| Issue |
A&A
Volume 586, February 2016
|
|
|---|---|---|
| Article Number | A117 | |
| Number of page(s) | 23 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201526963 | |
| Published online | 03 February 2016 | |
A study of a sample of high rotation-measure AGNs through multifrequency single-dish observations
1 Max-Planck Institut für Radioastronomie (MPIfR), Auf dem Hügel 69, 53121 Bonn, Germany
e-mail: apasetto@mpifr-bonn.mpg.de
2 Istituto di Radioastronomia-INAF (IRA-INAF), Via Gobetti 101, 40129 Bologna, Italy
3 Instituto de Radioastronomía y Astrofísica (IRyA-UNAM), Antigua Carretera a Pátzcuaro 8701, 58089 Morelia, Michoacán, Mexico
Received: 15 July 2015
Accepted: 28 September 2015
Context. We characterised and studied, in the radio band, a sample of candidates for high rotation measure (RM). These point-like objects show a strong depolarisation at 21 cm. This feature suggests the presence of a very dense medium surrounding them combined with a strong magnetic field.
Aims. This work aims at selecting and studying a sample of radio sources with high RM, thus studying their physical conditions and their status with respect to their surrounding medium. We want to understand whether any connection is present between the AGN-hosting galaxy medium with some evolutionary track and/or some restarting phase of the AGN itself.
Methods. Multifrequency single-dish observations were performed with the 100-m Effelsberg telescope to define the initial sample, to characterise the spectral energy distribution (SED) of the final sample (30 targets), and to determine their RM in the 11 to 2 cm wavelength range.
Results. From the observations, the SED and the polarisation information, i.e. the fractional polarisation and the polarisation angle, have been determined. Three different object types were revealed from the SED analysis: older, GPS-like, and mixed. For each of the targets, the rotation measure was found and the depolarisation modelled. No significant correlation is found between the depolarisation behaviours and the SEDs, while a correlation is found between sources with mixed SED (with an old component at low frequency and compact components at high frequencies) and high values of the rotation measure (with values in the rest frame greater than 1000 rad/m2).
Conclusions. This work helps us to define and identify a sample of sources with high RM. From the analysis we can conclude that the sources showing a restarting phase at high frequency (with a mixed SED) are characterised by a really dense and/or a magnetised medium that strongly rotates the polarisation angle at the different frequencies, leading to a high RM.
Key words: galaxies: active / polarization / galaxies: magnetic fields / quasars: general / radio continuum: galaxies
© ESO, 2016
1. Introduction
Active galactic nuclei (AGNs) are the most powerful objects in the Universe. Hosting a supermassive black hole (SMBH), AGNs have a spectrum that emits at all wavelengths from radio to gamma ray. This means that they have been studied well, but still our understanding about these objects is not completely clear. The unification scheme for radio loud AGN, where their appearance strongly depends on their orientation (Orr & Browne 1982; Urry & Padovani 1995), is by now accepted by most of the scientific community, but there are still several open questions. How the medium of the hosting galaxy in the vicinity of the SMBH is characterised and how strong their magnetic field is are important elements needed to understand the jets ejection mechanism. It is also important to understand whether AGNs are characterised, in the radio band, by some periodic activity phase (Marecki et al. 2006; Saikia & Jamrozy 2009; Czerny et al. 2009). Besides this, thanks to studies of samples of compact AGNs, O’Dea & Baum (1997) were able to identify an anti-correlation between the linear size and the peak frequency in their spectra as the result of the synchrotron self absorption (SSA) mechanism: the higher the peak frequency, the smaller the source. A possible reason could be found in their early evolutionary stage, which leads to very compact radio sources from the high-frequency peakers (HFP; Dallacasa et al. 2000), with the peak frequency around 8−10 GHz, to the compact steep-spectrum sources (CSS; Saikia 1988; Fanti et al. 1990), with a peak frequency around hundreds of MHz, passing through a state of giga-hertz peaked-spectrum sources (GPS; Gopal-Krishna et al. 1983; Stanghellini et al. 1990; O’Dea et al. 1991), where the peak frequency appears to be around a few GHz. However, whether AGNs are really experiencing the above evolution from young quasars to large-scale radio sources (O’Dea 1998) remains in doubt.
Study and analysis of the polarisation information in the radio band is a powerful tool that can help to clarify these questions. The Stokes parameters (I, Q, U, and V) are the observable quantities needed to obtain information on the linear polarization. The polarization flux density (SPol) is defined as 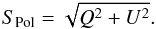 (1)The fractional polarisation is thus the ratio between the polarised flux density (Spol) with the total flux density, expressed with the Stokes I:
(1)The fractional polarisation is thus the ratio between the polarised flux density (Spol) with the total flux density, expressed with the Stokes I: 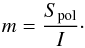 (2)The observed electric vector polarisation angle (EVPA) can also be expressed using the observable Stokes parameters Q and U:
(2)The observed electric vector polarisation angle (EVPA) can also be expressed using the observable Stokes parameters Q and U: ![\begin{equation} \chi = \frac{1}{2} \cdot \arctan \frac{U}{Q}\qquad [\rm{rad}] . \end{equation}](/articles/aa/full_html/2016/02/aa26963-15/aa26963-15-eq11.png) (3)From these quantities, it is possible to study two important aspects of this project: the Faraday rotation and the Faraday depolarisation. They can probe the interstellar medium (ISM) and the strength of the magnetic field of the host galaxy. To perform this kind of study, observations in a wide wavelength range are necessary.
(3)From these quantities, it is possible to study two important aspects of this project: the Faraday rotation and the Faraday depolarisation. They can probe the interstellar medium (ISM) and the strength of the magnetic field of the host galaxy. To perform this kind of study, observations in a wide wavelength range are necessary.
The Faraday rotation is the rotation of an electromagnetic wave that occurs when it passes through a magnetised plasma. Different unresolved regions of polarised emission will likely experience different amounts of Faraday rotation. Therefore, following the explanation proposed by Burn (1966), we can express the Faraday rotation using the Faraday depth: ![\begin{equation} \phi = \frac{e^3}{2\pi m_{\rm e}^2 c^4} \int_d^0 n_{\rm e} B_{\parallel}{\rm d}l \qquad[\rm{rad/m^2}], \end{equation}](/articles/aa/full_html/2016/02/aa26963-15/aa26963-15-eq12.png) (4)where ne is the electron density of the medium (expressed in cm-3), B∥ is the component of the magnetic field along the line of sight (expressed in μG), and l is the geometrical depth of the medium along the line of sight (expressed in parsecs). The integral is performed along the line of sight from the source (at distance d) to the observer. In the simplest case of a homogeneous medium, φ is equal to the rotation measure (RM), defined as the gradient of the polarisation angle χ with the observed λ2:
(4)where ne is the electron density of the medium (expressed in cm-3), B∥ is the component of the magnetic field along the line of sight (expressed in μG), and l is the geometrical depth of the medium along the line of sight (expressed in parsecs). The integral is performed along the line of sight from the source (at distance d) to the observer. In the simplest case of a homogeneous medium, φ is equal to the rotation measure (RM), defined as the gradient of the polarisation angle χ with the observed λ2: ![\begin{equation} \chi(\lambda) = RM \lambda^{2} + \chi(0) \qquad [\rm{rad}]. \end{equation}](/articles/aa/full_html/2016/02/aa26963-15/aa26963-15-eq21.png) (5)If the medium is inhomogeneous or unresolved, the RM can change within the source, and a deviation, more or less strong, from the λ2 law occurs (Burn 1966; Vallee 1980; Saikia & Salter 1988). This can indicate the presence of multiple RM components, hinting at the complexity of the source.
(5)If the medium is inhomogeneous or unresolved, the RM can change within the source, and a deviation, more or less strong, from the λ2 law occurs (Burn 1966; Vallee 1980; Saikia & Salter 1988). This can indicate the presence of multiple RM components, hinting at the complexity of the source.
Together with the RM, it is important to study the fractional polarisation (m) behaviour as a function of the observed wavelength. When the Faraday rotation causes the reduction of the fractional polarisation, the source is subjected to depolarisation. This can be internal or external; the first occurs when the Faraday rotating component is intermixed to the radio emitting region, and the second when several Faraday screens are somewhere between the radio source and the observer. Several depolarisation and repolarisation (where the fractional polarization increases at longer wavelengths) models have been developed (Burn 1966; Tribble 1991; Homan et al. 2002; Rossetti et al. 2009; Mantovani et al. 2009; Hovatta et al. 2012).
The analysis of these two features, the RM and the depolarisation, can give information about the density distribution of the ISM that surrounds the radio source, its clumpiness, and the strength of the magnetic field. The importance of connecting the polarisation properties, such as a very high RM value and strong depolarisation, with the ambient medium, has been evident for years (Burn 1966; Laing 1984; Tribble 1991; Rossetti et al. 2008). Some observational works have found sources with very high RM with single-dish and interferometric techniques (Kato et al. 1987; Benn et al. 2005; Trippe et al. 2012; Kravchenko et al. 2015) and also with studies with the higher resolution VLBI technique (Zavala & Taylor 2004; Attridge et al. 2005; Jorstad et al. 2007). However, a deep study of a relationship between the RM and the ambient medium is very difficult since it would require the study of a large sample in a wide range of frequencies and with simultaneous observations.
In this work we present a homogeneous observational study performed with the 100-m Effelsberg telescope of a medium-sized sample of radio sources. We selected sources from the full northern sky based on strong depolarisation at a low frequency, which defined a sample of high-RM candidates. This sample was then observed at several frequencies in the 2−15 GHz range with the single-dish telescope. We want to study whether any connection is present between the AGN-hosting galaxy medium with some evolutionary track and/or some periodic activity phase of the AGN itself. Further observations of our sample using the JVLA, EVN, and VLBA interferometers will be reported in future papers.
2. Sample selection criteria
Our sample was created by selecting sources from the NRAO VLA Sky Survey (NVSS; Condon et al. 1998), a survey at 1.4 GHz, which contains a total of 1 773 484 entries. From these, we considered only those sources that match the following criteria:
-
Flux density SNVSS ≥ 300 mJy;
-
Unresolved with major axis
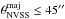 ;
; -
Declination δ ≥ –10
 ;
; -
Polarisation flux density
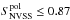 mJy, i.e. unpolarised sources.
mJy, i.e. unpolarised sources.
The minimum flux density of 300 mJy at 1.4 GHz was chosen in order to be able to detect enough total flux density at higher frequencies (roughly S = 70 mJy at 10.45 GHz) to perform polarisation studies, assuming that the majority of the AGNs could be characterised by a steep radio spectrum with α = −0.7. The last point is essential because we are interested in studying sources suffering from a strong depolarisation at 1.4 GHz, which is a hint of a possible high RM. The value 0.87 mJy represents the 3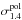 (where the rms fluctuation level
(where the rms fluctuation level 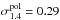 mJy/beam, for the NVSS survey; Condon et al. 1998). The result of this selection is a list of 2890 point-like sources with no detected polarisation flux density (thus ~20% of the brightest sources in the NVSS do not have polarisation detection).
mJy/beam, for the NVSS survey; Condon et al. 1998). The result of this selection is a list of 2890 point-like sources with no detected polarisation flux density (thus ~20% of the brightest sources in the NVSS do not have polarisation detection).
As a second step, we cross-correlated the obtained sample with the Faint Images of the Radio Sky at Twenty-cm (FIRST) catalogue (White et al. 1997). With a better angular resolution, only unresolved sources were selected, i.e. with a angular size ≤5″. The objective of this was to increase the probability of selecting possibly compact and/or high-redshift candidates. The result of the cross correlation is a list of 537 bright, point-like, and unpolarised sources.
Given the strong dependence of the Faraday depolarisation effect with the observing frequency (the lower the frequency, the stronger the depolarisation becomes), we observed the entire cross-correlated list with the 100-m Effelsberg telescope at 10.45 GHz (see Sect. 4.1), in order to search for polarised flux density, thus suggesting a strong depolarisation at 1.4 GHz. The final sample of high RM candidates is composed of 30 sources (~6% of the initial cross correlated sample). We checked that the targets are isolated sources by extracting images from the FIRST catalogue using an image size of 5′, which corresponds to the size of the Effelsberg beam at 11cm (2.64 GHz). The final sample was finally observed at several frequencies (see Sect. 4.2) in order to determine their SEDs and their RM (see Sects. 6.2 and 6.4 respectively).
3. Possible selection biases
The selection criteria we followed could result in the two possible biases present in our sample. The first is the lack of sensitivity of our observations for sources weaker than 150 mJy at 10.45 GHz. This could exclude a fraction of steep spectrum sources for which the polarised flux density drops below the minimum 3 mJy limit detectable in our observations. In fact, starting from the original list (537 unpolarised sources at 1.4 GHz), 30 sources show significant polarisation at 10.45 GHz, but the remaining 507 do not. Setting a 3 mJy upper limit (3σ, assuming the Effelsberg rms = 1 mJy/beam) on their polarised flux density and assuming that a typical detectable fractional polarisation is larger than 2% (Condon et al. 1998), we can only assert that the unpolarised sources are 77 targets with no polarisation detection at 10.45 GHz and S10.45 ≳ 150 mJy. Thus for the remaining 430 targets, we cannot discern whether they are polarised or not, so we cannot include them into our study.
In contrast, our flux density selection criterium (S1.4 GHz ≥ 300 mJy) should exclude potential sources with synchrotron spectra peaking at higher frequencies from our analysis, thus potential GPS-HFP targets. These sources, peaking in the range between 2 and 10 GHz, are optically thick at 1.4 GHz. Then, at this frequency their emission increases with a spectral index of 2.5. Therefore, while they can be very bright at high frequencies, we are excluding them from our analysis because of their weakness at 1.4 GHz.
4. Observations
In the following, we describe the observational campaign carried out for this work with the 100-m Effelsberg single-dish telescope.
4.1. 10.45 GHz observations
To identify high-RM candidates, we initially selected unpolarised sources at 1.4 GHz in the NVSS catalogue, assuming that the non-polarisation in some cases is caused by in-band depolarisation due to a very high RM. Therefore the strategy we adopted was to observe at higher frequencies searching for polarised flux density. Using the 100-m Effelsberg telescope, observations at 10.45 GHz on the initial sample of 537 targets were performed during the winter semester 2012−13. The 10.45 GHz receiver has a bandwidth of 300 MHz and a system temperature (Tsys) of ~50 K on the sky (zenith) and a FWHM of 69″. The system delivers right circular polarisation (RCP) and left circular polarisation (LCP) and is connected to an IF-polarimetry that provides full polarisation information, thus giving the Stokes parameters: I, Q, U and theoretically also V. Since the Stokes V is expected to be weak in extragalactic sources, it has not been taken into consideration for the purpose of our study. All 537 sources are point-like compared to the Effelsberg beam. Therefore they were observed in cross-scan mode, along azimuth and elevation with a scan length of 6′ and a scanning speed of ~7″/s, using a total of twelve subscans (6 scans for each direction). Since the sources are bright enough, focus and pointing were checked by the targets themselves. 3C 286, 3C 48, and 3C 161 have been observed as flux density calibrators, the flux densities of which were based on the scale of Baars et al. (1977) and counter-checked with more recent data coming from the 100-m Effelsberg calibrators monitoring programme (Kraus et al. 2003). The polarisation information (the fractional polarisation m and the polarisation angle χ) of the mentioned calibrators were checked using the recent and continuously updated values available in the Effelsberg wiki-page1. NGC 7027 and 0951+69 have been chosen as unpolarised calibrators to determine the leakage terms, the instrumental polarisation, which is of the order of 1%. This first observational session at high frequency led to a list of 30 sources, which became the high RM candidates (see Table 1).
4.2. Follow-up programme
For the sources with detected polarisation at 10.45 GHz, a follow-up programme was performed to determine their RM value. The 30 sources have been observed in cross-scan mode at 2.64 GHz (FWHM of 275″), 4.85 GHz (FWHM of 146″), 8.35 GHz (FWHM of 80.6″), 10.45 GHz (FWHM of 69″), and 14.60 GHz (FWHM of 50.8″) (see the Effelsberg wiki-page2 for more details on the receivers). The scan length and the scan velocity were chosen based on the technical parameters of the different receivers. As previously done with the observations at 10.45 GHz, suitable sources, such as 3C 286, 3C 48, and 3C 161, were observed to calibrate flux density and also to check for the polarisation information (m and χ). Again NGC 7027 and 0951+69 were observed for determining the instrumental polarisation. The total intensity and the polarisation information for all the 30 targets were collected and are presented in Sect. 6. The sample was observed quasi-simultaneously with time between observations from a few hours to a few days (in few cases in order to repeat some bad observations). Table B.1 contains the values of total intensity and the polarisation information of the high-RM candidates collected during this follow-up campaign.
4.3. Time variability
Flux density and polarization variability over the entire electromagnetic spectrum is a common phenomenon in AGN (Peterson 2001) and could therefore also influence our observations. However, strong variations are usually seen only at frequencies >10 GHz and mainly in blazar sources (radio-loud AGN seen at small angles to the axis of the jet) with variations of several factors in the total flux density (e.g. by a factor of ~4 for the sources BL Lac and 3C 273 at 15.0 GHz within 20 years) (Lister et al. 2009).
During the follow-up observations, the high RM candidates were observed nearly simultaneously at the various frequencies; the time between the individual scans was in most cases only a few minutes (except for a few cases where bad observations had to be repeated). From the obtained SEDs (presented in Sect. 6.2) of our targets, we can assert that the high RM sample is mainly composed of quasars, and we can most likely exclude contamination from blazar type sources. Besides this, most of our observations were performed at frequencies ≤10 GHz, so that strong variations are rather unlikely. Furthermore, our repeated observations at 10.45 GHz (for the follow-up campaign; Sect. 4.2) did not reveal any strong variations − at most, small oscillations (of a few %) have been seen on a time scale of a few months.
Because one observes at lower frequencies, time variability is not as strong. A considerable time window for this project is given by the NVSS and low-frequency surveys, which, as said, should not give any variability problems. Since our sources do not seem to be strongly variable at the higher observed frequency (10.45 GHz), we can expect that the combination of the new Effelsberg data and the data taken from literature is not strongly affected by a time variability that is significant for the purposes of this work. Therefore, we can safely assume that neither our RM determination nor the SEDs are significantly influenced by source variability.
4.4. Data reduction
Data was reduced using the TOOLBOX package for single-dish data (Max Planck Institute for Radio Astronomy; see the Effelsberg wiki-page3). For coherency, the same data reduction procedure has been followed for all frequencies, such as the correction for the opacity, determined by a fit between the Tsys versus airmass distribution and the pointing offsets, where the offsets in longitude are applied to the latitude data and vice versa. Moreover, a baseline subtraction, an averaging of all the subscans, and a few other standard adjustments were applied. Flux calibration was done using the [Jy/K] factor calculated from the flux calibrators opportunely observed during the different observational sessions. The leakage terms were adequately obtained through observations of unpolarised point like calibrators. The errors were calculated through error propagation taking uncertainties from the Gaussian fit to the cross-scanned data, pointing correction and various calibration uncertainties into account, e.g. changes in the noise diode or changes in the focus.
5. Comparison samples
We compared our results with two comparison samples. We used the 77 bona fide unpolarised sources at 10.45 GHz, listed in Table A.1, to compare their spectral indices with those of our high-RM candidates. We also compared our RM results with the sample of Farnes et al. (2014). They present a catalogue of multi-wavelength linear polarisation and total intensity radio data for polarised sources from the NVSS. The result of this work is a catalogue of 951 sources with the SEDs in both total intensity and fractional polarisation.
6. Results and discussion
In Table 1 we present information about the 30 high-RM candidates: the source coordinates taken from the FIRST catalogue (they are more precise, compared to the NVSS survey, thanks to the better angular resolution of the survey), their total flux density at 1.4 GHz from the NVSS catalogue, their total flux density measured with the Effelsberg telescope at 10.45 GHz (both expressed in mJy), the spectral index (α1.4−10.45), the observed RM value (RMobs), the redshifts (when available from the literature), the contribution of the RM of our Galaxy (RMmw), the values of which have been taken from the most recent work by Oppermann et al. (2015), and finally the rest-frame RM corrected by their redshifts (RMrf). Where the redshift was not available in the literature, we assumed a mean value: zmean = 1.5 in order to have a rough idea of the intrinsic RM value. For the source 0845+0439, we learned its redshift value via private communication after spectroscopic measurement tests at the Large Binocular Telescope (LBT). Almost all the targets are QSO type.
Parameters of the high-RM candidates.
In the following, we discuss the spectral index distribution, their SEDs, and their polarisation information with a detailed explanation of the RM determination and the depolarisation behaviour.
6.1. Spectral index distribution
From the first observational run, we were able to determine the spectral index (defined here as S ∝ να) between 1.4 GHz (from the NVSS catalogue) and 10.45 GHz. This allows us to have a qualitative idea of the source type presented in the sample. As mentioned in Sect. 5, we compared the 30 high-RM candidates with the 77 unpolarised sources at 10.45 GHz.
In Fig. 1 the spectral index distributions for the targets considered to have a high RM (red colours) are shown with the unpolarised targets (black colours) and its cumulative plot distribution. Both the histograms were normalised with the number of the sources. We chose the bin dimension larger than the 3σ of the larger error of the spectral index in our sample (in this case 3σα = 0.18). From the cumulative plot (Fig. 1b), the two distributions seem to follow a similar tendency up to a value of α ~ −0.6, then they separate. In fact, the spectral index distribution of the unpolarized sources (black histogram Fig. 1a) peaks at αpeak ≃ −0.5, thus we mainly see steep radio spectra sources. On the other hand, the spectral index distribution of the high RM candidates (red histogram Fig. 1a) shows three different groups of objects. The three distributions indeed peak at different spectral indices, revealing the following classes of spectra:
-
steep spectrum radio sources withαpeak ≃ −0.8;
-
flat spectrum radio sources with αpeak ≃ −0.1;
-
inverted spectrum radio sources with αpeak ≃ + 0.2.
The distribution of radio spectral indices can be symptomatic of the orientations of radio sources (Orr & Browne 1982). The first group could be associated to “lobe-dominated” objects where large-scale structures dominate the radio synchrotron emission and where the steepness of the spectrum is due to the radiative loss of the relativistic electrons. Flat-spectrum radio sources could be associated with objects where the lines of sight are closer to the radio axis. In these objects, we can see a superposition of several features, thus a continuous injection of relativistic electrons that become opaque at widely different frequencies. The latter kinds of objects could be representative of core-dominated objects where the dominant synchrotron component is very compact and where it is possible that the SSA occurs. If a turnover peak is revealed in the spectra of these objects, it is possible to associate them to the GPS source that is supposed to be AGNs in an early phase of activity (O’Dea 1998).
From the comparison of the histograms in Fig. 1, we can assert that, although they represent the low number in our sample, the high-RM candidates do not seem to be represented by a particular class of targets. Instead, the three main types of spectra seem to represent these peculiar objects equally. In contrast, the other sources without detected polarisation at high frequency seem to be dominated by very steep spectra. This could be an indication that the objects without high RM could be dominated by very extended and probably old synchrotron components, while high RM values could be found in different objects where the combined contribution of electron density and magnetic field is strong.
 |
Fig. 1 Spectral index distributions. a) Comparison of the spectral index distribution for the high-RM candidates (30 sources; red histogram) and the unpolarised sources (77 sources; black histogram). The distribution of the unpolarised sources peaks at αpeak ~ −0.5. The high-RM distribution shows 3 different types of objects: steep (αpeak ~ −0.8), flat (αpeak ~ −0.1), and inverted (αpeak ~ + 0.2) spectrum radio sources. b) The same but cumulative histograms. |
6.2. Spectral energy distribution
The wide frequency coverage obtained with our follow-up observations, plus data from the literature, allows us to study the SED shape of these sources that are all characterised by synchrotron emission. We indeed extended the SEDs to frequencies lower than 1.4 GHz, using the following surveys: VLSS (74 MHz with a resolution of 80″) (Cohen et al. 2007), 7C (151 MHz with a resolution of 70″) (Hales et al. 2007), WENSS (325 MHz with a resolution of 54″× 54″cosecδ) (Rengelink et al. 1997), and TEXAS (365 MHz with a resolution of ~50″) (Douglas et al. 1996). Their values are listed in Tables B.1. As discussed in Sect. 2, we checked that our targets are isolated up to 5′. Therefore, the different beam sizes of each frequency should not be affected by back- or foreground sources. Moreover, all the sources were selected to be compact in the FIRST survey, therefore effects on the flux density due to extended structures do not affect our analysis either.
For each source in our sample, we fit several models representing its SEDs:
-
a power law, representing a purely optically thin synchrotronspectrum with a slopeαthin:
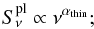 (6)
(6) -
a power law with a break (symptomatic of an ageing of the radio source) at frequency νb:
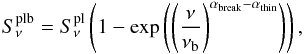 (7)where αthin is the spectral index at frequencies lower than νb and αbreak is the spectral index at higher frequencies;
(7)where αthin is the spectral index at frequencies lower than νb and αbreak is the spectral index at higher frequencies; -
a single SSA component:
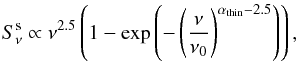 (8)where ν0 is the frequency where the emission changes from optically thick, with a spectral index of 2.5, to optically thin with a spectral index αthin;
(8)where ν0 is the frequency where the emission changes from optically thick, with a spectral index of 2.5, to optically thin with a spectral index αthin; -
a single synchrotron component with a break at frequency νb:
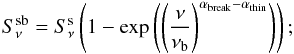 (9)
(9) -
a combination of several synchrotron components (
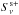 ) with fixed αthin = −0.7;
) with fixed αthin = −0.7; -
a combination of a power law with one or two synchrotron components (
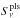 ) with αthin= free or αthin = −0.7.
) with αthin= free or αthin = −0.7.
For each source, we selected the best model according to the lowest residual value. Table C.1 shows the chosen parameters for the different fitting functions used for the SEDs study. Table 2 is a quick look at the values for αthick and αthin that we decided to use for each model.
Based on the fitted SEDs we noticed three main groups. We refer to them from now on with:
-
Older: sources fitted with a power law (with or without a break) and sources with one synchrotron component with a break (the presence of a frequency break is an indication of an ageing of the source);
-
GPS-like: SEDs with several synchrotron components peaking at frequencies ≥100 MHz;
-
Mixed: the combination of the two above, thus a combination of a power law or a synchrotron component peaked at low frequency (with peak frequency ≤100 MHz) and one or more synchrotron components at higher frequencies (with peak at frequencies ≥100 MHz).
Quick look at the spectral indices αthick and αthin used for each model.
In Fig. 2, we show three examples of the three object types we identified. Together with the total intensity SED, information on the polarisation flux density, the fractional polarisation (m) and the polarisation angle (χ) are shown for each of the targets. An explanation and a discussion about the polarisation characteristics is presented in Sects. 6.4 and 6.5. Similar plots for all the sources are available in Appendix D.
 |
Fig. 2 SEDs for the sources: 1015+0318 classified as Older, 2245+0324 classified as GPS-like, and 0845+0439 classified as Mixed. Black dot points are the Effelsberg and low-frequency data from the literature; 3-sigma upper limits are drawn as triangles. Where present, various synchrotron components are plotted with an orange dashed line. The fit of the spectra is the red straight line. Polarisation information is presented with the SEDs. |
From the analysis of the radio spectra, we find that the sample splits into three (equal sized) parts:
-
1/3 of the sample can be considered as Older sources. Since for these sources the synchrotron peak is not visible or it peaks at very low MHz value, it is possible to assert that these sources have an extended and probably old synchrotron component;
-
1/3 of the sample are characterised by a GPS-like SED. These targets could have a more compact and probably early-phase synchrotron components.
-
1/3 of the sample can be considered to have a Mixed spectrum, i.e. a combination of Older and GPS-like features. This behaviour could be an indication of sources in which a restart radio emission activity occurs.
These results suggest that the high-RM candidates are mainly (66%) sources with compact high-frequency components, thus probably new growing radio components. We can associate these targets with objects in a particular compact young phase (the GPS-like) or in a reactivated activity phase (Mixed).
For the Older sources, a possible explanation for a high-RM value could be a very dense intervening material surrounding the already extended radio component. From these considerations, in all the cases, the contribution inferred by the medium in which the source is embedded and/or the several Faraday screens that the radiation passes through (see Sects. 6.4 and 6.5 for details) is very important.
6.3. Magnetic field estimation
Estimation of the magnetic field for those targets with one or more synchrotron components in their SEDs.
Together with the characterisation of the type of the targets, the magnetic field was considered. Lower limits on the magnetic field were computed from observable quantities. Assuming that the spectral peaks seen on the SEDs are due to SSA, the magnetic field B of a homogeneous synchrotron component can be derived using the following relation (see e.g. Kellermann & Pauliny-Toth 1981): ![\begin{equation} B \sim \theta^{4} \nu_{\rm max}^{5} S_{\rm max}^{-2}(1+z)^{-1} \qquad [\rm{G}], \end{equation}](/articles/aa/full_html/2016/02/aa26963-15/aa26963-15-eq97.png) (10)where θ is the angular dimension [mas], Smax and νmax are the peak flux density [Jy] and the peak frequency [GHz] of the synchrotron component, and z is the redshift.
(10)where θ is the angular dimension [mas], Smax and νmax are the peak flux density [Jy] and the peak frequency [GHz] of the synchrotron component, and z is the redshift.
Since all our targets are unresolved for the FIRST beam, we do not have any information on their angular size. We obtained lower limits for the angular sizes by considering the inverse Compton limit for which the brightness temperature (TB) is assumed to not exceed its maximum value TB ≤ 1012 K (Kellermann & Pauliny-Toth 1981): ![\begin{equation} T_{\rm B} = 1.22\times10^{12}\frac{ S_{\rm max}}{\theta^{2}\cdot \nu_{\rm max}^{2}} \le 10^{12} \qquad [\rm{K}] ; \end{equation}](/articles/aa/full_html/2016/02/aa26963-15/aa26963-15-eq102.png) (11)therefore,
(11)therefore, ![\begin{equation} \theta = 1.1\cdot \frac{\sqrt{S_{\rm max}}}{ \nu_{\rm max}} \qquad [\rm{mas}] . \end{equation}](/articles/aa/full_html/2016/02/aa26963-15/aa26963-15-eq103.png) (12)From the lower limits in the angular size, we obtained lower limits for the magnetic field strength [μG] for those targets with synchrotron component/s in their SEDs. For the sources with no information on the redshift z, the mean value of the sample (zmean = 1.5) was used in order to have a rough estimation of their magnetic field strength. The lower limit values are listed in Table 3 and are, for most of the sources, in the range of 1−100 μG.
(12)From the lower limits in the angular size, we obtained lower limits for the magnetic field strength [μG] for those targets with synchrotron component/s in their SEDs. For the sources with no information on the redshift z, the mean value of the sample (zmean = 1.5) was used in order to have a rough estimation of their magnetic field strength. The lower limit values are listed in Table 3 and are, for most of the sources, in the range of 1−100 μG.
6.4. Rotation measure
The polarisation angle χ for all the targets was calculated and, by combining several frequencies, their RM estimated. To determine the RM value, we fit a straight line (linear regression fit) to the plot of the EVPA versus λ2. The data at our disposal cover a wide range in λ but with large gaps in the λ2 coverage, so the resulting RM values suffer from nπ ambiguity. The strategy we adopted was to trust the observed polarisation angle values at the highest frequency, which suffer less from Faraday rotation, and to apply, where necessary, wrapping by some integer multiple of 180 degrees to the lower frequencies data (mostly to the 2.64 GHz and to the 4.85 GHz data). The maximum number of wraps we decided to apply had been fixed to five.
In Table 1 the values of the observed RM (RMobs) are listed, together with the rest-frame RM (RMrf), both given in rad/m2. As is known, our Milky Way introduces a RM contribution that varies with the galactic latitude. The high RM targets are mainly at latitudes | b | > 30°, thus above the Galactic plane, but following pioneer works (Kronberg & Simard-Normandin 1976; Kronberg et al. 1977), the Galactic contribution should be subtracted to the observed RM value. Looking at the most recent foreground galactic RM (RMmw) map by Oppermann et al. (2015), we noticed that the RMmw contributions at the positions of our sources, are very small compared to the observed RMobs of our targets. However, the uncertainties of the RMmw are quite large. Therefore, since the correction for the Galactic contribution in our case would only increase the uncertainty of the measures without a significant correction on the RM value, we decided to not apply it. For the same reason we decided to ignore also the cosmic-web contribution that is only a few rad/m2, too (Akahori & Ryu 2011). The source rest frame RMrf was then calculated following the relation: ![\begin{equation} RM_{\rm rf} = RM_{\rm obs} \times (1+z)^{2} \qquad [\rm{rad/m^2}] . \end{equation}](/articles/aa/full_html/2016/02/aa26963-15/aa26963-15-eq108.png) (13)For those sources with unknown z, we used the approximate mean value of our sample (zmean = 1.5) to have at least an indication of the intrinsic RM of the source. In Appendix D all the plots showing the RM fit for the 30 targets are shown, along with the SEDs and other polarisation information.
(13)For those sources with unknown z, we used the approximate mean value of our sample (zmean = 1.5) to have at least an indication of the intrinsic RM of the source. In Appendix D all the plots showing the RM fit for the 30 targets are shown, along with the SEDs and other polarisation information.
The fitted data points for the RM almost always showed a linear regression with the lowest χ2 fit, as expected for the goodness of the fit. However, for 10 sources (~33% of the sample; 0239–0234, 0742+4900, 1043+2408, 1213+1307, 1616+2647, 1713+2813, 2050+0407, 2101+0341, 2200+0708, 2245+0324), we noticed a deviation from the λ2 law. Among these, six sources (~60%) are GPS-like. This suggests that these compact sources are characterised by several Faraday screens intervening in the medium. Indeed, if the radiation passes through different magnetised plasma, the latter could rotate the polarisation angle differently, leading to a non-linear behaviour by the data. This explains, in general, the low-RM (observed) associated with the majority of these 10 sources (~90%).
 |
Fig. 3 a) histogram showing the distribution of the fitted rotation measure of our targets (red histogram) together with the Farnes catalogue (blue histogram). b) the same but cumulative. |
 |
Fig. 4 a) Cumulative plot of the RMobs for the three object types. Yellow: Older type; grey: GPS-like type; green: Mixed type. b) Cumulative plot of the RMrf for the three object types. |
In Fig. 3 we show the distribution of the fitted RM (RMobs) for our 30 high-RM sources (red histogram) compared with the targets from the Farnes catalogue (Farnes et al. 2014) (blue histogram) and its cumulative plot. Both the histograms have been normalised with the number of the sources of each sample: 30 sources for our sample and 951 for the Farnes sample. For better visibility of the whole distribution, the histograms are shown on logarithmic scale. Farnes et al. (2014) show a RMobs distribution that is centred on zero with a σ ~ 100 rad/m2. From the two histograms in Fig. 3, it is evident that the distribution of the |RMobs| of our sample is different with respect to the sources chosen from the Farnes catalogue. The cumulative plot underlines that 80% of the Farnes targets have a |RMobs| value below 20 rad/m2, while 80% of our targets have a |RMobs| value of ≳100 rad/m2. To check the discrepancy, we also ran the Kolmogorov-Smirnov test to the distributions, and it gives a probability of 3 × 10-6 that the two distributions are comparable; the two distributions are different at a confidence level >95%.
We also compared the RM for the three main object types we found by analysing the SEDs. Their cumulative plot of the |RMobs| and the |RMrf| are shown in Fig. 4. In Fig. 4a it is clear that the three groups are different, and it seems that the Mixed targets are those with the highest values of |RMobs|. Indeed, after the correction of the observed RM to its value in the rest frame (Fig. 4b), we can assert that all the Mixed targets show |RMrf| higher than 1000 rad/m2, while for the two others, only 50% are above 500 rad/m2, still 5σ away from the Farnes distribution. This seems to suggest that sources that show a mixed SED, with an old component at low frequency and compact components at high frequencies, i.e. radio sources that are restarting their activity, are related to high values of the RM.
6.5. Fractional polarisation, depolarisation, and repolarisation
The analysis of the fractional polarisation (m), as a function of λ2 indicates that the majority of the sources have a fractional polarisation that decreases with increasing wavelength (Saikia & Salter 1988). This is indicative of a non-homogeneous medium that is present between the source and the observer.
Several depolarisation (DP) models have been developed to explain the physical processes behind this behaviour. The main models that one needs to consider are the Slab model (Burn 1966), the Tribble model (Tribble 1991), the Rossetti-Mantovani model (Rossetti et al. 2008; Mantovani et al. 2009), and the Repolariser model (Homan et al. 2002; Mantovani et al. 2009; Hovatta et al. 2012). Most of these models assume an optically thin emitting region, and all of them make the assumption that we detect the same emitting region at each frequency. We saw from our SEDs that the majority of the sources have different synchrotron components that contribute to the shape of the total intensity distribution. Thus, our unresolved sources can have several overlaps of optically thick and optically thin components together. This can, in the end, modify the polarisation behaviour from the simplified way described from the models.
Since we cannot be sure that the polarised emitting region comes from the same emitting region within the frequency range, and the lack of a complete coverage along the bandwidth led us to decide to follow a similar approach to the one adopted by Farnes et al. (2014), we chose three models that are just a mathematical generalisation that can mimic the wavelength dependence of polarisation of the various physical models: a Gaussian (DPGauss), a power law (DPPL), and a Gaussian with a constant term (DPGauss+):
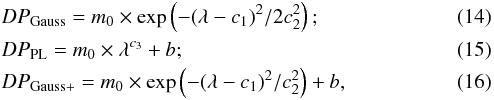 where λ is in centimetres, m0 in %, c1 and c2 in centimetres, c3 is unit-less, and b is a constant. The Gaussian model is representative of the Slab model, the power law model represents the Tribble or, thanks to its flexibility, the Repolariser model, and finally the Gaussian with the constant term can provide the Rossetti-Mantovani model.
where λ is in centimetres, m0 in %, c1 and c2 in centimetres, c3 is unit-less, and b is a constant. The Gaussian model is representative of the Slab model, the power law model represents the Tribble or, thanks to its flexibility, the Repolariser model, and finally the Gaussian with the constant term can provide the Rossetti-Mantovani model.
Owing to the different number of degrees of freedom for the various models, the Gaussian and the power law models have been used whenever three or more data points were available, and the Gaussian with constant model have been adopted when four or more data points were available. Proper fitting constraints were applied during the fitting process to ensure that only values of ci that correspond to physical solutions were obtained. Repolarised sources have been identified thanks to the flexibility of the power law model, which provides a polarisation spectral index c3> 0. The determination of the residuals, together with a visual inspection, provides a measure for the goodness of the fit. See the Appendix D for the plots of the depolarisation models.
Some of the sources (~30% of the sample; see 0845+0439 as an example, Fig. 2) show complex behaviour with rising and decaying of the fractional polarisation; for them, none of the three models fit the data properly. The behaviour of these sources can be studied better with better frequency-sampled data and/or higher angular resolution observations. Still from this first analysis, it is possible to note that:
-
1/3 of the sample follow a model of a Gaussian,DPGauss, or a Gaussian with a constant term, DPGauss+;
-
1/3 of the sample follow a power law model, DPPL; and
-
1/3 of the sample cannot be fitted by any of the three models because of their complex shape, thus we can assert the existence of a complex model DPcomplex not proposed here, owing to the lack of points for the fitting.
We did not find any correlation between the DP models and the SEDs shapes or the RM values. Thus from this first single-dish analysis of the polarisation fraction, it is not possible to indicate a possible trend that these objects are following.
7. Summary and conclusions
In this work, we presented the search for sources with a very high RM, as well as some follow-up studies of appropriate candidates. Assuming that a high RM causes strong in-band depolarisation, we observed a sample for unpolarised sources from the NVSS with the 100-m Effelsberg telescope at 10.45 GHz. After identifying 30 potential high-RM sources, we performed observations at 2.64, 4.85, 8.35, 10.45, and 14.60 GHz as well, in order to determine the SED and the RM of the sources. In some cases, exceptionally high RM were found, as in 1616+0459 where its RMobs of ~2550 rad/m2 corresponds to a RMrf of ~44 300 rad/m2. Our main conclusions can be summarised as follows.
-
From our statistical study it turned out that the high-RMcandidates are not characterised by a specific object type. Indeed,the spectral index distribution of the 30 high RM candidatesshows three peaks representing all the possible object type (steep,flat, and inverted spectrum radio sources).
-
SEDs were characterised and three groups (Older, GPS-like, Mixed) identified. The high-RM candidates are mainly (66%) sources with compact high-frequency components, probably new growing radio components, thus objects in a particular compact young phase (the GPS-like) or in a reactivated activity phase (Mixed). The Older sources showing high RM could be surrounded by a very dense intervening material.
-
Lower limits for the magnetic field strength were calculated for those sources with well-defined synchrotron component/s in their SEDs. The lack of angular resolution meant that no evidence of strong magnetic fields was detected.
-
The behaviour of the fractional polarisation m with λ2 were fitted using simpler mathematical representations of the main physical depolarisation models: the Slab model, the Tribble model, the Repolariser, and the Rossetti-Mantovani model. Three groups were detected: sources following a Gaussian or a Gaussian with a constant term model, sources following a power-law model, and sources having a complex behaviour for which we cannot fit any of the models because of their complex shape. No correlation between the SED type and the fractional polarisation behaviour has been found.
-
The RM was determined for all the sources in the sample, and among these, 10 sources show a deviation from simple linear behaviour. This feature could indicate that several Faraday screens within the medium are affecting the polarisation angle distribution differently. Owing to the lack of well sample data, we could not reconstruct their real behaviour.
-
A strong correlation between the mixed SEDs and a high value of the RM was found. Indeed, the mixed sources have a RMrf larger than 1000 rad/m2. This could be an indication that these particular sources, showing a restarting phase at high frequency, are characterised by a really dense and/or a magnetised medium that rotates the polarisation angle strongly.
https://eff100mwiki.mpifr-bonn.mpg.de/doku.php, “Calibrators and their polarisation” section in the Effelsberg User Guide.
https://eff100mwiki.mpifr-bonn.mpg.de/doku.php, the section “Receiver and calibration” in the Effelsberg User Guide.
https://eff100mwiki.mpifr-bonn.mpg.de/doku.php, section “Using the Toolbox to inspect cross-scans” in the Effelsberg User Guide.
Acknowledgments
Based on observations with the 100-m telescope of the MPIfR (Max-Planck-Institut für Radioastronomie) at Effelsberg. This research made use of the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. A.P. is a member of the International Max Planck Research School (IMPRS) for Astronomy and Astrophysics at the Universities of Bonn and Cologne. C.C.-G. acknowledges support by UNAM-DGAPA-PAPIIT grant number IA101214. We thank the Effelsberg operators for the useful help. We acknowledge Roberto Fanti for useful discussions and suggestions and Jochen Heidt for providing us with spectral redshifts of some of the sources. We thank the anonymous referee for careful revising of the paper and useful comments.
References
- Akahori, T., & Ryu, D. 2011, ApJ, 738, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Attridge, J. M., Wardle, J. F. C., Homan, D. C., & Phillips, R. B. 2005, in Future Directions in High Resolution Astronomy, eds. J. Romney, & M. Reid, ASP Conf. Ser., 340, 171 [Google Scholar]
- Baars, J. W. M., Genzel, R., Pauliny-Toth, I. I. K., & Witzel, A. 1977, A&A, 61, 99 [NASA ADS] [Google Scholar]
- Benn, C. R., Carballo, R., Holt, J., et al. 2005, MNRAS, 360, 1455 [NASA ADS] [CrossRef] [Google Scholar]
- Burn, B. J. 1966, MNRAS, 133, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, A. S., Lane, W. M., Cotton, W. D., et al. 2007, AJ, 134, 1245 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Czerny, B., Siemiginowska, A., Janiuk, A., Nikiel-Wroczyński, B., & Stawarz, Ł. 2009, ApJ, 698, 840 [NASA ADS] [CrossRef] [Google Scholar]
- Dallacasa, D., Stanghellini, C., Centonza, M., & Fanti, R. 2000, A&A, 363, 887 [NASA ADS] [Google Scholar]
- Douglas, J. N., Bash, F. N., Bozyan, F. A., Torrence, G. W., & Wolfe, C. 1996, AJ, 111, 1945 [NASA ADS] [CrossRef] [Google Scholar]
- Fanti, R., Fanti, C., Schilizzi, R. T., et al. 1990, A&A, 231, 333 [NASA ADS] [Google Scholar]
- Farnes, J. S., Gaensler, B. M., & Carretti, E. 2014, ApJS, 212, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Gopal-Krishna, Patnaik, A. R., & Steppe, H. 1983, A&A, 123, 107 [NASA ADS] [Google Scholar]
- Hales, S. E. G., Riley, J. M., Waldram, E. M., Warner, P. J., & Baldwin, J. E. 2007, MNRAS, 382, 1639 [NASA ADS] [Google Scholar]
- Homan, D. C., Ojha, R., Wardle, J. F. C., et al. 2002, ApJ, 568, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Hovatta, T., Lister, M. L., Aller, M. F., et al. 2012, AJ, 144, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Stevens, J. A., et al. 2007, AJ, 134, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, T., Tabara, H., Inoue, M., & Aizu, K. 1987, Nature, 329, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Kellermann, K. I., & Pauliny-Toth, I. I. K. 1981, ARA&A, 19, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, A., Krichbaum, T. P., Wegner, R., et al. 2003, A&A, 401, 161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kravchenko, E. V., Cotton, W. D., & Kovalev, Y. Y. 2015, in IAU Symp. 313, eds. F. Massaro, C. C. Cheung, E. Lopez, & A. Siemiginowska, 128 [Google Scholar]
- Kronberg, P. P., & Simard-Normandin, M. 1976, Nature, 263, 653 [NASA ADS] [CrossRef] [Google Scholar]
- Kronberg, P. P., Reinhardt, M., & Simard-Normandin, M. 1977, A&A, 61, 771 [NASA ADS] [Google Scholar]
- Laing, R. A. 1984, in Physics of Energy Transport in Extragalactic Radio Sources, ed. A. H. Bridle, 90 [Google Scholar]
- Lister, M. L., Cohen, M. H., Homan, D. C., et al. 2009, AJ, 138, 1874 [NASA ADS] [CrossRef] [Google Scholar]
- Mantovani, F., Mack, K.-H., Montenegro-Montes, F. M., Rossetti, A., & Kraus, A. 2009, A&A, 502, 61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marecki, A., Thomasson, P., Mack, K.-H., & Kunert-Bajraszewska, M. 2006, A&A, 448, 479 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’Dea, C. P. 1998, PASP, 110, 493 [NASA ADS] [CrossRef] [Google Scholar]
- O’Dea, C. P., & Baum, S. A. 1997, AJ, 113, 148 [NASA ADS] [CrossRef] [Google Scholar]
- O’Dea, C. P., Baum, S. A., & Stanghellini, C. 1991, ApJ, 380, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Oppermann, N., Junklewitz, H., Greiner, M., et al. 2015, A&A, 575, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Orr, M. J. L., & Browne, I. W. A. 1982, MNRAS, 200, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M. 2001, in Advanced Lectures on the Starburst-AGN, eds. I. Aretxaga, D. Kunth, & R. Mújica, 3 [Google Scholar]
- Rengelink, R. B., Tang, Y., de Bruyn, A. G., et al. 1997, A&AS, 124, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rossetti, A., Dallacasa, D., Fanti, C., Fanti, R., & Mack, K.-H. 2008, A&A, 487, 865 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rossetti, A., Mantovani, F., Dallacasa, D., et al. 2009, A&A, 504, 741 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saikia, D. J. 1988, in Active Galactic Nuclei, eds. H. R. Miller, & P. J. Wiita (Berlin: Springer Verlag), Lect. Notes Phys., 307, 317 [Google Scholar]
- Saikia, D. J., & Jamrozy, M. 2009, Bull. Astron. Soc. India, 37, 63 [NASA ADS] [Google Scholar]
- Saikia, D. J., & Salter, C. J. 1988, ARA&A, 26, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Stanghellini, C., Baum, S. A., O’Dea, C. P., & Morris, G. B. 1990, A&A, 233, 379 [NASA ADS] [Google Scholar]
- Tribble, P. C. 1991, MNRAS, 250, 726 [NASA ADS] [CrossRef] [Google Scholar]
- Trippe, S., Bremer, M., Krichbaum, T. P., et al. 2012, MNRAS, 425, 1192 [NASA ADS] [CrossRef] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Vallee, J. P. 1980, A&A, 86, 251 [NASA ADS] [Google Scholar]
- White, R. L., Becker, R. H., Helfand, D. J., & Gregg, M. D. 1997, ApJ, 475, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Zavala, R. T., & Taylor, G. B. 2004, ApJ, 612, 749 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional table
77 bona fide unpolarised sources at 10.45 GHz.
Appendix B:
Table of values.
Appendix C: Parameters used for the SEDs fit
Values of the SEDs best fit.
Appendix D: Plots of the high-RM candidates
 |
Fig. D.1 Sources 0239-0234, 0243-0550, and 0742+4900. For each source we present their SED S[Jy], the polarisation flux density Spol[Jy], the fractional polarisation m[%], and the polarisation angle PA[rad]. |
 |
Fig. D.2 Sources 0751+2716, 0845+0439, and 0925+3159. For each source we present their SED S[Jy], the polarisation flux density Spol[Jy], the fractional polarisation m[%], and the polarisation angle PA[rad]. |
 |
Fig. D.3 Sources 0958+3224, 1015+0318, and 1043+2408. For each source we present their SED S[Jy], the polarisation flux density Spol[Jy], the fractional polarisation m[%], and the polarisation angle PA[rad]. |
 |
Fig. D.4 Sources 1044+0655, 1048+0141, and 1146+5356. For each source we present their SED S[Jy], the polarisation flux density Spol[Jy], the fractional polarisation m[%], and the polarisation angle PA[rad]. |
 |
Fig. D.5 Sources 1213+1307, 1246-0730, and 1311+1417. For each source we present their SED S[Jy], the polarisation flux density Spol[Jy], the fractional polarisation m[%], and the polarisation angle PA[rad]. |
 |
Fig. D.6 Sources 1312+5548, 1351+0830 and 1405+0415. For each source we present their SED S[Jy], the polarisation flux density Spol[Jy], the fractional polarisation m[%], and the polarization angle PA[rad]. |
 |
Fig. D.7 Source 1435-0414, 1549+5038, and 1616+0459. For each source we present their SED S[Jy], the polarisation flux density Spol[Jy], the fractional polarisation m[%], and the polarisation angle PA[rad]. |
 |
Fig. D.8 Sources 1616+2647, 1647+3752, and 1713+2813. For each source we present their SED S[Jy], the polarisation flux density Spol[Jy], the fractional polarisation m[%], and the polarisation angle PA[rad]. |
 |
Fig. D.9 Sources 1723+3417, 2050+0407, and 2101+0341. For each source we present their SED S[Jy], the polrization flux density Spol[Jy], the fractional polarization m[%] and the polarization angle PA[rad]. |
 |
Fig. D.10 Source 2147+0929, 2200+0708 and 2245+0324. For each source we present their SED S[Jy], the polarisation flux density Spol[Jy], the fractional polarisation m[%], and the polarisation angle PA[rad]. |
All Tables
Estimation of the magnetic field for those targets with one or more synchrotron components in their SEDs.
All Figures
 |
Fig. 1 Spectral index distributions. a) Comparison of the spectral index distribution for the high-RM candidates (30 sources; red histogram) and the unpolarised sources (77 sources; black histogram). The distribution of the unpolarised sources peaks at αpeak ~ −0.5. The high-RM distribution shows 3 different types of objects: steep (αpeak ~ −0.8), flat (αpeak ~ −0.1), and inverted (αpeak ~ + 0.2) spectrum radio sources. b) The same but cumulative histograms. |
| In the text | |
 |
Fig. 2 SEDs for the sources: 1015+0318 classified as Older, 2245+0324 classified as GPS-like, and 0845+0439 classified as Mixed. Black dot points are the Effelsberg and low-frequency data from the literature; 3-sigma upper limits are drawn as triangles. Where present, various synchrotron components are plotted with an orange dashed line. The fit of the spectra is the red straight line. Polarisation information is presented with the SEDs. |
| In the text | |
 |
Fig. 3 a) histogram showing the distribution of the fitted rotation measure of our targets (red histogram) together with the Farnes catalogue (blue histogram). b) the same but cumulative. |
| In the text | |
 |
Fig. 4 a) Cumulative plot of the RMobs for the three object types. Yellow: Older type; grey: GPS-like type; green: Mixed type. b) Cumulative plot of the RMrf for the three object types. |
| In the text | |
 |
Fig. D.1 Sources 0239-0234, 0243-0550, and 0742+4900. For each source we present their SED S[Jy], the polarisation flux density Spol[Jy], the fractional polarisation m[%], and the polarisation angle PA[rad]. |
| In the text | |
 |
Fig. D.2 Sources 0751+2716, 0845+0439, and 0925+3159. For each source we present their SED S[Jy], the polarisation flux density Spol[Jy], the fractional polarisation m[%], and the polarisation angle PA[rad]. |
| In the text | |
 |
Fig. D.3 Sources 0958+3224, 1015+0318, and 1043+2408. For each source we present their SED S[Jy], the polarisation flux density Spol[Jy], the fractional polarisation m[%], and the polarisation angle PA[rad]. |
| In the text | |
 |
Fig. D.4 Sources 1044+0655, 1048+0141, and 1146+5356. For each source we present their SED S[Jy], the polarisation flux density Spol[Jy], the fractional polarisation m[%], and the polarisation angle PA[rad]. |
| In the text | |
 |
Fig. D.5 Sources 1213+1307, 1246-0730, and 1311+1417. For each source we present their SED S[Jy], the polarisation flux density Spol[Jy], the fractional polarisation m[%], and the polarisation angle PA[rad]. |
| In the text | |
 |
Fig. D.6 Sources 1312+5548, 1351+0830 and 1405+0415. For each source we present their SED S[Jy], the polarisation flux density Spol[Jy], the fractional polarisation m[%], and the polarization angle PA[rad]. |
| In the text | |
 |
Fig. D.7 Source 1435-0414, 1549+5038, and 1616+0459. For each source we present their SED S[Jy], the polarisation flux density Spol[Jy], the fractional polarisation m[%], and the polarisation angle PA[rad]. |
| In the text | |
 |
Fig. D.8 Sources 1616+2647, 1647+3752, and 1713+2813. For each source we present their SED S[Jy], the polarisation flux density Spol[Jy], the fractional polarisation m[%], and the polarisation angle PA[rad]. |
| In the text | |
 |
Fig. D.9 Sources 1723+3417, 2050+0407, and 2101+0341. For each source we present their SED S[Jy], the polrization flux density Spol[Jy], the fractional polarization m[%] and the polarization angle PA[rad]. |
| In the text | |
 |
Fig. D.10 Source 2147+0929, 2200+0708 and 2245+0324. For each source we present their SED S[Jy], the polarisation flux density Spol[Jy], the fractional polarisation m[%], and the polarisation angle PA[rad]. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


