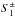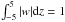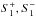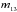| Issue |
A&A
Volume 586, February 2016
|
|
|---|---|---|
| Article Number | A33 | |
| Number of page(s) | 8 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201526494 | |
| Published online | 22 January 2016 | |
Research Note
Linear analysis of the vertical shear instability: outstanding issues and improved solutions
1
Space Sciences Division, NASA Ames Research Center, Moffett Field, CA
94035,
USA
e-mail:
orkan.m.umurhan@nasa.gov
2
SETI Institute, 189 Bernardo Way, Mountain
View, CA
94043,
USA
3
Queen Mary University of London, School of Physics and Astronomy,
327
Mile End Road London, E1 4NS, UK
4
Niels Bohr International Academy, The Niels Bohr Institute,
Blegdamsvej 17,
2100
Copenhagen Ø,
Denmark
Received: 8 May 2015
Accepted: 13 July 2015
Context. The vertical shear instability is one of several known mechanisms that are potentially active in the so-called dead zones of protoplanetary accretion disks. A recent analysis of the instability mechanism indicates that a subset of unstable modes shows unbounded growth – both as resolution is increased and when the nominal lid of the atmosphere is extended. This trend suggests that, possibly, the model system is ill-posed.
Aims. This research note both examines the energy content of these modes and questions the legitimacy of assuming separable solutions for a problem whose linear operator is fundamentally inseparable.
Methods. The reduced equations governing the instability are revisited and the generated solutions are examined using both the previously assumed separable forms and an improved non-separable solution form that is introduced in this paper.
Results. Reconsidering the solutions of the reduced equations by using the separable form shows that, while the low-order body modes have converged eigenvalues and eigenfunctions (for both variations in the model atmosphere’s vertical boundaries and radial numerical resolution). It is also confirmed that the corresponding high-order body modes and the surface modes indeed show unbounded growth rates. The energy contained in both the higher order body modes and surface modes diminishes precipitously due to the disk’s Gaussian density profile. Most of the energy of the instability is contained in the low-order modes. An inseparable solution form is introduced to filter out the inconsequential surface modes, leaving only body modes (both low- and high-order ones). The analysis predicts a fastest growing mode with a specific radial length scale. The growth rates associated with the fundamental corrugation and breathing modes match the growth and length scales observed in previous nonlinear studies of the instability.
Conclusions. Linear stability analysis of the vertical shear instability should be done assuming non-separable solutions, especially for settings involving boundaries in the radial direction. We also conclude that the surface modes are relatively inconsequential because of the little energy they contain, and are artifacts of imposing specific kinematic vertical boundary conditions in isothermals disk models.
Key words: protoplanetary disks / instabilities / turbulence / waves / methods: analytical
© ESO, 2016
1. Introduction
The vertical shear instability (VSI; Urpin 2003; Urpin & Brandenburg 1998; Arlt & Urpin 2004; Nelson et al. 2013; McNally & Pessah 2015; Stoll & Kley 2015), also known as the Goldreich Schubert Fricke instability (Goldreich & Schubert 1967; Fricke 1968) is a linear instability of axisymmetric inertial modes that relies on the vertical shear of the basic near-Keplerian flow state. This instability may be active in non-magnetized parts of protoplanetary accretion disks and is perhaps discernible in their dead zones (Turner et al. 2014). Nelson et al. (2013, NGU13 hereafter) and Stoll & Kley (2014) demonstrate that the instability can generate a modest amount of turbulence, with effective disk α ranging somewhere between 4 × 10-4 and 10-3. In both studies, the basic background setting is that of a locally isothermal disk with a radial temperature gradient arising either from some external imposition (NGU13) or appearing naturally, as a result of radiative transfer effects (Stoll & Kley 2014).
A satisfactory linear stability analysis is still missing for the disk setting. While the basic essence of the instability has been sketched out using a local point analysis (Goldreich & Schubert 1967; Fricke 1968; Urpin 2003), the way the instability manifests itself in a global or semi-global disk setting is difficult to assess because the basic linear stability problem is non-separable1 even in the simplest model reduction (NGU13; Barker & Latter 2015, BL15 hereafter). NGU13 and BL15 present a similar linear stability analysis using a reduced model set, and they show that, while the low-order modes that go unstable are consistent with the time scales of the instability seen in the numerical experiments, there are some serious shortcomings associated with the analysis that cast doubt on whether it accurately describes the physical manifestation of the VSI, especially when analyzed in the locally isothermal disk setting.
The mode analyses done by NGU13 and BL15 show that if one assumes radially propagating traveling waves, there are two classes of modes loosely referred to as body modes and surface modes. The surface modes come into existence if one imposes no-flow boundary conditions like an impenetrable lid at positions above and below the disk midplane (usually at least a few local disk scale heights or higher). The body modes are present irrespective of the kinematic conditions in the vertical, so long as their kinetic energies decay far enough away from the midplane (see below). BL15 also point out that the surface modes mulitply as the radial disturbance wavelengths become shorter. BL15 and NGU13 show that, for a given value of the radial wavenumber, there is a mode with the fastest growth rate, which corresponds, generally, to a surface mode.
However, there are three troubling features:
-
1.
As the nominal lid of the atmosphere is extended to infinity, the fastest growing eigenmodes have growth rates that become similarly unbounded, growing like
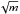 for integer m representing the number of vertical nodes in the disturbance (BL15).
for integer m representing the number of vertical nodes in the disturbance (BL15). -
2.
Where no-flow boundary conditions are imposed in the vertical direction, the number of unstable surface modes (with increasingly finer length scales) increases with higher radial resolution, possibly suggesting that the fundamental problem in the model VSI setup itself could be ill-posed – at least with respect to these surface modes (BL15).
-
3.
As the wavelength of the radially propagating traveling wave becomes larger, the growth rate similarly increases in an unbounded way.
With regards to the third feature, both numerical simulations of NGU13 and Stoll & Kley (2014) indicate that a radial scale of maximum linear growth exists, yet neither of the analyses of the asymptotically reduced equations examined by NGU13 or BL15 allow for such a trend. Is it possible that the reason for this is the breakdown in the validity of the reduced equations, which hinges on the assumption of radial geostrophy in the dynamics, or might this be a problem with the assumption of radial traveling waves? These questions are reviewed in more detail in Sect. 2.
In Sect. 3, we argue that the first two of the troubling features listed does not lead to any serious deficiency in either the reduced set of equations or in the robustness/validity of the VSI itself. This is because both the surface modes and the other high nodal modes (i.e. high m) carry very little of the total vertical kinetic energy of the system. For the third feature, we consider this pathology to be a shortcoming of adopting a traveling wave-like solution and not a deficiency of the reduced set of equations. This, in turn, is intimately related to incorrectly assuming separable solution forms for a problem that is inherently inseparable2. We present an improved approximation in Sect. 4, where we adopt a relatively tractable, non-separable solution form and reanalyze the reduced equations. We find that there are maximally growing disturbances at some finite radial length scale and that they, in turn, match the growth rates and fastest growing radial scales reported in NGU13. In Sect. 5 we briefly discuss our findings.
2. Background
In both NGU13 and BL15, the following asymptotic reduced set of equations governing the dynamics of the VSI was shown to be appropriate for describing the linear development of the instability of axisymmetric disturbances: 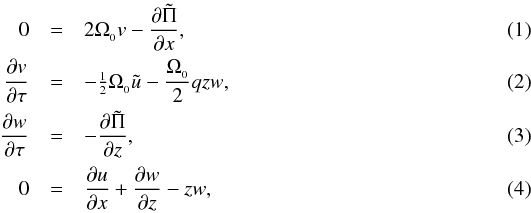 with
with 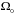 the local rotation rate of the disk section at a distance R0 from the parent star, the above set was obtained assuming that the spatial and temporal scales of motion are related to one another according to the following: temporal dynamics are given by
the local rotation rate of the disk section at a distance R0 from the parent star, the above set was obtained assuming that the spatial and temporal scales of motion are related to one another according to the following: temporal dynamics are given by 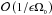 , radial dynamic scales x are
, radial dynamic scales x are 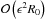 , and the vertical scales z are on the scale height
, and the vertical scales z are on the scale height 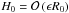 , in which the small parameter ϵ ≡ H0/R0 measures the relative thinness of the disk (which is usually taken to be approximately 0.05 in most theoretical studies, including the ones cited above). The scaled radial and vertical velocities are u and w, respectively, while v is the deviation azimuthal velocity with respect to the background near-Keplerian flow, and
, in which the small parameter ϵ ≡ H0/R0 measures the relative thinness of the disk (which is usually taken to be approximately 0.05 in most theoretical studies, including the ones cited above). The scaled radial and vertical velocities are u and w, respectively, while v is the deviation azimuthal velocity with respect to the background near-Keplerian flow, and  is the scaled pressure perturbation. These equations model disk inertial modes with very short radial wavelengths. The degree of the vertical shear, which varies with disk height z, is controlled by the parameter q (where no vertical shear is equivalent to q = 0). In both NGU13 and Stoll & Kley (2014), the value of q = −1 is adopted. Equation (1) states that the disturbances are largely in radial geostrophic balance. Equations (2), (3) are the azimuthal and vertical momentum equations while Eq. (4) is the anelastic equation of state. See both NGU13 and BL15 for further details regarding the derivation of this set of reduced equations. Because the equations have been appropriately non-dimensionalized, we henceforth set Ω0 = 1 on all of the Coriolis and vertical shear terms appearing in Eqs. (1), (2).
is the scaled pressure perturbation. These equations model disk inertial modes with very short radial wavelengths. The degree of the vertical shear, which varies with disk height z, is controlled by the parameter q (where no vertical shear is equivalent to q = 0). In both NGU13 and Stoll & Kley (2014), the value of q = −1 is adopted. Equation (1) states that the disturbances are largely in radial geostrophic balance. Equations (2), (3) are the azimuthal and vertical momentum equations while Eq. (4) is the anelastic equation of state. See both NGU13 and BL15 for further details regarding the derivation of this set of reduced equations. Because the equations have been appropriately non-dimensionalized, we henceforth set Ω0 = 1 on all of the Coriolis and vertical shear terms appearing in Eqs. (1), (2).
This simplified model may then be combined into a single partial differential equation (PDE) for the scaled pressure perturbation 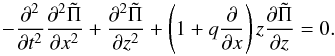 (5)Assuming normal mode solutions
(5)Assuming normal mode solutions 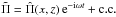 transforms the above PDE into the simpler one:
transforms the above PDE into the simpler one: 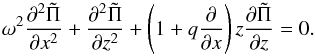 (6)The task still remains to construct solutions to this system and determine the eigenvalue ω that, in turn, determines the temporal response. Inspection of the above form shows that this system is inseparable when q ≠ 0, which introduces a number of problems with regards to linear stability analyses that we discuss briefly below.
(6)The task still remains to construct solutions to this system and determine the eigenvalue ω that, in turn, determines the temporal response. Inspection of the above form shows that this system is inseparable when q ≠ 0, which introduces a number of problems with regards to linear stability analyses that we discuss briefly below.
One might continue to analyze this system assuming an approximate separable form3. For instance, as was done by BL15, one can consider the relatively tractable traveling-wave ansatz as 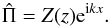 (7)Equation (6) can then be simplified further to
(7)Equation (6) can then be simplified further to 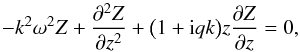 (8)where Z(z) is an, as yet undetermined, vertical structure function. The above equation, which is explicitly the same form as appear in BL15, is in the form of Hermite’s equation. One solution of this system that admits tractable analytic results is to allow perturbations to show (at most) algebraic growth as | z | → ∞, in which case
(8)where Z(z) is an, as yet undetermined, vertical structure function. The above equation, which is explicitly the same form as appear in BL15, is in the form of Hermite’s equation. One solution of this system that admits tractable analytic results is to allow perturbations to show (at most) algebraic growth as | z | → ∞, in which case 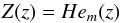 (9)is an acceptablesolution, where m is a positive index and Hem is the Hermite polynomial of order m. The index m counts the number of vertical nodes in the pressure eigenfunction, and is thus referred to as indicating this quality throughout the rest of this Research Note. When inserted into Eq. (6), we find that this solution form is an actual solution, provided the following relationship holds:
(9)is an acceptablesolution, where m is a positive index and Hem is the Hermite polynomial of order m. The index m counts the number of vertical nodes in the pressure eigenfunction, and is thus referred to as indicating this quality throughout the rest of this Research Note. When inserted into Eq. (6), we find that this solution form is an actual solution, provided the following relationship holds: 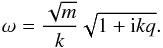 (10)As discussed in BL15, the growth rate associated with this form increases without bound as k → 0. We agree that this is pathological for a number of reasons, the following two being most prominent: (i) the approximation of radial geostrophy most likely breaks down when the horizontal wavelengths become large; and (ii) because, as we show in the next section, the traveling wave ansatz is also deeply flawed. This solution is also problematic because the growth rates increase without bound, both as the integer m increases and as k decreases. Nonetheless, this simplest solution indicates that the system is ill-posed as higher-order vertical modes (increased m) are included in the analysis.
(10)As discussed in BL15, the growth rate associated with this form increases without bound as k → 0. We agree that this is pathological for a number of reasons, the following two being most prominent: (i) the approximation of radial geostrophy most likely breaks down when the horizontal wavelengths become large; and (ii) because, as we show in the next section, the traveling wave ansatz is also deeply flawed. This solution is also problematic because the growth rates increase without bound, both as the integer m increases and as k decreases. Nonetheless, this simplest solution indicates that the system is ill-posed as higher-order vertical modes (increased m) are included in the analysis.
We note that this solution ansatz cannot recover surface modes for the obvious reason that no kinematic boundary conditions are either imposed or enforced in the vertical. We also observe the following: that since both the atmosphere density drops off as a Gaussian (i.e. ρ0 ~ exp−z2/ 2) and that eigenmodes have zm structure, the effect of adopting a free vertical boundary condition is to imply that kinetic energies of all modes decay to zero as z → ± ∞.
Another approach is the one taken by NGU13 and BL15 in which Eq. (8) is solved with no-normal-flow boundary conditions at the vertical boundaries at z = ± H (we note that H refers to the height of the solution domain and H0 refers to the disk scale height in this paper), which amounts to stating that 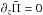 at z = ± H provided ω ≠ 0, which follows from the normal mode form of Eq. (3). The general solution of (8) is given by
at z = ± H provided ω ≠ 0, which follows from the normal mode form of Eq. (3). The general solution of (8) is given by 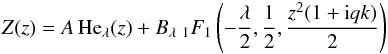 where 1F1 is a confluent hypergeometric function of the first kind and where λ is the usual separation constant which is determined through the application of boundary conditions. The second of these special functions does not offer very much in the form of analytical insight (NGU13) except in the guise of certain asymptotic limits (BL15), and as such, it is more convenient to numerically solve Eq. (8) directly.
where 1F1 is a confluent hypergeometric function of the first kind and where λ is the usual separation constant which is determined through the application of boundary conditions. The second of these special functions does not offer very much in the form of analytical insight (NGU13) except in the guise of certain asymptotic limits (BL15), and as such, it is more convenient to numerically solve Eq. (8) directly.
 |
Fig. 1 Growth rates, Im(ω), and frequencies, Re(ω), of solutions of Eq. (8) subject to no-normal-flow boundary conditions at z = ± H, where H is in units of scale heights. Top panel: distribution shown for k = 2, and H = 5 (diamonds), and H = 7 (open circles). As H increases, more surface modes become activated and high-order body modes have increased growth rates. In both cases shown, the frequency and growth rates of low-order body modes (labeled m1,m2,m3) remain unchanged. The surface modes generally appear in pairs as indicated by labeling the topmost surface mode with the superscript |
The numerical eigenvalues determined by this procedure recover the surface modes as well as the body modes of the VSI. The low-order body modes (the fundamental and first overtone breathing and corrugation modes) are also recovered with eigenvalues consistent with the numerical results of NGU13. However, this system introduces apparent pathologies, which are shown in Fig. 1. There are generally three branches of solutions: one associated with low-order body modes with relatively low frequencies, another branch of body modes with higher frequencies and a third short branch consisting of surface modes. The high-frequency branch of body modes shows decreasing growth rates as the mode frequency increases, while the low-order body modes show an increasing growth rate with increasing frequency.
However, as BL15 demonstrate, when the location of the vertical height is increased, the following occurs: (a) The growth rates of the high-frequency branch increases; (b) the growth rates of the surface body modes also increase; while (c) the growth rates and frequencies of the low-order body modes remain unchanged, and (d) as the lid of the atmosphere is raised to ± ∞, the low- and high-order body modes line up with the frequencies and growth rates expressed in Eq. (10). This corresponds to the response predicted assuming the ansatz found in Eq. (7). While it would seem that imposing vertical no-flow boundary conditions removes the ill-posed nature of the model problem, the system’s ill-posedness appears to manifest itself as H → ∞, since the growth rates in the high-order body modes and surface modes correspondingly increase, once again seemingly without bound. This is problematic and suggests that the model problem may be ill-posed after all.
The situation deteriorates even further if we consider the behavior of the surface modes, as BL15 indicate: an increase in the radial resolution (larger k) causes the number of surface modes attached to the upper and lower no-flow boundaries to proliferate, as the second panel of Fig. 1 clearly illustrates. Raising the position of the lid in the model also increases the growth rate of the fastest-growing surface modes, which is also indicative of an ill-posed model.
Moreover, another serious shortcoming implied by the results of the linear stability solutions developed in NGU13 and BL15, is that they do not predict finite, non-zero maximally growing radial wave disturbances, something that is observed in the numerical experiments of NGU13 and Stoll & Kley (2014). This suggests that assuming wavelike modes in the radial direction is either flawed or, at the very least, not physically relevant.
 |
Fig. 2 Vertical kinetic energy density plots, Ez, plotted for the modes labeled in the top panel of Fig. 1, which corresponds to solutions of Eq. (8) with H = 5 and k = 2. Each corresponding vertical velocity eigenfunction w is normalized, such that |
3. Mode kinetic energies
In spite of these troublesome features, these approximate theoretical solutions reveal a lot about the physical nature of the developing instability, especially in relation to the high frequency body modes and the proliferating surface modes. For example, they provide information on the relative energy content for each mode. The low-order body modes carry most of the inertia of the disk disturbances since their amplitudes are greatest near z = 0 (NGU13, BL15). Because these are also locations where most of the disk mass is concentrated, the energy contained in these low-order body modes dominate the corresponding energy contained in the higher order body and surface modes. This has a direct consequence on the interpretation of the VSI, even in the context of this somewhat incomplete analysis.
To illustrate this quantitatively, Fig. 2 shows a comparison of the relative energy densities contained in representative modes, labeled in the top panel of Fig. 1, which corresponds to solutions of Eq. (8) with H = 5 and k = 2. From Eq. (3) it follows that each eigenmode Z(z) generates a corresponding vertical velocity eigenfunction w = iω-1∂zZ. We normalize each vertical velocity eigenfunction so that 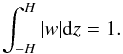 (11)Since the reduced equations represent an isothermal atmosphere, the steady-state density is given by ρ0 = exp(−z2/ 2). We also recall that this instability is one in which the perturbation vertical kinetic energy density dominates over the radial and azimuthal kinetic energy densities (NGU13, Stoll & Kley 2014). As such, we consider the vertical kinetic energy density Ez of each of the corresponding modes defined by Ez(z) ≡ 0.5ρ0 | w | 2. “m1” labels the fundamental corrugation mode (FCM), while “m2” labels the fundamental breathing mode (FBM) so that, for example, the expression Ez(z,m1) corresponds to the energy density of the FCM, and so on. For each mode we also define a total vertically integrated density
(11)Since the reduced equations represent an isothermal atmosphere, the steady-state density is given by ρ0 = exp(−z2/ 2). We also recall that this instability is one in which the perturbation vertical kinetic energy density dominates over the radial and azimuthal kinetic energy densities (NGU13, Stoll & Kley 2014). As such, we consider the vertical kinetic energy density Ez of each of the corresponding modes defined by Ez(z) ≡ 0.5ρ0 | w | 2. “m1” labels the fundamental corrugation mode (FCM), while “m2” labels the fundamental breathing mode (FBM) so that, for example, the expression Ez(z,m1) corresponds to the energy density of the FCM, and so on. For each mode we also define a total vertically integrated density 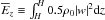 (i.e., a surface energy density). When we refer to the surface energy density of a particular mode, we write, for example,
(i.e., a surface energy density). When we refer to the surface energy density of a particular mode, we write, for example, 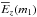 to indicate the surface energy density of the FCM, and so on.
to indicate the surface energy density of the FCM, and so on.
 |
Fig. 3 Total vertically integrated vertical kinetic energies |
Figure 2 plots the energy densities 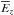 for the various modes admitted by the system with parameter values k = 2,H = 5, in which each vertical velocity normal mode is normalized according to Eq. (11). Here, we see that the relative energy density content is greatest with FCM and that it dominates the FBM by a factor of 10. The energy density distribution in the other higher order body modes are reduced by at least a factor of 100 compared to the FCM. The energy density contained in the two fastest growing surface modes is diminished by a factor of 1000 compared to the FCM.
for the various modes admitted by the system with parameter values k = 2,H = 5, in which each vertical velocity normal mode is normalized according to Eq. (11). Here, we see that the relative energy density content is greatest with FCM and that it dominates the FBM by a factor of 10. The energy density distribution in the other higher order body modes are reduced by at least a factor of 100 compared to the FCM. The energy density contained in the two fastest growing surface modes is diminished by a factor of 1000 compared to the FCM.
A comparison of the total vertically integrated energies in these various modes emphasizes further the relative unimportance of the high-order body and surface modes. To express this quantity, relative to the vertically integrated energy density of the FCM (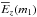 ), the following selected modes are used: for the FBM,
), the following selected modes are used: for the FBM, 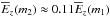 ; for the first overtone corrugation mode,
; for the first overtone corrugation mode, 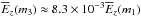 ; the selected high-order body mode
; the selected high-order body mode  :
: 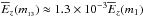 ; and for the two surface body modes, both of which have the same amount of vertically integrated energy contained within,
; and for the two surface body modes, both of which have the same amount of vertically integrated energy contained within, 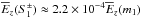 . Together with the first 50 vertical eigenmodes, the resulting trends are plotted in Fig. 3, which clearly shows that the energy contained in the modes drops with increased values of m. We similarly plot the relative vertically integrated kinetic energy densities for models where H = 7,k = 2 (Fig. 4) and H = 8,k = 5 (Fig. 5), and we see how, by increasing the resolution (going to larger k) and by extending the atmosphere lid, the low-order modes become increasingly populated (as BL15 point out) and how the
. Together with the first 50 vertical eigenmodes, the resulting trends are plotted in Fig. 3, which clearly shows that the energy contained in the modes drops with increased values of m. We similarly plot the relative vertically integrated kinetic energy densities for models where H = 7,k = 2 (Fig. 4) and H = 8,k = 5 (Fig. 5), and we see how, by increasing the resolution (going to larger k) and by extending the atmosphere lid, the low-order modes become increasingly populated (as BL15 point out) and how the 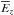 energies, contained in the corresponding surface and high-order body modes, diminish even further.
energies, contained in the corresponding surface and high-order body modes, diminish even further.
Most importantly we confirm the trend, reported by BL15m in which the energy in the low-order body modes remains steady as H is increased. This is especially true for the FCM and FBM but also becomes a characteristic feature of increasing overtones as H increased. With reference to Fig. 3, all the body modes to the left of the triple junction, where the surface mode branch meets the low-order and high-order body modes, display energies that remain unchanged as H increases. Increasing H, however, moves the location of the triple junction toward higher order body modes, whereas the energies of the low-order body modes (i.e., those left of the triple junction) do not change with increased H.
The relatively weak energy carrying potential of both the high-order body modes and the branch of surface modes comes about because the corresponding kinetic energy associated with them is severely diminished as a result of the Guassian drop-off that is associated with the mean density field 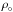 . This is despite their relatively large velocity amplitudes for large values of | z |.
. This is despite their relatively large velocity amplitudes for large values of | z |.
 |
Fig. 4 As in Fig. 3 except with H = 7. The power contained both in the surface and high-order body modes is diminished as the atmosphere lid is set farther away. Note that the energy in the low-order body modes remain unchanged, especially the FCM and FBM. |
 |
Fig. 5 As in Fig. 3, except that H = 8 and k = 5. The diminished energy-carrying capacity of both the surface modes and the high-order body modes when the lid of the atmosphere is made larger and when higher radial resolution modes are considered. The energy of the low-order body modes, especially the FCM, FBM and the first overtone corrugation mode remain unchanged compared to their energies for lower values of H, depicted in the two previous figures. |
4. An improved approximate solution
While we cannot address all of the concerns listed in Sect. 2, we offer an improved solution ansatz to the eigenvalue problem posed by Eq. (6). The simulations presented in NGU13 and Stoll & Kley (2014) employ a numerical set-up in which radial boundaries are enforced. These boundaries introduce effects that alter the growth rates and character of the low-frequency body modes, which are the very ones that have been observed to carry the instability into the nonlinear regime. We demonstrate here that (a) the unbounded growth predicted by assuming wavelike disturbances in the radial direction, is an artifact created by assuming radially-traveling wave solutions and (b) that this pathology is removed by the imposition of some kind of fixed radial boundary condition. Furthermore, the imposition of boundary conditions selects the fastest mode with radial length scales and growth rates that match those found in the aforementioned numerical experiments.
To represent the effect of radial boundaries, the following non-separable ansatz is assumed: 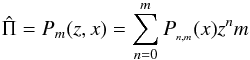 (12)where m is a positive integer, and Pn,m(x) a set of unknown functions of x4. This solution form is one borrowed from singular value decomposition methods, and has been used in other disk studies (e.g., Lubow & Pringle 1993). We note already that the ansatz found in Eq. (12) builds unbounded algebraic spatial growth into the solutions as | z | → ∞, which will predict the same kind of unbounded growth in which Im
(12)where m is a positive integer, and Pn,m(x) a set of unknown functions of x4. This solution form is one borrowed from singular value decomposition methods, and has been used in other disk studies (e.g., Lubow & Pringle 1993). We note already that the ansatz found in Eq. (12) builds unbounded algebraic spatial growth into the solutions as | z | → ∞, which will predict the same kind of unbounded growth in which Im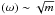 , just as the simple solution shown in Eq. (10). But, as we already note in Sect. 2, this means that these solutions are ones where the kinetic energies always decay as z → ± ∞. On a positive note, these solutions are not burdened by the introduction of surface modes.
, just as the simple solution shown in Eq. (10). But, as we already note in Sect. 2, this means that these solutions are ones where the kinetic energies always decay as z → ± ∞. On a positive note, these solutions are not burdened by the introduction of surface modes.
Based on the above, we adopt this solution form and insert it into Eq. (6). Separating out like-orders of powers of z turns this system into 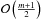 nested ODEs for the unknown functions
nested ODEs for the unknown functions 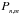 . For n = m we have the so-called “top” equation
. For n = m we have the so-called “top” equation 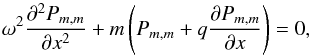 (13)while for 0 ≤ n<m we have the remaining so-called “slaved” equations
(13)while for 0 ≤ n<m we have the remaining so-called “slaved” equations 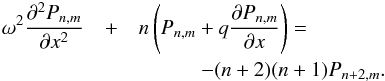 (14)The above system has even and odd symmetries associated with it, so that there are so-called breathing modes (even m) and corrugation modes (odd m). The fundamental corrugation mode (FCM) corresponds to m = 1 while the fundamental breathing mode (FBM) is associated with m = 2.
(14)The above system has even and odd symmetries associated with it, so that there are so-called breathing modes (even m) and corrugation modes (odd m). The fundamental corrugation mode (FCM) corresponds to m = 1 while the fundamental breathing mode (FBM) is associated with m = 2.
For this particular demonstration, we assume no-normal-flow boundary conditions at particular inner and outer radial positions, i.e., u = 0 at x = ± Lx, where Lx> 0. In terms of the variables we use, the expression of this condition is found by rewriting Eq. (2) in terms of the normal mode ansatz 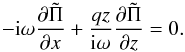 (15)Given the solution form (12) and since the polynomials zn are linearly independent with respect to one another (for integer n), each function Pn,m must separately satisfy
(15)Given the solution form (12) and since the polynomials zn are linearly independent with respect to one another (for integer n), each function Pn,m must separately satisfy 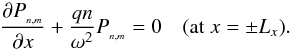 (16)The method for solving the full problem is now straightforward: (i) solve the “top” Eq. (13) subject to boundary conditions and then (ii) solve the “slaved” Eqs. (14) subject to the boundary conditions expressed in Eq. (16) for each Pn,m. This should be done by decreasing values of n (by 2) until one terminates either at n = 0 (breathing modes) or n = 1 (corrugation modes). A detailed depiction of the full solution will be the subject of a future study. Of concern to us here, however, is the fact that the top equation yields the eigenvalue ω. In fact, it is straightforward to show that
(16)The method for solving the full problem is now straightforward: (i) solve the “top” Eq. (13) subject to boundary conditions and then (ii) solve the “slaved” Eqs. (14) subject to the boundary conditions expressed in Eq. (16) for each Pn,m. This should be done by decreasing values of n (by 2) until one terminates either at n = 0 (breathing modes) or n = 1 (corrugation modes). A detailed depiction of the full solution will be the subject of a future study. Of concern to us here, however, is the fact that the top equation yields the eigenvalue ω. In fact, it is straightforward to show that 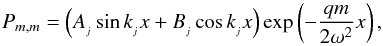 (17)is a solution to Eq. (13) provided ω = ω(kj) satisfies
(17)is a solution to Eq. (13) provided ω = ω(kj) satisfies 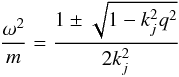 (18)together with k = kj ≡ jπ/ 2Lx, where j is any integer including zero. When j is an odd integer, then Aj = kj,Bj = −qm/ 2ω2. However, when j is an even integer (including zero) Aj = −qm/ 2ω2,Bj = −kj.
(18)together with k = kj ≡ jπ/ 2Lx, where j is any integer including zero. When j is an odd integer, then Aj = kj,Bj = −qm/ 2ω2. However, when j is an even integer (including zero) Aj = −qm/ 2ω2,Bj = −kj.
Since all the kj are real and their multitude are controlled by Lx, we can consider the set of kj as part of a continuum of real values given as k, and we can analyze these results accordingly. It follows that unstable solutions exist only if | kq | > 1, and after a little algebra it implies that the growth/decay rate is given by 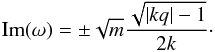 (19)This solution states that there is a wavelength of maximal growth
(19)This solution states that there is a wavelength of maximal growth 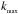 and corresponding growth rate
and corresponding growth rate 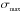 , which are given by
, which are given by  (20)Restoring these resultsin terms of the physical scalings of the disk, this indicates a maximally growing wavelength Λmax with corresponding growth rate Σmax expressed as
(20)Restoring these resultsin terms of the physical scalings of the disk, this indicates a maximally growing wavelength Λmax with corresponding growth rate Σmax expressed as
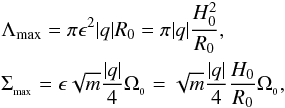 (21)of which the latter is given as
(21)of which the latter is given as 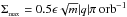 , expressed in units of local disk orbit times (orb = 2π/ Ω0).
, expressed in units of local disk orbit times (orb = 2π/ Ω0).
5. Discussion
The analysis developed in Sect. 4 is an improvement over previous ones reported in the literature (namely NGU13 and BL15). Below we itemize some relevant observations regarding this analysis.
-
1.
In the numerical experiments reported in NGU13, it is shown that in model disks where ϵ = 0.05 and q = −1, the growth rate of the perturbation kinetic energy during the early phase (between 10 and 25 orbits of the inner disk) of the growing VSI is about 0.25 orb-1 (see righthand panel of Fig. 1 of NGU13). Closer inspection of the dynamical response during this phase (see Fig. 3 of NGU13) primarily shows a breathing mode character in the vertical velocity. The radial wavelength of the response near the left boundary indicates a size of about 0.009R0. (This corresponds to approximately 17 grid points, resolving the fastest growing radial mode.) According to the theory developed in the previous section, the radial scale and growth rate of the fundamental breathing mode (FBM, m = 2) is given by Eq. (21), which predicts Λmax ≈ 0.0079R0, together with Σmax ≈ 0.11 orb-1. However, the growth rate in the kinetic energy is equal to 2Σmax ≈ 0.22 orb-1. These predictions, based on this improved approximation, compare favorably with the results of the numerical simulations.
-
2.
Similarly, for the same simulation reported in NGU13, after about 25 orbit times the simulations indicate slower growth, and the corresponding figures indicate that, in this latter phase, the disk response is primarily that of the FCM. For the FCM with k as given, the theory predicts a growth rate in the kinetic energy of about 2Σmax(m = 1) ≈ 0.15 orb-1, which approximately matches the decelerated growth seen in the kinetic energy growth rates displayed in Fig. 1 of NGU13.
-
3.
The analysis developed here, using the solution ansatz in Eq. (12), only captures the essence of the low-order body modes and cannot say anything about the surface modes. This is because no vertical boundary conditions are applied. However, based on our reflections in Sect. 3 regarding the kinetic energy density content of these modes, the surface modes are probably ephemeral, with no significant dynamical effect upon the development of the VSI in the bulk interior, where most of the disk inertia is contained.
-
4.
Despite the improved theoretical construction embodied in the ansatz of Eq. (12), especially in relation to the correct behavior predicted for a fastest growing radial mode, the theory still indicates unbounded growth as the vertical node number sm increases. Is this indicative of a profound flaw in the ansatz or is it a real effect? Based on our reflections upon the lack of energy contained in high-order body modes and surface modes (Sect. 3), it is possible that the theoretical predictions are actually valid, and that, despite the unbounded growth predicted for increasing m, the main instability and turbulent development in nonlinear calculations is driven primarily by the fundamental breathing and corrugation modes. The concomitant fast-growing high-order body modes and surface modes likely have little effect upon the overall development of the VSI primarily because they contain so little energy in comparison to the fundamental modes.
-
5.
We have compared the energy contained in each mode assuming a white-noise spectrum in the initial velocity field. Because the density field decays like a Gaussian in the vertical, the relative energy content in modes with many nodes in the vertical is shown to be very small. Just as the system evolves into the turbulent regime, so too will the corresponding energy/velocity spectrum and the relative energy content contained in each mode. Given the behavior observed in the numerical simulations reported in the literature to date, whereby energy appears to drain into low-order (vertical) m modes through nonlinear processes, the assumption and discussion of the modal energy content taking on a white spectrum in the velocity field is a conservative assumption and gives us an upper bound as to the real energy content in a simulation of well-developed turbulence. Of course, the meaning and physical structure of the linear modes will also probably change into the nonlinear regime, since the basic state upon which they are constructed also changes as the system evolves into the nonlinear regime.
-
6.
Related to the previous point, we believe that the VSI develops robustly and independently of the high-order and surface modes − even if artificial boundary conditions are emplaced on the upper and lower parts of a numerically modeled disk. This will not be true if, by conspiracy, most of the initial energy is placed in these same high-order modes and surface modes. This would be like stirring the low density parts of the disk with very large velocity perturbations, a scenario hard to imagine for a realistic disk. We agree with BL15 when they say that adding a bit of artificial viscosity, or possibly a sponge (an artifice commonly used in atmosphere GCMs) should either erase or strongly diminish these modes from a numerical calculation. We note that in both numerical experiments of NGU13 and Stoll & Kley (2014), the velocity fields are shown as timed snapshots of the instability as it develops, and they show a strong initial development in the velocity field near the boundaries that is primarily due to the fast growth rate of the surface modes. Nevertheless, the kinetic energy densities contained in disturbances high up in the atmosphere are diminished by a factor of e-12, as a result of the vanishingly small densities up there. It is hard to imagine that the ensuing instability within the bulk of the disk is dependent upon these surface modes and we view them as inconsequential as far as the long-term development of the VSI is concerned, including its aggregate turbulent transport. This can be verified by new numerical experiments in which, for instance, one replaces the upper hard boundary by a sponge or something similar.
-
7.
In simulations, the VSI manifests itself as very short radial wavelength disturbances. BL15 have suggested that this trend may be interpreted as the radial scale of the instability is being controlled by the action of viscosity. If this is the case, then the length scale of the fastest growing mode ought to change when the actual physical viscosity is lowered or when the effective numerical viscosity is reduced. We ran a very high resolution simulation that replicated the results displayed in Fig. 11 of NGU13, but with three times as many grid points in the radial direction (all other quantities remained fixed). These simulations were controlled by numerical viscosity alone and, because of this, an increased resolution effectively lowers the associated numerical dissipation. Essentially, we find no difference between these high resolution runs and the aforementioned results in Fig. 11 of NGU13. Furthermore, we confirm that during the early phases of the linear instability, the FBM gets expressed first, as predicted by theory.
-
8.
The results of the previous section show that enforcing boundary conditions at the inner and outer radial positions controls the growth of the VSI and selects for a fastest growing radial structure. As such, we see the unbounded growth rates resulting from the radial traveling wave ansatz (Sect. 2) as the result of the ansatz itself, which (we contend) is inappropriate to describe the dynamics in simulations with boundaries, and is not a result of a breakdown in the validity of the assumptions underpinning the equation set (1) to (4), namely the approximation of radial geostrophy of Eq. (1).
This last point naturally begets the following question: what are the appropriate boundary conditions to use in such disk models? How robust is the VSI to different radial boundary conditions, and how do these vouch for the true conditions of protoplanetary disk dead zones?
As observed by Urpin (2003) and Arlt & Urpin (2004), the local growth rates of the VSI scale approximately by ϵΩ0. While it has not yet been theoretically established to what degree the VSI is active in disk regions that also support the MRI, it is worthwhile noting that the growth rate of the VSI (when active in the absence of the MRI) is a factor of ϵ slower than the MRI underscoring the differing timescales of the two instabilities. Furthermore, there is also a disparity in the length scales on which the two instabilities operate, since the MRI is dynamically more potent on vertical disturbances with length scales that are comparable to the scale height H0, together with very little if no radial structure, whereas the VSI requires very short radial scales, ~ϵH0. It is quite conceivable that the two may operate concurrently in a given disk section, but so far there are no theoretical studies illustrating how the one modifies the other when they transition into the nonlinear regime, either separately or together.
The character of the turbulent state achieved by the VSI is different than in traditional turbulent cascades. Preliminary indications of the turbulent development of the VSI (NGU13, Stoll & Kley 2014, aforementioned unpublished studies) point to a complex expression including quasi-steady vertical vortices, as well as radially alternating vertical velocity fields with aperiodic interfacial roll-up, as well as attendant small scale unsteady fluctuations concentrated at about one scale height from the midplane. An analysis of the achievable outcome states of the VSI remains to be examined.
If the calculation domain is on a uniform rectangular grid, a sure way to guarantee an unambiguous determination of eigenvalues and eigenmodes is to apply a finite difference discretisation of Eq. (6). With Nz and Nx discretisation points in the vertical direction and radial direction, the resulting eigenvalue system requires inversion of (NxNz) × (NxNz) sized (relatively) sparse matrices. High resolution in both the radial and vertical direction are desirable and, therefore, Nz ≈ 150, Nx ≈ 100 are preferred resolutions, which means constructing matrices that are prohibitively large to invert and challenging to reconfigure into known sparse matrix formulations.
Acknowledgments
The authors express appreciation to A. Barker and H. Latter for their comments and views regarding several points of debate presented in this paper, when an earlier version of this work appeared on ArXiv. We also thank the anonymous referee who suggested a number of additional points for discussion, and we thank K. Shariff and J. Cuzzi (NASA Ames Research Center) for providing an internal review of this manuscript. Elements found in the discussion of this work used the DiRAC Complexity system, operated by the University of Leicester IT Services, which forms part of the STFC DiRAC HPC Facility (www.dirac.ac.uk). This equipment is funded by BIS National E-Infrastructure capital grant ST/K000373/1 and STFC DiRAC Operations grant ST/K0003259/1. DiRAC is part of the National E-Infrastructure.
References
- Arlt, R., & Urpin, V. 2004, A&A, 426, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barker, A. L., & Latter, H. N. 2015, MNRAS, 450, 21 (BL15) [NASA ADS] [CrossRef] [Google Scholar]
- Fricke, K. 1968, Z. Astrophys., 68, 317 [NASA ADS] [Google Scholar]
- Goldreich, P., & Schubert, G. 1967, ApJ, 150, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Lubow, S. H., & Pringle, J. E. 1993, ApJ, 409, 360 [NASA ADS] [CrossRef] [Google Scholar]
- McNally, C. P., & Pessah, M. 2015, ApJ, 811, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, R. P., Gressel, O., Umurhan, O. M. 2013, MNRAS, 435, 2610 (NGU13) [NASA ADS] [CrossRef] [Google Scholar]
- Stoll, M. H. R., & Kley, W. 2014, A&A, 572, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Turner, N. J., Fromang, S., Gammie, C., et al. 2014, Protostars and Planets VI, 411 [Google Scholar]
- Urpin, V. 2003, A&A, 404, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Urpin, V., & Brandenburg, A. 1998, MNRAS, 294, 399 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Growth rates, Im(ω), and frequencies, Re(ω), of solutions of Eq. (8) subject to no-normal-flow boundary conditions at z = ± H, where H is in units of scale heights. Top panel: distribution shown for k = 2, and H = 5 (diamonds), and H = 7 (open circles). As H increases, more surface modes become activated and high-order body modes have increased growth rates. In both cases shown, the frequency and growth rates of low-order body modes (labeled m1,m2,m3) remain unchanged. The surface modes generally appear in pairs as indicated by labeling the topmost surface mode with the superscript |
| In the text | |
 |
Fig. 2 Vertical kinetic energy density plots, Ez, plotted for the modes labeled in the top panel of Fig. 1, which corresponds to solutions of Eq. (8) with H = 5 and k = 2. Each corresponding vertical velocity eigenfunction w is normalized, such that |
| In the text | |
 |
Fig. 3 Total vertically integrated vertical kinetic energies |
| In the text | |
 |
Fig. 4 As in Fig. 3 except with H = 7. The power contained both in the surface and high-order body modes is diminished as the atmosphere lid is set farther away. Note that the energy in the low-order body modes remain unchanged, especially the FCM and FBM. |
| In the text | |
 |
Fig. 5 As in Fig. 3, except that H = 8 and k = 5. The diminished energy-carrying capacity of both the surface modes and the high-order body modes when the lid of the atmosphere is made larger and when higher radial resolution modes are considered. The energy of the low-order body modes, especially the FCM, FBM and the first overtone corrugation mode remain unchanged compared to their energies for lower values of H, depicted in the two previous figures. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.