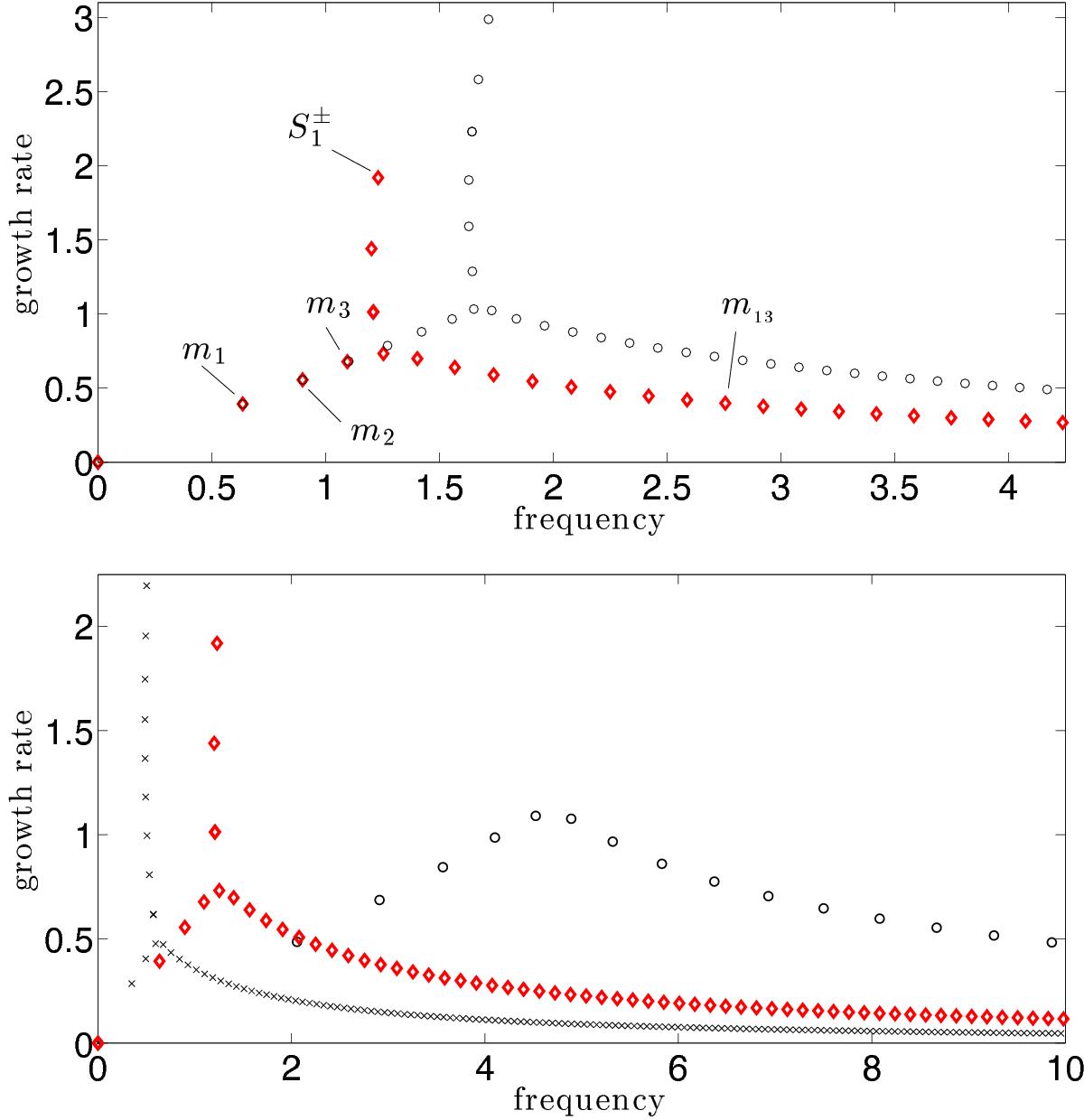
Growth rates, Im(ω), and frequencies, Re(ω), of solutions of Eq. (8) subject to no-normal-flow boundary conditions at z = ± H, where H is in units of scale heights. Top panel: distribution shown for k = 2, and H = 5 (diamonds), and H = 7 (open circles). As H increases, more surface modes become activated and high-order body modes have increased growth rates. In both cases shown, the frequency and growth rates of low-order body modes (labeled m₁,m₂,m₃) remain unchanged. The surface modes generally appear in pairs as indicated by labeling the topmost surface mode with the superscript . This panel confirms the trends reported by BL15. Bottom panel: distribution of the complex frequencies shown for differing values of k with fixed H = 5: k = 5 (crosses), k = 2 (diamonds), k = 0.5 (open circles). The growth rates increase without bound as k is decreased, with the same trend identified in the problem with no vertical boundaries as found in Expression (10). As k is increased, the number of surface modes increases, including the maximum growth rates which also confirms the results reported in BL15.