EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 586 (February 2016) A&A, 586 (2016) A147 Full HTML
Free Access
Issue
A&A
Volume 586, February 2016
Article Number A147
Number of page(s) 7
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/201525930
Published online 10 February 2016

© ESO, 2016

1. Introduction

Binary systems have been observed and characterized for almost 100 years (see, e.g., Aitken 1935). Since the seminal works by Duquennoy & Mayor (1991) and Fischer & Marcy (1992), the properties of stellar binaries have also been widely studied. One of the most interesting parameters of a binary system is the mass ratio q = M2/M1, defined as the ratio of the secondary (M2) over the primary mass (M1). The distribution of q values for a sample of binaries is the companion mass-ratio distribution (CMRD). Several surveys in the past decades focused on the detection of stellar binaries with the purpose of characterizing the occurrence of companions and their mass distribution both in the field (e.g., Raghavan et al. 2010; Janson et al. 2012) and in star-forming regions (e.g., Patience et al. 2002). Reggiani & Meyer (2013), in an update of Reggiani & Meyer (2011), have shown that in the field the CMRD is consistent with being universal, independent of primary mass and separation in the range covered by the observations, and can be fit by a single power-law slope dN/ dq ∝ qβ, with β = 0.25 ± 0.29. In addition, N-body simulations suggest that the CMRD is only modestly affected by dynamics, even in dense clusters, as opposed to the semimajor axis (SMA) distribution (Parker & Reggiani 2013). The CMRD therefore seems to be a good diagnostic for different star formation mechanisms.

While the distributions of masses and orbital parameters are very well established for stellar companions, the shape of the companion mass function (CMF) and of the SMA distribution in the substellar and planetary mass regime is still poorly understood. The more than 500 extrasolar planets discovered with the radial velocity (RV) method allowed astronomers to fit power-law slopes to the mass and SMA distributions for planets with masses between 0.3–10 MJupiter and within ~3 AU (see, e.g., Fischer & Valenti 2005; Cumming et al. 2008). However, nothing guarantees that the same behavior holds at larger separations or higher masses. Direct imaging is a detection method that allows us to characterize large-separation exoplanets. In the past decade many direct imaging surveys (e.g., Lowrance et al. 2005; Biller et al. 2007; Lafrenière et al. 2007; Chauvin et al. 2010; Heinze et al. 2010; Vigan et al. 2012; Biller et al. 2013; Rameau et al. 2013a; Wahhaj et al. 2013; Chauvin et al. 2015; Brandt et al. 2014a; Bowler et al. 2015) have been carried out to evaluate the occurrence of giant planets in wide orbits (10–500 AU). Other than a few planets (e.g., Kuzuhara et al. 2013; Rameau et al. 2013b) and brown dwarfs (BDs; e.g., Chauvin et al. 2005b; Biller et al. 2010; Mugrauer et al. 2010; Wahhaj et al. 2011; Carson et al. 2013) detected, many surveys found no planetary companions. The null results cannot be used to fit power-laws to the planetary distributions beyond 10 AU. However they suggest a truncation of the planet SMA distribution at a few tens of AU to reproduce the RV statistics below 3 AU (assuming the same power-law slope holds).

Regarding the substellar mass range, BDs were originally proposed as a separate class of objects with intermediate masses between stars and planets. High contrast observations have unambiguously revealed the presence of substellar objects, as companions to nearby stars, as well as BD-BD systems (e.g., Chauvin et al. 2005b; Dupuy & Liu 2011). Some were also found in isolation in the field (e.g., Burgasser et al. 2003). Their existence indicates that the formation mechanisms proposed to form stars (turbulent fragmentation, collapse and fragmentation, disk fragmentation) can actually form objects down to a few Jupiter masses. Star and planet formation mechanisms therefore overlap in the planetary-mass regime. Companions in this mass range could be the lower mass tail of the stellar CMRD as well as the higher mass end of the planet CMF, but they have usually been excluded by the statistical analyses of direct imaging surveys. Different features in the frequency of BD companions and planets as a function of mass and semimajor axis could help distinguish different formation mechanisms (see also Brandt et al. 2014b). Although spectroscopy may help in investigating whether a given detected object formed by one process or another, large surveys could contribute in assessing whether a stellar-like or planet-like formation process dominates the CMF in a given companion mass range.

As a project within the VLT/NaCo large program (hereafter NaCo-LP; P.I. J. Beuzit, Desidera et al. 2015; Chauvin et al. 2015), the work presented in this paper represents the first attempt to place some constraints on the full CMF in the substellar regime. It takes both BDs and planets into account and makes use of the results of most of the direct imaging surveys of solar-type primaries currently available. In Sects. 2 and 3, we present our model for the mass distribution of substellar companions and the Monte Carlo simulation tool that we developed to test our medel. Then, we describe the datasets that we adopted for the analysis (Sect. 4) and the results of the Monte Carlo simulations based on these data (Sect. 5). Finally, we discuss the results in Sect. 6 and summarize the conclusions in Sect. 7.

2. Model for the substellar CMF

Our model for the CMF is based on the hypothesis that both BDs and planets contribute to the substellar mass distribution. In this context, we consider as BDs all objects that, having formed through a stellar-like mechanism, constitute the lower mass tail of the CMRD, assuming that it can be extrapolated into the BD regime as suggested by Metchev & Hillenbrand (2009). We define as planets, instead, all companions that formed in standard planet-formation scenarios and gave rise to the RV measured CMF but extrapolated to larger separations. There are of course some caveats to these assumptions. For instance, we do not take into account how gravitational instability and core accretion differ in the distributions of orbital parameters of planets. The fact that there are multiple binary formation mechanisms and that both planets and BDs migrate makes everything more complicated. In this paper, we propose a simple, but new, model and test whether it works.

Instead of trying to fit the substellar CMF with a single power-law distribution (see, e.g., Brandt et al. 2014b), we assume the overall frequency of substellar companions to be the sum of two contributions as follows: d2NBD=CBD qαBD dlogq e−(loga−logacBD)22 σBD2 dloga,\begin{eqnarray} \label{eq:1} &&{\rm d}^2N_{\rm BD} = C_{\rm BD} \, q^{\alpha_{\rm BD}} \, {\rm d}\log q \, {\rm e}^{-\frac{(\log a-\log a_{c_{\rm BD}})^2}{2\,\sigma_{\rm BD}^2}} \, {\rm d}\log a, \\[3mm] &&{\rm d}^2N_{\rm pl}= C_{\rm pl} \, m^{\alpha_{\rm pl}} \, {\rm d}\log m \, a^{\beta_{\rm pl} } \,{\rm d} \log a \label{eq:2} \end{eqnarray}for BDs and planets, indicated with the BD and pl subscripts, respectively. The parameter q is the mass ratio, as defined in Sect. 1. The parameters αBD,pl and βpl are the exponents of the power-law mass and SMA distributions (c.f. Cumming et al. 2008), whereas acBD and σBD are the mean and standard deviation of the BD separation distribution, assuming it is log-normally distributed as for solar-type primaries (see, e.g., Raghavan et al. 2010). The parameters CBD and Cpl are normalization constants that can be obtained from measurements of the BD and planet frequency fBD,pl over a range of masses and semimajor axes.

We assume values for the parameters that we think are appropriate for solar-type primaries, typical of the dataset that we use to test this model. Our choices are presented in Table 1. Some of these values are measurement based, and some are extrapolations (e.g., the CMRD in the BD regime). The notes in Table 1 explain the extrapolations that have been made. The BD distribution is normalized to the companion frequency, fBD, measured by Raghavan et al. (2010) for stellar companions. If extrapolated to the BD mass regime (q = 0.012−0.072), it gives 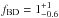fBD=1-0.6+1\hbox{$f_{\rm BD}=1^{+1}_{-0.6}$}% between 28–1590 AU, which is in agreement with the BD companion fraction presented by Metchev & Hillenbrand (2009), 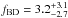fBD=3.2-2.7+3.1\hbox{$f_{\rm BD}=3.2^{+3.1}_{-2.7}$}%, over the same mass and separation ranges.

Table 1

Planet and BD distributions: model values.

Moreover, several physical mechanisms or observational constraints place upper and lower limits to the maximum and minimum mass (mmaxBD,pl, mminBD,pl) and separation (amaxBD,pl, aminBD,pl) for these distributions. For our analysis, we assume the following:

  • The minimum (mminBD) and maximum (mmaxBD) masses for the BD mass distribution are given by the opacity limit for fragmentation (Low & Lynden-Bell 1976) and the hydrogen burning limit (e.g., Burrows et al. 2001).

  • The minimum (aminBD) and maximum (aminBD) semimajor axes for the BD distribution can be set to exclude less than 1% of companions from the measured stellar separation distribution (e.g., Raghavan et al. 2010).

  • The maximum mass (mmaxpl) for the planet mass distribution is constrained by the disk mass (e.g., ≤10% of the mass of the star).

  • The maximum separation (amaxpl) for the planet separation distribution is possibly set by an outer truncation radius rcutoff (as suggested by previous direct imaging surveys), as long as planet-planet scattering does not significantly affect the distribution. Such a truncation radius is treated as a free parameter in our analysis.

The combined CMF in the substellar regime for this choice of parameters and assuming a 1 M⊙ star is shown in Fig. 1. We have assumed that the opacity limit for fragmentation sets a lower limit to the BD mass distribution, creating a discontinuity in the CMF. The opacity limit for fragmentation occurs when the gravitational potential energy that is released during the collapse of a molecular cloud core exceeds the energy that can be radiated away (Low & Lynden-Bell 1976). Theories of core fragmentation predict that fragmentation cannot take place at densities higher than 10-13 g cm-3, corresponding to a minimum mass of a few Jupiter masses (e.g., 1–10 MJupiter; Low & Lynden-Bell 1976; Silk 1977; Boss 2001). A challenging observational goal would be to test this aspect of our model. We assumed a minimum mass for BDs of 5 MJupiter.

thumbnail Fig. 1

Combined substellar CMF. The discontinuity at log M/M⊙ = −2.3 is due to the opacity limit for fragmentation that set a minimum mass for objects formed through core fragmentation. The minimum mass is assumed to be 5 MJupiter in our model.

The analysis presented does not take the uncertainties on the model parameters described in Table 1 into account, as this would be computationally too expensive. This aspect can certainly be improved in the future. Furthermore, better constraints on the BD and planet orbital parameter distributions from observations, as well as predictions from core accretion or gravitational instability theories will allow us to further test the model.

Previous studies have shown a dependence of the planet properties (e.g., frequency) on stellar properties (e.g., mass and metallicity, Johnson et al. 2010), however the analysis of the influence of the star properties on this model goes beyond the scope of the paper as our sample is restricted to a narrow range of primary masses. Future observations will allow us to study the dependence of the combined substellar CMF as a function of stellar mass.

3. Methodology

In this section we present the methodology that we developed to test the model for the substellar CMF presented in Sect. 2. We created a Monte Carlo simulation tool with the aim of predicting the frequency of planets and BDs around a given list of targets and the probability of detection in a given survey, assuming the combined CMF. The probability of the existence of substellar companions around a star depends on their mass and SMA distributions according to our model. The probability of detecting them instead depends on the parameters of the companions (mass, separation, eccentricity, inclination), on the properties of the star (age, distance, mass), and on the sensitivity (and contrast limits) of the instrument used.

The first step in our methodology is therefore to calculate the expected number of existing companions, both BDs and planets, per star. This quantity is generally expressed as the expectation value of the number of companions per star in a given range of masses and separations 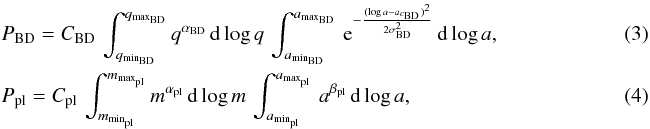\begin{eqnarray} &&\label{eq:3}P_{\rm BD}= C_{\rm BD} \, \int_{q_{\rm min_{\rm BD}}}^{q_{\rm max_{\rm BD}}}q^{\alpha_{\rm BD}} \, {\rm d}\log q \, \int_{a_{\rm min_{\rm BD}}}^{a_{\rm max_{\rm BD}}} \, {\rm e}^{-\frac{(\log a-a_{c_{\rm BD}})^2}{2 \sigma_{\rm BD}^2}} \, {\rm d}\log a,\\ &&\label{eq:4}P_{\rm pl}=C_{\rm pl} \, \int_{m_{\rm min_{\rm pl}}}^{m_{\rm max_{\rm pl}}}m^{\alpha_{\rm pl}} \, {\rm d}\log m \, \int_{a_{\rm min_{\rm pl}}}^{a_{\rm max_{\rm pl}}} \, a^{\beta_{\rm pl}} \, {\rm d}\log a, ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{eqnarray}where the integral limits indicate the mass/mass ratios and semimajor axis ranges of interest for BDs (BD subscript) and planets (pl subscript). The parameters qminBD and qmaxBD correspond to the mass ratios for mminBD and mmaxBD, respectively. The other parameters are described in Sect. 2.

Once we have calculated the average number of planets and BDs per star in the mass and semimajor axis ranges that we are interested in, we run N simulations of the survey, in which every target star is randomly assigned a number of planets and a number of BDs, based on Poisson statistics with mean Ppl and PBD for planets and BDs, respectively. In case the Poisson probability returns a number smaller than 0.5, the number of planets or BDs for the given star is zero. However, if the star turns out to have one or more planets (or BDs), the mass and semimajor axis for each one of them is randomly selected from the input planet (or BD) distributions (see Sect. 2). The eccentricity is randomly selected from the Jurić & Tremaine (2008) distribution, of the form P(ϵ) = ϵ × e[−ϵ2/ 2σ2] with σ = 0.3, and an inclination is randomly assigned. The time spent on the orbit, as a function of orbital location, is explicitly taken into account as a function of orbital parameters when converting the semimajor axis into a projected separation in AU.

Once every simulated planet or BD is assigned all its orbital properties, we compare its mass and separation with the sensitivity limits of the survey for a specific target to determine which planets or BDs could have been detected. Generally, the sensitivity limits are given for each star as a contrast curve, meaning apparent magnitude (or contrast) as a function of the angular separation. To perform a direct comparison of the simulated properties with the contrast curves, we use a family of substellar evolutionary models (e.g., COND models; Baraffe et al. 2003) and the information about distance and age of the stars to transform companion masses and projected separations into apparent magnitudes and angular separations. If the combination of magnitude and separation for a given companion falls below the sensitivity limits for the target, the companion is not detected.

At the end of the N runs of the artificial survey, we know how many planets or BDs we have created and how many we would have detected in each simulation. Finally, we can define the total probability for the survey of having found zero, one, or more objects, given the model that we assumed, and can compare this probability with the real outcome of the survey. Examples of applications of this tool are presented in Sect. 5. Here we show the results obtained by using the COND evolutionary models. Dupuy et al. (2014) present evidence for a substellar luminosity problem in the predictions from evolutionary models. The predicted luminosities from which we estimate planet and BD masses could in fact be underestimated (Dupuy et al. 2014), which would make our survey results more constraining regardless of the frequency of planetary mass objects. Although cloudless, the COND models show the smallest discrepancy with the observed luminosities compared to the DUSTY models (Chabrier et al. 2000) and the Saumon & Marley (2008) hybrid models. The DUSTY models might be more appropriate for some of the higher mass (and presumably hotter) BDs that we simulate, however, the simulations with both families of evolutionary models lead to consistent results.

thumbnail Fig. 2

Detection probability for the NaCo-LP observed sample for rcutoff = 100, 30, 20 AU (from left to right).

4. Dataset

The dataset that we used to test the model for the substellar CMF described in Sect. 2 consisted of the targets of the NaCo-LP (Chauvin et al. 2015; Desidera et al. 2015), a large observing program (ESO: 184.C-0157) in the context of the VLT/SPHERE scientific preparation. This program is a direct imaging survey providing a homogeneous statistically significant study of the occurrence of giant planets and BDs in wide (5–500 AU) orbits around young, nearby stars. It focused on a carefully selected sample, chosen with declinations δ ≤ 25°, ages t ≤ 200 Myr, distances d ≤ 100 pc, R-band brightnesses R ≤ 9.5, and the exclusion of spectroscopic binaries and visual binaries with separation <6′′. The sample was initially comprised of 84 targets, none of which had been observed before in a planet survey. These stars were then observed with VLT/NaCo in the H band between end 2009 and 2013 for a total of 16.5 nights. A complete description of the sample and its properties (distance, age, mass) can be found in Desidera et al. (2015). The summary of the program and of the observations is provided in Chauvin et al. (2015). As a result of the campaign, no substellar companions were detected around the targets. For 51 targets the observations were complete up to 300 AU and they constitute the statistical sample presented in Sect. 6.1 of Chauvin et al. (2015). Once only FGK stars are considered, the sample reduces to 47 targets. In the present work, we used these 47 objects to place some constraints on the BD and planet populations together. For simplicity we refer to the sample as NaCo-LP observed sample. The statistical analysis on this sample regarding the constraints on the planet distributions only is presented in a separate paper (Vigan et al., in prep.).

We complemented the observed sample with similar targets observed in previous surveys (not re-observed within the NaCo-LP) for which reduced data and detection limits were available: Lowrance et al. (2005), Masciadri et al. (2005), Biller et al. (2007), Kasper et al. (2007), Lafrenière et al. (2007), Chauvin et al. (2010), Heinze et al. (2010), Vigan et al. (2012), Rameau et al. (2013a), and Brandt et al. (2014a). We included in the so-called full sample targets, which share the same range of spectral types (from early-F to late-K) and distance (≤100 pc) as the NaCo-LP stars, for a total of 152 objects. No age or declination limit was applied in this case, while we adopted the same selection criteria as for NaCo-LP targets concerning binarity. Ages and other stellar parameters were redetermined for the full sample using the procedures described in Desidera et al. (2015) for the NaCo-LP sample. Full details on the revised stellar properties will be provided in (Vigan et al., in prep.).

While the outcome of the NaCo-LP was a null result, substellar companions have been found around four targets in the archive sample:

  • GSC 08047-00232 B

    is a 25 ± 10MJupiter mass BD with a derived spectral type M9.5 ± 1 (Chauvin et al. 2005a) at a projected separation of 278 AU. It is a probable member of the Tucana-Horologium association with an age of 10–50 Myrs.

  • AB Pic b

    is a ~13 MJupiter mass object at the planet/BD boundary (Chauvin et al. 2005b) and separation of 275 AU. It is also member of the Tucana-Horologium association.

  • HD 130948 BC

    is a BD binary system, companion to HD 130948 (Potter et al. 2002). The total mass was estimated to be 0.1095 ± 0.0022M⊙ (Dupuy & Liu 2011) and the age 0.93 Gyr.

  • PZ Telescopii B

    is a BD companion with a mass of 24–40 MJupiter at a projected separation of ~15 AU (Biller et al. 2010; Mugrauer et al. 2010). It is a member of the β Pic moving group.

The full sample (NaCo-LP + archive) is therefore comprised of 199 nearby (d ≤ 100 pc) solar-mass stars that have been observed in deep imaging with sensitivity down to planetary mass companions.

5. Monte Carlo simulation results

To test our model for the substellar CMF, we used the tool described in Sect. 3 to compare our predictions with the set of data presented in Sect. 4, beginning with the NaCo-LP observed sample and then with the full sample.

5.1. Results from the NaCo-LP observed sample

Concerning the 47 targets observed within the NaCo-LP, we initially ran 3000 Monte Carlo simulations of the survey, with the set of parameters shown in Table 1 and with an outer radius cutoff for the planet separation distribution of rcutoff = 100 AU, to quantify how likely the null result of the survey would be according to this model. In the 3000 simulations, 410 847 planets and 3714 BDs were created, of which we detected 5856 and 1527, respectively. The overall probability distribution of detections is shown in Fig. 2a. In 9% of the realizations, our survey found zero companions, while in 19% of the cases it found one and 71% of the time it found two or more planets or BDs. We then verified the dependence of this result on the choice of rcutoff. We repeated the set of 3000 Monte Carlo simulations for both rcutoff = 20 AU and rcutoff = 30 AU, but leaving all the other parameters unchanged. In this case, the probability of a null results is 53% and 45% for rcutoff = 20 AU and 30 AU, respectively (see Fig. 2). This result indicates that introducing a lower value for the outer radius cutoff better reproduces the outcome of the observations, assuming that the mass and SMA distributions from RV surveys (Cumming et al. 2008) are a good representation even at larger separations. However, the complete sample is needed to put more stringent constraints.

5.2. Results from the full sample

In the case of the full sample (199 targets), we repeated the same sets of simulations that we carried out for the NaCo-LP observed dataset. Besides the size, the main difference between the NaCo-LP subsample and the complete dataset is in the outcome of the observations.

thumbnail Fig. 3

Detection probability for the full sample for rcutoff = 100, 30, 20 AU (from left to right).

In this case, because of the detection of the BD companions listed in Sect. 4, we are interested in the probability of detecting three substellar objects. We do not consider the tight BD binary HD 130948 BC among the detections. It constitutes in fact a hierarchical triple system with the sun-like star HD 130948 A. This kind of system would generally contribute to the CMRD as two different binaries with masses MA and MBC, where MBC = MB + MC, and MB and MC, respectively. For HD 130948, in both binary systems either the primary or the secondary components would be outside the mass ranges of interest of this study.

Analogous to what has been done for the NaCo-LP observed sample, we simulated 3000 artificial observations of the targets in the full sample for the same three values of rcutoff = 20, 30 and 100 AU. The detection probability distributions are shown in Fig. 3. The probability of detecting three objects is 2%, 25%, and 19% for rcutoff = 100, 30, and 20 AU, respectively. The results from the full sample are similar to what was obtained for the NaCo-LP dataset only. The model described in Sect. 2 cannot be ruled out by the observations and smaller truncation radii give a better agreement.

To quantify this statement and assess which planet distributions could instead be excluded, we explored the SMA power-law index (βpl) vs. outer truncation radius (rcutoff) parameter space. Having fixed the BD mass and SMA distributions, we varied βpl from 0 to 1, with steps of 0.1, and rcutoff from 10 to 200 AU with steps of 10 AU. For each pair of βpl and rcutoff, we ran 300 simulations of the survey and we calculated the probability of detecting up to three objects. Regardless of the choice of values for βpl and rcutoff, every simulation was normalized to match the RV statistics within 3 AU. Figure 4 shows the probability of detecting up to three substellar companions as a function of βpl and rcutoff. Each grid cell point represents the 300 Monte Carlo simulations of the survey. In order to estimate confidence levels, the overall probability is normalized to be 1 within the figure. The confidence level shown in Fig. 4 indicates where the probability is lower than 0.3%. The region above the line therefore can be ruled out at a 99.7% confidence. For example, in the case of βpl = 0.39, as suggested by RV measurement (Cumming et al. 2008), all models with rcutoff ≳ 100 AU can be ruled out at a >3σ confidence.

thumbnail Fig. 4

Probability of our surveys detecting three substellar companions, as a function of the power-law slope of the SMA distribution βpl, and the outer radius cutoff of the SMA distribution. The overall probability is normalized to be 1 within the figure. The region above the line can be ruled out at 99.7% confidence.

6. Discussion

The results presented in Sect. 5 show that the current measurements of the occurrence of planets and BDs in wide orbits around solar-type stars do not rule out the model for the substellar CMF, presented in Sect. 2. The Kolmogorov-Smirnov test (KS test) between the masses of the detected BDs and the proposed CMF returns a probability PKS> 45%, for all choices of truncation radii. This probability does not reject the null hypothesis that they come from the same parent population. If the RV statistics (Cumming et al. 2008) provide a good estimate of the normalization and the power-law slopes of the planet distributions, an outer truncation radius of at most 100 AU is necessary to reproduce the observations (at a 99.7% confidence). These constraints on the planet population are consistent with previous survey analyses (Biller et al. 2007; Nielsen & Close 2010; Chauvin et al. 2010).

In past years, the observed dearth of close (≤5 AU) BD companions to solar-mass stars (e.g., Marcy et al. 2000), also known as the “brown dwarf desert”, has been used as evidence for a separate formation mechanism for BDs with respect to stars. Grether & Lineweaver (2006), in an attempt to quantify the relative number of stellar companions, planets, and BDs in close orbit (period ≤5 yrs) around nearby sun-like stars, found a paucity of objects in the BD mass regime compared to planetary and stellar companions, with the driest part of the “desert” being at 31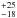+25-18\hbox{$^{+25}_{-18}$}MJupiter. Sahlmann et al. (2011) also measured the CMF for close BD companions to solar-type stars and found a minimum in the distribution between 25 and 45 MJupiter and claimed to have detected the high mass tail of the planet mass distribution.

Based on our analysis, the mass distribution of substellar companions is consistent with a superposition of the planet CMF and the stellar CMRD extrapolated into the BD mass regime provided that the planet distribution is truncated at a few tens of AU. This suggests that objects from the hydrogen burning limit down to a few Jupiter masses may still form as stellar companions, without the need of introducing a separate formation mechanism. From a theoretical point of view, recent turbulent fragmentation models have also explained the binary BD properties in terms of a single core fragmentation mechanism (Jumper & Fisher 2013). The paucity of companions in the mass range 10–50 MJupiter even at large (>10 AU) separations would naturally arise from the superposition of the two mass distributions (see Fig. 1). On the observational side, some planetary-mass companions identified by direct imaging in young clusters show evidence for active accretion and are surrounded by massive disks (see, e.g., Seifahrt et al. 2007; Bowler et al. 2011; Joergens et al. 2013; Zhou et al. 2014). This also argues for an extension of the stellar/BD formation mechanisms in the planetary-mass regime. Our results are also consistent with the conclusions of Brandt et al. (2014b) that some of the so-far directly imaged exoplanets could have formed by either core or disk fragmentation and constitute the low-mass tail of the BD mass distribution.

In the next few years, new instruments, such as the VLT Spectro-Polarimetric High-contrast Exoplanet REsearch (VLT/SPHERE) or the Gemini Planet Imager (GPI), will enable us to find new planetary-mass companions. To what extent large surveys with these new instruments will help us constrain the distributions of orbital parameters still remains to be seen. With the next generation of extremely large telescopes instead (e.g., the European Extremely Large Telescope, E-ELT), our understanding of planet statistics will make a huge step forward. It will be possible to directly measure the shape of the substellar CMF and locate with higher precision the minimum even for wide companions. In this context, it will be interesting to study how the distribution of companion masses in the substellar regime varies not only with respect to separation but also as a function of primary mass.

7. Conclusions

In this paper we propose a simple model for the substellar mass spectrum, as a combination of the planet CMF and an extrapolation of the stellar CMRD into the BD mass regime. Taking advantage of the largest sample to date of solar-type stars observed with direct imaging, we ran Monte Carlo simulations to compare predictions of our model with the observations from the NaCo-LP and archival data.

We conclude that the outcome of the direct imaging surveys is consistent with a superposition of the CMF derived by RV measurements (αpl = −0.31 and βpl = 0.39) and of the stellar CMRD down to 5 MJupiter, as long as rcutoff ≲ 100 AU (99.7% confidence). When all the other parameters are fixed, some combinations of βpl–rcutoff can be ruled out by the observations with a 99.7% confidence. The proposed CMF has a minimum between 10–50 MJupiter, in agreement with the results from RV observations (Sahlmann et al. 2011). The KS test probability between this CMF and the masses of the three detections is PKS> 45%, and does not reject the hypothesis that the data were drawn from the same distribution as the model. In this picture the so-called “BD desert” would naturally arise from the shape of the mass distribution, without having to introduce any different formation mechanism for BDs.

Future observations may allow us to measure directly the shape of the distribution and the precise location of the minimum in the substellar mass spectrum.

Acknowledgments

We are grateful to the referee for useful comments. Part of this work has been carried out within the frame of the National Centre for Competence in Research PlanetS supported by the Swiss National Science Foundation (SNSF). M.R. acknowledges funding from the European Research Council Under the European Union’s Seventh Framework Programme (ERC Grant Agreement No. 337569) and from the French Community of Belgium through an ARC grant for Concerted Research Action. M.R., S.P.Q., E.B., J.H., and M.R.M. acknowledge the financial support of the SNSF. JC is supported by the U.S. National Science Foundation under Award No. 1009203. S.D., A.L.M., R.G., and D.M. acknowledge partial support from PRIN-INAF 2010 “Planetary systems at young ages and the interactions with their active host stars”. A.Z. acknowledges support from the Millennium Science Initiative (Chilean Ministry of Economy), through grant “Nucleus RC130007”.

References

  1. Aitken, R. G. 1935, The binary stars (New York and London: McGraw-Hill book company, inc.) [Google Scholar]
  2. Baraffe, I., Chabrier, G., Barman, T. S., Allard, F., & Hauschildt, P. H. 2003, A&A, 402, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Biller, B. A., Close, L. M., Masciadri, E., et al. 2007, ApJS, 173, 143 [NASA ADS] [CrossRef] [Google Scholar]
  4. Biller, B. A., Liu, M. C., Wahhaj, Z., et al. 2010, ApJ, 720, L82 [NASA ADS] [CrossRef] [Google Scholar]
  5. Biller, B. A., Liu, M. C., Wahhaj, Z., et al. 2013, ApJ, 777, 160 [NASA ADS] [CrossRef] [Google Scholar]
  6. Boss, A. P. 2001, ApJ, 551, L167 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bowler, B. P., Liu, M. C., Kraus, A. L., Mann, A. W., & Ireland, M. J. 2011, ApJ, 743, 148 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bowler, B. P., Liu, M. C., Shkolnik, E. L., & Tamura, M. 2015, ApJS, 216, 7 [NASA ADS] [CrossRef] [Google Scholar]
  9. Brandt, T. D., Kuzuhara, M., McElwain, M. W., et al. 2014a, ApJ, 786, 1 [NASA ADS] [CrossRef] [Google Scholar]
  10. Brandt, T. D., McElwain, M. W., Turner, E. L., et al. 2014b, ApJ, 794, 159 [NASA ADS] [CrossRef] [Google Scholar]
  11. Burgasser, A. J., McElwain, M. W., & Kirkpatrick, J. D. 2003, AJ, 126, 2487 [NASA ADS] [CrossRef] [Google Scholar]
  12. Burrows, A., Hubbard, W. B., Lunine, J. I., & Liebert, J. 2001, Rev. Mod. Phys., 73, 719 [Google Scholar]
  13. Carson, J., Thalmann, C., Janson, M., et al. 2013, ApJ, 763, L32 [NASA ADS] [CrossRef] [Google Scholar]
  14. Chabrier, G., Baraffe, I., Allard, F., & Hauschildt, P. 2000, ApJ, 542, 464 [NASA ADS] [CrossRef] [Google Scholar]
  15. Chauvin, G., Lagrange, A.-M., Lacombe, F., et al. 2005a, A&A, 430, 1027 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Chauvin, G., Lagrange, A.-M., Zuckerman, B., et al. 2005b, A&A, 438, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Chauvin, G., Lagrange, A.-M., Bonavita, M., et al. 2010, A&A, 509, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Chauvin, G., Vigan, A., Bonnefoy, M., et al. 2015, A&A, 573, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Cumming, A., Butler, R. P., Marcy, G. W., et al. 2008, PASP, 120, 531 [CrossRef] [Google Scholar]
  20. Desidera, S., Covino, E., Messina, S., et al. 2015, A&A, 573, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Dupuy, T. J., & Liu, M. C. 2011, ApJ, 733, 122 [NASA ADS] [CrossRef] [Google Scholar]
  22. Dupuy, T. J., Liu, M. C., & Ireland, M. J. 2014, ApJ, 790, 133 [NASA ADS] [CrossRef] [Google Scholar]
  23. Duquennoy, A., & Mayor, M. 1991, A&A, 248, 485 [NASA ADS] [Google Scholar]
  24. Fischer, D. A., & Marcy, G. W. 1992, ApJ, 396, 178 [NASA ADS] [CrossRef] [Google Scholar]
  25. Fischer, D. A., & Valenti, J. 2005, ApJ, 622, 1102 [NASA ADS] [CrossRef] [Google Scholar]
  26. Grether, D., & Lineweaver, C. H. 2006, ApJ, 640, 1051 [NASA ADS] [CrossRef] [Google Scholar]
  27. Heinze, A. N., Hinz, P. M., Kenworthy, M., et al. 2010, ApJ, 714, 1570 [NASA ADS] [CrossRef] [Google Scholar]
  28. Janson, M., Hormuth, F., Bergfors, C., et al. 2012, ApJ, 754, 44 [NASA ADS] [CrossRef] [Google Scholar]
  29. Joergens, V., Bonnefoy, M., Liu, Y., et al. 2013, A&A, 558, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Johnson, J. A., Aller, K. M., Howard, A. W., & Crepp, J. R. 2010, PASP, 122, 905 [NASA ADS] [CrossRef] [Google Scholar]
  31. Jumper, P. H., & Fisher, R. T. 2013, ApJ, 769, 9 [NASA ADS] [CrossRef] [Google Scholar]
  32. Jurić, M., & Tremaine, S. 2008, ApJ, 686, 603 [NASA ADS] [CrossRef] [Google Scholar]
  33. Kasper, M., Apai, D., Janson, M., & Brandner, W. 2007, A&A, 472, 321 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Kuzuhara, M., Tamura, M., Kudo, T., et al. 2013, ApJ, 774, 11 [NASA ADS] [CrossRef] [Google Scholar]
  35. Lafrenière, D., Doyon, R., Marois, C., et al. 2007, ApJ, 670, 1367 [NASA ADS] [CrossRef] [Google Scholar]
  36. Lowrance, P. J., Becklin, E. E., Schneider, G., et al. 2005, AJ, 130, 1845 [NASA ADS] [CrossRef] [Google Scholar]
  37. Low, C., & Lynden-Bell, D. 1976, MNRAS, 176, 367 [NASA ADS] [Google Scholar]
  38. Marcy, G., Butler, P. R., Fischer, D. A., & Vogt, S. S. 2000, Bioastronomy 99, 213, 85 [NASA ADS] [Google Scholar]
  39. Masciadri, E., Mundt, R., Henning, T., Alvarez, C., & Barrado y Navascués, D. 2005, ApJ, 625, 1004 [NASA ADS] [CrossRef] [Google Scholar]
  40. Metchev, S. A., & Hillenbrand, L. A. 2009, ApJS, 181, 62 [NASA ADS] [CrossRef] [Google Scholar]
  41. Mugrauer, M., Vogt, N., Neuhäuser, R., & Schmidt, T. O. B. 2010, A&A, 523, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Nielsen, E. L., & Close, L. M. 2010, ApJ, 717, 878 [NASA ADS] [CrossRef] [Google Scholar]
  43. Parker, R. J., & Reggiani, M. M. 2013, MNRAS, 432, 2378 [NASA ADS] [CrossRef] [Google Scholar]
  44. Patience, J., Ghez, A. M., Reid, I. N., & Matthews, K. 2002, AJ, 123, 1570 [NASA ADS] [CrossRef] [Google Scholar]
  45. Potter, D., Martín, E. L., Cushing, M. C., et al. 2002, ApJ, 567, L133 [NASA ADS] [CrossRef] [Google Scholar]
  46. Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Rameau, J., Chauvin, G., Lagrange, A.-M., et al. 2013a, A&A, 553, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Rameau, J., Chauvin, G., Lagrange, A.-M., et al. 2013b, ApJ, 779, L26 [NASA ADS] [CrossRef] [Google Scholar]
  49. Reggiani, M., & Meyer, M. R. 2013, A&A, 553, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Reggiani, M. M., & Meyer, M. R. 2011, ApJ, 738, 60 [NASA ADS] [CrossRef] [Google Scholar]
  51. Sahlmann, J., Ségransan, D., Queloz, D., et al. 2011, A&A, 525, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Saumon, D., & Marley, M. S. 2008, ApJ, 689, 1327 [NASA ADS] [CrossRef] [Google Scholar]
  53. Seifahrt, A., Neuhäuser, R., & Hauschildt, P. H. 2007, A&A, 463, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Silk, J. 1977, ApJ, 214, 152 [NASA ADS] [CrossRef] [Google Scholar]
  55. Vigan, A., Patience, J., Marois, C., et al. 2012, A&A, 544, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Wahhaj, Z., Liu, M. C., Biller, B. A., et al. 2011, ApJ, 729, 139 [NASA ADS] [CrossRef] [Google Scholar]
  57. Wahhaj, Z., Liu, M. C., Nielsen, E. L., et al. 2013, ApJ, 773, 179 [NASA ADS] [CrossRef] [Google Scholar]
  58. Zhou, Y., Herczeg, G. J., Kraus, A. L., Metchev, S., & Cruz, K. L. 2014, ApJ, 783, L17 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Planet and BD distributions: model values.

In the text

All Figures

thumbnail Fig. 1

Combined substellar CMF. The discontinuity at log M/M⊙ = −2.3 is due to the opacity limit for fragmentation that set a minimum mass for objects formed through core fragmentation. The minimum mass is assumed to be 5 MJupiter in our model.

In the text
thumbnail Fig. 2

Detection probability for the NaCo-LP observed sample for rcutoff = 100, 30, 20 AU (from left to right).
In the text
thumbnail Fig. 3

Detection probability for the full sample for rcutoff = 100, 30, 20 AU (from left to right).

In the text
thumbnail Fig. 4

Probability of our surveys detecting three substellar companions, as a function of the power-law slope of the SMA distribution βpl, and the outer radius cutoff of the SMA distribution. The overall probability is normalized to be 1 within the figure. The region above the line can be ruled out at 99.7% confidence.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.