| Issue |
A&A
Volume 586, February 2016
|
|
|---|---|---|
| Article Number | A96 | |
| Number of page(s) | 20 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201525851 | |
| Published online | 29 January 2016 | |
Stellar models simulating the disk-locking mechanism and the evolutionary history of the Orion Nebula cluster and NGC 2264 ⋆
1
Universidade Federal de Viçosa,
Campus UFV Florestal,
Florestal,
35690-000
MG,
Brazil
e-mail:
nlandin@ufv.br; nlandin@fisica.ufmg.br
2
Depto. de Física, Universidade Federal de Minas
Gerais, Belo
Horizonte,702, 31161-901, MG,
Brazil
e-mail: lpv@fisica.ufmg.br; silvia@fisica.ufmg.br
3
Depto. de Engenharia Eletrônica, Universidade Federal de Minas
Gerais, Belo Horizonte,
702, 31270-901,
MG,
Brazil
e-mail:
luizt@cpdee.ufmg.br
Received: 9 February 2015
Accepted: 4 November 2015
Context. Rotational evolution in young stars is described by pre–main sequence evolutionary tracks including non-gray boundary conditions, rotation, conservation of angular momentum, and simulations of disk-locking.
Aims. By assuming that disk-locking is the regulation mechanism for the stellar angular velocity during the early stages of pre–main sequence evolution, we use our rotating models and observational data to constrain disk lifetimes (Tdisk) of a representative sample of low-mass stars in two young clusters, the Orion Nebula cluster (ONC) and NGC 2264, and to better understand their rotational evolution.
Methods. The period distributions of the ONC and NGC 2264 are known to be bimodal and to depend on the stellar mass. To follow the rotational evolution of these two clusters’ stars, we generated sets of evolutionary tracks from a fully convective configuration with low central temperatures (before D- and Li-burning). We assumed that the evolution of fast rotators can be represented by models considering conservation of angular momentum during all stages and of moderate rotators by models considering conservation of angular velocity during the first stages of evolution. With these models we estimate a mass and an age for all stars.
Results. The resulting mass distribution for the bulk of the cluster population is in the ranges of 0.2−0.4 M⊙ and 0.1−0.6 M⊙ for the ONC and NGC 2264, respectively. For the ONC, we assume that the secondary peak in the period distribution is due to high-mass objects still locked in their disks, with a locking period (Plock) of ~8 days. For NGC 2264 we make two hypotheses: (1) the stars in the secondary peak are still locked with Plock = 5 days, and (2) NGC 2264 is in a later stage in the rotational evolution. Hypothesis 2 implies in a disk-locking scenario with Plock = 8 days, a disk lifetime of 1 Myr and, after that, constant angular momentum evolution. We then simulated the period distribution of NGC 2264 when the mean age of the cluster was 1 Myr. Dichotomy and bimodality appear in the simulated distribution, presenting one peak at 2 days and another one at 5−7 days, indicating that the assumption of Plock = 8 days is plausible. Our hypotheses are compared with observational disk diagnoses available in the literature for the ONC and NGC 2264, such as near-infrared excess, Hα emission, and spectral energy distribution slope in the mid-infrared.
Conclusions. Disk-locking models with Plock = 8 days and 0.2 Myr ≤ Tdisk ≤ 3 Myr are consistent with observed periods of moderate rotators of the ONC. For NGC 2264, the more promising explanation for the observed period distribution is an evolution with disk-locking (with Plock near 8 days) during the first 1 Myr, approximately, but after this, the evolution continued with constant angular momentum.
Key words: stars: evolution / stars: interiors / stars: rotation / stars: pre-main sequence / stars: variables: T Tauri, Herbig Ae/Be / stars: low-mass
Full Table 1 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/586/A96
© ESO, 2016
1. Introduction
The evolution of angular momentum of pre-main sequence (pMS) stars is an important problem in star formation and is currently a controversial topic (Cieza & Baliber 2006 and Meibom et al. 2013). Gravitational contraction of the stars and only marginal loss of angular momentum can explain the spin-up of stars from pMS phase to zero-age main-sequence (zams) and, then, the existence of rapidly rotating stars on the zams. On the other hand, the broad period distribution of zams stars and the existence of slow rotators can only be explained if during early phases of evolution some stars lost significant fractions of their angular momenta, and this loss is, in addition, rather different from star to star (Lamm et al. 2005).
The observational basis for the study of stellar angular momentum starts with the knowledge that at about spectral type F5 a sharp break in the rotation velocity distributions of field stars occurs. Kraft (1967) proposed that rotation declines with advancing age as a result of magnetically coupled winds, even after a star reaches the main sequence (MS). Skumanich (1972) concluded, based on the available observed rotational velocities, that they decrease with time as t− 1 / 2. Benz at al. (1984) confirmed that for stars later than F8, the rotational velocities decrease with age, but this decay is only poorly fitted by the t− 1 / 2 law. When short-period photometric variations were discovered in young clusters, it was found that some stars do not follow the Skumanich law (Alphenaar & van Leeuwen 1981 and Meys et al. 1982). As soon as fast rotators were discovered in clusters of different ages, an interesting feature became clear: the mass dependence of the rapid rotation phenomenon. Several works (Stauffer et al. 1997b,a; 1987; Prosser et al. 1995; Stauffer & Hartmann 1987; and Soderblom et al. 1993), pointed out that rapid rotation disappears slower for stars of lower mass. The range in rotation for T Tauri stars appeared to be narrower than for the MS, which is problematic if the T Tauri star velocity distribution is to evolve into that seen on the MS. Since the works by Attridge & Herbst (1992) and Choi & Herbst (1996), it is well known that rotational periods of T Tauri stars in the Orion Nebula cluster (ONC) show a very characteristic distribution. Classical T Tauri stars (ctts) have a narrow period distribution that peaks at about 8 days. Weak-line T Tauri stars (wtts) have a much broader distribution, with some stars showing rotational periods lower by a factor of 4 relative to those presented by ctts. Herbst et al. (2002) found that the period distribution for ONC stars of spectral type M21 or earlier peaks at 2 and 8 days, while the distribution for ONC stars of later spectral types have a peak at 2 days and only a tail of slow rotators. Lamm et al. (2005) analyzed the period distribution of NGC 2264 stars as a function of their colors (which have a dependence on the masses), but not as a funtion of specifically their masses or spectral types. They found the same behavior as in the ONC: stars redder than a given color (lower mass stars) present only one peak in the period distribution, at around 1 day, and stars bluer than a given color (more massive stars) have a period histogram with two peaks: one around 1 day, and another one around 4−5 days.
These observations suggest that T Tauri stars in accretion disk systems are subjected to a regulation of their angular velocities, which counteracts the tendency to spin up both from accretion of disk material of high specific angular momentum and from readjustments in the moment of inertia as they contract toward the MS. The presence of a circumstellar disk apparently enforces nearly constant rotation in the central star, preventing the expected spin-up. The lower rotation period of wtts is consistent with an evolution without a circumstellar disk, being free to experience the spin-up. On the other hand, the observed range of MS rotation rates could be explained if a range in accretion disk lifetimes is assumed. According to Edwards et al. (1993), a mechanism proposed by Königl (1991), known as “disk-locking”, which consists of a magnetic star-disk interaction, could be responsible for this characteristic period distribution in young stellar clusters. This is the most acceptable picture of the problem, but Matt & Pudritz (2004) pointed out that observations by Stassun et al. (1999) and Johns-Krull et al. (1999) and theoretical considerations of Safier (1998) have called the standard disk-locking scenario into question. Based on the work by Uzdensky et al. (2002), which demonstrated that differential rotation between the star and disk leads to an opening of the field lines that drastically reduces the magnetic connection between the two, Matt & Pudritz (2004) emphasized that the disk-locking model cannot account for the angular momentum loss of the slow rotators, concluding that accretion-powered stellar winds are a promising scenario for solving the stellar angular momentum problem. On the other hand, Cauley et al. (2012) derived accretion parameters for 36 T Tauri stars in NGC 2264 and analyzed different models of magnetospheric accretion and found good support for disk-locking, but not for theories that assume a dipolar magnetic field geometry. In addition, their results found no support for accretion-powered stellar winds, although they agree that this mechanism certainly provides a mean of angular momentum removal for ctts.
Several works were carried on to examine the hypothesis that disk-locking regulates pMS angular momenta. These works were based on at least one observational property that indicates the presence of a circumstellar disk. Rebull et al. (2000) described the origin of some disk indicators commonly used in the literature, such as U − V excess, Hα emission (which are accretion diagnostics and, consequently, indicate the presence of circumstellar disks), and infrared excesses (I − K and H − K, which are diagnostics of dust heated in circumstellar disk). Rebull et al. (2002) used U − V, I − K, H − K excesses, and Hα emission to identify circumstellar disk candidates in NGC 2264. Makidon et al. (2004) used these same disk indicators to search for eventual correlations with period of NGC 2246 stars, but found no conclusive evidence that slower rotating stars have disk indicators, or that faster rotators are less likely to have disk indicators. Dahm & Simon (2005) analyzed the NGC 2264 rotational data from Lamm et al. (2004) and Makidon et al. (2004) and found a weak-to-moderate positive correlation between H − K color and rotation periods for the ctts, in the sense that longer period objects tend to have larger H − K colors. They found a similar positive correlation between LHα, Hα luminosity, and rotation period among the ctts. By using near-infrared excesses to identify disk candidates in the ONC, Hillenbrand et al. (1998) concluded that this disk indicator misses about 30% of disks that can be detected at longer wavelengths. Then, in the attempt to use a more reliable disk indicator, Cieza & Baliber (2007) used data from the Spitzer Space Telescope in the IRAC band passes to test the star-disk interaction paradigm in NGC 2264 and the ONC. By using Spitzer mid-infrared data, they observed a clear increase in the disk fraction with period in both clusters across the entire period range populated by their members. They also showed that the peak at 8 days of the distribution of ONC stars of spectral type M2 or earlier is dominated by stars possessing a disk, while the peak at 2 days is dominated by stars without disks. Their results present strong evidence that star-disk interaction regulates the angular momentum of these young stars. On the other hand, Cieza & Baliber (2006) made the same analysis for IC 348, a 1−3 Myr old cluster, and found no evidence that the tail of slow rotators (stars with M< 0.25M⊙) or the long-period peak (M> 0.25M⊙) are preferentially populated by objects with disks, as might be expected based on the current disk-braking model. In addition, they found no significant correlation between period and the IR-excess, regardless of the mass range considered. These results are in conflict with those by Nordhagen et al. (2006), who found that the variability observed in IC 348 wtts arises primarily from the rotation of a spotted photosphere and that the irregular variability of ctts is due to the presence of an accretion disk. Nordhagen et al. (2006) have also shown that the solar mass range stars present in IC 348 have a rotation period distribution similar to that of the ONC, but contain a larger portion of slow rotators than is seen in NGC 2264. As Nordhagen et al. (2006) considered an age of 3 Myr for IC 348, for them the IC 348 age is closer to NGC 2264 than to the ONC. Then, they concluded that another factor in addition to age and mass is probably important in establishing the rotation properties within a cluster, and their suggestion is that this factor is the environment. However, Affer et al. (2013) suggested that the results found by Cieza & Baliber (2006) suffer from several biases affecting the selected samples and even the disk and accretion indicators adopted. Based on CoRot light curves, Affer et al. (2013) determined high-accuracy rotation periods for 189 stars of NGC 2264. By using the Hα equivalent width, they found that rotational distributions of ctts and wtts are different, consistent with the disk-locking scenario.
To learn more about the initial conditions, it is necessary to obtain observational data for pMS stars. Through a monitoring campaign of some open clusters in star-forming regions, “The Monitor Project” researchers are trying to further our understanding of the angular momentum of young, low-mass stars (Aigrain et al. 2007). This survey measured photometric rotation periods for a large number of objects at a range of ages from the stellar birth line to the zero-age main sequence belonging to some young clusters (Irwin et al. 2007a,b, 2008a,b).
From the theoretical point of view, many of the angular momentum evolution models were developed in an attempt to address these questions. Kawaler (1987) used an extrapolation of the Kraft (1970) relation to infer the initial pMS angular momentum as a function of mass. Pinsonneault et al. (1989, 1990) constructed solar models with rotation using the Kawaler (1987) relations as initial conditions, and Kawaler (1988) presented a formulation for the angular momentum loss by magnetic stellar winds. Microscopic diffusion effects were considered in the models by Chaboyer et al. (1995a,b). Several authors explored the rotational evolution of solar analogs under a variety of assumptions about both the timescale for rotational coupling between the core and envelope, and the initial rotation rates (e.g., MacGregor & Brenner 1991 and Keppens et al. 1995). The role played by star-disk interaction in the origin of the initial conditions for stellar rotation was explored by Jianke & Cameron (1993) and Cameron et al. (1995). Bouvier et al. (1997) presented models for surface rotation of solar-like stars considering nearly solid-body rotation, pMS disk-locking, and wind braking, using the stellar moments of inertia and radii from the non-rotating stellar evolution model of Forestini (1994). They concluded that a median disk lifetime of 3 Myr would be necessary to make slow rotators, but long disk-coupling times (~10−20 Myr) are needed to explain the rotation rates of the slowest rotator stars. By using the Yale stellar evolution code2, Guenther et al. (1992) and Krishnamurthi et al. (1997) constructed angular momentum models and examined the effects of different assumptions about initial conditions on the angular momentum evolution of solar-type stars. For rotating models, they used moments of inertia calculated by non-rotating models. For differentially rotating models, modest disk lifetimes on the order of 3 Myr were needed to produce slow rotators, and for solid-body models, longer disk lifetimes (on the order of 20 Myr) were needed, in agreement with Bouvier et al. (1997). Barnes et al. (1999) and Barnes et al. (2001), also using the Yale code, constructed rotating models accounting for transport and redistribution of both chemical species and angular momentum within a star, as a result of various rotationally induced instabilities. To mimic the effect of disk-locking on the pMS, their models were allowed to lock the rotation rate of a young star on the Hayashi track for a specified time. Their models begin at the deuterium MS. Barnes et al. (1999) interpreted rotation period and B − V color data of young stars (30 Myr), present in the young clusters IC 2602 and IC 2391, in terms of these models. The ultrafast rotators (periods as slow as ~0.2 days) could be reproduced by assuming an initial rotation period of 4 days and no locking phase. For the majority of solar-type stars considered in their analysis, they explained the rotation period distribution with an initial rotation period of 16 days and disk lifetimes of up to 5 Myr.
Despite all these efforts, no model to date has been able to explain the presence of fast and slowly rotating stars in the same young cluster by a single mechanism intrinsic to the star. The introduction of rotation in the aton 2.3 stellar evolutionary code makes it possible to explore the physical mechanism that apparently maintains the stellar angular velocity constant.
We present our new rotating evolutionary tracks, including a simulation of the disk-locking mechanism, as a plausible explanation for the rotational evolution of slow rotator pMS stars. We do not model the star-disk interaction, but only mimic its effect on the stellar rotation by locking it for a while. The advantage of our models compared to those of Bouvier et al. (1997) and Krishnamurthi et al. (1997) is that we model not only the angular momentum, but also the structure and evolution of stars, and our moments of inertia are obtained by taking into account the rotation effects. This was also the approach followed by Barnes et al. (2001), but they began the calculations at the deuterium main sequence, disregarding the action of the thermostat of deuterium burning, which may introduce numerical uncertainties in stellar ages (see Landin et al. 2006 for a discussion). Our models instead reach the deuterium-burning phase by contracting in thermal equilibrium.
We consider a range of disk lifetimes and of initial rotation rates, and use our theoretical predictions to analyze the rotational properties of the ONC and NGC 2264 stars, which were found to vary considerably with mass. Objects with masses higher than a threshold value have a clear bimodal period distribution (which peaks ~2 and 8 days for the ONC and ~1 and 4−5 days for NGC 2264), while the less massive sample of each cluster only constitutes a tail of slow rotators. Assuming that disk-locking is responsible for the peak at 8 (4−5) days for the ONC (NGC 2264), we investigate the role of disk lifetimes on the rotational evolution of the stars in these two young clusters.
In Sect. 2 we present and describe our disk-locking models that we used to follow the evolution of moderate rotators present in the ONC and NGC 2264 clusters. Models with conservation of angular momentum during all evolution (also used in this work) are also described in Sect. 2. The observational evidence of an angular momentum regulation mechanism in pMS is discussed in Sect. 3. The ONC and NGC 2264 data used, the derivation of masses and ages, the results of the rotational period distributions (of both clusters), and a discussion of the possible interpretations are presented in Sect. 4. Our conclusions are given in Sect. 5.
2. Models
In this section we briefly present the version of the aton code we used and show how we introduced the effect of the presence of a disk in our models. The angular momentum evolution models, which are generally used in the literature to study the rotational evolution of low-mass stars, use as input parameters the moments of inertia and radii computed by stellar evolutionary models without rotation. The angular momentum evolution is calculated separately in another code (for example, see Bouvier et al. 1997 and Krishnamurthi et al. 1997). We used evolutionary models instead that include rotation. This is a more consistent approach because the structural effects caused by rotation are, thereby, taken into account. Some structural effects of rotation are discussed in this section. The evolutionary tracks were computed in the mass range of 0.15−0.8 M⊙. The solar chemical composition was adopted (Y = 0.27 and Z = 0.0175). We used the same boundary conditions as Hauschildt et al. (1999) and Allard et al. (2000). Convection was treated through the classical mixing length theory (mlt), with α = 2.0. Since most of the ONC and NGC 2264 objects are low-mass pMS stars, rigid body rotation was assumed. We used the opacities reported by Iglesias & Rogers (1993) and Alexander & Ferguson (1994) and the equations of state from Rogers et al. (1996) and Mihalas et al. (1988). The tracks start from a fully convective configuration with central temperatures in the range 5.3 < log Tc< 5.8, follow deuterium and lithium burning, and end at the MS configuration. For more details see Landin et al. (2006).
Attridge & Herbst (1992) and Choi & Herbst (1996) suggested that the mechanism acting on stars against the increase in their angular velocity during the pMS contraction could be disk-locking, due to magnetic coupling between the star and the disk (Königl 1991). This version of the aton code allows the evolution of stars with disk-locking simulation by keeping their angular velocity constant during the early stages of pMS. During this phase, the period of the star is fixed at a given locking-period, Plock. After this locked phase, the star is free to spin up, following a constant angular momentum evolution. For ONC stars, we used Plock = 8 days, following the suggestion by Herbst et al. (2002). For NGC 2264, we used Plock = 5 days, based on the value of the second peak in the rotation period distribution of this cluster (Lamm et al. 2005). These two values of Plock have corresponding values of initial angular momentum, which are used as input parameters by the model. Based on these initial rotation rates, we generated sets of evolutionary tracks taking into account the disk-locking mechanism, with disk lifetimes of 0.2, 0.5, 1.0, 3.0, and 10.0 Myr. To make a comparison with the evolution of stars without accretion disks, we generated another set of models considering angular momentum conservation since the beginning. In these cases, the initial angular momentum is a function of mass and is given by (Kawaler 1987) 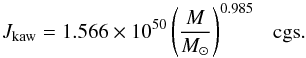 (1)It is important to emphasize that the results obtained with our rotating models depend on the initial angular momentum (or angular velocity) value, which is an input parameter of our models. For models with conservation of angular momentum from the beginning we used the Kawaler (1987) relations (Eq. (1)), and for disk-locking models we used an initial angular momentum that corresponds to a period of 5 or 8 days.
(1)It is important to emphasize that the results obtained with our rotating models depend on the initial angular momentum (or angular velocity) value, which is an input parameter of our models. For models with conservation of angular momentum from the beginning we used the Kawaler (1987) relations (Eq. (1)), and for disk-locking models we used an initial angular momentum that corresponds to a period of 5 or 8 days.
In Table 1 we present the 0.4 M⊙ models as an example of our calculations with the aton code version that includes disk-locking.
Pre-main sequence evolutionary tracks for 0.4 M⊙ star for disk-locking models with Plock = 5 days and Tdisk = 1 Myr(a).
 |
Fig. 1 Evolutionary tracks for 0.15, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, and 0.8 M⊙ (from low to high temperatures), considering constant angular momentum evolution (dashed lines) and disk-locking evolution with Plock = 8 days and Tdisk = 1 Myr (solid lines). Dotted lines represent the isochrones for 0.1, 1, 5, 10, and 100 Myr (from high to low luminosities). Crosses represent the ONC stars. Effective temperatures and luminosities were taken from Hillenbrand (1997). |
 |
Fig. 2 Color−magnitude diagram (Ic vs. Rc − Ic) and our evolutionary tracks for models of 0.15, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, and 0.8 M⊙ (from right to left) considering constant angular momentum evolution (dashed lines) and evolution with disk-locking with Plock = 5 days and Tdisk = 1 Myr (solid lines). Isochrones (dotted lines) for 0.1, 1, 5, 10, and 100 Myr are shown (from top to bottom). Crosses are NGC 2264 stars (Lamm et al. 2004). |
 |
Fig. 3 Time evolution of the rotation periods for some 0.4 M⊙ stellar models. |
In Figs. 1 and 2 we show the evolutionary tracks obtained with different sets of models. We note that a difference in the rotation evolution mainly affects low-mass tracks. Even a short disk lifetime of 1 Myr can shift the evolutionary paths followed by the tracks. In the beginning of the Hayashi phase (higher luminosities), the evolutionary tracks obtained with disk-locking models are slightly cooler than those obtained with conservation of angular momentum. When the tracks approach the MS (lower luminosities), the situation is reversed (Figs. 1, 2). This behavior can be connected with a structural effect caused by rotation, the mass-lowering effect, which produces a shift in the evolutionary tracks of rotating stars toward lower effective temperature and luminosity, simulating a non-rotating star of lower mass (Mendes 1999). This effect is more or less evident, depending on the intensity of rotation. In Fig. 3 we show as an example the time evolution of rotation periods of 0.4 M⊙ models. Rotation periods as a function of age are shown for models conserving angular momentum since the beginning and for disk-locking (DL) models with Plock = 5 days and Tdisk = 0.5 Myr, Plock = 5 days and Tdisk = 1 Myr, Plock = 8 days and Tdisk = 0.5 Myr, and Plock = 8 days and Tdisk = 1 Myr. In this work, models with conservation of angular momentum start the evolution with angular velocities given by Kawaler’s relation (Eq. (1)), which are lower than the locking velocities used in our disk-locking models for a given mass. This behavior is shown in Fig. 3, which plots the temporal evolution of periods, instead of velocities. For this reason, in the first stages of evolution (ages < 1 Myr), the tracks produced by the models conserving angular momentum seem to be more massive non-rotators than the disk-locking models, and then seem to have higher effective temperatures. For ages greater than ~1 Myr, the tracks of models with conservation of angular momentum evolve to configurations whose angular velocity is higher than disk-locking models with Tdisk = 1 Myr and Plock = 5 days, Tdisk = 1 Myr and Plock = 8 days, and Tdisk = 0.5 Myr and Plock = 8 days. Consequently, the tracks of models conserving angular momentum exhibit lower effective temperatures than the disk-locking models for the same mass, except for DL models with Tdisk = 0.5 Myr and Plock = 5 days.
 |
Fig. 4 Time evolution of the convective envelope relative mass for a 0.4 M⊙ model considering constant angular momentum evolution and evolution with disk-locking for different disk lifetimes. |
The impact of rotational evolution on the stellar structure can also be seen in Fig. 4, where we show the mass of the convective envelope of a 0.4 M⊙ model as a function of stellar age. During the first Myr, 0.4 M⊙ stars are completely convective, and so the relative mass of the convective envelope (Mconv/Mtot) is equal to 1. From this age on, the mass contents of the convective envelope changes depending on the kind of rotation evolution followed by the star. By comparing rotation periods and the mass of the convective envelope at a given age (Figs. 3 and 4), we note that the shorter the rotation period (or the greater the angular velocity), the larger the mass contents of the convective envelope. This behavior can also be understood by recalling the mass-lowering effect. The faster the star rotates, the more it mimics a lower mass star, and the larger its envelope. We discussed the case of 0.4 M⊙ models, but this is also valid for other mass models, with small differences. The relative mass of convective envelopes, for instance, is less sensitive to the rotational evolution model as the stellar mass increases.
Young stars are nearly completely convective and have large moments of inertia (or rotational inertia). As they contract, approaching the main-sequence, their surface convection zones retreat and their total rotational inertia, Itot, decreases. A fraction of Itot, the rotational inertia in the convection zone of the stars, Iconv, also decreases. This general behavior is visible Fig. 5, which shows the temporal evolution of rotational inertia in the convective envelope for 0.4 M⊙ stars. During the very early stages of evolution (ages shorter than 0.1 Myr), models with conservation of angular momentum since the beginning produce higher rotational inertia in the convective envelope, followed by disk-locking models with Plock = 8 days and disk-locking models with Plock = 5 days, in this order. A detailed inspection in the calculations reveals that values of rotational inertia in the convective envelope calculated with disk-locking models with the same locking period do not vary significantly. However, for more advanced stages of evolution (ages greater than 100 Myr) higher rotational inertia in the convection zone is produced by DL models with Plock = 5 days and Tdisk = 0.5 Myr, followed by models conserving angular momentum since the beginning, DL models with Plock = 8 days and Tdisk = 0.5 Myr, DL models with Plock = 5 days and Tdisk = 1 Myr, and DL models with Plock = 8 days and Tdisk = 1 Myr. This is shown in the upper right corner of Fig. 5, where we display an amplified view of rotational inertia in the convection zone obtained by the models for ages greater than 100 Myr. This behavior of Iconv for different rotational evolutions is also valid for other mass values, with small differences mainly for 0.8 M⊙.
 |
Fig. 5 Rotational inertia in the convective envelope versus stellar age of 0.4 M⊙ models considering constant angular momentum evolution and evolution with disk-locking for different disk lifetimes. |
3. Discussions
The ONC and NGC 2264 are the two best studied young star clusters, including analyses at different wavelengths. For the ONC we can cite, for example, Hillenbrand (1997), in the optical; Hillenbrand et al. (1998), in the near-infrared; Cieza & Baliber (2007) in the mid-infrared; Flaccomio et al. (2003a,b) and Stassun et al. (2004), in the X-ray; Stassun et al. (1999) and Herbst et al. (2002) in photometric variability studies to determine rotational periods. For NGC 2264, Rebull et al. (2002) conducted studies in the optical and near-infrared; Cieza & Baliber (2007) and Dahm et al. (2012) analyzed it in the mid-infrared; Flaccomio et al. (1999, 2006) and Rebull et al. (2006) investigated the cluster in X-rays; Teixeira et al. (2012) analyzed the nature of the disk population of NGC 2264 stars by using Spitzer data; Venuti et al. (2014) characterized the accretion process of NGC 2264 stars by performing deep ugri mapping and u- and r-band monitoring with CFHT/MegaCam; Lamm et al. (2004), Makidon et al. (2004) and Affer et al. (2013) performed photometric variability studies and identified several periodic and irregular variables. Favata et al. (2010) and Affer et al. (2013) observed NGC 2264 with the CoRoT space telescope, which allowed them to determine rotation periods (P< 12 days) with high accuracy and free of the biases imposed by ground-based observations. Preliminar results from Favata et al. (2010) showed that stars with M> 0.25 M⊙ have a single-peaked distribution and no short-period peak. The short-period peak (~1 day) present in the ground-based distribution appeared to be spurious. However, Affer et al. (2013) compared rotation periods obtained with CoRoT and ground-based data of Lamm et al. (2004) for 103 stars common in both samples. They found that 83% of the sample have consistent rotation periods, with the exception of only five stars that had one-day periods erroneously determined by the ground-based method.
This clearly shows that similar characteristics were detected in the ONC and NGC 2264, and some works are dedicated to compare their rotational properties (Lamm et al. 2005 and Cieza & Baliber 2007). This is also one of the purposes of the present work.
ctts were found to be remarkably slow rotators, having lost large amounts of angular momentum during the protostar or early pMS phase (Bouvier et al. 1986 and Hartmann et al. 1986), and the magnetic coupling between star and disk was proposed as the dominant mechanism of this process. Observational support for this picture includes evidence for a correlation of rotation properties with the presence of disks (Bouvier et al. 1993 and Edwards et al. 1993). This disk-locking scenario was observationally supported by rotation period studies in the ONC, where Attridge & Herbst (1992) first discovered a bimodal period distribution (with peaks around 2 and 8 days) and Herbst et al. (2001, 2002), in addition to confirming this, emphasized that it occurs for stars of spectral types earlier than M2. The bimodality observed in such stars was interpreted as an effect of disk-locking with a locking period of about 8 days, while stars with shorter periods are presumably not locked to their disks. Stassun et al. (1999) were unable to confirm the existence of a bimodal period distribution in the ONC and did not find differences between the rotation periods for ctts and wtts. This probably is a consequence of their study being strongly biased toward periods shorter than or equal to 8 days and toward lower mass stars. In addition, they did not analyze the influence of mass in the period distribution.
Makidon et al. (2004) and Lamm et al. (2005) studied the period distribution of pMS stars in NGC 2264. While the first authors have not observed bimodality in the total period distribution, Lamm and collaborators found it to be highly color dependent. They also reported that the period distribution is bimodal for bluer stars (Rc − Ic< 1.3, which corresponds to M> 0.25 M⊙ according to D’Antona & Mazzitelli 1997 models) and unimodal for redder ones (Rc − Ic> 1.3 or M< 0.25 M⊙). Lamm et al. (2005) noted that the median rotation periods of the bluer and redder stars in the ONC, a younger cluster, are 6.75 and 3.3 days, respectively, which means that stars with M< 0.25 M⊙ rotate on average faster by a factor of 2 than those with M> 0.25 M⊙. However, for NGC 2264, an older cluster than the ONC, they found that the median rotation periods of the bluer and redder stars are 4.7 and 1.9 days, respectively, which means that on average, stars with M< 0.25 M⊙ rotate faster than those with M> 0.25 M⊙ by a factor of 2.5. They estimated an age ratio of about 2 between the two clusters on the basis of pMS models. According to our models (with and without disk-locking), the estimate for this ratio is around 3. In addition, Lamm et al. (2005) found that the period distribution of NGC 2264 is similar in form to that of the ONC, but shifted to shorter periods. Their quantitative comparisons between the period distributions of the two clusters suggest that about 80% of the stars have spun up from the age of the ONC to the age of NGC 2264. Based on this suggestion and on the estimated age ratio between the two clusters, they found that the average spin-up by a factor of 1.5−1.8 from the age of the ONC to the age of NGC 2264 is consistent with a decreasing stellar radius and conservation of angular momentum. Lamm et al. (2005) assumed, based on their findings, that NGC 2264 represents a later stage in the rotational evolution of the stars than is shown by the ONC, meaning that when NGC 2264 was at the age of the ONC, its period distribution should have been close to that observed today in the ONC. Under this assumption, Lamm et al. (2005) proposed two possible explanations for the presence of the second peak (~4−5 days) in the period distribution of NGC 2264:
-
1.
stars with P ≳ 4−5 days are still locked, but at a locking period shorter than that in the ONC;
-
2.
stars with P ≳ 4−5 days were locked in the past, with a locking period similar to the locking period in the ONC, and were released from their disks presumably when they were at the age of the ONC stars.
After losing their disks (i.e., at about 1 Myr, the mean age of ONC objects), stars of the second group spun up, conserving angular momentum, which resulted in a shift of the period distribution of NGC 2264 toward shorter periods than are observed in the ONC distribution. Although about 30% of the stars with M> 0.25 M⊙ in NGC 2264 maintain a longer rotation period even as they have aged from the ONC, Lamm et al. (2005) considered hypothesis 2 as the more reliable and that a locking period of about 4−5 days is not trustworthy. In addition, most of the stars with P ≳ 4−5 days have an Hα index that is compatible with no accretion.
Recently, Gregory et al. (2012) studied the magnetic field of T Tauri stars and suggested that their magnetic field topologies are strongly dependent on the internal stellar structure. A star can begin to spin up even without losing its disk. If the magnetic field dipole component decreases, the magnetospheric radius (where the star-disk coupling occurs) moves inward, to values lower than the corotation radius, and the star begins to spin up. According to the findings of Gregory et al. (2012), this apparently occurs when the radiative core develops. Because NGC 2264 stars have a variety of masses and ages, this shift of the magnetospheric radius in this scenario would occur at different times and would result in different locking periods, whose values we would not know. By considering that NGC 2264 stars are older than those of the ONC, we expect that the number of stars that have already developed a radiative core and have then spun up is greater for NGC 2264. As a result, NGC 2264 should show a period distribution shifted to shorter periods than the ONC distribution. The arguments based on magnetic field topology evolution, presented by Gregory et al. (2012), imply stellar spin-up, favoring hypothesis 2.
The rotational properties of ONC and NGC 2264 stars are discussed and analyzed in Sect. 4, based on our previous discussions. The ONC was investigated by assuming that stars with periods greater than 8 days are locked to their disks (with Pdisk = 8 days) and the other stars, with P< 8 days, evolved without a disk. We decided to analyze the rotational properties of NGC 2264 under the assumptions that
-
stars with periods greater than 5 days are locked to their disks (with Pdisk = 5 days) and stars with P< 5 days evolved without disk, and
-
NGC 2264 stars were locked when they were at the age of the ONC stars, with Pdisk = 8 days, and since then they evolved, conserving angular momentum.
4. Results
4.1. ONC stars
The ONC is the massive star formation region closest to us, located at 470 pc from the Sun (Genzel et al. 1981). To study the angular momentum evolution in pMS phase, we compared our evolutionary track sets with observational data of the ONC stars. The ONC data we used have been kindly provided by Keivan Stassun, who has widely worked on the rotational properties of the ONC (Stassun et al. 1999, 2004). The data consist of rotation periods (Stassun et al. 1999 and Herbst et al. 2002), effective temperatures and luminosities (Hillenbrand 1997), and infrared excesses, Δ [ I − K ] (Hillenbrand et al. 1998).
In Fig. 1 we show the ONC stars in the theoretical Hertzsprung-Russell (HR) diagram together with our evolutionary tracks for disk-locking models and for models with constant angular momentum evolution. By using our evolutionary tracks and isochrones, we assigned a mass and an age to each ONC star. Figure 6 shows the mass distribution of the observed stars, obtained by using three sets of models. Two of them are models with disk-locking (with Plock = 8 days and disk lifetimes of 0.5 and 1 Myr). They produce very similar mass distributions, peaking at 0.3−0.35 M⊙. The third set of models, without disk-locking, produces a slightly different mass distribution that has a broader peak around 0.2−0.35 M⊙. The resulting mass distribution of the bulk of the ONC population is in the range 0.2−0.4 M⊙, independently of the model used.
 |
Fig. 6 Mass histogram of ONC stars. |
 |
Fig. 7 Age histogram of ONC stars. |
Figure 7 presents the age distribution of our ONC star sample. The age function peaks at the same age (~1 Myr) for all models, and they have roughly the same age distribution. According to the models, the bulk of the ONC population has ages between 0.6−2.5 Myr, and the mean age of the stars is 1 Myr.
It is important to emphasize here that, in general, the spread in luminosities observed in the ONC and in other young clusters, including NGC 2264, are interpreted as a genuine age dispersion. However, this interpretation is questionable (Hartmann 2001), and, as pointed out by Jeffries et al. (2011), a coeval pMS star sample may exhibit a luminosity dispersion caused by observational uncertainties and physical mechanism that change the conventional relation between luminosity and ages. Consequently, Fig. 7 should be taken as an apparent age distribution for ONC stars.
The ONC period distribution presents two main features: bimodality and dichotomy (e.g., Attridge & Herbst 1992; Choi & Herbst 1996; Herbst et al. 2002; and Landin et al. 2006). The bimodality is due to its two peaks (Fig. 8), and the dichotomy, which is related to bimodality, is due to the dependence of the rotational properties on mass, that is, the different behavior of the period distribution exhibited by objects with masses lower and higher than a given threshold (the transition mass, Mtr). Stars with masses higher than Mtr present a bimodal distribution, while those with masses lower than Mtr show only a tail of slow rotators. The value of transition mass depends on the model used to estimate the stellar masses. For gray models with α = 1.5 by D’Antona & Mazzitelli (1997), Mtr = 0.25M⊙. For non-gray models by Landin et al. (2006) with α = 2.0, Mtr ~ 0.35 M⊙. For our disk-locking models (Tdisk = 1 Myr and Plock = 8 days), the transition mass that better highlights the dichotomy is Mtr = 0.3 M⊙. We here defined as higher mass stars objects with M> 0.3M⊙ and as lower mass stars objects with M< 0.3 M⊙. In Fig. 9 we show period histograms for ONC stars of both higher and lower mass. It fully reproduces the results by Herbst et al. (2002): the period distribution of the whole sample of ONC stars has two peaks, at periods of 2 and 8 days, respectively.
From Fig. 9 we note that 67% of the lower mass objects (M< 0.3 M⊙) have P< 4 days and 14% have P> 6 days. Of the higher mass stars, 38% have periods shorter than 4 days and 48% have periods greater than 6 days.
We now establish a disk-locking criterion based on rotation periods. Stars with periods longer than a given threshold (Pthresh = 8 days for the ONC) are considered to be still locked to a disk (as suggested by Herbst et al. 2002). For stars with P<Pthresh (which is currently considered as unlocked), we determined the epoch at which their period was equal to 8 days. This would have been the time at which the stars would have lost their disks and, from then on, evolved with constant angular momentum. Following this approach, we found some stars that had P = 8 days at an age younger than 105 yr. Since they have lost their disk very early, these objects were considered to have evolved without a disk. A similar criterion was used by Landin et al. (2006).
 |
Fig. 8 Period histograms of all observed ONC stars (Landin et al. 2006). |
 |
Fig. 9 Period histograms of the ONC stars for lower and higher mass stars. Dotted lines represent the objects with M< 0.3M⊙ and solid lines stand for stars with M> 0.3M⊙. |
 |
Fig. 10 Δ [ I − K ] versus stellar mass for early fast (□ symbols), slow (×) and moderate (•) rotators in the ONC. Figure adapted from Landin et al. (2006). |
In this way, we identified three distinct populations:
-
i)
early fast rotators – stars locked only for ages <105 yr;
-
ii)
slow rotators – stars locked to their disks (P ≥ 8 d);
-
iii)
moderate rotators – unlocked stars (P< 8 d and ages >105 yr).
When we applied this criterion to our sample of 359 stars, 148 were classified as moderate rotators, 76 as slow rotators, 115 as early fast rotators, and 20 stars are younger than 105 yr. Stars of this last group did not enter our analysis.
Since the near-infrared excess Δ [ I − K ] is an observational indicator of the presence of disks, we compared our results with the near-infrared excess measurements for 324 of our objects. Landin et al. (2006) concluded that both methods agree well for slow and early fast rotators. IR excess provides a good diagnostic for passive disks, that is, for circumstellar disks not necessarily related to accreting processes. Still locked stars are expected to have Δ [ I − K ] > 0.3, while those evolving without a disk should have infrared excesses significantly lower than this threshold value (Herbst et al. 2002). In Fig. 10 we reproduce Fig. 8 of Landin et al. (2006) including the moderate rotators, showing Δ [ I − K ] as a function of stellar mass. From these, we found that 64% of slow rotators have Δ [ I − K ] ≥ 0.3, while 70% of early fast rotators and 42% of moderate rotators have Δ [ I − K ] < 0.3.
According to Landin et al. (2006), the evolution of the early fast rotators is consistent with an evolution conserving angular momentum from the beginning. Figure 11, taken from Landin et al. (2006), shows the ONC stars classified as early fast rotators in three mass intervals in the period-age plane, as well as their models corresponding to constant angular momentum evolution. To fully bracket the observed periods, it is necessary to assume a distribution of initial angular momenta Jin at least in the range Jkaw<Jin< 3Jkaw. Jkaw is described by the prescription of Kawaler (1987) and in Eq. (1). We used in this work models with α = 2, and Fig. 11 (and also Fig. 20) shows that even models with Jin = 3Jkaw are unable to fit some fast rotators ( days). However, models with lower convection efficiency (α = 1) can reproduce the period evolution of these objects along time (Landin et al. 2006). According to Barnes et al. (2001), these fast rotators can be fitted by solid body models with an initial rotation period of 4 days (at birthline) and conserving angular momentum from the beginning.
days). However, models with lower convection efficiency (α = 1) can reproduce the period evolution of these objects along time (Landin et al. 2006). According to Barnes et al. (2001), these fast rotators can be fitted by solid body models with an initial rotation period of 4 days (at birthline) and conserving angular momentum from the beginning.
 |
Fig. 11 Period versus age for early fast rotator pMS stars of the ONC. Their positions in the period-age plane are compared with models assuming evolution with constant angular momentum (Landin et al. 2006). Masses in the interval 0.2 <M/M⊙< 0.3 correspond to °, 0.3 <M/M⊙< 0.4 to ▪, and all the remaining to ×. Solid lines represent models with Jin = Jkaw, while dashed lines stand for models with Jin = 3Jkaw for M = 0.2, 0.3 and 0.4 M⊙. Figure adapted from Landin et al. (2006). |
The rotational evolution of slow and moderate rotators is not consistent with an evolution that conserves the angular momentum since the early phases. If our criterion is correct, slow rotators cannot evolve conserving angular momentum because they are still locked to their disks. Moderate rotators experience evolution with conservation of angular momentum only after going through the locking phase. To test our disk-locking models, which are based on the hypothesis that a mechanism preventing the stellar spin-up exists (for a while), we therefore investigated first the moderate rotators in the ONC. According to our criterion, the moderate rotators are not locked to their disks anymore (i.e., they have already lost their disks). Therefore, no significant observational evidence of (mainly active) disk is expected.
Of the 148 moderate rotators of our sample, 130 objects have near-infrared excess and 40 have mid-infrared measurements. Of the 130 objects of the first group, a considerable amount (58%) have Δ [ I − K ] > 0.3, as shown in Fig. 10. As they are assumed to be stars that have lost their disks, we expected a lower fraction of stars with indexes indicating the presence of disks. According to our estimates of age and of the time at which the disks were lost, the majority (60%) of the ONC stars with infrared excess compatible with locked stars have lost their disks relatively recently (less than 106 yr ago). The reason that most moderate rotators have Δ [ I − K ] > 0.3 might be that they probably did not have time to completely lose the surrounding material. An alternative explanation could be that they are still locked to their disks, but at a radius smaller than the corotation radius. As the radius of the star-disk interaction moves inward when the radiative core develops (Gregory et al. 2012), stars with masses greater than the transition to complete convection (~0.3 M⊙) may have been classified as moderate rotators, but show Δ [ I−K ]compatible with disk presence.
Figure 12 shows the ONC moderate rotators in the Prot vs. inferred age plane and also displays the results of our theoretical models, assuming that disk-locking is the mechanism preventing the stellar spinning up in the beginning of the pMS phase. According to our models, stars with 0.2, 0.3, and 0.4 M⊙ represent the bulk of the ONC population (see Fig. 6), and
 |
Fig. 12 Period versus age for moderate rotators pMS stars of the ONC. Their positions in the period-age plane are compared with models with disk-locking for three different locking times (Tdisk = 0.2, 1, and 3 Myr) and Pdisk = 8 days. The symbols are the same as in Fig. 11, and the lines represent our models for 0.2 (solid), 0.3 (dotted), and 0.4 M⊙ (dashed). |
our theoretical curves reproduce the observed loci of the ONC moderate rotators. The full distribution is well reproduced by using disk lifetimes between 0.2–3 Myr, which are good estimates for disk survival times. This is supported by Bouvier (2007), Barnes et al. (2001), and Irwin & Bouvier (2009). According to Bouvier (2007), 40−60% of the stars are still surrounded by circumstellar disks at 2 Myr, and this fraction decreases to 10−25% at 10 Myr. By using disk-locking models for solar-type stars (0.6−1.2 M⊙), Barnes et al. (2001) and Irwin & Bouvier (2009) reproduced the rotation period of stars that we classified as moderate rotators by using disk lifetimes similar to ours. The differentially rotating models of Barnes et al. (2001) required locking times of 0.3−1 Myr and initial rotation periods at birth line in the range of 4−16 days. The solid-body models of Irwin & Bouvier (2009) required locking times of 2−5 Myr and initial rotation periods of around 8-16 days. For the low-mass domain (0.1−0.4 M⊙), solid-body models of Irwin & Bouvier (2009) reproduced the ONC data with disk lifetimes of 4−8 Myr and initial rotation periods of around 8−23 days. These long initial periods (or Plock) are necessary to account for the slowest rotators, in this work called slow rotators.
4.2. NGC 2264 stars – hypothesis 1
NGC 2264 is a fairly populous nearby cluster, located at ~760 pc from the Sun (Sung et al. 1997). Our sample consists of 405 objects classified as periodic variables by Lamm et al. (2004), most of which probably are in the pMS phase. Most of the observational data of NGC 2264 stars used in this work (rotation periods, colors, and Hα based accretion disk diagnostic) come from Lamm et al. (2005). We used both the ground-based periods determined by Lamm et al. (2005) and the space-based CoRoT periods obtained by Affer et al. (2013), despite the fact that the number of stars whose periods may have been erroneously determined by the ground-based method represents only 3% of our sample. Since we lack information about their Teff and luminosities (except for a small sample of 109 objects by Flaccomio et al. 2006 and 256 objects by Venuti et al. 2014), we cannot show them all in the classical HR diagram. Instead, we have magnitudes and colors in the Johnson V and Cousins R, I systems. To compare our theoretical evolutionary tracks with observational data, we used color-temperature relations and bolometric corrections by VandenBerg & Clem (2003). As individual reddening and extinction are not available for a significant number of NGC 2264 stars, we followed Lamm et al. (2005) and calculated reddened isochrones and evolutionary tracks by using average values of reddening, E(Rc − Ic) = 0.10 ± 0.02, and extinction, AIc = 0.25, toward NGC 2264. These values were determined by Rebull et al. (2002) adopting R = E(B − V) /Av = 3.1.
We estimated mass and age to each NGC 2264 star by using our tracks and isochrones. Figure 2 shows our models (with conservation of angular momentum and disk-locking for Plock = 5 days and Tdisk = 1 Myr) and NGC 2264 data in the color−magnitude diagram Ic vs. Rc − Ic. Figure 13 shows the mass distribution of the observed stars obtained with models with conservation of angular momentum and disk-locking for Plock = 5 days (Tdisk = 1 and 0.5 Myr). For masses higher than 0.4 M⊙ the three distributions are quite similar, showing only small differences. However, for masses lower than 0.4 M⊙ they exhibit appreciable differences that are more pronounced for models with conservation of angular momentum. The mass distributions obtained with our models peak in the 0.1−0.2 M⊙ range. A secondary peak is seen in the 0.5−0.6 M⊙ range, while the resulting mass distribution of the bulk of NGC 2264 population is in the interval of 0.1−0.6 M⊙.
 |
Fig. 13 Mass histogram of NGC 2264 stars. |
Figure 14 displays the apparent age distribution obtained with our models for this sample of NGC 2264 stars, showing that the ages predicted by the three models are roughly similar, with only minor differences. The age function peaks in the range of 3.9−6.3 Myr and the bulk of the population lies in the interval of 1−10 Myr. The mean age of NGC 2264 obtained with our three models is 3.5 Myr.
 |
Fig. 14 Age histogram of NGC 2264 stars. |
Venuti et al. (2014) also determined stellar masses for 256 and ages for 218 NGC 2264 objects. The mean difference found for masses between their values and ours is 0.2 M⊙, with 59% of the objects having differences in mass determinations smaller than 0.2 M⊙. The ages of these stars, estimated by both works, are between 1 and 10 Myr, but the age distribution found by Venuti et al. (2014) has a narrow peak around 3.2 Myr, while our age determinations are mainly distributed in the range of 2.5 and 8 Myr (see right panel of Fig. 15). One source of the differences in mass and age estimates is the different evolutionary models used in each work. Venuti et al. (2014) used models of Siess et al. (2000), while we used the non-gray models described in Sect. 2, which are more suitable for p-MS than the gray atmospheric boundary conditions used by Siess et al. (2000). The use of non-gray models mainly affects mass determinations of low-mass stars. The left panel of Fig. 15 shows that the mass distribution of NGC 2264 stars obtained with our non-gray models (solid curve) is shifted to higher masses in comparison with the mass distribution determined by Venuti et al. (2014, dotted curve). Non-gray models yield evolutionary tracks cooler than gray models and, as a result, mass estimates obtained from the latter are systematically (and erroneously) lower than those obtained from the former.
 |
Fig. 15 Mass (left) and age (right) distributions for NGC 2264 stars in common in our sample and that of Venuti et al. (2014). Solid curves refer to masses and ages obtained with our models, dotted curves refer to masses and ages obtained with the models of Siess et al. (2000). |
As for the ONC, the rotation period distribution of NGC 2264 also exhibits features such as bimodality and dichotomy (Lamm et al. 2005 and Cieza & Baliber 2007), as shown in the period histograms for NGC 2264 stars, Figs. 16 and 17. The total period distribution (Fig. 16) is bimodal, with a primary peak at ~1 day and a secondary one at ~4−5 days. The distribution is clearly shifted toward lower periods than in the ONC one (see Fig. 8).
As shown in Fig. 17, NGC 2264 stars can be divided into two distinct populations: (i) a group with a unimodal period distribution, with a peak ~1−2 days and a tail of slow rotators, and (ii) another group with a bimodal distribution, with peaks at ~1 d and ~4−5 days. In the left panel of Fig. 17, these groups are divided into stars with Rc − Ic> 1.65 mag3 and with Rc − Ic< 1.65 mag. This transition color index corresponds to 0.3 M⊙, according to our disk-locking models (Tdisk = 1 Myr and Plock = 5 d). We chose this value for the transition mass to better highlight the dichotomy. However, a dichotomy is observed for a wide range of transition masses (0.2 ≤ Mtr/M⊙ ≤ 0.6, for NGC 2264), with different period distributions for each transition mass. For Mtr ~ 0.35 M⊙, the peak of low-mass stars and the primary peak of high-mass stars have nearly the same height. The right panel of Fig. 17 shows NGC 2264 objects divided into groups with masses greater and lower than 0.3 M⊙. This value of the transition mass is the same for models with either conservation of angular momentum or disk-locking, although the distributions are slightly different. However, Mtr is sensitive to other parameters such as atmospheric boundary conditions and convection treatment (Landin et al. 2006). Figure 17 gives a hint on how rotational properties of NGC 2264 behave as a function of mass. Of our sample of 405 stars, we estimated that 280 stars have M> 0.3 M⊙ and 125 have M< 0.3M⊙. Of the objects with M< 0.3 M⊙ 72.8% have P< 2.5 days and 16.8% have P> 3.5 days. Of the objects with M> 0.3 M⊙ 32.1% have P< 2.5 days and 57.9% have P> 3.5 days.
We used the same method as described in Sect. 4.1 to establish a disk-locking criterion based on the rotation period. For NGC 2264 we use in this section another value for the threshold period because the secondary peak in the period distribution for higher mass stars occurs around 4−5 days (instead of 8 days, as in the ONC). In the analysis of the rotational history of NGC 2264, we use Pthresh = 5 days and we have, again, three distinct groups:
-
i)
early fast rotators – stars locked only for ages <105 yr;
-
ii)
slow rotators – stars probably disk locked (P ≥ 5 d);
-
iii)
moderate rotators – unlocked stars (P< 5 d and ages > 105 yr).
The sample of Lamm et al. (2005) with its 405 stars has 240 that were found to be moderate rotators, 117 are slow and 48 early fast rotators.
We tested this disk-locking criterion against observational indicators of disk presence that are related, mainly, with Hα emission (Hα-index, Δ [ Rc − Hα ]) by Lamm (2003) and Lamm et al. (2004). These authors used nearly simultaneous observations in V, RC, IC, and Hα, obtained between December 2000 and March 2001, to search for rotation periods and to determine Hα-indexes. As chromospheric activity can also produce considerable Hα emission, its presence is an ambiguous sign of accretion disk, in particular close to an Hα emission equivalent width of Wλ(Hα) = 10 Å (Lamm 2003). As complementary data, we therefore used Spitzer IRAC data kindly provided by Paula Teixeira (Teixeira et al. 2012), who classified the circumstellar disks of NGC 2264 stars based on their spectral energy distribution slope between 3.6μm and 8μm, defined as αIRAC. These IRAC data were obtained in two epochs, March and October 2004, and can help us to distinguish the stars with a disk from diskless objects. In addition, we investigated Wλ(Hα), U − V and near-infrared excesses (I − K and H − K) by Rebull et al. (2002), near-infrared excess and Wλ(Hα) by Dahm & Simon (2005), mid-infrared excess by Cieza & Baliber (2007), and u-band exccess by Venuti et al. (2014). For disk identification purposes, we used the following values to indicate the presence of a disk: Wλ(Hα) ≥ 10 Å, Δ [ U − V ] ≤ −0.5, Δ [ I − K ] ≥ 0.3, Δ [ H − K ] ≥ 0.15, [ 3.8−8.0 ] ≥ 0.7, and αIRAC> −2.56.
 |
Fig. 16 Total period distribution for NGC 2264 stars. |
As in Lamm et al. (2004, 2005), we also dealt with the Hα index, Δ [ Rc − Hα ], which is a measure of the Hα emission. The Hα index is defined by the following equation: ![\begin{equation} \Delta[R_{\rm c}-{\rm H\alpha}]=(R_{\rm c}-{\rm H\alpha})_{\rm star}-(R_{\rm c}-{\rm H\alpha})_{\rm locus}, \label{haindex} \end{equation}](/articles/aa/full_html/2016/02/aa25851-15/aa25851-15-eq145.png) (2)where (Rc − Hα)star is the instrumental color of the star and (Rc − Hα)locus is the median (Rc − Hα) color as a function of Rc − Ic for the locus of pMS/MS stars. We obtained (Rc − Hα)locus for our sample by using the equation (Lamm et al. 2004)
(2)where (Rc − Hα)star is the instrumental color of the star and (Rc − Hα)locus is the median (Rc − Hα) color as a function of Rc − Ic for the locus of pMS/MS stars. We obtained (Rc − Hα)locus for our sample by using the equation (Lamm et al. 2004) 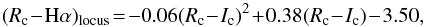 (3)which should be valid for an MS star.
(3)which should be valid for an MS star.
 |
Fig. 17 Period histograms for our sample of pMS stars of NGC 2264. The left panel shows the period distribution for stars with Rc − Ic<1.65 mag (solid line) and with Rc − Ic> 1.65 mag (dotted line). This corresponds approximately to a division into stars with M> 0.3 M⊙ (solid line) and M< 0.3 M⊙ (dotted line), in the right panel. |
To relate this Hα index to some physical property, Lamm (2003) and Lamm et al. (2004) used stars with a known Hα equivalent width, Wλ(Hα), to compare these two quantities. They found that 83% of the stars with Δ [ Rc − Hα ] ≥ 0.1 mag have Wλ(Hα) ≳ 10 Å and are likely ctts. On the other hand, about 85% of the stars with Δ [ Rc − Hα ] < 0.1 mag have Wλ(Hα) < 10 Å and are most likely wtts. In Fig. 18 we show Δ [ Rc − Hα ] versus stellar mass for NGC 2264 objects, indicating those classified as early fast, slow, and moderate rotators. Slow rotators are quite concentrated in the more massive region of the plot, early fast rotators in the less massive region. The sample of moderate rotators spreads throughout the entire mass interval. Figure 18 shows only objects with M ≤ 1.0 M⊙. However, Fig. 13 shows that only a few objects of our sample stay outside this range of mass.
Following Lamm (2003), we call stars with Δ [ Rc − Hα ] − δ [ Rc − Hα ] ≥ 0.1ctts and stars with Δ [ Rc − Hα ] + δ [ Rc − Hα ] ≤ 0.0wtts. The quantity δ [ Rc − Hα ] is the photometric error of Rc − Hα color. Stars that are neither ctts nor wtts according to these criteria are called intermediate cases. They have a small (positive) Hα-index and could be ctts.
 |
Fig. 18 Δ [ Rc − Hα ] versus stellar mass for NGC 2264 stars classified as early fast rotators (□), slow rotators (×), and moderate rotators (•). |
Lamm et al. (2004) noted that their periodic variables (which form our sample of stars in NGC 2264) are biased toward the wtts, objects with Δ [ Rc − Hα ] < 0.1, mentioning that this is a limitation of the photometric method used to study the rotational periods among T Tauri stars. In our sample of 405 stars, 81 have Δ [ Rc − Hα ] − δ [ Rc − Hα ]≥0.1 (ctts), 114 stars have Δ [ Rc − Hα ] + δ [ Rc − Hα ] ≤ 0.0 (wtts), and 210 were classified as “intermediate cases”. As expected, according to the classification of Lamm (2003), for ctts and wtts theHα-index values agree well with the Wλ(Hα) measurements by Rebull et al. (2002) and Dahm & Simon (2005). Of the 81 stars classified as ctts, 42 have a Wλ(Hα) measure in at least one of these two works, and 38 have Wλ(Hα) ≥ 10 Å. Of the 114 stars classified as wtts, 42 have at least one Wλ(Hα) measurement, and 39 of them have Wλ(Hα) < 10 Å. Of the 210 stars classified as intermediate cases, 98 have at least one Wλ(Hα) measurement, and 18 have Wλ(Hα) ≥ 10 Å and could be ctts.
Unfortunately, the only observational disk indicator for which we have measurements for all stars is Δ [ Rc − Hα ] , and this indicator is inconclusive for more than half of our sample stars, classifying 210 objects as intermediate cases. To distinguish these stars as objects with and without disks, we also used the αIRAC index reported by Teixeira et al. (2012). Of the 405 stars of our sample, 170 have αIRAC measurements, 75 have αIRAC> −2.56 (indicating that they have dust in the inner disk) and 95 have αIRAC ≤ −2.56 (indicating that they have naked photospheres). These IRAC data agree very well with the Hα index. Of the stars with αIRAC measurements, 35 were classified as ctts (34 have αIRAC> −2.56 and only 1 has αIRAC ≤ −2.56), 40 were classified as wtts (32 have αIRAC ≤ −2.56 and 8 have αIRAC> −2.56), and 95 were classified as intermediate cases (62 have αIRAC ≤ −2.56 and 33 have αIRAC> −2.56). By combining both indexes, Hα and αIRAC, we identified 114 objects with observational evidence of disk presence (ctts and intermediate cases with αIRAC> −2.56), 176 without such indications (wtts and intermediate cases with αIRAC ≤ −2.56), and 115 stars for which we do not have enough information to conclude whether they have a disk (intermediate cases without αIRAC measurements). By comparing our disk-locking criterion and these observational disk diagnostics, we found that only 40% of objects with observational indications of disk presence are slow rotators. For those without observational indications of a disk, the two methods agree well because 75.5% of them are early fast or moderate rotators. Of the 115 objects labeled intermediate cases that do not have αIRAC measurements, 66% are moderate rotators, 10.5% are early fast rotators, and 23.5% are slow rotators.
We can also compare the Hα index with other disk indicators, such as U − V, I − K, H − K excesses (Rebull et al. 2002) and the [3.6−8.0] excess (Dahm & Simon 2005). In the ctts group, 43 have measurements of another disk indicator, which for 23 stars (53.5%) indicate the presence of disks. In the wtts group, 52 stars have at least one measurement of another disk indicator, which for 40 stars (76.9%) suggests that they are diskless stars. In the group of 210 stars classified as intermediate cases, 128 have at least another measure of a disk indicator, which indicates for 60 the presence of a disk and that they might be ctts. This analysis reveals that we do not have enough UV and infrared data for our star sample to compare them with the Hα index. For the stars for which we have another disk indicator measurement, the comparison between them and Hα index do not agree well for stars classified as ctts, but they agree for the wtts stars.
We now compare the u-band survey by Venuti et al. (2014) with Hα-indexes and αIRAC measurements and with our disk-locking criterion. Of the 405 stars of our sample, 256 objects have u-band photometric measurements, 59 objects have u-band excess (compatible with ongoing accretion), and 197 stars have no u-band excess. Of the 59 stars with u-band excess, 31 are classified as ctts, 6 as wtts, and 22 as intermediate case stars. Of the 197 objects without u-band excess, 16 are classified as ctts, 62 as wtts, and 119 as intermediate case objects. Although u-band photometry data have been obtained on December 2010, some years after Δ [ Rc − Hα ] data, they agree reasonably well as accretion diagnostics. In addition, all 170 objects of our sample that have αIRAC measurements are present in the u-band survey, and the two diagnostics agree (Venuti et al. 2014). In this subsample, 89 stars have no u-band excess and αIRAC ≤ −2.56 (no dust in the inner disk), 40 objects do not show either u-band excess or an IRAC inner disk, and only 6 objects show u-band excess and do not have dusty inner disk. We still have 35 stars that do not exhibit u-band excess but have αIRAC> −2.56, suggesting that accretion processes are completed, but inner disks did not have time to dissipate. Finally, we compare our disk-locking criterion with u-band photometry. For early fast and moderate rotators our disk-locking criterion agrees with u-band data, with 88% of early fast rotators and 78% of moderate rotators having no u-band excess. On the other hand, u-band photometry is not compatible with expectations for slow rotators, with only 28% of these objects showing u-band excess.
We now compare our disk-locking criterion with observational evidence for disk presence. In this work, slow rotators (locked stars) are assumed to host circumstellar disks, and we expect that they are related to ctts and intermediate cases with αIRAC> −2.56. On the other hand, moderate rotators (unlocked objects) are assumed to be stars that have lost their disks in the past, and we expect that they are related to wtts and the intermediate cases that have αIRAC ≤ −2.56. wtts are stars without inner disks, have no accretion, and possibly are either objects whose disks are more evolved than ctts disks or even diskless stars. Finally, the early fast rotators are stars whose disk lifetimes were shorter than 105 years, which means that by definition, they are wtts with very short disk lifetimes and should exhibit low values of Hα and αIRAC indexes. However, they evolved practically without a disk. Figure 19 shows Δ [ Rc−Hα ] versus rotation period for NGC 2264 stars. The solid horizontal line at Δ [ Rc − Hα ] = 0.1 divides the sample into intermediate cases and classical T Tauri stars. The solid horizontal line at Δ [ Rc − Hα ] = 0 divides the sample into intermediate cases and weak-line T Tauri stars. The vertical line divides the sample into slow rotators (P ≥ 5 days), moderate, and fast rotators (P< 5 days).
Comparison between our disk-locking criterion and observational data.
In Table 2 we compare our disk-locking criterion with observational data by showing the number of stars that were classified as slow, early fast, and moderate rotators and the number of stars of each group that were classified as ctts, wtts, and intermediate cases according to their Hα emission. For each subgroup, we show the number of stars that present dust in the inner disk according to their αIRAC index. We also list the number of stars without αIRAC measurements. Of the 117 slow rotators found in our sample, only 40% (ctts and intermediate cases with αIRAC> −2.56) have an observational indication of a disk. However, this disagrees with our hypothesis that stars with P ≥ 5 days are locked to their disks. Here, it is worth mentioning that one of the slow rotators has Hα emission but no dust in the inner disk, which characterizes the so-called transitional disk4 class of objects. Of the 48 early fast rotators, 87.5% have an Hα index that indicates no accretion disk, as expected. In addition, αIRAC and Hα measurements for this group agree well. Of the 240 moderate rotators, 75% have no indication of disks (wtts and intermediate cases with αIRAC ≤ −2.56 or without αIRAC measurements). Although this is what we expected, we still found 60 stars classified as ctts or intermediate cases with αIRAC> −2.56. An alternative explanation for the existence of moderate rotators with observational indications of disk presence could be that the star-disk interaction has moved inward after the radiative core formed (Gregory et al. 2012). Thus, we can conclude that our disk-locking criterion agrees reasonably well with observational data for early fast and moderate rotators, but is not consistent with the data for slow rotators.
The group of 405 objects whose periods were determined from ground-based observations by Lamm et al. (2005), and the group of 189 objects by Affer et al. (2013), whose periods were determined by the CoRoT satelite, have 74 stars in common, 14 of which do not present the same periods in the two studies (considering the errors provided). By using these space-based periods, we again applied our criterion for a disk presence and compared the results with the Δ [ Rc − Hα ] indexes and with UV excesses by Venuti et al. (2014). This replacement of ground-based to space-based periods did not improve the comparison between our criterion for a disk presence and the observational disk indicators: even using CoRoT periods and more reliable disk indicators, the two criteria for a disk presence are not consistent for slow rotators. The 115 remaining stars of the Affer sample were not included in our study because they would prevented us from obtaining a unique observational disk indicator for all stars.
 |
Fig. 19 Δ [ Rc − Hα ] versus rotation period for NGC 2264 stars. The symbols are the same as in Fig. 18. |
We next analyzed the rotational evolution of NGC 2264 stars based on our disk-locking criterion. As for the ONC, we assumed that the 48 NGC 2264 stars classified as early fast rotators can be considered to evolve with conservation of angular momentum from the start. This implies that they evolved without a circumstellar disk, and this assumption seems to be supported by Hα emission observations because 24 of these stars were classified as wtts, 18 as intermediate cases, and only 6 as ctts. Even using a period as short as Pthresh, we found 48 early fast rotators in NGC 2264, which is not very significant, statistically, but enough to establish some constraints for pMS rotational evolution. The NGC 2264 early fast rotators are shown in Fig. 20 (similar to Fig. 11 for the ONC). Again, it is necessary to assume a distribution of initial angular momenta at least in the range Jkaw<Jin< 3 Jkaw, models with Jin = Jkaw being an upper limit for NGC 2264 objects classified as early fast rotators by the criterion of hypothesis 1. To reproduce the positions of stars with the lowest periods in the period-age plane, it is necessary to use models with high initial angular momentum (Jin> 3 Jkaw), as in the work by Barnes et al. (2001). Their solid-body models with initial periods of 4 days (at the birthline) and angular momentum conservation from the beginning can account for the slowest rotators of solar type of our sample. It is difficult to compare the initial conditions of our models and those of Yale. The starting point of the Yale models is placed at the birth line (defined on the deuterium main sequence), and our models start before it. For example, our 0.6 M⊙ calculations reach the deuterium-burning phase with a rotation period of about 10−15 days.
 |
Fig. 20 Period versus age for early fast rotator pMS stars of NGC 2264. Their positions in the period-age plane are compared with models assuming evolution with constant angular momentum. Masses in the interval 0.2 <M/M⊙< 0.3 correspond to °, 0.3 <M/M⊙< 0.4 to ▪, 0.4 <M/M⊙< 0.6 to △ and all the remaining to ×. Solid lines represent models with Jin = Jkaw , while the dashed lines stand for models with Jin = 3Jkaw. |
 |
Fig. 21 Period versus age for moderate rotators pMS stars of NGC 2264. Their positions in the period-age plane are compared with disk-locking models with Pdisk = 5 days and 0.2 (solid), 0.3 (dotted), 0.4 (dashed), and 0.5 M⊙ (dash-dotted). The symbols are the same as in Fig. 20. |
We assumed that the objects classified as moderate rotators can be used to test the hypothesis that disk-locking is the mechanism preventing stellar spin up. Then, we used the 240 moderate rotators found in our sample, which, according to our criterion, are currently unlocked stars, have lost their disks in the past time, and for which we expect to find no evidence of a disk. Observations related to Hα emission show that 45 stars were classified as ctts, 72 as wtts, and 123 as intermediate cases, partially supporting this hypothesis. Although 81,25% of the moderate rotators have Δ [ Rc − Hα ] < 0.1, a considerable number of stars (123) have low positive Hα indexes and 15 of these stars have dust in the inner disk, indicating that 25% of the moderate rotators could be ctts.
In Fig. 21 we show NGC 2264 moderate rotators in the rotation period-age plane together with our models for a series of disk lifetimes, Plock = 5 days and tracks for 0.2, 0.3, 0.4, and 0.5 M⊙. The 0.5 M⊙ models were included because of the considerable number of NGC 2264 objects in the mass range of 0.5−0.6 M⊙ (see Fig. 13), which are not seen in the ONC mass distribution (Fig. 6). Figure 21 shows that the observed positions of moderate rotators in the period-age plane are well reproduced by our theoretical models with disk-locking (Pdisk = 5 days and Tdisk = 0.2, 1, 3, and 10 Myr). However, disk lifetimes in the range of 5−10 Myr, which are needed to reproduce the period distribution of a considerable number of NGC 2264 stars, seem to be only poor estimates. According to Bouvier (2007), at 10 Myr the fraction of stars that still have disk is around 10−25%. Sicilia-Aguilar et al. (2006) reported that at an age of 5 Myr, about 90% of disks have already dispersed, and within 10 Myr, almost all pMS stars are diskless. More recently, Fedele et al. (2010) determined an accretion timescale of 2.3 Myr and a near-to-mid infrared excess timescale of 3 Myr, indicating that mass accretion in pMS stars seems to drop below the detectable level earlier than near-to-mid infrared excess.
The analysis we made in hypothesis 1, which assumes that NGC 2264 stars with rotation periods longer than 5 days evolved with a constant angular velocity (locked to their disks), shows that our disk-locking criterion is not compatible with Hα and αIRAC observational data. In our slow rotators sample (117 objects), 30 are classified as ctts and 69 stars are classified as intermediate cases. In the intermediate case group, 42 stars have αIRAC measurements and 17 of these have αIRAC> −2.56 and could be ctts (see Table 2). This means that we have observational evidence of a disk only for 40% of our slow rotators. Furthermore, it is worth remembering that according to Lamm et al. (2005) and based on the model by Shu et al. (1994), estimates for the locking period of NGC 2264 stars indicate that a Plock = 5 days is very short for higher mass stars. This short locking period and disk lifetimes of 5−10 Myr assumed in this section are very unlikely. As a result of these discrepancies in our physical hypothesis, we investigated another scenario for the period distribution of NGC 2264, in which ctts are not associated with stars with P ≥ 5 days. We describe this in the next section.
4.3. NGC 2264 stars – hypothesis 2
Another possible interpretation of the rotation evolution of NGC 2264 stars was presented by Lamm et al. (2005), who suggested that the period distribution of both NGC 2264 and the ONC were similar when the clusters had the same age. In this view, stars in NGC 2264 with P ≥ 4−5 days are assumed to have been locked in the past with the locking period attributed to the ONC (Plock ~ 8 days) and released from their disks presumably when they were at the age of ONC stars. Since then, these stars would have spun up conserving angular momentum.
To test this hypothesis, we tried to simulate the NGC 2264 period distribution at 1 Myr. If we simply used the stars’ estimated ages and projected them back to 1 Myr, we would be assuming that all the stars were formed together, disregarding the apparent spread on age of 1−10 Myr seen in Fig. 14. According to our age determinations, the apparent age dispersions in NGC 2264 and the ONC are similar: 83% (96%) of ONC stars and 75% (95%) of NGC 2264 stars lie within one (two) standard deviation from their respective mean ages. Therefore it makes more sense to simulate the NGC 2264 period distribution when the mean age of its stars was 1 Myr. In this way, if the current mean age of NGC 2264 stars is 3.5 Myr, 2.5 Myr ago the cluster’s mean age was about 1 Myr. It is important to stress that this period distribution simulation of NGC 2264 stars at the ONC age is very simplistic because the dynamical evolution of stellar clusters is subject to many competing physical conditions (see, e.g., Lada & Lada 2003); nevertheless, we believe it is a valid approach for obtaining some insight about the evolutionary history of NGC 2264. We then defined a quantity named “age difference” to describe the difference between the stellar age (estimated in Sect. 4.2 by our stellar models) and 2.5 Myr. We computed the age difference for all stars in our sample. However, stars in NGC 2264 are as young as 1 Myr and as old as 10 Myr (see Fig. 7); therefore, 121 stars with age difference <0 had not been formed 2.5 Myr ago and they will not enter our simulation of the NGC 2264 period distribution at the mean age of 1 Myr. To estimate the rotation period of NGC 2264 stars with an age difference ≥0, we proceed in the following way. For the stars without observational evidence of disks (wtts and intermediate cases with αIRAC ≤ −2.56 or intermediate cases without αIRAC measurements), we calculated with our evolutionary tracks their radii at 2.5 Myr ago and their current radii. By considering conservation of angular momentum and the observed rotation period, we also calculated their rotation period at 2.5 Myr ago, that is, when the mean age of NGC 2264 stars was 1 Myr. For the ctts and intermediate cases with αIRAC> −2.56 (those that probably still have their disks), we assumed that their rotation periods have not changed during these 2.5 Myr, so that, when the mean age of NGC 2264 was 1 Myr, they had the same period as they have now.
 |
Fig. 22 Present period distribution of NGC 2264 stars that probably do not have a disk (left panel). Simulation of the period distribution of NGC 2264 stars when the objects had, on average, 1 Myr (right panel). |
The present and simulated period distributions are shown in the left and right panels of Fig. 22, for comparison purposes. A shift in the peaks of the rotation periods between these two histograms is clearly seen. In the current distribution (left panel of Fig. 22) the primary peak is formed by two bins in the interval of 0.5−2 days. In the simulated distribution (right panel of Fig. 22) this peak is also formed by two bins and is shifted to the interval of 2−3 days. The secondary peak shifts from 4−5 days to 5−7 days. Our simulated period distribution for NGC 2264 at 1 Myr is similar to that exhibited by the ONC, but the secondary peak of the ONC occurs around 8 days.
We now investigated the behavior of period distributions of NGC 2264 stars by dividing the objects into the groups of low (M< 0.3 M⊙) and high (M> 0.3 M⊙) mass. In the left panel of Fig. 23 we show the current period distributions of these stars. It is fairly similar to the right panel of Fig. 17, the difference is due to the absence of objects with an age difference lower than 1 Myr in Fig. 23. The simulated distribution (right panel of Fig. 23) agrees reasonably well with our expectation: a distribution with one peak around 2 days for lower mass stars, and a bimodal distribution for higher mass stars with one peak around 2 days and another one around 5−7 days. The distribution shown in the right panel of Fig. 23 is similar to the one exhibited by the ONC. The differences remain mainly in the rotation period of the secondary peak, which is slightly shorter than the ONC value (~8 days).
 |
Fig. 23 Same as Fig. 22, but distinguishing between lower (dotted lines) and higher (solid lines) mass stars (Mtr = 0.3 M⊙). |
 |
Fig. 24 Simulated period distributions for lower and higher mass stars (Mtr = 0.3 M⊙) of NGC 2264 at mean ages of 0.8 Myr (left) and 1.3 Myr (right). |
Our results depend on the assumption that NGC 2264 stars lost their disks when the mean age of the cluster was the current mean age of the ONC (1 Myr). Studies of near-infrared excesses (Hillenbrand 2008) for several young clusters contain information about the disk fraction of each cluster. Since the age of each cluster is known, a diagram with the fraction of stars with a disk as a function of time can be obtained and, in this way, Meyer (2009) found that clusters with ages ~0.8−1.3 Myr often present considerable fractions of stars with disks (around 70%). To take this into account, we investigated the period distribution for NGC 2264 assuming its stars had lost their disks slightly before or after the mean age of 1 Myr. We repeated the above calculations and found the rotation period distribution of NGC 2264, when the mean age of the cluster was 0.8 Myr and 1.3 Myr. These histograms are shown in the left (0.8 Myr) and right (1.3 Myr) panels of Fig. 24. The period distribution does not change significantly for lower mass stars in either simulation. For the higher mass objects, the secondary peak produced for the simulated distribution of periods at 0.8 Myr is broader than that in the right panel of Fig. 23, ranging between 4−7 days. In the simulated distribution at 1.3 Myr, the secondary peak, formed by the higher mass stars, ranges between 4−6 days. Our simulated distributions in Figs. 23 and 24 show that there are 89 stars (lower and higher mass stars) with periods in the range 3.5 days<P< 8 days in the simulated distribution at 0.8 Myr, 90 stars in the simulated distribution at 1 Myr, and 95 stars in the simulated distribution at 1.3 Myr. Our simulations do not show significant changes in the disk fraction from 0.8 Myr to 1 Myr, and it increases only in 5.3% from 1 Myr to 1.3 Myr. The secondary peak of higher mass stars at 0.8 Myr is present, but less evident than those obtained for the simulations at 1 and 1.3 Myr; several stars have periods longer than 8 days. The secondary peak of higher mass stars of the simulated period distribution at 1.3 Myr ranges from 4−6 days, which is shorter than those for 0.8 and 1 Myr. Although NGC 2264 stars may have lost their disks when the age of the cluster was in the interval of 0.8 and 1.3 Myr, the dichotomy is clearly highlighted by the simulated distribution at 1 Myr.
Even for a NGC 2264 sample biased toward wtts and without 121 stars with a negative age difference, we reproduced the period distribution of NGC 2264 at the mean age of 1 Myr, preserving its two main characteristics: bimodality and dichotomy with Mtr = 0.3 M⊙. Moreover, since we obtained a simulated distribution similar to that of the ONC, with a secondary peak close to 8 days, our results indicate that the hypothesis that NGC 2264 is in a rotational stage later than that of the ONC as a promising explanation for the current period distribution exhibited by NGC 2264. In addition, this hypothesis is consistent with the observational disk diagnostics available in the literature.
5. Summary and conclusions
We presented new rotating models that can simulate one of the effects of the disk-locking mechanism by keeping the stellar angular velocity constant. The action of disk-locking lasts for a given time (Tdisk = 0.2, 0.5, 1.0, 3.0, and 10.0 Myr) and takes place in the initial stages of pMS evolution. We assumed that disk-locking is the mechanism that regulates the stellar angular velocity in the early stages of pMS and consequently is responsible for the very characteristic distribution of rotation periods of higher mass, slowly rotating T Tauri stars. Models considering angular momentum conservation were generated for comparison purposes and to explain the rotational evolution of fast rotators. We found that distinct rotation evolutions can alter not only the evolutionary paths followed by the tracks in the HR diagram, but also the mass contained in the convective envelope relative to the total mass and the rotational inertia in the convection region of the star. Disk-locking models produce less massive convective envelopes and lower rotational inertia in the convective envelope than models with angular momentum conservation.
We used the observed stellar populations of both the ONC and NGC 2264 to test our pMS models. By comparing our tracks (obtained with our models conserving angular momentum and disk-locking with Tdisk = 0.5 and 1.0 Myr and Prot = 8 and 5 days) with the position of the observed objects in the HR diagram, we assigned mass and age to each star of each cluster. We found that the bulk of the observed ONC stars have masses and ages in the ranges from 0.2 to 0.4 M⊙ and 0.6 Myr≤Age≤2.5 Myr, for all models. The bulk of NGC 2264 population is concentrated between 0.1 and 0.6 M⊙ and between 1 and 10 Myr. According to our models, the age ratio between the two clusters is ~3.5.
We confirmed the dichotomy in the clusters’ rotational properties: objects with M<Mtr (whose period distribution peaks at short periods) and with M>Mtr (with a primary peak at short periods and a secondary peak at longer periods). For disk-locking models the transition value of masses is Mtr ~ 0.3 M⊙ for both clusters. We also found that a high percentage (~70%) of lower mass stars (M< 0.3 M⊙) rotate fast (with P< 4 days for the ONC and P< 2.5 days for NGC 2264).
We established a disk-locking criterion based on rotation periods and identified three groups of stars. Stars with P ≥ Pthresh (slow rotators) were considered to be still locked to the disk. Stars with P<Pthresh were considered unlocked, and we determined the time at which these stars have lost their disks. Some stars were found to be locked only for ages younger than 105 years and were classified as early fast rotators. The remaining unlocked stars were identified as moderate rotators. We used a different threshold period for each cluster, Pthresh = 8 days for the ONC and Pthresh = 5 days for NGC 2264. We compared our results with an observational indicator for a disk that is available in the literature. Our findings for the ONC agree with infrared excess, and those for NGC 2264 only poorly agree with Hα and αIRAC indexes. This might be because some of the ctts in NGC 2264 have already spun up as a result of the evolution of their magnetic field topologies. For NGC 2264 ctts, disk indicators related to Hα emission do not agree well with U − V and IR-excesses. Only 30 objects were simultaneously classified as ctts and slow rotators (representing 37% of ctts and 25.6% of slow rotators). Moreover, the hypothesis that the higher mass stars of NGC 2264 are locked at Plock = 5 days (hypothesis 1, Sect. 4.2) implies a short locking period and long disk lifetimes, which are unlikely to occur.
According to our disk-locking criterion, the lower mass stars probably evolved without a disk while the longer period, higher mass stars most likely had a disk during some time in the beginning of their evolution. Our results indicate that the evolution of the early fast rotators is consistent with an evolution conserving angular momentum for both clusters. The comparison of the period evolution predicted by the models with the observed values suggests that the initial angular momenta should be at least three times higher than those provided by Kawaler (1987). On the other hand, the evolution of the moderate rotators agrees with an evolution with disk-locking. For ONC objects, the observed periods of moderate rotators can be explained by means of disk-locking models with 0.2 ≤ Tdisk(Myr)≤3 and Plock = 8 days. For NGC 2264 stars, although disk-locking models with 0.2 ≤ Tdisk(Myr)≤10 and Plock = 5 days fit the observed periods of moderate rotators reasonably well, this result must be considered with caution. Short locking periods of 5 days and long disk lifetimes of 10 Myr are questionable. Studies point out that at this age the fraction of stars with disks is considerably small (<10−25%).
Therefore, because hypothesis 1 for NGC 2264 requires odd assumptions (short locking period and long disk lifetimes), we tested hypothesis 2 (Sect. 4.3) proposed by Lamm et al. (2005): when NGC 2264 stars had the same mean age as the ONC, they had the same period distribution. In this scenario, NGC 2264 stars with observational evidence of a disk remained locked during their evolution, while stars with no such evidence remained locked only during the first 1 Myr with Plock = 8 days, and after this, they evolved with constant angular momentum. By assuming angular momentum conservation, we simulated the period distribution of NGC 2264 stars when they had, on average, 1 Myr. We found that the total distribution was shifted to longer periods, resulting in a double-peaked histogram similar to that observed for ONC stars, but the secondary peak of NGC 2264 occurs for periods slightly shorter than for the ONC (around 5 to 7 days). In addition, we found a dichotomy in the simulated distribution at the same transition value, Mtr = 0.3 M⊙.
Our results show that a disk-locking criterion based on rotation periods is consistent with observations, but not for any values of Plock and Tdisk. Typical values are estimated as Plock ≈ 8 days and Tdisk ≤ 3 Myr. As rotation periods of pre-MS stars seem to decrease with age, the period distribution of a young cluster seems to evolve as it ages. In the specific case of the clusters analyzed in this work, the period distribution of the ONC seems to represent a previous stage of the NGC 2264 cluster, indicating that hypothesis 2 (Sect. 4.3) is a promising scenario to explain the period distribution of NGC 2264. This interpretation is supported by Monte Carlo simulations results by Vasconcelos & Bouvier (2015), who used similar disk-locking hypotheses and reproduced the disk fraction as a function of period of ONC and NGC 2264 stars and their accretion-rotation and mass-rotation connections.
The corresponding mass of this spectral type division is model dependent. According to theoretical evolutionary tracks by D’Antona & Mazzitelli (1997), it corresponds to 0.25 M⊙ and, according to the models presented in this work, to 0.30 M⊙.
Several authors cited in this work used the Yale Rotating Stellar Evolution Code (YREC) to study angular momentum evolution, for instance, Pinsonneault et al. (1989, 1990), Guenther et al. (1992), Chaboyer et al. (1995a), Krishnamurthi et al. (1997), Barnes et al. (1999, 2001).
We chose a transition color index of 1.65 mag, which most clearly shows the phenomenon of dichotomy. On the other hand, Lamm et al. (2005) used a value of 1.3 mag, which corresponds to the same transition mass adopted for the ONC by using gray models, i.e., 0.25 M⊙. As can be seen in their Fig. 3a, the peak of the lower mass stars is more than twice as large as the peak of higher mass stars in the period distributions.
According to Pott et al. (2010), transitional disks are defined as systems that are significantly depleted of optically thick dust on scales of a few astronomical units. It is believed that the transition from optically thick accretion to optically thin disks depleted of gas and dust is short lived (Hillenbrand 2008).
Acknowledgments
The authors thank Francesca D’Antona (INAF-OAR, Italy) and Italo Mazzitelli (INAF-IASF, Italy) for granting them full access to the ATON evolutionary code. We also thank an anonymous referee for the comments and suggestions. The financial support from the Brazilian agencies CAPES, CNPq and FAPEMIG is gratefully acknowledged.
References
- Affer, L., Micela, G., Favata, F., et al. 2013, MNRAS, 430, 1433 [NASA ADS] [CrossRef] [Google Scholar]
- Aigrain, S., Hodgkin, S., Irwin, J., et al. 2007, MNRAS, 375, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, D. R., & Ferguson, J. W. 1994, ApJ, 437, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Allard, F., Hauschildt, P. H., & Schweitzer, A. 2000, ApJ, 539, 366 [NASA ADS] [CrossRef] [Google Scholar]
- Alphenaar, P., & van Leeuwen, F. 1981, Inf, Bull. Variable Stars, No. 1957 [Google Scholar]
- Attridge, J. M., & Herbst, W. 1992, ApJ, 398, 61 [Google Scholar]
- Barnes, S. A., Sofia, S., Prosser, C. F., & Satuffer, J. R. 1999, ApJ, 516, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, S., Sofia, S., & Pinsonneault, M. H. 2001, ApJ, 548, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Benz, W., Mayor, M., & Mermilliod, J. C. 1984, A&A, 138, 93 [NASA ADS] [Google Scholar]
- Bouvier, J. 2007, IAU Symp., 243, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Bouvier, J., Bertout, C., Benz, W., & Mayor, M. 1986, A&A, 165, 110 [NASA ADS] [Google Scholar]
- Bouvier, J., Cabrit, S., Fernandex, M., Martin, E. L., & Matthews, J. M. 1993, A&A, 272, 176 [NASA ADS] [Google Scholar]
- Bouvier, J., Forestini, M., & Allain, S. 1997, A&A, 326, 1023 [NASA ADS] [Google Scholar]
- Cameron, A. C., Campbell, C. G., & Qauintrell, H. 1995, A&A, 298, 133 [NASA ADS] [Google Scholar]
- Chaboyer, B., Demarque, P., & Pinsonneault, M. H. 1995a, ApJ, 441, 865 [NASA ADS] [CrossRef] [Google Scholar]
- Chaboyer, B., Demarque, P., & Pinsonneault, M. H. 1995b, ApJ, 441, 876 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, P. I., & Herbst, W. 1996, AJ, 111, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Cieza, L., & Baliber, N. 2006, ApJ, 649, 862 [NASA ADS] [CrossRef] [Google Scholar]
- Cieza, L., & Baliber, N. 2007, ApJ, 671, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Cieza, L., Padgett, D. L., Stapelfeldt, K. R., et al. 2007, ApJ, 667, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Cauley, P. W., Johns-Krull, C. M., Hamilton, C. M., & Lockhart, K. 2012, ApJ, 756, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Dahm, S. E., & Simon, T. 2005, AJ, 129, 829 [NASA ADS] [CrossRef] [Google Scholar]
- Dahm, S. E., Slesnick, C. L., & White, R. J., 2012, ApJ, 745, 56 [NASA ADS] [CrossRef] [Google Scholar]
- D’Antona, F., & Mazzitelli, I. 1997, in Cool stars in Clusters and Associations, eds. R. Pallavicini, & G. Micela, Mem. Soc. Astron. It., 68 [Google Scholar]
- Edwards, S., Stron, S. E., Hartigon, et al. 1993, AJ, 106, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Favata, F., Micela, G., Alencar, S. H. P., et al. 2010, in Highlights of Astronomy, IAU Symp., 15, 752 [Google Scholar]
- Fedele, D., van den Ancker, M. E., Henning, Th., Jayawardhana, R., & Oliveira, J. M. 2010, A&A, 510, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flaccomio, E., Micela, G., Sciortino, S., et al. 1999, A&A, 345, 521 [NASA ADS] [Google Scholar]
- Flaccomio, E., Damiani, F., Micela, G., et al. 2003a, ApJ, 582, 382 [NASA ADS] [CrossRef] [Google Scholar]
- Flaccomio, E., Damiani, F., Micela, G., et al. 2003b, ApJ, 582, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Flaccomio, E., Micela, G., & Sciortino, S. 2006, A&A, 455, 903 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Forestini, M. 1994, A&A, 285, 473 [Google Scholar]
- Genzel, R., Downes, D., Schneps, M. H., et al. ApJ, 247, 1039 [Google Scholar]
- Gregory, S. G., Donati, J.-F., Morin, J., et al. 2012, ApJ, 755, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Guenther, D. B., Demarque, P., Kim, Y. C., & Pinsonneault, M. H. 1992, ApJ, 387, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L. W. 2001, AJ, 121, 1030 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L. W., Soderblom, D. R., & Stauffer, J. R. 1986, AJ, 93, 852 [Google Scholar]
- Hauschildt, P. H., Allard, F., & Baron, E. 1999, ApJ, 512, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, W., Bailer-Jones, C. A. L., & Mundt, R. 2001, ApJ, 554, L197 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, W., Bailer-Jones, C. A. L., Mundt, R., et al. 2002, A&A, 396, 513 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hillenbrand, L. A. 2008, PhST, 130, 4024 [NASA ADS] [Google Scholar]
- Hillenbrand, L. A. 1997, AJ, 113, 1733 [NASA ADS] [CrossRef] [Google Scholar]
- Hillenbrand, L. A., Strom, S. E., Calvet, N., et al. 1998, AJ, 116, 1816 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1993, ApJ, 412, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J., & Bouvier, J. 2009, IAU Symp. 258, 363 [NASA ADS] [Google Scholar]
- Irwin, J., Irwin, M., Aigrain, S., et al. 2007a, MNRAS, 375, 1449 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J., Irwin, M., Aigrain, S., et al. 2007b, MNRAS, 377, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J., Hodgkin, S., Aigrain, S., et al. 2008a, MNRAS, 383, 1602 [Google Scholar]
- Irwin, J., Hodgkin, S., Aigrain, S., et al. 2008b, MNRAS, 384, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffries, R. D., Littlefair, S. P., Naylor, T., & Mayne, N. J., MNRAS, 418, 1948 [Google Scholar]
- Jianke, L., & Cameron, A. C. 1993, MNRAS, 261, 766 [NASA ADS] [CrossRef] [Google Scholar]
- Johns-Krull, C. M., Valenti, J. A., Hatzes, A. P., et al. 1999, ApJ, 510, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Kawaler, S. D. 1987, PASP, 99, 1322 [NASA ADS] [CrossRef] [Google Scholar]
- Kawaler, S. D. 1988, ApJ, 333, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Keppens, R., MacGregor, K. B., & Charbonneau, P. 1995, A&A, 294, 469 [NASA ADS] [Google Scholar]
- Königl, A. 1991, ApJ, 370, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Kraft, R. 1967, ApJ, 150, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Kraft, R. 1970, in Spectroscopic Astrophysics, ed. G. H. Herbig (Berkeley: Univiversity of California Press), 385 [Google Scholar]
- Krishnamurthi, A., Pinsonneault, M. H., Barnes, S., & Sofia, S. 1997, ApJ, 480, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. L., & Lada, E. A. 2003, ARA&A, 41, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Lamm, 2003, Ph.D. Thesis, University of Heidelberg, http://www.ub.uni-heidelberg.de/archiv/4105 [Google Scholar]
- Lamm, M. H., Bailer-Jones, C. A. L., Mundt, R., et al. 2004, A&A, 417, 557 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lamm, M. H., Mundt, R., Bailer-Jones, C. A. L., Herbst, W. 2005, A&A, 430, 1005 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Landin, N. R., Ventura, P., D’Antona, F., et al. 2006, A&A, 456, 269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Makidon, R. B., Rebull, L. M., Strom, S. E., et al. 2004, AJ, 127, 2228 [NASA ADS] [CrossRef] [Google Scholar]
- MacGregor, K. B., & Brenner, M. 1991, ApJ, 376, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, S., & Pudritz, R. E. 2004, ApJ, 607, 43 [Google Scholar]
- Matt, S., & Pudritz, R. E. 2007, IAU Symp., 243, 299 [Google Scholar]
- Meibom, S., Barnes, S. A., Covey, K., et al. 2013, Astrom. Nachr., 334, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Mendes, L. T. S. 1999, Ph.D. Thesis, Universidade Federal de Minas Gerais, Brazil [Google Scholar]
- Meyer, M. R. 2009, IAU Symp., 258, 111 [NASA ADS] [Google Scholar]
- Meys, J. J. M., Alphenaar, P., & van Leeuwen, F. 1982, Inf. Bull. Variable Stars, No. 2115 [Google Scholar]
- Mihalas, D., Dappen, W., Hummer, D. G. 1988, ApJ, 331, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Nordhagen, S, Herbst, W., Rhode, K. L., & Williams, E. C. 2006, AJ, 132, 1555 [NASA ADS] [CrossRef] [Google Scholar]
- Pinsonneault, M. H., Kawaler, S. D., Sfia, S., & Demarque, P. 1989, ApJ, 338, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Pinsonneault, M. H., Kawaler, S. D., & Demarque, P. 1990, ApJS, 74, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Pott, J.-U., Perrin, M. D., Furlan, E., et al. 2010, ApJ, 710, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Prosser, C. F.,Shetrone, M. D., Dasgupta, A., et al. 1995, PASP, 107, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Rebull, L. M., Hillenbrand, L. A., Strom, S. E., et al. 2000, AJ, 119, 3026 [NASA ADS] [CrossRef] [Google Scholar]
- Rebull, L. M., Makidon, R. B., Strom, S. E., et al. 2002, AJ, 123, 1528 [NASA ADS] [CrossRef] [Google Scholar]
- Rebull, L. M., Stauffer, J. R., Ramirez, S. V., et al. 2006, AJ, 131, 2934 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, F. J., Swenson, F. J., Iglesias, C. A. 1996, ApJ, 456, 902 [NASA ADS] [CrossRef] [Google Scholar]
- Safier, P. N. 1998, ApJ, 494, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H., Najita, J., Ostriker, E., et al. 1994, ApJ, 429, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Sicilia-Aguilar, A., Hartmann, L., Calvet, N., et al. 2006, ApJ, 638, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M., 2000, A&A, 358, 593 [Google Scholar]
- Skumanich, A. 1972, ApJ, 171, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Soderblom, D. R., Stauffer, J. R., MacGregor, K. B., et al. 1993, ApJ, 409, 624 [NASA ADS] [CrossRef] [Google Scholar]
- Stauffer, J. R., & Hartmann, L. W. 1987, ApJ, 318, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Stauffer, J. R., Hartmann, L. W., & Latham, D. 1987, ApJ, 320, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Stauffer, J. R., Balachandran, S. C., Krishnamurthi, A., et al. 1997a, ApJ, 475, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Stauffer, J. R., Hartmann, L. W., Prosser, C. F., et al. 1997b, ApJ, 479, 776 [NASA ADS] [CrossRef] [Google Scholar]
- Stassun, K. G., Mathieu, R. D., Mazeh, T., Vrba, F. J. 1999, AJ, 117, 2941 [NASA ADS] [CrossRef] [Google Scholar]
- Stassun, K. G., Ardila, D. R., Basri, G., et al. 2004, AJ, 127, 3537 [NASA ADS] [CrossRef] [Google Scholar]
- Sung, H., Bessel, M. S., & Lee, S.-W. 1997, AJ, 114, 2644 [NASA ADS] [CrossRef] [Google Scholar]
- Teixeira, P. S., Lada, C. J., Marengo, M., & Lada, E. A. 2012, A&A, 540, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Uzdensky, D. A., Königl, A., & Litwin, C. 2002, ApJ, 565, 1191 [NASA ADS] [CrossRef] [Google Scholar]
- VandenBerg, D. A., & Clem, J. L. 2003, AJ, 126, A778 [NASA ADS] [CrossRef] [Google Scholar]
- Vasconcelos, M. J., & Bouvier, J. 2015, A&A, 578, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venuti, L., Bouvier, G., Flaccomio, E., et al. 2014, A&A, 570, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Pre-main sequence evolutionary tracks for 0.4 M⊙ star for disk-locking models with Plock = 5 days and Tdisk = 1 Myr(a).
All Figures
 |
Fig. 1 Evolutionary tracks for 0.15, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, and 0.8 M⊙ (from low to high temperatures), considering constant angular momentum evolution (dashed lines) and disk-locking evolution with Plock = 8 days and Tdisk = 1 Myr (solid lines). Dotted lines represent the isochrones for 0.1, 1, 5, 10, and 100 Myr (from high to low luminosities). Crosses represent the ONC stars. Effective temperatures and luminosities were taken from Hillenbrand (1997). |
| In the text | |
 |
Fig. 2 Color−magnitude diagram (Ic vs. Rc − Ic) and our evolutionary tracks for models of 0.15, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, and 0.8 M⊙ (from right to left) considering constant angular momentum evolution (dashed lines) and evolution with disk-locking with Plock = 5 days and Tdisk = 1 Myr (solid lines). Isochrones (dotted lines) for 0.1, 1, 5, 10, and 100 Myr are shown (from top to bottom). Crosses are NGC 2264 stars (Lamm et al. 2004). |
| In the text | |
 |
Fig. 3 Time evolution of the rotation periods for some 0.4 M⊙ stellar models. |
| In the text | |
 |
Fig. 4 Time evolution of the convective envelope relative mass for a 0.4 M⊙ model considering constant angular momentum evolution and evolution with disk-locking for different disk lifetimes. |
| In the text | |
 |
Fig. 5 Rotational inertia in the convective envelope versus stellar age of 0.4 M⊙ models considering constant angular momentum evolution and evolution with disk-locking for different disk lifetimes. |
| In the text | |
 |
Fig. 6 Mass histogram of ONC stars. |
| In the text | |
 |
Fig. 7 Age histogram of ONC stars. |
| In the text | |
 |
Fig. 8 Period histograms of all observed ONC stars (Landin et al. 2006). |
| In the text | |
 |
Fig. 9 Period histograms of the ONC stars for lower and higher mass stars. Dotted lines represent the objects with M< 0.3M⊙ and solid lines stand for stars with M> 0.3M⊙. |
| In the text | |
 |
Fig. 10 Δ [ I − K ] versus stellar mass for early fast (□ symbols), slow (×) and moderate (•) rotators in the ONC. Figure adapted from Landin et al. (2006). |
| In the text | |
 |
Fig. 11 Period versus age for early fast rotator pMS stars of the ONC. Their positions in the period-age plane are compared with models assuming evolution with constant angular momentum (Landin et al. 2006). Masses in the interval 0.2 <M/M⊙< 0.3 correspond to °, 0.3 <M/M⊙< 0.4 to ▪, and all the remaining to ×. Solid lines represent models with Jin = Jkaw, while dashed lines stand for models with Jin = 3Jkaw for M = 0.2, 0.3 and 0.4 M⊙. Figure adapted from Landin et al. (2006). |
| In the text | |
 |
Fig. 12 Period versus age for moderate rotators pMS stars of the ONC. Their positions in the period-age plane are compared with models with disk-locking for three different locking times (Tdisk = 0.2, 1, and 3 Myr) and Pdisk = 8 days. The symbols are the same as in Fig. 11, and the lines represent our models for 0.2 (solid), 0.3 (dotted), and 0.4 M⊙ (dashed). |
| In the text | |
 |
Fig. 13 Mass histogram of NGC 2264 stars. |
| In the text | |
 |
Fig. 14 Age histogram of NGC 2264 stars. |
| In the text | |
 |
Fig. 15 Mass (left) and age (right) distributions for NGC 2264 stars in common in our sample and that of Venuti et al. (2014). Solid curves refer to masses and ages obtained with our models, dotted curves refer to masses and ages obtained with the models of Siess et al. (2000). |
| In the text | |
 |
Fig. 16 Total period distribution for NGC 2264 stars. |
| In the text | |
 |
Fig. 17 Period histograms for our sample of pMS stars of NGC 2264. The left panel shows the period distribution for stars with Rc − Ic<1.65 mag (solid line) and with Rc − Ic> 1.65 mag (dotted line). This corresponds approximately to a division into stars with M> 0.3 M⊙ (solid line) and M< 0.3 M⊙ (dotted line), in the right panel. |
| In the text | |
 |
Fig. 18 Δ [ Rc − Hα ] versus stellar mass for NGC 2264 stars classified as early fast rotators (□), slow rotators (×), and moderate rotators (•). |
| In the text | |
 |
Fig. 19 Δ [ Rc − Hα ] versus rotation period for NGC 2264 stars. The symbols are the same as in Fig. 18. |
| In the text | |
 |
Fig. 20 Period versus age for early fast rotator pMS stars of NGC 2264. Their positions in the period-age plane are compared with models assuming evolution with constant angular momentum. Masses in the interval 0.2 <M/M⊙< 0.3 correspond to °, 0.3 <M/M⊙< 0.4 to ▪, 0.4 <M/M⊙< 0.6 to △ and all the remaining to ×. Solid lines represent models with Jin = Jkaw , while the dashed lines stand for models with Jin = 3Jkaw. |
| In the text | |
 |
Fig. 21 Period versus age for moderate rotators pMS stars of NGC 2264. Their positions in the period-age plane are compared with disk-locking models with Pdisk = 5 days and 0.2 (solid), 0.3 (dotted), 0.4 (dashed), and 0.5 M⊙ (dash-dotted). The symbols are the same as in Fig. 20. |
| In the text | |
 |
Fig. 22 Present period distribution of NGC 2264 stars that probably do not have a disk (left panel). Simulation of the period distribution of NGC 2264 stars when the objects had, on average, 1 Myr (right panel). |
| In the text | |
 |
Fig. 23 Same as Fig. 22, but distinguishing between lower (dotted lines) and higher (solid lines) mass stars (Mtr = 0.3 M⊙). |
| In the text | |
 |
Fig. 24 Simulated period distributions for lower and higher mass stars (Mtr = 0.3 M⊙) of NGC 2264 at mean ages of 0.8 Myr (left) and 1.3 Myr (right). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


