EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 585 (January 2016) A&A, 585 (2016) A83 Full HTML
Free Access
Issue
A&A
Volume 585, January 2016
Article Number A83
Number of page(s) 11
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201526720
Published online 23 December 2015

© ESO, 2015

1. Introduction

A key ingredient for many astrophysical calculations is a reliable equation of state (EoS) for isospin asymmetric matter, covering symmetric nuclear matter (SNM) and pure neutron matter (PNM), from low to high densities (≃4−5 times saturation density). The EoS is applied to describe neutron stars (NS) properties as the mass-radius relation or their inhomogeneous crust. Restricting ourselves to the category of nucleonic EoS, one of the most popular EoS is derived from (Baldo et al. 1997) and was obtained within the context of Brueckner-Bethe-Goldstone (BBG) many-body theory, using the Argonne v14 potential plus the Urbana model for the three-body nuclear interaction. Such an EoS has been tabulated for given values of the density of the system. For this reason, it is customary to fit the EoS with some analytical expressions which are much simpler to handle in numerical codes (Typel et al. 2013) suited for astrophysical simulations.

A possible alternative to the fit is the use of an effective Skyrme interaction (Skyrme 1959) as suggested earlier by (Cao et al. 2006). These authors have shown that it is possible to fit an effective Skyrme functional (which they named LNS) onto BBG, conserving some of the main features of the original BBG EoS. The main advantage of using a functional, instead of a generic interpolation, as done by, for instance (Haensel & Potekhin 2004), is that once the parameters of the functional are fixed, all basic properties as pressure or symmetry energy can simply be obtained by standard derivative operations. In the case where the vector part of the functional is also taken into account, one can describe collective phenomena within the NS, with a simple formalism based on the Linear Response (LR) theory (Pastore et al. 2015). Collective excitations play a crucial role in understanding different phenomena in the NS as the thermal properties of the inner crust (Chamel et al. 2013) or the neutrino mean free path (Iwamoto & Pethick 1982). Another important advantage is that the same functional can also be consistently used to describe the region of the crust of the NS (Chamel & Haensel 2008), thus enabling a unified description of the star. Although LNS gives a nice reproduction on infinite matter properties up to two times saturation density, its EoS in pure neutron matter deviates from the BBG results remarkably, leading to a different behavior of the symmetry energy at high density. It follows that the LNS EoS only supports NS with mass lower than 1.6 Solar-masses as shown by (Singh et al. 2013). The authors of (Gambacurta et al. 2011) recently refitted the LNS functional, but the new LNS1 and LNS5 do not substantially improve the properties of the homogeneous nuclear medium, as compared to the original LNS, although they improve the description of the finite nuclei. In the present article, we generalize the analysis done by (Cao et al. 2006), which concerns the possibility of constraining a phenomenological Skyrme functional on microscopic results, by using an extended Skyrme functional that includes up to sixth order derivative terms (Carlsson et al. 2008; Raimondi et al. 2011), and which aims to also give a reliable EoS in the high density region and thus be in better agreement with BBG results.

Indeed, the Skyrme interaction can be interpreted as a low-momentum expansion of a finite-range interaction (Skyrme 1959). The standard form of the interaction is the one given by (Vautherin & Brink 1972) that takes into account only gradient terms up to the second power, as for LNS. Although this can be viewed as a good approximation to be used in finite nuclei calculations (Bender et al. 2003), it is not adapted to the study of dense nuclear matter. For example, the standard Skyrme interaction is not able to reproduce the correct isovector splitting of the effective mass of BBG results (Baldo et al. 2014b) at the same time, nor the high density behavior of nuclear matter. Among the different strategies one can adopt to overcome these difficulties, the most promising implies either the addition of extra density dependencies on the velocity dependent terms (Chamel & Goriely 2010) or the inclusion of higher order derivative terms (Carlsson et al. 2008). We prefer to follow the latter approach since it enables us to grasp the correct behavior of the EoS of BBG calculations, especially at high density. In particular, it has been shown (Davesne et al. 2015b) that the different terms follow a precise hierarchy, and thus high-order terms have stronger influence on the high-density part, inducing almost negligible modification to the low-density part. Such a result is also in good agreement with previous findings of (Carlsson & Dobaczewski 2010), based on density matrix expansion methods in finite nuclei. In this respect, the functional presented here can be considered as the natural extension of the LNS to correct the high density region. In the present article, we thus present an extended Skyrme functional, hereafter called LYVA1 to treat these higher order gradients properly, and providing all necessary analytical expressions for astrophysical calculations. A numerical code and the tabulated values of this new EoS will be available at the CompOSE webpage1.

The article is organized as follows. In Sect. 2 we present the general formalism of the extended Skyrme functional. In Sect. 3 we give the general formula for the binding energy per particle for isospin asymmetric nuclear matter, while in Sect. 4 we present the case of polarized matter. In Sect. 5, we study the behavior of the symmetry energy. In Sect.6 we discuss further the behavior of the effective mass, and in Sect. 7 we examine the applications of our model to the description of an NS. Our conclusions are then drawn in Sect. 8.

2. Extended Skyrme interaction

The most general form of the Skyrme functional up to sixth order in the gradient expansion has been derived by (Carlsson et al. 2008). In the present article, we prefer to relate this functional to an effective interaction, thus reducing the number of free coupling constants, as shown in (Davesne et al. 2013). The corresponding Skyrme interaction reads (Raimondi et al. 2011; Davesne et al. 2014)

vSk=t0(0)(1+x0(0)Pσ)+16t3(0)(1+x3(0)Pσ)nα(R)+12t1(2)(1+x1(2)Pσ)[k′2+k2]+t2(2)(1+x2(2)Pσ)k′·k+14t1(4)(1+x1(4)Pσ)[(k′2+k2)2+4(k′·k)2]+t2(4)(1+x2(4)Pσ)(k′·k)(k′2+k2) +12t1(6)(1+x1(6)Pσ)(k′2+k2)[(k′2+k2)2+12(k′·k)2]+t2(6)(1+x2(6)Pσ)(k′·k)[3(k′2+k2)2+4(k′·k)2].\begin{eqnarray} \label{sk:ext} v^{}_{Sk}&=&t^{(0)}_{0}\left(1+x^{(0)}_{0}P_{\sigma}\right)+\frac{1}{6}t^{(0)}_{3}\left(1+x^{(0)}_{3}P_{\sigma}\right)n^{\alpha}(\vec{R})\nonumber\\ &&+\frac{1}{2}t^{(2)}_{1}\left(1+x^{(2)}_{1}P_{\sigma}\right)\left[\vec{k}^{'2}+\vec{k}^{2} \right]+t^{(2)}_{2}\left(1+x^{(2)}_{2}P_{\sigma}\right)\vec{k}^{'}\cdot \vec{k}\nonumber\\ &&+\frac{1}{4}t_{1}^{(4)}\left(1+x^{(4)}_{1}P_{\sigma}\right)\left[(\vec{k}^{'2}+\vec{k}^{2})^{2}+4(\vec{k}'\cdot\vec{k})^{2} \right]\nonumber\\ &&+t_{2}^{(4)}\left(1+x^{(4)}_{2}P_{\sigma}\right)(\vec{k}^{'}\cdot \vec{k})(\vec{k}^{'2}+\vec{k}^{2})\,\nonumber\\ &&+\frac{1}{2}t_{1}^{(6)}\left(1+x^{(6)}_{1}P_{\sigma}\right)(\vec{k}^{'2}+\vec{k}^{2})\left[(\vec{k}^{'2}+\vec{k}^{2})^{2}+12(\vec{k}'\cdot\vec{k})^{2} \right]\nonumber\\ &&+t_{2}^{(6)}\left(1+x^{(6)}_{2}P_{\sigma}\right)(\vec{k}^{'}\cdot \vec{k})\left[3(\vec{k}^{'2}+\vec{k}^{2})^{2}+4(\vec{k}^{'}\cdot\vec{k})^{2}\right]. \end{eqnarray}(1)The notations used here are standard and more details can be found in (Bender et al. 2003). The spin-orbit and tensor terms are discarded here since they do not contribute to the total EoS, although they do contribute to its multipolar partial wave decomposition, as shown by (Davesne et al. 2015a). The corresponding functional form can be obtained by performing an average on Hartree-Fock states. Results for a homogeneous medium are given in Eq. (5). An important advantage of deriving a functional from an effective interaction is that, when applied to a single nucleon, the functional leads to vanishing internal energy. This is not an automatic guarantee for a generic phenomenological functional, which thus implyies that the nucleon may be interacting with itself (Chamel 2010).

The parameters 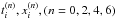ti(n),xi(n),(n=0,2,4,6)\hbox{$t^{(n)}_{i}, x^{(n)}_{i}, (n=0,2,4,6)$} of this effective interaction were fitted following the method illustrated by (Davesne et al. 2015b), to the results of a BBG calculation (Baldo et al. 1997; Baldo 2014), based on the microscopic Argonne v14 nucleon-nucleon two-body interaction plus the Urbana model for the three-body term. Although more recent BBG calculations for the EoS are available (as for instance Zhou et al. 2004), to determine the parameters completely, we also require the spin/isospin decomposition of the potential energy. To the best of our knowledge, the BBG results of (Baldo et al. 1997) are the most complete, and include results for other important astrophysical quantities. Other ab initio results also exist that were obtained from chiral effective field calculations at Vlow−k (Hebeler et al. 2011) or the many-body perturbation theory (Bogner et al. 2005; Rotival 2008). In (Davesne et al. 2015b), we show that it is possible to fix the parameters of the extended Skyrme functional by also using these calculations. However, they presently cover a narrower density range than BBG results, and are therefore not yet suited for our present purpose. We thus rely on the BBG results of (Baldo et al. 1997). The inputs for the fit include the projection of the energy per particle in the different spin (S) and isospin (T) channels in symmetric nuclear matter, and the EoS of both SNM and pure neutron matter. As discussed by (Davesne et al. 2015b), no density-dependent term, i.e., 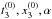t3(0),x3(0),α\hbox{$t^{(0)}_3, x^{(0)}_3, \alpha$} parameters, is required to get satisfactory fits, but the resulting parameterizations give too low a value for the Landau effective mass of SNM at saturation (m∗/m ≃ 0.4). In this paper, the density-dependent term is thus taken into account, and we have fixed its parameters to the values α = 1/6, 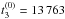t3(0)=13 763\hbox{$t^{(0)}_{3}=13\,763$} [MeV fm3+α], and 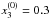x3(0)=0.3\hbox{$x^{(0)}_{3}=0.3$}. In such a way, we can properly constrain the higher order derivative terms, whose role is mainly to give the correct asymptotic behavior at high density.

thumbnail Fig. 1

Equations of state of SNM and PNM (panel a)) and projections (S,T) in SNM (panel b)), both expressed in MeV. The solid lines represent the result obtained with our extended Skyrme interaction, while the dots represent the EoS obtained by (Baldo et al. 1997). The LNS results are represented by dashed-lines.

thumbnail Fig. 2

Equations of state of SNM (panel a)) and PNM (panel b)) obtained using the LYVA1 interaction (solid) the BSk models (dashed) and the BCMP functional (dotted).

Table 1

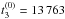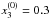Parameters of the extended LYVA1 Skyrme interaction, with α = 1/6, t3(0)=13 763\hbox{$t^{(0)}_{3}=13\,763$} [MeVfm3+α], and x3(0)=0.3\hbox{$x^{(0)}_{3}=0.3$}.

To fix the remaining parameters we proceeded using two steps. In a first step, we considered the interaction (1) up to fourth order in the gradient expansion only. The parameters 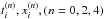ti(n),xi(n),(n=0,2,4)\hbox{$t^{(n)}_{i}, x^{(n)}_{i}, (n=0,2,4)$} were determined by fitting BBG results for SNM EoS and (S,T) channels. However, since the resulting EoS for PNM is too rigid at high densities, we added sixth order parameters on top of the previously determined fourth order values. 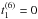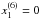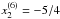To keep the quality of the SNM EoS, we imposed the values t1(6)=0\hbox{$t^{(6)}_{1}=0$}, x1(6)=0\hbox{$x^{(6)}_{1}=0$}, and x2(6)=−5/4\hbox{$x^{(6)}_{2}=-5/4$}. The remaining sixth order parameter 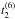t2(6)\hbox{$t^{(6)}_2$} was then determined by fitting the PNM EoS in the full density interval. The resulting parameters of the LYVA1 interaction are given in Table 1.

Figure 1 shows the EoS for SNM and PNM (see panel a), and the SNM potential energy decomposition in the different spin-isospin (S,T) channels (see panel b). Our fit is clearly very good for both EoS. The results obtained using LNS are also displayed, and one can see a rapid deviation of the PNM EoS, starting from n ≈ 0.4 fm-3; one can expect this deviation to have an impact on other quantities, such as the symmetry energy at high values of the density. Let us now turn to the results for the (S,T)-channels shown in panel b. As already discussed in (Lesinski et al. 2006), a general drawback of the standard Skyrme functional is that the simultaneous reproduction of the (S,T)-channels is very difficult, to say the least. In Fig. 1, we can see the particular LNS case, which fails to reproduce BBG results. In contrast, with the extended functional, the S = 1 channels are nicely fitted in the full range of density values, whereas the S = 0 channels show a deviation for n ≥ 0.6 fm-3, as a consequence of our giving more weight to PNM data in the fit. All the other quantities presented hereafter in the article have not been fitted, and they can be considered as a prediction of our model.

It is worth mentioning that some other functionals have been developed with particular attention to the properties of NS. Among the non-relativistic ones, we consider the BCPM (Baldo et al. 2013, 2014a; Sharma et al. 2015) and the BSk family (Goriely et al. 2009, 2013). The BCPM functional has been derived in a complete Khon-Sham scheme (thus not related to any interaction) and it was explicitly constrained to reproduce BBG results in homogeneous matter. The BSk models were derived from an effective Skyrme interaction with the addition of a power of the density into the momentum dependent terms of the standard Skyrme interaction. The BSk models were constrained on several nuclear observables as masses and radii of finite nuclei together with additional pseudo-observables of homogeneous nuclear matter. In Fig. 2, we compare the EoS in both SNM and PNM obtained with LYVA1, the BCPM functional, and three representative BSk interactions, BSk19, BSk20, and BSk21 (Chamel et al. 2011). Since the BCPM functional fits the same microscopic EoS as LYVA1, we observe that the resulting curves are almost on top of each other, except in the saturation region where the BCPM has been adjusted to give a value of saturation density n0 = 0.16fm-3 and E/A = −16 MeV. We note that the BCMP was fitted up to n = 0.6 fm-3 and that beyond that value the microscopic results of (Burgio & Schulze 2010) were used. To be consistent, we thus omit the points beyond 0.6 fm-3 in this paper.

With regard to the BSk functionals, we used the generalized expressions given in (Lesinski et al. 2007) to obtain their (S,T) decomposition. We note that, as for the SLy4 case (Chabanat et al. 1997), the coupling constants in front of the so-called J2 term are switched to zero. This choice is justified in (Chamel & Goriely 2010) to avoid the appearance of spurious ferromagnetic phase-transitions in the homogeneous medium (Margueron et al. 2002) and anomalous behavior of the entropy. In Fig. 3, we compare the results obtained with the BSk models and the BBG calculations. We observe that the BSk19-21 behave more consistently than any standard Skyrme interactions (Lesinski et al. 2007) since, in the low-density region (≈n0), they give the correct sign and trend of the energy per particle. In the same figure, we also report the chiral effective field theory (χ-EFT) calculations at low momentum k (Hebeler et al. 2011). The χ-EFT results are in very good agreement with the BBG results, apart from the (S = 1,T = 1) channel. Such a comparison gives us the level of uncertainty related to the adopted interaction and/or calculation technique.

thumbnail Fig. 3

Same as Fig. 1, but for the BSk model discussed in the text.

3. Energy per particle

In this section, we give the analytical expression of the binding energy per particle (E/A) for infinite systems with isospin unbalance, which we call asymmetric nuclear matter (ANM). Other relevant quantities can be easily derived from this, including SNM and PNM. It is convenient to define an isospin asymmetry parameter as 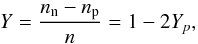Y=nn−npn=1−2Yp,\begin{eqnarray} Y=\frac{n_{\text{n}}-n_{\text{p}}}{n}=1-2Y_{p}, \end{eqnarray}(2)where nn(p) is the neutron (proton) density, n = nn + np is the total density of the system, and Yp is the proton fraction. When the asymmetry parameter is equal to Y = 0 we are in the SNM case, while for Y = 1, we are in the other extreme case, i.e. PNM. To present the expressions in a compact, yet transparent, form we define the coefficients a = (3π2/ 2)1/3 and b = (3π2)1/3, and the following functions of the asymmetry parameter Fx=12[(1+Y)x+(1−Y)x],Gx=12[(1+Y)x−(1−Y)x].\begin{eqnarray} F_x &=& \frac{1}{2} \left[(1+Y)^x + (1-Y)^x \right], \\ G_x &=& \frac{1}{2} \left[(1+Y)^x - (1-Y)^x \right]. \end{eqnarray}The EoS in ANM reads EA=35ħ22ma2F5/3n2/3+t0(0)8[3−(2x0(0)+1)Y2]n+t348[3−(2x3+1)Y2]nα+1+380a2[C0(2)F5/3+C1(2)YG5/3]n5/3+3a41120[C0(4)(5F7/3+7F5/32)+C1(4)(5YG7/3+7G5/32)]n7/3+a6240[C0(6)(5F3+27F7/3F5/3)]n3+a6240[C1(6)(5YG3+27G7/3G5/3)]n3.\begin{eqnarray} \label{eosanm} \frac{E}{A} &=&\frac{3}{5}\frac{\hbar^{2}}{2m} a^2 F_{5/3} n^{2/3}\nonumber\\ && +\frac{t^{(0)}_{0}}{8} \left[3 - \left(2x^{(0)}_{0}+1\right) Y^2 \right] n +\frac{t_{3}}{48} \left[3 - (2x_{3}+1) Y^2 \right] n^{\alpha+1} \nonumber\\ && +\frac{3}{80} a^2 \left[C^{(2)}_{0} F_{5/3} + C^{(2)}_{1} Y G_{5/3} \right] n^{5/3} \nonumber\\ && +\frac{3 a^4}{1120} \left[C^{(4)}_{0} \left( 5 F_{7/3} +7 F_{5/3}^2 \right) + C^{(4)}_{1} \left( 5 Y G_{7/3} +7 G_{5/3}^2\right) \right] n^{7/3} \nonumber\\ &&+\frac{a^6}{240} \left[C^{(6)}_{0} \left( 5 F_{3} +27 F_{7/3} F_{5/3} \right) \right] n^3 \nonumber\\ &&+\frac{a^6}{240} \left[C^{(6)}_{1} \left( 5 Y G_{3} +27 G_{7/3} G_{5/3} \right) \right] n^3 . 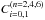\end{eqnarray}(5)The constants Ci=0,1(n=2,4,6)\hbox{$C^{(n=2,4,6)}_{i=0,1}$} are the following combinations of Skyrme parameters 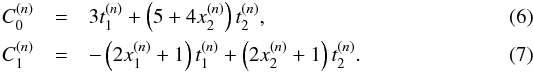C0(n)=3t1(n)+(5+4x2(n))t2(n),C1(n)=−(2x1(n)+1)t1(n)+(2x2(n)+1)t2(n).\begin{eqnarray} C^{(n)}_{0}&=& 3t^{(n)}_{1}+\left(5+4x^{(n)}_{2}\right)t^{(n)}_{2} ,\\ C^{(n)}_{1}&=& -\left(2x_{1}^{(n)}+1\right)t_{1}^{(n)}+\left(2x^{(n)}_{2}+1\right)t^{(n)}_{2}. \end{eqnarray}In Fig. 4, we show the binding energy per particle obtained with our new functional as a function of the density and the asymmetry parameter Y of the system. As expected, the energy minimum is located at Y = 0 with the values E/A = −17.02 [MeV] and n0 = 0.169 [fm-3]. These values are slightly larger than commonly adopted ones (Dutra et al. 2012). This is a drawback of the BBG calculations used to fix the parameters that have E/A = −16.46 [MeV] and n0 = 0.178 [fm-3] (Baldo et al. 1997). We decided not to adjust the saturation point to the standard value as extracted, for example from mass formulas (Bohr & Mottelson 1998), and keep the value obtained by the direct fit, as performed for LNS (Cao et al. 2006). Due to uncertainties related to three-body forces (Baldo 1999) and the methods adopted for the calculations (Baldo et al. 2012), these values can change from one ab-initio method to another. The goal of the present article is to prove that a simple Skyrme functional can grasp the main features of a more complicated calculation, based on realistic nucleon-nucleon interactions. As a consequence we prefer not to do any fine-tuning around the saturation point, since it will not change the main conclusions of the present work.

thumbnail Fig. 4

Equations of states in asymmetric nuclear matter as a function of the density n and asymmetry parameter Y.

Table 2

Basic SNM properties calculated with the LYVA1 parametrization given in Tab.1, the BCPM and the BSk19-21 functionals at saturation density n0.

From Eq. (5), we can also extract other quantities, as the pressure of the system 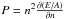P=n2∂(E/A)∂n\hbox{$P=n^2\frac{\partial (E/A)}{\partial n}$} or the nuclear incompressibility 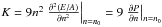K=9n2∂2(E/A)∂n2|n=n0=9∂P∂n|n=n0\hbox{$K=9n^2\left.\frac{\partial^2 (E/A)}{\partial n^2}\right|_{n=n_0}=9\left.\frac{\partial P}{\partial n}\right|_{n=n_0}$}, as functions of the asymmetry parameter Y. In Table 2, we report several relevant SNM quantities that were calculated at saturation density. Our parametrization gives a value of the incompressibility of K = 231 MeV at saturation density, which is within the range of acceptable values as discussed by (Dutra et al. 2012). The third derivative of the EoS gives us the skewness Q.

The two limiting cases of symmetric nuclear matter and pure neutron matter can be immediately obtained from Eq. (5), as E/A|SNM=35ħ22ma2n2/3+38t0(0)n+116t3nα+1+380a2C0(2)n5/3+9280a4C0(4)n7/3+215a6C0(6)n3,E/N|PNM=35ħ22mb2nn2/3+14(1−x0(0))t0(0)nn+124(1−x3)t3nnα+1+380b2[C0(2)+C1(2)]nn5/3+9280b4[C0(4)+C1(4)]nn7/3+215b6[C0(6)+C1(6)]nn3.\begin{eqnarray} \left.\phantom{\frac{1}{1}} E/A \right|_{\rm SNM}\! &=&\! \frac{3}{5}\frac{\hbar^{2}}{2m} a^2 n^{2/3} + \frac{3}{8} t^{(0)}_{0}n + \frac{1}{16} t_{3}n^{\alpha+1} \nonumber\\ &&+\frac{3}{80} a^2 C^{(2)}_{0} n^{5/3}\! +\!\frac{9}{280} a^4 C^{(4)}_{0} n^{7/3}\!+\! \frac{2}{15} a^6 C^{(6)}_{0} n^3 ,\\ \left.\phantom{\frac{1}{1}}E/N \right|_{\rm PNM} \!&=&\! \frac{3}{5}\frac{\hbar^{2}}{2m} b^2 n_{\text n}^{2/3} + \frac{1}{4} \left(1-x^{(0)}_0\right) t^{(0)}_0 n_{\text{n}}\nonumber\\ &&+ \frac{1}{24} (1-x_3) t_3 n_{\text{n}}^{\alpha+1}+\frac{3}{80} b^2 \left[C^{(2)}_{0}+ C^{(2)}_{1}\right] n_{\text{n}}^{5/3} \nonumber\\ &&+\frac{9}{280} b^4 \left[C^{(4)}_{0}\!+\! C^{(4)}_{1}\right] n_{\text{n}}^{7/3} \!+\!\frac{2}{15} b^6 \left[C^{(6)}_{0}\!+\! C^{(6)}_{1}\right] n_{\text{n}}^3 .\nonumber\\ \end{eqnarray}In Fig. 5, we show the evolution of the pressure P as a function of the density in SNM for LYVA1, BSk19-21, and BCPM. The two areas represent the constraints obtained on the EoS by using experimental observations of heavy-ion collisions (Danielewicz et al. 2002) and by observations of experiments on kaons (Fuchs 2006). We observe that the LYVA1 functional is perfectly consistent with such results.

thumbnail Fig. 5

The pressure as a function of the density in SNM for the different models considered in the article. See text for details.

In Fig. 6, we compare the resulting EoS in PNM for the LYVA1 functional and the results of several microscopic calculations (Akmal et al. 1998; Li & Schulze 2008; Baldo et al. 1997; Gandolfi et al. 2012). We observe that our EoS is compatible with these calculations up to three times the saturation density; beyond that value the different calculations differ strongly from each other. It is thus very important to adopt the same microscopic calculation to constrain both the PNM and SNM EoS, otherwise one would obtain untrustworthy results concerning the behavior of the symmetry energy.

thumbnail Fig. 6

The EoS in PNM for the different models discussed in the text. The shaded area represents the constraints extracted from (Gandolfi et al. 2012).

In Fig. 7, we show the pressure P in PNM for the different models discussed here as well as some additional constraints derived in (Danielewicz 2003), and based on the analysis of heavy-ion collisions. We observe that both the BCPM and LYVA1 models are in good agreement with the constraints extracted, assuming a soft EoS. See (Danielewicz 2003) for more details.

thumbnail Fig. 7

The pressure as a function of the density in PNM for the different models considered in the article. The grey areas are derived from the analysis of (Danielewicz 2003).

The sound velocity vs of a system is obtained in the non-relativistic limit from the isothermal incompressibility ∂n/∂P. We refer to (Haensel et al. 2007) for a more detailed discussion. The explicit expression for PNM reads mnc2(vsc)2=23ħ22mb2nn2/3+12(1−x0(0))t0(0)nn+124(1−x3(0))t3(0)(1+α)(2+α)nnα+1+16b2[C0(2)+C1(2)]nn5/3+14b4[C0(4)+C1(4)]nn7/3+85b6[C0(6)+C1(6)]nn3.\begin{eqnarray} m_{\rm n} c^2 \left(\frac{v_{\rm s}}{c} \right)^2 &=&\frac{2}{3}\frac{\hbar^{2}}{2m} b^2 n_{\text n}^{2/3} +\frac{1}{2} \left(1-x_0^{(0)}\right)t_0^{(0)} n_{\text n}\nonumber\\ &&+\frac{1}{24}\left(1-x_3^{(0)}\right)t_3^{(0)}(1+\alpha)(2+\alpha)n_{\text{n}}^{\alpha+1} \nonumber\\ &&+\frac{1}{6} b^2 \left[C^{(2)}_{0}+ C^{(2)}_{1}\right] n_{\text{n}}^{5/3} +\frac{1}{4} b^4 \left[C^{(4)}_{0}+ C^{(4)}_{1}\right] n_{\text{n}}^{7/3}\nonumber\\ &&+\frac{8}{5} b^6 \left[C^{(6)}_{0}+ C^{(6)}_{1}\right] n_{\text{n}}^3. \end{eqnarray}(10)In Fig. 8, we show the evolution of vs in PNM as a function of the density. We observe that our parametrization respects the causality principle (there is actually a maximum around 1.1 fm-3 with vs/c = 0.97), and is thus reliable for the description of high density neutron matter. In the same figure, we also compare the results obtained with the BSk models. We notice that the BSk21 model violates causality in PNM at n ≈ 0.8 fm-3. As discussed in (Goriely et al. 2010), the BSk models assure the causality principle in β-equilibrium nuclear matter for the density ranges found in NS. We exclude the BCPM model from this analysis since its analytical expressions are strictly valid, by construction, only in the low density regime.

We note that, although the causality principle is always respected by the LYVA1 functional, a speed of sound, which is very close to the speed of light, is clearly a symptom of the use of the non-relativistic approximation to treat matter very close to the relativisitic limit.

thumbnail Fig. 8

The speed of sound in PNM as a function of the density of the system. The notation is as in Fig.1.

4. Polarized matter

A major drawback of several effective interactions is the presence of a spontaneous ferromagnetic transition (Vidaurre et al. 1984) at densities relevant for the physics of nuclei and NS. However, no such a spontaneous phase transition has so far been observed by any microscopic calculation (Pandharipande et al. 1972; Fantoni et al. 2001; Vidana et al. 2002). It is thus interesting to determine the behavior of our interaction in relation to this aspect.

The expressions for the energy per particle in fully polarized pure neutron matter (PolPNM) reads 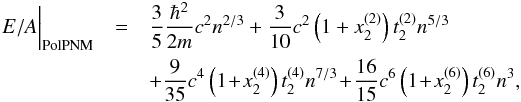E/A|PolPNM=35ħ22mc2n2/3+310c2(1+x2(2))t2(2)n5/3+935c4(1+x2(4))t2(4)n7/3+1615c6(1+x2(6))t2(6)n3,\begin{eqnarray} \left.\phantom{\frac{1}{1}} E/A \right|_{\rm PolPNM} &=&\frac{3}{5}\frac{\hbar^{2}}{2m} c^2 n^{2/3} +\frac{3}{10} c^2\left(1+x^{(2)}_{2}\right) t^{(2)}_{2} n^{5/3}\nonumber\\ &&+\frac{9}{35} c^4\left(1\!+\!x^{(4)}_{2}\right) t^{(4)}_{2} n^{7/3}\!+\!\frac{16}{15} c^6\left(1\!+\!x^{(6)}_{2}\right) t^{(6)}_{2} n^{3},\nonumber\\ \end{eqnarray}(11)where we have used the notation c = (6π2)1/3. In the following we compare the results obtained with the LYVA1 functional and available BBG calculations of (Bombaci et al. 2006). More precisely, in Fig. 9, we show the difference of energy per particle between PolPNM and PNM, that is ΔE/A = E/A|PolPNM−E/A|PNM obtained with the LYVA1 functional and the BBG results of (Bombaci et al. 2006). To be consistent, we consider only, for this particular case, the results up to ≈3 n0, since the treatment of the three-body term at high density is not the same as that used in BBG results of (Baldo et al. 1997) and used here for the fit of the LYVA1 functional. We observe that the LYVA1 as well as BSk20 follow pretty closely the BBG results, while the BSk19(21) tends to underestimate (overestimate) the energy difference between the two systems. The LNS functional is not stable against polarization and at densities n ≈ 0.6 [fm-3] favors the appearance of polarized neutron matter. The BCPM functional has not been included in such analysis since the functional has not been tailored to describe polarized systems.

thumbnail Fig. 9

Energy difference between PolPNM and PNM for the different models considered in the text.

thumbnail Fig. 10

Symmetry energy as a function of the density of the system for different models (left panel). The dots correspond to the BBG calculations. In the right panel we compare the constraints extracted using IAS (Danielewicz & Lee 2014). See text for details.

5. Symmetry energies

We give now the LYVA1 expression for the isospin symmetry energy εT(n), which plays a crucial role in determining the composition of the NS, since the β-equilibrium condition strongly depends on it. It follows that reproducing the symmetry energy, not only at saturation but also as a function of the density, is a necessary condition to have a reliable extrapolation of the high density part of the NS. Starting from the complete expression of Eq. (5), we can expand the binding energy per particle up to second order in the following way 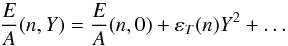EA(n,Y)=EA(n,0)+εT(n)Y2+...\begin{equation} \frac{E}{A}(n,Y)= \frac{E}{A}(n,0)+ \varepsilon_{T}(n)Y^2+\dots \end{equation}(12)to get the result 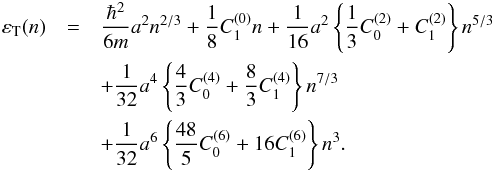εT(n)=ħ26ma2n2/3+18C1(0)n+116a2{13C0(2)+C1(2)}n5/3+132a4{43C0(4)+83C1(4)}n7/3+132a6{485C0(6)+16C1(6)}n3.\begin{eqnarray} \label{eq:sym} \varepsilon_{\rm T}(n)&=&\frac{\hbar^{2}}{6m} a^2 n^{2/3}+\frac{1}{8}C_{1}^{(0)}n +\frac{1}{16} a^2 \left\{\frac{1}{3} C_{0}^{(2)}+C_{1}^{(2)} \right\} n^{5/3} \nonumber\\ &&+\frac{1}{32} a^4 \left\{\frac{4}{3}C_{0}^{(4)}+\frac{8}{3}C_{1}^{(4)} \right\} n^{7/3} \nonumber\\ &&+ \frac{1}{32} a^6 \left\{\frac{48}{5}C_{0}^{(6)}+16C_{1}^{(6)}\right\} n^3. \end{eqnarray}(13)In Fig. 10, we show the evolution of the symmetry energy εT as a function of the density of the system. At saturation density, we obtain a value of the symmetry energy εT(n0) = J = 33.8 MeV, a value compatible with most recent constraints on J that has been obtained combining different experimental data (Tsang et al. 2009). Furthermore, we observe an excellent agreement – up to several times the saturation density value – between our results and the BBG ones. In the same figure, we also compare the evolution of the symmetry energy for the BCPM and BSk models. We observe that, while BCPM gives by construction results that overlap with ours for low density, the BSk19-21 give very different behaviors, especially beyond saturation density. There is no agreement between different microscopic approaches concerning the behavior of εT beyond saturation density. We refer to the discussion in (Goriely et al. 2010). A possible way to determine the correct trend of εT at high density is the predicted proton fraction and, thus, the possibility or not of allowing direct Urca process (Haensel 1995). We refer to Sect. 7 for a more detailed discussion. In any case, we can anticipate that BSk19-20 and LNS are not compatible with such additional constraints. In Panel (b), we compare the results at low density that were obtained with the different models and the constraints obtained in (Danielewicz & Lee 2014). The large yellow area represents the constraints extracted by analyzing data on isobaric analog states (IAS), while the smaller area, delimitated by the solid line contour, were obtained by studying data on the neutron skin properties of some selected nuclei. All the functionals considered in the text respect these constraints.

It is important to remember that a parabolic approximation was used in (Baldo et al. 1997) to extract the symmetry energy and the validity of such an approximation has been tested only in the region n ∈ [0,0.4] fm-3 (Bombaci & Lombardo 1991; Goriely et al. 2010). In this case the symmetry energy is obtained as the difference between the EoS in PNM and SNM 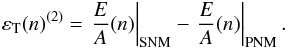εT(n)(2)=EA(n)|SNM−EA(n)|PNM.\begin{eqnarray} \label{eq:sym:parab} \varepsilon_{\rm T}(n)^{(2)}= \left.\frac{E}{A}(n)\right|_{\rm SNM}- \left.\frac{E}{A}(n)\right|_{\rm PNM}. \end{eqnarray}(14)In Fig. 11, we compare the results for the LYVA1 functional using the definition of Eqs. (13) and (14). We observe that using the parabolic approximation we obtain a better reproduction of the high density part of the BBG results of (Baldo et al. 1997). The agreement is still not perfect because of the small overestimate of the EoS for PNM, which results in our fit and is shown in Fig. 1. We note that, in our calculations, the two definitions of the symmetry energy of Eqs. (13) and (14) overlap up to n ≈ 0.6 [fm-3].

thumbnail Fig. 11

Symmetry energy as a function of the density of the system using different definition of the symmetry energy. The dots represent the BBG results. See text for details.

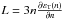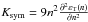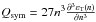For completeness, we also define additional quantities related to the symmetry energy as L=3n∂εT(n)∂n\hbox{$L= 3n\frac{\partial \varepsilon_{\rm T}(n)}{\partial n}$}, Ksym=9n2∂2εT(n)∂n2\hbox{$K_{\rm sym}= 9n^2\frac{\partial^2 \varepsilon_{\rm T}(n)}{\partial n^2}$}, and Qsym=27n3∂3εT(n)∂n3\hbox{$Q_{\rm sym}= 27 n^3\frac{\partial^3 \varepsilon_{\rm T}(n)}{\partial n^3}$}. Their values at saturation density are reported in Tab. 2. The constraints on these quantities are much less strict, leading to larger error bars (Dutra et al. 2012). However, the value obtained here, e.g., for L, is compatible with some recent estimates (Chen et al. 2010) and extracted from finite nuclei analysis.

6. Effective mass

The effective mass is directly related to some important processes as neutrino emissivity (Yakovlev et al. 2001). We thus give the explicit expressions for the neutron (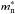mn∗\hbox{$m^*_{\rm n}$}) and proton (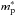mp∗\hbox{$m^*_{\rm p}$}) Landau effective masses at the Fermi surface as a function of the density and of the asymmetry of the system. For neutrons it reads ħ22mn∗−ħ22mn=116(C0(2)+C1(2)Y)n+a216[(C0(4)+C1(4)Y)(F2/3+G2/3)+C0(4)F5/3+C1(4)G5/3]n5/3+a416n7/3[3(C0(6)+C1(6)Y)(F4/3+G4/3)+425(C0(6)F5/3+C1(6)G5/3)(F2/3+G2/3)+3(C0(6)F7/3+C1(6)G7/3)].\begin{eqnarray} &&\frac{\hbar^2}{2m_{\rm n}^*}-\frac{\hbar^2}{2m_{\rm n}}=\frac{1}{16}\left( C^{(2)}_0 + C^{(2)}_1 Y \right) n \nonumber\\ &&~+\frac{a^2}{16} \left[\left( C^{(4)}_0 + C_1^{(4)} Y \right) \left( F_{2/3} + G_{2/3} \right) + C_0^{(4)} F_{5/3} + C_1^{(4)} G_{5/3} \right] n^{5/3} \nonumber\\ &&~+ \frac{a^4}{16} n^{7/3} \left[3 (C_0^{(6)} + C_1^{(6)} Y )( F_{4/3}+G_{4/3}) \right.\nonumber\\ &&~+\left.\frac{42}{5} ( C_0^{(6)} F_{5/3} \!+\! C_1^{(6)} G_{5/3} ) (F_{2/3} \!+\! G_{2/3} ) \!+\! 3 ( C_0^{(6)} F_{7/3}\! +\! C_1^{(6)} G_{7/3} ) \right].\nonumber\\[-1mm] \end{eqnarray}(15)The proton effective mass is obtained simply by replacing Y → −Y in the previous expression. It is worth noting that, contrary to the standard Skyrme interaction, the effective mass for our pseudopotential has an explicit dependence on the momentum k, as happens in the case of real BBG calculations. See (Becker et al. 2014) for more details.

In Fig. 12, we show the evolution of the effective mass for neutrons and protons as a function of the asymmetry parameter at saturation density. We observe that the mass splitting 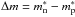Δm=mn∗−mp∗\hbox{$\Delta m=m^*_{\rm n}-m^*_{\rm p}$} has the correct sign and density behavior, compared with BBG results (Baldo et al. 2014b), although the resulting effective masses are slightly lower at saturation in the SNM case (m∗/m ≃ 0.7) compared to the BBG result (m∗/m ≃ 0.8). Such a difference can be further reduced by a better fine-tuning of the 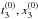t3(0),x3(0)\hbox{$t_3^{(0)},x_3^{(0)}$} parameters without inducing side-effects on other quantities.

thumbnail Fig. 12

Neutron and proton effective mass at saturation density as a function of the asymmetry parameter Y. The dots correspond to the BBG calculations (Baldo et al. 2014b), the solid line to LYVA1 interaction.

In Fig. 13a, we compare the effective mass in SNM calculated with the LYVA1 functional and the corresponding BBG results as a function of the density of the system. Although the difference between the two calculations increases with the density reaching at most 30% in the high density region, the asymptotic behavior is correct with a positive slope at high densities. On the same figure, we also show the results obtained from the different BSk models (concerning BCPM, it was fitted by imposing the bare nucleon mass at all densities and all asymmetries). The major difference between the BSk and LYVA models is related to the high density behavior, where the former lead to a much smaller effective mass compared to BBG results. In Fig. 13b, we show the evolution of the difference between neutron and proton effective mass 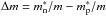Δm=mn∗/m−mp∗/m\hbox{$\Delta m= m^*_{\rm n}/m- m^*_{\rm p}/m$} at n0 = 0.169 fm-3 for the different models discussed in this article. We notice that the BSk19-20 models give a much larger splitting than the one observed with BBG calculations.

thumbnail Fig. 13

In panel a), we show the neutron effective mass in SNM (Y = 0) for the BBG calculations (dots), LYVA1 (solid) and BSk19-21 (dashed). Panel b) shows the evolution of the effective mass splitting at n0 = 0.169 fm-3 .

The presence of magnetic fields inside a star could lead to spin-unbalanced systems. As discussed in Sect.4, such a configuration does not constitute the ground state of the system up to several times the saturation density, but the presence of an external field could change the situation. Limiting ourselves to polarized pure neutron matter, it is possible to write the explicit expression for the spin-up (↑) and spin-down (↓) effective mass as ħ22m↑∗−ħ22m=18(C2(2)+C3(2)Δ)n+18C2(4)nkF2(1+Δ)2/3+18C3(4)nkF2Δ(1+Δ)2/3+116C2(4)nkF2[(1+Δ)5/3+(1−Δ)5/3]+116C3(4)nkF2[(1+Δ)5/3−(1−Δ)5/3]+38C2(6)nkF4(1+Δ)4/3+38C3(6)nkF4Δ(1+Δ)4/3+2140C2(6)nkF4(1+Δ)2/3[(1+Δ)5/3+(1−Δ)5/3]+2140C3(6)nkF4(1+Δ)2/3[(1+Δ)5/3−(1−Δ)5/3]+316C2(6)nkF4[(1+Δ)7/3+(1−Δ)7/3]+316C3(6)nkF4[(1+Δ)7/3−(1−Δ)7/3],\begin{eqnarray} \label{effmassup} \frac{\hbar^2}{2m_{\uparrow}^*}-\frac{\hbar^2}{2m}&=&\frac{1}{8}\left( C^{(2)}_2 + C^{(2)}_3 \Delta \right) n\nonumber \\[-0.5mm] &&+\frac{1}{8} C^{(4)}_2 n k_F^2 (1+\Delta)^{2/3}+\frac{1}{8} C^{(4)}_3 n k_F^2 \Delta(1+\Delta)^{2/3}\nonumber\\[-0.5mm] &&+\frac{1}{16} C^{(4)}_2 n k_F^2\left[(1+\Delta)^{5/3} +(1-\Delta)^{5/3}\right]\nonumber\\[-0.5mm] &&+\frac{1}{16} C^{(4)}_3 n k_F^2\left[(1+\Delta)^{5/3} -(1-\Delta)^{5/3}\right]\nonumber\\[-0.5mm] &&+\frac{3}{8} C^{(6)}_2 n k_F^4 (1+\Delta)^{4/3}+\frac{3}{8} C^{(6)}_3 n k_F^4 \Delta(1+\Delta)^{4/3} \nonumber\\[-0.5mm] &&+\frac{21}{40} C^{(6)}_2 n k_F^4(1+\Delta)^{2/3}\left[(1+\Delta)^{5/3} +(1-\Delta)^{5/3}\right] \nonumber\\[-0.5mm] &&+\frac{21}{40} C^{(6)}_3 n k_F^4(1+\Delta)^{2/3}\left[(1+\Delta)^{5/3} -(1-\Delta)^{5/3}\right] \nonumber\\[-0.5mm] &&+\frac{3}{16} C^{(6)}_2 n k_F^4\left[(1+\Delta)^{7/3} +(1-\Delta)^{7/3}\right] \nonumber\\[-0.5mm] &&+\frac{3}{16} C^{(6)}_3 n k_F^4\left[(1+\Delta)^{7/3} -(1-\Delta)^{7/3}\right], \end{eqnarray}(16)where we have defined Δ = (ρ↑−ρ↓) /ρ. 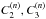The coupling constants C2(n),C3(n)\hbox{$C^{(n)}_2,C^{(n)}_3$} are related to the 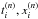ti(n),xi(n)\hbox{$t_i^{(n)},x_i^{(n)}$} as follows 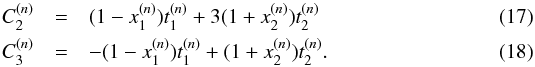C2(n)=(1−x1(n))t1(n)+3(1+x2(n))t2(n)C3(n)=−(1−x1(n))t1(n)+(1+x2(n))t2(n).\begin{eqnarray} C^{(n)}_2&=&(1-x_1^{(n)})t_1^{(n)}+3(1+x_2^{(n)})t_2^{(n)} \\ C^{(n)}_3&=&-(1-x_1^{(n)})t_1^{(n)}+(1+x_2^{(n)})t_2^{(n)} . \end{eqnarray}The explicit expressions for the spin-down effective mass can be derived from Eq. (16) by replacing Δ → −Δ. In Fig. 14, we show the evolution of the spin-up (-down) effective mass for the LYVA1 model and the original BBG results (Bombaci et al. 2006).

In Fig. 15, we compare the effective mass for the spin-up (-down) component for the different functionals considered in the present article in polarized neutron matter. The BCPM results are not present here: this functional cannot be used for polarized systems since information on the vector part is missing by construction. Contrary to the LYVA1 functional, the BSk models do not produce any splitting in the effective mass. This is due to the absence of terms CTs·T (see Eqs. (A.1)–(A.2) of Pastore et al. 2014) in the functional which governs such a splitting. The effective mass given by BSk19 is particularly high compared to BBG results. We refer to (Goriely et al. 2010) for a more detailed discussion.

7. Neutron stars

In this section, we present the basic properties of a nonaccreting NS at zero temperature using our interaction. To calculate the mass and the radius of a NS we have to solve the Tolman-Oppenheimer-Volkoff (TOV) equations for the total pressure P and the enclosed mass mdP(r)dr=−Gm(r)ε(r)r2×[(1+P(r)ε(r)c2)(1+4πr3P(r)ε(r)c2)][1−2Gm(r)rc2]-1,dm(r)dr=4πr2ε(r),\begin{eqnarray} \label{eq:tov} \frac{{\rm d}P(r)}{{\rm d}r}&=&-\frac{G m(r) \varepsilon(r)}{r^{2}}\nonumber\\ &&\times\left[\left(1+\frac{P(r)\varepsilon(r)}{c^{2}} \right) \left(1+\frac{4\pi r^{3}P(r)}{\varepsilon(r)c^{2}} \right)\right] \left[1-\frac{2G m(r)}{rc^{2}}\right]^{-1},\nonumber\\ \frac{{\rm d}m(r)}{{\rm d}r}&=&4\pi r^{2} \varepsilon(r), \end{eqnarray}(19)where G is the gravitational constant and ε(r) is the total energy density of the system. Since in our model we consider only neutrons, protons, and electrons, the β-equilibrium condition at each value of the density of the star translates into the equation μp + μn = μe for the chemical potentials, the possible contribution of muons being neglected. In Fig. 16, we show the proton fraction inside the star, calculated using our EoS. According to (Haensel 1995), the direct Urca process, which is very important for a fast cooling during stellar evolution (Lattimer et al. 1991), can take place when the proton fraction is x ≈ 0.11. We observe that our model predicts the possibility for direct Urca process at already three times saturation density. On the same plot, we also present the BBG results. The agreement between the two calculations is very good, up to n ≃ 0.6 fm-3.

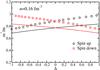thumbnail Fig. 14

Spin-up and spin-down neutron effective mass at saturation density as a function of the polarization parameter Δ. The dots correspond to the BBG calculations (Bombaci et al. 2006), the solid line to LYVA1 interaction.

thumbnail Fig. 15

Same as Fig. 12, but for other models considered in the text. Up (down) triangles stand for spin-up (-down) component.

thumbnail Fig. 16

Proton fraction Yp as a function of the density of the star. The dashed line represents the proton fraction threshold to activate the direct Urca process during the cooling stage of the NS. The open dots represent the BBG calculations.

As anticipated in Sect. 5, the possibility of allowing or not a direct Urca process can be used to consider the behavior of the symmetry energy in the high density region. The β-equilibrium condition for nucleonic equation of state can be related directly, within the parabolic approximation, to the symmetry energy, we have 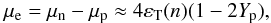μe=μn−μp≈4εT(n)(1−2Yp),\begin{eqnarray} \mu_{\rm e}=\mu_{\rm n}-\mu_{\rm p}\approx 4\varepsilon_{\rm T}(n)(1-2Y_{\rm p}), \end{eqnarray}(20)where μe,np, are the chemical potential of the different species included in the EoS. From Fig. 16, we can conclude that only the LYVA1, BSk21 and BCPM functionals allow for a direct Urca process in NS.

To describe the structure of the NS, we need to solve Eq. (19) imposing the β-equilibrium for each value of the density. In the most external layers, the crust, it is possible to observe the presence of structures, either nuclei or more exotic pasta-phases (Chamel & Haensel 2008). This part of the star will be described using the EoS of (Douchin & Haensel 2001), which has been derived using the SLy4 functional, and by means of the compressible liquid drop model (Douchin et al. 2000). This allows for a simple description of both the crust (inner and outer), as well as the liquid-core transition. We match our EoS with the that of (Douchin & Haensel 2001)) at n ≈ 0.08 fm-3. This small inconsistency in the EoS will not affect the value of the maximum mass of the star, but it introduces an error of, at most, 5% on its radius (Hebeler et al. 2010). The study of the inhomogeneous phase of the NS with our functional will be the subject of a forthcoming study. Our results concerning the mass-radius relation are shown in Fig. 17a. On the same plot, we also show the recent measurements of masses of NS (Demorest et al. 2010; Antoniadis et al. 2013), both of which are compatible with a 2 MSun neutron star. We observe that our EoS gives a prediction compatible with the latest experimental measurements, giving a maximal value of M = 1.96 MSun in the nonrotating case. The inclusion of extra degrees of freedom as pions, kaons, or hyperons would affect that result (Heiselberg & Hjorth-Jensen 2000), as well as the effect of rotation (Salgado et al. 1994a; Stergioulas 2003). Considering the results of (Salgado et al. 1994b), we could expect an increase of ~10−15% for the results of our EoS. The detailed study of these effects goes beyond the scope of this paper and we leave it for the future.

thumbnail Fig. 17

In panel a), we show the mass-radius relation for NS obtained with our EoS by solving TOV equations. The two horizontal bars refers to the two recent of NS masses measurements M/MSun = 1.97 ± 0.04 given in (Demorest et al. 2010) and M/MSun = 2.01 ± 0.04 given in (Antoniadis et al. 2013). In panel b), the mass-density relation.

The radius of an NS is very difficult to extract from observations because of the several hypothesis one has to perform on their atmospheric composition. Different models (Suleimanov et al. 2011; Steiner et al. 2010) lead to slightly different values for the radius, but it is nevertheless possible to give an upper value of around 12.5 km for a NS with a mass 1.4 MSun. See also discussion in (Fortin et al. 2015). From the EoS of our functional, we get 11.6 km, which is in fair agreement with the original BBG results. In Fig. 17b, we show the evolution of the maximum mass of the NS as a function of the central density of the star. It is worth noting that recent constraints of (Klähn et al. 2006) imply the absence of a direct Urca process for NS within a mass range of 1−1.5 MSun. From Fig. 17b, we can observe that the lowest value of the density at which the Urca process takes place corresponds to an NS of mass 1.54 MSun.

8. Conclusions

We have presented a new nucleonic equation of state based on the extended Skyrme functional. The inclusion of higher order derivative terms has allowed us to give a more precise description of the high-density region. By fixing the coupling constants of our functional on the EoS of ab-initio calculations, we have shown the possibility of analytically extracting several quantities of strong astrophysical interest, such as incompressibility, pressure or effective mass. As shown in (Davesne et al. 2015b), the higher order gradients enable us to grasp the correct physical behavior, obtained with a microscopic calculation. Our functional can be fitted to other microscopic calculations, thus providing a more powerful tool for astrophysics than a simple interpolation procedure. The Skyrme functional can be easily implemented to perform calculations in all layers of the star, not only in its uniform phase (Douchin & Haensel 2001; Pearson et al. 2012).

We have compared our results with other commonly adopted functionals, namely the BCPM (Baldo et al. 2013, 2014a; Sharma et al. 2015) and the BSk functionals (Goriely et al. 2009, 2010, 2013; Chamel & Goriely 2010). We have shown that our model is complementary to the results obtained by these different groups since it aims at reproducing BBG results in nuclear matter (including polarized matter) as accurately as possible, so that the functional can be used to describe both ground state properties and excited states.

As a result of the simplicity of the calculations, the formalism can easily be extended to include finite-temperature effects properly. In this case, it is necessary to replace the step function, used to evaluate the EoS of the system, by a Fermi-Dirac distribution (Bonche & Vautherin 1981). These integrals can be approximated with analytical expressions, as shown by (Antia 1993). The possible temperature dependence of the coupling constants can be also studied by direct comparison with existing microscopic calculations at finite temperatures (Pandharipande & Ravenhall 1989; Lejeune et al. 1986).

Acknowledgments

We thank M. Oertel for enlightening discussions and a careful reading of the manuscript. We thank N. Chamel for interesting suggestions for the manuscript. We thank M. Baldo and K. Hebeler for providing us with the results of their calculations. J.N. has been supported by grant FIS2014-51948-C2-1-P, Mineco (Spain).

References

  1. Akmal, A., Pandharipande, V. R., & Ravenhall, D. G. 1998, Phys. Rev. C, 58, 1804 [NASA ADS] [CrossRef] [Google Scholar]
  2. Antia, H. 1993, ApJS, 84, 101 [NASA ADS] [CrossRef] [Google Scholar]
  3. Antoniadis, J., Freire, P. C., Wex, N., et al. 2013, Science, 340, 1233232 [Google Scholar]
  4. Baldo, M. 1999, Nuclear methods and the nuclear equation of state, Vol. 8 (World Scientific) [Google Scholar]
  5. Baldo, M. 2014, priv. comm. [Google Scholar]
  6. Baldo, M., Bombaci, I., & Burgio, G. 1997, A&A, 328, 274 [NASA ADS] [Google Scholar]
  7. Baldo, M., Polls, A., Rios, A., Schulze, H.-J., & Vidaña, I. 2012, Phys. Rev. C, 86, 064001 [NASA ADS] [CrossRef] [Google Scholar]
  8. Baldo, M., Robledo, L. M., Schuck, P., & Viñas, X. 2013, Phys. Rev. C, 87, 064305 [NASA ADS] [CrossRef] [Google Scholar]
  9. Baldo, M., Burgio, G., Centelles, M., Sharma, B., & Viñas, X. 2014a, Phys. At. Nucl., 77, 1157 [Google Scholar]
  10. Baldo, M., Burgio, G. F., Schulze, H.-J., & Taranto, G. 2014b, Phys. Rev. C, 89, 048801 [NASA ADS] [CrossRef] [Google Scholar]
  11. Becker, P., Davesne, D., Meyer, J., Pastore, A., & Navarro, J. 2014, J. Phys. G, 42, 034001 [NASA ADS] [CrossRef] [Google Scholar]
  12. Bender, M., Heenen, P.-H., & Reinhard, P.-G. 2003, Rev. Mod. Phys., 75, 121 [NASA ADS] [CrossRef] [Google Scholar]
  13. Bogner, S., Schwenk, A., Furnstahl, R., & Nogga, A. 2005, Nucl. Phys. A, 763, 59 [NASA ADS] [CrossRef] [Google Scholar]
  14. Bohr, A., & Mottelson, B. R. 1998, Nuclear structure, Vol. 1 (World Scientific) [Google Scholar]
  15. Bombaci, I., & Lombardo, U. 1991, Phys. Rev. C, 44, 1892 [NASA ADS] [CrossRef] [Google Scholar]
  16. Bombaci, I., Polls, A., Ramos, A., Rios, A., & Vidana, I. 2006, Phys. Lett. B, 632, 638 [NASA ADS] [CrossRef] [Google Scholar]
  17. Bonche, P., & Vautherin, D. 1981, Nucl. Phys. A, 372, 496 [NASA ADS] [CrossRef] [Google Scholar]
  18. Burgio, G., & Schulze, H.-J. 2010, A&A, 518, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Cao, L. G., Lombardo, U., Shen, C. W., & Giai, N. V. 2006, Phys. Rev. C, 73, 014313 [NASA ADS] [CrossRef] [Google Scholar]
  20. Carlsson, B. G., & Dobaczewski, J. 2010, Phys. Rev. Lett., 105, 122501 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  21. Carlsson, B. G., Dobaczewski, J., & Kortelainen, M. 2008, Phys. Rev. C, 78, 044326 [NASA ADS] [CrossRef] [Google Scholar]
  22. Chabanat, E., Bonche, P., Haensel, P., Meyer, J., & Schaeffer, R. 1997, Nucl. Phys. A, 627, 710 [NASA ADS] [CrossRef] [Google Scholar]
  23. Chamel, N. 2010, Phys. Rev. C, 82, 061307 [NASA ADS] [CrossRef] [Google Scholar]
  24. Chamel, N., & Goriely, S. 2010, Phys. Rev. C, 82, 045804 [NASA ADS] [CrossRef] [Google Scholar]
  25. Chamel, N., & Haensel, P. 2008, Liv. Rev. Relat., 11, 10 [Google Scholar]
  26. Chamel, N., Fantina, A., Pearson, J., & Goriely, S. 2011, Phys. Rev. C, 84, 062802 [Google Scholar]
  27. Chamel, N., Page, D., & Reddy, S. 2013, Phys. Rev. C, 87, 035803 [NASA ADS] [CrossRef] [Google Scholar]
  28. Chen, L.-W., Ko, C. M., Li, B.-A., & Xu, J. 2010, Phys. Rev. C, 82, 024321 [NASA ADS] [CrossRef] [Google Scholar]
  29. Danielewicz, P. 2003, Nucl. Phys. A, 727, 233 [NASA ADS] [CrossRef] [Google Scholar]
  30. Danielewicz, P., & Lee, J. 2014, Nucl. Phys. A, 922, 1 [NASA ADS] [CrossRef] [Google Scholar]
  31. Danielewicz, P., Lacey, R., & Lynch, W. G. 2002, Science, 298, 1592 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  32. Davesne, D., Pastore, A., & Navarro, J. 2013, J. Phys. G, 40, 095104 [NASA ADS] [CrossRef] [Google Scholar]
  33. Davesne, D., Pastore, A., & Navarro, J. 2014, J. Phys. G, 41, 065104 [NASA ADS] [CrossRef] [Google Scholar]
  34. Davesne, D., Meyer, J., Pastore, A., & Navarro, J. 2015a, Phys. Scr., 90, 114002 [NASA ADS] [CrossRef] [Google Scholar]
  35. Davesne, D., Navarro, J., Becker, P., et al. 2015b, Phys. Rev. C, 91, 064303 [NASA ADS] [CrossRef] [Google Scholar]
  36. Demorest, P., Pennucci, T., Ransom, S., Roberts, M., & Hessels, J. 2010, Nature, 467, 1081 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  37. Douchin, F., & Haensel, P. 2001, A&A, 380, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Douchin, F., Haensel, P., & Meyer, J. 2000, Nucl. Phys. A, 665, 419 [NASA ADS] [CrossRef] [Google Scholar]
  39. Dutra, M., Lourenço, O., SáMartins, J. S., et al. 2012, Phys. Rev. C, 85, 035201 [NASA ADS] [CrossRef] [Google Scholar]
  40. Fantoni, S., Sarsa, A., & Schmidt, K. E. 2001, Phys. Rev. Lett., 87, 181101 [NASA ADS] [CrossRef] [Google Scholar]
  41. Fortin, M., Zdunik, J., Haensel, P., & Bejger, M. 2015, A&A, 576, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Fuchs, C. 2006, Prog. Part. Nucl. Phys., 56, 1 [NASA ADS] [CrossRef] [Google Scholar]
  43. Gambacurta, D., Li, L., Colò, G., et al. 2011, Phys. Rev. C, 84, 024301 [NASA ADS] [CrossRef] [Google Scholar]
  44. Gandolfi, S., Carlson, J., & Reddy, S. 2012, Phys. Rev. C, 85, 032801 [NASA ADS] [CrossRef] [Google Scholar]
  45. Goriely, S., Chamel, N., & Pearson, J. M. 2009, Phys. Rev. Lett., 102, 152503 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  46. Goriely, S., Chamel, N., & Pearson, J. M. 2010, Phys. Rev. C, 82, 035804 [NASA ADS] [CrossRef] [Google Scholar]
  47. Goriely, S., Chamel, N., & Pearson, J. M. 2013, Phys. Rev. C, 88, 024308 [NASA ADS] [CrossRef] [Google Scholar]
  48. Haensel, P. 1995, Space Sci. Rev., 74, 427 [NASA ADS] [CrossRef] [Google Scholar]
  49. Haensel, P., & Potekhin, A. Y. 2004, A&A, 428, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Haensel, P., Potekhin, A. Y., & Yakovlev, D. G. 2007, in Neutron stars 1: Equation of state and structure (Springer Science & Business Media), 326 [Google Scholar]
  51. Hebeler, K., Lattimer, J. M., Pethick, C. J., & Schwenk, A. 2010, Phys. Rev. Lett., 105, 161102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  52. Hebeler, K., Bogner, S. K., Furnstahl, R. J., Nogga, A., & Schwenk, A. 2011, Phys. Rev. C, 83, 031301 [NASA ADS] [CrossRef] [Google Scholar]
  53. Heiselberg, H., & Hjorth-Jensen, M. 2000, Phys. Rep., 328, 237 [NASA ADS] [CrossRef] [Google Scholar]
  54. Iwamoto, N., & Pethick, C. J. 1982, Phys. Rev. D, 25, 313 [NASA ADS] [CrossRef] [Google Scholar]
  55. Klähn, T., Blaschke, D., Typel, S., et al. 2006, Phys. Rev. C, 74, 035802 [NASA ADS] [CrossRef] [Google Scholar]
  56. Lattimer, J. M., Pethick, C., Prakash, M., & Haensel, P. 1991, Phys. Rev. Lett., 66, 2701 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  57. Lejeune, A., Grangé, P., Martzolff, M., & Cugnon, J. 1986, Nucl. Phys. A, 453, 189 [NASA ADS] [CrossRef] [Google Scholar]
  58. Lesinski, T., Bennaceur, K., Duguet, T., & Meyer, J. 2006, Phys. Rev. C, 74, 044315 [NASA ADS] [CrossRef] [Google Scholar]
  59. Lesinski, T., Bender, M., Bennaceur, K., Duguet, T., & Meyer, J. 2007, Phys. Rev. C, 76, 014312 [NASA ADS] [CrossRef] [Google Scholar]
  60. Li, Z. H., & Schulze, H.-J. 2008, Phys. Rev. C, 78, 028801 [NASA ADS] [CrossRef] [Google Scholar]
  61. Margueron, J., Navarro, J., & Nguyen, V. G. 2002, Phys. Rev. C, 66, 014303 [NASA ADS] [CrossRef] [Google Scholar]
  62. Pandharipande, V., & Ravenhall, D. 1989, in Nuclear matter and heavy ion collisions (Springer), 103 [Google Scholar]
  63. Pandharipande, V., Garde, V., & Srivastava, J. 1972, Phys. Lett. B, 38, 485 [NASA ADS] [CrossRef] [Google Scholar]
  64. Pastore, A., Martini, M., Davesne, D., et al. 2014, Phys. Rev. C, 90, 025804 [NASA ADS] [CrossRef] [Google Scholar]
  65. Pastore, A., Davesne, D., & Navarro, J. 2015, Phys. Rep., 563, 1 [NASA ADS] [CrossRef] [Google Scholar]
  66. Pearson, J., Chamel, N., Goriely, S., & Ducoin, C. 2012, Phys. Rev. C, 85, 065803 [NASA ADS] [CrossRef] [Google Scholar]
  67. Raimondi, F., Carlsson, B. G., & Dobaczewski, J. 2011, Phys. Rev. C, 83, 054311 [NASA ADS] [CrossRef] [Google Scholar]
  68. Rotival, V. 2008, Ph.D. Thesis, Université Paris-Diderot – Paris VII [Google Scholar]
  69. Salgado, M., Bonazzola, S., Gourgoulhon, E., & Haensel, P. 1994a, A&A, 291, 155 [NASA ADS] [Google Scholar]
  70. Salgado, M., Bonazzola, S., Gourgoulhon, E., & Haensel, P. 1994b, A&AS, 108, 455 [Google Scholar]
  71. Sharma, B., Centelles, M., Vinas, X., Baldo, M., & Burgio, G. 2015, A&A, 584, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Singh, S. K., Biswal, S., Bhuyan, M., Jha, T., & Patra, S. 2013, ArXiv e-prints [arXiv:1312.5840] [Google Scholar]
  73. Skyrme, T. H. R. 1959, Nucl. Phys., 9, 615 [CrossRef] [Google Scholar]
  74. Steiner, A. W., Lattimer, J. M., & Brown, E. F. 2010, ApJ, 722, 33 [NASA ADS] [CrossRef] [Google Scholar]
  75. Stergioulas, N. 2003, Liv. Rev. Relat., 6, 3 [Google Scholar]
  76. Suleimanov, V., Poutanen, J., & Werner, K. 2011, A&A, 527, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Tsang, M. B., Zhang, Y., Danielewicz, P., et al. 2009, Phys. Rev. Lett., 102, 122701 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  78. Typel, S., Oertel, M., & Klaehn, T. 2013, ArXiv e-prints [arXiv:1307.5715] [Google Scholar]
  79. Vautherin, D., & Brink, D. M. 1972, Phys. Rev. C, 5, 626 [NASA ADS] [CrossRef] [Google Scholar]
  80. Vidana, I., Polls, A., & Ramos, A. 2002, Phys. Rev. C, 65, 035804 [NASA ADS] [CrossRef] [Google Scholar]
  81. Vidaurre, A., Navarro, J., & Bernabeu, J. 1984, A&A, 135, 361 [NASA ADS] [Google Scholar]
  82. Yakovlev, D., Kaminker, A., Gnedin, Oleg, Y., & Haensel, P. 2001, Phys. Rep., 354, 1 [NASA ADS] [CrossRef] [Google Scholar]
  83. Zhou, X. R., Burgio, G. F., Lombardo, U., Schulze, H.-J., & Zuo, W. 2004, Phys. Rev. C, 69, 018801 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

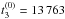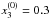Parameters of the extended LYVA1 Skyrme interaction, with α = 1/6, t3(0)=13 763\hbox{$t^{(0)}_{3}=13\,763$} [MeVfm3+α], and x3(0)=0.3\hbox{$x^{(0)}_{3}=0.3$}.

In the text
Table 2

Basic SNM properties calculated with the LYVA1 parametrization given in Tab.1, the BCPM and the BSk19-21 functionals at saturation density n0.

In the text

All Figures

thumbnail Fig. 1

Equations of state of SNM and PNM (panel a)) and projections (S,T) in SNM (panel b)), both expressed in MeV. The solid lines represent the result obtained with our extended Skyrme interaction, while the dots represent the EoS obtained by (Baldo et al. 1997). The LNS results are represented by dashed-lines.
In the text
thumbnail Fig. 2

Equations of state of SNM (panel a)) and PNM (panel b)) obtained using the LYVA1 interaction (solid) the BSk models (dashed) and the BCMP functional (dotted).
In the text
thumbnail Fig. 3

Same as Fig. 1, but for the BSk model discussed in the text.
In the text
thumbnail Fig. 4

Equations of states in asymmetric nuclear matter as a function of the density n and asymmetry parameter Y.
In the text
thumbnail Fig. 5

The pressure as a function of the density in SNM for the different models considered in the article. See text for details.
In the text
thumbnail Fig. 6

The EoS in PNM for the different models discussed in the text. The shaded area represents the constraints extracted from (Gandolfi et al. 2012).
In the text
thumbnail Fig. 7

The pressure as a function of the density in PNM for the different models considered in the article. The grey areas are derived from the analysis of (Danielewicz 2003).
In the text
thumbnail Fig. 8

The speed of sound in PNM as a function of the density of the system. The notation is as in Fig.1.
In the text
thumbnail Fig. 9

Energy difference between PolPNM and PNM for the different models considered in the text.
In the text
thumbnail Fig. 10

Symmetry energy as a function of the density of the system for different models (left panel). The dots correspond to the BBG calculations. In the right panel we compare the constraints extracted using IAS (Danielewicz & Lee 2014). See text for details.
In the text
thumbnail Fig. 11

Symmetry energy as a function of the density of the system using different definition of the symmetry energy. The dots represent the BBG results. See text for details.
In the text
thumbnail Fig. 12

Neutron and proton effective mass at saturation density as a function of the asymmetry parameter Y. The dots correspond to the BBG calculations (Baldo et al. 2014b), the solid line to LYVA1 interaction.
In the text
thumbnail Fig. 13

In panel a), we show the neutron effective mass in SNM (Y = 0) for the BBG calculations (dots), LYVA1 (solid) and BSk19-21 (dashed). Panel b) shows the evolution of the effective mass splitting at n0 = 0.169 fm-3 .
In the text
thumbnail Fig. 14

Spin-up and spin-down neutron effective mass at saturation density as a function of the polarization parameter Δ. The dots correspond to the BBG calculations (Bombaci et al. 2006), the solid line to LYVA1 interaction.
In the text
thumbnail Fig. 15

Same as Fig. 12, but for other models considered in the text. Up (down) triangles stand for spin-up (-down) component.

In the text
thumbnail Fig. 16

Proton fraction Yp as a function of the density of the star. The dashed line represents the proton fraction threshold to activate the direct Urca process during the cooling stage of the NS. The open dots represent the BBG calculations.
In the text
thumbnail Fig. 17

In panel a), we show the mass-radius relation for NS obtained with our EoS by solving TOV equations. The two horizontal bars refers to the two recent of NS masses measurements M/MSun = 1.97 ± 0.04 given in (Demorest et al. 2010) and M/MSun = 2.01 ± 0.04 given in (Antoniadis et al. 2013). In panel b), the mass-density relation.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.