| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A109 | |
| Number of page(s) | 5 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201527151 | |
| Published online | 01 December 2015 | |
A jet model for Galactic black-hole X-ray sources: The correlation between cutoff energy and phase lag
1 IESL, Foundation for Research and Technology-Hellas, 711 10 Heraklion, Crete, Greece
e-mail: pau@physics.uoc.gr
2 University of Crete, Physics Department & Institute of Theoretical & Computational Physics, 70013 Heraklion, Crete, Greece
Received: 10 August 2015
Accepted: 15 October 2015
Context. Galactic black-hole X-ray binaries emit a compact, optically thick, mildy relativistic radio jet when they are in the hard and hard-intermediate states, that is, typically at the beginning and the end of an X-ray outburst. In a series of papers, we have developed a jet model and have shown through Monte Carlo simulations that our model can explain many observational results.
Aims. In this work, we investigate one more constraining relationship between the cutoff energy and the phase lag during the early stages of an X-ray outburst of the black-hole X-ray binary GX 339–4: the cutoff energy decreases while the phase lag increases during the brightening of the hard state.
Methods. We performed Monte Carlo simulations of the Compton upscattering of soft accretion-disk photons in the jet and computed the phase lag between soft and hard photons and the cutoff energy of the resulting high-energy power law.
Results. We demonstrate that our jet model naturally explains the above correlation, with a minor modification consisting of introducing an acceleration zone at the base of the jet.
Conclusions. The observed correlation between the cutoff energy and the phase lag in the black-hole binary GX 339–4 suggests that the lags are produced by the hard component. Here we show that this correlation arises naturally if Comptonization in the jet produces these two quantities.
Key words: black hole physics / accretion, accretion disks / methods: statistical / radiation mechanisms: non-thermal
© ESO, 2015
1. Introduction
The continuum X-ray spectra of black-hole binaries (BHB) are well described by just two components: i) a soft component, normally modelled as a multi-colour black-body component dominating the spectrum below ~10 keV (Mitsuda et al. 1984; Merloni et al. 2000), whose origin is attributed to a geometrically thin, optically thick disk (Shakura & Sunyaev 1973); and ii) a power-law hard tail with an exponential cutoff, which is believed to be the result of Comptonization of low-energy photons from the disk by energetic electrons in a configuration that is still under debate. The Comptonizing medium could be an optically thin, very hot corona in the vicinity of the compact object (Sunyaev & Titarchuk 1980; Hua & Titarchuk 1995; Zdziarski 1998), an advection-dominated accretion flow (Narayan & Yi 1994; Esin et al. 1997), a low angular momentum accretion flow (Ghosh et al. 2011; Garain et al. 2012), or the base of a radio jet (Band & Grindlay 1986; Georganopoulos et al. 2002). In addition to these components, a discrete line at 6.4 keV is generally observed and attributed to reflection of the hard X-rays from the accretion disk (Fabian et al. 1989).
Depending on the strength of these two spectral components and the different shapes and characteristic frequencies of the noise components in the power spectra, including quasi-periodic oscillations (QPO), black-hole systems can be found in several states (McClintock & Remillard 2006; Belloni 2010), of which the two main ones are called soft and hard states (Done et al. 2007). In the soft state, the thermal black-body component dominates the energy spectrum with no or very weak power-law emission (Remillard & McClintock 2006; Dexter & Quataert 2012). Weak power-law noise (rms < 5%) is detected in the power spectrum, and sometimes also a QPO at 10–20 Hz (van der Klis 2006). In the hard state, the soft component is weak or absent, whereas the hard tail extends to a few hundred keV in the form of a power law with photon-number index in the range 1.5–2. The power law falls exponentially at a few tens to about a hundred keV (McClintock & Remillard 2006; Castro et al. 2014). The power spectrum shows strong band-limited noise with a typical strength of 20–40% rms and a break frequency below 1 Hz (Homan & Belloni 2005; Belloni & Stella 2014). In addition, the phase (time) lag between the light curves at two different energy bands obtained simultaneously is well established. The magnitude of this lag strongly depends on Fourier frequency and on the energy bands considered (Miyamoto et al. 1988; Vaughan & Nowak 1997; Nowak et al. 1999; Poutanen 2001; Pottschmidt et al. 2003).
The hard and hard-intermediate states are prominent because in these states a compact, optically thick, mildy relativistic jet is detected in the radio band (Fender et al. 2009), hence the relation between accretion and outflow in accreting black holes can be best studied. For the formation and destruction of jets in black-hole and neutron star binaries, we refer to Kylafis et al. (2012). For an interpretation of the observed phenomenology of black-hole X-ray transients, we refer to Kylafis & Belloni (2015).
In a series of papers, we have developed a model for the hard state of BHBs. We have shown that Compton upscattering in the jet of soft photons from the accretion disk can explain a number of observational relations between the spectral and timing parameters. Our results demonstrate that jets play a central role in all the observed phenomena, not only in the radio emission.
Reig et al. (2003; hereafter Paper I) reproduced the X-ray energy spectra and the dependence of time lag on Fourier frequency and investigated the effect of the optical depth and extent of the base of the jet on the spectral continuum. For simplicity, we assumed that the jet has a constant flow velocity v∥ and that in the rest frame of the flow the electrons are mono-energetic, with a velocity component perpendicular to the magnetic field v⊥. The observed parabolic shape of the jet implies that the density of the electrons in the jet drops inversely proportional to the vertical distance z from the black hole.
Giannios et al. (2004; hereafter Paper II) showed that both the hardening of the high-frequency power spectra and, equivalently, the narrowing of the auto-correlation function with photon energy observed in Cygnus X-1 can be explained by simply assuming that the electrons close to the core of the jet are more energetic than those at its periphery. Specifically, v⊥ was assumed to drop linearly with polar distance from the axis of the jet.
To explain the entire spectrum from radio to X-rays, Giannios (2005; hereafter Paper III) assumed that the electrons have a power-law energy distribution. This assumption helps explain the radio part of the spectrum, but has no effect on the Comptonization. This is because the distribution is steep and Comptonization is performed by the electrons with the lowest Lorentz factor γmin.
Kylafis et al. (2008; hereafter Paper IV) explained the correlation observed in Cyg X-1 between the photon index Γ and the average time lag without any additional modification to the model. We also explained the correlation between Γ and the characteristic frequencies of the Lorenztian peaks (Pottschmidt et al. 2003).
In this work, we aim at reproducing the correlation between the cutoff energy Ec and the phase lag φlag between hard and soft photons, as measured for the BHB GX 339–4 with no or only very slight modifications to our jet model. Motta et al. (2009) studied the evolution of the high-energy cutoff in the X-ray spectrum of GX 339–4 across a hard-to-soft transition and found that the cutoff energy decreased monotonically from 120 to 60 keV during the brightening of the hard state. Altamirano & Méndez (2015) studied the evolution of the phase lag of GX 339–4 as a function of the position of the source in the hardness-intensity diagram (q-diagram) and found that the phase lag increases as the sources moves up in the q-diagram through the hard state. They also showed that Ec and φlag appear to be correlated.
In Sect. 2 we briefly present our model, in Sect. 3 we give the results of our calculations, in Sect. 4 we discuss our results, and in Sect. 5 we draw our conclusions.
2. Model
One of the models that we used in this work (model 1) is a simplified version of that used in Paper III. Since we are not interested in reproducing the radio spectrum of GX 339-4, we have assumed mono-energetic electrons in the jet with a Lorentz factor equal to the smallest in the distribution, namely 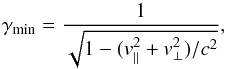 (1)where v∥ = v0 = const. is the flow velocity of the jet and v⊥ is the lowest perpendicular velocity of the electrons in the rest frame of the flow. Our model is otherwise identical to that used in Paper IV.
(1)where v∥ = v0 = const. is the flow velocity of the jet and v⊥ is the lowest perpendicular velocity of the electrons in the rest frame of the flow. Our model is otherwise identical to that used in Paper IV.
Simplicity is a preferred quality in models, but there are limits. In our model 1 above, we have assumed that the flow velocity in the jet is v0 = const. throughout the jet, or equivalently that the acceleration region of the jet is infinitesimal. This is an unphysical description of the base of the jet. For this reason, we considered a second model (model 2), where the flow velocity in the jet is given by 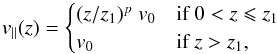 (2)where z1 and p are parameters. In other words, the jet has an acceleration region of thickness z1 beyond which the flow has a constant velocity v0, equal to that of model 1.
(2)where z1 and p are parameters. In other words, the jet has an acceleration region of thickness z1 beyond which the flow has a constant velocity v0, equal to that of model 1.
For a parabolic jet, that is, one whose radius at height z is R(z) = R0(z/z0)1/2, the electron density in model 1 is inversely proportional to z, namely ne(z) = n0(z0/z) (see Paper IV), while in model 2 it is obtained from the continuity equation.
The fixed parameters of our models and their reference values are as follows: the radius R0 = 100rg of the base of the jet, where rg = GM/c2 is the gravitational radius of the black hole, the distance z0 = 5rg of the bottom of the jet from the black hole, the height H = 105rg of the jet, the velocity v0 = 0.8c of the jet, the thickness z1 = 50rg of the acceleration zone, the exponent p = 0 (model 1) or p = 1/2 (model 2), and the temperature Tbb = 0.2 keV of the soft-photon input.
The parameters of our models that we varied are either the Thomson optical depth along the axis of the jet 1 ≤ τ∥ ≤ 10 or the minimum Lorentz factor 2 ≤ γmin ≤ 2.4, or both with a linear relation between the two. Since v0 is a constant in our models, the variation of γmin is caused by the variation of 0.35c ≤ v⊥ ≤ 0.42c.
As the source moves from the hard to the hard-intermediate state, the jet weakens (Homan & Belloni 2005) and eventually disappears at the jet line. We interpret this weakening of the jet as a decrease of the parameter τ∥. At the same time, the luminosity increases and the jet cooling is enhanced, and we interpret this as a decrease of the parameter γmin. This means that τ∥ and γmin decrease with time during the initial rise of the outburst.
Since the jet is mildly relativistic, the results also depend on the angle θ of observation with respect to the jet axis. As in Papers II–IV, we here focus in an intermediate range of observing angles 0.2 < cosθ< 0.6. This means practically for the Monte Carlo simulation that we only count photons that leave the jet in this range of angles.
3. Results
The output of our Monte Carlo code consists of energy spectra and light curves. In this work, the light curves were obtained for the energy bands 2−5.7 keV and 5.7−15 keV to match those of Altamirano & Méndez (2015) for the BHB GX 339–4.
The output energy spectrum was fitted by a power law with an exponential cutoff to extract the photon index Γ and the cutoff energy Ec. We applied a Fourier analysis to the light curves to obtain the phase lag of the hard X-rays with respect to the soft ones as a function of Fourier frequency. The final phase lag considered, φlag, is the average over the frequency range 0.01−5 Hz.
In reality, the parameters γmin and τ∥ decrease simultaneously, but for clarity of presentation, we first varied τ∥, then γmin, and in the end, both of them. The result that we wish to reproduce in this work is the decrease of the cutoff energy and the increase of the phase lag of GX 339–4 as the X-ray intensity increases and the source traverses the hard state. As explained above, we expect τ∥ and γmin to decrease with time. However, for plotting purposes, we left these two parameters, the independent variables of the plots, to increase towards the right in the X-axis, as is common practice. For this reason, Ec increases and φlag decreases with τ∥ and γmin.
 |
Fig. 1 Cutoff energy and phase lag as functions of τ∥ without (filled circles) and with an acceleration zone (empty circles). Each point represents a calculation with the same γmin = 2.21 (v⊥ = 0.395c) and different τ∥. The horizontal dotted lines bracket the ranges of observed values as in Motta et al. (2009) for Ec and Altamirano & Méndez (2015) for φlag. |
 |
Fig. 2 Cutoff energy and phase lag as functions of γmin without (filled circles) and with an acceleration zone (empty circles). Each point represents a calculation with the same τ∥ = 5 and different γmin (v⊥). The horizontal dotted lines bracket the ranges of observed values as in Motta et al. (2009) for Ec and Altamirano & Méndez (2015) for φlag. |
3.1. Variation of τ∥
In Fig. 1 we show the variations of Ec and φlag as functions of the Thomson optical depth τ∥. The solid line represents the case where no acceleration zone is considered (model 1, p = 0), while the dashed one represents the case when an acceleration zone is taken into account (model 2, p = 0.5). The Lorentz factor of the electrons is fixed at γmin = 2.21 (v∥ = 0.8c, v⊥ = 0.395c) and the remaining parameters at their reference values. In both panels, the horizontal dotted lines bracket the observed values of Ec and φlag, as determined by Motta et al. (2009) and Altamirano & Méndez (2015).
It is important to stress that the variation of Ec and φlag has the correct trend for both model 1 and model 2. On the other hand, the variation of only τ∥ is not enough to simultaneously reproduce the observed ranges of variation of Ec and φlag for the same range of variation of τ∥.
Whereas Ec nicely covers the whole range of observed variation when the optical depth τ∥ decreases from 10 to 1, the phase lag φlag is outside the range of the observations at low optical depth and lies short at high optical depth. The introduction of an acceleration zone (model 2, p = 0.5) makes the φlag trend somewhat steeper, but again the two parameters do not cover the observed ranges of allowed values for the same range of optical depth. Similar curves are found for values of p different from 0.5, as long as p<~1.
As we showed in Papers I–IV, maintaining the remaining parameters at their reference values and decreasing the density n0 (or equivalently the Thomson optical depth along the axis of the jet τ∥, see Eq. (2) in Paper IV) softens the emerging spectra. A decrease in the optical depth τ∥ also causes a decrease in the cutoff energy Ec as a result of the reduced number of scatterings. The effect on the time lag or the phase lag is less obvious, however. At high optical depth, the soft input photons penetrate the base of the jet superficially, that is, on average, a region equivalent to an optical depth of unity. There, they are scattered, but because of the high density, the mean free path is short and the photons sample a small region at the base of the jet before they escape. As the optical depth (or equivalently the density) decreases, the mean free path increases, and at low optical depths the photons sample the entire volume of the jet. Thus, the time lag or the phase lag increases.
In the top panel of Fig. 1 we show that for model 2 (p = 0.5) Ec is consistently higher than the corresponding value for model 1 (p = 0). This is because the mean number of scatterings of the photons in model 2 is larger than that in model 1, which in turn is due to the higher density of the electrons at the base of the jet in model 2 than in model 1.
3.2. Variation of γmin
In Fig. 2 we show the variation of Ec and φlag as functions of the Lorentz factor γmin. The optical depth is fixed to τ∥ = 5 and the remaining parameters to their reference values. Again, the trend followed by the computed quantities matches that of the observations. It is natural to expect that Ec would decrease as the energy of the electrons decreases. The increase of φlag as γmin decreases requires an explanation.
At large γmin, that is, large v⊥, there is a tendency for the photons after scattering to have directions with polar angle θ closer to 90 degrees than to zero degrees. Thus, the random walk of the photons occurs close to the base of the jet, and the time lag or phase lag is relatively short because the size of the jet is small there. As γmin decreases, that is, v⊥ decreases, the photons after scattering have the tendency to have directions closer to θ = 0 than to θ = 90 degrees. Thus, the input photons are pushed in the flow direction and are forced to sample the entire volume of the jet, which results in a comparatively longer time lag or phase lag.
 |
Fig. 3 Cutoff energy and phase lag as a function of τ∥ without (filled symbols) and with an acceleration zone (open symbols). Each point represents a calculation with different τ∥ and γmin. The horizontal dotted lines bracket the ranges of observed values as in Motta et al. (2009) for Ec and Altamirano & Méndez (2015) for φlag. The vertical dot-dashed lines show the range in τ∥ (hence in γmin also, see text) where the two quantities simultaneously cover the entire observed ranges. |
As in Fig. 1, only Ec covers the entire range of observed values (indicated by the horizontal dotted lines). The phase lag lies short of one or both extremes. The introduction of an acceleration zone (model 2, p = 0.5) changes the amplitude of the lags substantially. This is because in the acceleration zone v∥<v0, hence scattering in directions with θ closer to 90 degrees is enhanced. Thus, the phase lag becomes shorter than in the case without an acceleration zone.
3.3. Variation of τ∥ and γmin
In reality, both τ∥ and γmin decrease simultaneously as the source moves in the hard state, therefore we varied them both in the simplest way possible, one proportional to the other. In Fig. 3 we show Ec and φlag as functions of τ∥. In this figure, γmin is linked to τ∥ by γmin = 2.023−0.019 τ∥.
With two parameters, τ∥ and γmin, working in the same direction, it is not surprising that we are now able to demonstrate that for 3 ≤ τ∥ ≤ 10, both computed quantities with model 2, simultaneously cover the entire observed ranges (see the vertical dot-dashed lines in Fig. 3).
To better illustrate the good agreement between the observations and our model, we plot the phase lag as a function of the cutoff energy in Fig. 4. The data points are taken from Motta et al. (2009) and Altamirano & Méndez (2015). The solid and dashed lines correspond to the models shown in Fig. 3.
 |
Fig. 4 Phase lags as a function of cutoff energy. Circles represent data from the observations. The cutoff energy and phase lag values were taken from Motta et al. (2009) and Altamirano & Méndez (2015), respecively. Solid and dashed lines correspond to the models shown in Fig. 3. |
4. Summary and conclusion
Observations from space-based X-ray telescopes over the past decades have provided a wealth of data that has led to a revolution in our understanding of BHB. Numerous studies of these observations have allowed characterizing their spectral and temporal properties and defining source states. Correlations between the spectral and timing parameters impose tight observational constraints that any model seeking to explain the observations must address. Our jet model has so far been able to quantitatively explain a number of results regarding the hard state of BHB (Papers I–IV): i) the emerging spectrum from radio to hard X-rays; ii) the time (phase)-lags as a function of Fourier frequency; iii) the flattening of the power spectra at high frequencies with increasing photon energy and the narrowing of the autocorrelation function; and iv) the correlation observed in Cyg X-1 between the photon index and the average time lag.
Motta et al. (2009) and Altamirano & Méndez (2015) provided one more stringent constraint: the cutoff energy of the power law and the phase lag of hard photons with respect to soft ones vary in unison as the black-hole binary GX 339–4 evolves through the hard state and moves up in the q-diagram (see Fig. 1 in Altamirano & Méndez 2015). In this work, we showed that we can reproduce this correlation with a minor modification of our model: by introducing an acceleration zone.
The correlation between the cutoff energy and the phase lag suggests that the most likely origin of the lag is the same region as the one where the hard X-rays are formed (Altamirano & Méndez 2015). Because the spectrum of the radiation at the energies where the cutoff is measured (tens of keV) cannot be formed in the accretion disk, the Ec−φlag correlation strongly suggests that the lags are due to Comptonization. In our model, Comptonization takes place in the jet. Hence we conclude that the phase lag must originate in the jet. Another result that supports the association between lag and jet stems from the fact that, at least for Cyg X–1, the lag drops as the source moves into the soft-intermediate state (see Fig. 6 in Altamirano & Méndez 2015), that is, when the radio emission is quenched.
Acknowledgments
We thank the anonymous referee for useful comments and especially for the suggestion of Fig. 4. We acknowledge useful discussions with Dimitrios Gannios. This research has been supported in part by the “RoboPol” project, which is implemented under the “ARISTEIA” Action of the “OPERATIONAL PROGRAM EDUCATION AND LIFELONG LEARNING” and is co-funded by the European Social Fund (ESF) and National Resources.
References
- Altamirano, D., & Méndez, M. 2015, MNRAS, 449, 4027 [NASA ADS] [CrossRef] [Google Scholar]
- Band, D. L., & Grindlay, J. E. 1986, ApJ, 311, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Belloni, T. M. 2010, in Lect. Notes Phys. 794 (Berlin: Springer Verlag), ed. T. Belloni, 53 [Google Scholar]
- Belloni, T. M., & Stella, L. 2014, Space Sci. Rev., 183, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Castro, M., D’Amico, F., Braga, J., et al. 2014, A&A, 569, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dexter, J., & Quataert, E. 2012, MNRAS, 426, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Done, C., Gierliński, M., & Kubota, A. 2007, A&ARv, 15, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Esin, A. A., McClintock, J. E., & Narayan, R. 1997, ApJ, 489, 865 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Rees, M. J., Stella, L., & White, N. E. 1989, MNRAS, 238, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Fender, R. P., Homan, J., & Belloni, T. M. 2009, MNRAS, 396, 1370 [NASA ADS] [CrossRef] [Google Scholar]
- Garain, S. K., Ghosh, H., & Chakrabarti, S. K. 2012, ApJ, 758, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Georganopoulos, M., Aharonian, F. A., & Kirk, J. G. 2002, A&A, 388, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghosh, H., Garain, S. K., Giri, K., & Chakrabarti, S. K. 2011, MNRAS, 416, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Giannios, D. 2005, A&A, 437, 1007 (Paper III) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giannios, D., Kylafis, N. D., & Psaltis, D. 2004, A&A, 425, 163 (Paper II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Homan, J., & Belloni, T. 2005, Ap&SS, 300, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Hua, X.-M., & Titarchuk, L. 1995, ApJ, 449, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Kylafis, N. D., & Belloni, T. M. 2015, A&A, 574, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kylafis, N. D., Papadakis, I. E., Reig, P., Giannios, D., & Pooley, G. G. 2008, A&A, 489, 481 (Paper IV) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kylafis, N. D., Contopoulos, I., Kazanas, D., & Christodoulou, D. M. 2012, A&A, 538, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McClintock, J. E., & Remillard, R. A. 2006, Black hole binaries, eds. W. H. G. Lewin, & M. van der Klis (Cambridge University Press), 157 [Google Scholar]
- Merloni, A., Fabian, A. C., & Ross, R. R. 2000, MNRAS, 313, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Mitsuda, K., Inoue, H., Koyama, K., et al. 1984, PASJ, 36, 741 [NASA ADS] [Google Scholar]
- Miyamoto, S., Kitamoto, S., Mitsuda, K., & Dotani, T. 1988, Nature, 336, 450 [NASA ADS] [CrossRef] [Google Scholar]
- Motta, S., Belloni, T., & Homan, J. 2009, MNRAS, 400, 1603 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., & Yi, I. 1994, ApJ, 428, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Nowak, M. A., Vaughan, B. A., Wilms, J., Dove, J. B., & Begelman, M. C. 1999, ApJ, 510, 874 [NASA ADS] [CrossRef] [Google Scholar]
- Pottschmidt, K., Wilms, J., Nowak, M. A., et al. 2003, A&A, 407, 1039 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poutanen, J. 2001, Adv. Space Res., 28, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Reig, P., Kylafis, N. D., & Giannios, D. 2003, A&A, 403, L15 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Remillard, R. A., & McClintock, J. E. 2006, ARA&A, 44, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Sunyaev, R. A., & Titarchuk, L. G. 1980, A&A, 86, 121 [NASA ADS] [Google Scholar]
- van der Klis, M. 2006, Rapid X-ray Variability, eds. W. H. G. Lewin, & M. van der Klis (Cambridge University Press), 39 [Google Scholar]
- Vaughan, B. A., & Nowak, M. A. 1997, ApJ, 474, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A. 1998, MNRAS, 296, L51 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Cutoff energy and phase lag as functions of τ∥ without (filled circles) and with an acceleration zone (empty circles). Each point represents a calculation with the same γmin = 2.21 (v⊥ = 0.395c) and different τ∥. The horizontal dotted lines bracket the ranges of observed values as in Motta et al. (2009) for Ec and Altamirano & Méndez (2015) for φlag. |
| In the text | |
 |
Fig. 2 Cutoff energy and phase lag as functions of γmin without (filled circles) and with an acceleration zone (empty circles). Each point represents a calculation with the same τ∥ = 5 and different γmin (v⊥). The horizontal dotted lines bracket the ranges of observed values as in Motta et al. (2009) for Ec and Altamirano & Méndez (2015) for φlag. |
| In the text | |
 |
Fig. 3 Cutoff energy and phase lag as a function of τ∥ without (filled symbols) and with an acceleration zone (open symbols). Each point represents a calculation with different τ∥ and γmin. The horizontal dotted lines bracket the ranges of observed values as in Motta et al. (2009) for Ec and Altamirano & Méndez (2015) for φlag. The vertical dot-dashed lines show the range in τ∥ (hence in γmin also, see text) where the two quantities simultaneously cover the entire observed ranges. |
| In the text | |
 |
Fig. 4 Phase lags as a function of cutoff energy. Circles represent data from the observations. The cutoff energy and phase lag values were taken from Motta et al. (2009) and Altamirano & Méndez (2015), respecively. Solid and dashed lines correspond to the models shown in Fig. 3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


