| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A43 | |
| Number of page(s) | 8 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201526440 | |
| Published online | 18 November 2015 | |
Angular momentum evolution for galaxies in a Λ-CDM scenario
1
Instituto de Astronomía y Física del Espacio, CONICET-UBA,
Casilla de Correos 67, Suc. 28,
C1428ZAA
Ciudad Autónoma de Buenos Aires
Argentina
e-mail:
supe@iafe.uba.ar
2
Departamento de Ciencias Fisicas, Universidad Andres
Bello, Av. Republica 220,
837-0134
Santiago,
Chile
3
Millennium Institute of Astrophysics, Av. Republica 220, 837-0134
Santiago,
Chile
Received: 30 April 2015
Accepted: 28 August 2015
Context. Galaxy formation in the current cosmological paradigm is a very complex process in which inflows, outflows, interactions, and mergers are common events. These processes can redistribute the angular momentum content of baryons. Recent observational results suggest that disc formed conserving angular momentum while elliptical galaxies, although they lose angular momentum, determine a correlation between the specific angular momentum of the galaxy and the stellar mass. These observations provide stringent constraints for galaxy formation models in a hierarchical clustering scenario.
Aims. We aim to analyse the specific angular momentum content of the disc and bulge components as a function of virial mass, stellar mass, and redshift. We also estimate the size of the simulated galaxies and compare them with observations.
Methods. We use cosmological hydrodynamical simulations that include an effective, physically motivated supernova feedback which is able to regulate the star formation in haloes of different masses. We analyse the morphology and formation history of a sample of galaxies in a cosmological simulation by performing a bulge-disc decomposition of the analysed systems and their progenitors. We estimate the angular momentum content of the stellar and gaseous discs, stellar bulges, and total baryons.
Results. In agreement with recent observational findings, our simulated galaxies have disc and spheroid components whose specific angular momentum content determine correlations with the stellar and dark matter masses with the same slope, although the spheroidal components are offset by a fixed fraction. The average angular momentum efficiency for the simulated discs is η ~ 1, while for bulges it is η ~ 0.10−0.20. For the simulated sample, the correlations found for the specific angular momentum content as a function of virial mass or stellar mass are found not to evolve significantly with redshift (up to z ~ 2). Both dynamical components seem to move along the correlations as they evolve. The total specific angular momentum of galaxies occupy different positions filling the gap between pure rotational-dominated and dispersion-dominated systems. The scaling relations derived from the simulated galaxies determine a similar relation with the virial radius, which is in agreement with recent observations.
Key words: Galaxy: abundances / Galaxy: evolution / dark matter
© ESO, 2015
1. Introduction
The understanding of the morphology of galaxies and its relation to their physical properties has evolved during the last decades as new insights are provided by observations. It is well known that the angular momentum content correlates with the morphology of galaxies along the Hubble sequence. Fall (1983) has found evidence suggesting that the specific angular momentum content of both disc and elliptical galaxies holds a clear correlation with the stellar mass, but with the elliptical systems it shifts to lower values. Recently Romanowsky & Fall (2012) have analysed a larger database of galaxies with different morphologies, revisiting and confirming the Fall (1983) findings. These authors estimated the specific angular momentum of the stellar component js using kinetic and photometric data and the stellar mass obtained from near-infrared luminosities. Using this larger database, they found that disc-dominated galaxies follow this relation, as do elliptical galaxies. However, the latter have lower js at a given Mstar. The authors suggested that observed galaxies of all morphological types lie along almost parallel sequences with exponents α ~ 0.6 in the js − Mstar diagram, but with an offset between late and early types. More recently, Fall & Romanowsky (2013) showed that position of galaxies in the js − Mstar diagram is correlated with their position in the disc-to-bulge-ratio-Mstar plane relating the disc-to-bulge ratio and Mstar. They concluded that the description of galaxies in terms of js − Mstar may be regarded as a physically motivated alternative to the traditional morphological classification. The detected js − Mstar relation for spheroidal galaxies suggests an angular momentum efficiency of 10−20% regardless of Mstar (Fall & Romanowsky 2013).
In a hierarchical clustering universe, protogalaxies acquire their angular momenta via tidal torques due to small density fluctuations (Peebles 1969). As baryons are initially drawn by the same tidal torques as the dark matter haloes, they are expected to acquire similar specific angular momenta. The specific angular momentum of the dark matter haloes is supposed to grow as 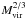 . Hence, if baryons collapse conserving their angular momentum, they should also determine a similar relation. Based on this hypothesis, Fall & Efstathiou (1980) postulated the standard disc model (SDM). This model was able to explain the observed correlation between the angular momentum of discs and the stellar masses (Mo et al. 1998).
. Hence, if baryons collapse conserving their angular momentum, they should also determine a similar relation. Based on this hypothesis, Fall & Efstathiou (1980) postulated the standard disc model (SDM). This model was able to explain the observed correlation between the angular momentum of discs and the stellar masses (Mo et al. 1998).
Several numerical works have shown that if a disc component is able to assemble, then it does so conserving its specific angular momentum, although within the hierarchical scenario for galaxy formation this might imply a combination of processes that could contribute to retaining or balancing the angular momentum content so that discs are formed as expected from the SDM (e.g. Agertz et al. 2011; Brook et al. 2011; De Rossi et al. 2012; Padilla et al. 2014; Nelson et al. 2015). In particular, SN feedback plays a critical role in determining the fraction of disc components, as well as mergers and interactions (e.g Domínguez-Tenreiro et al. 1998; Scannapieco et al. 2009; Guedes et al. 2011; Sales et al. 2012; Pedrosa et al. 2014; Lagos et al. 2015). Elliptical galaxies are expected to be affected by major mergers or repetitive minor ones. This tends to decrease the angular momentum content of the material, which ends up dominated by velocity dispersion (e.g. Meza et al. 2003; Parry et al. 2009; Hopkins et al. 2010; Bournaud et al. 2011; Sales et al. 2010; Pedrosa et al. 2014). Internal disc instabilities could also contribute to shaping bulges and elliptical galaxies (e.g. Efstathiou et al. 1982).
As the final morphology of a galaxy is directly linked to its angular momentum content, there must also be a connection with its characteristic size: when angular momentum is conserved, structures that are more extended are able to form. Recently, Kravtsov (2013) has found that characteristic sizes of stellar and gas distributions in galaxies scale approximately linearly with the virial radius derived from the abundance matching ansatz. This author found that the relation is in agreement with expectations from the model of Mo et al. (1998). Interestingly, he also found that this relation is present not only for late-type galaxies but also for early-type systems. From these findings, he concluded that the angular momentum content plays a crucial role in determining the sizes of galaxies of all morphological types, not only of those dominated by rotation.
In a recent paper, we have made a thorough study of the relation between the morphology of galaxies and their formation history, Pedrosa et al. (2014). The central role played by the angular momentum content of galaxies was studied. We found that when a disc component is able to form it does so following the expected relation from the standard disc formation model in agreement with previous works (see also Governato et al. 2010; Sales et al. 2012). More interestingly, in this simulation, spheroidal components are shown to follow a similar correlation, but offset with respect to that of rotational-supported systems. It became clear from this work that SN feedback played a major role.
In this paper, we analyse the angular momentum content of the disc and bulge components of the best resolved galaxies in a Λ-cold dark matter (Λ-CDM) scenario. Pedrosa et al. (2014) analysed a sister simulation (S230A) from the Fenix Project with a stronger feedback parameter. We explore a run (S230D) with a slightly weaker SN feedback and a different chemical distribution of the synthetized metals, which reproduces better the observational results of the metallicity gradients (Tissera et al. 2015). This is a very important point that helps to set constraints on the strength of the SN feedback (e.g. Gibson et al. 2013). The simulated galaxies also have larger D/T stellar ratios than those measured in S230A. We also follow them back in time to establish the possible existence of a redshift dependence.
This work is organized as follows. In Sect. 2 we describe the initial conditions and free parameters used to run the analysed simulation and the methods used to identify and decompose galaxies. In Sect. 3 we analyse the angular momentum content of our galaxies and their dynamical components. In Sect. 4 we study the characteristic sizes of the galaxies and the connection with their angular momentum content. Finally, in Sect. 5 we summarize our main findings.
2. Numerical experiments
We used a version of the code GADGET-3, an update of GADGET-2 (Springel & Hernquist 2003; Springel 2005), optimized for massive parallel simulations of highly inhomogeneous systems. This version of GADGET-3 includes treatments for metal-dependent radiative cooling, stochastic star formation (SF), chemical enrichment, and the multiphase model for the interstellar medium (ISM) and the supernova (SN) feedback scheme of Scannapieco et al. (2005, 2006). The SN feedback model is able to successfully trigger galactic mass-loaded winds without introducing mass-scale parameters.
 |
Fig. 1 Upper panels: density map for a face-on and an edge-on view of a late-type galaxy from the 230D simulation catalogue. Lower panels: disc and central spheroid components. |
Our code considers energy feedback by Type II (SNII) and Type Ia (SNIa) supernovae. These processes are grafted into a multiphase model for the ISM, both developed by Scannapieco et al. (2006). The energy released by each SN event is distributed between the cold and the hot phases of the simulated ISM. The adopted multiphase model allows the coexistence of diffuse and dense gas phases. In this model, each gas particle defines the cold and hot phases by using a local entropy criteria. This definition allows particles to decouple hydrodynamically from particular low-entropy ones if they are not part of a shock front. Each cold gas particle has a reservoir where injected SN energy is stored until they fulfil the conditions for joining their local hot phase. It is worth mentioning that this SN feedback scheme does not include parameters that depend on the global properties of the given galaxy (e.g. the total mass, size), thus making it suitable for cosmological simulations where systems with different masses have formed in a complex way. Our code also includes the chemical evolution model developed by Mosconi et al. (2001). SNII and SNIa contribute with chemical elements estimated by adopting the chemical yields of Woosley & Weaver (1995) and Iwamoto et al. (1999), respectively.
As already mentioned, for this study, we used one of the simulations from the Fenix Project (S230D). They share the same initial conditions but assume different parameters for the SF and SN feedback subgrid physics. The initial conditions are consistent with the concordance model with ΩΛ = 0.7, Ωm = 0.3, Ωb = 0.04, a normalization of the power spectrum of σ8 = 0.9, and H0 = 100 h km s-1 Mpc-1 with h = 0.7. The simulated volume represents a box of 10 Mpc h-1 comovil with 2 × 2303 initial particles, achieving a mass resolution of 5.9 × 106 h-1 M⊙ and 9.1 × 105 h-1 M⊙ for the dark matter and initial gas particles, respectively. The gravitational softening is 0.5 kpc h-1. We acknowledge that the initial condition represents a small volume of the Universe. It was chosen to represent a typical region of the Universe with no large structure nearby. Using the S230A run, De Rossi et al. (2013) verified that halo growth is reproduced well by comparing the results with those obtained from the Millennium simulation by Fakhouri et al. (2010). The S230A was also analysed by Pedrosa et al. (2014) to study the morphology and angular momentum content of the simulated galaxies. Recently, Artale et al. (2015) introduced the effects of high-mass X-ray binary feedback in the very early Universe in a counterpart run of S230D.
Simulation S230D used a higher gas density threshold for star formation and a lower energy per SN event (0.7 × 1051 erg) than in S230A (e.g. De Rossi et al. 2013; Pedrosa et al. 2014). Simulation 230D injects a larger fraction of new synthesized chemical elements into the cold phase, while the fraction of SN energy is equally distributed between the cold and hot phases (S230A injected an equal fraction of energy and chemical elements into the cold and hot phases close to the SF region). This different combination of SF and SN feedback parameters and metal distribution produced a good representation of chemical abundances on the disc components (Tissera et al. 2015).
2.1. Simulated galaxy sample
Our galaxy sample was built up by using a friends-of-friends algorithm to identify the virialized structures. Then, the substructures were discerned by using the SUBFIND scheme (Springel et al. 2001), which iteratively determines the self-bound substructures within the virial radius, r200. For illustration purposes, an example of a late-type galaxy of our simulated catalogue is shown in Fig. 1, (upper panels).
To diminish resolution problems, we restricted our study to systems with a total number of particles greater than 2000 in the main galaxy (which corresponds to Mvir ~ 1010.3 M⊙). We also tested that the estimated relations are conserved when this particle number limit is increased to ~10 000.
In order to classify our simulated galaxies into early-type and late-type systems, we estimated the parameter ϵ of the star (gas) particles defined as ϵ = Jz/Jz,max(E), where Jz is the angular momentum component in the direction of the total angular momentum and Jz,max(E) is the maximum Jz over all particles at a given binding energy, E. A particle on a perfect prograde circular orbit in the disc plane should have ϵ = 1. We considered particles with ϵ higher than 0.5 to be part of a disc. The particles that did not satisfy this requirement were considered to belong to the spheroidal component. By inspecting the ϵ − E plane, we checked whether the adopted limits were suitable to individualize the rotationally supported components. This threshold is less restrictive than those usually adopted (e.g. Tissera et al. 2012), so if there were stars in a thick disc they would contribute by decreasing the signals for angular momentum conservation, for example. We also distinguished between the central spheroid and the stellar halo components depending on their bounding energy following Tissera et al. (2012). In Fig. 1 (lower panels) we display the disc and central spheroid components for the galaxy shown after the decomposition.
Therefore, for each simulated galaxy, we determine the disc (i.e. rotational-dominated) and the central spheroids components (i.e. dispersion-dominated) based on these dynamical criteria. This procedure was also applied to galaxies identified at z = 1 and z = 2 in order to study the evolution of the angular momentum content in the galaxies, their central spheroids and disc components, and the dark matter haloes.
 |
Fig. 2 Relation ji − mi medians for the stellar (red dashed lines) and gaseous (green dashed lines) disc components, the stellar spheroidal components (pink dashed lines), the total stellar component (blue line), and the total baryonic component (black lines). The solid black line represents the relation in the case of angular momentum conservation. The stellar and gas disc components are consistent with angular momentum conservation, while the spheroidal components determine a relation with a similar slope but offset by a constant factor suggesting that spheroids have lost a similar fraction of angular momentum with respect to the total angular momentum of their virial haloes. The relation has been estimated for z = 0 (upper panels, in the right panel we include the scatter data for the stellar disc component), and for z = 1 and z = 2 (bottom panels, left and right, respectively), and shows similar trends. |
3. Angular momentum
To calculate the properties of the simulated galaxies, we adopted the half-mass stellar ratio (rHM), defined as the radius that enclosed 50% of the total stellar mass. This characteristic radius was chosen in order to make an adequate comparison with observational results. The half-mass radius is usually adopted to estimate galaxy properties in observations. In the case of Kravtsov (2013) for example, he uses the stellar half-mass radius to estimate his Rhm − Rvir relation. We estimated the ratio between the angular momentum of the stars (gas) in the discs (JD) within rHM and the corresponding angular momentum of the dark matter haloes within the virial radius (JH), jd = JD/JH, as a function of the ratio between the corresponding masses, md = MD/MH1. We followed the classical notation of Mo et al. (1998) to define jd and md. Similarly, we defined the js and ms ratios by using the star particles identified as belonging to the central spheroidal components. Those corresponding to the whole stellar mass and the total baryonic mass were also estimated and analysed. These relations can be seen in Fig. 2 for z = 0 (upper panel), z = 1 (middle panel), and z = 2 (lower panel). As shown, there is a clear correlation for the disc and central spheroidal components in the three redshifts (see also Domínguez-Tenreiro et al. 1998; Pedrosa et al. 2014).
We first analyse the relations at z = 0. As can be seen in Fig. 2, there is a one-to-one relation between ji and mi, where i represents the gas or stellar disc components as expected in the case of angular momentum conservation. As discussed before, the one-to-one correlation is the consequence of the fact that all the material in the system experienced the same external torques before it collapsed to form a bounded system, and that the collapse occurred with angular momentum conservation. Interestingly, a clear correlation is also detected for the stellar central spheroidal components, but it is offset from that determined by the disc components. This indicates that the material that ended up dominated by dispersion lost angular momentum as expected, but it did so by a similar fraction, regardless of the final stellar fraction, mi. This trend was previously shown in Pedrosa et al. (2014, Fig. 3,) and in Pedrosa & Tissera (2015, see also Domínguez-Tenreiro et al. 1998.
In Fig. 2 the same relations are estimated at z = 1 and z = 2. As can be seen, both the stellar and gaseous discs are always consistent with the one-to-one relation. However, the most interesting result is again provided by the spheroidal components, which determine a similar correlation as a function of redshift. Regardless of their formation history, the disc and spheroidal components determine relations with the stellar and dark matter masses, which are statistically unchanged up to z ~ 2. The gap between the angular momentum content of the galaxy with respect to that of the dark matter does not show a systematic change with redshift.
Hence, our simulated galaxies have disc and central spheroidal components consistent with the relation 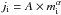 , where A ~ 1 for the disc components and A ~ 0.10−0.20 for the central spheroidal components. We fit a linear regression to the log-log relations finding slopes of α ~ 0.9 and α ~ 1.1 for the stellar discs and central spheroids, respectively, at z = 0.
, where A ~ 1 for the disc components and A ~ 0.10−0.20 for the central spheroidal components. We fit a linear regression to the log-log relations finding slopes of α ~ 0.9 and α ~ 1.1 for the stellar discs and central spheroids, respectively, at z = 0.
These relations are found not to evolve significantly with redshift at least up to z ~ 2 (α ~ 0.90,0.87 and α ~ 0.96,0.86 for the stellar discs and spheroids at z = 1 and z = 2, respectively) Therefore, the spheroidal components, although they are dominated by dispersion, retain a similar fraction of the angular momentum imprinted by tidal torques onto the small perturbations during the first stages of the evolution of the structure (Peebles 1969), regardless of their assembly histories or mi.
The slope of the relation ji − mi changes when the total stellar mass (i.e. total stellar discs and bulges) or the baryonic mass are considered for the estimation of these ratios (blue and black lines, respectively), reaching values close to α ~ 2 due to the combination of angular momentum content of both disc and bulge components. This is in agreement with the results obtained by previous works where the angular momentum of baryons were studied without distinguishing between disc and spheroidal components (e.g. Sales et al. 2012). In this case, the gap is filled with the combination of contributions from the two components and the slope of the mean relation gets steeper. We found indications of a flattening in the relation for the total baryonic mass with redshift (α ~ 1.54,1.40 for z = 1 and z = 2, respectively ). However, a larger sample is needed to confirm the level of evolution since the dispersion in our sample increases with increasing redshift.
We have also analysed the angular momentum efficiency ηi for both components, defined as the ratio between jD (jS) of the disc component (central spheroids) and jH of the dark matter halo, following Sales et al. (2010). In Fig. 3 we plot ηi versus mi for the three analysed redshifts. As expected, the disc components are found to have η ~ 1, on average, reflecting the conservation of angular momentum during their formation. Conversely, the central spheroid has η ~ 0.10−0.20, on average. In both cases, there is no clear evolution with redshift (although the dispersion increases slightly with increasing z). The different locations of η for the two dynamical components reflect their different evolutionary histories that introduce dispersion but, nevertheless, take place in an organized fashion. The narrow range of mi values detected for the spheroids indicate that there are no tiny bulges or massive spheroids in our simulations. Hence, our results should be verified using larger and higher-resolution simulations.
 |
Fig. 3 Angular momentum efficiency ηi as a function of mi ratio for disc (squares) and central spheroid (circles) components at z = 0 (red), z = 1 (green), and z = 2 (blue). |
3.1. Specific angular momenta of galaxies and their dark matter haloes
Here we analyse in detail the j of the disc and central spheroids in relation to that of their dark matter haloes. In Fig. 4 we show j for the stellar disc and spheroidal components as a function of virial mass of their host galaxies. They define parallel relations consistent with j ∝ M2/3. This is in agreement with the expected theoretical relation derived under the hypothesis that the dark matter halo spin parameter is constant. For comparison purposes, we have also included the estimations for the gaseous disc components and the simulated dark matter haloes, which agree well with the expected theoretical relation under the hypothesis of angular momentum conservation (solid line).
Both the spheroidal and disc components determine relations with the same slopes, which indicates that the stellar spheroids have formed from material of lower content of angular momentum (by a similar fraction), regardless of the virial mass of their host galaxy (or the relative fraction of stellar mass accumulated in the central region as shown in Fig. 2). This trend is similar to that reported by Genel et al. (2015). This agreement is highly encouraging considering the differences in the codes, subgrid physics, and criteria adopted to classify the simulated galaxies.
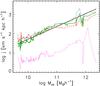 |
Fig. 4 Medians of the specific stellar angular momentum of the gaseous (green line) and stellar disc (red dashed line) components and the central stellar spheroidal components (pink dotted line) as a function of the virial mass of their host haloes. For comparison purposes, the relation estimated for the dark matter haloes (black dotted line) and the expected theoretical relation (black solid line) have been also included. |
3.2. Evolution with redshift
A question naturally arises about the possible evolution of j in the disc and central spheroidal components with redshift. This might imply a change in the slope or fraction of lost angular momentum, or both, as galaxies evolve. To explore this, we estimated the j values for the stellar discs and central spheroids as a function of Mvir for z = 1 and z = 2. We note that at each redshift, we apply the dynamical decomposition explained in Sect. 2.1.
As shown in Fig. 5, we found no significant evolution of these relations since z ~ 2. The gap between the j of rotational-dominated and dispersion-dominated components remains approximately constant, implying a loss of 80−90% of the initial angular momentum content by the material which ends up in the spheroidal component, regardless of the virial mass of the halo or of the redshift. This is a remarkable trend which suggests again that, independently of the assembly history of galaxies, their disc and bulge components will contain similar amounts of angular momentum as they evolve.
We note that in Fig. 5 we show the j for the stellar disc and bulge components, independently of the global morphology of the galaxies. Hence, some of the simulated galaxies are disc-dominated while others are spheroid-dominated systems. So, their total j will be distributed by filling the gap and determining a steeper mean relation as shown in Fig. 2. Therefore, these trends of conservation of the j by rotational-dominated components and equally lost of j by dispersion-dominated ones will be erased as the gap is filled with the combination of systems. The separation of discs and central spheroids is crucial for a deeper insight into the physical problem. Nevertheless, we cannot explain the origin of the similar angular momentum efficiency for central spheroids yet.
 |
Fig. 5 Specific stellar angular momentum for the stellar disc (empty triangles) and central spheroid (empty circles) components as a function of the virial mass for z = 0 (red), z = 1 (green), and z = 2 (blue). The gap between the two dynamical components does not evolve with redshift. For comparison purposes, j for the dark matter haloes have been also included (filled squares). We note that the angular momenta of the discs and central spheroids are given at rHM. |
3.3. Comparison with observations
Recently, Fall & Romanowsky (2013) reported results that support the existence of a relation between the j and stellar mass with the same slope for both ellipticals and disc-dominated galaxies, as found by Fall & Efstathiou (1980). The gap between them indicates a loss of angular momentum by the material which formed the ellipticals by a similar fraction, regardless of stellar mass. Our simulations seem to reproduce this trend naturally as can be seen in Fig. 2 and more clearly seen in Fig. 6 where the observational estimations from Fall & Romanowsky (2013) are included. As shown in this figure, the stellar disc component determines a relation that agrees well with the one estimated for observed discs. In the case of central spheroids, they are also consistent with observations provided that stellar bulges behave similarly to elliptical galaxies (as also suggested by Fall & Romanowsky 2013). The good agreement between the observations and simulations suggests that the latter are able to grasp the relevant aspects of the physics at play well enough.
 |
Fig. 6 Relation between j and the total stellar mass for the simulated stellar disc components (blue filled squares) and the stellar spheroids (red open circles). The observational estimations reported by Fall & Romanowsky (2013) are depicted for comparison: disc components (blue open squares) and elliptical galaxies (red filled circles). The theoretical relation j ∝ M2/3 is also included for comparison (black continuous line). |
In order to improve the comparison of our results with observations, we estimated the total j defined by the whole stellar populations within the galaxy radius2. Previous figures show results estimated at rHM. The morphology of a simulated galaxy is defined by the ratio D/T between the stellar disc mass, D, and the total stellar mass of the galaxy, T = D + B. Simulated galaxies are classified according to the D/T in four subsamples from disc-dominated (D/T> 0.6) to spherodial-dominated (D/T< 0.2) ones.
We should keep in mind that the comparison should be taken as indicative since differences between the observed and simulated parameters are always expected. For example, while observations use the gas information to trace the angular momentum content of the stellar discs under the hypothesis that they should be dynamically comparable, the simulated calculations make use of the information store directly in the stellar populations. As we show below, the gaseous discs conserve their angular momentum and they compare well to the relation determined by Sc galaxies, where the dispersion-dominated component is small. This indicates that this galaxy type is missing in the simulations.
In Fig. 7 we show j as a function of galaxy stellar mass with different D/T ratios. A correlation can be seen in the sense that higher D/T ratios are related to higher contents of specific angular momentum, as expected. It also presents a good agreement with the observational trend found by Fall & Romanowsky (2013). The gap between disc-dominated systems (D/T> 0.6) and spheroidal-dominated ones (D/T< 0.2) is filled with the corresponding intermediate morphological types. Our results support the claim that this relation opens the possibility to an alternative way of mapping the morphologies of the galaxies. However, and more importantly, the agreement between the observational and numerical results suggests that the hierarchical clustering signature is not erased in spheroidal galaxies as previously assumed.
It is remarkable that the gap between both morphological types does not depend on the mass of the galaxy or the virial mass of the haloes. In Pedrosa et al. (2014) a detailed study of the D/T fraction was done. The evolution of the morphology was quantified by analysing the D/T ratios as a function of the redshift for a group of 15 selected galaxies and the correlation of that parameter with their assembly history. As galaxies evolve, the D/T ratios of the progenitor systems can drastically change, reflecting their different formation histories (major and minor mergers, accretions, etc.). The D/T fraction is a highly dynamic parameter, which indicates that the disc can be destroyed and rebuilt several times along its evolution, as shown in Fig. 4 of Pedrosa et al. (2014).
 |
Fig. 7 Relation between j and the total stellar mass for simulated galaxies with different disc-to-bulge ratios: D/T> 0.6 (red filled triangles), 0.4 <D/T< 0.6 (green filled triangles), 0.4 <D/T< 0.2 (blue filled triangles), and D/T< 0.2 (pink filled triangles) calculated at the galaxy radius. The relation for the gaseous discs are also included (cyan crosses). The observational estimations reported by Fall & Romanowsky (2013) are depicted for comparison: Sa-Sab (black triangles), Sb-Sbc (black squares), Sc-Sm (black diamonds), E (black filled circles), S0 (black filled squares, and sE (black circles). The theoretical relation j ∝ M2/3 is also included (black continuous line). |
 |
Fig. 8 Size relations for the simulated galaxies and their host dark matter haloes: rHM = 0.04 × λr200. Upper panel: simulated galaxies are colour-coded according to the D/T ratio: D/T> 0.6 (red filled squares), 0.4 <D/T< 0.6 (green filled diamonds), 0.4 <D/T< 0.2 (blue crosses), and D/T< 0.2 (pink filled circles). Lower panel: the colours correspond to the different redshifts: z = 0 (red circles), z = 1 (green squares), z = 2 (blue triangles) |
During galaxy assembly, angular momentum is exchanged through different physical processes. Previous works such as Brook et al. (2011) have found that preferential removal of low angular momentum material at early redshift also contributes to the redistribution of the angular momentum. They found that low angular momentum material is accreted and rapidly expelled when star formation peaks at early times, with shallow potential wells that favour early gas ejection. Later accreted material has higher angular momentum and is accreted preferentially onto the disc, contributing to re-building it. Also, gas might flow into galaxies through the dark matter filaments, feeding the galaxy with high angular momentum material, as found by Dekel et al. (2009). Using a more observational approach, Genel et al. (2015) studied the angular momentum content of galaxies in the Illustris simulations. They found, in agreement with our results, that the retention factor of the early-type galaxies is approximately 30%. They also analysed the evolution track of a group of selected galaxies, finding that different processes, such as mergers, could drastically redistribute the angular momentum content (see also Teklu et al. 2015).
Therefore, bulges are formed by important contributions of low angular momentum material which might have lost it during the galaxy formation process (Pedrosa et al. 2014).
4. Size relations
As shown in previous sections, the disc components in our simulations were formed in agreement with the hypothesis of j conservation, while the central spheroids were formed from material with lower content of j, by a similar fraction. From these results, we would expect a clear scaling relation between the galaxy and halo size.
The proportionality between the specific angular momentum of the baryons and that of the halo assumed by the disc galaxy formation models would also imply the existence of a linear relation between the galactic and virial radius of the hosting halo (Kravtsov 2013; Tonini et al. 2006). The galaxy size is expected to scale as rgal ∝ λr200.
Kravtsov (2013) analysed the relation between sizes of stellar systems of galaxies characterized by their half-mass radius and the virial radius of their dark matter haloes. The latter are derived by using the abundance matching ansatz. They found that the characteristic size of stellar and gas distributions in galaxies spanning several orders of magnitude in stellar mass scales approximately linearly with a fraction of the virial radius with a proportionality factor of ~0.015. However, this author did not consider the effects of baryons on the dark matter potential well, which are naturally provided by our hydrodynamical simulations (e.g. Pedrosa et al. 2010; Tissera et al. 2010). In fact, Diemer et al. (2013) claimed that the most common definition of the dark matter halo that considers a spherical overdensity of matter with respect to a reference density, such as the critical density or the mean matter density of the Universe, could lead to a spurious pseudo-evolution of halo mass due to redshift evolution of the reference density. They found that for all halo masses a significant fraction of the halo mass growth since z ~ 1 is due to this so-called pseudo-evolution rather than the actual physical accretion of matter. They obtained a corrected value for the size relation of 0.03−0.04. by taking the contraction effect into account.
In Fig. 8 (upper panel) we show the stellar rHM as a function of a fraction of r200 for our simulated systems. Interestingly, we determined that the best factor relating both characteristic radii is ~0.04. In this figure, we show the relation for galaxies with different D/T ratios. It is clear that higher D/T values correspond to more extended structures. And this is consistent with Fig. 7 where it can also be seen that higher D/T ratios correspond to higher values of angular momentum content. The size correlation is in place since z ~ 2 as expected since the angular momentum relation is also present and unchanged overall since this time Fig. 8 (lower panel).
5. Conclusions
We used hydrodynamical cosmological simulation to perform a comparative analysis of the angular momentum content in the disc and bulge components of the simulated galaxies. We focused our analysis on the best resolved galaxies and used a dynamical criterion to identify the disc and bulge components at z = 0 and for their progenitor galaxies at z = 1 and z = 2.
Our most important findings are the following:
-
We found that both discs and bulges determine a relation in the ji − mi plane. Both the rotational-supported and the dispersion-dominated components follow a relation with the same slope (ji ∝ mi). For the disc components, the correlation is the expected one-to-one relation in the case of angular momentum conservation (Mo et al. 1998). Remarkably, the dispersion-dominated systems determine a parallel relation but are offset by an approximately constant factor. Our simulated bulges conserved η ~ 10−20% of their original angular momentum regardless of the D/T ratio of the galaxy (see also Domínguez-Tenreiro et al. 1998 ; Pedrosa et al. 2014 ). This is in agreement with observational findings ( Fall & Romanowsky 2013 , and references therein).
-
A similar analysis was carried out for the progenitor systems up to z ~ 2, finding that the central spheroids and discs determine similar relations. Hence, regardless of the formation history of these galaxies, their disc and spheroidal components have angular momentum contents which determine relations with the stellar and dark matter masses with similar slope up to z ~ 2. In the case of the spheroidal components a similar off-set is detected showing an angular momentum efficiency of ~ 0.10 − 0.20. These values vary slightly with redshift. A larger sample is required to assess robustly the level of evolution.
-
Regarding the specific angular momentum, we found that the spheroidal and disc components determine relations with the same slopes, j ∝ M2/3. This indicates that the stellar spheroids have been formed by material of low angular momentum content or that have lost it by similar fraction during the assembly process regardless of the virial mass of their host galaxy. We have analysed this relation at different redshifts, finding no evolution. Remarkably, this trend suggests that independently of virial masses, the disc and bulge components will conserve similar amounts of angular momentum as they evolve.
-
In good agreement with the trend found by Fall & Romanowsky (2013) , we found a clear correlation between the morphological type of a galaxy and its total specific angular momentum content: higher D/T ratios are related with higher contents of specific angular momentum, as expected. The gap between disc-dominated systems (D/T> 0.6) and spheroidal-dominated ones (D/T< 0.2) is filled with the corresponding intermediate morphological types. This supports the claim that this relation opens the possibility to an alternative way of mapping the morphology of galaxies. This also implies that the hierarchical clustering signature is still present in spheroidal galaxies. It is remarkable that the gap between the two morphological types does not depend on the mass of the galaxy or the virial mass of the haloes.
-
In agreement with Kravtsov (2013) , we found that the characteristic size of stellar distributions in the simulated galaxies scales approximately linearly with the virial radius in the log-log plane. The proportionality factor for our simulated systems is ~ 0.04 (Diemer et al. 2013). This relation is found not to evolve with time: galaxies move along the relation as one moves to higher redshift.
Acknowledgments
The authors thanks Michael Fall for kindly providing the data electronically. This work was partially supported by PICT 2011-0959 and PIP 2012-0396 (Mincyt, Argentina). P.B.T. acknowledges partial support from the Regular Grant UNAB 2014, Nucleo UNAB 2015 of Universidad Andres Bello and Fondecyt 1150334.
References
- Agertz, O., Teyssier, R., & Moore, B. 2011, MNRAS, 410, 1391 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Artale, M. C., Tissera, P. B., & Pellizza, L. J. 2015, MNRAS, 448, 3071 [NASA ADS] [CrossRef] [Google Scholar]
- Bournaud, F., Chapon, D., Teyssier, R., et al. 2011, ApJ, 730, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Brook, C. B., Governato, F., Roškar, R., et al. 2011, MNRAS, 415, 1051 [NASA ADS] [CrossRef] [Google Scholar]
- De Rossi, M. E., Tissera, P. B., & Pedrosa, S. E. 2012, A&A, 546, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Rossi, M. E., Avila-Reese, V., Tissera, P. B., González-Samaniego, A., & Pedrosa, S. E. 2013, MNRAS, 435, 2736 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., Sari, R., & Ceverino, D. 2009, ApJ, 703, 785 [Google Scholar]
- Diemer, B., More, S., & Kravtsov, A. V. 2013, ApJ, 766, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Domínguez-Tenreiro, R., Tissera, P. B., & Sáiz, A. 1998, ApJ, 508, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Efstathiou, G., Lake, G., & Negroponte, J. 1982, MNRAS, 199, 1069 [NASA ADS] [CrossRef] [Google Scholar]
- Fakhouri, O., Ma, C.-P., & Boylan-Kolchin, M. 2010, MNRAS, 406, 2267 [NASA ADS] [CrossRef] [Google Scholar]
- Fall, S. M. 1983, in Internal Kinematics and Dynamics of Galaxies, ed. E. Athanassoula, IAU Symp., 100, 391 [Google Scholar]
- Fall, S. M., & Efstathiou, G. 1980, MNRAS, 193, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Fall, S. M., & Romanowsky, A. J. 2013, ApJ, 769, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Genel, S., Fall, S. M., Hernquist, L., et al. 2015, ApJ, 804, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, B. K., Pilkington, K., Brook, C. B., Stinson, G. S., & Bailin, J. 2013, A&A, 554, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Governato, F., Brook, C., Mayer, L., et al. 2010, Nature, 463, 203 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Guedes, J., Callegari, S., Madau, P., & Mayer, L. 2011, ApJ, 742, 76 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hopkins, P. F., Bundy, K., Croton, D., et al. 2010, ApJ, 715, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Iwamoto, K., Brachwitz, F., Nomoto, K., et al. 1999, ApJS, 125, 439 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kravtsov, A. V. 2013, ApJ, 764, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Lagos, C. d. P., Padilla, N. D., Davis, T. A., et al. 2015, MNRAS, 448, 1271 [NASA ADS] [CrossRef] [Google Scholar]
- Meza, A., Navarro, J. F., Steinmetz, M., & Eke, V. R. 2003, ApJ, 590, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Mo, H. J., Mao, S., & White, S. D. M. 1998, MNRAS, 295, 319 [Google Scholar]
- Mosconi, M. B., Tissera, P. B., Lambas, D. G., & Cora, S. A. 2001, MNRAS, 325, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, D., Genel, S., Vogelsberger, M., et al. 2015, MNRAS, 448, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Padilla, N. D., Salazar-Albornoz, S., Contreras, S., Cora, S. A., & Ruiz, A. N. 2014, MNRAS, 443, 2801 [Google Scholar]
- Parry, O. H., Eke, V. R., & Frenk, C. S. 2009, MNRAS, 396, 1972 [NASA ADS] [CrossRef] [Google Scholar]
- Pedrosa, S., & Tissera, P. 2015, Proc. of AAA Meeting 2014 [arXiv:1503.01798] [Google Scholar]
- Pedrosa, S., Tissera, P. B., & Scannapieco, C. 2010, MNRAS, 402, 776 [NASA ADS] [CrossRef] [Google Scholar]
- Pedrosa, S. E., Tissera, P. B., & De Rossi, M. E. 2014, A&A, 567, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peebles, P. J. E. 1969, ApJ, 155, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Romanowsky, A. J., & Fall, S. M. 2012, ApJS, 203, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Sales, L. V., Navarro, J. F., Schaye, J., et al. 2010, MNRAS, 409, 1541 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Sales, L. V., Navarro, J. F., Theuns, T., et al. 2012, MNRAS, 423, 1544 [NASA ADS] [CrossRef] [Google Scholar]
- Scannapieco, C., Tissera, P. B., White, S. D. M., & Springel, V. 2005, MNRAS, 364, 552 [NASA ADS] [CrossRef] [Google Scholar]
- Scannapieco, C., Tissera, P. B., White, S. D. M., & Springel, V. 2006, MNRAS, 371, 1125 [NASA ADS] [CrossRef] [Google Scholar]
- Scannapieco, C., White, S. D. M., Springel, V., & Tissera, P. B. 2009, MNRAS, 396, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., & Hernquist, L. 2003, MNRAS, 339, 289 [Google Scholar]
- Springel, V., Yoshida, N., & White, S. D. M. 2001, New A, 6, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Teklu, A. F., Remus, R.-S., Dolag, K., et al. 2015, ApJ, 812, 29 [Google Scholar]
- Tissera, P. B., White, S. D. M., Pedrosa, S., & Scannapieco, C. 2010, MNRAS, 406, 922 [NASA ADS] [Google Scholar]
- Tissera, P. B., White, S. D. M., & Scannapieco, C. 2012, MNRAS, 420, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Tissera, et al. 2015, submitted [Google Scholar]
- Tonini, C., Lapi, A., Shankar, F., & Salucci, P. 2006, ApJ, 638, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Upper panels: density map for a face-on and an edge-on view of a late-type galaxy from the 230D simulation catalogue. Lower panels: disc and central spheroid components. |
| In the text | |
 |
Fig. 2 Relation ji − mi medians for the stellar (red dashed lines) and gaseous (green dashed lines) disc components, the stellar spheroidal components (pink dashed lines), the total stellar component (blue line), and the total baryonic component (black lines). The solid black line represents the relation in the case of angular momentum conservation. The stellar and gas disc components are consistent with angular momentum conservation, while the spheroidal components determine a relation with a similar slope but offset by a constant factor suggesting that spheroids have lost a similar fraction of angular momentum with respect to the total angular momentum of their virial haloes. The relation has been estimated for z = 0 (upper panels, in the right panel we include the scatter data for the stellar disc component), and for z = 1 and z = 2 (bottom panels, left and right, respectively), and shows similar trends. |
| In the text | |
 |
Fig. 3 Angular momentum efficiency ηi as a function of mi ratio for disc (squares) and central spheroid (circles) components at z = 0 (red), z = 1 (green), and z = 2 (blue). |
| In the text | |
 |
Fig. 4 Medians of the specific stellar angular momentum of the gaseous (green line) and stellar disc (red dashed line) components and the central stellar spheroidal components (pink dotted line) as a function of the virial mass of their host haloes. For comparison purposes, the relation estimated for the dark matter haloes (black dotted line) and the expected theoretical relation (black solid line) have been also included. |
| In the text | |
 |
Fig. 5 Specific stellar angular momentum for the stellar disc (empty triangles) and central spheroid (empty circles) components as a function of the virial mass for z = 0 (red), z = 1 (green), and z = 2 (blue). The gap between the two dynamical components does not evolve with redshift. For comparison purposes, j for the dark matter haloes have been also included (filled squares). We note that the angular momenta of the discs and central spheroids are given at rHM. |
| In the text | |
 |
Fig. 6 Relation between j and the total stellar mass for the simulated stellar disc components (blue filled squares) and the stellar spheroids (red open circles). The observational estimations reported by Fall & Romanowsky (2013) are depicted for comparison: disc components (blue open squares) and elliptical galaxies (red filled circles). The theoretical relation j ∝ M2/3 is also included for comparison (black continuous line). |
| In the text | |
 |
Fig. 7 Relation between j and the total stellar mass for simulated galaxies with different disc-to-bulge ratios: D/T> 0.6 (red filled triangles), 0.4 <D/T< 0.6 (green filled triangles), 0.4 <D/T< 0.2 (blue filled triangles), and D/T< 0.2 (pink filled triangles) calculated at the galaxy radius. The relation for the gaseous discs are also included (cyan crosses). The observational estimations reported by Fall & Romanowsky (2013) are depicted for comparison: Sa-Sab (black triangles), Sb-Sbc (black squares), Sc-Sm (black diamonds), E (black filled circles), S0 (black filled squares, and sE (black circles). The theoretical relation j ∝ M2/3 is also included (black continuous line). |
| In the text | |
 |
Fig. 8 Size relations for the simulated galaxies and their host dark matter haloes: rHM = 0.04 × λr200. Upper panel: simulated galaxies are colour-coded according to the D/T ratio: D/T> 0.6 (red filled squares), 0.4 <D/T< 0.6 (green filled diamonds), 0.4 <D/T< 0.2 (blue crosses), and D/T< 0.2 (pink filled circles). Lower panel: the colours correspond to the different redshifts: z = 0 (red circles), z = 1 (green squares), z = 2 (blue triangles) |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


