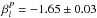| Issue |
A&A
Volume 583, November 2015
|
|
|---|---|---|
| Article Number | A137 | |
| Number of page(s) | 16 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201526638 | |
| Published online | 05 November 2015 | |
Linear polarization structures in LOFAR observations of the interstellar medium in the 3C 196 field ⋆
1 Kapteyn Astronomical Institute, University of Groningen, PO Box 800, 9700 AV Groningen, The Netherlands
e-mail: vjelic@astro.rug.nl
2 ASTRON – The Netherlands Institute for Radio Astronomy, PO Box 2, 7990 AA Dwingeloo, The Netherlands
3 Ruđer Bošković Institute, Bijenička cesta 54, 10000 Zagreb, Croatia
4 Department of Astrophysics/IMAPP, Radboud University Nijmegen, PO Box 9010, 6500 GL Nijmegen, The Netherlands
5 Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
6 Department of Physics & Astronomy, University College London, Gower Street, London WC1E 6BT, UK
7 SKA SA, 3rd Floor, The Park, Park Road, 7405 Pinelands, South Africa
8 Max-Planck Institute for Astrophysics, Karl-Schwarzschild-Strasse 1, 85748 Garching bei München, Germany
9 Astronomy Centre, Department of Physics & Astronomy, Pevensey II Building, University of Sussex, Brighton BN1 9QH, UK
10 Department of Astronomy and Oskar Klein Centre, Stockholm University, AlbaNova, 10691 Stockholm, Sweden
11 ASTRON & IBM Center for Exascale technology, Oude Hoogeveensedijk 4, 7991 PD Dwingeloo, The Netherlands
Received: 30 May 2015
Accepted: 2 September 2015
Aims. This study aims to characterize linear polarization structures in LOFAR observations of the interstellar medium (ISM) in the 3C 196 field, one of the primary fields of the LOFAR-Epoch of Reionization key science project.
Methods. We have used the high band antennas (HBA) of LOFAR to image this region and rotation measure (RM) synthesis to unravel the distribution of polarized structures in Faraday depth.
Results. The brightness temperature of the detected Galactic emission is 5−15 K in polarized intensity and covers the range from –3 to +8 rad m-2 in Faraday depth. The most interesting morphological feature is a strikingly straight filament at a Faraday depth of +0.5 rad m-2 running from north to south, right through the centre of the field and parallel to the Galactic plane. There is also an interesting system of linear depolarization canals conspicuous in an image showing the peaks of Faraday spectra. We used the Westerbork Synthesis Radio Telescope (WSRT) at 350 MHz to image the same region. For the first time, we see some common morphology in the RM cubes made at 150 and 350 MHz. There is no indication of diffuse emission in total intensity in the interferometric data, in line with results at higher frequencies and previous LOFAR observations. Based on our results, we determined physical parameters of the ISM and proposed a simple model that may explain the observed distribution of the intervening magneto-ionic medium.
Conclusions. The mean line-of-sight magnetic field component, B∥, is determined to be 0.3 ± 0.1 μG and its spatial variation across the 3C 196 field is 0.1 μG. The filamentary structure is probably an ionized filament in the ISM, located somewhere within the Local Bubble. This filamentary structure shows an excess in thermal electron density (neB∥> 6.2 cm-3μG) compared to its surroundings.
Key words: ISM: general / ISM: magnetic fields / ISM: structure / radio continuum: ISM / techniques: interferometric / techniques: polarimetric
The RM cubes (FITS files) are available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/583/A137
© ESO, 2015
1. Introduction
The Galactic interstellar medium (ISM) is filled with cold, warm, and hot thermal gas (the multi-phase medium; e.g. McKee & Ostriker 1977) in a mixture of ionized, neutral, atomic, and molecular components. In addition, the ISM is permeated with non-thermal plasma (mostly relativistic protons and electrons) pervaded by a large-scale magnetic field. In general, the energy density in the various components is approximately equal, but large deviations in energy balance occur in various situations. Observations of diffuse polarized emission are valuable in exploring both the distribution and the properties of the ISM. Magnetic fields, relativistic electrons, and thermal electrons can be constrained through the action of Faraday rotation, which changes the morphology of the observed emission.
Studies of Galactic polarized emission are mostly done at high radio frequencies (>1 GHz; for an overview see Reich 2006, and references therein). At lower radio frequencies, these studies were performed mainly at 325 MHz with the Westerbork Synthesis Radio Telescope (WSRT). These studies revealed a large number of unusually-shaped polarized, small-scale structures, which have no counterpart in the total intensity (e.g. Wieringa et al. 1993; Haverkorn et al. 2003a,b; Schnitzeler et al. 2009). They are attributed to a combination of Faraday rotation and depolarization effects due to variable Faraday depth in the ISM. In many areas, linear structures dominate the morphology and have so far defied explanation. This is especially the case at higher Galactic latitudes where line-of-sight superposition effects would not inherently randomize anisotropic structures.
Faraday rotation is proportional to the square of the wavelength. Therefore, low radio frequency observations are very sensitive to small column densities of magnetized plasma in the ISM that are difficult to detect at higher radio frequencies. The wide frequency coverage and good angular resolution of the Low-Frequency Array (LOFAR; van Haarlem et al. 2013), make LOFAR an excellent instrument for studying Galactic polarized emission (Iacobelli et al. 2013; Jelić et al. 2014). In combination with the rotation measure (RM) synthesis technique (Brentjens & de Bruyn 2005), LOFAR observations allow us to study the relative distribution of synchrotron-emitting and Faraday-rotating regions at an exquisite resolution of ~1 rad m-2 in Faraday depth. In addition, the high angular resolution available in LOFAR allows us to study the medium at a resolution hardly affected by beam depolarization.
Recent observations with LOFAR revealed diffuse polarization in several fields at high Galactic latitudes with surprisingly high brightness temperature. For example, polarized emission in the ELAIS-N1 field is ~4 K at 150 MHz (Jelić et al. 2014). This is much greater than was anticipated on the basis of earlier WSRT (e.g. Bernardi et al. 2009, 2010; Pizzo et al. 2011) and Giant Metrewave Radio Telescope (GMRT; e.g. Pen et al. 2009) observations in the same frequency band. Early results from the Murchison Widefield Array (MWA) also indicated much higher levels of observed polarization (Bernardi et al. 2013). In this paper, we present LOFAR observations of diffuse polarized emission detected in the 3C 196 field, one of the primary fields of the LOFAR-Epoch of Reionization key science project.
The 3C 196 field is centred on the very bright quasar 3C 196, in a cold region towards the Galactic anticentre (l = 171°, b = + 33°). It has been observed previously with the Low Frequency Front Ends (LFFE; 138−156 MHz) on the WSRT radio telescope (Bernardi et al. 2010). These data revealed only faint patchy polarized emission, restricted to Faraday depths smaller than 4 rad m-2. The surface brightness of this emission was close to the thermal noise on angular scales smaller than 10′. On scales greater than 30′, emission has an rms value of 0.7 K. The resolution in Faraday depth space of the WSRT data was three times poorer than that of the LOFAR observations presented in this paper, which have three times wider frequency coverage.
The paper is organized as follows. In Sect. 2 we give an overview of the observational set-up and the data reduction. The widefield images of the 3C 196 field in total intensity and polarization are presented in Sect. 3. In Sect. 4 we discuss the fidelity of the data. In Sect. 5 we discuss properties of the detected diffuse polarized structures and give a possible theoretical interpretation, while analysis of the observed discrete polarized sources will be presented in a separate paper. We summarize and conclude in Sect. 6.
2. Observations and data reduction
The 3C 196 field was observed multiple times during winter 2012/13 and 2013/14 with the LOFAR high band antennas (HBA). During this period we accumulated ~450 h of data. For this paper we have fully processed five syntheses with durations of 8 h (2012) and 6 h (2013), as a representative sample of the observations. An overview of these five observations is given in Table 1.
An overview of observational parameters of the five LOFAR-HBA observations used in this study.
The array was used in the so-called HBA DUAL INNER configuration (van Haarlem et al. 2013), consisting of 48 core stations (CS) and 14 remote stations (RS), which were tapered to have the same size and shape as the CS. Data were taken in the frequency range from 115 MHz to 189 MHz, divided into 380 sub-bands of width 195.3125 kHz. Each sub-band was further divided in 64 channels. The correlator integration time was 2 s. All four correlation products between pairs of orthogonal dipoles were recorded. The total time per observation was 8 h in 2012 and 6 h in 2013. All observations were symmetric around transit and were taken during the nighttime. The uv coverage was fully sampled up to baselines of about 800 wavelengths. To compare observations taken in different observing cycles, we used 6 h symmetric around transit of each 8 h observation.
The processing of the data was done on a CPU/GPU1 cluster dedicated to the LOFAR-EoR project, located at the University of Groningen, the Netherlands. During the processing we used the LOFAR-EoR Diagnostic Database (LEDDB), which is used for the storage and management of the LOFAR-EoR observations (Martinez-Rubi et al. 2013).
2.1. Initial processing and calibration
The first step in our initial processing is the automatic flagging of radio frequency interference (RFI) using AOFlagger (Offringa et al. 2010, 2012). In the frequency range from 115–177 MHz on average only ~3% of our data is flagged. This percentage, however, is much higher (>40%) for frequencies above 177 MHz where signals from Digital Audio Broadcasting (DAB) corrupt the data in a few 1.75 MHz wide bands. For an overview of the LOFAR RFI-environment we refer to Offringa et al. (2013).
After flagging, the data are averaged to reduce the data volume for further processing. The bandwidth and time smearing resulting from this averaging only affects the longer baselines, which are not used in this study. To remove edge effects from the polyphase filter the 4 edge channels from the initial 64 channels are excluded in the averaging process. The resulting data set has a spectral resolution of 183 kHz (henceforth called a sub-band) and a time resolution of 10 s.
The calibration proceeds in two steps. First, we perform a direction-independent calibration with the Black Board Selfcal (BBS) package (Pandey et al. 2009). Each sub-band is calibrated separately. The source 3C 196, which is located in the pointing and phase centre, dominates the visibilities on all baselines, making this step of the calibration straightforward. We use a four-component model for 3C 196, which accurately represents the high-resolution structure of the source (Pandey et al., in prep.). The total flux of 3C 196 (84 ± 2 Jy at 150 MHz) is set by the broadband spectral model given by Scaife & Heald (2012). The BBS step removes the clock and ionospheric phase errors, and sets the frequency-dependent intensity as well as the astrometric reference frame for the field. The BBS solves for all four complex elements of the station Jones matrices taking the changing location of 3C 196 within the dipole element beam into account. Because the station phased array centre tracks 3C 196, the varying station gain is automatically accounted for in this process. When applying the gains we also correct for the varying parallactic angle. This leads to a very stable and small polarimetric response over the inner part of station beam.
 |
Fig. 1 Frequency-averaged Stokes I image of the 3C 196 region, based on the four nights of data taken in December 2012. The image is 8.3° × 8.3° in size, with a PSF of 45′′, and the noise level is 170 μJy PSF-1. The nine bright sources towards which we performed direction-dependent calibration are indicated with red circles. The 3C 196 source is subtracted from direction-independent calibrated visibilities, while eight other sources are not. A location of the discovered pulsar J081558+461155 (see Sect. 3.3) is shown with a blue asterisk. The image is de-convolved using the CLEAN algorithm implemented in CASA. |
The second step is more involved. There are at least eight additional sources with integrated apparent flux densities in excess of 2 Jy (at 150 MHz) within 2.5° of 3C 196. To remove their time-variable polarized response, together with one of the 3C 196, requires direction-dependent calibration. This is done using SAGECal (Yatawatta et al. 2008; Kazemi et al. 2011, 2013a,b; Kazemi & Yatawatta 2013) in nine directions. This corrects for time- and frequency-dependent errors due to the station beam and the slight position-dependent ionospheric delays. Each direction is associated with one source. The solution interval is 20 min for the eight bright sources and 2 min for 3C 196. This interval is sufficient to remove these sources down to the confusion noise on the short core baselines. During SAGECal we are only using baselines >800 wavelengths to minimize suppression of the ubiquitous extended diffuse (polarized) emission, which is not included in the sky model and mostly appears at baselines <800 wavelengths. All nine sources are unpolarized down to a fraction of a percent. These nine sources (3C 196, and eight bright, discrete sources; see Fig. 1) were subsequently subtracted from the residual visibilities with the directional gains derived for their directions.
2.2. Faraday rotation in the Earth’s ionosphere
Ionospheric Faraday rotation is a time- and direction-dependent propagation effect, whose size is proportional to the total electron content (TEC) of plasma in the ionosphere. If variability in Faraday rotation happens on a timescale that is smaller than the total integration time of an observation, the observed polarized emission is partially decorrelated. To correct for this effect we predict the RM variations in the ionosphere using the Global Ionospheric Maps of the Centre for Orbit Determination in Europe (CODE2) and the World Magnetic Model (WMM3). A full description of this procedure is given in Jelić et al. (2014, Sect. 3.2).
Figure 2 shows the estimated RM variations in the ionosphere that we apply to the data. The curves are given for different nights as a function of observing time. The RM variations are the largest during the L79324 observation. This observation also shows the largest absolute RM values. We emphasize that at 150 MHz, a RM variation of 0.2 rad m-2 rotates the plane of polarization by 45°.
 |
Fig. 2 The estimated RM variations in the ionosphere using the Global Ionospheric Maps of CODE. The RM are given as a function of observing time and for each night. |
2.3. Imaging and RM synthesis
If not stated otherwise, images we present are produced using the excon imager (Yatawatta 2014)4. To analyse the polarization of diffuse emission, which mostly appears on spatial scales greater than a few arcmin, we make lower resolution images in all Stokes parameters (IQUV). These images are produced using baselines between 10 and 800 wavelengths, providing a frequency independent resolution of about 3 arcmin. We use robust (Briggs) weighting with robustness parameter equal to 0.
 |
Fig. 3 Two images of the 3C 196 region in polarized intensity at Faraday depth 0 rad m-2 after performing direction-independent calibration (image on the left) and direction-dependent calibration and source subtraction (image on the right). Images are 8.3° × 8.3° in size, with a PSF of 3.6′ × 3.9′. The 3C 196 source is also subtracted from direction-independent calibrated visibilities. Eight bright sources, used for direction-dependent calibration and source subtraction, are indicated with red circles. The images have not been corrected for polarization noise bias nor for Faraday rotation in the Earth’s ionosphere. |
To study the linearly polarized emission as a function of Faraday depth (Φ), we apply RM synthesis (Brentjens & de Bruyn 2005) to the Stokes Q, U images of 310 sub-bands, which have comparable noise levels. These sub-bands cover the frequencies between 115 MHz and 175 MHz. We first synthesize a cube over a wide range in Faraday depth to determine where polarized emission could be detected. The final cube covers a Faraday depth range from −25 rad m-2 to + 25 rad m-2 in 0.25 rad m-2 steps. The resolution in Faraday depth space, defined by a width of a RMSF (rotation measure spread function), is δΦ = 0.9 rad m-2, while the largest Faraday structure that can be resolved is ΔΦ = 1.1 rad m-2. Since the resolution is comparable to the maximum detectable scale, we can only detect Faraday thin structures (λ2ΔΦ ≪ 1Brentjens & de Bruyn 2005).
 |
Fig. 4 Widefield images of the 3C 196 field in polarized intensity (PI), Stokes Q, and Stokes U at Faraday depths of −1.5, −0.0, +1.0, +1.5, +2.0, +2.5, +3.0, and +3.5 rad m-2. Images are 8.3° × 8.3° in size with a PSF of 3.6′ × 3.9′. The noise level is 71 μJy PSF-1 RMSF-1 in polarized intensity and 108 μJy PSF-1 RMSF-1 in Stokes Q, U. The images in polarized intensity have not been corrected for polarization noise bias nor for the primary beam. |
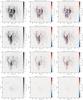 |
Fig. 4 continued. |
To determine the brightness temperature of emission and its angular power spectrum, we correct the RM cube for the relative variation of the element beam pattern across the field of view and for the primary beam. These corrections are applied using the AWimager (Tasse et al. 2013). We have not attempted to deconvolve the RM cube for the effects of the side lobes of the RMSF. The sidelobes are small and the signal-to-noise ratio is generally so low that this would have had very little effect on the images.
3. Observational results
3.1. Direction-dependent calibration: instrumentally polarized sources
The beam pattern of a LOFAR-HBA station can be described as the product of an element beam pattern and the array beam pattern of the station (van Haarlem et al. 2013). The element beam pattern is strongly polarized. Its polarization response is related to the projection of two beam patterns of two orthogonal dipoles on the sky and the changing parallactic angle. As a result of this, spurious polarization is produced. We correct the data for the beam pattern during calibration to first order, using BBS. The data are corrected for both the array and the element beam gain at the centre of the image. However, the relative variation of the element beam pattern across the field of view, as well as the temporal changes, are still be present in the data (for more details, see Asad et al. 2015). The direction-dependent calibration and source subtraction can correct for these effects to some extent.
The results of direction-dependent calibration and source subtraction are illustrated in Fig. 3. We show images in polarized intensity before and after performing direction-dependent calibration and source subtraction. Images are shown at a Faraday depth of 0 rad m-2. The instrumental polarization leakage, after calibrating on 3C 196, is to first order independent of frequency, and therefore all instrumentally polarized signals are located around a Faraday depth of 0 rad m-2.
All sources included in the sky model are removed successfully. Their side lobes are significantly suppressed and they are not visible in the images. The morphology of diffuse emission is preserved. A flux scale of diffuse emission agrees on average over all directions within 5−10% with the data calibrated using only BBS (direction-independent calibration).
3.2. Diffuse polarized emission
A series of widefield images of the 3C 196 field in both polarized intensity and Stokes Q, U are presented in Fig. 4. The images are 8.3° × 8.3° in size with a PSF (point spread function) of 3.6′ × 3.9′. The noise level is 71 μJy PSF-1 RMSF-1 in polarized intensity and 108 μJy PSF-1 RMSF-1 in Stokes Q, U. The images are given at Faraday depths of −1.5, 0, +1, +1.5, +2, +2.5, +3.0, and + 3.5 rad m-2 to emphasize the various detected structures in linear polarization.
 |
Fig. 5 Faraday spectra of a few representative lines-of-sight through the RM cube of polarized intensity. We have not attempted to deconvolve the spectra for the effects of the side lobes of the RMSF. |
Diffuse emission (≲3 mJy PSF-1 RMSF-1) is detected over a range of Faraday depths from −3 to + 8 rad m-2. A triangular feature in the south-west side of the primary beam (marked with C in Fig. 4) dominates at negative Faraday depths. At positive Faraday depths, emission first appears as two extended north-south structures (denoted with A and B in Fig. 4). A striking filamentary structure A, running right across 3C 196, is at least 4° long and 7.5′ wide. Its mean surface brightness is 3.2 mJy PSF-1 RMSF-1 and it peaks at Faraday depth ~0.5 rad m-2. The two-legged puppet structure B has the mean surface brightness of 2.5 mJy PSF-1 RMSF-1, peaking at Faraday depth ~0.25 rad m-2. Towards the higher Faraday depths, emission fills up the east side of the primary beam. The mean surface brightness of this emission is 1.6 mJy PSF-1 RMSF-1.
A few representative Faraday spectra of detected features are shown in Fig. 5. The largest Faraday structure that can be resolved is 1.1 rad m-2 wide. Information contained in the Faraday spectra is summarized in Fig. 6. We follow Schnitzeler et al. (2009) and show a map of the highest peak of the Faraday depth spectrum at each spatial pixel and a map of the RM value of each peak. The highest peaks in the Faraday spectra have on average a surface brightness of ~2.5 mJy PSF-1 RMSF-1, located mostly at positive Faraday depths.
While the polarized intensity shows only the amplitude of polarized emission, images in Stokes Q, U also reflect the morphology of polarization angle. There are a number of striking patterns and features in Stokes Q, U (see Fig. 4). Most of them are outlined by regions that show emission in Stokes Q, U of opposite sign. They have a typical width of 5′−10′.
3.3. Polarized sources
In addition to the widespread diffuse emission, we identified ~15 discrete polarized sources in the 3C 196 field. All but one of these sources are (giant) radio galaxies with typical polarization fractions of a few percent, and a detailed analysis of their properties will be presented in de Bruyn et al. (in prep.). One source, J081558+461155 (see Figs. 1 and 6), has a steep spectrum, is spatially unresolved and shows about 50% polarization. These properties are reminiscent of those of pulsars.
A follow-up observation of this field, in Director’s Discretionary Time, with the LOFAR Full HBA Core in tied-array mode (van Haarlem et al. 2013) indeed revealed a pulsar with a period of 434 ms and a dispersion measure (DM) of 11.28 pc cm-3 (priv. comm., J. W. T. Hessels and V. Kondratiev; see the LOFAR Tied-Array All-Sky Survey Discoveries5).
The RM of the pulsar is + 2.7 ± 0.1 rad m-2, as determined from our RM cubes. In the direction of the pulsar the NE2001 model of the Galactic distribution of thermal electrons (Cordes & Lazio 2002, 2003) predicts a thermal electron density of ⟨ne⟩ = 0.028 cm-3. Given its DM, we estimate its distance to be ~400 pc. Given the sparsity of sources in this direction, however, both the density and the distance derived from the model must be considered uncertain.
4. Fidelity of the data
In this section, we make qualitative and quantitative comparisons between five LOFAR observations. The analysis is performed on RM cubes in polarized intensity, Stokes Q and U. Table 2 gives an overview of the noise in the RM cubes for different nights. Variation of the noise from night to night is small. The L79324 observation shows the largest variations in RM and has the highest noise. L80273 has the lowest noise. The ratio of the rms values between the polarized intensity and Stokes Q, U is ~0.65. This implies consistent normally distributed noise in Stokes Q, U.
We then compare maps of the highest peak of the Faraday depth spectrum at each spatial pixel for different nights. An example of this kind of map is given in Fig. 6. For each pair of maps, we calculate the Pearson correlation coefficient using only the inner 5° × 5° of the images. We find that the peak fluxes agree well, with a correlation of 96 ± 1% from night to night. The L80273 and L80508 observations show the highest correlation, of 98%. This shows that LOFAR performance from night to night is very stable and that we are able to correct for Faraday rotation in the ionosphere to first order. The small difference in the peak fluxes between the observations is mainly caused by the low time resolution of the CODE data (2 h).
To check the alignment of the RM cubes in Faraday depth, we calculate the cross-correlation between two observations as a function of the lag in Faraday depth. In this comparison we take only spectra that have a peak flux in polarized intensity >1.5 mJy PSF-1 RMSF-1 (at least two times above the noise). We then average the cross-correlation functions to determine their common peak by fitting a parabola. The position of this peak gives the misalignment of the two RM cubes. On average we find that the five RM cubes are misaligned by 0.10 ± 0.08 rad m-2. The best alignment is between L79324 and L80508 (0.02 ± 0.01 rad m-2) and the worst is between L80508 and L192832 (0.14 ± 0.01 rad m-2). A misalignment between different observations can be attributed to systematic errors in the CODE data, resulting in a bias in TEC maps from day to day. This bias leads to uncertenties of ~1 TEC unit, corresponding to an error in RM around 0.1 rad m-2.
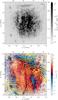 |
Fig. 6 Upper image: highest peak of the Faraday depth spectrum in polarization at each spatial pixel. Bottom image: map of the RM value of each peak, shown in red-blue colour scale. Yellow contours are showing Hα intensity on a one degree scale (Finkbeiner 2003; Haffner et al. 2003), given in units of Rayleighs (see Sect. 5). A white box indicates the boundaries of the WSRT 350 MHz image in Fig. 10. A location of the discovered pulsar J081558+461155 (see Sect. 3.3) is shown with a yellow asterisk. |
The noise in the RM cubes of different observations.
To get a better signal-to-noise ratio in the RM cubes, one can average the cubes from different nights. However, the RM cubes should be aligned in Faraday depth to high accuracy. Even a small misalignment decorrelates the signal to some extent. The detected diffuse emission is ~25× above the noise, so an additional improvement of 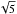 does not make an impact on our results and our current conclusions.
does not make an impact on our results and our current conclusions.
Finally, we compare our LOFAR observations with observations of the same field by Bernardi et al. (2010) in the same frequency range, obtained using the LFFE on the WSRT radio telescope. Emission detected with the WSRT-LFFE is fainter and its morphology appears much simpler (see Figs. 9–11 in Bernardi et al. 2010) than the morphology of emission detected with LOFAR. There is just faint patchy emission, without any more distinctive morphological features.
The difference between the WSRT-LFFE and LOFAR observations can be attributed to the three times better resolution of LOFAR in Faraday depth. Multiple Faraday-thin structures (ΔΦ <δφWSRT−LFFE) detected in the LOFAR observations decorrelate when we observe them with a broader RMSF if their emission shows different polarization angle. Moreover, WSRT-LFFE observations were showing some instrumental artefacts that contaminated RM cubes (Bernardi et al. 2010). Given these restrictions a more quantitative comparison between the LOFAR and WSRT-LFFE observations is not very meaningful and we restrict our analysis to the superior quality LOFAR data.
5. Discussion
5.1. General properties of detected diffuse polarized emission and the underlying magnetic field component
 |
Fig. 7 Angular power spectrum of integrated polarized emission. The best power-law fit (solid line) to the power spectrum (“Cl−l”) between l = 150 and l = 2700 gives a slope of |
The diffuse emission presented in Sect. 3.2 is of Galactic origin. To analyse its properties, we follow our previous work (Jelić et al. 2014) and compute the total polarized intensity at each pixel by integrating the polarized intensity RM cube along Faraday depth. The brightness temperature of the resulting integrated emission varies from 5 to 15 K. This is comparable to the brightness temperature of emission detected in the ELAIS-N1 field (Jelić et al. 2014), also a field at high Galactic latitude. Using only the inner 3° × 3° of the field, we estimate the angular power spectrum of the integrated polarized emission, Cl. In the calculation we assume the “flat-sky” approximation (e.g. White et al. 1999), i.e. 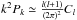 for l = 2πk, where Pk is the 2D Fourier transform of an image and l = 180°/θ [°] is a spherical harmonic multipole. Figure 7 shows the resulting averaged dimensionless angular power spectrum. We then fit a power law to “Cl−l” between l = 150 and l = 2700. The best fit (solid line in Fig. 7) gives a slope of βl = −1.64 ± 0.05.
for l = 2πk, where Pk is the 2D Fourier transform of an image and l = 180°/θ [°] is a spherical harmonic multipole. Figure 7 shows the resulting averaged dimensionless angular power spectrum. We then fit a power law to “Cl−l” between l = 150 and l = 2700. The best fit (solid line in Fig. 7) gives a slope of βl = −1.64 ± 0.05.
In total intensity a slope of the synchrotron emission is usually steeper (−3.0 ≲ βl ≲ −2.5 e.g. Baccigalupi et al. 2001; Tucci et al. 2002; Bernardi et al. 2009; Ghosh et al. 2012). A difference between the two slopes can be explained by redistribution of power between different angular scales of polarized emission, mostly from large scales to small scales, as a result of small-scale structure of intervening Faraday-rotating medium. At LOFAR frequencies even a very small RM of the medium leaves a signature in the power spectrum.
On the same angular scales, 100 <l< 3000, and in the same frequency range as our observations, but in an area located in the Galactic plane (Fan region), Bernardi et al. (2009) found a slope for polarized emission of βl = −1.65 ± 0.15, which is very similar to the 3C 196 field. The morphology of emission in the two fields is different, yet integrated emission along Faraday depth of both fields shows a very similar power spectrum slope. This indicates that in both fields redistribution of power through Faraday rotation is similar.
In the current data we have not detected diffuse emission in total intensity. This can be attributed to a lack of short baselines in our observations. We are only sensitive to structures on scales smaller than two degrees, meaning that synchrotron emission in total intensity appears mostly on scales larger than two degrees. This is in line with the discussed steeper slope of the observed synchrotron emission in total intensity, and with previous observations with LOFAR (Jelić et al. 2014) and WSRT (e.g. Bernardi et al. 2010) at high Galactic latitudes. Unfortunately, a lack of detected emission in total intensity prevents us from making a more detailed study of Galactic interstellar turbulence through fluctuations in synchrotron emission, as was done by Iacobelli et al. (2013) for a low Galactic latitude field.
In near future the AARTFAAC6 (Amsterdam – ASTRON Radio Transients Facility and Analysis Centre) project might help to mitigate a lack of a very short baselines in our current LOFAR observations. Six stations at the heart of LOFAR will be used as a 288-element array. This will then provide almost full uv coverage at short baselines and will enable us to map large-scale Galactic emission that is currently not accessible.
To estimate the fraction of polarization, we divide the integrated polarized intensity by the 408 MHz total intensity map (Haslam et al. 1981, 1982) scaled to 160 MHz. The spectral index between 45 and 408 MHz of Galactic synchrotron emission in this region is β = −2.5 (Guzmán et al. 2011). If we scale the brightness temperature of ~23 K from 408 MHz to 160 MHz, we deduce a brightness temperature of 236 K in total emission. The observed polarization levels therefore imply a polarization of ≈4%.
A high degree of polarization indicates a regular large-scale magnetic field topology, coming from either uniform or anisotropically random magnetic fields. The uniform magnetic field component, following the spiral arms of our Galaxy, is almost perpendicular to the line of sight at the direction of 3C 196 (for a description of Galactic magnetic field models, see Sun et al. 2008, and references therein). Its contribution to Faraday rotation towards the 3C 196 field is therefore expected to be small.
This assumption is supported by the estimated mean line-of-sight magnetic field component in the direction of pulsar J081558+461155 (see Sect. 3.3). Given the known relation between the RM and DM of a pulsar (e.g. Manchester 1972), i.e. ![\begin{equation} \frac{\left<B_{||}\right>}{[{\rm \mu G}]}=\frac{\rm RM~[{\rm rad~m^{-2}}]}{\rm 0.812~DM~[{\rm pc~cm^{-3}}]}, \end{equation}](/articles/aa/full_html/2015/11/aa26638-15/aa26638-15-eq113.png) (1)we get ⟨B||⟩ = 0.3 ± 0.1 μG. A typical strength of magnetic field in the Galactic halo (thick disk) is ~3 μG, with an expected random component of ~1 μG (Mao et al. 2010; Haverkorn 2015, and references therein).
(1)we get ⟨B||⟩ = 0.3 ± 0.1 μG. A typical strength of magnetic field in the Galactic halo (thick disk) is ~3 μG, with an expected random component of ~1 μG (Mao et al. 2010; Haverkorn 2015, and references therein).
Variations of the mean line-of-sight magnetic field component across the 3C 196 field, σ⟨B||⟩, can be estimated from variations in the RM values of detected diffuse structures and in thermal electrons. We obtain the RM variations directly from the image in Fig. 6, σRM ≃ 4 rad m-2. A good tracer of warm ionized gas is the Hα line. From the composite all-sky Hα map (Finkbeiner 2003, v1.1)7, we find the Hα intensity across the 3C 196 field to be 0.6 ± 0.1 R (Rayleighs; 1 R = 106 (4π)-1 photons cm-2 s-1 sr-1). However, the given Hα intensity reflects the integrated emission over different velocities (|v| < 100 km s-1) and over the line-of-sight through the whole Galaxy, while the polarized structures detected with LOFAR are probably limited to distances ≲1−1.5 kpc from us (see Sect. 5.2). Electron densities that we derive from Hα intensity should therefore be taken more as an upper limit. We do not know whether we see polarized emission all the way to the edge of the Galaxy.
We convert the observed Hα intensity into emission measure (EM), according to (Reynolds 1991), ![\begin{equation} \label{eq:em} \frac{{\rm EM}}{[\rm pc~cm^{-6}]}= \int_0^L n_{{\rm e}}^2 {\rm d}l = 2.75 \left(\frac{T}{[10^4~{\rm K}]}\right)^{0.9}\frac{I_{{\rm H}\alpha}}{\rm [R]}, \end{equation}](/articles/aa/full_html/2015/11/aa26638-15/aa26638-15-eq123.png) (2)where T is the temperature of the ionized gas, ne is the local electron density, and L is the total path length. Assuming T = 104 K at high Galactic latitudes (e.g. Sun et al. 2008; Akahori et al. 2013, and references therein), we derive the related emission measure of EM = 1.7 ± 0.3 pc cm-6 across the 3C 196 field. This corresponds to a large-scale mean electron density of ⟨ne⟩ ≃ 0.03 cm-3 over an assumed path length of 1.5 kpc. Its spatial variation across the 3C 196 field is σ⟨ne⟩ ≃ 0.003 cm-3. In our calculation, we do not take observed vertical temperature gradient in the diffuse ionized gas into account (Reynolds et al. 1999; Haffner et al. 2009), as the gradient is small and our results are not sensitive to it.
(2)where T is the temperature of the ionized gas, ne is the local electron density, and L is the total path length. Assuming T = 104 K at high Galactic latitudes (e.g. Sun et al. 2008; Akahori et al. 2013, and references therein), we derive the related emission measure of EM = 1.7 ± 0.3 pc cm-6 across the 3C 196 field. This corresponds to a large-scale mean electron density of ⟨ne⟩ ≃ 0.03 cm-3 over an assumed path length of 1.5 kpc. Its spatial variation across the 3C 196 field is σ⟨ne⟩ ≃ 0.003 cm-3. In our calculation, we do not take observed vertical temperature gradient in the diffuse ionized gas into account (Reynolds et al. 1999; Haffner et al. 2009), as the gradient is small and our results are not sensitive to it.
We can now use the equation for rotation measure, ![\begin{equation} \label{eq:fardep} \frac{\left<{\rm RM}\right>}{\rm [rad~m^{-2}]}=0.81\int^L_0 \frac{\left<n_{\rm e}\right>}{\rm [cm^{-3}]} \frac{\left<B_\parallel\right>}{\rm [\mu G]}{\rm d} l , \end{equation}](/articles/aa/full_html/2015/11/aa26638-15/aa26638-15-eq132.png) (3)and estimate σ⟨B∥⟩ according to
(3)and estimate σ⟨B∥⟩ according to  (4)In our case, the first term in Eq. (4) dominates over the second term. Using L = 1.5 kpc and ⟨RM⟩ = 1 rad m-2, we get variations of the mean line-of-sight magnetic field component across the 3C 196 field to be σ⟨B∥⟩ ≃ 0.1 μG. This is in agreement with an upper limit, σ⟨B∥⟩ ≲ 0.4 μG, derived by Schnitzeler (2010) using the rotation measure of NVSS sources.
(4)In our case, the first term in Eq. (4) dominates over the second term. Using L = 1.5 kpc and ⟨RM⟩ = 1 rad m-2, we get variations of the mean line-of-sight magnetic field component across the 3C 196 field to be σ⟨B∥⟩ ≃ 0.1 μG. This is in agreement with an upper limit, σ⟨B∥⟩ ≲ 0.4 μG, derived by Schnitzeler (2010) using the rotation measure of NVSS sources.
If B∥, ne, or both show a large-scale gradient across the sky, this should be seen in observed RM cubes. Polarized structures appear to move in the direction of the gradient as we go through different Faraday depths. We see this behaviour in our RM cubes from + 1 to + 2.75 rad m-2. Polarized emission moves mostly from the west to the east (see Fig. 4 and 6). To quantify this, we calculate the centroid of emission at each Faraday depth as 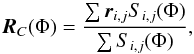 (5)where sums are taken over all pixels of an image Si,j at Faraday depth Φ, where Si,j> 1.5 mJy PSF-1 RMSF-1 (at least two times above the noise). The vector ri,j contains the coordinates of the pixels.
(5)where sums are taken over all pixels of an image Si,j at Faraday depth Φ, where Si,j> 1.5 mJy PSF-1 RMSF-1 (at least two times above the noise). The vector ri,j contains the coordinates of the pixels.
We find that the centroid of emission changes systematically by ~0.8° per rad m-2 from west to east and by 0.3° per rad m-2 from north to south. From Faraday depth + 1 to + 2.75 rad m-2 the polarized structures have moved by 1.4° towards the east and by 0.6° towards the south. This is indeed an indication of a large-scale gradient in RM.
Based on our previous discussion that the σ⟨RM⟩ term in Eq. (4) dominates over the σ⟨ne⟩ term, the large-scale gradient that we observe seems to be a gradient of B∥ across the 3C 196 field. However, the distribution of the thermal plasma is known to be extremely inhomogeneous with a very small filling factor for the Warm Ionized Medium (WIM, e.g. Berkhuijsen et al. 2006; Gaensler et al. 2008), which is mostly responsible for the Faraday rotation (e.g. Heiles & Haverkorn 2012). The estimated ne from the Finkbeiner (2003) Hα map is just an average of the true distribution along a line-of-sight. Therefore, it is possible that inhomogeneity of ne also contributes to the observed gradient in Faraday depth.
Finally, B∥ across the 3C 196 field varies both in strength and in orientation. This is seen through the presence of observed structures both at positive and negative Faraday depths (see Fig. 6). Positive RM values are associated with B∥ orientated towards us and negative RM values with B∥ orientated away form us. This does not necessarily mean that B∥ has the same orientation along the line of sight. The field can reverse, sometimes even multiple times.
Direct evidence for field reversal(s) can be seen in the Faraday spectrum, where structures are found at both positive and negative depths. In our RM cubes there are ~5% of Faraday spectra that we directly associate with field reversal(s) (for an example see Fig. 5). However, spectra with structures, which are only on one side of the Faraday spectrum, do not exclude field reversals. If two regions with opposite magnetic field orientations change the polarization angle of incoming emission, but they do not themselves emit, and there is no additional emission between the two, the polarization angle of incoming emission is first rotated in one direction and then derotated in the other. The observed polarization angle is then a net effect of Faraday rotations along these two regions (for an illustration, see Fig. 2 in Brentjens & de Bruyn 2005). In the Faraday spectrum, this only manifests as one structure, despite the fact that in reality we have two physically separated regions.
 |
Fig. 8 A cartoon of the possible layout of polarized emission and magnetic fields towards the 3C 196 field. Solid arrows indicate orientation and strength of B∥. For display purposes, the filamentary structures are shown along the viewing direction in this sideways projection. |
5.2. Physical picture and relative distribution of intervening magneto-ionic medium
The synchrotron emission of our Galaxy is known to have many components: the disk, a thick disk, and possibly a halo (e.g. Subrahmanyan & Cowsik 2013, and references therein). At high Galactic latitudes the bulk of the emission comes from the thick disk with a width of about 1−1.5 kpc. The polarized emission builds up over the same path length, but along the way it gets depolarized by the magneto-ionic ISM. Depolarization is stronger at lower frequencies. A typical observed polarization at LOFAR frequencies is about 1−4% (Iacobelli et al. 2013; Jelić et al. 2014), while intrinsically synchrotron radiation is polarized at the 70% level. Hence only a small fraction of the synchrotron emission of our Galaxy is observed in polarization.
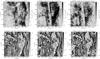 |
Fig. 9 Examples of higher resolution images of the 3C 196 field in polarized intensity (PI) and polarization angle (PHI) given at Faraday depths of +1.0, +1.5, and +2.0 rad m-2. Images show the central 2.5° × 2.5° of the field. During the imaging we used baselines between 10 and 4000 wavelengths, providing a frequency-independent resolution of about 1 arcmin. |
A possible geometric configuration and distribution of the random and uniform component of the magnetic field and magneto-ionic medium are very difficult to get directly from observations. Analysis of observations in Faraday depth helps to constrain the relative distribution of structures. However, the distribution in Faraday depth does not necessarily reflect the true physical distribution (see discussion in Brentjens & de Bruyn 2005). Magnetic field reversals and inhomogeneous distribution of regions (i) that only emit; (ii) with only Faraday rotation; and (iii) with a combination of both, give a rise to a discrepancy between the two distributions. Full radiative transfer simulations are needed to disentangle this problem.
To visualize the complexity of the problem, we have constructed a simple physical model (see Fig. 8), which we believe contains the essential ingredients to explore the conditions in the ISM that are required to explain observed structures in the 3C 196 field. Observed features are organized in four distinctive groups: (i) filaments A and B: relatively straight filamentary structures running from north to south at Faraday depths around + 0.5 rad m-2 and parallel to the Galactic plane; (ii) diffuse emission BG1: prominent diffuse background emission at Faraday depths from +1.0 to + 4.5 rad m-2, showing a large-scale gradient; (iii) diffuse emission BG2: very faint patchy emission at Faraday depths from +4.5 to + 7.5 rad m-2 and at negative Faraday depths from −3 to −0.5 rad m-2 (iv) a horizontal structure located in the upper north of the field; and (v) a “triangular” feature C in the south-west.
We now describe and discuss our crude model. At first, we assume that dominant orientation of B∥ is towards us. This is consistent with the observed, mostly positive, values of Faraday depth. Based on Eq. (3), assuming a path length of 1.5 kpc, taking estimated values from Sect. 5.1 of ⟨ne⟩ ≃ 0.03 cm-3 and ⟨B∥⟩ ≃ 0.3 μG, and including a vertical gradient in electron density8, we expect to see polarized emission at Faraday depths up to Φ ≲ + 10 rad m-2. This is in an agreement with our observations, where we have detected faint patchy structures up to + 8 rad m-2. Simulated RM profiles towards the 3C 196 field (l = + 171, b = + 33°; see Fig. 12 in Sun et al. 2008), based on the regular double-torus halo field and disk field models described in Sun et al. (2008), also agree with our observations. These profiles predict RM values up to ≲+ 10 rad m-2.
At the negative side of the Faraday spectrum, structures are only observed up to −3 rad m-2. Under the same assumptions, but with the magnetic field pointing away from us, the thickness of the negative Faraday rotating region appears to be much smaller than the positive: Eq. (3) gives L ≃ 250 pc.
A relative distribution of the observed features is as follows. Filaments seem to be displaced from the background diffuse emission BG1 by only ~1.5 rad m-2. Their brightness is comparable to the background emission that shows a very uniform large-scale structure of polarization angle on both sides of the filaments (see high-resolution images in Fig. 9). We therefore conclude that filaments are non-emitting magnetized plasma located in front of the prominent background BG1.
The Faraday depth of the filaments is smaller than that of the background emission. This implies B∥ with an orientation in the opposite direction to the background. Parts of the background emission are derotated within the filaments, giving a deficit in Faraday depth compared to the other parts of the background emission.
Prominent background emission BG1 is closer to us than the fainter background emission BG2, and is probably a very nearby component. BG1 emission might be associate with the synchrotron emission coming somewhere from the edge of the Local Bubble, which is estimated to have a radius of approximately 200 pc (see e.g. Sun et al. 2008). To be consistent with our observations, in front of this emission there must be a non-emitting magnetized plasma, with B∥ orientated towards us.
The same orientation of B∥ we also expect for a region associated with the fainter emission BG2. This emission is the most distant component and probably reflects the global emission of the thick disk. Along the way, two types of depolarization occur (for an overview, Haverkorn et al. 2004, and references therein), resulting in the observed very faint and patchy emission. The first is wavelength-independent depolarization, due to turbulent magnetic fields in the ISM, and the second is due to differential Faraday rotation occurring in regions where emitting and Faraday rotating areas are mixed.
The horizontal structure in the north, at negative Faraday depths, does not have any positive Faraday depth components along the line of sight and, therefore, it is a region with a dominant B∥ component orientated away from us. This horizontal structure also seems to be spatially a part of the large-scale gradient observed in BG1. If this is true, in front of the synchrotron emitting region BG1, there is one layer of a non-emitting magnetized plasma with B∥ orientated towards us and one layer with B∥ orientated away from us. The second region should have a large-scale gradient in B∥. Since the strength of B∥ along the gradient is different, some part of the background emission appears at positive and some at negative Faraday depths. Then, in this case, the observed filamentary structures and the horizontal structure in the north reflect the regions with an excess in thermal electron density and/or magnetic field strength. However, the filaments should be located in the front of all other components since they cast shadows both across emission observed at positive and negative Faraday depths.
Finally, Faraday spectrum at a location of the negative triangular structure C peaks both at positive and negative Faraday depths. Positive Faraday components are associated with the background emission BG1 and BG2. The negative triangular component is probably associate with an additional emitting region, located somewhere in front of the background emission BG1 and BG2. We tried to incorporate all of these into our model. A cartoon of this model is shown in Fig. 8.
5.3. Possible associations with the filamentary structure A and its proper motion
The elongated straight filament A running in the north-to-south direction is displaced by ~1.5 rad m-2 in Faraday depth relative to the surrounding background emission, suggesting a magneto-ionic structure located in front of the bulk of the emission. It is interesting to compare it to other linear ISM features that have been reported in the literature. McCullough & Benjamin (2001) discovered an extremely narrow, linear, ionized filament in the ISM, which resembles some characteristics of our filament at Faraday depth + 0.5 rad m-2. Their filament is 2.5° long, 20′′ wide and has an Hα surface brightness of IHα ≈ 0.5 R. It is located at a comparable Galactic latitude (b = + 38.5°) to the 3C 196 field. McCullough & Benjamin (2001) argued that the most probable origin of the filament is an ionized trail left by photoionization from a star or compact object. As an alternative, but unlikely scenario, they mentioned an extremely low density nearby stellar jet, or an unusually linear filament associated with a large-scale nearby bubble, or an ionized trail left by mechanical input from a star or compact object. They also argued that this kind of filament would show a displacement in Faraday depth against the background radio emission, regardless of its true nature of origin.
Unfortunately, up to now there are no observations in the radio that can support this prediction. This is similarly true for our filament. Available data in Hα of 3C 196 field do not have the angular resolution needed to resolve the filament. For the purpose of further discussion, we assume that our filament has the Hα surface brightness of the McCullough & Benjamin (2001) filament, and then estimate the thermal electron density of the filament and its distance.
Combining Eq. (2) and (3), we find that the thermal electron density of the filament is ![\begin{equation} \frac{n_{\rm e}}{[\rm cm^{-3}]}=0.81B_\parallel \frac{\rm EM}{\rm RM}\frac{[\rm rad~m^{-2}]}{\rm [\mu G][pc~cm^{-6}]}, \end{equation}](/articles/aa/full_html/2015/11/aa26638-15/aa26638-15-eq167.png) (6)where to calculate ne we need to assume the strength of B∥. Once that ne is known, one can get dl from Eq. (2) or (3) and then estimate a distance, d, to the filament based on its angular diameter, Dθ = 9.4′, and assuming axial symmetry.
(6)where to calculate ne we need to assume the strength of B∥. Once that ne is known, one can get dl from Eq. (2) or (3) and then estimate a distance, d, to the filament based on its angular diameter, Dθ = 9.4′, and assuming axial symmetry.
Taking IHα = 0.5 R and RM = 1.5 rad m-2 with the results from the previous sections, T = 104 K and B∥ = 0.3 μG, we get EM = 1.37 pc cm-6, ne = 0.2 cm-3, dl = 28 pc, and d = 20 kpc. The calculated distance is obviously not realistic. The filament cannot be located behind the background emission (see discussion in Sect. 5.2). This means that some of our assumptions in the calculation are not correct.
First, it is possible that our filamentary structure is not a filament but rather a sheet-like structure observed edge-on. Axial symmetry in that case is not valid, and the distance based on this assumption would not be valid either. Second, if we keep the assumption about the filamentary nature, then either B∥ or ne or both must be larger. If we assume that our filament is located somewhere within the Local Bubble, i.e. d< 200 pc, this implies that dl< 0.3 pc and neB∥> 6.2 cm-3μG. A filament is a region showing an excess in ne and/or B∥ compared to its surroundings.
For a proper understanding of the nature of the filament, it is crucial to know its distance and proper motion. We assume that the filament is at 50 pc distance and has a transverse velocity of 50 km s-1. It should then move 50 × 10-6 pc yr-1, which is equivalent to 0.2′′ yr-1. This causes a parallax with an amplitude of about 0.03′′ over the course of one year. Obviously it is easier to measure the filment’s proper motion than its distance. We therefore try to measure the first using our 1 arcmin resolution images (see Fig. 9), observed one year apart (L80508 and L192832 observations).
The edges of the filament are well defined by the depolarization canals seen so clearly in the upper left image in Fig. 9. We use these canals to create a mask and isolate the filament from its surrounding background emission. We repeat this for the two observations and then determine if the position of the filament has changed on the timescale of one year. We find no change in position between the L80508 and L192832 observations. The estimated error on our current measurement is ~1′′. Assuming a typical transverse velocity of 50 km s-1, we can set a lower limit to the distance of ≳10 pc.
To achieve the precision needed to measure a real proper motion, we can reduce the noise by averaging the RM cubes from many nights in each of the two seasons. However, for this to work for a very small fraction of the width of these filaments, it is essential to compare the structures at exactly the same Faraday depth. The RM cubes must therefore be aligned in RM to much better accuracy than provided by the CODE ionospheric data. Recently, Brentjens et al. (in prep.) developed a new method, which yields the required accuracy limited only by the available signal within the field of view. The method cross-correlates the Galactic polarized emission in Faraday depth as a function of time, both within each night and between nights and season. Initial results suggest that the ionospheric Faraday rotation can be aligned to levels on the order of 0.01 rad m-2, i.e. a very small fraction of the width of the RMSF. The results of this analysis will be presented in a future paper.
5.4. The system of depolarization canals
Figure 6 shows many organized patterns of linear structures with no or very weak polarized signal. Many of these resemble the depolarization canals first discussed and studied by Haverkorn et al. (2000, 2004). We also refer to these structures as canals. Haverkorn et al. (2004) described two characteristics of these depolarization canals. They are one PSF wide and the polarization angle changes across the canal by 90°. Mechanisms that create them are as follows. The canals are at the boundary between two regions, which each have similar polarized intensities but a difference in polarization angle of ΔΘ = (n + 1/2)180° (where n = 0,1,2,...). This causes almost total depolarization through vector addition, and the resulting canal is by definition one PSF wide. The other mechanism is connected to differential Faraday rotation. A linear gradient in RM produces a long, narrow depolarization canal at a certain value RMc, where 2RMcλ2 = nπ. Across every null in the sinc-function, the polarization angle changes by 90°. A third possibility is beam depolarization due to the presence of turbulent magneto-ionic medium, which is extremely small-scale, in front of a polarized background. To explore this possibility, we also made a RM cube with a spatial resolution of 12′′. At this scale the canals appear resolved, but they do not show an increased polarization signal. We therefore consider this possibility unlikely as a cause for the creation of canals.
We believe that most of the canals are probably of the first kind, that is they are due to beam depolarization due to discontinuity in the polarization angle. The best example are the canals associated with the edges of the prominent filament discussed previously and the spaghetti-like structure located to the east of it (see Fig. 9). They are indeed one PSF wide, the intensity of the emission on either side of the canal is comparable, and there is a 90° polarization angle change when crossing the canal. Adopting this mechanism for the creation of a canal there is, however, a clear prediction: the polarized emission cannot go to zero at all frequencies that were used in the creation of the RM cube, which by necessity spans a wide range of frequencies (in our case from 115–175 MHz). The Stokes Q and U signals at the edges of this frequency range should therefore increase again within the canals. Unfortunately the signal-to-noise ratio in our data at this stage is not yet sufficient to confirm this prediction. We stress that the residual polarized signal within the canals also carries valuable information about the polarization signal emitted between the location of the filament and the observer at any Faraday depth. In this picture the deepest canals must be closest to the observer. We will return to this interesting aspect in a future paper when we have aligned and analysed, the RM cubes from the many nights we have accumulated on this field.
There are also some canals in our observations that are broader than one PSF. One of these is located in the south-west part of the image, along the boundary between a triangular region showing emission at negative Faraday depth and surrounding emission at positive depths (see Fig. 6). This type of canal must be either a region in the ISM showing no emission, all along the line of sight, or a region with an extremely turbulent magneto-ionic medium, causing wavelength-independent beam depolarization.
5.5. Straightness of observed structures and canals
Without regard to the origin of observed structures and canals, a real puzzle is their extraordinary straightness. Their axial ratio is larger than 100:1. It is possible that they are the results of a fortunate projection of a three-dimensional morphology of the magnetic field (e.g. the folding of magnetic sheets and loops) and the ISM.
Recent magneto-hydrodynamical simulations of the ISM, by Choi & Stone (2012), showed that thermal conduction plays an important role in shaping the geometry of structures formed by the thermal instabilities by stabilizing small scales and limiting the size of the smallest condensates. If the magnetic field is uniform and weak (~3 nG), the heat is conducted anisotropically, primary along magnetic field lines. As a result of this, the thermal instabilities saturate into very long thin filaments of dense gas aligned with the magnetic field. In the linear regime, this can be explained by the variation of the Field length (Field 1965) with respect to the direction of magnetic field. Isobaric perturbations with wavelength smaller than the Field length do not grow at all. Perpendicular to the magnetic field, the Field length is very small, so very short wavelength perturbations are unstable. Parallel to the magnetic field, the Field length is much longer, so only longer wavelength modes grow. As the perturbations grow non-linear, conduction tends to enforce isothermality along magnetic field lines, leading to long filaments. If the magnetic field is uniform and strong (~3 μG), only motions along field lines are allowed, and, moreover, magnetic pressure provides some support in dense regions, resulting in fragmented filaments aligned with the field lines (for more details we refer to Choi & Stone 2012). Therefore, it is possible that filamentary structures observed in our data were shaped through thermal instabilities. To get better statistics on observed structures/filaments, and to study their distribution and orientation with regard to the regular magnetic field component, we plan to survey a larger area of the sky. This will then allow us to directly associate observed structures with the results of magneto-hydrodynamical simulations of the ISM.
Another explanation of observed linear structures can be connected to interactions of close-by moving stars with the ISM, as discussed by McCullough & Benjamin (2001). Bow shocks around stars and neutron stars (pulsars) can leave long and narrow trails in the ISM, because of their large speeds. Or, trails can be left by an ionizing source of sufficiently low ionizing luminosity that its Strömgren radius is small compared with the distance it travels in a recombination time. However, to make such trails long in angular size, of a few degrees, these sources should be rather close, less than about 100 pc, and located somewhere within the Local Bubble. We will leave a more detailed study of this possibility for future work.
 |
Fig. 10 An image of the 3C 196 field in polarized intensity (PI) observed with the 28 WSRT mosaic pointings at 350 MHz (based on preliminary calibration and analysis). In making this image, we used only the central 9 of the 28 observed pointings. The image is given at Faraday depth 0 rad m-2 and has not been corrected for polarization noise bias. It measures 6.9° × 6.9° in size and the PSF is 2.8 × 3.8′. |
6. WSRT observations from 312–381 MHz
The 3C 196 field was also observed with the WSRT at 350 MHz in 2013 and 2014. These observations form part of a large-area mosaic survey to complement LOFAR polarization studies. Thus far we have finished the reduction and analysis of the part, which overlaps with the LOFAR field of view so we can make a comparison with the features seen at LOFAR frequencies.
Figure 10 shows the WSRT 350 MHz image in polarized intensity at Faraday depth 0 rad m-2. The RMSF in the WSRT 350 MHz data (δΦ = 11 rad m-2) is an order of magnitude less than in the LOFAR data. Hence, almost all Faraday depths that show emission in the LOFAR data are captured in this one frame in the WSRT data. The linear filament A passing over 3C 196 is clearly detected. It has a surface brightness of ~7 mJy PSF-1 RMSF-1. This is the first time that we see some common morphology in the RM cubes made in the LOFAR 115−175 MHz and WSRT 315−380 MHz bands. Diffuse emission surrounding the filament is not as prominent (≲3 mJy PSF-1 RMSF-1) as observed with LOFAR (see Fig. 4) and its morphology is very patchy.
In addition to the filament A passing over 3C 196, we detected yet another straight filamentary structure (marked with D in Fig. 10) at the WSRT frequencies. It is located in the south-east part of the image. Its surface brightness is ~8 mJy PSF-1 RMSF-1 and is probably associated with emission at + 2.5 rad m-2 in the LOFAR RM cubes. The two filaments in the WSRT data seem to have similar orientation.
Bright horizontal emission (~15 mJy PSF-1 RMSF-1) located to the north of the filaments in the WSRT data coincides with the region showing weak emission and horizontal depolarization canals at LOFAR frequencies, just below horizontal emission in the north at negative Faraday depths. Some parts of this bright emission in the WSRT data are probably Faraday-thick structures at LOFAR frequencies and not detectable with LOFAR (ΔΦ >δΦLOFAR).
The different observed morphology of the diffuse emission surrounding the filament in the two different frequency bands may be attributed to the poor resolution in Faraday depth at 350 MHz. To test this, we generated an RM cube at LOFAR frequencies using an RMSF that has a resolution of δΦ350 MHz ≈ 10 δΦ150 MHz. It is possible that multiple Faraday thin structures (ΔΦ <δΦ350 MHz) detected in the LOFAR low-frequency images decorrelate when we observe them with a much broader RMSF. We find that ~50% of the flux is depolarized, but the overall morphology of emission is not much different from the original LOFAR RM cubes. Thus, the lack of prominent background emission detected with LOFAR cannot be explained by the much broader RMSF at 350 MHz.
Another possible explanation for the lack of emission in the WSRT 350 MHz data may be related to the missing large-scale structures. The shortest baseline of the WSRT is 36 m, so at 350 MHz structure on angular scales larger than about a degree is not adequately measured. As we discussed in Sect. 5, the synchrotron radiation is emitted on large scales, but its polarization is altered on smaller scales by Faraday effects. Faraday rotation is much stronger at lower radio frequencies. We thus expect the missing large-scale emission in polarization to be more prominent at higher frequencies. This was discussed first by Haverkorn et al. (2004). For the case of a uniformly polarized background propagating through a small-scale Faraday screen, the expected offset for Stokes Q and U depends on the wavelength, λ, and the width of the Faraday depth distribution, σΦ, as 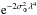 . In WSRT 350 MHz observations, this condition is not well satisfied and one needs to take it into account during interpretation of the data (e.g. Haverkorn et al. 2004; Schnitzeler et al. 2009).
. In WSRT 350 MHz observations, this condition is not well satisfied and one needs to take it into account during interpretation of the data (e.g. Haverkorn et al. 2004; Schnitzeler et al. 2009).
To correct for these undetectable large-scale structures, one needs first to observe the same region at the same frequencies with a single-dish telescope with absolute intensity scaling. Then, these large-scale data can be added to the interferometer data (Uyaniker et al. 1998; Stanimirovic 2002). However, for the WSRT 350 MHz observations this is not possible. We can only estimate it based on other existing absolutely calibrated observations at higher frequencies, e.g. Berkhuijsen & Brouw (1963) map of polarized emission at 408 MHz. This frequency is close enough to 350 MHz to allow a comparison, although the polarized intensity at 408 MHz is expected to be slightly higher due to the larger polarization horizon.
The polarized brightness temperature at 408 MHz at the location of the 3C 196 field is 2.1 ± 0.4 K (Berkhuijsen & Brouw 1963). Using a power-law spectral index of −2.5, this corresponds to ~3 K at 350 MHz. If we now smooth our 350 MHz data to the 2° FWHM of Berkhuijsen & Brouw (1963) we get 0.08 K. This means that indeed we have a missing large-scale component in polarized intensity.
7. Summary and conclusions
We have presented results from LOFAR HBA observations of a field centred on the 3C 196 source, taken as part of the LOFAR-EoR project. We applied RM synthesis to the data to reveal a very rich morphology of polarized emission. Detected structures are spread over a wide range of Faraday depths, ranging from −3 to + 8 rad m-2. Their average brightness temperature is 5−15 K, which is comparable to the emission in the ELAIS-N1 field and also to a field observed with LOFAR at high Galactic latitudes (Jelić et al. 2014).
The most interesting features detected in polarization are (i) a straight and long filamentary structure at Faraday depth + 0.5 rad m-2, parallel to the Galactic plane and (ii) a system of linear depolarization canals. The first is probably an ionized structure in the ISM located very close by, somewhere within the Local Bubble. It is displaced by 1.5 rad m-2 from the surrounding background emission. This implies that, within the filament, the thermal electron density and magnetic field must satisfy neB∥> 6.2 cm-3μG. With the current accuracy of the position measurement of 1′′, we can set a lower limit to its distance of 10 pc, assuming a transverse velocity of 50 kms-1.
The same filament was also observed with the WSRT at 350 MHz. This is the first time that we see some common morphology in the RM cubes made in two different frequency regimes. Interestingly, in the south-east part of the WSRT mosaic there is another filament. This filament is probably associated with emission at + 2.5 rad m-2 in the LOFAR RM cubes. Its orientation is the same as the filament located in the centre of the image. This is a tentative indication that these two filaments might be a part of the same large-scale structure in the ISM.
A follow up study of the filaments discussed in this paper showed their strong correlation with the orientation of the sky projected magnetic field component as probed by the Planck maps of the dust emission in polarization (Zaroubi et al. 2015). Dust particles are usually embedded within neutral hydrogen (Hi) gas, as seen through Hi/dust correlation at high Galactic latitudes (Planck Collaboration Int. XVII 2014). Therefore, high angular resolution Hi data of 3C 196 field can be very usefully in providing potential kinematic information about the features studied in this paper. This is also supported by Clark et al. (2014) analysis of Hi data from the Galactic Arecibo L-Band Feed Array Hi (GALFA-Hi) Survey and the Parkes Galactic All Sky Survey (GASS), which revealed many slender, linear Hi features (“fibers”) that extent for many degrees at high Galactic latitude. These fibers are orientated along the interstellar magnetic field as probed by starlight polarization and are most likely a component of the Local Bubble wall.
Most of the depolarization canals detected in our LOFAR data are due to beam depolarization. However, some of them might be associated with regions in the ISM that show a very turbulent magneto-ionic medium, causing wavelength-independent beam depolarization. Without regard to their origin, the straightness of these canals is a real puzzle. Are they a projection effect of complicated morphology in the magnetic field and the ISM, or are they associated with fast-moving close-by stars interacting with the ISM? This needs to be investigated further. Planned observations covering a much larger area of this region, along with observations at other wavelengths, will help towards this goal.
Results presented in this paper are also of concern for epoch of reionization experiments. The instrumentally polarized response of an interferometer needs to be calibrated to a small fraction of a percent to limit leakage of polarization signals to levels of a few mK. Otherwise, the leakage can contaminate the cosmological 21-cm signal in total intensity (e.g. Jelić et al. 2010). The contamination depends strongly on the brightness temperature of polarized emission, its morphology, and its spread in Faraday depth. In the case of the polarized emission detected in the 3C 196 field, which is limited to small Faraday depths (| Φ | ≲ 10 rad m-2), this is not a big concern. Asad et al. (2015) showed that in the spherical power spectrum the leakage power of emission presented in this paper is lower than the cosmological signal at k< 0.3 Mpc-1. Moreover, there is a window in the cylindrical power spectrum where the cosmological signal dominates over the leakage.
This map is a composite of three separate surveys. The 3C 196 field is covered only by the Wisconsin H-Alpha Mapper (WHAM; Haffner et al. 2003) survey, which means that given Hα emission is at 1° resolution. The WHAM survey provides velocity resolved spectra, but for this work we use only integrated emission.
The vertical electron density gradient can be described as 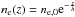 , where ne,0 is a mid-plane electron density and h is a scale height (e.g. Haffner et al. 2009; Schnitzeler 2012, and references therein). In our calculation, we normalize it to give ⟨ne⟩ ≃ 0.03 cm-3.
, where ne,0 is a mid-plane electron density and h is a scale height (e.g. Haffner et al. 2009; Schnitzeler 2012, and references therein). In our calculation, we normalize it to give ⟨ne⟩ ≃ 0.03 cm-3.
Acknowledgments
We thank an anonymous referee for useful comments that improved the manuscript. V.J. would like to thank the Netherlands Foundation for Scientific Research (NWO) for financial support through VENI grant 639.041.336. A.Gd.B., A.R.O., M.M., S.Y. and V.N.P. acknowledge support by the ERC for project 339743 (LOFARCORE). L.V.E.K., A.G., K.M.B.A. and H.K.V. acknowledge the financial support from the European Research Council under ERC-Starting Grant FIRSTLIGHT – 258942. F.B.A. acknowledges the support of the Royal Society for a University Research Fellowship. G.H. acknowledges funding from the People Programme (Marie Curie Actions) of the European Union’s Seventh Framework Programme (FP7/2007–2013) under REA grant agreement No. 327999. I.T.I. was supported by the Science and Technology Facilities Council [grant number ST/L000652/1]. The Low-Frequency Array (LOFAR) was designed and constructed by ASTRON, the Netherlands Institute for Radio Astronomy, and has facilities in several countries, which are owned by various parties (each with their own funding sources) and are collectively operated by the International LOFAR Telescope (ILT) foundation under a joint scientific policy. The Westerbork Synthesis Radio Telescope (WSRT) is operated by the ASTRON with support from the Netherlands Foundation for Scientific Research (NWO). The Wisconsin H-Alpha Mapper is funded by the National Science Foundation.
References
- Akahori, T., Ryu, D., Kim, J., & Gaensler, B. M. 2013, ApJ, 767, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Asad, K. M. B., Koopmans, L. V. E., Jelić, V., et al. 2015, MNRAS, 451, 3709 [NASA ADS] [CrossRef] [Google Scholar]
- Baccigalupi, C., Burigana, C., Perrotta, F., et al. 2001, A&A, 372, 8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berkhuijsen, E. M., & Brouw, W. N. 1963, Bull. Astron. Inst. Netherlands, 17, 185 [Google Scholar]
- Berkhuijsen, E. M., Mitra, D., & Mueller, P. 2006, Astron. Nachr., 327, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Bernardi, G., de Bruyn, A. G., Brentjens, M. A., et al. 2009, A&A, 500, 965 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bernardi, G., de Bruyn, A. G., Harker, G., et al. 2010, A&A, 522, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bernardi, G., Greenhill, L. J., Mitchell, D. A., et al. 2013, ApJ, 771, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Brentjens, M. A., & de Bruyn, A. G. 2005, A&A, 441, 1217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Choi, E., & Stone, J. M. 2012, ApJ, 747, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, S. E., Peek, J. E. G., & Putman, M. E. 2014, ApJ, 789, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Cordes, J. M., & Lazio, T. J. W. 2002, ArXiv e-prints [arXiv:astro-ph/0207156] [Google Scholar]
- Cordes, J. M., & Lazio, T. J. W. 2003, ArXiv e-prints [arXiv:astro-ph/0301598] [Google Scholar]
- Field, G. B. 1965, ApJ, 142, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Finkbeiner, D. P. 2003, ApJS, 146, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Gaensler, B. M., Madsen, G. J., Chatterjee, S., & Mao, S. A. 2008, PASA, 25, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Ghosh, A., Prasad, J., Bharadwaj, S., Ali, S. S., & Chengalur, J. N. 2012, MNRAS, 426, 3295 [NASA ADS] [CrossRef] [Google Scholar]
- Guzmán, A. E., May, J., Alvarez, H., & Maeda, K. 2011, A&A, 525, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haffner, L. M., Reynolds, R. J., Tufte, S. L., et al. 2003, ApJS, 149, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Haffner, L. M., Dettmar, R.-J., Beckman, J. E., et al. 2009, Rev. Mod. Phys., 81, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Haslam, C. G. T., Klein, U., Salter, C. J., et al. 1981, A&A, 100, 209 [NASA ADS] [Google Scholar]
- Haslam, C. G. T., Salter, C. J., Stoffel, H., & Wilson, W. E. 1982, A&AS, 47, 1 [NASA ADS] [Google Scholar]
- Haverkorn, M. 2015, in Astrophys. Space Sci. Lib. 407, eds. A. Lazarian, E. M. de Gouveia Dal Pino, & C. Melioli, 483 [Google Scholar]
- Haverkorn, M., Katgert, P., & de Bruyn, A. G. 2000, A&A, 356, L13 [NASA ADS] [Google Scholar]
- Haverkorn, M., Katgert, P., & de Bruyn, A. G. 2003a, A&A, 403, 1031 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haverkorn, M., Katgert, P., & de Bruyn, A. G. 2003b, A&A, 404, 233 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haverkorn, M., Katgert, P., & de Bruyn, A. G. 2004, A&A, 427, 549 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heiles, C., & Haverkorn, M. 2012, Space Sci. Rev., 166, 293 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iacobelli, M., Haverkorn, M., Orrú, E., et al. 2013, A&A, 558, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jelić, V., Zaroubi, S., Labropoulos, P., et al. 2010, MNRAS, 409, 1647 [NASA ADS] [CrossRef] [Google Scholar]
- Jelić, V., de Bruyn, A. G., Mevius, M., et al. 2014, A&A, 568, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kazemi, S., & Yatawatta, S. 2013, MNRAS, 435, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Kazemi, S., Yatawatta, S., Zaroubi, S., et al. 2011, MNRAS, 414, 1656 [NASA ADS] [CrossRef] [Google Scholar]
- Kazemi, S., Yatawatta, S., & Zaroubi, S. 2013a, MNRAS, 430, 1457 [NASA ADS] [CrossRef] [Google Scholar]
- Kazemi, S., Yatawatta, S., & Zaroubi, S. 2013b, MNRAS, 434, 3130 [NASA ADS] [CrossRef] [Google Scholar]
- Manchester, R. N. 1972, ApJ, 172, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Mao, S. A., Gaensler, B. M., Haverkorn, M., et al. 2010, ApJ, 714, 1170 [NASA ADS] [CrossRef] [Google Scholar]
- Martinez-Rubi, O., Veligatla, V. K., de Bruyn, A. G., et al. 2013, in Astronomical Data Analysis Software and Systems XXII, ed. D. N. Friedel, ASP Conf. Ser., 475, 377 [Google Scholar]
- McCullough, P. R., & Benjamin, R. A. 2001, AJ, 122, 1500 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Ostriker, J. P. 1977, ApJ, 218, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Offringa, A. R., de Bruyn, A. G., Biehl, M., et al. 2010, MNRAS, 405, 155 [NASA ADS] [Google Scholar]
- Offringa, A. R., van de Gronde, J. J., & Roerdink, J. B. T. M. 2012, A&A, 539, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Offringa, A. R., de Bruyn, A. G., Zaroubi, S., et al. 2013, A&A, 549, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pandey, V. N., van Zwieten, J. E., de Bruyn, A. G., & Nijboer, R. 2009, in The Low-Frequency Radio Universe, eds. D. J. Saikia, D. A. Green, Y. Gupta, & T. Venturi, ASP Conf. Ser., 407, 384 [Google Scholar]
- Pen, U.-L., Chang, T.-C., Hirata, C. M., et al. 2009, MNRAS, 399, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Pizzo, R. F., de Bruyn, A. G., Bernardi, G., & Brentjens, M. A. 2011, A&A, 525, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XVII. 2014, A&A, 566, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reich, W. 2006, ArXiv e-prints [arXiv:astro-ph/0603465] [Google Scholar]
- Reynolds, R. J. 1991, ApJ, 372, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, R. J., Haffner, L. M., & Tufte, S. L. 1999, ApJ, 525, L21 [Google Scholar]
- Scaife, A. M. M., & Heald, G. H. 2012, MNRAS, 423, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Schnitzeler, D. H. F. M. 2010, MNRAS, 409, L99 [NASA ADS] [Google Scholar]
- Schnitzeler, D. H. F. M. 2012, MNRAS, 427, 664 [NASA ADS] [CrossRef] [Google Scholar]
- Schnitzeler, D. H. F. M., Katgert, P., & de Bruyn, A. G. 2009, A&A, 494, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stanimirovic, S. 2002, in Single-Dish Radio Astronomy: Techniques and Applications, eds. S. Stanimirovic, D. Altschuler, P. Goldsmith, & C. Salter, ASP Conf. Ser., 278, 375 [Google Scholar]
- Subrahmanyan, R., & Cowsik, R. 2013, ApJ, 776, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, X. H., Reich, W., Waelkens, A., & Enßlin, T. A. 2008, A&A, 477, 573 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tasse, C., van der Tol, S., van Zwieten, J., van Diepen, G., & Bhatnagar, S. 2013, A&A, 553, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tucci, M., Carretti, E., Cecchini, S., et al. 2002, ApJ, 579, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Uyaniker, B., Fuerst, E., Reich, W., Reich, P., & Wielebinski, R. 1998, A&AS, 132, 401 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Haarlem, M. P., Wise, M. W., Gunst, A. W., et al. 2013, A&A, 556, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- White, M., Carlstrom, J. E., Dragovan, M., & Holzapfel, W. L. 1999, ApJ, 514, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Wieringa, M. H., de Bruyn, A. G., Jansen, D., Brouw, W. N., & Katgert, P. 1993, A&A, 268, 215 [NASA ADS] [Google Scholar]
- Yatawatta, S. 2014, MNRAS, 444, 790 [NASA ADS] [CrossRef] [Google Scholar]
- Yatawatta, S., Zaroubi, S., de Bruyn, G., Koopmans, L., & Noordam, J. 2008, ArXiv e-prints [arXiv:0810.5751] [Google Scholar]
- Zaroubi, S., Jelić, V., de Bruyn, A. G., et al. 2015, MNRAS, submitted [arXiv:1508.06652] [Google Scholar]
All Tables
An overview of observational parameters of the five LOFAR-HBA observations used in this study.
All Figures
 |
Fig. 1 Frequency-averaged Stokes I image of the 3C 196 region, based on the four nights of data taken in December 2012. The image is 8.3° × 8.3° in size, with a PSF of 45′′, and the noise level is 170 μJy PSF-1. The nine bright sources towards which we performed direction-dependent calibration are indicated with red circles. The 3C 196 source is subtracted from direction-independent calibrated visibilities, while eight other sources are not. A location of the discovered pulsar J081558+461155 (see Sect. 3.3) is shown with a blue asterisk. The image is de-convolved using the CLEAN algorithm implemented in CASA. |
| In the text | |
 |
Fig. 2 The estimated RM variations in the ionosphere using the Global Ionospheric Maps of CODE. The RM are given as a function of observing time and for each night. |
| In the text | |
 |
Fig. 3 Two images of the 3C 196 region in polarized intensity at Faraday depth 0 rad m-2 after performing direction-independent calibration (image on the left) and direction-dependent calibration and source subtraction (image on the right). Images are 8.3° × 8.3° in size, with a PSF of 3.6′ × 3.9′. The 3C 196 source is also subtracted from direction-independent calibrated visibilities. Eight bright sources, used for direction-dependent calibration and source subtraction, are indicated with red circles. The images have not been corrected for polarization noise bias nor for Faraday rotation in the Earth’s ionosphere. |
| In the text | |
 |
Fig. 4 Widefield images of the 3C 196 field in polarized intensity (PI), Stokes Q, and Stokes U at Faraday depths of −1.5, −0.0, +1.0, +1.5, +2.0, +2.5, +3.0, and +3.5 rad m-2. Images are 8.3° × 8.3° in size with a PSF of 3.6′ × 3.9′. The noise level is 71 μJy PSF-1 RMSF-1 in polarized intensity and 108 μJy PSF-1 RMSF-1 in Stokes Q, U. The images in polarized intensity have not been corrected for polarization noise bias nor for the primary beam. |
| In the text | |
 |
Fig. 4 continued. |
| In the text | |
 |
Fig. 5 Faraday spectra of a few representative lines-of-sight through the RM cube of polarized intensity. We have not attempted to deconvolve the spectra for the effects of the side lobes of the RMSF. |
| In the text | |
 |
Fig. 6 Upper image: highest peak of the Faraday depth spectrum in polarization at each spatial pixel. Bottom image: map of the RM value of each peak, shown in red-blue colour scale. Yellow contours are showing Hα intensity on a one degree scale (Finkbeiner 2003; Haffner et al. 2003), given in units of Rayleighs (see Sect. 5). A white box indicates the boundaries of the WSRT 350 MHz image in Fig. 10. A location of the discovered pulsar J081558+461155 (see Sect. 3.3) is shown with a yellow asterisk. |
| In the text | |
 |
Fig. 7 Angular power spectrum of integrated polarized emission. The best power-law fit (solid line) to the power spectrum (“Cl−l”) between l = 150 and l = 2700 gives a slope of |
| In the text | |
 |
Fig. 8 A cartoon of the possible layout of polarized emission and magnetic fields towards the 3C 196 field. Solid arrows indicate orientation and strength of B∥. For display purposes, the filamentary structures are shown along the viewing direction in this sideways projection. |
| In the text | |
 |
Fig. 9 Examples of higher resolution images of the 3C 196 field in polarized intensity (PI) and polarization angle (PHI) given at Faraday depths of +1.0, +1.5, and +2.0 rad m-2. Images show the central 2.5° × 2.5° of the field. During the imaging we used baselines between 10 and 4000 wavelengths, providing a frequency-independent resolution of about 1 arcmin. |
| In the text | |
 |
Fig. 10 An image of the 3C 196 field in polarized intensity (PI) observed with the 28 WSRT mosaic pointings at 350 MHz (based on preliminary calibration and analysis). In making this image, we used only the central 9 of the 28 observed pointings. The image is given at Faraday depth 0 rad m-2 and has not been corrected for polarization noise bias. It measures 6.9° × 6.9° in size and the PSF is 2.8 × 3.8′. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.