| Issue |
A&A
Volume 583, November 2015
|
|
|---|---|---|
| Article Number | A54 | |
| Number of page(s) | 10 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201526598 | |
| Published online | 27 October 2015 | |
Modelling low-lying, cool solar loops with optically thick radiative losses
1
INAF–Osservatorio Astronomico di Capodimonte, Salita Moiariello
16,
80131
Napoli,
Italy
e-mail: csasso@oacn.inaf.it
2
INAF–Osservatorio Astrofisico di Catania, via S. Sofia
78, 95123
Catania,
Italy
Received: 25 May 2015
Accepted: 21 August 2015
Aims. We investigate the increase of the differential emission measure (DEM) towards the chromosphere due to small and cool magnetic loops (height ≲8 Mm, T ≲ 105 K). In a previous paper, we analysed the conditions of existence and stability of these loops through hydrodynamic simulations, focussing on their dependence on the details of the optically thin radiative loss function.
Methods. In this paper, we extend those hydrodynamic simulations to verify if this class of loops exists and is stable when using an optically thick radiative loss function. We study two cases: constant background heating and a heating depending on the density. The contribution to the transition region extreme-UV output of these loops is also calculated and presented.
Results. We find that stable, quasi-static cool loops can be obtained using an optically thick radiative loss function and a background heating depending on the density. The DEMs of these loops, however, fail to reproduce the observed DEM for temperatures between 4.6 < log T < 4.8. We also show the transient phase of a dynamic loop obtained by considering constant heating rate and find that its average DEM, interpreted as a set of evolving dynamic loops, reproduces the observed DEM very well.
Key words: Sun: transition region / Sun: UV radiation / hydrodynamics
© ESO, 2015
1. Introduction
The origin of the extreme-UV (EUV) output at temperatures below 1 MK is still widely debated in solar physics. The classical picture that the transition region (TR) emission originates from the base of the hot large-scale coronal loops greatly underestimates the observed EUV emission below 0.1 MK, but no alternative, quantitative view has gained consensus to date. One of the proposed explanations hypothesizes that much of the TR plasma is confined in relatively small and cool magnetic loops (height ≲8 Mm, T ≲ 105 K), which are directly connected to the chromosphere but thermally insulated from the corona (Dowdy et al. 1986; Dowdy 1993; Feldman 1983; Feldman et al. 2001).
From an observational point of view, these loops are indeed very difficult to observe. The first, presumed direct observations present in the literature have been obtained with the instrument Very High Angular Ultraviolet Telescope (VAULT, Korendyke et al. 2001) in the H i Ly-α line. They show loop-like structures with estimated temperatures and densities (T = 104−3 × 104 K, P = 0.1−0.3 dyne cm-2) that could be appropriate for the low-temperature end of cool loops (Patsourakos et al. 2007; Vourlidas et al. 2010). This interpretation has been debated by Judge & Centeno (2008). More recently, the launch of the IRIS spacecraft (De Pontieu et al. 2014), in June 2013, has provided new possibilities to observe these loops. The analysis of the data obtained in spectral lines and continua, covering a range of temperatures log T = 3.7−7 K with a spatial resolution of ~0.4′′, represents a very good opportunity to look for structures with the dimension and temperatures of the class of loops described above. It is therefore not surprising that observations have recently been reported (Hansteen et al. 2014) of highly dynamical cool, low-lying loops that are in many respects similar to those we discuss.
In a previous paper (Sasso et al. 2012, hereafter referred to as Paper I), we analysed the general properties of quasi-static (velocity along the loop lower than 1 km s-1) cool loops with T ≲ 0.1 MK and their conditions of stability and existence under different and more realistic assumptions about the optically thin radiative loss function with respect to previous works (i.e. Cally & Robb 1991). In particular, we obtained stable low-lying, cool loops through hydrodynamic simulations, even for a set of parameters that would prevent the formation of rigorously static loops. The existence of the loops we found is indeed due to small departures from static conditions, i.e. to the presence of a small, but non-zero conductive flux and velocities, and to the requirement of nearly constant pressure (implying that our loops are limited to low heights above the chromosphere). In our simulations, we only considered the case of constant heating rate. We also showed that the emission of these cool loops, plus the emission of intermediate temperature loops (0.1 <T < 1 MK), can account for the observed radiative output below 1 MK.
From a theoretical point of view, there are still several points that need to be explored to determine the conditions under which cool loops could exist in the solar atmosphere. One important point is the shape of the radiative loss function below 0.1 MK, due to the presence of the H i Ly-α peak, which is very important for the existence of cool loops.
Our work is based on 1D hydrodynamic simulations and aims to study the conditions of existence of cool loops to understand, in particular, the mechanisms of their heating and energy balance through comparison between their simulated differential emission measure (DEM) and the observed DEM. Peter et al. (2004, 2006) made the first successful attempt to reproduce the shape of the DEM curve quantitatively and qualitatively, even at temperatures below log T = 5.3 K. They synthesized spectra from three-dimensional (3D) MHD simulations of the whole Sun atmosphere, finding structures that could be related to the kind of loops we are studying. However, the cool loops we describe would be covered by only very few resolution elements in their simulation, and in any case resolving the gradients and dynamics of the relevant quantities in our loop models would require a much higher resolution. Therefore, we regard our study as complementary to large-scale 3D simulations.
As in Paper I, while looking for cool loops, we have also found low-lying, quasi-static loops with temperatures in the range 1−5 × 105 K. Following one of the latest loop classifications (Reale 2014), we should also refer to these loops as cool coronal loops. We refer to these loops as intermediate-temperature loops to avoid confusion.
In this paper, we want to make a further step in the direction of considering more realistic assumptions for the simulations of cool loops with respect to Paper I, by introducing an optically thick radiative loss function. In Sect. 2, we describe the numerical model and introduce the radiative loss function adopted. In Sect. 3, we present the hydrodynamic simulations and loops obtained (cool and intermediate-temperature loops) with different assumptions about the heating rate, and we discuss and analyse their properties. Section 3.4 is dedicated to the calculated DEMs of the loops obtained and to the comparison with the observed DEM. Finally, in the conclusions (Sect. 4), we treat the role of the cool and intermediate-temperature loops in the solar atmosphere and the comparison with the observations.
2. Numerical calculations
The set of hydrodynamic equations for mass, momentum, and plasma energy conservation for a fully ionized hydrogen plasma have been solved in a unidimensional, magnetically confined loop of constant cross-section with ARGOS, a 1D hydrodynamic code with the fully adaptive-grid package PARAMESH (Antiochos et al. 1999; MacNeice et al. 2000). A fully adaptive-grid is necessary to adequately resolve one or more evolving regions of steep gradients. The hydrodynamic equations for mass, momentum, and energy, respectively, solved by ARGOS are 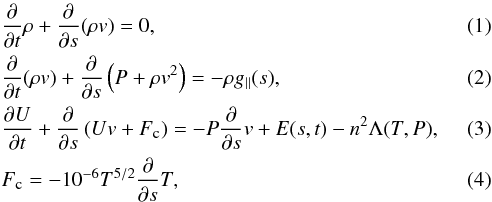 where t is the time, ρ the mass density, v the velocity, P, T and n are the gas pressure, temperature, and electron number density, respectively. The parameter U is the internal energy, s the curvilinear coordinate along the loop, E(s,t) the assumed form for the input heating rate, n2Λ(T,P) the plasma radiative losses specified by the radiative loss function Λ(T,P), g∥(s) the component of the solar gravity along the loop axis, and Fc the thermal conductive flux, in CGS units.
where t is the time, ρ the mass density, v the velocity, P, T and n are the gas pressure, temperature, and electron number density, respectively. The parameter U is the internal energy, s the curvilinear coordinate along the loop, E(s,t) the assumed form for the input heating rate, n2Λ(T,P) the plasma radiative losses specified by the radiative loss function Λ(T,P), g∥(s) the component of the solar gravity along the loop axis, and Fc the thermal conductive flux, in CGS units.
The code is based on a loop geometry, which assumes an arched loop of a given length L and apex height above the chromosphere h as described in Karpen et al. (2001), Spadaro et al. (2003). At each footpoint of the loop there is a thick chromosphere (26.7 Mm deep) acting as a mass reservoir, with temperature set to T = 9.5 × 103 K. Since we take, by definition, the top of the chromosphere as the level at which the plasma drops below 9.5 × 103 K, the exact position of the top of the chromosphere (s = ± Li/ 2 at the beginning of the simulation, s being the curvilinear coordinate along the field lines) changes during the calculation with the plasma filling or evacuating the loop. Hence, at end of the simulation, we find a new position for the top of the chromosphere s = ± Lf/ 2 and, consequently, a new value of h = hf, where hf is no longer the geometrical parameter defining the shape of the loop, but the height of the loop apex above the T = 9.5 × 103 K level.
The main input parameters for the calculations are the radiative loss function, heating rate, pressure (or the density) at the chromospheric reference temperature, and loop geometry (h and L). In Paper I, we used constant heating rates per unit volume throughout the loop. Following the more general approach of Antiochos & Noci (1986), we also consider the case of a constant heating rate per particle. The two cases are parametrized as follows: ![\begin{equation} E(s,t) = E_\mathrm{h}\: f(s)\: [ n(s,t)/n_\circ ]^\gamma , \label{eq:heating} \end{equation}](/articles/aa/full_html/2015/11/aa26598-15/aa26598-15-eq38.png) (5)where γ = 0 is the case of constant heating per unit volume, and γ = 1 corresponds to the case of constant heating per particle, and n° = 3.9882 × 109 cm-3 is the value of the density at the base of the loop, taken from the work of Kuin & Poland (1991). The function f(s) specifies the variability of the heating rate (per particle or per volume) along the loop. With the exception of the discussion of Sect. 2.2, we assume f(s) = 1 throughout. The radiative loss function we adopt is described more in detail in the following section.
(5)where γ = 0 is the case of constant heating per unit volume, and γ = 1 corresponds to the case of constant heating per particle, and n° = 3.9882 × 109 cm-3 is the value of the density at the base of the loop, taken from the work of Kuin & Poland (1991). The function f(s) specifies the variability of the heating rate (per particle or per volume) along the loop. With the exception of the discussion of Sect. 2.2, we assume f(s) = 1 throughout. The radiative loss function we adopt is described more in detail in the following section.
2.1. Radiative loss function
To estimate the radiative losses in the optically thick H Ly-α line, we used the calculations by Kuin & Poland (1991). Those authors computed the contribution to radiative losses of hydrogen and helium taking the effects of geometry and optical depths and the non-local thermodynamic equilibrium (non-LTE) ionization state of hydrogen and helium into account. They generated 3D tables of radiative losses as a function of T, P, and slab thickness, for H and He. We combine those tables with the radiative losses of the other elements from the CHIANTI database (version 7.1, Landi et al. 2013) and the code interpolates these tables depending on the temperature and pressure of the loop. We refer to the resulting radiative loss function as Λkp. In the following calculations, we only consider the case of slab thickness equal to 200 km. This value is consistent with the dimensions of these loops as inferred from observations (Vourlidas et al. 2010; Hansteen et al. 2014).
There are other calculations of optically thick radiative losses in the literature, such as the more recent work of Carlsson & Leenaarts (2012). This work is dedicated to the radiative cooling and heating only in the chromosphere, by combining detailed, non-LTE radiative transfer calculations and time-dependent 2D MHD simulations. We decided to use the radiative losses calculated by Kuin & Poland (1991), even if they are older because their results are presented in a form that can be easily incorporated in hydrodynamic flux-tube calculations and are expressly aimed at flux-tube modelling. In addition, their calculations are relevant to a broader temperature range more suitable for our calculations.
In Fig. 1 we show the radiative loss function Λkp plotted for different pressure values (log P = −2, −1, 0, 3, red, yellow, green, and blue lines, respectively) and that from the CHIANTI database, version 7.1 (Landi et al. 2013, black line) from which we start to compute the radiative loss function used in this work. They are compared to some of the radiative loss functions used in Paper I, for which we obtained stable cool loops. These include: power-law segments function equal to T2 for log T < 4.95 K and T-1 for log T> 4.95 K (AN, dark grey line, Antiochos & Noci 1986); AN function plus a peak mimicking the H Ly-α losses (dark grey line plus diamond symbols); from the work of Dere et al. (2009) without the H contribution (light grey line). The black and blue lines represent the upper and lower limits for the radiative loss functions, corresponding to the optically thin and optically thick cases, respectively.
 |
Fig. 1 Radiative loss function Λkp plotted for different pressure values (log P = −2, −1,0,3, red, yellow, green, and blue lines, respectively) and radiative loss function from the CHIANTI database, version 7.1 (Landi et al. 2013, black line). Moreover, we plot some of the radiative loss functions used in Paper I: Antiochos & Noci (AN, dark grey line, 1986); AN function plus a peak mimicking the H Ly-α losses (dark grey line plus diamond symbols); from the CHIANTI database, version 6 (Dere et al. 2009), without the H contribution (light grey line). |
2.2. Preliminary considerations on cool loop solutions
Antiochos & Noci (1986) addressed the solutions of the hydrodynamic equations of loops with negligible conductive flux, and studied the properties and conditions of existence of their solutions under specific hypotheses about the radiative loss functions. In particular, they approximated the optically thin function Λ(T) with power-law segments: Λ(T) ~ Ta for T < 0.1 MK, and Λ(T) ~ T− b for T> 0.1 MK, where a and b are positive values. The conditions of existence and stability of these solutions were studied more extensively by e.g. Klimchuk et al. (1987), Cally & Robb (1991). Here we revisit some of those previous analyses, extending the results to consider the specific radiation losses functions we used in our simulations.
Antiochos & Noci (1986) solved the hydrodynamic equations Eqs. (1)–(3), assuming negligible conductive flux. The energy equation, Eq. (3), can then be rewritten as 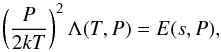 (6)where now we consider the more general case of optically thick radiative loss function, Λ(T,P), while E(s,P) is given by Eq. (5).
(6)where now we consider the more general case of optically thick radiative loss function, Λ(T,P), while E(s,P) is given by Eq. (5).
It is convenient to define the following quantities:  The quantity a(T,P) can be interpreted as the local power-law index of the radiative loss function at a given temperature and pressure. The values of a(T,P) for Λkp in the interval log T = 4.3–5 range from ≈0.5 to ≈2. The values for b(T,P) are substantially smaller, ranging from ≈−0.15 to ≈0.2 around the peak temperature of the Ly-α line.
The quantity a(T,P) can be interpreted as the local power-law index of the radiative loss function at a given temperature and pressure. The values of a(T,P) for Λkp in the interval log T = 4.3–5 range from ≈0.5 to ≈2. The values for b(T,P) are substantially smaller, ranging from ≈−0.15 to ≈0.2 around the peak temperature of the Ly-α line.
Substituting Eqs. (6) and (5) into the momentum equation, Eq. (2), with the above definitions the the equation for T becomes ![\begin{equation} \left[a(T,P)\!+\!\gamma\!-\!2\right] \frac{\mathrm{d}T}{\mathrm{d}s}\! =\! T \frac{1}{f(s)}\frac{\mathrm{d}f(s)}{\mathrm{d}s} + \left[b(T,P)\!+\!2\!-\!\gamma\right] \frac{T_\circ}{H(T_\circ)} \eta(s) , \label{eq:gradT} \end{equation}](/articles/aa/full_html/2015/11/aa26598-15/aa26598-15-eq70.png) (11)where T° is the temperature at the lower boundary of the loop.
(11)where T° is the temperature at the lower boundary of the loop.
The special case a(T,P) = constant = 2 − γ (power-law dependence of Λ(T,P) with temperature, with exponent either 2 or 1, depending on the value of γ), reduces the above differential equation to the simpler expression, i.e. ![\begin{eqnarray*} H(T) = \left[-\frac{1}{f(s)}\frac{\mathrm{d}f(s)}{\mathrm{d}s}\right]^{-1} \left[b(T,P)+2-\gamma\right]\:\eta(s) . \end{eqnarray*}](/articles/aa/full_html/2015/11/aa26598-15/aa26598-15-eq75.png) In this case, any function f(s) that is monotonically decreasing with height produces a loop solution, provided that b(T,P) > −2 + γ (true for Λkp). The case b = 0 and a = 2 is the case we labelled “AN”, and is shown in Fig. 1 with a grey line.
In this case, any function f(s) that is monotonically decreasing with height produces a loop solution, provided that b(T,P) > −2 + γ (true for Λkp). The case b = 0 and a = 2 is the case we labelled “AN”, and is shown in Fig. 1 with a grey line.
In the remainder, we only consider the case f(s) = 1; for simplicity, we further neglect the dependence of Λ on pressure, i.e.: b(T,P) = 0. In this case, Eq. (11) can be integrated to obtain an implicit dependence of T on s, i.e. 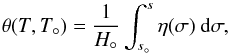 (12)where the function θ(T,T°) is defined as
(12)where the function θ(T,T°) is defined as ![\begin{equation} \theta(T,T_\circ) \equiv \left[\frac{\bar{a}(T,T_\circ)+\gamma-2}{2-\gamma}\right] \left(\frac{T}{T_\circ}-1\right) , \label{eq:theta_T} \end{equation}](/articles/aa/full_html/2015/11/aa26598-15/aa26598-15-eq83.png) (13)while the quantity
(13)while the quantity 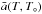 is the “mean” power-law index
is the “mean” power-law index 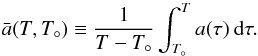 (14)The above equations highlights a first constraint for the existence of this kind of solution:
(14)The above equations highlights a first constraint for the existence of this kind of solution: 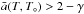 . We mentioned before that for the radiative loss function we are using, we have a< 2 for log T> 4.3, and it is clear that it would be very difficult to obtain cool solutions for the case of uniform heating per unit volume, γ = 0.
. We mentioned before that for the radiative loss function we are using, we have a< 2 for log T> 4.3, and it is clear that it would be very difficult to obtain cool solutions for the case of uniform heating per unit volume, γ = 0.
The upper limit to the loop temperature as mapped by function θ(T,T°) is given by the maximum of 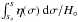 ; in the case of a semicircular loop of radius h, this is h/H°. However, a stronger constraint obviously follows from the consideration that
; in the case of a semicircular loop of radius h, this is h/H°. However, a stronger constraint obviously follows from the consideration that 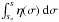 is a monotonically increasing function, whereas θ(T,T°), in general, is not. Single-value solutions are therefore limited to the first local maximum of θ(T,T°), shown in Fig. 2 for the radiative loss function of Fig. 1 in the case γ = 0 and γ = 1. The simple considerations above highlight one of the basic characteristics of cool loop solutions, namely, their strong sensitivity to the details of the heating and of the radiation loss function.
is a monotonically increasing function, whereas θ(T,T°), in general, is not. Single-value solutions are therefore limited to the first local maximum of θ(T,T°), shown in Fig. 2 for the radiative loss function of Fig. 1 in the case γ = 0 and γ = 1. The simple considerations above highlight one of the basic characteristics of cool loop solutions, namely, their strong sensitivity to the details of the heating and of the radiation loss function.
 |
Fig. 2 Function θ(T,T°) for the radiative loss functions shown in Fig. 1 in the case of γ = 0 (left panel) and γ = 1 (right panel). |
3. Results and discussion
We ran numerous simulations, extensively exploring the parameter space, under different initial conditions. We consider a loop in a quasi-static equilibrium state when the plasma velocities are lower than 1−2 km s-1. We took as an initial equilibrium state (t = 0 s) for new simulations some of the cool loops obtained in Paper I, changing only the heating rate and radiative loss function. The list of simulated loops, together with the relevant parameters, is listed in Table 1 (cool loops) and Table 2 (intermediate temperature loops).
Cool loop parameters at the end of the simulations when the loops reach a quasi-static condition (γ = 1).
3.1. Loops from spatially uniform and temporally constant heating rate per unit volume
We start by making simulations with constant heating rate (γ = 0) and using the radiative loss function Λkp. As expected from the discussion in Sect. 2.2, we are not able to obtain stable cool loops since during the simulations, they become all hot (T ~ 8 × 105 K).
As an example, Fig. 3 shows the evolution of the mean temperature, density, and pressure of a loop (hereafter, Loop 0) during a simulation started from a stable cool loop of a high temperature ~1.2 × 104 K (Loop 24 of Table 1 in Paper I), assuming constant heating rate.
Loop 0 stays for ~42 min in a cool state (T < 105 K) even if it is not stable. The mean temperature of the loop oscillates between 1−2 × 104 K (see left panel of Fig. 3) for ~38 min and then in ~4 min reaches much higher values. It becomes a quasi-static coronal loop, after ~2.5 h from the beginning of the simulation, reaching a high temperature of ~8.5 × 105 K. ARGOS allows us to follow the evolution of the loop by storing the loop’s parameters at previously defined time steps. During the four minutes mentioned before, the simulation records three states characterized by maximum temperatures of ~5,7, and 9 × 104 K, progressively. During the evolution of the loop, the maximum temperature is not always localized at s = 0 (loop centre) but also along the loop, i.e. at different values of s.
In Paper I, we obtained indeed quasi-static cool loops by using constant heating rate but we used different radiative loss functions. From Fig. 1, it is clear that Λkp for pressure values characteristic of cool loops (log P ~ −2) is higher than the losses used in Paper I and requires a higher thermal conductive flux from warmer regions to be balanced.
 |
Fig. 3 Evolution of the mean temperature, mean density, and mean pressure of Loop 0, obtained from a simulation starting from a stable cool loop of high temperature ~1.2 × 104 K and constant heating rate per unit volume. |
3.2. Loops from constant heating rate per particle
We perform new simulations with the radiative loss function Λkp, and use constant heating rate per particle, setting γ = 1 in Eq. (5). We list in Table 1 and discuss below a representative selection of cool loops in quasi-static equilibrium that we obtained in these conditions. All loops are obtained starting from four different loops of Paper I (Loops 17, 24, 26, and 27; the initial loop parameters are at the top of each loop group in Table 1) by changing the value of the constant Eh and the radiative loss function. We are able to obtain quasi-static cool loops with maximum temperatures between ~1.5 and 6.2 × 104 K, using Eh in the range 0.2−140 × 10-4 ergs cm-3 s-1. We are not able to obtain cool loops with maximum temperatures in the range 4.3 ≲ log T ≲ 4.5 K, since at those temperatures, a, defined in Eq. (9), is lower than 1 (see Sect. 2.2) because of the change of the slope of Λkp. The cool loops found have the properties analytically predicted by Antiochos & Noci (1986), which are small (L/ 2 = 7.5−8.8 Mm and h = 1.67−3.05 Mm), nearly isobaric, and in approximate balance between the heating rate and radiative losses. They also have low-pressure values in the range predicted by Antiochos & Noci (1986), even if some loops have higher pressure (up to ~7 times) compared with the cool loops obtained in Paper I. In Fig. 4 we plot the behaviour of the loop parameters as well as of the terms of the energy equation for three loops chosen as examples (loops 13, 16, and 22 from top to bottom) at the end of the simulation. The left panels show the temperature (solid line) and pressure (dashed line) profiles as a function of the curvilinear coordinate, s, while the right panels show the radiative losses energy term, n2Λ (crosses), the heating rate, E (solid line), and the divergence of the conductive flux, ∇Fc (asterisks), as a function of the temperature. For all the loops, the pressure is constant along the loop (within 1% above the chromosphere) and the terms n2Λ and E are in approximate balance, while the divergence of the conductive flux is only a small term. From the left panels of Fig. 4 we see that the temperature of the loops starts to increase slowly up to a certain value of s and then increases rapidly up to the maximum temperature value reached by the loop. The values of L/ 2 in Table 1 for these loops include the piece where the temperature rises slowly.
 |
Fig. 4 Top panel, left: temperature (solid line) and pressure (dashed line) as a function of the curvilinear coordinate along the field lines, s. Right: divergence of the conductive flux (asterisks), radiative losses (crosses) and heating rate, E (solid line), as a function of the temperature, for loop 13. Middle and bottom panels: as in the top panels for loops 16 and 22, respectively. |
 |
Fig. 5 Left: temperature (solid line) and pressure (dashed line) as a function of the curvilinear coordinate along the field lines, s. Right: divergence of the conductive flux (asterisks), radiative losses (crosses), and heating rate, E (solid line), as a function of the temperature, for loop 26. |
Using the same radiative loss function and γ = 1, we also obtained quasi-static intermediate-temperature loops (0.1 <T < 0.5 × 105 MK), listed in Table 2. These loops are obtained by starting the simulations from the quasi-static cool loop 17 of Table 1 in Paper I. We show in Fig. 5 the behaviour of the temperature and pressure as a function of s (left) and of the terms of the energy equation as a function of the temperature (right) for loop 26. The divergence of the conductive flux, comparable to the radiative losses, contributes to dissipating the heating in excess.
3.3. Relations between loop parameters and scaling laws
In Fig. 6 we show the relations between the thermodynamic parameters (P, Tmax and L/ 2) and Eh for the loops in Table 1 (loops 1–3 are represented by triangles, loops 4–15 by crosses, loops 16–18 by asterisks, and loops 19–24 by diamonds) and Table 2 (represented by squares). The solid lines in the bottom panels of Fig. 6 represent the “static” scaling laws for coronal loops described by Rosner et al. (1978, hereafter RTV) for different values of L/ 2. The pressure of all cool loops with T < 0.1 MK is proportional to Eh and is dependent on their length and maximum temperatures. Indeed, in the simulations, we increase Eh to obtain higher temperature loops, which also yields higher pressure and longer loops. There is, however, a maximum limit of Eh (different for each initial condition loop) at which, even increasing its value, the loops continue increasing their pressure but not their maximum temperatures (see bottom left panel of Fig. 6).
Intermediate-temperature loops obey the RTV scaling law for coronal loops for temperature and pressure (see bottom left panel of Fig. 6) in the same way as the intermediate-temperature loops we found in Paper I. Observed intermediate-temperature loops do not obey the coronal scaling laws (Brown 1996), but as we already discussed in Paper I, the static model used by Rosner et al. (1978) to derive the relationships between coronal temperature, pressure, length and heating in coronal loops does not seem to predict the physical conditions of these loops accurately. We obtained intermediate-temperature loops with pressures that are 1–2 orders of magnitudes lower than measured in observed loops with the same temperatures (Brown 1996). Loops 25–26 have the correct pressure to fall on the scaling law lines.
 |
Fig. 6 Behaviour of the physical parameters for loops 1–3 (triangles), 4–15 (crosses), 16–18 (asterisks), and 19–24 (diamonds) of Table 1, and loops 25–26 (squares) of Table 2. The solid lines represent the RTV scaling laws for coronal loops for different values of L/2. |
3.4. Calculated DEMs for cool and intermediate-temperature loops
The theoretical DEMs for a single or isolated loop were computed for the quasi-static loops we found according to Spadaro et al. (2003), with a temperature bin of 0.05 dex on a log T scale along the loop 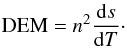 (15)This simplified approach permits us to study the overall properties of the DEM of this class of loops without the need for taking details into account, such as the shape of the loop, geometry of the observations, loop cross-section, etc.
(15)This simplified approach permits us to study the overall properties of the DEM of this class of loops without the need for taking details into account, such as the shape of the loop, geometry of the observations, loop cross-section, etc.
The top panel of Fig. 7 shows the calculated DEMs versus temperature of the quasi-static cool loops 1–3 (solid blue lines), 4–15 (black), 16–18 (red), 19–24 (green) of Table 1, and the quasi-static, intermediate-temperature loops 25–26 (magenta) of Table 2. In Fig. 7 and in the figures that follow, we plot, for comparison, the observed DEMs of the quiet Sun and active region (dashed and dotted lines, respectively), derived using the Vernazza & Reeves (1978) average quiet Sun and active region intensities, and produced as part of the CHIANTI atomic database collaboration (Landi et al. 2013). In the bottom panel of Fig. 7, we plot the total theoretical DEMs for each group of loops obtained starting from a different initial loop condition (distinguished with the different colours). Assuming that the loops are equiprobable (uniformly distributed in log T) and with the same cross-section, we divided the temperature range into bins of amplitude 0.2 dex on a log T scale, and for each bin considered a representative loop, i.e. a loop whose maximum temperature belongs to that bin (our loops are almost isothermal). The total DEMs are obtained by summing the DEMs of these representative loops. When more loops have their maximum temperatures falling in the same bin, we averaged their DEMs.
 |
Fig. 7 Top: calculated DEMs for the quasi-static cool loops 1–3 (solid blue lines), 4–15 (black), 16–18 (red), 19–24 (green) of Table 1, and the intermediate-temperature loops 25–26 (magenta) of Table 2, compared to the DEMs of the quiet Sun (dashed) and active region (dotted) from the CHIANTI atomic database (Dere et al. 2009). Bottom: total DEMs for each group of loops shown in the top panel. |
 |
Fig. 8 Total DEM resulting from the combination of the DEMs of the loops 1–24 and 25–26 (solid line), compared to the DEMs of the quiet Sun (dashed) and active region (dotted) from the CHIANTI atomic database (Landi et al. 2013). |
We obtain cool loops with maximum temperatures covering the temperature range up to the position of its peak (log T ~ 4.8 K), except for the interval 4.3 ≲ log T ≲ 4.5, using Λkp (and γ = 1). By adding the DEMs of the intermediate-temperature loops 25–26, the resulting DEM (black solid line in Fig. 8) follows the shape of the observed DEMs, except for the interval 4.6 ≲ log T ≲ 4.8, where we have an excess of emission due to the high density of the loops with maximum temperatures falling in that interval. Only loops 2 and 3, with maximum temperatures belonging to this interval, have pressures such that their DEMs would resemble the observed DEM, but the solar total pressures at these temperatures and heights, according to the model of Avrett & Loeser (2008), are estimated around 0.1 dyne cm-2, which is much higher than the pressures of loops 2 and 3 and closer to that of all other loops of Table 1. Moreover, the presence of the Ly-α peak at logT ~ 4.2 K and, in particular, the negative slope of the radiative loss function (as explained in Sect. 2.2), produces a relative minimum in all DEMs, which remains in the total DEM (bottom panel of Fig. 7, blue, black, green, or red lines). In the literature, however, there are derived quiet Sun DEMs (Macpherson & Jordan 1999) that exhibit a minimum around logT ~ 4.2 K.
There is a also minimum in the total DEM at around logT = 4.9 K, which is caused by the lack of cool loops with that maximum temperature. This minimum almost corresponds to the maximum of the function Λkp or better to the point where its slope starts to change and we have a< 1. Therefore, the lack of cool loops with maximum temperatures around log T = 4.9 K is not caused by an incomplete exploration of the parameter space, but by the negative slope of Λkp that prevents their formation. However, the shape of the averaged DEM of the loops 25–26, with a flat minimum and a tail extended towards low temperatures, helps fill this gap, improving the agreement with the observed DEM. Since we considered a filling factor of 100% the total DEM has its highest value. The height of the DEM would be lower with a lower filling factor.
We also calculate the emission due to Loop 0, obtained in Sect. 3.1 by performing a simulation using constant heating rate per unit volume (γ = 0) and starting from a quasi-static cool loop of maximum temperature Tmax ~ 1.2 × 104 K. The loop becomes a quasi-static coronal loop, after ~2.5 h from the beginning of the simulation, reaching a high temperature of ~8.5 × 105 K. The evolution of Loop 0’s mean temperature, density and pressure is shown in Fig. 3.
The discussion that follows is based on considering each recorded step of the simulation as a single dynamic loop at a particular instant of its evolution (for example, cooling down or heating up depending whether we keep the heating on or we shut it down). Indeed, we show in Fig. 9 that the DEM of each loop obtained at each time step of the simulation (black dot-dashed lines) during the first 42 min in which Loop 0 evolves keeping its temperature lower than 105 K. The red line is the total DEM obtained by combining all the loops as already explained. Another possible way to calculate the total DEM is described in Susino et al. (2010). They simulated the DEM of a multi-stranded loop by averaging instantaneous DEMs calculated at n different times, randomly selected throughout the simulation. This approach is based on the assumption that the states of the model at n randomly selected times can be used to describe the behaviour of n independent strands observed at the same time. In this analysis, we do not want to concentrate on how the loops are obtained, rather we only want to show what the emission measure produced by this particular distribution of loops looks like. The total DEM resembles the observed DEM very well and we do not have any of the problems observed with the total DEM obtained from static loops. We are also able to obtain loops with maximum temperatures that are prohibitive for the quasi-static loops (log T ~ 4.2 and ~4.9 K).
 |
Fig. 9 Calculated DEM of Loop 0 over the first 42 min of the simulation (red line). This DEM is obtained by averaging the DEM of each loop obtained at each time step of the simulation (black dash-dotted lines), and is compared to the DEMs of the quiet Sun (green dashed line) and active region (green dotted line) from the CHIANTI atomic database (Landi et al. 2013). |
Obviously, the resulting DEM depends on the assumption we are making, and, in particular, on the number of the loops that fall in a certain temperature interval and/or filling factor, and in addition, the resulting DEM depends on the distribution of the loops, and, ultimately, on the distribution of the heating rates (Antiochos & Noci 1986).
3.5. Non-equilibrium phase of Loop 0
We have additionally examined the behaviour of the vertical component of velocites in Loop 0. At each time step of the simulation we computed the mean value weighted by the DEM (e.g. Spadaro et al. 2003) of the vertical component of velocities in the temperature bins of 0.20 dex in log T, considering the two halves of the loop separately. The temperature bins chosen are centred at log T = 4.1, 4.3, 4.5, 4.7, and 4.9. The last two bins are populated only towards the end of the transient phase. We found that in the transient phase we are considering, the vertical velocities are of the same magnitude and sign at both footpoints.
During the transient phase, the mean vertical component of velocities averaged on the whole loop for the different temperature bins appear in a few bursts lasting 1−4 min and reaching values of the order of 5−10 km s-1 or more in absolute value. After the first 10−15 min of the simulation, the velocities in these bursts are systematically negative, adopting a sign convention that corresponds to negative Doppler shifts (redshifts). Considering the episodic character of these Doppler shifts, the average values in each temperature bin over the 42 min interval correspond to redshifts of the order of −1 km s-1 or less. These redshifts, however, are limited to the range of temperatures covered by the transient phase (see Fig. 9). At later times, as the loop reaches near coronal temperatures, the vertical velocities start to oscillate between blue- and redshifts, with decreasing amplitudes until a quasi-static situation is attained. Peter & Judge (1999) report observed values of about −5 km s-1 in the range log T = 4.5−5, with one exception of nearly zero wavelength shift. These redshifts are higher than our average redshifts, even though it should be noted that there are only a few measurements in the temperature range best covered by the transient phase of the simulations (log T < 4.6). Their Table 3 lists only three lines nominally forming at or below log T = 4.7, i.e. He i 584 Å, C ii 1036 Å and C ii 1037 Å. It is encouraging, however, that our results for transient phase of Loop 0 show a predominance of redshifts, although this result should be confirmed and extended with simulations spanning a variety of loop parameters.
4. Conclusions
We have studied the conditions of existence and stability of cool loops with T ≲ 0.1 MK through hydrodynamic simulations, introducing an optically thick radiative loss function. We analysed two different cases, i.e. the constant heating rate either per volume or per particle. We found that it is possible to obtain quasi-static (velocities lower than 1 km s-1) cool loops, as predicted by Antiochos & Noci (1986), only by using a constant heating rate per particle, unlike the previous work in which we used different radiative loss functions, with a less pronounced Ly-α peak.
We also obtained quasi-static loops with maximum temperatures in the range 1−5 × 105 K, using the same optically thick radiative loss function. These loops are smaller with respect to coronal loops, but have different characteristics compared to the static cool loops proposed by Antiochos & Noci (1986) and others. These loops obey the scaling laws for coronal loops, contrary to results of previous works based on observational data (e.g. Brown 1996). The loops obtained have indeed low pressures that make their parameters obey the RTV scaling laws, but these pressures are 1–2 orders of magnitudes lower than those estimated from observations (Brown 1996).
We examined and discussed the quasi-static solutions we found and analysed the contributions of the cool and intermediate-temperature loops to the TR DEM. We find that a combination of these loops, precisely because of their computed pressures and assuming that they were uniformly distributed, can yield a DEM with a shape that is not too far from the observed DEM for log T < 4.3 and log T> 5.0. However, there is a pronounced excess emission due to the high density of the cool loops between 4.6 ≲ log Tmax ≲ 4.8 and a deficit around log T ~ 4.4 (see Sect. 2.2).
We also showed a dynamic loop (Loop 0) obtained by performing a simulation using constant heating rate per unit volume and starting from a quasi-static cool loop of maximum temperature Tmax ~ 1.2 × 104 K. The loop becomes a quasi-static “coronal” loop, after ~2.5 h from the beginning of the simulation, reaching a high temperature of ~8.5 × 105 K. While the final state does not reproduce the observed DEM for temperatures lower than 105 K, the average DEM of Loop 0, interpreted as a combination of a set of evolving dynamic loops, reproduces the observed DEM very well. The whole simulation that we called Loop 0 can also be considered the evolution of a single loop emerging from lower atmospheric layers to the corona. The dimensions of this emerging loop, its initial and final temperatures, and the timescale of the event are comparable to the observations and simulations of an emerging magnetic loop, from photosphere to low corona, as that described in the work of Guglielmino et al. (2010).
In principle, cool and intermediate-temperature loops could be observed with current telescopes, but to resolve them in all their temperature extension, we would need multi-temperature observations, i.e. different UV lines formed at temperatures between 0.01−1 MK with resolution of at least 1′′. Highly dynamical cool, low-lying loops have recently been reported by Hansteen et al. (2014) using observations obtained with the IRIS spacecraft (De Pontieu et al. 2014). These kinds of loops are usually observed as time-dependent, short-lived segments, and not as complete loops. This could depend on the fact that those loops extend over a range of temperatures not entirely covered by the IRIS spectral lines. These observations suggest that the class of loops reported by Hansteen et al. (2014) is related to short-lived, episodic heating, and “temporary” loops would therefore be created and then rapidly collapse. Hansteen et al. also stress that these are high-density structures and postulate that these loops follow a near-horizontal magnetic field; hence, they are low-lying.
Based on the work of Antiochos & Noci (1986) and Paper I, we expect cool loops to be low-lying even though we focus our attention on steady-state heating. In this work, we confirm that the existence, stability, and properties of cool loops greatly depend on the details of the radiative loss function. We also find that considering a more realistic function, the derived DEMs depart from the observations (see Fig. 7). On the other hand, transient loops, like Loop 0, display characteristics that are appealingly closer to observations, and this class of transient loops does not necessarily imply impulsive heating. The similarity between the DEM of the transient phase of Loop 0 and the observed DEM, together with the new observations of dynamic small scale structures on the Sun, suggest that we focus our attention on simulating dynamic cool loops. In addition, we emphasize that this dynamical loop is characterized, in its non-equilibrium phase, by the predominance of redshifts at its footpoints appearing in bursts of the order of −5−−10 km s-1 and on average of the order of −1 km s-1 or less over the 42 min of the transient phase. Redshifts of this magnitude could be marginally consistent with existing spectroscopic observations of redshifts in the transition region in the relative low-temperature range best covered by the transient phase of the simulation (log T < 4.6). The episodic nature of these redshifts could be investigated by IRIS time-resolved, spectroscopic observations. We also plan to further investigate this intriguing result with more simulations spanning a wider range of loop parameters.
With this perspective, an important point to consider is the effect of partial ionization of hydrogen on the hydrodynamics of the loop plasma. The equations for mass, momentum, and energy conservation we adopt are for a fully ionized hydrogen plasma. This assumption is well verified in our cool loops, which are characterized by plasma pressures in the range 10-2−10-1 dyne cm-2, according to the calculations reported in Table 3 of Kuin & Poland (1991). In only three cases, the pressure in the loop is above 10-1 dyne cm-2, resulting in a significant fraction of neutral hydrogen just below 2 × 104 K (see Kuin & Poland 1991). The fraction increases and becomes important even at higher temperatures as the pressure becomes higher. Since Hansteen et al. (2014) stress that the episodically heated loops they observe are high-density structures, the simulation of dynamic cool loops should take the fraction of neutral hydrogen in the hydrodynamic equations into account.
Acknowledgments
This work was supported by the ASI/INAF contracts I/013/12/0 for the program “Solar Orbiter – Supporto scientifico per la realizzazione degli strumenti METIS e SWA/DPU nelle fasi B2-C”.
References
- Antiochos, S. K., & Noci, G. 1986, ApJ, 301, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Antiochos, S. K., MacNeice, P. J., Spicer, D. S., & Klimchuk, J. A. 1999, ApJ, 512, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Avrett, E. H., & Loeser, R. 2008, ApJS, 175, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, S. F. 1996, A&A, 305, 649 [NASA ADS] [Google Scholar]
- Cally, P. S., & Robb, T. D. 1991, ApJ, 372, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Carlsson, M., & Leenaarts, J. 2012, A&A, 539, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Pontieu, B., Title, A. M., Lemen, J. R., et al. 2014, Sol. Phys., 289, 2733 [NASA ADS] [CrossRef] [Google Scholar]
- Dere, K. P. 1982, Sol. Phys., 75, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Dere, K. P., Landi, E., Young, P. R., et al. 2009, A&A, 498, 915 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dowdy, J. F., Jr. 1993, ApJ, 411, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Dowdy, J. F., Jr., Rabin, D., & Moore, R. L. 1986, Sol. Phys., 105, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Durrant, C. J., & Brown, S. F. 1989, PASA, 8, 137 [NASA ADS] [Google Scholar]
- Feldman, U. 1983, ApJ, 275, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Feldman, U., Dammasch, I. E., & Wilhelm, K. 2001, ApJ, 558, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Guglielmino, S. L., Bellot Rubio, L. R., Zuccarello, F., et al. 2010, ApJ, 724, 1083 [Google Scholar]
- Hansteen, V., De Pontieu, B., Carlsson, M., et al. 2014, Science, 346, 1255757 [CrossRef] [Google Scholar]
- Judge, P., & Centeno, R. 2008, ApJ, 687, 1388 [NASA ADS] [CrossRef] [Google Scholar]
- Karpen, J. T., Antiochos, S. K., Hohensee, M., Klimchuk, J. A., & MacNeice, P. J. 2001, ApJ, 553, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Klimchuk, J. A., Antiochos, S. K., & Mariska, J. T. 1987, ApJ, 320, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Korendyke, C. M., Vourlidas, A., Cook, J. W., et al. 2001, Sol. Phys., 200, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Kuin, N. P. M., & Poland, A. I. 1991, ApJ, 370, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Landi, E., Young, P. R., Dere, K. P., et al. 2013, ApJS, 763, 86 [NASA ADS] [CrossRef] [Google Scholar]
- MacNeice, P. J., Olson, K. M., Mobarry, C., de Fainchtein, R., & Packer, C. 2000, Comput. Phys. Commun., 126, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Macpherson, K. P., & Jordan, C. 1999, MNRAS, 308, 510 [NASA ADS] [CrossRef] [Google Scholar]
- Patsourakos, S., Gouttebroze, P., & Vourlidas, A. 2007, ApJ, 664, 121 [Google Scholar]
- Peter, H., & Judge, P. 1999, ApJ, 522, 1148 [NASA ADS] [CrossRef] [Google Scholar]
- Peter, H., Gudiksen, B. V., & Nordlund, A. 2004, ApJ, 617, 85 [Google Scholar]
- Peter, H., Gudiksen, B. V., & Nordlund, A. 2006, ApJ, 638, 1086 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Reale, F. 2010, Liv. Rev. Sol. Phys., 11, 4 [Google Scholar]
- Rosner, R., Tucker, W. H., & Vaiana, G. S. 1978, ApJ, 220, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Sasso, C., Andretta, V., Spadaro, D., & Susino, R. 2012, A&A, 537, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spadaro, D., Lanza, A. F., Lanzafame, A. C., et al. 2003, ApJ, 582, 486 [NASA ADS] [CrossRef] [Google Scholar]
- Susino, R., Lanzafame, A. C., Lanza, A. F., & Spadaro, D. 2010, ApJ, 709, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Vernazza, J. E., & Reeves, E. M. 1978, ApJS, 37, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Vourlidas, A., Sanchez Andrade-Nuño, B., Landi, E., et al. 2010, Sol. Phys., 261, 53 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Cool loop parameters at the end of the simulations when the loops reach a quasi-static condition (γ = 1).
All Figures
 |
Fig. 1 Radiative loss function Λkp plotted for different pressure values (log P = −2, −1,0,3, red, yellow, green, and blue lines, respectively) and radiative loss function from the CHIANTI database, version 7.1 (Landi et al. 2013, black line). Moreover, we plot some of the radiative loss functions used in Paper I: Antiochos & Noci (AN, dark grey line, 1986); AN function plus a peak mimicking the H Ly-α losses (dark grey line plus diamond symbols); from the CHIANTI database, version 6 (Dere et al. 2009), without the H contribution (light grey line). |
| In the text | |
 |
Fig. 2 Function θ(T,T°) for the radiative loss functions shown in Fig. 1 in the case of γ = 0 (left panel) and γ = 1 (right panel). |
| In the text | |
 |
Fig. 3 Evolution of the mean temperature, mean density, and mean pressure of Loop 0, obtained from a simulation starting from a stable cool loop of high temperature ~1.2 × 104 K and constant heating rate per unit volume. |
| In the text | |
 |
Fig. 4 Top panel, left: temperature (solid line) and pressure (dashed line) as a function of the curvilinear coordinate along the field lines, s. Right: divergence of the conductive flux (asterisks), radiative losses (crosses) and heating rate, E (solid line), as a function of the temperature, for loop 13. Middle and bottom panels: as in the top panels for loops 16 and 22, respectively. |
| In the text | |
 |
Fig. 5 Left: temperature (solid line) and pressure (dashed line) as a function of the curvilinear coordinate along the field lines, s. Right: divergence of the conductive flux (asterisks), radiative losses (crosses), and heating rate, E (solid line), as a function of the temperature, for loop 26. |
| In the text | |
 |
Fig. 6 Behaviour of the physical parameters for loops 1–3 (triangles), 4–15 (crosses), 16–18 (asterisks), and 19–24 (diamonds) of Table 1, and loops 25–26 (squares) of Table 2. The solid lines represent the RTV scaling laws for coronal loops for different values of L/2. |
| In the text | |
 |
Fig. 7 Top: calculated DEMs for the quasi-static cool loops 1–3 (solid blue lines), 4–15 (black), 16–18 (red), 19–24 (green) of Table 1, and the intermediate-temperature loops 25–26 (magenta) of Table 2, compared to the DEMs of the quiet Sun (dashed) and active region (dotted) from the CHIANTI atomic database (Dere et al. 2009). Bottom: total DEMs for each group of loops shown in the top panel. |
| In the text | |
 |
Fig. 8 Total DEM resulting from the combination of the DEMs of the loops 1–24 and 25–26 (solid line), compared to the DEMs of the quiet Sun (dashed) and active region (dotted) from the CHIANTI atomic database (Landi et al. 2013). |
| In the text | |
 |
Fig. 9 Calculated DEM of Loop 0 over the first 42 min of the simulation (red line). This DEM is obtained by averaging the DEM of each loop obtained at each time step of the simulation (black dash-dotted lines), and is compared to the DEMs of the quiet Sun (green dashed line) and active region (green dotted line) from the CHIANTI atomic database (Landi et al. 2013). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


