| Issue |
A&A
Volume 583, November 2015
|
|
|---|---|---|
| Article Number | A78 | |
| Number of page(s) | 10 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201425594 | |
| Published online | 30 October 2015 | |
Modeling of magnetic cloud expansion
1
Astronomical Institute of the Czech Academy of
Sciences, Boční II
1401, 141 00
Praha 4, Czech Republic
e-mail: vandas@asu.cas.cz
2
University Park, LSC, Houston, TX
77070,
USA
3
Physics Department, Nuclear and Particle Physics Section,
University of Athens, 15771
Ilissia,
Greece
Received: 29 December 2014
Accepted: 8 August 2015
Aims. Magnetic clouds are large interplanetary flux ropes that propagate in the solar wind from the Sun and that expand during their propagation. We check how magnetic cloud models, represented by cylindrical magnetic flux ropes, which include expansion, correspond to in situ observations.
Methods. Spacecraft measurements of magnetic field and velocity components inside magnetic clouds with clearly expressed expansion are studied in detail and fit by models. The models include expanding cylindrical linear force-free flux ropes with circular or elliptic cross sections.
Results. From the period of 1995–2009, 26 magnetic clouds were fit by the force-free model of an expanding circular cylindrical flux rope. Expansion velocity profiles qualitatively correspond to model ones in the majority of cases (81%) and quantitatively in more than half of them (58%). In four cases an elliptic cross section significantly improved a match between observed and modeled expansion velocity profiles.
Conclusions. Analysis of velocity components tests magnetic cloud models more strictly and may reveal information on magnetic cloud shapes.
Key words: solar wind / magnetic fields / magnetohydrodynamics (MHD)
© ESO, 2015
1. Introduction
Magnetic clouds were discovered in late 1970s (Burlaga et al. 1981) and defined as special regions in the solar wind with the following properties (Burlaga 1991): the magnetic field is higher and proton temperature lower than in the background, and the magnetic field vector smoothly rotates through a large angle (~180°). These properties can be easily seen in Fig. 1, which depicts solar wind observations during the passage of a magnetic cloud, which followed after a big solar eruption, the so-called Bastille Day Event (e.g. Lepping et al. 2001; Mulligan et al. 2001; Watari et al. 2001). The duration of magnetic cloud events is on the order of one day, which implies that their sizes are on the order of 0.1 au. The specific behavior of the magnetic field and the decrease in temperature led to the supposition that magnetic clouds were magnetically isolated bodies, i.e., large interplanetary flux ropes propagating in the solar wind.
In the beginning, magnetic clouds were modeled by force-free configurations (Goldstein 1983; Marubashi 1986; Burlaga 1988), because they have very low plasma β, so magnetic field dominates. These configurations were quite successful in describing magnetic field rotation within magnetic clouds. Later, non-force-free models were also developed (e.g., Mulligan & Russell 2001; Hidalgo et al. 2002; Hu & Sonnerup 2002; Hidalgo & Nieves-Chinchilla 2012; Hidalgo 2013, 2014) to account for asymmetric magnetic field profiles or plasma quantities. In the present analysis, we deal with linear force-free models.
Also from the beginning, it has been argued that magnetic clouds expanded during their propagation in the inner heliosphere (Burlaga et al. 1981; Burlaga 1991). This followed from their presumably originating at the Sun, but near the Earth they were much larger than the Sun. Expansion manifests itself as a smooth decrease in the solar wind velocity during the passage of a magnetic cloud (Fig. 1). Low proton temperature is also understood as a result of expansion (Burlaga 1991). Ivanov et al. (1993) attempted to interpret the velocity profiles as a combined effect of expansion and deceleration by the ambient medium; they found that both effects are present. The first modeling of magnetic cloud expansion was done by Osherovich et al. (1993) and later followed by others (e.g., Marubashi 1997; Hidalgo 2003; Vandas et al. 2006; Marubashi & Lepping 2007). These models try to fit velocity magnitude profiles in magnetic clouds, in addition to profiles of magnetic field components. Wu et al. (2002) did the first investigation of velocity vectors in magnetic clouds observed near the Earth. In their statistical study, they found a clear cloud expansion only along the Sun-Earth line. Vandas et al. (2005b) presented the first comparison of velocity vectors between observations and their model. It was concluded that velocity component profiles in magnetic clouds had regular patterns, but fits with the model were not satisfactory.
Magnetic cloud expansion causes a distortion of the cloud magnetic field profile, namely a shift of the magnetic field maximum toward the cloud leading boundary (see Fig. 1). Statistical analysis by Lepping et al. (2003) shows reasonable agreement between this shift and the assumption of a self-similar expansion. Hidalgo (2003) studied distortion of the magnetic field profile due to expansion in his non-force-free model.
 |
Fig. 1 Magnetic cloud of July 15–16, 2000 observed near the Earth. Measurements (hourly averages) of the solar wind quantities are plotted: magnetic field magnitude B and components Bx, By, and Bz in the geocentric solar ecliptic (GSE) system, velocity V, density N, and proton temperature T. Estimated cloud boundaries are drawn by the vertical dashed lines. Observations are plotted by the thin line, and the thick line is a fit by a model (static circular cylindrical flux rope). More details on it are given in Sect. 2. The cloud is numbered 46.0 in Table 1. |
During recent years we have observed an increasing interest in the magnetic cloud expansion. Lepping et al. (2007) conclude that the enhancement of the magnetic cloud front field is mainly due to compression and a lesser effect to expansion. The expansion velocity is usually well below the local Alfvén speed (Lepping et al. 2008). Dasso et al. (2007) used a self-similar expansion to model an observation of a magnetic cloud. Démoulin et al. (2008) and Démoulin & Dasso (2009) theoretically studied the causes of magnetic cloud expansion and concluded that the radial expansion of flux ropes is close to self-similar, resulting in a nearly linear radial velocity profile, and the expansion rate is proportional to the radius. Nakwacki et al. (2008) compared large scale MHD quantities (helicity, magnetic flux, and magnetic energy) in static or expanding flux ropes, and Nakwacki et al. (2011) investigated changes in these quantities caused by expansion for a particular magnetic cloud and found agreement with theoretical predictions. Lynnyk & Vandas (2009, 2010) statistically studied how incorporation of expansion into a model improved fits of magnetic-field components in magnetic clouds. Gulisano et al. (2010, 2012) investigated the expansion rates of magnetic clouds throughout the heliosphere and found that the self-similar expansion and its distance dependence is consistent with theoretical expectations. Dalakishvili et al. (2011) assumed a self-similar expansion of magnetic clouds and derived analytical solutions of the cloud evolution; they show that their solutions are consistent with results from (more general) numerical simulations.
In the present paper we investigate the behavior of velocity components in magnetic clouds in more detail. Magnetic clouds for this study were taken from the magnetic cloud table published on the World Wide Web1. It is referred to as the www magnetic cloud table in the present paper.
2. Models and a fitting procedure
Burlaga (1988) suggested using a simple model of a linear force-free field in a cylindrical flux rope, given by Lundquist (1950). In cylindrical coordinates it reads as  This solution solves the force-free equation curlB = αB, α = const., Jn are the Bessel functions of the first kind, B0 determines the level of the magnetic field, and α is related to the flux rope size (radius). The success of this solution at describing magnetic field rotation satisfactorily in magnetic cloud observations caused this model to be widely used to fit magnetic cloud events (e.g., Lepping et al. 1990, 2006, 2008) until it could be regarded as a standard model.
This solution solves the force-free equation curlB = αB, α = const., Jn are the Bessel functions of the first kind, B0 determines the level of the magnetic field, and α is related to the flux rope size (radius). The success of this solution at describing magnetic field rotation satisfactorily in magnetic cloud observations caused this model to be widely used to fit magnetic cloud events (e.g., Lepping et al. 1990, 2006, 2008) until it could be regarded as a standard model.
Vandas & Romashets (2003) generalized this model to account for magnetic cloud oblateness. They have found a linear force-free field in a cylinder with an elliptic cross section. In elliptic cylindrical coordinates, it reads as 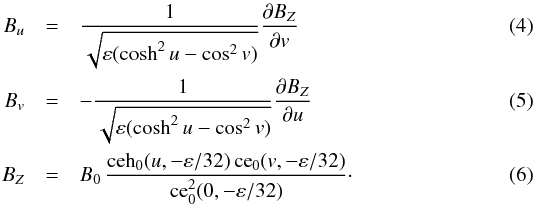 Elliptic cylindrical coordinates u, v, and Z are related to Cartesian ones by
Elliptic cylindrical coordinates u, v, and Z are related to Cartesian ones by  where c is a parameter related to oblateness (
where c is a parameter related to oblateness (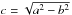 , with a and b being the major and minor semi-axes of a generating ellipse, respectively; contours with u = const. are ellipses in the xy plane). The parameter ε = (αc)2 is related to the size and oblateness of the flux rope, ce0 and ceh0 are angular and radial even Mathieu functions of zero order, and B0 determines the level of the magnetic field.
, with a and b being the major and minor semi-axes of a generating ellipse, respectively; contours with u = const. are ellipses in the xy plane). The parameter ε = (αc)2 is related to the size and oblateness of the flux rope, ce0 and ceh0 are angular and radial even Mathieu functions of zero order, and B0 determines the level of the magnetic field.
The component BZ reaches its maximum at the axis (Z) in both solutions. Usually the boundary of a magnetic cloud is taken at r0 (Burlaga 1988; Lepping et al. 1990) or u0 (Vandas & Romashets 2003; Vandas et al. 2005a) where BZ reaches zero, i.e. where functions J0 or ceh0 have their first roots. It relates α to the size of the magnetic cloud. For the Lundquist solution, it is α ≈ 2.4048 /r0 where the number stands for the first root of J0. For the elliptic flux rope, u0 defines the ellipse with the semi-axes a and b, coshu0 = a/c, and α is determined from an implicit equation and depends not only on the size of the flux rope, but also on its oblateness (Vandas & Romashets 2003). We use this location of the boundary in the present analysis.
To model magnetic cloud expansion, Vandas et al. (2006) used a heuristic approach and replaced the constant parameters α and B0 in both solutions by time-dependent ones: 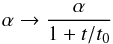 (10)and
(10)and 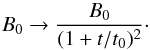 (11)These replacements are based on the asymptotic behavior of an exact solution of MHD equations for a circular cylindrical flux rope with self-similar expansion, as found by Shimazu & Vandas (2002; see also Berdichevsky et al. 2003) and inspired by works of Osherovich et al. (1993, 1995) (who used a less general solution, resulting in a slightly different time dependence in their modification of the Lundquist solution). According to the asymptotic behavior, it is assumed that the flux rope is radially expanding with velocity
(11)These replacements are based on the asymptotic behavior of an exact solution of MHD equations for a circular cylindrical flux rope with self-similar expansion, as found by Shimazu & Vandas (2002; see also Berdichevsky et al. 2003) and inspired by works of Osherovich et al. (1993, 1995) (who used a less general solution, resulting in a slightly different time dependence in their modification of the Lundquist solution). According to the asymptotic behavior, it is assumed that the flux rope is radially expanding with velocity 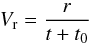 (12)where r is the radial distance from the flux rope axis (Z) in both solutions. Such a form ensures that the oblateness of the flux rope is conserved during expansion. The field is time dependent but force-free at any instant. A new parameter, the expansion time t0, is introduced.
(12)where r is the radial distance from the flux rope axis (Z) in both solutions. Such a form ensures that the oblateness of the flux rope is conserved during expansion. The field is time dependent but force-free at any instant. A new parameter, the expansion time t0, is introduced.
When comparing the standard model (Lepping et al. 1990) with observations, the model and its relationship to a spacecraft passage is described by eight parameters: ϑc, φc, r0, B0, h, Vsw, tm, and p. It is assumed that a cylindrical flux rope with the radius r0 is conveyed by the solar wind with velocity Vsw. The magnetic field in the flux rope is static and described by the Lundquist solution (1)–(3) with B0 and α = 2.41h/r0, where h = ± 1 is the magnetic field chirality. The orientation of the flux rope axis is given by two angles, the inclination ϑc and azimuth φc in the ecliptic plane. Usually the geocentric solar ecliptic (GSE) system (x, y, z) is used for observations near the Earth. The last parameter p, the impact factor, is related to a minimum approach of a spacecraft to the cloud axis, and it is described in Appendix A. If p = 0, it is a central crossing, so the spacecraft crossed the axis. The time of the minimum approach is given by tm.
If the flux rope oblateness is included in the model, Eqs. (4)–(6), two additional parameters appear: oblateness a/b and the angle ψc, which determines the orientation of the semi-axis b. The angle ψc is the azimuthal angle between the x axis and the projection of the semi-axis b to the ecliptic (xy) plane. To maintain correspondence with the standard model, we define r0 ≡ b, which also enables the same definition of p to be kept (see Appendix A). When a/b → 1 (and ψc arbitrary), the model converges to the standard model. Because this limit is difficult to calculate numerically, and calculations using Eqs. (4)–(6) are much more computationally expensive than formulae (1)–(3), we maintain two models separately with (i) circular and (ii) elliptic cross sections.
The models with expansion (Fig. 2) introduce the last parameter, the expansion time t0. Modeled velocity magnitude profile during a passage of an expanding flux rope is shown in Fig. 2b and yields a nearly linear decrease. Nearly linear decreases in velocity profiles are common in magnetic cloud observations (see Fig. 1). The expansion time t0 is estimated from the velocity slope. It determines instant values of α and B0 (10)–(11) in both solutions (1)–(6), the radial velocity profile by Eq. (12), and instant flux rope radius/semi-axes (with help of the other parameters in the latter case). When t0 → ∞, the models converge to the static ones, either circular (standard) or elliptic.
 |
Fig. 2 a) Spacecraft crossing an expanding circular flux rope. The spacecraft trajectory is drawn by a straight thin line, the boundary of the cloud/rope at the spacecraft entry (leading boundary) is the solid-line circle, the boundary at the spacecraft exit (trailing boundary) is the dashed-line circle. The bullet indicates the position of the rope axis. b) The ambient solar wind and expansion (Vr) velocities add at the leading boundary and subtract at the trailing one, which results in a decrease in observed velocity magnitude; the vertical lines indicate the flux rope boundaries, and their line types match the ones in panel a). c) Radial velocity Vr is highest near the boundary and drops to zero at the axis. It yields a characteristic “U” shape profile in the modeled Vr. |
Before making a fit, boundaries of a magnetic cloud must be identified or estimated from observed profiles of solar wind quantities, which are times t1 and t2 of the spacecraft entry and exit of the magnetic cloud, respectively (see the dashed vertical lines in Fig. 1). There are many discussions of how to determine magnetic cloud boundaries (see Burlaga 1991; Lepping et al. 1990, 2006; Gosling 1990; Crooker et al. 1990; Wei et al. 2003), but no general procedure or consensus exists. For fitting purposes, the boundaries usually determine the time interval where solar wind quantities vary sufficiently smoothly and fit the definition of a magnetic cloud. Subsequently, the interval may be slightly adjusted to get the best fit possible. It follows from the above description that determining the cloud boundaries includes a subjective element. In the present analysis we take the times t1 and t2 from the www magnetic cloud table (i.e., the start and end times in this table set to whole hours, since we use hourly data). In a few cases the boundaries were shifted by a few hours to exclude a peculiar velocity behavior or to obtain a significantly better fit (most notably in Case 46.0, Fig. 1, as explained below), that is, to have the times t1 and t2 closer to the same-magnetic-surface crossings (since the cloud boundary represents a magnetic surface).
Eleven parameters of the models in total were mentioned above (ϑc, φc, r0, B0, h, Vsw, tm, p, a/b, ψc, and t0); some of them are given in advance and some are free parameters to be searched by a fitting procedure. We search free parameters by a non-linear mean square fitting. Powell’s method (Press et al. 2002) is used to minimize a difference between observed and modeled quantities, that is to say, 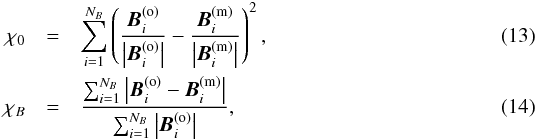 and
and 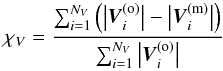 (15)are minimized. The superscripts (o) and (m) denote observed and modeled values, respectively; NB and NV are numbers of observed values of the magnetic field components and velocity magnitude, respectively. This can be NB ≠ NV if some observations are missing or not reliable.
(15)are minimized. The superscripts (o) and (m) denote observed and modeled values, respectively; NB and NV are numbers of observed values of the magnetic field components and velocity magnitude, respectively. This can be NB ≠ NV if some observations are missing or not reliable.
We have five free parameters entering the automatic fitting procedure in the present analysis, ϑc, φc, p, B0, and Vsw. The fitting procedure needs initial guesses for them. A guess of the axis orientation is determined from the standard variance analysis of the magnetic field vectors (Lepping et al. 1990). The parameters B0 and Vsw are taken as the maximum observed field magnitude and the average solar wind velocity within the cloud interval ⟨t1,t2⟩, respectively, and p is set to 0.5. The t0 is calculated from the velocity magnitude slope in the beginning of the fitting procedure (and does not change). In principle, t0 could be included as a free parameter in the fitting procedure, but in practice this approach has not yielded the desired results. Magnetic field component profiles are not very sensitive to oblateness (Vandas et al. 2005a), so we try several values of it (e.g., 1.5, 2, 3, 5) and select one with minimum χB (and not significantly worse χV). For simplicity, we set ψc = 0. The chirality h has only two values, and they can be checked subsequently. Usually one fit is much better, so the choice is evident. However, in the present analysis, we took h values from the www magnetic cloud table. The initial (at t = t1) radius r0 (or b) and the time tm of the minimum axis approach are determined from the geometric situation using t1, t2, and above given parameters (for the standard model, tm = (t1 + t2)/2). Here our approach is different from that of Lepping et al. (1990, 2006), who regard r0 and tm as free parameters. Then the boundaries of a cloud may not coincide with t1 and t2, they may be inside or outside the interval ⟨t1,t2⟩, and the measure of coincidence is given by the asymmetry factor in the www magnetic cloud table. The factor is zero for a perfect coincidence. We regard t1 and t2 as times of (model) boundary crossings; i.e., model BZ is zero there, as discussed above. Other differences concern the solar wind velocity, Vsw, and B0; they are searched for in our case, but the former quantity is prescribed and the latter one determined after the fitting procedure from minimum mean square differences of magnetic field magnitudes in the cited works.
Our fitting procedure runs in three steps: (i) ϑc, φc, and p (three free parameters) are determined via χ0 minimization; B0 is determined by a least square method from 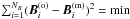 ; (ii) B0 is added (four free parameters) for determination and χB minimized; (iii) Vsw is added (five free parameters) for determination and χB + χV minimized. Steps (i)–(iii) are repeated several times to check convergence.
; (ii) B0 is added (four free parameters) for determination and χB minimized; (iii) Vsw is added (five free parameters) for determination and χB + χV minimized. Steps (i)–(iii) are repeated several times to check convergence.
Figure 1 shows a fit of the magnetic cloud by the standard (static) model (i.e., it has a/b = 1 and t0 → ∞ within our model parameters). The fit yielded ϑc = 13°, φc = 41°, and p = −0.27. Passage of the model flux rope by a constant velocity (Vsw) is indicated by a horizontal line in the velocity plot. While matches of the magnetic field components are plausible, it is not so for the magnetic field magnitude. The modeled B profile is symmetric (intrinsic feature of the model), but the measured profile is highly asymmetric, because it is affected by a strong expansion of the magnetic cloud. And this type of disagreement is the reason expansion is incorporated into models. We later show how the model with expansion can improve the fit shown in Fig. 1. The modeled B profile is symmetric and centered within the cloud interval, because times t1 and t2 are the model cloud boundaries. The meaning of a (non-zero) asymmetry factor in the www magnetic cloud table is that the modeled B profile is symmetric, but its maximum is shifted in time within the cloud interval ⟨t1,t2⟩.
The magnetic field components (such as in Fig. 1) are compared with models in numerous analyses of magnetic cloud observations. More rarely, the velocity magnitude profiles are also compared. In the present analysis, the models further specify the radial component of the velocity, Vr, defined in Eq. (12); the other two components are set to zero. Figure 2c shows how a model profile of Vr looks like with its “U” shape. We investigate to what extent modeled and observed radial velocities are similar. The use of “observed” is somewhat inexact because radial velocities are not directly measured but are instead calculated from observed velocity components, but the calculations depend on geometric situation drawn from a model, so the observed radial velocities are not strictly model independent. Nevertheless, radial velocities usually represent small fractions of the total velocities, so their comparison is a stricter test of the models than only a comparison of the velocity magnitude would be.
The first comparison of modeled and observed radial velocity profiles has been presented by Vandas et al. (2009), who used the circular model with expansion. Here we make a more comprehensive analysis and examine whether the introduction of oblateness into the model can improve radial-velocity profile matches.
 |
Fig. 3 Histograms of magnetic clouds from the www magnetic cloud table. a), b) The magnetic clouds sorted by the velocity difference ΔV, with a) the ΔV selection criterion (by the arrow) and b) selected cases displayed. c) The magnetic clouds sorted by the velocity slope |
3. Data analysis
We have analyzed magnetic cloud observations from the www magnetic cloud table; it is an extended version of Table 1 in Lepping et al. (2006). The table lists 121 magnetic clouds for the period 1995–2009 with parameters derived from fits by the standard model. The quality of their fit is marked by 1–3 (1 is the best). We only considered clouds of quality levels 1 and 2: there are 73 cases. Figure 3a is a histogram of clouds from the table grouped according to the quality and velocity difference ΔV within the cloud interval, that is, the difference between the maximum and minimum solar wind velocities, ΔV = Vmax − Vmin.
We used hourly averages of solar wind data from OMNIWeb2 in our work. The analysis was subsequently restricted to clouds with well-expressed expansion (see Fig. 2b): sufficiently large velocity decrease and slope. We considered clouds with ΔV> 50 km s-1 (Fig. 3a shows this selection). The histogram in Fig. 3c displays clouds grouped according to velocity slopes 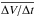 . The slopes were determined from a linear fit of the velocity magnitude profiles within the cloud interval. Positive slopes (contraction) are not rare and indicate the interaction of magnetic clouds with their surroundings (other ejecta or fast streams). These cases often have non-monotonous velocity magnitude profiles. Occasionally the slope reaches nearly 700 km s-1 per day in both signs (Fig. 3c; these are the Bastille Day Event, Fig. 1, and the cloud on 22 July 2004 in the considered table). Our analysis included only cases with
. The slopes were determined from a linear fit of the velocity magnitude profiles within the cloud interval. Positive slopes (contraction) are not rare and indicate the interaction of magnetic clouds with their surroundings (other ejecta or fast streams). These cases often have non-monotonous velocity magnitude profiles. Occasionally the slope reaches nearly 700 km s-1 per day in both signs (Fig. 3c; these are the Bastille Day Event, Fig. 1, and the cloud on 22 July 2004 in the considered table). Our analysis included only cases with 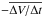 > 50 km s-1 per day (Fig. 3c shows this selection). Low
> 50 km s-1 per day (Fig. 3c shows this selection). Low 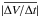 values have slowly expanding clouds, but they may also result from non-monotonic velocity magnitude profiles. After applying all the above given criteria, 30 magnetic clouds remained (Fig. 3b), which are listed in Table 1.
values have slowly expanding clouds, but they may also result from non-monotonic velocity magnitude profiles. After applying all the above given criteria, 30 magnetic clouds remained (Fig. 3b), which are listed in Table 1.
List of 30 analyzed magnetic clouds.
4. Results
Using our fitting procedure with the circular model with expansion, the cloud parameters were determined, and the radial velocity profiles (observed and modeled) were visually inspected. The results of our visual Vr comparison are summarized in the last column of Table 1. Of course, these judgments are somewhat subjective, but below we explain their meanings and demonstrate them in figures.
We mean by “reasonable fit” those cases where the observed Vr profile exhibits the “U” profile, and it is at least partly met quantitatively by the model profile. Figure 4 shows one example where the magnetic field components, velocity magnitude, and radial velocity are met quite well.
 |
Fig. 4 Magnetic cloud of April 22, 2001. It has number 58.0 in Table 1. The format is similar to Fig. 1, and only the radial velocity profiles Vr are added: the observed radial velocity is plotted by the thin line, and the thick line is the profile following from the model (expanding circular cylindrical flux rope). |
Figure 5 shows the magnetic cloud from the Bastille Day Event, which was already displayed in Fig. 1 but now fit by the cylindrical model with expansion. The introduction of expansion does not automatically mean that fits of magnetic field components improve. Some may improve, but others are better matched by the static model. What improves is the match of the magnetic magnitude profile, and the velocity magnitude profile is fit, sometimes very well, but this is not the current case. As the figure demonstrates, expansion causes an asymmetry in the magnetic field’s magnitude profile, and the maximum is shifted toward the leading boundary, that is, the field increase is shorter and its decline is longer.
We could not get a fit of this case with reasonable parameters when using t1 and t2 from the www magnetic cloud table. The event is also treated by Lepping et al. (2001), who present a different time interval, which we used here in Figs. 1 and 5. One can notice in Table 1 a large difference between the axis orientations following from our fitting and the values from the www magnetic cloud table (numbers in parentheses). It reports a flux rope with a relatively large inclination. A similar axis orientation is given in Lepping et al. (2001) with a relatively large asymmetry (33%).
Our fitting procedure converges to a low inclined flux rope in both static and expanding model cases (with the initial radius around 0.1 au), and the resulting fits are seen in Figs. 1 and 5. Mulligan et al. (2001) also deduce a low-inclined flux rope. The magnetic-field and velocity magnitude profiles are not fit very well. The case is an extreme, with an extraordinary velocity decrease. The fit of the magnetic field magnitude suggests that the model cloud should expand more slowly, but the fit of the velocity magnitude indicates a faster expansion. These requirements are in contradiction, and the fit represents a compromise. An introduction of oblateness does not help in this case and makes the fit of the velocity magnitude even worse. Apparently our simple model cannot adequately describe in detail the evolution of this cloud. Both observed and modeled Vr have “U” profiles, but they do not agree quantitatively, so we label this case as ““U” shape expressed, fit only qualitative”.
 |
Fig. 5 Magnetic cloud of July 15–16, 2000, already displayed in Fig. 1 (number 46.0 in Table 1), but fit by the expanding circular cylindrical flux rope. The format is the same as in Fig. 4. |
 |
Fig. 6 Magnetic cloud of February 8, 1995 (number 1.0 in Table 1) fit by expanding cylindrical flux ropes with a) circular or b) elliptic cross sections. The format of panels is the same as in Fig. 4. |
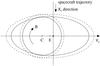 |
Fig. 7 Geometric situation depicting a spacecraft passage through modeled magnetic clouds in Case 1.0. Two magnetic cloud systems are superposed, one (with the origin C) related to an expanding circular magnetic cloud and Fig. 6a, and the second one (with the origin E) related to an expanding elliptic magnetic cloud and Fig. 6b. The systems are aligned with the Yc axes and the XcYc projections of the spacecraft trajectory (shown by the labeled straight vertical line). The Xc axes (not shown) are parallel to this vertical line and cross either the point C, or E. The solid-line circle and ellipse are magnetic-cloud cross sections at the spacecraft entry, while the dashed-line shapes display them at the spacecraft exit. The sense of the magnetic field rotation is shown by a bent arrow, and there is also BZ component pointing toward the viewer (i.e., the field is lefthanded, h = −1). |
Figure 6a shows the first entry in Table 1, the magnetic cloud of February 8, 1995, fit by an expanding model with a circular cross section. Inspecting the Vr panel, we see that the radial velocity profiles are only partly met. However, an introduction of oblateness significantly improves this fit (see Fig. 6b). The reason can be deduced from parameters given in Table 1, and it is also demonstrated in Fig. 7. Axis orientations following from these two fits are relatively close together, so Fig. 7 plausibly displays a spatial relationship of the models. However, the spacecraft crosses boundaries of the circular and elliptic magnetic clouds in different places owing to different cloud-axis orientations. If the axis orientations (given by ϑc and φc) following from the two fits were the same, then the spacecraft trajectory would pass through the mutual crossing points of the circular and elliptic cloud boundaries. It nearly occurs in Case 11.0, discussed later and shown in Fig. 9, where the cloud axis directions resulting from the two fits only differ by 15°, unlike the current case with the value of 38°. (Another reason for the boundary crossing discrepancy can be different times t1 and/or t2 of the two fits, but it is not the case for the clouds displayed in Figs. 7 and 9; compare, for example, these times in Figs. 6a and b.) Returning to the current case, 1.0, impact parameters p are quite different for the two fits, the elliptic fit brings the spacecraft much closer to the cloud axis, so Vr becomes lower and is more consistent with the data (Fig. 6b versus Fig. 6a).
 |
Fig. 8 Magnetic cloud of September 22, 1997 (number 22.0 in Table 1) fit by expanding cylindrical flux ropes with a) circular or b) elliptic cross sections. The format of panels is the same as in Fig. 4. |
Figure 8a displays the magnetic cloud of September 22, 1997 (number 22.0 in Table 1) fit by an expanding circular cylindrical flux rope. While the fits of magnetic field components and the field and velocity magnitudes are reasonable (but note a large difference in parameters in Table 1 between this fit and values in parentheses taken from the www magnetic cloud table), it is not true for the radial velocity. Their difference is very large. Moreover, the observed radial velocity is negative (therefore the label “Vr< 0” in Table 1) in the center, which is strange because it should indicate a compression. The model’s radial velocity is always positive (or zero at the axis). The negative observed Vr indicates that something is wrong with the correspondence between the cloud and the model. We again tested that the oblateness of the cloud could improve the situation. Figure 8b shows how the fit improves when oblateness is introduced into our model. Here the fitting procedure brings the axis orientation closer to the values in parentheses, and the large change in the axis orientation and impact parameter yields a different geometric situation and makes Vr more consistent with the data. We consider this fit to be reasonable, and it is the meaning of words “negative Vr fixed by an elliptic shape” in Table 1.
Another case with negative Vr fixed is the magnetic cloud of December 24, 1996 (Case 11.0 in Table 1). It has been treated in Vandas et al. (2009), who fit it by an expanding circular cylindrical flux rope. Figure 4 there shows this fit with the negative Vr profile. The modeled axes of circular and elliptic clouds have similar directions (see Table 1), so the clouds are suitable for superposed analysis (Fig. 9). These two fits have opposite signs of p, so the model axes are located at opposite sites with respect to the spacecraft trajectory (see Fig. 9). Assuming that the correct axis follows from the elliptic fit (origin/axis in point E) and the cloud expands from the axis, then Vr (shown in Fig. 9) is directed away from E (Vr> 0), but toward C (Vr< 0).
 |
Fig. 9 Geometric situation depicting a spacecraft passage through modeled magnetic clouds related to Case 11.0 in Table 1 (magnetic cloud of December 24, 1996). The format is the same as in Fig. 7. In addition, the direction of the radial velocity Vr for the elliptic model is shown. The cloud is righthanded (h = +1). |
 |
Fig. 10 Magnetic cloud of April 29, 2001 (number 59.0 in Table 1) fit by an expanding circular cylindrical flux rope. The format is the same as in Fig. 4. |
Fit of the cloud from April 29, 2001 (Case 59.0 in Table 1) also yields a negative Vr (Fig. 10). There is a very good match of the magnetic field components and velocity magnitude, but still a large difference in the Vr profiles, and observed Vr is negative. The model with oblateness does not help. The case is labeled as “Vr< 0, not fixed by an elliptic shape”. There are three such cases in Table 1. Another possibility for explaining (removing) the observed negative radial velocity is that the cloud axis is bent. We have suggested it in Vandas et al. (2009) but did not treat it in detail. Such an analysis goes beyond the scope of the present paper where models with straight axes are used. We shall treat them in a paper under preparation on toroidal magnetic clouds.
Figure 11a shows the magnetic cloud of January 10, 1997 (number 12.0 in Table 1) fit by an expanding circular cylindrical flux rope. The fit of the magnetic field and velocity is reasonable, as is the radial velocity. The magnetic-field magnitude profile is very flat, and we have suggested earlier (Vandas et al. 2006) that it may indicate an oblate shape of the magnetic cloud. In this paper the cloud was fit by an elliptic flux rope. Within the scope of the present paper we examined how this fit changes radial velocity profiles. The result is shown in Fig. 11b. We see that the quality of the Vr fit does not change (does not get worse), but the fit of the field magnitude did improve.
Some cases could not be analyzed by the present model as can be inferred from Table 1. Our selection criteria did not exclude all non-monotonous velocity profiles. A few cases have unusual B profiles, with B increasing toward the trailing edge (i.e., the opposite of what is expected by the model). When these features dominate, it makes no sense to use the present model, because its assumptions are violated.
 |
Fig. 11 Magnetic cloud of January 10, 1997 (number 12.0 in Table 1) fit by expanding cylindrical flux ropes with a) circular or b) elliptic cross sections. The format of panels is the same as in Fig. 4. |
5. Summary and conclusions
We have analyzed 30 magnetic clouds with clearly expressed expansion in detail: 26 of them were fit by the linear force-free model of an expanding circular or elliptic cylindrical flux rope, and the remaining four violated assumptions in the model by having strongly non-monotonous velocity profiles. Radial velocities in 21 cases (81% of 26) behave as expected and were quantitatively compatible with the model in 15 cases (58%). The observed negative radial velocities were present in six cases, three of which were converted into expected positive values by the model including the flux rope oblateness. This model changed the parameters of the flux ropes, meaning they changed the geometric situation of the spacecraft passage through the clouds and usually brought the spacecraft closer to the cloud axis, which removes the observed negative radial velocity profiles. The remaining three cases have relatively large impact factors. This might be the reason for the discrepancy, but we cannot exclude that the discrepancy might be explained by a flux rope curvature (future task). There were two cases where the radial velocities even behave differently qualitatively, but they were accompanied by peculiar magnetic field magnitude profiles.
To conclude, radial velocity profiles qualitatively correspond to model ones in the majority of cases and quantitatively in more than half of them. In general, analyses of velocity components test models more strictly and may reveal information about magnetic cloud shapes.
Acknowledgments
We acknowledge the use of data from OMNIWeb and PIs who provided them. This work was supported by projects 205/09/0170 and 14-19376S from GA ČR and by the AV ČR grant RVO:67985815.
References
- Berdichevsky, D., Lepping, R. P., & Farrugia, C. J. 2003, Phys. Rev. E, 67, 036405 [NASA ADS] [CrossRef] [Google Scholar]
- Burlaga, L. F. 1988, J. Geophys. Res., 93, 7217 [NASA ADS] [CrossRef] [Google Scholar]
- Burlaga, L. F. 1991, in Physics of the Inner Heliosphere 2, eds. R. Schwenn, & E. Marsch (New York: Springer-Verlag), 1 [Google Scholar]
- Burlaga, L., Sittler, E., Mariani, F., & Schwenn, R. 1981, J. Geophys. Res., 86, 6673 [Google Scholar]
- Crooker, N. U., Gosling, J. T., Smith, E. J., & Russell, C. T. 1990, in Physics of Magnetic Flux Ropes, eds. C. T. Russell, E. R. Priest, & L. C. Lee (Washington, D.C.: AGU), Geophys. Monogr. Ser., 58, 365 [Google Scholar]
- Dalakishvili, G., Rogava, A., Lapenta, G., & Poedts, S. 2011, A&A, 526, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dasso, S., Nakwacki, M. S., Démoulin, P., & Mandrini, C. H. 2007, Sol. Phys., 244, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Démoulin, P., & Dasso, S. 2009, A&A, 498, 551 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Démoulin, P., Nakwacki, M. S., Dasso, S., & Mandrini, C. H. 2008, Sol. Phys., 250, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Goldstein, H. 1983, in Solar Wind Five, NASA CP, ed. M. Neugebauer (NASA), 2280, 731 [Google Scholar]
- Gosling, J. T. 1990, in Physics of Magnetic Flux Ropes, Geophys. Monogr. Ser., eds. C. T. Russell, E. R. Priest, & L. C. Lee (Washington, D.C.: AGU), 58, 343 [Google Scholar]
- Gulisano, A. M., Démoulin, P., Dasso, S., Ruiz, M. E., & Marsch, E. 2010, A&A, 509, A39 [Google Scholar]
- Gulisano, A. M., Démoulin, P., Dasso, S., & Rodriguez, L. 2012, A&A, 543, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hidalgo, M. A. 2003, J. Geophys. Res., 108, DOI: 10.1029/2002JA009818 [Google Scholar]
- Hidalgo, M. A. 2013, ApJ, 766, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Hidalgo, M. A. 2014, ApJ, 784, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Hidalgo, M. A., & Nieves-Chinchilla, T. 2012, ApJ, 748, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Hidalgo, M. A., Cid, C., Viñas, A. F., & Sequeiros, J. 2002, J. Geophys. Res., 107, DOI: 10.1029/2001JA900100 [Google Scholar]
- Hu, Q., & Sonnerup, B. U. Ö. 2002, J. Geophys. Res., 107, DOI: 10.1029/2001JA000293 [Google Scholar]
- Ivanov, K. G., Kharshiladze, A. F., & Romashets, E. P. 1993, Geomag. Aeronom., 33, 90 [NASA ADS] [Google Scholar]
- Lepping, R. P., Jones, J. A., & Burlaga, L. F. 1990, J. Geophys. Res., 95, 11957 [NASA ADS] [CrossRef] [Google Scholar]
- Lepping, R. P., Berdichevsky, D. B., Burlaga, L. F., et al. 2001, Sol. Phys., 204, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Lepping, R. P., Berdichevsky, D. B., Szabo, A., Arqueros, C., & Lazarus, A. J. 2003, Sol. Phys., 212, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Lepping, R. P., Berdichevsky, D. B., Wu, C.-C., et al. 2006, Ann. Geophys., 24, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Lepping, R. P., Narock, T. W., & Chen, H. 2007, Ann. Geophys., 25, 2641 [NASA ADS] [CrossRef] [Google Scholar]
- Lepping, R. P., Wu, C.-C., Berdichevsky, D. B., & Ferguson, T. 2008, Ann. Geophys., 26, 1919 [NASA ADS] [CrossRef] [Google Scholar]
- Lundquist, S. 1950, Ark. Fys., 2, 361 [Google Scholar]
- Lynnyk, A., & Vandas, M. 2009, Planet. Space Sci., 57, 1375 [NASA ADS] [CrossRef] [Google Scholar]
- Lynnyk, A., & Vandas, M. 2010, in Twelve International Solar Wind Conference, eds. M. Maksimovic, K. Issautier, N. Meyer-Vernet, M. Moncuquet, & F. Pantellini (Melville, New York: AIP), AIP Conf. Proc., 1216, 395 [Google Scholar]
- Marubashi, K. 1986, Adv. Space Res., 6, 6, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Marubashi, K. 1997, in Coronal Mass Ejections, eds. N. Crooker, J. Joselyn, & J. Feyman (Washington, D. C.: AGU), Geophys. Monogr. Ser. 99, 147 [Google Scholar]
- Marubashi, K., & Lepping, R. P. 2007, Ann. Geophys., 25, 2453 [NASA ADS] [CrossRef] [Google Scholar]
- Mulligan, T., & Russell, C. T. 2001, J. Geophys. Res., 106, 10581 [NASA ADS] [CrossRef] [Google Scholar]
- Mulligan, T., Russell, C. T., Anderson, B. J., & Acuna, M. H. 2001, Geophys. Res. Lett., 28, 4417 [NASA ADS] [CrossRef] [Google Scholar]
- Nakwacki, M. S., Dasso, S., Mandrini, C. H., & Démoulin, P. 2008, J. Atm. Sol.-Terr. Phys., 70, 1318 [Google Scholar]
- Nakwacki, M. S., Dasso, S., Démoulin, P., Mandrini, C. H., & Gulisano, A. M. 2011, A&A, 535, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Osherovich, V. A., Farrugia, C. J., & Burlaga, L. F. 1993, Adv. Space Res., 13, 6, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Osherovich, V. A., Farrugia, C. J., & Burlaga, L. F. 1995, J. Geophys. Res., 100, 12307 [NASA ADS] [CrossRef] [Google Scholar]
- Press, V. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 2002, Numerical Recipes in C, The Art of Scientific Computing, 2nd edn. (New York: Cambridge University Press) [Google Scholar]
- Shimazu, H., & Vandas, M. 2002, Earth Planets Space, 54, 783 [NASA ADS] [CrossRef] [Google Scholar]
- Vandas, M., & Romashets, E. P. 2003, A&A, 398, 801 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vandas, M., Romashets, E. P., & Watari, S. 2005a, Planet. Space Sci., 53, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Vandas, M., Romashets, E. P., & Watari, S. 2005b, in Proc. Solar Wind 11 – SOHO 16 Connecting Sun and Heliosphere, eds. B. Fleck, T. H. Zurbuchen, & H. Lacoste (Noordwijk: ESA), ESA SP, 592, 775 [Google Scholar]
- Vandas, M., Romashets, E. P., Watari, S., et al. 2006, Adv. Space Res., 38, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Vandas, M., Geranios, A., & Romashets, E. P. 2009, Astrophys. Space Sci. Trans., 5, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Watari, S., Kunitake, M., & Watanabe, T. 2001, Sol. Phys., 204, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Wei, F., Liu, R., Fan, Q., & Feng, X. 2003, J. Geophys. Res., 108, DOI: 10.1029/2002JA009511 [Google Scholar]
- Wu, C.-C., Lepping, R. P., Berdichevsky, D. B., Ferguson, T., & Lazarus, A. J. 2002, in AGU Fall Meeting 2002 (abstract SH21A-0513) [Google Scholar]
Appendix A: Impact parameter and its sign
Let us assume that a spacecraft is located in the origin of a GSE system (x, y, z). A magnetic cloud approximated by a cylindrical flux rope is traveling radially from the Sun. Its axis crosses the ecliptic plane in a point (ignoring a singular case when ϑc = 0° exactly) that is conveyed by the solar wind parallel to the x axis; in other words, the point has its y coordinate, YG, constant. Following Lepping et al. (1990), a magnetic cloud system is introduced, Zc, the axis of which coincides with the cloud axis. If denoting a unit vector in the direction of the spacecraft trajectory within the magnetic cloud system by S, then the Yc axis is defined by a unit vector in its direction, 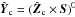 , where
, where 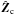 is similarly a unit vector in the Zc axis direction. The Xc axis completes the system by its unit vector
is similarly a unit vector in the Zc axis direction. The Xc axis completes the system by its unit vector 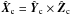 . These unit vectors can be easily calculated in the GSE system when we realize that S = (1,0,0) and
. These unit vectors can be easily calculated in the GSE system when we realize that S = (1,0,0) and 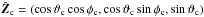 . The spacecraft in the magnetic cloud system moves along a trajectory that also has a constant Yc coordinate, denoted by Y0 in Lepping et al. (1990). Here, | Y0 | is the closest distance of the spacecraft from the cloud axis, and the impact parameter p = Y0/r0 where r0 is the cloud radius, so the sign of p is the sign of Y0, and its absolute value is the relatively closest distance. When the cloud is elliptic, we define p = Y0/b, where b is the minor radius. If the cloud is expanding, the values of r0 or b are taken at the spacecraft entry into the cloud. The angle δ between the x and Xc axes is given by
. The spacecraft in the magnetic cloud system moves along a trajectory that also has a constant Yc coordinate, denoted by Y0 in Lepping et al. (1990). Here, | Y0 | is the closest distance of the spacecraft from the cloud axis, and the impact parameter p = Y0/r0 where r0 is the cloud radius, so the sign of p is the sign of Y0, and its absolute value is the relatively closest distance. When the cloud is elliptic, we define p = Y0/b, where b is the minor radius. If the cloud is expanding, the values of r0 or b are taken at the spacecraft entry into the cloud. The angle δ between the x and Xc axes is given by 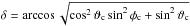 . These two axes therefore have similar directions for low inclined flux ropes (ϑc ≈ 0°), the axes of which are roughly perpendicular to the Sun-Earth line (φc ≈ 90° or 270°). In a very crude approximation, these conditions hold for the clouds shown in Figs. 7 and 9. Values of Y0 and YG are related by Y0 = −YGsinϑc/ cosδ.
. These two axes therefore have similar directions for low inclined flux ropes (ϑc ≈ 0°), the axes of which are roughly perpendicular to the Sun-Earth line (φc ≈ 90° or 270°). In a very crude approximation, these conditions hold for the clouds shown in Figs. 7 and 9. Values of Y0 and YG are related by Y0 = −YGsinϑc/ cosδ.
Lepping et al. (1990) do not specify explicitly the orientation of the vector S in the text, but their Fig. 1 suggests that it is in the direction of the spacecraft motion through the cloud. Our vector S has this direction. However, comparison of their magnetic cloud parameters with data lead us to the conclusion that their S goes in the opposite direction, against the spacecraft motion, so the values of p in parentheses in Table 1 are defined as p = −CA/100, where CA is the parameter from the www magnetic cloud table related to the impact parameter. This is supported by, e.g., Figs. 7 and 6. The cloud has a positive impact parameter (see Table 1), so Y0 is also positive, in accord with the geometric situation given in Fig. 7. The cloud is lefthanded, as it is indicated in this figure, so the spacecraft should observe positive Bx, which is confirmed by Fig. 6. When p is opposite, as suggested by the www magnetic cloud table, the observed Bx should be negative, which is not the case.
All Tables
All Figures
 |
Fig. 1 Magnetic cloud of July 15–16, 2000 observed near the Earth. Measurements (hourly averages) of the solar wind quantities are plotted: magnetic field magnitude B and components Bx, By, and Bz in the geocentric solar ecliptic (GSE) system, velocity V, density N, and proton temperature T. Estimated cloud boundaries are drawn by the vertical dashed lines. Observations are plotted by the thin line, and the thick line is a fit by a model (static circular cylindrical flux rope). More details on it are given in Sect. 2. The cloud is numbered 46.0 in Table 1. |
| In the text | |
 |
Fig. 2 a) Spacecraft crossing an expanding circular flux rope. The spacecraft trajectory is drawn by a straight thin line, the boundary of the cloud/rope at the spacecraft entry (leading boundary) is the solid-line circle, the boundary at the spacecraft exit (trailing boundary) is the dashed-line circle. The bullet indicates the position of the rope axis. b) The ambient solar wind and expansion (Vr) velocities add at the leading boundary and subtract at the trailing one, which results in a decrease in observed velocity magnitude; the vertical lines indicate the flux rope boundaries, and their line types match the ones in panel a). c) Radial velocity Vr is highest near the boundary and drops to zero at the axis. It yields a characteristic “U” shape profile in the modeled Vr. |
| In the text | |
 |
Fig. 3 Histograms of magnetic clouds from the www magnetic cloud table. a), b) The magnetic clouds sorted by the velocity difference ΔV, with a) the ΔV selection criterion (by the arrow) and b) selected cases displayed. c) The magnetic clouds sorted by the velocity slope |
| In the text | |
 |
Fig. 4 Magnetic cloud of April 22, 2001. It has number 58.0 in Table 1. The format is similar to Fig. 1, and only the radial velocity profiles Vr are added: the observed radial velocity is plotted by the thin line, and the thick line is the profile following from the model (expanding circular cylindrical flux rope). |
| In the text | |
 |
Fig. 5 Magnetic cloud of July 15–16, 2000, already displayed in Fig. 1 (number 46.0 in Table 1), but fit by the expanding circular cylindrical flux rope. The format is the same as in Fig. 4. |
| In the text | |
 |
Fig. 6 Magnetic cloud of February 8, 1995 (number 1.0 in Table 1) fit by expanding cylindrical flux ropes with a) circular or b) elliptic cross sections. The format of panels is the same as in Fig. 4. |
| In the text | |
 |
Fig. 7 Geometric situation depicting a spacecraft passage through modeled magnetic clouds in Case 1.0. Two magnetic cloud systems are superposed, one (with the origin C) related to an expanding circular magnetic cloud and Fig. 6a, and the second one (with the origin E) related to an expanding elliptic magnetic cloud and Fig. 6b. The systems are aligned with the Yc axes and the XcYc projections of the spacecraft trajectory (shown by the labeled straight vertical line). The Xc axes (not shown) are parallel to this vertical line and cross either the point C, or E. The solid-line circle and ellipse are magnetic-cloud cross sections at the spacecraft entry, while the dashed-line shapes display them at the spacecraft exit. The sense of the magnetic field rotation is shown by a bent arrow, and there is also BZ component pointing toward the viewer (i.e., the field is lefthanded, h = −1). |
| In the text | |
 |
Fig. 8 Magnetic cloud of September 22, 1997 (number 22.0 in Table 1) fit by expanding cylindrical flux ropes with a) circular or b) elliptic cross sections. The format of panels is the same as in Fig. 4. |
| In the text | |
 |
Fig. 9 Geometric situation depicting a spacecraft passage through modeled magnetic clouds related to Case 11.0 in Table 1 (magnetic cloud of December 24, 1996). The format is the same as in Fig. 7. In addition, the direction of the radial velocity Vr for the elliptic model is shown. The cloud is righthanded (h = +1). |
| In the text | |
 |
Fig. 10 Magnetic cloud of April 29, 2001 (number 59.0 in Table 1) fit by an expanding circular cylindrical flux rope. The format is the same as in Fig. 4. |
| In the text | |
 |
Fig. 11 Magnetic cloud of January 10, 1997 (number 12.0 in Table 1) fit by expanding cylindrical flux ropes with a) circular or b) elliptic cross sections. The format of panels is the same as in Fig. 4. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


