| Issue |
A&A
Volume 582, October 2015
|
|
|---|---|---|
| Article Number | A108 | |
| Number of page(s) | 4 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201526882 | |
| Published online | 20 October 2015 | |
Mass fluxes for O-type supergiants with metallicity Z = Z⊙/5
Astrophysics Group, Blackett Laboratory, Imperial College London,
Prince Consort
Road
London
SW7 2AZ
UK
e-mail:
l.lucy@imperial.ac.uk
Received: 3 July 2015
Accepted: 3 September 2015
A code used previously to predict O-star mass fluxes as a function of metallicity is used to compute a grid of models with the metallicity of the Small Magellanic Cloud (SMC). These models allow mass-loss rates to be derived by interpolation for all O-type supergiants in the SMC, with the possible exception of extremely massive stars close to the Eddington limit.
Key words: stars: early-type / stars: mass-loss / stars: winds, outflows
© ESO, 2015
1. Introduction
A recent paper by Bouret et al. (2015) is a major contribution to our understanding of mass loss by O-type supergiants at low metallicity (Z).
Earlier papers by Tramper et al. (2011, 2014) analysing optical spectra of extragalactic O stars in low-Z environments derive mass-loss rates which, they claim, challenge the current paradigm of massive-star evolution, both in the local universe as well as at cosmic distances. They make this claim because their estimates exceed predicted rates for radiatively-driven winds. The implication, therefore, is that a new, unknown mass-loss mechanism operates, and that evolutionary tracks for massive stars require revision.
However, the Bouret et al. analyses of the far-UV HST/COS spectra of three of these stars decisively contradicts − see their Fig. 5 − the rates found by Tramper et al. Moreover, the origin of the discrepacy is fully understood: Tramper et al had perforce to rely on weak optical signatures of mass loss, namely the partial infilling of the Hα and He ii 4686 Å absorption lines as a result of recombinations in the winds. But these diagnostics have long been known (e.g., Lucy 1975) to overestimate mass-loss rates because of wind clumping, an effect neglected by Tramper et al.
With the revised rates of Bouret et al., there is now no case for a mass-loss mechanism other than radiative driving, especially since their estimates are in good agreement with previously-computed mass fluxes (Lucy 2012; L12). This is an important conclusion since the Tramper et al. rates could imply a Z-independent mass- and angular momentum loss mechanism that might even operate for Population III stars.
Nevertheless, Bouret et al. emphasize that this conclusion is based on just three stars, so that confirmation from a larger sample is desirable. To this end, they promise a subsequent paper analysing archived spectra of O stars in the Small Magellanic Cloud (SMC). To support this effort, this paper reports mass fluxes for models with SMC metallicity, Z = Z⊙/ 5.
Throughout this paper, mass flux in units gm s-1 cm-2 is denoted by J, whence the mass-loss rate Φ = 4πR2J in solar masses per yr is given by 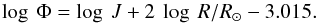 (1)
(1)
2. Computing mass loss rates
In the light of the Bouret at al. (2015) analysis, this section briefly comments on two methods of predicting Φ.
2.1. The Monte Carlo method
In addition to the disagreement with Tramper et al., the Φ’s determined by Bouret et al. are ~1 dex below − see their Fig. 9 − those derived from the Vink et al. (2001) fitting formula. Given that similarly large overpredictions occur in the weak-wind domain (Marcolino at al. 2009; Lucy 2010a; L10a) the Monte Carlo (MC) method used by Vink et al. would appear to be discredited. This merits discussion.
The semi-empirical MC method used by Vink et al. was introduced by Abbott & Lucy (1985; AL85) to investigate the differential effect of multi-line scattering, with the aim of explaining the high Φ’s of Wolf-Rayet stars (Lucy & Abbott 1993). The method is well-founded physically and should give reliable Φ’s provided that, in the supersonic wind, 1) radiative driving is the acceleration mechanism; and 2) that the interaction of radiation and matter is accurately modelled. This second point is where difficulties arise.
Detailed modelling of far-UV line profiles − see Sect. 8.2 of Bouret et al. (2015) and references therein − demonstrates that the standard model of a homogeneous wind with a laminar outflow obeying a monotonic velocity law is contradicted: parameterized descriptions of severe clumping and highly supersonic turbulence must be incorporated to fit the profiles. Since these effects impact on the transfer of momentum from radiation to matter, they evidently must be included in the MC method. Accordingly, when using this method, the predicted emergent spectrum − see Fig. 2 in AL85 − should be compared to an observed spectrum to see if the chosen clumping and turbulence parameters reproduce the observed P Cygni line profiles.
2.2. Prediction
In principle, the structure of radiatively-driven winds can be predicted from the equations of radiation gas dynamics. The results could then be used to eliminate parameterized phenomenological models. But this requires combining a treatment of 3D, time-dependent, multi-frequency, non-LTE radiative transfer with that of 3D, time-dependent gas dynamics with multiple shocks. This is way beyond our capabilities, and so quantitative prediction from first principles is not possible.
But note that the supersonic wind arises from a stable stellar envelope. Accordingly, as the Mach number m → 0, the wind solution converges to that of a 1D, static photosphere in mechanical, statistical and thermal equilibrium − i.e, to a structure that is eminently computable.
Plausibly, the transition from computable to non-computable occurs early in the supersonic zone with the growth of instability (Lucy & Solomon 1970; LS70; Owocki et al. 1988), in which case the sonic point lies within the computable domain. A first-principles treatment of transonic flow is then feasible, and this includes a determination of the mass flux J as an eigenvalue. This assumption of computability is the fundamental basis of the moving reversing layer (MRL) method used to compute the low-Z mass fluxes (L12) tested by Bouret et al. (2015).
However, if extreme clumpiness and multiple shocks already arise when the bulk motion is still subsonic, then the MRL method is undermined, and this should evidence itself in predictions that conflict with observations.
2.3. The MRL method
The MRL method is an updating of the crude treatment of dynamical reversing layers given in LS70. The model was initially updated (Lucy 2007; L07) in order to investigate claims (Bouret et al. 2005; Fullerton et al. 2006) that the theory of radiatively-driven winds overpredicts Φ’s. The same code was later used (L10a) to investigate the weak-wind problem. Subsequently, the model was further refined (Lucy 2010b; L10b) by introducing a flexible, non-parametric representation for the variation of the radiative acceleration due to lines gℓ with flow velocity v.
The physical picture (LS70) motivating this model is that of the radiative expulsion of a stellar atmosphere’s highest layers followed by a relatively gentle up-welling of deeper layers in response to the unbalanced pressure. The MRL method assumes that this up-welling adjusts to a 1D, time-independent outflow, with a smooth transition from sub- to supersonic velocity. This regularity constraint at the sonic point can only be satisfied for a particular value of the mass flux J, which is therefore an eigenvalue.
As originally formulated, MRL models could be computed from first principles. But there is ample evidence that the quasi-static reversing layers of O-stars are turbulent, and this is a phenomenon that we cannot yet predict from first principles. Accordingly, the MRL models computed here and previously follow Lanz & Hubeny (2003) in assuming a canonical microturbulent velocity vt = 10 km s-1 when computing the Doppler widths of line profiles. In this regard, therefore, the MRL models also acquire a semi-empirical aspect. This is a presently- unavoidable departure from the ideal of calculation from first principles.
3. Numerical solutions
Mass fluxes J are now computed for O-type supergiants in the SMC.
3.1. Input data
The composition has NHe/NH = 0.1 and metals are reduced from solar (Grevesse & Sauval 1998) by a factor 5. The included ions are as in Table 1 of Lanz & Hubeny (2003).
The basic line data is from Kurucz & Bell (1995). This is reduced to a working line list of the ~105 transitions relevant for the ions and atomic levels included in the TLUSTY models of Lanz & Hubeny (2003).
3.2. Parameters
The parameters are plotted on the (log Teff,log g)-plane in Fig. 1, together with evolutionary tracks for masses 25 and 60 ℳ⊙ (Brott et al. 2011). The models thus encompass the H-burning phase of SMC O-stars with 25 ≲ ℳ/ℳ⊙ ≲ 80.
The points selected in Fig. 1 are dictated by the availability of TLUSTY models. As explained in L07 and L10a, continuum fluxes and photospheric departure coefficients are derived from models downloaded from the TLUSTY website. In effect, each MRL model is grafted onto the corresponding TLUSTY model. This is justified because significant departures from the static TLUSTY models occur only when m2 ≳ 0.1, and this corresponds to small optical depths. In this paper, the downloaded data refers to the S series of TLUSTY models, for which Z = Z⊙/ 5.
For technical reasons, the TLUSTY models do not more closely approach the Eddington limit than shown in Fig. 1. Stars in the resulting gap − i.e., with ℳ/ℳ⊙ ≳ 80− may indeed exist in the SMC, and estimates of their Φ’s are of great interest. But MRL predictions for such stars would require individual treatment. Note that extrapolation with a scaling law is not justified − see Fig. 7 in L10b.
The MRL models are conveniently identified with the TLUSTY notation. Thus St400g350 is the S series model with Teff = 40 000 K and log g(cgs) = 3.50.
 |
Fig. 1 Domain of interest in (Teff,log g)-space. The filled circles are loci of the O-star MRL models with Z/Z⊙ ∈ (1/30,2) reported in L12. The open circles are the loci of models with Z/Z⊙ = 1/5 reported in this paper. The Eddington limit for static radiative envelopes is shown as well as H-burning evolutionary tracks (Brott et al. 2011) for masses 25 and 60 ℳ⊙. |
3.3. Mass fluxes
The predicted log J’s and other quantities of interest are given in Table 1 for each circled point (Teff,log g)in Fig. 1. For the filled circles, the values are the Z/Z⊙ = 1/5 models from L12, Table 1.
In addition to log J, Table 1 gives φ = c2Φ /L, the effective number of strong lines; η, the percentage of MC quanta that propagate through the MRL without interaction; and ζ, the percentage contribution of Fe and Ni to radiative driving by lines in the MRL layer. These quantities are given as a function of Z in L12, Table 1 and are useful in understanding curve-of-growth effects and the Z-dependence of the J’s − see Sects. 2.3 and 3.3 in L12.
The new quantity in Table 1 is 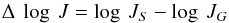 (2)where log JS is the S series value from Table 1 and log JG is the corresponding G series (Z/Z⊙ = 1) value from L10b, Table 1. The initial reason for tabulating this quantity is to identify possible anomalies arising in the time-consuming, trial-and-error solution procedure. But this quantity may also be useful for differential, model-insensitive comparisons of the spectra of Galactic and SMC O-type stars − see Sect. 3 in Bouret et al (2015).
(2)where log JS is the S series value from Table 1 and log JG is the corresponding G series (Z/Z⊙ = 1) value from L10b, Table 1. The initial reason for tabulating this quantity is to identify possible anomalies arising in the time-consuming, trial-and-error solution procedure. But this quantity may also be useful for differential, model-insensitive comparisons of the spectra of Galactic and SMC O-type stars − see Sect. 3 in Bouret et al (2015).
Computed mass fluxes J(gm s-1 cm-2) for Z = Z⊙/ 5 and vt = 10 km s-1.
For each value of log g, the dependence of log J on log Teff is plotted in Fig. 2. The corresponding plot for Galactic metallicity Z = Z⊙ is Fig. 5 in L10b. As in that previous plot, Fig. 2 shows the expected trends that J increases with increasing Teff and decreasing g.
 |
Fig. 2 Mass flux J as a function of Teff for log g = 3.00(0.25)4.25. Lines of constant φ = c2Φ /L are also plotted. The metallicity Z/Z⊙ = 1/5, and the microturbulent velocity vt = 10km s-1. |
3.4. Failed solutions
Inspection of Fig. 1 or the Δlog J values in Table 1 can lead one to suspect that some solutions are in error, perhaps reflecting mistakes in the iterative, trial and error procedure adopted in the absence of an automatic search algorithm. Such suspected anomalies can be investigated with the procedure described in L12, Sect. 5.2. Specifically, a value J† is selected that is more consistent with smooth variation, and this value is fixed as the vector gℓ is adjusted. If the best solution thus found fails to achieve consistency between the input and output vectors gℓ, then the solution search fails and J† is contradicted. Typically, failure is evident by the need to add or subtact momentum in the neighbourhood of the sonic point − see L12, Fig. 2.
Failures of this kind are as follows: St400g350 at J† = −5.0 dex; St400g375 at J† = −6.3 dex; and St375g350 at J† = −6.25 dex.
The implication of these failures is that these apparent anomalies indicate that the TLUSTY sampling in Fig. 1 is somewhat too coarse to reveal all the real structure in the function J(Teff,g).
3.5. Particular cases
Given the importance of the SMC as an accessible low-Z environment, it merits the attention of spectroscopists, as Bouret et al. (2015) recognize. This should then also prompt developers of stellar-wind codes to compute models for O stars in the SMC.
Although comparisons with spectroscopic estimates are of primary importance, conflicts between different codes should also be identified and understood. With respect to the MRL method, Table 1 provides data for such comparisons. But in addition, Figs. 3 and 4 plot the converged solutions of transonic flows for St350g325 and St450g375. In these diagrams, the input assumption for the radiative acceleration due to lines (open circles) is compared to the estimates derived from the MC experiment (filled circles). Not only does output match input rather well, but the solutions exhibit smooth transitions from sub- to supersonic flow, illustrating the constraints that determine the eigenvalues J.
 |
Fig. 3 MRL model St350g325. Radiative acceleration due to lines as a function of Mach number v/a for the transonic flow. The open circles define the assumed, non-parametric input model; the filled circles are the MC estimates. |
 |
Fig. 4 MRL model St450g375. |
3.6. Accuracy
A lengthy discussion of the accuracy of the J’s is given in L10b, Sect. 4.2 − see also L12, Sect. 5.2.
Because of the steep gradients of J(Teff,g)− see Fig. 2, a further source of error in predicting J for a particular star arises due to errors in the spectroscopic estimates of Teff and g. Such an error in the predicted J is minimized if Teff and g derive from diagnostics calibrated with the predictions of TLUSTY atmospheres.
Yet another source of error is incompleteness of the line list. The working line list (Sect. 3.1) comprises 87,469 transitions, of which 50% have log gf < −3.0. Since incompletness will predominantly concern weak transitions, it is instructive to
exclude those with log gf < −3.0 and then to recompute log J. This has been done for the models plotted in Figs. 3 and 4. For St350g325, the revised log J = −5.35, so that including the weakest 50% increases J by 0.05 dex. For St450g375, the corresponding increment in J is again 0.05 dex. These calculations suggest that incompleteness of the line list is less of a problem than other sources of error discussed above and in L10b. Nevertheless, future investigators of transonic flows should certainly update the line list.
4. Conclusion
With motivation provided by Bouret et al. (2015), the limited aim of this paper has been to use an existing code (L10b, L12) to predict mass fluxes for O-type supergiants in the SMC. The results presented in Table 1 cover the full range of Teff and g expected for such stars. Accordingly, for most observed stars, a prediction for its mass-loss rate should be derivable by interpolation. Possible exceptions are massive stars closer to the Eddington limit than the TLUSTY models allow (see Fig. 1). For such stars, prediction by extrapolation or by guessing a scaling law is not recommended.
In comparing with spectroscopic estimates, a discrepancy for an individual star might be due to errors in the assigned Teff and g. Of more significance would be a pattern of discrepancies that might point the way to an improved theory.
Given the importance in understanding the Z-dependence of mass loss by massive stars, this paper also includes data (Table 1) and diagrams (Figs. 3 and 4) for comparisons with extant and future stellar-wind codes. Again, by analysing discrepancies, we should eventually achieve greater predictive power.
Acknowledgments
I thank the referee, W.-R. Hamann, for a careful reading of the manuscript and for thoughtful suggestions.
References
- Abbott, D. C., & Lucy, L. B. 1985, ApJ, 288, 679 (AL85) [NASA ADS] [CrossRef] [Google Scholar]
- Brott, I., de Mink, S. E., Cantiello, M., et al. 2011, A&A, 530, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouret, J.-C., Lanz, T., & Hillier, D. J. 2005, A&A, 438, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouret, J.-C., Lanz, T., Hillier, D. J., et al. 2015, MNRAS, 449, 1545 [NASA ADS] [CrossRef] [Google Scholar]
- Fullerton, A. W., Massa, D. L., & Prinja, R. K. 2006, ApJ, 637, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L., & Bell, B. 1995, Kurucz CD-ROM No. 23 (Cambridge, Mass: Smithsonian Astrophysical Observatory) [Google Scholar]
- Lanz, T., & Hubeny, I. 2003, ApJS, 146, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 1975, Mem. Soc. R. Sci. Liège, 8, 359 [Google Scholar]
- Lucy, L. B. 2007, A&A, 468, 649 (L07) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lucy, L. B. 2010a, A&A, 512, A33 (L10a) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lucy, L. B. 2010b, A&A, 524, A41 (L10b) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lucy, L. B. 2012, A&A, 543, A18 (L12) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lucy, L. B., & Abbott, D. C. 1993, ApJ, 405, 738 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B., & Solomon, P. M. 1970, ApJ, 159, 879 (LS70) [NASA ADS] [CrossRef] [Google Scholar]
- Marcolino, W. L. F., Bouret, J.-C., Martins, F., et al. 2009, A&A, 498, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Owocki, S. P., Castor, J. I., & Rybicki, G. B. 1988, ApJ, 335, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Tramper, F., Sana, H., de Koter, A., & Kaper, L. 2011, ApJ, 741, 8 [Google Scholar]
- Tramper, F., Sana, H., de Koter, A., Kaper, L., & Ramrez-Agudelo, O. H. 2014, A&A, 572, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Domain of interest in (Teff,log g)-space. The filled circles are loci of the O-star MRL models with Z/Z⊙ ∈ (1/30,2) reported in L12. The open circles are the loci of models with Z/Z⊙ = 1/5 reported in this paper. The Eddington limit for static radiative envelopes is shown as well as H-burning evolutionary tracks (Brott et al. 2011) for masses 25 and 60 ℳ⊙. |
| In the text | |
 |
Fig. 2 Mass flux J as a function of Teff for log g = 3.00(0.25)4.25. Lines of constant φ = c2Φ /L are also plotted. The metallicity Z/Z⊙ = 1/5, and the microturbulent velocity vt = 10km s-1. |
| In the text | |
 |
Fig. 3 MRL model St350g325. Radiative acceleration due to lines as a function of Mach number v/a for the transonic flow. The open circles define the assumed, non-parametric input model; the filled circles are the MC estimates. |
| In the text | |
 |
Fig. 4 MRL model St450g375. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


