| Issue |
A&A
Volume 582, October 2015
|
|
|---|---|---|
| Article Number | A16 | |
| Number of page(s) | 9 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201526731 | |
| Published online | 30 September 2015 | |
The ALHAMBRA survey: Estimation of the clustering signal encoded in the cosmic variance⋆
1
Centro de Estudios de Física del Cosmos de Aragón, Plaza San Juan
1,
44001
Teruel,
Spain
e-mail:
clsj@cefca.es
2
Observatori Astronòmic, Universitat de València,
C/ Catedràtic José Beltrán 2,
46980
Paterna,
Spain
3
Instituto de Física de Cantabria (CSIC-UC),
39005
Santander,
Spain
4
Unidad Asociada Observatorio Astronómico (IFCA-UV),
46980
Paterna,
Spain
5
Departament d’Astronomia i Astrofísica, Universitat de
València, 46100
Burjassot,
Spain
6
IAA-CSIC, Glorieta de la Astronomía s/n,
18008
Granada,
Spain
7
GEPI, Observatoire de Paris, CNRS, Université Paris Diderot, 61
avenue de l’Observatoire, 75014
Paris,
France
8
Instituto de Astronomía, Geofísica e Ciéncias Atmosféricas,
Universidade de São Paulo, 05508-090
São Paulo,
Brazil
9
Instituto de Astrofísica de Canarias, Vía Láctea s/n, 38200 La Laguna, Tenerife, Spain
10
Departamento de Astrofísica, Facultad de Física, Universidad de La
Laguna, 38206
La Laguna,
Spain
11
Observatório Nacional-MCT, Rua José Cristino 77, CEP 20921-400, Rio de Janeiro - RJ, Brazil
12
Department of Theoretical Physics, University of the Basque
Country UPV/EHU, 48080
Bilbao,
Spain
13
IKERBASQUE, Basque Foundation for Science,
48013
Bilbao,
Spain
14
Departamento de Física Atómica, Molecular y Nuclear, Facultad de
Física, Universidad de Sevilla, 41012
Sevilla,
Spain
15
Institut de Ciències de l’Espai (IEEC-CSIC), Facultat de
Ciències, Campus
UAB, 08193
Bellaterra,
Spain
16
Departamento de Astronomía, Pontificia Universidad Católica.
782-0436
Santiago,
Chile
17
Instituto de Física Teórica, UAM/CSIC, Universidad Autónoma de
Madrid, Cantoblanco, 28049
Madrid,
Spain
18
Campus of International Excellence UAM+CSIC,
Cantoblanco, 28049
Madrid,
Spain
Received: 12 June 2015
Accepted: 1 August 2015
Aims. The relative cosmic variance (σv) is a fundamental source of uncertainty in pencil-beam surveys and, as a particular case of count-in-cell statistics, can be used to estimate the bias between galaxies and their underlying dark-matter distribution. Our goal is to test the significance of the clustering information encoded in the σv measured in the ALHAMBRA survey.
Methods. We measure the cosmic variance of several galaxy populations selected with B-band luminosity at 0.35 ≤ z< 1.05 as the intrinsic dispersion in the number density distribution derived from the 48 ALHAMBRA subfields. We compare the observational σv with the cosmic variance of the dark matter expected from the theory, σv,dm. This provides an estimation of the galaxy bias b.
Results. The galaxy bias from the cosmic variance is in excellent agreement with the bias estimated by two-point correlation function analysis in ALHAMBRA. This holds for different redshift bins, for red and blue subsamples, and for several B-band luminosity selections. We find that b increases with the B-band luminosity and the redshift, as expected from previous work. Moreover, red galaxies have a larger bias than blue galaxies, with a relative bias of brel = 1.4 ± 0.2.
Conclusions. Our results demonstrate that the cosmic variance measured in ALHAMBRA is due to the clustering of galaxies and can be used to characterise the σv affecting pencil-beam surveys. In addition, it can also be used to estimate the galaxy bias b from a method independent of correlation functions.
Key words: dark matter / galaxies: statistics
© ESO, 2015
1. Introduction
One fundamental uncertainty in any observational measurement derived from galaxy surveys is the relative cosmic variance (σv, also called sample variance), arising from the underlying large-scale density fluctuations and leading to variances larger than those expected from simple Poisson statistics. The most efficient way to tackle the cosmic variance is to split the survey into several independent areas on the sky. This minimises the sampling problem and it is better than increasing the volume in a wide contiguous field (e.g. Driver & Robotham 2010). However, the uncertainties in many existing surveys are dominated by the cosmic variance because of the observational constraints (depth vs. area). Thus, a proper estimation of σv is needed to fully describe the error budget in deep cosmological surveys.
The impact of the cosmic variance in a given survey and redshift range can be estimated using two basic methods: theoretically, by analysing cosmological simulations (e.g. Somerville et al. 2004; Trenti & Stiavelli 2008; Stringer et al. 2009; Moster et al. 2011), or empirically, by sampling a larger survey (e.g. Driver & Robotham 2010; López-Sanjuan et al. 2014; Keenan et al. 2014). Unfortunately, the value of previous empirical work is limited by the precise understanding of the measured cosmic variance: the estimated σv must encode, by definition, the clustering of the studied populations, but no previous work in the literature has tested this requirement.
The galaxy bias b is the relationship between the spatial distribution of galaxies and the underlying dark-matter density field (Kaiser 1984; Bardeen et al. 1986; Mo & White 1996). The cosmic variance σv is a particular case of count-in-cell statistics (Peebles 1980; Efstathiou et al. 1990; Efstathiou 1995; Andreani et al. 1994; Adelberger et al. 1998; Dekel & Lahav 1999; Marinoni et al. 2005; Robertson 2010; Yang & Saslaw 2011; Di Porto et al. 2014), and can be therefore used to estimate b by comparison with σv,dm, the cosmic variance of the dark matter expected from the theory. The galaxy bias computed from the cosmic variance, noted bv, encodes the clustering information of σv and has to be the same that the bias estimated with an independent method at similar scales. We use the bias computed from the two-point correlation function, noted bξ, as a benchmark because it is a well-tested method widely used in the literature. The agreement between bv and bξ implies that the origin of the observational σv is the clustering of galaxies, as desired, while the discrepancy reflects deficiencies in our methodology to measure σv.
We take advantage of the unique design, depth, and photometric redshift accuracy of the Advanced, Large, Homogeneous Area, Medium-Band Redshift Astronomical (ALHAMBRA) survey1 (Moles et al. 2008) to study the clustering signal encoded in the cosmic variance. We compare the observed cosmic variance with the expectations from non-linear theory to estimate the galaxy bias bv. Then, we compare bv with the bξ reported by Arnalte-Mur et al. (2014, AM14 hereafter) from two-point correlation function analysis using the same data set, cosmological parameters, and theoretical expectations.
The paper is organised as follows. In Sect. 2, we present the ALHAMBRA survey and its photometric redshifts and probability distribution functions, and in Sect. 3 our estimation of the cosmic variance and the galaxy bias. We compare our results with the bias estimated from correlation function analysis in Sect. 4. Finally, we present our summary and conclusions in Sect. 5. Throughout this paper we use a standard cosmology with Ωm = 0.27, ΩΛ = 0.73, H0 = 100h km s-1 Mpc-1, and σ8 = 0.816. To avoid systematics in our results, these cosmological parameters are the same as in AM14. Magnitudes are given in the AB system (Oke & Gunn 1983) and the absolute B-band magnitudes are given as MB − 5log 10h, even when not explicitly indicated.
ALHAMBRA survey fields.
2. ALHAMBRA survey
The ALHAMBRA survey provides a photometric data set over 20 contiguous, equal-width (~300 Å), non-overlapping, medium-band optical filters (3500−9700 Å) plus three standard broad-band near-infrared (NIR) filters (J, H, and Ks) over eight different regions of the northern sky (Moles et al. 2008). The survey has the aim of understanding the evolution of galaxies throughout cosmic time by sampling a large cosmological fraction of the Universe, for which reliable spectral energy distributions (SEDs) and precise photometric redshifts (zp) are needed. The simulations of Benítez et al. (2009), which relate the image depth and the accuracy of the photometric redshifts to the number of filters, have demonstrated that the filter set chosen for ALHAMBRA can achieve a photometric redshift precision that is three times better than a classical 4−5 optical broad-band filter set. The final survey parameters and scientific goals, as well as the technical requirements of the filter set, were described by Moles et al. (2008). The survey has collected its data for the 20+3 optical-NIR filters in the 3.5 m telescope at the Calar Alto observatory, using the wide-field camera LAICA (Large Area Imager for Calar Alto) in the optical and the OMEGA−2000 camera in the NIR. The full characterisation, description, and performance of the ALHAMBRA optical photometric system were presented in Aparicio-Villegas et al. (2010). A summary of the optical reduction can be found in Cristóbal-Hornillos et al. (in prep.), the NIR reduction is reported in Cristóbal-Hornillos et al. (2009).
The ALHAMBRA survey has observed eight well-separated regions of the sky. The wide-field camera LAICA has four chips, each with a 15′ × 15′ field of view (0.22 arcsec pixel-1). The separation between chips is 13′. Thus, each LAICA pointing provides four distinct areas in the sky, one per chip. Six ALHAMBRA regions comprise two LAICA pointings. In these cases, the pointings define two separate strips in the sky. We assumed the four chips in each LAICA pointing to be independent subfields. We summarise the properties of the seven fields included in the first ALHAMBRA data release in Table 1. Currently, ALHAMBRA comprises 48 subfields of ~183.5 arcmin2, which can be assumed to be independent for cosmic variance studies as demonstrated by López-Sanjuan et al. (2014).
2.1. Bayesian photometric redshifts in ALHAMBRA
The photometric redshifts used throughout were fully presented and tested in Molino et al. (2014), and we summarise their principal characteristics below.
The photometric redshifts of ALHAMBRA were estimated with BPZ2.0, a new version of the Bayesian Photometric Redshift (BPZ, Benítez 2000) estimator. This is a SED-fitting method based on a Bayesian inference, where a maximum likelihood is weighted by a prior probability. ALHAMBRA relied on the ColorPro software (Coe et al. 2006) to perform point spread function (PSF) matched aperture-corrected photometry, which provided both total magnitudes and isophotal colours for the galaxies. In addition, a homogeneous photometric zero-point recalibration was performed using either spectroscopic redshifts (when available) or accurate photometric redshifts from emission-line galaxies (Molino et al. 2014). Sources were detected in a synthetic F814W filter image, noted I in the following, defined to resemble the HST/F814W filter. The areas of the images affected by bright stars and those with lower exposure times (e.g. the edges of the images) were masked following Arnalte-Mur et al. (2014). The total area covered by the current ALHAMBRA data after masking is 2.38 deg2 (Table 1). Finally, a statistical star/galaxy separation was encoded in the variable Stellar_Flag of the ALHAMBRA catalogues, and we kept ALHAMBRA sources with Stellar˙Flag≤ 0.5 as galaxies.
The photometric redshift accuracy, as estimated by comparison with ~7200 spectroscopic redshifts (zs), was encoded in the normalised median absolute deviation (NMAD) of the photometric vs. spectroscopic redshift distribution (Ilbert et al. 2006; Brammer et al. 2008),  (1)where δz = zp − zs and ⟨·⟩ is the median operator. The fraction of catastrophic outliers η is defined as the fraction of galaxies with | δz | /(1 + zs) > 0.2. In the case of ALHAMBRA, σNMAD = 0.011 for I ≤ 22.5 galaxies with a fraction of catastrophic outliers of η = 2.1%. We refer to Molino et al. (2014) for a more detailed discussion of the ALHAMBRA photometric redshifts.
(1)where δz = zp − zs and ⟨·⟩ is the median operator. The fraction of catastrophic outliers η is defined as the fraction of galaxies with | δz | /(1 + zs) > 0.2. In the case of ALHAMBRA, σNMAD = 0.011 for I ≤ 22.5 galaxies with a fraction of catastrophic outliers of η = 2.1%. We refer to Molino et al. (2014) for a more detailed discussion of the ALHAMBRA photometric redshifts.
2.2. Probability distribution functions in ALHAMBRA
This section is devoted to the description of the probability distribution functions (PDFs) of the ALHAMBRA sources. When dealing with photometric redshifts, several studies show that it is better to use the full PDF than to use only the best zp (e.g. Fernández-Soto et al. 2002; Cunha et al. 2009; Wittman 2009; Myers et al. 2009; Schmidt & Thorman 2013; Carrasco Kind & Brunner 2014). The ALHAMBRA PDFs have been successfully used to study high-redshift (z> 2) galaxies (Viironen et al. 2015), to detect galaxy groups and clusters (Ascaso et al. 2015), to estimate the merger fraction (López-Sanjuan et al. 2015), or to improve the estimation of stellar population parameters (Díaz-García et al. 2015).
The probability that a galaxy i is located at redshift z and has a spectral type T is PDFi (z,T). This probability density function is the posterior provided by BPZ2.0. The probability that the galaxy i is located at redshift z is then 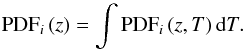 (2)Moreover, the total probability that the galaxy i is located at z1 ≤ z<z2 is
(2)Moreover, the total probability that the galaxy i is located at z1 ≤ z<z2 is 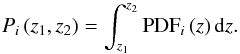 (3)The probability density function PDFi (z,T) is normalised to one by definition; in other words, the probability of any galaxy i being found in the whole parameter space is one. Formally,
(3)The probability density function PDFi (z,T) is normalised to one by definition; in other words, the probability of any galaxy i being found in the whole parameter space is one. Formally,  (4)The B-band absolute magnitude of a galaxy with observed magnitude I = 20 and spectral type T that is located at redshift z is denoted as
(4)The B-band absolute magnitude of a galaxy with observed magnitude I = 20 and spectral type T that is located at redshift z is denoted as 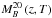 , which is also provided by BPZ2.0. This function condenses the information about the luminosity distance, which depends on z, and the k correction, which depends on z and T, needed to translate observed I-band magnitudes to absolute B-band magnitudes. Thus, the MB of the galaxy i depends on its z and T, and we have to weight
, which is also provided by BPZ2.0. This function condenses the information about the luminosity distance, which depends on z, and the k correction, which depends on z and T, needed to translate observed I-band magnitudes to absolute B-band magnitudes. Thus, the MB of the galaxy i depends on its z and T, and we have to weight 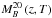 with the corresponding PDFi (z,T) to obtain MB,i. Formally, we estimate MB as a function of z as
with the corresponding PDFi (z,T) to obtain MB,i. Formally, we estimate MB as a function of z as  (5)where Ii is the observed I-band magnitude of the source.
(5)where Ii is the observed I-band magnitude of the source.
Thanks to the probability functions defined in this section, we are able to statistically use the output of current photometric redshift codes without losing information.
2.3. Sample selection
We focus our analysis on the galaxies in the ALHAMBRA first data release2. This catalogue comprises ~500 k sources and is complete (5σ, 3″ aperture) for I ≤ 24.5 galaxies (Molino et al. 2014).
We perform our study in a given redshift range z ∈ [ zmin,zmax) with B-band luminosity selected samples. Because the MB of a galaxy depends on its redshift as shown in Sect. 2.2, we manage the galaxy samples under study with the function  , defined as
, defined as 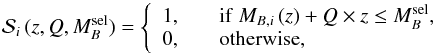 (6)where MB,i (z) is the B-band luminosity of the galaxy i from Eq. (5),
(6)where MB,i (z) is the B-band luminosity of the galaxy i from Eq. (5),  is the selection magnitude of the sample, and the term Q × z accounts for the evolution of the luminosity function with redshift. This last term ensures that we explore similar
is the selection magnitude of the sample, and the term Q × z accounts for the evolution of the luminosity function with redshift. This last term ensures that we explore similar  luminosities at every z, where
luminosities at every z, where  is the typical B-band luminosity at a given redshift reported by Ilbert et al. (2006).
is the typical B-band luminosity at a given redshift reported by Ilbert et al. (2006).
Our goal is to compare the galaxy bias derived from the cosmic variance with the bias measured from the two-point correlation function analysis performed by AM14. To minimise any possible difference between the two studies, we define the same redshift ranges and B-band luminosity selections as AM14. The studied samples, defined with Q = 0.6 to mimic AM14 selection, are summarised in the first two columns of Table 2, and cover a B-band luminosity from  to 2 at 0.35 ≤ z< 1.05. The
to 2 at 0.35 ≤ z< 1.05. The  values in the table are those reported by AM14.
values in the table are those reported by AM14.
3. Estimation of the galaxy bias from the cosmic variance
In this section we present the steps we follow to estimate the galaxy bias from the cosmic variance in ALHAMBRA. First, we expose the theoretical relation between the cosmic variance and b (Sect. 3.1). Then, we detail how to measure the cosmic variance from ALHAMBRA data (Sect. 3.2). Finally, we estimate the cosmic variance of the dark matter expected from theory (Sect. 3.3).
3.1. Theoretical link between σv and b
To connect the cosmic variance with the galaxy bias, we follow Somerville et al. (2004) and Moster et al. (2011). The mean ⟨ N ⟩ and the variance ⟨ N2 ⟩ − ⟨ N ⟩ 2 in the distribution of galaxies are given by the first and second moments of the probability distribution PN (V), which describes the probability of counting N objects within a volume V. The relative cosmic variance is defined as 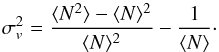 (7)The second term represents the correction for the Poisson shot noise. The second moment of the object counts is
(7)The second term represents the correction for the Poisson shot noise. The second moment of the object counts is  (8)where ξ is the two-point correlation function of the sample under study (Peebles 1980). Combining this with Eq. (7), the relative cosmic variance can be written as
(8)where ξ is the two-point correlation function of the sample under study (Peebles 1980). Combining this with Eq. (7), the relative cosmic variance can be written as  (9)We can approximate the galaxy correlation function in Eq. (9) using the correlation function for dark matter ξdm as ξ = b2ξdm, where b is the galaxy linear bias and we assume that b does not depend on scale. With this definition of the correlation function, we find that
(9)We can approximate the galaxy correlation function in Eq. (9) using the correlation function for dark matter ξdm as ξ = b2ξdm, where b is the galaxy linear bias and we assume that b does not depend on scale. With this definition of the correlation function, we find that 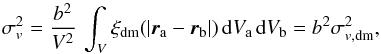 (10)where σv,dm is the cosmic variance of the dark matter. Finally, the galaxy bias from the cosmic variance is
(10)where σv,dm is the cosmic variance of the dark matter. Finally, the galaxy bias from the cosmic variance is 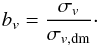 (11)We estimate σv from ALHAMBRA data in Sect. 3.2, and σv,dm from theory in Sect. 3.3.
(11)We estimate σv from ALHAMBRA data in Sect. 3.2, and σv,dm from theory in Sect. 3.3.
3.2. Measuring the cosmic variance σv in ALHAMBRA
In this section we define the procedure used to measure the cosmic variance from ALHAMBRA data. We estimate the number density of galaxies (n) in the ALHAMBRA subfield j for a given B-band luminosity selection  and redshift range z ∈ [ zmin,zmax) as
and redshift range z ∈ [ zmin,zmax) as 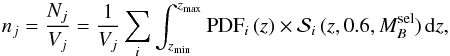 (12)where Nj is the number of galaxies that fulfil the selection, and Vj is the cosmic volume probed by the subfield j at zmin ≤ z<zmax. The index i spans all the galaxies in the subfield; that is, no pre-selection of the sources is performed. A similar probabilistic approach is used by Viironen et al. (2015) to study the number counts of high-redshift galaxies.
(12)where Nj is the number of galaxies that fulfil the selection, and Vj is the cosmic volume probed by the subfield j at zmin ≤ z<zmax. The index i spans all the galaxies in the subfield; that is, no pre-selection of the sources is performed. A similar probabilistic approach is used by Viironen et al. (2015) to study the number counts of high-redshift galaxies.
 |
Fig. 1 Number density distribution of |
Galaxy bias estimated from the cosmic variance in ALHAMBRA.
The 48 number densities nj from the ALHAMBRA subfields follow a log-normal distribution, ![\begin{equation} P_{\rm LN}\,(n\,|\,\mu, \sigma) = \frac{1}{n\sqrt{2 \pi}\,\sigma}\,{\rm exp}\,\bigg[-\frac{(\ln n - \mu)^2}{2 \sigma^2}\bigg]\,,\label{Plog} \end{equation}](/articles/aa/full_html/2015/10/aa26731-15/aa26731-15-eq202.png) (13)where μ and σ are the median and the dispersion of a Gaussian function in log-space,
(13)where μ and σ are the median and the dispersion of a Gaussian function in log-space, ![\begin{equation} P_{\rm G}\,(n'\,|\,\mu, \sigma) = \frac{1}{\sqrt{2 \pi}\,\sigma}\,{\rm exp}\,\bigg[-\frac{(n' - \mu)^2}{2 \sigma^2}\bigg]\,,\label{Pg} \end{equation}](/articles/aa/full_html/2015/10/aa26731-15/aa26731-15-eq205.png) (14)where n′ = lnn. This log-normal distribution of the number densities was expected because the distribution of overdense structures in the Universe is described by a log-normal function (e.g. Coles & Jones 1991; de la Torre et al. 2010; Kovač et al. 2010; Yang & Saslaw 2011). We present two representative examples in Fig. 1. We checked that the number densities of all the samples under study follow a log-normal distribution with an Anderson & Darling (1952) test. This test confirms that the distribution of the number densities is compatible with a log-normal shape and always disfavours a Gaussian distribution.
(14)where n′ = lnn. This log-normal distribution of the number densities was expected because the distribution of overdense structures in the Universe is described by a log-normal function (e.g. Coles & Jones 1991; de la Torre et al. 2010; Kovač et al. 2010; Yang & Saslaw 2011). We present two representative examples in Fig. 1. We checked that the number densities of all the samples under study follow a log-normal distribution with an Anderson & Darling (1952) test. This test confirms that the distribution of the number densities is compatible with a log-normal shape and always disfavours a Gaussian distribution.
There are two origins of the observed σ: the intrinsic dispersion σint (i.e. the field-to-field variation due to the clustering of the galaxies), and the dispersion due to the Poisson shot noise σP. We estimate the Poisson shot noise in each subfield as  (15)and apply the maximum likelihood estimator (MLE) presented in López-Sanjuan et al. (2014) to measure the median number density of the distribution
(15)and apply the maximum likelihood estimator (MLE) presented in López-Sanjuan et al. (2014) to measure the median number density of the distribution 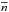 , the intrinsic dispersion σint, and their uncertainties.
, the intrinsic dispersion σint, and their uncertainties.
Applying Eq. (7) to PLN (n), we conclude that the observed relative cosmic variance is 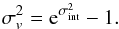 (16)We estimate the σv uncertainty by propagating the uncertainty in σint, as estimated with the MLE (see López-Sanjuan et al. 2014, for details). We summarise the median number density
(16)We estimate the σv uncertainty by propagating the uncertainty in σint, as estimated with the MLE (see López-Sanjuan et al. 2014, for details). We summarise the median number density 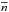 and the measured cosmic variance σv of the studied samples in Cols. 3 and 4 of Table 2. We note that the average number densities reported by AM14 differ from our values. This discrepancy is explained by the number density definition: we estimate a probabilistic number density from Eq. (12) and AM14 assumed the galaxies located at their best photometric redshift.
and the measured cosmic variance σv of the studied samples in Cols. 3 and 4 of Table 2. We note that the average number densities reported by AM14 differ from our values. This discrepancy is explained by the number density definition: we estimate a probabilistic number density from Eq. (12) and AM14 assumed the galaxies located at their best photometric redshift.
3.3. Estimation of the dark-matter cosmic variance σv,dm
The final ingredient needed to estimate the galaxy bias bv from Eq. (11) is σv,dm, the cosmic variance of the dark matter expected from the theory. We calculate σv,dm in each volume by solving the integral in Eq. (9) for dark matter using the code QUICKCV3, which is described in Newman & Davis (2002). The code computes the cosmic variance from the dark-matter power spectrum using a window function which is 1 inside the interest volume and 0 otherwise. We obtain the dark-matter power spectrum at each redshift bin using the CAMB software (Lewis et al. 2000), including the non-linear corrections of HALOFIT (Smith et al. 2003).
The cosmic variance is a particular case of count-in-cell statistics, and the procedure used to estimate the galaxy linear bias is similar if either spherical or cubic volumes are used instead (see references in Sect. 1). In the next section, we compare the galaxy bias bv estimated from the cosmic variance with the values reported in ALHAMBRA by AM14 from two-point correlation function analysis. They estimate the galaxy bias as  (17)where wp is the measured projected correlation function and wp,dm is the projected dark-matter correlation function expected from the theory.
(17)where wp is the measured projected correlation function and wp,dm is the projected dark-matter correlation function expected from the theory.
4. Clustering signal encoded in the cosmic variance
We summarise the studied samples, the measured cosmic variance σv, the inferred galaxy bias from the cosmic variance bv, and the galaxy bias bξ reported by AM14 from correlation function analysis in Table 2. We show the comparison between bv and bξ in three redshift bins and for several B-band luminosity selections in Fig. 2.
We find that the galaxy bias from the cosmic variance nicely agrees with the values from AM14, with all the estimations consistent at the 1σ level. This result has two important implications. First, it confirms that the cosmic variance measured in ALHAMBRA is due to the clustering of galaxies and the methodology applied to measure σv is therefore correct. Thus, the ALHAMBRA σv can be used to characterise the cosmic variance affecting pencil-beam surveys, reinforcing the results and the parametrisation of σv for close-pair studies presented by López-Sanjuan et al. (2014). Second, we can estimate the galaxy bias b from the cosmic variance, complementing the bias measurements from correlation function analysis with an independent method. The σv is measured in large volumes defined by the observational strategy of the survey, and it is unaffected by the photometric redshift precision and peculiar motions as the counts-in-cells performed with spherical or cubic volumes (Papageorgiou et al. 2012).
Regarding the observed trends, we find that bv increases with the B-band luminosity of the sample and, for a fixed selection, increases with redshift. These trends have already been found in several studies (e.g. Benoist et al. 1996; Norberg et al. 2001; Pollo et al. 2006; Coil et al. 2006; Coupon et al. 2012; Skibba et al. 2014; AM14). The quantitative comparison with the galaxy bias measured by other surveys is beyond the scope of this paper. Because of the excellent agreement with the AM14 values, we refer the reader to AM14 for a detailed discussion of the galaxy bias measurements in ALHAMBRA and a comparison with previous work in the literature.
In the next sections we explore the impact on the bv vs. bξ comparison of the ALHAMBRA fields explored (Sect. 4.1), the power-spectrum model used (Sect. 4.2), the probed scale (Sect. 4.3), and the colour of the galaxies (Sect. 4.4).
 |
Fig. 2 Galaxy bias b as a function of the B-band luminosity in three redshift bins (labelled in the panels). The dots are from this work by cosmic variance analysis, bv. The red crosses are from Arnalte-Mur et al. (2014) from the two-point correlation function analysis, bξ. The dotted line marks unity. A colour version of this plot is available in the electronic edition. |
4.1. Dependence on the explored fields
Arnalte-Mur et al. (2014) conclude that the fields ALHAMBRA-4 (COSMOS) and ALHAMBRA-7 (ELAIS-N1) have significantly different clustering properties from the other ALHAMBRA fields. Thus, in addition to the global measurements presented in the previous section, AM14 also reported the bξ estimated without using the fields ALHAMBRA-4 and ALHAMBRA-7. To further check the ALHAMBRA cosmic variance, we also estimated the galaxy bias bv without the 12 subfields corresponding to the ALHAMBRA-4 and ALHAMBRA-7 fields. The results are summarised in Fig. 3. As in the global case, the agreement between both estimations of the galaxy bias is remarkable and further support that the clustering measured by the correlation function is encoded in the estimated cosmic variance, as desired.
4.2. Dependence on the power-spectrum model
The power spectrum that we used to estimate σv,dm accounts for the non-linear evolution of the dark matter. The popular work of Moster et al. (2011) also uses QUICKCV but with a linear power spectrum. We checked that the values from Moster et al. (2011) are recovered if linear theory is used, and we estimated the impact of non-linear evolution in the theoretical models. We find that the σv,dm from non-linear theory is larger by 15%, 9%, and 6% than the cosmic variance from linear theory reported by Moster et al. (2011) at 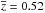 , 0.74, and 0.91, respectively. These differences are below the 20% accuracy targeted by Moster et al. (2011) and decrease with redshift for two main reasons: first, the impact of the non-linear evolution increases with the growth of the structures, and therefore decreases with z. Second, the non-linear effects are important at scales smaller than ~1 h-1 Mpc. The scale probed by each ALHAMBRA subfield increases with z, decreasing the impact of the non-linear evolution.
, 0.74, and 0.91, respectively. These differences are below the 20% accuracy targeted by Moster et al. (2011) and decrease with redshift for two main reasons: first, the impact of the non-linear evolution increases with the growth of the structures, and therefore decreases with z. Second, the non-linear effects are important at scales smaller than ~1 h-1 Mpc. The scale probed by each ALHAMBRA subfield increases with z, decreasing the impact of the non-linear evolution.
4.3. Dependence on the probed scale
Throughout this paper, we assume that the galaxy bias b does not depend on scale, but b is a scale-dependent parameter (e.g. Heavens et al. 1998; Mann et al. 1998; Cresswell & Percival 2009). The observational studies find that the bias is nearly constant for scales larger than r ~ 1 h-1 Mpc (the linear bias regime), with larger b values at smaller scales (e.g. White et al. 2011; Parejko et al. 2013). The values of bξ reported by AM14 are computed in the linear bias regime, from 1 h-1 Mpc to 10 h-1 Mpc. In the cosmic variance case, we integrate all the scales inside the volume of interest, and the measurements of bv are affected by scales smaller than r = 1 h-1 Mpc. The integration in Eq. (9) weights each scale by r2, so the impact of the small scales decreases with the area subtended by the ALHAMBRA subfields. This subtended area increases from ~3.6 × 3.6 h-2 Mpc2 at 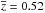 to ~4.5 × 4.5 h-2 Mpc2 at
to ~4.5 × 4.5 h-2 Mpc2 at 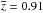 . We find that bv and bξ are similar, implying that bv is dominated by the linear bias regime and that the ALHAMBRA subfields are large enough to reduce the scale dependence of the bias.
. We find that bv and bξ are similar, implying that bv is dominated by the linear bias regime and that the ALHAMBRA subfields are large enough to reduce the scale dependence of the bias.
We further test the impact of small scales with a toy model. In our model, we assumed a scale-dependent bias of the form  (18)as suggested by observations (White et al. 2011; Parejko et al. 2013). We applied this bias model to the non-linear power spectrum and computed the cosmic variance of this biased power spectrum, noted
(18)as suggested by observations (White et al. 2011; Parejko et al. 2013). We applied this bias model to the non-linear power spectrum and computed the cosmic variance of this biased power spectrum, noted 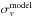 . The comparison between
. The comparison between 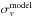 and σv,dm provides an effective bias beff that should be close to beff = 2 if the signal is dominated by the linear bias regime. We find beff = 2.2,2.1, and 2.1 at
and σv,dm provides an effective bias beff that should be close to beff = 2 if the signal is dominated by the linear bias regime. We find beff = 2.2,2.1, and 2.1 at 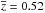 , 0.74, and 0.91, respectively. This confirms that small scales should affect our measurements by less than 10%, supporting that bv is comparable to the linear bias measured with bξ given the geometry of the ALHAMBRA survey.
, 0.74, and 0.91, respectively. This confirms that small scales should affect our measurements by less than 10%, supporting that bv is comparable to the linear bias measured with bξ given the geometry of the ALHAMBRA survey.
 |
Fig. 3 Galaxy bias b as a function of the B-band luminosity in three redshift bins (labelled in the panels) with the 12 subfields from ALHAMBRA-4 and ALHAMBRA-7 removed. The dots are from this work by cosmic variance analysis, bv. The red crosses are from Arnalte-Mur et al. (2014) by two-point correlation function analysis, bξ. The dotted line marks unity. A colour version of this plot is available in the electronic edition. |
Galaxy bias of galaxies with 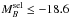 as a function of colour estimated from the cosmic variance in ALHAMBRA.
as a function of colour estimated from the cosmic variance in ALHAMBRA.
 |
Fig. 4 Galaxy bias b of E/S0 (red symbols) and S/SB (blue symbols) galaxies with |
4.4. Dependence on the colour
Following the work of AM14, Hurtado-Gil et al. (2015) study the two-point correlation function and the galaxy bias of red and blue galaxies with 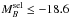 in the ALHAMBRA survey. To complete the comparison between bv and bξ, we also estimated the galaxy bias of red and blue galaxies with
in the ALHAMBRA survey. To complete the comparison between bv and bξ, we also estimated the galaxy bias of red and blue galaxies with 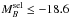 from the cosmic variance.
from the cosmic variance.
To define red and blue galaxies, we take advantage of the profuse information encoded in the PDFs. Instead of selecting galaxies according to their observed colour or their best spectral template, we split each PDF into red templates (T = E/S0), denoted PDFred, and blue templates (T = S/SB), denoted PDFblue. Formally,  (19)In practice, the red templates have T ∈ [1,5.5] and the blue templates have T ∈ (5.5,11] in the ALHAMBRA catalogues. Thus, we can reliably work with colour segregations without any pre-selection of the sources (e.g. López-Sanjuan et al. 2015).
(19)In practice, the red templates have T ∈ [1,5.5] and the blue templates have T ∈ (5.5,11] in the ALHAMBRA catalogues. Thus, we can reliably work with colour segregations without any pre-selection of the sources (e.g. López-Sanjuan et al. 2015).
We summarise the basic properties of the samples under study, the measured σv and bv, and the bξ reported by Hurtado-Gil et al. (2015) in Table 3. We note that the subfields from ALHAMBRA-4 are not included in this analysis because Hurtado-Gil et al. (2015) discard this field owing to its peculiar clustering properties. As in the general case, bv agrees with bξ at the 1σ level both for red and blue galaxies, reinforcing our results and conclusions (Fig. 4). We find that red galaxies are more biased than blue galaxies, with bv being compatible with a constant bias in the redshift range under study. The error-weighted averages at 0.35 ≤ z< 1.0 are  and
and 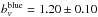 . This implies a relative bias of
. This implies a relative bias of 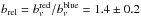 , in agreement with previous work that find brel ~ 1.3−1.7 at z< 1 (e.g. Madgwick et al. 2003; Meneux et al. 2006; Coil et al. 2008; de la Torre et al. 2011; Skibba et al. 2014; Hurtado-Gil et al. 2015).
, in agreement with previous work that find brel ~ 1.3−1.7 at z< 1 (e.g. Madgwick et al. 2003; Meneux et al. 2006; Coil et al. 2008; de la Torre et al. 2011; Skibba et al. 2014; Hurtado-Gil et al. 2015).
5. Summary and conclusions
We estimate the significance of the clustering signal encoded in the cosmic variance σv measured in the ALHAMBRA survey. With this aim, we measured the galaxy bias b from the ALHAMBRA cosmic variance. The cosmic variance is defined as the intrinsic dispersion (i.e. due to the field-to-field variations) in the number density distribution of the 48 ALHAMBRA subfields. The number densities were computed using the full probability distribution functions (PDFs) of the ALHAMBRA photometric redshifts. We compared the observed σv with the cosmic variance of the dark matter expected from non-linear theory to estimate the galaxy bias b.
The galaxy bias from the cosmic variance nicely agrees with the bias estimated by AM14 in ALHAMBRA from two-point correlation function analysis. This confirms that the cosmic variance measured in ALHAMBRA is due to the clustering of galaxies and the methodology applied to measure σv is therefore correct. Thus, the ALHAMBRA σv can be used to characterise the cosmic variance affecting pencil-beam surveys, reinforcing the results and the parametrisation of the cosmic variance for close-pair studies presented by López-Sanjuan et al. (2014). We find that the bias increases with the B-band luminosity of the sample and, for a fixed selection, increases with redshift, in agreement with previous studies (e.g. Norberg et al. 2001; Coupon et al. 2012; AM14). Moreover, red galaxies have a larger bias than blue galaxies, with a relative bias of brel = 1.4 ± 0.2 (e.g. Madgwick et al. 2003; Meneux et al. 2006; Skibba et al. 2014).
The technique outlined in this paper can be used to estimate the galaxy bias b of high-redshift galaxies and of different galaxy populations at z< 1 (Sect. 4.4) simply from the dispersion of the observed number densities, complementing the bias measurements from correlation function analysis with an independent method. These number densities are measured in large volumes defined by the observational strategy of the survey rather than in the common spherical or cubic volumes, which are affected by the photometric redshift precision and peculiar motions (Papageorgiou et al. 2012). In addition to its cosmological and observational value, the study of the number density distribution can be useful in order to detect systematics and photometric inhomogeneities in the next generation of large photometric surveys, such as the Dark Energy Survey (DES, Flaugher 2012), the Javalambre-Physics of the accelerating Universe Astrophysical Survey (J-PAS, Benítez et al. 2014), and the Large Synoptic Survey Telescope (LSST, Ivezic et al. 2008).
QUICKCV is available at www.phyast.pitt.edu/~janewman/quickcv
Acknowledgments
We dedicate this paper to the memory of our six IAC colleagues and friends who met with a fatal accident in Piedra de los Cochinos, Tenerife, in February 2007, with special thanks to Maurizio Panniello, whose teachings of python were so important for this paper. We thank R. Angulo, S. Bonoli, A. Ederoclite, A. Orsi, and all the CEFCA staff for useful and productive discussions. We thank the anonymous referee for his/her suggestions, and K. Xu for the pertinent comments that motivated this work. This work has been mainly funded by the FITE (Fondos de Inversiones de Teruel) and the projects AYA2012-30789, AYA2006-14056, and CSD2007-00060. We also acknowledge support from the Spanish Ministry for Economy and Competitiveness and FEDER funds through grants AYA2010-15081, AYA2010-15169, AYA2010-22111-C03-01, AYA2010-22111-C03-02, AYA2011-29517-C03-01, AYA2012-39620, AYA2013-40611-P, AYA2013-42227-P, AYA2013-43188-P, AYA2013-48623-C2-1, AYA2013-48623-C2-2, ESP2013-48274, AYA2014-58861-C3-1, Aragón Government Research Group E103, Generalitat Valenciana projects Prometeo 2009/064 and PROMETEOII/2014/060, Junta de Andalucía grants TIC114, JA2828, P10-FQM-6444, and Generalitat de Catalunya project SGR-1398. A.J.C. and C.H.-M. are Ramón y Cajal fellows of the Spanish government. A. M. acknowledges the financial support of the Brazilian funding agency FAPESP (Post-doc fellowship - process number 2014/11806-9). M.P. acknowledges financial support from JAE-Doc program of the Spanish National Research Council (CSIC), co-funded by the European Social Fund. This research made use of Astropy, a community-developed core Python package for Astronomy (Astropy Collaboration et al. 2013), and Matplotlib, a 2D graphics package used for Python for publication-quality image generation across user interfaces and operating systems (Hunter 2007).
References
- Adelberger, K. L., Steidel, C. C., Giavalisco, M., et al. 1998, ApJ, 505, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Aihara, H., Allen de Prieto, C., An, D., et al. 2011, ApJS, 193, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, T. W., & Darling, D. A. 1952, Ann. Math. Statist., 23, 193 [CrossRef] [Google Scholar]
- Andreani, P., Cristiani, S., Lucchin, F., Matarrese, S., & Moscardini, L. 1994, ApJ, 430, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Aparicio-Villegas, T., Alfaro, E. J., Cabrera-Caño, J., et al. 2010, AJ, 139, 1242 [NASA ADS] [CrossRef] [Google Scholar]
- Arnalte-Mur, P., Martínez, V. J., Norberg, P., et al. 2014, MNRAS, 441, 1783 [NASA ADS] [CrossRef] [Google Scholar]
- Ascaso, B., Benítez, N., Fernández-Soto, A., et al. 2015, MNRAS, 452, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration, Robitaille, T. P., Tollerud, E. J., et al. 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bardeen, J. M., Bond, J. R., Kaiser, N., & Szalay, A. S. 1986, ApJ, 304, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Benítez, N. 2000, ApJ, 536, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Benítez, N., Moles, M., Aguerri, J. A. L., et al. 2009, ApJ, 692, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Benítez, N., Dupke, R., Moles, M., et al. 2014, in Highlights of Spanish Astrophysics VIII, Proc. XI Scientific Meeting of the Spanish Astronomical Society, eds. A. J. Cenarro, F. Figueras, C. Hernández- Monteagudo, J. Trujillo Bueno, & L. Valdivielso 148 [Google Scholar]
- Benoist, C., Maurogordato, S., da Costa, L. N., Cappi, A., & Schaeffer, R. 1996, ApJ, 472, 452 [NASA ADS] [CrossRef] [Google Scholar]
- Brammer, G. B., van Dokkum, P. G., & Coppi, P. 2008, ApJ, 686, 1503 [NASA ADS] [CrossRef] [Google Scholar]
- Carrasco Kind, M., & Brunner, R. J. 2014, MNRAS, 442, 3380 [NASA ADS] [CrossRef] [Google Scholar]
- Coe, D., Benítez, N., Sánchez, S. F., et al. 2006, AJ, 132, 926 [NASA ADS] [CrossRef] [Google Scholar]
- Coil, A. L., Newman, J. A., Cooper, M. C., et al. 2006, ApJ, 644, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Coil, A. L., Newman, J. A., Croton, D., et al. 2008, ApJ, 672, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Coles, P., & Jones, B. 1991, MNRAS, 248, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Coupon, J., Kilbinger, M., McCracken, H. J., et al. 2012, A&A, 542, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cresswell, J. G., & Percival, W. J. 2009, MNRAS, 392, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Cristóbal-Hornillos, D., Aguerri, J. A. L., Moles, M., et al. 2009, ApJ, 696, 1554 [NASA ADS] [CrossRef] [Google Scholar]
- Cunha, C. E., Lima, M., Oyaizu, H., Frieman, J., & Lin, H. 2009, MNRAS, 396, 2379 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, M., Guhathakurta, P., Konidaris, N. P., et al. 2007, ApJ, 660, L1 [NASA ADS] [CrossRef] [Google Scholar]
- de la Torre, S., Guzzo, L., Kovač, K., et al. 2010, MNRAS, 409, 867 [NASA ADS] [CrossRef] [Google Scholar]
- de la Torre, S., Le Fèvre, O., Porciani, C., et al. 2011, MNRAS, 412, 825 [Google Scholar]
- Dekel, A., & Lahav, O. 1999, ApJ, 520, 24 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Díaz-García, L. A., Cenarro, A. J., López-Sanjuan, C., et al. 2015, A&A, 582, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Porto, C., Branchini, E., Bel, J., et al. 2014, A&A, submitted [arXiv:1406.6692] [Google Scholar]
- Driver, S. P., & Robotham, A. S. G. 2010, MNRAS, 407, 2131 [NASA ADS] [CrossRef] [Google Scholar]
- Efstathiou, G. 1995, MNRAS, 276, 1425 [Google Scholar]
- Efstathiou, G., Kaiser, N., Saunders, W., et al. 1990, MNRAS, 247, 10P [Google Scholar]
- Fernández-Soto, A., Lanzetta, K. M., Chen, H.-W., Levine, B., & Yahata, N. 2002, MNRAS, 330, 889 [NASA ADS] [CrossRef] [Google Scholar]
- Flaugher, B. 2012, in APS April Meet. Abstr., D7007 [Google Scholar]
- Giavalisco, M., Ferguson, H. C., Koekemoer, A. M., et al. 2004, ApJ, 600, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Heavens, A. F., Matarrese, S., & Verde, L. 1998, MNRAS, 301, 797 [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
- Hurtado-Gil, Ll., Arnalte-Mur, P., Martínez, V. J., et al. 2015, ApJ, submitted [Google Scholar]
- Ilbert, O., Lauger, S., Tresse, L., et al. 2006, A&A, 453, 809 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ivezic, Z., Tyson, J. A., Acosta, E., et al. 2008, ArXiv e-prints [arXiv:0805.2366] [Google Scholar]
- Kaiser, N. 1984, ApJ, 284, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Keenan, R. C., Foucaud, S., De Propris, R., et al. 2014, ApJ, 795, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Kovač, K., Lilly, S. J., Cucciati, O., et al. 2010, ApJ, 708, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, A., Challinor, A., & Lasenby, A. 2000, ApJ, 538, 473 [NASA ADS] [CrossRef] [Google Scholar]
- López-Sanjuan, C., Cenarro, A. J., Hernández-Monteagudo, C., et al. 2014, A&A, 564, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López-Sanjuan, C., Cenarro, A. J., Varela, J., et al. 2015, A&A, 576, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Madgwick, D. S., Hawkins, E., Lahav, O., et al. 2003, MNRAS, 344, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Mann, R. G., Peacock, J. A., & Heavens, A. F. 1998, MNRAS, 293, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Marinoni, C., Le Fèvre, O., Meneux, B., et al. 2005, A&A, 442, 801 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meneux, B., Le Fèvre, O., Guzzo, L., et al. 2006, A&A, 452, 387 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mo, H. J., & White, S. D. M. 1996, MNRAS, 282, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Moles, M., Benítez, N., Aguerri, J. A. L., et al. 2008, AJ, 136, 1325 [Google Scholar]
- Molino, A., Benítez, N., Moles, M., et al. 2014, MNRAS, 441, 2891 [NASA ADS] [CrossRef] [Google Scholar]
- Moster, B. P., Somerville, R. S., Newman, J. A., & Rix, H.-W. 2011, ApJ, 731, 113 [Google Scholar]
- Myers, A. D., White, M., & Ball, N. M. 2009, MNRAS, 399, 2279 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, J. A., & Davis, M. 2002, ApJ, 564, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, J. A., Cooper, M. C., Davis, M., et al. 2013, ApJS, 208, 5 [Google Scholar]
- Norberg, P., Baugh, C. M., Hawkins, E., et al. 2001, MNRAS, 328, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Oke, J. B., & Gunn, J. E. 1983, ApJ, 266, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Papageorgiou, A., Plionis, M., Basilakos, S., & Ragone-Figueroa, C. 2012, MNRAS, 422, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Parejko, J. K., Sunayama, T., Padmanabhan, N., et al. 2013, MNRAS, 429, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E. 1980, The large-scale structure of the universe (Princeton University Press) [Google Scholar]
- Pollo, A., Guzzo, L., Le Fèvre, O., et al. 2006, A&A, 451, 409 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robertson, B. E. 2010, ApJ, 716, L229 [CrossRef] [Google Scholar]
- Rowan-Robinson, M., Lari, C., Perez-Fournon, I., et al. 2004, MNRAS, 351, 1290 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, S. J., & Thorman, P. 2013, MNRAS, 431, 2766 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N., Aussel, H., Brusa, M., et al. 2007, ApJS, 172, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Skibba, R. A., Smith, M. S. M., Coil, A. L., et al. 2014, ApJ, 784, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. E., Peacock, J. A., Jenkins, A., et al. 2003, MNRAS, 341, 1311 [NASA ADS] [CrossRef] [Google Scholar]
- Somerville, R. S., Lee, K., Ferguson, H. C., et al. 2004, ApJ, 600, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Stringer, M. J., Benson, A. J., Bundy, K., Ellis, R. S., & Quetin, E. L. 2009, MNRAS, 393, 1127 [NASA ADS] [CrossRef] [Google Scholar]
- Trenti, M., & Stiavelli, M. 2008, ApJ, 676, 767 [Google Scholar]
- Viironen, K., Marín-Franch, A., López-Sanjuan, C., et al. 2015, A&A, 576, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- White, M., Blanton, M., Bolton, A., et al. 2011, ApJ, 728, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Wittman, D. 2009, ApJ, 700, L174 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, A., & Saslaw, W. C. 2011, ApJ, 729, 123 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Galaxy bias of galaxies with 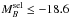 as a function of colour estimated from the cosmic variance in ALHAMBRA.
as a function of colour estimated from the cosmic variance in ALHAMBRA.
All Figures
 |
Fig. 1 Number density distribution of |
| In the text | |
 |
Fig. 2 Galaxy bias b as a function of the B-band luminosity in three redshift bins (labelled in the panels). The dots are from this work by cosmic variance analysis, bv. The red crosses are from Arnalte-Mur et al. (2014) from the two-point correlation function analysis, bξ. The dotted line marks unity. A colour version of this plot is available in the electronic edition. |
| In the text | |
 |
Fig. 3 Galaxy bias b as a function of the B-band luminosity in three redshift bins (labelled in the panels) with the 12 subfields from ALHAMBRA-4 and ALHAMBRA-7 removed. The dots are from this work by cosmic variance analysis, bv. The red crosses are from Arnalte-Mur et al. (2014) by two-point correlation function analysis, bξ. The dotted line marks unity. A colour version of this plot is available in the electronic edition. |
| In the text | |
 |
Fig. 4 Galaxy bias b of E/S0 (red symbols) and S/SB (blue symbols) galaxies with |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




