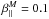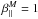EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 582 (October 2015) A&A, 582 (2015) A124 Full HTML
Free Access
Issue
A&A
Volume 582, October 2015
Article Number A124
Number of page(s) 7
Section The Sun
DOI https://doi.org/10.1051/0004-6361/201526509
Published online 26 October 2015

© ESO, 2015

1. Introduction

Largely extended in space, most astrophysical plasmas are dilute and low-collisional (see, e.g., Table 8.1 in the textbook by Schlickeiser 2002), and the plasma particles are expected to be out of thermal (Maxwellian) equilibrium in these systems. Direct in-situ measurements of the solar wind plasma confirm this hypothesis, providing evidence for the existence of departures from thermal equilibrium, as well as clues for their origin (Marsch 2006). Described by the velocity distribution functions (VDFs) of plasma particles (electrons, protons, heavier ions), nonequilibrium plasma states are indicated by the anisotropy of the distribution (for instance, in the solar wind the anisotropy is measured with respect to the uniform magnetic field), and especially by the suprathermal populations, which enhance the high-energy tails of the distributions and are ubiquitous in space plasmas (see the reviews by Pierrard & Lazar 2010; and Lazar et al. 2012). More pronounced in the electron distributions, the suprathermal populations (also known as the halo component) are reported for all species of plasma particles observed in the solar wind. The existence of suprathermal particles is not conditioned (maybe not directly) by the uniform magnetic field, but it seems to be well explained by a certain level of wave turbulence that keeps these populations energized and in a quasi-stationary equilibrium with the main thermal component (the core) of the solar wind particles.

Functional models, used for decades to describe the anisotropic distributions of plasma particles in the solar wind and supporting waves and fluctuations, were limited to standard bi-Maxwellians (see textbooks by Gary 1993; and Treumann & Baumjohann 1997). Bi-Maxwellians offer a simple description of the gyrotropic distributions (with a bi-axis temperature anisotropy), and are supported by the solar wind observations, as the best-fitting models for the core (low-energy) components of the distribution, representing roughly 90−95% of the total density. However, the suprathermal (halo) components are less dense but much hotter than the core, and, in general, highly anisotropic, such that their kinetic effects, especially those leading to instabilities and fluctuations cannot be ignored. According to the observations, the suprathermal tails of the distribution are best described by power laws. Of these, the best known is the Kappa VDF with its bi-Kappa variant to model the anisotropic temperature. To keep the analysis straightforward with a reduced number of parameters, the anisotropic Kappas are applied as “global” models, incorporating both the core and halo components (Summers & Thorne 1992; Fichtner & Sreenivasan 1993; Hellberg et al. 2005; Pierrard & Lazar 2010), mainly based on the fact that a Kappa is nearly Maxwellian at low energies and decreases smoothly as a power law at high energies. Although the core can be less anisotropic or much different than the halo, these two components cannot be decoupled, but are in fact interconnected. For that reason, a global bi-Kappa may be a convenient starting basis for studying the anisotropic suprathermal populations and their instabilities.

The bi-Kappa model is a generalization of the more idealized bi-Maxwellian approach, which is recovered in the limit of a very high power index κ → ∞. The comparison with a bi-Maxwellian becomes then possible, enabling us to quantify the effects of suprathermal populations. However, one major conclusion that emerges from the existing comparative studies is very intriguing: the excess of free energy stored by a nonequilibrium bi-Kappa plasma is not reflected in the effects on the kinetic instabilities. Precisely, in comparison with bi-Maxwellians, in bi-Kappa plasmas with the same temperatures and the same temperature anisotropy, the resulting instabilities are not enhanced. Contrary to expectations, the instability growth rates are inhibited by the increase of suprathermal populations, i.e., decreasing kappa index (Xue et al. 1996; Lazar & Poedts 2009; Mace & Sydora 2010; Lazar et al. 2011; 2013; Lazar 2012). An enhancing effect of the growth rates may also be apparent, but only for low values of the temperature anisotropy close to the marginal condition of stability where the growth rates Im(ω) ≡ γ → 0 (Summers & Thorne 1992; Xue et al. 1993; Mace 1998).

In this paper we revisit these two approaches: namely, the bi-Kappa and bi-Maxwellian models, and we propose to identify a method of comparative analysis that unveils the destabilizing effects of suprathermal populations. As an application, we analyze the electromagnetic electron cyclotron (EMEC) instability, also known as the whistler instability. The EMEC modes (whistlers) are right-handed (RH) circularly polarized modes with frequencies between the proton and electron gyrofrequencies (Ωp<ω< | Ωe |). These modes are destabilized by an excess of the electron perpendicular temperature, e.g., Te,⊥>Te,∥, where ∥,⊥ indicate directions with respect to the magnetic field direction. The observations have shown whistlers induced in atmospherics for the first time (Helliwell 1956), and later their existence was also proven in terrestrial magnetospheres (Cattell et al. 2008; Breneman et al. 2011) and the solar wind (Lacombe et al. 2014).

In the next section (Sect. 2), we introduce the bi-Maxwellian and bi-Kappa distribution functions to model the thermal core and global distribution, respectively. Basic concepts of comparative analysis are contrasted to depict a realistic method of characterization of the suprathermal populations and their destabilizing effects. In Sect. 3 this method is particularized to the EMEC instability, making a detailed comparison with the previous results, and showing major differences for the effects of suprathermal populations on this instability. Our results and their implications are concluded in Sect. 4.

2. Models for the VDFs

The anisotropic plasma systems are assumed to be collisionless and spatially homogeneous. To describe the initially unperturbed plasma, we first introduce the standard bi-Maxwellian model FM(v∥,v⊥)=1π3/2u⊥2u∥ exp(−v∥2u∥2−v⊥2u⊥2)=\begin{eqnarray} F_M (v_{\parallel}, v_{\perp}) &= & {1 \over \pi^{3/2} u_{\perp}^2 u_{\parallel}} \, \exp \left(- {v_{\parallel}^2\over u_{\parallel}^2 } - {v_{\perp}^2\over u_{\perp}^2 }\right) \notag \\ &=& \left(m \over 2 \pi k_{\rm B}\right)^{3/2} {1 \over T^M_\perp \sqrt{T^M_\parallel}} \exp \left[- {m \over 2 k_{\rm B}} \left( {v_{\parallel}^2\over T^M_{\parallel} } - {v_{\perp}^2\over T^M_{\perp} }\right) \right], \label{e1} \end{eqnarray}(1)using polar coordinates (vx,vy,vz) = (v⊥cosφ,v⊥sinφ,v∥) in the velocity space. This VDF is normalized to unity, 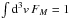d3∫v FM=1\hbox{$\int {\rm d}^3v\, F_M = 1$}, and describes a temperature anisotropy 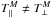T∥M≠T⊥M\hbox{$T^M_\parallel \ne T^M_\perp$} in terms of thermal velocities u∥,⊥ defined by 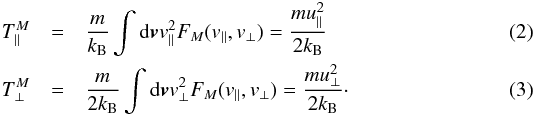T∥M=T⊥M=\begin{eqnarray} T_{\parallel}^M & =& {m \over k_{\rm B}} \int {\rm d}{\vec v} v_{\parallel}^2 F_M (v_{\parallel}, v_{\perp}) = {m u_{\parallel}^2 \over 2 k_{\rm B}}\label{e2} \\ T_{\perp}^M & = &{m \over 2 k_{\rm B}} \int {\rm d}{\vec v} v_{\perp}^2 F_M (v_{\parallel}, v_{\perp}) = {m u_{\perp}^2 \over 2 k_{\rm B}} \label{e3}\cdot \end{eqnarray}For the anisotropic distributions with suprathermal tails, we invoke a bi-Kappa distribution function FK(v∥,v⊥)=1π3/2θ⊥2θ∥ Γ[κ+1]κ3/2Γ[κ−1/2](1+v∥2κθ∥2+v⊥2κθ⊥2)−κ−1=[mπkB(2κ−3)]3/21T⊥KT∥KΓ[κ+1]Γ[κ−1/2]\begin{eqnarray} F_K (v_{\parallel}, v_{\perp}) &= & {1 \over \pi^{3/2} \theta_{\perp}^2 \theta_{\parallel}} \, {\Gamma[\kappa +1] \over \kappa^{3/2} \Gamma[\kappa -1/2]} \left(1 + {v_{\parallel}^2\over \kappa \theta_{\parallel}^2 } + {v_{\perp}^2\over \kappa \theta_{\perp}^2 }\right)^{-\kappa-1} \notag \\ & = &\left[m \over \pi k_{\rm B} (2\kappa-3)\right]^{3/2} {1 \over T^K_\perp \sqrt{T^K_\parallel}} {\Gamma[\kappa +1] \over \Gamma[\kappa -1/2]} \notag \\ && \times \left[1+ {m \over k_{\rm B} (2\kappa-3)} \left( {v_{\parallel}^2\over T^K_{\parallel} } - {v_{\perp}^2\over T^K_{\perp} }\right) \right]^{-\kappa-1}, \label{e4} \end{eqnarray}(4)which is normalized to unity 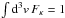d3∫v Fκ=1\hbox{$\int {\rm d}^3v\, F_\kappa = 1$}, and describes a temperature anisotropy 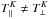T∥K≠T⊥K\hbox{$T^K_\parallel \ne T^K_\perp$} in terms of the equivalent thermal velocities θ∥,⊥ defined by 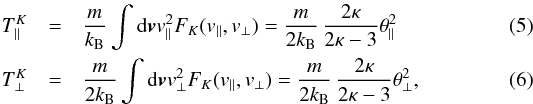T∥K=T⊥K=\begin{eqnarray} T_{\parallel}^K & =& {m \over k_{\rm B}} \int {\rm d}{\vec v} v_{\parallel}^2 F_K (v_{\parallel}, v_{\perp}) = {m \over 2 k_{\rm B}} \, {2 \kappa \over 2 \kappa -3} \theta_{\parallel}^2 \label{e5} \\ T_{\perp}^K & =& {m \over 2 k_{\rm B}} \int {\rm d}{\vec v} v_{\perp}^2 F_K (v_{\parallel}, v_{\perp}) = {m \over 2 k_{\rm B}} \, {2 \kappa \over 2 \kappa -3} \theta_{\perp}^2 \label{e6}, \end{eqnarray}for a spectral index κ> 3/2. To compare with a bi-Maxwellian, the bi-Kappa model may be built in two ways:

(A): Firstly, we can keep the temperature constant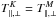T∥,⊥K=T∥,⊥M\hbox{$T^K_{\parallel,\perp} = T^M_{\parallel,\perp}$}, and only let the power-index κ> 3/2 vary. In this case, θ becomes κ-dependent by 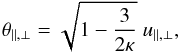θ∥,⊥=1−32κu∥,⊥,\begin{equation} \theta_{\parallel,\perp} = \sqrt{1- {3 \over 2 \kappa}} \; u_{\parallel,\perp} \label{e7}, \end{equation}(7)but the temperature anisotropy is also constant 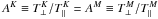AK≡T⊥K/T∥K=AM≡T⊥M/T∥M\hbox{$A^K \equiv T_\perp^K /T_\parallel^K = A^M \equiv T_\perp^M /T_\parallel^M$}. This method of comparison has been extensively used to evaluate the effects of the suprathermal populations on the kinetic instabilities (Xue et al. 1993, 1996; Mace 1998; Hellberg et al. 2005; Xiao et al. 2006; Lazar & Poedts 2009; Mace & Sydora 2010; Lazar et al. 2011, 2013; Mace et al. 2011; Lazar 2012), and contrary to the expectations, the results indicate a suppression of the instability with the increase of suprathermal populations for a wide range of plasma parameters and a wide spectrum of eigenmodes (e.g., the high-frequency electron cyclotron instability and low-frequency proton cyclotron instability). Moreover, in contrast to the Maxwellian limit, the Kappa model shows a pronounced (excentrical) peak (see Fig. 1a), making their comparison inappropriate to provide a plausible characterization of the suprathermal populations and their effects.

(B): Alternatively, we can assume θ∥,⊥ = u∥,⊥, implying higher Kappa temperatures 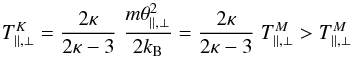T∥,⊥K=2κ2κ−3mθ∥,⊥22kB=2κ2κ−3T∥,⊥M>T∥,⊥M\begin{equation} T^K_{\parallel,\perp} = {2\kappa \over 2 \kappa - 3}\; {m \theta_{\parallel,\perp}^2 \over 2k_{\rm B}} = {2\kappa \over 2 \kappa - 3}\; T^M_{\parallel,\perp} > T^M_{\parallel,\perp} \label{e8} \end{equation}(8)(equality satisfied only for κ → ∞), but equal temperature anisotropies 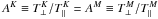AK≡T⊥K/T∥K=AM≡T⊥M/T∥M\hbox{$A^K \equiv T_\perp^K /T_\parallel^K = A^M \equiv T_\perp^M /T_\parallel^M$}. To our knowledge, this comparative method was only invoked to analyze a hypothetical presence of suprathermal ions in the solar corona by their effects as seeds for solar energetic particle (SEP) production and the initiation of coronal mass ejections (CMEs; Laming et al. 2013). This method is fully motivated, however, by the particle distributions measured in-situ in the solar wind plasma. Thus, the first attempts to describe fluxes of electrons measured in the solar wind proposed a Kappa model, see Vasyliunas (1968) after an original idea by Olbert (1968), fκ(v)=Nπ3/2w03 Γ[κ+1]κ3/2Γ[κ−1/2](1+v2κw02)−κ−1=\begin{eqnarray} f_\kappa (v) &=& {N \over \pi^{3/2} w_0^3} \, {\Gamma[\kappa +1] \over \kappa^{3/2} \Gamma[\kappa -1/2]} \left(1 + {v^2\over \kappa w_0^2 } \right)^{-\kappa-1} \notag \\ &=& {N \over (2\pi E_0/m)^{3/2}} \, {\Gamma[\kappa +1] \over \kappa^{3/2} \Gamma[\kappa -1/2]} \left(1 + {v^2\over 2 \kappa E_0/m } \right)^{-\kappa-1}, \label{e9} \end{eqnarray}(9)where N is the total number density, κ is the same power-index, and w0 is the most probable speed defined by a measurable quantity, the energy 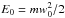E0=mw02/2\hbox{$E_0 = m w_0^2/2$} corresponding to the peak in the differential flux (~ v2f(v) /m). Here E0 can be related to the average thermal energy by E0 = kBT(1−1.5 /κ), and the two are identical only for κ → ∞ (Baumjohann & Treumann 1997). On the other hand, in this case the Kappa model at low energies is well shaped (see Fig. 1a) by the Maxwellian limit 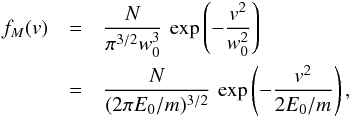fM(v)=Nπ3/2w03 exp(−v2w02)=\begin{eqnarray} f_M(v) &=& {N \over \pi^{3/2} w_0^3} \, \exp \left(-{v^2\over w_0^2 } \right) \notag \\ &=& {N \over (2\pi E_0/m)^{3/2}} \, \exp \left(-{v^2\over 2 E_0/m } \right), \label{e10} \end{eqnarray}(10)enabling a realistic comparison between a global best-fitting Kappa, which incorporates both the core and suprathermal tails, and the Maxwellian core.

Figure 1 shows parallel cuts (panel a) and contour plots (panels b and c) of these models, bi-Kappa variants A and B, and their bi-Maxwellian limit. The bi-Maxwellian model from Eq. (1) is plotted with solid lines for u⊥/c = 2u∥/c = 0.02. The bi-Kappa model (κ = 2) from Eq. (4) is shown for both cases: (A) when T∥,⊥K=T∥,⊥M\hbox{$T^K_{\parallel, \perp} = T^M_{\parallel, \perp}$} and θ∥,⊥ is provided by Eq. (7) (dash-dotted lines); and (B) for θ∥,⊥ = u∥,⊥, when T∥,⊥K>T∥,⊥M\hbox{$T^K_{\parallel,\perp} > T^M_{\parallel,\perp}$} (dashed lines). Both variants A and B of the bi-Kappa distribution function approach the same bi-Maxwellian in the limit of a very high power index κ → ∞, while for low values of κ → 1.5 the difference between these two variants becomes significant, the hotter bi-Kappa (variant B) showing pronounced high-energy tails and a potential excess of free energy. This is the second feature showing a significant contrast between the variants A and B of the bi-Kappa model, and indicating the new variant B as a more appropriate choice to include the suprathermal populations in the analysis and realistically predict their destabilizing effects.

thumbnail Fig. 1

Models of VDFs: bi-Maxwellian from Eq. (1) with u⊥/c = 2u∥/c = 0.02 (solid lines), and bi-Kappa from Eq. (4) with κ = 2 and θ∥,⊥ provided by Eq. (7) (dash-dotted lines) or with θ∥,⊥ = u∥,⊥ (dashed lines). Parallel cuts F(v∥) are shown in panel a), and isocontours at 10-3 in panel b) and 10-2 in panel c), corresponding to dotted lines in panel a). Note the enhanced high-energy tails shown by the hotter Kappa with dashed lines. (Color online.)

3. EMEC instability

The EMEC mode is destabilized by the electrons with an excess of perpendicular temperature (T⊥>T∥, where ∥,⊥ are directions with respect to the magnetic field), leading to an instability of finite frequency Re(ω) ≡ ωr ≠ 0, and growth rate Im(ω) ≡ γ> 0. We propose to describe the effects of suprathermal populations on this instability through a comparative analysis of the bi-Maxwellian and bi-Kappa models A and B, invoked here to parameterize the temperature anisotropy (A = T⊥/T∥> 1) of the electrons. The analysis is restricted to the parallel propagation (k = k∥) of the EMEC modes because in parallel direction these modes exhibit maximum growth rates and decouple from the electrostatic modes (Kennel & Petschek 1966). The parallel electromagnetic modes with RH polarization are described by the general dispersion relation (Gary 1993) 0=1−k2c2ω2+πω2∑aωp,a2∫−∞∞ dv∥ω−kv∥+Ωa∫0∞ dv⊥\begin{eqnarray} 0 &=& 1 -{k^2c^2 \over \omega^2} + {\pi \over \omega^2} \sum_a \omm_{p,a}^2 \int_{-\infty}^{\infty} \, {{\rm d}v_{\parallel} \over \omm - k v_{\parallel} + \Omega_a} \int_0^{\infty} \, {\rm d}v_{\perp} \notag \\ && \quad \times v_{\perp}^2 \left[(\omm - k v_{\parallel}) {\partial F_a \over \partial v_{\perp}} + k v_{\perp} {\partial F_a \over \partial v_{\parallel}} \right], \label{e11} \end{eqnarray}(11)where Ωa = qaB0/ (mac) is the (nonrelativistic) gyrofrequency, and ωp,a = (4πnae2/ma)1/2 is the plasma frequency for particles of sort a. 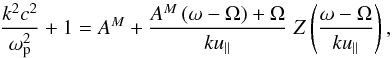For a standard bi-Maxwellian the dispersion relation simplifies to k2c2ωp2+1=AM+AM (ω−Ω)+Ωku∥Z(ω−Ωku∥),\begin{equation} {k^2c^2 \over \omega_{\rm p}^2} + 1 = A^M + {A^M \,(\omega - \Omega)+\Omega \over k u_{\parallel}} \; Z\left({\omega - \Omega \over k u_{\parallel}}\right), \label{e12} \end{equation}(12)in terms of the plasma dispersion function (Fried & Conte 1961) 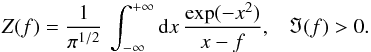Z(f)=1π1/2 ∫−∞+∞dx exp(−x2)x−f,ℑ(f)>0.\begin{eqnarray} Z(f) = {1 \over \pi^{1/2}} \, \int_{-\infty}^{+\infty} {\rm d}x \, {\exp(-x^2)\over x - f}, \; \;\; \Im (f) > 0. \label{e13} \end{eqnarray}(13)At high frequencies of the EMEC modes only electrons react (ion contribution can be neglected), and for simplicity, we omit the subscript “e” for all symbols, e.g., ωp = ωp,e, Ω = | Ωe |. Moreover, the EMEC modes are subluminal, such that ω2 ≪ k2c2.

For a bi-Kappa model in Eq. (4) the dispersion relation (11) becomes (Lazar et al. 2013) 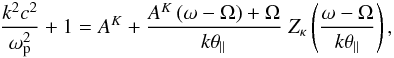k2c2ωp2+1=AK+AK (ω−Ω)+Ωkθ∥Zκ(ω−Ωkθ∥),\begin{eqnarray} {k^2c^2 \over \omega_{\rm p}^2} + 1 = A^K + {A^K \,(\omega - \Omega)+\Omega \over k \theta_{\parallel}} \; Z_{\kappa} \left({\omega - \Omega \over k \theta_{\parallel}}\right), \label{e14} \end{eqnarray}(14)this time written in terms of the modified (Kappa) plasma dispersion function (Lazar et al. 2008) Zκ(f)=\begin{eqnarray} Z_{\kappa}(f) &= & {1 \over \pi^{1/2} \kappa^{1/2}} \, {\Gamma [\kappa] \over \Gamma \left[\kappa - 1/2\right]} \int_{-\infty}^{+\infty} {\rm d}x \, {(1+x^2/\kappa)^{- \kappa } \over x - f}, \; \;\; \Im (f) > 0. \label{e15} \end{eqnarray}(15)

thumbnail Fig. 2

Thresholds of the EMEC instability for two levels of the maximum growth rates γm/ Ω = 10-2 and 10-3.

3.1. The instability thresholds

By specifying the plasma parameters, the instability thresholds are derived from dispersion relations (12) and (14) for sufficiently low levels of the maximum growth rate γm/ Ω = 10-2,10-3, such that the effects of the suprathermal populations shown for the lowest level (γm/ Ω = 10-3) are relevant for all the other lower thresholds, down to the marginal limit of stability (γm → 0). After the normalization of the wave frequency ωr/ Ω, growth rate γ/ Ω and wave number kc/ωp only two parameters remain to describe the dispersion relation (12) for bi-Maxwellian plasmas: namely, the anisotropy AM = AK = A and the parallel plasma beta 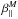β∥M\hbox{$\beta_\parallel^M$}, while the power index κ emerges as an additional parameter for the bi-Kappa dispersion Eq. (14). The anisotropy thresholds are computed numerically for an extended range of the plasma beta parameter 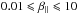\hbox{$0.01 \leqslant \beta_{\parallel} \leqslant 10$}, relevant for the solar wind conditions (Stverak et al. 2008). The plasma beta parameter 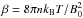β=8πnkBT/B02\hbox{$\beta = 8 \pi n k_{\rm B} T /B_0^2$} is defined by the ratio of the thermal pressure (energy) to the magnetic pressure (energy). Contours of the maximum growth rates (in units of Ω) are shown in Fig. 2 for both bi-Kappa models (κ = 2), case A (dash-dotted lines) and case B (dashed lines), and for the bi-Maxwellian limit (solid lines). An inverse correlation law between the temperature anisotropy, A = T⊥/T∥, and the plasma beta, β∥, is obtained by fitting the anisotropy thresholds with (Gary & Wang 1996) 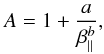A=1+aβ∥b,\begin{eqnarray} A = 1 + {a \over \beta_{\parallel}^b}, \label{e16} \end{eqnarray}(16)where a and b are fitting parameters with values given in Table 1.

Table 1

Electron temperature anisotropy fitting parameters from Eq. (14).

In case A, the comparison between different Kappa plasmas, including the Maxwellian limit κ → ∞ is straightforward because all these systems are characterized by the same temperature, 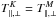T∥,⊥K=T∥,⊥M\hbox{$T^K_{\parallel,\perp} = T^M_{\parallel,\perp}$}, and implicitly by the same plasma beta 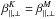β∥,⊥K=β∥,⊥M\hbox{$\beta^K_{\parallel,\perp} = \beta^M_{\parallel, \perp}$}. It is probably for this reason that previous comparative studies have preferentially chosen method A to investigate the destabilizing effects of suprathermal populations in Kappa distributed plasmas. With the new method B we compare plasma systems with different temperatures, see Eq. (8), and implicitly with different plasma betas 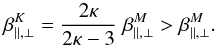β∥,⊥K=2κ2κ−3β∥,⊥M>β∥,⊥M.\begin{equation} \beta^K_{\parallel, \perp} = {2\kappa \over 2 \kappa - 3}\; \beta^M_{\parallel,\perp} > \beta^M_{\parallel,\perp}. \label{e17} \end{equation}(17)Whether in case A or B, for a bi-Kappa plasma the instability thresholds are derived with the same dispersion relation (14), such that, for the comparison in Fig. 2, the same instability threshold derived in case A (dot-dashed lines) may also be used in case B (dashed lines). However, the instability threshold must appear translated to the left, i.e., to lower values of β∥, by the corresponding increase of β∥ in Eq. (17).

The anisotropy thresholds decrease with plasma beta as for hotter or less magnetized plasmas we need lower anisotropies to ignite the instability. The same argument applies in the new case B, where the Kappa plasma becomes hotter with the increase of suprathermal populations yielding instability thresholds (dashed lines) markedly lower than those predicted in case A (dash-dotted lines) as well as for a bi-Maxwellian plasma (solid lines). This result indicates that suprathermal populations present in the solar wind facilitate the conditions favorable to the EMEC instability. The same effect was previously shown with method A, but less pronounced and only for sufficiently low anisotropies (bottom panel in Fig. 2), while for higher temperature anisotropies the instability appeared to be inhibited by the suprathermals (top panel in Fig. 2). For higher anisotropies (far from marginal stability), in the next section we check whether the new method B reveals a stimulation or an inhibition of the instability in the presence of suprathermals.

thumbnail Fig. 3

Unstable solutions derived for a bi-Maxwellian (solid lines) and a bi-Kappa, case A (dot-dashed lines) and case B (dashed lines): the wave frequency in panel a) and the growth rates in panel b). Plasma parameters: A = 4, β∥M=0.1\hbox{$\beta_\parallel^M = 0.1$} and κ = 2.

thumbnail Fig. 4

Unstable solutions derived for a bi-Maxwellian (solid lines) and a bi-Kappa, case A (dot-dashed lines) and case B (dashed lines): the wave frequency in panel a) and the growth rates in panel b). Plasma parameters: A = 4, β∥M=1\hbox{$\beta_\parallel^M = 1$} and κ = 2.

3.2. Unstable solutions

We calculated the unstable EMEC solutions for an extended range of plasma parameters relevant for conditions in the solar wind and terrestrial magnetosphere (i.e., 0.01 <β< 10), as well as for small or large deviations from isotropy. Representative for all these cases, Figs. 3−6 show the unstable solutions, i.e., the normalized wave frequency ωr/ Ω (top panels) and growth rate γ/ Ω (bottom panels) vs. the normalized wave number (kc/ωp), covering plasma regimes of low β∥ = 0.1 (Figs. 3 and 5) or moderately high β∥ = 1 (Figs. 4 and 6).

For all these four cases, the EMEC growth rates predicted for a bi-Kappa plasma by method B are always higher than those predicted by method A or for a bi-Maxwellian limit, confirming an important stimulation of the EMEC instability by the suprathermal populations. This effect remains valid for the whole range of the unstable wave numbers, which extends to very low values in the presence of suprathermals. This reduces the inhibiting effect of the magnetic field (for bi-Maxwellian distributed plasmas there is a minimum cutoff wave number, which increases with the magnetic field strength). The maximum cutoff of the unstable wave numbers does not change in the presence of suprathermals, as it only depends on the temperature anisotropy. This cutoff coincides with a particular value of the wave frequency common to all dispersion curves (top panels of Figs. 3−6), where all electron thermal effects, and hence all κ dependencies vanish (Mace & Sydora 2010). Differences shown by the wave frequency of the EMEC modes, as predicted for a bi-Kappa with methods A and B and for the bi-Maxwellian limit, only become significant for sufficiently large anisotropies (Figs. 3 and 4).

thumbnail Fig. 5

Unstable solutions derived for a bi-Maxwellian (solid lines) and a bi-Kappa, case A (dot-dashed lines) and case B (dashed lines): the wave frequency in panel a) and the growth rates in panel b). Plasma parameters: A = 1.8, β∥M=0.1\hbox{$\beta_\parallel^M = 0.1$} and κ = 2.

thumbnail Fig. 6

Unstable solutions derived for a bi-Maxwellian (solid lines) and a bi-Kappa, case A (dot-dashed lines) and case B (dashed lines): the wave frequency in panel a) and the growth rates in panel b). Plasma parameters: A = 1.8, β∥M=1\hbox{$\beta_\parallel^M = 1$} and κ = 2.

4. Discussions and conclusions

Suprathermal populations present in the solar wind indicate plasma states out of thermal equilibrium and an excess of free energy expected to enhance the kinetic instabilities. The potential destabilizing effect of the suprathermal populations can only be unveiled by a comparison with the effects of the Maxwellian core. The existing theories, which compare Kappa and Maxwellian distribution models with the same effective temperature, do not reveal this effect, which should stimulate kinetic instabilities. These instabilities, including the EMEC instability studied in the present paper, are in general inhibited by the suprathermal populations (e.g., decreasing the power-index κ → 1.5), with the exception of very small wave numbers or low temperature anisotropies (close to the marginal condition of stability). Profiles of the velocity distribution functions shown in Fig. 1 may be relevant for the origin of these nonmonotonous effects. Thus, the main inhibiting effect seems to be well explained by the depression shown by the Kappa model (variant A) at energies about the mean kinetic energy of plasma particles, with values lower than the Maxwellian limit over an extended velocity range (see panels a and b in Fig. 1). Otherwise, at lower energies the same Kappa model exhibits a pronounced eccentrical peak (enhanced fraction of particles at low speeds) in comparison to its Maxwellian limit (panel a), providing a plausible explanation for the marginal stimulating effect on the low wave numbers of the instability. However, this eccentrical peak makes these two models inappropriate to be used for a plausible comparison between the Maxwellian core and the global best-fitting Kappa, incorporating both the core and suprathermal tails.

The method we propose compares Kappa distribution functions with the effective temperature naturally increasing with the increase of the suprathermal populations. In this case, the high-energy tails of the Kappa model (variant B) are markedly enhanced, see Fig. 1, indicating an important surplus of free energy. Moreover, at low energies the Kappa model is well shaped by the Maxwellian limit (with the lowest temperature) enabling a realistic comparison between the Maxwellian core and the global Kappa (see panel a in Fig. 1). The reliability of the new method to unveil the potential destabilizing effects of the suprathermal populations present in the solar wind is demonstrated by investigations on the EMEC instability driven by a temperature anisotropy of electrons. We have compared the instability thresholds, growth rates, and wave frequencies with the previous calculations. The new method reveals an important stimulation of this instability in the presence of suprathermal populations by a significant lowering of the threshold conditions (and implicitly of the marginal stability) as well as a systematic and significant increase of the growth rates for any level of the temperature anisotropy. We can conclude pointing out that the results of our present study provide valuable premises for a realistic re-evaluation of the whole spectrum of kinetic instabilities driven by the temperature anisotropies in the solar wind.

Acknowledgments

The authors acknowledge support from the Katholieke Universiteit Leuven, the Ruhr-Universität Bochum, and the Deutsche Forschungsgemeinschaft (DFG). These results were obtained in the framework of the projects GOA/2009-009 (KU Leuven), G.0729.11 (FWO-Vlaanderen) and C 90347 (ESA Prodex 9). The research leading to these results has also received funding from the European Commission’s Seventh Framework Programme (FP7/2007-2013) under the grant agreements SOLSPANET (project No. 269299, www.solspanet.eu), SPACECAST (project No. 262468, fp7-spacecast.eu), eHeroes (project No. 284461, www.eheroes.eu), and SWIFF (project No. 263340, www.swiff.eu).

References

  1. Baumjohann, W., & Treumann, R. A. 1997, Basic Space Plasma Physics (London: Imperial College Press) [Google Scholar]
  2. Breneman, A., Cattell, C., Wygant, J., et al. 2011, J. Geophys. Res., 116, A06310 [NASA ADS] [Google Scholar]
  3. Cattell, C., Wygant, J. R., Goetz, K., et al. 2008, Geophys. Res. Lett., 35, L01105 [NASA ADS] [CrossRef] [Google Scholar]
  4. Fichtner, H., & Sreenivasan, S. R. 1993, J. Plasma Phys., 49, 101 [NASA ADS] [CrossRef] [Google Scholar]
  5. Fried, B. D., & Conte, S. D. 1961, The plasma dispersion function (New York: Academic Press) [Google Scholar]
  6. Gary, S. P. 1993, Theory of space plasma microinstabilities (Cambridge: University Press) [Google Scholar]
  7. Gary, S. P., & Wang, J. 1996, J. Geophys. Res., 101, 10,749 [Google Scholar]
  8. Hellberg, M., Mace, R., & Cattaert, T. 2005, Space Sci. Rev., 121, 127 [NASA ADS] [CrossRef] [Google Scholar]
  9. Helliwell, R., Crary, J., Pope, J., & Smith, R. 1956, J. Geophys. Res., 61, 139 [NASA ADS] [CrossRef] [Google Scholar]
  10. Kennel, C. F., & Petschek, H. E. 1966, J. Geophys. Res., 71, 1 [NASA ADS] [CrossRef] [Google Scholar]
  11. Lacombe, C., Alexandrova, O., Matteini, L., et al. 2014, ApJ, 796, 1 [NASA ADS] [CrossRef] [Google Scholar]
  12. Laming, J. M., Moses, J. D., Ko, Y.-K., et al. 2013, ApJ, 770, 73 [NASA ADS] [CrossRef] [Google Scholar]
  13. Lazar, M. 2012, A&A, 547, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Lazar, M., & Poedts, S. 2009, A&A, 494, 311 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Lazar, M., Schlickeiser, R., & Shukla, P. K. 2008, Phys. Plasmas, 15, 042103 [NASA ADS] [CrossRef] [Google Scholar]
  16. Lazar, M., Poedts, S., & Schlickeiser, R. 2011, A&A, 534, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Lazar, M., Schlickeiser, R., & Poedts, S. 2012, Suprathermal particle populations in the solar wind and corona, in exploring the solar wind (InTech), Ch. 11, http://www.intechopen.com/books/exploring-the-solar-wind [Google Scholar]
  18. Lazar, M., Poedts, S., & Michno, M. J. 2013, A&A, 554, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Mace, R. L. 1998, J. Geophys. Res., 103, 14643 [NASA ADS] [CrossRef] [Google Scholar]
  20. Mace, R. L., & Sydora, R. D. 2010, J. Geophys. Res., 115, A07206 [NASA ADS] [CrossRef] [Google Scholar]
  21. Mace, R. L., Sydora, R. D., & Silin, I. 2011, J. Geophys. Res., 116, A05206 [NASA ADS] [Google Scholar]
  22. Marsch, E. 2006, Liv. Rev. Solar Phys., 3, http://www.livingreviews.org/lrsp-2006-1 [Google Scholar]
  23. Olbert, S. 1968, Summary of experimental results from M. I. T. detector on IMP-1, in Physics of the magnetosphere, eds. R. L. Carovillano, J. F. McClay, & H. R. Radoski (Dordrecht: D. Reidel Publishing Company), 641 [Google Scholar]
  24. Pierrard, V., & Lazar, M. 2010, Sol. Phys., 267, 153 [NASA ADS] [CrossRef] [Google Scholar]
  25. Schlickeiser, R. 2002, Cosmic Ray Astrophysics (Heidelberg: Springer) [Google Scholar]
  26. Stverak, S., Travnicek, P., Maksimovic, M., et al. 2008, J. Geophys. Res., 113, A03103 [Google Scholar]
  27. Summers, D., & Thorne, R. M. 1992, J. Geophys. Res., 97, 16827 [NASA ADS] [CrossRef] [Google Scholar]
  28. Treumann, R. A., & Baumjohann, W. 1997, Adv. Space Plasma Physics (London: Imperial College Press) [Google Scholar]
  29. Vasyliunas, V. M. 1968, J. Geophys. Res., 73, 2839 [NASA ADS] [CrossRef] [Google Scholar]
  30. Xiao, F., Zhou, Q., Zheng, H., & Wang, S. 2006, J. Geophys. Res., 111, A08208 [NASA ADS] [Google Scholar]
  31. Xue, S., Thorne, R. M., & Summers, D. 1993, J. Geophys. Res., 98, 17475 [NASA ADS] [CrossRef] [Google Scholar]
  32. Xue, S., Thorne, R. M., & Summers, D. 1996, J. Geophys. Res., 101, 15467 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Electron temperature anisotropy fitting parameters from Eq. (14).

In the text

All Figures

thumbnail Fig. 1

Models of VDFs: bi-Maxwellian from Eq. (1) with u⊥/c = 2u∥/c = 0.02 (solid lines), and bi-Kappa from Eq. (4) with κ = 2 and θ∥,⊥ provided by Eq. (7) (dash-dotted lines) or with θ∥,⊥ = u∥,⊥ (dashed lines). Parallel cuts F(v∥) are shown in panel a), and isocontours at 10-3 in panel b) and 10-2 in panel c), corresponding to dotted lines in panel a). Note the enhanced high-energy tails shown by the hotter Kappa with dashed lines. (Color online.)
In the text
thumbnail Fig. 2

Thresholds of the EMEC instability for two levels of the maximum growth rates γm/ Ω = 10-2 and 10-3.
In the text
thumbnail Fig. 3

Unstable solutions derived for a bi-Maxwellian (solid lines) and a bi-Kappa, case A (dot-dashed lines) and case B (dashed lines): the wave frequency in panel a) and the growth rates in panel b). Plasma parameters: A = 4, β∥M=0.1\hbox{$\beta_\parallel^M = 0.1$} and κ = 2.
In the text
thumbnail Fig. 4

Unstable solutions derived for a bi-Maxwellian (solid lines) and a bi-Kappa, case A (dot-dashed lines) and case B (dashed lines): the wave frequency in panel a) and the growth rates in panel b). Plasma parameters: A = 4, β∥M=1\hbox{$\beta_\parallel^M = 1$} and κ = 2.
In the text
thumbnail Fig. 5

Unstable solutions derived for a bi-Maxwellian (solid lines) and a bi-Kappa, case A (dot-dashed lines) and case B (dashed lines): the wave frequency in panel a) and the growth rates in panel b). Plasma parameters: A = 1.8, β∥M=0.1\hbox{$\beta_\parallel^M = 0.1$} and κ = 2.
In the text
thumbnail Fig. 6

Unstable solutions derived for a bi-Maxwellian (solid lines) and a bi-Kappa, case A (dot-dashed lines) and case B (dashed lines): the wave frequency in panel a) and the growth rates in panel b). Plasma parameters: A = 1.8, β∥M=1\hbox{$\beta_\parallel^M = 1$} and κ = 2.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.