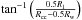| Issue |
A&A
Volume 582, October 2015
|
|
|---|---|---|
| Article Number | A20 | |
| Number of page(s) | 27 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201525758 | |
| Published online | 30 September 2015 | |
Inverse-Compton emission from clusters of galaxies: Predictions for ASTRO-H⋆
GRAPPA Institute, University of Amsterdam, 1098 XH Amsterdam, The Netherlands
e-mail: r.t.bartels@uva.nl
Received: 27 January 2015
Accepted: 8 June 2015
The intra-cluster medium of several galaxy clusters hosts large-scale regions of diffuse synchrotron radio emission, known as radio halos and relics, which demonstrates the presence of magnetic fields and relativistic electrons in clusters. These relativistic electrons should also emit X-rays through inverse-Compton scattering off of cosmic microwave background photons. The detection of such a non-thermal X-ray component, together with the radio measurement, would permit the magnetic field to be clearly separated from the relativistic electron distribution because the inverse-Compton emission is independent of the magnetic field in the cluster. However, non-thermal X-rays have not been conclusively detected from any cluster of galaxies so far. In this paper, for the first time, we model the synchrotron and inverse-Compton emission of all clusters hosting radio halos and relics for which the spectral index can be determined. We provide constraints on the volume-average magnetic field by comparing with current X-ray measurements. We then estimate the maximum volume-average magnetic field that will allow detection of inverse-Compton hard X-rays by the ASTRO-H satellite. We find that several clusters are good targets for ASTRO-H to detect their inverse-Compton emission, in particular for what corresponds to radio relics, so we propose a list of promising targets for which ASTRO-H can test ≥ 1μG magnetic fields. We conclude that the already operating NuSTAR and the soon-to-be-launched ASTRO-H definitely have the potential of shedding light on the long-sought non-thermal hard-X-ray emission in clusters of galaxies.
Key words: galaxies: clusters: intracluster medium / radiation mechanisms: non-thermal / radio continuum: general / X-rays: galaxies: clusters / magnetic fields
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
The observation of diffuse synchrotron emission in clusters of galaxies proves that there are magnetic fields and relativistic electrons in the intra-cluster medium (ICM). This diffuse radio emission is observationally classified into two phenomena: peripheral radio relics that show irregular morphology and appear to trace merger and accretion shocks, and radio halos centred on clusters that show a regular morphology resembling that of the thermal X-ray emission (e.g., Feretti et al. 2012).
The electrons generating the observed radio emission can also produce X-rays by inverse-Compton (IC) scattering off of cosmic microwave background (CMB) photons. IC emission has been searched for extensively in the past, with a few claims of detection (see, e.g., Rephaeli & Gruber 2002; Fusco-Femiano et al. 2004; Rephaeli et al. 2006, 2008; Eckert et al. 2008). However, more recent observations did not confirm most of the earlier claims (Molendi & Gastaldello 2009; Ajello et al. 2009, 2010; Wik et al. 2012, 2014; Ota 2012; Ota et al. 2014; Gastaldello et al. 2015) and IC emission from clusters remains elusive.
The dominant emission in clusters of galaxies is the thermal bremsstrahlung from the ICM. Since this falls quickly above ~ 10 keV, hard X-rays (HXRs) offer the best prospect for detecting IC emission from clusters. In coming years, next-generation X-ray satellites will increase the chances. Especially, ASTRO-H (Takahashi et al. 2012, 2014; Kitayama et al. 2014), to be launched this year (2015), and the recently launched NuSTAR (Harrison et al. 2013) are excellent instruments for probing IC emission in HXRs.
In this work, we model, for the first time, the synchrotron and IC emission of all galaxy clusters hosting radio halos and relics for which the spectral index can be determined. The radio-emitting electrons in clusters can have different origins (see, e.g., Brunetti & Jones 2014, for a review). Our approach is phenomenological, we do not make any assumption about the injection and acceleration history of the relativistic electrons, and we only assume that the same electron distribution that generates the observed synchrotron radio emission also IC scatters off of the CMB photons. We provide detailed predictions for the ASTRO-H satellite and compare with current X-ray observations, where available. In particular, we estimate cap values for the volume-averaged magnetic field below which an IC signal would be detectable by ASTRO-H.
The detection of IC emission from clusters of galaxies is crucial for breaking the degeneracy in the determination of the electron distribution and magnetic field value in clusters. Because the synchrotron radio emission depends on both, while the IC emission is independent of the cluster’s magnetic field, the detection of the latter in HXR is important. This will shed new light not only on non-thermal emission in clusters, but also on the impact of non-thermal phenomena on the thermal content of galaxy clusters, which is fundamental for robustly using galaxy clusters for cosmological studies (Voit 2005).
This paper is organised as follows. We introduce our sample of radio halos and relics in Sect. 2 and describe how we treat the relativistic electrons in Sect. 3. In Sect. 4, we briefly discuss how the non-thermal synchrotron and IC emission is modelled, while in Sect. 5, we discuss the considered background emissions. We describe the main characteristics of the ASTRO-H satellite that are important for this work in Sect. 6, and explain the procedures adopted for determining the IC detectability by ASTRO-H in Sect. 7. Finally, we present all results in Sect. 8 and our conclusions in Sect. 9. We work in cgs units and adopt a cosmological model with Ωm = 0.27, ΩΛ = 0.73, and H0 = 70 km s-1 Mpc-1.
2. Galaxy cluster sample
We have analysed the radio halos and relics from the September2011-Halo and September2011-Relic collections of Feretti et al. (2012). We limited our final sample to objects that have at least two radio measurements at different wavelengths in order to be able to determine the corresponding photon spectral index α and reduce the degeneracy in our modelling. There are a few sources for which the spectral index was estimated from neighbouring wavelengths, making the estimate subject to uncertainty. These sources were therefore excluded from our sample (A545 halo, A115, and A548 relics). Additionally, we searched the literature for radio data published after Feretti et al. (2012), which led to including the Toothbrush (1RXS J0603.3+4214), A3376, A3411, the A3667 south-eastern relic, El-Gordo (ACT-CL J0102-4915), MACSJ1149.5+2223, MACSJ1752.0+4440, PLCK G171.9-40.7, and ZwCl2341.1+0000 in our final sample.
We excluded from the present analysis radio mini-halos hosted in cool-core clusters because the magnetic field estimates in the centre of these environments are high, up to ~ 10μG (Clarke 2004; Enßlin & Vogt 2006), implying very low relativistic electron densities for which it would be extremely difficult to aim for an IC detection1. Tables 1 and 2 contain the information about our sample of radio halos and relics, respectively, including current X-ray upper limits where available. A note on the latter: most of the current HXR upper limits come from observations pointed at the centre of clusters. There are a just few works dedicated to radio relics, but in most cases, these HXR upper limits contain contributions from both halo and relic regions.
Radio halo sample.
Radio relic sample.
3. The electron population distribution
As anticipated above, we take a phenomenological approach to the radio-emitting electrons. We assume a power-law distribution of electrons, 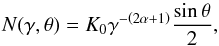 (1)with K0 the normalisation, γ the Lorentz factor, and α the photon spectral index, where we consider an isotropic distribution of pitch angles θ. The electron distribution is then integrated between γmin and γmax. In some of the analysed cases, where spectral steepening is clearly observed, γmin and γmax can be determined from the radio data. However, more often there is no evidence of any such feature, in which case the cutoffs are fixed to theoretically motivated values.
(1)with K0 the normalisation, γ the Lorentz factor, and α the photon spectral index, where we consider an isotropic distribution of pitch angles θ. The electron distribution is then integrated between γmin and γmax. In some of the analysed cases, where spectral steepening is clearly observed, γmin and γmax can be determined from the radio data. However, more often there is no evidence of any such feature, in which case the cutoffs are fixed to theoretically motivated values.
The low-energy cutoff is estimated from the lifetime of relativistic electrons in the ICM. At low energies (γ ≲ 102), Coulomb cooling dominates, whereas at high energies IC cooling dominates (Rephaeli 1979; Sarazin 1999). For typical values in the centre of clusters, where there is a thermal electron number density of ne ~ 10-3 cm-3 and B = 1 μG, this yields a maximum lifetime of γ ≈ 300. However, outskirts of the cluster are characterised by lower ICM densities, which implies γ ≈ 200. Therefore, the low-energy cutoff is fixed to γmin = 300 for halos and to 200 for relics. The high-energy cutoff γmax is more arbitrary given that we do not make assumptions on the injection and acceleration history of the radio-emitting electrons. If no spectral steepening at high radio frequencies is observed, it is fixed to γmax = 2 × 105, corresponding to electron energies of 100 GeV. At any rate, as we also show in Sect. 8, our conclusions are not affected by changing γmin and/or γmax, unless, of course, spectral steepening is observed.
4. Radiative processes
In this work, we assume that the magnetic field is tangled on much smaller scales than the observed emitting volume, therefore adopting an isotropic distribution of magnetic field orientations. Such a distribution is motivated by Faraday rotation (FR) measurements in clusters, which indicate that the coherence scales of magnetic fields are of the order of 10 kpc, which is much smaller than the typical Mpc-size of radio halos and relics (Carilli & Taylor 2002; Murgia et al. 2004, 2010). The synchrotron flux density is then given by 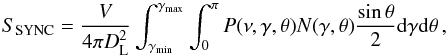 (2)where P(ν,γ,θ) is the synchrotron spectrum emitted by a single electron (Blumenthal & Gould 1970), V is the emitting volume, and DL is the luminosity distance. The factor sinθ/ 2 is due to our assumption about the magnetic field distribution.
(2)where P(ν,γ,θ) is the synchrotron spectrum emitted by a single electron (Blumenthal & Gould 1970), V is the emitting volume, and DL is the luminosity distance. The factor sinθ/ 2 is due to our assumption about the magnetic field distribution.
The presence of this factor leads to slightly higher estimates of the magnetic field with respect to assuming coherent magnetic fields on large scales (e.g., Wik et al. 2009; Ajello et al. 2009, 2010). This assumption of tangled magnetic fields releases part of the tension between the typically high FR measurements and equipartition estimates of the magnetic field, on the one hand, and claimed IC detections, on the other. Indeed, there are several uncertainties that affect magnetic field estimates from IC emission, and therefore the comparison with results from FR measurements. While some of these sources of uncertainties will be discussed in more detail in the next sections, we remind the reader to look at, for example, Petrosian (2001), Brunetti (2003), and Bonafede et al. (2010) for extensive discussions.
Low-energy photons scattering off of relativistic electrons can produce X-rays through IC emission. We assume that all incoming photons are from the CMB2. While starlight at the very centre of galaxy clusters can be as important as the CMB, this is not true when considering larger areas, such as the ones corresponding to radio halos or the clusters’ outskirts where radio relics lie (see, e.g., Pinzke et al. 2011). The IC flux density is then given by  (3)where ϵ is the incoming photon energy, ϵ1 is the outgoing photon energy, and FIC is the IC kernel function (Blumenthal & Gould 1970) for the Thomson limit, which is valid for the energy range of interest here. Here,
(3)where ϵ is the incoming photon energy, ϵ1 is the outgoing photon energy, and FIC is the IC kernel function (Blumenthal & Gould 1970) for the Thomson limit, which is valid for the energy range of interest here. Here, 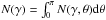 .
.
We conclude this section with an estimate of which HXR IC energies correspond to electrons that emit synchrotron radiation at a given frequency. This depends on the magnetic field strength. The average energy of an IC up-scattered photon is ⟨ϵ1⟩ = (4/3) γ2⟨ϵ⟩ ≈ 8.6 × 10-7γ2 keV, where we assumed the incoming CMB photon to be at redshift 0. We can use the monochromatic approximation for the synchrotron emission, which yields (ν/ 1 GHz) = 1.05 × 10-9γ2 (B/ 1 μG). In the case of B = 1 μG, synchrotron radiation at ~ 100 (20) MHz is produced by the electrons that generate IC emission at 80 (20) keV, while for B = 5 μG, one finds that ~ 480 (120) MHz radio waves correspond to 80 (20) keV X-rays. Therefore, low-frequency radio observations are crucial for precisely predicting HXR IC emission, as discussed in Sect. 8, and for eventually clarifying whether our assumption of Sect. 3 regarding the electron distribution holds down to low energies.
5. Background emission
In this section, we discuss the main background emission for IC searches in clusters. These are the thermal ICM bremsstrahlung and the cosmic X-ray background (CXB) emission. In Sect. 7, we also introduce the instrumental background.
5.1. Thermal bremsstrahlung from ICM
To model the thermal bremsstrahlung emission from the ICM, we use the APEC code (Smith et al. 2001) as provided in the XSPEC software (Arnaud 1996). The input parameters are the ICM temperature (taken, for most nearby clusters, from Chen et al. 2007), the redshift z, the metal abundance, which we fix to 0.3 times the solar abundance for simplicity (e.g., Böhringer & Werner 2010), and the normalisation. The latter contains information about the ICM gas distribution that, for our purposes, can be approximated with a beta model (e.g., Cavaliere & Fusco-Femiano 1976), ![\begin{equation} n_\mathrm{e}(r) = \left[\sum_i n_{0,i}^2 \left(1 + \frac{r^2}{r_{c,i}^2}\right)^{-3 \beta_i}\right]^{1/2}, \label{eq:ne} \end{equation}](/articles/aa/full_html/2015/10/aa25758-15/aa25758-15-eq79.png) (4)where n0 is the central ICM electron density, and rc the core radius. Most clusters are described well by a single beta model (i = 1), whereas others are better described by a double beta model (i = 1,2). The values of n0, rc, and β are derived from X-ray observations. For most nearby clusters, these values are taken from Pinzke et al. (2011).
(4)where n0 is the central ICM electron density, and rc the core radius. Most clusters are described well by a single beta model (i = 1), whereas others are better described by a double beta model (i = 1,2). The values of n0, rc, and β are derived from X-ray observations. For most nearby clusters, these values are taken from Pinzke et al. (2011).
In the few cases where we cannot find a gas density model in the literature, we adopt the phenomenological ICM model of Zandanel et al. (2014) which provides a gas density once the mass M500 of the cluster is known. In the few cases where no mass estimate is present in the literature, we adopt the X-ray luminosity-mass relation from Mantz et al. (2010). If there is no ICM temperature available in the literature, we also use the mass-temperature relation of Mantz et al. (2010). Obviously, such approximations are a source of uncertainty when used in particular cases, so the modelling of those clusters should be taken with caution. This is also true in general for relics where the gas density profiles have been inferred from X-ray observations of the clusters’ centre.
In the case of radio halos, the bremsstrahlung luminosity, LB, is obtained by integrating over the full extent of the halo, where we approximate the halo to be spherical and use the largest linear size as given in Feretti et al. (2012) as halo diameter. In the case of radio relics in the outskirts of clusters, we only integrate over the relic region as 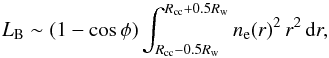 (5)where Rcc is the distance to the cluster centre, Rw the approximate width of the relic, and φ = tan-1 [0.5Rl/ (Rcc−0.5Rw)] with Rl the largest linear size of the relic (see Fig. 1). For relics that are classified as roundish by Feretti et al. (2012), we use Rw = Rl.
(5)where Rcc is the distance to the cluster centre, Rw the approximate width of the relic, and φ = tan-1 [0.5Rl/ (Rcc−0.5Rw)] with Rl the largest linear size of the relic (see Fig. 1). For relics that are classified as roundish by Feretti et al. (2012), we use Rw = Rl.
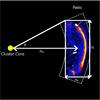 |
Fig. 1 The geometry used in determining the normalisation for the APEC modelling of the radio relic regions (Eq. (5)). Rcc corresponds to the distance between the relic and the cluster center as projected on the sky. Rl is the relic largest linear size and Rw is the relic width. For relics that are classified as roundish by Feretti et al. (2012) we use Rw = Rl. φ is given by |
The parameters that enter the APEC model are shown in Tables 1 and 2 for all the clusters in our sample.
5.2. Cosmic X-ray background
The CXB (e.g., Gilli et al. 2007) is another important background for the case of radio relics in the outskirts of clusters, where it often outweighs the thermal ICM emission. We assume the CXB to be isotropic across the sky and model it in the 0.5−100 keV regime as follows (Gruber 1992; Comastri et al. 1995): 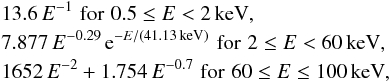 in units of keV cm-2 s-1 sr-1 keV-1 and with E the photon energy in units of keV. Below 0.5 keV, the galactic emission becomes an important source of background, but these low energies are not considered in this work.
in units of keV cm-2 s-1 sr-1 keV-1 and with E the photon energy in units of keV. Below 0.5 keV, the galactic emission becomes an important source of background, but these low energies are not considered in this work.
6. The ASTRO-H and NuSTAR satellites
In this section, we describe the characteristics of ASTRO-H that are relevant for this work. While we provide detailed predictions for the IC-emission detection by ASTRO-H, we also discuss in the same context the recently launched NuSTAR satellite.
6.1. ASTRO-H
ASTRO-H is a next-generation X-ray satellite that is scheduled for launch in 2015 (Takahashi et al. 2012, 2014). The instruments that are of interest for our purposes are the Hard X-ray Imager (HXI) and the Soft X-ray Imager (SXI). In Table 3, we summarise the main characteristics of these instruments.
Properties of the SXI and HXI detectors that will be on-board ASTRO-H.
To estimate the detectability of the non-thermal X-ray component in galaxy clusters, we make use of the sensitivity curves as published by the ASTRO-H collaboration for both point and extended sources (ASTRO-H Quick Reference3, Takahashi et al. 2010, 2012). We adopt the sensitivity curve for 1 Ms of observation, and scale it to other observation times as 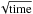 . The ASTRO-H sensitivity curves are 3σ sensitivities, and the sensitivity curve for extended sources assumes a uniform source of 1 deg2.
. The ASTRO-H sensitivity curves are 3σ sensitivities, and the sensitivity curve for extended sources assumes a uniform source of 1 deg2.
We assume, for simplicity, that halos and relics are uniform sources. To scale the sensitivity to the size, Ω arcmin2, of a given object, we proceed as follows. For sources that are smaller than the HXI field of view, we scale the point-source sensitivity as 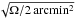 , where 2 arcmin2 is roughly the pixel size. For sources that are larger, we apply a linear scaling to the 1 deg2 diffuse source sensitivity as Ω/3600 arcmin2 (Hiroki Akamatsu, Madoka Kawaharada, priv. comm.).
, where 2 arcmin2 is roughly the pixel size. For sources that are larger, we apply a linear scaling to the 1 deg2 diffuse source sensitivity as Ω/3600 arcmin2 (Hiroki Akamatsu, Madoka Kawaharada, priv. comm.).
6.2. NuSTAR
The NuSTAR satellite was launched on June 13, 2012. Its performances in HXR should be comparable to ASTRO-H (Harrison et al. 2013), with the exception that ASTRO-H will be equipped with a pre-collimator designed to mitigate stray light (Mori et al. 2012).
Recently, Wik et al. (2014) have pointed out that a possible IC signal has to be extracted from both the thermal and instrumental backgrounds, with the former dominating at low and the latter at high energies. In fact, the instrumental background is likely to dominate the count rate in the HXR. Since the instrumental background is modelled by a power law, any claim of IC detection is extremely sensitive to the applied model. While the HXI detector onboard ASTRO-H will not improve much upon NuSTAR – in fact, our predictions are approximately valid in both cases – the presence of the SXI detector will greatly improve the modelling of the thermal component in clusters over the NuSTAR results.
7. Multi-band modelling and HXR detectability
For any given object in Tables 1 and 2, we proceed as follows. If an upper limit exists on the non-thermal hard X-ray flux FX,UL, we calculate the corresponding lower limit on the volume-average magnetic field BV. First, we fix K0 by fitting the IC spectrum of Eq. (3) to FX,UL. Next, we fit the synchrotron emission of Eq. (2) to the radio data4, with BV as free parameter. Depending on whether spectral steepening at low and/or high frequencies is observed, γmin and/or γmax are also determined from the data (see Sect. 3). The spectral index α is taken from the literature, unless it returns a poor fit, in which case we determine a new spectral index. The resulting broadband spectrum provides a lower limit on the magnetic field.
Results for halos.
Results for relics.
We then compare the background spectra (thermal bremsstrahlung and the CXB) to the properly scaled ASTRO-H sensitivity. We use the intersection between the ASTRO-H sensitivity curve and the dominant background component, either thermal ICM or CXB, to fix a new normalisation of the electron distribution K0 using Eq. (3). This represents the lower limit on the normalisation detectable by ASTRO-H. If no upper limit on the hard X-ray flux, FX,UL, exists for a given object, we start from this step. Finally, we fit the synchrotron emission of Eq. (2) again to the radio data. The resulting magnetic field value is a cap on the volume-average magnetic field below which HXR IC emission would be detectable by ASTRO-H, and we call it Bdt. To be clearer, HXR IC emission would be detectable by ASTRO-H if the cluster’s magnetic field was lower than or equal to Bdt, always meaning a volume average. We underline that this simple approach is meant to be just a first-order approximation to what can really be achieved. In fact, the CXB background is well known and can be easily subtracted. We provide the result in such a case, along with the rest, in Tables 4 and 5.
The above approach leads to a rough estimate that we complement with one based on the total number of counts in the 20−80 keV band as follows. We require the signal-to-noise ratio 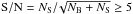 , where NS is the total number of source counts and
, where NS is the total number of source counts and 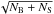 is the corresponding noise, with NB = NICM + NCXB + Ninstr including all background counts (ICM, CXB and instrumental).
is the corresponding noise, with NB = NICM + NCXB + Ninstr including all background counts (ICM, CXB and instrumental).
We approximate the instrumental background by a power law corresponding to 6 × 10-3 counts/s/keV/FoV at 10 keV and 2 × 10-4 counts/s/keV/FoV at 50 keV, which are values adopted from the ASTRO-H Quick Reference (Table 2). For our purpose, a simple power-law approximation of the instrumental noise suffices, since uncertainties will be dominated by the modelling of the thermal and IC emission5. We convert the thermal bremsstrahlung and CXB fluxes into count rates by multiplying by the HXI effective area taken from the ASTRO-H Quick Reference (Fig. 1). Here, NS is then related to the HXR flux density, Sx(E) = kxE− α, through 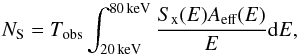 (6)where Tobs is the observation time and Aeff(E) the effective area. Using the NS for which S/N ≥ 5, we solve for kx and, finally, calculate the corresponding flux as
(6)where Tobs is the observation time and Aeff(E) the effective area. Using the NS for which S/N ≥ 5, we solve for kx and, finally, calculate the corresponding flux as 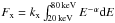 . The spectral index used here is the same as above. This flux is then converted into a magnetic field,
. The spectral index used here is the same as above. This flux is then converted into a magnetic field, 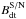 , using
, using ![\begin{eqnarray} & &\frac{F _{x} \nu_r^{-\alpha} }{s_r \int_{\nu_\mathrm{min}}^{\nu_\mathrm{max}} \nu_{x}^{-\alpha} \mathrm{d}\nu_x} = \nonumber \\[0.5mm] && \quad \frac{2.46 \times 10^{-19} T_\mathrm{CMB}^3}{B_\mathrm{dt}^\mathrm{S/N}} \frac{b(p)}{a(p)} \left(\frac{4.96 \times 10^3 T_\mathrm{CMB}}{B_\mathrm{dt}^\mathrm{S/N}}\right)^\alpha, \label{eq:Banalytic1} \end{eqnarray}](/articles/aa/full_html/2015/10/aa25758-15/aa25758-15-eq168.png) (7)where TCMB = T0(1 + z) is the CMB temperature, Fx the X-ray flux, sr the radio flux density at νr, p = 2α + 1, and
(7)where TCMB = T0(1 + z) is the CMB temperature, Fx the X-ray flux, sr the radio flux density at νr, p = 2α + 1, and ![% subequation 6843 0 \begin{eqnarray} a(p) &=& \frac{2^{(p-1)/2} \sqrt 3 \Gamma\left(\frac{3p -1}{12}\right)\Gamma\left(\frac{3p +19}{12}\right) \Gamma\left(\frac{p +7}{4}\right)} {16 \pi^{1/2} \Gamma\left(\frac{p + 9}{4}\right)}, \label{eq:anew1} \\[1.5mm] b(p) &=& 2^{p+3} \frac{(p^2 + 4p + 11) \Gamma\left(\frac{p + 5}{2}\right) \zeta\left(\frac{p+5}{2}\right)}{(p+3)^2(p+1)(p+5)}\cdot \end{eqnarray}](/articles/aa/full_html/2015/10/aa25758-15/aa25758-15-eq174.png) Here Γ and ζ are the gamma and Riemann zeta functions, respectively (Pacholczyk 1970; Blumenthal & Gould 1970; Sarazin 1988; Longair 2011)6. In this approach, for objects whose size in the sky (Ω arcmin2) is larger than the HXI FoV (9 × 9 arcmin2), the radio flux density sr is scaled down roughly as 9 × 9/Ω. This implies slightly conservative results since halos and relics are not uniform sources. Eventually, the resulting magnetic field value,
Here Γ and ζ are the gamma and Riemann zeta functions, respectively (Pacholczyk 1970; Blumenthal & Gould 1970; Sarazin 1988; Longair 2011)6. In this approach, for objects whose size in the sky (Ω arcmin2) is larger than the HXI FoV (9 × 9 arcmin2), the radio flux density sr is scaled down roughly as 9 × 9/Ω. This implies slightly conservative results since halos and relics are not uniform sources. Eventually, the resulting magnetic field value, 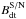 , is again a cap on the volume-average magnetic field below which HXR IC emission is detectable by ASTRO-H.
, is again a cap on the volume-average magnetic field below which HXR IC emission is detectable by ASTRO-H.
The analysis based on the signal-to-noise ratio is done assuming a straight power law in the 20–80 keV energy band. That is, we ignore any possible cutoff effect in that range, otherwise Eq. (7) would not be valid anymore. In most cases, the cutoffs are at much lower and higher energies. However, for A0085 and A1914 (see Fig. 3) and for A2063 and A0013 (see Appendix A for the corresponding figures), for example, this method could give slightly optimistic results.
In some cases (only radio relics, see Appendix A for the figures), the CXB dominates the thermal ICM emission, and the intersection point between the ASTRO-H sensitivity and the CXB emission is at an energy lower than the rise in the CXB spectrum. The corresponding results for Bdt should be taken with caution, and in fact, in these cases, the signal-to-noise approach gives more conservative results. We underline again that our simple approach is meant to be only a first approximation and that, in the following, we base all our conclusions only on the more robust signal-to-noise approach. Nevertheless, we note that the two approaches turn out to give similar results.
 |
Fig. 2 Synchrotron and IC modelling of the radio halo (H) in A2255. The black points and arrow are the currently available radio data and HXR upper-limit, respectively, from Table 1. We show the thermal ICM and CXB emissions, together with the ASTRO-H HXI sensitivity for 1 Ms of observations scaled to the halo angular size. The green lines show the models for the current volume-average lower limit BV (solid), and for Bdt (dashed) and |
We eventually decided to exclude the A2218 halo and the ZwCl0008.8-5215 western relic from the final modelling. This is due to their low radio flux and to the apparent presence of quite high γmin, or break in the radio spectra, that would render the IC search in these objects fairly impossible.
 |
Fig. 3 Synchrotron and IC modelling of the A0085, AS753, and A3667-NW radio relics (R), and of the Bullet, A1914 and A2319 radio halos (H). Caption as in Fig. 2. For A3667-NW and A2319, the lines corresponding to Bdt are not shown as they correspond to that of BV. |
We show an example of synchrotron and IC modelling in Fig. 2 for the case of the radio halo hosted by A2255, and we present and discuss all results in the next sections.
Signal-to-noise results for halo.
Signal-to-noise results for relics.
8. Results
The results of our analysis are given in Tables 4 and 5 for radio halos and relics, respectively. The third column contains the current lower limit on the magnetic field for objects where an HXR flux upper limit is available in literature. Our lower limits on the magnetic field are slightly higher than those in the original works from which the HXR upper limits fluxes are taken because of our assumption on the magnetic field distribution (see Sect. 4). The sixth column contains Bdt, which corresponds to the cap value of the volume-averaged magnetic field up to which ASTRO-H can still detect non-thermal IC for 1 Ms of observation time. The eighth column shows an optimistic value for the detection sensitivity on the volume-average magnetic field, 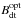 , obtained assuming that the CXB can be perfectly subtracted and, therefore, always considering the intersection of the ASTRO-H sensitivity curve with the thermal ICM emission as estimation point for
, obtained assuming that the CXB can be perfectly subtracted and, therefore, always considering the intersection of the ASTRO-H sensitivity curve with the thermal ICM emission as estimation point for 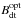 (see Sect. 7 for details).
(see Sect. 7 for details).
In Tables 6 and 7, we show the estimate of the ASTRO-H detection sensitivity of the volume-average magnetic field, 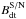 , obtained with the signal-to-noise approach in the 20–80 keV band, for halos and relics, respectively. We show the results for 100 ks, 500 ks, and 1 Ms of observation time.
, obtained with the signal-to-noise approach in the 20–80 keV band, for halos and relics, respectively. We show the results for 100 ks, 500 ks, and 1 Ms of observation time.
Comparing the results in Tables 4−7, it is clear that the results based on the intersection point between the background emission and the ASTRO-H sensitivity are more pessimistic. In particular, for sources larger than the HXI FoV (e.g., the halos of Coma and A2319, and the relics of Coma and A3667), our initial analysis shows little room for improvement on the current constraints, while the signal-to-noise analysis shows something different. The simplified assumption of a uniform source in our initial analysis is the most obvious reason for the pessimistic perspective for sources that cover a large area on the sky. This is also the origin for the Bdt values of the Coma and A2319 radio halos and the Coma and A3667-NW relic being at the same level of current upper limits. Additionally, assuming that the IC emission is only detectable at energies where it dominates the background is a conservative approach, given that backgrounds are known and can be modelled in detail in a real analysis. Indeed, as already stressed earlier, this simple method is meant to be just a first-order approximation, and we take our signal-to-noise approach as reference when drawing conclusions.
The soft X-ray (SXR) and extreme ultra-violet (EUV) bands could also be promising for the detection of IC emission, since the flux would be much higher at those lower frequencies (e.g., Sarazin & Lieu 1998). However, this is only advantageous if the background can be well constrained, and it crucially depends on the low-energy cutoff of the relativistic electron population, γmin, which is, in most cases, unconstrained by current radio data. Indeed, assuming an electron spectrum cutoff of γmin ~ 102, as discussed in Sect. 3, implies IC spectra peaking in the EUV band and often dominating the X-ray background in SXRs, in particular in case of very steep radio spectra. However, such steep spectra down to very low frequencies seem unlikely. The radio spectrum depends on the acceleration history of relativistic electrons, and as an example, steady state injection models feature a spectral break and would imply a low-frequency flattening (e.g., Sarazin 1999). In the near future, low-frequency observations with LOFAR (Röttgering et al. 2012) will provide crucial information and certainly shed more light on the spectrum of cosmic-ray electrons in clusters. This will be vital for assessing the possible IC contribution in the SXR and EUV regimes.
Magnetic field equipartition estimates.
Promising targets for ASTRO-H observations.
8.1. Promising targets
To pinpoint the most promising targets for ASTRO-H HXR observations, we focus on magnetic field estimates (e.g., Govoni & Feretti 2004). FR measurements range from ~ μG for merging clusters up to 10 μG for cool-core clusters (Carilli & Taylor 2002; Clarke 2004; Vogt & Enßlin 2005; Bonafede et al. 2010, 2013). Therefore, μG-level magnetic fields in clusters are nowadays widely acknowledged.
Analytical estimates can be obtained by the equipartition argument, that is, by minimising the total energy content (the sum of the energy in the magnetic field and that in relativistic particles) of a radio source. While standard equipartition estimates, Beq, are based on computing the synchrotron radio luminosity between two fixed frequencies, the so-called revised equipartition estimates, 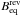 , are based on integrating over the relativistic electron distribution (Brunetti et al. 1997; Beck & Krause 2005). In Table 8, we summarise all the (revised) equipartition estimates that we could find in literature for the clusters in our sample.
, are based on integrating over the relativistic electron distribution (Brunetti et al. 1997; Beck & Krause 2005). In Table 8, we summarise all the (revised) equipartition estimates that we could find in literature for the clusters in our sample.
We stress that the equipartition estimates compiled in Table 8 should only be considered as reference values for comparison purposes. Not only do these suffer from several uncertainties, such as the ratio of electrons to protons in the source and the low-energy cutoff of the electron distribution, which are, a priori, unknown (see Govoni & Feretti 2004 for a discussion), but also one could question whether the equipartition assumption is justified because the evolution of relativistic electrons and magnetic fields in clusters may be decoupled given the short lifetime of the electrons compared to that of clusters. We also note that different authors often adopt different assumptions when applying the equipartition argument.
We consider a given halo or relic to be a promising candidate for ASTRO-H if its 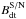 in 100 ks of observations is ≥ 1μG; while if smaller, we consider it promising when that value is comparable to, or higher than, the corresponding (revised) equipartition estimate (where available). The value of 1μG is just a rough educated guess that assumes the magnetic field value of the Coma cluster as prototype for which the volume average is ~ 2 μG (Bonafede et al. 2010, 2013). We summarise all objects that meet these criteria in Table 9.
in 100 ks of observations is ≥ 1μG; while if smaller, we consider it promising when that value is comparable to, or higher than, the corresponding (revised) equipartition estimate (where available). The value of 1μG is just a rough educated guess that assumes the magnetic field value of the Coma cluster as prototype for which the volume average is ~ 2 μG (Bonafede et al. 2010, 2013). We summarise all objects that meet these criteria in Table 9.
There is a crucial point to be considered when looking at our summary list of promising targets in Table 9, the size in the sky of a given halo. Halo size plays a crucial role in our predictions. Several objects in Table 9 have a size well below the ASTRO-H HXI FoV of 9 × 9 = 81 arcmin2. The smaller the size of a given object with respect to the FoV, the higher the contamination given by the thermal ICM emission, which obviously peaks in the centre of clusters. This is particularly important for radio relics in the cluster’s outskirts, which are the best targets for HXR IC detection, as is clear from the results presented in the tables in this work. On the other hand, an object that is much larger than the ASTRO-H FoV will call for multiple pointings with the corresponding increase in observation time. Regarding their morphology, ASTRO-H observation simulations of these objects are needed in order to give a definitive answer to which the most promising targets are.
We included Coma in our list of promising targets mainly because it is one of the best-studied clusters, and its observation by ASTRO-H is desirable. In fact, Coma represents one of the best targets for detecting and mapping the bulk of the ICM turbulent velocities for the first time with the Soft X-ray Spectrometer (SXS) on-board ASTRO-H (Kitayama et al. 2014). However, it does not represent the best hopes for the HXR IC detection.
To facilitate interpretation of our results, we provide a simple, approximate scaling of the ASTRO-H observation time with the magnetic field value 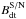 that corresponds to the signal-to-noise approach. We note that the number of background counts scales linearly with time NB ∝ Tobs, and under the assumption that NB ≫ NS, one finds that the number of source counts needed to reach a fixed signal-to-noise ratio scales as
that corresponds to the signal-to-noise approach. We note that the number of background counts scales linearly with time NB ∝ Tobs, and under the assumption that NB ≫ NS, one finds that the number of source counts needed to reach a fixed signal-to-noise ratio scales as 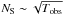 . From Eq. (6),
. From Eq. (6), 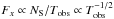 , and eventually, from Eq. (7), we find that, for any given α,
, and eventually, from Eq. (7), we find that, for any given α, 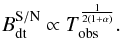 (9)Analogously, it can be shown that for a fixed observation time, i.e., fixed NB, the detectable magnetic field depends on the signal-to-noise ratio as follows:
(9)Analogously, it can be shown that for a fixed observation time, i.e., fixed NB, the detectable magnetic field depends on the signal-to-noise ratio as follows: 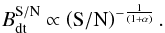 (10)
(10)
 |
Fig. 4 Synchrotron and IC modelling of the radio halo (H) and relic (R) hosted by Coma. Caption as in Fig. 2. In the case of the relic, we do not show the line corresponding to Bdt because it gives worst estimates than that of BV. This is due to our assumption of uniform radio sources which is particularly inappropriate in case of objects with a large size in the sky, like Coma. See main text for details. |
8.2. Comments on individual clusters
We report in the following some comments on the individual clusters in our final list of the most promising objects – A0085, AS753, A3667, Bullet, A1914, A2255, A2319, and Coma – while we leave the rest for Appendix A. We show the corresponding synchrotron and IC modelling in Figs. 2−4.
A0085. As can be seen from the top left-hand panel of Fig. 3, the radio relic of A0085 appears to have a low-energy cutoff in the radio spectrum. While this cutoff does not seem to affect our conclusion for the ASTRO-H detectability, if the magnetic field is much larger than BS/N, the low-energy turnover of the spectrum would move to higher energies and could affect the detectability estimates. The current HXR upper limit for this cluster (Ajello et al. 2010) refers to a much larger area than that of the relic. We remind the reader that the result of the signal-to-noise approach should be taken with caution in this case because its assumes a straight power law in the 20−80 keV range, while some spectral features could be expected.
AS753. The top right-hand panel of Fig. 3 shows the synchrotron and IC modelling for the radio relic hosted by this cluster. There are two things that should be noted: first, the very steep radio spectrum that implies a very-large IC flux in SXRs if we stick to the theoretically motivated γmin = 200. For this reason, we also show in the figure the case with γmin = 1000 and see that it does not change our predictions much for the HXR regime. Second, we must note that, since we lacked information on the gas density in this cluster, we used the phenomenological ICM model of Zandanel et al. (2014). This is, obviously, a source of a uncertainty and has very likely resulted in an underestimation of the gas density at the relic location.
A3667. This cluster hosts the prototype double relic system (Rottgering et al. 1997). The 1.9 Mpc northwestern relic contains most of the diffuse emission. HXR emission from the A3667-NW relic has been studied by Ajello et al. (2009) and Nakazawa et al. (2009). We used the latter group’s upper limit on the HXR non-thermal emission since it specifically refers to the relic region. In addition, a detailed X-ray study of the ICM can be found in Finoguenov et al. (2010) and Akamatsu et al. (2012). We show the corresponding synchrotron and IC modelling in the central left panel of Fig. 3. The current HXR upper limit is at the same level of our Bdt prediction due to our assumption of uniform radio sources. We try to assess this issue in Table 7 by providing an alternative estimate by assuming that all the radio emission comes from a region within the ASTRO-H HXI FoV.
Recently, Kitayama et al. (2014) have pointed out that the A3667-NW relic is one of the more promising targets for ASTRO-H to detect non-thermal HXR emission. They predict that HXI can constrain the magnetic field to B ≥ 4 μG in 200 ks of observations. This is significantly higher than our predicted values of Tables 5 and 7 by about a factor of two. However, their approach is quite different because they estimate the 90% confidence-level (CL) upper limit obtainable with ASTRO-H in 200 ks of observations. Moreover, the discrepancy mostly occurs because they assume that the SXR observed by Finoguenov et al. (2010) with XMM-Newton has a non-thermal origin, a hypothesis that cannot be excluded, and extrapolate this to HXRs with a power-law spectrum with a photon index of α = 2.
Bullet. We included the Bullet cluster for the broad interest in it and because it has been recently observed by NuSTAR, even if it does not fulfil our criteria of being in the promising targets list. Wik et al. (2014) have recently reported the results of the NuSTAR observations of the Bullet cluster where they do not find any evidence of non-thermal HXR emission from the radio halo. We derive slightly better prospects for ASTRO-H than their derived upper limit, as can be seen in the central right panel of Fig. 3. Although ASTRO-H and NuSTAR show comparable performances in HXR, the former has the advantage of the simultaneous operation of the SXI, allowing for a better determination of the thermal ICM emission.
A1914. The radio halo of A1914 has a very steep spectrum (Bacchi et al. 2003; Komissarov & Gubanov 1994). While we modelled the low-energy flattening in radio with a spectral cutoff, the data is insufficient to distinguish it from a broken power law, as can be seen in the bottom left-hand panel of Fig. 3. In this sense, therefore, the result of the signal-to-noise approach should be taken with caution because its assumes a straight power law in the 20–80 keV range, while some spectral features could be expected. The X-ray upper limit is from Ajello et al. (2010).
A2255. This cluster hosts both a radio halo and a relic (Feretti et al. 1997a). Since the relic is at ~ 10′ of the cluster centre and the XMM-Newton FoV is 30′, current HXR upper limits likely contain contributions from both the halo and the relic (Turner et al. 2001; Wik et al. 2012). The synchrotron and IC emission modelling of the radio halo is shown in Fig. 2. While we use radio observations from Feretti et al. (1997a) and Govoni et al. (2005), more recent observations were performed by Pizzo & de Bruyn (2009). However, considering the different areas used for the flux extraction, the later results are comparable to the former for the purpose of our modelling.
A2319. We used the HXR upper limit from Ajello et al. (2009) and point out that we obtain a more constraining lower limit BV> 0.7μG as a result of our assumptions regarding the magnetic field distribution (see Sect. 4). The bottom right-hand panel of Fig. 3 shows the corresponding synchrotron and IC modelling. The current HXR upper limit is at the same level of our Bdt prediction owing to our assumption of uniform radio sources, and we try to assess this issue in Table 6 by providing an alternative estimate by assuming that all the radio emission comes from a region within the ASTRO-H HXI FoV.
Coma. We included the Coma cluster more for historical reasons than for it being a very promising target. Coma is one of the best-studied clusters, and it hosts the prototype radio halo and relic (e.g., Thierbach et al. 2003; Brown & Rudnick 2011). A HXR excess at the halo location was claimed by Rephaeli & Gruber (2002) and Fusco-Femiano et al. (2004), but later never confirmed (Wik et al. 2009, 2011; Gastaldello et al. 2015). The radio relic (1253+275) is located at 75′ from the cluster centre. Figure 4 shows the synchrotron and IC modelling for both the radio halo and relic.
For the relic, the current upper limit (Feretti & Neumann 2006) appears more constraining than what is achievable with ASTRO-H HXI in 1 Ms of observation according to the signal-to-noise analysis. However, this upper limit is determined in the 20−80 keV band and could be evaded with a low-energy spectral cutoff or flattening. Therefore, as for AS753, we also show the case with γmin = 1000 in the right-hand panel of Fig. 4. Also in the case of the halo, the current HXR upper limit is at the same level as our predictions for Bdt. This is due to our assumption of uniform radio sources, which is particularly inappropriate for objects with a large size in the sky, like Coma. In fact, in Tables 6 and 7, we try to assess this by providing alternative estimates by i) assuming that all the radio emission comes from a region within the ASTRO-H HXI FoV (we show this also for a few other objects); and ii) by computing the thermal ICM emission for the case of the halo only within the halo boundaries. (We normally integrate over the full halos size, but again, owing to the large sky size of Coma, here the difference is appreciable.)
Kitayama et al. (2014) have recently discussed the prospects for 500 ks of ASTRO-H observation of the halo region. They estimate a corresponding 90%CL upper limit of B ~ 0.4 μG, which is slightly more optimistic than our estimates, but they assumed a photon index of α = 2.
9. Conclusions
In this work, we modelled the synchrotron and IC emission of all known radio halos and relics for which the spectral index can be determined. Our approach is phenomenological towards the generation mechanism of relativistic electrons. We simply assumed that the same electrons generating the observed radio synchrotron emission are responsible for HXR IC emission, where we adopted a power-law distribution with low- and high-energy cutoffs that we either fitted to the radio data, if steepening was observed, or we fixed to theoretically motivated values.
We provided updated lower limits on the magnetic field values for those objects for which an HXR upper limit is available. Subsequently, by considering the thermal ICM and CXB emissions and the instrumental background, we provided predictions for the volume-average magnetic filed values up to which HXR IC emission can be detected by the ASTRO-H HXI instrument, adopting different approaches and considering different observations times.
Our first approach was to estimate the magnetic field testable by ASTRO-H by taking the intersection point between the dominant background emission as reference, either thermal ICM or CXB, and the properly scaled ASTRO-H sensitivity for 1 Ms of observations. We then adopted a more robust approach based on photon counts in the 20−80 keV regime, requiring the signal-to-noise ratio to be higher than 5, where the noise includes the ICM and CXB emissions and the instrumental background. With this approach, on which we have based our conclusions, we estimated the magnetic field values testable by ASTRO-H in 100 ks, 500 ks, and 1 Ms of observations. With this estimate, we found that the observation time needed to test a certain magnetic field value B roughly scales as 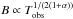 .
.
We identified as promising all those halos and relics for which the magnetic field testable by ASTRO-H in 100 ks is larger than 1μG or than the equipartition estimates, where available. We provided the corresponding list of 15 halos and relics in Table 9. Among the most promising targets, we have the AS753 and A3667-NW relics and the A2255 and A2319 halos, with an extension in the sky close to or larger than the ASTRO-H HXI FoV. Additionally, we can also identify the A0085, A2048, and A2063 relics as very promising, and the A1914 halo, with an extension smaller than the HXI FoV. The size in the sky of the considered object plays a crucial role in such observations, both for evaluating the contribution of the thermal ICM emission to the observed spectrum and for planning multiple pointings with a corresponding increase in observation time.
We stress that we have provided a theoretical expectation that suffers from several approximations that we discuss openly in the text. While we estimate that most of these approximations imply conservative results, some of them could go in the other direction: in particular, the uncertainty in the ICM density distribution of some objects, particularly for radio relics in the clusters’ outskirts, and the assumption of a power-law distribution of electrons down to low energies that are not tested by current radio observations, but could be tested soon by LOFAR. Therefore, while it is clear that detailed ASTRO-H observation simulations should be performed to select the best target amongst those we have proposed here, in particular against their angular dimension in the sky, we conclude that HXR IC detection could be at hand for ASTRO-H in several objects.
With the operation of NuSTAR and the upcoming launch of ASTRO-H, we will eventually be able to probe HXR IC emission in clusters for magnetic fields ≥ 1μG. Although detailed observation simulation are needed case by case, for a few clusters we might finally break the degeneracy between the magnetic field and the relativistic electrons distribution, and be able to shed new light on the non-thermal phenomena in clusters of galaxies.
Online material
Appendix A: Other figures and comments on individual clusters
This appendix contains the figures for the synchrotron and IC modelling of all clusters not shown in the main text. For some of these, the IC emission peaks in SXRs or EUV above the CXB and ICM emissions, so we also show the case with γmin = 1000.
Several objects, mainly radio relics, have the peculiarity of very low thermal ICM emission, probably an underestimation by observations pointed to the cluster’s centre or by using the phenomenological model of Zandanel et al. (2014) for the gas density. In some cases (A0781, A2163, MACSJ1149, 5-2223-E and W,
MACSJ1752.0+4440-SW, PLCK G287.0+32.9-N and S), the CXB outweighs the thermal ICM emission, and in addition, the intersection point between the ASTRO-H and CXB emissions is at an energy lower than the rise in the CXB spectrum. The corresponding results for Bdt should be taken with caution, and in fact, in these cases, the signal-to-noise approach gives more conservative and reasonable results.
We also remind the reader that the signal-to-noise approach assumes a straight power law in the 20−80 keV energy band (see Sect. 7). While in most cases the cutoffs are at much lower and higher energies, for A2063 and A0013 this method could give slightly optimistic results.
All figures can be read as explained in the caption of Fig. 2.
 |
Fig. A.1 Synchrotron and IC modelling for all clusters that are not shown in the main text. Caption as in Fig. 2. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
See, however, Eckert et al. (2008), Pérez-Torres et al. (2009), and Murgia et al. (2010) for the case of the Ophiuchus galaxy cluster, hosting a radio mini-halo, for which the detection of non-thermal HXR emission has been claimed.
Synchrotron-self Comptonisation is also possible (e.g., Ensslin & Sunyaev 2002).
We neglect the possible effect at high frequencies of thermal Sunyaev-Zeldovich (SZ) decrement (e.g., Enßlin 2002) which should, however, have a small impact (e.g., Brunetti et al. 2013). Anyhow, ignoring the SZ decrement implies more conservative results.
Additionally, comparing our power-law estimate to the ASTRO-H response files (http://astro-h.isas.jaxa.jp/researchers/sim/response.html) in the 20−80 keV band shows that we overestimate the predicted instrumental background by just a few percent.
Acknowledgments
We thank the anonymous referee for helping to improve our manuscript. We thank Hiroki Akamatsu, Madoka Kawaharada, Matteo Murgia, Anders Pinzke, Jacco Vink, and Franco Vazza for useful comments and discussions. We also profited from the Radio Observation of Galaxy Clusters database, collected by Klaus Dolag. This work was supported by the Netherlands Organisation for Scientific Research (NWO) through a Veni and a Vidi grant (F.Z. and S.A.).
References
- Ajello, M., Rebusco, P., Cappelluti, N., et al. 2009, ApJ, 690, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Ajello, M., Rebusco, P., Cappelluti, N., et al. 2010, ApJ, 725, 1688 [NASA ADS] [CrossRef] [Google Scholar]
- Akamatsu, H., de Plaa, J., Kaastra, J., et al. 2012, PASJ, 64, 49 [NASA ADS] [Google Scholar]
- Bacchi, M., Feretti, L., Giovannini, G., & Govoni, F. 2003, A&A, 400, 465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
- Bagchi, J., Enßlin, T. A., Miniati, F., et al. 2002, New Astron., 7, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Bagchi, J., Sirothia, S. K., Werner, N., et al. 2011, ApJ, 736, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Barrena, R., Girardi, M., Boschin, W., & Dasi, M. 2009, A&A, 503, 357 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, R., & Krause, M. 2005, Astron. Nach., 326, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Blumenthal, G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Böhringer, H., & Werner, N. 2010, A&ARv, 18, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Bonafede, A., Feretti, L., Giovannini, G., et al. 2009a, A&A, 503, 707 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonafede, A., Giovannini, G., Feretti, L., Govoni, F., & Murgia, M. 2009b, A&A, 494, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonafede, A., Feretti, L., Murgia, M., et al. 2010, A&A, 513, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonafede, A., Brüggen, M., van Weeren, R., et al. 2012, MNRAS, 426, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Bonafede, A., Vazza, F., Brüggen, M., et al. 2013, MNRAS, 433, 3208 [NASA ADS] [CrossRef] [Google Scholar]
- Boschin, W., Girardi, M., & Barrena, R. 2013, MNRAS, 434, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Brentjens, M., A. 2008, A&A, 489, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, S., & Rudnick, L. 2011, MNRAS, 412, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, S., Duesterhoeft, J., & Rudnick, L. 2011, ApJ, 727, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Brunetti, G. 2003, in Matter and Energy in Clusters of Galaxies, eds. S. Bowyer, & C.-Y. Hwang, ASP Conf. Ser., 301, 349 [Google Scholar]
- Brunetti, G., & Jones, T. W. 2014, Int. J. Mod. Phys. D, 23, 30007 [Google Scholar]
- Brunetti, G., Setti, G., & Comastri, A. 1997, A&A, 325, 898 [NASA ADS] [Google Scholar]
- Brunetti, G., Giacintucci, S., Cassano, R., et al. 2008, Nature, 455, 944 [NASA ADS] [CrossRef] [Google Scholar]
- Brunetti, G., Rudnick, L., Cassano, R., et al. 2013, A&A, 558, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carilli, C. L., & Taylor, G. B. 2002, ARA&A, 40, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Cavagnolo, K. W., Donahue, M., Voit, G. M., & Sun, M. 2009, ApJ, 182, 12 [Google Scholar]
- Cavaliere, A., & Fusco-Femiano, R. 1976, A&A, 49, 137 [NASA ADS] [Google Scholar]
- Chen, Y., Reiprich, T. H., Böhringer, H., Ikebe, Y., & Zhang, Y. Y. 2007, A&A, 466, 805 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, C. M. H., Harris, D. E., Harrison, F. A., & Mao, P. H. 2008, MNRAS, 383, 1259 [NASA ADS] [CrossRef] [Google Scholar]
- Clarke, T. E. 2004, J. Kor. Astron. Soc., 37, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Clarke, T. E., & Ensslin, T. A. 2006, AJ, 131, 2900 [Google Scholar]
- Cohen, A. S., & Clarke, T. E. 2011, AJ, 141, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Comastri, A., Setti, G., Zamorani, G., & Hasinger, G. 1995, A&A, 296, 1 [NASA ADS] [Google Scholar]
- Eckert, D., Produit, N., Paltani, S., Neronov, A., & Courvoisier, T. J.-L. 2008, A&A, 479, 27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Enßlin, T. A. 2002, A&A, 396, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Enßlin, T. A., & Vogt, C. 2006, A&A, 453, 447 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ensslin, T. A., & Sunyaev, R. A. 2002, A&A, 383, 423 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ensslin, T. A., Biermann, P. L., Klein, U., & Kohle, S. 1998, A&A, 332, 395 [NASA ADS] [Google Scholar]
- Feretti, L., & Neumann, D. M. 2006, A&A, 450, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feretti, L., Boehringer, H., Giovannini, G., & Neumann, D. 1997a, A&A, 317, 432 [NASA ADS] [Google Scholar]
- Feretti, L., Giovannini, G., & Boehringer, H. 1997b, New Astron., 2, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Feretti, L., Fusco-Femiano, R., Giovannini, G., & Govoni, F. 2001, A&A, 373, 106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feretti, L., Orru, E., Brunetti, G., et al. 2004, A&A, 423, 111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feretti, L., Schuecker, P., Böhringer, H., Govoni, F., & Giovannini, G. 2005, A&A, 444, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feretti, L., Giovannini, G., Govoni, F., & Murgia, M. 2012, A&ARv, 20, 1 [CrossRef] [Google Scholar]
- Finoguenov, A., Sarazin, C. L., Nakazawa, K., Wik, D. R., & Clarke, T. E. 2010, ApJ, 715, 1143 [NASA ADS] [CrossRef] [Google Scholar]
- Fukazawa, Y., Makishima, K., & Ohashi, T. 2004, PASJ, 56, 965 [NASA ADS] [Google Scholar]
- Fusco-Femiano, R., Orlandini, M., Brunetti, G., et al. 2004, ApJ, 602, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Gastaldello, F., Wik, D. R., Molendi, S., et al. 2015, ApJ, 800, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Gavazzi, G., & Trinchieri, G. 1983, ApJ, 270, 410 [NASA ADS] [CrossRef] [Google Scholar]
- Giacintucci, S. 2011, Mem. Soc. Astron. It., 82, 541 [NASA ADS] [Google Scholar]
- Giacintucci, S., Venturi, T., Brunetti, G., et al. 2005, A&A, 440, 867 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giacintucci, S., Venturi, T., Brunetti, G., et al. 2009, A&A, 505, 45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giacintucci, S., Dallacasa, D., Venturi, T., et al. 2011, A&A, 534, A109 [Google Scholar]
- Giacintucci, S., Kale, R., Wik, D. R., Venturi, T., & Markevitch, M. 2013, ApJ, 766, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Gilli, R., Comastri, A., & Hasinger, G. 2007, A&A, 463, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giovannini, G., & Feretti, L. 2000, New Astron., 5, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Giovannini, G., Feretti, L., & Stanghellini, C. 1991, A&A, 252, 528 [NASA ADS] [Google Scholar]
- Giovannini, G., Bonafede, A., Feretti, L., et al. 2009, A&A, 507, 1257 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Govoni, F., & Feretti, L. 2004, Int. J. Mod. Phys. D, 13, 1549 [NASA ADS] [CrossRef] [Google Scholar]
- Govoni, F., Feretti, L., Giovannini, G., et al. 2001, A&A, 376, 803 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Govoni, F., Murgia, M., Feretti, L., et al. 2005, A&A, 430, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gruber, D. E. 1992, in The X-ray Background, eds. X. Barcons, & A. C. Fabian, 44 [Google Scholar]
- Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Henriksen, M., & Mushotzky, R. 2001, ApJ, 553, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Hindson, L., Johnston-Hollitt, M., Hurley-Walker, N., et al. 2014, MNRAS, 445, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Johnston-Hollitt, M. 2004, in The Riddle of Cooling Flows in Galaxies and Clusters of galaxies, eds. T. Reiprich, J. Kempner, & N. Soker, 51 [Google Scholar]
- Juett, A. M., Sarazin, C. L., Clarke, T. E., et al. 2008, ApJ, 672, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Kale, R., & Dwarakanath, K. S. 2012, ApJ, 744, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Kale, R., Dwarakanath, K. S., Bagchi, J., & Paul, S. 2012, MNRAS, 426, 1204 [NASA ADS] [CrossRef] [Google Scholar]
- Kassim, N. E., Clarke, T. E., Enßlin, T. A., Cohen, A. S., & Neumann, D. M. 2001, ApJ, 559, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Kawano, N., Fukazawa, Y., Nishino, S., et al. 2009, PASJ, 61, 377 [NASA ADS] [Google Scholar]
- Kempner, J. C., & Sarazin, C. L. 2001, ApJ, 548, 639 [NASA ADS] [CrossRef] [Google Scholar]
- Kitayama, T., Bautz, M., Markevitch, M., et al. 2014, ArXiv e-prints [arXiv:1412.1176] [Google Scholar]
- Komissarov, S. S., & Gubanov, A. G. 1994, A&A, 285, 27 [NASA ADS] [Google Scholar]
- Liang, H., Hunstead, R. W., Birkinshaw, M., & Andreani, P. 2000, ApJ, 544, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Lindner, R. R., Baker, A. J., Hughes, J. P., et al. 2014, ApJ, 786, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Longair, M. 2011, High Energy Astrophysics (Cambridge University Press) [Google Scholar]
- Ma, C.-J., Ebeling, H., Donovan, D., & Barrett, E. 2008, ApJ, 684, 160 [Google Scholar]
- Macario, G., Venturi, T., Intema, H. T., et al. 2013, A&A, 551, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mantz, A., Allen, S. W., Ebeling, H., Rapetti, D., & Drlica-Wagner, A. 2010, MNRAS, 406, 1773 [NASA ADS] [Google Scholar]
- Marini, F., Bardelli, S., Zucca, E., et al. 2004, MNRAS, 353, 1219 [NASA ADS] [CrossRef] [Google Scholar]
- Menanteau, F., Hughes, J. P., Sifón, C., et al. 2012, ApJ, 748, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Million, E. T., & Allen, S. W. 2009, MNRAS, 399, 1307 [NASA ADS] [CrossRef] [Google Scholar]
- Molendi, S., & Gastaldello, F. 2009, A&A, 493, 13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mori, H., Maeda, Y., Ishida, M., et al. 2012, in SPIE Conf. Ser., 8443, 5 [Google Scholar]
- Murgia, M., Govoni, F., Feretti, L., et al. 2004, A&A, 424, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murgia, M., Eckert, D., Govoni, F., et al. 2010, A&A, 514, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakazawa, K., Sarazin, C. L., Kawaharada, M., et al. 2009, PASJ, 61, 339 [NASA ADS] [Google Scholar]
- Ogrean, G. A., Brüggen, M., van Weeren, R. J., et al. 2013, MNRAS, 433, 812 [NASA ADS] [CrossRef] [Google Scholar]
- Orru, E., Murgia, M., Feretti, L., et al. 2007, A&A, 467, 943 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ota, N. 2012, RA&A, 12, 973 [Google Scholar]
- Ota, N., Nagayoshi, K., Pratt, G. W., et al. 2014, A&A, 562, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pacholczyk, A. 1970, Radio Astrophysics: Nonthermal Processes in Galactic and Extragalactic Sources, Astronomy and Astrophysics Series (W. H. Freeman) [Google Scholar]
- Pandey-Pommier, M., Richard, J., Combes, F., et al. 2013, A&A, 557, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pérez-Torres, M. A., Zandanel, F., Guerrero, M. A., et al. 2009, MNRAS, 396, 2237 [NASA ADS] [CrossRef] [Google Scholar]
- Petrosian, V. 2001, ApJ, 557, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Petrosian, V., Madejski, G., & Luli, K. 2006, ApJ, 652, 948 [NASA ADS] [CrossRef] [Google Scholar]
- Piffaretti, R., Arnaud, M., Pratt, G. W., Pointecouteau, E., & Melin, J. B. 2011, A&A, 534, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinzke, A., Pfrommer, C., & Bergström, L. 2011, Phys. Rev. D, 84, 12 3509 [Google Scholar]
- Pizzo, R. F., & de Bruyn, A. G. 2009, A&A, 507, 639 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIX. 2014, A&A, 571, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popesso, P., Biviano, A., Böhringer, H., & Romaniello, M. 2007, A&A, 461, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reid, A. D., Hunstead, R. W., Lémonon, L., & Pierre, M. M. 1999, MNRAS, 302, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Rephaeli, Y. 1979, ApJ, 227, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Rephaeli, Y., & Gruber, D. 2002, ApJ, 579, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Rephaeli, Y., Gruber, D., & Arieli, Y. 2006, ApJ, 649, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Rephaeli, Y., Nevalainen, J., Ohashi, T., & Bykov, A. M. 2008, Space Sci. Rev., 134, 71 [Google Scholar]
- Röttgering, H., Afonso, J., Barthel, P., et al. 2012, JA&A, 557, 34 [Google Scholar]
- Röttgering, H., van Weeren, R., Brüggen, M., et al. 2013, Astron. Nachr., 334, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Rottgering, H. J. A., Wieringa, M. H., Hunstead, R. W., & Ekers, R. D. 1997, MNRAS, 290, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Sarazin, C. 1999, ApJ, 520, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Sarazin, C. L. 1988, X-ray emission from clusters of galaxies (Cambridge: Cambridge University Press) [Google Scholar]
- Sarazin, C. L., & Lieu, R. 1998, ApJ, 494, L177 [NASA ADS] [CrossRef] [Google Scholar]
- Sehgal, N., Hughes, J. P., Wittman, D., et al. 2008, ApJ, 673, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, S., Kauffmann, G., Von Der Linden, A., White, S. D. M., & Best, P. N. 2008, MNRAS, 389, 1074 [NASA ADS] [CrossRef] [Google Scholar]
- Shimwell, T. W., Brown, S., Feain, I. J., et al. 2014, MNRAS, 440, 2901 [NASA ADS] [CrossRef] [Google Scholar]
- Slee, O. B., Roy, A. L., Murgia, M., Andernach, H., & Ehle, M. 2001, AJ, 122, 1172 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. K., Brickhouse, N. S., Liedahl, D. A., & Raymond, J. C. 2001, ApJ, 556, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Storm, E., Jeltema, T. E., & Rudnick, L. 2015, MNRAS, 448, 2495 [NASA ADS] [CrossRef] [Google Scholar]
- Stroe, A., Rumsey, C., Harwood, J. J., et al. 2014, MNRAS, 441, 41 [Google Scholar]
- Subrahmanyan, R., Beasley, A. J., Goss, W. M., Golap, K., & Hunstead, R. W. 2003, AJ, 125, 1095 [NASA ADS] [CrossRef] [Google Scholar]
- Takahashi, T., Mitsuda, K., Kelley, R., et al. 2010, in SPIE Conf. Ser., 7732 [Google Scholar]
- Takahashi, T., Mitsuda, K., Kelley, R., et al. 2012, in SPIE Conf. Ser., 8443 1 [Google Scholar]
- Takahashi, T., Mitsuda, K., Kelley, R., et al. 2014, in SPIE Conf. Ser., 9144, 25 [Google Scholar]
- Thierbach, M., Klein, U., & Wielebinski, R. 2003, A&A, 397, 53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vacca, V., Feretti, L., Giovannini, G., et al. 2014, A&A, 561, A11 [Google Scholar]
- van Weeren, R. J., Röttgering, H. J. A., Bagchi, J., et al. 2009, A&A, 506, 1083 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Weeren, R. J., Brüggen, M., Röttgering, H. J. A., et al. 2011a, A&A, 533, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Weeren, R. J., Hoeft, M., Röttgering, H. J. A., et al. 2011b, A&A, 528, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Weeren, R. J., Röttgering, H. J. A., & Brüggen, M. 2011c, A&A, 527, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Weeren, R. J., Bonafede, A., Ebeling, H., et al. 2012a, MNRAS, 425, L36 [NASA ADS] [CrossRef] [Google Scholar]
- van Weeren, R. J., Röttgering, H. J. A., Intema, H. T., et al. 2012b, A&A, 546, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Weeren, R. J., Röttgering, H. J. A., Rafferty, D. A., et al. 2012c, A&A, 543, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Weeren, R. J., Fogarty, K., Jones, C., et al. 2013, ApJ, 769, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Venturi, T., Bardelli, S., Dallacasa, D., et al. 2003, A&A, 402, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venturi, T., Giacintucci, S., Brunetti, G., et al. 2007, A&A, 463, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venturi, T., Giacintucci, S., Cassano, R., et al. 2009, in The Low-Frequency Radio Universe, eds. D. J. Saikia, D. A. Green, Y. Gupta, & T. Venturi, ASP Conf. Ser., 407, 232 [Google Scholar]
- Vogt, C., & Enßlin, T. A. 2005, A&A, 434, 67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voit, G. M. 2005, Rev. Mod. Phys., 77, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Wik, D. R., Sarazin, C. L., Finoguenov, A., et al. 2009, ApJ, 696, 1700 [NASA ADS] [CrossRef] [Google Scholar]
- Wik, D. R., Sarazin, C. L., Finoguenov, A., et al. 2011, ApJ, 727, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Wik, D. R., Sarazin, C. L., Zhang, Y.-Y., et al. 2012, ApJ, 748, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Wik, D. R., Hornstrup, A., Molendi, S., et al. 2014, ApJ, 792, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, J. H., Schawinski, K., Sheen, Y.-K., Ree, C. H., & Yi, S. K. 2008, ApJS, 176, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Zandanel, F., Pfrommer, C., & Prada, F. 2014, MNRAS, 438, 116 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 The geometry used in determining the normalisation for the APEC modelling of the radio relic regions (Eq. (5)). Rcc corresponds to the distance between the relic and the cluster center as projected on the sky. Rl is the relic largest linear size and Rw is the relic width. For relics that are classified as roundish by Feretti et al. (2012) we use Rw = Rl. φ is given by |
| In the text | |
 |
Fig. 2 Synchrotron and IC modelling of the radio halo (H) in A2255. The black points and arrow are the currently available radio data and HXR upper-limit, respectively, from Table 1. We show the thermal ICM and CXB emissions, together with the ASTRO-H HXI sensitivity for 1 Ms of observations scaled to the halo angular size. The green lines show the models for the current volume-average lower limit BV (solid), and for Bdt (dashed) and |
| In the text | |
 |
Fig. 3 Synchrotron and IC modelling of the A0085, AS753, and A3667-NW radio relics (R), and of the Bullet, A1914 and A2319 radio halos (H). Caption as in Fig. 2. For A3667-NW and A2319, the lines corresponding to Bdt are not shown as they correspond to that of BV. |
| In the text | |
 |
Fig. 4 Synchrotron and IC modelling of the radio halo (H) and relic (R) hosted by Coma. Caption as in Fig. 2. In the case of the relic, we do not show the line corresponding to Bdt because it gives worst estimates than that of BV. This is due to our assumption of uniform radio sources which is particularly inappropriate in case of objects with a large size in the sky, like Coma. See main text for details. |
| In the text | |
 |
Fig. A.1 Synchrotron and IC modelling for all clusters that are not shown in the main text. Caption as in Fig. 2. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.