| Issue |
A&A
Volume 581, September 2015
|
|
|---|---|---|
| Article Number | A113 | |
| Number of page(s) | 6 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201526236 | |
| Published online | 17 September 2015 | |
Sparsely sampling the sky: Regular vs. random sampling
1
Mullard Space Science Laboratory, University College London,
Holmbury St. Mary, Dorking,
Surrey
RH5 6NT,
UK
e-mail:
p.paykari@ucl.ac.uk
2
Laboratoire AIM, Irfu, Service d’Astrophysique, CEA
Saclay, 91191
Gif-sur-Yvette,
France
3
Department of Physics, Blackett Laboratory,
Imperial College, London
SW7 2AZ,
UK
Received: 1 April 2015
Accepted: 20 June 2015
Aims. The next generation of galaxy surveys, aiming to observe millions of galaxies, are expensive both in time and money. This raises questions regarding the optimal investment of this time and money for future surveys. In a previous work, we have shown that a sparse sampling strategy could be a powerful substitute for the – usually favoured – contiguous observation of the sky. In our previous paper, regular sparse sampling was investigated, where the sparse observed patches were regularly distributed on the sky. The regularity of the mask introduces a periodic pattern in the window function, which induces periodic correlations at specific scales.
Methods. In this paper, we use a Bayesian experimental design to investigate a “random” sparse sampling approach, where the observed patches are randomly distributed over the total sparsely sampled area.
Results. We find that in this setting, the induced correlation is evenly distributed amongst all scales as there is no preferred scale in the window function.
Conclusions. This is desirable when we are interested in any specific scale in the galaxy power spectrum, such as the matter-radiation equality scale. As the figure of merit shows, however, there is no preference between regular and random sampling to constrain the overall galaxy power spectrum and the cosmological parameters.
Key words: methods: data analysis / cosmological parameters / cosmology: observations
© ESO, 2015
1. Introduction
The accurate measurement of the cosmological parameters relies on accurate measurements of a type of power spectrum that describes the spatial distribution of an isotropic random field. The power spectrum is enough to completely define the perturbations when the perturbations are assumed uncorrelated Gaussian random fields in the Fourier space. A power spectrum (or its Fourier transform, the correlation function) is what the surveys measure, from which cosmological parameters are inferred. These spectra are normally a convolution of the primordial power spectrum and a transfer function, which depends on the cosmological parameters. One of the most important observed spatial power spectra is the galaxy power spectrum, first formulated by Peebles (1973), which is defined as 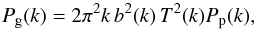 (1)where Pp(k) = Askns−1 is the primordial power spectrum, which measures the statistical distribution of perturbations in the early Universe – for example, just after the inflationary era. The transfer function T(k) is responsible for the evolution of the Universe and depends on the cosmological parameters, such as the cold dark matter Ωc and the baryonic content of the Universe Ωb. The galaxy power spectrum, which is the observed quantity, is related to the underlying matter power spectrum via the bias b (Kaiser 1984) – galaxies trace dark matter up to this b factor. The galaxy power spectrum is very rich in terms of constraining a wide range of cosmological parameters. On large scales, it probes the structures that are less affected by clustering and evolution and hence have a “memory” of the initial state of the Universe. On intermediate scales, the spectrum informs us about the evolution of the Universe; for example, the epoch of matter-radiation equality. On relatively small scales, there is a great deal of information about galaxy clustering via the baryonic acoustic oscillations (BAO), which, for example, encodes information about the sound horizon at the time of recombination. Therefore, measuring the galaxy power spectrum on a wide range of scales helps us constrain a range of cosmological parameters.
(1)where Pp(k) = Askns−1 is the primordial power spectrum, which measures the statistical distribution of perturbations in the early Universe – for example, just after the inflationary era. The transfer function T(k) is responsible for the evolution of the Universe and depends on the cosmological parameters, such as the cold dark matter Ωc and the baryonic content of the Universe Ωb. The galaxy power spectrum, which is the observed quantity, is related to the underlying matter power spectrum via the bias b (Kaiser 1984) – galaxies trace dark matter up to this b factor. The galaxy power spectrum is very rich in terms of constraining a wide range of cosmological parameters. On large scales, it probes the structures that are less affected by clustering and evolution and hence have a “memory” of the initial state of the Universe. On intermediate scales, the spectrum informs us about the evolution of the Universe; for example, the epoch of matter-radiation equality. On relatively small scales, there is a great deal of information about galaxy clustering via the baryonic acoustic oscillations (BAO), which, for example, encodes information about the sound horizon at the time of recombination. Therefore, measuring the galaxy power spectrum on a wide range of scales helps us constrain a range of cosmological parameters.
For accurate measurements of the galaxy power spectrum, surveys aim to maximize the observed number of galaxies to overcome the Poisson noise. Considering the large investments in time and money for these surveys, one would like to know the optimal survey strategy. For example, to investigate larger scales, it may be more efficient to observe a larger but sparsely sampled area of sky instead of a smaller contiguous area. In this case, one gathers a higher density of states in Fourier space, but at the expense of an increased correlation between different scales – aliasing. This would smooth out features on certain scales and decrease their statistical significance. The sparse sampling approach was investigated in a previous paper (Paykari & Jaffe 2013), where the advantages and disadvantages of such a design was studied. It was shown that sparse sampling could be a powerful substitute for the usually favoured contiguous sampling. In particular, it was shown that for a survey similar to the Dark Energy Survey (DES)1, a sparse design could help reduce the observing time – and hence cost – of the survey without significantly reducing the constraining power of the survey. Alternatively, for the same amount of observing time, one can observe a larger but sparsely sampled area of the sky to improve the constraining power of the survey.
In Paykari & Jaffe (2013), the observed patches were regularly distributed over the total sampled area of the sky. The fixed and determined position of the patches introduces a periodic pattern in the window function, which induce a periodic aliasing of scales: This means that certain scales, corresponding to the fixed distances between the patches, are more aliased than other scales (Fig. 8 in Paykari & Jaffe 2013). As a result of this effect, the regular design may not be desirable.
In this paper, we investigate the optimal strategy for sparse sampling. We study and compare the advantages and disadvantages of random vs. regular sparse sampling. As in Paykari & Jaffe (2013), we used a Bayesian experimental design and various figures of merit (FoMs) to select the optimal design for constraining the galaxy power spectrum bins and a set of cosmological parameters.
Chiang et al. (2013) also investigated regular and random sparse sampling of redshift surveys. They found a bias in the power spectrum recovery when a regular mask is randomly perturbed. Such a bias can be eliminated by explicitly accounting for the window function corresponding to the particular mask (selection function) used with an appropriate unbiased estimator (e.g., Feldman et al. 1994) to recover the power spectrum. Here, we focus on comparing the induced aliasing of power amongst scales due to regular and random sampling.
Paper content
In Sect. 2 we present a brief introduction to our methodology. A full description can be found in Paykari & Jaffe (2013). In Sect. 3 we present the regular and random sparse designs. Our results are presented in Sect. 4, and in Sect. 5 we conclude and give some potential perspectives.
2. Methodology
Bayesian methods have recently been used in cosmology for model comparison and for deriving posterior probability distributions for parameters of different models. Bayesian statistics can be used to investigate the performance of future experiments, based on our knowledge from current experiments (Liddle et al. 2006; Trotta 2007a,b; Mukherjee et al. 2006). We will use this strength of Bayesian statistics to optimise the observing strategy for galaxy surveys. For such an optimisation, we need to satisfy three requirements: 1. specify the parameters that define the experiment; 2. specify the parameters to constrain (with respect to which the survey is optimised); 3. specify a quantity of interest, generally called the figure of merit (FoM), associated with the proposed experiment. We wish to extremise the FoM subject to constraints imposed by the experiment or by our knowledge about the nature of the Universe.
We assume e denotes the different experimental designs, Mi are the different models with their parameters θi, and experiment o has already been performed. The posterior P(θ | o) of experiment o forms our prior probability function for the new experiment. The FoM depends on the parameters of interest, the previous experiment (data), and the characteristics of the future experiment, U(θ,e,o). From this, we can build the expected FoM E[U] as ![\begin{equation} E[U|e,o]=\sum_{i}P(M^{i}|o)\int {\rm d}\hat{\theta}^{i}\; U(\hat{\theta}^{i},e,o)P(\hat{\theta}^{i}|o,M^{i}), \end{equation}](/articles/aa/full_html/2015/09/aa26236-15/aa26236-15-eq15.png) (2)where
(2)where 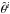 represents the fiducial parameters for model Mi. Our knowledge of the Universe is described by the current posterior distribution
represents the fiducial parameters for model Mi. Our knowledge of the Universe is described by the current posterior distribution 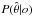 . Averaging U over the posterior accounts for the present uncertainty in the parameters and summing over all the available models would account for the uncertainty in the underlying true model. The aim is to select an experiment that extremises the FoM (or its expectation). One of the common choices for the FoM is some scalar function of the Fisher matrix, which is the expectation of the inverse covariance of the parameters in the Gaussian limits (this is explained further in this section)2. The three common FoMs (Hobson et al. 2009) we use here are
. Averaging U over the posterior accounts for the present uncertainty in the parameters and summing over all the available models would account for the uncertainty in the underlying true model. The aim is to select an experiment that extremises the FoM (or its expectation). One of the common choices for the FoM is some scalar function of the Fisher matrix, which is the expectation of the inverse covariance of the parameters in the Gaussian limits (this is explained further in this section)2. The three common FoMs (Hobson et al. 2009) we use here are
-
A-optimality = log (trace(F)); trace of the Fisher matrix F (or its log ), which is proportional to sum of the variances.
-
D-optimality = log (|F|); determinant of the Fisher matrix F (or its log ), which measures the inverse of the square of the parameter volume enclosed by the posterior.
-
Entropy (also called the Kullback-Leibler divergence)
![\begin{eqnarray} \textrm{Entropy} & = & \int {\rm d}\theta\; P(\theta|\hat{\theta},e,o)\log\frac{P(\theta|\hat{\theta},e,o)}{P(\theta|o)}\nonumber \\ & = & \frac{1}{2}\left[\log\left|\mathbf{F}\right|-\log|\mathbf{\Pi}|-\textrm{Tr}(\mathbb{I}-\mathbf{\Pi}\mathbf{F}^{-1})\right], \end{eqnarray}](/articles/aa/full_html/2015/09/aa26236-15/aa26236-15-eq23.png) (3)where
(3)where 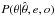 is the posterior distribution with Fisher matrix F and P(θ | o) is the prior distribution with Fisher matrix Π. The posterior Fisher matrix is F = L + Π, where L is the likelihood Fisher matrix, which is the current sparse survey we have designed.
is the posterior distribution with Fisher matrix F and P(θ | o) is the prior distribution with Fisher matrix Π. The posterior Fisher matrix is F = L + Π, where L is the likelihood Fisher matrix, which is the current sparse survey we have designed.
Here, the FoMs are defined so that they need to be maximised for an optimal design. For a detailed comparison between the above FoMs we refer to Hobson et al. (2009) and Paykari & Jaffe (2013). We note that these are not the “expected” FoM – in our current models of the Universe, we do not expect a significant difference between the parameters of the same model.
The Fisher matrix (e.g., Kendall & Stuart 1977; Tegmark 1997) has frequently been used for optimisation and forecasting. The Fisher matrix is defined as the ensemble average of the curvature of the likelihood function ℒ (i.e., it is the average of the curvature over many realisations of signal and noise), ![\begin{eqnarray} F_{ij} &=& \left\langle \mathcal{F}_{ij}\right\rangle \nonumber\\ &=&\left\langle -\frac{\partial^{2}\ln\mathcal{L}}{\partial\theta_{i}\partial\theta_{j}}\right\rangle \label{eq:General_FM} \nonumber\\ &=&\frac{1}{2}\textrm{Tr}[C_{,i}C^{-1}C_{,j}C^{-1}]\:, \end{eqnarray}](/articles/aa/full_html/2015/09/aa26236-15/aa26236-15-eq29.png) (4)where subscript,i means differentiation with respect to parameter i. The last equality is appropriate for a Gaussian distribution with correlation matrix C determined by the parameters θi. The inverse of the Fisher matrix is an approximation of the covariance matrix of the parameters, by analogy with a Gaussian distribution in the θi, for which this would be exact. The Cramer-Rao inequality states that the smallest frequentist error measured for θi by any unbiased estimator is
(4)where subscript,i means differentiation with respect to parameter i. The last equality is appropriate for a Gaussian distribution with correlation matrix C determined by the parameters θi. The inverse of the Fisher matrix is an approximation of the covariance matrix of the parameters, by analogy with a Gaussian distribution in the θi, for which this would be exact. The Cramer-Rao inequality states that the smallest frequentist error measured for θi by any unbiased estimator is 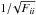 or
or 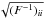 , for non-marginalised and marginalised one-sigma errors, respectively. The derivatives in Eq. (4) generally depend on where they are calculated in the parameter space, and hence the Fisher matrix is a function of the fiducial parameters. We furthermore note that any results obtained from the Fisher matrix must be taken with the caveat that these relations only map onto realistic error bars for a Gaussian distribution, usually most appropriate in the limit of high signal-to-noise ratios, where the conditions of the central limit theorem hold. In case of no extremely degenerate parameter directions, we expect that our results are indicative of a full analysis (Trotta 2007b).
, for non-marginalised and marginalised one-sigma errors, respectively. The derivatives in Eq. (4) generally depend on where they are calculated in the parameter space, and hence the Fisher matrix is a function of the fiducial parameters. We furthermore note that any results obtained from the Fisher matrix must be taken with the caveat that these relations only map onto realistic error bars for a Gaussian distribution, usually most appropriate in the limit of high signal-to-noise ratios, where the conditions of the central limit theorem hold. In case of no extremely degenerate parameter directions, we expect that our results are indicative of a full analysis (Trotta 2007b).
Following Tegmark (1997), the data in pixel i is defined as ![\hbox{$ \Delta_{i}\equiv\int d^{3}x \; \psi_{i}(\underbar{x})\left[{n(\underbar{x})-\bar{n}}\right]/{\bar{n}}, $}](/articles/aa/full_html/2015/09/aa26236-15/aa26236-15-eq36.png) where
where 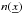 is the galaxy density at position
is the galaxy density at position 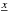 and
and 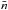 is the expected number of galaxies at that position. The weighting function,
is the expected number of galaxies at that position. The weighting function, 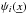 , which determines the pixelisation and the shape of the survey, is defined as a set of Fourier pixels
, which determines the pixelisation and the shape of the survey, is defined as a set of Fourier pixels 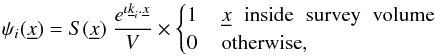 (5)where V is the total volume of the survey and
(5)where V is the total volume of the survey and 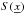 is the mask, which, for example, defines the distribution of the observed patches. We design the sparsely sampled area of the sky as a distribution np × np square patches of size M × M, as shown in Fig. 1. Therefore, the structure of the mask S on the sky is defined as a series of top-hat functions in both x and y directions and a single top-hat function in the z direction3
is the mask, which, for example, defines the distribution of the observed patches. We design the sparsely sampled area of the sky as a distribution np × np square patches of size M × M, as shown in Fig. 1. Therefore, the structure of the mask S on the sky is defined as a series of top-hat functions in both x and y directions and a single top-hat function in the z direction3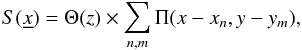 (6)where xn and ym mark the centres of the patches in our coordinate system and the top-hat functions are defined as
(6)where xn and ym mark the centres of the patches in our coordinate system and the top-hat functions are defined as 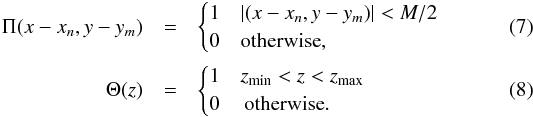 Dividing the survey volume into sub-volumes i, Δi is then the fractional over-density in pixel i. Using this pixelisation, we can define a covariance matrix as
Dividing the survey volume into sub-volumes i, Δi is then the fractional over-density in pixel i. Using this pixelisation, we can define a covariance matrix as 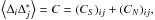 where CS and CN are the signal and noise covariance matrices, respectively, and are assumed independent of each other. For generality, we take the complex conjugate of one member of the pair. By equating the number over-density
where CS and CN are the signal and noise covariance matrices, respectively, and are assumed independent of each other. For generality, we take the complex conjugate of one member of the pair. By equating the number over-density ![\hbox{$\left[n(\underbar{x})-\bar{n}\right]/\bar{n}$}](/articles/aa/full_html/2015/09/aa26236-15/aa26236-15-eq58.png) with the continuous over-density
with the continuous over-density ![\hbox{$\delta(\underbar{x})=\left[\rho(\underbar{x})-\bar{\rho}\right]/\bar{\rho}$}](/articles/aa/full_html/2015/09/aa26236-15/aa26236-15-eq59.png) , the signal and the noise covariance matrices can be defined as
, the signal and the noise covariance matrices can be defined as 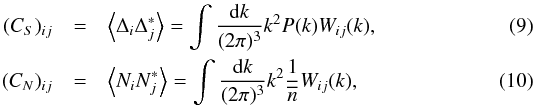 where the window function Wij(k) is defined as the angular average of the square of the weighting function in the Fourier space
where the window function Wij(k) is defined as the angular average of the square of the weighting function in the Fourier space 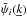 ,
, 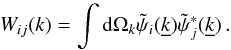 (11)This prescription gives us a data covariance matrix for a galaxy survey, from which we can obtain a Fisher matrix for the parameters of interest using Eq. (4) above. For a full analysis of these equations we refer to Dodelson (2003) or Paykari & Jaffe (2013).
(11)This prescription gives us a data covariance matrix for a galaxy survey, from which we can obtain a Fisher matrix for the parameters of interest using Eq. (4) above. For a full analysis of these equations we refer to Dodelson (2003) or Paykari & Jaffe (2013).
3. Survey design
We chose a geometrically flat ΛCDM model with adiabatic perturbations with a five-parameter model: Ωc = 0.214, Ωb = 0.044, ΩΛ = 0.742, τ = 0.087 and h = 0.719, where H0 = 100h km s-1 Mpc-1. We expect our results to be fairly insensitive to the exact values of the parameters in the ΛCDM model. As explained above, the FoMs we used here are entropy, A-optimality and D-optimality, where a SDSS-LRG-like survey was chosen as the prior Fisher matrix Π.
 |
Fig. 1 Design of the mask for random (left) and regular (right) sparse sampling. The patches (we observe through the white square patches in the figure) are distributed randomly and regularly on the surface of the sky. The fractional sky coverage, fsky, is the same in both designs – we verified that the patches do not overlap to satisfy this condition. |
As in Paykari & Jaffe (2013), we used a flat sky approximation to sparsify our survey. We divided the total sparsely sampled area of the sky into small square patches and distributed them randomly (left panel of Fig. 1) and regularly (right panel of Fig. 1). The total observed area is the sum of the areas of all the patches, (np × M)2, and the total sampled area is the total area that bounds both the masked and the unmasked areas. Hence the fractional sky coverage is fsky = (np × M)2/Atot, which is the same in both designs. The patches have a size of 41 Mpc in both x and y directions. This patch size avoids entering the non-linear regime.
We note that there are three scales that control the behaviour of the window function; one is the size of the patches, the other is the distance between them, and the third one is total size of the survey, that is, the extent of the survey. In both the regular and the random designs, the size of the patches and the total size of the survey is exactly the same. In this scenario, the only difference between the two designs is the distribution of the distances/separation between the patches; in the regular design, the patches are placed at 180 Mpc from one another, while in the random case the distances span a range.
We also note that we had the same number of patches in both designs, and we verified that the patches did not overlap. This is so that the fractional sky coverage fsky is the same in both cases to ensure that we have the same information gain for both surveys. We note that in practice, random pointings on the sky may not be optimal from the instrument point of view (for example, taking into account the overheads). However, in this work we aim to optimise a survey for our cosmological purposes. Optimising the instruments to best match the cosmologically optimised survey is beyond the scope of this paper.
4. Results
In Fig. 2 we compare the power spectrum Fisher matrix Fij for regular and random sampling. The main peak in the middle is the expected inverse error of the middle bin of the power spectrum, that is, 1 /σii. Moving away from the main peak, each point represents the correlation between that bin and the middle one, that is, 1 /σij. In the case of regular sampling, there are secondary peaks at other scales in addition to the main peak at the centre, which indicates an induced correlation at these scales. The position of the secondary peaks is a consequence of the fixed distances between the patches in the mask. The patches are placed at 180 Mpc from one another, meaning the distance between the peaks in Fourier space are at 2π/ (180 Mpc) ≃ 0.035 Mpc-1, as shown in Fig. 2. The regularity in the mask introduces a periodic pattern in the window function, which in turn induces correlations at that period. In this design, certain scales are therefore measured with less statistical significance. This could be a disadvantage if we wish to constrain the behaviour of the power spectrum at a certain scale, such as the BAO scale.
On the other hand, the patches are placed at random positions in the case of random sampling. As there is no preferred scale in the mask, all scales are on average constrained with almost the same statistical significance. This means that the power leakage from the main peak is evenly distributed amongst all scales.
The amplitude and the width of the main peak are controlled by the fractional sky coverage fsky and the total sparsely sampled volume Vtot, respectively. As fsky and Vtot are the same in both regular and random sampling, the amplitude and width of the main peaks are the same in both cases.
 |
Fig. 2 Top panel: middle row of the power spectrum Fisher matrix Fij for five realisations of the random sparse sampling. The main peak in the middle is the inverse error of the middle bin of the power spectrum 1 /σii. Moving away from the main peak, each point represents the correlation between that bin and the middle one 1 /σij. Bottom panel: same for regular (black) and average of the realisations of the random (blue) sampling. In the case of regular sampling, there are secondary peaks at specific scales, which is a consequence of the fixed position of the patches. On the other hand, for random sampling, there is no preferred scale and correlation is evenly distributed between all scales. The symmetric shoulders on the main peak, at k ≃ 0.037 Mpc-1 and k ≃ 0.06 Mpc-1, in the random case are due to the design of the random mask, which has been obtained by a reflection in the x and y plane for simplicity (see main text). Note that the y-axis is in log scale. |
Table 1 shows the FoM for the galaxy power spectrum bins on the left and the cosmological parameters on the right. As can be seen, both regular and random designs have very similar values for both the power spectrum bins and the parameters. This shows that for the same fsky, the arrangement of the patches does not play an important role in constraining the galaxy spectrum bins or the parameters. Therefore, the constraining power of the survey is not controlled by the distribution of the patches, but, as investigated in Paykari & Jaffe (2013), by the total extent of the sampled area. We also note that the FoMs we chose are only sensitive to the integrated constraining power over all scales of the spectrum; that is, the total information gain of the survey, which is proportional to fsky. As this is the same for both designs, we do expect similar values for the FoMs for both cases. However, if we are interested in any particular scale, random sampling would be the preferred approach as it causes evenly distributed leakage of power into all scales, as demonstrated in Fig. 2. That is, the error at any particular scale has low correlations with all other scales.
Figure of merit (FoM) for the galaxy power spectrum and the cosmological parameters for regular and random sampling.
To this end, we summarise the main features of Fig. 2:
-
1.
The width of the main peak in both designs (and the secondary peaks in the regular case) is controlled by the total size of the survey. As this is the same in both designs, the width is the same in both cases.
-
2.
The position of the secondary peaks in the regular case is controlled by the position of the patches in the mask. We note that apart from the periodicity in x and y directions, there is also periodicity at all angles, especially at the 45° line.
-
3.
The size of the patches generates an envelope function over the whole k range. As the sizes of the patches are so much smaller than the total size of the survey, their effect over our k range is negligible. The patches also have the same size in both designs, therefore their effect in the window function is exactly the same.
-
4.
As the random mask has been designed as a reflection of a smaller random mask in x and y and is hence not completely randomised over the whole area, some regularities are expected. For example, the symmetric shoulders at k ≃ 0.037 Mpc-1 and k ≃ 0.06 Mpc-1 on the main peak of the random case is due to the patches placed at the edges of the mask.
-
5.
As fsky is the same in both designs, the total information gained in both surveys is the same. We note that an average over the positions of the patches in the mask is constant:
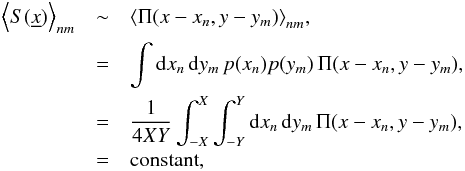 (12)where 2X and 2Y are the total extent of the survey in x and y directions, respectively, and p(xn) and p(ym) are the probability distribution of the patches in x and y directions. We note that this equation is correct in the case where fsky is constant in each realisation, or in other words, we verified that we have the same number of non-overlapping patches for each realisation. Therefore, in terms of the FoMs, both designs have the same constraining power for the galaxy power spectrum and the cosmological parameters.
(12)where 2X and 2Y are the total extent of the survey in x and y directions, respectively, and p(xn) and p(ym) are the probability distribution of the patches in x and y directions. We note that this equation is correct in the case where fsky is constant in each realisation, or in other words, we verified that we have the same number of non-overlapping patches for each realisation. Therefore, in terms of the FoMs, both designs have the same constraining power for the galaxy power spectrum and the cosmological parameters.
5. Conclusion
For future surveys, one would like to know the optimal investment of time and money. In the current era, where statistical errors have been greatly reduced and compete with systematic errors, observing a greater number of galaxies (to overcome the Poisson noise) may not necessarily improve our results. One desires more strategic ways to make observations and take control of systematics. This inspired a new approach in making observations (see Paykari & Jaffe 2013), in which the sampled area was covered sparsely as opposed to contiguously. In this case, one gathers a higher density of states in Fourier space, but at the expense of an increased correlation between different scales – aliasing. This would smooth out features on certain scales and decrease their statistical significance. In the previous work, the area of the sky was divided into small square patches, regularly distributed across the total area. It was shown that the loss of the constraining power of the survey induced by the sparse sampling is negligible.
More interestingly, it was shown that for the same amount of observing time, one could sparsely sample a larger total area of sky, which improves the constraining power of the survey. One therefore gains a great deal by spending the same amount of time on a larger but sparsely sampled area. Hence the sparse sampling could be a promising substitute for the contiguous observations and the way forward for designing future surveys.
In this work, we have investigated the best strategy for sparse sampling. One constraint in this previous design was the fixed and determined positions of the observed patches. The regular design of the mask introduces a periodic pattern in the window function, which induces periodic correlations at specific scales corresponding to the distances between the patches. This can be a problem if we are interested in a specific scale in the power spectrum. Here, we compared random sparse sampling to regular sparse sampling. Because there is no preferred scale in the mask in the random design, we found that all scales are constrained with almost the same level of statistical significance. This means that the power leakage from the main peak is evenly distributed amongst all scales. Hence the random sparse sampling is the preferred approach if we are interested in any specific scale.
Moreover, in terms of constraining the power spectrum over all scales or constraining the cosmological parameters, there is no difference between regular or random sampling. This means that the arrangement of the patches does not control the constraining power of the survey for the galaxy power spectrum or the cosmological parameter measurements. This therefore means we can design our mask in a way that is practically or cosmologically more suitable. This helps because in realistic cases there are always regions in the sky one would like to avoid, such as the plane of the Milky Way.
One can refer to the Dark Energy Task Force (DETF; Albrecht et al. 2006) FoM, which uses Fisher-matrix techniques to investigate how well each model experiment would be able to restrict the dark energy parameters w0, wa, ΩDE for their purposes.
Acknowledgments
The authors would like to thank A. Woiselle and F. Lanusse for the kind discussions. This work was supported by the European Research Council grant SparseAstro (ERC-228261).
References
- Albrecht, A., Bernstein, G., Cahn, R., et al. 2006, ArXiv e-prints [arXiv:astro-ph/0609591] [Google Scholar]
- Chiang, C.-T., Wullstein, P., Jeong, D., et al. 2013, JCAP, 12, 30 [Google Scholar]
- Dodelson, S. 2003, Modern cosmology, ed. S. Dodelson (Amsterdam: Academic Press) [Google Scholar]
- Feldman, H. A., Kaiser, N., & Peacock, J. A. 1994, ApJ, 426, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Hobson, M. P., Jaffe, A. H., Liddle, A. R., Mukherjee, P., & Parkinson, D. 2009, Bayesian Methods in Cosmology (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Kaiser, N. 1984, ApJ, 284, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Kendall, M., & Stuart, A. 1977, The advanced theory of statistics. Vol. 1: Distribution theory [Google Scholar]
- Liddle, A., Mukherjee, P., & Parkinson, D. 2006, Astron. Geophys., 47, 040000 [CrossRef] [Google Scholar]
- Mukherjee, P., Parkinson, D., Corasaniti, P. S., Liddle, A. R., & Kunz, M. 2006, MNRAS, 369, 1725 [NASA ADS] [CrossRef] [Google Scholar]
- Paykari, P., & Jaffe, A. H. 2013, MNRAS, 433, 3523 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. 1973, ApJ, 185, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Tegmark, M. 1997, Phys. Rev. Lett., 79, 3806 [NASA ADS] [CrossRef] [Google Scholar]
- Trotta, R. 2007a, MNRAS, 378, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Trotta, R. 2007b, MNRAS, 378, 819 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Figure of merit (FoM) for the galaxy power spectrum and the cosmological parameters for regular and random sampling.
All Figures
 |
Fig. 1 Design of the mask for random (left) and regular (right) sparse sampling. The patches (we observe through the white square patches in the figure) are distributed randomly and regularly on the surface of the sky. The fractional sky coverage, fsky, is the same in both designs – we verified that the patches do not overlap to satisfy this condition. |
| In the text | |
 |
Fig. 2 Top panel: middle row of the power spectrum Fisher matrix Fij for five realisations of the random sparse sampling. The main peak in the middle is the inverse error of the middle bin of the power spectrum 1 /σii. Moving away from the main peak, each point represents the correlation between that bin and the middle one 1 /σij. Bottom panel: same for regular (black) and average of the realisations of the random (blue) sampling. In the case of regular sampling, there are secondary peaks at specific scales, which is a consequence of the fixed position of the patches. On the other hand, for random sampling, there is no preferred scale and correlation is evenly distributed between all scales. The symmetric shoulders on the main peak, at k ≃ 0.037 Mpc-1 and k ≃ 0.06 Mpc-1, in the random case are due to the design of the random mask, which has been obtained by a reflection in the x and y plane for simplicity (see main text). Note that the y-axis is in log scale. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


