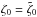| Issue |
A&A
Volume 581, September 2015
|
|
|---|---|---|
| Article Number | A128 | |
| Number of page(s) | 14 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201526175 | |
| Published online | 22 September 2015 | |
Detectability of quasi-circular co-orbital planets. Application to the radial velocity technique
1
ASD, IMCCE-CNRS UMR8028, Observatoire de Paris, UPMC,
77 Av. Denfert-Rochereau,
75014
Paris,
France
e-mail:
adrien.leleu@obspm.fr
2
CIDMA, Departamento de Física, Universidade de
Aveiro, Campus de
Santiago, 3810-193
Aveiro,
Portugal
Received: 24 March 2015
Accepted: 8 June 2015
Several celestial bodies in co-orbital configurations exist in the solar system. However, co-orbital exoplanets have not yet been discovered. This lack may result from a degeneracy between the signal induced by co-orbital planets and other orbital configurations. Here we determine a criterion for the detectability of quasi-circular co-orbital planets and develop a demodulation method to bring out their signature from the observational data. We show that the precision required to identify a pair of co-orbital planets depends only on the libration amplitude and on the planet’s mass ratio. We apply our method to synthetic radial velocity data, and show that for tadpole orbits we are able to determine the inclination of the system to the line of sight. Our method is also valid for planets detected through the transit and astrometry techniques.
Key words: planets and satellites: detection / planets and satellites: dynamical evolution and stability / celestial mechanics
© ESO, 2015
1. Introduction
Lagrange (1772) found an equilibrium configuration for the three-body problem where the bodies are located at the vertices of an equilateral triangle. For relatively small eccentricities, the libration around the stable Lagrangian equilibrium points L4 and L5 is one of the two possible configurations of a stable co-orbital system, called a tadpole orbit (by analogy with the restricted three-body problem, we define L4 as the equilibrium point when the less massive planet is 60° ahead of the more massive one and L5 when it is behind). The first object of this kind was observed by Wolf (1906), the asteroid Achilles, which shares its orbit with Jupiter around L4. At present, more than 6000 bodies in tadpole orbits are known in the solar system (MPC 2014). For objects in the second configuration, called a horseshoe orbit after the shape the trajectories of the bodies in the corotating frame, the libration encompasses the equilibrium points L4, L5, and L3. A single example is known, for a pair of satellites of Saturn (see Dermott & Murray 1981b).
The Lagrangian equilibria points are stable if the masses of the planets are low enough. In the quasi-circular case, Gascheau (1843) showed that there is a stability condition for the Lagrangian equilibrium 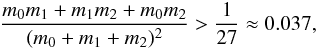 (1)where m0 is the mass of the star, and m1 and m2 the mass of the co-orbital planets. The mass repartition between the two co-orbitals has a small impact on the stability. Within this limit, Gascheau’s criterion guarantees the stability of the linearized equations in the vicinity of L4 or L5. The lower the masses of the co-orbitals with respect to the total mass, the larger is the possible libration amplitude. The horseshoe domain is stable when the planets have a Saturn-mass or less (Laughlin & Chambers 2002).
(1)where m0 is the mass of the star, and m1 and m2 the mass of the co-orbital planets. The mass repartition between the two co-orbitals has a small impact on the stability. Within this limit, Gascheau’s criterion guarantees the stability of the linearized equations in the vicinity of L4 or L5. The lower the masses of the co-orbitals with respect to the total mass, the larger is the possible libration amplitude. The horseshoe domain is stable when the planets have a Saturn-mass or less (Laughlin & Chambers 2002).
For eccentric orbits, the range of stable mass ratios between the co-orbital and the central body decreases as the eccentricity increases (Roberts 2000; Nauenberg 2002). Moreover, an additional co-orbital configuration exists in the eccentric case, called quasi-satellite, as the co-orbitals seem to gravitate around each other in the rotating frame. For high eccentricities, co-orbitals have a much larger stable domain for quasi-satellites than for tadpole or horseshoe configurations (Giuppone et al. 2010).
Since the discovery of the first exoplanets (Wolszczan & Frail 1992), a great diversity of systems has been found, some of them in mean motion resonances (MMR). A few of these resonant systems are highly populated (like the 2 / 1 MMR), but so far no system has been identified in a co-orbital configuration (1 / 1 MMR). However, many theoretical works suggest that co-orbital exoplanets may also exist. Laughlin & Chambers (2002) introduced two possible processes that form these systems: (i) planet-planet gravitational scattering and (ii) accretion in situ at the L4-L5 points of a primary.
The assumptions made on the gas disc density profile in scenario (i) can either lead to systems with a high diversity of mass ratio (Cresswell & Nelson 2008) or to equal mass co-orbitals when a density jump is present (Giuppone et al. 2012). In their model, Cresswell & Nelson (2008) form co-orbitals in over 30% of the runs. Initially in horseshoe configurations, the co-orbital systems are generally damped into tadpole configurations. The co-orbitals formed by this process usually have very low inclinations and eccentricities (e< 0.02).
Lyra et al. (2009) showed that in scenario (ii), up to 5−20 Earth-mass planets may form in the tadpole of a Jupiter-mass primary. For existing co-orbitals, the gas accretion seems to increase the mass difference between co-orbitals, the more massive of the two reaching Jovian mass while the starving one stays below 70 M⊕ (Cresswell & Nelson 2009).
Models that produce co-orbital planets due to dissipation within a disc may also experience significant inward migration. Such migration increases the libration amplitude of trojan planets for late migrating stages with low gas friction. This may lead to instability, but the damping of the disc usually forces the libration to remain small. Equal mass co-orbitals (from super-Earths to Saturns) are heavily disturbed during large scale orbital migration (Pierens & Raymond 2014). In some cases, Rodríguez et al. (2013) have shown as well that long-lasting tidal evolution may perturb equal mass close-in systems. Overall, significantly different mass trojans may thus be more common, especially in close-in configurations.
Co-orbital planets can also be disturbed in the presence of additional planetary companions, in particular by a significantly massive planet in another MMR with the co-orbitals (Morbidelli et al. 2005; Robutel & Bodossian 2009). Moreover, horseshoe orbits are more easily disturbed than tadpole orbits owing to the higher variation of frequencies in the system with respect to the libration amplitude (Robutel & Pousse 2013).
Detecting co-orbital planets is not an easy task because the signatures of each body are usually superimposed. The transit method can solve this degeneracy, either by observing both co-orbitals transiting (Janson 2013), or when only one co-orbital is transiting by coupling with another detection method (Ford & Gaudi 2006). When the libration amplitude is large enough, the transit timing variation (TTV) method can also find co-orbital candidates even when only one body is transiting (Janson 2013; Vokrouhlický & Nesvorný 2014).
If the bodies are exactly at the Lagrangian equilibrium point (with no libration), the radial velocity (RV) signal is the same as for a single planet, overestimating the mass of the system by ≈13% (Dobrovolskis 2013). Laughlin & Chambers (2002) showed that the libration of co-orbitals modulates the RV signal from the star, allowing them to determine a co-orbital system from a simulated RV signal. Cresswell & Nelson (2009) estimated that for the co-orbitals obtained in their simulation, this modulation is 10−20% of the total amplitude of the signal. Giuppone et al. (2012) showed that a short-term RV signal (duration inferior to the period of libration) did not allow co-orbitals to be distinguished from an eccentric planet or from two planets in 2 / 1 MMR (Goździewski & Konacki 2006; Anglada-Escudé et al. 2010).
Theoretical and numerical studies seem to agree that tadpole and horseshoe co-orbitals tend to have low eccentricities and mutual inclinations. In addition, in the solar system we observe among the moons of Saturn (Dermott & Murray 1981b, and references therein) three co-orbital systems, all with inclinations <1° and eccentricities <0.01. Jupiter’s trojans have a mean inclination of about ≈12° and eccentricities bellow 0.3. We thus conclude that quasi-circular orbits are a good approximation for many co-orbital systems. As the study of quasi-circular and coplanar orbits is easier than the full case, in this paper we restrict our analysis to this simpler situation. We first give a brief overview of the co-orbital dynamics and an analytical approximation of the co-orbital motion valid for small eccentricities. In Sect. 3 we derive an analytical method that can be used to extract the signature of co-orbitals from the motion of the host star. In Sect. 4 we exemplify our method with the radial velocity technique using synthetic data, and we conclude in the last section.
2. Co-orbital dynamics
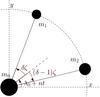 |
Fig. 1 Reference angles represented for the circular co-orbital system with respect to an inertial frame (x,y). m0 is the mass of the central star, m1 and m2 the masses of the co-orbitals. ri is the distance of the co-orbital i to the central star, and λi its true longitude. Following Eq. (3) one can write λi as a function of λ0, ζ, and of the mass ratio δ. |
We denote m0 the mass of the central star, and m1 and m2 the masses of the co-orbital planets. Adapting the theory developed by Érdi (1977) for the restricted three-body problem to the case of three massive bodies, and neglecting the quantities of second order and more in 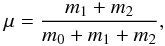 (2)the mean longitudes λi and the semi-major axes ai of the co-orbitals can be approximated by the expressions (see Robutel et al. 2011)
(2)the mean longitudes λi and the semi-major axes ai of the co-orbitals can be approximated by the expressions (see Robutel et al. 2011) 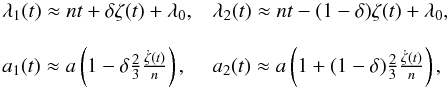 (3)where n is the averaged mean motion of the barycentre of m1 and m2, λ0 is a constant equal to the initial value of the barycentre of the longitudes (λ1m1 + λ2m2) / (m1 + m2), and
(3)where n is the averaged mean motion of the barycentre of m1 and m2, λ0 is a constant equal to the initial value of the barycentre of the longitudes (λ1m1 + λ2m2) / (m1 + m2), and 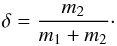 (4)At first order in μ, we have the constant quantity a = (1 − δ)a1 + δa2, which can be seen as the mean semi-major axis, and is linked to n by Kepler’s third law n2a3 = G(m0 + m1 + m2), where G is the gravitational constant. Finally, the variable ζ = λ1 − λ2 satisfies the second-order differential equation
(4)At first order in μ, we have the constant quantity a = (1 − δ)a1 + δa2, which can be seen as the mean semi-major axis, and is linked to n by Kepler’s third law n2a3 = G(m0 + m1 + m2), where G is the gravitational constant. Finally, the variable ζ = λ1 − λ2 satisfies the second-order differential equation ![\begin{equation} \ddot\zeta=-3\mu n^2\left[1-(2-2\cos\zeta)^{-3/2}\right]\sin\zeta , \label{eq:sol_orb_zeta} \end{equation}](/articles/aa/full_html/2015/09/aa26175-15/aa26175-15-eq40.png) (5)which is one of the most common representations of the co-orbital motion (see Morais 1999, and references therein). For small eccentricities, it describes the relative motion of the two bodies and is valid as long as the co-orbital bodies are not too close to the collision (ζ = 0).
(5)which is one of the most common representations of the co-orbital motion (see Morais 1999, and references therein). For small eccentricities, it describes the relative motion of the two bodies and is valid as long as the co-orbital bodies are not too close to the collision (ζ = 0).
Equation (5) is invariant under the symmetry ζ − → 2π − ζ, so the study of its phase portrait can be reduced to the domain ![\hbox{$(\zeta,\dot\zeta) \in [0, \pi]\times \RR$}](/articles/aa/full_html/2015/09/aa26175-15/aa26175-15-eq43.png) (see Fig. 2) (this symmetry will be developed later on). The equilibrium point located at
(see Fig. 2) (this symmetry will be developed later on). The equilibrium point located at 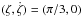 corresponds to one of the two Lagrangian equilateral configurations1, which are linearly stable for sufficiently small planetary masses (see below). Another equilibrium point, whose coordinates are (π,0), corresponds to the unstable Eulerian collinear configuration of the type L3. The separatrices emanating from this last unstable point split the phase space in three different regions: two corresponding to the tadpole trajectories surrounding one of the two Lagrangian equilibria (in red in Fig. 2), and another one corresponding to the horseshoe orbits that surround the three above-mentioned fixed points (in blue in Fig. 2).
corresponds to one of the two Lagrangian equilateral configurations1, which are linearly stable for sufficiently small planetary masses (see below). Another equilibrium point, whose coordinates are (π,0), corresponds to the unstable Eulerian collinear configuration of the type L3. The separatrices emanating from this last unstable point split the phase space in three different regions: two corresponding to the tadpole trajectories surrounding one of the two Lagrangian equilibria (in red in Fig. 2), and another one corresponding to the horseshoe orbits that surround the three above-mentioned fixed points (in blue in Fig. 2).
 |
Fig. 2 Phase portrait of Eq. (5). The separatrix (black curve) splits the phase space in two different domains: inside the separatrix the region associated with the tadpole orbits (in red) and the horseshoe domain (blue orbits) outside. The phase portrait is symmetric with respect to ζ = 180°. The horizontal purple segment indicates the range of variation of ζ0 while the vertical one shows the section used as initial condition to draw Fig. 5. See the text for more details. |
As shown in Fig. 2, any trajectory given by a solution of Eq. (5) can be entirely determined by the initial conditions (t0,ζ0) such that ζ(t0) = ζ0 and 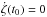 , where ζ0 is the minimum value of ζ along the trajectory, and t0 the first positive instant for which the value ζ0 is reached.
, where ζ0 is the minimum value of ζ along the trajectory, and t0 the first positive instant for which the value ζ0 is reached.
The possible values of ζ0, represented by the purple horizontal line in Fig. 2, are included in the interval ] 0°,60° ]; ζ0 = 60° corresponds to the equilateral configuration where m1 is the leading body and m2 is the trailing one2. The tadpole orbits are associated with ζ0 ∈ ] ζs,60° [, ζs ≈ 23.9° being associated with the separatrix, while ζ0 ranges from ζs to 0 for horseshoe orbits. As a result, the shape of the trajectory of the relative motion (as the libration amplitude of the resonant angle ζ) is entirely determined by the quantity ζ0.
In contrast, t0 and 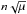 are necessary to know the exact position on the trajectory, and in particular, the amplitude of the variations of the semi-major axes. We can rewrite Eq. (5) by rescaling the time with
are necessary to know the exact position on the trajectory, and in particular, the amplitude of the variations of the semi-major axes. We can rewrite Eq. (5) by rescaling the time with 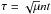 ,
, ![\begin{equation} \frac{{\rm d}^2 \tilde{\zeta}}{{\rm d}\tau^2}=-3\left[1-(2-2\cos\tilde{\zeta})^{-3/2}\right]\sin\tilde{\zeta} \ , \label{eq:sol_orb_zeta_tau} \end{equation}](/articles/aa/full_html/2015/09/aa26175-15/aa26175-15-eq60.png) (6)where
(6)where 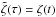 . As a consequence, this differential equation does not depend on
. As a consequence, this differential equation does not depend on 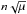 . Its solutions are solely determined by the initial conditions
. Its solutions are solely determined by the initial conditions 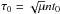 and
and 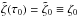 .
.
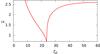 |
Fig. 3 Variation of the libration frequency |
In a small vicinity of the Lagrangian equilibria, the frequencies of the motion are close to 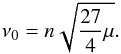 (7)More generally, excluding the separatrix, the solutions of Eq. (5) (respectively (6)) are periodic. The associated frequency, denoted by ν (respectively
(7)More generally, excluding the separatrix, the solutions of Eq. (5) (respectively (6)) are periodic. The associated frequency, denoted by ν (respectively 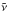 ), depends on the considered trajectory. However, the time-normalized frequency associated with Eq. (6),
), depends on the considered trajectory. However, the time-normalized frequency associated with Eq. (6), 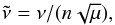 (8)depends only on ζ0 (
(8)depends only on ζ0 (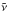 is plotted versus ζ0 in Fig. 3). In tadpole configurations, this dimensionless frequency remains almost constant in the vicinity of the Lagrangian equilibrium ν ≈ ν0 (Eq. (7)) and tends to 0 as the separatrix is reached at ζ0 = ζs. In horseshoe configurations, ν can take any value. In Fig. 3, one can see that far from the separatrix,
is plotted versus ζ0 in Fig. 3). In tadpole configurations, this dimensionless frequency remains almost constant in the vicinity of the Lagrangian equilibrium ν ≈ ν0 (Eq. (7)) and tends to 0 as the separatrix is reached at ζ0 = ζs. In horseshoe configurations, ν can take any value. In Fig. 3, one can see that far from the separatrix, 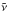 is always of order unity. This imposes that the variations of the difference of the longitudes, ζ, are slow with respect to the orbital time scale, i.e. ν ≪ n. It turns out that
is always of order unity. This imposes that the variations of the difference of the longitudes, ζ, are slow with respect to the orbital time scale, i.e. ν ≪ n. It turns out that 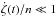 and as a consequence, the quantities aj can be approximated by a (Eq. (3)). Thus, in the circular planar case, at order 0 in ν, the position of m1 and m2 in the heliocentric system r = (x + iy) are given by
and as a consequence, the quantities aj can be approximated by a (Eq. (3)). Thus, in the circular planar case, at order 0 in ν, the position of m1 and m2 in the heliocentric system r = (x + iy) are given by 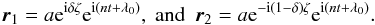 (9)Within the same approximation, we can also write the derivative of previous equation, which gives us the heliocentric velocity of the co-orbitals
(9)Within the same approximation, we can also write the derivative of previous equation, which gives us the heliocentric velocity of the co-orbitals 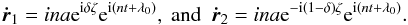 (10)While searching for co-orbital bodies, the stability of each configuration also needs to be taken into account. In order to determine the influence of the planetary masses on the global stability of planar co-orbital systems, we show the results of two numerical simulations indicating the width of the stable co-orbital region in different directions. In Fig. 4, we consider two planets orbiting around a star of mass m0 = 1 M⊙, with fixed initial elements a1 = a2 = 1 au, e1 = e2 = 0.05, and λ1 = ϖ1 = 0, and we vary the initial element λ2 = ϖ2 = −ζ0 in [ 0°,60° ] and their masses m1 = m2 = μm0/ 2, with μ/ 2 ∈ [ 10-8,10-1 ]. For each set of initial conditions, the system is integrated over 5 Myr using the symplectic integrator SABA4 (Laskar & Robutel 2001) with a time-step of 0.0101 year.
(10)While searching for co-orbital bodies, the stability of each configuration also needs to be taken into account. In order to determine the influence of the planetary masses on the global stability of planar co-orbital systems, we show the results of two numerical simulations indicating the width of the stable co-orbital region in different directions. In Fig. 4, we consider two planets orbiting around a star of mass m0 = 1 M⊙, with fixed initial elements a1 = a2 = 1 au, e1 = e2 = 0.05, and λ1 = ϖ1 = 0, and we vary the initial element λ2 = ϖ2 = −ζ0 in [ 0°,60° ] and their masses m1 = m2 = μm0/ 2, with μ/ 2 ∈ [ 10-8,10-1 ]. For each set of initial conditions, the system is integrated over 5 Myr using the symplectic integrator SABA4 (Laskar & Robutel 2001) with a time-step of 0.0101 year.
 |
Fig. 4 Stability of co-orbitals as a function of log 10(μ) and ζ0. The initial conditions are chosen as t0 = 0 (Δa/a = 0) and ζ0 ∈ [ 0°,60° ]: purple horizontal line in Fig. 2. In black is the separatrix between the tadpole and the horseshoe domain. The stability criteria of Gascheau (1843), corresponding to ν/n = 1/ |
Strongly chaotic systems or systems that quit the co-orbital resonance before the integration stops are removed from the computation. In this case, in Fig. 4 white dots are assigned to their initial parameters (ζ0,μ). This strong short-term instability is mainly due to the overlapping of low-order secondary resonances (Páez & Efthymiopoulos 2015). After the elimination of these initial conditions, long-term diffusion along secondary resonances may also destabilize the co-orbital systems on a much longer time scale. Measuring the temporal variation of the libration frequency identifies this diffusion (Laskar 1990, 1999). The black dots indicate a relative variation of over 10-6 between the first and second half of the 5 million years integration (to compare with ≈10-10 for the long-term stable configurations). They are mainly located in the vicinity of the separatrix and near the ejection boundary. In the remaining regions, the small variation of the frequency ν guarantees, in most cases, the stability for a billion years (Robutel & Gabern 2006). For long-term stable systems, a colour depending on its libration frequency ν is assigned to regular resonant co-orbital systems (see the colour code at the bottom of Fig. 4). We observe that for large planetary masses, slightly lower than the limit value μ ≈ 0.037 (Gascheau 1843), the stability region is extremely small and strongly perturbed by low-order secondary resonances. The chaos generated by the main secondary resonances, namely the ν = n/ 2, ν = n/ 3, and ν = n/ 4, shrink the stability region significantly, reducing it to a small region near the equilateral configuration (see Roberts 2002; Nauenberg 2002). As μ decreases, the width of the stable tadpole region increases, and the destabilizing influence of the secondary resonances becomes dominant only on the boundary of the stability region (see Páez & Efthymiopoulos 2015; Robutel & Gabern 2006; Érdi et al. 2007, for the restricted problem). When μ ≈ 3 × 10-4 ≈ 2MSaturn/M⊙, the whole tadpole domain becomes stable, except for a small region around the separatrix (ζ0 = ζs ≈ 23.9°). On the other side of the separatrix, for ζ0<ζs, stable horseshoe orbits start to appear (see Laughlin & Chambers 2002). For lower planetary masses, the size of the horseshoe orbital domain increases as μ decreases, to reach the outer boundary of the Hill sphere at a distance to the separatrix of the order of μ1 / 3 (see Robutel & Pousse 2013).
 |
Fig. 5 Stability of co-orbitals as a function of log 10(μ) and Δa/a. The initial conditions are ζ0 = π/ 3 and Δa/a ∈ [ 0,0.06 ]: vertical purple line in Fig. 2. The black line indicates the separatrix between the tadpole and the horseshoe domains. The dots follow a curve Δa ∝ μ1 / 3, delimiting the stability region of the horseshoe domain. The colour code indicates the value of the libration frequency, i.e. log 10(ν/n) (see Fig. 4 for the scale). |
In Fig. 5 we show another section of the co-orbital region. Instead of varying the angle ζ0, we change the initial value of the difference of the semi-major axes from the equilateral equilibrium L4 towards the outside of the co-orbital region (vertical purple line in Fig. 2). More precisely, the initial conditions of the planetary systems are e1 = e2 = 0.05, λ1 = ϖ1 = 0, λ2 = ϖ2 = π/ 3, and aj = 1 − (−1)jΔa with Δa ∈ [ 0:0.06 ]. As they do in figure 4, the planetary masses vary as m1 = m2 = μm0/ 2, with μ/ 2 ∈ [ 10-8,10-1 ].
The tadpole domaine lies above the solid black line corresponding to the equation 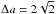 /
/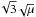 (Robutel & Pousse 2013). In this case, contrarily to the ζ0 direction where the width of the stable tadpole region is a monotonous function of μ, the extent of the stability region reaches a maximum for Δa/a ≈ 0.052 at μ = 3.5 × 10-3 and then tends to zero with μ as indicated by the above-mentioned curve. For lower values of μ, the size of this region decreases until μ reaches the value for which horseshoe orbits begins to be stable. After these critical masses, the two domains shrink together but at a different rate. The asymptotical estimates of the tadpole’s width in this direction is of the order of μ1 / 2 (black solid line in Fig. 5), while an estimation for the horseshoe region is of the order of μ1 / 3 (black dashed line in Fig. 5, corresponding to the equation Δa = 0.47μ1 / 3) has been fitted to the lower bound of the stable horseshoe region (see Robutel & Pousse 2013, for more details). As a consequence, the stability domain of the horseshoe configurations becomes larger than the tadpole domain when the planetary masses tend to zero (Dermott & Murray 1981a).
(Robutel & Pousse 2013). In this case, contrarily to the ζ0 direction where the width of the stable tadpole region is a monotonous function of μ, the extent of the stability region reaches a maximum for Δa/a ≈ 0.052 at μ = 3.5 × 10-3 and then tends to zero with μ as indicated by the above-mentioned curve. For lower values of μ, the size of this region decreases until μ reaches the value for which horseshoe orbits begins to be stable. After these critical masses, the two domains shrink together but at a different rate. The asymptotical estimates of the tadpole’s width in this direction is of the order of μ1 / 2 (black solid line in Fig. 5), while an estimation for the horseshoe region is of the order of μ1 / 3 (black dashed line in Fig. 5, corresponding to the equation Δa = 0.47μ1 / 3) has been fitted to the lower bound of the stable horseshoe region (see Robutel & Pousse 2013, for more details). As a consequence, the stability domain of the horseshoe configurations becomes larger than the tadpole domain when the planetary masses tend to zero (Dermott & Murray 1981a).
3. One planet or two co-orbitals?
In some particular situations, co-orbital planets can be identified independently from the orbital libration: when both planets are transiting (Janson 2013) or when we combine data from transits with radial velocities (Ford & Gaudi 2006). However, in general the detection of co-orbitals requires identifying the effect of the libration in the data. Vokrouhlický & Nesvorný (2014) showed that the TTV of only one of the co-orbital planets is enough if the libration is large. Laughlin & Chambers (2002) showed that the libration induced by co-orbital can have an important effect on the radial velocity of a star, while Giuppone et al. (2012) showed that co-orbitals can be mistaken for a single planet if the data span is short with respect to the libration period.
In the previous section we saw that co-orbital planets can be stable for large libration amplitudes, depending on the parameter μ (see Figs. 2 and 4). However, the libration period is always longer than the orbital period of the bodies (see the colour code in Fig. 4). The faster ζ librates, the higher the chances of detecting the co-orbital bodies, because this reduces the time span needed to detect the libration. We write Pν the period associated to the libration frequency ν. The value of Pν decreases when μ and n increase (see Eq. (7) and Fig. 3). Therefore, high mass ratios and the proximity to the star maximize the detectability of co-orbitals, although high mass ratios also lead to the instability of most of the co-orbital configurations (Fig. 4). Hereafter we consider that the time span of the observations is always longer than Pν.
3.1. Signals induced by co-orbital planets
 |
Fig. 6 Motion of the two co-orbital bodies (red and blue) and their barycentre (purple) in a co-rotating frame with frequency n. Tadpole (left) and horseshoe (right). δ = 0.6. Here μ = 2 × 10-4 and the planets are located at 1 AU from the star. By eliminating the influence of n, one can see the long-term motion of the barycentre of the planets. Pν is the period of the periodic trajectories represented by the coloured lines. See the text for more details. |
 |
Fig. 7 Motion of the star in the configurations of Fig. 6 in the direction x in the inertial frame. In black is the tadpole orbit and in red the horseshoe. The top graph represents the evolution of the position of the star over time and the bottom graph its spectrum. In these examples, the libration period of the horseshoe orbits is about twice the period of the tadpole orbits. See the text for more details. |
Most important observational techniques used to detect exoplanets (transits, radial-velocity, astrometry) are indirect, i.e. we do not directly observe the planets, but rather their effect on the host star. In order to get an idea of the effect of the libration of co-orbital planets on the star, we take two examples of co-orbital configurations (see Fig. 6) with the following initial conditions: λ1 = 0°, a1 = a2 = 1 AU, e1 = e2 = 0, m1 = 0.8 × 10-4M⊙ (red), and m2 = 1.2 × 10-4M⊙ (blue). In the left graph, ζ0 = 25°, leading to a large amplitude tadpole orbit, and in the right graph, ζ0 = 23°, leading to a horseshoe orbit. The position of the barycentre of the system composed of the two planets is represented in purple. With μ = 2 × 10-4 and ζ0 near the separatrix, these two examples are at the limit of the stability domain, but give a clear idea of what we can expect.
In Fig. 7 we show the projection of the stellar orbit on the x-axis for these two configurations. We observe that the signal induced by the Keplerian motion of the co-orbitals is indeed modulated over a period of libration of the resonant angle ζ. This phenomenon was described by Laughlin & Chambers (2002) in the case of a radial velocity signal. It is due to the oscillation, with a frequency ν, of the distance between the barycentre of the two planets and the star, clearly visible in Fig. 6. The larger the amplitude of variation of ζ, the larger the amplitude of modulation. For a given ζ0 value, the maximum oscillation amplitude is achieved when δ = 1 / 2, that is, for m1 = m2. In the horseshoe configuration, δ = 1 / 2 leads the barycentre of m1 and m2 to pass by the position of m0, periodically cancelling the signal.
The bottom panel of Fig. 7 shows the spectrum of those signals. The features of the spectrum of a modulated signal appear clearly: one peak located at the high frequency n and harmonics located on both sides n + pν, where p is an integer and ν is the frequency of the modulation. In general, the peaks located in n and n ± ν are the ones with the largest amplitude. However, there is an exception when the signal is at the limit of the over-modulation, that is, when the peak located in n disappears. This can happen only in the horseshoe configuration when m1 ≈ m2. In this case, the main components of the spectrum would be two peaks separated by 2ν and the system would then be easier to identify. In this paper we focus on the possibility of detecting the main three peaks.
3.2. Motion of a star hosting co-orbital planets
If the centre of mass of the system is at rest, the position of a star hosting two co-orbital planets is given by (in barycentric coordinates) ![\begin{eqnarray} \vec{r}_0= \mu [(1-\delta)\vec{r}_1+ \delta \vec{r}_2] , \label{eq:r0_v1} \end{eqnarray}](/articles/aa/full_html/2015/09/aa26175-15/aa26175-15-eq145.png) (11)where r1 and r2 are given by Eqs. (9). Since ζ(t) is a periodic function with frequency ν, we can expand the terms eiδζ in Fourier series as
(11)where r1 and r2 are given by Eqs. (9). Since ζ(t) is a periodic function with frequency ν, we can expand the terms eiδζ in Fourier series as 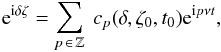 (12)where cp(δ,ζ0,t0) is a complex coefficient. Replacing Eqs. (9) and (12) into Eq. (11), we get
(12)where cp(δ,ζ0,t0) is a complex coefficient. Replacing Eqs. (9) and (12) into Eq. (11), we get 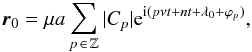 (13)with
(13)with 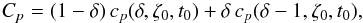 (14)and
(14)and 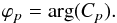 (15)For the velocity, we thus have (at order 0 in ν)
(15)For the velocity, we thus have (at order 0 in ν) 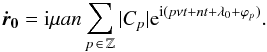 (16)For instance, if the observational data is acquired through astrometry, we get the projection of Eq. (13) on the plane of the sky, while for radial velocities we use the projection of Eq. (16) in the line of sight.
(16)For instance, if the observational data is acquired through astrometry, we get the projection of Eq. (13) on the plane of the sky, while for radial velocities we use the projection of Eq. (16) in the line of sight.
The stellar motion can be expressed as the sum of a signal of frequency n, which we call the “Keplerian component”, and other signals of frequency n + pν, which we call the “modulating components”. For simplicity, we consider only the two main modulation components p = ± 1, which are the ones with the largest amplitude, hence the ones that are easier to detect. We thus introduce the quantity S(t), which represents a projection of r0 (Eq. (11)) or ṙ0 (Eq. (16)) over an observable direction, restricted to its main two components, 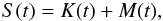 (17)where
(17)where 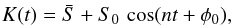 (18)and
(18)and 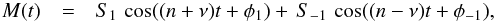 (19)where φ0, φ1, and φ-1 depend on ϕ− 1,0,1, λ0, and the direction of the projection. Our purpose is to check if the Keplerian signal that we have detected is modulated, and if our data can be approximated by a signal under the form S(t).
(19)where φ0, φ1, and φ-1 depend on ϕ− 1,0,1, λ0, and the direction of the projection. Our purpose is to check if the Keplerian signal that we have detected is modulated, and if our data can be approximated by a signal under the form S(t).
3.3. Demodulation
We assume that the Keplerian part of the signal is well determined (S0 and 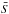 terms in Eq. (18)), otherwise it would be impossible to look for something else. However, the modulating signal (S1 and S-1) can be hidden in the noise. In order to isolate the effect of the modulation, we suggest using a frequency mixing method similar to the one used in the demodulation of radio signals. This method is called “superheterodyne” and was introduced by Armstrong (1914). It consists in multiplying the modulated signal by a signal that has the same frequency as the carrier. As a result, we obtain a peak at the modulating signal’s period in the spectrum. We propose using this method on data from co-orbital systems, but it can also be used on any other modulated signal produced by a different source (e.g. Morais & Correia 2008).
terms in Eq. (18)), otherwise it would be impossible to look for something else. However, the modulating signal (S1 and S-1) can be hidden in the noise. In order to isolate the effect of the modulation, we suggest using a frequency mixing method similar to the one used in the demodulation of radio signals. This method is called “superheterodyne” and was introduced by Armstrong (1914). It consists in multiplying the modulated signal by a signal that has the same frequency as the carrier. As a result, we obtain a peak at the modulating signal’s period in the spectrum. We propose using this method on data from co-orbital systems, but it can also be used on any other modulated signal produced by a different source (e.g. Morais & Correia 2008).
We consider a set of N observational data measurements. We denote tk the time of each observation and sk the corresponding observed measurement. First, we fit the data with a simple sinusoidal function that contains only the Keplerian part K(t) (Eq. (18)). This provides us with an initial approximation for 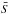 , S0, n, and φ0. Then, we perform a transformation on the raw data sk to subtract the Keplerian part,
, S0, n, and φ0. Then, we perform a transformation on the raw data sk to subtract the Keplerian part, 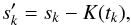 (20)and then, to isolate the modulation frequency,
(20)and then, to isolate the modulation frequency, 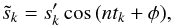 (21)where φ is an arbitrary phase angle. This modified data set can be fitted with a similarly modified function
(21)where φ is an arbitrary phase angle. This modified data set can be fitted with a similarly modified function ![\begin{eqnarray} \tilde \vS(t) & =& \left[\vS(t) - \vK(t) \right] \cos(n t+\phi) = \vM (t) \cos (n t + \phi) \nonumber \\ &=& \frac{\vS_1}{2} \cos((2n+\nu)t +\phi_1+\phi) \nonumber \\ &&+ \frac{\vS_{-1}}{2} \cos((2n-\nu)t +\phi_{-1}+\phi) \nonumber \\ &&+ \hat \vS_1 \cos (\nu t + \Delta \phi) + \Delta \vS \cos(\nu t + \phi - \phi_{-1}) , \label{eq:demc} \end{eqnarray}](/articles/aa/full_html/2015/09/aa26175-15/aa26175-15-eq180.png) (22)where
(22)where
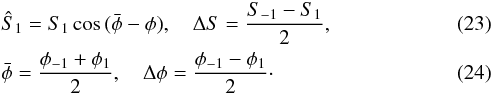 The libration frequency ν is now clearly separated from the Keplerian frequency n. As we will see in the following sections, we have ΔS ≪ S1. The libration contribution can therefore be fitted by the term in Ŝ1, and the signal is maximized if we are able to choose
The libration frequency ν is now clearly separated from the Keplerian frequency n. As we will see in the following sections, we have ΔS ≪ S1. The libration contribution can therefore be fitted by the term in Ŝ1, and the signal is maximized if we are able to choose 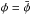 . However,
. However, 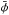 is a priori unknown, so we propose computing the
is a priori unknown, so we propose computing the 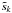 for two values of φ dephased by π/ 2, for example φ = φ0 and φ = φ0 + π/ 2. By proceeding in this way, in the worst case we get
for two values of φ dephased by π/ 2, for example φ = φ0 and φ = φ0 + π/ 2. By proceeding in this way, in the worst case we get 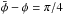 , corresponding to a minimum amplitude of S1/
, corresponding to a minimum amplitude of S1/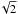 . Moreover, by taking the ratio of the fitted amplitudes with the two φ values, we can additionally estimate
. Moreover, by taking the ratio of the fitted amplitudes with the two φ values, we can additionally estimate 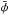 , and thus
, and thus 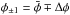 .
.
The initial determination of n using Eq. (18) always has an error ϵn, which leads to the splitting of the libration term in ν into two terms in ν ± ϵn. Since these two frequencies are very close to each other, the Fast Fourier Transform (FFT) usually shows a widened peak around ν, preventing an optimal determination of ν, S1, and Δφ. Therefore, once we have some estimations for these parameters, in the last step of the demodulation process, we return to the original data set sk, and directly fit it with the full equation S(t) (Eq. (17)), using the previously determined 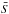 , S0, S1, S-1 = S1, n, ν, φ0, φ1, and φ-1 as initial values for the fit.
, S0, S1, S-1 = S1, n, ν, φ0, φ1, and φ-1 as initial values for the fit.
4. Detection using the radial-velocity technique
In this section we apply the general method described previously to the case where the data is acquired thorough the radial-velocity technique. In this case, the data corresponds to the projection of Eq. (16) in the line of sight, given by an arbitrary direction eiθsin I in the space (Murray & Correia 2011) 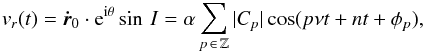 (25)where
(25)where 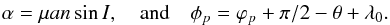 (26)We note that Eq. (25) could also be the projection of Eq. (13) over a direction in the plane of the sky (for example in the case of an astrometric measurement). Within our approximation that would only change the value of the parameter α. However, most of our results on the detectability do not depend on this parameter, thus hold true for any measurement technique. For reasons of clarity, we return to the example of the radial velocity measurements.
(26)We note that Eq. (25) could also be the projection of Eq. (13) over a direction in the plane of the sky (for example in the case of an astrometric measurement). Within our approximation that would only change the value of the parameter α. However, most of our results on the detectability do not depend on this parameter, thus hold true for any measurement technique. For reasons of clarity, we return to the example of the radial velocity measurements.
Considering only the first harmonics of Eq. (25), one can identify the RV signal to the Eq. (17), which is 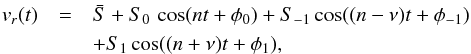 (27)with Sp = α | Cp |. We can therefore apply the demodulation process from Sect. 3.3 to extract the orbital information from the observational data. Our aim now is to determine which configurations can be detected for a given precision in the RV observations, and explain how to retrieve the orbital parameters from the Sp and φp parameters.
(27)with Sp = α | Cp |. We can therefore apply the demodulation process from Sect. 3.3 to extract the orbital information from the observational data. Our aim now is to determine which configurations can be detected for a given precision in the RV observations, and explain how to retrieve the orbital parameters from the Sp and φp parameters.
4.1. Detectability
We introduce the following quantity  (28)which represents the power of the modulation terms with respect to the Keplerian term. When we search for co-orbital planets, the product S0Am must be distinguishable from the noise.
(28)which represents the power of the modulation terms with respect to the Keplerian term. When we search for co-orbital planets, the product S0Am must be distinguishable from the noise.
4.1.1. Detection near the Lagrangian equilibrium
We consider a system in a tadpole configuration with a low libration amplitude. In this case we can use a linear approximation for ζ near the Lagrangian equilibrium. Within this approximation, we can obtain an explicit expression for vr(t) in terms of the orbital parameters. We introduce the small parameter z = ζ0 − π/ 3 and write 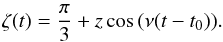 (29)At first order in z and using Eq. (10), the derivative of Eq. (11) becomes
(29)At first order in z and using Eq. (10), the derivative of Eq. (11) becomes ![\begin{eqnarray} \vec{\dot{r}}_0&=& - i \mu a n \Big[(1-\delta) \big(1+i \delta z \cos\,(\nu(t-t_0)) \big) \notag\\ && + \delta \big(1+ i (1-\delta) z \cos\,(\nu(t-t_0))\big) {\rm e}^{{\rm -i} \frac{\pi}{3}} \Big] {\rm e}^{{\rm i}(nt+ \lambda_0+\delta \frac{\pi}{3})}. \label{eq:rp0_v1} \end{eqnarray}](/articles/aa/full_html/2015/09/aa26175-15/aa26175-15-eq212.png) (30)Following Eq. (25), we project Eq. (30) in the line of sight, and identify the terms appearing in Eq. (27) as
(30)Following Eq. (25), we project Eq. (30) in the line of sight, and identify the terms appearing in Eq. (27) as
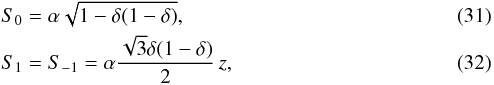 which allow us to compute Am as well:
which allow us to compute Am as well: 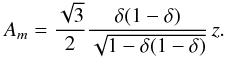 (33)When m0 ≫ m2 ≥ m1 the modulation terms can be simplified as
(33)When m0 ≫ m2 ≥ m1 the modulation terms can be simplified as 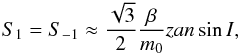 (34)where β = m1m2/ (m1 + m2) is the reduced mass of the planets’ subsystem. We thus see that the power in these terms is proportional to β and to the angular separation from the Lagrangian equilibrium z. The detection is therefore maximized for large libration amplitudes and planets with large similar masses (m1 ≈ m2). Nevertheless, we note that for planetary systems with mass ratios very different from one, for instance, m1/m2 ≪ 1, the reduced mass converges to the mass of the smaller planet (β = m1 in this case), while for equal mass planets it converges to β = m1/ 2. As a consequence, although planets with large equal masses are easier to detect than planets with small equal masses, a small mass planet is two times easier to detect if it is accompanied by a large mass planet rather than another small similar mass planet.
(34)where β = m1m2/ (m1 + m2) is the reduced mass of the planets’ subsystem. We thus see that the power in these terms is proportional to β and to the angular separation from the Lagrangian equilibrium z. The detection is therefore maximized for large libration amplitudes and planets with large similar masses (m1 ≈ m2). Nevertheless, we note that for planetary systems with mass ratios very different from one, for instance, m1/m2 ≪ 1, the reduced mass converges to the mass of the smaller planet (β = m1 in this case), while for equal mass planets it converges to β = m1/ 2. As a consequence, although planets with large equal masses are easier to detect than planets with small equal masses, a small mass planet is two times easier to detect if it is accompanied by a large mass planet rather than another small similar mass planet.
4.1.2. Detection in any tadpole or horseshoe configuration
For large libration amplitudes, we cannot have an explicit expression for Sp with respect to the orbital parameters. Nevertheless, similarly to the linear case, we can prove that Am and | C0 | depend only on ζ0 and δ. Indeed, since cp are Fourier coefficients of the expression of eiδζ, see Eq. (12), we can write 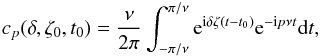 (35)or, in terms of τ (see Sect. 2),
(35)or, in terms of τ (see Sect. 2), 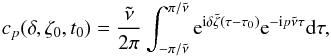 (36)where
(36)where 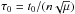 . Since
. Since 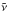 depends only on ζ0, it turns out that
depends only on ζ0, it turns out that 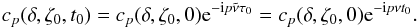 (37)As a result, the dependence of cp on τ0 is explicit. Using the definition of Cp given by Eq. (14), we see that | Cp |, and consequently Am, do not depend on t0.
(37)As a result, the dependence of cp on τ0 is explicit. Using the definition of Cp given by Eq. (14), we see that | Cp |, and consequently Am, do not depend on t0.
The dependence of Am and | C0 | on the parameters (δ, ζ0) is shown in Figs. 9 and 10 for tadpole configurations and in Fig. 11 for horseshoe configurations. These figures were obtained by integrating the differential Eq. (5) satisfied by ζ, with initial conditions 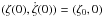 . The outputs of these integrations were then replaced into the expression of ṙ0 for a given set of δ (Eq. (10)). For each simulation, the spectrum of a projection of ṙ0 has been computed in order to get the value of the displayed quantities. These quantities have also been computed from three-body direct integrations, which give the same results.
. The outputs of these integrations were then replaced into the expression of ṙ0 for a given set of δ (Eq. (10)). For each simulation, the spectrum of a projection of ṙ0 has been computed in order to get the value of the displayed quantities. These quantities have also been computed from three-body direct integrations, which give the same results.
The RV signal that we obtain for the general cases follows the trends of the linear approach. For given values of a, μ, and δ, the detectability of a co-orbital system increases as the amplitude of the libration of ζ increases, i.e. when ζ0 decreases. This is still true when ζ0 crosses the separatrix. When δ tends to 1 or 0, the modulation peak disappears and the signal is similar to the one induced by a single planet. For a given ζ0, Am reaches its maximum when δ = 1 / 2. In the horseshoe case, the modulating terms have higher amplitudes than the Keplerian term for 0.35 ≲ δ ≲ 0.65, the Keplerian term being cancelled when δ tends to 1 / 2.
We showed at the end of the previous section that a planet of mass m1 (fixed) will be easier to detect if its co-orbital companion is significantly more massive (m2 ≫ m1), rather than m2 ≈ m1. This holds true in the horseshoe domain, as shown in Appendix A.2.
4.1.3. Detectability for a given data set
While searching for co-orbital companions of an already detected planet, it is possible to put some constraints on what we can expect to observe, based on the observational limitations. In addition to the main Keplerian signal, characterized by K0 and Pn, we also know the time span of the observations, T, and the precision of the instrument, ϵ.
The modulation signal of a co-orbital configuration is detectable if AmK0>ϵ (Eq. (28)). Thus, the detection of a co-orbital companion can only occur for 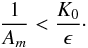 (38)We also know that the libration period Pν is proportional to the orbital period Pn (Eq. (8), Fig. 3). One complete libration period can only be contained in the data when Pν>T, therefore
(38)We also know that the libration period Pν is proportional to the orbital period Pn (Eq. (8), Fig. 3). One complete libration period can only be contained in the data when Pν>T, therefore 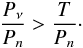 (39)The parameter Am depends on δ and ζ0, while the ratio Pν/Pn depends on ζ0 and μ. The detectability of a co-orbital configuration therefore depends on the mass of both planets and on the libration amplitude.
(39)The parameter Am depends on δ and ζ0, while the ratio Pν/Pn depends on ζ0 and μ. The detectability of a co-orbital configuration therefore depends on the mass of both planets and on the libration amplitude.
In Fig. 8 we show the ratio K0/ϵ as a function of the ratio T/Pν, which correspond to the observable quantities. We denote m2 the most massive of the two planets (which is the main contributor to K0 and μ), and m1 the mass of the less massive planet that we are looking for. We fix m2/m0 = 10-3 (which is near the maximum value allowed for the stability of co-orbital systems) and show the detection limits for three different values of m1. Co-orbital companions below each threshold limit can be ruled out.
These detection limits are constrained by the observational limitations (ϵ and T), but also by the stability of the co-orbital systems, which is parametrized by the values of ζ0. As ζ0 → π/ 3 (Lagrange point, with no libration amplitude) or m1/m2 → 0, we have that K0/ϵ> 1 /Am → ∞. On the other hand, as ζ0 → 0, the chances of detection increase (the libration amplitude increases), but the system also tends to become unstable (Fig. 4).
 |
Fig. 8 Detectability of a co-orbital companion for m2/m0 ≈ 10-3. For a given data set (K0/ϵ,T/Pn), co-orbital companions with a mass m1 can only be detected if they lie above the respective threshold limit. |
4.2. Characterization of the co-orbital system
The orbits of the co-orbital planets are fully characterized by the quantities n, ν, a, ζ0, λ0, t0, and sinI. In addition, assuming that the mass of the star is known, we can determine the mass of the planets through μ and δ. The frequencies n and ν are directly obtained when we fit the data with our model (Eq. (27)), while a is obtained by the third Kepler law from n. Since 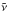 depends only on ζ0 (Fig. 3), for each configuration there is a bijective map that links μ and ζ0 given by
depends only on ζ0 (Fig. 3), for each configuration there is a bijective map that links μ and ζ0 given by 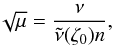 (40)where
(40)where 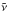 is defined by Eq. (8). We are thus left with five parameters, ζ0 (or μ), δ, λ0, t0, and sinI, that need to be determined in order to characterize the system.
is defined by Eq. (8). We are thus left with five parameters, ζ0 (or μ), δ, λ0, t0, and sinI, that need to be determined in order to characterize the system.
We can start looking for the shape of the orbit rather than the exact trajectories of the planets as a function of time. Therefore, we ignore by now all quantities that depend on λ0 and t0, i.e. we restrict our analysis to Am (Eq. (28)) and | C0 | (Eq. (37)).
We define the quantity Ψ as 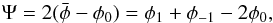 (41)with φp = λ0 + arg(Cp) + π/ 2 − θ (Eq. (26)). Thus
(41)with φp = λ0 + arg(Cp) + π/ 2 − θ (Eq. (26)). Thus 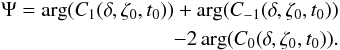 (42)From Eq. (37), we know that arg(Cp(δ,ζ0,t0)) = arg(Cp(δ,ζ0,0)) − pνt0. Hence Ψ depends only on ζ0 and δ. One can show that any quantity defined as a function of φp with p ∈ { −1,0,1 } and independent of t0 and λ0 is a function of Ψ.
(42)From Eq. (37), we know that arg(Cp(δ,ζ0,t0)) = arg(Cp(δ,ζ0,0)) − pνt0. Hence Ψ depends only on ζ0 and δ. One can show that any quantity defined as a function of φp with p ∈ { −1,0,1 } and independent of t0 and λ0 is a function of Ψ.
The parameters Am, | C0 |, and Ψ evolve in a different way depending on the orbital configuration of the system (tadpole or horseshoe). We thus need to split our analysis for these two different configurations.
4.2.1. Characterization near the Lagrangian equilibrium
In the linear case, we can entirely determine the trajectories of the co-orbitals analytically. According to Eqs. (31) and (32), the amplitudes S0 and S1 = S-1 depend on α, ζ0, and δ. By identifying the phases angles appearing in Eq. (27) to the data and then comparing with expression (30), we get three additional equations 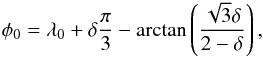 (43)and
(43)and 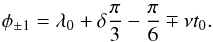 (44)These three equations, combined with the Eqs. (31) and (32) lead to a system of five equations of the form (S0,S1,φ0,φ1,φ-1) = F(α,δ,ζ0,λ0,t0), where F is a non-linear function of the five unknown parameters. We can thus get an explicit expression for these parameters from the observational data. Then, the expression of ν near the Lagrangian equilibrium (Eq. (7)) can be used to get the value of μ. Finally, the inclination I can be deduced from the definition of α (Eq. (26)):
(44)These three equations, combined with the Eqs. (31) and (32) lead to a system of five equations of the form (S0,S1,φ0,φ1,φ-1) = F(α,δ,ζ0,λ0,t0), where F is a non-linear function of the five unknown parameters. We can thus get an explicit expression for these parameters from the observational data. Then, the expression of ν near the Lagrangian equilibrium (Eq. (7)) can be used to get the value of μ. Finally, the inclination I can be deduced from the definition of α (Eq. (26)): 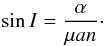 (45)We can thus remove the classic μ sin I degeneracy in this case and fully determine the exact masses of the planets and their trajectories in space.
(45)We can thus remove the classic μ sin I degeneracy in this case and fully determine the exact masses of the planets and their trajectories in space.
Replacing expressions (43) and (44) for φp in the expression of Ψ (Eq. (41)) gives 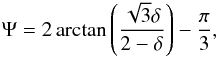 (46)i.e. near the Lagrangian equilibrium Ψ only depends on δ. Since 0 ≤ δ ≤ 1, we have Ψ ∈ [ −π/ 3,π/ 3 ], and for δ = 1 / 2 we get Ψ = 0, which corresponds to equal mass planets.
(46)i.e. near the Lagrangian equilibrium Ψ only depends on δ. Since 0 ≤ δ ≤ 1, we have Ψ ∈ [ −π/ 3,π/ 3 ], and for δ = 1 / 2 we get Ψ = 0, which corresponds to equal mass planets.
 |
Fig. 9 Level curves of δ (black) and ζ0 (red) for the tadpole configuration, with respect to Am and Ψ. See the text for more details. |
4.2.2. Large amplitude tadpole orbits
As discussed in Sect. 4.1.2, for large libration amplitudes it is not possible to obtain an explicit expression for the orbital parameters from the Sp terms. The same applies to the phase angles φp. However, for tadpole configurations it is still possible to inverse the problem using implicit functions and to fully characterize the orbits from the modulation terms in Eq. (27).
In Fig. 9, we show iso-values of the parameters ζ0 and δ with respect to the quantities Am and Ψ (see Sect. 4.1.2 for more details). For tadpole orbits, we see that each couple (Am, Ψ) corresponds to a unique couple (ζ0, δ). One can thus determine the values of ζ0 and δ directly from Am and Ψ.
We also know that | C0(δ,ζ0) | depends only on ζ0 and δ (see Sect. 4.1.2). In Fig. 10 we show iso-values of | C0 |. Since S0 = α | C0 |, we can directly obtain the value of α from (ζ0, δ), and hence from (Am, Ψ). We can thus determine sinI (Eq. (45)), since μ is linked to ζ0 through expression (40). The parameters δ, ζ0, μ, and sinI are then fully determined for the tadpole configuration.
Finally, similarly to the linear case (Sect. 4.1.1), for a given δ one can show that φ0 is a bijective map for λ0 ∈ [ 0,2π/n [, and φ1 − λ0 is a bijective map for t0 ∈ [ 0,2π/ν [ (see Eqs. (43) and (44)). The values of λ0 and t0 are therefore determined by the values of φ0 and φ1. Then, one can use Eqs. (3) and (5) to obtain the orbital parameters of the co-orbitals.
 |
Fig. 10 Level curves of | C0 | for the tadpole configuration with respect to ζ0 and δ. See the text for more details. |
4.2.3. Horseshoe orbits
For the horseshoe configuration, it is also not possible to obtain explicit expressions for the orbital parameters from the Sp terms. However, a symmetry in ζ allows us to compute this (see Appendix A.1): 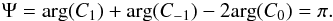 (47)Since Ψ is constant in horseshoe configurations, we cannot use it to get an additional constraint on the couple (δ,ζ0).
(47)Since Ψ is constant in horseshoe configurations, we cannot use it to get an additional constraint on the couple (δ,ζ0).
 |
Fig. 11 Left:| C0 | with respect to δ in the horseshoe configuration. As Am(δ = 1 / 2) = + ∞, we plot the quantity Am | C0 |. Right: Am | C0 | versus δ in the horseshoe configuration. These quantities are symmetric with respect to δ = 0.5. red: ζ0 = 23°, purple: ζ0 = 19°, blue: ζ0 = 15°. See the text for more details. |
In Fig. 11 we plot | C0 | and Am | C0 | = ( | C1 | + | C-1 | ) / 2 versus δ (see Sect. 4.1.2 for more details). The graphs are symmetric in δ = 1 / 2. One can see that these quantities vary significantly with δ, but are are almost constant in regard to ζ0 (different colour curves in Fig. 11), except near δ = 1 / 2 for Am | C0 |. Thus, we can assume an average value for ζ0 in the horseshoe domain. From this average value, we get approximated values of δ and α by knowing Am and | C0 |. Then, we can obtain approximated values for the parameters t0 and λ0 from φ0 and φ1, as explained in the tadpole case. However, the degeneracy in μ sin I remains, because of the strong dependence of 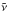 on ζ0 in the horseshoe domain (see Fig. 3). One of the ways to get this information is to consider higher order harmonics in the expansion of the radial velocity, Eq. (25). However, as these harmonics are about 10 times smaller than S1, much more accurate data is required.
on ζ0 in the horseshoe domain (see Fig. 3). One of the ways to get this information is to consider higher order harmonics in the expansion of the radial velocity, Eq. (25). However, as these harmonics are about 10 times smaller than S1, much more accurate data is required.
4.2.4. Tadpole or horseshoe?
Since the method that we use to determine the orbital parameters of a co-orbital system depends on its configuration (tadpole or horseshoe), it is legitimate to ask whether it is possible to know the configuration type before we choose one method or another for reducing the observational data.
Once the signature of a co-orbital system is detected (by the observation of a modulation in the radial-velocity data) we can compute Ψ from Eq. (42). One can see from Eq. (A.9) that Ψ = π in the horseshoe configuration, while Ψ ∈ [ −2,2 ] in the tadpole configuration (Fig. 9). Since the domains for Ψ are exclusive in the different configurations, by computing Ψ we can immediately distinguish between a horseshoe and a tadpole configuration.
When the detected signal is at the limit of the instrumental precision, the phases can be improperly determined. In this case, one can always compute Am using expression (28). As shown in Appendix A.2, Am ranges within [ 0, + ∞ [ in the horseshoe configuration. In the tadpole configuration, Am reaches its maximum value for δ = 1 / 2 and ζ0 near the separatrix. We can see in Fig. 9 that this quantity remains below 1 / 3. Therefore, Am> 1 / 3 is also a sufficient condition to know that a co-orbital system is in a horseshoe configuration.
4.3. Application to synthetic data
We now apply the methods developed in the previous sections to two concrete situations of stars hosting a pair of coobital planets in quasi-circular orbits, one for tadpole and another for horseshoe orbits. In Table 1 we list the initial osculating orbital elements for these two hypothetical systems orbiting a solar-mass star. We then generate synthetic radial-velocity data for these systems by numerically integrating the equations of motion using an n-body model. In order to create a realistic data set, we use the same observational dates taken for the HD 10180 system (Lovis et al. 2011) to simulate the acquisition days, and associate with each measurement a Gaussian error with σ = 1 m/s. These synthetic data sets contain 160 measurements spanning 4600 days and correspond to an instrumental precision of ~1 m/s. The orbital periods of the planets are around 11.5 days in both examples, such that we can observe at least three complete libration cycles over the length of the observations.
Osculating orbital elements for a given date of two hypothetical co-orbital systems orbiting a solar-mass star.
4.3.1. Tadpole orbits
 |
Fig. 12 Periodograms of the synthetic radial velocity of the tadpole configuration presented in Table 1. a) raw data sk; b) modified data |
Our tadpole system is composed of two Saturn-like planets at 0.1 au (comparable masses and eccentricities). The individual RV amplitudes of both planets are K ~ 10 m/s, well above the instrument precision. Therefore, the signatures of the planets can be easily identified in the data, and we use this example to illustrate how to retrieve the complete set of orbital parameters listed in Table 1 with our method.
In Fig. 12a, we show a generalized Lomb-Scargle periodogram of the radial velocity data (Zechmeister & Kürster 2009). The Keplerian component of the signal with a period Pn ≈ 11 days can clearly be identified. We fit the raw data with a Keplerian function (Eq. (18)) and obtain an initial estimation for Pn ≈ 11.46 days, 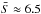 m/s, S0 ≈ 61.1 m/s, and φ0 ≈ 341.6°. We then subtract the Keplerian contribution to the data and obtain a modified data set
m/s, S0 ≈ 61.1 m/s, and φ0 ≈ 341.6°. We then subtract the Keplerian contribution to the data and obtain a modified data set 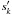 (Eq. (20)). In Fig. 12b, we show a periodogram of this modified data. We observe that the main peak with a period of approximately 11 days is replaced by two nearby smaller peaks. This is a clear indication of the presence of a modulation, each peak corresponding to the n ± ν terms (Eq. (27)).
(Eq. (20)). In Fig. 12b, we show a periodogram of this modified data. We observe that the main peak with a period of approximately 11 days is replaced by two nearby smaller peaks. This is a clear indication of the presence of a modulation, each peak corresponding to the n ± ν terms (Eq. (27)).
In order to better determine the libration frequency, we modify the data again following expression (21) adopting φ = φ0 = 341.6° and φ = φ0 + π/ 2 = 71.6°. In Figs. 12c and d we show the periodograms of 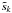 for these two transformations, respectively. In both transformations we observe that the peak around 11 days is replaced by some power at the periods near 5 and 150 days, corresponding to the frequencies 2n and ν, respectively (Eq. (22)). However, while for φ = φ0 the maximum power is observed for ν (Fig. 12 c), for φ = φ0 + π/ 2 it is observed for 2n (Fig. 12 d). From expression (23), we see that the amplitude Ŝ1 associated with the term with frequency ν is reduced by
for these two transformations, respectively. In both transformations we observe that the peak around 11 days is replaced by some power at the periods near 5 and 150 days, corresponding to the frequencies 2n and ν, respectively (Eq. (22)). However, while for φ = φ0 the maximum power is observed for ν (Fig. 12 c), for φ = φ0 + π/ 2 it is observed for 2n (Fig. 12 d). From expression (23), we see that the amplitude Ŝ1 associated with the term with frequency ν is reduced by 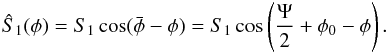 (48)For tadpole orbits we have Ψ ~ 0 (Fig. 9), which means that
(48)For tadpole orbits we have Ψ ~ 0 (Fig. 9), which means that 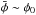 (Eq. (41)). Therefore, Ŝ1 is maximized for φ ~ φ0 and minimized for φ ~ φ0 + π/ 2 (Eq. (48)). Performing a FFT to
(Eq. (41)). Therefore, Ŝ1 is maximized for φ ~ φ0 and minimized for φ ~ φ0 + π/ 2 (Eq. (48)). Performing a FFT to 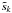 allows us to estimate Pν ≈ 154.66 days, S1 ≈ 4.23 m/s, and Δφ ≈ −116.5°. We can also estimate
allows us to estimate Pν ≈ 154.66 days, S1 ≈ 4.23 m/s, and Δφ ≈ −116.5°. We can also estimate 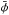 (and hence φ1 and φ-1) using the ratio between the two amplitudes
(and hence φ1 and φ-1) using the ratio between the two amplitudes 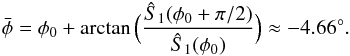 (49)Finally, adopting these values as initial parameters, we refit the raw data sk by performing a minimization of expression (27) using the Levenberg-Marquardt method (e.g. Press 1992). The results corresponding to the minimum of χ2 are shown in Table 2.
(49)Finally, adopting these values as initial parameters, we refit the raw data sk by performing a minimization of expression (27) using the Levenberg-Marquardt method (e.g. Press 1992). The results corresponding to the minimum of χ2 are shown in Table 2.
From the observational parameters listed in Table 2, we can obtain the corresponding orbital parameters using the inversion method explained in Sect. 4.2.2. The osculating orbital elements are then obtained through the Eqs. (3) and (5). The results are given Table 3. Except for the eccentricities and the longitudes of the pericentre, which cannot be determined with a Keplerian circular orbit approximation (Eq. (18)), we obtain a very good agreement for the remaining parameters (cf. Table 1).
We can still improve the quality of the fit in a last step, by performing an adjustment to the data using the direct n-body equations of motion (e.g. Correia et al. 2010). By adopting the orbital parameters listed in Table 3 as the starting point, the algorithm converges rapidly to the best fit. The results are given in Table 4. This last step slightly improves the orbital parameters obtained previously (lower χ2 and rms), because it is able to additionally fit the eccentricities and the longitudes of the pericentre. We note, however, that the n-body algorithm is only able to converge to the correct orbital solution because it used the parameters from Table 3 as starting point. Indeed, the phase space of co-orbital planets has many other local minima that provide alternative solutions that are not real.
4.3.2. Horseshoe orbits
 |
Fig. 13 Periodograms of the synthetic radial velocity of the horseshoe configuration presented in Table 1. a) raw data sk; b) modified data |
Our horseshoe system is composed of a Neptune-mass and a 3 Earth-mass planet at 0.1 au. It is at the limit of detection, since the individual RV amplitudes of each planet are K = 4.85 m/s and K = 0.85 m/s, respectively. With this example we intend to show the limitations of our method.
In Fig. 13a, we show a generalized Lomb-Scargle periodogram of the RV data. As for the tadpole example in the previous section (Fig. 12), the Keplerian component of the signal can clearly be identified for a period Pn ≈ 11 days. We thus fit the raw data with a Keplerian function (Eq. (18)) obtaining an initial estimation for Pn ≈ 11.55 days, 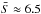 km s-1, S0 ≈ 4.9 m/s, and φ0 ≈ 23°, subtract its contribution to the data, and obtain a modified data set
km s-1, S0 ≈ 4.9 m/s, and φ0 ≈ 23°, subtract its contribution to the data, and obtain a modified data set  (Eq. (20)). However, unlike the tadpole case, in the new periodogram of the residual data, there is no clear peak above the noise (Fig. 13 b). Therefore, such a system can easily be mistaken with a system hosting a single planet at 11 days.
(Eq. (20)). However, unlike the tadpole case, in the new periodogram of the residual data, there is no clear peak above the noise (Fig. 13 b). Therefore, such a system can easily be mistaken with a system hosting a single planet at 11 days.
We can nevertheless apply our method to search for the traces of a co-orbital companion. We thus modify the data  according to expression (21) adopting φ = φ0 = 23° and φ = φ0 + π/ 2 = 113°. In Figs. 13c and d we show the periodograms corresponding to these transformations, respectively. For φ = φ0 the periodogram is very similar to the one with the residual data (Fig. 13b), so we conclude there is nothing else above the noise in the data. However, for φ = φ0 + π/ 2 the scenario is completely different as a significant peak appears around 1500 days, corresponding to the libration frequency (Fig. 13d). Indeed, for horseshoe orbits we have Ψ = π (Eq. (A.9)), which means that
according to expression (21) adopting φ = φ0 = 23° and φ = φ0 + π/ 2 = 113°. In Figs. 13c and d we show the periodograms corresponding to these transformations, respectively. For φ = φ0 the periodogram is very similar to the one with the residual data (Fig. 13b), so we conclude there is nothing else above the noise in the data. However, for φ = φ0 + π/ 2 the scenario is completely different as a significant peak appears around 1500 days, corresponding to the libration frequency (Fig. 13d). Indeed, for horseshoe orbits we have Ψ = π (Eq. (A.9)), which means that 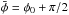 (Eq. (41)). Therefore, Ŝ1 is null for φ = φ0 and maximized for φ = φ0 + π/ 2 (Eq. (48)).
(Eq. (41)). Therefore, Ŝ1 is null for φ = φ0 and maximized for φ = φ0 + π/ 2 (Eq. (48)).
Performing a FFT to 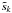 allow us to estimate Pν ≈ 1340 days, S1 ≈ 1.2 m/s, and Δφ ≈ 295°. Adopting these values as initial parameters, we refit the raw data sk with expression (27). The results corresponding to the minimum of χ2 are shown in Table 2. Comparing these results to the tadpole case, we observe that the uncertainty associated with the Sp and φp terms is larger, but still near 1 m/s, which corresponds to the considered precision of the instrument. Our method is therefore able to extract any information on the existence of a co-orbital companion, provided that the information on the libration terms is accessible in the data.
allow us to estimate Pν ≈ 1340 days, S1 ≈ 1.2 m/s, and Δφ ≈ 295°. Adopting these values as initial parameters, we refit the raw data sk with expression (27). The results corresponding to the minimum of χ2 are shown in Table 2. Comparing these results to the tadpole case, we observe that the uncertainty associated with the Sp and φp terms is larger, but still near 1 m/s, which corresponds to the considered precision of the instrument. Our method is therefore able to extract any information on the existence of a co-orbital companion, provided that the information on the libration terms is accessible in the data.
Once the existence of a co-orbital companion is confirmed, we can determine the corresponding orbital parameters. The parameter ζ0 (which gives the departure of the semi-major axis and the mean longitudes from their mean value) has a low impact on the orbital parameters and cannot be easily determined in horseshoe configuration (see Sect. 4.2.3). However, its value is constrained by the stability of the system: in the horseshoe configuration, it ranges between its lowest stable value for μmin = μ sinI, in our case ≈6 × 10-5 (see Fig. 4), and the separatrix. We therefore have ζ0 ∈ [ 13°,24° ]. We take ζ0 = 18.5° (average value on this interval) and compute the corresponding orbital parameters. We obtain a system close to the original one (Table 3).
In the horseshoe case, we cannot determine either the eccentricities and the longitudes of the pericentre, because we used a Keplerian circular orbit approximation (Eq. (18)), or the inclination to the line of sight, because we only fit the first three harmonics (Eq. (27)). In a final step, we perform an adjustment to the data using the direct n-body equations of motion, and we obtain a similar adjustment (Table 4).
5. Discussion and conclusion
In this paper we have revisited the dynamics of quasi-circular co-orbital planets. By computing their gravitational effect on the parent star, we have found a simple method for detecting this kind of planets, provided that the orbital libration can be seen in the observational data. Indeed, when the star is accompanied by co-orbital planets, in addition to the Keplerian orbital motion, there is a modulation at a longer period, corresponding to the libration frequency. Therefore, commonly used methods for signal demodulation (see Sect. 3.3) can also be applied to co-orbital systems, allowing the amplitude and the frequency of the modulation to be identified more accurately.
Every time a modulation is observed in the motion of a single planet, an inquiry should be made to check if it can correspond to the libration induced by another co-orbital planet. In this paper, we explain a way to quantify which co-orbital configurations can be expected: for stability reasons, we can put boundaries for pairs of the parameters (μ, ζ0); for data span duration reasons, we can estimate the frequency of libration ν, depending on (n, μ, ζ0); for measurement precision reasons, we can estimate the amplitude of the modulating peaks, which depends on the parameters (μ, n, δ, ζ0).
For reasons of clarity, we exemplify our method in the case of a radial velocity signal. However, our results are valid for any other method that measures a projection of the stellar motion. We have shown that the relative amplitude of the modulation signal depends only on the distance to the Lagrangian equilibrium, ζ0, and mass ratio, δ. Therefore, the detection of co-orbital planets is enhanced for large libration amplitudes around the Lagrangian equilibrium (i.e. small ζ0 values), and for planetary masses equally distributed between the two co-orbitals (δ ≈ 1 / 2).
In order to reduce the data, we proposed a direct inversion from the periodograms of the signal to the osculating elements of the system. For systems in the tadpole configuration we are able to determine the inclination of the orbital plane with respect to the plane of the sky and hence the true masses of the planets (and not only the minimum masses). In the horseshoe case this is not possible without considering higher harmonics for the modulation.
Acknowledgments
We acknowledge support from CIDMA strategic project UID/MAT/04106/2013. The “conseil scientifique de l’Observatoire de Paris” is acknowledged for their financial support.
References
- Anglada-Escudé, G., López-Morales, M., & Chambers, J. E. 2010, ApJ, 709, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Armstrong, E. 1914, Wireless receiving system., uS Patent 1, 113, 149 [Google Scholar]
- Correia, A. C. M., Couetdic, J., Laskar, J., et al. 2010, A&A, 511, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cresswell, P., & Nelson, R. P. 2008, A&A, 482, 677 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cresswell, P., & Nelson, R. P. 2009, A&A, 493, 1141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dermott, S. F., & Murray, C. D. 1981a, Icarus, 48, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Dermott, S. F., & Murray, C. D. 1981b, Icarus, 48, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Dobrovolskis, A. R. 2013, Icarus, 226, 1635 [NASA ADS] [CrossRef] [Google Scholar]
- Érdi, B., Nagy, I., Sándor, Z., Süli, Á., & Fröhlich, G. 2007, MNRAS, 381, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Ford, E. B., & Gaudi, B. S. 2006, ApJ, 652, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Gascheau, G. 1843, C. R. Acad. Sci. Paris, 16, 393 [Google Scholar]
- Giuppone, C. A., Beaugé, C., Michtchenko, T. A., & Ferraz-Mello, S. 2010, MNRAS, 407, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Giuppone, C. A.Benitez-Llambay, P., & Beaugé, C. 2012, MNRAS, 421, 356 [NASA ADS] [Google Scholar]
- Goździewski, K., & Konacki, M. 2006, ApJ, 647, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Janson, M. 2013, ApJ, 774, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Lagrange. 1772, Œuvres complètes (Paris: Gouthier-Villars) [Google Scholar]
- Laskar, J. 1990, Icarus, 88, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J. 1999, in Hamiltonian Systems with Three or More Degrees of Freedom, ed. C. Simó, NATO ASI (Dordrecht: Kluwer), 134 [Google Scholar]
- Laskar, J., & Robutel, P. 2001, Celes. Mech. Dyn. Astron., 80, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Laughlin, G., & Chambers, J. E. 2002, AJ, 124, 592 [NASA ADS] [CrossRef] [Google Scholar]
- Lovis, C., Ségransan, D., Mayor, M., et al. 2011, A&A, 528, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lyra, W., Johansen, A., Klahr, H., & Piskunov, N. 2009, A&A, 493, 1125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morais, M. H. M. 1999, A&A, 350, 318 [NASA ADS] [Google Scholar]
- Morais, M. H. M., & Correia, A. C. M. 2008, A&A, 491, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morbidelli, A., Levison, H. F., Tsiganis, K., & Gomes, R. S. 2005, Nature, 435, 462 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- MPC 2014, http://www.minorplanetcenter.org/ [Google Scholar]
- Murray, C. D., & Correia, A. C. M. 2011, Keplerian Orbits and Dynamics of Exoplanets, ed. S. Seager (Tucson: The University of Arizona Press), 15 [Google Scholar]
- Nauenberg, M. 2002, AJ, 124, 2332 [NASA ADS] [CrossRef] [Google Scholar]
- Páez, R. I., & Efthymiopoulos, C. 2015, Celes. Mech. Dyn. Astron. 121, 139 [Google Scholar]
- Pierens, A., & Raymond, S. N. 2014, MNRAS, 442, 2296 [NASA ADS] [CrossRef] [Google Scholar]
- Press, N. A. 1992, J. Br. Astron. Assoc., 102, 62 [NASA ADS] [Google Scholar]
- Roberts, G. 2002, Differ. Equ., 182, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, G. E. 2000, in Hamiltonian Systems and Celestial Mechanics (HAMSYS-98), Proc. III Int. Symp., 303 [Google Scholar]
- Robutel, P., & Bodossian, J. 2009, MNRAS, 399, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Robutel, P., & Gabern, F. 2006, MNRAS, 372, 1463 [NASA ADS] [CrossRef] [Google Scholar]
- Robutel, P., & Pousse, A. 2013, Celes. Mech. Dyn. Astron., 117, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Robutel, P., Rambaux, N., & Castillo-Rogez, J. 2011, Icarus, 211, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez, A., Giuppone, C. A., & Michtchenko, T. A. 2013, Celest. Mech. Dyn. Astron., 117, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlický, D., & Nesvorný, D. 2014, ApJ, 791, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, M. 1906, Astron. Nachr., 170, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Wolszczan, A., & Frail, D. A. 1992, Nature, 355, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Symmetries
Equation (5), respectively (6), possesses several symmetries. We use two of them to study analytically some features of the horseshoe configuration. On the one hand, we have the symmetry with respect to 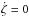 (Δa/a = 0 in Fig. 2):
(Δa/a = 0 in Fig. 2): 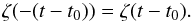 (A.1)On the other hand, we have the central symmetry of the phase space (ζ,Δa/a) in ζ = π and Δa/a = 0:
(A.1)On the other hand, we have the central symmetry of the phase space (ζ,Δa/a) in ζ = π and Δa/a = 0: 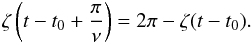 (A.2)Similar expressions can be obtained for
(A.2)Similar expressions can be obtained for 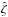 . In the tadpole configuration, these symmetries exist as well, but the symmetry (A.2) maps a vicinity of L4 to a vicinity of L5.
. In the tadpole configuration, these symmetries exist as well, but the symmetry (A.2) maps a vicinity of L4 to a vicinity of L5.
We can use these symmetries to simplify the expression of the coefficients Cp given by Eq. (14). Our purpose is to study the values of Am(δ,ζ0) and Ψ(δ,ζ0). Since none of them depends on the value of τ0, we take τ0 = 0 from now on. The coefficients cp (Eq. (36)) become 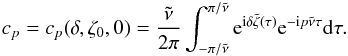 (A.3)Since we took τ0 = 0, e− iδζ is an even function in the case of a horseshoe orbit. Hence
(A.3)Since we took τ0 = 0, e− iδζ is an even function in the case of a horseshoe orbit. Hence  becomes
becomes 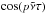 in the expressions of the Cp. By splitting this expression into two integrals and changing τ to
in the expressions of the Cp. By splitting this expression into two integrals and changing τ to 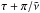 in the first one, we get
in the first one, we get ![\appendix \setcounter{section}{1} \begin{eqnarray} c_p=\frac{\tilde{\nu}}{2\pi} \int^{\frac{\pi}{\tilde{\nu}}}_{0} \left[{\rm e}^{{\rm i}\delta \tilde{\zeta}(\tau+\frac{\pi}{\tilde{\nu}})}{\rm e}^{{\rm -i}p\pi}+{\rm e}^{{\rm i}\delta\tilde{\zeta}(\tau)} \right] \cos(p\tilde{\nu}\tau) {\rm d}\tau . \label{eq:cp_v2} \end{eqnarray}](/articles/aa/full_html/2015/09/aa26175-15/aa26175-15-eq448.png) (A.4)Then, using the symmetry given by expression (A.2), the previous integral simplifies as
(A.4)Then, using the symmetry given by expression (A.2), the previous integral simplifies as ![\appendix \setcounter{section}{1} \begin{eqnarray} c_p=\frac{\tilde{\nu}}{2\pi} \int^{\frac{\pi}{\tilde{\nu}}}_{0} \left[{\rm e}^{{\rm i}\delta (2\pi -\tilde{\zeta}(\tau))}{\rm e}^{{\rm -i}p\pi}+{\rm e}^{{\rm i}\delta\tilde{\zeta}(\tau)} \right] \cos(p\tilde{\nu}\tau) {\rm d}\tau , \label{eq:cp_v3} \end{eqnarray}](/articles/aa/full_html/2015/09/aa26175-15/aa26175-15-eq449.png) (A.5)hence
(A.5)hence 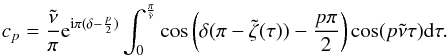 (A.6)As a consequence, using Eq. (14), we get for p = 0
(A.6)As a consequence, using Eq. (14), we get for p = 0![\appendix \setcounter{section}{1} \begin{eqnarray} \begin{split} C_0= \frac{\tilde{\nu}}{\pi} {\rm e}^{{\rm i}\delta\pi} \int^{\frac{\pi}{\tilde{\nu}}}_{0} \left[ (1-\delta)\cos (\delta(\pi-\tilde{\zeta}(\tau))) \right. \\ \left. - \delta \cos ((\delta-1)(\pi-\tilde{\zeta}(\tau))) \right] {\rm d}\tau , \end{split} \label{eq:C0_v2} \end{eqnarray}](/articles/aa/full_html/2015/09/aa26175-15/aa26175-15-eq452.png) (A.7)and for q = ± 1
(A.7)and for q = ± 1![\appendix \setcounter{section}{1} \begin{eqnarray} \begin{split} C_{q}= \frac{\tilde{\nu}}{\pi} {\rm e}^{{\rm i}(\delta\pi-\frac{\pi}{2})} \int^{\frac{\pi}{\tilde{\nu}}}_{0} \left[ (1-\delta)\sin (\delta(\pi-\tilde{\zeta}(\tau))) \right. \\ \left. - \delta \sin ((\delta-1)(\pi-\tilde{\zeta}(\tau))) \right] \cos(q\tilde{\nu}\tau) {\rm d}\tau . \end{split} \label{eq:C1_v1} \end{eqnarray}](/articles/aa/full_html/2015/09/aa26175-15/aa26175-15-eq454.png) (A.8)We obtain C1 = C-1.
(A.8)We obtain C1 = C-1.
Appendix A.1: Computation of Ψ
From Eq. (A.7), we have arg(C0(δ)) = δπ if δ ∈ [ 0,1 / 2 [ and δπ + π if δ ∈ ] 1 / 2,1 ]. Since arg(C1) = arg(C-1) = (δ−1/2)π (Eq. (A.8)), we conclude that for any horseshoe configuration 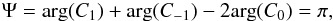 (A.9)i.e. Ψ is constant and equal to π.
(A.9)i.e. Ψ is constant and equal to π.
Appendix A.2: Computation of Am
Generally, the | Cq | (Eq. (A.8)) does not have an explicit expression. However, Am can be computed for some specific values of δ. We denote 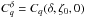 . For δ = 1 / 2, we have
. For δ = 1 / 2, we have ![\appendix \setcounter{section}{1} \begin{eqnarray} \begin{split} C_{q}^{1/2}= \frac{\tilde{\nu}}{\pi} \int^{\frac{\pi}{\tilde{\nu}}}_{0} \left[ \sin ((\pi-\tilde{\zeta}(\tau))/2) \right] \cos(q\tilde{\nu}\tau) {\rm d}\tau . \end{split} \label{eq:C1_v3} \end{eqnarray}](/articles/aa/full_html/2015/09/aa26175-15/aa26175-15-eq466.png) (A.10)The amplitude of the first harmonics (q = ± 1) of the Fourier series of an odd function is not null. Thus, since from expression (A.7) we have that
(A.10)The amplitude of the first harmonics (q = ± 1) of the Fourier series of an odd function is not null. Thus, since from expression (A.7) we have that 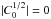 , we can conclude that in the horseshoe configuration
, we can conclude that in the horseshoe configuration 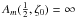 (Eq. (28)). Similarly, one can also see from Eqs. (A.7) and (A.8) that Am(0,ζ0) = Am(1,ζ0) = 0.
(Eq. (28)). Similarly, one can also see from Eqs. (A.7) and (A.8) that Am(0,ζ0) = Am(1,ζ0) = 0.
Appendix B: Mass ratios
In Sect. 4.1.1, we have shown that in the vicinity of the Lagrangian equilibrium, a planet with mass m1 is easier to identify when its co-orbital companion is much more massive (m1 ≪ m2) rather than when m1 ≈ m2. We show here that this result holds true in the horseshoe configuration. Using the symmetries (A.1) and (A.2), one can rewrite C1 (Eq. (A.8)) as ![\appendix \setcounter{section}{2} \begin{eqnarray} \begin{split} C_{1}= \frac{2\tilde{\nu}}{\pi} {\rm e}^{{\rm i}(\delta\pi-\frac{\pi}{2})} \int^{\frac{\pi}{2\tilde{\nu}}}_{0} \left[ (1-\delta)\sin (\delta(\pi-\tilde{\zeta}(\frac{\pi}{2\tilde{\nu}}-\tau))) \right. \\ \left. - \delta \sin \left(\left(\delta-1\right)\left(\pi-\tilde {\zeta}\left(\frac{\pi}{2\tilde{\nu}}-\tau\right)\right)\right) \right] \sin(\tilde{\nu}\tau) {\rm d} \tau. \end{split} \end{eqnarray}](/articles/aa/full_html/2015/09/aa26175-15/aa26175-15-eq473.png) (B.1)For a mass m1, we want to compare the quantity S1 = AmS0 = α | C1 | in the case of m1 = m2 (δ = 1 / 2) against the case when m1 ≪ m2 (δ ≈ 1 − m1/m2 = 1 − ϵ). Writing
(B.1)For a mass m1, we want to compare the quantity S1 = AmS0 = α | C1 | in the case of m1 = m2 (δ = 1 / 2) against the case when m1 ≪ m2 (δ ≈ 1 − m1/m2 = 1 − ϵ). Writing 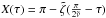 , from Eq. (A.8) we have
, from Eq. (A.8) we have ![\appendix \setcounter{section}{2} \begin{eqnarray} \begin{split} |C_{1}^{1/2}|= \left|\frac{2\tilde{\nu}}{\pi} \int^{\frac{\pi}{2\tilde{\nu}}}_{0} \left[ \sin (X(\tau)/2) \right] \sin(\tilde{\nu}\tau) {\rm d}\tau \right|, \end{split} \label{eq:C1_1s2} \end{eqnarray}](/articles/aa/full_html/2015/09/aa26175-15/aa26175-15-eq477.png) (B.2)and at first order in ϵ, Eq. (A.8) yields
(B.2)and at first order in ϵ, Eq. (A.8) yields ![\appendix \setcounter{section}{2} \begin{eqnarray} \begin{split} |C_{1}^{1-\epsilon}|= \left|\epsilon \frac{\tilde{2\nu}}{\pi} \int^{\frac{\pi}{2\tilde{\nu}}}_{0} \left[ X(\tau) + \sin (X(\tau)) \right] \sin(\tilde{\nu}\tau) {\rm d}\tau \right|. \end{split} \label{eq:C1_eps} \end{eqnarray}](/articles/aa/full_html/2015/09/aa26175-15/aa26175-15-eq478.png) (B.3)We have X(0) = 0 and
(B.3)We have X(0) = 0 and 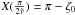 . One can show that X is a monotonous function in the interval
. One can show that X is a monotonous function in the interval ![\hbox{$\tau \in [0, \pi/(2\tilde{\nu})]$}](/articles/aa/full_html/2015/09/aa26175-15/aa26175-15-eq482.png) , hence sin(X/ 2) and X + sin(X) are a positive function in this interval. Moreover, for X ∈ [ 0,π ], we have the following inequality:
, hence sin(X/ 2) and X + sin(X) are a positive function in this interval. Moreover, for X ∈ [ 0,π ], we have the following inequality: 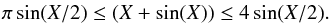 (B.4)Since
(B.4)Since  is also a positive function on the considered interval, the inequality in Eq. (B.4) holds true when we multiply each term by
is also a positive function on the considered interval, the inequality in Eq. (B.4) holds true when we multiply each term by  and integrate over
and integrate over ![\hbox{$\tau \in [0, \pi/(2\tilde{\nu})]$}](/articles/aa/full_html/2015/09/aa26175-15/aa26175-15-eq482.png) . Finally, we get
. Finally, we get 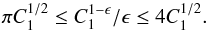 (B.5)When δ = 1 / 2, we have μ ≈ 2m1/m0, while when δ = 1 − ϵ, we get μ ≈ m1/ (ϵm0). Multiplying Eq. (B.5) by α, we obtain
(B.5)When δ = 1 / 2, we have μ ≈ 2m1/m0, while when δ = 1 − ϵ, we get μ ≈ m1/ (ϵm0). Multiplying Eq. (B.5) by α, we obtain 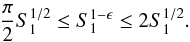 (B.6)We finally conclude that in the horseshoe case, for a given mass m1, the co-orbital couple (m1,m2) is up to two times easier to identify when m1 ≪ m2 rather than when m1 ≈ m2.
(B.6)We finally conclude that in the horseshoe case, for a given mass m1, the co-orbital couple (m1,m2) is up to two times easier to identify when m1 ≪ m2 rather than when m1 ≈ m2.
All Tables
Osculating orbital elements for a given date of two hypothetical co-orbital systems orbiting a solar-mass star.
All Figures
 |
Fig. 1 Reference angles represented for the circular co-orbital system with respect to an inertial frame (x,y). m0 is the mass of the central star, m1 and m2 the masses of the co-orbitals. ri is the distance of the co-orbital i to the central star, and λi its true longitude. Following Eq. (3) one can write λi as a function of λ0, ζ, and of the mass ratio δ. |
| In the text | |
 |
Fig. 2 Phase portrait of Eq. (5). The separatrix (black curve) splits the phase space in two different domains: inside the separatrix the region associated with the tadpole orbits (in red) and the horseshoe domain (blue orbits) outside. The phase portrait is symmetric with respect to ζ = 180°. The horizontal purple segment indicates the range of variation of ζ0 while the vertical one shows the section used as initial condition to draw Fig. 5. See the text for more details. |
| In the text | |
 |
Fig. 3 Variation of the libration frequency |
| In the text | |
 |
Fig. 4 Stability of co-orbitals as a function of log 10(μ) and ζ0. The initial conditions are chosen as t0 = 0 (Δa/a = 0) and ζ0 ∈ [ 0°,60° ]: purple horizontal line in Fig. 2. In black is the separatrix between the tadpole and the horseshoe domain. The stability criteria of Gascheau (1843), corresponding to ν/n = 1/ |
| In the text | |
 |
Fig. 5 Stability of co-orbitals as a function of log 10(μ) and Δa/a. The initial conditions are ζ0 = π/ 3 and Δa/a ∈ [ 0,0.06 ]: vertical purple line in Fig. 2. The black line indicates the separatrix between the tadpole and the horseshoe domains. The dots follow a curve Δa ∝ μ1 / 3, delimiting the stability region of the horseshoe domain. The colour code indicates the value of the libration frequency, i.e. log 10(ν/n) (see Fig. 4 for the scale). |
| In the text | |
 |
Fig. 6 Motion of the two co-orbital bodies (red and blue) and their barycentre (purple) in a co-rotating frame with frequency n. Tadpole (left) and horseshoe (right). δ = 0.6. Here μ = 2 × 10-4 and the planets are located at 1 AU from the star. By eliminating the influence of n, one can see the long-term motion of the barycentre of the planets. Pν is the period of the periodic trajectories represented by the coloured lines. See the text for more details. |
| In the text | |
 |
Fig. 7 Motion of the star in the configurations of Fig. 6 in the direction x in the inertial frame. In black is the tadpole orbit and in red the horseshoe. The top graph represents the evolution of the position of the star over time and the bottom graph its spectrum. In these examples, the libration period of the horseshoe orbits is about twice the period of the tadpole orbits. See the text for more details. |
| In the text | |
 |
Fig. 8 Detectability of a co-orbital companion for m2/m0 ≈ 10-3. For a given data set (K0/ϵ,T/Pn), co-orbital companions with a mass m1 can only be detected if they lie above the respective threshold limit. |
| In the text | |
 |
Fig. 9 Level curves of δ (black) and ζ0 (red) for the tadpole configuration, with respect to Am and Ψ. See the text for more details. |
| In the text | |
 |
Fig. 10 Level curves of | C0 | for the tadpole configuration with respect to ζ0 and δ. See the text for more details. |
| In the text | |
 |
Fig. 11 Left:| C0 | with respect to δ in the horseshoe configuration. As Am(δ = 1 / 2) = + ∞, we plot the quantity Am | C0 |. Right: Am | C0 | versus δ in the horseshoe configuration. These quantities are symmetric with respect to δ = 0.5. red: ζ0 = 23°, purple: ζ0 = 19°, blue: ζ0 = 15°. See the text for more details. |
| In the text | |
 |
Fig. 12 Periodograms of the synthetic radial velocity of the tadpole configuration presented in Table 1. a) raw data sk; b) modified data |
| In the text | |
 |
Fig. 13 Periodograms of the synthetic radial velocity of the horseshoe configuration presented in Table 1. a) raw data sk; b) modified data |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.