| Issue |
A&A
Volume 580, August 2015
|
|
|---|---|---|
| Article Number | A109 | |
| Number of page(s) | 19 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201526108 | |
| Published online | 11 August 2015 | |
Infrequent visitors of the Kozai kind: the dynamical lives of 2012 FC71, 2014 EK24, 2014 QD364, and 2014 UR⋆
Apartado de Correos 3413, 28080 Madrid, Spain
e-mail: carlosdlfmarcos@gmail.com
Received: 16 March 2015
Accepted: 2 June 2015
Context. Asteroids with semi-major axes very close to that of a host planet can avoid node crossings when their nodal points are at perihelion and at aphelion. This layout protects the asteroids from close encounters, and eventual collisions, with the host planet.
Aims. Here, we study the short-term dynamical evolution of four recently discovered near-Earth asteroids (NEAs) – 2012 FC71, 2014 EK24, 2014 QD364, and 2014 UR – that follow very Earth-like orbits.
Methods. Our analysis is based on results of direct N-body calculations that use the most updated ephemerides and include perturbations from the eight major planets, the Moon, the barycentre of the Pluto-Charon system, and the three largest asteroids.
Results. These four NEAs exhibit an orbital evolution unlike any other known near-Earth object (NEO). Beyond horseshoe, tadpole, or quasi-satellite trajectories, they follow co-orbital passing orbits relative to the Earth within the Kozai domain. Our calculations show that secular interactions induce librations of their relative argument of perihelion with respect to our planet but also to Venus, Mars, and Jupiter. Secular chaos is also present. The size of this transient population is probably large.
Conclusions. Although some of these NEAs can remain orbitally stable for many thousands of years, their secular dynamics are substantially more complicated than commonly thought and cannot be properly described within the framework of the three-body problem alone owing to the overlapping of multiple secular resonances. Objects in this group are amongst the most atypical NEOs regarding favourable visibility windows because these are separated in time by many decades or even several centuries.
Key words: methods: numerical / minor planets, asteroids: general / chaos / celestial mechanics
© ESO, 2015
1. Introduction
In a seminal paper, Milani et al. (1989) pointed out that for asteroids with semi-major axes very close to that of a host planet, node crossings can be avoided when the nodal points are at perihelion and at aphelion, i.e. at ω ≃ 0° and ω ≃ 180°. This arrangement protects the asteroids from close encounters and possible collisions with the host planet, and corresponds to one of the variants of a more general mechanism known as the Kozai resonance (Kozai 1962). This form of the Kozai resonance is particularly important for objects moving in low-eccentricity, low-inclination orbits.
This special, dynamically cold case was explored by Michel & Thomas (1996) who confirmed that, at low inclinations, the argument of perihelion of near-Earth objects (NEOs) can librate around either 0° or 180°. These authors found that, in the future, 4660 Nereus (1982 DB) will stay in the Kozai resonance for almost 2 × 105 yr with ω librating around 180° and its inclination oscillating between 5° and 11°. A similar behaviour was found for the future dynamical evolution of 4034 Vishnu (1986 PA). Such orbital architecture indeed provides a protection mechanism against close encounters with our planet.
This interesting topic received additional attention from Namouni (1999) who predicted the existence of minor bodies following passing orbits with small Jacobi constants but still moving in unison with their host planets. Namouni labelled this orbital regime “the Kozai domain” as it is characterised by a libration about 0° of the variation of the relative argument of perihelion (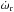 ) with the variation of the relative longitude of the ascending node being negative (
) with the variation of the relative longitude of the ascending node being negative (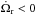 ). No such objects were found until de la Fuente Marcos & de la Fuente Marcos (2013) identified 2012 FC71 as a Kozai librator that is currently following an Earth-like passing orbit with a small Jacobi constant. This object is locked in a Kozai resonance with ω librating around 0°. In sharp contrast with horseshoe librators, NEOs trapped in the Kozai regime exhibit a very slow orbital evolution and may remain relatively unperturbed for hundreds of thousands of years (Michel & Thomas 1996; Gronchi & Milani 1999; de la Fuente Marcos & de la Fuente Marcos 2013).
). No such objects were found until de la Fuente Marcos & de la Fuente Marcos (2013) identified 2012 FC71 as a Kozai librator that is currently following an Earth-like passing orbit with a small Jacobi constant. This object is locked in a Kozai resonance with ω librating around 0°. In sharp contrast with horseshoe librators, NEOs trapped in the Kozai regime exhibit a very slow orbital evolution and may remain relatively unperturbed for hundreds of thousands of years (Michel & Thomas 1996; Gronchi & Milani 1999; de la Fuente Marcos & de la Fuente Marcos 2013).
Here we present three recently discovered NEOs – 2014 EK24, 2014 QD364, and 2014 UR – that are following dynamically cold, passing orbits with small Jacobi constants with respect to the Earth; i.e. they are co-orbital to our planet. Like in the case of 2012 FC71, the argument of perihelion of 2014 EK24 and 2014 QD364 currently librates around 0°. On the other hand, a libration of ω about 180° is observed for 2014 UR. This paper is organised as follows. In Sect. 2, we briefly outline our numerical model. Section 3 reviews the case of 2012 FC71. The dynamics of 2014 EK24 is studied in Sect. 4. Sections 5 and 6 focus on 2014 QD364 and 2014 UR, respectively. In Sect. 7, we show the multi-planet erωr-portrait for these objects. Our results are discussed in Sect. 8. Artificial interlopers are considered in Sect. 9. Section 10 summarises our conclusions.
Heliocentric Keplerian orbital elements of asteroids 2012 FC71, 2014 EK24, 2014 QD364, and 2014 UR.
2. Numerical model
Our physical model takes into account the perturbations by eight major planets and treats the Earth–Moon system as two separate objects; it also includes the barycentre of the dwarf planet Pluto-Charon system and the three largest asteroids (for further details, see de la Fuente Marcos & de la Fuente Marcos 2012). Initial conditions (positions and velocities in the barycentre of the solar system) have been obtained from the Jet Propulsion Laboratory (JPL) HORIZONS system (Giorgini et al. 1996; Standish 1998) and they are referred to as the JD 2 457 000.5 epoch (2014-December-9.0), which is the t = 0 instant in our figures. The numerical integrations discussed in this paper have been performed using the Hermite scheme described by Makino (1991) and implemented by Aarseth (2003). The standard version of this direct N-body code is publicly available from the IoA web site1.
In our calculations, relativistic and oblateness terms and the role of the Yarkovsky and Yarkovsky–O’Keefe–Radzievskii–Paddack (YORP) effects (see e.g. Bottke et al. 2006) have been ignored. Neglecting these effects has no impact on the evaluation of the present dynamical status of the objects discussed here, but may affect both the reconstruction of their dynamical past and any predictions made regarding their future evolution. Accurate modelling of the Yarkovsky force requires relatively precise knowledge of the physical properties of the objects affected, which is not the case here. In addition to – and because of – the co-orbital status of these bodies, the orbital drifts induced by non-gravitational forces may be smaller than those observed in standard NEOs. In general, oblateness terms induce circulation of the relative argument of perihelion, which can dominate over the objects interaction and terminate the librations of the relative argument of perihelion (Namouni 1999). However, for the objects studied here this contribution could be negligible owing to the low orbital eccentricity and the absence of very close encounters with our planet.
In addition to the integrations performed making use of the nominal orbital parameters in Table 1, we have computed 50 control simulations for each object with sets of orbital elements obtained from the nominal ones within the quoted uncertainties and assuming Gaussian distributions for them (up to 9σ in the cases of 2012 FC71 and 2014 QD364, and 6σ for 2014 EK24 and 2014 UR). For the sake of clarity, only a few characteristic orbits are shown in the figures. Additional sets of 100 shorter control simulations are discussed in Appendix A (see Figs. A.1 to A.4). Relative errors in the total energy at the end of the calculations are <1 × 10-15. The corresponding error in the total angular momentum is several orders of magnitude smaller.
It may be argued that presenting these objects here could be premature because some of their orbits are still not well known (see Table 1 and Sects. 3–6), in particular those of 2012 FC71 and 2014 QD364. However, not all orbital solutions with relatively short data-arc spans are “born equal”. It is not the same short data-arc for an object that moves in a low-inclination orbit that crosses the paths of all the planets from Jupiter to Mercury as another similarly short data-arc for an object that is only directly perturbed by the Earth–Moon system. In general, these are peculiar, very stable minor bodies with very long synodic periods. The synodic period of an object relative to the Earth is the time interval for the object to return to the same position as seen from our planet (e.g. Green 1985). The synodic period, S, is given by 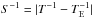 , where T and TE are the orbital periods of the object and the Earth, respectively. For a given object (natural or artificial), it is the characteristic timescale between favourable visibility windows. The relative mean longitude of these objects does not librate as it does in the case of quasi-satellite, tadpole, or horseshoe orbits because
, where T and TE are the orbital periods of the object and the Earth, respectively. For a given object (natural or artificial), it is the characteristic timescale between favourable visibility windows. The relative mean longitude of these objects does not librate as it does in the case of quasi-satellite, tadpole, or horseshoe orbits because 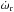 librates about 0°. Therefore, if an object is only observed a few times after discovery, we have to wait an entire synodic period (not just a fraction of it) to be able to observe it again. In the case of 2012 FC71, the waiting time is nearly 56 yr and for 2014 EK24 could be as high as 166 yr. For objects in this group, it may take many decades or even several centuries to recover them. No other group of NEOs, except for horseshoe librators, is so dramatically restricted regarding favourable visibility windows.
librates about 0°. Therefore, if an object is only observed a few times after discovery, we have to wait an entire synodic period (not just a fraction of it) to be able to observe it again. In the case of 2012 FC71, the waiting time is nearly 56 yr and for 2014 EK24 could be as high as 166 yr. For objects in this group, it may take many decades or even several centuries to recover them. No other group of NEOs, except for horseshoe librators, is so dramatically restricted regarding favourable visibility windows.
3. Asteroid 2012 FC71, an Aten Kozai librator
Asteroid 2012 FC71 was discovered on 2012 March 31 by A. Boattini observing with the Steward Observatory 0.9 m Spacewatch telescope at Kitt Peak (Scotti et al. 2012). It is a small object with H = 25.2, which translates into a diameter in the range 20–60 m for an assumed albedo of 0.20–0.04. The orbital elements of 2012 FC71 (see Table 1) are suggestive of a NEO that moves co-orbitally with the Earth. The source of the Heliocentric Keplerian osculating orbital elements and uncertainties in Table 1 is the JPL Small-Body Database2. Its current orbit is reliable enough (see discussion above) to assess its short-term dynamical evolution as it is based on 34 observations for a data-arc span of 21 d. The quality of the orbit of this object is at present lower than that of 2014 EK24 or 2014 UR and is on par with that of 2014 QD364 (see Table 1). In addition, it is similar (34 observations spanning 21 d versus 18 observations spanning 24 d) to that of the orbital solution of 2013 LX28, another very stable Earth co-orbital, when it was recognised as a quasi-satellite of our planet by Connors (2014).
With a value of the semi-major axis a = 0.9885 AU, very close to that of our planet (0.9992 AU), this Aten asteroid is a NEO moving in a very Earth-like orbit with low-eccentricity, e = 0.09, and little inclination, i = 4.̊9. With such an orbit, close encounters are only possible with the Earth–Moon system, and they take place with a cadence equal to its synodic period (see above). One of the reasons for its inclusion here is to encourage further observations of this interesting and unusual (at least dynamically) minor body that is characterised by very sparse favourable visibility windows; the last one occurred around 1959. This object will experience close encounters with our planet under 0.5 AU in June 2015 (0.18 AU), 2016 (0.28 AU), 2017 (0.39 AU), and 2018 (0.50 AU), but after this last relatively favourable flyby, the next one under 0.5 AU will take place in 2061 February (0.44 AU).
 |
Fig. 1 Short-term dynamical evolution of various parameters for the nominal orbit of 2012 FC71 as presented in Table 1. The distance from the Earth (panel A)); the value of the Hill sphere radius of the Earth, 0.0098 AU, is shown (red line). The parameter |
In order to study the possible co-orbital nature of 2012 FC71 with the Earth, we have performed N-body calculations in both directions of time for 250 kyr using the physical model described above. Regular co-orbitals are characterised by the libration of the relative mean longitude, λr, or the difference between the mean longitudes of the object and its host planet. The mean longitude of an object is given by λ = M + Ω + ω, where M is the mean anomaly, Ω is the longitude of ascending node, and ω is the argument of perihelion (see e.g. Murray & Dermott 1999). Asteroid 2012 FC71 is not a co-orbital of the Earth in the classical sense (see e.g. Morais & Morbidelli 2002) because its λr does not currently librate but circulates (not shown in the figures); however, its ω does librate around 0° which means that it is submitted to a secular resonance, see panel F in Figs. 1 (nominal orbit) and 2, the Kozai resonance (Kozai 1962). There is no libration of λr because 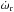 librates about 0°. In a Kozai resonance, the apse and the node are in resonance with one another (Kozai 1962). Because of the Kozai resonance, both eccentricity and inclination oscillate with the same frequency but out of phase; when the value of the eccentricity reaches its maximum the value of the inclination is the lowest and vice versa (
librates about 0°. In a Kozai resonance, the apse and the node are in resonance with one another (Kozai 1962). Because of the Kozai resonance, both eccentricity and inclination oscillate with the same frequency but out of phase; when the value of the eccentricity reaches its maximum the value of the inclination is the lowest and vice versa (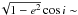 constant, panel B in Figs. 1 and 2). The values of the eccentricity and inclination are coupled, and the value of the semi-major axis remains nearly constant (see panels C, D, and E in Figs. 1 and 2). At a proper average inclination of 5.̊5, this object was – when discovered – the coldest (dynamically speaking) known Kozai resonator (de la Fuente Marcos & de la Fuente Marcos 2013). Asteroids 2014 EK24 and 2014 QD364 are even colder Kozai librators, but are less stable.
constant, panel B in Figs. 1 and 2). The values of the eccentricity and inclination are coupled, and the value of the semi-major axis remains nearly constant (see panels C, D, and E in Figs. 1 and 2). At a proper average inclination of 5.̊5, this object was – when discovered – the coldest (dynamically speaking) known Kozai resonator (de la Fuente Marcos & de la Fuente Marcos 2013). Asteroids 2014 EK24 and 2014 QD364 are even colder Kozai librators, but are less stable.
In Figs. 2, 3, 5, 7, and 9 when an orbit is labelled “± nσ”, where n is an integer, it has been obtained by adding (+) or subtracting (−) n-times the uncertainty from the orbital parameters (the six elements) in Table 1. All the control orbits exhibit consistent behaviour within a few hundred thousand years of t = 0. This object can only experience close encounters with the Earth–Moon system, see panel G in Figs. 1 and 2. Close encounters place the object inside the Kozai resonance, see panel A in Figs. 1 and 2. To further support the idea that the relatively low quality of the present orbit of this particular object is not an obstacle to obtaining a clear and reliable picture of its past and future orbital evolution, Fig. 3 shows additional control orbits where the orbital elements have been further modified at the ± 9σ level. The short-term dynamical evolution of these orbits is still consistent with that in Fig. 1. Although based on a relatively short data-arc (21 d), the orbital evolution of 2012 FC71 is remarkably stable. The nodes of 2012 FC71 remain far from our planet for very long periods of time (see panel G in Figs. 1–3). The present quality of the orbit is obviously not an issue regarding the study of the dynamical evolution of this object. The duration of its current co-orbital state is at least 330 kyr, but episodes lasting nearly 500 kyr are feasible. Longer calculations, spanning 3 Myr, show that recurrent episodes are also possible.
4. Asteroid 2014 EK24, an Apollo Kozai librator
Asteroid 2014 EK24 was discovered on 2014 March 10 by S. M. Larson observing for the Catalina Sky Survey with the 0.68 m Schmidt telescope (Larson et al. 2014). It is larger than 2012 FC71 at H = 23.2 or a diameter in the range 60–150 m if an albedo of 0.20–0.04 is assumed. It is the largest of the objects studied here. As in the previous case, the orbital elements of 2014 EK24 (see Table 1) resemble those of a co-orbital NEO. Its orbit is well defined as it is based on 267 observations with a data-arc span of 390 d. The value of its semi-major axis is also very close to that of our planet, a = 1.0043 AU. This Apollo asteroid is a NEO that also follows a very Earth-like orbit with e = 0.07 and i = 4.̊7. As in the case of 2012 FC71, its path is only directly perturbed by the Earth–Moon system during relatively distant close encounters (the minimum distance is currently >0.03 AU). Asteroid 2014 EK24 is included on NASA’s list of potential human mission targets (the NHATS list), which means that improving our understanding of the dynamics of this object is particularly important. Based on observations made with the IAC80 and ESA-OGS telescopes operated in Tenerife by the Instituto de Astrofísica de Canarias (IAC) in the Spanish Observatorio del Teide, Radu Cornea and Ovidiu Vaduvescu (priv. comm.) from the EURONEAR network (Vaduvescu et al. 2008, 2015) have reported a rotation period of 6 min. Its very fast rotation is also characterised by a large amplitude of 0.79 mag. Elongated asteroids have large lightcurve amplitudes (see e.g. Kaasalainen & Torppa 2001).
Figure 4 shows the short-term dynamical evolution of this object under the same conditions used for 2012 FC71 except that only the time interval (−30, 30) kyr is given because the object is considerably less stable. We show the results for three illustrative orbits, the nominal one (Fig. 4) and those of two representative orbits that are the most different from the nominal one (Fig. 5). A smaller value of the dispersion has been used because the orbit of this object is considerably more robust, statistically speaking. All the control orbits exhibit coherent behaviour within a few thousand years of t = 0. As in the previous case and for the same reason, its λr does not currently librate (not shown), but its orbital period (1.01 yr) matches that of the Earth and its ω librates around 0° (see panel F in Figs. 4 and 5), the signposts of a co-orbital passing orbit with a small Jacobi constant. This assessment is statistically robust according to the current observational uncertainties or at a confidence level >99.99% (6σ). Brief (~40–200 yr) co-orbital episodes of the horseshoe and quasi-satellite type are also observed. During these episodes λr librates and 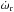 is positive (horseshoe) or negative (quasi-satellite). The value of the parameter
is positive (horseshoe) or negative (quasi-satellite). The value of the parameter 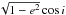 (see panel B in Figs. 4 and 5) remains approximately constant for most of the evolution shown.
(see panel B in Figs. 4 and 5) remains approximately constant for most of the evolution shown.
This minor body started following a co-orbital passing orbit nearly 4.5 kyr ago and it will continue in this state for at least 5.5 more kyr. The duration of the entire episode is in the range 15 to 40 kyr with shorter episodes being more likely. Asteroid 2014 EK24 is an even colder (dynamically speaking) Kozai resonator than 2012 FC71, with a proper average inclination of just 3.̊3 (see panel E in Figs. 4 and 5), which means that the encounters with the Earth–Moon system are closer and take place more often than in the case of 2012 FC71 (compare panel A in Figs. 1 or 3 and 4 or 5). This explains why 2014 EK24 is overall less dynamically stable than 2012 FC71. Close encounters are responsible for both injection into and ejection from the Kozai state.
5. Asteroid 2014 QD364, a small Aten Kozai librator
Asteroid 2014 QD364 was discovered on 2014 August 30 by the Catalina Sky Survey (Kowalski et al. 2014). Its orbit is reasonably well known and is based on 29 observations with a data-arc span of 17 d similar to that of 2012 FC71, although the orbit is significantly less stable. In principle, it is the smallest of the four objects studied here at H = 27.2 or a diameter in the range 10–24 m if an albedo of 0.20–0.04 is assumed. As in the previous two cases, the orbital parameters of this object (see Table 1) are comparable to those of a co-orbital NEO. The value of its semi-major axis is very close to that of our planet, a = 0.9891 AU. This Aten asteroid is a NEO that follows a very Earth-like orbit with e = 0.04 and i = 4.̊0; its path is at present only directly perturbed by the Earth–Moon system during relatively distant close encounters (currently the minimum distance is >0.01 AU), well separated in time (nearly 60 yr).
Figure 6 shows the short-term dynamical evolution of this object under the same conditions used for the previous two. As in the case of 2014 EK24, only the time interval (−30, 30) kyr is shown because the object is not very stable; in fact, it is perhaps the most unstable of the four minor bodies studied here. Following the same reasoning applied to 2012 FC71, we display the results for three illustrative orbits, the nominal one (Fig. 6) and those of two representative orbits that are the most different from the nominal one (Fig. 7). All the control orbits exhibit consistent behaviour within a few thousand years of t = 0.
Asteroid 2014 QD364 appears to be precariously perched on the threshold of instability. The descending node is dangerously close to Earth’s aphelion (see panel G in Figs. 6 and 7). Very similar control orbits evolve rather differently after just a few thousand years. It began following a co-orbital passing orbit nearly 2 kyr ago and it will continue doing so for at least the next 1.5 kyr. As in the previous two cases, its argument of perihelion currently librates around 0°. Close encounters are responsible for both injection into and ejection from the Kozai state that lasts at least 4 kyr and as long as 10 kyr, the shortest episodes being more common. Kozai states characterised by the libration of the argument of perihelion around 90°, − 90°, or 180° for a few thousand years are possible. Brief (~40 yr to 1.5 kyr) co-orbital episodes of the horseshoe and quasi-satellite type are also observed. The horseshoe episodes last longer.
6. Asteroid 2014 UR, yet another small Aten Kozai librator
Asteroid 2014 UR was discovered on 2014 October 17, also by the Catalina Sky Survey (Hill et al. 2014). It is smaller than 2014 EK24 and 2012 FC71 but larger than 2014 QD364 at H = 26.6 or a diameter in the range 14–32 m if an albedo of 0.20–0.04 is assumed. As in the previous cases, the orbital parameters of 2014 UR (see Table 1) are similar to those of a co-orbital NEO. Its orbital solution is very robust and it is based on 146 observations, including 2 radar observations, with a data-arc span of 14 d. Its orbit uncertainty is similar to that of 2014 EK24. The value of its semi-major axis (a = 0.9991 AU) is very close to that of our planet. This Aten asteroid is a NEO that also follows an Earth-like orbit with e = 0.01 and i = 8.̊2. Like the previous three, its path is at the moment only directly perturbed by the Earth–Moon system during close encounters (the minimum distance is currently >0.008 AU).
Figure 8 shows the short-term dynamical evolution of this minor body during the time interval (− 30, 30) kyr. It presents the past and future behaviour of the nominal solution; those of two additional representative control orbits where the orbital elements have been modified at the ± 6σ level (see above) are displayed in Fig. 9. Its overall past and future dynamical evolution is quite uncertain and it may be as unstable and chaotic as that of 2014 QD364. Some of the control orbits show long Kozai episodes in which the argument of perihelion librates around 180° for many thousands of years (see right-hand panel F in Fig. 9). The close encounters with the Earth–Moon system experienced by 2014 UR are stronger than those of the previous three objects and that explains why it is so unstable.
7. Relative eccentricity-relative argument of perihelion
The secular evolution of co-orbital objects is viewed naturally in the erωr-plane, where er = e − ep and ωr = ω − ωp; ep and ωp are, respectively, the eccentricity and argument of perihelion of a given planet. In Namouni (1999), the analysis is carried out within the framework of the restricted elliptic three-body problem; his Fig. 19 shows a selection of orbits in the erωr-plane and they all look very regular. In sharp contrast, our erωr maps for 2012 FC71, 2014 EK24, 2014 QD364, and 2014 UR relative to the Earth (second from top panels in Figs. 10, 12, 14, and 16) display a rather convoluted evolution, in particular those of 2012 FC71 and 2014 QD364. We cannot conclude that the Kozai dynamics followed by these objects are the result of the dominant secular perturbation of Venus, Earth, Mars, or Jupiter. The superposition of these secular perturbations creates a very rich dynamics instead.
In addition to being trapped in a near 1:1 mean motion resonance with our planet, these asteroids orbit the Sun in a near 13:8 mean motion resonance with Venus, so this planet completes 13 orbits around the Sun in the same amount of time that the asteroids complete 8; they also move in a near 2:1 mean motion resonance with Mars, so Mars completes one orbit while the minor bodies do two, and a 12:1 mean motion resonance with Jupiter, completing 12 orbits around the Sun approximately in the same amount of time Jupiter completes only one. These near resonances induce the dramatic changes observed in the erωr-portraits. The irregular evolution displayed in Figs. 10, 12, 14, and 16 shows that the dynamics of these objects cannot be properly described within the framework of the restricted elliptic three-body problem alone, at least not during the entire time-span studied here.
 |
Fig. 10 The erωr-portrait relative to Venus, the Earth, Mars, and Jupiter for 2012 FC71. |
Jupiter is not the single dominant factor regarding the Kozai resonance affecting these objects. The argument of perihelion relative to Jupiter of 2012 FC71 was librating around 180° from 120 to 60 kyr ago and around 90° for nearly 30 kyr soon afterwards, but in general the evolution is very irregular with no persistent periodicities (see Fig. 11). Less irregular is the equivalent evolution of 2014 EK24; in fact, it is the most stable of the four in the erωr-portrait. For this object, Jupiter is dominant in the time frame − 11 to 6 kyr with its relative argument of perihelion librating around 90° (see Fig. 13); during the same time interval the argument of perihelion relative to Venus librates around − 90° and the one relative to Earth flips from − 90° to 90°. During libration episodes, we observe intersecting closed cycles in the erωr-plane that resemble ripples in a pond. Mars only seems to affect 2014 EK24, a shifting oscillation from − 10 to − 5 kyr in Fig. 13. The remarkable periodic behaviour often observed, but without libration, may be understood as resulting from being very close to the separatrix in the phase space of the mean motion resonance. For 2012 FC71 there is no actual stable libration of the relative argument of perihelion with respect to any planet in Fig. 11 during the Kozai episode.
In sharp contrast, the evolution displayed by 2014 QD364 in the erωr-plane (see Fig. 15) is very irregular, although multiple but short libration episodes can be identified. The evolution of 2014 UR is cleaner (see Fig. 17), but the relative arguments of perihelion hardly circulate. In any case, the superposition of secular resonances makes them more unstable. Short episodes of simultaneous libration break the Kozai state in the case of these objects. The average relative eccentricity with respect to the Earth is also higher for them. The average orbital inclination of 2014 QD364 is the lowest, which further explains the observed differences with respect to 2012 FC71.
It is well known that chaos arises where resonances overlap. Overlapping secular resonances have been identified as the source of long-term chaos in the orbits of the terrestrial planets (Lecar et al. 2001; Morbidelli 2002; Lithwick & Wu 2014). The topic of overlapping secular resonances and its effects on the dynamics of asteroids was first studied by Michel (1997) in the particular case of objects moving in Venus horseshoe orbits. He concluded that overlapping of secular resonances is possible, complicating the dynamics of horseshoe orbits significantly. Furthermore, this author found that the presence of overlapping secular resonances provides a transport mechanism to induce high inclinations, switching orbits between different regimes of the Kozai resonance. On a more practical and pragmatic note, overlapping secular resonances have a significant impact on active debris removal and the design of disposal strategies for deactivated artificial satellites (Rosengren et al. 2015).
In our case, Figs. 10–17 show that it is certain that the overlapping of multiple secular resonances – with Venus, Earth, Mars, and Jupiter – plays an important role, perhaps dominant, for these four objects and, in general, for those moving within the Arjuna orbital domain (see de la Fuente Marcos & de la Fuente Marcos 2013). Such interplay affects the long-term stability of this type of orbits.
Ito & Tanikawa (1999) argued that the terrestrial planets share the effect of the secular perturbation from Jupiter. In particular, the Earth shares the increase in eccentricity of Venus on the long term; the two planets exchange angular momentum (Ito & Tanikawa 2002). These authors stated that the terrestrial planets maintain their stability by sharing and weakening the secular perturbation from Jupiter (Jupiter’s perihelion has a periodicity of nearly 300 kyr); i.e. the Earth–Venus pair distributes the effects of this perturbation. Tanikawa & Ito (2007) further extended this analysis concluding that, regarding the secular perturbation from Jupiter, the inner planets are a planetary group or collection of loosely connected mutually dynamically dependent planets. This planetary grouping has direct implications on the case studied here; if Jupiter is removed from the calculations, the overlapping secular resonances disappear. Removing the Earth–Moon system or Venus also breaks (but only slightly) the status quo. Only the removal of Mars has virtually negligible effects on the dynamics of the objects discussed in this work. Within this context, objects part of the Arjuna orbital domain are indeed a very singular NEO group. Under certain circumstances, 2012 FC71-like orbits, the secular perturbations of Jupiter become negligible (see Fig. 11, bottom panel) and relatively long-term stability could be achieved.
Namouni (1999) opened a window to the study of the Kozai realm within the framework of the restricted elliptic three-body problem. Unfortunately, the orbital architecture of the terrestrial zone is significantly more complicated with strong secular coupling between planets inducing overlapping of multiple secular resonances. The ultimate source of the perturbation is Jupiter, but that perturbation is shared and weakened by the terrestrial planets.
Orbital properties of objects currently moving in Arjuna-type orbits.
8. Comparative dynamics and discussion
First we will focus on 2012 FC71 and 2014 EK24, the most stable minor bodies in the set of four discussed here. Asteroids 2012 FC71 and 2014 EK24 represent two incarnations of the same paradigm, passing orbits with small Jacobi constants as described by Namouni (1999). Asteroid 2012 FC71 is an Aten and occupies an orbit interior (for the most part) to that of the Earth; in contrast, 2014 EK24 is an Apollo that follows an orbit exterior (for the most part) to that of the Earth, yet both currently exhibit the same secular resonance with libration of ω around 0°. The orbit of 2012 FC71 is far more stable than that of 2014 EK24, however. Asteroid 2012 FC71 stays in the Kozai resonance for at least 330 kyr, but 2014 EK24 only remains there for 10 to 30 kyr, suggesting that Apollo passing companions are far less stable than Aten ones. Our calculations show that the stable island occupied by Aten asteroid 2012 FC71 is less perturbed and its volume in orbital parameter space is much larger than the one hosting Apollo asteroid 2014 EK24. The near mean motion resonances and secular resonances discussed above are clearly stronger for the stable Apollo island. The key to understanding this is in the behaviour of the argument of perihelion relative to Mars: in Fig. 11 it circulates rapidly, but in Fig. 13 an almost proper libration around 90° for nearly 5 kyr is observed. The effect of the secular perturbations linked to near resonances significantly reduces the stability of the Apollo island with respect to that of the Aten island.
Unlike horseshoe librators, NEOs trapped in the Kozai resonance have a very slow orbital evolution (see Figs. 1–5) and can remain relatively unperturbed for hundreds of thousands of years (Michel & Thomas 1996; Gronchi & Milani 1999) as they never get excessively close to the Earth–Moon system (see panel A in Figs. 1–5), well beyond the Hill radius of our planet (0.0098 AU) during the span of the passing co-orbital phase. They do not librate in λr; in other words, they are not classical co-orbitals like Trojans, quasi-satellites, or horseshoe librators. However, their paths resemble those of the classical co-orbitals (see Figs. 1 and 5 in de la Fuente Marcos & de la Fuente Marcos 2013). For these objects, close encounters below the Hill radius are observed prior to their insertion in the Kozai resonance and immediately before their eviction from it. Critical close encounters for 2012 FC71 always happen at the descending node, but for 2014 EK24 they take place at both nodes (see panel G in Figs. 1–5). In most of the control orbits of 2014 EK24, the object was a horseshoe librator to the Earth before becoming a passing co-orbital; in some cases it returns to that state right after leaving the Kozai resonance. Although not shown, during the passing co-orbital episodes 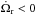 in agreement with predictions made in Namouni (1999).
in agreement with predictions made in Namouni (1999).
Asteroids 2014 QD364 and 2014 UR are clearly more unstable than the previous two (see Appendix A) and this is not the result of having more uncertain orbits. The current orbital solution of 2014 UR is as robust as that of 2014 EK24, but the object is far less stable. Both 2014 QD364 and 2014 UR are likely smaller than the other two, they could be fragments of fragments. The current catastrophic disruption rate of asteroids in the main belt has been recently studied by Denneau et al. (2015). These authors have found that the rate is significantly higher than previously thought with rotational disruptions being the dominant source of most fragments. Asteroidal decay could be induced by collisional processes (see e.g. Dorschner 1974; Ryan 2000), but could also be the combined result of thermal fatigue (see e.g. Čapek & Vokrouhlický 2010) and rotational (see e.g. Walsh et al. 2008) or tidal stresses (see e.g. Tóth et al. 2011). These last three processes can easily produce secondary fragments. Planetary ejecta from Mars, the Earth–Moon system, and Venus are also possible sources (Warren 1994; Gladman et al. 1995; Bottke et al. 1996; Gladman 1996, 1997). Asteroid 2014 EK24 is a fast rotator (see above) and the largest of the group. From a theoretical standpoint, it may be producing additional fragments via rotational stress. These putative fragments will follow similar orbits, at least initially. Asteroid 2013 RZ53 (see Table 3) follows a very similar orbit and it has a size in the range 1–4 m, typical of a fragment of a fragment.
9. Artificial interlopers
The four objects studied here are part of a subclass of a larger group of dynamically cold, resonant asteroids known as the Arjunas (see de la Fuente Marcos & de la Fuente Marcos 2013, 2015). Nearly every time a new object moving in a very Earth-like orbit is discovered, it is speculated that it may be a relic of human space exploration which has returned to the neighbourhood of the Earth–Moon system. Items of space debris are routinely found when looking for asteroids. Spectral and photometric observations, and orbital analysis concluded that J002E3, initially considered a new minor body, was an Apollo rocket body (Jorgensen et al. 2003). The Rosetta spacecraft was also mistaken as an asteroid and given the designation 2007 VN84 (Kowalski et al. 2007)3. Even the European Space Agency telescope Gaia was erroneously given a minor body designation, 2015 HP116 (Anderson et al. 2015)45.
Therefore, within the Arjuna orbital domain sit artificial interlopers, objects that left low-Earth parking orbits and headed out to interplanetary space. A recent example is 2014 XX39, which has been identified as hardware from the Hayabusa 2 mission, specifically the Hayabusa 2 spacecraft. Hayabusa 2 is an asteroid sample return mission aimed at the C-type asteroid 162173 (1999 JU3) (Tsuda et al. 2013; Giancotti et al. 2014). This recent misidentification and the ones pointed out above highlight the fact that the positional information available on distant artificial objects is incomplete. Table 2 shows the heliocentric Keplerian orbital elements of 2014 XX39 before it was identified as the Hayabusa 2 spacecraft. Its orbit is quite uncertain because it was observed just six times after its discovery on 2014 December 6. Figure 18 shows the evolution of this object as well as that of the nominal orbit of the actual Hayabusa 2 spacecraft (data from the JPL HORIZONS system). Hayabusa 2 was launched on December 3, therefore the orbital evolution prior to that date is only displayed here as a mere dynamical curiosity. The aim of our analysis is to compare the orbital evolution of a confirmed human-made piece of hardware to that of natural objects like 2012 FC71, 2014 EK24, 2014 QD364, or 2014 UR. For both orbits displayed in Fig. 18 the overall evolution is different from that in Figs. 1–9; the object tends to drift away from Earth’s co-orbital region rather quickly. The launch of a spacecraft has to be very fine tuned so its subsequent dynamical evolution resembles that of a natural object like the Arjunas. This is not surprising taking into account that the phase space in the neighbourhood of our planet is threaded by a dense stochastic web of instabilities.
In the case of known objects moving in Arjuna-type orbits, we can easily conclude that they are unlikely to be human-made. The first unambiguously documented objects sent out of the atmosphere were launched in the second half of 1957. Objects in Table 3 were all discovered near their most recent perigee; their previous perigee appear listed in the table under column L. Only four objects had a previous perigee after the second half of 1957: 2006 JY26, 2006 RH120, 2012 FC71, and 2012 LA11. With the exception of 2006 RH120, none of their perigees can be matched to any known rocket launch. Asteroid 2006 RH120 reached perigee on 1979 May 15, the same day the Russian satellite Kosmos 1098 was launched. However, this was just a coincidence because 2006 RH120 is a confirmed natural object (Kwiatkowski et al. 2009; Granvik et al. 2012). None of the objects in Table 3 are expected to be human-made.
10. Conclusions
Our calculations confirm that, in accordance with predictions made by Namouni (1999), minor bodies moving in passing orbits with a small Jacobi constant relative to a host planet, or co-orbital passing orbits, do exist. Asteroids 2012 FC71, 2014 EK24, 2014 QD364, and 2014 UR exhibit an orbital evolution unlike any other known NEO; however, they are all part of a little studied group of dynamically cold, resonant asteroids known as the Arjunas (see de la Fuente Marcos & de la Fuente Marcos 2013, 2015) that occupy the most dynamically stable region of the NEO orbital parameter space. This region is affected by multiple mean motion, near mean motion, and secular resonances. The superposition of this relatively large set of resonances contributes to both stabilising and destabilising the trajectories of the bodies moving within this peculiar orbital parameter space. The four objects studied in this work are submitted to Kozai resonances.
They are small objects that can only be observed when they arrive close to the Earth, with a frequency of many decades or even centuries, remaining within 0.5 AU from the Earth for about 10–20 yr with typical close approaches at minimum distances of 0.05 AU. This implies that the vast majority of them may be well beyond reach of current NEO surveys (see the analysis in de la Fuente Marcos & de la Fuente Marcos 2015); however, they could be numerous because they are dynamically stable (in particular the Atens with orbits similar to that of 2012 FC71), significantly more stable than typical NEOs or even Earth quasi-satellites like 2013 LX28 (Connors 2014). Most known Earth quasi-satellites also exhibit Kozai-like dynamics (de la Fuente Marcos & de la Fuente Marcos 2014). Asteroid 2014 EK24 represents a rare instance of an object that is in very near mean motion resonance with multiple planets (Venus, Earth, Mars, and Jupiter). The chance discovery of three objects with similar dynamical properties within a few months during 2014 strongly suggests that the size of this population may not be as negligible as considered in typical studies (see e.g. Rabinowitz et al. 1993; Bottke et al. 2002; Brasser & Wiegert 2008).
As members of the unofficial Arjuna class, these minor bodies moving in orbits with low-eccentricity, low-inclination, and Earth-like period eventually suffer a close encounter with the Earth–Moon system that changes their dynamical status, turning them into traditional co-orbitals of the horseshoe, Trojan, or quasi-satellite type, or – more often – ejecting them outside Earth’s co-orbital region. Objects of this dynamical class may experience repeated co-orbital and Kozai episodes, and transitions are driven by the encounters (de la Fuente Marcos & de la Fuente Marcos 2013). The most usual (and persistent) state is symmetric horseshoe, but quasi-satellite and Trojan episodes have also been observed during the simulations. Prior to the Kozai episode and after it, these minor bodies often follow horseshoe trajectories. When trapped in the Kozai resonant state, these objects exhibit libration of their arguments of perihelion around 0° or 180°, characteristic of passing orbits with small Jacobi constants.
Although NEOs in this group can remain orbitally stable for many thousands of years, their secular dynamics are quite complex and cannot be properly described within the framework of the three-body problem alone. The orbital evolution of these objects, and the Arjuna asteroids in general, is organised to a large extent by secular chaos. From an observational point of view, minor bodies in this group are amongst the most dramatically restricted NEOs regarding favourable visibility windows because these are separated in time by many decades or even several centuries. Failure to secure more observations of 2012 FC71 or 2014 QD364 before they leave Earth’s neighbourhood in the near future can definitely place them in the category of “lost asteroids” because their next visibility window comes half a century from now.
Online material
 |
Fig. 2 Comparative short-term dynamical evolution of various parameters for two representative examples of orbits that are the most different from the nominal one of 2012 FC71 (± 3σ deviations, see text for details). The distance from the Earth (panel A)); the value of the Hill sphere radius of the Earth, 0.0098 AU, is shown (red line). The parameter |
 |
Fig. 11 Time evolution of ωr relative to Venus, the Earth, Mars, and Jupiter for 2012 FC71. |
Heliocentric Keplerian orbital elements of 2014 XX39.
Appendix A: Average short-term evolution of 2012 FC71, 2014 EK24, 2014 QD364, and 2014 UR
Figures A.1 to A.4 show the short-term evolution of the orbital elements a, e, i, Ω, and ω of the objects studied here. The thick black curves show the average results of the evolution of 100 control orbits computed as described in Sect. 2. The thin red curves show the ranges (minimum and maximum) in the values of the parameters at a given time. Asteroid 2012 FC71 is the most dynamically stable of the four objects, followed by 2014 EK24; 2014 UR is quite unstable and the least stable is 2014 QD364. Asteroid 2014 QD364 has an e-folding time, or characteristic timescale on which two arbitrarily close orbits diverge exponentially, of a few dozen years. In sharp contrast, the e-folding time of 2014 EK24 is several hundred years. Surprisingly, the e-folding time of 2014 EK24 is somewhat longer than that of 2012 FC71, even if its orbital evolution is significantly less stable.
 |
Fig. A.1 Time evolution of the orbital elements a, e, i, Ω, and ω of 2012 FC71. The thick curve shows the average evolution of 100 control orbits, the thin curves show the ranges in the values of the parameters at the given time. |
Acknowledgments
The authors thank the referee for his/her constructive report and very helpful suggestions regarding the presentation of this paper. The authors would like to thank S. J. Aarseth for providing the code used in this research, and O. Vaduvescu and R. L. Cornea for sharing their results on 2014 EK24 prior to publication. This work was partially supported by the Spanish “Comunidad de Madrid” under grant CAM S2009/ESP-1496. Some of the calculations presented here were completed on the “Servidor Central de Cálculo” of the Universidad Complutense de Madrid. In preparation of this paper, we made use of the NASA Astrophysics Data System, the ASTRO-PH e-print server, the MPC data server, and the NEODyS information service.
References
- Aarseth, S. J. 2003, Gravitational N-Body Simulations (Cambridge: Cambridge University Press), 27 [Google Scholar]
- Anderson, R., Gibson, B., Goggia, T., et al. 2015, MPEC 2015-H123 [Google Scholar]
- Bottke, W. F., Jr., Nolan, M. C., Melosh, H. J., Vickery, A. M., & Greenberg, R. 1996, Icarus, 122, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Bottke, W. F., Morbidelli, A., Jedicke, R., et al. 2002, Icarus, 156, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Bottke, W. F., Jr., Vokrouhlický, D., Rubincam, D. P., & Nesvorný, D. 2006, Annu. Rev. Earth Planet. Sci., 34, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brasser, R., & Wiegert, P. 2008, MNRAS, 386, 2031 [NASA ADS] [CrossRef] [Google Scholar]
- Čapek, D., & Vokrouhlický, D. 2010, A&A, 519, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Connors, M. 2014, MNRAS, 437, L85 [NASA ADS] [CrossRef] [Google Scholar]
- de la Fuente Marcos, C., & de la Fuente Marcos, R. 2012, MNRAS, 427, 728 [NASA ADS] [CrossRef] [Google Scholar]
- de la Fuente Marcos, C., & de la Fuente Marcos, R. 2013, MNRAS, 434, L1 [NASA ADS] [CrossRef] [Google Scholar]
- de la Fuente Marcos, C., & de la Fuente Marcos, R. 2014, MNRAS, 445, 2985 [NASA ADS] [CrossRef] [Google Scholar]
- de la Fuente Marcos, C., & de la Fuente Marcos, R. 2015, Astron. Nachr., 336, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Denneau, L., Jedicke, R., Fitzsimmons, A., et al. 2015, Icarus, 245, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Dorschner, J. 1974, Astron. Nachr., 295, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Giancotti, M., Campagnola, S., Tsuda, Y., & Kawaguchi, J. 2014, Celest. Mech. Dyn. Astron., 120, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Giorgini, J. D., Yeomans, D. K., Chamberlin, A. B., et al. 1996, BAAS, 28, 1158 [NASA ADS] [Google Scholar]
- Gladman, B. 1997, Icarus, 130, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Gladman, B. J. 1996, Ph.D. Thesis, Cornell University [Google Scholar]
- Gladman, B. J., Burns, J. A., Duncan, M. J., & Levison, H. F. 1995, Icarus, 118, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Granvik, M., Vaubaillon, J., & Jedicke, R. 2012, Icarus, 218, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Green, R. M. 1985, Spherical Astronomy (Cambridge: Cambridge University Press), 416 [Google Scholar]
- Gronchi, G. F., & Milani, A. 1999, A&A, 341, 928 [NASA ADS] [Google Scholar]
- Hill, R. E., Christensen, E. J., Gibbs, A. R., et al. 2014, MPEC 2014-U13 [Google Scholar]
- Ito, T., & Tanikawa, K. 1999, Icarus, 139, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Ito, T., & Tanikawa, K. 2002, MNRAS, 336, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Jorgensen, K., Rivkin, A., Binzel, R., et al. 2003, BAAS, 35, 981 [NASA ADS] [Google Scholar]
- Kaasalainen, M., & Torppa, J. 2001, Icarus, 153, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Kowalski, R. A., Beshore, E. C., Boattini, A., et al. 2007, MPEC 2007-V69 [Google Scholar]
- Kowalski, R. A., Christensen, E. J., Gibbs, A. R., et al. 2014, MPEC 2014-R01 [Google Scholar]
- Kozai, Y. 1962, AJ, 67, 591 [Google Scholar]
- Kwiatkowski, T., Kryszczyńska, A., Polińska, M., et al. 2009, A&A, 495, 967 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larson, S. M., Christensen, E. J., Gibbs, A. R., et al. 2014, MPEC 2014-E65 [Google Scholar]
- Lecar, M., Franklin, F. A., Holman, M. J., & Murray, N. W. 2001, ARA&A, 39, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Lithwick, Y., & Wu, Y. 2014, Proc. Natl. Acad. Sci. USA, 111, 12610 [NASA ADS] [CrossRef] [Google Scholar]
- Makino, J. 1991, ApJ, 369, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Michel, P. 1997, A&A, 328, L5 [NASA ADS] [Google Scholar]
- Michel, P., & Thomas, F. 1996, A&A, 307, 310 [NASA ADS] [Google Scholar]
- Milani, A., Carpino, M., Hahn, G., & Nobili, A. M. 1989, Icarus, 78, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Morais, M. H. M., & Morbidelli, A. 2002, Icarus, 160, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A. 2002, Modern Celestial Mechanics: Aspects of Solar System Dynamics (London: Taylor & Francis) [Google Scholar]
- Murray, C. D., & Dermott, S. F. 1999, Solar System Dynamics (Cambridge: Cambridge University Press), 97 [Google Scholar]
- Namouni, F. 1999, Icarus, 137, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Rabinowitz, D. L., Gehrels, T., Scotti, J. V., et al. 1993, Nature, 363, 704 [NASA ADS] [CrossRef] [Google Scholar]
- Rosengren, A. J., Alessi, E. M., Rossi, A., & Valsecchi, G. B. 2015, MNRAS, 449, 3522 [NASA ADS] [CrossRef] [Google Scholar]
- Ryan, E. V. 2000, Ann. Rev. Earth Planet. Sci., 28, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Scotti, J. V., Bressi, T. H., Boattini, A., et al. 2012, MPEC 2012-G13 [Google Scholar]
- Standish, E. M. 1998, JPL Planetary and Lunar Ephemerides, DE405/LE405, Interoffice Memo, 312.F-98-048, Jet Propulsion Laboratory, Pasadena, California [Google Scholar]
- Tanikawa, K., & Ito, T. 2007, PASJ, 59, 989 [NASA ADS] [Google Scholar]
- Tóth, J., Vereš, P., & Kornoš, L. 2011, MNRAS, 415, 1527 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuda, Y., Yoshikawa, M., Abe, M., Minamino, H., & Nakazawa, S. 2013, Acta Astron., 91, 356 [Google Scholar]
- Vaduvescu, O., Birlan, M., Colas, F., Sonka, A., & Nedelcu, A. 2008, Planet. Space Sci., 56, 1913 [NASA ADS] [CrossRef] [Google Scholar]
- Vaduvescu, O., Hudin, L., Tudor, V., et al. 2015, MNRAS, 449, 1614 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, K. J., Richardson, D. C., & Michel, P. 2008, Nature, 454, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Warren, P. H. 1994, Icarus, 111, 338 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Heliocentric Keplerian orbital elements of asteroids 2012 FC71, 2014 EK24, 2014 QD364, and 2014 UR.
All Figures
 |
Fig. 1 Short-term dynamical evolution of various parameters for the nominal orbit of 2012 FC71 as presented in Table 1. The distance from the Earth (panel A)); the value of the Hill sphere radius of the Earth, 0.0098 AU, is shown (red line). The parameter |
| In the text | |
 |
Fig. 4 Same as Fig. 1 but for 2014 EK24. |
| In the text | |
 |
Fig. 6 Same as Fig. 1 but for 2014 QD364. |
| In the text | |
 |
Fig. 8 Same as Fig. 1 but for 2014 UR. |
| In the text | |
 |
Fig. 10 The erωr-portrait relative to Venus, the Earth, Mars, and Jupiter for 2012 FC71. |
| In the text | |
 |
Fig. 12 Same as Fig. 10 but for 2014 EK24. |
| In the text | |
 |
Fig. 14 Same as Fig. 10 but for 2014 QD364. |
| In the text | |
 |
Fig. 16 Same as Fig. 10 but for 2014 UR. |
| In the text | |
 |
Fig. 2 Comparative short-term dynamical evolution of various parameters for two representative examples of orbits that are the most different from the nominal one of 2012 FC71 (± 3σ deviations, see text for details). The distance from the Earth (panel A)); the value of the Hill sphere radius of the Earth, 0.0098 AU, is shown (red line). The parameter |
| In the text | |
 |
Fig. 3 Same as Fig. 2 but for ± 9σ (see text for details). |
| In the text | |
 |
Fig. 5 Same as Fig. 2 but for 2014 EK24 and ± 6σ (see text for details). |
| In the text | |
 |
Fig. 7 Same as Fig. 2 but for 2014 QD364 and ± 9σ (see text for details). |
| In the text | |
 |
Fig. 9 Same as Fig. 2 but for 2014 UR and ± 6σ (see text for details). |
| In the text | |
 |
Fig. 11 Time evolution of ωr relative to Venus, the Earth, Mars, and Jupiter for 2012 FC71. |
| In the text | |
 |
Fig. 13 Same as Fig. 11 but for 2014 EK24. |
| In the text | |
 |
Fig. 15 Same as Fig. 11 but for 2014 QD364. |
| In the text | |
 |
Fig. 17 Same as Fig. 11 but for 2014 UR. |
| In the text | |
 |
Fig. 18 Same as Fig. 1 but for 2014 XX39 and Hayabusa 2 (see text for details). |
| In the text | |
 |
Fig. A.1 Time evolution of the orbital elements a, e, i, Ω, and ω of 2012 FC71. The thick curve shows the average evolution of 100 control orbits, the thin curves show the ranges in the values of the parameters at the given time. |
| In the text | |
 |
Fig. A.2 Same as Fig. A.1 but for 2014 EK24. |
| In the text | |
 |
Fig. A.3 Same as Fig. A.1 but for 2014 QD364. |
| In the text | |
 |
Fig. A.4 Same as Fig. A.1 but for 2014 UR. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


