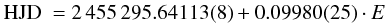| Issue |
A&A
Volume 580, August 2015
|
|
|---|---|---|
| Article Number | A117 | |
| Number of page(s) | 6 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201425581 | |
| Published online | 14 August 2015 | |
A new HW Vir binary from the Palomar Transient Factory
PTF1 J072455.75+125300.3: An eclipsing subdwarf B binary with a M-star companion⋆
1 Dr. Remeis-Observatory & ECAP, Astronomical Institute, Friedrich-Alexander University Erlangen-Nürnberg, Sternwartstr. 7, 96049 Bamberg, Germany
e-mail: markus.schindewolf@fau.de
2 Division of Physics, Mathematics and Astronomy, California Institute of Technology, Pasadena, CA 91125, USA
3 Institute for Astro- and Particle Physics, University of Innsbruck, Technikerstr. 25/8, 6020 Innsbruck, Austria
4 Department of Astrophysics/IMAPP, Radboud University Nijmegen, PO Box 9010, 6500 GL Nijmegen, The Netherlands
Received: 23 December 2014
Accepted: 10 June 2015
We report the discovery of an eclipsing binary – PTF1 J072456+125301– composed of a subdwarf B (sdB) star (g′ = 17.2m) with a faint companion. Subdwarf B stars are core helium-burning stars, which can be found on the extreme horizontal branch. About half of them reside in close binary systems, but few are known to be eclipsing, for which fundamental stellar parameters can be derived. We conducted an analysis of photometric data and spectra from the Palomar 60′′ and the 200′′ Hale telescope, respectively. A quantitative spectral analysis found an effective temperature of Teff = 33 900 ± 350 K, log g = 5.74 ± 0.08, and log (nHe/nH) = −2.02 ± 0.07, typical for an sdB star. The companion does not contribute to the optical light of the system, except through a distinct reflection effect. From the light curve an orbital period of 0.09980(25) d and a system inclination of 83.56 ± 0.30° were derived. The radial velocity curve yielded an orbital semi-amplitude of K1 = 95.8 ± 8.1 km s-1. The mass for the M-type dwarf companion is 0.155 ± 0.020 M⊙. PTF1 J072456+125301 has similar atmospheric parameters to those of pulsating sdB stars (V346 Hya stars). Therefore it could be a high-priority object for asteroseismology, if pulsations were detected such as in the enigmatic case of NY Vir.
Key words: binaries: eclipsing / stars: early-type / stars: evolution / stars: fundamental parameters / stars: horizontal-branch / subdwarfs
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Hot subdwarf stars (sdBs and sdOs) are core helium-burning stars with thin hydrogen envelopes that are unable to sustain hydrogen shell burning (Heber 2009). This type of star dominates the population of faint blue stars at high galactic latitudes and can be found both in the old disk as well as in the halo (Ferraro et al. 1997). With regard to galaxy evolution, sdB stars play an important role because they are believed to be a dominating source for the UV upturn phenomenon that can be observed in elliptical galaxies and galaxy bulges (Brown et al. 1997).
Subluminous B stars are identified with evolutionary models for extreme horizontal branch (EHB) stars. To form an sdB star, the progenitor star has to lose almost all of its hydrogen envelope rather quickly, right at the onset of helium burning. The remaining thin part of the envelope is inert. Close binary evolution is very likely to be responsible for the mass loss on the red giant branch (RGB) that is needed to form an sdB star (Maxted et al. 2001). A significant fraction of sdB stars have composite spectra indicating the presence of a main-sequence companion of F, G, or K type (Ferguson et al. 1984; Stark & Wade 2003). Such binaries have long periods of several hundreds of days to more than 1000 days (Vos et al. 2013). About 50% of the known single-lined sdB stars reside in close binaries with periods of less than 30 days, hosting invisible companions that are either white dwarfs or very low-mass dwarfs (Maxted et al. 2001; Copperwheat et al. 2011). To understand the formation of the sdB binaries, two possible channels have been proposed, both requiring interacting binary systems (Han et al. 2002, 2003):
-
(i)
The first is called the “stable Roche lobeoverflow (RLOF) channel”. Stable mass transferis taking place, originating from a low-mass giant filling its Rochelobe close to the tip of the RGB. During this time it loses most of itsenvelope as a result of the Roche lobe overflow. When thehydrogen envelope has been reduced sufficiently, the masstransfer stops and the star begins to shrink. If the degenerate core ismassive enough, a helium flash is possible. Subdwarf B systemsoriginating from the RLOF channel are predicted to have longperiods from 10 d upto 1000 d.
-
(ii)
The second is the “common envelope ejection channel” (CEEC). Again, mass transfer occurs close to the tip of the red giant branch of the sdB progenitor, but the mass transfer rate is so high that a common envelope (CE) is formed. Owing to friction in the envelope, both stars approach each other. This leads to a release of orbital energy and angular momentum, which is used to eject the envelope. This process results in a close binary system. If the core of the initially more massive star is still able to ignite helium burning, it becomes an sdB. The result would be an sdB star with a main-sequence companion in a short period binary such as the HW Vir star discussed in this paper. If a second common envelope phase occurs, the companion would be a white dwarf in a close orbit to the sdB star.
The mass distribution of sdB stars is found to peak at the canonical sdB mass of 0.47 M⊙ (Dorman et al. 1993). Observational mass determinations for a few objects are consistent with such predictions (0.47 ± 0.031 M⊙, Van Grootel et al. 2014; Fontaine et al. 2012).
Subdwarf B stars in close binary systems with low-mass dwarf companions have been known for decades (Kilkenny et al. 1978). These companions were discovered by means of the reflection effect in their light curves. If these systems are eclipsing, they are called HW Vir systems, named after the first discovered system (Menzies et al. 1986). They mostly have short periods (around 0.1 days) and a late M-type companion (which can usually only be detected by its reflection effect, caused by the high temperature difference of both components). The short period indicates that they have undergone a common envelope phase followed by a spiral-in phase. Up to now, only fifteen such systems are known (Schaffenroth et al. 2014a,b).
The canonical mass remains valid for HW Vir systems, even though it is the result of binary evolution (Han et al. 2003).
Because such eclipsing binaries offer the opportunity of determining the stellar masses, detailed analyses are crucial for as many of these objects as possible.
In this paper, we present observations and analysis of a new HW Vir star discovered by the Palomar Transient Factory (PTF). The PTF is a wide-field survey that searches for variable sources and optical transients. It makes use of the 1.2 m Oschin Telescope at Palomar Observatory, equipped with eleven 12k × 8k CCD cameras, and the Palomar 60-inch telescope (Law et al. 2009). With each exposure 7.2 square degrees are covered. In a typical night 200 square degrees or more are observed (Levitan et al. 2011).
We describe the spectroscopic and photometric observations in Sect. 2 and their analysis in Sect. 3 (spectroscopy) and Sect. 4 (photometry). In Sect. 5 we give a summary of the results from the analysis.
2. Observations
Photometric and spectroscopic data presented here were obtained at the Palomar 60-inch (hereafter P60; Cenko et al. 2006) and Palomar 200-inch (hereafter P200) telescopes, respectively.
2.1. Spectroscopy
The spectra of PTF1 J072456+125301 (hereafter PTF0724) were taken at the P200 telescope with the Double Spectrograph (DBSP; Oke et al. 1982) using a low resolution (R ~ 1500). The observations took place on August 10, 2010 and were scheduled to cover the entire orbit at equally distributed phases. Thirty-eight spectra were collected, covering a range from 3000 Å to 11 000 Å. The exposure time was set between 600 s and 900 s per spectrum to prevent orbital smearing. A grating of 600 lines/4000 mm-blaze was used at a grating angle of 27°17′′. All P200 spectra were reduced using optimal extraction (Horne 1986) as implemented in the Pamela Code (Marsh 1989), as well as the Starlink packages kappa, figaro, and convert. The spectrum is readily classified as that of an sdB star, according to the strong Stark-broadened Balmer and weak helium lines.
2.2. Photometry
We obtained a total of 1162 photometric observations of PTF0724 with the P60 over seven nights (details of each night are in Table A.2. All observations were made using a g′ filter and with an exposure time of 45 s with a dead time of approximately 21 s between exposures.
The P60 photometric observations were de-biased, flat-fielded, and astrometrically calibrated using the P60 pipeline (Cenko et al. 2006). Stars in each individual image were identified using the Sextractor Package (Bertin & Arnouts 1996) and instrumental magnitudes were measured using optimal point-spread function photometry (Naylor 1998) as implemented by the Starlink package Autophotom1.
Calibrated light curves were calculated using the relative photometry algorithm described in the appendix of Ofek et al. (2011) and in Sect. 3.1 of Levitan et al. (2011). Briefly, this algorithm identifies non-varying (over the course of the observations) “calibration” stars in the field of view and minimizes the scatter of their instrumental magnitudes by adjusting the zero-point of each individual exposure. We simultaneously fit to a reference catalog (here, USNO-B 1.0) to find an absolute calibration. This minimization is calculated using an iterative, matrix-based, least-squares approach and the resulting zero-points can then be applied to the target of interest. We note that we did not utilize the de-trending features of the algorithm as described in Levitan et al. (2011) since only one telescope/instrument was used. Measurement uncertainties are calculated from a combination of the Poisson error and the fit error. However, we note that this estimate does not include systematic errors and they are thus likely underestimated. Calculating the systematic error accurately can be done by finding the minimum scatter observed for bright stars on each exposure, but doing so requires substantially more sources than are present in the small field of view here.
The light curve is characterized by a strong reflection effect and primary as well as secondary eclipses. This, together with the spectral properties of the star (see Sect. 3.2), classifies PTF0724 as an HW Vir star.
The primary minimum is quite deep, with the flux descending to about 25% of the flux at phase 0.25 (g′ = 17.2m at this phasepoint). For further analysis the light curve was normalized to 1 at phase 0.25. The ephemeris was determined by fitting Gaussians to the primary eclipses via the standard Marquardt-Levenberg algorithm (Levenberg 1944). The period could be easily derived, because several light curves covered more than one full orbit and contained two primary minima.
The ephemeris of the primary minimum was found to be:
3. Spectroscopic analysis
3.1. Radial velocity curve
We begin by measuring and plotting the radial velocity (RV) curve. Since the system is single-lined, the analysis is straightforward. We made use of the Spectrum Plotting and Analysis Suite (SPAS; Hirsch 2009) to determine the radial velocity for each blue spectrum (see Table A1). The RVs were measured by fitting a set of mathematical functions (Gaussians, Lorentzians, and polynomials) to the spectral lines (see Fig. 2). Three functions are used to match the continuum (polynomials), the line (Lorentzians), and the line core (Gaussians), respectively and to mimic the typical Voigt profile of spectral lines. The profiles are fitted to all suitable lines simultaneously using χ2 minimization and the RV shift with respect to the rest wavelengths with the associated 1σ error is measured.
Because we find the phase shift between the primary and secondary minima is 0.5009 ± 0.001, the eccentricity of the orbit of PTF0724 must be very small (Fig. 4). Therefore we fitted a sine curve to the RVs. Figure 1 shows the phased RV curve with the best-fit solution. All phases of the orbit are well covered. We derived a semiamplitude of K = 95.7 ± 8.1 km s-1 and a system velocity of γ = −26.7 ± 5.5 km s-1 with a bootstrapping approach using 1200 iterations. Thereby the observational data is resampled randomly and fitted again. The standard deviation of a parameter is regarded as the 1σ error of the parameter. To estimate the contribution of systematic effects to the error budget, we modified the χ2 of the best solution by adding systematic errors in quadrature until the reduced χ2 reached ~1.0.
The period derived from the sinusoidal fit (P = 0.0976 ± 0.0042 d) is consistent with the period derived from photometry (P = 0.09980(25) d) resulting in a mass function of f(m) = 0.0093 ± 0.002 M⊙. The inclination of the orbit is well constrained by photometry (i = 83.56 ± 0.30°, see Sect. 4). Adopting the canonical mass of 0.47 M⊙ we find a mass ratio of q = 0.327 ± 0.033 by making use of the mass function.
 |
Fig. 1 Radial velocity plotted against orbital phase of PTF0724. In the bottom panel the residuals can be seen. |
3.2. Atmospheric parameters
Because of the poor signal-to-noise ratio (S/N ~ 10) of the individual spectra, we shifted and coadded the individual velocity-corrected spectra to improve the S/N to be able to derive reliable atmospheric parameters.
Effective temperature, surface gravity and helium abundance were determined by fitting synthetic spectra to the Balmer and helium lines of the coadded spectra. The synthetic spectra were calculated by using LTE model atmospheres with solar metallicity and metal line blanketing (Heber et al. 2000). The derived parameters are: Teff = 33 900 ± 350 K, log g = 5.74 ± 0.08, and log y = −2.02 ± 0.07.
The errors of the parameters were calculated with a bootstrapping approach.
 |
Fig. 2 Example fit to several Balmer lines of an individual spectrum, to determine the radial velocities. |
 |
Fig. 3 Position of PTF0724 (black triangle) in a (Teff, log g) diagram compared to the known sdB+dM systems in close binary systems with known periods (gray circles, Kupfer et al. 2015). Overplotted EHB evolutionary tracks by Han et al. (2002) using 0.50 M⊙ models (dash-dotted lines). In addition the zero-age horizontal branch (ZAEHB) as well as the helium main sequence (HeMS) are shown. |
In Fig. 3 the position of PTF0724 in a (Teff, log g) diagram is compared to the known sdB+dM systems in close binary systems with known periods (Kupfer et al. 2015). Its position in the graph indicates that the primary component in PTF0724 is a normal sdB close to core helium exhaustion. Similar systems lie in the same regime. There are two classes of multi-periodic pulsating stars known among the sdB stars, which show either g-modes (361 Hya stars) or p-modes (V1093 Her stars). It is worth mentioning that its atmospheric parameters place PTF0724 in a regime where the driving of g-mode pulsations is predicted to be largest (Charpinet et al. 2007).
4. Light curve analysis
The seven light curves derived from the observations in Table 2 were phased, normalized, and merged into one light curve (see Fig. 4). Its analysis proceeds as described in Drechsel et al. (2001); for details see also Schaffenroth et al. (2013).
The light curve analysis was performed by using the MORO code (MOdified ROche Program, see Drechsel 1995). The program is based on the Wilson-Devinney approach Wilson (1971), but uses a modified Roche model that takes the radiative pressure of the stars into account. The optimization of parameters, is achieved by the simplex algorithm.
 |
Fig. 4 Phased light curve of PTF0724. The solid line represents the best fitting model for q = 0.33. In the bottom panel the residuals can be seen. Some outlying data points, mainly before and after the primary eclipse, are visible. This was most likely caused by the changing air mass. As the exact coverage of the depth and form of the bottom of the primary eclipse is crucial for correct results, the data points around phase 1 were weighted higher, resulting in smaller residuals. |
One of the main problems with light curve analysis is the large number of free parameters. For a single light curve 17 parameters have to be adjusted but parameter correlations exist. However, some of the parameters could be constrained from the spectroscopic analysis or on theoretical grounds, e.g. limb and gravity darkening parameters (see Table 1). Too many free parameters tend to generate underdetermined solutions and there is no guarantee of uniqueness.
In particular the mass ratio, one of the most important solution parameters, is strongly correlated with other parameters (i.e., the Roche potentials Ω) and causes a degeneracy of solutions. Therefore, in a first step, the mass ratio was fixed, while the other parameters were adjusted. Thereafter the mass ratio was changed by a certain increment and the iterative process started again.
The effective temperature and the surface gravity of the primary component were derived from the spectroscopic analysis (see Sect. 3.2). Because of its early spectral type, the gravity darkening exponent can be fixed at g1 = 1, as one would expect for radiative outer envelopes (von Zeipel 1924). For the companion, we used g2 = 0.32 (Lucy 1967), as expected for convective envelopes. The linear limb darkening coefficient for the primary was interpolated from the table of Wade & Rucinski (1985) and fixed at x1 = 0.190. The radiation pressure parameter Drechsel (1995) of the secondary was set to zero because of the low temperature of the secondary star. That means that the effects of the radiation pressure exerted by this star are negligible. All trial runs with different sets of parameters resulted in negligible third light. Hence there is no evidence for a third body in the system, and l3 was set to zero. We constrain the mass ratio to the range 0.29 <q< 0.36, as indicated by the spectroscopic measurements. For each mass ratio a large grid of synthetic light curves was calculated to ensure that the final solution corresponds to the global minimum.
To estimate the quality of the light curve fit, the sum of the squared residuals of all points to the synthetic light curve is calculated. The solution with the smallest sum is best. We define 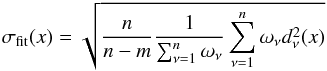 (1)as an indicator for the quality of the fit, where dν are the residuals, the difference between observational data and the calculated model; ων are weights that can be used to increasingly consider several data points, i.e., the bottom of the primary eclipse; m is the number of start parameters for the simplex algorithm; and n is the number of data points.
(1)as an indicator for the quality of the fit, where dν are the residuals, the difference between observational data and the calculated model; ων are weights that can be used to increasingly consider several data points, i.e., the bottom of the primary eclipse; m is the number of start parameters for the simplex algorithm; and n is the number of data points.
Model parameters of the light curve solution for q = 0.33.
Adopted stellar parameters for the components of PTF0724.
It was found that there is a solution for a mass ratio of q = 0.33 that reproduces the light curve best (see Table 1). The reflection effect dominates the shape of the light curve between the eclipses. No sign of ellipsoidal variations was found.
The solution requires an albedo for the companion that exceeds 1 (A2 = 1.8), which means the concept of pure reflection is inadequate and reprocessing of radiation in the atmosphere of the companion has to be taken into account, which is beyond the scope of this work. An albedo exceeding unity has been found for other HW Vir systems as well (Schaffenroth et al. 2013). No reasonable fits for values of A2 = 1 or less were found. Light curves at other wavelengths are required to better constrain the secondary’s albedo.
As the reduced χ2 for the solution is well above 1, the question arises if the errors in the photometric measurements are estimated accurately. If so, this could be a hint for unresolved pulsations superposed on the eclipse curve.
5. Summary
The star PTF1 J072456+125301 was found to be an eclipsing binary with an orbital period of 0.09980(25) d or 2 h 23.71 min showing a strong reflection effect typical for HW Vir Stars. We obtained time series with the Palomar P60 telescope and spectroscopic data with the P200 telescope and performed an analysis of the light curves and radialvelocity curves in order to pin down the system parameters. A quantitative spectral analysis of the co-added spectrum allowed us to determine the atmospheric parameters of the sdB. The effective temperature of Teff = 39 000 ± 350 K, log (g) = 5.74 ± 0.08, and a helium abundance of log NHe / H = −2.02 ± 0.07 are typical for sdB stars and place it on or near the EHB.
From the radial velocity curve we derive the mass ratio of 0.327 ± 0.033 by adopting the canonical sdB mass (0.47 M⊙) for the primary. The analysis of the light curve results reveal the mass, radius and temperature of the companion of Mcomp = 0.155 ± 0.020 M⊙, Rcomp = 0.165 ± 0.015 R⊙ and Teff = 3300 ± 300 K, indication that the companion is a late M dwarf.
Further observations of this interesting system should be aimed at gaining spectra with better quality. High-resolution spectra may reveal lines of the companion and would allow the mass ratio to be determined directly from the spectra and would check if there are any discrepancies with our light-curve-based solution.
Most important would be high-quality light curves (short cadence, high S/N), preferably in several wavebands, to search for short-period, multi-periodic light variations caused by pulsations. Their detection would make PTF0724 an ideal target for asteroseismolgy similar to the enigmatic NY Vir (Vučković et al. 2007, 2009), providing two independent tools of mass determination to be combined (Van Grootel et al. 2013).
Online material
Appendix A: Additional tables
Radial velocities with errors of PTF0724.
Beginning and end-time of the photometric observations.
The Starlink Software Group homepage can be found at http://starlink.jach.hawaii.edu/starlink
Acknowledgments
Based on observations collected at the Palomar Observatory with the 200-inch Hale Telescope, operated by the California institute of Technology, its divisions Caltech Optical Observations, the Jet Propulsion Laboratory (operated for NASA) and Cornell University. Based on observations of the Palomar Transient Factory. The Palomar Transient Factory is a scientific collaboration between the California Institute of Technology, Columbia University, Las Cumbres Observatory, the Lawrence Berkely National Laboratory, the National Energy Research Scientific Computing Center, the University of Oxford, and the Weizmann Institute of Science. T. Kupfer acknowledges support by the Netherlands Research School of Astronomy (NOVA). V. Schaffenroth is supported by the Deutsches Zentrum für Luft- und Raumfahrt (grant 50 OR 1110). This research has made use of ISIS functions provided by ECAP/Remeis Obervatory.
References
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, T. M., Ferguson, H. C., Davidsen, A. F., & Dorman, B. 1997, ApJ, 482, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Charpinet, S., Fontaine, G., Brassard, P., et al. 2007, Commun. Asteroseismol., 150, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Cenko, S. B., Fox, D. B., Moon, D.-S., et al. 2006, PASP, 118, 1396 [NASA ADS] [CrossRef] [Google Scholar]
- Copperwheat, C. M., Morales-Rueda, L., Marsh, T. R., Maxted, P. F. L., & Heber, U. 2011, MNRAS, 415, 1381 [NASA ADS] [CrossRef] [Google Scholar]
- Dorman, B., Rood, R. T., & O’Connell, R. W. 1993, ApJ, 419, 596 [CrossRef] [Google Scholar]
- Drechsel, H., Haas, S., Lorenz, R., & Gayler, S. 1995, A&A, 294, 723 [NASA ADS] [Google Scholar]
- Drechsel, H., Heber, U., Napiwotzki, R., et al. 2001, A&A, 379, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferguson, D. H., Green, R. F., & Liebert, J. 1984, ApJ, 287, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Ferraro, F., Paltrinieri, B., Fusi Pecci, F., et al. 1997, ApJ, 184, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Fontaine, G., Brassard, P., Charpinet, S., et al. 2012, A&A, 539, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Han, Z., Podsiadlowski, Ph., Maxted, P. F. L., Marsh, T. R., & Ivanova, N. 2002, MNRAS, 336, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., Podsiadlowski, Ph., Maxted, P. F. L., & Marsh, T. R. 2003, MNRAS, 341, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Heber, U. 2009, ARA&A, 47, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Heber, U., Reid, I. N., & Werner, K. 2000, A&A, 363, 198 [NASA ADS] [Google Scholar]
- Hirsch, H. 2009, Ph.D Thesis, Friedrich Alexander Universität Erlangen Nürnberg [Google Scholar]
- Horne, K. 1986, PASP, 98, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kilkenny, D., Hilditch, R. W., & Penfold, J. E. 1978, MNRAS, 183, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Kupfer, T., Geier, S., Heber, U., et al. 2015, A&A, 576, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Law, N. M., 2009, PASP, 121, 1395 [NASA ADS] [CrossRef] [Google Scholar]
- Levenberg, K. 1944, Quarterly of Applied Mathematics 2, 164 [Google Scholar]
- Levitan, D., Fulton, B. J., Groot, P. J., et al. 2011, ApJ, 739, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 1967, Z. Astrophys., 65, 89 [Google Scholar]
- Marsh, T. R. 1989, PASP, 101, 1032 [NASA ADS] [CrossRef] [Google Scholar]
- Maxted, P. F. L., Heber, U., Marsh, T. R., & North, R. C. 2001, MNRAS, 326, 1391 [NASA ADS] [CrossRef] [Google Scholar]
- Menzies, J. W., & Marang, F. 1986, IAU Symp., 118, 305 [NASA ADS] [Google Scholar]
- Naylor, T. 1998, MNRAS, 296, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Ofek, E. O., Frail, D. A., Breslauer, B., et al. 2011, ApJ, 740, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Oke, J. B., & Gunn, J. E. 1982, PASP, 94, 586 [NASA ADS] [CrossRef] [Google Scholar]
- Schaffenroth, V., Geier, S., Drechsel, H., et al. 2013, A&A, 553, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaffenroth, V., Geier, S., Heber, U., et al. 2014a, A&A, 564, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaffenroth, V., Geier, S., Barbu-Barna, I., et al. 2014b, 6th Meeting on Hot Subdwarf Stars and Related Objects, 481, 253 [Google Scholar]
- Stark, M. A., & Wade, R. A. 2003, AJ, 126, 1455 [NASA ADS] [CrossRef] [Google Scholar]
- Van Grootel, V., Charpinet, S., Brassard, P., Fontaine, G., & Green, E. M. 2013, A&A, 553, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Grootel, V., Charpinet, S., Fontaine, G., Brassard, P., & Green, E. 2014, ASP Conf. Ser., 481, 229 [NASA ADS] [Google Scholar]
- von Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Vos, J., Østensen, R. H., Nemeth, P., et al. 2013, A&A, 559, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vučković, M., Aerts, C., Östensen, R., et al. 2007, A&A, 471, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vučković, M., Østensen, R. H., Aerts, C., et al. 2009, A&A, 505, 239 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wade, R. A., & Rucinski, S. M. 1985, A&A, 60, 471 [Google Scholar]
- Wilson, R. E., & Devinney, E. J. 1971, ApJ, 166, 605 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Radial velocity plotted against orbital phase of PTF0724. In the bottom panel the residuals can be seen. |
| In the text | |
 |
Fig. 2 Example fit to several Balmer lines of an individual spectrum, to determine the radial velocities. |
| In the text | |
 |
Fig. 3 Position of PTF0724 (black triangle) in a (Teff, log g) diagram compared to the known sdB+dM systems in close binary systems with known periods (gray circles, Kupfer et al. 2015). Overplotted EHB evolutionary tracks by Han et al. (2002) using 0.50 M⊙ models (dash-dotted lines). In addition the zero-age horizontal branch (ZAEHB) as well as the helium main sequence (HeMS) are shown. |
| In the text | |
 |
Fig. 4 Phased light curve of PTF0724. The solid line represents the best fitting model for q = 0.33. In the bottom panel the residuals can be seen. Some outlying data points, mainly before and after the primary eclipse, are visible. This was most likely caused by the changing air mass. As the exact coverage of the depth and form of the bottom of the primary eclipse is crucial for correct results, the data points around phase 1 were weighted higher, resulting in smaller residuals. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.