| Issue |
A&A
Volume 580, August 2015
|
|
|---|---|---|
| Article Number | A41 | |
| Number of page(s) | 13 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201425115 | |
| Published online | 24 July 2015 | |
How are Forbush decreases related to interplanetary magnetic field enhancements?⋆
1 Indian Institute of Science Education and Research, Dr. Homi Bhabha Road, Pashan, 411 021 Pune, India
e-mail: gupta@grapes.tifr.res.in
2 The GRAPES–3 Experiment, Cosmic Ray Laboratory, Raj Bhavan, 643 001 Ooty, India
3 Tata Institute of Fundamental Research, Homi Bhabha Road, Mumbai, Maharashtra, India
4 Graduate School of Science, Osaka City University, Osaka 558-8585, Japan
5 College of Engineering, Chubu University, Kasugai, Aichi 487-8501, Japan
Received: 6 October 2014
Accepted: 24 April 2015
Aims. A Forbush decrease (FD) is a transient decrease followed by a gradual recovery in the observed galactic cosmic ray intensity. We seek to understand the relationship between the FDs and near-Earth interplanetary magnetic field (IMF) enhancements associated with solar coronal mass ejections (CMEs).
Methods. We used muon data at cutoff rigidities ranging from 14 to 24 GV from the GRAPES-3 tracking muon telescope to identify FD events. We selected those FD events that have a reasonably clean profile, and magnitude >0.25%. We used IMF data from ACE/WIND spacecrafts. We looked for correlations between the FD profile and that of the one-hour averaged IMF. We wanted to find out whether if the diffusion of high-energy protons into the large scale magnetic field is the cause of the lag observed between the FD and the IMF.
Results. The enhancement of the IMF associated with FDs occurs mainly in the shock-sheath region, and the turbulence level in the magnetic field is also enhanced in this region. The observed FD profiles look remarkably similar to the IMF enhancement profiles. The FDs typically lag behind the IMF enhancement by a few hours. The lag corresponds to the time taken by high-energy protons to diffuse into the magnetic field enhancement via cross-field diffusion.
Conclusions. Our findings show that high-rigidity FDs associated with CMEs are caused primarily by the cumulative diffusion of protons across the magnetic field enhancement in the turbulent sheath region between the shock and the CME.
Key words: Sun: coronal mass ejections / solar wind / Sun: flares / cosmic rays
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Forbush decreases (FDs), are short-term decreases in the intensity of galactic cosmic rays that were first observed by Forbush (1937, 1938). It was the work of Simpson using neutron monitors (Simpson 1954) that showed that the origin of the FDs was in the interplanetary (IP) medium. Solar transients such as the coronal mass ejections (CMEs) cause enhancements in the interplanetary magnetic field (IMF). The near-Earth manifestation of a CME from the Sun typically has two major components: i) the interplanetary counterpart of CME (commonly called an ICME); and ii) the shock, which is driven ahead of it. Both the shock and the ICME cause significant enhancement in the IMF. Interplanetary CMEs, which possess some well defined criteria such as reduction in plasma temperature and smooth rotation of magnetic field are called magnetic clouds (e.g., Burlaga et al. 1981; Bothmer & Schwenn 1998).
Correlations between the parameters characterizing FDs and solar wind parameters have been a subject of considerable study. Belov et al. (2001) and Kane (2010) maintain that there is a reasonable correlation between the FD magnitude and the product of maximum magnetic field and maximum solar wind velocity. Dumbović et al. (2012) also found reasonable correlation between the FD magnitude | FD |, and duration with the solar wind parameters such as the amplitude of magnetic field enhancement B, amplitude of the magnetic field fluctuations δB, maximum solar wind speed associated with the disturbance v, and duration of the disturbance tB. We note that the FD magnitude also depends strongly on other solar wind parameters like the velocity of the CME, turbulence level in the magnetic field, size of the CME, etc. The contributions of these parameters are explained in the CME-only cumulative diffusion model described in Arunbabu et al. (2013).
Arunbabu et al. (2013) described the CME-only cumulative diffusion model for FDs, where the cumulative effects of diffusion of cosmic ray protons through the turbulent sheath region as the CME propagated from the Sun to the Earth was invoked to explain the FD magnitude. However, the diffusion was envisaged to occur across an idealized thin boundary. In this paper we relax the ideal, thin boundary assumption and examine the detailed relationship between the FD profile and the IMF compression.
2. Data analysis
2.1. The GRAPES-3 experiment
The GRAPES-3 experiment is located at Ooty (11.4°N latitude, 76.7°E longitude, and 2200 m altitude) in India. It contains two major components, first an air shower array of 400 scintillation detectors (each 1 m2), with a distance of 8 m between adjacent detectors deployed in a hexagonal geometry (Gupta et al. 2005; Mohanty et al. 2009; Mohanty et al. 2012). The GRAPES-3 array is designed to measure the energy spectrum and composition of the primary cosmic rays in the energy region from 10 TeV to 100 PeV (Gupta et al. 2009; Tanaka et al. 2012). The second component of the GRAPES-3 experiment, a large area tracking muon telescope is a unique instrument used to search for high-energy protons emitted during the active phase of a solar flare or a CME. The muon telescope provides a high statistics, directional measurement of the muon flux. The GRAPES-3 muon telescope covers an area of 560 m2, consisting of a total of 16 modules, each 35 m2 in area. The energy threshold of the telescope is sec (θ) GeV for the muons arriving along a direction with zenith angle θ. The observed muon rate of ~3000 s-1 per module yields a total muon rate of ~3 × 106 min-1 for the entire telescope (Hayashi et al. 2005; Nonaka et al. 2006). This high rate permits even a small change of ≲0.1% in the muon flux to be accurately measured over a time scale of ~5 min, after appropriate corrections are applied for the time dependent variation in the atmospheric pressure (Mohanty et al. 2013).
We identified the FDs using the data from the GRAPES-3 muon telescope. By using the tracking capability of the muon telescope the direction of detected muons are binned into nine different solid angle directions, named NW (northwest), N (north), NE (northeast), W (west), V (vertical), E (east), SW (southwest), S (south), and SE (southeast). The cutoff rigidity due to the geomagnetic field at Ooty is 17 GV along the vertical direction and varies from 14 to 42 GV across the 2.2 sr. field of view of the muon telescope. Details of the muon telescope are given in Hayashi et al. (2005), Nonaka et al. (2006), and Subramanian et al. (2009).
2.2. Broad shortlisting criteria
The GRAPES-3 muon telescope has observed a large number of FD events exhibiting a variety of characteristics. We now describe the broad criteria that we use to shortlist events used for analysis in this paper. In addition to the criteria described here, we will have occasion to apply further criteria, which will be described in subsequent sections. We have examined all FD events observed by the GRAPES-3 muon telescope during the years 2001−2004. We shortlist events that have a clean FD profile and FD magnitude >0.25%, and are also associated with an enhancement in the near-Earth IMF. Here, the term “clean profile” is used to refer to an FD event characterized by a sudden decrease and a gradual recovery in the cosmic ray flux. Although 0.25% might seem like a small number, according to Arunbabu et al. (2013) these are fairly significant events in the GRAPES-3 data, given its high sensitivity. This yields a sample of 65 events, which is used in the analysis reported in Sect. 3. We note that the event of 29 September 2001 is not included in this list since it was associated with many IMF enhancements, which could be due to multiple Halo and partial halo CMEs. Similarly, the event of 29 October 2003 is not included (even though it was the biggest FD event observed in the solar cycle 23) since the near-Earth magnetic field data is incomplete for this event.
We used GRAPES-3 data summed over a time interval of one hour for each direction. This improves the signal-to-noise ratio, but the diurnal variation in the muon flux is still present. We used a low-pass filter to remove oscillations having frequency >1 d-1. This filter was explained in Subramanian et al. (2009). The measured variation of the muon flux in percent for the 24 November 2001 event is shown in Fig. 1, where the dotted black lines are the unfiltered data and the solid black lines are the filtered data after using the low-pass filter to remove the frequencies >1 d-1. Although the filtering may change the amplitude of the decrease and possibly shift the onset time for the FD by a few hours in some cases, it is often difficult to determine whether these differences are artifacts of filtering or if the unfiltered data showed different amplitude because a diurnal oscillation happened to have the right phase so as to enhance or suppress the amplitude of the FD. Some fluctuations in the muon flux could be due to FD and associated events, but it is unlikely that they will be periodic in nature and are not likely to be affected by the filter.
 |
Fig. 1 FD event on 24 Nov. 2001. Percent deviation in the muon flux for different directions are shown in separate panels. The solid line shows percent deviation for filtered data and the dotted line shows the same for unfiltered data. |
The FDs that we study are associated with near-Earth CME counterparts, which contribute to significant increases in the IMFs. We intend to investigate the relation between these IMF enhancements and FDs. We used the IMF data observed by the ACE and WIND spacecraft available from the OMNI database. We used hourly resolution data on magnetic field Btotal, Bx, By, Bz in the geocentric solar ecliptic (GSE) coordinate system: Btotal is the magnitude of the magnetic field, Bx is the magnetic field component along the Sun-Earth line in the ecliptic plane pointing towards the Sun, Bz the component parallel to the ecliptic north pole, and By the component in the ecliptic plane pointing towards dusk. For a consistent data analysis we applied the same low-pass filter to the magnetic field data as we did to the muon flux, which removes any oscillations having frequency >1 d-1. Since FD events are associated with enhancements in the IMF, we use the quantity 100− | B | and calculate the average value and the percent deviation of this quantity over the same data interval as the FD. This effectively flips the magnetic field increase and makes it appear as a decrease, enabling easy comparison with the FD profile. Figure 2 shows the FD event on 24 November 2001, A.1 shows the FD event on 11 April 2001, and A.2 shows the FD event on 23 May 2002, together with the IMF data processed in this manner.
 |
Fig. 2 FD event of 24 Nov. 2001 and magnetic field for 9 directions in GRAPES-3 muon telescope. Black solid line is percentage deviation of cosmic ray intensity in each direction. The red-dotted, blue-dash-dot-dotted, green-dash-dotted and orange-dash lines are percentage deviation of IMFs Btotal, Bz, By and Bx respectively, that are scaled down by a factor of 10 to fit in the frame. |
3. Correlation of FD magnitude with peak IMF
Before studying the detailed relationship between the IMF and FD profiles, we examine the relationship between the peak IMF and the FD magnitudes. For this study we considered all 65 FD events shortlisted using the criteria explained in Sect. 2.2. The FD magnitude for a given direction is calculated as the difference between the pre-event intensity of the cosmic rays and the intensity at the minimum of the decrease. We examine the corresponding IMF during these events. We denote By and Bz “perpendicular” fields, because they are tangential to a flux rope CME approaching the Earth. They are perpendicular to a typical cosmic ray proton that seeks to enter the CME radially; it will therefore have to cross these perpendicular fields. We study the relation between the FD magnitude and the peak of the total magnetic field 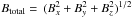 and the peak of the net perpendicular magnetic field
and the peak of the net perpendicular magnetic field 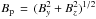 .
.
The correlation coefficients of the peak Btotal with the FD magnitude for different directions are listed in Table 1 and shown in Fig. 3. The correlation coefficients of the peak Bp with FD magnitude are listed in Table 1 and shown in Fig. 4. We find that the correlation coefficient between peak Bp and peak Btotal with the FD magnitude ranges from 63% to 72%. We note that the correlations in Figs. 3 and 4 are fairly similar because the longitudinal magnetic field (Bx) is fairly small for most events. We will have further occasion to discuss this in Sect. 5. We also carried out the same study using Tibet neutron monitor data; this yields a correlation coefficient of 60.0% and 61.9% respectively for Btotal and Bp. The error on the correlation coefficients are calculated using Eq. (1) below, and are listed in Table 1: 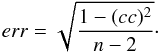 (1)Here cc is the correlation coefficient, n−2 gives the degree of freedom, and n is the number of points considered for the correlation.
(1)Here cc is the correlation coefficient, n−2 gives the degree of freedom, and n is the number of points considered for the correlation.
From the CME-only cumulative diffusion model described in Arunbabu et al. (2013) we know that the FD magnitude depends on various parameters associated with CME, such as velocity of CME, turbulence level in the magnetic field, and the size of the CME. It is thus not surprising that the FD magnitude correlates only moderately with the peak value of the IMF.
 |
Fig. 3 Correlation of maximum total magnetic field in the magnetic field enhancement to FD magnitude observed in different directions using GRAPES-3. |
 |
Fig. 4 Correlation of maximum perpendicular magnetic field in the magnetic field enhancement to FD magnitude observed in different directions using GRAPES-3. |
 |
Fig. 5 FD event on 24 November 2001. The black solid line denotes percentage deviation of the cosmic ray intensity, black dotted line percentage deviation of total magnetic field | 100−B | as explained in Sect. 2 which is scaled down to fit the frame. The vertical brown-dotted, magenta-dash-dotted, blue-dash-dot-dotted, green-long-dashed, and black-dashed lines denote the timings corresponding to the FD onset, shock arrival, magnetic cloud start, magnetic cloud end, and FD minimum, respectively. The solid red vertical line corresponds to the maximum of the magnetic field compression. |
Correlation of the FD magnitude with the maximum total and perpendicular IMF.
4. IMF compression: shock-sheath or ICME?
As mentioned earlier, we considered FD events associated with the magnetic field enhancements that are due to the shock propagating ahead of the ICME. An example of this is shown in Figs. 5, A.3, and A.4 where the nine different panels show the cosmic ray flux (FD profile) of the nine directions of the GRAPES-3 muon telescope for the FD observed on 24 November 2001, 11 April 2001, and 23 May 2002, respectively. It is clear that the magnetic field compression responsible for the FD is in the sheath region, i.e., the region between the shock and magnetic cloud.
The CME-only model described in Arunbabu et al. (2013) deals with the diffusion of cosmic rays through the turbulent magnetic field in the sheath region. The cross-field diffusion coefficient depends on the rigidity of the proton and the turbulence level in the magnetic field (e.g., Candia & Roulet 2004). The turbulence level in the magnetic field is an important parameter in this context. We have calculated the turbulence level using one-minute averaged data from the ACE/WIND spacecraft available from the OMNI data base. To calculate the turbulence level σ we use a one-hour running average of the magnetic field (B0) and the fluctuation of the IMF around this average (Btur = B−B0). We define the quantity σ as 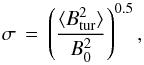 (2)where
(2)where 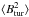 denotes the average of
denotes the average of 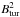 over the one-hour window. Figure 6 shows a representative event. The top panel shows the one-minute average magnetic field for 21−30 November 2001. The bottom panel in this figure shows the turbulence level σ calculated for this event. We note that the magnetic field compression responsible for the FD occurs in the shock sheath region, i.e., the region between the shock and the magnetic cloud. The turbulence level enhancement also occurs in this region.
over the one-hour window. Figure 6 shows a representative event. The top panel shows the one-minute average magnetic field for 21−30 November 2001. The bottom panel in this figure shows the turbulence level σ calculated for this event. We note that the magnetic field compression responsible for the FD occurs in the shock sheath region, i.e., the region between the shock and the magnetic cloud. The turbulence level enhancement also occurs in this region.
For events selected using the criteria described in Sect. 2, we narrow down the ones that have a well-defined shock and associated magnetic cloud. Such events allow us to clearly distinguish the shock, sheath, and CME regions associated with the magnetic field compression. We studied ten such FD events, which are listed in Table 2.The timings of the shock, maximum of the magnetic field compression, magnetic cloud start and end timings, along with the FD onset times for different directions are given in Table 2. The peak of the magnetic field enhancement in the filtered data generally occurs before the start of the magnetic cloud or at the start of the magnetic cloud, whereas in the unfiltered data the enhancement lies in the sheath region. We note that the filtering procedure using the low-pass filter shifts the maximum by a small amount (−5 to 10 h).
Shock arrival time, time of maximum magnetic field enhancement, magnetic cloud start and end timings and FD onset timings for different directions for FD events that have a well-defined shock and magnetic clouds associated with them.
 |
Fig. 6 Magnetic field compression associated with the FD event on 24 November 2001. In the first panel the continuous line denotes Btotal and the dotted line denotes Bp. The continuous line in the second panel shows the turbulence level for Btotal. In both panels the vertical solid, dotted, and dashed lines corresponds to shock arrival time, magnetic cloud start time, magnetic cloud end time, respectively. |
It is clear from Figs. 5, A.3, A.4, 6, and Table 2that the peak of the magnetic field compression responsible for the FD lies in the sheath region, and the turbulence level is also enhanced in this region. This is in broad agreement with Richardson & Cane (2011).
5. How similar are the FD and the IMF profiles?
One of the near-Earth effects of a CME is the compression of (and consequent increase in) the IMF. The IMF measured by spacecrafts such as WIND and ACE can detect these magnetic field compressions. We investigate the relation of these magnetic field compressions to the FD profile. We work with the hourly resolution IMF data from the ACE and WIND spacecrafts obtained from the OMNI database. Applying the low-pass filter described in Sect. 2 to this data yields a combined magnetic field compression comprising the shock and ICME/magnetic cloud. A visual comparison of the FD profile with the magnetic field compression often reveals remarkable similarities. To quantify the similarity between these two profiles, we studied the cross correlation of the cosmic ray intensity profile with the IMF profile. In order to do this, we shift the magnetic field profile (with respect to the FD profile) by amounts ranging from −36 h to 12 h. We identify the peak correlation value and the shift corresponding to this value is considered to be the time lag between the IMF and the cosmic ray FD profile. Most of the FD events exhibit correlations ≥60% with at least one of the four IMF components (Btotal, Bx, By, Bz). Examples of the correlation between the FD profile and Btotal for the events of 24 November 2001, 11 April 2001, and 23 May 2002 are shown in Figs. 7, A.5, and A.6, respectively. The top panel in these figures shows the percentage deviation of the cosmic ray flux and the Btotal. The percentage deviation of Btotal is scaled to fit in the frame. The middle panel shows the same percentage deviations, but the magnetic field is shifted by the peak correlation lag and the bottom panel shows the correlation coefficients corresponding to different lags. The correlation lag means that the IMF profile precedes the FD profile by 21 h for the 24 November 2001 event, by 19 h for the 11 April 2001 event and 13 h for the 23 May 2003 event. In particular, Table 3 gives the maximum cross correlation values obtained for different FD profile of different directions of GRAPES-3 to the total magnetic field compression and different components of magnetic field for the 24 November 2001 event. The same quantities for Tibet neutron monitor data are also shown in last row of this table. In further discussion we consider only those events showing a cross correlation ≥70% for lags between −36 to 12 h. The events thus shortlisted are presented in Table B.1. From these, we will further narrow down events for which the FD profile exhibits a high correlation with the perpendicular component of the IMF.
Correlation of FD profile in different direction observed in GRAPES-3 with magnetic fields for the 24 November 2001 event.
 |
Fig. 7 Cross correlation of the cosmic ray flux with Btotal. The top panel shows the percentage deviation of cosmic ray flux using solid black lines and the magnetic field using dotted black lines (scaled to fit in the frame). The middle panel shows the same with magnetic field shifted to the right corresponding to the time lag and the bottom panel shows the correlation coefficient for different lags. |
Cross-field diffusion into the ICME through the sheath
The time lag between the cosmic ray flux and the IMF occurs because the high-energy protons do not respond to magnetic field compressions immediately; they are subjected to the classical magnetic mirror effect arising from the gradient in the longitudinal magnetic field and to turbulent cross-field (also referred as perpendicular) diffusion (e.g., Kubo & Shimazu 2010). Here, we concentrate only on the cross-field diffusion of the high-energy protons through the turbulent sheath region between the shock and the CME. As discussed earlier, we have identified the IMF compression to be comprised mainly of this sheath region; we therefore use the observed values of the mean field and turbulent fluctuations in the sheath region to calculate representative diffusion timescales for cosmic rays. The time delay between the IMF compression and the FD profile (i.e., the correlation lag) can be interpreted as the time taken by the cosmic rays to diffuse into the magnetic compression. Our approach may be contrasted with that of Kubo & Shimazu (2010), who use a computational approach to investigate cosmic ray dynamics (thus incorporating both the mirror effect and cross-field diffusion) in a magnetic field configuration that comprises an idealized flux rope CME. They do not consider the sheath region, and neither do they use observations to guide their choice of magnetic field turbulence levels.
To calculate the cross-field diffusion timescale, we proceed as follows: considering the flux rope geometry of a near-Earth CME, the magnetic field along the Sun-Earth (BX) represents the longitudinal magnetic field. The fields By and Bz represent the perpendicular magnetic fields encountered by the diffusing protons. In our discussion we consider only cross-field diffusion; we therefore choose events that exhibit good correlation with the By and Bz magnetic field compressions and poor correlation with compressions in Bx. The events shortlisted using these criteria are listed in Table 4.
Events for which the FD profile correlates well only with the perpendicular component of the IMF enhancement.
6. Cross-field diffusion coefficient (D⊥)
The cross-field diffusion coefficient D⊥ governs the diffusion of the ambient high-energy protons into the CME across the magnetic fields that enclose it. The topic of cross-field diffusion of charged particles across magnetic field lines in the presence of turbulence is the subject of considerable research. Analytical treatments include classical scattering theory (e.g., Giacalone & Jokipii 1999, and references therein) and non-linear guiding center theory (Matthaeus et al. 2003; Shalchi 2010) for cross-field diffusion. Numerical treatments of cross-field diffusion of charged particle in turbulent magnetic fields include Giacalone & Jokipii (1999), Casse et al. (2002), Candia & Roulet (2004), Tautz & Shalchi (2011), and Potgieter et al. (2014). We seek a concrete prescription for D⊥ that can incorporate observationally determined quantities.
D⊥ : Candia & Roulet (2004)
The D⊥ prescription we use is given by Candia & Roulet (2004), obtained from extensive Monte Carlo simulations of cosmic rays propagating through tangled magnetic fields. Their results reproduce the standard results of Giacalone & Jokipii (1999) and Casse, Lemoine & Pelletier (2002), and also extend the regime of validity to include strong turbulence and high rigidities. The extent of cross-field diffusion of protons depends on the proton rigidity, which indicates how tightly the proton is bound to the magnetic field, and the level of magnetic field turbulence, which can contribute to field line transport.
Candia & Roulet (2004) give the following fit for the “parallel” diffusion coefficient D∥ (which is due to scattering of the particles back and forth along the mean field, as the field is subject to random turbulent fluctuations), 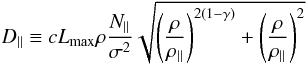 (3)where c is the speed of light and the quantities N∥, γ, and ρ∥ are constants specific to different kinds of turbulence whose values are listed in Table 1 of Candia & Roulet (2004). The parameter Lmax is the maximum length scale of turbulence; in our case we considered it as the size of the CME near the Earth. The quantity ρ is related to the rigidity of the proton Rg as
(3)where c is the speed of light and the quantities N∥, γ, and ρ∥ are constants specific to different kinds of turbulence whose values are listed in Table 1 of Candia & Roulet (2004). The parameter Lmax is the maximum length scale of turbulence; in our case we considered it as the size of the CME near the Earth. The quantity ρ is related to the rigidity of the proton Rg as 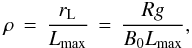 (4)where rL is the Larmor radius and B0 is the magnetic field. The quantity σ2 is the magnetic turbulence level, which is defined as in Eq. (2).
(4)where rL is the Larmor radius and B0 is the magnetic field. The quantity σ2 is the magnetic turbulence level, which is defined as in Eq. (2).
The cross-field diffusion coefficient (D⊥) is related to the parallel one (D∥ ) by, 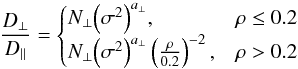 (5)The quantities N⊥ and a⊥ are constants specific to different kinds of turbulent spectra, and are given in Table 1 of Candia & Roulet (2004). We note that the exponent characterizing the IMF turbulence may vary through the magnetic field compression associated with FD (Alania & Wawrzynczak 2012). Although the treatment of Candia & Roulet (2004), which we use, cannot accommodate arbitrary turbulent spectrum indices, it can address the Kolmogorov (γ = 5/3), Kraichnan (γ = 3/2), and Bykov-Toptygin (γ = 2) spectra. We therefore quote results for all three turbulence spectra.
(5)The quantities N⊥ and a⊥ are constants specific to different kinds of turbulent spectra, and are given in Table 1 of Candia & Roulet (2004). We note that the exponent characterizing the IMF turbulence may vary through the magnetic field compression associated with FD (Alania & Wawrzynczak 2012). Although the treatment of Candia & Roulet (2004), which we use, cannot accommodate arbitrary turbulent spectrum indices, it can address the Kolmogorov (γ = 5/3), Kraichnan (γ = 3/2), and Bykov-Toptygin (γ = 2) spectra. We therefore quote results for all three turbulence spectra.
7. The IP B field compression-FD lag: how many diffusion lengths?
We have shown that the FD profile is often very similar to that of the IMF compression, and lags behind it by a few hours. This observed lag is poorly correlated with the FD magnitude and the CME speeds (both near the Sun and near the Earth). We interpret the observed time lag between the IMF and the FD profiles as the time taken by the protons to diffuse through the magnetic field compression via cross-field diffusion. The time taken for a single diffusion random walk of a high-energy proton into the magnetic structure of CME is given by 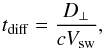 (6)where c is the speed of light (which is the typical propagation speed for the highly relativistic galactic cosmic rays we are concerned with) and Vsw is the solar wind velocity upstream of the CME.
(6)where c is the speed of light (which is the typical propagation speed for the highly relativistic galactic cosmic rays we are concerned with) and Vsw is the solar wind velocity upstream of the CME.
When using the D⊥ from Candia & Roulet (2004), we use two different methods for computing the turbulence level σ. In the first one, we calculate σ as a function of time using the one-minute averaged IMF data, as described in Eq. (2). In the second, we assume a constant value of 15% for σ, which is typically expected to be the maximum level of turbulence in quiet solar wind (Spangler 2002). We used both these methods to calculate tdiff for Kolmogorov, Kraichnan, and Bykov-Toptygin turbulent spectra. Using these values of tdiff, we estimated the number of diffusion lengths required to account for the observed time lag between the FD profile and the IMF profile using 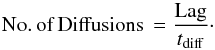 (7)The results for the number of diffusion times needed to account for the observed lag between the IMF enhancement and the FD profile are shown in Table B.2. These numbers are calculated using the peak value of the IMF profile. It is evident that the observed lags can be accounted for by a few tens to a few hundred diffusion times. There are two exceptional events on 2001 December 14 and 2003 December 27, where the number of diffusions are ~1000 using the time-varying σ prescription. There are three events in this list that have no correlation lag between the IMF profile and FD profile. The FD on 2001 May 27 correlates well with Btotal, the FD on 2002 December 22 correlates well with By, and the FD on 2003 May 04 correlates with the Bz with no correlation lag.
(7)The results for the number of diffusion times needed to account for the observed lag between the IMF enhancement and the FD profile are shown in Table B.2. These numbers are calculated using the peak value of the IMF profile. It is evident that the observed lags can be accounted for by a few tens to a few hundred diffusion times. There are two exceptional events on 2001 December 14 and 2003 December 27, where the number of diffusions are ~1000 using the time-varying σ prescription. There are three events in this list that have no correlation lag between the IMF profile and FD profile. The FD on 2001 May 27 correlates well with Btotal, the FD on 2002 December 22 correlates well with By, and the FD on 2003 May 04 correlates with the Bz with no correlation lag.
8. Summary
We studied all FD events observed by the GRAPES-3 muon telescope during the years 2001–2004 satisfying the broad criteria listed in Sect. 2.2. For a sample of especially well-observed events, we find that the magnetic field compression responsible for the FD as well as the turbulence level gets enhanced in the shock-sheath region. For these events, details regarding shock timing, magnetic cloud start and end timings along with the FD onset time for different directions are given in Table 2.
We find that the FD profile looks remarkably similar to that of the corresponding IMF compression and lags behind it by few hours (Table B.1). Since we want to focus on cross-field diffusion, we selected the FD events whose profiles correlate well with the enhancements in the perpendicular magnetic fields (By, Bz) and not with the radial magnetic field (Bx); these events are listed in Table 4. We have calculated the number of diffusions using Eq. (7) for 14.3 GV and 24.0 GV protons. The number of diffusions corresponding to the observed lag for the selected events are listed in Table B.2. For most events we find that the observed time lag corresponds to a few tens to a few hundred diffusions.
9. Conclusion
The results of Arunbabu et al. (2013) show that FDs are due to cumulative diffusion of galactic cosmic ray protons into the CME as it propagates from the Sun to the Earth. However, the precise nature of the diffusive barrier was left unspecified, and the diffusion was assumed to occur across an idealized thin boundary that presumably had to do with the turbulent sheath region. The results from this work clearly show that the magnetic field enhancement responsible for the FD comprises the sheath region. The FD profile looks like a lagged (and inverted) copy of the magnetic field enhancement (Table 1). The FD lags behind the magnetic field enhancement by a few hours (Tables B.1 and 4). We have quantitatively shown that the time lag between the FD and the magnetic field enhancement can be accounted for by cross-field diffusion through the turbulent sheath region (Table B.2). This work establishes i) the importance of the turbulent sheath region between the shock and ICME; we show that the magnetic field enhancement responsible for the FD comprises the shock-sheath, and the magnetic turbulence level is also enhanced in this region (Sect. 4) and ii) the viability of cross-field diffusion through the turbulent CME sheath as the primary mechanism for FDs (Sect. 7).
Online material
Appendix A: Additional figures
 |
Fig. A.1 FD event of 11 April 2001 and magnetic field for nine directions in GRAPES-3 muon telescope. The linestyles are the same as used in Fig. 2. |
 |
Fig. A.2 FD event of 23 May 2002 and magnetic field for nine directions in GRAPES-3 muon telescope. The linestyles are the same as used in Fig. 2. |
 |
Fig. A.5 Cross correlation of the cosmic ray flux with Btotal. The top panel shows the percentage deviation of cosmic ray flux using solid black lines and the magnetic field using dotted black lines (scaled to fit in the frame). The middle panel shows the same with magnetic field shifted to the right corresponding to the time lag and the bottom panel shows the correlation coefficient for different lags. |
 |
Fig. A.6 Cross correlation of the cosmic ray flux with Btotal. The top panel shows the percentage deviation of cosmic ray flux using solid black lines and the magnetic field using dotted black lines (scaled to fit in the frame). The middle panel shows the same with magnetic field shifted to the right corresponding to the time lag and the bottom panel shows the correlation coefficient for different lags. |
Appendix B: Additional Tables
FD events for which the correlation coefficient between the profiles of the FD and the IMF enhancement ≥70%.
Acknowledgments
K.P. Arunbabu acknowledges support from a Ph.D. studentship at IISER Pune. P. Subramanian acknowledges partial support via the CAWSES-II program administered by the Indian Space Research Organization and via a grant from the Asian Office of Aerospace Research and Development, Tokyo. We thank D. B. Arjunan, A. Jain, the late S. Karthikeyan, K. Manjunath, S. Murugapandian, S. D. Morris, B. Rajesh, B. S. Rao, C. Ravindran, and R. Sureshkumar for their help in the testing, installation, and operation of the proportional counters and the associated electronics and during data acquisition. We thank G. P. Francis, I. M. Haroon, V. Jeyakumar, and K. Ramadass for their help in the fabrication, assembly, and installation of various mechanical components and detectors. We are thankful to the Tibet neutron monitor groups for making the data available on the internet. We thank the anonymous referee for a thorough and helpful review.
References
- Alania, M. V., & Wawrzynczak, A. 2012, Adv. Space Res., 50, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Arunbabu, K. P., Antia, H. M., Dugad, S. R., et al. 2013, A&A, 555, A139 [Google Scholar]
- Belov, A. V., Eroshenko, E. A., Oleneva, V. A., Struminsky, A. B., & Yanke, V. G. 2001, Adv. Space Res., 27, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Bothmer, V., & Schwenn, R. 1998, Ann. Geophys., 16, 1 [Google Scholar]
- Burlaga, L. F., Sittler, E., Mariani, F., & Schwenn, R. 1981, J. Geophys. Res., 86, 6673 [Google Scholar]
- Candia, J., & Roulet, E. 2004, J. Cosmol. Astropart. Phys., 10, 007 [Google Scholar]
- Casse, F., Lemoine, M., & Pelletier, G. 2002, Phys. Rev. D, 65, 023002 [Google Scholar]
- Dumbović, M., Vršnak, B., Čalogovi, J., & Župan, R. 2012, A&A, 538, A28 [Google Scholar]
- Forbush, S.E. 1937, Phys. Rev. 51, 1108 [Google Scholar]
- Forbush, S. E. 1938, Phys. Rev., 54, 975 [NASA ADS] [CrossRef] [Google Scholar]
- Giacalone, J., & Jokipii, J. R. 1999, ApJ, 520, 204 [Google Scholar]
- Gupta, S. K., Aikawa, Y., Gopalakrishnan, N. V., et al. 2005, Nucl. Instrum. Meth. A, 540, 311 [Google Scholar]
- Gupta, S. K., Antia, H. M., Dugad, S. R., et al. 2009, Nucl. Phys. B Proc. Suppl. 196, 153 [Google Scholar]
- Hayashi, Y., Aikawa, Y., Gopalakrishnan, N. V., et al. 2005, Nucl. Instrum. Meth. A, 545, 643 [Google Scholar]
- Kane, R. P. 2010, Ann. Geophys., 28, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Kubo, Y., & Shimazu, H. 2010, ApJ, 720, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Matthaeus, W. H., Qin, G., Bieber, J. W., & Zank, G. P. 2003, ApJ, 590, 53 [Google Scholar]
- Mohanty, P. K., Dugad, S. R., Goswami, U. D., et al. 2009, Astropart. Phys., 31, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Mohanty, P. K., Dugad, S. R., & Gupta, S. K. 2012, Rev. Sci. Instrum., 83, 043301 [NASA ADS] [CrossRef] [Google Scholar]
- Mohanty, P. K., Atri, D., Dugad, S. R., et al. 2013, Pramana J. Phys., 81, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Nonaka, T., Hayashi, Y., Ito, N., et al. 2006, Phys. Rev. D., 74, 052003 [NASA ADS] [CrossRef] [Google Scholar]
- Potgieter, M. S., Vos, E. E., Boezio, M., et al. 2014, Sol. Phys., 289, 391 [Google Scholar]
- Richardson, I. G., & Cane, H. V. 2011, Sol. Phys., 270, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Shalchi, A. 2010, ApJ, 720, 127 [Google Scholar]
- Simpson, J. A. 1954, Phys. Rev., 94, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Spangler, S. R. 2002, ApJ, 576, 997 [NASA ADS] [CrossRef] [Google Scholar]
- Subramanian, P., Antia, H. M., Dugad, S. R., et al. Grapes-3 Collaboration. 2009, A&A, 494, 1107 [Google Scholar]
- Tanaka, H., Dugad, S. R., Gupta, S. K., et al. 2012, J. Phys. G, 39, 025201 [Google Scholar]
- Tautz, R. C., & Shalchi, A. 2011, ApJ, 735, 92 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Shock arrival time, time of maximum magnetic field enhancement, magnetic cloud start and end timings and FD onset timings for different directions for FD events that have a well-defined shock and magnetic clouds associated with them.
Correlation of FD profile in different direction observed in GRAPES-3 with magnetic fields for the 24 November 2001 event.
Events for which the FD profile correlates well only with the perpendicular component of the IMF enhancement.
FD events for which the correlation coefficient between the profiles of the FD and the IMF enhancement ≥70%.
All Figures
 |
Fig. 1 FD event on 24 Nov. 2001. Percent deviation in the muon flux for different directions are shown in separate panels. The solid line shows percent deviation for filtered data and the dotted line shows the same for unfiltered data. |
| In the text | |
 |
Fig. 2 FD event of 24 Nov. 2001 and magnetic field for 9 directions in GRAPES-3 muon telescope. Black solid line is percentage deviation of cosmic ray intensity in each direction. The red-dotted, blue-dash-dot-dotted, green-dash-dotted and orange-dash lines are percentage deviation of IMFs Btotal, Bz, By and Bx respectively, that are scaled down by a factor of 10 to fit in the frame. |
| In the text | |
 |
Fig. 3 Correlation of maximum total magnetic field in the magnetic field enhancement to FD magnitude observed in different directions using GRAPES-3. |
| In the text | |
 |
Fig. 4 Correlation of maximum perpendicular magnetic field in the magnetic field enhancement to FD magnitude observed in different directions using GRAPES-3. |
| In the text | |
 |
Fig. 5 FD event on 24 November 2001. The black solid line denotes percentage deviation of the cosmic ray intensity, black dotted line percentage deviation of total magnetic field | 100−B | as explained in Sect. 2 which is scaled down to fit the frame. The vertical brown-dotted, magenta-dash-dotted, blue-dash-dot-dotted, green-long-dashed, and black-dashed lines denote the timings corresponding to the FD onset, shock arrival, magnetic cloud start, magnetic cloud end, and FD minimum, respectively. The solid red vertical line corresponds to the maximum of the magnetic field compression. |
| In the text | |
 |
Fig. 6 Magnetic field compression associated with the FD event on 24 November 2001. In the first panel the continuous line denotes Btotal and the dotted line denotes Bp. The continuous line in the second panel shows the turbulence level for Btotal. In both panels the vertical solid, dotted, and dashed lines corresponds to shock arrival time, magnetic cloud start time, magnetic cloud end time, respectively. |
| In the text | |
 |
Fig. 7 Cross correlation of the cosmic ray flux with Btotal. The top panel shows the percentage deviation of cosmic ray flux using solid black lines and the magnetic field using dotted black lines (scaled to fit in the frame). The middle panel shows the same with magnetic field shifted to the right corresponding to the time lag and the bottom panel shows the correlation coefficient for different lags. |
| In the text | |
 |
Fig. A.1 FD event of 11 April 2001 and magnetic field for nine directions in GRAPES-3 muon telescope. The linestyles are the same as used in Fig. 2. |
| In the text | |
 |
Fig. A.2 FD event of 23 May 2002 and magnetic field for nine directions in GRAPES-3 muon telescope. The linestyles are the same as used in Fig. 2. |
| In the text | |
 |
Fig. A.3 FD event on 11 April 2001. The linestyles are the same as used in Fig. 5. |
| In the text | |
 |
Fig. A.4 FD event on 23 May 2002. The linestyles are the same as used in Fig. 5. |
| In the text | |
 |
Fig. A.5 Cross correlation of the cosmic ray flux with Btotal. The top panel shows the percentage deviation of cosmic ray flux using solid black lines and the magnetic field using dotted black lines (scaled to fit in the frame). The middle panel shows the same with magnetic field shifted to the right corresponding to the time lag and the bottom panel shows the correlation coefficient for different lags. |
| In the text | |
 |
Fig. A.6 Cross correlation of the cosmic ray flux with Btotal. The top panel shows the percentage deviation of cosmic ray flux using solid black lines and the magnetic field using dotted black lines (scaled to fit in the frame). The middle panel shows the same with magnetic field shifted to the right corresponding to the time lag and the bottom panel shows the correlation coefficient for different lags. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


