| Issue |
A&A
Volume 579, July 2015
|
|
|---|---|---|
| Article Number | A15 | |
| Number of page(s) | 10 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201525646 | |
| Published online | 19 June 2015 | |
Dust evolution in the transition towards the denser ISM: impact on dust temperature, opacity, and spectral index
Institut d’Astrophysique Spatiale (IAS), Université Paris Sud & CNRS, Bât. 121, Orsay 91405, France
e-mail: mkoehler@ias.u-psud.fr
Received: 12 January 2015
Accepted: 29 March 2015
Context. Variations in the observed dust emission and extinction indicate a systematic evolution of grain properties in the transition from the diffuse interstellar medium (ISM) to denser molecular clouds.
Aims. The differences in the dust spectral energy distribution (SED) observed from the diffuse ISM to denser regions, namely an increase in the spectral index at long wavelengths, an increase in the FIR opacity, and a decrease in temperature, are usually assumed to be the result of changes in dust properties. We investigate if evolutionary processes, such as coagulation and accretion, are able to change the dust properties of grains in a way that is consistent with observations.
Methods. We use a core-mantle grain model to describe diffuse ISM-type grains, and using a discrete-dipole approximation, we calculate how the accretion of mantles and coagulation into aggregates vary the grain optical properties. We calculate the dust SED and extinction using DustEM and the radiative transfer code CRT.
Results. We show that the accretion of an aliphatic carbon mantle on diffuse ISM-type dust leads to an increase in the FIR opacity by a factor of about 2 and in the FIR/submm spectral index from 1.5 to 1.8, and to a decrease in the temperature by about 2 K. We also show that the coagulation of these grains into aggregates further decreases the temperature by 3 K and increases the spectral index up to a value of ~2. The FIR opacity is increased by a factor of 3 (7) for these aggregates (with an additional ice-mantle) compared to the diffuse ISM-dust.
Conclusions. Dust evolution in the ISM resulting from coagulation and accretion, leads to significant changes in the optical properties of the grains that can explain the observed variations in the dust SED in the transition from the diffuse ISM to denser regions.
Key words: dust, extinction / evolution / ISM: abundances
© ESO, 2015
1. Introduction
Indications of dust evolution from the diffuse interstellar medium (ISM) to molecular cloud environments (n > 103H/cm3) have recently been observed with the Herschel (Pilbratt et al. 2010) and Planck (Lamarre et al. 2010) space observatories in the far-infrared (FIR) and submillimetre (submm) wavelength range. Earlier, dust evolution was already indicated with ISO, Spitzer, SPM/PRONAOS, and IRAS data. For example, a temperature decrease of large grains, which are in thermal equilibrium with the radiation field, from 20.3 K in the diffuse ISM (Planck Collaboration XI 2014) to less than 14 K in denser regions (e.g., Lagache et al. 1998; Stepnik et al. 2003; Planck Collaboration XXIV 2011) was observed together with an increase in the dust opacity by a factor of 2 to 4 in the FIR/submm (e.g., Stepnik et al. 2003; Planck Collaboration XXIV 2011; Juvela et al. 2012; Roy et al. 2013). Additionally, the mid-infrared emission, which comes mainly from stochastically heated very small grains (e.g., Draine & Li 2001; Compiègne et al. 2011; Jones et al. 2013), decreases by 80−100% from diffuse to denser regions (e.g., Laureijs et al. 1991; Stepnik et al. 2003; Juvela et al. 2012). In many of these papers, an anti-correlation of the dust colour temperature T with the opacity spectral index β has been observed with increasing column density in the environment (Dupac et al. 2003; Stepnik et al. 2003; Désert et al. 2008; Paradis et al. 2010; Veneziani et al. 2010; Bracco et al. 2011; Planck Collaboration XXIV 2011; Juvela et al. 2013; Sadavoy et al. 2013). Values for β and T are derived by fitting observations at wavelengths longer than around 60 μm with a modified blackbody. As was shown by Juvela et al. (2013) the values derived for β and T depend strongly on the fitting method and the wavelength range of the observations where the modified blackbody has been fitted. In general, the χ2 approach overestimates β and underestimates T when fitting noisy observations. In the literature, we therefore find a wide range for values of β, from 0.8 (Dupac et al. 2003) to 5 (Veneziani et al. 2010), and of T, from 7 K (Désert et al. 2008; Paradis et al. 2010) to 80 K (Dupac et al. 2003). A systematic study of the various fitting methods (χ2, hierarchical models, and the Bayesian method) was carried out by Juvela et al. (2013). Their main result was that the observed anti-correlation cannot be explained only by bias in the fitting methods but must originate, at least partly, in intrinsic variations in dust properties. It is usually assumed that all four changes in the observed SEDs occur because of the evolution of dust from diffuse to dense regions. These variations result from the evolutionary processes acting on dust as it responds to its environment.
Changes in the environment include variations in the local gas density and in the radiation field. Coagulation, accretion, fragmentation, sputtering, and photoevaporation change the properties of dust grains, such as their structure, shape, material composition, and size. This results in a modification of the optical properties of the grains and therefore to changes in the spectral energy distribution (SED). Variations in dust optical properties resulting from coagulation have been explored in many papers (e.g. Bazell & Dwek 1990; Ossenkopf 1993; Ossenkopf & Henning 1994; Stognienko et al. 1995; Dwek 1997; Fogel & Leung 1998; Ormel et al. 2009, 2011; Köhler et al. 2011, 2012). In the transition from the diffuse ISM to denser regions, the main evolutionary processes are the accretion of mantles composed mainly of amorphous carbon, water ice, and other molecular species (Jones et al. 1990; Mathis 1992; Whittet et al. 1996; del Burgo et al. 2003; Kiss et al. 2006) and grain coagulation (Bernard et al. 1999; del Burgo et al. 2003; Stepnik et al. 2003; Kiss et al. 2006; Ridderstad et al. 2006; Paradis et al. 2009; Ysard et al. 2013). Observational evidence of grain coagulation in denser clouds was found by Jura (1980) through an analysis of the extinction towards ρ Oph.
The β-T anti-correlation is seen for amorphous carbon and silicate materials in laboratory measurements (Agladze et al. 1996; Mennella et al. 1998; Boudet et al. 2005; Coupeaud et al. 2011) and the DCD/TLS model (Meny et al. 2007). We do not take variations of β with grain temperatures into account in our model, but plan to in future studies. Since these variations occur mainly at long wavelengths and for large temperature variations, the influence on the SED and extinction are likely to be small for our assumed dust composition and size distribution.
However, so far, no dust model or dust-evolution model have been able to self-consistently explain all four observed changes in the SED from the diffuse ISM to denser regions, i.e. changes in temperature, spectral index (and their anti-correlation), opacity (emissivity) and the mid-infrared emission. Model calculations taking into account the coagulation of separate grains into aggregates could explain the decrease in temperature and the increase in opacity, but were not able to explain the observed increase in β (e.g. Köhler et al. 2012). This theoretical study was later confirmed by simulations including radiative transfer calculations (Ysard et al. 2012) and the analysis of Herschel observations of a dense filament in the Taurus molecular cloud complex (Ysard et al. 2013). These three studies were based on the Compiègne et al. (2011) dust model, which consists of neutral and charged polycyclic aromatic hydrocarbons, very small grains (VSGs, ~1.2−15 nm in radius) of amorphous carbon (Zubko et al. 1996) and big grains (BGs, 15−110 nm in radius) of astronomical silicate (Draine & Lee 1984) and of amorphous carbon (Zubko et al. 1996).
Recently, new optical constants for hydrogenated amorphous carbon were derived (Jones 2012a,b,c). A new dust model that uses these materials, in conjunction with new silicate data, explains the observational data of dust in the diffuse ISM, such as the IR to far-ultraviolet (FUV) extinction and the dust SED (Jones et al. 2013; Köhler et al. 2014; Ysard et al. 2015). In the present study, we use this new dust model and coagulate the grains into aggregates following the same approach as in Köhler et al. (2012). We also consider the accretion of carbonaceous material and ice from the gas phase onto the surfaces of the aggregates.
This paper is organised as follows: in Sect. 2 we present the dust model and dust evolution. In Sect. 3 we describe the method and calculations and present the results in Sect. 4. We summarise and conclude our study in Sect. 5.
2. Dust model and dust evolution
Our study is based on the recently published dust model from Jones et al. (2013) for the diffuse ISM (nH< 100 H/cm3). In the diffuse ISM, we assume that VSGs and BGs are mainly separated. Very small grains up to about 20 nm in radius consist purely of aromatic-rich amorphous carbon because of UV photo-processing. Larger VSGs and BGs of amorphous carbon show a core-mantle structure, where the mantle with a thickness of ~20 nm is aromatic rich, while the core is aliphatic rich. Another BG population consists of amorphous silicates, with Fe/FeS nano-particle inclusions and a mantle of aromatic-rich amorphous carbon, which is formed by accretion and the coagulation of VSGs and has a thickness of ~5 nm. We assume amorphous silicates of forsterite-type and of enstatite-type and the inclusions occupy a volume of 10% and consist of a mixture of 30% FeS and 70% Fe as described in Köhler et al. (2014). Starting from these grain populations, we consider dust evolution based on the processes of accretion and coagulation, which we assume to occur in relatively dense interstellar environments (nH> 1500H/cm3, as in Ysard et al. 2013).
2.1. Accretion of carbonaceous mantles
The first process that we consider is accretion. Because of the accretion of C and H atoms from the gas phase, an additional amorphous carbon mantle is formed on the surface of grains (Jones et al. 2014). Parvathi et al. (2012) show that more carbon is available than usually assumed (see e.g. Compiègne et al. 2011), so that there appears to be sufficient gas phase carbon to form such a carbonaceous mantle. In low-density regions, this newly accreted mantle would aromatise quickly because of UV photo-processing (Jones et al. 2014). As a result, the grain properties would not change dramatically, since the aromatic amorphous mantle would only increase the particle size but would not change the material properties. This would have the strongest influence for the small grains, where the mantle would increase the particle size by a larger factor. However, this case was already studied in Ysard et al. (2015). In denser regions, where UV photons are significantly attenuated (AV ≳ 1), the accretion of C and H atoms will result in an aliphatic-rich amorphous carbon mantle (Jones et al. 2014), so that BGs will have a core-mantle-mantle structure. We investigate how the optical properties of the grains change because of the accretion of such an aliphatic-rich amorphous carbon mantle.
In the following, we use abbreviations to describe the particles with accreted mantles:
-
CM:
core-mantle grains from the Joneset al. (2013) and Köhleret al. (2014) model.
-
CMM:
core-mantle-mantle grains, which are the original grains with an additional aliphatic-rich mantle.
2.2. Coagulation into aggregates
In denser regions of the ISM (nH> 103 H/cm3, AV ≳ 1), grains are expected to coagulate into aggregates. Considering the time scales (see e.g. Köhler et al. 2012), the coagulation of VSGs onto the surface of BGs is relatively fast, so that the mantles on the BGs thicken with time. We assume that all VSGs coagulate onto the surfaces of BGs and that the population of VSGs is therefore incorporated into the BG population aggregates. The time scales to coagulate a few BGs into aggregates (t = 4 × 105−106 yr, Köhler et al. 2012) are consistent with typical cloud lifetimes (t ≈ 107 yr, Walmsley et al. 2004). Furthermore, amorphous carbon mantles tend to favour the coagulation of BGs, since they act as a sort of glue (Chokshi et al. 1993). Observations indicate that the relative velocities between the BGs can be small and hence fragmentation processes minimal (Ormel et al. 2009; Pagani et al. 2010).
We assume aggregates that are formed of 4 BGs (monomers) in an intermediate elongated shape, as described by Köhler et al. (2012). At long wavelengths, the difference in optical properties compared to separated grains, is largest for the coagulation of a few monomers and remains rather constant for larger aggregates (see e.g. Mackowski 2006; Köhler et al. 2011). The time scales to coagulate 4 BGs are realistic in comparison to the cloud lifetime in relatively dense media (nH = 4 × 103 cm-3) as shown by Köhler et al. (2012). With the increasing density of the environment, the coagulation rate between BGs increases so that larger aggregates are able to form. Larger aggregates have lower temperatures, but the differences in β and the FIR opacity are small compared to smaller aggregates (see e.g. Mackowski 2006; Köhler et al. 2011). We therefore only consider small aggregates consisting of 4 BGs in this study.
The constituents of the aggregates are one BG of aliphatic-rich amorphous carbon and three BGs of amorphous silicate of olivine and pyroxene type with Fe/FeS inclusions as described above. This distribution agrees with the mass fractions of BGs in the ISM as derived by Jones et al. (2013). We then consider the accretion of a second mantle in denser regions as in Sect. 3.1. This second mantle consists of aliphatic-rich amorphous carbon, which is unprocessed because of the high UV extinction.
With increasing density (line of sight AV> 1.5, Jones et al. 2014), the formation of a water-ice mantle occurs. We therefore assume the formation of such ice mantles on the surface of the grains after forming the aggregate.
In the following we use abbreviations to describe the coagulated aggregates:
-
AMM:
aggregates consisting of CMM grains.
-
AMMI:
aggregates consisting of CMM grains with an additional ice mantle.
3. Theory and calculations
Model calculations to derive the optical properties of aggregates are carried out with the discrete-dipole approximation (DDA Purcell & Pennypacker 1973; Draine 1988; Draine & Flatau 2010). We use the DDA code DDSCAT 7.1.0 (for a detailed description see Draine 1988; Draine & Flatau 2010) including the lattice dispersion relations (LDR; Draine & Goodman 1993).
3.1. Accretion
In order to study the accretion process, we consider grain radii from 0.04 to 1.0 μm. Up to a radius of 0.441 μm we use DDA to derive the optical properties. For DDA calculations, the grains are represented by interacting dipoles. In order to obtain the correct size ratios between BGs and VSGs, we assume that BGs of radius (cores) 0.02 μm are 7 dipoles across, BGs of 0.06 μm are 17 dipoles across and all larger BGs are 35 dipoles across. Since we want to coagulate these grains into aggregates containing 4 BGs, we cannot consider more dipoles because the DDA calculations are then computationally too expensive. We assume that 1000 dipoles, 3 nm in radius, form the original mantle plus the first coagulated VSGs of aromatic amorphous carbon and that another 1000 dipoles of aliphatic amorphous carbon, 3 nm in radius, form the accreted mantle on each BG. For cores of 0.02, 0.06 and 0.11 μm, where each dipole is 3 nm in size, 1000 dipoles are distributed on the grain surface. For larger BGs, the dipole size is larger than 3 nm, since we keep the number of dipoles across the BG constant but increase the radius. We therefore reduce the number of dipoles in the mantle when increasing the grain size, so that the mantle mass is constant for each BG. In order to avoid an antenna effect (see e.g. Köhler et al. 2012), the mantles form a layer so that chains of dipoles protruding from the surface are prevented. The optical property results are averaged over 125 grain orientations as discussed in Köhler et al. (2012), which allows a relatively fast calculation and gives sufficient accuracy.
For grains with radii larger than 0.441 μm, we use the Maxwell-Garnett effective medium theory (Bohren & Huffman 1983) to derive the best mixture of aromatic and aliphatic amorphous carbon in the mantle and amorphous silicate in the core. We then use BHMIE (Bohren & Huffman 1983) to derive the optical properties for the grains1. The best mixture was derived by comparing the optical properties for smaller grains, where DDA results are available. We find the best mantle mixture of 50% aromatic-rich and 50% aliphatic-rich amorphous carbon in volume and a mantle to core volume relation of 0.08% to 99.2%.
The mass distribution of CMM grains is shown in Fig. 1. The range of the mass distribution is determined by amin, which is the smallest grain size which is possible when adding the accreted mantle and by amax, which is the largest grain size we calculate. We see clearly an increase in the mass as a result of the accretion of material. For the CMM grains, we use 182 ppm of C for the first mantle and 224 ppm of C for the second mantle. The total of 406 ppm is in good agreement with the carbon abundance (Compiègne et al. 2011; Parvathi et al. 2012). We derived the average density to be 1.46 g/cm3 for a core of amorphous carbon and and 1.59 g/cm3 for a core of amorphous silicate.
 |
Fig. 1 Mass distribution of the CM dust grains as described in Jones et al. (2013), of core-mantle-mantle (CMM) grains and of aggregates (AMM) and aggregates with an accreted ice mantle (AMMI). |
 |
Fig. 2 Qabs (solid lines) and Qsca (dashed lines) for CMM grains with cores of amorphous carbon (left) and cores of amorphous silicate of olivine type (middle) and pyroxene type (right) for different grain radii in μm. The inner mantle is aromatic-rich and the outer mantle aliphatic-rich amorphous carbon. At long wavelengths Qabs and Qsca increase with increasing grain size. |
3.2. Coagulation
We now coagulate the CMM grains as described in Sect. 3.1 into aggregates of 4 BGs, where the cores of 2 BGs are of amorphous silicate of olivine type, 1 BG of amorphous silicate of pyroxene type and 1 BG of amorphous carbon. The optical properties of the aggregates are calculated with DDA for six sizes, with volume-equivalent sphere radii, aV, of 0.05, 0.06, 0.09, 0.17, 0.318, 0.476 and 0.70 μm, averaged over 125 aggregate orientations. The aggregate size distribution is shown in Fig. 1. The maximum is shifted to larger grains because of the coagulation process. With our adopted formalism the smallest aggregates, with radius amin, actually only consist of carbonaceous mantle materials. We assume amax = 0.70μm, since it was computationally too expensive to calculate the optical properties of larger aggregates. We derive the averaged density to be 1.55 g/cm3.
In a second step, we also study the changes in the optical properties when accreting an ice mantle on the surface of the aggregates. For the ice mantles we assume 6000 dipoles of 3 nm in size per BG. We take the optical constants of ice from Warren (1984). The mass distribution for these icy aggregates is also shown in Fig. 1. The amin is again shifted to larger grain sizes. The increase in mass due to the accreted ice mantle is clearly visible. The average density decreases to 1.18 g/cm3. For the ice mantle we use 500 ppm of O which is in agreement with the abundances given in Compiègne et al. (2011).
As shown by Köhler et al. (2011), the optical properties of an aggregate depend on the connections between the monomers. In this study we consider a contact area of 3, 5 and 9 dipoles across for BGs of 7, 17 and 35 dipoles across, respectively. We also consider that the BGs form the aggregate and VSGs are connected to their surfaces, so that in the contact area the BGs “touch”. As shown by Köhler et al. (2011), the increase in the absorption coefficient depends on the real part, n, of the optical constants. This is at the origin of the increase in opacity (emissivity) at 250 μm. Since the amorphous silicate and the amorphous carbon (Eg = 0.1) have similar values of n at 250 μm, the differences in the absorption coefficient are small when VSGs provide the contact area. This was tested by using dimers. Initially, we connect silicate BGs and coagulate VSGs of amorphous carbon on their surfaces. In follow-up calculations, we separate the silicate BGs by two dipoles and fill the contact area and the surface of the BGs with VSGs of amorphous carbon. The number of VSGs is the same in each case. The absorption coefficients vary at most by only 4% and 5% for aromatic and aliphatic amorphous carbon, respectively.
3.3. Dust emission
Firstly, we use the DustEM code2 (Compiègne et al. 2011) to calculate the SEDs and the extinction of our grains. We assume a diffuse (transparent) medium illuminated by the interstellar radiation field (ISRF) of Mathis et al. (1983) for a galacto-centric distance of 10 kpc.
Secondly, we simulate denser environments by coupling DustEM to the 3D continuum radiative transfer code CRT as described in Juvela (2005) and Ysard et al. (2012). We consider spherical clouds with the following radial hydrogen density distribution, 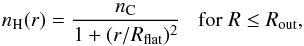 (1)where nC is the central density, Rflat is the internal flat radius, and Rout the external radius set to 0.5 pc. We define the (nC,Rflat)-parameters for the clouds to be at equilibrium, with their masses per unit length equal to the critical mass defined by Ostriker (1964),
(1)where nC is the central density, Rflat is the internal flat radius, and Rout the external radius set to 0.5 pc. We define the (nC,Rflat)-parameters for the clouds to be at equilibrium, with their masses per unit length equal to the critical mass defined by Ostriker (1964), 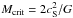 , where G is the gravitational constant. The sound speed cS is computed for a gas temperature of 12 K. These spherical clouds are then embedded in a more diffuse medium with 100 H/cm3. We simulate a series of clouds with central visual extinctions of AV ~ 0.1 to 20 and illuminate them with the standard ISRF.
, where G is the gravitational constant. The sound speed cS is computed for a gas temperature of 12 K. These spherical clouds are then embedded in a more diffuse medium with 100 H/cm3. We simulate a series of clouds with central visual extinctions of AV ~ 0.1 to 20 and illuminate them with the standard ISRF.
In order to study the variations in dust populations inside the clouds, we consider the following models:
-
Model
CM:
no variation in the dust properties and the diffusemedium as well as the spherical clouds are filled with CM dust ofthe diffuse-ISM type (Joneset al. 2013; Köhleret al. 2014).
-
Model
CMM:
the diffuse medium is filled with CM dust while the spherical clouds are filled with CMM dust.
-
Model
AMM:
the diffuse medium is filled with CM dust, and the dense cloud with CMM dust for nH < 1500 H/cm3 and AMM for higher densities.
-
Model
AMMI:
same as Model AMM, with the central region filled with AMMI grains.
To compare our dust models with observational results, we finally fit our modelled SEDs with a modified blackbody, 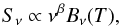 (2)where Bν is the Planck function, β the spectral index, and T the colour temperature. We perform the fits in the Planck-HFI bands at 857, 545, 353, and 143 GHz, and the IRAS 100 μm filter. We also make fits to the Herschel PACS and SPIRE filters at 100, 160, 250, 350, and 500 μm. A last pair of fits is performed, without instrumental filters, continuously between 100 and 500 μm, or 100 and 870 μm. We do standard weighted least square fits, where all bands/wavelengths are given an equal weight (i.e. we do not consider the effect of noise), in order to determine T and β.
(2)where Bν is the Planck function, β the spectral index, and T the colour temperature. We perform the fits in the Planck-HFI bands at 857, 545, 353, and 143 GHz, and the IRAS 100 μm filter. We also make fits to the Herschel PACS and SPIRE filters at 100, 160, 250, 350, and 500 μm. A last pair of fits is performed, without instrumental filters, continuously between 100 and 500 μm, or 100 and 870 μm. We do standard weighted least square fits, where all bands/wavelengths are given an equal weight (i.e. we do not consider the effect of noise), in order to determine T and β.
 |
Fig. 3 Qabs (solid lines) and Qsca (dashed lines) of AMM structure (left) and of AMMI structure (right) for different radii in μm of volume-equivalent spheres aV. At long wavelengths Qabs and Qsca increase with increasing grain size. |
 |
Fig. 4 Differences in Qabs/aV and Qsca/aV for the evolution of grains with CM grain radii of 0.06 μm. Left: Qabs/aV (dashed-dotted and solid lines) and Qsca/aV (dotted and dashed lines) for CM and CMM grains, respectively. Right: Qabs/aV (solid and dashed-dotted lines) and Qsca/aV (dashed and dotted lines) for CMM grains (as in left panel) and for AMM and AMMI grains, respectively. Ol indicates amorphous silicate of olivine-type, Py indicates amorphous silicate of pyroxene-type and Ca indicates amorphous carbon. |
4. Results of model calculations
4.1. Absorption and scattering coefficients
In Fig. 2 the calculated absorption coefficients Qabs and scattering coefficients Qsca for the CMM grains with different sizes and different core materials (amorphous carbon left, amorphous silicate olivine type middle and pyroxene type right) are presented. A difference in Qabs and Qsca with grain size is clearly visible for all core materials. The peak in Qsca shifts to longer wavelengths with increasing particle size. Qabs increases with increasing grain size for amorphous silicate cores and decreases at wavelengths longer than 1 μm for the amorphous carbon core. This decrease is due to the more dominant core material when the grain sizes increase. For amorphous carbon cores an increase in the features at 3.4 and around 7 μm can be seen. For grains with an amorphous silicate core, an increase in the strength of the silicate features can be observed and differences in the slope at long wavelengths are evident (λ> 50μm).
In Fig. 3Qabs and Qsca are presented for different sized aggregates, AMM (left) and AMMI (right). With increasing grain size both Qabs and Qsca increase. With increasing grain size the silicate features become more pronounced. The differences in the slope at long wavelengths are strongest for small aggregates. The smallest aggregates only consists of amorphous carbon material and therefore show strong hydrocarbon features in the spectrum. For AMMI grains, the ice features are clearly visible for small aggregates and become less evident with increasing grain size while the silicate features become more pronounced. The smallest grains consist of the pure carbonaceous AMM with a thick ice mantle and we find that the ice features clearly dominate the spectrum.
In Fig. 4, we present the variation in the optical properties due to the evolution of CM grains with a radius of a = 0.06μm. It can be seen that Qabs and Qsca vary with accretion (left) and coagulation (right). The accretion of an aliphatic amorphous carbon mantle on the amorphous carbon grains shows a decrease in Qabs and a change in slope at long wavelengths, while differences in Qsca are rather small. For grains with an amorphous silicate core, we find a decrease in the silicate feature and an increase between 5 and 10 μm in Qabs due to the accretion of carbonaceous material. For AMM grains, Qabs and Qsca increase compared to the single grains, but the overall shape of the curve is comparable to the curves of the amorphous silicate CMM grains. For AMMI grains, the ice features are clearly visible in Qabs. Compared to AMM grains, Qabs decreases between 0.1 and ~5 μm and for wavelength larger than 200 μm. For Qsca the differences are small compared to the AMM grains.
4.2. Temperature, spectral index, and opacity derived with modified blackbody fits
Using the optical properties described in the previous section, we calculate the corresponding SEDs for grains illuminated by the standard ISRF (Mathis et al. 1983) using DustEM (Compiègne et al. 2011). The results are presented in Fig. 5 for CM, CMM, AMM and AMMI grains. The SED of the CM grains is the one presented in Köhler et al. (2014), where VSGs are still separated and contribute to the emission up to ~70 μm. At longer wavelengths, the SED of CMM grains shows an increase in the intensity of the far-IR emission and a shift to shorter wavelengths indicating an increase in temperature due to stronger absorption at short wavelengths compared to CM grains. The steepening of the slope (i.e. an increase in the FIR opacity spectral index) is also clearly visible.
For AMM grains the SED maximum is shifted to longer wavelengths, which is an indication of the decrease in temperature when coagulating grains. We can also see a small bump at shorter wavelengths (magenta curve) which is due to the smallest grains which only consist of carbonaceous material. The temperature of these grains is around 52 K while all other AMM aggregates are colder than 20 K. Because of their high temperatures and small intensity these smallest grains do not contribute to the SED at longer wavelengths. Excluding these smallest grains, show indeed no variation in the SED at the maximum and longer wavelengths (red line). The SED of the AMM grains decreases significantly at 70 μm as observed by e.g. Stepnik et al. (2003).
 |
Fig. 5 SED of the CM grains, CMM grains and aggregates, AMM and AMMI. |
 |
Fig. 6 Colour temperature, spectral index β and opacity derived with DustEM for the Jones et al. (2013) and Köhler et al. (2014) model (CM), CMM grains and AMM and AMMI aggregates. |
When adding the ice mantle the far-IR emission increases and the emission peak shifts to longer wavelengths. Since an ice band occurs at the wavelength, where the maximum is reached, it is not clear if there is a real shift due to a temperature decrease or if the ice band is dominant. The calculated temperatures of AMM and AMMI grains show a small decrease of less than 1.5 K for the larger aggregates. The temperature of the smallest purely carbonaceous AMM grain decreases to 14 K when adding the ice mantle. Excluding these smallest AMMI grains, we find no variations in the SED (blue line compared to cyan line).
Temperature, spectral index, β, and increase in opacity derived with the modified blackbody approach, 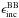 , at 250 μm for the separate grains and aggregates, derived in different wavelength ranges.
, at 250 μm for the separate grains and aggregates, derived in different wavelength ranges.
 |
Fig. 7 Infrared extinction of single grains and aggregates normalised at 10 μm (left) and at the K-band (right) compared to observational data. The normalisation wavelength is indicated by the star. Solid lines: CM grains (black), CMM grains (green), AMM grains (red), AMMI grains (blue). |
Fitting the calculated SEDs with a modified blackbody, we can derive the dust colour temperature, the spectral index and opacity at 250 μm. In Fig. 6 and Table 1, these values are summarised for the SEDs of the different grain populations, integrated over the Herschel and Planck bands and over the 100 to 500 μm and 100 to 870 μm wavelength ranges. The separate BGs have colour temperatures of around 20 K, in agreement with the findings of Planck Collaboration XI (2014), while the colour temperatures of CMM grains decrease to about 18.7 K. The SED consists of three different components, each having a different size distribution. The colour temperature is the value to fit the SED with a modified backbody and not the temperature of the grains. Compared to CM grains CMM grains with an amorphous carbon core are hotter while CMM grains with an amorphous silicate core have similar temperatures. The SED therefore does not show a shift of the peak position, but because of the additional change in the spectral slope, the best modified blackbody fit gives a lower temperature. For the aggregates, the colour temperature is about 2 to 3 K lower than the CM grains. Compared to the calculated temperatures for grains larger than 100 nm, the colour temperatures are on average around 1 K higher. The spectral index increases from around 1.5 for separate grains to about 1.8 for CMM and AMM grains and up to 2 for AMMI grains. The opacity at 250 μm for the original model of Jones et al. (2013) is found to be 0.5 × 1025 cm2/ H, which is essentially the same as the observed value of 0.49 × 1025 cm2/ H (Planck Collaboration XI 2014; Planck Collaboration Int. XVII 2014). We see an opacity increase of around 2.3 for CMM grains and 2.9 for AMM grains, which is in good agreement with the observational results discussed in Sect. 1. For AMMI grains, the increase is up to a factor of 7, which is due to the increase in mass when accreting the ice mantle.
4.3. Extinction
Using DustEM, we also derive the extinction of the CMM grains and the aggregates and compare them to observations. In Fig. 7, we show the derived extinction compared to observations normalised at 10 μm (left) and at the K-band (right). The normalisation at 10 μm, as suggested by van Breemen et al. (2011), shows the variations at different wavelengths in the extinction curves between AMM and AMMI. The ice features are visible and an increase between 6 and 8 μm and between the two silicate features occurs. The usual normalisation to the K-band is problematic, since we find differences in the dust extinction in this wavelength range when coagulating grains and/or accretion mantles3. However, in order to compare the modelled results to observations the data have to be normalised. The comparison to observations show that the original model by Jones et al. (2013) and Köhler et al. (2014) agrees well with the observational data for the diffuse ISM from Mathis (1990). The silicate features of the aggregates are in agreement with observations from Rieke & Lebofsky (1985) but vary at wavelengths shorter than 5 μm. The silicate features observed by McClure (2009) are in general much less pronounced than for the model of the diffuse ISM and the aggregates. However, the differences between our model and the observational data might be due to the different methods and assumptions used in the normalisation of the observational data. This topic will be discussed in detail in a following paper. For our model we derive RV values of 3.5 ± 0.2 for CM grains, 3.9 ± 0.2 for CMM grains, and 4.9 ± 0.2 for AMM and AMMI grains. The relatively large uncertainties are due to the appearance of the ripple and interference structures in the extinction curves, which result from the rather narrow size distributions.
The mass extinction coefficient κ in cm2/g at λ = 250, 350 and 500 μm for the four models presented in the paper.
 |
Fig. 8 UV extinction of single grains and aggregates normalised at 1 μm-1. |
In Fig. 8 the extinction normalised to 1 μm-1 in the visible-UV is shown. For evolved grains, we find strong differences in the UV bump and FUV extinction, which are characteristic of the diffuse ISM and where they appear to arise from small carbonaceous grains (VSGs). We assume that the VSGs are completely coagulated onto the surface of the BGs and this is why the UV bump disappears for our aggregates. Coagulation and accretion leads to a strong increase in extinction compared to separate grains. We find the same decrease as seen in observations published by Fitzpatrick & Massa (2007), except that in those observations the UV bump is still slightly visible. This might be due to VSGs belonging to the diffuse gas surrounding denser regions or distributed along the line of sight and thus contributing to the observed extinction.
 |
Fig. 9 κ shown for the different grains. The grey lines indicate the wavelengths 250, 350 and 500 μm. Ol indicates amorphous silicate of olivine-type, Py indicates amorphous silicate of pyroxene-type and Ca indicates amorphous carbon. |
In Fig. 9 the mass extinction coefficient κ is presented for the original CM grains as well as for the CMM, AMM, and AMMI grains. For CM grains the amorphous carbons show the highest κ values at the longest wavelengths and the lowest κ values with the addition of the aliphatic-rich mantle. For CM grains with amorphous silicate cores, κ increases by about a factor of 2 with the addition of the aliphatic-rich mantle. For AMM grains, κ is similar to the values for CMM grains with amorphous silicate cores, and increases slightly with the addition of an ice mantle. It is therefore less than ideal to choose a single value of κ to derive the total mass of the dust in a galaxy, since dust evolution leads to large differences in κ. In Table 2 we present κ for the different models.
 |
Fig. 10 β-T correlation for cloud cylinders derived with radiative transfer calculations for the four models described in Sect. 3.3. |
4.4. Radiative transfer approach
We also combine DustEM with the CRT radiative transfer code as described in Sect. 3.3. The results for the derived spectral index β and colour temperature are presented in Fig. 10 for the four different models presented in Sect. 3.3 and for the analysis with SEDs integrated in the Planck and Herschel bands and in the 100 to 500 μm and 100 to 870 μm wavelength ranges.
For the CM and CMM grains (Models CM and CMM), β decreases with decreasing temperature in all cases. This correlation is a pure radiative transfer effect: when the clouds are denser, the mixture of temperatures along the line of sight increases resulting in broader SEDs and thus lower β values. This plot clearly shows the increase in beta, when accreting a second mantle of aliphatic-rich amorphous carbon. Assuming grain coagulation into aggregates and ice-mantle formation (Models AMM and AMMI), we can clearly see that β increases with decreasing temperature down to about 15 K. At even lower temperatures, β starts to decrease again. This means that the radiative transfer effects are strong enough to overcome the increase in β of the aggregates. The β-T anti-correlation is strong for all considered bands but is more distinct when analysing the data in the Planck bands, i.e. over a wider wavelength range. The colour temperatures decrease from around 19.5 to 15 K and β increases from 1.45 to 1.8. These values are reached in regions with AV ≈ 16. The results match the values measured by Planck Collaboration XXV (2011) and Planck Collaboration XI (2014).
5. Conclusions
We investigate how evolutionary processes, i.e. accretion and coagulation, change the optical properties of grains in the transition from the diffuse ISM to denser regions. For dust in the diffuse ISM we assume the dust properties of the Jones et al. (2013) and Köhler et al. (2014) model. We also assume that in denser regions these grains undergo evolutionary processes: the accretion of material from the gas phase forms an additional aliphatic-rich mantle of amorphous carbon and the grains then coagulate into aggregates. In even denser regions ice mantles form on the surface of the aggregates. With detailed model calculations we derive the optical properties of these evolved grains and use the DustEM tool and the CRT radiative transfer code to derive the SED and extinction. With the presented dust-evolution model we are able, for the first time, to self-consistently explain the four observed changes in the SED in going from the diffuse ISM to denser regions with AV of up to 16, namely the changes in temperature, spectral index (and their anti-correlation), opacity (emissivity) and the mid-infrared emission.
The β-T anti-correlations that we find in the Herschel bands differ from the observational results. The PACS and SPIRE channels have a high level of noise which might significantly influence the measured relation, as shown by Ysard et al. (2012). This is not the case for the Planck HFI+IRAS bands, where we find a good correspondence between the model and observations. We note that the changes that we observe in β are actually driven by gas density-dependent dust evolution processes (accretion and coagulations). Thus, the β-T effect is actually a β-nH effect according to the predictions of our model.
Using BHCOAT (Bohren & Huffman 1983) is not possible, since the mantle on the large grains would be too thin to derive reasonable results.
DustEM is a publicly available numerical tool to calculate the SED, the extinction and the grain temperature distribution for dust in the ISM, available at http://www.ias.u-psud.fr/DUSTEM/
As pointed out by Jones et al. (2013), it is likely that the extinction in the B and V bands, as we note for the K band here, varies and so normalisation of the extinction curve at the B and V (and K) bands biases the interpretations.
Acknowledgments
This research acknowledges the support of the French Agence National de la Recherche (ANR) through the program “CIMMES” (ANR-11-BS56-0029).
References
- Agladze, N. I., Sievers, A. J., Jones, S. A., Burlitch, J. M., & Beckwith, S. V. W. 1996, ApJ, 462, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Bazell, D., & Dwek, E. 1990, ApJ, 360, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Bernard, J. P., Abergel, A., Ristorcelli, I., et al. 1999, A&A, 347, 640 [NASA ADS] [Google Scholar]
- Bohren, C., & Huffman, D. 1983, Absorption and Scattering of Light by Small Particles (New York, Chichester, Brisbane, Toronto, Singapore: Wiley and Sons) [Google Scholar]
- Boudet, N., Mutschke, H., Nayral, C., et al. 2005, ApJ, 633, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Bracco, A., Cooray, A., Veneziani, M., et al. 2011, MNRAS, 412, 1151 [NASA ADS] [Google Scholar]
- Chokshi, A., Tielens, A. G. G. M., & Hollenbach, D. 1993, ApJ, 407, 806 [Google Scholar]
- Compiègne, M., Verstraete, L., Jones, A., et al. 2011, A&A, 525, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coupeaud, A., Demyk, K., Meny, C., et al. 2011, A&A, 535, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- del Burgo, C., Laureijs, R. J., Ábrahám, P., & Kiss, C. 2003, MNRAS, 346, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Désert, F.-X., Macías-Pérez, J. F., Mayet, F., et al. 2008, A&A, 481, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. 1988, ApJ, 333, 848 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Flatau, P. J. 2010, User Guide for the Discrete Dipole Approximation Code DDSCAT 7.1 [arXiv:1002.1505] [Google Scholar]
- Draine, B. T., & Goodman, J. 1993, ApJ, 405, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Lee, H. M. 1984, ApJ, 285, 89 [Google Scholar]
- Draine, B. T., & Li, A. 2001, ApJ, 551, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Dupac, X., Bernard, J.-P., Boudet, N., et al. 2003, A&A, 404, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dwek, E. 1997, ApJ, 484, 779 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 2007, ApJ, 663, 320 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fogel, M. E., & Leung, C. M. 1998, ApJ, 501, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, A. P. 2012a, A&A, 540, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, A. P. 2012b, A&A, 540, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, A. P. 2012c, A&A, 542, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, A. P., Duley, W. W., & Williams, D. A. 1990, QJRAS, 31, 567 [NASA ADS] [Google Scholar]
- Jones, A. P., Fanciullo, L., Köhler, M., et al. 2013, A&A, 558, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, A. P., Ysard, N., Köhler, M., et al. 2014, Faraday Discussion Meeting [Google Scholar]
- Jura, M. 1980, ApJ, 235, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Juvela, M. 2005, A&A, 440, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Juvela, M., Malinen, J., & Lunttila, T. 2012, A&A, 544, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Juvela, M., Montillaud, J., Ysard, N., & Lunttila, T. 2013, A&A, 556, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kiss, C., Ábrahám, P., Laureijs, R. J., Moór, A., & Birkmann, S. M. 2006, MNRAS, 373, 1213 [NASA ADS] [CrossRef] [Google Scholar]
- Köhler, M., Guillet, V., & Jones, A. 2011, A&A, 528, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Köhler, M., Stepnik, B., Jones, A. P., et al. 2012, A&A, 548, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Köhler, M., Jones, A., & Ysard, N. 2014, A&A, 565, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagache, G., Abergel, A., Boulanger, F., & Puget, J. 1998, A&A, 333, 709 [NASA ADS] [Google Scholar]
- Lamarre, J.-M., Puget, J.-L., Ade, P. A. R., et al. 2010, A&A, 520, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laureijs, R. J., Clark, F. O., & Prusti, T. 1991, ApJ, 372, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Mackowski, D. W. 2006, JQSRT, 100, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S. 1990, ARA&A, 28, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S. 1992, Science, 258, 1384 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 128, 212 [NASA ADS] [Google Scholar]
- McClure, M. 2009, ApJ, 693, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Mennella, V., Brucato, J. R., Colangeli, L., et al. 1998, ApJ, 496, 1058 [NASA ADS] [CrossRef] [Google Scholar]
- Meny, C., Gromov, V., Boudet, N., et al. 2007, A&A, 468, 171 [Google Scholar]
- Ormel, C. W., Paszun, D., Dominik, C., & Tielens, A. G. G. M. 2009, A&A, 502, 845 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ormel, C. W., Min, M., Tielens, A. G. G. M., Dominik, C., & Paszun, D. 2011, A&A, 532, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ossenkopf, V. 1993, A&A, 280, 617 [NASA ADS] [Google Scholar]
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Ostriker, J. 1964, ApJ, 140, 1056 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Pagani, L., Ristorcelli, I., Boudet, N., et al. 2010, A&A, 512, A3 [Google Scholar]
- Paradis, D., Bernard, J., & Mény, C. 2009, A&A, 506, 745 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paradis, D., Veneziani, M., Noriega-Crespo, A., et al. 2010, A&A, 520, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parvathi, V. S., Sofia, U. J., Murthy, J., & Babu, B. R. S. 2012, ApJ, 760, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIV. 2011, A&A, 536, A24 [Google Scholar]
- Planck Collaboration, XXV. 2011, A&A, 536, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration, XI. 2014, A&A, 571, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration, Int. XVII. 2014, A&A, 566, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Purcell, E. M., & Pennypacker, C. R. 1973, ApJ, 186, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Ridderstad, M., Juvela, M., Lehtinen, K., Lemke, D., & Liljeström, T. 2006, A&A, 451, 961 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieke, G. H., & Lebofsky, M. J. 1985, ApJ, 288, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Roy, A., Martin, P. G., Polychroni, D., et al. 2013, ApJ, 763, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Sadavoy, S. I., Di Francesco, J., Johnstone, D., et al. 2013, ApJ, 767, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Stepnik, B., Abergel, A., Bernard, J., et al. 2003, A&A, 398, 551 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stognienko, R., Henning, T., & Ossenkopf, V. 1995, A&A, 296, 797 [NASA ADS] [Google Scholar]
- van Breemen, J. M., Min, M., Chiar, J. E., et al. 2011, A&A, 526, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Veneziani, M., Ade, P. A. R., Bock, J. J., et al. 2010, ApJ, 713, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Walmsley, C. M., Flower, D. R., & Pineau des Forêts, G. 2004, A&A, 418, 1035 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Warren, S. G. 1984, Appl. Opt., 23, 1206 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Whittet, D. C. B., Schutte, W. A., Tielens, A. G. G. M., et al. 1996, A&A, 315, L357 [NASA ADS] [Google Scholar]
- Ysard, N., Juvela, M., Demyk, K., et al. 2012, A&A, 542, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ysard, N., Abergel, A., Ristorcelli, I., et al. 2013, A&A, 559, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ysard, N., Koehler, M., Jones, A., et al. 2015, A&A, 577, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zubko, V. G., Mennella, V., Colangeli, L., & Bussoletti, E. 1996, MNRAS, 282, 1321 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Temperature, spectral index, β, and increase in opacity derived with the modified blackbody approach, 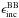 , at 250 μm for the separate grains and aggregates, derived in different wavelength ranges.
, at 250 μm for the separate grains and aggregates, derived in different wavelength ranges.
The mass extinction coefficient κ in cm2/g at λ = 250, 350 and 500 μm for the four models presented in the paper.
All Figures
 |
Fig. 1 Mass distribution of the CM dust grains as described in Jones et al. (2013), of core-mantle-mantle (CMM) grains and of aggregates (AMM) and aggregates with an accreted ice mantle (AMMI). |
| In the text | |
 |
Fig. 2 Qabs (solid lines) and Qsca (dashed lines) for CMM grains with cores of amorphous carbon (left) and cores of amorphous silicate of olivine type (middle) and pyroxene type (right) for different grain radii in μm. The inner mantle is aromatic-rich and the outer mantle aliphatic-rich amorphous carbon. At long wavelengths Qabs and Qsca increase with increasing grain size. |
| In the text | |
 |
Fig. 3 Qabs (solid lines) and Qsca (dashed lines) of AMM structure (left) and of AMMI structure (right) for different radii in μm of volume-equivalent spheres aV. At long wavelengths Qabs and Qsca increase with increasing grain size. |
| In the text | |
 |
Fig. 4 Differences in Qabs/aV and Qsca/aV for the evolution of grains with CM grain radii of 0.06 μm. Left: Qabs/aV (dashed-dotted and solid lines) and Qsca/aV (dotted and dashed lines) for CM and CMM grains, respectively. Right: Qabs/aV (solid and dashed-dotted lines) and Qsca/aV (dashed and dotted lines) for CMM grains (as in left panel) and for AMM and AMMI grains, respectively. Ol indicates amorphous silicate of olivine-type, Py indicates amorphous silicate of pyroxene-type and Ca indicates amorphous carbon. |
| In the text | |
 |
Fig. 5 SED of the CM grains, CMM grains and aggregates, AMM and AMMI. |
| In the text | |
 |
Fig. 6 Colour temperature, spectral index β and opacity derived with DustEM for the Jones et al. (2013) and Köhler et al. (2014) model (CM), CMM grains and AMM and AMMI aggregates. |
| In the text | |
 |
Fig. 7 Infrared extinction of single grains and aggregates normalised at 10 μm (left) and at the K-band (right) compared to observational data. The normalisation wavelength is indicated by the star. Solid lines: CM grains (black), CMM grains (green), AMM grains (red), AMMI grains (blue). |
| In the text | |
 |
Fig. 8 UV extinction of single grains and aggregates normalised at 1 μm-1. |
| In the text | |
 |
Fig. 9 κ shown for the different grains. The grey lines indicate the wavelengths 250, 350 and 500 μm. Ol indicates amorphous silicate of olivine-type, Py indicates amorphous silicate of pyroxene-type and Ca indicates amorphous carbon. |
| In the text | |
 |
Fig. 10 β-T correlation for cloud cylinders derived with radiative transfer calculations for the four models described in Sect. 3.3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


