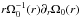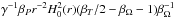| Issue |
A&A
Volume 579, July 2015
|
|
|---|---|---|
| Article Number | A100 | |
| Number of page(s) | 15 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201424663 | |
| Published online | 07 July 2015 | |
Quasi-steady vortices in protoplanetary disks
I. From dwarfs to giants
1 Max Planck Institut für Astronomie, Königsthul 17, 69117 Heidelberg, Germany
2 Institute for Computational Science, University of Zurich, Winterthurerstrasse 190, 8057 Zurich, Switzerland
e-mail: clement.surville@physik.uzh.ch
3 Aix Marseille Université, CNRS, Laboratoire d’Astrophysique de Marseille, UMR 7326, 13388 Marseille, France
e-mail: pierre.barge@lam.fr
Received: 23 July 2014
Accepted: 27 April 2015
Aims. We determine the size, structure, and evolution of persistent vortices in 2D and inviscid Keplerian flows.
Methods. A Gaussian model of the vortices is built and compared with numerical solutions issued from non-linear hydrodynamical simulations. Test vortices are also produced using a fiducial method based on the Rossby wave instability to help explore the vortex parameters. Numerical simulations are performed using a second order finite volume method. We assume a perfect-gas law and a non-homentropic adiabatic flow.
Results. The new model nicely fits the numerical vortex solution. In the vortex centre it is consistent with existing models, whereas in the outer regions it enables the vortex to be connected with the background flow. Two families of vortices can be distinguished following the importance of the compressional effects. The model also permitted a new class of vortices to be discovered corresponding to huge perturbations of pressure and density and whose radial sizes are significantly larger than the disk scale height, in contrast with the standard way to define the maximum vortex size.
Conclusions. Our Gaussian model of the vortex solutions of the 2D Euler’s equations is a useful tool for studying vortex properties. Among the large number of vortex solutions, the possible existence of giant vortices could open interesting perspectives in planetary formation, particularly during the building stage of the giant gas planets.
Key words: hydrodynamics / instabilities / accretion, accretion disks
© ESO, 2015
1. Introduction
In the context of planet formation, the early disk evolution as well as grain growth processes are of critical interest. The turbulent flow of the disk, responsible for the accretion, usually reorganizes into vortex structures. This may be the consequence of the inverse cascade of energy in nearly 2D flows or the result of specific instabilities. The role of long-lived vortices in angular momentum transport (see Paardekooper et al. 2010; Surville & Barge 2012, 2013) and in solid particles capture to form planetesimals (see Barge & Sommeria 1995; Johansen et al. 2004; Heng & Kenyon 2010) has been already invoked, but detailed studies are still necessary.
In particular, the diversity of vortices is unclear. They can be produced by different instabilities, like the Rossby waves instability (RWI, Lovelace et al. 1999; Li et al. 2000, 2001) or by what is now known as convective overstability (see Klahr & Bodenheimer 2003; Petersen et al. 2007a,b; Lyra & Klahr 2011), in 2D and 3D flows, but the vortex structure is strongly dependent on the initial conditions. Vortex models can avoid this bias, as the widely used elliptical vortex (Kida 1981; Goodman et al. 1987; Chavanis 2000). However, other vortex solutions may exist and may overcome the limitations of this old model. Motivated by recent numerical results showing that, in most cases, 3D vortices appear as nearly columnar vorticity (see Lin 2013; Richard et al. 2013), we keep on working on 2D models. This also permits faster numerical simulations, leading to the ability to explore a wider space of vortex structures.
We provide a detailed study of the structure and evolution of 2D vortices when considered as solutions of the compressible Euler’s equations, however they form. They are also studied for different models of protoplanetary disks. To this end, we will develop a new model of the vortices that permits us to fully describe their structure and to better understand their evolution.
This first paper is organized as follows. Section 2 is devoted to describing the main disk assumptions and the basic equations. The fiducial method used to produce the test vortices is presented in Sect. 3. A Gaussian vortex model is built in Sect. 4, with an accurate fit of control parameters of the vortices. In Sect. 5, we present a detailed study of the Gaussian parameters and discriminate the various vortex families. In Sect. 6, we claim the discovery of a new class of vortices whose size and mass largely exceed the expected values in standard simulations; finally, we speculate on the possible role of this class of vortices for planet formation.
2. Disk model and numerical method
2.1. Governing equations
We assume that the disk is composed of a mixture of molecular hydrogen and helium for which the perfect gas description can be applied. Integrations over the disk thickness lead to a surface density σ and a pressure P ∝ σT, where T is the gas temperature. A parcel of this fluid, moving at an average velocity V, has a specific total energy 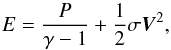 (1)where γ = 1.4 is the adiabatic index. In the adiabatic assumption, the entropy of a gas parcel, S = ln(P/σγ), remains constant in the Lagrangian sense and its time derivative, DtS, is zero.
(1)where γ = 1.4 is the adiabatic index. In the adiabatic assumption, the entropy of a gas parcel, S = ln(P/σγ), remains constant in the Lagrangian sense and its time derivative, DtS, is zero.
The conservation of mass, momentum, and energy lead to the standard time evolution equations of an inviscid compressible gas flowing around the star. In a polar coordinate system, these equations read 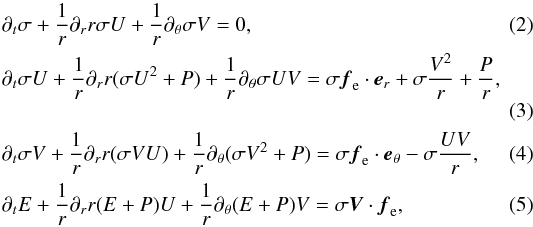 where V = Uer + Veθ is the gas velocity, and the gravitational force fe reduces to the Keplerian gravity of the star:
where V = Uer + Veθ is the gas velocity, and the gravitational force fe reduces to the Keplerian gravity of the star: 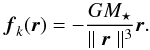 (6)The energy equation Eq. (5) includes the adiabatic property of the flow. We also used ∂∗ instead of ∂/∂ ∗.
(6)The energy equation Eq. (5) includes the adiabatic property of the flow. We also used ∂∗ instead of ∂/∂ ∗.
We will focus on the possible vortex solutions of these equations neglecting the self-gravity of the disk.
2.2. Equilibrium state of the disk
The equilibrium state of the disk corresponds to the steady solution of equations Eqs. (2)−(5). The various physical quantities are constrained by the observations of protoplanetary disks that provide models for the density and the temperature. Here we will use the MMSN model (Hayashi 1981) assuming that the density and temperature of the gas vary as power laws of the radial distance to the star,  with typical values of the gradient parameters βσ = −1.5 and βT = −0.5. It must be noted that the density σ0(r0) does not change the global flow since self-gravity is not taken into account. Then, using the perfect gas law, the pressure reads
with typical values of the gradient parameters βσ = −1.5 and βT = −0.5. It must be noted that the density σ0(r0) does not change the global flow since self-gravity is not taken into account. Then, using the perfect gas law, the pressure reads 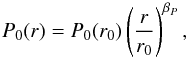 (9)with βP = βσ + βT, and the adiabatic expression of the sound speed is
(9)with βP = βσ + βT, and the adiabatic expression of the sound speed is 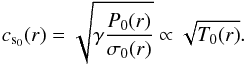 (10)At steady state, the gas is in circular motion around the star (U0 = 0) and fk(r) imposes a Keplerian angular velocity
(10)At steady state, the gas is in circular motion around the star (U0 = 0) and fk(r) imposes a Keplerian angular velocity 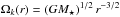 , which in a more general way can be written
, which in a more general way can be written 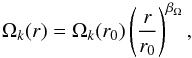 (11)where the parameter βΩ is equal to −3/2 in the Keplerian case. However, the centrifugal balance (in Eq. (3)) must account for the radial pressure gradient of the gas, so the steady angular velocity of the flow reads
(11)where the parameter βΩ is equal to −3/2 in the Keplerian case. However, the centrifugal balance (in Eq. (3)) must account for the radial pressure gradient of the gas, so the steady angular velocity of the flow reads 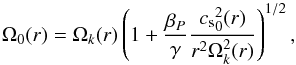 (12)which is generally sub-Keplerian, because in most cases βP< 0.
(12)which is generally sub-Keplerian, because in most cases βP< 0.
Now, we can close the system and normalize the various disk quantities assuming a pressure scale height 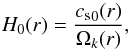 (13)with H0(r0) = 0.06r0 at the reference radius r0. This value is commonly used by the other workers and makes the comparison easier; it also corresponds to an aspect ratio of the disk small enough to be consistent with the 2D assumption.
(13)with H0(r0) = 0.06r0 at the reference radius r0. This value is commonly used by the other workers and makes the comparison easier; it also corresponds to an aspect ratio of the disk small enough to be consistent with the 2D assumption.
At equilibrium, the vorticity of the flow is defined by the simple scalar ω0(r) = r-1∂rrV0(r), where V0(r) = rΩ0(r) is the steady azimuthal velocity. It also writes 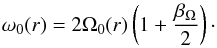 (14)The precision of this expression is ~ 5 × 10-4 for the values of the disk parameters chosen in this study. 1 The vorticity of the background flow is thus ω0(r) = Ω0(r)/2 when βΩ = −3/2, and differs from that of a pure Keplerian motion when the flow of the disk is sub-Keplerian (βP< 0).
(14)The precision of this expression is ~ 5 × 10-4 for the values of the disk parameters chosen in this study. 1 The vorticity of the background flow is thus ω0(r) = Ω0(r)/2 when βΩ = −3/2, and differs from that of a pure Keplerian motion when the flow of the disk is sub-Keplerian (βP< 0).
 |
Fig. 1 Formation of vortices by the RWI (fiducial case). From left to right: evolution of the density in the (r,θ) plane at t = 0, t = 30, and t = 190 rotations. The density is relative to the disk, σ/σ0(r)−1, and shows the formation of a chain of six vortices, in agreement with the m = 6 most unstable azimuthal mode. After fewer than 200 rotations, the chain merges in a single vortex. The aspect ratio of the vortices is of the order of 5.2 at t = 30 rotations and 7.4 at t = 190 rotations. |
2.3. Numerical method
The system of equations Eqs. (2)−(5) is solved using a finite volume method in order to preserve at best compressibility effects and shocks. It is inspired by the work of Inaba et al. (2005). A fixed grid is defined on an annular computational domain between rin = 5 and rout = 10 measured in astronomical units (AU). The domain is divided into Nr cells in the radial direction and Nθ cells in the azimuthal direction; in practice the typical values we used were Nr = 500 and Nθ = 1000. The spatial resolution in the radial direction, in terms of the disk scale height, depends on the distance to the star; for a reference radius at r0 = 7.5 AU we get 75 cells per scale height at rin, 45 cells at r0, and 32 cells at rout, as H0(r) varies in the disk as (r/r0)βT/ 2−βΩ.
The evolution of the conserved quantities in each cell is solved in time using a second order Runge-Kutta method and with a simultaneous determination of the flux and the source terms. The numerical fluxes are computed thanks to a third order limited parabolic interpolation at the cell boundaries. We also use an exact Riemann solver (Toro 1999). Combined with a non-splitting of the radial and azimuthal directions and a balance of the flux and source residual errors, inspired by Guillard & Daniel (2005), we obtain a stable and accurate numerical scheme that is perfectly appropriate for the long-term evolutions (more than 1000 rotations) necessary in the present work.
The boundary conditions are established at each sub-time-step of the second order time integration. We use two ghost-cells outside the computational domain with periodic conditions in the azimuthal direction and sheared damping conditions in the radial direction. The use of sheared damping conditions permits a smooth continuity with the steady solution assumed outside the computational domain and avoids spurious reflections at the inner and outer boundaries.
This numerical method, first developed for the simulation of protoplanetary disks, has been adapted for the simulation of other rotating fluids. The present code is called ROtating System Simulation for BI-fluids (ROSSBI) and will be fully described in an upcoming paper.
3. A fiducial way to get test vortices
The RWI is presently one of the most efficient ways to form vortices in 2D protoplanetary disks, particularly in the dead zone where the gas is assumed to be inviscid (Varnière & Tagger 2006). The choice of this non-homentropic instability is also adapted to form vortices in adiabatic disks (Lin 2013). Once the instability has grown and saturated, a single vortex remains in the computational domain; it survives independently of the initial conditions and for a large number of rotation periods (Li et al. 2001). Such vortices forget the initial conditions from which they grow and can be considered as quasi-steady solutions of Euler’s equations. Below, they will be used as test vortices for the purpose of exploring the space of the parameters and the long term evolution (cf. Paper II).
3.1. Vortex formation by RWI
Various initial conditions can make the disk unstable to RWI. Here we have used a locally isothermal density bump with a Gaussian radial profile, ![\begin{eqnarray} \sigma(r) & = &\sigma_0(r)\left[1 + f(r) \right] , \\ P(r) & =& P_0(r) \left[1 + f(r) \right] , \end{eqnarray}](/articles/aa/full_html/2015/07/aa24663-14/aa24663-14-eq64.png) where
where 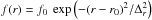 . The amplitude of the bump is set to f0 = 20% and its radial width to Δr = 0.3 AU. On the other hand, the initial velocity field is directly issued from the centrifugal balance:
. The amplitude of the bump is set to f0 = 20% and its radial width to Δr = 0.3 AU. On the other hand, the initial velocity field is directly issued from the centrifugal balance: ![\begin{eqnarray} &&U = 0, \\ &&V(r) = V_0(r) \left[1 - 2 r \frac{r-r_0}{\Delta_r^2} \frac{f(r)}{1 + f(r)} \frac{ {c_{\rm s}}_0^2(r)}{\gamma V_0^2(r)} \right]^{1/2}\cdot \end{eqnarray}](/articles/aa/full_html/2015/07/aa24663-14/aa24663-14-eq68.png) First, in order to test the consistency of our results with those from other workers (Li et al. 2001; Meheut et al. 2013), we perturbed the surface density and the pressure with periodic azimuthal perturbations of amplitude 1% and mode m. We found that m = 6 is the most unstable mode with an exponential growth rate of 0.71T-1, where
First, in order to test the consistency of our results with those from other workers (Li et al. 2001; Meheut et al. 2013), we perturbed the surface density and the pressure with periodic azimuthal perturbations of amplitude 1% and mode m. We found that m = 6 is the most unstable mode with an exponential growth rate of 0.71T-1, where 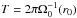 is the reference orbital period of the gas. This is in good agreement with the previous results cited above.
is the reference orbital period of the gas. This is in good agreement with the previous results cited above.
Then the instability was triggered with a random white noise of 1% amplitude and the evolution of the disk was followed on 200 periods (see Fig. 1). The density map shows (i) the formation of a chain of six vortices after 30 rotation periods, in agreement with the quick preeminence of the m = 6 mode (growth in ~ 1 rotation); (ii) the progressive merging of these vortices in a big solitary vortex. In fact, the duration of the merging process depends on the radial distribution of the noise initially injected in the system; for example in Fig. 1 the time necessary to obtain a single vortex was of the order of 190 rotations.
Inside the vortex, the density increases up to 55% above the disk level or nearly three times the amplitude of the initial bump. The radial width of the vortex is also larger than the initial Δr. Thus, in practice, it is difficult to completely control the shape of a test vortex produced with the RWI probably because a vortex also excites sound waves, which appear as spiral density patterns in the disk (see Bodo et al. 2005). After ~ 30 rotations, each vortex of the chain resulting from the instability is coupled to spiral arms whose amplitude is a significant fraction of the vortex amplitude. On the other hand, after 190 rotations, the solitary vortex is accompanied only by very tiny waves. This is due to the gradual increase of the aspect ratio of the vortices during the merging process.
We checked that the extent of the computational zone has no influence on the vortex formation and evolution. A run with a disk of size [1/4,4] r0 having the same radial resolution as with the standard disk size [2/3,4/3] r0 used in the paper poduces similar results. The RWI saturation and the structure of the final vortex both agree with better than 10% accuracy. Indeed, as disk gravity is ignored, the disk size has no consequence on the simulation.
3.2. Vortex structure and GNG model
In this section our goal is to describe the structure of the vortices, but we will neglect the closely related density waves which are difficult to take into account. To this end, we have plotted in Fig. 2 (top panel) the radial profiles of the relative density and pressure, defined as σ/σ0(r)−1 and P/P0(r)−1, respectively. A parabola or a Gaussian function can fit the radial structure of the vortex fairly well. The azimuthal structure is very similar and can also be adjusted by the same functions.
 |
Fig. 2 Structure of a quasi-steady Rossby vortex. Top: radial profiles of the density (solid line) and the pressure (dashed line) relative to the disk: σ/σ0(r)−1 and P/P0(r)−1, respectively. These radial cuts nicely well fit a Gaussian profile. Bottom: radial profile of the vorticity inside the vortex and relative to the disk. It is expressed as a Rossby number Ro(r) (see text). |
The higher amplitude of the relative pressure with respect to the relative density indicates that the vortex is a region of higher temperature than the background disk. Of course this property is in relation with the adiabatic assumption made for the gas and could be different in the presence of thermal transfer. Once estimated with the relation P0(r)[σ/σ0(r)]γ−1, we find that the relative pressure has an amplitude nearly equal to 0.8, a value in very good agreement with what can be measured on the plot.
In the lower part of Fig. 2 the Rossby number, defined as Ro(r) = [| ∇ × V | −ω0(r)]/[2Ω0(r)], is plotted as a function of the distance to the star. As expected, we see the signature of an anticyclonic vortex with a negative Rossby number, nearly constant on the vortex area and equal to Ro ~ −0.08. The positive values on each side of the vortex are residuals from the initial bump that triggered the RWI.
The velocity field of the vortex is presented in Fig. 3. The upper panel is the radial velocity of the gas in the azimuthal direction, whereas the lower panel is the azimuthal velocity V−V0(r) in the radial direction. Far from the vortex, the flow can be considered to be unperturbed by the presence of the vortex. From the vortex centre to the rest of the disk, the gas velocities begin to vary linearly, then reach an extremum, and finally smoothly recover the zero value corresponding to the background disk flow.
 |
Fig. 3 Velocity structure of a quasi-steady Rossby vortex (normalized to V0(r0)). Top: radial velocity in the vortex core located at r0 ~ 7.5 AU, in the azimuthal direction. We note the nearly linear behaviour around the centre at θ0 = 1.8. Bottom: azimuthal velocity V−V0(r) in the vortex core in the radial direction. We also note the linear shape between 7 and 8 AU. |
In the central part of the vortex, a simple linear model like the one derived by Kida (1981) or by Goodman et al. (1987; hereafter GNG), can account for the nearly linear spatial dependance of the velocity field. Here we will briefly describe the widely used standard GNG model for the purpose of comparison with our new vortex model.
The GNG model describes the velocity field of an incompressible elliptic vortex in a shearing sheet approximation. Using a cartesian frame of reference centred on the vortex core, with the x-axis in the er direction and the y-axis in the eθ direction, the two components of the gas velocity field are  In this model, η is the ratio of the internal turn-over frequency of the vortex to its orbital frequency, here Ω0 = Ωk(r0), and χ is the aspect ratio of the elliptic streamlines. Assuming also that the background has constant density and temperature, along with a polytropic equation of state with index n, we find by following GNG that the enthalpy
In this model, η is the ratio of the internal turn-over frequency of the vortex to its orbital frequency, here Ω0 = Ωk(r0), and χ is the aspect ratio of the elliptic streamlines. Assuming also that the background has constant density and temperature, along with a polytropic equation of state with index n, we find by following GNG that the enthalpy 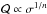 reads
reads 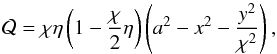 (21)and
(21)and 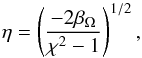 (22)where a is the extent of the vortex in the x direction. In the central part of the vortex the model clearly shows a linear dependance of the velocity field and a parabolic dependance of the enthalpy (with approximately the same dependance for the density and the pressure). This is in good agreement with the structure of our test vortices.
(22)where a is the extent of the vortex in the x direction. In the central part of the vortex the model clearly shows a linear dependance of the velocity field and a parabolic dependance of the enthalpy (with approximately the same dependance for the density and the pressure). This is in good agreement with the structure of our test vortices.
Finally, in the local rotating frame, the vorticity is 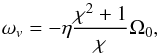 (23)which contains the shearing sheet vorticity.
(23)which contains the shearing sheet vorticity.
However, the GNG model also has a number of limitations:
-
the transition between the inner part of the vortex and thebackground flow cannot be taken into account, resulting indiscontinuous velocity field and enthalpy;
-
it is limited to constant profiles of the density and the temperature backgrounds (it is hard to account for radial stratification);
-
in principle, the model is limited to closed elliptic streamlines and excludes the compressional effects of strong vortices.
We now propose a vortex model that can fulfill the above requirements and that allows us to consider a wider range of the vortex parameters.
4. A Gaussian model of the vortices
We search for a vortex model in a polar system of coordinates, avoiding the local shearing-sheet approximation. We will conserve the radial dependance of Ω0, σ0 and T0, thus preserving the radial stratification of the disk.
4.1. Velocity equations
The evolution equations of the fluid velocity, derived from the continuity and the momentum equations, read 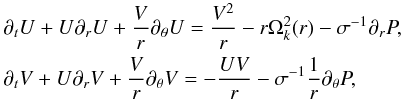 (24)and obviously account for the compressibility of the gas. When the disk contains a vortex, the gas velocity field can be decomposed into the superimposition of a vortex velocity field (u, v) on top of the background flow:
(24)and obviously account for the compressibility of the gas. When the disk contains a vortex, the gas velocity field can be decomposed into the superimposition of a vortex velocity field (u, v) on top of the background flow: 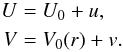 (25)Of course when the vortex velocities u and v tend to zero or cancel, the gas flow equals the unperturbed background flow.
(25)Of course when the vortex velocities u and v tend to zero or cancel, the gas flow equals the unperturbed background flow.
Then, the vortex orbiting at r0 is assumed to be a quasi-steady pattern rotating at the angular velocity Ω0(r0), which means that the background advection operator cancels, ∂t + Ω0(r0)∂θ = 0. Combining with Eq. (11), one obtains the non-linear system of equations that must satisfy a vortex solution 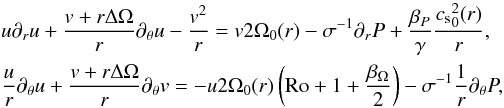 (26)where ΔΩ = Ω0(r)−Ω0(r0), indicates the sub-Keplerian nature of the flow.
(26)where ΔΩ = Ω0(r)−Ω0(r0), indicates the sub-Keplerian nature of the flow.
The expression between parentheses (normalized to 2Ω0(r)) is the sum of the vorticity of the vortex, 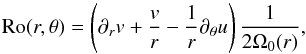 (27)and of the background vorticity in the inertial frame, 1 + βΩ/ 2, as presented in Sect. 2.2. The parameter Ro will be referred to as a relative Rossby number in the rest of the paper; it is negative for an anticyclonic vortex and usually larger than 5% for large scale structures.
(27)and of the background vorticity in the inertial frame, 1 + βΩ/ 2, as presented in Sect. 2.2. The parameter Ro will be referred to as a relative Rossby number in the rest of the paper; it is negative for an anticyclonic vortex and usually larger than 5% for large scale structures.
The left hand sides of the equations contain terms that are either of third order in space (like u∂ru or (v + rΔΩ)r-1∂θv) or smaller than the others in the limit of small velocities. If they are completely neglected, we obtain a linear system of equations that can provide the vortex velocity field as a function of the density and the pressure gradients: 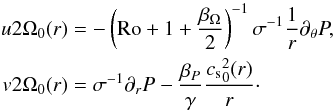 (28)It must be noted that these expressions correspond to a generalized geostrophic balance in which local and background vorticities are taken into account; this is in contrast with the standard geostrophic equilibrium (e.g. Adams & Watkins 1995).
(28)It must be noted that these expressions correspond to a generalized geostrophic balance in which local and background vorticities are taken into account; this is in contrast with the standard geostrophic equilibrium (e.g. Adams & Watkins 1995).
To get the solution of the velocity equations, it is obviously necessary to close the system for density and pressure. To this end, we used the identities 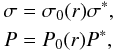 (29)with σ∗ = P∗ = 1 for an unperturbed disk. In the polytropic assumption for the perturbed disk, one sets
(29)with σ∗ = P∗ = 1 for an unperturbed disk. In the polytropic assumption for the perturbed disk, one sets 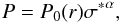 (30)with α = γ for an adiabatic vortex, α = 1 for an isothermal vortex, and other values of α for different thermodynamical assumptions.
(30)with α = γ for an adiabatic vortex, α = 1 for an isothermal vortex, and other values of α for different thermodynamical assumptions.
 |
Fig. 4 Velocity field of a Rossby vortex: comparison of the numerical solution with the Gaussian model. Top row: values issued from the simulation of the radial velocity, the azimuthal velocity V−V0(r), and the Rossby number, from left to right, respectively. Bottom row: residual difference between the numerical data and the values issued from the model for the radial and azimuthal velocities and for the Rossby number, from left to right, respectively (see text for details). |
Inspired by the GNG model, we define a pseudo-enthalpy: 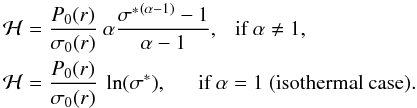 (31)We thus obtain the velocity field of the vortex solution:
(31)We thus obtain the velocity field of the vortex solution: 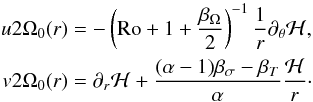 (32)This new model provides vortex-shaped velocity fields from approximate enthalpy functions. This is in contrast with the GNG model, which derives density and pressure from the elliptic streamlines of the Kida’s incompressible model. This approach leads to more general solutions because any profile of ℋ can define a velocity field that accurately satisfies the equations near the vortex centre.
(32)This new model provides vortex-shaped velocity fields from approximate enthalpy functions. This is in contrast with the GNG model, which derives density and pressure from the elliptic streamlines of the Kida’s incompressible model. This approach leads to more general solutions because any profile of ℋ can define a velocity field that accurately satisfies the equations near the vortex centre.
In order to test the relevance and accuracy of this model, we have compared the velocity field in Eq. (32), in the adiabatic case (α = γ), with the velocity field directly issued from the numerical simulation. To this end, we have used the pressure P∗ = P/P0(r) in addition to σ∗ in Eq. (31) to compute ℋnum, to better fit the equations, since σ∗α−1 = P∗/σ∗. The results we get for a test vortex, resulting from a RWI after 190 rotations, are presented in Fig. 4.
In the top row of Fig. 4, we clearly see how smoothly the velocity field merges with the unperturbed disk in both radial and azimuthal directions. Week spiral patterns reveal the emission of sound waves, but their amplitude is a very small fraction of the vortex values in that case. An axisymmetric pattern due to the residual vorticity left after RWI has saturated is noticeable at corotation. In the vortex core, we also observe small scale structures in the vorticity distribution, that are remnants of the successive merging processes and also indicative of the very small viscosity of our code.
The bottom row of Fig. 4 shows the differences between the numerical data and the theoretical values given by the vortex model. The residuals can be a small percentage of the highest values reached inside the vortex. This occurs in the regions where the quasi-geostrophic equilibrium, on which our model is based, is satisfied: (i) in the vortex core; and (ii) close to the corotation zone where Rossby waves have been generated by the instability. On the other hand, stronger residuals are observed in the vicinity of the spiral-wave patterns because the associated compressional effects cannot be properly described by our model.
Thus, the vortex solution derived from the first order approximation model of the steady-state Euler’s equations and based on a pseudo-enthalpy function ℋ is able to describe with a good accuracy the full numerical solution of the non-linear conservation equations. Now, the next step is to find an analytic expression of ℋ in order to construct a complete vortex model.
4.2. Gaussian approximation
Guided by the shape of the test vortices derived in Sect. 3 and in accordance with a common assumption in incompressible fluid dynamics (see e.g. Bodo et al. 2007), we have represented ℋ by a Gaussian function of r and θ. This 2D vortex model is centred on r0 and θ0 and can be parametrized with three quantities:
-
ℋ0, the amplitude at (r0,θ0);
-
χr, a normalized radial extent (or width Δr = r0χr);
-
χθ, an azimuthal aspect ratio (or width Δθ = χrχθ).
Thus, as a function of r and θ, the pseudo-enthalpy ℋ is approximated by ![\begin{equation} \label{Def_enthalpy} \mathcal{H}= \mathcal{H}_0 \exp \left[-\chi_r^{-2} \left[\left(\frac{r}{r_0}-1 \right)^2 + \chi_\theta^{-2}\left(\theta-\theta_0\right)^2 \right] \right], \end{equation}](/articles/aa/full_html/2015/07/aa24663-14/aa24663-14-eq151.png) (33)which reaches a maximum at the vortex centre and smoothly connects to zero at the background level. We note that
(33)which reaches a maximum at the vortex centre and smoothly connects to zero at the background level. We note that  in the GNG model behaves in roughly the same way as ℋ but presents a discontinuity; its parabolic expression can, in fact, be obtained through a second order expansion of ℋ.
in the GNG model behaves in roughly the same way as ℋ but presents a discontinuity; its parabolic expression can, in fact, be obtained through a second order expansion of ℋ.
With this Gaussian model of ℋ, the system Eq. (32) leads to the approximate expression of the velocity field of a quasi-steady vortex solution: ![\begin{equation} \label{Velocity_gauss} \begin{aligned} u & = \frac{1}{2 \Omega_0(r)} \left( {\rm Ro} + 1 + \beta_\Omega /2 \right)^{-1} \frac{2}{r \chi_r^2} \frac{\theta -\theta_0}{\chi_\theta^2} \mathcal{H}, \\ v & = \frac{1}{2 \Omega_0(r)} \left[- \frac{2}{r_0 \chi_r^2} \left(\frac{r}{r_0}-1\right) + \frac{(\alpha -1) \beta_\sigma - \beta_T}{\alpha} \frac{1}{r} \right] \mathcal{H}. \end{aligned} \end{equation}](/articles/aa/full_html/2015/07/aa24663-14/aa24663-14-eq153.png) (34)A second order expansion of this velocity field permits the recovery of the linear behaviours u ∝ θ−θ0 and v ∝ r−r0, which are obtained from the Kida and GNG models. This Gaussian model, combined with the velocity field obtained before, can therefore be interpreted as a higher order class of vortex models.
(34)A second order expansion of this velocity field permits the recovery of the linear behaviours u ∝ θ−θ0 and v ∝ r−r0, which are obtained from the Kida and GNG models. This Gaussian model, combined with the velocity field obtained before, can therefore be interpreted as a higher order class of vortex models.
However, in the first equation of the above system, the Rossby number Ro appears as an undetermined function of r and θ. A simple way to close the system is to assume Ro as a constant equal to its value at the vortex centre Ro(r0,θ0). This can be obtained by solving the equation Ro(r,θ) = ω/ [2Ω0(r)], where ω = r-1∂r(rv)−r-1∂θu. As a function of the parameters defining the Gaussian, we found the relation ![\begin{eqnarray} {\rm Ro} & =& - \left( r_0 \chi_r \Omega_0(r_0) \sqrt{2} \right)^{-2} \mathcal{H}_0 \nonumber \\ &&\quad \times \left[1 + \left(\chi_\theta^2 ({\rm Ro} + 1 + \beta_\Omega /2) \right)^{-1} + \frac{\beta_\Omega}{2} \chi_r^2 \frac{(\alpha -1) \beta_\sigma - \beta_T}{\alpha} \right] \cdot \end{eqnarray}](/articles/aa/full_html/2015/07/aa24663-14/aa24663-14-eq159.png) (35)In brackets at the right-hand side of this equation, the last term is much smaller than the others for a huge range of disk gradients. Indeed, it is less than 10-2 since χr is generally smaller than 10-1; moreover, in the case of an isentropic flow, it exactly cancels since βT = (γ−1)βσ. In contrast, the second term in brackets cannot be neglected, especially when χθ ≲ 5 and Ro ≲ −0.1, as in many of the numerical simulations.
(35)In brackets at the right-hand side of this equation, the last term is much smaller than the others for a huge range of disk gradients. Indeed, it is less than 10-2 since χr is generally smaller than 10-1; moreover, in the case of an isentropic flow, it exactly cancels since βT = (γ−1)βσ. In contrast, the second term in brackets cannot be neglected, especially when χθ ≲ 5 and Ro ≲ −0.1, as in many of the numerical simulations.
So, we found that the Rossby number is related to the vortex parameters, but is independent from the global disk parameters (βσ, βT) and from the thermodynamical index α. This property makes Ro a better parameter than ℋ0 to define a vortex, as Ro also permits us to directly quantify the vortex strength or vorticity. This is the reason why, in the rest of the paper, each vortex will be parametrized with a triplet (Ro,χr,χθ), replacing the pseudo-enthalpy ℋ0 by ![\begin{equation} \label{Equ_H0} \mathcal{H}_0 =- 2 {\rm Ro} \left(r_0^{ } \chi_r \Omega_0(r_0)\right)^2 \left[1 + \left(\chi_\theta^2 ({\rm Ro} + 1 + \beta_\Omega /2) \right)^{-1} \right]^{-1}\!. \end{equation}](/articles/aa/full_html/2015/07/aa24663-14/aa24663-14-eq168.png) (36)This relation is very instructive regarding the main properties of the vortices. In particular, it indicates that the amplitude of the bump, associated with a vortex, increases (i) linearly with the Rossby number (or vorticity) and (ii) quadratically with the radial extent χr. The amplitude also changes as a function of the azimuthal aspect ratio, very weakly for χθ> 7 but more significantly for χθ< 7, with variations that can modulate by more than 30% the estimation of ℋ0.
(36)This relation is very instructive regarding the main properties of the vortices. In particular, it indicates that the amplitude of the bump, associated with a vortex, increases (i) linearly with the Rossby number (or vorticity) and (ii) quadratically with the radial extent χr. The amplitude also changes as a function of the azimuthal aspect ratio, very weakly for χθ> 7 but more significantly for χθ< 7, with variations that can modulate by more than 30% the estimation of ℋ0.
In summary, starting from a triplet of parameters (Ro,χr,χθ), it is possible to derive an approximate vortex solution of the steady Euler equations. First, the Gaussian enthalpy ℋ is determined from the triplet using Eqs. (33) and (36); second, the velocity field is deduced from Eq. (34); and, finally, the density and pressure are derived thanks to equations Eqs. (31), (30), and (29).
 |
Fig. 5 Comparison of the velocity field issued from the numerical simulation (solid line) and from the model, when using ℋnum (dashed line) and when using ℋGauss (dashed-dot line) (see text for details). Top: for the radial component of the velocity. Bottom: for the azimuthal component of the velocity, V−V0(r). |
To test relevance and accuracy of our model, we have compared the theoretical vortex solution with the test vortices directly issued from the numerical integration of Euler’s equations. To this end, we used the same method as in Sect. 4.1: (i) a test vortex is produced by a RWI; (ii) its enthalpy ℋnum is calculated and its characteristic parameters (Ro,χr,χθ) are measured to provide ℋGauss, the Gaussian approximation of ℋ; and (iii) the theoretical vortex solution and its Gaussian approximation are compared with the numerical vortex solution.
The results we have found for the velocity field in the case of the last vortex obtained from the RWI are presented in Fig. 5. The following values are plotted simultaneously: the numerical values of the test vortex (solid line), the theoretical values obtained with ℋnum (dashed line), and the theoretical values obtained with the Gaussian approximation (dot-dashed line). We note that these are the velocity differences to the background flow.
We clearly see that both the radial velocity (top panel) and the azimuthal velocity (bottom panel) are accurately fitted by the Gaussian model in the inner part of the vortex between the position of the two extrema. It gives the correct values of the velocities and of the gradients inside the vortex core. The model also makes a smooth connection with the background flow, but the intermediate values deviate from the numerical solution. In fact, the Gaussian approximation tends to underestimate the extreme values of the two velocity components and also the sharpness of the connection between the vortex and the background flow. However, the estimated values derived from ℋnum (dashed lines) fit the numerical data with a good accuracy.
Despite these small discrepancies, our Gaussian model is the first to provide a consistent and continuous description of quasi-steady vortices in Keplerian flows. It can be considered as an analytical tool for vortex studies and provides excellent initial conditions and test vortices for numerical simulations. In particular, it permits the vortex shape to be controlled, avoiding the use of discontinuous models like the GNG model that strongly disturb the disk evolution during the first rotations.
4.3. A library of Gaussian vortices
In this section we use the Gaussian model to build up a large sample of test vortices for studying vortex stability in a wide range of the parameters (Ro,χr,χθ). Some authors have already addressed the stability problem (Bodo et al. 2007; Godon & Livio 1999; Davis et al. 2000), but their studies are limited (i) by a lower performance of the vortex model based on the Kida velocity field, such as the GNG model; (ii) by an inappropriate choice of the control parameters; and (iii) by a poor sample of the test vortices.
In contrast, we are able to produce a wide sample of vortices by performing about 300 simulations from numerous triplets of parameters and also for different values of the disk parameters. Our choice of the disk parameters deviates from the standard minimum mass solar nebula (MMSN) by assuming −2 <βσ< 0.5 for the density gradient and −2 <βT< 0.5 for the temperature gradient; we have also considered various values of the disk scale height with H0(r0) /r0 =0.042, 0.06, 0.073 or 0.085.
Figure 6 shows the distributions of the parameters for the quasi-steady vortices of our sample. In the top panel the Rossby number ranges from −0.07 to −0.33, but for most of the vortices we have −0.17 < Ro < −0.11. In the middle panel the radial extent ranges from χr = 0.02 to χr = 0.15, but for most of the vortices 0.05 <χr< 0.08, consistently with the assumed values of the scale height. Finally, in the bottom panel, the aspect ratio ranges from 2 to 18, but most of the vortices have χθ ~ 6. We must stress that these three distributions do not reflect which vortex parameters are the most frequent in protoplanetary disks since many simulations were performed with the same Gaussian parameters but different choices for the disk profile. This, of course, biases the morphological sorting of the simulated vortices.
 |
Fig. 6 Distribution of the vortex parameters in our sample of simulated vortices. From top to bottom: the Rossby number Ro, the radial extent ratio χr, and the azimuthal aspect ratio χθ. In each case the number of vortices we get for a given value of the parameter is plotted. |
This sample of test vortices is large enough to check the analytical results obtained with the Gaussian model, but also to explore new classes of vortices. All the vortex parameters we have tested are reported in the above sample, except in a number of additional cases explicitly mentioned in the text.
5. Morphology and classification of the vortices
5.1. Radial extent: from dwarf to giant vortices
The radial extent of vortices can be an important parameter for disk evolution and planet formation scenarios. Indeed, the more extended a vortex is, the larger its gas mass, the stronger the disk/vortex interaction, and the higher the number of captured particles. The local increase of the densities of gas and solid particles can make collisional growth and gravitational instabilities easier. Setting realistic boundaries on this quantity is thus required in order to constrain such possibilities.
A vortex in a sheared flow is commonly characterized by its radial extent Δr, which roughly scales in Keplerian disks as the vertical scale height at the vortex position, H0(r0). In our sample, Δr ranges from 0.33H0 to 2.5H0, but additional simulations have shown that vortices as small as Δr = 0.1H0 can also survive many hundreds of rotations. These tiny vortices can form by RWI if the initial bump is narrow enough, or by other instabilities like the baroclinic instability.
In Fig. 7 are reported the vorticity and density associated with very small vortices obtained by the numerical relaxation of initially Gaussian vortices (of course numerical resolution has been adapted to the vortex size). The vorticity, plotted in terms of the Rossby Number (top panel), is as small as Ro = −0.05; it spreads over a very small radial extent (Δr<H0/ 10) around the core and nearly vanishes elsewhere. The density map (lower panel) displays differently to the vorticity with a bigger core and two long spiral arms; the density perturbation is at a very low level with only 3 × 10-3 the disk density.
It is striking that such small vortices, associated with such weak density perturbations, can keep a coherent structure for very long durations. Their lifetime is found longer than 500 rotation periods and can reach the limits imposed by numerical viscosity. Such properties were never pointed out for isolated vortices and we have called them “dwarf vortices”. The existence of these vortices could also affect the evolution of small scale turbulence as described by (Johnson & Gammie 2005; Mamatsashvili & Chagelishvili 2007; Mamatsashvili & Rice 2009) with the possible formation of small scale persistent structures. Our model would be well suited to mimic such a situation. Of course, we must keep in mind that the study of these tiny vortices could be inappropriate in a 2D context, particularly if the typical scales in the mid-plane are much smaller than the vertical scales. In this case 3D studies are necessary, but this is out of the scope of the present paper.
 |
Fig. 7 Dwarf vortex simulated from an initial Gaussian vortex with parameters (Ro,χr,χθ) = (−0.05,5 × 10-3,8). Top: the very weak but coherent vorticity (Rossby number) of the flow inside the vortex. Bottom: the density, relative to the disk, shows the nearly Gaussian vortex core associated with spiral waves. |
By contrast, larger values of Δr are more frequently investigated. However, since a coherent vortex must keep a subsonic structure, it is commonly thought that Δr has to be less than H0 to avoid destruction by the background shear, e.g. Bodo et al. (2007). At larger distances from the vortex centre, the gas parcels no longer belong to a coherent pattern since sound waves cannot cross the vortex in less than an orbital period. Actually, these simple arguments do not account for the true vortex properties.
Here, our Gaussian model is used to revisit the problem since it permits us to approximatively describe the connection between inner regions of the vortex and background flow. First, the norm of the gas velocity inside the vortex is required to be smaller than the local sound speed. Then, we assume that the norm of the velocity vector can be maximized by its azimuthal component, which also contains the main dependance in the radial direction. In the context of the Gaussian model, this velocity reads 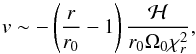 (37)where we have neglected the additional term in 1 /r (which is zero in the case of an isentropic disk). From Eqs. (33) and (36), we find that the maximum value of the velocity is reached for
(37)where we have neglected the additional term in 1 /r (which is zero in the case of an isentropic disk). From Eqs. (33) and (36), we find that the maximum value of the velocity is reached for 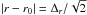 and is equal to
and is equal to 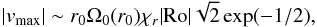 (38)where the exponential term comes from the Gaussian part of ℋ.
(38)where the exponential term comes from the Gaussian part of ℋ.
With the subsonic requirement, | vmax | <cs, we find the maximum value of the radial extent ratio 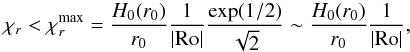 (39)which is a function of the Rossby number. In the limit of very strong vortices (Ro ~ −1), we find again that
(39)which is a function of the Rossby number. In the limit of very strong vortices (Ro ~ −1), we find again that 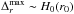 . For the typical vortices of our sample we obtain Ro ~ −0.12, and we get
. For the typical vortices of our sample we obtain Ro ~ −0.12, and we get 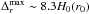 , a much larger value than commonly thought.
, a much larger value than commonly thought.
A large vortex also corresponds to a strong enhancement of the surface density, which can be estimated with Eqs. (36) and (31) of the Gaussian model; this over-density writes in the form ![\begin{equation} \label{Equ_sima_max} \begin{aligned} \sigma^* = \left[{2(\gamma-1)} {\frac{r_0^2~|{\rm Ro}| ~\chi_r^2}{ H_0^2(r_0)}} \right. \left. \left[1+\frac{1}{\chi_\theta^2 ({\rm Ro}+1+ \beta_\Omega /2)} \right]^{-1} \right]^{1/(\gamma-1)}. \end{aligned} \end{equation}](/articles/aa/full_html/2015/07/aa24663-14/aa24663-14-eq212.png) (40)We have tested numerically the existence of such vortices starting from a vortex solution with (Ro,χr,χθ) = (−0.2,0.19,4.5) in a disk with H0(r0) /r0 = 0.06. This initial approximate solution rapidly stabilizes into a giant vortex whose radial size is 3H0(r0), in agreement with the maximum value
(40)We have tested numerically the existence of such vortices starting from a vortex solution with (Ro,χr,χθ) = (−0.2,0.19,4.5) in a disk with H0(r0) /r0 = 0.06. This initial approximate solution rapidly stabilizes into a giant vortex whose radial size is 3H0(r0), in agreement with the maximum value 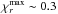 associated with this Rossby number. Figure 8 presents the simulated vortex after 65 rotations around the star; the upper panel shows the density map relative to the background, σ/σ0(r)−1. This vortex corresponds to a strong density bump, with a maximum of about 4.5 that can survive many hundreds of rotation periods.
associated with this Rossby number. Figure 8 presents the simulated vortex after 65 rotations around the star; the upper panel shows the density map relative to the background, σ/σ0(r)−1. This vortex corresponds to a strong density bump, with a maximum of about 4.5 that can survive many hundreds of rotation periods.
Thus, we have found a new class of very large vortices associated with very strong perturbations of the density and the pressure. They survive as stable structures in the disk and stay in a quasi-steady equilibrium for a large number of rotation periods. This is a new result that deserves a more detailed study.
 |
Fig. 8 Structure of a giant vortex obtained with the parameters (Ro,χr,χθ) = (−0.2,0.19,4.5). Top: density inside the vortex; the maximum value in the vortex centre is more than 4 times higher than in the disk. Bottom: mach number inside the vortex (see text). Ma< 0.5 in the core, but is of the order of ~ 0.8 near the shocked region of the right spiral arm. The streamlines show the anticyclonic motion. |
It is interesting to note that, inputing the above vortex parameters, Eq. (40) provides a density enhancement σ∗−1 = 4.4 very similar to the one measured in the simulation. This indicates that the Gaussian model can provide a suitable vortex solution of the non-linear quasi-steady equations, even in the case of very strong perturbations. This was not possible with Kida and GNG models.
The lower part of Fig. 8 shows the magnitude of the velocity relative to the background flow and compared to the local sound speed. We have plotted this Mach number defined as 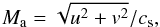 (41)with the local adiabatic sound speed
(41)with the local adiabatic sound speed 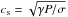 . It is important to use the local sound speed here and not the background value cs0.
. It is important to use the local sound speed here and not the background value cs0.
The results confirm the subsonic property of the vortex since Ma has a typical value ~ 0.5 and is everywhere under unity. The grey streamlines indicate the vortical motion of the gas. Owing to the compressional effects, they are not exactly closed ellipses but rather lines spiraling outward from the vortex centre. In the south-east direction, they tend to converge to a discontinuity that characterizes a spiral shock-wave, clearly visible on the density map. In this region, the Mach number increases to a maximum of 0.8 near the vortex boundary.
One can observe that the Mach number already reaches the sonic limit Ma ~ 1, even if the radial extent of the vortex (χr = 0.19) is significantly smaller than the limit 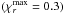 . Indeed, the radial velocity is strongly perturbed in the spiral arms and, particularly, close to the vortex border; this contributes to locally increase the Mach number. Nevertheless, the criterion defined in Eq. (39), which is only based on azimuthal velocity perturbations, empirically provides a satisfying condition for the existence and survival of giant vortices in protoplanetary disks.
. Indeed, the radial velocity is strongly perturbed in the spiral arms and, particularly, close to the vortex border; this contributes to locally increase the Mach number. Nevertheless, the criterion defined in Eq. (39), which is only based on azimuthal velocity perturbations, empirically provides a satisfying condition for the existence and survival of giant vortices in protoplanetary disks.
5.2. Vorticity and aspect ratio: from weak to strong vortices
The function Ro(r,θ) defined in Eq. (27) quantifies the rotating strength of a vortex. From the Gaussian structure of the velocity field, we can expect Ro to be a bump function. However, in this paper, we will avoid too complex developments and Ro will be approximated by a negative top-hat function centred on the vortex core and with an amplitude chosen as the minimum value of Ro(r,θ). We will refer to this constant as the Rossby number of the vortex.
In the vortex library, this Rossby number reaches values that range from −0.33 for the strongest vortex to −0.07 for the weakest. In terms of vorticity, this corresponds to the background vorticity scaled by a factor of −1.3 to −0.3, respectively. As a consequence, we find that the total vorticity at the vortex centre, 2Ω0(r0)(Ro + 1 + βΩ/ 2), may reach inappropriate negative values. This occurs for Ro ≤ −0.25 and results from the assumptions made while constructing the Gaussian model, particularly when neglecting u∂θu in front of the other terms. Thus, this Gaussian model provides suitable vortex solutions for the weak vorticities (i.e. −0.2 < Ro < 0) for which 2Ω0Ro ~ r-1∂r(rv).
On the other hand, for stronger vorticities (Ro ≤ −0.25), the model discards from the exact vortex solution, but still provides appropriate initial conditions for numerical simulations. The quasi-steady vortices resulting from these simulations have strong vorticities and also other quantities that slightly differ from the initial values; only the radial velocity is found to change a lot from the initial condition. In the library, a number of vortices were produced with −0.75 < Ro < −0.25.
Now, since the actual dependance of Ro could have consequences on the structure and evolution of the vortices, it is important to examine the limitations of the top-hat approximation. Figure 9 shows the comparison of two radial profiles taken at the vortex centre, obtained for a same radial extent χr = 0.09, but for different values of the Rossby number, namely Ro = −0.1 (solid line) and Ro = −0.29 (dashed line). In this figure, the radial extent, between r = 7 AU and r = 8AU, is consistent with the total Gaussian width of the vortices, 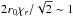 AU. It is also striking that the two radial profiles have the same slopes at the vortex border.
AU. It is also striking that the two radial profiles have the same slopes at the vortex border.
The differences between the two cases appear in the inner regions, near the vortex centre. A top-hat is a good fit on 80% of the vortex surface for Ro = −0.1, whereas it is a poor fit for the case with Ro = −0.29. As a general trend, we also find that the radial profile of Ro(r,θ) can be approximated by a top-hat when the value at the vortex centre Ro ≳ −0.12, but this is hardly possible for more negative values. The Gaussian shape of the vorticity resulting from our model is thus a better fit to the data than the top-hat profile produced by the GNG model. One can expect limitations of elliptic streamline models, when Ro ≲ −0.12.
 |
Fig. 9 Comparison of the radial dependance of Ro for two vortices with χr = 0.09. The vortex with Ro = −0.1 (solid line) can easily be approximated with a top-hat whereas the strongest vortex with Ro = −0.29 (dashed line) cannot be approximated in the same way. |
This effect is even stronger for smaller radial extent since the vorticity profile inside the vortex is, then, steeper (for a constant value of Ro at the centre). In the limit of χr → 0, we get the so-called point vortex, with a Dirac vorticity profile, of the 2D turbulence (see Adams & Watkins 1995). This is consistent with the Gaussian profiles we found in our simulations and which were placed at the core of our model. Indeed, a Dirac profile can be expressed as a limit of Gaussian functions 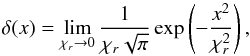 (42)so for standard values of χr we retrieve the Gaussian profiles of our model. However, further analytical developments would be necessary to go from a useful Gaussian approximation to true Gaussian vortex solutions. Finally, this model does not exhibit any dependence between the radial extent χr and the Rossby number Ro, except in the case of giant vortices, where χr is limited by an additional subsonic condition, as discussed in Sect. 5.1.
(42)so for standard values of χr we retrieve the Gaussian profiles of our model. However, further analytical developments would be necessary to go from a useful Gaussian approximation to true Gaussian vortex solutions. Finally, this model does not exhibit any dependence between the radial extent χr and the Rossby number Ro, except in the case of giant vortices, where χr is limited by an additional subsonic condition, as discussed in Sect. 5.1.
On the other hand, the azimuthal aspect ratio χθ is known to decrease for increasing absolute values of the Rossby number. This was pointed out in previous models (Kida and GNG) and was also observed in our vortex library. This property comes out from the linearized continuity equation, after assuming that the density (or the enthalpy) is steady at the lowest order. As the velocity field has a linear behaviour in the vortex centre (cf. Eq. (34)), the second order terms in r/r0−1 and θ−θ0 left in the conservation of enthalpy must cancel. We have respected this condition in the case of the GNG model, and obtained the following equation relating Ro to χθ, in accordance with Chavanis (2000): 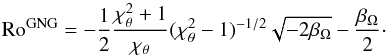 (43)In the case of an isentropic and homogeneous background, we also derived a similar relation between Ro and the aspect ratio χθ for Gaussian vortices:
(43)In the case of an isentropic and homogeneous background, we also derived a similar relation between Ro and the aspect ratio χθ for Gaussian vortices: 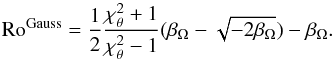 (44)The two models lead to different equations; however, they both confirm that elongated vortices have a small vorticity. When χθ → ∞, the Rossby number tends toward
(44)The two models lead to different equations; however, they both confirm that elongated vortices have a small vorticity. When χθ → ∞, the Rossby number tends toward 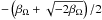 which is approximately −0.1 for βΩ = −3/2. Interestingly, both models converge to the same asymptotic value corresponding to the smallest vorticity required for the existence of elongated vortices. This conclusion appears consistent with the building up of the vortex library, since we were not able to obtain stable numerical solutions for Ro > −0.07. In this case, vortices are sheared away in a nearly axisymmetric ring. This numerical value is also in rough agreement, within 30%, with the ~−0.1 analytical value.
which is approximately −0.1 for βΩ = −3/2. Interestingly, both models converge to the same asymptotic value corresponding to the smallest vorticity required for the existence of elongated vortices. This conclusion appears consistent with the building up of the vortex library, since we were not able to obtain stable numerical solutions for Ro > −0.07. In this case, vortices are sheared away in a nearly axisymmetric ring. This numerical value is also in rough agreement, within 30%, with the ~−0.1 analytical value.
 |
Fig. 10 Rossby number at the vortex centre, as a function of the aspect ratio χθ for the vortices used in our sample (black circles). Different expressions relating these two quantities are shown: the GNG model (solid line) which underestimates Ro as soon as χθ< 7, and the Gaussian model (dashed line) which better fits the data for 2 <χθ< 20. We note the logarithmic scale for χθ. |
In Fig. 10, we compared the correlation bewteen the Rossby number Ro (measured at the vortex centre) and χθ of the vortex library, with the relations derived from the GNG model RoGNG, and from the Gaussian model RoGauss. We note, however, that we have included a shift of 10% in the values of χθ, to better fit the data. This shift is probably due to errors in the measurement of the aspect ratios on the numerical data. The best agreement between the analytical relations and the numerical data is in the case of elongated vortices (χθ> 7), as expected. For smaller aspect ratios, however, the Gaussian model is the most accurate since the deviation in the determination of the Rossby number can reach 50% when χθ< 4 for the GNG model. This discrepancy arises from the failure of the top-hat approximation in the GNG model.
Surprisingly, the relation derived from the Gaussian model quite nicely fits the numerical data even for χθ as small as 2.5 and for Ro < −0.25, which is beyond the limit of validity of our model. This suggests that some analytical improvements of the Gaussian model could be possible providing a larger accessible domain for the parameters.
5.3. Two parameters to initiate numerical vortex solutions
Following the above model, three parameters (Ro,χr,χθ) are necessary to define a Gaussian vortex and start the numerical simulations. However, as the Rossby number also depends on the azimuthal aspect ratio (see Eq. (43) or (44)), only two parameters are sufficient. In practice, we have chosen the radial extent χr and the Rossby number Ro, while the azimuthal aspect ratio is derived by inverting Eq. (44): ![\begin{equation} \label{Eq_Chi_Theta_Gauss} \chi_\theta = \left[\frac{{\rm Ro} + \beta_\Omega + \left(\beta_\Omega - \sqrt{-2\beta_\Omega}\right)/2}{{\rm Ro} + \beta_\Omega - \left(\beta_\Omega - \sqrt{-2\beta_\Omega}\right)/2}\right]^{1/2}\cdot \end{equation}](/articles/aa/full_html/2015/07/aa24663-14/aa24663-14-eq269.png) (45)From the vortex library we observed that χθ approximately scales as
(45)From the vortex library we observed that χθ approximately scales as 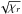 , an empirical relation that enables us (i) to adjust relation Eq. (45); (ii) to get a better fit of the data, and (iii) to provide more appropriate initial conditions for the numerical simulations. This property is likely due to the contribution of higher order terms in the present model, which could be justified in a future more elaborate model.
, an empirical relation that enables us (i) to adjust relation Eq. (45); (ii) to get a better fit of the data, and (iii) to provide more appropriate initial conditions for the numerical simulations. This property is likely due to the contribution of higher order terms in the present model, which could be justified in a future more elaborate model.
5.4. Identifing two families of vortices
The study of the correlation between the Rossby number and the aspect ratio (see Sect. 5.2), has shown that the GNG model, based on closed streamlines and constant vorticity, can be a suitable model for elongated vortices with χθ ≳ 7. On the other hand, for less elongated vortices (χθ ≲ 7) the Gaussian model is more accurate and produces better predictions than the GNG model.
This can be raised as a criterion on the space of the parameters and help to identify two families of vortices following the importance of compressibility:
-
incompressible vortices, for whichRo > −0.15 and χθ> 7 (closed streamlines with elliptical shape) ,
-
compressible vortices, for which Ro < −0.15 and χθ< 7 (open streamlines spiraling outward from the core).
They have been identified in the vortex library by checking that ∇·V is increasing for decreasing χθ. The transition between the two families is also smooth since Ro and χθ are continuous parameters.
Figure 11 illustrates the two classes of vortices: the top panel shows the relative density and streamlines of a vortex of the incompressible family with parameters (Ro,χr,χθ) = (−0.10,0.10,12); the bottom panel shows a vortex of the compressible family with parameters (Ro,χr,χθ) = (−0.33,0.08,3.2). Incompressible vortices have elongated structures with an amplitude of the density and pressure much larger than for compressible ones. At the vortex centre, they show a nearly axial symmetry with respect to the azimuthal and radial axes. On the contrary, compressible vortices are characterized by a peanut-shaped density structure, with some central symmetry to the vortex centre.
 |
Fig. 11 The two vortex families. Top: relative density and streamlines of a vortex of the incompressible family. We note the closed structure of the streamlines in the vortex. Bottom: relative density and streamlines of a vortex of the compressible family. The streamlines are now open curves spiraling from the vortex centre. In the core, the density shows a peculiar structure, with a peanut shape. Such vortices are also characterized by exciting strong spiral waves and possibly shocks. The compressible vortex has a Rossby number ~ 3 larger than the incompressible while its amplitude is smaller by a factor of ~ 2/3. |
 |
Fig. 12 Density map of the two vortex families in a shadowing depiction that brings out the small scale structures. Top: incompressible vortex with an amplitude 90% larger than the background density; some weak spiral waves are excited by the vortex. Bottom: compressible vortex with an amplitude about 60% larger than the background value; two spiral waves are excited, with a density perturbation nearly equal to half the amplitude of the vortex. |
In the incompressible family the streamlines are closed with an anticyclonic motion of the gas around the vortex centre. Such vortices gently bend the background flow, which is significantly perturbed up to 4 scale heights from the centre (here H0(Ro) ~ 0.45 AU). In the compressible case, the streamlines do not loop but rather spiral out from the vortex centre. The global flow around the vortex is broken, and spiral waves as well as shock waves are excited directly from the vortex core. This is the reason for the peanut shape of the vortex, with two outgoing waves on the north-east and the south-west, and two incoming shock waves on the south-east and the north-west.
In Fig. 12, shadowing plots highlight the structure of these vortices and their associated spiral waves. In the incompressible case (top), the vortex is embedded in an annular bump centred on the corotation region (a residual of the initial conditions) and is also associated with tiny spiral waves whose amplitude is less than 5% of the vortex one. In the compressible case (bottom), the vortex core splits in a cross-like feature and connects with spiral waves. This 3D visualization of the density map more clearly shows that the amplitude of these density waves can reach up to 20% that of the vortex. To the south, we can see a secondary vortex which is much smaller than the primary one and associated with spiral waves of the same amplitude as the core. However, this is a transient situation since, after ten rotations, this secondary vortex will merge with the primary.
The emission of compressional waves that brakes the flow around the vortex is thus the turning point between the families, and is closely related to the Rossby number. The amplitude of these waves can reach a significant fraction of the amplitude of the central bump (of density or velocity). Thus, the most relevant way to sort vortices is not the amplitude of the central density bump, but rather the vorticity or Rossby number which quantifies the strength of vortices.
Finally, the global evolution of the vortices in the disk and particularly their migration will be different depending on whether the vortices are compressible or not. This is in relation with the strength of the waves emitted by the vortices and will be studied in the second paper.
6. Discussion and conclusions
A detailed study of the role of vortices in the evolution of solid particles (see Chavanis 2000; Chang & Oishi 2010) or in the transport of angular momentum in disks (Paardekooper et al. 2010; Johnson & Gammie 2005) requires a better understanding of their structure and evolution. This paper addresses the problem by studying the possible shape and strength of the vortices. Two-dimensional vortices can be produced by various instabilities like RWI and most of them can reach a quasi-steady state in the disk flow. However, numerically produced Rossby vortices only cover a limited domain of the vortex-solution space. Indeed, the accessible range of the parameters is often biased by the choice of unstable initial conditions. This is the reason for using vortex models since they permit a broader space of the parameters to explored.
The linear vortex model derived by GNG is widely used in analytical studies of the stability and evolution of vortices. However, it is not well adapted to the comparisons with simulated vortices, mainly owing to the discontinuities produced in the velocity field and the density map. On the other hand, our model derived from a Gaussian pseudo-enthalpy ℋ function, is more general and accurate than the GNG model; it more closely fits the numerical vortex solutions than the GNG model and offers the possibility of exploring new vortex solutions of Euler’s equations.
6.1. A convenient model for numerical studies
The Gaussian model developed in this paper can provide suitable initial conditions for the numerical simulation of vortices in Keplerian disks. Choosing a triplet of parameters (Ro,χr,χθ), in agreement with the prescriptions given in Sect. 5.3, one is able to derive continuous maps for velocity, density, and pressure. The numerical readjustment of this approximate vortex solution takes place gently and disk perturbations relax in a few rotation periods; finally, the readjusted vortex have parameters quite similar to the initial triplet. On the other hand, starting from a GNG vortex a soft evolution is impossible because of the discontinuities of the variables inherent to the incompleteness of the model; moreover, in practice, the numerical scheme of the code used might not be sufficiently accurate to manage such discontinuities.
The new model we developed makes possible the creation of libraries of vortex solutions for a larger number of parameters than in previous studies and also the identification of two possible families. Further, it can help to plan statistical studies for dust capture or to mimic the end result of a turbulent disk evolution. Thus it can be a very useful tool for numerical studies in this context.
6.2. A vorticity threshold
Another advantage of the Gaussian model is to make analytical approaches of the problem easier. For example, in Sect. 4 we used a quasi-linear approximation that sheds light on the relations between the various vortex parameters and particularly between the elongation χθ and the vorticity of the core (Ro). A similar relation was found by GNG but in a less general context. This approach is important to clarify the link between the morphology of quasi-steady vortices and their stability in Keplerian flows. Vortices issued from the analytical model and from the numerical library clearly show strong similarities, mainly when their aspect ratio is larger than 7.
From the models we also deduce that a minimum vorticity (Ro ≲ −0.1) is required to get stable vortices. This limitation is consistent with the existence of a threshold for the development of the RWI, as was suggested by Lovelace et al. (1999). Indeed, if the initial axisymmetric condition of the RWI does not have enough vorticity, i.e. Ro ≳ −0.1, it will not be possible for vortices with Ro < −0.1 to form. However, a more detailed study is necessary to confirm this point, which is beyond the scope of the present paper.
6.3. Giant vortices
The other main result discussed in Sect. 5.1 is the possible existence of giant vortices whose radial size is significantly larger than the mean scale height of the disk. With a simple subsonic condition we derived a maximum value for the vortex radial extent and found that it depends on the relative Rossby number Ro. Here, we quickly explore the main properties of giant vortices produced with our numerical method and discuss their possible impact on disk evolution and planetary formation.
6.3.1. Main properties
We have formed giant vortices through the numerical re-adjustment of Gaussian vortex-solutions initially located at r0 = 7.5 AU from the star and in a disk with σ0(r0) = 83 g cm-2. These vortices have a radial size that ranges from 1 to 3H0; their main properties (shape, temperature, and density at the centre, total-mass estimate) are presented in Table 1. It is noticeable that each quantity reported in the table increases with the radial extent of the vortices. For the largest of them, the density at the centre can reach 415% of the background density (at the vortex orbit).
Of course, this rises the problem of their possible existence in actual disks. It is, however, striking to see that such strong perturbations of the disk can keep a coherent structure and rapidly stabilize without drastically changing the basic flow. This robustness of vortex solutions in Keplerian flows must be emphasized, even if the formation and persistence of giant vortices in protoplanetary disks remains to be clarified. Successive merging of vortices (in a 2D flow) or baroclinic amplification (see Raettig et al. 2013) could be invoked as a possible formation mechanism; however, this question has to be addressed in a deeper study. We want to stress that the increase of the temperature in the core of these vortices is observed in adiabatic disks but not in locally isothermal disks; this is in agreement with Eq. (30).
Main properties of the giant vortices produced in our numerical simulations and their associated Toomre parameters (values are compared to the background values).
These vortices are also big mass reservoirs which contain from 1 to 200 Earth masses, a mass range that also depends on the surface density of the disk and on the vortex position with respect to the star. Because of the local density enhancement, these vortices are favorable places for the gravitational instability and for planet growth. A simple way to quantify the occurrence of the gravitational instability is to use the Toomre parameter, 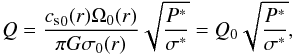 (46)where P = P0(r)P∗ and σ = σ0(r)σ∗ like in the Gaussian model. As an example, at the vortex orbit and for an unperturbed disk, we get Q0 = Q(r0) ~ 40, which obviously depends on r0, on the disk scale height, and on the disk-to-star mass ratio. The values of the Toomre parameter at the centre of the vortex and for various giant vortices are reported in the last column of Table 1. We found that the larger the vortex, the smaller the Toomre parameter; however, the collapse condition (i.e. Q ≲ 2) can be reached only for very large vortices (with a reduction factor Q/Q0 ~ 1/4) orbiting in regions of the disk where Q0 ≲ 8.
(46)where P = P0(r)P∗ and σ = σ0(r)σ∗ like in the Gaussian model. As an example, at the vortex orbit and for an unperturbed disk, we get Q0 = Q(r0) ~ 40, which obviously depends on r0, on the disk scale height, and on the disk-to-star mass ratio. The values of the Toomre parameter at the centre of the vortex and for various giant vortices are reported in the last column of Table 1. We found that the larger the vortex, the smaller the Toomre parameter; however, the collapse condition (i.e. Q ≲ 2) can be reached only for very large vortices (with a reduction factor Q/Q0 ~ 1/4) orbiting in regions of the disk where Q0 ≲ 8.
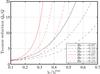 |
Fig. 13 Reduction factor N of the Toomre parameter as Q = Q0/N, as a function of the radial extent of the vortex, for different values of the Rossby number and in the case of an isothermal disk, α = 1 (red curves) or an adiabatic disk, α = γ (black curves). The radial extent χr is scaled to the maximal size |
An analytical estimate of the Toomre parameter can be obtained with the Gaussian model and the vortex over-density in Eq. (40). It is plotted as a function of the radial extent of the vortices in Fig. 13 in which are also considered the vortex strength (Ro) and the gas properties (adiabatic or isothermal). For typical vortices with 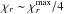 , the Toomre parameter is only reduced by a factor of 1/3. This is not a sufficient reduction to reach the collapse condition when Q0 ~ 40. Stronger reductions are possible either for fast cooling disks (nearly isothermal case) or extremely large vortices (
, the Toomre parameter is only reduced by a factor of 1/3. This is not a sufficient reduction to reach the collapse condition when Q0 ~ 40. Stronger reductions are possible either for fast cooling disks (nearly isothermal case) or extremely large vortices (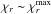 ). One can remark that smaller Ro values lead to higher reduction, since the maximum radial extent
). One can remark that smaller Ro values lead to higher reduction, since the maximum radial extent 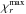 increases in these cases. As a conclusion, giant vortices could contribute to planet formation thanks to their high mass, and their possible collapse when orbiting in a moderate Q0 region. Deeper study of these questions is planned in an upcoming publication.
increases in these cases. As a conclusion, giant vortices could contribute to planet formation thanks to their high mass, and their possible collapse when orbiting in a moderate Q0 region. Deeper study of these questions is planned in an upcoming publication.
6.3.2. Consequences on the disk structure
 |
Fig. 14 Effective scale height of the disk, relative to the local background value H0(r). a): case of the giant vortex of Fig. 8. The scale height is 31% larger than H0(r) in the vortex centre but can reach 50% in the outer part of the spiral arm because of the shock wave. b): case of the large incompressible vortex of Fig. 11 (top). In the centre of the vortex the scale height is 14% larger than the background value. c): case of the compressible vortex of Fig. 11 (bottom). Even with a smaller density maximum, the scale height is about 10% larger than the background, owing to a warmer temperature in this vortex; there is also a slight increase in the spiral waves. |
Our numerical simulations show that the presence of a giant vortex in a Keplerian flow does not drastically change the global evolution of the disk. However, the possible large density and pressure perturbations associated with giant vortices may change the local disk scale height. In Fig. 14 we plot the change of the disk scale height relative to the background value H0(r) for three examples of vortices presented in the above sections.
First, we confirm that inside the vortex, the modification of the local H is only a small fraction of the background H0(r). Even for the giant vortex shown in Fig. 8 (left), the scale height at the centre is only 30% larger than H0. It is a small effect when we consider the density and pressure at the vortex centre, which are more than 400% larger than the disk background values. In the other cases, the changes are less than 15%.
Following the Gaussian vortex model, one can write 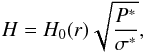 (47)and in the adiabatic case one has P∗ = σ∗ γ. Thus, even if the density in the centre is 4 times larger than the in background (σ∗ = 5), one obtains H ~ 1.38 H0 in agreement with the numerical results. The effect of a giant vortex on the scale height would be even smaller in a radiative disk, and in the limit of an isothermal disk (P∗ = σ∗), no change at all would be noticed.
(47)and in the adiabatic case one has P∗ = σ∗ γ. Thus, even if the density in the centre is 4 times larger than the in background (σ∗ = 5), one obtains H ~ 1.38 H0 in agreement with the numerical results. The effect of a giant vortex on the scale height would be even smaller in a radiative disk, and in the limit of an isothermal disk (P∗ = σ∗), no change at all would be noticed.
A second consequence is the formation of a ring outside the vortex orbit in which the scale height H is approximately 40% larger than the background value H0. This ring can be observed in simulations performed in large enough computational disks and is due to the heating of the gas by the periodic sweeping of the matter by the spiral shock waves emitted from the vortex. The stronger dissipation in the outer regions than in the inner ones explains why the ring is mainly observed outside the vortex orbit. We must again point out that this heating mechanism could be weaker in a gas allowing thermal transfer than in an adiabatic gas (as in the present simulation).
Such a ring of warm gas could also be a pressure maximum where the solid particles could be trapped, providing a signature in the IR and millimetre wavelengths, possibly observable with the new generation of high-resolution instruments. Indeed, the possible existence of large scale vortices has been suggested in a number of transitional disks to explain the observed asymmetrical dust features (van der Marel et al. 2013).
6.4. From two to three dimensions
Our 2D approach of the problem has permitted us to explore possible properties of quasi-steady vortices in protoplanetary disks. However, we wonder how these results stand in a 3D context. Recent 3D numerical simulations of the RWI (Richard et al. 2013) have shown that vortices can form and grow in 3D stratified disks. The aspect ratio of these Rossby vortices is significantly larger than 4, so they are stable against the elliptical instability (Lesur & Papaloizou 2009) and can reach a quasi-steady equilibrium. They keep a columnar structure in the whole thickness of the disk and survive for a very large number of rotation periods.
Thus, from the recent 3D studies we learned that the results obtained for 2D vortices are comparable only for vortices with χθ ≳ 4. Other results of our 2D study should be compared to future more detailed 3D studies. For example, what are the maximum and the minimum sizes of quasi-steady vortices? Are they similar to what we have found in the present 2D approach? Three-dimensional numerical simulations are certainly necessary to answer these questions, but the possible generalization of our 2D Gaussian model to a 3D model would certainly help to explore the properties and role of vortices in 3D protoplanetary disks. This will be addressed in a future work.
Acknowledgments
This work is issued from the Ph.D. Thesis defended by Clément Surville at Aix-Marseille University (AMU). Part of the numerical simulations was performed on a Bull multicore system funded by the AMU and the Laboratore d’Astrophysique de Marseille. Clément Surville would also like to thank the Max Planck Institute for Astronomy in Heidelberg for the financial support and the access to the local AMD multicore cluster, where most of the simulations were performed.
References
- Adams, F. C., & Watkins, R. 1995, ApJ, 451, L314 [NASA ADS] [CrossRef] [Google Scholar]
- Barge, P., & Sommeria, J. 1995, A&A, 295, L1 [NASA ADS] [Google Scholar]
- Bodo, G., Chagelishvili, G., Murante, G., et al. 2005, A&A, 437, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bodo, G., Tevzadze, A., Chagelishvili, G., et al. 2007, A&A, 475, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chang, P., & Oishi, J. S. 2010, ApJ, 721, 1593 [NASA ADS] [CrossRef] [Google Scholar]
- Chavanis, P. H. 2000, A&A, 356, 1089 [NASA ADS] [Google Scholar]
- Davis, S. S., Sheehan, D. P., & Cuzzi, J. N. 2000, ApJ, 545, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Godon, P., & Livio, M. 1999, ApJ, 523, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, J., Narayan, R., & Goldreich, P. 1987, MNRAS, 225, 695 [Google Scholar]
- Guillard, H., & Daniel, E. 2005, in Finite Volumes for Complex Applications IV: Problems and Perspectives, eds. F. Benkhaldoun, D. Ouazar, & S. Raghay (Hermes Science Publisher), 355 [Google Scholar]
- Hayashi, C. 1981, Progr. Theor. Phys. Suppl., 70, 35 [Google Scholar]
- Heng, K., & Kenyon, S. J. 2010, MNRAS, 408, 1476 [NASA ADS] [CrossRef] [Google Scholar]
- Inaba, S., Barge, P., Daniel, E., & Guillard, H. 2005, A&A, 431, 365 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johansen, A., Andersen, A. C., & Brandenburg, A. 2004, A&A, 417, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnson, B. M., & Gammie, C. F. 2005, ApJ, 635, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Kida, S. 1981, J. Phys. Soc. Jap., 50, 3517 [Google Scholar]
- Klahr, H. H., & Bodenheimer, P. 2003, ApJ, 582, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Lesur, G., & Papaloizou, J. C. B. 2009, A&A, 498, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, H., Finn, J. M., Lovelace, R. V. E., & Colgate, S. A. 2000, ApJ, 533, 1023 [NASA ADS] [CrossRef] [Google Scholar]
- Li, H., Colgate, S. A., Wendroff, B., & Liska, R. 2001, ApJ, 551, 874 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, M.-K. 2013, ApJ, 765, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Lovelace, R. V. E., Li, H., Colgate, S. A., & Nelson, A. F. 1999, ApJ, 513, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Lyra, W., & Klahr, H. 2011, A&A, 527, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mamatsashvili, G. R., & Chagelishvili, G. D. 2007, MNRAS, 381, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Mamatsashvili, G. R., & Rice, W. K. M. 2009, MNRAS, 394, 2153 [NASA ADS] [CrossRef] [Google Scholar]
- Meheut, H., Lovelace, R. V. E., & Lai, D. 2013, MNRAS, 430, 1988 [NASA ADS] [CrossRef] [Google Scholar]
- Paardekooper, S.-J., Lesur, G., & Papaloizou, J. C. B. 2010, ApJ, 725, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Petersen, M. R., Julien, K., & Stewart, G. R. 2007a, ApJ, 658, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Petersen, M. R., Stewart, G. R., Julien, K., et al. 2007b, ApJ, 658, 1252 [NASA ADS] [CrossRef] [Google Scholar]
- Raettig, N., Lyra, W., & Klahr, H. 2013, ApJ, 765, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Richard, S., Barge, P., & Le Dizès, S. 2013, A&A, 559, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Surville, C., & Barge, P. 2012, 20th French Congress of Mechanics, Besançon, France [arXiv:1201.3257] [Google Scholar]
- Surville, C., & Barge, P. 2013, EPJ Web Conf., 46, 05002 [CrossRef] [EDP Sciences] [Google Scholar]
- Toro, E. F. 1999, Riemann Solvers and Numerical Methods for Fluid Dynamics, 2nd edn. (Berlin: Springer-Verlag), 646 [Google Scholar]
- van der Marel, N., van Dishoeck, E. F., Bruderer, S., et al. 2013, Science, 340, 1199 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Varnière, P., & Tagger, M. 2006, A&A, 446, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Main properties of the giant vortices produced in our numerical simulations and their associated Toomre parameters (values are compared to the background values).
All Figures
 |
Fig. 1 Formation of vortices by the RWI (fiducial case). From left to right: evolution of the density in the (r,θ) plane at t = 0, t = 30, and t = 190 rotations. The density is relative to the disk, σ/σ0(r)−1, and shows the formation of a chain of six vortices, in agreement with the m = 6 most unstable azimuthal mode. After fewer than 200 rotations, the chain merges in a single vortex. The aspect ratio of the vortices is of the order of 5.2 at t = 30 rotations and 7.4 at t = 190 rotations. |
| In the text | |
 |
Fig. 2 Structure of a quasi-steady Rossby vortex. Top: radial profiles of the density (solid line) and the pressure (dashed line) relative to the disk: σ/σ0(r)−1 and P/P0(r)−1, respectively. These radial cuts nicely well fit a Gaussian profile. Bottom: radial profile of the vorticity inside the vortex and relative to the disk. It is expressed as a Rossby number Ro(r) (see text). |
| In the text | |
 |
Fig. 3 Velocity structure of a quasi-steady Rossby vortex (normalized to V0(r0)). Top: radial velocity in the vortex core located at r0 ~ 7.5 AU, in the azimuthal direction. We note the nearly linear behaviour around the centre at θ0 = 1.8. Bottom: azimuthal velocity V−V0(r) in the vortex core in the radial direction. We also note the linear shape between 7 and 8 AU. |
| In the text | |
 |
Fig. 4 Velocity field of a Rossby vortex: comparison of the numerical solution with the Gaussian model. Top row: values issued from the simulation of the radial velocity, the azimuthal velocity V−V0(r), and the Rossby number, from left to right, respectively. Bottom row: residual difference between the numerical data and the values issued from the model for the radial and azimuthal velocities and for the Rossby number, from left to right, respectively (see text for details). |
| In the text | |
 |
Fig. 5 Comparison of the velocity field issued from the numerical simulation (solid line) and from the model, when using ℋnum (dashed line) and when using ℋGauss (dashed-dot line) (see text for details). Top: for the radial component of the velocity. Bottom: for the azimuthal component of the velocity, V−V0(r). |
| In the text | |
 |
Fig. 6 Distribution of the vortex parameters in our sample of simulated vortices. From top to bottom: the Rossby number Ro, the radial extent ratio χr, and the azimuthal aspect ratio χθ. In each case the number of vortices we get for a given value of the parameter is plotted. |
| In the text | |
 |
Fig. 7 Dwarf vortex simulated from an initial Gaussian vortex with parameters (Ro,χr,χθ) = (−0.05,5 × 10-3,8). Top: the very weak but coherent vorticity (Rossby number) of the flow inside the vortex. Bottom: the density, relative to the disk, shows the nearly Gaussian vortex core associated with spiral waves. |
| In the text | |
 |
Fig. 8 Structure of a giant vortex obtained with the parameters (Ro,χr,χθ) = (−0.2,0.19,4.5). Top: density inside the vortex; the maximum value in the vortex centre is more than 4 times higher than in the disk. Bottom: mach number inside the vortex (see text). Ma< 0.5 in the core, but is of the order of ~ 0.8 near the shocked region of the right spiral arm. The streamlines show the anticyclonic motion. |
| In the text | |
 |
Fig. 9 Comparison of the radial dependance of Ro for two vortices with χr = 0.09. The vortex with Ro = −0.1 (solid line) can easily be approximated with a top-hat whereas the strongest vortex with Ro = −0.29 (dashed line) cannot be approximated in the same way. |
| In the text | |
 |
Fig. 10 Rossby number at the vortex centre, as a function of the aspect ratio χθ for the vortices used in our sample (black circles). Different expressions relating these two quantities are shown: the GNG model (solid line) which underestimates Ro as soon as χθ< 7, and the Gaussian model (dashed line) which better fits the data for 2 <χθ< 20. We note the logarithmic scale for χθ. |
| In the text | |
 |
Fig. 11 The two vortex families. Top: relative density and streamlines of a vortex of the incompressible family. We note the closed structure of the streamlines in the vortex. Bottom: relative density and streamlines of a vortex of the compressible family. The streamlines are now open curves spiraling from the vortex centre. In the core, the density shows a peculiar structure, with a peanut shape. Such vortices are also characterized by exciting strong spiral waves and possibly shocks. The compressible vortex has a Rossby number ~ 3 larger than the incompressible while its amplitude is smaller by a factor of ~ 2/3. |
| In the text | |
 |
Fig. 12 Density map of the two vortex families in a shadowing depiction that brings out the small scale structures. Top: incompressible vortex with an amplitude 90% larger than the background density; some weak spiral waves are excited by the vortex. Bottom: compressible vortex with an amplitude about 60% larger than the background value; two spiral waves are excited, with a density perturbation nearly equal to half the amplitude of the vortex. |
| In the text | |
 |
Fig. 13 Reduction factor N of the Toomre parameter as Q = Q0/N, as a function of the radial extent of the vortex, for different values of the Rossby number and in the case of an isothermal disk, α = 1 (red curves) or an adiabatic disk, α = γ (black curves). The radial extent χr is scaled to the maximal size |
| In the text | |
 |
Fig. 14 Effective scale height of the disk, relative to the local background value H0(r). a): case of the giant vortex of Fig. 8. The scale height is 31% larger than H0(r) in the vortex centre but can reach 50% in the outer part of the spiral arm because of the shock wave. b): case of the large incompressible vortex of Fig. 11 (top). In the centre of the vortex the scale height is 14% larger than the background value. c): case of the compressible vortex of Fig. 11 (bottom). Even with a smaller density maximum, the scale height is about 10% larger than the background, owing to a warmer temperature in this vortex; there is also a slight increase in the spiral waves. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\hbox{$\chi_r^{\rm max} \sim \left[H_0(r_0)/r_0\right]/ |{\rm Ro}|$}](/articles/aa/full_html/2015/07/aa24663-14/aa24663-14-eq329.png)