| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | L6 | |
| Number of page(s) | 7 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201526011 | |
| Published online | 05 June 2015 | |
Asymmetric features in the protoplanetary disk MWC 758⋆,⋆⋆,⋆⋆⋆
1 Université Grenoble Alpes, IPAG, 38000 Grenoble, France ;
CNRS, IPAG, 38000 Grenoble, France
e-mail: Myriam.Benisty@obs.ujf-grenoble.fr
2 Institute of Astronomy, Madingley Road, Cambridge CB3 OHA, UK
3 LESIA, Observatoire de Paris, CNRS, Université Pierre et Marie Curie Paris 6, Université Denis Diderot Paris 7, 5 place Jules Janssen, 92195 Meudon, France
4 Departamento de Astronomìa, Universidad de Chile, Casilla 36-D, Santiago, Chile
5 ESO, Alonso de Córdova 3107, Vitacura, Casilla 19001, Santiago de Chile, Chile
6 Institute for Astronomy, ETH Zurich, Wolfgang-Pauli-Strasse 27, 8093 Zurich, Switzerland
7 Sterrenkundig Instituut Anton Pannekoek, Science Park 904, 1098 XH Amsterdam, The Netherlands
8 Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
9 Max-Planck Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
10 Institute of Theoretical Astrophysics, Heidelberg University, Albert-Ueberle-Strasse 2, 69120 Heidelberg, Germany
11 Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA
12 Eureka Scientific and Goddard Space Flight Center, Code 667, Goddard Space Flight Center, Greenbelt, MD 20771, USA
13 Centro de Astrobiología (INTA-CSIC); ESAC Campus, PO Box 78, 28691 Villanueva de la Canada, Spain
14 Department of Physics & Astronomy, Rice University, 6100 Main Street, Houston, TX 77005, USA
15 Observatoire de Lyon, Centre de Recherche Astrophysique de Lyon, École Normale Supérieure de Lyon, CNRS, Université Lyon 1, UMR 5574, 9 avenue Charles André, 69230 Saint-Genis Laval, France
16 UMI-FCA, CNRS/INSU, France (UMI 3386), and Dept. de Astronomía, Universidad de Chile, Santiago, Chile
17 Laboratoire AIM, CEA/DSM – CNRS – Université Paris Diderot, IRFU/SAp, 91191 Gif-sur-Yvette, France
18 Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
Received: 3 March 2015
Accepted: 17 May 2015
Context. The study of dynamical processes in protoplanetary disks is essential to understand planet formation. In this context, transition disks are prime targets because they are at an advanced stage of disk clearing and may harbor direct signatures of disk evolution.
Aims. We aim to derive new constraints on the structure of the transition disk MWC 758, to detect non-axisymmetric features and understand their origin.
Methods. We obtained infrared polarized intensity observations of the protoplanetary disk MWC 758 with VLT/SPHERE at 1.04 μm to resolve scattered light at a smaller inner working angle (0.093′′) and a higher angular resolution (0.027′′) than previously achieved.
Results. We observe polarized scattered light within 0.53′′ (148 au) down to the inner working angle (26 au) and detect distinct non-axisymmetric features but no fully depleted cavity. The two small-scale spiral features that were previously detected with HiCIAO are resolved more clearly, and new features are identified, including two that are located at previously inaccessible radii close to the star. We present a model based on the spiral density wave theory with two planetary companions in circular orbits. The best model requires a high disk aspect ratio (H/r ~ 0.20 at the planet locations) to account for the large pitch angles which implies a very warm disk.
Conclusions. Our observations reveal the complex morphology of the disk MWC 758. To understand the origin of the detected features, the combination of high-resolution observations in the submillimeter with ALMA and detailed modeling is needed.
Key words: techniques: high angular resolution / protoplanetary disks
Appendices are available in electronic form at http://www.aanda.org
ESO data is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/578/L6
© ESO, 2015
1. Introduction
The planetary systems detected so far show a great diversity in their architectures and natures which may originate in the variety of initial conditions of their formation (Mordasini et al. 2012). It is thus of fundamental importance to study the physical conditions in the circumstellar disks in which they form, and the processes that rule their evolution. Direct-imaging observations at high angular resolution of young disks provide an efficient way to constrain these processes because they may leave clear signatures in the disk structure. As an example, planet-disk interactions will naturally generate asymmetric features, such as vortices, spiral arms or eccentric gaps, and may be used to indirectly detect planets embedded in their parent disk (e.g. Kley & Nelson 2012; Baruteau et al. 2014). In this context, disks with gaps or cavities, called transition disks, are prime targets to study because they may be at an advanced stage of disk evolution (Espaillat et al. 2014). Asymmetric features have already been observed in transition disks with high-contrast observations in the infrared (IR), which probe the disk surface layers (e.g., Hashimoto et al. 2011; Muto et al. 2012; Rameau et al. 2012; Casassus et al. 2012; Boccaletti et al. 2013; Canovas et al. 2013; Garufi et al. 2013; Avenhaus et al. 2014; Thalmann et al. 2014). Some of these features were traced deeper in the disk with CO submillimeter imaging (e.g., Christiaens et al. 2014).
In this context, the transition disk around the Herbig A5 star MWC 758 (HD 36112) is particularly interesting. It is 3.5 ± 2 Myr old (Meeus et al. 2012), and is located near the edge of the Taurus star-forming region. The revised Hipparcos parallax data provide a distance of 279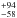 pc (van Leeuwen 2007). It is most likely a single star, as any stellar companion down to a mass limit of 80 MJup was ruled out based on sparse aperture masking observations (Grady et al. 2013). Submillimeter observations show a circumstellar disk extending up to 385 ± 26 astronomical units (au) (Chapillon et al. 2008), with an inclination and position angle of 21°± 2° and 65°± 7°, respectively, as determined from the CO line (Isella et al. 2010). Modeling indicates that the surface density steeply increases between 40 and 100 au, which supports the idea that the disk might be gravitationally perturbed by one or more companions. The observations marginally resolved a cavity with a radial extent in the submillimeter estimated between 70 and 100 au (Isella et al. 2010; Andrews et al. 2011). Using Ks (2.15 μm) direct imaging and H-band (1.65 μm) polarimetric imaging with the High Contrast Instrument for the Subaru Next Generation Adaptive Optics (HiCIAO), Grady et al. (2013) found no evidence for a cavity in scattered light down to 0.1′′ (28 au) from the star and detected two small-scale spiral arms. The authors suggested that the southeast spiral might be launched by a 5
pc (van Leeuwen 2007). It is most likely a single star, as any stellar companion down to a mass limit of 80 MJup was ruled out based on sparse aperture masking observations (Grady et al. 2013). Submillimeter observations show a circumstellar disk extending up to 385 ± 26 astronomical units (au) (Chapillon et al. 2008), with an inclination and position angle of 21°± 2° and 65°± 7°, respectively, as determined from the CO line (Isella et al. 2010). Modeling indicates that the surface density steeply increases between 40 and 100 au, which supports the idea that the disk might be gravitationally perturbed by one or more companions. The observations marginally resolved a cavity with a radial extent in the submillimeter estimated between 70 and 100 au (Isella et al. 2010; Andrews et al. 2011). Using Ks (2.15 μm) direct imaging and H-band (1.65 μm) polarimetric imaging with the High Contrast Instrument for the Subaru Next Generation Adaptive Optics (HiCIAO), Grady et al. (2013) found no evidence for a cavity in scattered light down to 0.1′′ (28 au) from the star and detected two small-scale spiral arms. The authors suggested that the southeast spiral might be launched by a 5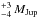 companion at 1.55′′ (432 au; beyond the submillimeter dust emission) in a dynamically warm disk.
companion at 1.55′′ (432 au; beyond the submillimeter dust emission) in a dynamically warm disk.
In this Letter, we report IR polarized intensity observations of the transition disk MWC 758 obtained with the SPHERE instrument in the Y band (1.04 μm). The use of an extreme adaptive optics system, combined with high-contrast coronagraphic and differential imaging techniques led to deeper observations, at a smaller inner working angle (IWA; 0.093′′, 26 au) and a higher angular resolution (0.027′′, 7.5 au) than previously achieved.
 |
Fig. 1 Left and middle: polarized intensity images (Qφ) obtained in December 2014 and March 2015, respectively. East is toward the left. Right: radial map of the deprojected Qφ image from March 2015 using i = 21° and PA = 65°. The dashed line indicates a radius of 0.23′′. Each pixel has been scaled with the square of its distance from the star, r2, to compensate for the r-2 dependency of the stellar illumination. The color scale is arbitrary. |
2. Observations and data reduction
The observations were carried out on 2014 December 5 and 2015 March 3 with the SPHERE instrument (Beuzit et al. 2008, and in prep.), equipped with an extreme adaptive-optics (AO) system (Fusco et al. 2006; Petit et al. 2014; Sauvage et al. 2014) at the Very Large Telescope at Cerro Paranal, Chile. The observations were executed in Science Verification Time. MWC 758 was observed in the Y-band filter (1.04 μm) using the infrared dual-band imager and spectrograph (IRDIS; Dohlen et al. 2008; Langlois et al. 2014), with a plate scale of 12.25 milli-arcseconds (mas) per pixel. We used a 185 mas-diameter coronagraphic mask combined with a Lyot apodizer. MWC 758 was observed during ~51 min at both epochs. These data were taken in challenging AO conditions with moderate to poor seeing (between 0.9′′ and 1.2′′ in the optical), high airmass (between 1.5 and 2), and relatively short wavelength. The Strehl ratio reached about ~70% in the H band, that is, ~45% in the Y band. The December dataset suffered from a number of defects (regarding spider alignment and centering onto the mask), leading to a lower signal-to-noise (S/N) ratio than in the March dataset.
The images were obtained using differential polarimetric imaging (DPI), a powerful technique for studying the spatial distribution of small dust grains in the disk surface layers through their scattered light by suppressing the unpolarized stellar light (e.g. Apai et al. 2004; Quanz et al. 2011). IRDIS provides two beams, in which wire-grid polarizers are inserted in DPI mode, and lead to ordinary and extraordinary polarization states. The half-wave plate (HWP) that controls the orientation of the polarization was set to four positions shifted by 22.5° in order to construct a set of linear Stokes vectors. To minimize uncertainties related to the relative positioning of the star with respect to the coronagraphic mask, the frame registration was accurately performed using a background star located at ~2.35′′ from MWC 758. The data were corrected for the distortion and true North. We then followed a procedure developed for high-contrast imaging and used the double-ratio method to calculate the Stokes parameters Q and U (Avenhaus et al. 2014). Since the scattered light from a circumstellar disk is expected to be linearly polarized in the azimuthal direction under the assumption of single scattering, it is beneficial to describe the polarization vector field in polar rather than Cartesian coordinates. We define the polar-coordinate Stokes parameters Qφ, Uφ as: 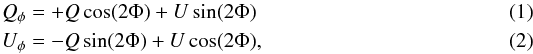 where φ refers to the azimuth in polar coordinate, Φ is the position angle of the location of interest (x, y) with respect to the star location (x0,y0), and is written as:
where φ refers to the azimuth in polar coordinate, Φ is the position angle of the location of interest (x, y) with respect to the star location (x0,y0), and is written as: 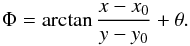 (3)θ corrects for instrumental effects such as the angular misalignment of the HWP. In this coordinate system, the azimuthally polarized flux from a circumstellar disk appears as a consistently positive signal in the Qφ image, whereas the Uφ image remains free of disk signal and provides a convenient estimate of the residual noise in the Qφ image (Schmid et al. 2006). Because the DPI mode of IRDIS was still in commissioning at the time of publication, the absolute level of polarization could not be accurately retrieved, and we are only able to report polarized intensity images with arbitrary surface brightness levels.
(3)θ corrects for instrumental effects such as the angular misalignment of the HWP. In this coordinate system, the azimuthally polarized flux from a circumstellar disk appears as a consistently positive signal in the Qφ image, whereas the Uφ image remains free of disk signal and provides a convenient estimate of the residual noise in the Qφ image (Schmid et al. 2006). Because the DPI mode of IRDIS was still in commissioning at the time of publication, the absolute level of polarization could not be accurately retrieved, and we are only able to report polarized intensity images with arbitrary surface brightness levels.
3. Polarized intensity images
Figure 1 shows the Qφ images at both epochs and the radial mapping of the March data, obtained after deprojection (with i = 21°, PA = 65°; Isella et al. 2010). Each pixel was scaled with r2 to compensate for the r-2 dependency of the stellar illumination. The dark central region corresponds to the area masked by the coronagraph. The residual spiders from the coronagraph are visible in the December 2014 image (Fig. 1, left). Scattered light is detected from ~0.093′′ to ~0.53′′ (~26 to ~148 au) in polarized intensity, and we did not resolve any depleted cavity. Six distinct non-axisymmetric features are detected, the innermost ones being at previously inaccessible radii. The features are indicated by arrows in Fig. 1: (1) a spiral arm located in the south and east (hereafter, the SE spiral) at deprojected distances r ~ 0.26″−0.53′′; (2) an arc in the west at r ~ 0.2′′–0.3′′; (3) a spiral arm in the northwest (hereafter, the NW spiral) at r ~ 0.22′′–0.34′′; (4) an arc located north of the NW spiral at r ~ 0.32′′–0.53′′; (5) substructures inside the spirals at r ~ 0.1′′–0.2′′ and (6) a substructure branching off the SE spiral at r ~ 0.21′′–0.27′′. We note that although there is some clear scattered light signal very close to the coronagraph, the exact morphology of feature (5) may be affected by the efficiency of the AO correction and the coronagraph centering. Appendix A provides the Uφ images (Fig. A.1) and S/N maps (Fig. A.2). The features are detected above the disk background at more than 3σ and do not appear in the Uφ images. This suggests that they are real and not diffraction residuals that would affect the Qφ and Uφ images alike. Although one could naturally see a single spiral arm in the west, extending from PA ~ 180° to 350°, the radial mapping (Fig. 1, right) shows that it consists of different features that have a very distinct dependence on the PA, with a sharp transition at PA ~ 240°. In the December 2014 image, feature (2) hosts an area that is ~1.5 times brighter than the NW spiral, at PA ~ 240°−260°. In the March dataset, the area at PA ~ 260° in contrast seems fainter than the background spiral. Since it is very close to the residual spiders, it is difficult to conclude whether it is an instrumental effect, or if it has a physical origin which, considering the timescale of the variations, would point to a variability in the inner disk. While the detected structures agree with the HiCIAO H-band image (Grady et al. 2013), we did not detect a significant difference in the extent of the scattered light signal between the west and the east sides.
4. Spiral feature modeling
Planets embedded in circumstellar disks are known to launch spiral waves at Lindblad resonances both inside and outside of their orbit (e.g. Ogilvie & Lubow 2002). The shape of the spiral wake is determined by the disk rotation profile and by the sound speed (i.e., temperature) distribution in the disk. In this section, we attempt to fit the shape of the two regions where there is a significant departure from circular symmetry, features (1) and (3), with a model based on the spiral density wave theory. As the spiral features are very similar in both datasets, and since the observations in March were obtained under better conditions, we only fit the corresponding dataset. We assume that the observed scattered light traces small dust grains that are well coupled to the gas, and thus, that it indirectly traces the gas. Following the prescription of Rafikov (2002) and Muto et al. (2012), the spiral wake in polar coordinates (r,Φ) follows 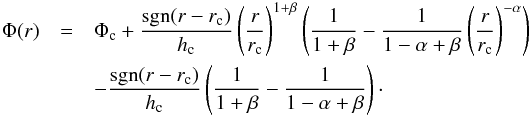 (4)where α and β are the exponents of the disk rotation and sound speed profiles, respectively: Ω ∝ r− α, cs ∝ r− β. hc = cs(rc) /rcΩ(rc) is the ratio of the pressure scale height H to the radius (also called disk aspect ratio) at the location of the planet (rc,Φc). The pitch angle of the spirals depends on the disk temperature (hence on the aspect ratio) and the distance from the launching planet. The flaring index, α − β − 1, determines the variation of H/r with radius. Equation (4) is valid in the linear or weakly nonlinear regimes, in which a single spiral wave is launched by an embedded planet, and approximates well the shape of the density wave given by the WKB theory (Rafikov 2002).
(4)where α and β are the exponents of the disk rotation and sound speed profiles, respectively: Ω ∝ r− α, cs ∝ r− β. hc = cs(rc) /rcΩ(rc) is the ratio of the pressure scale height H to the radius (also called disk aspect ratio) at the location of the planet (rc,Φc). The pitch angle of the spirals depends on the disk temperature (hence on the aspect ratio) and the distance from the launching planet. The flaring index, α − β − 1, determines the variation of H/r with radius. Equation (4) is valid in the linear or weakly nonlinear regimes, in which a single spiral wave is launched by an embedded planet, and approximates well the shape of the density wave given by the WKB theory (Rafikov 2002).
We attempted to fit both spirals simultaneously assuming that they are launched by two planets in circular orbit at different radii in the disk. We assumed that the disk is in Keplerian rotation and fixed α = 3/2. Varying β has little influence on the fit, and we fixed β = 0.45, following Andrews et al. (2011). We considered that hc is a global disk parameter, meaning that the values of aspect ratios at the locations of the planets should be consistent. This leads to five free parameters in total. We restricted our models to planets located inside the submillimeter cavity, whose extent is ~0.36′′ within large uncertainties (Isella et al. 2010; Andrews et al. 2011) and considered disk aspect ratios of at most 0.20 to be consistent with the modeling of the spectral energy distribution (SED; Andrews et al. 2011). The parameters are thus varied as 0.03 ≤ hc ≤ 0.20, 0.01″ ≤ rc,NW/SE ≤ 0.36″, 0 ≤ Φc,NW/SE ≤ 360°, in 20, 50, and 50 linearly spaced values, respectively.
We deprojected the image and fit the locations of the surface brightness maxima along a set of azimuth angles (PA ~ 70°−200° (80 linearly spaced values) and 280°–340° (50 values), for the SE and NW spirals, respectively). We minimized a χ2 function assuming that the uncertainty on each location is the FWHM of the point spread function (PSF). The best-fit parameters are for the SE arm: (hc, rc, Φc) = (0.20, 0.253′′, 72°), and for the NW arm: (hc, rc, Φc) = (0.20, 0.196′′, 266°). This corresponds to planets located at ~55 and 71 au for the NW and SE arms, respectively. The spiral shapes with these parameters are plotted in the polarized intensity image in Fig. 2. As noted by Muto et al. (2012), the degeneracy of the model is significant. Figure B.1 shows the 2D probability distributions for each pair of free parameters. The Bayesian probabilities were derived as exp( − χ2/ 2) and normalized such that their integral over the whole parameter domain is unity. We obtained a lower limit of the disk aspect ratio hc = 0.2. A high value of hc is needed to account for the large pitch angle, and while higher values may be favored by the spiral fit, they would produce too much infrared flux to account for the SED. In addition, we note that hc and rc are not independent. The lower hc, the closer to the spiral the planet must be, as the spiral pitch angle is only large very close to the planet.
Although we restricted the planets to be inside the submillimeter cavity, we note that the only way to fit the northern tip of the SE spiral (up to PA ~ 45°) is to consider a planet outside of the submillimeter continuum emission as in Grady et al. (2013). However, extending the range in rc to 2′′ strongly increases the degeneracy of the model. We do not favor this solution because companions are likely to be located inside the submillimeter cavity since other clearing mechanisms, such as photo evaporation, can be ruled out by near-IR interferometric observations of the inner disk (Isella et al. 2008).
 |
Fig. 2 Best-fit model in dashed lines. The locations of the planets are indicated by white diamonds. The dotted ellipse is a projected circle with radius 0.25′′. The color scale is arbitrary. |
5. Discussion and conclusions
We presented Y-band polarized intensity images of the scattered light from the protoplanetary disk around the Herbig Ae star MWC 758 and studied the morphology of non-axisymmetric features. The image shows six distinct features, including arc-like features and two spiral arms with a large winding angle. Fitting the shape of the spirals, with a model based on the spiral density wave theory, showed that only a warm disk with a high aspect ratio (~0.2) at the locations of the planets can lead to such large pitch angle spirals (Rafikov 2002). Assuming that the disk is in hydrostatic equilibrium, this corresponds to midplane temperatures of ~315 K and ~250 K at 55 and 71 au, respectively, slightly higher than the predictions from SED and submillimeter continuum modeling (~200 K at these locations; Andrews et al. 2011), but significantly different from the temperature measured with CO (~53 K at 50 AU; Isella et al. 2010). Such a high disk aspect ratio also reduces the contrast and the observability of the spirals in scattered light (Juhasz et al. 2014). This suggests that the vertically isothermal assumption implied in the spiral model may not hold (e.g. Richert et al. 2015). Alternatively, a planet on an eccentric orbit, an inclined planet or a planet massive enough to exert disk eccentricity may affect the shape of the spirals and induce a different pitch angle than in the case of a circular orbit.
The two spiral arms were interpreted in the context of planet-disk interaction, but other mechanisms, such as self-gravity, can trigger spiral features with lower winding numbers (Rice et al. 2006b), while keeping enough contrast to detect them in scattered light (Pohl et al., in prep.) and at longer wavelengths (Dipierro et al. 2014). The disk mass has been estimated to be ~0.01 M⊙ from submillimeter observations (Andrews et al. 2011), which is probably too low to trigger gravitational instabilities, although these estimates are very uncertain and strongly depend on the assumed dust opacities and gas-to-dust ratio. If a significant part of the solid mass is in planets or particles larger than 1 cm, the gas mass can be much higher than currently estimated.
Assuming that the observed spirals are trailing, the SE spiral arm is located on the far side of the disk and interestingly, does not appear darker than the near side (unlike SAO206462, Garufi et al. 2013). This may indicate an isotropic scattering phase function of the dust grains, which would imply submicron sized grains, or a high polarization efficiency. We note that the detected scattered light is quite symmetric and the western side of the image does not show the extended emission seen in the HiCIAO image (Grady et al. 2013), which was interpreted as being due to an asymmetric irradiation of the disk. Considering that the observations were obtained only three years apart, it is unlikely that this would result from variable shadowing and should be investigated further.
We found no indication of a fully depleted cavity in micron-size dust grains beyond the coronagraph radius (consistent with 12CO peaking at the star position; Isella et al. 2010) while a cavity in millimeter grains has been marginally resolved at a much larger radius (Isella et al. 2010; Andrews et al. 2011). Such spatial segregation of small and large grains can be a natural outcome of particle trapping at the edge of a cavity carved by a planet (Pinilla et al. 2012, 2015). The requirement of a continuous replenishment of small particles through the cavity translates into a maximum planet mass, above which any companion would filter all dust particles (Rice et al. 2006a; Zhu et al. 2012). With typical disk viscosities, a companion with a planet-to-star mass ratio above 10-2 (i.e., a 5.5 MJup planet around MWC 758) would filter all dust grains (Pinilla et al. 2012).
Features (2) and (3) have a very distinct dependence on the PA, with a sharp transition at PA ~ 240°, therefore no spiral model can fit the full NW structure (features (2) and (3) together). A projected circle of 0.25′′ radius is shown in Fig. 2 and can only partly account for the region between PA ~ 190 − 270°. The circular region between features (2) and (3) may trace the edge of a cavity, although high-resolution submillimeter observations are required to determine whether this is the case. Alternatively, a slightly eccentric ellipse (e ~ 0.1) oriented with PA = −30°, that would trace an eccentric gap, can fit part of feature (3) in addition to feature (2). In addition to the two spiral arms, four more structures are detected. Feature (4) is located beyond the NW spiral and indicates that the NW arm does not shadow the outer disk in this direction. Its small angular extent is puzzling, and its nature is unclear. Features (5) and (6) are located closer in than the two arms and the submillimeter cavity, at previously inaccessible radii close to the star. Feature (5) may trace the optically thick innermost disk (Isella et al. 2008), or alternatively, the inner arm of the SE spiral.
Considering that the best-fit aspect ratio from the spiral models is difficult to reconcile with the expected temperatures in this disk, and that on the other hand, the disk mass seems to be too low to account for gravitational instability, additional observations coupled with advanced modeling are needed to understand which processes these non-axisymmetric features may trace. In particular, complementary observations on similar spatial scales with ALMA, which will trace different optical depths in the disk, is very promising. Future DPI observations with SPHERE and its visible-light instrument ZIMPOL (Roelfsema et al. 2010) are also expected to place new constraints on the innermost structures.
Online material
Appendix A: Uφ image and S/N map
Figure A.1 presents the Uφ images. Since the scattered light from a circumstellar disk is expected to be linearly polarized in the azimuthal direction under the assumption of single scattering, Uφ contains no signal, but only noise of the same magnitude as the noise in the Qφ image. For multiple scattering, the assumption of polarization only in azimuthal direction still holds approximately, especially for close to face-on disks, and the deviations from azimuthal polarizations are expected to be well below the noise level (Avenhaus et al. 2014).
Figure A.2 provides qualitative S/N maps. They were obtained by first smoothing both Qφ and Uφ with a Gaussian kernel of 37 mas (close to the instrument PSF) and then dividing
the Qφ by the standard deviation in the Uφ images. The standard deviation in the Uφ image was calculated over a Gaussian-weighted area centered on the respective image point with a FWHM of 260 mas. We note that these do not strictly provide S/N estimates. Indeed, the noise reported in these maps depends on the area considered for the calculation of the variance from the Uφ images. Moreover, the first step smoothes out the readout noise and other small-scale (smaller than the smoothing kernel) noise (but not large-scale systematic noise). These maps are still very useful, as a feature detected in the Qφ image and appearing at a location of the map that has a high S/N value, should be considered as real. An example is feature 4, which lies in an area of high S/N and can thus be considered real, even though it does not seem apparent from the S/N maps alone.
 |
Fig. A.1 Uφ images (left, December 2014; right, March 2015). East is toward the left. Each pixel has been scaled with the square of its distance from the star, r2, to compensate for the r-2 dependency of the stellar illumination. The color scale is arbitrary. |
 |
Fig. A.2 S/N maps with contours every 3σ (left, December 2014; right, March 2015). |
Appendix B: Probability plot
Figure B.1 shows the 2D probability distributions for each pair of free parameters.
 |
Fig. B.1 Bayesian probabilities for the simultaneous fit of the two spirals. The top panel of each column provides the integrated 1D probability for each parameter. The lower panels in each column are the 2D probability maps for each pair of parameters. |
Acknowledgments
We acknowledge the SVT team at ESO HQ for their help during the preparation of the OBs and the VLT team for conducting the observations. We thank C. P. Dullemond, G. Lesur, M. Min, and M. Tauras for fruitful discussions, and the referee for providing useful comments. M.B. acknowledges financial support from “Programme National de Physique Stellaire” (PNPS) of CNRS/INSU, France. C.G. was supported under the NASA Origins of Solar Systems program on NNG13PB64P. T.B. acknowledges support from NASA Origins of Solar Systems grant NNX12AJ04G.
References
- Andrews, S. M., Wilner, D. J., Espaillat, C., et al. 2011, ApJ, 732, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Apai, D., Pascucci, I., Brandner, W., et al. 2004, A&A, 415, 671 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Avenhaus, H., Quanz, S. P., Schmid, H. M., et al. 2014, ApJ, 781, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Baruteau, C., Crida, A., Paardekooper, S.-J., et al. 2014, Protostars and Planets VI, 667 [Google Scholar]
- Beuzit, J.-L., Feldt, M., Dohlen, K., et al. 2008, in SPIE Proc., 7014, 18 [Google Scholar]
- Boccaletti, A., Pantin, E., Lagrange, A.-M., et al. 2013, A&A, 560, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Canovas, H., Ménard, F., Hales, A., et al. 2013, A&A, 556, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casassus, S., Perez, M. S., Jordán, A., et al. 2012, ApJ, 754, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Chapillon, E., Guilloteau, S., Dutrey, A., & Piétu, V. 2008, A&A, 488, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Christiaens, V., Casassus, S., Perez, S., van der Plas, G., & Ménard, F. 2014, ApJ, 785, L12 [Google Scholar]
- Dipierro, G., Lodato, G., Testi, L., & de Gregorio Monsalvo, I. 2014, MNRAS, 444, 1919 [NASA ADS] [CrossRef] [Google Scholar]
- Dohlen, K., Langlois, M., Saisse, M., et al. 2008, in SPIE Proc., 7014 [Google Scholar]
- Espaillat, C., Muzerolle, J., Najita, J., et al. 2014, Protostars and Planets VI, 497 [Google Scholar]
- Fusco, T., Rousset, G., Sauvage, J.-F., et al. 2006, Opt. Express, 14, 7515 [NASA ADS] [CrossRef] [Google Scholar]
- Garufi, A., Quanz, S. P., Avenhaus, H., et al. 2013, A&A, 560, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grady, C. A., Muto, T., Hashimoto, J., et al. 2013, ApJ, 762, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Hashimoto, J., Tamura, M., Muto, T., et al. 2011, ApJ, 729, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Isella, A., Tatulli, E., Natta, A., & Testi, L. 2008, A&A, 483, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Isella, A., Natta, A., Wilner, D., Carpenter, J., & Testi, L. 2010, ApJ, 725, 1735 [NASA ADS] [CrossRef] [Google Scholar]
- Juhasz, A., Benisty, M., Pohl, A., et al. 2014, MNRAS, submitted [arXiv:1412.3412] [Google Scholar]
- Kley, W., & Nelson, R. P. 2012, ARA&A, 50, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Langlois, M., Dohlen, K., Vigan, A., et al. 2014, in SPIE Proc., 9147, 1 [Google Scholar]
- Meeus, G., Montesinos, B., Mendigutía, I., et al. 2012, A&A, 544, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C., Alibert, Y., Klahr, H., & Henning, T. 2012, A&A, 547, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muto, T., Grady, C. A., Hashimoto, J., et al. 2012, ApJ, 748, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Ogilvie, G. I., & Lubow, S. H. 2002, MNRAS, 330, 950 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, C., Sauvage, J.-F., Fusco, T., et al. 2014, in SPIE Proc., 9148 [Google Scholar]
- Pinilla, P., Benisty, M., & Birnstiel, T. 2012, A&A, 545, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinilla, P., de Juan Ovelar, M., Ataiee, S., et al. 2015, A&A, 573, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quanz, S. P., Schmid, H. M., Geissler, K., et al. 2011, ApJ, 738, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Rafikov, R. R. 2002, ApJ, 569, 997 [NASA ADS] [CrossRef] [Google Scholar]
- Rameau, J., Chauvin, G., Lagrange, A.-M., et al. 2012, A&A, 546, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rice, W., Armitage, P. J., Wood, K., & Lodato, G. 2006a, MNRAS, 373, 1619 [NASA ADS] [CrossRef] [Google Scholar]
- Rice, W. K. M., Lodato, G., Pringle, J. E., Armitage, P. J., & Bonnell, I. A. 2006b, MNRAS, 372, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Richert, A. J. W., Lyra, W., Boley, A., Mac Low, M.-M., & Turner, N. 2015, ApJ, accepted [arXiv:1504.00066] [Google Scholar]
- Roelfsema, R., Schmid, H. M., Pragt, J., et al. 2010, in SPIE Proc., 7735, 4 [Google Scholar]
- Sauvage, J., Fusco, T., Petit, C., et al. 2014, in SPIE Proc., 9148 [Google Scholar]
- Schmid, H. M., Joos, F., & Tschan, D. 2006, A&A, 452, 657 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thalmann, C., Mulders, G. D., Hodapp, K., et al. 2014, A&A, 566, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhu, Z., Nelson, R., Dong, R., Espaillat, C., & Hartmann, L. 2012, ApJ, 755, 6 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Left and middle: polarized intensity images (Qφ) obtained in December 2014 and March 2015, respectively. East is toward the left. Right: radial map of the deprojected Qφ image from March 2015 using i = 21° and PA = 65°. The dashed line indicates a radius of 0.23′′. Each pixel has been scaled with the square of its distance from the star, r2, to compensate for the r-2 dependency of the stellar illumination. The color scale is arbitrary. |
| In the text | |
 |
Fig. 2 Best-fit model in dashed lines. The locations of the planets are indicated by white diamonds. The dotted ellipse is a projected circle with radius 0.25′′. The color scale is arbitrary. |
| In the text | |
 |
Fig. A.1 Uφ images (left, December 2014; right, March 2015). East is toward the left. Each pixel has been scaled with the square of its distance from the star, r2, to compensate for the r-2 dependency of the stellar illumination. The color scale is arbitrary. |
| In the text | |
 |
Fig. A.2 S/N maps with contours every 3σ (left, December 2014; right, March 2015). |
| In the text | |
 |
Fig. B.1 Bayesian probabilities for the simultaneous fit of the two spirals. The top panel of each column provides the integrated 1D probability for each parameter. The lower panels in each column are the 2D probability maps for each pair of parameters. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


