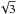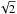| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A16 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201525704 | |
| Published online | 25 May 2015 | |
Dynamical masses of the low-mass stellar binary AB Doradus B
1 Departament d’Astronomia i Astrofísica, Universitat de València, C. Dr. Moliner 50, 46100 Burjassot, València, Spain
e-mail: Rebecca.Azulay@uv.es
2 Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
3 Observatori Astronòmic, Universitat de València, Parc Científic, C. Catedrático José Beltrán 2, 46980 Paterna, València, Spain
4 Onsala Space Observatory, Chalmers University of Technology, 439 92 Onsala, Sweden
5 CSIRO Astronomy and Space Science, Canberra, 2122 Marsfield, Australia
6 Research School of Astronomy & Astrophysics, Australian National University, 0200 Canberra, Australia
7 Observatoire de Paris/LERMA, 61 rue de l’Observatoire, 75014 Paris, France
8 Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Drive, Pasadena, California 91109, USA
9 University of Roma Tor Vergata, Department of Physics, via della Ricerca Scientifica 1, 00133 Roma, Italy
10 INFN, Section of Pisa, Largo Bruno Pontecorvo 3, 56127 Pisa, Italy
11 INAF–Observatory of Rome, via Frascati 33, 00040 Monteporzio Catone (RM), Italy
Received: 21 January 2015
Accepted: 31 March 2015
Context. AB Doradus is the main system of the AB Doradus moving group. It is a quadruple system formed by two widely separated binaries of pre-main-sequence (PMS) stars: AB Dor A/C and AB Dor Ba/Bb. The pair AB Dor A/C has been extensively studied and its dynamical masses have been determined with high precision, thus making AB Dor C a benchmark for calibrating PMS stellar models. If the orbit and dynamical masses of the pair AB Dor Ba/Bb could be determined, they could play a similar role to that of AB Dor C in calibrating PMS models, and would also help to better understand the dynamics of the whole AB Doradus system.
Aims. We aim to determine the individual masses of the pair AB Dor Ba/Bb using VLBI observations and archive infrared data as part of a larger program that monitors binary systems in the AB Doradus moving group.
Methods. We observed the system AB Dor B between 2007 and 2013 with the Australian Long Baseline Array (LBA) at a frequency of 8.4 GHz in phase-reference mode.
Results. We detected, for the first time, compact radio emission from both stars in the binary, AB Dor Ba and AB Dor Bb. This result allowed us to determine the orbital parameters of both the relative and absolute orbits and, consequently, their individual dynamical masses: 0.28 ± 0.05 M⊙ and 0.25 ± 0.05 M⊙, respectively.
Conclusions. Comparisons of the dynamical masses with the prediction of PMS evolutionary models show that the models underpredict the dynamical masses of the binary components Ba and Bb by 10–30% and 10–40%, respectively, although they still agree at the 2σ level. Some of the stellar models considered favor an age between 50 and 100 Myr for this system, while others predict older ages. We also discuss the evolutionary status of AB Dor Ba/Bb in terms of an earlier double-double star scenario that might explain the strong radio emission detected in both components.
Key words: astrometry / binaries: close / stars: fundamental parameters / stars: pre-main sequence
© ESO, 2015
1. Introduction
Stellar evolution models are used to predict fundamental parameters of the stars, such as their mass. The estimates from mass-luminosity theoretical relationships are not in agreement for the particular case of pre-main-sequence (PMS) stars with masses <1.2 M⊙. Either more accurate observations or revised models are needed. As reported in Azulay et al. (2014), a VLA/VLBI program to detect binary stars with substantial emission at radio wavelengths is underway. This program focuses on stars members of the AB Doradus moving group, AB Dor-MG (Zuckerman et al. 2004), which includes the already studied pairs AB Dor A/C (Guirado et al. 2006, G06) and HD 160934 A/c (Azulay et al. 2014).
Located at a distance of ~15 pc (G06), the stellar system AB Doradus has a pair of binaries, AB Dor A and AB Dor B, separated by ~9′′. The K1 star AB Dor A, the main star of the system, is an active star with detectable emission at all wavelengths. In particular, it has strong radio emission (Guirado et al. 1997) generated by a dynamo effect caused by its rapid rotation (0.514 days). This star has a low-mass companion, AB Dor C (0.090 M⊙), whose study is important in order to calibrate the stellar evolution models of young low-mass stars (Close et al. 2005).
Journal of observations of AB Dor B.
The other binary of the AB Doradus system is AB Dor B (=Rossiter 137 B), which consists of two components, AB Dor Ba and AB Dor Bb, with spectral types M5 and M5-6 (Close et al. 2007), respectively. These components are separated by an angular distance of ~0.06′′ (G06; Janson et al. 2007). The combined system shows a high rotation rate with a period of 0.38 days (Lim 1993; Wolter et al. 2014) and displays strong radio emission detected both by the Australian Telescope Compact Array (ATCA; Lim 1993; Wolter et al. 2014) and the Australian VLBI Network (G06; this paper). Close et al. (2007) and Wolter et al. (2014) report information on the relative orbit from near-infrared (NIR) VLT observations at H and K bands. The latter authors estimated a value of the sum of the masses of the components Ba and Bb of 0.69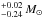 that is somewhat larger than the model-dependent estimates from Janson et al. (2007) (0.13–0.20 and 0.11–0.18 M⊙ for Ba and Bb, respectively).
that is somewhat larger than the model-dependent estimates from Janson et al. (2007) (0.13–0.20 and 0.11–0.18 M⊙ for Ba and Bb, respectively).
An important point of debate is the age of the AB Doradus system, which has not been determined with sufficient accuracy and presents different estimates in different publications: from 40–50 Myr (Zuckerman et al. 2004; Lòpez-Santiago et al. 2006; Guirado et al. 2011) to 50–100 Myr (Nielsen et al. 2005; Janson et al. 2007; Boccaletti et al. 2008) and 100–140 Myr (Luhman et al. 2005; Ortega et al. 2007; Barenfeld et al. 2013). The determination of the age of the AB Doradus system is fundamental to calibrating the evolution models of PMS stars.
In this paper we report the results of three epochs of VLBI observations of AB Dor B, leading to the discovery of radio emission from both components, the determination of the dynamical masses for the individual components, and their comparisons with theoretical models. We also discuss a possible evolutionary scenario for AB Dor Ba and AB Dor Bb in terms of an earlier quadruple system that evolved to its present state via Kozai cycling and tidal friction (Mazeh & Shaham 1979; Fabrycky & Tremaine 2007).
2. Observations and data reduction
We carried out three epochs of observations with the Long Baseline Array (LBA), the Australian VLBI Network, between 2007 and 2013 (see Table 1). Each observation lasted 12 h at the frequency of 8.4 GHz. Both RCP and LCP polarizations were recorded with a rate of 1024 Mbps (two polarizations, eight subbands per polarization, 16 MHz per subband, 2 bits per sample), except at Hobart and Ceduna, with a recording rate of 512 Mbps (two polarizations, four subbands per polarization, 8 MHz per subband, 2 bits per sample). We used the phase-reference technique, interleaving scans of the ICRF1-defining source BL Lac PKS 0516−621 and the star AB Dor B (separated by 3.6°). The observation sequence target-calibrator-target lasted about four minutes.
We reduced the data using the Astronomical Image Processing System (AIPS) program, of the National Radio Astronomy Observatory (NRAO), following standard procedures: (i) we calibrated the visibility amplitude using system temperatures and antenna gains; (ii) we removed the ionospheric contribution (using GPS-based Global Ionospheric Maps2); and corrected the parallactic angle; (iii) we performed a fringe-search on the calibrator to remove residual contributions to the phases; and (iv) we interpolated these solutions from the calibrator onto the star data.
We imaged the radio sources with the program DIFMAP (Shepherd et al. 1994) and cross-checked the results with the IMAGR task in AIPS. To re-scale the visibility amplitudes of the calibrator PKS 0516−621, known to be a variable source (Sadler et al. 2006; Murphy et al. 2010), we used the 8.4 GHz flux density values obtained from ATCA measurements of this calibrator taken at the same time as our LBA observations (0.85, 1.40, and 1.50 Jy for epochs 2007.863, 2010.816, and 2013.625, respectively). We iterated amplitude and phase self-calibrations with deconvolutions using the clean algorithm to finally obtain the uniformly weighted maps of PKS 0516−621 (see Fig. 1). For each epoch, this iterative procedure allowed us to determine both the amplitude scaling corrections and self-calibrated phase for each telescope. Back to the AIPS program, these corrections were then interpolated and applied to the AB Dor B data. The phase-referenced naturally weighted images of AB Dor B are shown in Fig. 2. We note that in this phase-reference mapping process the positional information of AB Dor B with respect to the external quasar is conserved, thus relating the position of AB Dor B to the ICRF.
Circular Gaussian fits corresponding to the VLBI maps of the components of AB Dor B.
 |
Fig. 1 Contour images of the calibrator PKS 0516−621 at the three LBA epochs. In each map, the lowest contour level corresponds to 3 times the statistical root-mean-square (3, 1.5, and 3 mJy beam-1) with a scale factor between contiguous contours of |
 |
Fig. 2 Clean maps of the binary AB Dor B at the three LBA epochs. In each map, the lowest contour level corresponds to 3 times the statistical root-mean-square (0.08, 0.19, and 0.12 mJy beam-1) with a scale factor between contiguous contours of |
3. Results
3.1. Maps of AB Dor Ba/Bb
At each of the three observing epochs, two sources are clearly distinguishable in Fig. 2; we identify both spots with the components Ba and Bb previously seen in NIR images (Janson et al. 2007). We determined the flux and position of both components from a circular Gaussian least-squares fit (see Table 2). Both components appear unresolved for all three epochs. These are the first VLBI images of AB Dor B where we confirm that both components are compact and strong radio emitters. Previous studies (Lim 1993; Wolter et al. 2014) already found the system to have an intense radio emission with rapid rotation rate (0.38 days) and strong magnetic activity, as shown by the high X-ray luminosity, close to the saturation limit for active late-type stars. Our radio maps show that each component Ba and Bb should retain a high rotation rate to maintain such intense activity. The AB Dor B IR spectral analysis reported in Wolter et al. (2014) is compatible with two rapid rotators (although a model based on a single high-rotation star is not excluded). Using the fluxes and sizes listed in Table 2, we derived a mean radio luminosity for Ba and Bb of LR = 2.7 × 1014 erg Hz-1 s-1, similar to other radio star members of the AB Dor-MG, indicating that gyrosynchrotron emission originating at the stellar corona is the responsible mechanism for the radio emission.
For a proper astrometric analysis, we still need to identify the components Ba and Bb, as labeled by Janson et al. (2007) in their NIR images, in each of our images of AB Dor B. These authors selected component Ba to be the brightest one; however, the flux density of both stars is very variable at radio wavelengths (see Table 2) making an identification under the same criteria difficult. To break this ambiguity, and based on the similar relative position of components Ba and Bb in both the NIR and radio images, we selected the easternmost component of the radio maps to be Ba. This choice was confirmed to be correct after the analysis of the orbital motion (see Sect. 3.2). It must be noted that the appropriate registration of Ba and Bb through the three epochs is guaranteed by the use of the quasar PKS 0516−621 as an external astrometric reference.
3.2. Orbit determination of AB Dor Ba/Bb
To estimate the orbital elements of AB Dor Ba/Bb, we used the positions of AB Dor Ba/Bb resulting from the astrometric analysis of our three LBA observations, both the relative positions (as measured directly on the maps shown in Fig. 2) and the absolute positions (in turn referenced to the position of the quasar PKS 0516−621). We included the NIR relative positions available in the literature (Wolter et al. 2014, and references therein) in our fit. We complemented our data sets with the absolute positions reported in G06 and re-interpreted here. These authors made a first attempt to estimate the orbital elements with LBA epochs ranging from 1992 to 1996, but their least-squares analysis did not converge to any plausible solution. A possible reason for this non-convergence could be the misidentification of the only component detected, wrongly associated with AB Dor Ba at all epochs. Preliminary fits of the G06 positions along with the new ones presented in this paper show that only the positions at epochs 1992.685 (corresponding to Bb) and 1993.123 (corresponding to Ba) are compatible with the new LBA data. Accordingly, only those positions are included in our fit. The rest of the positions of AB Dor Ba/Bb in G06 are therefore not included in our analysis. Table 3 summarizes all the positions used in this work.
To find the astrometric and Keplerian parameters of the AB Dor B system, we selected a non-redundant data set from the positions shown in Table 3. In practice, in our fit we combined the absolute positions of AB Dor Bb and all relative positions of AB Dor Bb to AB Dor Ba. The reason for this choice is that the absolute orbit of AB Dor Bb and the relative orbit constructed using AB Dor Ba as reference (Bb–Ba) are identical, except for their semimajor axes, which are related by the mass ratio. An equivalently valid choice would have been a combination of absolute data of Ba and relative data constructed as Ba–Bb. We note that other combinations of absolute and relative data would have produced an extra difference of π radians in the longitude of the periastron (ω) between the absolute and relative orbits, which would have complicated our orbit analysis (see below). We used a least-squares fit approach similar to that described in G06, but slightly improved to deal with relative data, which we outline here.
We define the absolute position of AB Dor Bb (αBb,δBb) at epoch t through the expressions 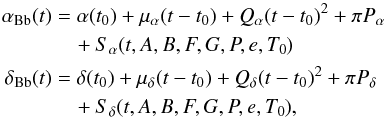 where t0 is the reference epoch, μα and μδ are the proper motions in each coordinate, Qα and Qδ are the secular perspective accelerations in each coordinate (i.e., time variation of the proper motions), π is the parallax, Pα and Pδ are the parallax factors (Green 1985), and Sα and Sδ are the absolute orbital motions of AB Dor Bb in α and δ, respectively. The acceleration terms are intended to model the long-term expected curvature of the sky trajectory of AB Dor B due to the gravitational pull of AB Dor A 9′′ away (see G06). We used the Thieles-Innes elements (A,B,F,G), which are combinations of the semimajor axis of the absolute orbit aBb, the inclination i, the longitude of the ascending node Ω, and the longitude of periastron ω. The three remaining non-linear parameters are the period P, the eccentricity e, and the time of periastron passage T0.
where t0 is the reference epoch, μα and μδ are the proper motions in each coordinate, Qα and Qδ are the secular perspective accelerations in each coordinate (i.e., time variation of the proper motions), π is the parallax, Pα and Pδ are the parallax factors (Green 1985), and Sα and Sδ are the absolute orbital motions of AB Dor Bb in α and δ, respectively. The acceleration terms are intended to model the long-term expected curvature of the sky trajectory of AB Dor B due to the gravitational pull of AB Dor A 9′′ away (see G06). We used the Thieles-Innes elements (A,B,F,G), which are combinations of the semimajor axis of the absolute orbit aBb, the inclination i, the longitude of the ascending node Ω, and the longitude of periastron ω. The three remaining non-linear parameters are the period P, the eccentricity e, and the time of periastron passage T0.
Compilation of astrometric measurements for the AB Dor B system.
Similarly, the relative positions (αrel,δrel, constructed as Bb−Ba) at epoch t′ (not necessarily different from t) are included in the fit through the expressions 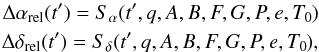 where q is the ratio between the semimajor axes of the relative and absolute orbit, arel/aBb. We note that q behaves as a scale factor between the absolute and relative orbit, both sharing all the orbital elements but the semimajor axes (provided that the absolute and relative data sets have been chosen appropriately, as explained above). Accordingly, the true Thieles-Innes constants of the relative orbit can be written as (qA,qB,qC,qG), so that q remains as the only additional free parameter in our fit when adding the relative orbit data. Given the definition of both data types, the χ2 to be minimized is
where q is the ratio between the semimajor axes of the relative and absolute orbit, arel/aBb. We note that q behaves as a scale factor between the absolute and relative orbit, both sharing all the orbital elements but the semimajor axes (provided that the absolute and relative data sets have been chosen appropriately, as explained above). Accordingly, the true Thieles-Innes constants of the relative orbit can be written as (qA,qB,qC,qG), so that q remains as the only additional free parameter in our fit when adding the relative orbit data. Given the definition of both data types, the χ2 to be minimized is 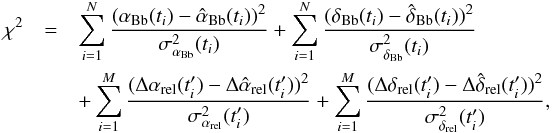 where N is the number of absolute positions, M the number of relative positions, σ the corresponding standard deviations, and the circumflexed quantities are the theoretical positions derived from the a priori values of the astrometric and orbital parameters. We have used the Levenberg-Marquardt algorithm (L-M; e.g., Press et al. 1992) to minimize the χ2. Like other methods used to find minima in a non-linear χ2 space, the efficiency of the L-M algorithm is much improved if good a priori values are used for the orbital elements. In our particular case, exploration of the relative orbit data yields a reasonable initial value for the period: as seen in Table 3, the two NIR positions are similar, indicating that the time difference between both epochs, nearly one year, could be a promising initial value for the period. In addition, the separation and the position angle in the first two LBA epochs (2007.863 and 2010.816) are almost coincident, with a difference of less than two milliarcseconds. This strongly suggests that the time difference between the two LBA epochs (2.95 years) should be approximately an integer number of the true orbital period. If we assume that three complete orbits have elapsed between the two epochs, the orbital period would be 0.98 yr, coincident with the estimate made from the relative infrared data. The use of an a priori value for the period of 1 yr did facilitate the convergence of the L-M algorithm. Of course, the previous argumentation is also valid for shorter periods as long as P ~ 1 /n yr, with n being an integer number; however, no convergence is found in our fit for periods with n ≥ 2.
where N is the number of absolute positions, M the number of relative positions, σ the corresponding standard deviations, and the circumflexed quantities are the theoretical positions derived from the a priori values of the astrometric and orbital parameters. We have used the Levenberg-Marquardt algorithm (L-M; e.g., Press et al. 1992) to minimize the χ2. Like other methods used to find minima in a non-linear χ2 space, the efficiency of the L-M algorithm is much improved if good a priori values are used for the orbital elements. In our particular case, exploration of the relative orbit data yields a reasonable initial value for the period: as seen in Table 3, the two NIR positions are similar, indicating that the time difference between both epochs, nearly one year, could be a promising initial value for the period. In addition, the separation and the position angle in the first two LBA epochs (2007.863 and 2010.816) are almost coincident, with a difference of less than two milliarcseconds. This strongly suggests that the time difference between the two LBA epochs (2.95 years) should be approximately an integer number of the true orbital period. If we assume that three complete orbits have elapsed between the two epochs, the orbital period would be 0.98 yr, coincident with the estimate made from the relative infrared data. The use of an a priori value for the period of 1 yr did facilitate the convergence of the L-M algorithm. Of course, the previous argumentation is also valid for shorter periods as long as P ~ 1 /n yr, with n being an integer number; however, no convergence is found in our fit for periods with n ≥ 2.
Estimates of the astrometric and orbital parameters of AB Dor B.
The set of orbital parameters that produces a minimum in the χ2 (1.2) is shown in Table 4. Plots of the relative and absolute orbits are shown in Figs. 3 and 4, respectively. These parameters coincide with those of Wolter et al. (2014) to within their standard deviations (except for Ω, with a difference of ~π/ 2, which may reflect a quadrant ambiguity). The sum of the masses of the system can be calculated from arel and the period P using Kepler’s Third Law (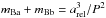 ), which resulted in 0.53 ± 0.05 M⊙, somewhat lower, but within uncertainties, than the Wolter et al. (2014) estimate of 0.69
), which resulted in 0.53 ± 0.05 M⊙, somewhat lower, but within uncertainties, than the Wolter et al. (2014) estimate of 0.69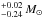 . More importantly, since our data also provide the semimajor axis of the absolute orbit of AB Dor Bb, aBb, we can also calculate the mass of the component Ba, mBa, using Kepler’s third law in the form
. More importantly, since our data also provide the semimajor axis of the absolute orbit of AB Dor Bb, aBb, we can also calculate the mass of the component Ba, mBa, using Kepler’s third law in the form 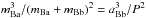 . This yields a value of mBa = 0.28 ± 0.05 M⊙, with the uncertainty calculated from the propagation of the standard deviations of the semimajor axis aBb, the period P, and mBa + mBb. Since we also have the absolute data of AB Dor Ba, we can estimate, independently of the previous fit, a value of mBb (i.e., not just the difference between mass sum and mBa). To this end, we repeated the fit described throughout this section but using the absolute positions of AB Dor Ba and the relative positions constructed as Ba-Bb. As explained above, this is an equivalent fit to the previous one, except that it provides an estimate of aBa instead of aBb. Again, using Kepler’s Third Law, now with aBa, we obtain a value of mBb = 0.25 ± 0.05 M⊙, this estimate being largely independent of mBa and the total mass.
. This yields a value of mBa = 0.28 ± 0.05 M⊙, with the uncertainty calculated from the propagation of the standard deviations of the semimajor axis aBb, the period P, and mBa + mBb. Since we also have the absolute data of AB Dor Ba, we can estimate, independently of the previous fit, a value of mBb (i.e., not just the difference between mass sum and mBa). To this end, we repeated the fit described throughout this section but using the absolute positions of AB Dor Ba and the relative positions constructed as Ba-Bb. As explained above, this is an equivalent fit to the previous one, except that it provides an estimate of aBa instead of aBb. Again, using Kepler’s Third Law, now with aBa, we obtain a value of mBb = 0.25 ± 0.05 M⊙, this estimate being largely independent of mBa and the total mass.
Regarding the astrometric parameters in Table 4, we note that the long-term orbit of the pair AB Dor B around AB Dor A is reflected in the values of the perspective acceleration; solving for Qα and Qδ reduced the rms of the residuals by a factor of three. The magnitude of the acceleration can be easily reproduced from the simple expression (circular orbit) (2π/PAB)2 × rAB, taking the A/B distance rAB = 9.22′′ at the reference epoch (2000.0) and assuming reasonable values of the period of B around A, PAB (~2000 yr; within the plausible orbits defined in G06).
Finally, as seen in Figs. 3 and 4, the orbit of the pair in AB Dor B is not fully covered. However, the orbital elements in Table 4 are satisfactorily determined. This apparent contradiction may be explained in two ways. First, the so-called Eggen’s effect (Lucy 2014), which predicts that for poorly covered orbits, the quantity a3/P2 has little variation for the values of the parameters (a,P) that minimize the χ2 defined in Sect. 3.2. We note that a3/P2 is proportional to the star masses, and therefore sensitive to any trace of orbital motion present in one of the components of the binary. Second, we have a precise a priori value for the orbital period, which when combined with the previous effect leads to a reliable estimate of the semimajor axis, greatly constraining the rest of the orbital elements.
 |
Fig. 3 Relative orbit for the binary AB Dor Bb using to the orbital elements in Table 4 (with arel). The AB Dor Ba component is indicated by the asterisk at the origin. Star symbols and epochs correspond to the VLBI data. For the sake of clarity, the NIR points are marked with numbers, following a chronological order which corresponds with their entries in Table 3. A prediction of the relative position at epoch 2008.605 is shown as an empty circle, indicating that the upper bound of 19 mas suggested by Wolter et al. (2014) is fully accomplished. |
 |
Fig. 4 Absolute orbits of AB Dor Ba and AB Dor Bb using the orbital elements in Table 4 (with aBa and aBb, respectively). The positions of components Ba (triangles) and Bb (star symbols) are marked along with their respective epochs. The center of mass (CM) of the system is placed at the origin. |
4. Discussion
4.1. Stellar evolution models for PMS stars
 |
Fig. 5 Comparison of AB Dor B components with some PMS theoretical models (Baraffe et al. 1998, top left; Siess et al. 2000, top right; Montalán & D’Antona 2006, bottom left; Tognelli et al. 2011; bottom right). For each model isomasses (solid lines) and isochrones (dashed lines) are plotted. We highlight the nearest tracks available corresponding to our dynamical mass values. The theoretical masses are consistent with our dynamical estimates just at the extreme of their uncertainties. |
The measurements of dynamical masses are essential in order to check PMS stellar evolution models. The mass is the most important stellar parameter, but determinations of the luminosity and the temperature are also necessary in order to calibrate the theoretical models. Extensive description and comparison between existing stellar models can be seen in Hillenbrand & White (2004).
In this paper, we have considered isochrones and isomasses corresponding to the PMS models of Baraffe et al. (1998, BCAH98), Siess et al. (2000, S00), Montalbán & D’Antona (2006, MD06), and Tognelli et al. (2011; 2012, TDP12). A metallicity value of [Fe/H] = 0.0 has been adopted as the average value of the AB Doradus moving group was reported to be [Fe / H] = 0.02 ± 0.02 (Barenfeld et al. 2013). All the quoted models provide theoretical masses for stars down to 0.1 M⊙, but for different mass spacing. Low convection efficiency (i.e., mixing length parameter αML = 1.0), which optimizes the comparison with our data, have been used in the case of the BCAH98, MD06, and TDP12 models. For the S00 models, tracks are available only for solar calibration, with αML = 1.61.
In addition to the convection treatment, other differences among the quoted PMS low-mass star models are relevant, in particular the adopted equation of state, the radiative opacity, the atmospheric structures used to specify the outer boundary conditions, and the adopted initial abundances of the chemical elements (mainly helium and total metallicity) at a fixed [Fe/H] value (see, e.g., Siess et al. 2001; Mathieu et al. 2007, Tognelli et al. 2011). As a result, the age and mass inferred by comparing evolutionary tracks and data might change significantly for different stellar models (i.e., input physics).
These models are shown in Fig. 5, where different isomasses and isochrones are plotted. We have placed AB Dor Ba and Bb in the Hertzsprung-Russell (H-R) diagrams in Fig. 5 using the spectroscopically determined effective temperatures of Wolter et al. (2014) and the K magnitude measured by Janson et al. (2007). The BCAH98 and TDP12 models suggest that AB Dor Ba and Bb are coeval, with an age between ~50 Myr and 100 Myr, similar to that reported by Janson et al. (2007) and Wolter et al. (2004). S00 provides a slightly older age, but non-coevality. Finally, MD06 predicts substantially older ages, 100–125 Myr for both stars. This last age range seems to agree with the age derived by Barenfeld et al. (2013) for the nucleus of the AB Dor-MG (>110 Myr).
On the other hand, the theoretical masses predicted from the models agree with our dynamical estimates just at the extreme of their uncertainties. The models of BCAH98 and TDP12 (with a denser distribution of isomasses than S00) predict mass ranges of 0.18–0.25 M⊙ for component Ba and 0.14–0.21 M⊙ for component Bb. The MD06 models also underpredict the masses of Ba and Bb but with a better agreement, in practice within the standard deviations of our dynamical measurements. Therefore, for the BCAH98, TDP12, and S00 models the dynamical masses reported in this paper are 30% and 40% larger than the central values of the range predicted for AB Dor Ba and Bb, respectively. This disagreement decreases to 10% for the MD06 models. Our results seem consistent with similar comparisons of dynamical and theoretical masses done by other authors (Hillenbrand & White 2004; Stassun et al. 2004; Mathieu et al. 2007) who concluded that models underpredict stellar masses by 10–30% for PMS stars with masses in the range 0.3–1.2 M⊙. Our comparisons suggest that this disagreement holds for masses below 0.3 M⊙. We note that other stellar models designed specifically for lower mass objects (e.g., DUSTY models, Chabrier et al. 2000) do not cover the range 0.2–0.3 M⊙.
4.2. Alternative scenario for the binary AB Dor B
As noted in Sect. 3.1, both AB Dor Ba and AB Dor Bb are strong, compact radio emitters, which contributes to the emerging perception that many radio stars reside in double or multiple systems (Melis et al. 2013; Azulay et al. 2014). Considering the radio/X-ray activity correlation (Güdel et al. 1993), this perception finds support in other, better reported statistics which relates X-ray activity and binarity, namely, that about 79% of the X-ray emitters are in binary systems (Makarov & Eggleton 2009). Many of these binaries correspond to close binaries, but interestingly, a large fraction of the total X-ray binaries (67%; Makarov & Eggleton 2009) are part of hierarchical triple systems, with the third body in a wider orbit. In this scheme, the presence of the wide companion induces dynamical perturbations to the orbit of the close binary at each periastron passage through the Kozai cycles and tidal friction mechanism (e.g., Mazeh & Shaham 1979; Fabrycky & Tremaine 2007). Provided that the inner and outer orbits are misaligned, such an interaction progressively produces a loss of angular momentum that leads the close binary to shrink, to increment its orbital period, and in some cases to begin a merging process. The resulting merger will retain part of the angular momentum showing, as a consequence, an extraordinarily high rotational velocity, which will translate to high levels of activity both at X-ray and radio. This appears precisely to be the scenario found in some of the young radio stars in binary systems. Makarov & Eggleton (2009) explained the origin of the high rotation rate of AB Dor A (0.5 days) via Kozai cycling and tidal interaction between a close binary (now merged in AB Dor A) and the 0.090 M⊙ low-mass companion AB Dor C, orbiting AB Dor A at a mean distance of 2 AU with a period of 11.74 yr.
Could a similar mechanism be acting in AB Dor B? The remarkably high radio emission in both AB Dor Ba and AB Dor Bb reported in this paper and the rapid rotation suspected to occur in the two stars, <0.88 days (Wolter et al. 2014), provide support for this hypothesis. In addition, the separation Ba–Bb is only 0.15 AU at periastron with a much faster period than the pair AB Dor A/C, ~1 yr. Therefore, a more efficient Kozai cycling and tidal interaction might be taking place. Interestingly, this hypothesis would imply a double-double scenario where both components, Ba or Bb, resulting from their respective mergers, would act as mutual “third bodies” with respect to each other. This double-double scenario does not appear to be rare and it has been proposed to explain the light curves of quadruple systems of eclipsing binaries (Cagaš & Pejcha 2012).
5. Conclusions
We have shown the first VLBI images of the binary AB Dor B where we detect the presence of compact radio emission in both components. The scientific output of our LBA astrometric monitoring has been optimized, since both the absolute and relative orbits have been determined in combination with published NIR relative positions. The dynamical masses of the individual components of AB Dor B are very similar (0.28 and 0.25 M⊙, for Ba and Bb, respectively). Depending on the models, these values are 10–30% (10–40%) larger than the theoretical estimates of PMS evolutionary models for AB Dor Ba (AB Dor Bb), emphasizing the known tendency of these models to underpredict the masses, yet within 2σ of the predicted values. Comparisons in H-R diagrams favor an age between 50 Myr and 100 Myr, although the Montalbán & D’Antona (2006) models predicts ages older than 100 Myr. AB Dor B is one of the systems in the AB Dor-MG whose two components are radio emitters, contributing to the evidence that many young, wide binaries are strong radio emitters (like AB Dor A and HD 160934; see Azulay et al. 2014). This radio/binarity correlation may be the radio counterpart of the better established relationship between wide binaries and X-ray activity, which can be explained under the assumption that the present wide binaries were originated by dynamical interaction of hierarchical triple systems. This means that AB Dor Ba/Bb could be understood as two earlier close binaries, a double-double system, where both binaries were forced to shrink and merge via mutually induced, cyclic dynamical perturbations. The two evolved mergers (the present stars Ba and Bb) would thus keep part of the angular momentum as a very rapid rotation, responsible in turn for both the X-ray and radio activity.
New and more precise estimates of the dynamical masses would be desirable via an improved coverage of the orbit, where the resolution and sensitivity of the LBA array has been shown to be essential. Likewise, as pointed out by Janson et al. (2007) and Wolter et al. (2014), high-resolution spectroscopy of the components in AB Dor B would also better constrain their placement in H-R diagrams. These observations would also help to confirm the suspected rapid rotation of both components, as well as to determine the tilt of the spin axis of each star with respect to the orbital plane, which could add arguments in favor of the interpretation of the binary AB Dor B as an earlier double close-binary system.
International Celestial Reference Frame. http://hpiers.obspm.fr/icrs-pc/
Acknowledgments
This work has been partially supported by the Spanish MINECO projects AYA2009-13036-C02-02 and AYA2012-38491-C02-01 and by the Generalitat Valenciana projects PROMETEO/2009/104 and PROMETEOII/2014/057. The Long Baseline Array is part of the Australia Telescope National Facility which is funded by the Commonwealth of Australia for operation as a National Facility managed by CSIRO. We thank J. Montalbán for providing the PMS models and for the guidance to use them appropriately. The data used in this study were acquired as part of NASA’s Earth Science Data Systems and archived and distributed by the Crustal Dynamics Data Information System (CDDIS). This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. R.A. acknowledges the Max-Planck-Institute für Radioastronomie for its hospitality and especially J. A. Zensus for support.
References
- Azulay, R., Guirado, J. C., Marcaide, J. M., Martí-Vidal, I., & Arroyo-Torres, B. 2014, A&A, 561, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 1998, A&A, 337, 403 [NASA ADS] [Google Scholar]
- Barenfeld, S. A., Bubar, E. J., Mamajek, E. E., & Young, P. A. 2013, ApJ, 766, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Boccaletti, A., Chauvin, G., Baudoz, P., & Beuzit, J.-L. 2008, A&A, 482, 939 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cagaš, P., & Pejcha, O. 2012, A&A, 544, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chabrier, G., Baraffe, I., Allard, F., & Hauschildt, P. H. 2000, ApJ, 542, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Close, L. M., Lenzen, R., Guirado, J. C., et al. 2005, Nature, 433, 286 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Close, L. M., Thatte, N., Nielsen, E. L., et al. 2007, ApJ, 665, 736 [NASA ADS] [CrossRef] [Google Scholar]
- Fabrycky, D., & Tremaine, S. 2007, ApJ, 669, 1298 [NASA ADS] [CrossRef] [Google Scholar]
- Green, R. M. 1985, Spherical astronomy (Cambridge, New York: Cambridge University Press) [Google Scholar]
- Gudel, M., Schmitt, J. H. M. M., Bookbinder, J. A., & Fleming, T. A. 1993, ApJ, 415, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Guirado, J. C., Reynolds, J. E., Lestrade, J.-F., et al. 1997, ApJ, 490, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Guirado, J. C., Martí-Vidal, I., Marcaide, J. M., et al. 2006, A&A, 446, 733 (G06) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guirado, J. C., Marcaide, J. M., Martí-Vidal, I., et al. 2011, A&A, 533, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hillenbrand, L. A., & White, R. J. 2004, ApJ, 604, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Janson, M., Brandner, W., Lenzen, R., et al. 2007, A&A, 462, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lim, J. 1993, ApJ, 405, 33 [NASA ADS] [CrossRef] [Google Scholar]
- López-Santiago, J., Montes, D., Crespo-Chacón, I., & Fernández-Figueroa, M. J. 2006, ApJ, 643, 1160 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 2014, A&A, 563, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luhman, K. L., Stauffer, J. R., & Mamajek, E. E. 2005, ApJ, 628, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Makarov, V. V., & Eggleton, P. P. 2009, ApJ, 703, 1760 [NASA ADS] [CrossRef] [Google Scholar]
- Mathieu, R. D., Baraffe, I., Simon, M., Stassun, K. G., & White, R. 2007, Protostars and Planets V, 411 [Google Scholar]
- Mazeh, T., & Shaham, J. 1979, A&A, 77, 145 [Google Scholar]
- Melis, C., Reid, M. J., Mioduszewski, A. J., Stauffer, J. R., & Bower, G. C. 2013, IAU Symp., 289, 60 [NASA ADS] [Google Scholar]
- Montalbán, J., & D’Antona, F. 2006, MNRAS, 370, 1823 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, T., Sadler, E., Ekers, R. D., et al. 2010, MNRAS, 402, 2403 [NASA ADS] [CrossRef] [Google Scholar]
- Nielsen, E. L., Close, L. M., Guirado, J. C., et al. 2005, Astron. Nachr., 326, 1033 [NASA ADS] [CrossRef] [Google Scholar]
- Ortega, V. G., Jilinski, E., de La Reza, R., & Bazzanella, B. 2007, MNRAS, 377, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, 2nd edn. (Cambridge: University Press) [Google Scholar]
- Sadler, E. M., Ricci, R., Ekers, R. D., et al. 2006, MNRAS, 371, 891 [Google Scholar]
- Shepherd, M. C., Pearson, T. J., & Taylor, G. B. 1994, BAAS, 26, 987 [NASA ADS] [Google Scholar]
- Siess, L. 2001, in From Darkness to Light: Origin and Evolution of Young Stellar Clusters, eds. T. Montmerle, & P. André, ASP Conf. Ser., 243, 581 [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [Google Scholar]
- Stassun, K. G., Mathieu, R. D., Vaz, L. P. R., Stroud, N., & Vrba, F. J. 2004, ApJS, 151, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Tognelli, E., Prada Moroni, P. G., & Degl’Innocenti, S. 2011, A&A, 533, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tognelli, E., Degl’Innocenti, S., & Prada Moroni, P. G., 2012, A&A, 548, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolter, U., Czesla, S., Fuhrmeister, B., et al. 2014, A&A, 570, A95 [Google Scholar]
- Zuckerman, B., Song, I., & Bessell, M. S. 2004, ApJ, 613, L65 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Circular Gaussian fits corresponding to the VLBI maps of the components of AB Dor B.
All Figures
 |
Fig. 1 Contour images of the calibrator PKS 0516−621 at the three LBA epochs. In each map, the lowest contour level corresponds to 3 times the statistical root-mean-square (3, 1.5, and 3 mJy beam-1) with a scale factor between contiguous contours of |
| In the text | |
 |
Fig. 2 Clean maps of the binary AB Dor B at the three LBA epochs. In each map, the lowest contour level corresponds to 3 times the statistical root-mean-square (0.08, 0.19, and 0.12 mJy beam-1) with a scale factor between contiguous contours of |
| In the text | |
 |
Fig. 3 Relative orbit for the binary AB Dor Bb using to the orbital elements in Table 4 (with arel). The AB Dor Ba component is indicated by the asterisk at the origin. Star symbols and epochs correspond to the VLBI data. For the sake of clarity, the NIR points are marked with numbers, following a chronological order which corresponds with their entries in Table 3. A prediction of the relative position at epoch 2008.605 is shown as an empty circle, indicating that the upper bound of 19 mas suggested by Wolter et al. (2014) is fully accomplished. |
| In the text | |
 |
Fig. 4 Absolute orbits of AB Dor Ba and AB Dor Bb using the orbital elements in Table 4 (with aBa and aBb, respectively). The positions of components Ba (triangles) and Bb (star symbols) are marked along with their respective epochs. The center of mass (CM) of the system is placed at the origin. |
| In the text | |
 |
Fig. 5 Comparison of AB Dor B components with some PMS theoretical models (Baraffe et al. 1998, top left; Siess et al. 2000, top right; Montalán & D’Antona 2006, bottom left; Tognelli et al. 2011; bottom right). For each model isomasses (solid lines) and isochrones (dashed lines) are plotted. We highlight the nearest tracks available corresponding to our dynamical mass values. The theoretical masses are consistent with our dynamical estimates just at the extreme of their uncertainties. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.