| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A22 | |
| Number of page(s) | 26 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201424811 | |
| Published online | 27 May 2015 | |
Unprecedented study of the broadband emission of Mrk 421 during flaring activity in March 2010⋆,⋆⋆
1 IFAE, Campus UAB, 08193 Bellaterra, Spain
2 Università di Udine, and INFN Trieste, 33100 Udine, Italy
3 INAF National Institute for Astrophysics, 00136 Rome, Italy
4 Università di Siena, and INFN Pisa, 53100 Siena, Italy
5 Croatian MAGIC Consortium, Rudjer Boskovic Institute, University of Rijeka and University of Split, 10000 Zagreb, Croatia
6 Max-Planck-Institut für Physik, 80805 München, Germany
7 Universidad Complutense, 28040 Madrid, Spain
8 Inst. de Astrofísica de Canarias, 38200 La Laguna, Tenerife, Spain
9 University of Łódź, 90236 Lodz, Poland
10 Deutsches Elektronen-Synchrotron (DESY), 15738 Zeuthen, Germany
11 ETH Zurich, 8093 Zurich, Switzerland
12 Universität Würzburg, 97074 Würzburg, Germany
13 Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas, 28040 Madrid, Spain
14 Institute of Space Sciences, 08193 Barcelona, Spain
15 Università di Padova and INFN, 35131 Padova, Italy
16 Technische Universität Dortmund, 44221 Dortmund, Germany
17 Unitat de Física de les Radiacions, Departament de Física, and CERES-IEEC, Universitat Autònoma de Barcelona, 08193 Bellaterra, Spain
18 Universitat de Barcelona, ICC, IEEC-UB, 08028 Barcelona, Spain
19 Japanese MAGIC Consortium, Division of Physics and Astronomy, Kyoto University, 277-8582 Chiba, Kashiwa, Japan
20 Finnish MAGIC Consortium, Tuorla Observatory, University of Turku and Department of Physics, University of Oulu, 90014 Oulu, Finland
21 Inst. for Nucl. Research and Nucl. Energy, 1784 Sofia, Bulgaria
22 Università di Pisa, and INFN Pisa, 56126 Pisa, Italy
23 ICREA and Institute of Space Sciences, 08193 Barcelona, Spain
24 Università dell’Insubria and INFN Milano Bicocca, Como, 22100 Como, Italy
25 Now at: Centro Brasileiro de Pesquisas Físicas (CBPF/MCTI), R. Dr. Xavier Sigaud, 150 − Urca, 22290-180 Rio de Janeiro – RJ, Brazil
26 NASA Goddard Space Flight Center, Greenbelt, MD 20771, USA
27 Department of Physics and Department of Astronomy, University of Maryland, College Park, MD 20742, USA
28 Now at: École polytechnique fédérale de Lausanne (EPFL), 1015 Lausanne, Switzerland
29 Now at: Institut für Astro- und Teilchenphysik, Leopold-Franzens- Universität Innsbruck, 6020 Innsbruck, Austria
30 Now at: Finnish Centre for Astronomy with ESO (FINCA), 20100 Turku, Finland
31 Now at: Astrophysics Science Division, Bhabha Atomic Research Centre, 400085 Mumbai, India
32 Now at: School of Chemistry & Physics, University of Adelaide, 5005 Adelaide, Australia
33 Physics Department, McGill University, Montreal, QC H3A 2T8, Canada
34 Department of Physics, Washington University, St. Louis, MO 63130, USA
35 Fred Lawrence Whipple Observatory, Harvard-Smithsonian Center for Astrophysics, Amado, AZ 85645, USA
36 Department of Physics and Astronomy and the Bartol Research Institute, University of Delaware, Newark, DE 19716, USA
37 School of Physics, University College Dublin, Belfield, Dublin 4, Ireland
38 Santa Cruz Institute for Particle Physics and Department of Physics, University of California, Santa Cruz, CA 95064, USA
39 Institute of Physics and Astronomy, University of Potsdam, 14476 Potsdam-Golm, Germany
40 Astronomy Department, Adler Planetarium and Astronomy Museum, Chicago, IL 60605, USA
41 Department of Physics and Astronomy, Purdue University, West Lafayette, IN 47907, USA
42 Department of Physics and Astronomy, Iowa State University, Ames, IA 50011, USA
43 Department of Astronomy and Astrophysics, 525 Davey Lab, Pennsylvania State University, University Park, PA 16802, USA
44 School of Physics and Astronomy, University of Minnesota, Minneapolis, MN 55455, USA
45 School of Physics, National University of Ireland Galway, University Road, Galway, Ireland
46 Department of Physics and Astronomy, University of Iowa, Van Allen Hall, Iowa City, IA 52242, USA
47 Department of Physics and Astronomy, University of Utah, Salt Lake City, UT 84112, USA
48 Department of Physics and Astronomy, DePauw University, Greencastle, IN 46135-0037, USA
49 Enrico Fermi Institute, University of Chicago, Chicago, IL 60637, USA
50 Kavli Institute for Cosmological Physics, University of Chicago, Chicago, IL 60637, USA
51 School of Physics and Center for Relativistic Astrophysics, Georgia Institute of Technology, 837 State Street NW, Atlanta, GA 30332-0430, USA
52 Department of Physics, Anderson University, 1100 East 5th Street, Anderson, IN 46012, USA
53 Department of Life and Physical Sciences, Galway-Mayo Institute of Technology, Dublin Road, Galway, Ireland
54 Department of Physics and Astronomy, University of California, Los Angeles, CA 90095, USA
55 Instituto de Astronomia y Fisica del Espacio, Casilla de Correo 67 − Sucursal 28, (C1428ZAA) Ciudad Autònoma de Buenos Aires, Argentina
56 Physics Department, California Polytechnic State University, San Luis Obispo, CA 94307, USA
57 Department of Applied Physics and Instrumentation, Cork Institute of Technology, Bishopstown, Cork, Ireland
58 Space Science Division, Naval Research Laboratory, Washington, DC 20375-5352, USA
59 INAF, Osservatorio Astronomico di Torino, 10025 Pino Torinese (TO), Italy
60 Department of Astronomy, University of Michigan, Ann Arbor, MI 48109-1042, USA
61 Department of Physics, University of Trento, 38050 Povo, Trento, Italy
62 Graduate Institute of Astronomy, National Central University, 32054 Jhongli, Taiwan
63 Harvard-Smithsonian Center for Astrophysics, Cambridge, MA 02138, USA
64 Institute for Astrophysical Research, Boston University, 725 Commonwealth Avenue, Boston, MA 02215, USA
65 Astronomical Institute, St. Petersburg State University, Universitetskij Pr. 28, Petrodvorets, 198504 St. Petersburg, Russia
66 Institute of Astronomy, National Tsing Hua University, 101 Guanfu Rd., 30013 Hsinchu, Taiwan
67 Abastumani Observatory, Mt. Kanobili, 0301 Abastumani, Georgia
68 Landessternwarte, Zentrum für Astronomie der Universität Heidelberg, Königstuhl 12, 69117 Heidelberg, Germany
69 Aalto University Metsähovi Radio Observatory, Metsähovintie 114, 02540 Kylmälä, Finland
70 Aalto University Department of Radio Science and Engineering, PO Box 13000, 00076 Aalto, Finland
71 Astron. Inst., St.-Petersburg State University, 198504 St. Peetersburg, Russia
72 Pulkovo Observatory, St.-Petersburg, 198504 St. Peetersburg, Russia
73 Isaac Newton Institute of Chile, St.-Petersburg Branch, Russia
74 Department of Physics and Astronomy, Brigham Young University, Provo, UT 84602, USA
75 Cahill Center for Astronomy and Astrophysics, California Institute of Technology, 1200 E California Blvd, Pasadena, CA 91125, USA
76 ASI-Science Data Center, via del Politecnico, 00133 Rome, Italy
77 Agrupació Astronòmica de Sabadell, 08206 Sabadell Barcelona, Spain
78 Department of Physics, University of Colorado Denver, Denver, Colorado, Co 80217-3364, USA
79 Department of Physics and Mathematics, College of Science and Engineering, Aoyama Gakuin University, 5-10-1 Fuchinobe, 1105 Chuoku, 252-5258 Sagamihara-shi Kanagawa, Japan
80 Steward Observatory, University of Arizona, Tucson, AZ 85721, USA
81 Space Science Institute, Boulder, CO 80301, USA
82 School of Cosmic Physics, Dublin Institute for Advanced Studies, Belfield, Dublin 2, Ireland
⋆⋆⋆
Corresponding author: David Paneque, e-mail: dpaneque@mpp.mpg.de; Shangyu Sun, e-mail: sysun@mpp.mpg.de; Hajime Takami, e-mail: takami@post.kek.jp
Received: 14 August 2014
Accepted: 5 December 2014
Context. Because of its proximity, Mrk 421 is one of the best sources on which to study the nature of BL Lac objects. Its proximity allows us to characterize its broadband spectral energy distribution (SED).
Aims. The goal is to better understand the mechanisms responsible for the broadband emission and the temporal evolution of Mrk 421. These mechanisms may also apply to more distant blazars that cannot be studied with the same level of detail.
Methods. A flare occurring in March 2010 was observed for 13 consecutive days (from MJD 55 265 to MJD 55 277) with unprecedented wavelength coverage from radio to very high energy (VHE; E> 100 GeV) γ-rays with MAGIC, VERITAS, Whipple, Fermi-LAT, MAXI, RXTE, Swift, GASP-WEBT, and several optical and radio telescopes. We modeled the day-scale SEDs with one-zone and two-zone synchrotron self-Compton (SSC) models, investigated the physical parameters, and evaluated whether the observed broadband SED variability can be associated with variations in the relativistic particle population.
Results. The activity of Mrk 421 initially was high and then slowly decreased during the 13-day period. The flux variability was remarkable at the X-ray and VHE bands, but it was minor or not significant at the other bands. The variability in optical polarization was also minor. These observations revealed an almost linear correlation between the X-ray flux at the 2–10 keV band and the VHE γ-ray flux above 200 GeV, consistent with the γ-rays being produced by inverse-Compton scattering in the Klein-Nishina regime in the framework of SSC models. The one-zone SSC model can describe the SED of each day for the 13 consecutive days reasonably well, which once more shows the success of this standard theoretical scenario to describe the SEDs of VHE BL Lacs such as Mrk 421. This flaring activity is also very well described by a two-zone SSC model, where one zone is responsible for the quiescent emission, while the other smaller zone, which is spatially separated from the first, contributes to the daily variable emission occurring at X-rays and VHE γ-rays. The second blob is assumed to have a smaller volume and a narrow electron energy distribution with 3 × 104<γ< 6 × 105, where γ is the Lorentz factor of the electrons. Such a two-zone scenario would naturally lead to the correlated variability at the X-ray and VHE bands without variability at the optical/UV band, as well as to shorter timescales for the variability at the X-ray and VHE bands with respect to the variability at the other bands.
Conclusions. Both the one-zone and the two-zone SSC models can describe the daily SEDs via the variation of only four or five model parameters, under the hypothesis that the variability is associated mostly with the underlying particle population. This shows that the particle acceleration and cooling mechanism that produces the radiating particles might be the main mechanism responsible for the broadband SED variations during the flaring episodes in blazars. The two-zone SSC model provides a better agreement with the observed SED at the narrow peaks of the low- and high-energy bumps during the highest activity, although the reported one-zone SSC model could be further improved by varying the parameters related to the emitting region itself (δ, B and R), in addition to the parameters related to the particle population.
Key words: radiation mechanisms: non-thermal / galaxies: active / BL Lacertae objects: individual: Mrk 421 / gamma rays: galaxies
Appendices are available in electronic form at http://www.aanda.org
Multi-wavelength light curves (data in Fig. 1) and broadband spectral energy distributions (the data in Figs. 7, 8a–9f, 12a–13f) are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/578/A22
© ESO, 2015
1. Introduction
Markarian 421 (Mrk 421; RA = 11h4′27.31″, Dec = 38°12′31.8″, J2000) is a BL Lac object that is believed to have a pair of relativistic jets flowing in opposite directions closely aligned to our line of sight. It is also one of the closest (z = 0.031; de Vaucouleurs et al. 1991) and brightest BL Lac objects in the extragalactic X-ray and very high energy (VHE; E> 100 GeV) sky. This object was the first BL Lac object detected by the Energetic Gamma Ray Experiment Telescope (EGRET; Lin et al. 1992) at energies above 100 MeV, and was also the first extragalactic source detected by imaging atmospheric Cherenkov telescopes (IACTs; Punch et al. 1992). Mrk 421 is one of the best-studied BL Lac objects at VHE because it can be detected by modern IACTs within several minutes, and its broadband spectral energy distribution (SED) can be well measured by operating instruments covering energies from radio to VHE. Nearly all the IACTs have measured its VHE γ-ray spectrum (Krennrich et al. 2002; Aharonian et al. 2003, 2002; Okumura et al. 2002; Aharonian et al. 2005; Albert et al. 2007a).
The SED of a blazar is dominated by the emission of the jet components magnified by relativistic beaming. The observed spectrum and polarization indicate that the low-energy bump is synchrotron radiation of electrons in turbulent magnetic fields in the jet. Mrk 421 has a peak frequency of the low-energy bump above 1015 Hz, and therefore it is categorized as a high-synchrotron-peaked (HSP) BL Lac object based on the classification criterion presented in Abdo et al. (2010). The peak frequency of the high-energy bump for HSP blazars detected at VHE is usually below 100 GeV1. This bump may be interpreted as the inverse-Compton scattering of the same population of electrons off synchrotron photons (synchrotron self-Compton, SSC; Maraschi et al. 1992; Dermer & Schlickeiser 1993; Bloom & Marscher 1996). Alternatively, hadronic models can also explain this bump (e.g., Mannheim 1993; Mücke et al. 2003). Although both leptonic and hadronic models can reproduce the time-averaged broadband SED of Mrk 421 (e.g. Abdo et al. 2011), it is difficult to produce short-time variability (<1 h) with hadronic models, which has been observed in Mrk 421 (e.g. Gaidos et al. 1996). Thus, leptonic models are favored, at least in active states. A recent study on Mrk 421 also supports leptonic models during low blazar activity (Aleksić et al. 2015). In leptonic scenarios, one-zone SSC models with an electron distribution described by one or two power-law functions can typically describe the observed SEDs (e.g., Katarzyński et al. 2003; Błażejowski et al. 2005; Rebillot et al. 2006; Fossati et al. 2008; Horan et al. 2009).
Because Mrk 421 is bright and highly variable, long-term multiwavelength (MW) monitoring campaigns have been organized to intensely study its SED and its temporal evolution from radio to VHE γ-rays. Since 2009, an exceptionally long and dense monitoring of the broadband emission of Mrk 421 has been performed. The results of the 2009 MW campaign, which is related to Mrk 421 during nonflaring (typical) activity, were reported in Abdo et al. (2011). The SED was successfully modeled by both a leptonic and a hadronic model, but the authors commented that the hadronic model required extreme conditions for particle acceleration and confinement. Moreover, the densely sampled SED revealed that the leptonic one-zone SSC model required two breaks in the electron energy distribution (EED) to satisfactorily describe the smooth bumps in the quiescent state SED.
Mrk 421 showed high activity during the entire multi-instrument campaign in 2010. During the period from March 10 (modified Julian day [MJD] 55 265) to March 22 (MJD 55 277), the VHE activity decreased from a high flux ~2 Crab units (c.u.)2 down to the typical value ~0.5 c.u (Acciari et al. 2014), hence offering the possibility of studying the evolution of the SED during the decay of a flaring event. The extensive MW data collected allow measuring the broadband SED over the largest available fraction of wavelengths with simultaneous observations (mostly within 2−3 h) during 13 consecutive days. The present study is unprecedented for any blazar. The SED and indicated physical parameters in the emission region at different epochs and their temporal evolution have been studied (e.g., Mankuzhiyil et al. 2011; Acciari et al. 2011; Aleksić et al. 2012a), but based on sparse sampling. The observational data for 13 consecutive days provide a first opportunity to directly study the temporal evolution of the SED.
In Sect. 2, we report the observations and data analysis performed with the various instruments. In Sect. 3 we present the observational results on multi-band variability. In Sect. 4, all the broadband SEDs during the flaring activity are characterized within two SSC models and physical parameters in emission regions are derived. In Sect. 5 we discuss the interpretation of the experimental results, and then we summarize this study in Sect. 6. Throughout this paper, the ΛCDM cosmology with H0 = 71 km s-1, ΩM = 0.27, and ΩΛ = 0.73 is adopted.
Participating instruments in the campaign on Mrk 421 during 2010 March.
2. Observation and data analysis
All instruments that observed Mrk 421 during this campaign are listed in Table 1. The details of observations by each instrument are described below.
2.1. MAGIC
The Major Atmospheric Gamma-ray Imaging Cherenkov (MAGIC) telescope system consists of two 17-meter telescopes that are located on the island of La Palma, 2200 m above sea level. Stereo observation can provide a sensitivity of ~0.008 c.u. above ~300 GeV in 50 h of observation and allows detecting VHE photons between 50 GeV and 50 TeV. A detailed description of the performance of the MAGIC stereo system can be found in Aleksić et al. (2012b).
During this flare, MAGIC made 11 observations, all in stereoscopic mode. The exposure time ranged from ~10 to ~80 min, with the zenith angle ranging from 5 to 30 deg. In total we collected 4.7 h of good-quality data. The MAGIC data presented in this paper were taken in dark conditions and were not affected by bright moonlight. All these observations were conducted in the false-source-tracking (wobble) mode (Fomin et al. 1994): alternatively tracking two positions in the sky that are symmetric with respect to the true source position and 0.4° away from it. The MAGIC data on MJD 55 272 and 55 275 suffered from bad weather and occasional technical problems and were therefore removed from the analysis.
The MAGIC data were analyzed using the MAGIC Standard Analysis Software (MARS; Moralejo et al. 2010). In the analysis routine, signals are first calibrated and then an image-cleaning algorithm that involves the time structure of the shower images, and removes the contribution from the night sky background is applied. Afterward, the shower images are parameterized with an extended set of Hillas parameters (Hillas 1985), and another parameter, hadronness, to reject background showers resulting from charged cosmic rays. The hadronness is determined through a random forest classification (Breiman 2001), which is trained based on shower-image parameters and time information.
Then, all these parameters from the two telescopes are combined to reconstruct the arrival directions and energies of the γ-ray candidate events. The number of signal (excess) events is the number of events around the source position after subtracting the number of background events, which is estimated using the number of events in a source-free region. Flux and a preliminary spectrum are calculated based on this number. Finally, this preliminary spectrum is unfolded to correct for the effect of the limited energy resolution of the detector, as reported in Albert et al. (2007b), which leads to the final (true) observed VHE spectrum of the source.
The systematic uncertainties in the spectral measurements with MAGIC stereo observations are 11% in the normalization factor (at >300 GeV) and 0.15−0.20 in the photon index. The error on the flux does not include uncertainty on the energy scale. The energy scale of the MAGIC telescopes is determined with a precision of about 17% at low energies (E< 100 GeV) and 15% at medium energies (E> 300 GeV). Further details are reported in Aleksić et al. (2012b).
2.2. VERITAS
The Very Energetic Radiation Imaging Telescope Array System (VERITAS) is an array of four imaging atmospheric Cherenkov telescopes 12 m in diameter that are located in southern Arizona (Weekes et al. 2002) and are designed to detect emission from astrophysical objects in the energy range from ~100 GeV to greater than 30 TeV. VERITAS has an energy resolution of ~15% and an angular resolution (68% containment) of ~0.1° per event at 1 TeV. A source with a flux of 0.01 c.u. is detected in ~25 h of observations, while a 0.05 c.u. source is detected in less than 2 h. The field of view of the VERITAS cameras is 3.5°. For more details on the VERITAS instrument and its imaging atmospheric Cherenkov technique, see Perkins & Maier (2009).
VERITAS monitored Mrk 421 in March 2010 with a 10-min run each day on MJD 55 260, 55 265, 55 267−55 274. Observations were taken near culmination at zenith angles in the range 18° − 23° to benefit from the lowest possible energy threshold. All data were taken in wobble mode where the telescopes are pointed away from the source by 0.5° north, south, east, and west to allow for simultaneous background estimation using events from the same field of view.
Before event selection and background subtraction, all shower images are calibrated and cleaned as described in Cogan (2006) and Daniel et al. (2007). Following the calibration and cleaning of the data, the events are parameterized using a moment analysis (Hillas 1985). From this moment analysis, scaled parameters are calculated and used to select the γ-ray-like events (Aharonian et al. 1997; Krawczynski et al. 2006). The event-selection cuts are optimized a priori for a Crab-like source (power-law spectrum photon index Γ = 2.5 and Crab nebula flux level).
2.3. Whipple 10 m
The Whipple 10 m γ-ray telescope was situated at the Fred Lawrence Whipple Observatory in southern Arizona. It operated in the 300 GeV to 20 TeV energy range, with a peak response energy (for a Crab-like spectrum) of approximately 400 GeV. The telescope had a 10 m optical reflector with a camera consisting of 379 photomultiplier tubes, covering a field of view of 2.6° (Kildea et al. 2007). The Whipple 10-m was decommissioned in July 2011.
The Whipple 10 m telescope made ten observations performed in the ON/OFF and TRK (tracking) modes, in which the telescope tracked the source, which was centered in the field of view, for 28 min (ON and TRK runs). The duration of the observations ranged from about one to six hours, with half of the observations more than four hours long. The corresponding OFF run was collected at an offset of 30 min from the source’s right ascension for a period of 28 min. The two runs were taken at the same declination over the same range of telescope azimuth and elevation angles. This removed systematic errors that depend on slow changes in the atmosphere. In the TRK mode, only ON runs were taken without corresponding OFF observations, and the background was estimated from events whose major axis points away from the center of the camera (the source position). The data set amounts to 36 h and was analyzed using the University College Dublin analysis package as described in Acciari (2011). The photon fluxes, initially derived in Crab units for energies above 400 GeV, were converted into photon fluxes above 200 GeV using a Crab nebula flux of 2.2 × 10-10 cm-2 s-1 (Aleksić et al. 2012b). Because the spectrum of Mrk 421 is variable (and sometimes slightly harder or softer than that of the Crab nebula), this conversion could overestimate or underestimate the photon fluxes, but only at the level of ~10%, which is not critical for the results reported in this paper.
2.4. Fermi-LAT
The Fermi Large Area Telescope (LAT) is a γ-ray telescope operating from 20 MeV to more than 300 GeV. The LAT is an array of 4 × 4 identical towers, each one consisting of a tracker (where the photons are pair-converted) and a calorimeter (where the energies of the pair-converted photons are measured). LAT has a large peak effective area (0.8 m2 for 1 GeV photons), an energy resolution typically better than 10%, and a field of view of about 2.4 sr with an angular resolution (68% containment angle) better than 1° for energies above 1 GeV. Further details on the description of LAT are given in Atwood et al. (2009) and Ackermann et al. (2012). The analyses of the Fermi-LAT data were performed here with the ScienceTools software package version v9r32p5. We used the reprocessed Fermi-LAT events3 belonging to the P7REP_SOURCE_V15 class that are located in a circular region of interest (ROI) of 10° radius around Mrk 421, after applying a cut of <52° in the rocking angle, and <100° on the zenith angle to reduce contamination from the γ-rays produced in the upper atmosphere and observed along Earth’s limb. The background model used to extract the γ-ray signal includes a Galactic diffuse-emission component and an isotropic component. The model we adopted for the Galactic component is given by the file gll_iem_v05.fit, and the isotropic component, which is the sum of the extragalactic diffuse emission and the residual charged particle background, is parameterized by the file iso_source_v05.txt4. The normalizations of the two components in the background model were allowed to vary freely during the spectral-point fitting. The spectral parameters were estimated using the unbinned maximum-likelihood technique (Mattox et al. 1996) in the energy range 300 MeV to 300 GeV. We used the P7REP_SOURCE_V15 instrument response function5 and took into account all the sources from the second Fermi-LAT catalog (2FGL, Nolan et al. 2012) that are located within 15° of Mrk 421. When performing the fit, the spectral parameters of sources within 10° of Mrk 421 were allowed to vary, while those between 10° and 15° were fixed to their values from the 2FGL. When performing the likelihood fit in differential energy bins (spectral bins in the SED), the photon indices of the sources were frozen to the best-fit values obtained from the full spectral analysis.
The sensitivity of Fermi-LAT is not good enough to detect Mrk 421 within a few hours, and hence we integrated over two days to have significant detections and to be able to produce γ-ray spectra. Despite the two-day integration window, the number of collected photons above 300 MeV is only about 8 to 15 for each of the two-day intervals. Most of these photons have energies below a few GeV, since photons above 10 GeV are rarely detected from Mrk 421 in a two-day interval. Upper limits at 95% confidence level were calculated for the differential energy bins whenever the maximum-likelihood test statistic (TS)6 was below 4, or when the detected signal had fewer than two events. The systematic uncertainty in the flux is dominated by the systematic uncertainty in the effective area, which is estimated as 10% below 0.1 GeV, 5% in the energy range between 0.3 GeV and 10 GeV and 10% above 10 GeV(Ackermann et al. 2012). The systematic uncertainties are substantially smaller than the statistical uncertainties of the data points in the light curve and spectra.
2.5. X-ray observations
All 11 Swift-XRT (Burrows et al. 2005) observations were carried out using the windowed timing (WT) readout mode. The data set was first processed with the XRTDAS software package (v.2.9.3) developed at the ASI Science Data Center (ASDC) and distributed by HEASARC within the HEASoft package (v. 6.15.1)7. Event files were calibrated and cleaned with standard filtering criteria with the xrtpipeline task using the calibration files available in the Swift-XRT CALDB version 20140120. Events for the spectral analysis were selected within a 20-pixel (~46 arcsec) radius, which encloses about 90% of the PSF, centered on the source position. The background was extracted from a nearby circular region of 40 pixel radius. The ancillary response files were generated with the xrtmkarf task applying corrections for PSF losses and CCD defects using the cumulative exposure map. Before the spectral fitting, the 0.3−10 keV source energy spectra were binned to ensure a minimum of 20 counts per bin. The spectra were corrected for absorption with a neutral hydrogen column density fixed to the Galactic 21 cm value in the direction of Mrk 421, namely 1.9 × 1020 cm-2 (Kalberla et al. 2005).
The Rossi X-ray Timing Explorer (RXTE; Bradt et al. 1993) satellite performed daily pointing observations of Mrk 421 during the time interval from MJD 55 265 to MJD 55 277. The data analysis was performed using FTOOLS v6.9 and following the procedures and filtering criteria recommended by the NASA RXTE Guest Observer Facility8. The observations were filtered following the conservative procedures for faint sources. Only the first xenon layer of PCU2 was used. We used the package pcabackest to model the background and the package saextrct to produce spectra for the source and background files and the script9pcarsp to produce the response matrix. The PCA average spectra above 3 keV were fitted using the XSPEC package using a power-law function with an exponential cutoff (cutoffpl) with the same neutral hydrogen column density as was used in the Swift-XRT data analysis. However, since the PCA bandpass starts at 3 keV, the results do not depend strongly on the column density adopted.
We also used data from the all-sky X-ray instruments available in 2010, namely RXTE/ASM, MAXI, and Swift/BAT. The data from RXTE/ASM were obtained from the ASM web page10 and were filtered according to the prescription provided in the ASM web page. The daily fluxes from Swift/BAT were gathered from the BAT web page11 and the daily fluxes from MAXI were retrieved from a dedicated MAXI web page12.
2.6. Optical and UV observations
The optical fluxes reported in this paper were obtained within the GLAST-AGILE Support Program (GASP) within the Whole Earth Blazar Telescope (WEBT; e.g. Villata et al. 2008, 2009), with various optical telescopes around the globe. Additionally, many observations were performed with the Perkins, Rovor, New Mexico Skies, and the Bradford telescopes. Optical polarization measurements are also included from the Steward, Crimean, and St Petersburg observatories. All the instruments use the calibration stars reported in Villata et al. (1998) for calibration, and the Galactic extinction was corrected with the reddening corrections given in Schlegel et al. (1998). The flux from the host galaxy (which is significant only below ν ~ 1015 Hz) was estimated using the flux values across the R band from Nilsson et al. (2007) and the colors reported in Fukugita et al. (1995), and then subtracted from the measured flux.
The Swift Ultraviolet/Optical Telescope (UVOT; Roming et al. 2005) obtained data cycling through each of the three ultraviolet pass bands, UVW1, UVM2, and UVW2 with central wavelengths of 260 nm, 220 nm, and 193 nm, respectively. The photometry was computed using a 5 arcsec source region around Mrk 421 using a custom UVOT pipeline that performs the calibrations presented in Poole et al. (2008). Moreover, the custom pipeline also allows for separate, observation-by-observation, corrections for astrometric misalignments (Acciari et al. 2011). The flux measurements obtained were corrected for Galactic extinction with EB − V = 0.015 mag (Schlegel et al. 1998) at each spectral band (Fitzpatrick 1999). The contribution of the host galaxy to the UV fluxes is negligible and hence not considered.
2.7. Radio observations
The radio data reported in this manuscript were taken with the 14 m Metsähovi Radio Observatory at 37 GHz, the 40 m Owens Valley Radio Observatory (OVRO) telescope at 15 GHz, and the 26 m University of Michigan Radio Astronomy Observatory (UMRAO) at 14.5 GHz. Details of the observing strategy and data reduction are given by Teraesranta et al. (1998, Metsähovi), Richards et al. (2011, OVRO), and Aller et al. (1985, UMRAO). The 225 GHz (1.3 mm) light curve was obtained at the Submillimeter Array (SMA) near the summit of Mauna Kea (Hawaii). During the period covered in this work, Mrk 421 was observed as part of a dedicated program to follow sources on the Fermi-LAT Monitored Source List (PI: A. Wehrle). Observations of available LAT sources were made periodically for several minutes, and the measured source signal strength was calibrated against known standards, typically solar system objects (Titan, Uranus, Neptune, or Callisto).
Mrk 421 is a point-like and unresolved source for these three single-dish radio instruments and for SMA, which means that the measured fluxes are the flux densities integrated over the full source extension, and hence should be considered as upper limits in the SED model fits reported in this paper. However, it is worth noting that the radio flux of Mrk 421 resolved with the VLBA for a region of 1 − 2 × 1017 cm (hence comparable to the size of the blazar emission) is a very large part of the radio flux measured with the single-dish radio instruments (see Abdo et al. 2011), and thus it is reasonable to assume that the blazar emission contributes substantially to the radio flux measured by single-dish radio telescopes such as Metsähovi, OVRO, and UMRAO. Moreover, there are several works reporting a correlation between radio and GeV emission in blazars as a population (see e.g. Ackermann et al. 2011), which implies that at least a fraction of the radio emission is connected to the gamma-ray (blazar) emission. The 225 GHz observations from SMA connect the bottom (radio) to the peak (optical/X-rays) of the synchrotron (low-energy) bump of the SED, and hence it is also expected to be strongly dominated by the blazar emission of the source. Therefore, it seems reasonable to adjust the theoretical model in such a way that the predicted energy flux for the millimeter band is close to the SMA measurement, and the predicted energy flux for the radio band is not too far below the measurements performed by the single-dish instruments.
3. Multiband variability
In this section, we present the experimental results derived from the MW campaign observations described in Sect. 2. Figure 1 shows the multiband light curves during the decline observed between 2010 March 10 (MJD 55 265) and 2010 March 22 (MJD 55 277). In the top left panel, the VHE band includes nine observations from MAGIC, nine from VERITAS, and ten from Whipple.
 |
Fig. 1 Light curves of Mrk 421 between MJD 55 264 and 55 278, from VHE to radio (including optical polarization). The Whipple data were converted into fluxes above 200 GeV, and the host galaxy contribution was subtracted from the reported optical fluxes. Popt and EVPAopt stand for the polarization degree and the electric vector polarization angle. For details, see text in Sect. 3. |
The flux above 200 GeV decreases roughly steadily with time. Before MJD 55 272 the fluxes are ~1 − 2 c.u., while on subsequent days they are below 1 c.u., showing that only the decay (perhaps including the peak) of the flare was observed with the VHE γ-ray instruments in 2010 March. It is worth noting that the VHE flux measured with MAGIC for MJD 55 268 is roughly 50% lower than that measured with VERITAS for that day: 2.1 ± 0.3 vs. 4.0 ± 0.6 in units of 10-10 cm-2 s-1. Taking into account the measured errors, these fluxes are different by three to four standard deviations. This might result (at least partially) from systematics related to the instruments or observations during that night, but it might also be due to intra-night variability over the MAGIC and VERITAS observation windows, which are about seven hours apart.
The photon flux above 300 MeV (measured by Fermi-LAT in two-day long time intervals) does not show any significant variability. A fit with a constant line gives a flux level of (6.8 ± 0.9) × 10-8 cm-2 s-1, with χ2/ ndf = 2.5 / 6, which is similar to the mean flux of ~7.2 × 10-8 cm-2 s-1 observed during the first 1.5 yr of Fermi operation, from 2008 August to 2010 March (Abdo et al. 2011).
The variability at the X-ray band as measured with RXTE, Swift and MAXI is high, with light curves that resemble those at VHE. The Swift-XRT energy flux at the band 0.3−10 keV decreases from ~2.2 × 10-9 erg cm-2 s-1 down to ~0.8 × 10-9 erg cm-2 s-1. The low X-ray fluxes measured during this 13-day period are comparable to the mean 0.3−10 keV X-ray flux of ~0.9 × 10-9 erg cm-2 s-1, measured during the first seven years of Swift operation, from 2005 to 2012 (Stroh & Falcone 2013).
At UV and optical frequencies, the variability is also rather small, in contrast to the VHE and X-ray bands. The emission at the UV and optical bands is variable. For instance, a constant fit yields χ2/ ndf of 174/11 and 144/60 for the UVOT-UVM2 and GASP/R band, respectively. Hence Mrk 421 showed some activity at these bands, although it is substantially weaker than that shown at VHE and X-rays. The optical flux at the R band measured during this 13-day period is ~16 mJy (~24 mJy if the host galaxy is included), which is comparable to the typical flux of ~25 mJy measured during the first eight years of the Tuorla blazar monitoring program, from 2003 to 201113.
Optical polarization measurements are also reported in Fig. 1. The errors on these observations are smaller than 0.1% and 3° for the polarization degree and the electric vector polarization angle and are therefore too small to be visible in the plot. The collected data do not show any flare in the polarization degree or high rotation in the electric vector polarization angle as is observed during the flaring activities in other blazars (e.g. Marscher et al. 2008). There are some small variations in the polarization degree and angle, however, but such random fluctuations are common and expected due to continuous noise processes and not by singular events (see Marscher 2014).
In the radio bands, there were only seven observations during this period, which were performed at frequencies from 14 GHz to 225 GHz. All of them reported a flux of about 0.4−0.5 Jy. We did not find significant variability in any of these single-dish radio observations, which are ≲1 h long. The radio fluxes measured during this 13-day period are comparable to the typical 15 GHz radio flux of ~0.45 mJy measured during the first three years of the OVRO monitoring program, from 2008 to 2011 (Richards et al. 2013).
To quantify the overall variability during these 13 consecutive days, we followed the method provided in Vaughan et al. (2003). The fractional variability Fvar at each energy band is computed as 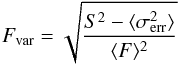 (1)where ⟨ F ⟩ is the mean photon flux, S is the standard deviation of the N flux points, and
(1)where ⟨ F ⟩ is the mean photon flux, S is the standard deviation of the N flux points, and 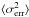 is the mean-squared error. The error in Fvar is calculated according to the prescription in Sect. 2.2 of Poutanen et al. (2008),
is the mean-squared error. The error in Fvar is calculated according to the prescription in Sect. 2.2 of Poutanen et al. (2008), 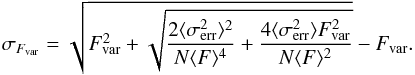 (2)This prescription is more precise than the method used in Vaughan et al. (2003) when the σerr is comparable to or larger than S.
(2)This prescription is more precise than the method used in Vaughan et al. (2003) when the σerr is comparable to or larger than S.
The Fvar values derived from the light curves in Fig. 1 are plotted in Fig. 2. The values of Fvar are plotted only for instruments with 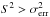 . When there is no variability detectable with the sensivity of the instrument,
. When there is no variability detectable with the sensivity of the instrument, 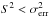 might occur (as is the case for Fermi-LAT).
might occur (as is the case for Fermi-LAT).
The Fvar is highest at the X-ray band. The values of Fvar measured by Swift-XRT and RXTE-PCA agree well at the 2−10 keV band. We note that Swift-XRT shows a higher Fvar at the 2−10 keV band than at the 0.3−2 keV band. The uncertainty in the Fvar values at these two bands is small because the measured X-ray flux variations are very large in comparison to the flux uncertainties (which are smaller than 1%), and that makes the difference in the measured variability very significant. This difference cannot be attributed to different temporal coverage, as they were observed with the same instrument (and hence the same time).
To study this difference, we calculated the normalized deviations of the fluxes, Fdev = (F − ⟨F⟩) / ⟨F⟩ computed with the Swift-XRT light curves at both energy bands (0.3−2 keV and 2−10 keV). Figure 3 shows that the absolute values of Fdev, |Fdev|, at the 2−10 keV band are always higher than those at the 0.3−2 keV band. This shows that the flux at the 2−10 keV band is intrinsically more variable than at the 0.3−2 keV band across the whole temporal range, and hence that the higher Fvar is not due to one or a few observations, but rather dominated by a higher overall relative dispersion at the 2−10 keV flux values during the 13 consecutive days.
 |
Fig. 2 Fractional variability Fvar as a function of frequency. |
 |
Fig. 3 Temporal evolution of the absolute value of the normalized deviation of the Swift-XRT flux, Fdev. See text for further details. |
 |
Fig. 4 Correlation between VHE γ-ray flux (MAGIC, black solid circles, and VERITAS, blue empty circles) and X-ray fluxes. Top: X-ray flux at the 0.3−2 keV band measured with Swift-XRT. Middle: X-ray flux at the 2−10 keV band measured with Swift-XRT. Bottom: X-ray flux at the 2−10 keV band measured with RXTE-PCA. The lines show the fits with linear and quadratic functions. Only MAGIC data points were used for the fits to ensure VHE-X-ray simultaneity (see Appendix A). |
The Fvar at VHE γ-rays is similar to that at X-rays. The flux points from VERITAS and Whipple are more concentrated around their mean values, which yield slightly lower Fvar than that of MAGIC. In conclusion, both VHE γ-rays and X-rays show higher variability than the flux at the other bands, which is additional evidence that they have a closer relation to each other, as reported in several other Mrk 421 flaring episodes (e.g. Maraschi et al. 1999).
To better understand the relation between X-rays and VHE γ-rays, we examined the correlation between the X-ray energy flux at the 0.3−2 keV and 2−10 keV bands and the VHE γ-ray energy flux above 200 GeV. For this exercise we used the X-ray fluxes from Swift and RXTE and the VHE fluxes from MAGIC and VERITAS. The VHE photon fluxes given in [cm-2 s-1] were converted into energy fluxes reported in [erg cm-2 s-1] using a power-law spectrum with index 2.5 above 200 GeV14. The top panel in Fig. 4 shows the VHE γ-ray flux vs. X-ray flux at the 0.3−2 keV band, and the resulting fits with a linear (FVHE = k·FX - ray) and a quadratic (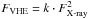 ) function. For the fits we used only MAGIC data, which are the VHE observations taken simultaneously or almost simultaneously with the X-ray observations (see Appendix A for details on simultaneity of the observations). The middle and bottom panels of Fig. 4 also show the X-ray flux vs. VHE-γ-ray flux, but using the X-ray flux at the 2−10 keV band measured with Swift and RXTE. Neither a linear nor a quadratic function describes the data perfectly. However, for the 2−10 keV energy range, the VHE to X-ray flux closely follows a linear trend, which it is clearly not the case for the 0.3−2 keV energy range. The physical interpretation of these results is discussed in Sect. 5.
) function. For the fits we used only MAGIC data, which are the VHE observations taken simultaneously or almost simultaneously with the X-ray observations (see Appendix A for details on simultaneity of the observations). The middle and bottom panels of Fig. 4 also show the X-ray flux vs. VHE-γ-ray flux, but using the X-ray flux at the 2−10 keV band measured with Swift and RXTE. Neither a linear nor a quadratic function describes the data perfectly. However, for the 2−10 keV energy range, the VHE to X-ray flux closely follows a linear trend, which it is clearly not the case for the 0.3−2 keV energy range. The physical interpretation of these results is discussed in Sect. 5.
4. Temporal evolution of the broadband spectral energy distribution
To study this flaring activity, we built 13 successive simultaneous broadband SEDs for 13 consecutive days. We study these SEDs within one-zone and two-zone SSC scenarios in Sects. 4.1 and 4.2. The characteristics of the MW data are described in Appendix B. Specifically, we investigate whether the temporal evolution of the EED in SSC models can explain the observed variations in the SED during the 13-day period, and hence we try to fix (to their quiescent values) the model parameters related to the environment, namely the blob radius (R), magnetic field (B), and Doppler factor (δ). We cannot exclude that other model realizations with a different set of model parameters (e.g., changing the environment parameters, or varying more model parameters) can also provide a satisfactory description of the broadband SEDs, but in this paper we wish to vary as few model parameters as possible to most directly study the evolution of the EED, which is the part of the model directly connected to the particle acceleration and cooling mechanisms.
We applied steady-state SSC models instead of time-dependent models to the SEDs of each day and estimated physical parameters in the emission regions, which gives us an estimate of the temporal evolution of these physical parameters. Time-dependent models, as developed by Krawczynski et al. (e.g. 2002), Chen et al. (e.g. 2011), are a direct way to derive the physical properties of the emission regions, but they include many detailed processes, such as synchrotron or inverse-Compton cooling of electrons, adiabatic cooling of electrons due to the expansion of an emission blob, and the injection of relativistic electrons and its time evolution, and therefore are very complex and have an arbitrarily large number of degrees of freedom. The snapshot approach with steady-state SSC models allows us to observe the time evolution of basic physical parameters averaged over a day in the blobs independently of the difficulty associated with time-dependent models. The time evolution of the averaged basic parameters observed in this study reflects physical mechanisms that are not considered explicitly, but gives us hints about them. A caveat of this approach is that the SEDs are observationally determined from short (about one hour) observations distributed over a relatively long (13 day) period of time, and hence we cannot exclude that some of the SEDs relate to short-lived active states that do not necessarily fit in the scheme of a slowly varying activity phase.
Given the known multiband variability in the emission of Mrk 421 (and blazars in general), we paid special attention to organize observations that were as close in time as possible (see Appendix A for the simultaneity of the observations). The observations performed with MAGIC, RXTE, and Swift were scheduled many weeks in advance, which resulted in actual observations occurring always within temporal windows of less than two hours. The observations with VERITAS/Whipple were triggered by the high activity detected in 2010 March, and performed typically about seven hours after MAGIC observations because VERITAS and Whipple are located at a different longitude from that of MAGIC. At radio frequencies we have only seven observations during this period, but we neither expected nor detected variability at radio during these short (a few days) timescales. Based upon these observations, we show in Appendix B.13 consecutive days of SEDs. Each SED is characterized with a one-zone and a two-zone SSC model as described in the following two subsections.
The peak luminosities and peak frequencies of the low- and high-energy bumps shift during high activity. In general, the peak frequency and peak luminosity decrease as the flare decays. In addition to the migration in the SED peak positions, the shapes of these SED bumps change. The X-ray and γ-ray bumps of the SEDs from MJD 55 265 and 55 266, when Mrk 421 emitted the highest flux, are narrow, and they widen as the flare decays. A quantitative evaluation of the widening of the two SED bumps is reported in Sect. 5.
4.1. SED modeling: one-zone SSC model
In this SSC model, we assume that emission comes from a single, spherical and homogeneous region in the jet, which is moving relativistically toward us. The one-zone SSC model describes most of the SEDs of high-frequency-peaked BL Lac objects with the fewest parameters, and hence it is the most widely adopted. The emission from radio to X-ray results from synchrotron radiation of electrons inside a blob of comoving radius R, with a Doppler factor δ. In this emission blob, there is a randomly oriented magnetic field with uniform strength B. The γ-ray emission is produced by inverse-Compton scattering of the synchrotron photons with the same population of electrons that produce them. We used the numerical code of the SSC model described in Takami (2011). The algorithm implemented in this code allows us to very quickly determine the parameters that accurately describe the SED.
Integral flux above 200 GeV and parameters of the one-zone SSC model.
The one-zone homogeneous SSC scenario with an EED described with a broken power-law function (seven free parameters plus the two parameters defining the edges of the EED) can be formally constrained from the seven characteristic observables that can be obtained from the multi-instrument data covering the two SED bumps, namely the spectral indices below and above the synchrotron peak, the peak frequencies and luminosities of the synchrotron and inverse-Compton bumps, and the variability timescale (Tavecchio et al. 1998). However, in reality, the collected data do not allow us to determine these seven parameters with very good precision (particularly for the variability timescale and the peak frequency of the inverse-Compton bump), which implies some degeneracy in the seven (+two) model parameters, which unavoidably necessitates making some approximations or assumptions.
In previous works related to Mrk 421, it was common to use only one or two power-law functions (that is, zero or one break) to describe the EED. However, such a simple model cannot adequately describe the broadband SED from the campaign organized in 2009, when Mrk 421 was in its typical nonflaring VHE state (Abdo et al. 2011). The SED from this paper was better sampled (more instruments with higher sensitivity) than those reported previously, and an additional break (two additional parameters) was required to properly describe the shape of the measured synchrotron bump (from 1 eV to 100 keV), together with the full inverse-Compton bump (from 100 MeV to 10 TeV). Given the similar energy coverage and activity of the source during many days of the 13-day period considered here, we also used three power-law functions (i.e., two breaks) to parameterize the EED: 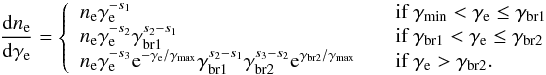 (3)where ne is the number density of electrons, γe is the Lorentz factor of the electrons, γmin and γmax define the range of γe, s1, s2 and s3 are the indices of the power-law functions, and γbr1 and γbr2 are the Lorentz factors where the power-law indices change. In total, this model has two more free parameters than the model with a broken power-law EED. The SEDs from the days with highest activity can be described with an EED with only one break, but for the nonflaring activity, we need to use an EED with two breaks. The requirement for a more complex parameterization of the EED in the recent works might be due to the better energy coverage (more instruments involved in the campaigns), and better sensitivity to cover the γ-ray bump. Future observations of Mrk 421 during nonflaring states with as good or better energy coverage will reveal whether the two-break EED is always needed, or whether this is something that was required only to describe the 2009 and 2010 data.
(3)where ne is the number density of electrons, γe is the Lorentz factor of the electrons, γmin and γmax define the range of γe, s1, s2 and s3 are the indices of the power-law functions, and γbr1 and γbr2 are the Lorentz factors where the power-law indices change. In total, this model has two more free parameters than the model with a broken power-law EED. The SEDs from the days with highest activity can be described with an EED with only one break, but for the nonflaring activity, we need to use an EED with two breaks. The requirement for a more complex parameterization of the EED in the recent works might be due to the better energy coverage (more instruments involved in the campaigns), and better sensitivity to cover the γ-ray bump. Future observations of Mrk 421 during nonflaring states with as good or better energy coverage will reveal whether the two-break EED is always needed, or whether this is something that was required only to describe the 2009 and 2010 data.
Despite the extensive MW data collected in this campaign, there is still some degeneracy in the choice of the eleven parameter values required to adjust the SED model to the observational data. Given the similarities between the SEDs of the last few days and the SED reported in Abdo et al. (2011), we used the SED model parameter values from Abdo et al. (2011) as a reference for the choice of SSC parameters to describe the 2010 March broadband observations. In particular, we wish to test whether the temporal evolution of the EED can explain the observed variations in the SED during the 13-day period, and hence we fixed γmin, γmax and the model parameters related to the environment R, B, and δ to the values reported in Abdo et al. (2011). The value of the Doppler factor, 21, is higher than the value inferred from VLBA measurements of the blob movement in Piner et al. (2010). This is a common circumstance for VHE sources, which has been dubbed the “bulk Lorentz factor crisis”, and requires the radio and TeV emission to be produced in regions with different Lorentz factors (Georganopoulos & Kazanas 2003; Ghisellini et al. 2005; Henri & Saugé 2006). During the adjustment of the model to the measured SED, the VHE and X-ray data provide the primary constraint because the variability is highest in these two energy bands.
The model parameters inferred from the observed SEDs (shown in Appendix B) are reported in Table 2. Only one break in the EED (instead of two) is sufficient to describe the narrow SED bumps on MJD 55 265 and 55 266, while two breaks are necessary to properly describe the wider X-ray and γ-ray bumps from MJD 55 267 to MJD 55 277, when Mrk 421 shows a somewhat lower X-ray and VHE activity. The changes in the SED during the flaring activity are dominated by the parameters, ne, γbr1, and γbr2: lower activity can be parameterized with a lower ne and a decrease in the values of the two break Lorentz factors in the EED. The spectral index s2 is equal to 2.5 for MJD 55 272, while s2 = 2.7 for the adjacent days. The X-ray bump for MJD 55 272 (see Fig. 3a) is rather narrow, and therefore s2, which affects the SED slope of the lower energy side of the bump, needs to be closer to s1 to properly describe the data.
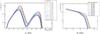 |
Fig. 5 One-zone SSC model curves and the related EEDs used to describe the measured SEDs during the 13-day flaring activity. The parameter values are given in Table 2. |
Given the values of the blob radius and Doppler factor used here, the shortest time of the flux variation tmin = (1 + z)R/βcδ is about one day. This value is reasonable, given the flux variations measured during the March flaring activity (see Fig. 1), but it would not be consistent with the potential intra-night variability that might have occurred in MJD 55 268, as hinted by the disagreement in the VHE fluxes measured by MAGIC and VERITAS. The predicted radiative cooling break by synchrotron radiation15, γc = 6πmec2/ (σTB2R), where me is the electron mass and σT is the Thomson cross-section, is 3.2 × 105 in this model. This formula is derived by equating the timescale of synchrotron radiation to the timescale of electrons staying in the blob ~R/c, on the assumption that the timescale of adiabatic cooling is much longer than that of synchrotron cooling. This assumption is reasonable because R is fixed in this study. The γbr2 values in the model range from 3.9 × 105 to 7.0 × 105, which is comparable to γc, hence suggesting that the second break in the EED might be related to the synchrotron cooling break. Thus, the decrease of γbr2 and the weak dependence on ne implies that the end of a flare is dominated by cooling. However, the change in the power-law index does not match the canonical change expected from synchrotron cooling, Δs = 1, which is similar to the situation reported in Abdo et al. (2011). The result that s3 is softer than expected can be explained by inhomogeneity of the emission blob, or by a weakening of the electron injection.
In general, the agreement between the one-zone SSC model and the observational data is quite acceptable, which shows one more the success of the one-zone SSC model in describing the SEDs of blazars. However, there are several problems. At the low-energy end of the VHE spectra, the model is slightly higher than the data for the SEDs from MJD 55 265, 55 266, 55 268, 55 269, and 55 273; and the model also goes slightly beyond the data in the X-ray bump for MJD 55 265 and 55 266. We cannot exclude that these data-model mismatches arise from the requirement that the EED is the only mechanism responsible for the blazar variability. For instance, if in addition to changing the model parameters related to the EED, the parameters B, R and δ were varied as well, the relative position of the synchrotron and SSC peak could be modified, possibly achieving better agreement with the data.
Overall, the temporal evolution of the broadband SEDs can be described by changes in the EED, keeping γmin, γmax, and the model parameters related to the environment (blob radius, magnetic field, and the Doppler factor) constant at the values reported in Abdo et al. (2011). Figures 5a and b depict the one-zone SSC model curves and the parameterized EEDs for the 13 consecutive days. We can divide the whole activity into three periods: MJD 55 265−55 266 (period 1), MJD 55 268−55 271 (period 2), and MJD 55272-55277 (period 3), which correspond to a VHE flux of ~2 c.u., ~1.5 c.u., and ~0.5 c.u., respectively. The EEDs of period 1 have one break, while those of period 2 and 3 have two breaks. Moreover, the EEDs of period 1 have a higher electron number density (ne) than those of periods 2 and 3. Figure 5b shows that the greatest variability occurs above the first break (γbr1) in the EED.
4.2. SED modeling: two-zone SSC model
The one-zone SSC model curves reported in the previous section describe the overall temporal evolution of the low- and high-energy bumps of the SED during this flaring activity reasonably well. However, we cannot ignore the model-data mismatches mentioned in the last section. This was our main motivation for trying a model with two distinct blobs: one producing the steady emission, the other producing the temporal evolution of the SED, which is evident primarily at the X-ray and VHE γ-ray bands. The two blobs are assumed to be separated by a long distance and the individual radiation fields do not interact with each other. We call these the quiescent blob and the flaring blob. The quiescent blob is described with the parameter values from the one-zone SSC model reported in Table 2 for MJD 55 274, which is the SED with the lowest activity among the 13 consecutive days. While the EED of the quiescent-state blob is described by three power-law functions, we employ only two power-law functions to describe the EED of the flaring blob: 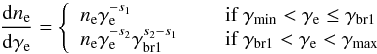 (4)where ne is the electron number density, γe is the Lorentz factor of the electrons, γmin and γmax define the range of γe, s1 and s2 are the indices of the power-law function, and γbr1 is the Lorentz factor where the power-law index changes.
(4)where ne is the electron number density, γe is the Lorentz factor of the electrons, γmin and γmax define the range of γe, s1 and s2 are the indices of the power-law function, and γbr1 is the Lorentz factor where the power-law index changes.
 |
Fig. 6 Largely simultaneous broadband SED of Mrk 421 on MJD 55 265. The correspondence between markers and instruments is given in the legend. The full names of the instruments can be found in Table 1. Because of space limitations, R-band instruments other than GASP, GRT, and NMS are denoted with the symbol “++”. Whenever a simultaneous observation is not available, the fluxes from the closest date are reported, and their observation time in MJD is reported next to the instrument name in the legend. The red curve depicts the two-zone SSC model matching the SED data, while the black line shows the contribution of the flaring blob. The gray circles depict the averaged SED from the 2009 MW campaign reported in Abdo et al. (2011), which is a good representation of the nonflaring (typical) SED of Mrk 421. |
In the overall process of adjusting the model to the 13 measured SEDs, we used a flaring blob size R about one order of magnitude smaller than the quiescent blob, which naturally allows faster variability. The size of the blob was kept constant, while the other parameters were allowed to change to describe the characteristics of the flare evolution.
Parameters for the flaring blob in the two-zone SSC model.
 |
Fig. 7 Two-zone SSC model curves (sum of the emission from the quiescent and the flaring blobs) and the related EEDs from the flaring blob used to describe the measured SEDs during the 13-day flaring activity. The parameter values are given in Table 3. |
Figure 6 depicts the two-zone model curve adjusted to the broadband SED from MJD 55 265. It is worth noting that the contribution from the flaring blob is relevant only at the X-ray and VHE bands. The model curves related to the remaining 12 consecutive SEDs are shown in Figs. B.4 and B.5, and Table 3 reports the two-zone SSC model parameters that adequately describe the measured SEDs. Except for the magnetic field, which decreases during the decay of the flare, the other model parameters related to the environment remain constant. The changes occur in the three model parameters ne, γmin, and γbr1, while s1, s2, γmax can be kept constant for all the 13 SEDs. With this two-zone SSC model, the shortest variability timescale tmin is about one hour, which is comparable to the length of our single-instrument observations, during which we did not measure significant variability. This shortest variability timescale would be consistent with the potential intra-night VHE variability on MJD 55 268. The predicted synchrotron cooling break γc for the flaring blob is 7 × 105 for MJD 55 265. For this day, the parameter γbr1 for the flaring blob is 3 × 105, with a change in the EED power-law index of 1, which is the canonical change for synchrotron cooling. During the following three days 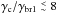 , and after MJD 55 269 γc/γbr1 is much larger, which means that the break in the EED of the flaring blob is intrinsic to the acceleration mechanism, and cannot be directly related to the synchrotron cooling during these days.
, and after MJD 55 269 γc/γbr1 is much larger, which means that the break in the EED of the flaring blob is intrinsic to the acceleration mechanism, and cannot be directly related to the synchrotron cooling during these days.
The flaring blob is characterized by an EED with a very high γmin (>3 × 104), which means that it lacks low-energy electrons, and so does not contribute to the radio/optical emission. This is necessary for improving (with respect to the one-zone SSC model from Sect. 4.1) the description of the very narrow peaks at the X-ray and the γ-ray bumps occurring on some days (e.g. MJD 55 265 and 55 266).
Figures 7a and b depict the two-zone SSC model curves and the parameterized EEDs for the 13 consecutive days. In this case, by construction, all the SED variations occur at the X-ray and the VHE bands, and the SED peaks are narrower than those from the one-zone SSC scenario. Overall, the decay of the flaring activity is dominated by a reduction in ne and γbr1. The magnetic field also varies with time (not shown in this plot, see Table 3); lower activity is related to lower values of B.
The two-zone SSC model is described by 20 parameters, the one-zone SSC model by 11. However, after fixing the parameters of the quiescent-state blob, we only needed to change the values of four parameters (γmin, γbr1, ne, and B) in the flaring blob, while in the one-zone SSC model we had to change five parameters (γbr1, γbr2, s1, s2, ne) to describe the SEDs during these 13 consecutive days (see Sect. 4.1). Therefore, once the parameters of the quiescent blob are fixed, the two-zone SSC model describes the measured temporal evolution of the broadband SED with one free parameter less than the one-zone SSC model.
5. Discussion
The broadband SEDs during this flaring episode, resolved on timescales of one day, allows for an unprecedented characterization of the time evolution of the radio to γ-ray emission of Mrk 421. We find that both the one-zone SSC and the two- zone SSC models can describe the daily SEDs by varying five and four model parameters, mostly related to the EED. This shows that the particle acceleration and cooling mechanism producing the EED could be the main mechanism responsible for the broadband SED variations during the flaring episodes in blazars.
In this theoretical framework, the two-zone SSC model provides better data-model agreement at the peaks of the low- and high-energy SED bumps. Additionally, the two-zone SSC scenario presented here naturally provides shorter timescales (one hour vs. one day) for variability at the X-ray and VHE bands, as the correlated variability at X-ray and VHE bands without any variation at the optical and radio bands. Because low-energy electrons are absent, the peak frequency of the γ-ray bump becomes sensitive to γmin as a result of the strong Klein-Nishina effect, which provides a rather independent channel to adjust the γ-ray bump for the flaring state. On the other hand, the X-ray bump is more sensitive to the magnetic field and γbr1. Hence this phenomenological scenario of two distinct zones (quiescent+flaring) allows for more flexibility in the locations and shapes of the two bumps than in the one-zone SSC model, while still varying fewer parameters. This was particularly useful to adequately describe the evolution of the width of the two SED bumps. We can quantify this effect by computing the widths of the bumps as the full width at half maximum (FWHM) in the logarithmic scale, log (ν2/ν1), where ν1 and ν2 are the frequencies at which the energy flux is half of that at the peak position. The widths of the SED bumps for the 13 consecutive days are reported in Table 4, showing that both the synchrotron and inverse-Compton peak widths increase from log (ν2/ν1) ~ 2 to log (ν2/ν1) ~ 3 during the decay of the flare, which means that the width of the two bumps (in logarithmic scale) is about 50% greater during the nonflaring (low) activity.
The additional flexibility of the two-zone SSC model helps to improve the agreement of the model SEDs with the data from MJD 55 265, 55 266, 55 268, 55 269, and 55 273. The largest data-model differences occur for the first two days, which are the days with the highest activity and the narrowest low- and high-energy bumps. Figures 8a and b compare the data-model agreement for these two days. Note the better agreement of the two-zone SSC model curves with the X-ray data points and, especially, the γ-ray data points. The agreement can be quantified using χ2 on the broadband SEDs, after excluding the radio data, which are considered as upper limits for the models. In total, we have 50 and 51 data points for MJD 55 265 and MJD 55 266, respectively. With a one-zone SSC model we obtain a χ2 of 4.0 × 103 for MJD 55 265 and 3.6 × 103 for MJD 55 266, while we obtain 1.2 × 103 for MJD 55 265 and 0.7 × 103 for MJD 55 266 with the two-zone SSC model, which shows that the agreement of the model with the data is better for the latter theoretical scenario. An F-test on the obtained χ2 values, and assuming conservatively that the one-zone model has 11 free parameters and the two-zone model has 20 free parameters (hence not considering that many of these parameters are kept constant) rejects the one-zone model in favor of the two-zone model for the given set of model parameters with a p-value lower than 10-5. If one considers that many model parameters are kept constant, the rejection of the reported one-zone model in favor of the reported two-zone model would be even clearer. The reduced χ2 for all cases is well above 1, which shows that none of the models describe the observations perfectly well. Both models oversimplify the complexity in the blazar jets, and hence we do not intend to explain the data at the percent level.
 |
Fig. 8 Broadband SEDs from MJD 55 265 and 55 266 (the two days with the highest activity) with the one-zone and two-zone model curves described in Sects. 4.2 and 4.3. We refer to Figs. B.1 and 2a for details of the data points. |
It is worth noting that the EED of the flaring blob is constrained to a very narrow range of energies, namely γmin − γmax ~ 3 × 104 − 6 × 105. One theoretical possibility to produce such a narrow EED is stochastic particle acceleration via scattering by magnetic inhomogeneities in the jet, namely second-order Fermi acceleration (e.g., Stawarz & Petrosian 2008; Lefa et al. 2011; Asano et al. 2014). The spectrum in this model is localized around a characteristic Lorentz factor γch determined by the power spectrum of magnetic turbulence q and the cooling timescale of electrons, with a shape proportional to ![\hbox{$\gamma_{\rm e}^2 \exp \left[- (\gamma_{\rm e} / \gamma_{\rm ch})^{3-q} \right]$}](/articles/aa/full_html/2015/06/aa24811-14/aa24811-14-eq191.png) (e.g., Schlickeiser 1985). Such a spectrum can realize the narrow peaks of synchrotron radiation and inverse-Compton scattering that we measured for Mrk 421 during the 2010 March flare.
(e.g., Schlickeiser 1985). Such a spectrum can realize the narrow peaks of synchrotron radiation and inverse-Compton scattering that we measured for Mrk 421 during the 2010 March flare.
The treatment made with the one- and two-zone homogeneous SSC models is a simplification of the problem. For instance, relativistic travel within a jet can change the properties of a blob (e.g. expansion of the size R of the emitting region, and decrease in the magnetic field B). This issue has been discussed in several papers (e.g. Tagliaferri et al. 2008, for the case of 1ES 1959+650). The fact that we can explain the temporal evolution of the SED during 13 consecutive days without changing the model parameters related to the environment could be interpreted as meaning that the blazar emission region is not traveling relativistically, but rather is stationary in one or several regions of the jet where there is a standing shock. Such standing shocks could be produced, for instance, by recollimation in the jet, and the particles would be accelerated as the jet flows or the superluminal knots cross it (Komissarov & Falle 1997; Sokolov et al. 2004; Marscher 2014). The Lorentz factor of the plasma, as it flows through the standing shock, would be the Lorentz factor that would lead to the Doppler factor (depending on the angle) used in the model.
This MW campaign reveals that the correlation between the X-ray flux at the 2 − 10 keV band and the VHE γ-ray flux above 200 GeV shows an approximately linear trend (see Fig. 4 middle and bottom panels), while the correlation between X-ray flux at the 0.3-2 keV band and the VHE γ-ray flux is equally close to both a linear and quadratic trend (see Fig. 4 top panel). This is an interesting result because the 0.3−2 keV band reports the synchrotron emission below or at the low-energy (synchrotron) peak of the SED, while the 2−10 keV band reports the emission at or above the low-energy peak. During the Mrk 421 flaring activity observed in 2001, it was also noted that the VHE-to-X-ray (above 2 keV) correlation was linear when considering day timescales, but the correlation was quadratic when considering few-hour long variability (see Fossati et al. 2008). A quadratic (or more-than-quadratic) correlation between X-ray and VHE γ-ray fluxes in the decaying phase is hard to explain with conventional SSC models (Katarzyński et al. 2005). During the flaring activity observed in 2010 March, we do not detect any significant intra-night variability, which might be due to the shorter (about one hour) duration of the observations (in comparison to the many-hour long observations reported in Fossati et al. 2008), or perhaps due to the lower X-ray and VHE activity (in contrast to that of 2001).
The almost linear correlation at 2 − 10 keV X-rays can be explained as follows: In the framework of the one-zone SSC model, the SED peaks at γ-ray frequencies are produced by the smaller cross-section in the Klein-Nishina regime, rather than by the breaks γbr,1 / 2 in the EED. Therefore, the γ-ray emission with energies above the SED peak energy is affected by the lower Klein-Nishina cross-section and is dominated by inverse-Compton scattering off infrared-to-optical photons. Since these target photons are produced by the synchrotron radiation of electrons with a Lorentz factor well below γbr1, whose density is almost constant during this decaying phase (see Fig. 5b), the density of target photons is almost constant. Thus, the change in the number density of electrons above γbr2 is directly reflected in the γ-ray flux, resulting in the almost linear correlation between X-ray and γ-ray fluxes. A similar mechanism also works in the two-zone SSC model in each blob. In a flaring blob, γ-ray SED peaks originate from the Klein-Nishina effect. Therefore, γ-rays with energies above the SED peak result from inverse-Compton scattering of electrons off photons below the SED peak at the X-ray band as well as in the one-zone SSC model. Thus, the almost linear relation is realized in both the quiescent and flaring blobs, and hence it is also realized in the total spectra.
The correlation between X-rays and γ-rays was analyzed with a great level of detail in Katarzyński et al. (2005), where the evolution of several quantities such as the number density of electrons, magnetic fields, and the size of the emission region, are simply parameterized to study their contribution to the index of the correlation. Evolution of the emission region volume is a possibility to naturally explain the reduction of the electron number density in the emission region. In the results presented here we fixed the size R to properly study the evolution of the electron spectrum with the steady SSC models at each moment. Further studies of the temporal broadband emission evolution involving such additional parameters will be performed elsewhere.
The SED model results described in Sects. 4.1 and 4.2 allow for an estimate of several physical properties of Mrk 421 during the flaring activity from 2010 March: the total electron number density Ne, mean electron Lorentz factor ⟨ γe ⟩, the jet power carried by electrons Le, the jet power carried by the magnetic field LB, the ratio of comoving electron and magnetic field energy densities  , the synchrotron luminosity Lsyn (integrated from 109.5 Hz to 1020.5 Hz), the inverse-Compton luminosity LIC (integrated from 1020.5 Hz to 1028 Hz), and the total photon luminosity from the SSC model Lph = Lsyn + LIC. We can also compute the jet power carried by protons Lp assuming one proton per electron (Np = Ne). The total jet power is Ljet = Lp + Le + LB. We follow the prescriptions given in Celotti & Ghisellini (2008). Specifically, the following formulae are used:
, the synchrotron luminosity Lsyn (integrated from 109.5 Hz to 1020.5 Hz), the inverse-Compton luminosity LIC (integrated from 1020.5 Hz to 1028 Hz), and the total photon luminosity from the SSC model Lph = Lsyn + LIC. We can also compute the jet power carried by protons Lp assuming one proton per electron (Np = Ne). The total jet power is Ljet = Lp + Le + LB. We follow the prescriptions given in Celotti & Ghisellini (2008). Specifically, the following formulae are used:
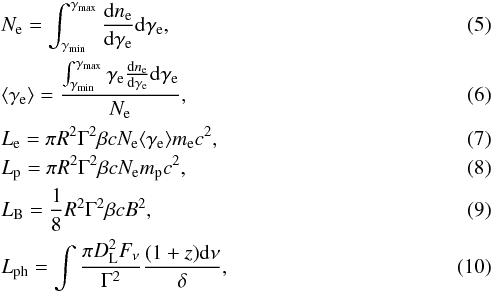 where Γ ~ δ,
where Γ ~ δ, 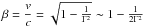 , DL = 134 Mpc. In the jet power calculation, only one side is considered, differently to what was done in Finke et al. (2008), who used a two-sided jet. The details of these quantities derived with the SSC model parameters are tabulated in Appendix C.
, DL = 134 Mpc. In the jet power calculation, only one side is considered, differently to what was done in Finke et al. (2008), who used a two-sided jet. The details of these quantities derived with the SSC model parameters are tabulated in Appendix C.
In both the one-zone and two-zone model, the electron luminosity Le and magnetic luminosity LB are more than one order of magnitude away from equipartition, which was reported in Abdo et al. (2011), Mankuzhiyil et al. (2011), Aleksić et al. (2012a). In addition, we found that the ratio Le/LB does not vary much during the 13-day period considered here.
In the two-zone model, the total power Lp + Le + LB of the flaring blob is about one order of magnitude smaller than that of the quiescent-state blob (~1043 erg s-1 vs. ~1044 erg s-1) even though ⟨ γe ⟩ is 20−30 times higher. This is caused by the smaller size of the flaring blob, in spite of its stronger magnetic field and higher electron density. Nevertheless, the flaring blob is responsible for about half of the photon luminosity Lph( =Lsyn + LIC) of the quiescent-state blob during the highest X-ray/VHE γ-ray activity. This indicates that the radiative efficiency of electrons is high in the flaring blob as a result of the strong magnetic field B and high electron number density ne. Since the contribution of the flaring blob to the total photon luminosity decreases with the decline of the X-ray/VHE activity, the total photon luminosity in the two-zone model does not change substantially during the 13-day period with the VHE flux going from ~2 c.u. down to ~0.5 c.u., remaining at about (3 − 5) × 1042 erg s-1. On the other hand, the variation of the total photon luminosity in the one-zone model is from 9 × 1042 erg s-1 to 3 × 1042 erg s-1, and hence, in terms of jet energetics, the production of the measured X-ray/VHE flaring activity is more demanding in the one-zone scenario than in the two-zone scenario.
6. Conclusion
We have reported the MW observations of the decaying phase of a Mrk 421 flare from 2010 March, and characterized it with two leptonic scenarios: a one-zone SSC model, and a two-zone SSC model where one zone is responsible for the quiescent emission, while the other (smaller) zone, which is spatially separated from the former one, contributes to the daily-variable emission occurring mostly at X-rays and VHE γ-rays. We found that flux variability is noticeable at the X-ray and VHE γ-ray bands, while it is minor or not significant in the other bands. These observations revealed an almost linear correlation between the X-ray flux at the 2−10 keV band and the VHE γ-ray flux above 200 GeV, consistent with the γ-rays being produced by inverse-Compton scattering in the Klein-Nishina regime in the framework of SSC models.
The broadband SEDs during this flaring episode, resolved on timescales of one day, allowed for an unprecedented characterization of the time evolution of the radio to γ-ray emission of Mrk 421. Such a detailed study has not been performed on Mrk 421 or any other blazar before. Both the one-zone SSC and the two-zone SSC models can describe the daily SEDs via the variation of only five and four model parameters respectively, under the hypothesis that the variability is associated mostly with the underlying particle population. This shows that blazar variability might be dominated by the acceleration and cooling mechanisms that produce the EED. For both cases (one-zone and two-zone SSC models), an EED parameterized by two power-law functions is sufficient to describe the emission during the very high states (MJD 55 265 and 55 266), but an EED with three power-law functions is needed during the somewhat lower blazar activity.
We also found that the two-zone SSC model describes the measured SED data at the peaks of the low- and high-energy bumps better, although the reported one-zone SSC model could be further improved by the variation of the parameters related to the emitting region itself, in addition to the parameters related to the particle population. The two-zone SSC scenario presented here naturally provides shorter timescales (one hour vs. one day) for variability at the X-ray and VHE bands, as well as lack of correlation between the radio/optical/GeV emission and the variability in the X-ray/VHE bands. Within this two-zone SSC scenario, the EED of the flaring blob is constrained to a very narrow range of energies, namely γmin − γmax ~ 3 × 104 − 6 × 105, which could be produced through stochastic particle acceleration via scattering by magnetic inhomogeneities in the jet.
Online material
Appendix A: Simultaneity in the multi-instrument observations
The energy coverage as a function of the time for the daily multi-instrument observations from 2010 March 10 (MJD 55 265) to
 |
Fig. A.1 Temporal and energy coverage during the flaring activity from 2010 March 10 (MJD 55 265) to 2010 March 16 (MJD 55 271). Fermi-LAT data were accumulated during two-day time intervals to ensure significant detections of Mrk 421, and is depicted here with a blue band. For better visibility of the observations at UV, optical, and radio band, where the observation time is usually short and the covered frequency band is narrow, an additional 20 min in time and half a decade in frequency are included when displaying the results. The names of all the optical instruments are listed in Table 1. |
2010 March 22 (MJD 55 277) is depicted in Figs. A.1 and A.2, which show that most of the observations used to determine the SEDs reported in Appendix B occur within less than 2 h.
 |
Fig. A.2 Temporal and energy coverage during the flaring activity from 2010 March 17 (MJD 55 272) to 2010 March 22 (MJD 55 277). See the caption of Fig. A.1 for further details. |
Appendix B: Broadband SEDs for the 13 consecutive days
The measured SEDs for these 13 consecutive days are shown in Figs. B.1 to B.5 with one-zone SSC model curves (from Figs. B.1 to Fig. B.3) and two-zone SSC model curves (Figs. B.4 and B.5). The SED with a two-zone SSC model curve measured on the first day (MJD 55 265) was shown in Fig. 6 in the main text. For comparison, the average SED from the 2009 MW campaign (Abdo et al. 2011) is shown in all the figures, which is a good representation of the SED of Mrk 421 during its nonflaring (typical) state. The details of the models and the characterization of the SED evolution were discussed in Sects. 4.1 and 4.2 in the main text.
The actual MJD date for each data entry is given in the legend of each figure. For optical bands, the reported SED data points correspond to the averaged values (host-galaxy
subtracted) for the specified observing night. As reported in Sect. 3, the variability at the optical band is small and occurs on timescales of several days. Therefore, if there was no instrument observing at a particular optical energy band, then the nearest observation was used, and the corresponding MJD date is described in the legend of the figure.
Although Mrk 421 is cosmologically nearby, at a redshift of 0.03, the absorption of γ-rays by the extragalactic background light (EBL) is not negligible at TeV energies. The VHE spectra are corrected (de-absorbed) with the EBL model provided by Franceschini et al. (2008), where e− τγγ = 0.58 at 4 TeV. At this energy, which is roughly the highest energy bin in the VHE spectra, most models provide 0.5 < e− τγγ< 0.6, such as models from Kneiske et al. (2004), Finke et al. (2010), and Domínguez et al. (2011), which means that the results are not sensitive to the particular published EBL model that we selected.
 |
Fig. B.1 Largely simultaneous broadband SED of Mrk 421 on MJD 55 265. The correspondence between markers and instruments is given in the legend. The full names of the instruments can be found in Table 1. Because of space limitations, R-band instruments other than GASP, GRT, and NMS are denoted with the symbol “++”. Whenever a simultaneous observation is not available, the fluxes from the closest date are reported, and their observation time in MJD is reported next to the instrument name in the legend. The red curve depicts the one-zone SSC model matching the data. The gray circles depict the average SED from the 2009 MW campaign reported in Abdo et al. (2011), which is a good representation of the nonflaring (typical) SED of Mrk 421. |
 |
Fig. B.2 Simultaneous broadband SEDs and their one-zone SSC model fits. See caption of Fig. B.1 for further details. |
 |
Fig. B.3 Simultaneous broadband SEDs and their one-zone SSC model fits. See caption of Fig. B.1 for further details. |
 |
Fig. B.4 Simultaneous broadband SEDs and their two-zone SSC model fits. See caption of Fig. 6 for further details. |
 |
Fig. B.5 Simultaneous broadband SEDs and their two-zone SSC model fits. See caption of Fig. 6 for further details. The emission of the quiescent blob was set to the one describing the SED from MJD 55 274, which is the lowest SED among all the 13 dates considered in this paper. Consequently, there is no flaring blob emission for MJD 55 274. |
Appendix C: Physical parameters derived from one-zone and two-zone SSC scenarios
Physical parameters inferred from spectral modeling are tabulated in Table C.1 for the one-zone SSC model and in Table C.2 for the two-zone SSC model. The definition of these quantities are provided by Eqs. (5) to (10).
See the TeV catalog at http://tevcat.uchicago.edu/
The VHE flux of the Crab nebula between 200 GeV and 10 TeV used in this paper is 2.2 × 10-10 cm-2 s-1 (Aleksić et al. 2012b).
The maximum-likelihood test statistic TS (Mattox et al. 1996) is defined as TS = 2Δlog (likelihood) between models with and without a point source at the position of Mrk 421.
The CALDB files are located at http://heasarc.gsfc.nasa.gov/FTP/caldb
Acknowledgments
The authors thank the anonymous referee for providing a very detailed and constructive list of remarks that helped us to improve the manuscript. The MAGIC collaboration would like to thank the Instituto de Astrofísica de Canarias for the excellent working conditions at the Observatorio del Roque de los Muchachos in La Palma. The financial support of the German BMBF and MPG, the Italian INFN and INAF, the Swiss National Fund SNF, the ERDF under the Spanish MINECO, and the Japanese JSPS and MEXT is gratefully acknowledged. This work was also supported by the Centro de Excelencia Severo Ochoa SEV-2012-0234, CPAN CSD2007-00042, and MultiDark CSD2009-00064 projects of the Spanish Consolider-Ingenio 2010 programme, by grant 268740 of the Academy of Finland, by the Croatian Science Foundation (HrZZ) Project 09/176 and the University of Rijeka Project 13.12.1.3.02, by the DFG Collaborative Research Centers SFB823/C4 and SFB876/C3, and by the Polish MNiSzW grant 745/N-HESS-MAGIC/2010/0. The VERITAS collaboration acknowledges supports from the grants from the US Department of Energy Office of Science, the US National Science Foundation and the Smithsonian Institution, by NSERC in Canada, by Science Foundation Ireland (SFI 10/RFP/AST2748) and by STFC in the UK. We acknowledge the excellent work of the technical support staff at the Fred Lawrence Whipple Observatory and at the collaborating institutions in the construction and operation of the instrument. The Fermi-LAT collaboration acknowledges generous ongoing support from a number of agencies and institutes that have supported both the development and the operation of the LAT as well as scientific data analysis. These include the National Aeronautics and Space Administration and the Department of Energy in the United States, the Commissariat à l’Énergie Atomique and the Centre National de la Recherche Scientifique/Institut National de Physique Nucléaire et de Physique des Particules in France, the Agenzia Spaziale Italiana and the Istituto Nazionale di Fisica Nucleare in Italy, the Ministry of Education, Culture, Sports, Science and Technology (MEXT), High Energy Accelerator Research Organization (KEK) and Japan Aerospace Exploration Agency (JAXA) in Japan, and the K. A. Wallenberg Foundation, the Swedish Research Council and the Swedish National Space Board in Sweden. Additional support for science analysis during the operations phase is gratefully acknowledged from the Istituto Nazionale di Astrofisica in Italy and the Centre National d’Études Spatiales in France. The research at Boston University was funded in part by NASA Fermi Guest Investigator grant NNX11AQ03G. The Submillimeter Array is a joint project between the Smithsonian Astrophysical Observatory and the Academia Sinica Institute of Astronomy and Astrophysics and is funded by the Smithsonian Institution and the Academia Sinica. The OVRO 40-m monitoring program is supported in part by NASA grants NNX08AW31G and NNX11A043G, and NSF grants AST-0808050 and AST-1109911. The Metsähovi team acknowledges the support from the Academy of Finland to our observing projects (numbers 212656, 210338, 121148, and others). This work was partly supported by Russian RFBR grant 12-02-00452 and St.Petersburg University research grants 6.0.163.2010, 6.38.71.2012. The Abastumani Observatory team acknowledges financial support by the Georgian National Science Foundation through grant GNSF/ST07/4-180 and by the Shota Rustaveli National Science Foundation through the grant FR/577/6-320/13. We acknowledge the use of public data from the Swift and RXTE data archive.
References
- Abdo, A. A., Ackermann, M., Agudo, I., et al. 2010, ApJ, 716, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2011, ApJ, 736, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Abeysekara, A. U., Allen, B. T., et al. 2014, ApJ, 782, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Acciari, V., 2011, Ph.D. Thesis, Galway-Mayo Institute of Technology http://veritas.sao.arizona.edu/documents/Theses/Acciari_Thesis.pdf [Google Scholar]
- Acciari, V. A., Aliu, E., Aune, T., et al. 2009, ApJ, 703, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Acciari, V. A., Aliu, E., Arlen, T., et al. 2011, ApJ, 738, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Acciari, V. A., Arlen, T., Aune, T., et al. 2014, Astropart. Phys., 54, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Allafort, A., et al. 2011, ApJ, 741, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Albert, A., et al. 2012, ApJS, 203, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F. A., Hofmann, W., Konopelko, A. K., & Völk, H. J. 1997, Astropart. Phys., 6, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F., Akhperjanian, A., Beilicke, M., et al. 2002, A&A, 393, 89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A., Beilicke, M., et al. 2003, A&A, 410, 813 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Aye, K.-M., et al. 2005, A&A, 437, 95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2007a, ApJ, 663, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2007b, Nucl. Instrum. Methods Phys. Res. A, 583, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Aller, H. D., Aller, M. F., Latimer, G. E., & Hodge, P. E. 1985, ApJS, 59, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Aleksić, J., Alvarez, E. A., Antonelli, L. A., et al. 2012a, A&A, 542, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aleksić, J., Alvarez, E. A., Antonelli, L. A., et al. 2012b, Astropart. Phys., 35, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Aleksić, J., Ansoldi, S., Antonelli, L. A., et al. 2015, A&A, 576, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asano, K., Takahara, F., Kusunose, M., Toma, K., & Kakuwa, J. 2014, ApJ, 780, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Błażejowski, M., Blaylock, G., Bond, I. H., et al. 2005, ApJ, 630, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Bloom, S. D., & Marscher, A. P. 1996, ApJ, 461, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Boone, L. M., Hinton, J. A., Bramel, D., et al. 2002, ApJ, 579, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Bradt, H. V., Rothschild, R. E., & Swank, J. H. 1993, A&AS, 97, 355 [NASA ADS] [Google Scholar]
- Breiman, L. 2011, Machine Learning, 45, 5 [Google Scholar]
- Brinkmann, W., Papadakis, I. E., Raeth, C., Mimica, P., & Haberl, F. 2005, A&A, 443, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, Space Sci. Rev., 120, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Celotti, A., & Ghisellini, G. 2008, MNRAS, 385, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, X., Fossati, G., Liang, E. P., & Böttcher, M. 2011, MNRAS, 416, 2368 [NASA ADS] [CrossRef] [Google Scholar]
- Cogan, P. 2006, Ph.D. Thesis, School of Physics, University College Dublin [Google Scholar]
- Daniel, M. K., et al. 2007, Proc. 30th International Cosmic Ray Conf., eds. R. Caballero, et al. (Mexico City, Mexico: Universidad Nacional Autónoma de México), 3, 1325 [Google Scholar]
- Dermer, C. D., & Schlickeiser, R. 1993, ApJ, 416, 458 [NASA ADS] [CrossRef] [Google Scholar]
- de Vaucouleurs, G., de Vaucouleurs, A., Corwin, H. G., Jr., et al. 1991, Third Reference Catalogue of Bright Galaxies, Vol. 1−3 (Berlin, Heidelberg, New York: Springer-Verlag) [Google Scholar]
- Domínguez, A., Primack, J. R., Rosario, D. J., et al. 2011, MNRAS, 410, 2556 [NASA ADS] [CrossRef] [Google Scholar]
- Edelson, R., Turner, T. J., Pounds, K., et al. 2002, ApJ, 568, 610 [NASA ADS] [CrossRef] [Google Scholar]
- Finke, J. D., Dermer, C. D., & Böttcher, M. 2008, ApJ, 686, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Finke, J. D., Razzaque, S., & Dermer, C. D. 2010, ApJ, 712, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Fomin, V. P., Fennell, S., Lamb, R. C., et al. 1994, Astropart. Phys., 2, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, G., Buckley, J. H., Bond, I. H., et al. 2008, ApJ, 677, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Franceschini, A., Rodighiero, G., & Vaccari, M. 2008, A&A, 487, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fukugita, M., Shimasaku, K., & Ichikawa, T. 1995, PASP, 107, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Gaidos, J. A., Akerlof, C. W., Biller, S., et al. 1996, Nature, 383, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Georganopoulos, M., & Kazanas, D. 2003, ApJ, 594, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Tavecchio, F., & Chiaberge, M. 2005, A&A, 432, 401 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henri, G., & Saugé, L. 2006, ApJ, 640, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Hillas, A. M. 1985, Proc. 19th International Cosmic Ray Conf., San Diego, USA, 3, 445 [Google Scholar]
- Horan, D., Acciari, V. A., Bradbury, S. M., et al. 2009, ApJ, 695, 596 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Katarzyński, K., Sol, H., & Kus, A. 2003, A&A, 410, 101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Katarzyński, K., Ghisellini, G., Tavecchio, et al. 2005, A&A, 433, 479 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kildea, J., Atkins, R. W., Badran, H. M., et al. 2007, Astropart. Phys., 28, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Kneiske, T. M., Bretz, T., Mannheim, K., & Hartmann, D. H. 2004, A&A, 413, 807 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Komissarov, S. S., & Falle, S. A. E. G. 1997, MNRAS, 288, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Krawczynski, H., Coppi, P. S., & Aharonian, F. 2002, MNRAS, 336, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Krawczynski, H., Carter-Lewis, D. A., Duke, C., et al. 2006, Astropart. Phys., 25, 380 [NASA ADS] [CrossRef] [Google Scholar]
- Krennrich, F., Bond, I. H., Bradbury, S. M., et al. 2002, ApJ, 575, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Lefa, E., Rieger, F. M., & Aharonian, F. 2011, ApJ, 740, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y. C., Bertsch, D. L., Chiang, J., et al. 1992, ApJ, 401, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Mannheim, K. 1993, A&A, 269, 67 [NASA ADS] [Google Scholar]
- Maraschi, L., Ghisellini, G., & Celotti, A. 1992, ApJ, 397, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Maraschi, L., Fossati, G., Tavecchio, F., et al. 1999, ApJ, 526, L81 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Marscher, A. P. 2014, ApJ, 780, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P., Jorstad, S. G., D’Arcangelo, F. D., et al. 2008, Nature, 452, 966 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mankuzhiyil, N., Ansoldi, S., Persic, M., & Tavecchio, F. 2011, ApJ, 733, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Mattox, J. R., Bertsch, D. L., Chiang, J., et al. 1996, ApJ, 461, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Moralejo, R. A., Gaug, M., Carmona, E., et al. 2010, Astrophys. Source Code Lib., 11004 [Google Scholar]
- Mücke, A., Protheroe, R. J., Engel, R., Rachen, J. P., & Stanev, T. 2003, Astropart. Phys., 18, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Nandra, K., George, I. M., Mushotzky, R. F., Turner, T. J., & Yaqoob, T. 1997, ApJ, 476, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Nilsson, K., Pasanen, M., Takalo, L. O., et al. 2007, A&A, 475, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nolan, P. L., Abdo, A. A., Ackermann, M., et al. 2012, ApJS, 199, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Okumura, K., Asahara, A., Bicknell, G. V., et al. 2002, ApJ, 579, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Perkins, J. & Mayer, G. 2009, eConf Proc. C091122 [arXiv:astro-ph:0912.3841] [Google Scholar]
- Piner, B. G., Pant, N., & Edwards, P. G. 2010, ApJ, 723, 1150 [NASA ADS] [CrossRef] [Google Scholar]
- Poole, T. S., Breeveld, A. A., Page, M. J., et al. 2008, MNRAS, 383, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Poutanen, J., Zdziarski, A. A., & Ibragimov, A. 2008, MNRAS, 389, 1427 [NASA ADS] [CrossRef] [Google Scholar]
- Punch, M., Akerlof, C. W., Cawley, M. F., et al. 1992, Nature, 358, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Rebillot, P. F., Badran, H. M., Blaylock, G., et al. 2006, ApJ, 641, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, J. L., Max-Moerbeck, W., Pavlidou, V., et al. 2011, ApJS, 194, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, J. L., Hovatta, T., Lister, M. L., et al. 2013, Eur. Phys. J. Web Conf., 61, 04010 [CrossRef] [EDP Sciences] [Google Scholar]
- Roming, P. W. A., Kennedy, T. E., Mason, K. O., et al. 2005, Space Sci. Rev., 120, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schlickeiser, R. 1985, A&A, 143, 431 [NASA ADS] [Google Scholar]
- Sokolov, A., Marscher, A. P., & McHardy, I. M. 2004, ApJ, 613, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Stawarz, L., & Petrosian, V. 2008, ApJ, 681, 1725 [NASA ADS] [CrossRef] [Google Scholar]
- Stroh, M. C., & Falcone, A. D. 2013, ApJS, 207, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Tagliaferri, G., Foschini, L., Ghisellini, G., et al. 2008, ApJ, 679, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- Takami 2011, MNRAS, 413, 1845 [NASA ADS] [CrossRef] [Google Scholar]
- Tavecchio, F., Maraschi, L., & Ghisellini, G. 1998, ApJ, 509, 608 [NASA ADS] [CrossRef] [Google Scholar]
- Teraesranta, H., Tornikoski, M., Mujunen, A., et al. 1998, A&AS, 132, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tramacere, A., Massaro, F., & Cavaliere, A. 2007, A&A, 466, 521 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tramacere, A., Giommi, P., Perri, M., Verrecchia, F., & Tosti, G. 2009, A&A, 501, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vaughan, S., Edelson, R., Warwick, R. S., & Uttley, P. 2003, MNRAS, 345, 1271 [NASA ADS] [CrossRef] [Google Scholar]
- Villata, M., Raiteri, C. M., Lanteri, L., Sobrito, G., & Cavallone, M. 1998, A&AS, 130, 305 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Villata, M., Raiteri, C. M., Larionov, V. M., et al. 2008, A&A, 481, L79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Villata, M., Raiteri, C. M., Gurwell, M. A., et al. 2009, A&A, 504, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weekes, T. C., Badran, H., Biller, S. D., et al. 2002, Astropart. Phys., 17, 221 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Light curves of Mrk 421 between MJD 55 264 and 55 278, from VHE to radio (including optical polarization). The Whipple data were converted into fluxes above 200 GeV, and the host galaxy contribution was subtracted from the reported optical fluxes. Popt and EVPAopt stand for the polarization degree and the electric vector polarization angle. For details, see text in Sect. 3. |
| In the text | |
 |
Fig. 2 Fractional variability Fvar as a function of frequency. |
| In the text | |
 |
Fig. 3 Temporal evolution of the absolute value of the normalized deviation of the Swift-XRT flux, Fdev. See text for further details. |
| In the text | |
 |
Fig. 4 Correlation between VHE γ-ray flux (MAGIC, black solid circles, and VERITAS, blue empty circles) and X-ray fluxes. Top: X-ray flux at the 0.3−2 keV band measured with Swift-XRT. Middle: X-ray flux at the 2−10 keV band measured with Swift-XRT. Bottom: X-ray flux at the 2−10 keV band measured with RXTE-PCA. The lines show the fits with linear and quadratic functions. Only MAGIC data points were used for the fits to ensure VHE-X-ray simultaneity (see Appendix A). |
| In the text | |
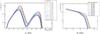 |
Fig. 5 One-zone SSC model curves and the related EEDs used to describe the measured SEDs during the 13-day flaring activity. The parameter values are given in Table 2. |
| In the text | |
 |
Fig. 6 Largely simultaneous broadband SED of Mrk 421 on MJD 55 265. The correspondence between markers and instruments is given in the legend. The full names of the instruments can be found in Table 1. Because of space limitations, R-band instruments other than GASP, GRT, and NMS are denoted with the symbol “++”. Whenever a simultaneous observation is not available, the fluxes from the closest date are reported, and their observation time in MJD is reported next to the instrument name in the legend. The red curve depicts the two-zone SSC model matching the SED data, while the black line shows the contribution of the flaring blob. The gray circles depict the averaged SED from the 2009 MW campaign reported in Abdo et al. (2011), which is a good representation of the nonflaring (typical) SED of Mrk 421. |
| In the text | |
 |
Fig. 7 Two-zone SSC model curves (sum of the emission from the quiescent and the flaring blobs) and the related EEDs from the flaring blob used to describe the measured SEDs during the 13-day flaring activity. The parameter values are given in Table 3. |
| In the text | |
 |
Fig. 8 Broadband SEDs from MJD 55 265 and 55 266 (the two days with the highest activity) with the one-zone and two-zone model curves described in Sects. 4.2 and 4.3. We refer to Figs. B.1 and 2a for details of the data points. |
| In the text | |
 |
Fig. A.1 Temporal and energy coverage during the flaring activity from 2010 March 10 (MJD 55 265) to 2010 March 16 (MJD 55 271). Fermi-LAT data were accumulated during two-day time intervals to ensure significant detections of Mrk 421, and is depicted here with a blue band. For better visibility of the observations at UV, optical, and radio band, where the observation time is usually short and the covered frequency band is narrow, an additional 20 min in time and half a decade in frequency are included when displaying the results. The names of all the optical instruments are listed in Table 1. |
| In the text | |
 |
Fig. A.2 Temporal and energy coverage during the flaring activity from 2010 March 17 (MJD 55 272) to 2010 March 22 (MJD 55 277). See the caption of Fig. A.1 for further details. |
| In the text | |
 |
Fig. B.1 Largely simultaneous broadband SED of Mrk 421 on MJD 55 265. The correspondence between markers and instruments is given in the legend. The full names of the instruments can be found in Table 1. Because of space limitations, R-band instruments other than GASP, GRT, and NMS are denoted with the symbol “++”. Whenever a simultaneous observation is not available, the fluxes from the closest date are reported, and their observation time in MJD is reported next to the instrument name in the legend. The red curve depicts the one-zone SSC model matching the data. The gray circles depict the average SED from the 2009 MW campaign reported in Abdo et al. (2011), which is a good representation of the nonflaring (typical) SED of Mrk 421. |
| In the text | |
 |
Fig. B.2 Simultaneous broadband SEDs and their one-zone SSC model fits. See caption of Fig. B.1 for further details. |
| In the text | |
 |
Fig. B.3 Simultaneous broadband SEDs and their one-zone SSC model fits. See caption of Fig. B.1 for further details. |
| In the text | |
 |
Fig. B.4 Simultaneous broadband SEDs and their two-zone SSC model fits. See caption of Fig. 6 for further details. |
| In the text | |
 |
Fig. B.5 Simultaneous broadband SEDs and their two-zone SSC model fits. See caption of Fig. 6 for further details. The emission of the quiescent blob was set to the one describing the SED from MJD 55 274, which is the lowest SED among all the 13 dates considered in this paper. Consequently, there is no flaring blob emission for MJD 55 274. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


