| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A85 | |
| Number of page(s) | 12 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201424401 | |
| Published online | 11 June 2015 | |
Relative drifts and temperature anisotropies of protons and α particles in the expanding solar wind: 2.5D hybrid simulations
1
Centre for mathematical Plasma Astrophysics, KU Leuven, Celestijnenlaan
200B,
3001
Leuven,
Belgium
e-mail:
yana.maneva@wis.kuleuven.be
2
Department of Physics, Catholic University of
America, 620 Michigan Ave
NE, Washington
DC
20064,
USA
3
NASA Goddard Space Flight Center, 8800 Greenbelt Rd,
Greenbelt,
Maryland
20771,
USA
Received: 13 June 2014
Accepted: 26 April 2015
Context. We perform 2.5D hybrid simulations to investigate the origin and evolution of relative drift speeds between protons and α particles in the collisionless turbulent low-
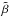 solar wind plasma.
solar wind plasma.
Aims. We study the generation of differential streaming by wave-particle interactions and absorption of turbulent wave spectra. Next we focus on the role of the relative drifts for the turbulent heating and acceleration of ions in the collisionless fast solar wind streams.
Methods. The energy source is given by an initial broad-band spectrum of parallel propagating Alfvén-cyclotron waves, which co-exists with the plasma and is self-consistently coupled to the perpendicular ion bulk velocities. We include the effect of a gradual solar wind expansion, which cools and decelerates the minor ions. We here consider for the first time the combined effect of self-consistently initialized dispersive turbulent Alfvénic spectra with differentially streaming protons and α particles in the expanding solar wind outflows within a 2.5D hybrid simulation study.
Results. For differential streaming of Vαp < 0.5VA, the selected initial wave spectrum accelerates the minor ions in the non-expanding wind. At Vαp = 0.5VA the relative drift speed remains nearly steady. For ions that stream below this threshold value, the waves act to increase the magnitude of the relative drift speed. Ions that stream faster than the threshold value become subject to a nonlinear streaming instability, and as the system evolves, their bulk velocities decrease. We find that the solar wind expansion strongly affects the relative drift speed and significantly slows down both ion species for all values of the relative drift speeds considered in this study. The initial nonresonant wave spectra interact with the particles, resulting in preferential and anisotropic heating for the minor ions with a prominent increase of their perpendicular temperature, which overcomes the effect of the double-adiabatic cooling that is due to the solar wind expansion. Finally, the initial parallel spectra undergo a micro-turbulent nonlinear cascade during which oblique waves are generated, whose intensity depends on the value of the relative drift speed.
Key words: solar wind / plasmas / turbulence / waves / instabilities / acceleration of particles
© ESO, 2015
1. Introduction
Remote-sensing and in situ measurements in coronal holes and fast solar wind show that heavy ions are preferentially heated and accelerated, despite the higher inertia and the stronger gravitational force they experience in the vicinity of the solar surface (Marsch et al. 1982; Kohl et al. 1998, 2006; Cranmer et al. 1999). In situ observations of the temperature anisotropies and the relative drift speed between protons and α particles in collisionless fast solar wind streams indicate a relation between the wave activity and the bulk properties of the ion species in the range 0.3−1 AU (Bourouaine et al. 2010, 2011, 2013; Maruca et al. 2011, 2012; Kasper et al. 2008, 2013). Recent observations indicate that doubly ionized solar wind helium ions near Earth can on average be nearly seven times hotter than protons (Kasper et al. 2013). The causes of this strong heating for the α particles and the reason for the onset of preferential acceleration and generation of the observed temperature anisotropies are still open questions that remain to be solved by future observations and models. Currently, there are no measurements of helium ions in the inner solar corona, but spectroscopic observations of other ions such as O5+ and Mg9+ in coronal holes imply high outflow speeds, temperatures, and anisotropies for the heavy species there (Kohl et al. 1997, 1999; Cranmer et al. 1999; Ofman et al. 2001, 2011a, 2013). This indicates that the onset of the preferential heating, differential acceleration, and temperature anisotropies for the heavy ions takes place in the low-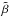 coronal plasma, where turbulence is important and wave amplitudes can be higher than at 0.3 AU (Jian et al. 2009, 2010).
coronal plasma, where turbulence is important and wave amplitudes can be higher than at 0.3 AU (Jian et al. 2009, 2010).
In this paper we perform 2.5D hybrid simulations to investigate the generation of ion temperature anisotropies and differential streaming by broadband turbulent spectra of low-frequency Alfvén-cyclotron waves. We also study the influence of the relative drift speeds between protons and minor ions and the solar wind expansion on the ion heating and differential acceleration. The results of this study provide insight into the physical mechanisms that are responsible for the observed preferential heating and acceleration of minor ions in the solar wind. The work relates the particle properties to the existing solar wind wave spectra in terms of the generation and absorption of waves through nonlinear wave-wave and wave-particle interactions and the evolution of the micro-turbulence in the solar wind.
The scope of our paper is of broad interest to the solar plasma community and extends various previous studies that were based on hybrid numerical modeling, for instance, Gary et al. (2003, 2006), Xie et al. (2004b), Ofman et al. (2005, 2014), Ofman & Viñas (2007), Hellinger & Trávníček (2006), Perrone et al. (2013), Hellinger & Trávníček (2013), linear Vlasov kinetic instability theory, Gary et al. (2001, 2002), Verscharen et al. (2013), Chandran et al. (2013) and numerous observations, such as Reisenfeld et al. (2001), Gary et al. (2002), Hellinger et al. (2006), Kasper et al. (2008, 2013), Bourouaine et al. (2010, 2011, 2013), Maruca et al. (2012). Podesta & Gary (2011) performed a linear theory analysis to explore the effects of the α-proton differential streaming in the solar wind. Hellinger & Trávníček (2006, 2013) discussed the role of α-proton relative drifts in destabilizing the plasma in nonlinear 2.5D hybrid simulations. Verscharen et al. (2013), Chandran et al. (2013), and Bourouaine et al. (2013) considered the limits of differential streaming and ion temperature anisotropies from the point of view of linear kinetic instabilities and observations. Hellinger & Trávníček (2013) have studied the effects of the solar wind expansion on the plasma instabilities in a high-plasma-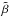 system consisting of a differentially streaming proton core, beam, and α particles in the heliosphere at a distance of r > 0.3 AU. In the current paper, we investigate the effect of the solar wind expansion for an initially drifting α-proton plasma in plasma-
system consisting of a differentially streaming proton core, beam, and α particles in the heliosphere at a distance of r > 0.3 AU. In the current paper, we investigate the effect of the solar wind expansion for an initially drifting α-proton plasma in plasma-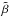 conditions that are appropriate in particular to the inner heliosphere and the solar corona. We initialize the system with an α-proton population and let the ion beams be self-consistently generated by the model ambient wave-spectra as the system evolves in time. We load the particle populations with equal temperatures for the two ion species and study the temporal evolution of their temperature ratio as a function of the relative drift speed. With the goal of constructing a more realistic model of the solar wind, we consider the effects of turbulent initial wave spectra that obey the three-species electron-proton-α cold-plasma dispersion relation. This allows for additional wave-particle and wave-wave interactions that are absent when there are no waves, and it provides essential information on the relation between plasma waves and the properties of ions in collisionless low-
conditions that are appropriate in particular to the inner heliosphere and the solar corona. We initialize the system with an α-proton population and let the ion beams be self-consistently generated by the model ambient wave-spectra as the system evolves in time. We load the particle populations with equal temperatures for the two ion species and study the temporal evolution of their temperature ratio as a function of the relative drift speed. With the goal of constructing a more realistic model of the solar wind, we consider the effects of turbulent initial wave spectra that obey the three-species electron-proton-α cold-plasma dispersion relation. This allows for additional wave-particle and wave-wave interactions that are absent when there are no waves, and it provides essential information on the relation between plasma waves and the properties of ions in collisionless low-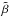 solar wind. Recently, Ofman et al. (2014) have considered the effect of the solar wind expansion for the cases of super-Alfvénic initial relative drifts or α particle temperature anisotropies, and a driven wave spectrum. The waves are injected in time at one side of the periodic boundaries with a prescribed power law consistent with observations within a certain range in frequency space. Ozak et al. (2015) used a 2.5D hybrid model to consider the effects of inhomogeneous background plasma on the ion heating by a turbulent Alfvén-cyclotron wave spectrum and the generation of oblique waves in expanding solar wind plasma. While the study of Ofman et al. (2014) was based on introducing time-dependent magnetic fluctuations, in the present study the magnetic spectrum is introduced as an initial-value problem. By construction, the broad-band spectra preserve the magnetic field as divergence-free, conserve the sense of magnetic helicity, and obey Parseval’s theorem for energy conservation. The waves represent solutions of the cold plasma dispersion relation for a given narrow range in wave-vector space, for which a k-1 spectral slope is considered. Previous 1.5D and 2.5D hybrid simulations (Xie et al. 2004b; Araneda et al. 2009; Ofman & Viñas 2007; Ofman et al. 2011b, 2014; Maneva et al. 2013b, 2014) showed that monochromatic pumps and broad-band spectra of waves can preferentially heat and accelerate the α particles. In this 2.5D study we have narrowed the spectral range of the initial turbulent fluctuations to avoid the slow evolution of the very low-frequency MHD-type Alfvén waves, which would not interact with the particles within the simulation timescales considered here (hundreds of gyroperiods). Details of the simulation setup and the initial wave-spectra are presented in Sect. 2. Simulation results are described in Sect. 3, and conclusions are given in Sect. 4.
solar wind. Recently, Ofman et al. (2014) have considered the effect of the solar wind expansion for the cases of super-Alfvénic initial relative drifts or α particle temperature anisotropies, and a driven wave spectrum. The waves are injected in time at one side of the periodic boundaries with a prescribed power law consistent with observations within a certain range in frequency space. Ozak et al. (2015) used a 2.5D hybrid model to consider the effects of inhomogeneous background plasma on the ion heating by a turbulent Alfvén-cyclotron wave spectrum and the generation of oblique waves in expanding solar wind plasma. While the study of Ofman et al. (2014) was based on introducing time-dependent magnetic fluctuations, in the present study the magnetic spectrum is introduced as an initial-value problem. By construction, the broad-band spectra preserve the magnetic field as divergence-free, conserve the sense of magnetic helicity, and obey Parseval’s theorem for energy conservation. The waves represent solutions of the cold plasma dispersion relation for a given narrow range in wave-vector space, for which a k-1 spectral slope is considered. Previous 1.5D and 2.5D hybrid simulations (Xie et al. 2004b; Araneda et al. 2009; Ofman & Viñas 2007; Ofman et al. 2011b, 2014; Maneva et al. 2013b, 2014) showed that monochromatic pumps and broad-band spectra of waves can preferentially heat and accelerate the α particles. In this 2.5D study we have narrowed the spectral range of the initial turbulent fluctuations to avoid the slow evolution of the very low-frequency MHD-type Alfvén waves, which would not interact with the particles within the simulation timescales considered here (hundreds of gyroperiods). Details of the simulation setup and the initial wave-spectra are presented in Sect. 2. Simulation results are described in Sect. 3, and conclusions are given in Sect. 4.
2. Simulation setup
In this section we introduce the normalization units and the characteristic parameters used for the simulations. The expanding box model and the construction of the initial wave spectra are presented in separate subsections.
The simulation time is given in units of proton gyrofrequency 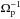 and the velocities are normalized to the local Alfvén speed,
and the velocities are normalized to the local Alfvén speed, 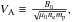 as defined by the magnitude of the homogeneous background magnetic field B0, the electron number density ne, and the proton mass mp. The length of the simulation box is the same in both spatial directions. In units of the proton inertial length it reads Lx = Ly = 384VA/Ωp. The simulations were performed with 256 × 256 cells and 127 particles per cell per species, or in total >16.6 million particles. The time step used is a small fraction of the proton gyroperiod,
as defined by the magnitude of the homogeneous background magnetic field B0, the electron number density ne, and the proton mass mp. The length of the simulation box is the same in both spatial directions. In units of the proton inertial length it reads Lx = Ly = 384VA/Ωp. The simulations were performed with 256 × 256 cells and 127 particles per cell per species, or in total >16.6 million particles. The time step used is a small fraction of the proton gyroperiod, 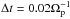 .
.
Summary of the parameters used in the 2.5D hybrid simulation study.
2.1. Initial wave spectra
To initialize the simulations, we assumed that the magnetic field consists of a constant background and a fluctuating part, which corresponds to a broad-band spectrum of low-frequency parallel propagating Alfvén-cyclotron waves:
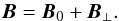 (1)To construct the initial spectra for the two-dimensional simulations, we performed a one-dimensional parallel propagating broad-band reconstruction, based on the procedure described in Viñas et al. (2014), and distributed it homogeneously at each point in the transverse direction until the entire simulation domain was filled with waves. For the one-dimensional reconstruction we assumed that the ambient magnetic field is along the x axis,
(1)To construct the initial spectra for the two-dimensional simulations, we performed a one-dimensional parallel propagating broad-band reconstruction, based on the procedure described in Viñas et al. (2014), and distributed it homogeneously at each point in the transverse direction until the entire simulation domain was filled with waves. For the one-dimensional reconstruction we assumed that the ambient magnetic field is along the x axis, 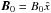 , and the fluctuating part B⊥(x) represents left-hand polarized transverse waves propagating along the background field. For the magnetic fluctuations we considered plane-wave decomposition:
, and the fluctuating part B⊥(x) represents left-hand polarized transverse waves propagating along the background field. For the magnetic fluctuations we considered plane-wave decomposition: ![\begin{equation} \vec{B}_{\perp}= {\rm Re}\left[\sum_{k>0} C_k^L \exp({\rm i} \phi_k) (\hat{y} + {\rm i} \hat{z})\exp({\rm i}kx) \right], \end{equation}](/articles/aa/full_html/2015/06/aa24401-14/aa24401-14-eq41.png) (2)where the phases φk are randomly set between ±[ 0,2π ]. The Fourier coefficients for left-hand polarized waves
(2)where the phases φk are randomly set between ±[ 0,2π ]. The Fourier coefficients for left-hand polarized waves 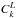 were computed based on the following physical conditions: 1) a divergence-free magnetic field ∇·B = 0; 2) preservation of the sense of magnetic helicity; and 3) conservation of energy between configuration and Fourier spaces, also known as Parseval’s theorem. For left-hand circularly polarized waves the conservation of energy can be expressed as
were computed based on the following physical conditions: 1) a divergence-free magnetic field ∇·B = 0; 2) preservation of the sense of magnetic helicity; and 3) conservation of energy between configuration and Fourier spaces, also known as Parseval’s theorem. For left-hand circularly polarized waves the conservation of energy can be expressed as 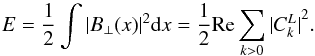 (3)The total magnetic helicity for all fluctuations, defined as the scalar product of the vector potential A with the fluctuating magnetic field B, can be represented as a superposition of the spectral magnetic helicity Hmk for each mode
(3)The total magnetic helicity for all fluctuations, defined as the scalar product of the vector potential A with the fluctuating magnetic field B, can be represented as a superposition of the spectral magnetic helicity Hmk for each mode 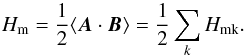 (4)For a spectrum that consists of purely left-hand polarized waves, the spectral magnetic helicity can easily be expressed in terms of the Fourier amplitudes of the fluctuations as follows:
(4)For a spectrum that consists of purely left-hand polarized waves, the spectral magnetic helicity can easily be expressed in terms of the Fourier amplitudes of the fluctuations as follows: 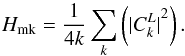 (5)To construct magnetic field power spectra that resemble solar wind observations, we assumed a power-law dependence for the amplitude of the waves
(5)To construct magnetic field power spectra that resemble solar wind observations, we assumed a power-law dependence for the amplitude of the waves 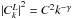 , where γ is a prescribed power spectral index. The constant C depends on the total amplitude of the magnetic field fluctuations
, where γ is a prescribed power spectral index. The constant C depends on the total amplitude of the magnetic field fluctuations 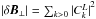 , the spectral slope, and the selected spectral range
, the spectral slope, and the selected spectral range 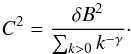 (6)The spectra were constructed in Fourier space, and we used an inverse Fourier transform to provide the magnetic and velocity field fluctuations in configuration space. A detailed description of the method used to construct the initial broad-band spectra for a general combination of left-hand and right-hand circularly polarized parallel propagating waves can be found in Viñas et al. (2014). For the power spectral slope in our simulation study we chose γ = −1. We note that the observed solar wind power spectra close to the Sun are in frequency domain. Thus the observed power spectral slope at large scales ω-1 can be directly related to the k-1 spectrum only for the low-frequency linear part of the dispersion relation, where ω = VAk.
(6)The spectra were constructed in Fourier space, and we used an inverse Fourier transform to provide the magnetic and velocity field fluctuations in configuration space. A detailed description of the method used to construct the initial broad-band spectra for a general combination of left-hand and right-hand circularly polarized parallel propagating waves can be found in Viñas et al. (2014). For the power spectral slope in our simulation study we chose γ = −1. We note that the observed solar wind power spectra close to the Sun are in frequency domain. Thus the observed power spectral slope at large scales ω-1 can be directly related to the k-1 spectrum only for the low-frequency linear part of the dispersion relation, where ω = VAk.
 |
Fig. 1 Initial parallel-propagating Alfvén-α-cyclotron wave spectra – solution of the coupled set of cold quasi-neutral multifluid plasma and the nonrelativistic Maxwell equations. Top panel: the solution for nondrifting plasma. Middle panel: the solution for relative drift speed Vαp = 0.2VA. Bottom panel: the solution for the special case of a relative drift speed of Vαp = 0.5VA. The initial wave spectra was selected from the Alfvén-α-cyclotron branch, and its [ ω0,k0 ] range is shown as a solid brown line. |
To self-consistently couple the initial ion velocities to the reconstructed magnetic field, one needs to prescribe a certain dispersion relation for the waves and solve it to find the relation between the ion motion and the prescribed electromagnetic fluctuations. Complementary to the wave-spectra initialization in our previous 1.5D work (Maneva et al. 2013b), in the present 2.5D study we constructed the initial ion bulk velocity fluctuations as solutions of the three-fluid cold plasma dispersion relation, see Eq. (11)and Fig. 1. In other words, we took into account the fact that the given spectrum of parallel propagating Alfvén-cyclotron waves imposes separate transverse bulk velocity fluctuations for the protons and the α particles, cf. Eq. (12). Using a consistent initialization for both ion species is important to avoid artificial pressure imbalances and instabilities, which can affect the resulting ion heating and acceleration. We note that for the chosen range of wave numbers in the low plasma 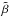 regime considered here (see Table 1), the solution of the cold plasma dispersion relation for parallel wave propagation in drifting isotropic plasma is practically identical to the solution of the full Vlasov linear theory dispersion relation, as there is no damping for the Alfvén-cyclotron branch at wave numbers k0< 0.5Ωp/VA. Thus the chosen spectra are stable with respect to linear plasma instabilities, which become important at higher wave numbers of k0> 0.5Ωp/VA, as shown for example by Ofman & Viñas (2007). To derive the cold plasma dispersion for parallel wave propagation, we started with the combined set of multifluid-Maxwell equations that govern the behavior of low-frequency waves and particles in a drifting isotropic plasma:
regime considered here (see Table 1), the solution of the cold plasma dispersion relation for parallel wave propagation in drifting isotropic plasma is practically identical to the solution of the full Vlasov linear theory dispersion relation, as there is no damping for the Alfvén-cyclotron branch at wave numbers k0< 0.5Ωp/VA. Thus the chosen spectra are stable with respect to linear plasma instabilities, which become important at higher wave numbers of k0> 0.5Ωp/VA, as shown for example by Ofman & Viñas (2007). To derive the cold plasma dispersion for parallel wave propagation, we started with the combined set of multifluid-Maxwell equations that govern the behavior of low-frequency waves and particles in a drifting isotropic plasma: 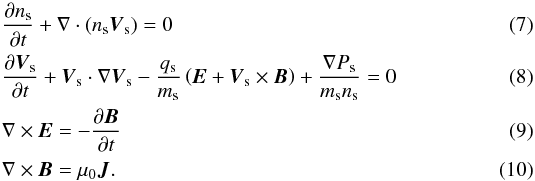 The solution of this system for parallel wave propagation is given by the dispersion relation (Smith & Brice 1964; Sonnerup & Su 1967; Araneda et al. 2009):
The solution of this system for parallel wave propagation is given by the dispersion relation (Smith & Brice 1964; Sonnerup & Su 1967; Araneda et al. 2009): 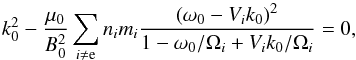 (11)where quasi-neutrality and current conservation are assumed to eliminate the electron contribution, and the summation is carried over the ions. Since we are interested in low-frequency waves in nonrelativistic plasma, we have neglected the vacuum electromagnetic fluctuations described by the
(11)where quasi-neutrality and current conservation are assumed to eliminate the electron contribution, and the summation is carried over the ions. Since we are interested in low-frequency waves in nonrelativistic plasma, we have neglected the vacuum electromagnetic fluctuations described by the 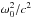 term. The dispersion relation for warm drifting multispecies plasma can be found for example in Davidson & Ogden (1975), Gary (1993), Xie et al. (2004a). For the velocity fluctuations of the ion species we obtain the relation
term. The dispersion relation for warm drifting multispecies plasma can be found for example in Davidson & Ogden (1975), Gary (1993), Xie et al. (2004a). For the velocity fluctuations of the ion species we obtain the relation 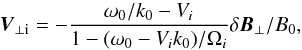 (12)where Vi is the bulk velocity speed for each species, which determines the differential streaming between the protons and the α particles: Vαp = Vα − Vp. The velocity and the magnetic field fluctuations are coupled, so that the initially isotropic ions acquire a bulk transverse motion, determined by the properties of the wave. When no drifts are considered, the corresponding velocity fluctuations for the α particles are much higher than the velocity fluctuations for the protons for the same given choice of initial parallel Alfvén-cyclotron waves, see Ofman et al. (2005), for example. In the presence of relative drifts, the bulk velocity fluctuations for the protons and the α particles change. For Vαp = 0.2VA the transverse velocity fluctuations for the two species become of the same order, and for Vαp = 0.5VA the proton velocity fluctuations are dominant.
(12)where Vi is the bulk velocity speed for each species, which determines the differential streaming between the protons and the α particles: Vαp = Vα − Vp. The velocity and the magnetic field fluctuations are coupled, so that the initially isotropic ions acquire a bulk transverse motion, determined by the properties of the wave. When no drifts are considered, the corresponding velocity fluctuations for the α particles are much higher than the velocity fluctuations for the protons for the same given choice of initial parallel Alfvén-cyclotron waves, see Ofman et al. (2005), for example. In the presence of relative drifts, the bulk velocity fluctuations for the protons and the α particles change. For Vαp = 0.2VA the transverse velocity fluctuations for the two species become of the same order, and for Vαp = 0.5VA the proton velocity fluctuations are dominant.
The initial spectrum consists of 17 modes laying on the left-hand circularly polarized Alfvén-α-cyclotron branch (with a frequency below the α-cyclotron frequency). As noted above, the spectra is chosen from the low-frequency solution of the dispersion relation (see Fig. 1), which is stable with respect to the warm plasma linear Vlasov instability theory and contains no significant wave amplification or damping. The selected normalized wave-number space given in terms of the ion inertial length as given by the local proton gyrofrequency Ωp and the local Alfvén speed VA is k0 ∈ [ 0.26−0.52 ] Ωp/VA, or equivalently, by the ratio of the proton plasma frequency to the speed of light ωp/c. The corresponding frequencies for the individual runs are presented in Table 1. Note that in a previous 1.5D study (Maneva et al. 2013b), we found that spreading the wave power within a rather wide range of frequencies and wave numbers, including very low-frequency MHD-type nondispersive waves, leads to significant reduction in the ion heating and particularly in acceleration rate. This is due to the slow direct cascade and the low left-over power at the relevant kinetic scales. To investigate the ion heating and acceleration, we here considered initial wave spectra within the intermediate frequency range given above (in between the low-frequency MHD-type Alfvén waves and the resonant ion-cyclotron waves), where dispersive effects facilitate a nonlinear cascade and the energy transfer toward the relevant scales for wave-particle interactions. For this test study, the simulations were performed with a total magnitude for the entire initial wave spectra of 20% of the magnitude of the external background magnetic field | δB⊥ | = 0.2B0. If the constituent waves had the same phase (which was randomly selected in our model), this would translate into amplitudes of the individual waves of about 1% of the ambient magnetic field. Recent in situ observations of monochromatic Alfvén-cyclotron waves with similar amplitudes at 1 AU have been presented in Jian et al. (2009). The authors argued that larger amplitudes should be expected at smaller heliocentric distances, closer to the Sun. Large-amplitude magnetic fluctuations, presumably of Alfvénic nature, have also been detected by Helios at various distances in the inner heliosphere (Bourouaine et al. 2011). Wind observations of large-amplitude Alfvén waves at 1 AU have recently been reported in Wang et al. (2012). We note that the initial wave spectra used in our model is based on a linear superposition of Alfvén-cyclotron waves, which are solutions of Sonnerups dispersion relation in a drifting plasma species (Sonnerup & Su 1967). The reconstruction of the magnetic field fluctuations preserves energy, magnetic helicity, and cross-helicity in Fourier and configuration space. It ensures that the magnetic field is divergence free, and as shown by Viñas et al. (2014), this superposition corresponds to an almost constant magnetic field with negligible variations of | B |. Although the mode-mode coupling is neglected in the initial state because the linear principle of superposition is not strictly applicable to nonlinear equations, the hybrid model treats the wave-wave interactions and the magnitude variations of the total magnetic field | B | self-consistently already in the first time-step.
2.2. Expanding-box model
The expanding-box model used in our simulation setup follows the original work by Grappin & Velli (1996) and Liewer et al. (2001), which has since been used by many authors, for example, Hellinger et al. (2005), Hellinger & Trávníček (2006, 2013), Ofman et al. (2011b, 2014), Maneva et al. (2013b). The expanding-box equations for the hybrid simulation settings read 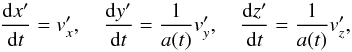 (13)where x is the direction of radial expansion and the external magnetic field, a(t) = 1 + U0t/R0 and the ion velocities in the expanding (prime) frame and at rest are related by the magnitude of the constant solar wind bulk speed U0 and the initial distance from the Sun R0,
(13)where x is the direction of radial expansion and the external magnetic field, a(t) = 1 + U0t/R0 and the ion velocities in the expanding (prime) frame and at rest are related by the magnitude of the constant solar wind bulk speed U0 and the initial distance from the Sun R0,
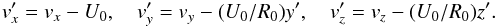 The substantial derivative of the individual ion velocities vi in the expanding and nonexpanding frames are related as follows
The substantial derivative of the individual ion velocities vi in the expanding and nonexpanding frames are related as follows
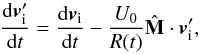 where R(t) = R0 + U0t is the time-dependent radial heliocentric distance from the center of the numerical box in the expanding-box model and
where R(t) = R0 + U0t is the time-dependent radial heliocentric distance from the center of the numerical box in the expanding-box model and 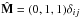 is the transformation matrix, see Grappin & Velli (1996).
is the transformation matrix, see Grappin & Velli (1996).
The equation of motion for the ions in the expanding frame reads
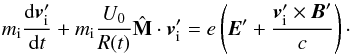 (14)The electric field in the expanding (prime) frame of reference is computed from the momentum equation for the massless fluid isothermal electrons
(14)The electric field in the expanding (prime) frame of reference is computed from the momentum equation for the massless fluid isothermal electrons 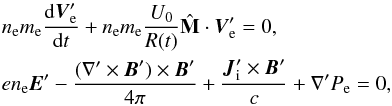 (15)where the electron inertia was neglected,
(15)where the electron inertia was neglected, 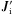 is the ion current in the co-moving reference frame, and Pe = nekBTe is the electron pressure. The transformations for the electric field and the bulk velocities for all species are E′ = E + U0 × B/c and
is the ion current in the co-moving reference frame, and Pe = nekBTe is the electron pressure. The transformations for the electric field and the bulk velocities for all species are E′ = E + U0 × B/c and 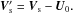 The evolution of the magnetic field is modified by the expansion as follows
The evolution of the magnetic field is modified by the expansion as follows 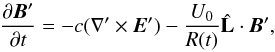 (16)where
(16)where 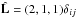 is the transformation matrix that accounts for the effect of the slow expansion, determined by the small expansion parameter ε ≡ U0/R0 with εt ≪ 1, and t is given in units of
is the transformation matrix that accounts for the effect of the slow expansion, determined by the small expansion parameter ε ≡ U0/R0 with εt ≪ 1, and t is given in units of 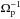 . In these considerations, the second and higher order terms of the type O(ε2) were neglected in the equation of motion for the ion species. In the induction equation we kept the second-order term ε/a(t) = ε/ (1 + εt) as in the original derivations. The approximation for the ion equations of motion we used, ε/R(t) ≈ ε/R0, is equivalent to neglecting the second-order terms in the small expansion parameter ε, assuming (U0/R0) / (1 + U0t/R0) = ε/ (1 + εt) ≈ ε. Repeating the simulations by keeping the higher order terms in the momentum equation introduces insignificant difference, and all results remain the same within 1% variation for the case of ε = 10-4 Ωp, whereas the ion temperature anisotropies at the end of the simulations at Ωpt = 600 vary within 4−5% for the faster expansion with ε = 5 × 10-4 Ωp. Within the approximation discussed above, the expanding-box equations reproduce the original model derivations that were initially developed for magnetohydrodynamic (MHD) systems in Grappin & Velli (1996) and were later applied to hybrid systems by Liewer et al. (2001). The model is valid for radial solar wind expansion and neglects the effects of the curvature within the expanding box as well as the variation of the cross-section of the box in radial direction at any given time. In our hybrid model we solved this system of equations by conserving the net charge and the total current. The charge neutrality for the three species plasma was set by ne = np + 2nα, and the simulations were initialized with zero net current, which was conserved throughout the dynamical evolution of the system. As an initial state we considered isotropic plasma with an equal ion temperature for the protons and the α particles, Tα = Tp, and a different value of the parallel relative drift speed between the two species, Vαp. The parallel components of the corresponding ion plasma beta
. In these considerations, the second and higher order terms of the type O(ε2) were neglected in the equation of motion for the ion species. In the induction equation we kept the second-order term ε/a(t) = ε/ (1 + εt) as in the original derivations. The approximation for the ion equations of motion we used, ε/R(t) ≈ ε/R0, is equivalent to neglecting the second-order terms in the small expansion parameter ε, assuming (U0/R0) / (1 + U0t/R0) = ε/ (1 + εt) ≈ ε. Repeating the simulations by keeping the higher order terms in the momentum equation introduces insignificant difference, and all results remain the same within 1% variation for the case of ε = 10-4 Ωp, whereas the ion temperature anisotropies at the end of the simulations at Ωpt = 600 vary within 4−5% for the faster expansion with ε = 5 × 10-4 Ωp. Within the approximation discussed above, the expanding-box equations reproduce the original model derivations that were initially developed for magnetohydrodynamic (MHD) systems in Grappin & Velli (1996) and were later applied to hybrid systems by Liewer et al. (2001). The model is valid for radial solar wind expansion and neglects the effects of the curvature within the expanding box as well as the variation of the cross-section of the box in radial direction at any given time. In our hybrid model we solved this system of equations by conserving the net charge and the total current. The charge neutrality for the three species plasma was set by ne = np + 2nα, and the simulations were initialized with zero net current, which was conserved throughout the dynamical evolution of the system. As an initial state we considered isotropic plasma with an equal ion temperature for the protons and the α particles, Tα = Tp, and a different value of the parallel relative drift speed between the two species, Vαp. The parallel components of the corresponding ion plasma beta 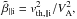 defined in terms of the parallel ion thermal speed vth, ∥ i and the local Alfvén speed VA, is
defined in terms of the parallel ion thermal speed vth, ∥ i and the local Alfvén speed VA, is 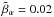 for the He++ ions and
for the He++ ions and 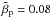 for the protons. The α particles constitute 5% of the background electron density, nα = 0.05ne and the plasma beta of the isothermal fluid electrons is
for the protons. The α particles constitute 5% of the background electron density, nα = 0.05ne and the plasma beta of the isothermal fluid electrons is 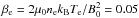 . Most simulations are computed until
. Most simulations are computed until 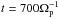 , whereas the simulations with higher expansion factor (see Table 1) are computed until
, whereas the simulations with higher expansion factor (see Table 1) are computed until 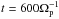 to comply with the approximation used in the expanding-box model, εt ≪ 1. We note that for a faster expansion the value of εt at the end of the simulations is still sufficiently low, εt = 5 × 10-4×600 = 0.3 because the second-order terms are an order of magnitude smaller, ε2t2 = 0.09 ≪ 1.
to comply with the approximation used in the expanding-box model, εt ≪ 1. We note that for a faster expansion the value of εt at the end of the simulations is still sufficiently low, εt = 5 × 10-4×600 = 0.3 because the second-order terms are an order of magnitude smaller, ε2t2 = 0.09 ≪ 1.
 |
Fig. 2 Magnetic field (blue lines) and transverse velocity fluctuations (red lines) for the protons (to the left) and α particles (to the right), corresponding to the initial broad-band spectra of Alfvén-cyclotron waves. The plot shows the strong dependence of the induced transverse velocity fluctuations for the minor ions on the value of the initial relative drift speed. The initial drift varies top to bottom as follows: Vαp = 0,0.2VA and 0.5VA. |
3. Results
Figure 1 describes the shift of the dispersion relation branches that is due to the relative drift speed between the protons and the α particles within the cold quasi-neutral plasma approximation considered here. The red line represents the right-hand polarized fast mode, excited by the electrons. The blue line corresponds to the left-hand polarized proton-cyclotron branch, and the orange curve represents the left-hand polarized Alfvén-cyclotron waves, related to the heaviest α particles in the three-species plasma considered here. The selected initial wave spectra belongs to the latter low-frequency Alfvén-α-cyclotron branch and is overplotted in brown. The relative drift leads to asymmetries in the forward − and backward-propagating Alfvén-cyclotron branches and increases the forbidden bands between the proton- and the α-cyclotron branches found in the linear dispersion relation. Note that the relative drift has no visible influence over the initially selected frequency range for our simulations. Nevertheless, it significantly changes the bulk velocity fluctuations for the different ions, see Eq. (12)and Fig. 2. The relative drifts also influence the turbulent evolution of the initial wave spectra, as shown below in Figs. 10−13.
Figure 2 shows the strong dependence of the induced transverse velocity fluctuations for the minor ions on the value of the initial relative drift speed. The panels show the Alfvénic correlation between the reconstructed initial ion bulk velocities and the magnetic field fluctuations as a function of the simulation box length in “x” direction, parallel to the background magnetic field. For the sake of simplicity, the figure shows only one component of the transverse velocities (given in red) and magnetic field fluctuations (plotted as blue lines). The other transverse components exhibit an identical correlation. The left panel shows the correlation for protons, the right panel the α particles. The plots illustrate the change in the magnitude of the velocity fluctuations for the different ion species depending on the value of the initial relative drift speed. The top panels correspond to nondrifting distributions. The middle panels show the case with Vαp = 0.2VA, the lower panels show the case with Vαp = 0.5VA. The figure demonstrates how the transverse velocity fluctuations for the α particles decrease with increasing relative drift speed. Since the current conservation condition in a frame co-moving with the electrons implies Vα ≫ Vp, the proton velocity fluctuations are in the opposite direction to those of α and remain nearly unaffected by the values of the relative drift considered here.
 |
Fig. 3 Temporal evolution of the ion temperature anisotropies and relative drift speed, showing the generation of differential streaming between protons and α particles. The solid lines indicate simulations without expansion, and the dashed lines show the results when a gradual expansion with ε = 10-4 Ωp was considered. The apparent initial anisotropies are caused by the waves. |
 |
Fig. 4 Temporal evolution of the ion temperature anisotropies and relative drift speed for differentially streaming α particles with Vαp = 0.2VA. The dashed lines denote the ion bulk properties for a gradual expansion with ε = 10-4 Ωp. |
 |
Fig. 5 Temporal evolution of the ion temperature anisotropies and relative drift speed for differentially streaming α particles with Vαp = 0.5VA. The solid lines indicate simulations without expansion, the dashed lines denote the results with ε = 10-4 Ωp. |
Figure 3 shows the temporal evolution of the ion temperature anisotropies and the relative drift speed. Overplotted with dashed lines is the effect of a gradual solar wind expansion with ε = 10-4 Ωp, where 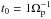 . The initial temperature anisotropy for both species is apparent and is caused by the nonthermal transverse velocity fluctuations that are induced by the waves. The onset of the differential streaming between the protons and the α particles is caused by the acceleration of the proton beam in the system with zero net currents. The reasonable expansion factor considered here leads to a minor change in the bulk ion properties. Note that in Figs. 3−8 the initial state (t = 0) is not plotted to avoid the sharp anisotropy and temperature jumps (within a single time step) that is due to the presence of the nonthermal wave component in the bulk velocities of the ions, see Eq. (12).
. The initial temperature anisotropy for both species is apparent and is caused by the nonthermal transverse velocity fluctuations that are induced by the waves. The onset of the differential streaming between the protons and the α particles is caused by the acceleration of the proton beam in the system with zero net currents. The reasonable expansion factor considered here leads to a minor change in the bulk ion properties. Note that in Figs. 3−8 the initial state (t = 0) is not plotted to avoid the sharp anisotropy and temperature jumps (within a single time step) that is due to the presence of the nonthermal wave component in the bulk velocities of the ions, see Eq. (12).
Figures 4 and 5 also describe the temporal evolution of the ion anisotropies and relative drift speed, but for the case of initially drifting distributions with Vαp = 0.2VA and Vαp = 0.5VA, respectively. The effect of the gradual expansion varies with the value of the initial relative drift speed. It leads to a change of less than 2% in the ion temperature anisotropies and a change of 4.5% in the relative drift speed for Vαp = 0.2VA. With increasing initial relative drift speed, the solar wind expansion leads to about 17% reduction for the temperature anisotropy of the α particles and a 8.9% reduction of the proton temperature anisotropy, whereas the evolution of the relative drift speed is almost unchanged. For interpreting Figs. 3−5, we note that the decrease of the magnetic field and the density B(t),n(t) ∝ 1 /a2(t) lead to a temporal dependence of the local Alfvén speed VA(t)/VA(t = 0) = 1 /a(t). Nevertheless, all physical quantities (ion temperatures and velocities) in our simulations were normalized to the initial constant Alfvén speed VA(t = 0), as defined by the initial background magnetic field and the total density. If we had normalized all quantities with respect to the time-dependent Alfvén speed VA(t), the evolution paths of the relative drift speeds in the nonexpanding and in the expanding box model would have become closer to each other. Still, the temporal evolution of the ion temperatures presented below differs in the expanding and nonexpanding cases even if the temporal dependence of the local Alfvén speed is taken into account.
 |
Fig. 6 Temporal evolution of the parallel and perpendicular components of the ion temperatures for initially nondrifting distributions. Panel a) shows a nonexpanding case. Panel b) illustrates the expansion with ε = 10-4 Ωp. The top rows describe the α particles, whereas the bottom rows depict the protons. The solid red lines denote the perpendicular and the dashed-dotted blue lines stand for the parallel temperature components. The solid green lines denote the perpendicular temperature decrease as predicted by the CGL model. |
To understand the relation between the initial wave spectra and the apparent temperature anisotropy of the ions, we need to take into account several factors. To begin with, the simulations were initialized with equal temperatures for both ion species. The normalized parallel ion temperature for each species was set at half the product of their mass ratio and the parallel plasma 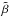 , that is,
, that is, 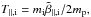 so that T∥,p = T∥,α = 0.04. Since we assumed an initially isotropic plasma, the initial perpendicular temperatures for the two ion species are also equal. What appears on the plots instead are the apparent temperatures and anisotropies, which are calculated based on the thermal velocities of the ions and the nonthermal ion motions, imposed by the initial wave spectra, see Eq. (12). Since we considered only parallel waves, their effect on the ions is only in perpendicular direction. Therefore the larger nonthermal component of the velocity fluctuations induces higher apparent temperature anisotropies. This picture changes for oblique wave propagation, where the waves also affect the parallel motion of the ions and induce parallel bulk velocity fluctuations as well (Maneva et al. 2015). For the initial wave spectra used in our simulations, the magnitude of the velocity fluctuations of the α particles and the protons constitutes from 42% to almost twice the value of their initial perpendicular thermal speeds (
so that T∥,p = T∥,α = 0.04. Since we assumed an initially isotropic plasma, the initial perpendicular temperatures for the two ion species are also equal. What appears on the plots instead are the apparent temperatures and anisotropies, which are calculated based on the thermal velocities of the ions and the nonthermal ion motions, imposed by the initial wave spectra, see Eq. (12). Since we considered only parallel waves, their effect on the ions is only in perpendicular direction. Therefore the larger nonthermal component of the velocity fluctuations induces higher apparent temperature anisotropies. This picture changes for oblique wave propagation, where the waves also affect the parallel motion of the ions and induce parallel bulk velocity fluctuations as well (Maneva et al. 2015). For the initial wave spectra used in our simulations, the magnitude of the velocity fluctuations of the α particles and the protons constitutes from 42% to almost twice the value of their initial perpendicular thermal speeds (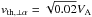 and
and 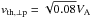 ). The ratio of the average wave-induced perpendicular bulk velocity fluctuations to the thermal velocities of the ions at the beginning of the simulations as a function of the relative drift speed between the two species is presented in Table 1. At zero drifts the motion of the α particles is strongly affected by the wave spectra, see Fig. 2, and the average of their perpendicular velocity flucutations for the chosen broad-band spectrum is ⟨ V⊥ α ⟩ = 0.26VA vs. ⟨ V⊥ p ⟩ = 0.15VA for the protons. As the relative drift speed increases to Vαp = 0.2VA, the selected wave spectrum affects the α particles and the protons in a similar manner and the imposed velocity flucutuations for the two species are of the same order: ⟨ V⊥ α ⟩ ≈ ⟨ V⊥ p ⟩ ≈ 0.16VA. For higher drifts, Vαp = 0.5VA, the influence of the electromagnetic field of the wave spectrum on the α particles is negligible ⟨ V⊥ α ⟩ = 0.06VA, whereas its effect on the protons remains almost unchanged ⟨ V⊥ p ⟩ = 0.17VA. We note that for a fixed type of waves the relation between the velocity fluctuations and the relative drift speed strongly depends on the selected spectral range, as a shift in ω − k space would change the resonant condition according to Eq. (12). This relation is only valid for parallel wave propagation within the cold isotropic homogeneous plasma limit, and it would change once oblique waves and anisotropic ions or plasma inhomogeneities are introduced.
). The ratio of the average wave-induced perpendicular bulk velocity fluctuations to the thermal velocities of the ions at the beginning of the simulations as a function of the relative drift speed between the two species is presented in Table 1. At zero drifts the motion of the α particles is strongly affected by the wave spectra, see Fig. 2, and the average of their perpendicular velocity flucutations for the chosen broad-band spectrum is ⟨ V⊥ α ⟩ = 0.26VA vs. ⟨ V⊥ p ⟩ = 0.15VA for the protons. As the relative drift speed increases to Vαp = 0.2VA, the selected wave spectrum affects the α particles and the protons in a similar manner and the imposed velocity flucutuations for the two species are of the same order: ⟨ V⊥ α ⟩ ≈ ⟨ V⊥ p ⟩ ≈ 0.16VA. For higher drifts, Vαp = 0.5VA, the influence of the electromagnetic field of the wave spectrum on the α particles is negligible ⟨ V⊥ α ⟩ = 0.06VA, whereas its effect on the protons remains almost unchanged ⟨ V⊥ p ⟩ = 0.17VA. We note that for a fixed type of waves the relation between the velocity fluctuations and the relative drift speed strongly depends on the selected spectral range, as a shift in ω − k space would change the resonant condition according to Eq. (12). This relation is only valid for parallel wave propagation within the cold isotropic homogeneous plasma limit, and it would change once oblique waves and anisotropic ions or plasma inhomogeneities are introduced.
 |
Fig. 7 Temporal evolution of the individual ion temperatures for an initially drifting plasma with Vαp = 0.2VA. Similar to Fig. 6, the right panel shows the effect of a gradual expansion with ε = 10-4 Ωp. |
 |
Fig. 8 Temporal evolution of the individual ion temperatures for initially drifting plama with Vαp = 0.5VA. Right panel: the effect of the gradual expansion with ε = 10-4 Ωp. The notations are the same as in Figs. 6 and 7. |
Figures 6−8 describe the temporal evolution of the parallel and perpendicular temperature components for protons and α particles for the three sets of values for the initial relative drift speed, starting with nondrifting distributions and increasing the drift to Vαp = 0.2VA and Vαp = 0.5VA. Each figure consists of two panels that show the difference between the ion heating and cooling in the nonexpanding wind, panel (a), and the effect of a gradual expansion with ε = 10-4 Ωp, panel (b). The perpendicular component of the ion temperature is given by the solid red lines, whereas the parallel component is plotted with dashed-dotted blue lines. The expected perpendicular cooling as predicted by the double-adiabatic CGL model is described by the solid green lines. In all cases, the expansion leads to significant perpendicular cooling for both ion species and minor cooling in parallel direction. We observe a decrease of about 16−20% in the perpendicular temperature for the α particles and a decrease of about 6−11% in the perpendicular temperature for the protons. The parallel cooling is less prominent for both protons and α particles, and it decreases with increase of the initial relative drift speed. Thus the highest reduction of the ion temperature anisotropy for the α particles due to the effect of the gradual expansion is at Vαp = 0.5VA, see Fig. 5. As discussed above, the presence of relative drifts decreases the nonthermal component of the transverse velocity for the minor ions, which reduces their apparent perpendicular temperature. Despite the substantial perpendicular cooling caused by the expansion, the perpendicular temperature decrease for the minor ions is weaker than is expected from the CGL model, and preferential heating for the α particles is present in all simulation cases. The protons, on the other hand, are less affected by initial and induced waves throughout the simulations, and their evolution is close to the double-adiabatic expectations. In Fig. 9 we show the contour plot of the two-dimensional ion velocity distribution function at the final stage of the simulations for initially drifting plasma with Vαp = 0.2VA. The parallel velocity component is along the x axis and the perpendicular one is along the ordinate. The ion acceleration and anisotropic heating lead to a deviation from the initial isotropic distributions. Ion acceleration associated with prominent ion beam formations occurs for both species. The beams are caused by the turbulence-generated ion-acoustic fluctuations, similar to the parametric instability scenario described in Araneda et al. (2009), Maneva et al. (2009, 2013b). The perpendicular heating is a combination of the quasilinear diffusion in phase-space from the forced bouncing caused by the initial wave-spectra and additional resonant scattering with the ion-cyclotron waves generated during the nonlinear evolution of the system. To facilitate the comparison of their distributions, in this figure we use the same isotropic range in vx and vz for both protons and the α particles. The 2D velocity distributions for the two ion species are symmetric in the phase-space formed by the transverse velocity components vy and vz, because of the circular polarization of the waves and the ion gyro motion. This makes the particle velocity distributions in vx,vy and vx,vz identical. The velocity distribution functions, corresponding to the nondrifting plasma case, show similar features for both ion species. However, in this case, the proton beams are stronger and the α particles are heated to higher temperatures in both parallel and perpendicular direction. The stronger proton beams and parallel minor ion heating are most likely related to Landau damping of the turbulence-generated ion density fluctuations, whose resonant absorption depends on the relative drift speed.
 |
Fig. 9 Snapshot of the two-dimensional velocity distribution functions for protons (left) and α particles (right) for the case of initially drifting isotropic and isothermal plasma with Vαp = 0.2VA. The reduced distributions in the lower panel show the number of particles as a function of the parallel component of the ion thermal speeds. A best-fit Maxwellian velocity distribution is overplotted with the dotted line. |
Figures 10 and 11 show the power spectral density of the magnetic field fluctuations in Fourier space as a function of frequency and wave numbers. Figure 10 corresponds to a nondrifting non-expanding plasma, whereas Fig. 11 refers to a drifting nonexpanding plasma with Vαp = 0.2VA. The top panels describe the redistributed wave power for the duration of the simulations as a function of the parallel wave number, as projected along the ambient magnetic field. In both simulation cases, with and without relative drifts, the power spectra is asymmetric with respect to the direction of propagation. There are strong forward-propagating ion-cyclotron modes at k∥ ≤ 0.35Ωp/VA, remnants from the initial broad-band spectra, together with powerful forward-propagating fast modes, which are excited in the course of evolution. The initial waves with k∥> 0.35Ωp/VA quickly decay and are absorbed by the plasma. A broad-band spectrum of powerful backward-propagating higher order proton-cyclotron and some α-cyclotron modes is also generated and intersects with the backward-propagating Alfvén-α-cyclotron branch. The parallel dispersion relation was calculated by fixing a certain point in perpendicular y direction and making a fast Fourier transform of the magnetic field fluctuations in time t and along the parallel spatial coordinate x. The transverse dispersion relation is shown in the bottom panels of Figs. 10, 11. It was calculated following a similar procedure, but the fast-Fourier transform was performed in t and y for a fixed point in x. The perpendicular power spectra indicate the presence of oblique modes, propagating across the ambient magnetic field. The oblique waves have a higher intensity in the nondrifting case. The magnetic power spectra for both figures were computed over a long time interval, starting at the beginning of the simulations at t = 0 and ending toward the end of the simulations at 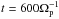 . In this way, the plots illustrate the turbulent evolution of the fluctuations and the wave coupling at the fully nonlinear stage of the simulations.
. In this way, the plots illustrate the turbulent evolution of the fluctuations and the wave coupling at the fully nonlinear stage of the simulations.
 |
Fig. 10 Dispersion diagram ω vs. k, representing the wave intensity as a function of wave frequency vs. parallel (up) and perpendicular (bottom) wave-number space. The graph corresponds to nondrifting initial distributions. |
 |
Fig. 11 Wave intensity as a function of wave frequency vs. parallel (up) and perpendicular (bottom) wave number for a drifting nonexpanding plasma with Vαp = 0.2VA. |
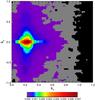 |
Fig. 12 Wave power as a function of the parallel vs. perpendicular wave number for a nondrifting nonexpanding plasma at the end stage of the simulations Ωpt = 700. |
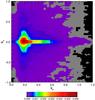 |
Fig. 13 Wave power as a function of the parallel vs. perpendicular wave number at Ωpt = 700 for a drifting nonexpanding plasma with Vαp = 0.2VA. |
Figures 12 and 13 show the power spectral density of the magnetic field fluctuations (wave power) as a function of the parallel and perpendicular wave numbers at the end of the simulations for the same cases as described in Figs. 10, 11 above. These complementary plots show the nonlinear anisotropic cascade of wave energy from parallel toward perpendicular wave numbers. In addition to the generation of oblique fluctuations, the figures show a dependence of the parallel cascade on the value of the initial relative drift speed: for initially nondrifting ion distributions, there is a shift toward smaller parallel wave numbers (Fig. 12), and there is a parallel cascade to both smaller and higher k∥ for an initial drift Vαp = 0.2VA (Fig. 13). The two-dimensional spectra were computed with a two-dimensional Fourier transform (along both spatial coordinates) of the fluctuating component of the magnetic field at the end stage of the simulations. The figures show the role of the differential streaming for the perpendicular energy cascade and oblique mode generation. The initial state for both cases is a broad-band spectrum of parallel Alfvén-cyclotron waves with parallel wave numbers in the range k0 = k∥ = [ 0.26−0.52 ] Ωp/VA. For nondrifting plasma the initial spectrum is strongly depleted above k∥ ≤ 0.35Ωp/VA and parallel waves at longer wavelengths are generated, so that the initial spectra are shifted toward lower parallel wave numbers. For drifting plasma, the initial spectra for k∥ > 0.35Ωp/VA is not fully depleted and the generated oblique waves are slightly stronger. For both cases the strongest parallel waves are concentrated within | k∥ | ∈ [ 0.1−0.3 ] Ωp/VA, whereas the power of the generated oblique waves is concentrated within the limited range | k⊥ | ∈ [ 0−0.1 ] Ωp/VA. If we were to think of the spectra as a superposition of individual monochromatic waves, then we could try to understand the turbulent evolution in terms of superposition of the daughter waves generated by the parametric instabilities of the individual constituent pump waves. If we assume such an analogy, we could say that there are strong modulational and decay instabilities (Kauffmann & Araneda 2008; Maneva et al. 2009). There is an interplay between the modulational and the decay-like instabilities in the nondrifting and the drifting case. We note that the analogy with the linear superposition of parametrically unstable waves is given only as an illustration of a possible way to introduce nonlinear effects. A realistic treatment of the solar wind turbulence requires fully nonlinear wave-wave couplings and consequent wave-particle interactions achieved in the present hybrid model.
4. Discussion and conclusions
We have performed 2.5D hybrid simulations to investigate the role of initially imposed broad-band wave spectra in a drifting and expanding solar wind plasma. We have studied the relaxation and evolution of the initial turbulent spectra and their effect on the ions. The results from the 2.5D simulations yield heating and acceleration rates for the ion species that are similar to the rates observed in 1.5D simulations (Maneva et al. 2013a,b, 2014). The threshold value for the differential acceleration, Vαp = 0.5VA, agrees with previous results from 1.5D hybrid simulations with single monochromatic pump waves (Maneva et al. 2014), and the power spectra of the magnetic field fluctuations shows that the initial parallel waves evolve and grow predominantly parallel to the background magnetic field with less wave activity in the perpendicular direction. The combination of these effects suggests that the parametric instabilities and the turbulent evolution of low-frequency finite-amplitude Alfvén-cyclotron waves in 1.5D studies could serve as a starting point for understanding parallel wave propagation in two-dimensional turbulent problems.
The direct comparison between the nonlinear evolution of turbulence generated by parametrically unstable pump waves and a broad-band initial turbulent wave spectra based on a 1.5D hybrid simulation study showed similar spectral slopes for the late-stage magnetic field and density fluctuations. Nevertheless, the resulting minor ion heating and differential acceleration are significantly different because of the different fluctuations at the early stage of their evolution, cf. Fig. 3 from Maneva et al. (2013a). This suggests that the plasma processes induced by initial pump waves and initial turbulent wave spectra need to be considered as complementary to each other because both of them can be realized in the solar wind, but with different consequences on the ions. We note that although the initial turbulent magnetic fluctuations are characterized by random phases, the present hybrid model significantly differs from weak-turbulence studies, which do not take into account wave-particle interactions.
For the plasma parameters considered within our model, the linear Vlasov theory predicts a much higher threshold value for the relative drift speed required for the onset of the two-streaming instability, Vαp > 1.8VA. In this respect,the observed deceleration of the α particles at Vαp > 0.5VA is a nonlinear phenomenon, which requires higher-order analytical treatment or direct numerical simulations. We constructed a self-consistent initial wave spectra of parallel Alfvén-cyclotron waves and computed the related velocity fluctuations in the presence of differential streaming. We estimated the apparent temperature anisotropies corresponding to the nonthermal velocity components generated by the initial wave spectra. We demonstrated the effect of the differential streaming on the apparent temperature anisotropies for the minor ions. In a nondrifting plasma the α particles are strongly influenced by the initial spectra. They acquire high transverse bulk velocity fluctuations with a higher magnitude than the corresponding transverse component of the minor ion thermal speed. These fluctuations are significantly reduced in the presence of relative drifts. The protons are much less affected by the selected wave spectra, and their nonthermal velocity component constitutes a fraction of the relevant proton thermal speed for all simulation cases. For the sake of clarity, we note that 2.5D simulations with higher initial relative drifts Vαp> 0.5VA clearly show that the relative drift speed decreases in time. Furthermore, 1.5D simulations show a similar decrease of the relative drift speed for Vαp ≤ 1.8VA− that is, throughout the entire linearly stable regime of the magnetosonic instability (without waves) for the given plasma parameters (see Fig. 9 from Maneva et al. 2014). For larger drifts the system is prone to the linear theory streaming instability, which again causes a decrease of the relative drift speed in time.
Although one-dimensional simulations can provide useful indications for understanding the solar wind properties, they fail to capture other factors such as oblique wave generation, anisotropic turbulence, and plasma structures. The solar wind expansion by construction is strongly influenced by the degrees of freedom in the system, and its role can be stronger in two-dimensional systems. In addition, many of the observed solar wind magnetic fluctuations are oblique in nature, and their scattering and interaction with the co-existing parallel waves requires more than one spatial dimension. Our 2.5D simulation study provides a further step toward a proper treatment of the dynamic ion properties in the solar wind and the anisotropic evolution of the solar wind micro-turbulence, which cannot be captured by 1.5D modeling.
We find that the relative drift speed prolongs the lifetime of the parallel waves at short wavelengths, as new waves with | k∥ | ≥ 0.35Ωp/VA are generated and the wave power is replenished after the initial spectra is damped. This implies that the turbulent evolution of the plasma waves and the nonlinear wave-wave interactions are affected by the differential streaming. In addition, the relative drifts enter the cyclotron damping resonant condition and Doppler-shift the frequency of the Alfvén-cyclotron waves, which is required for resonant wave-particle interactions with the minor ions. The selected initial spectra is far from resonance with the protons for all values of the relative drift speeds we considered. In addition, the direct turbulent cascade is not strong enough to bring sufficient wave power at the proton-cyclotron scales during the short (kinetic) timescale of the simulations. Hence there is no perpendicular heating for the protons at any time throughout the simulations. The differential streaming also suppresses the parallel wave generation at large wavelengths | k∥ | < 0.125Ωp/VA and facilitates the oblique-mode generation with enhanced energy transfer in the perpendicular direction. In both drifting and nondrifting plasmas the oblique waves appear confined within the range of | k⊥ | ∈ [ 0,0.3 ] Ωp/VA, with most of their power concentrated in | k⊥ | ∈ [ 0−0.1 ] Ωp/VA.
The almost realistic values of the solar wind expansion factor in the inner heliosphere used here, ε = 10-4 Ωp, lead to a change of only a few percent in the evolution of the differential streaming on the temporal scales considered here. This holds true when we keep the second-order terms in ε in the ion equations of motion, which results in a difference of 1% for the final value of the differential streaming with respect to the currently used expanding box for the two cases of ε = 10-4 Ωp and ε = 5 × 10-4 Ωp. Still, the expansion plays a significant role in decreasing the ion temperature anisotropies and the perpendicular ion temperatures − up to 20% for the α particles. As the minor ions are preferentially heated by the existing waves in the system, their perpendicular temperature remains higher than the double adiabatic prediction. The protons, on the other hand, experience no wave heating, and their cooling in time is practically given by the CGL model. The slight additional cooling comes from the lack of exact energy conservation in the system, where the total electromagnetic energy is preserved within 14%, the kinetic energy of the protons is preserved with 1.5%, and the kinetic energy for the α particles is preserved to within 11%. Although the energy is quasi-conserved, there is still some energy loss in the system because all these energies slightly decrease in time. If we account for this numerical effect, we would expect an even higher heating rate for the minor ions. We note that the gradual solar wind expansion considered here would have a stronger net effect as we follow the plasma evolution over a longer time interval. Assuming an expansion factor of ε = 5 × 10-4 Ωp already leads to a substantial reduction of the relative drift speed (by up to 40%) and the ion temperature anisotropies (by up to 51%), as visible from Table 1. This causes some questions as to how strongly the observed high values of the relative drift speed between protons and minor ions can be attributed to the sweeping mechanism. If we were to renormalize the differential streaming and the ion temperatures to the time-dependent local Alfvén speed in the expanding case, the temporal evolution of the relative drift speed would be similar to the nonexpanding case, but the perpendicular ion temperatures would remain slightly lower in the expanding case. The faster expansion also changes the nonlinear evolution of the initial wave spectra, affecting the wave-particle interactions and the resulting shape of the ion velocity distribution functions. Since the wave-particle interactions operate much faster than the expansion timescales, however, a pure increase in the expansion factor might not properly describe the plasma evolution. A self-consistent description of the evolution of the turbulent fast solar wind plasma requires long simulation times and is computationally very expensive even in 2.5D hybrid kinetic models. It is beyond the scope of this paper to investigate the turbulent cascade at very large MHD scales. However, we were able to capture the dynamics at the ion scales and demonstrate the back-reaction of the ions on the cascade processes and the evolution of the turbulent wave spectra at the intermediate ion scales and some limited part of the large-scale MHD spectra.
Acknowledgments
This work was supported by NASA, grant NNX10AC56G. Y. G. Maneva would like to acknowledge the F+ fellowship at KU Leuven, (FP7/2007-2013) under the grant agreement SOLSPANET (project 269299) and C 90347 (ESA Prodex) for partial support. A. F. Viñas would like to acknowledge the Wind/SWE project for partial support. Fruitful discussions with P. Hunana are highly appreciated.
References
- Araneda, J. A., Maneva, Y., & Marsch, E. 2009, Phys. Rev. Lett., 102, 175001 [NASA ADS] [CrossRef] [Google Scholar]
- Bourouaine, S., Marsch, E., & Neubauer, F. M. 2010, Geophys. Res. Lett., 37, 14104 [NASA ADS] [CrossRef] [Google Scholar]
- Bourouaine, S., Marsch, E., & Neubauer, F. M. 2011, ApJ, 728, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Bourouaine, S., Verscharen, D., Chandran, B. D. G., Maruca, B. A., & Kasper, J. C. 2013, ApJ, 777, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Chandran, B. D. G., Verscharen, D., Quataert, E., et al. 2013, ApJ, 776, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Cranmer, S. R., Field, G. B., & Kohl, J. L. 1999, ApJ, 518, 937 [NASA ADS] [CrossRef] [Google Scholar]
- Davidson, R. C., & Ogden, J. M. 1975, Phys. Fluids, 18, 1045 [NASA ADS] [CrossRef] [Google Scholar]
- Gary, S. P. 1993, Theory of Space Plasma Microinstabilities (New York: Cambridge University Press) [Google Scholar]
- Gary, S. P., Goldstein, B. E., & Steinberg, J. T. 2001, J. Geophys. Res., 106, 24955 [NASA ADS] [CrossRef] [Google Scholar]
- Gary, S. P., Goldstein, B. E., & Neugebauer, M. 2002, J. Geophys. Res. Space Phys., 107, 1169 [NASA ADS] [CrossRef] [Google Scholar]
- Gary, S. P., Yin, L., Winske, D., et al. 2003, J. Geophys. Res. Space Phys., 108, 1068 [NASA ADS] [CrossRef] [Google Scholar]
- Gary, S. P., Yin, L., & Winske, D. 2006, J. Geophys. Res., 111, 6105 [NASA ADS] [CrossRef] [Google Scholar]
- Grappin, R., & Velli, M. 1996, J. Geophys. Res., 101, 425 [Google Scholar]
- Hellinger, P., & Trávníček, P. 2006, J. Geophys. Res. Space Phys., 111, 1107 [Google Scholar]
- Hellinger, P., & Trávníček, P. M. 2013, J. Geophys. Res. Space Phys., 118, 5421 [Google Scholar]
- Hellinger, P., Velli, M., Trávníček, P., et al. 2005, J. Geophys. Res., 110, 12109 [NASA ADS] [CrossRef] [Google Scholar]
- Hellinger, P., Trávníček, P., Kasper, J. C., & Lazarus, A. J. 2006, Geophys. Res. Lett., 33, 9101 [Google Scholar]
- Jian, L. K., Russell, C. T., Luhmann, J. G., et al. 2009, ApJ, Lett., 701, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Jian, L. K., Russell, C. T., Luhmann, J. G., et al. 2010, J. Geophys. Res., 115, 12115 [CrossRef] [Google Scholar]
- Kasper, J. C., Lazarus, A. J., & Gary, S. P. 2008, Phys. Rev. Lett., 101, 261103 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kasper, J. C., Maruca, B. A., Stevens, M. L., & Zaslavsky, A. 2013, Phys. Rev. Lett., 110, 091102 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, K., & Araneda, J. A. 2008, Phys. Plasmas, 15, 062106 [NASA ADS] [CrossRef] [Google Scholar]
- Kohl, J. L., Noci, G., Antonucci, E., et al. 1997, Sol. Phys., 175, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Kohl, J. L., Noci, G., Antonucci, E., et al. 1998, ApJ, 501, L127 [Google Scholar]
- Kohl, J. L., Esser, R., Cranmer, S. R., et al. 1999, ApJ, 510, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Kohl, J. L., Noci, G., Cranmer, S. R., & Raymond, J. C. 2006, A&ARv, 13, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Liewer, P. C., Velli, M., & Goldstein, B. E. 2001, J. Geophys. Res., 106, 29261 [NASA ADS] [CrossRef] [Google Scholar]
- Maneva, Y. G., Araneda, J. A., & Marsch, E. 2009, AIP Conf. Ser., 1121, 122 [Google Scholar]
- Maneva, Y. G., Ofman, L., & Viñas, A. F. 2013a, in AIP Conf. Ser. 1539, eds. G. P. Zank, J. Borovsky, R. Bruno, et al., 34 [Google Scholar]
- Maneva, Y. G., Viñas, A. F., & Ofman, L. 2013b, J. Geophys. Res. Space Phys., 118, 2842 [NASA ADS] [CrossRef] [Google Scholar]
- Maneva, Y. G., Araneda, J.-A., & Marsch, E. 2014, ApJ, 783, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Maneva, Y. G., Viñas, A.-F., Moya, P. S., Wicks, R. T., & Poedts, S. 2015, ApJ, submitted [Google Scholar]
- Marsch, E., Schwenn, R., Rosenbauer, H., et al. 1982, J. Geophys. Res., 87, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Maruca, B. A., Kasper, J. C., & Bale, S. D. 2011, Phys. Rev. Lett., 107, 201101 [NASA ADS] [CrossRef] [Google Scholar]
- Maruca, B. A., Kasper, J. C., & Gary, S. P. 2012, ApJ, 748, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Ofman, L., & Viñas, A. F. 2007, J. Geophys. Res. Space Phys., 112, 6104 [Google Scholar]
- Ofman, L., Viñas, A., & Gary, S. P. 2001, ApJ, 547, L175 [NASA ADS] [CrossRef] [Google Scholar]
- Ofman, L., Davila, J. M., Nakariakov, V. M., & Viñas, A.-F. 2005, J. Geophys. Res. Space Phys., 110, 9102 [NASA ADS] [CrossRef] [Google Scholar]
- Ofman, L., Abbo, L., & Giordano, S. 2011a, ApJ, 734, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Ofman, L., Viñas, A.-F., & Moya, P. S. 2011b, Annales Geophysicae, 29, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Ofman, L., Abbo, L., & Giordano, S. 2013, ApJ, 762, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Ofman, L., Viñas, A.-F., & Maneva, Y. G. 2014, J. Geophys. Res., 119, 4223 [CrossRef] [Google Scholar]
- Ozak, N., Ofman, L., & Viñas, A.-F. 2015, ApJ, 799, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Perrone, D., Valentini, F., Servidio, S., Dalena, S., & Veltri, P. 2013, ApJ, 762, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Podesta, J. J., & Gary, S. P. 2011, ApJ, 742, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Reisenfeld, D. B., Gary, S. P., Gosling, J. T., et al. 2001, J. Geophys. Res., 106, 5693 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. L., & Brice, N. 1964, J. Geophys. Res., 69, 5029 [NASA ADS] [CrossRef] [Google Scholar]
- Sonnerup, B. U. Ö., & Su, S.-Y. 1967, Physics of Fluids, 10, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Verscharen, D., Bourouaine, S., Chandran, B. D. G., & Maruca, B. A. 2013, ApJ, 773, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Viñas, A.-F., Moya, P. S., Araneda, J. A., & Maneva, Y. G. 2014, ApJ, 786, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, X., He, J., Tu, C., et al. 2012, ApJ, 746, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Xie, H., Ofman, L., & Viñas, A. 2004a, J. Geophys. Res., 109, 8103 [Google Scholar]
- Xie, H., Ofman, L., & Viñas, A. 2004b, J. Geophys. Res. Space Phys., 109, 8103 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Initial parallel-propagating Alfvén-α-cyclotron wave spectra – solution of the coupled set of cold quasi-neutral multifluid plasma and the nonrelativistic Maxwell equations. Top panel: the solution for nondrifting plasma. Middle panel: the solution for relative drift speed Vαp = 0.2VA. Bottom panel: the solution for the special case of a relative drift speed of Vαp = 0.5VA. The initial wave spectra was selected from the Alfvén-α-cyclotron branch, and its [ ω0,k0 ] range is shown as a solid brown line. |
| In the text | |
 |
Fig. 2 Magnetic field (blue lines) and transverse velocity fluctuations (red lines) for the protons (to the left) and α particles (to the right), corresponding to the initial broad-band spectra of Alfvén-cyclotron waves. The plot shows the strong dependence of the induced transverse velocity fluctuations for the minor ions on the value of the initial relative drift speed. The initial drift varies top to bottom as follows: Vαp = 0,0.2VA and 0.5VA. |
| In the text | |
 |
Fig. 3 Temporal evolution of the ion temperature anisotropies and relative drift speed, showing the generation of differential streaming between protons and α particles. The solid lines indicate simulations without expansion, and the dashed lines show the results when a gradual expansion with ε = 10-4 Ωp was considered. The apparent initial anisotropies are caused by the waves. |
| In the text | |
 |
Fig. 4 Temporal evolution of the ion temperature anisotropies and relative drift speed for differentially streaming α particles with Vαp = 0.2VA. The dashed lines denote the ion bulk properties for a gradual expansion with ε = 10-4 Ωp. |
| In the text | |
 |
Fig. 5 Temporal evolution of the ion temperature anisotropies and relative drift speed for differentially streaming α particles with Vαp = 0.5VA. The solid lines indicate simulations without expansion, the dashed lines denote the results with ε = 10-4 Ωp. |
| In the text | |
 |
Fig. 6 Temporal evolution of the parallel and perpendicular components of the ion temperatures for initially nondrifting distributions. Panel a) shows a nonexpanding case. Panel b) illustrates the expansion with ε = 10-4 Ωp. The top rows describe the α particles, whereas the bottom rows depict the protons. The solid red lines denote the perpendicular and the dashed-dotted blue lines stand for the parallel temperature components. The solid green lines denote the perpendicular temperature decrease as predicted by the CGL model. |
| In the text | |
 |
Fig. 7 Temporal evolution of the individual ion temperatures for an initially drifting plasma with Vαp = 0.2VA. Similar to Fig. 6, the right panel shows the effect of a gradual expansion with ε = 10-4 Ωp. |
| In the text | |
 |
Fig. 8 Temporal evolution of the individual ion temperatures for initially drifting plama with Vαp = 0.5VA. Right panel: the effect of the gradual expansion with ε = 10-4 Ωp. The notations are the same as in Figs. 6 and 7. |
| In the text | |
 |
Fig. 9 Snapshot of the two-dimensional velocity distribution functions for protons (left) and α particles (right) for the case of initially drifting isotropic and isothermal plasma with Vαp = 0.2VA. The reduced distributions in the lower panel show the number of particles as a function of the parallel component of the ion thermal speeds. A best-fit Maxwellian velocity distribution is overplotted with the dotted line. |
| In the text | |
 |
Fig. 10 Dispersion diagram ω vs. k, representing the wave intensity as a function of wave frequency vs. parallel (up) and perpendicular (bottom) wave-number space. The graph corresponds to nondrifting initial distributions. |
| In the text | |
 |
Fig. 11 Wave intensity as a function of wave frequency vs. parallel (up) and perpendicular (bottom) wave number for a drifting nonexpanding plasma with Vαp = 0.2VA. |
| In the text | |
 |
Fig. 12 Wave power as a function of the parallel vs. perpendicular wave number for a nondrifting nonexpanding plasma at the end stage of the simulations Ωpt = 700. |
| In the text | |
 |
Fig. 13 Wave power as a function of the parallel vs. perpendicular wave number at Ωpt = 700 for a drifting nonexpanding plasma with Vαp = 0.2VA. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


