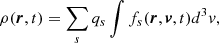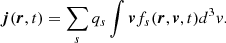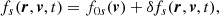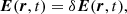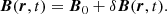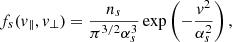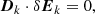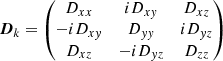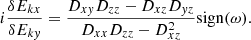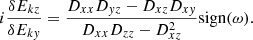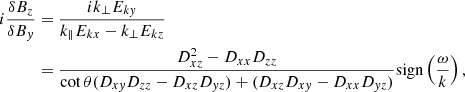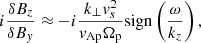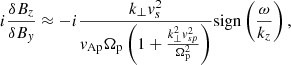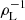EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 689 (September 2024) A&A, 689 (2024) A261 Full HTML
Open Access
Issue
A&A
Volume 689, September 2024
Article Number A261
Number of page(s) 12
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/202449471
Published online 19 September 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Since the first half of the 20th century, plasma waves have become fundamental to the study and comprehension of the dynamics of space and astrophysical plasmas. Many of these physical environments, such as the solar wind, planetary magnetospheres, and outer heliosphere (Livadiotis 2017), as well as supernova remnants (Barnes & Scargle 1973; Kato 2007), are weakly collisional, meaning that the long-range forces due to the electromagnetic fields dominate over the short-range forces from particle-particle interactions (Landau et al. 1981). In this type of plasma, in which the effect of particle collisions may be neglected, wave-particle interactions play a major role in the regulation of the large-scale global behaviour of the system. Fluctuations in the electromagnetic fields extend over a broad range of spatial and temporal scales, with energy flowing from the larger magnetohydrodynamic (MHD) scales to the smaller kinetic scales in which the energy dissipates as the plasma is heated. Mechanisms from linear (or quasi-linear) kinetic theory, like plasma instabilities and Landau damping, can effectively exchange energy between the particles and the oscillating electromagnetic fields, shaping the velocity distribution of the plasma (Gary 1992; Livadiotis 2017; Verscharen et al. 2019; Roberts et al. 2022), and have therefore been proposed as candidates for the collisionless dissipation of the energy cascade, although non-linear effects like turbulent decay may also play an important role (Matthaeus et al. 2020). Thus, the study of plasma wave modes from kinetic theory and their dispersion properties acquire a fundamental role in our understanding of the small-scale physics of space plasmas.

One of the candidate wave modes that forms part of the turbulent spectrum at sub-proton scales is the kinetic Alfvén wave (KAW), as the power spectrum and characteristics of the electromagnetic fluctuations exhibit signature properties of this mode both in the solar wind (Salem et al. 2012) and terrestrial magnetosphere (Roberts et al. 2022), and can therefore be expected to do the same in other magnetised astrophysical plasma environments (Alfvén 1987). The KAW is the small-scale extension of the MHD shear-Alfvén when kinetic effects acquire relevance and the wave develops fluctuations in the electrostatic potential and the field-parallel component of the electric field. In low β plasmas (β < me/mp, where β = 8πnkBT/B2 in a one-temperature isotropic plasma and me, mp are the mass of electrons and protons, respectively), the KAW (often referred to as inertial Alfvén wave, in this particular case) appears when the perpendicular wavelength becomes of the order of the electron’s inertial length, and the wave is driven by inertial electron effects (Goertz & Boswell 1979; Lysak & Lotko 1996; Nandal et al. 2016; Barik et al. 2019c, 2020). In higher-β plasmas (β > me/mp), thermal effects dominate, and the wave appears when the perpendicular wavelength becomes comparable to the proton’s (or ion’s) Larmor radius (Hasegawa 1977; Hollweg 1999). The latter is the case that corresponds to the β regime that is considered for this article. A detailed discussion and even an illustrative cartoon regarding the difference between the inertial and kinetic limits of the Alfvén wave are provided by Chen & Boldyrev (2017), Barik et al. (2021), and Barik et al. (2023).

Kinetic Alfvén waves have been widely observed in a varied range of space plasma environments; spacecraft measurements have provided direct evidence of this mode propagating in Earth’s magnetopause (Chaston et al. 2005, 2007; Yao et al. 2011), plasma sheet (Wygant et al. 2002; Chaston et al. 2012; Stawarz et al. 2017; Zhang et al. 2022), magnetosheath (Trávníček & Chaston 2022), and inner magnetosphere (Chaston et al. 2014, 2015; Malaspina et al. 2015; Moya et al. 2015; Saikin et al. 2015; Tian et al. 2022), as well as in the solar wind (He et al. 2011; Perschke et al. 2013; Salem et al. 2012; He et al. 2015; Huang et al. 2020). Furthermore, evidence of these waves through the detection of particle energisation along magnetic field lines has been observed in the heliosphere (Wu & Yang 2006; Artemyev et al. 2016) as well as in Earth’s (Artemyev et al. 2015; Tian et al. 2022; Zhang et al. 2022) and Jupiter’s magnetospheres (Gershman et al. 2019; Sulaiman et al. 2020; Damiano et al. 2023). The large number of observations of KAWs in different astrophysical environments and their theoretical prediction in many others prove that they are ubiquitous in space plasma environments, making their study essential for understanding the underlying physics behind many of the phenomena observed in these kinds of systems, such as collisionless plasma heating (Gershman et al. 2017), electron energisation (Zhou et al. 2023), and magnetic reconnection (Boldyrev & Loureiro 2019).

One of the signature properties of KAWs is their right-handed polarisation; in the plane transverse to the background magnetic fields, the perturbed electromagnetic fields rotate in the sense of the electron’s Larmor gyration (Gary 1986). This makes this mode resonant with electrons, which leads to wave-particle interactions at sub-proton scales. As the propagation angle decreases, the transverse polarisation becomes linear and shifts to being left-handed as the wave transitions to the quasi-parallel electromagnetic ion-cyclotron (EMIC) wave. The EMIC mode is resonant with the Larmor gyration of positive ions and is of great relevance in the plasma dynamics of Earth’s magnetosphere (Usanova & Mann 2016; Usanova 2021). The transition angle between the KAW and EMIC modes has been shown to depend heavily on the wavenumber and plasma β (Gary 1986; Hollweg 1999; Hunana et al. 2013), as well as on the temperature anisotropy (Moya et al. 2021) and ion composition of the plasma (Moya et al. 2015, 2021, 2022; Villarroel-Sepúlveda et al. 2023). These studies, however, consider fixed temperature ratios between electrons and ions. The ion-to-electron temperature ratio, Ti/Te, varies considerably on average between different astrophysical environments, and it also may vary in time between a large range of values in a single system (Wilson et al. 2018). In Earth’s plasma sheet, the most frequently observed values are 3 ≤ Ti/Te ≤ 5 (Grigorenko et al. 2016); in Earth’s magnetotail, Ti/Te ∼ 3, while 5 ≤ Ti/Te ≤ 7 can be observed for low electron temperatures (Artemyev et al. 2011). Other measurements in the magnetosheath and plasma sheet have found that 6 ≤ Ti/Te ≤ 10 when the plasma is cool, and 2 ≤ Ti/Te ≤ 5 when the plasma is warm (Wang et al. 2012). In the solar wind near 1 au, most frequent observations show 0.28 ≤ Ti/Te ≤ 0.47 with an average of Ti/Te ∼ 0.61, with important variations during coronal mass ejections (Wilson et al. 2018; Mizuno et al. 2021). In the solar corona, Ti/Te ∼ 3.5 has been observed (Boldyrev et al. 2020). Observations in Balmer-dominated supernova remnants show 3 ≤ Ti/Te ≤ 10 (van Adelsberg et al. 2008), while in astrophysical shocks (Raymond et al. 2023) and low-luminosity accretion disks (Shapiro et al. 1976; Quataert & Narayan 1999; Mizuno et al. 2021) the ion temperature can surpass that of electrons by several orders of magnitude. Thermal and inertial effects are known to play important roles in the kinetic dispersion properties of plasma waves, and the temperature ratio between electrons and ions is thus expected to affect the transition from the EMIC mode to the KAW one.

The role of electron properties from a fully kinetic theory has been studied with a focus on fire-hose instability (Maneva et al. 2016; López et al. 2022). Howes (2009) studied the limitations of Hall MHD compared to Vlasov-Maxwell theory in weakly collisional plasmas by comparing the dispersion relations of whistler and Alfvén waves obtained from both theories. He found that discrepancies between the two theories depend on the wavenumber, propagation angle, Tp/Te, and βp. Previous studies on the effect of electron properties on the dispersion of KAWs have used fluid approximations (Jana et al. 2017) or taken the limit of near-perpendicular propagation in kinetic theory (Quataert 1998; Agarwal et al. 2011; Tong et al. 2015; Zhao 2015). In this study, we present an extensive investigation of the effect of the ion-to-electron temperature ratio on the dispersive properties of KAWs from a full kinetic theory. This will allow us to understand the effect of electron properties on the transition from EMIC to KAW in astrophysical plasmas and develop an insight into the kinetic scale effects of Tp/Te and how electron inertia becomes relevant for the propagation of these waves.

2. Linear theory for a weakly collisional plasma

The particles of each of the species comprising the plasma are described statistically by phase-space distribution functions, fs(r, v, t), where the sub-index, s, represents a particular species. These distribution functions satisfy Vlasov’s equation for a weakly collisional plasma,

∂ f s ∂ t + v · ∇ r f s + q s m s [ E + v c × B ] · ∇ v f s = 0 , $$ \begin{aligned} \frac{\partial f_{s}}{\partial t}+\boldsymbol{v}\cdot \nabla _{\boldsymbol{r}}f_{s}+\frac{q_s}{m_s}[\boldsymbol{E}+\frac{\boldsymbol{v}}{c}\times \boldsymbol{B}]\cdot \nabla _{\boldsymbol{v}}f_s&=0, \end{aligned} $$(1)

where ∇r is the usual spatial gradient and ∇v is the gradient in velocity space, and qs is the electric charge of the s-th species. The system is coupled with Maxwell’s equation through the charge and current densities:

ρ ( r , t ) = ∑ s q s ∫ f s ( r , v , t ) d 3 v , $$ \begin{aligned} \rho (\boldsymbol{r},t)&=\sum _{s}q_s\int f_s(\boldsymbol{r},\boldsymbol{v},t)d^3v, \end{aligned} $$(2)

j ( r , t ) = ∑ s q s ∫ v f s ( r , v , t ) d 3 v . $$ \begin{aligned} \boldsymbol{j}(\boldsymbol{r},t)&=\sum _{s}q_s\int \boldsymbol{v}f_{s}(\boldsymbol{r},\boldsymbol{v},t)d^3v. \end{aligned} $$(3)

We considered linearised quantities, such that the system is in equilibrium at the zeroth order and perturbations, preceded by the letter δ, vary rapidly in time:

f s ( r , v , t ) = f 0 s ( v ) + δ f s ( r , v , t ) , $$ \begin{aligned} f_{s}(\boldsymbol{r},\boldsymbol{v},t)&=f_{0s}(\boldsymbol{v})+\delta f_{s}(\boldsymbol{r},\boldsymbol{v},t),\end{aligned} $$(4)

E ( r , t ) = δ E ( r , t ) , $$ \begin{aligned} \boldsymbol{E}(\boldsymbol{r},t)&=\delta \boldsymbol{E}(\boldsymbol{r},t),\end{aligned} $$(5)

B ( r , t ) = B 0 + δ B ( r , t ) . $$ \begin{aligned} \boldsymbol{B}(\boldsymbol{r},t)&=\boldsymbol{B}_0 + \delta \boldsymbol{B}(\boldsymbol{r},t). \end{aligned} $$(6)

The stable equilibrium solution of Vlasov’s equation is given by a Maxwellian velocity distribution function,

f s ( v ‖ , v ⊥ ) = n s π 3 / 2 α s 3 exp ( − v 2 α s 2 ) , $$ \begin{aligned} f_{s}(v_\parallel ,v_\perp )=\frac{n_{s}}{\pi ^{3/2}\alpha _{s}^3 }\exp \left(-\frac{v^2}{\alpha _{s}^2}\right), \end{aligned} $$(7)

for each particle species, where v2 = v⊥2 + v∥2, with v∥, ⊥ indicating the kinetic field-aligned and transverse velocity of the particles, respectively. The thermal speed of each species is given by 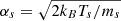α s = 2 k B T s / m s $ \alpha_{s}=\sqrt{2k_BT_{s}/m_s} $, where ms and Ts are the mass and temperature of the corresponding species, while ns is the particle density. We are interested in studying the oblique propagation of electromagnetic waves. We therefore set the propagation direction, without loss of generality, as 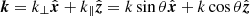k = k ⊥ x ̂ + k ‖ z ̂ = k sin θ x ̂ + k cos θ z ̂ $ \boldsymbol{k}=k_\perp\hat{\boldsymbol{x}}+k_\parallel\hat{\boldsymbol{z}} = k\sin\theta\hat{\boldsymbol{x}}+k\cos\theta\hat{\boldsymbol{z}} $, where the propagation or wave-normal angle, θ, is the angle between the wave-vector and the background magnetic field, B 0 = B 0 z ̂ $ \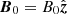boldsymbol{B}_0=B_0\hat{\boldsymbol{z}} $.

Following Landau’s approach (Landau 1965), we used Laplace transforms for time and Fourier transforms for the spatial co-ordinates of the linearised quantities, and by treating (1) in reciprocal space, we obtained, at the first order, the dispersion relation

D k · δ E k = 0 , $$ \begin{aligned} \boldsymbol{D}_k\cdot \delta \boldsymbol{E}_k=0, \end{aligned} $$(8)

where

D k = ( D xx i D xy D xz − i D xy D yy i D yz D xz − i D yz D zz ) $$ \begin{aligned} \boldsymbol{D}_k&=\begin{pmatrix} D_{xx}&iD_{x{ y}}&D_{xz}\\ -iD_{x{ y}}&D_{{ yy}}&iD_{{ y}z}\\ D_{xz}&-iD_{{ y}z}&D_{zz} \end{pmatrix} \end{aligned} $$(9)

is the full dispersion tensor for oblique waves (see (Villarroel-Sepúlveda et al. 2023) for further detail), and the eigenvectors, δEk, represent the electric field perturbations. The Laplace transform on the time co-ordinate implies that the solutions will be damped oscillations, and we refer to the real part of the complex frequency as ω and the imaginary part as γ. With the information on the dispersion tensor, we can compute the polarisation of the transverse component of the waves taken with respect to the background magnetic field, defined by Stix (1992), using

i δ E kx δ E ky = D xy D zz − D xz D yz D xx D zz − D xz 2 sign ( ω ) . $$ \begin{aligned} i\frac{\delta E_{kx}}{\delta E_{k{ y}}}=\frac{D_{x{ y}}D_{zz}-D_{xz}D_{{ y}z}}{D_{xx}D_{zz}-D_{xz}^2}\mathrm{sign}(\omega ). \end{aligned} $$(10)

By convention, a right(left)-handed polarisation is defined by a time-wise rotation of the fields according to the right(left)-hand rule around the magnetic field, B0, such that field-perpendicular electric fields in a right-hand polarised wave gyrate in the sense of the Larmor motion of electrons, while in a left-hand polarised wave the fields rotate in the sense of the Larmor gyration of positive ions.

The MHD Alfvén wave is linearly polarised, with its electric perturbations appearing only in the 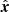x ̂ $ \hat{\boldsymbol{x}} $ direction, such that the transverse electric polarisation (Eq. (10)) is infinite in k → 0, and becomes finite as Ey becomes different than 0 when kinetic effects become relevant, indicating that the wave becomes elliptically polarised. In general, the complex nature of the fields implies that they possess both linear and elliptical polarisation, with Re[iδEkx/δEky] being a measure of the mode’s elliptical polarisation and Im[iδEkx/δEky] representing the linear polarisation of the wave. We are particularly interested in the elliptical polarisation of the waves, so the quantity to be analysed will be the real part of Eq. (10). We note, however, that the polarisation is completely linear whenever Re[iδEkx/δEky] = 0 or Re[iδEkx/δEky]= ± ∞. Circular polarisation occurs when Re[iδEkx/δEky]= ± 1, where right-handed polarisation is obtained when the right-hand-side of the equation equals +1, and left-handed polarisation occurs for −1.

Other polarisation ratios can be obtained from (8), such as

i δ E kz δ E ky = D xx D yz − D xz D xy D xx D zz − D xz 2 sign ( ω ) . $$ \begin{aligned} i\frac{\delta E_{kz}}{\delta E_{k{ y}}}&=\frac{D_{xx}D_{{ y}z}-D_{xz}D_{x{ y}}}{D_{xx}D_{zz}-D_{xz}^2}\mathrm{sign}(\omega ). \end{aligned} $$(11)

Replacing both (10) and (11) in Faraday’s law allows us to evaluate

i δ B z δ B y = i k ⊥ E ky k ‖ E kx − k ⊥ E kz = D xz 2 − D xx D zz cot θ ( D xy D zz − D xz D yz ) + ( D xz D xy − D xx D yz ) sign ( ω k ) , $$ \begin{aligned} i\frac{\delta B_z}{\delta B_{ y}}&=\frac{ik_\perp E_{k{ y}}}{k_{\parallel }E_{kx} -k_{\perp }E_{kz} }\nonumber \\&=\frac{D_{xz}^2-D_{xx}D_{zz}}{\cot \theta (D_{x{ y}}D_{zz}-D_{xz}D_{{ y}z})+(D_{xz}D_{x{ y}}-D_{xx}D_{{ y}z})}\mathrm{sign}\left(\frac{\omega }{k}\right), \end{aligned} $$(12)

whose characteristic behaviour for the KAW has been thoroughly analysed in two-fluid theory by Hollweg (1999). He obtained the first- and second-order finite Larmor radius corrections to this quantity, which is zero in MHD:

i δ B z δ B y ≈ − i k ⊥ v s 2 v Ap Ω p sign ( ω k z ) , $$ \begin{aligned} i\frac{\delta B_z}{\delta B_{ y}}&\approx -i\frac{k_{\perp }v_s^2}{v_{\rm Ap}\Omega _{\rm p}}\mathrm{sign}\left(\frac{\omega }{k_z}\right), \end{aligned} $$(13a)

i δ B z δ B y ≈ − i k ⊥ v s 2 v Ap Ω p ( 1 + k ⊥ 2 v sp 2 Ω p 2 ) sign ( ω k z ) , $$ \begin{aligned} i\frac{\delta B_z}{\delta B_{ y}}&\approx -i\frac{k_{\perp }v_s^2}{v_{\rm Ap}\Omega _{\rm p}\left(1+\frac{k_\perp ^2v_{sp}^2}{\Omega _{\rm p}^2}\right)}\mathrm{sign}\left(\frac{\omega }{k_z}\right), \end{aligned} $$(13b)

Here, vs = [kB(γpTp + γeTe)/mp]1/2 is the plasma sound speed, where kB is Boltzmann’s constant, γj is the heat capacity ratio of species j, mj is its mass and Tj is its temperature. The proton Alfvén speed is given by 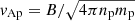v Ap = B / 4 π n p m p $ v_{\mathrm{Ap}}=B/\sqrt{4\pi n_{\mathrm{p}} m_{\mathrm{p}}} $, where np is the proton density and B is the magnitude of the background magnetic field. The gyrofrequency associated with this species is 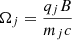Ω j = q j B m j c $ \Omega_j=\frac{q_jB}{m_j c} $, with qj its charge, and c is the speed of light in vacuum. The proton sound speed is then defined as vsp = (kBγpTp/mp)1/2.

The dispersion relation of the KAW can be obtained directly by assuming k⊥ ≫ k∥, me/mp ≪ β ≪ 1, and |ω|≫|γ| (see Lakhina 1990, 2008; Barik et al. 2019a, 2019b, for example). Since we are interested in studying the transition of left-hand polarised Alfvén waves to their right-hand polarised counterparts, which depends on both the propagation angle and the plasma temperature, and because the waves can become strongly damped for smaller angles, we must relax the aforementioned approximations and solve the full dispersion relation of oblique Alfvénic waves using the DIS-K solver1 (López et al. 2021; López 2023) in the limit of isotropic Maxwellian distributions given by Eq. (7). We checked our results by comparing them with the NHDS code2 (Verscharen & Chandran 2018). Because no approximations have been made regarding the frequency of the waves, these solutions are valid even in the strong-damping wavenumber domain (|γ(k)| ≥ |ω(k)|, where γ and ω represent the imaginary and real parts of the complex frequency, respectively).

In the Alfvén mode, we refer to the continuous extension of the MHD Alfvén wave to the large-wavenumber domain, which we identified and differentiated from other solutions that possess right-handed polarisation at near-perpendicular angles by analysing the phase velocity of the waves in the MHD limit (see Appendix B). It is worth noting that this extension may differ considerably from the cold plasma solutions because of the effects of finite temperature, especially for propagation angles that depart from near-parallel or near-perpendicular propagation. In this context, it is not unusual for the real frequency of the continuous kinetic extended MHD Alfvén wave to surpass the proton gyrofrequency at relatively large wavenumbers; this has then been referred to as the Alfvén-whistler solution in two-fluid theory (Sahraoui et al. 2012), although a similar effect can happen due to mixing between wave modes in kinetic theory (Krauss-Varban et al. 1994). This phenomenon is very complex and highly dependent on the temperature of each of the plasma species (Isenberg 1984) and, although interesting by itself, its in-depth analysis and discussion lie beyond the scope of this article.

For a fixed value of the β parameter, we obtained the real and imaginary parts of the wave’s frequency normalised to the protons’ cyclotron frequency, Ωp, as well as their polarisation, all as a function of the wavenumber normalised to the inverse of the proton inertial length, ωpp/c, with ωpp the protons’ plasma frequency, and c the speed of light in vacuum.

3. Results

Figure 1 displays the real and imaginary frequency of the Alfvén mode, as well as its transverse electrical polarisation, for βp = 0.1 and βp = 1.0, as functions of the normalised wavenumber, with the different colours indicating different electron-to-proton temperature ratios. The solutions are plotted in different styles depending on the sign of |ω|−|γ| to make a distinction between weakly and strongly damped solutions, as strongly damped solutions will not effectively propagate, and thus cannot represent realistic electromagnetic waves.

thumbnail Fig. 1.

Real (ω) and imaginary (γ) frequency of the Alfvén wave and its transverse polarisation for different electron-to-proton temperature ratios, with βp = 0.1 (top) and βp = 1.0 (bottom). The dispersion relation is plotted with continuous lines for |γ|< |ω| and in dotted lines for |γ|> |ω|, indicating that the mode is strongly damped. Dash-dotted lines indicate k⊥ρ = 1 for the different configurations, and the segmented line in the real frequency panels corresponds to the MHD dispersion relation of the Alfvén wave.

For all of the cases considered, as the propagation angle approaches perpendicular propagation, the waves acquire the typical characteristics of the KAW, with their polarisation becoming elliptically right-handed and their real frequency lying above MHD prediction. As can be seen in the figure, this transition appears at different propagation angles in the different plasmas that are being considered. Both βp and the electron-to-proton temperature ratio, Te/Tp, play an important role in this matter, as raising any of these quantities will effectively lower the transition angle, allowing right-hand polarised Alfvén waves to propagate at angles that depart from the near-perpendicular limit. Vertical lines indicate k⊥ρL = 1.0 for the different curves, where ρL = vS/Ωp is referred to as the ion-acoustic Larmor radius (Choi et al. 2023). This Larmor radius, which depends on both the electron and ion temperatures, can also be expressed as 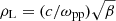ρ L = ( c / ω pp ) β $ \rho_{\mathrm{L}}=({c}/{\omega_{\mathrm{pp}}})\sqrt{\beta} $, with β = (βe + βp)/2(1 + me/mp) being the ion-acoustic β defined in Choi et al. (2023), with βj = 2vsj2/vA2 for the j-th species. This quantity is often utilised in two-fluid theory in the me/mp → 0 limit and with γi = γe = 1. This choice of heat capacity ratios is characteristic of an isothermic process and provides the correct dispersion relation for the magnetosonic waves in this plasma setting (see Appendix B of Villarroel-Sepúlveda et al. 2023), as well as the low-wavenumber limit of the magnetic polarisation (see Figure 2), and allows us to use the usual definition of βj = 8πkBTj/B2 from kinetic theory.

thumbnail Fig. 2.

Magnitude of the real part of the magnetic ratio iBz/By for different values of Te/Tp. Continuous lines are the results obtained from kinetic theory and indicate the rough predictions from the two-fluid theory given in Eq. (13a).

Figure 2 depicts in continuous colored lines the absolute value of the aforementioned magnetic polarisation for different propagation angles, electron-to-proton temperature ratios, and βp. Dashed lines indicate the first-order two-fluid approximation of this quantity, given in Eq. (13a) with γe = γp = 1. This expression provides an approximation for the behaviour of this quantity in the quasi-perpendicular limit, although it deviates from the kinetic solutions at approximately the same wavenumbers as the first-order approximation and has therefore been omitted in the figure in favor of readability. As was expected, for a fixed value of βp, the wavenumber range in which this quantity and the prediction from fluid theory coincide becomes larger as the propagation angle approaches perpendicular propagation. This agreement in the small-wavenumber domain between the kinetic theory results and two-fluid theory predictions for the KAW is an indication that the displayed solution can be associated with the KAW most described in the literature. It is noteworthy that the agreement is not restricted to near-perpendicular propagation, as for Te > Tp, the fluid prediction can be a good approximation even at θ = 75° for βp = 0.25. In general, if βp is sufficiently small, an increase in both Te/Tp and βp will allow the kinetic solution to coincide with the two-fluid KAW at a wider range of propagation angles. For large β, the fluid predictions exhibit completely different slopes from those of the results from kinetic theory, and thus cannot approximate the kinetic solutions even at near-perpendicular propagation.

Figure 3 depicts the real and imaginary frequency, transverse electrical polarisation (Eq. (10)), and magnetic polarisation (Eq. (12)) for different values of Te/Tp and fixed values of βe + βp. As can be seen, deviations between the solutions considering different Te/Tp for a fixed total, β, appear to be small, even for k⊥ρ ≥ 1. Although there are considerable differences in the transverse electrical polarisation, the behaviour of these quantities remains qualitatively the same; the polarisation goes from linear at small wavenumbers to elliptical for larger wavenumbers, which can be seen in that Re[iEx/Ey] decreases monotonically as k increases, and plateaus for k⊥ρ ≥ 1.

thumbnail Fig. 3.

Real and imaginary frequency, transverse electrical polarisation, and magnetic polarisation of the Alfvén wave. The summed β of the plasma, β = βe + βp, was fixed at 0.12, 0.60, 1.20, and for each value of β different electron-to-proton temperature ratios were considered. Dash-dotted lines indicate k⊥ρL = 1 for the different values of βe + βp. The segmented line in the real frequency panels corresponds to the MHD dispersion relation of the Alfvén wave. In the two middle panels it indicates the line corresponding to zero, and in the bottom panel it represents the improved two-fluid approximation of this quantity given in Eq. (13b).

Figure 4 shows the relative amplitude of the electric field components as functions of the wavenumber for different values of Te/Tp, with βp = 0.1 and βp = 1.0. The linearised electric field appears to be sustained mostly by the field in the x direction, which lies in the wave’s propagation plane but is perpendicular to the background magnetic field. As the mode becomes dispersive, the field in the direction of the background magnetic field becomes excited at the expense of the perpendicular electric field. The way in which this occurs depends on β. For a smaller β (βp = 0.1, in our case), the field in the x direction decreases as its z component increases until |Ex2|/|E2| reaches a local minimum and |Ez2|/|E2| a local maximum. Both quantities then plateau at large wavenumbers, with |Ez2|/|E2| reaching a constant value different from 0. The similarly perpendicular electric field in the y direction is much smaller in magnitude but exhibits the same rise and decay as the one in the parallel direction. When Te > Tp, the field’s z component may even become the dominant electric component for a considerable range of wavenumbers, although this does not take place in the near-perpendicular propagation limit. For a larger β, the asymptotic values of the amplitude ratios at large wavenumbers depend largely on the propagation angle and can differ significantly between the solutions with different Te/Tp, which is not seen in the small β case. Nevertheless, the core of the previous statement remains valid; the Ex electric component recedes at larger wavenumbers as Ez becomes large, although now |Ey2|/|E2| can also achieve significant values that can be larger than those of the other amplitude ratios. It is also worth noting that for the solution considering βp = 0.1 propagating at θ = 60°, there are wavenumbers at which |Ey2|/|E2| = 0. Since this is a complex modulus, the equality implies that both the real and imaginary parts of this field component must become zero. These wavenumbers coincide with local critical points in the corresponding transverse electrical polarisations depicted in Figure 1. Since these local maxima and minima are finite, this implies that one of the components of Ex must also become null. These zeroes in Ey roughly coincide with the local maximum in Ez and minimum in Ex, while for near-perpendicular propagation the minimum in |Ex2|/|E2| coincides with maxima in the amplitude ratios |Ez2|/|E2| and |Ey2|/|E2|. It is also worth mentioning that the nature of the excitation in the parallel electric field is different for different propagation angles and electron-to-proton temperature ratios. As Te/Tp becomes larger, the relative amplitudes of the Ez and Ey fields also become significantly larger. For larger wavenumbers, all cases approach the same constant value, implying that the rise in the amplitude of the parallel electric field is likely a consequence of the inclusion of highly thermal electrons. The maxima in the parallel electric field appear to be displaced to larger wavenumbers as the wave approaches perpendicular propagation. Although for these propagation angles the Ez field does not become larger in magnitude than Ex, this drift towards small scales of the maxima of the relative amplitude of Ez ensures that the parallel electric field can acquire relatively high values at sub-proton scales, where wave-particle interactions are highly relevant.

thumbnail Fig. 4.

Amplitude of the perturbed electric field ratios for different values of Te/Tp and different propagation angles. Results are displayed for βp = 0.1 and βp = 1.0. Vertical dashed lines correspond to k⊥ρL = 1.0 for the corresponding electron-to-proton temperature ratio indicated by the color code.

Figure 5 displays the wave’s parallel electric perturbations, its transverse electrical polarisation, and magnetic polarisation for different βp values as functions of the electron-to-proton temperature ratio for two fixed values of the wavenumber. The parallel perturbed electric field appears to be monotonically increasing with Te/Tp until it plateaus at a constant value, which is larger the smaller βp is. This plateau is also highly dependent on the propagation angle. For smaller propagation angles, the transverse electrical polarisation is susceptible to changes in sign. At ck/ωpp = 1.0 with βp = 0.1 and βp = 0.5, an increase in Te/Tp, which increases the total β, changes this polarisation from left-handed to right-handed, as has been predicted by previous studies (Gary 1986). In the latter case, however, since |Ex| does not become zero in magnitude for any of the studied cases, the behaviour suggests that at two points, Ex/Ey and Bz/By become purely real, indicating that the fields become linearly polarised but not zero.

thumbnail Fig. 5.

Amplitude of the squared parallel electric field ratio, Ez/|E|, real part of the transverse electric polarisation, iEx/Ey, and magnitude of the real part of the magnetic polarisation, iBz/By, for different values of βp and propagation angles. The results are displayed as functions of the electron-to-proton temperature ratio contained in βe/βp for kρp = 0.5 and kρp = 1.0.

Figure 6 displays the mode’s polarisation in heat maps as functions of the wavenumber, for fixed values of βp, and of Te/Tp, for fixed values of the wavenumber. The contours of Re[iEx/Ey] = 0 are plotted in white, while the contours of characteristic values of the damping rate are overplotted in black. The usual behaviour of the transition from left-handed to right-handed polarisation of the Alfvénic waves in an electron-proton plasma, as was seen in the early groundbreaking work by Gary (1986) and a recent study by Villarroel-Sepúlveda et al. (2023), can be seen here for βp = 0.1. For this value of βp, an increase in βe has the same effect as increasing β for Te = Tp. For higher values of βp, the results exhibit a different behaviour; at small wavenumbers, a rise in Te/Tp tends to bring the transition curve to smaller wave-normal angles, while for larger wavenumbers, the transition occurs at larger propagation angles. This can be seen both in panels depicting the transverse electric polarisation as a function of the wavenumber and in panels depicting the transverse electric polarisation as a function of the ratio βe/βp. It is also noteworthy that increasing the ratio Te/Tp tends to reduce the mode’s damping rate in scales normalised to the ion-acoustic Larmor radius, ρL, which depends on this ratio. When normalised to a value independent of Te, however, an increase in the electron-to-proton temperature ratio will in most cases increase the wave’s damping rates, as can be seen in Figures 1 and 3.

thumbnail Fig. 6.

Heat maps displaying the transverse electric polarisation for a wide range of propagation angles and different combinations of βp and βe/βp as a function of the wavenumber in units of ρ L − 1 $ \rho_{\mathrm{L}}^{-1} $ and for different combinations of βp and kρp as functions of βe/βp. The white lines indicate the contour of Re[iEx/Ey] = 0 and black lines represent contours of characteristic values of −γ/Ωp, where γ is the imaginary part of the wave frequency.

Figure 7 depicts the contours of Re[iEx/Ey] = 0 with respect to the wavenumber and wave-normal angle for different combinations of βp and Te/Tp in the top row, and with respect to βe/βp and the wave-normal angle for different combinations of ck/ωpp and βp in the bottom row. For both βp = 0.01 and βp = 0.10, there is a segment of the transition curve for relatively large angles that is independent of the wavenumber until kρL ∼ 1, when kinetic effects dominate, and the transition curve becomes heavily dependent on the wavenumber in some complicated ways. This is not true for larger values of βp, as can be deduced from Figure 6, where the transition may depend on the wavenumber even in the large-scale domain of the waves. For larger values of Te/Tp and βp = 0.10, the transition tilts towards larger propagation angles. The same behaviour can be appreciated for βp = 0.01, although in this case the curve is disjointed, implying that there are certain wavenumbers around 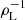ρ L − 1 $ \rho_{\mathrm{L}}^{-1} $ for which Re[iEx/Ey] > 0 and the transverse electric fields rotate in a right-handed sense, at least for all wave-normal angles depicted in this Figure. We also observe that for kρL ≥ 1 and larger wave-normal angles, the polarisation of the waves may shift from right-handed to left-handed, as can also be seen in Figure 1. In the bottom panel, we see that an increase in βp reduces the propagation angle at which Alfvénic waves change from being left-hand to right-hand polarised for βp ≥ βe. When βe > βp, the behaviour tends to change, especially for larger values of βp.

thumbnail Fig. 7.

Contours of Re[iEx/Ey] = 0 for different electron-to-proton temperature ratios and βp as functions of the propagation angle and kρL in the top two panels, and for different combinations of the βp and kρp as functions of the propagation angle and the ratio βe/βp in the bottom two panels.

4. Discussion

In this work, we present an extensive study on the effect of the thermal properties of electrons on the propagation of Alfvénic waves in warm, magnetised plasmas. Considering typical values of the electron-to-proton temperature ratio in space plasmas, such as Earth’s magnetosphere and the solar wind, we show that the electron temperature can considerably modify the dispersive properties of KAW and EMIC waves, especially in the sub-protonic domain.

The results in Figures 1 and 3 show that an increase in the electron-to-proton temperature ratio for fixed values of βp results in an increased wave damping with respect to the wave number. This is to be expected, as electron heating dominates the KAW’s power dissipation (Quataert 1998; Podesta 2012; Tong et al. 2015; Zhao et al. 2022). The results also show that, for a fixed proton temperature, an increase in the electron temperature raises the frequency of the waves as the mode becomes dispersive, which is consistent with previous results (Agarwal et al. 2011). Comparing our results for the magnetic polarisation, iBz/By, to predictions from two-fluid theory in Figure 2, we show that an increase in the electron-to-proton temperature ratio allows the wave to acquire signature characteristics of the KAW at propagation angles significantly lower than θ ∼ π/2. For higher βp values, the results do not adjust well with the two-fluid theory predictions, although the difference between the three cases seems to be dependent on the combined β. For the fluid prediction to adjust our results in the large β case requires that the heat capacity ratios, γe, γp, of electrons and protons, respectively, both be less than unity, which cannot represent any thermodynamic process in either a plasma or ideal gas. Thus, the discrepancy is assumed to be a consequence of the limitations of fluid theories in the description of a high-temperature plasma. This is consistent with results by Krauss-Varban et al. (1994), which indicate that results from kinetic theory deviate from their fluid theory equivalents for β ≳ 0.5. As is seen in the different panels of Figure 1, the electron temperature plays an important role in the mode’s transition from the large scales for which solutions can be approximated by fluid theories to the small scales that require a fully kinetic description. The mode becomes dispersive and wave damping appears at different wavenumbers for different electron-to-proton temperature ratios. In general, a larger electron temperature will cause the real frequency to depart from the MHD solution at smaller wavenumbers, and the same is true for the apparition of kinetic damping. It is often mentioned in the literature that for the KAW, these effects arise when the perpendicular wavenumber becomes comparable to the inverse proton gyroradius or, equivalently, k⊥ρp ∼ 1. This criterion, however, completely excludes the thermal effects of electrons. Our results show that an increase in the electron temperature yields a similar outcome to that of raising β in a plasma in which Tp = Te. Thus, we conclude that βe contributes to a total β = (βe + βp)/2, where for the s-th plasma species we have used βs = 8πnskBTs/B2. A consequence of this is that a large value of Te/Tp allows the Alfvén mode to acquire signature characteristics of the KAW at smaller propagation angles than for Te/Tp ≤ 1. The use of the ion-acoustic Larmor radius, ρL, instead of ρp provides an electron-temperature-sensible characteristic scale for the lower limit of the kinetic domain, which appears to be in good agreement with the departure of the kinetic solution from its MHD counterpart for the different temperature ratios considered, especially as the propagation angle becomes near-perpendicular and the mode can be identified as the KAW. This is further supported by the results displayed in Figure 3. Here, the ion-acoustic β is held fixed, while the electron-to-proton temperature ratio varies. The results show only small differences in the real and imaginary frequencies, contrasting with those of Figure 1. Also, as was expected, the two-fluid prediction for the magnetic polarisation does not provide a faithful approximation of the kinetic solution for large β values, as is seen in the case in which βe + βp = 1.20. Interestingly, however, this does not hold true for the case with Te/Tp = 5, for which the two-fluid solution provides a good approximation at small wavenumbers. This is somewhat in contrast with Yang et al. (2014), which shows that fluid theory solutions agree better with kinetic theory results for Tp ≫ Te, although this study focuses on small β values. Figure 4 provides a useful insight into how the Aflvénic mode transitions from linear polarisation in MHD scales to elliptical polarisation in the kinetic domain. As was expected from classical MHD, the mode’s electric perturbations are sustained mostly by those in the wave’s propagation direction in the perpendicular plane with respect to the background magnetic field (Ex, in this case). As the wave becomes dispersive, the mode acquires significant electric perturbations along the background field (Ez) and small but non-null perturbations orthogonal to the wave vector (Ey). This makes the polarisation elliptical, although the reason for the fields’ rotations changing from left-hand to right-handed as the propagation angle increases is yet unclear. With the larger β values, the Ey field becomes larger, even becoming the largest component of the electric perturbations for some of the studied configurations. This makes the Ex field decrease in magnitude, and thus makes the transverse electric polarisation of the waves become almost linear for large wavenumbers and even change its sign from right-hand to left-handed, as can be seen for large Te/Tp in Figure 1. It is also worth noting that the parallel electric perturbations arise even for smaller propagation angles than those that can be considered as propitious for KAW propagation, but for relatively small β values, only near perpendicular propagation does the magnitude of this electric component have maxima at sub-protonic scales.

Figure 5 displays relevant quantities in the study of the KAW as functions of the electron-to-proton temperature ratios. These results imply that high Te/Tp tends to increase the value of the field-aligned electric perturbations. We also note that varying Te/Tp at lower wave-normal angles may reverse the sign of the transverse electric polarisation. It is noteworthy, however, that the nature of the changes in the rotation sense of the transverse electric fields is different for βp = 0.1 and βp = 0.5. In the former case, the behaviour in the polarisation suggests that the Ey component becomes zero, something that is supported by the fact that iBz/By, which has Ey in its numerator through Faraday’s law, becomes zero at the same electron-to-proton temperature ratio.

Figure 6 displays the transverse electric polarisation as heat maps, with contours of Re[iEx/Ey] = 0 in white, indicating the transition from left-hand to right-hand polarised Alfvén waves and damping rate contours in black. As was expected, for small β values, an increase in Te/Tp has the same effect as increasing β in an isothermic plasma, as is reported in Villarroel-Sepúlveda et al. (2023). For larger β values, the result tends to be counter-intuitive; for smaller wavenumbers, augmenting Te/Tp lowers the transition curve, while for larger wavenumbers, this curve drifts towards larger propagation angles. This is corroborated by the results for fixed wavenumbers as functions of βe/βp. It is also interesting to note that, although under the proton intertial length normalisation of the wavenumber, an increase in Te/Tp results in stronger Landau damping (Figures 1, 3), when normalised to ρL, the opposite holds.

Figure 7 exhibits different Re[iEx/Ey] = 0 contours for different plasma configurations, for fixed βp with respect to the propagation angle and wavenumber and for fixed wavenumber with respect to the propagation angle and electron-to-proton temperature ratio. The results show that normalizing to ρL allows us to identify a region where the transition from left-hand to right-hand polarised Alfvén waves is independent of the wavenumber. For small values of β, there are two disjointed regions where left-handed polarisation is allowed, which implies that there are particular wavenumbers near 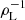ρ L − 1 $ \rho_{\mathrm{L}}^{-1} $ for which the waves acquire right-handed polarisation for a wide range of propagation angles. From the bottom panels of this figure, we observe that an increase in Te/Tp has a similar effect to raising the total β only until Te ∼ Tp for high values of βp. Kinetic effects related to electrons are likely the reason why this does not hold for Te > Tp in cases where β ≳ 0.5.

In summary, we have shown that the thermal properties of electrons have strong and non-trivial effects on the dispersive properties of Alfvénic waves in the kinetic domain. We propose that electrons contribute to a total β as in two-fluid theories, which sets the gateway of the kinetic domain through an ion-acoustic Larmor radius, ρL. Fixing the total β results in very similar dispersion relations with different electron-to-proton temperature ratios, while only fixing βp results in very different ones. The results from kinetic theory deviate from the fluid picture at large β values, which is consistent with previous results.

1

The full code is publicly available and can be found at https://github.com/ralopezh/dis-k.

2

Also publicly available at https://github.com/danielver02/NHDS.

Acknowledgments

N.V.S. thanks the support of ANID, Chile, through National Doctoral Scholarship N°21220616. P.S.M is supported by Fondecyt Grant 1240281, and by the Research Vice-Rectory of the University of Chile (VID) through Grant ENL08/23. R.A.L is supported by Fondecyt Initiation Grant 11201048. D.V. is supported by STFC Consolidated Grant ST/W001004/1.

References

  1. Agarwal, P., Varma, P., & Tiwari, M. M. S. 2011, Indian J. Pure Appl. Phys., 49, 91 [Google Scholar]
  2. Alfvén, H. 1987, Phys. Scr., T18, 20 [CrossRef] [Google Scholar]
  3. Artemyev, A. V., Baumjohann, W., Petrukovich, A. A., et al. 2011, Ann. Geophys., 29, 2253 [Google Scholar]
  4. Artemyev, A. V., Rankin, R., & Blanco, M. 2015, J. Geophys. Res.: Space Phys., 120, 305 [Google Scholar]
  5. Artemyev, A. V., Zimovets, I. V., & Rankin, R. 2016, A&A, 589, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Barik, K. C., Singh, S., & Lakhina, G. 2019a, URSI Radio Science Bulletin, 2019, 17 [Google Scholar]
  7. Barik, K. C., Singh, S. V., & Lakhina, G. S. 2019b, Phys. Plasmas, 26, 022901 [NASA ADS] [CrossRef] [Google Scholar]
  8. Barik, K. C., Singh, S. V., & Lakhina, G. S. 2019c, Phys. Plasmas, 26, 112108 [NASA ADS] [CrossRef] [Google Scholar]
  9. Barik, K. C., Singh, S. V., & Lakhina, G. S. 2020, ApJ, 897, 172 [NASA ADS] [CrossRef] [Google Scholar]
  10. Barik, K. C., Singh, S. V., & Lakhina, G. S. 2021, ApJ, 919, 71 [NASA ADS] [CrossRef] [Google Scholar]
  11. Barik, K. C., Singh, S. V., & Lakhina, G. S. 2023, ApJ, 951, 53 [NASA ADS] [CrossRef] [Google Scholar]
  12. Barnes, A., & Scargle, J. D. 1973, ApJ, 184, 251 [NASA ADS] [CrossRef] [Google Scholar]
  13. Boldyrev, S., Forest, C., & Egedal, J. 2020, Proc. Natl. Acad. Sci., 117, 9232 [Google Scholar]
  14. Boldyrev, S., & Loureiro, N. 2019, Phys. Rev. Res., 1, 012006 [NASA ADS] [CrossRef] [Google Scholar]
  15. Chaston, C. C., Phan, T. D., Bonnell, J. W., et al. 2005, Phys. Rev. Lett., 95, 065002 [NASA ADS] [CrossRef] [Google Scholar]
  16. Chaston, C. C., Wilber, M., Mozer, F. S., et al. 2007, Phys. Rev. Lett., 99, 175004 [NASA ADS] [CrossRef] [Google Scholar]
  17. Chaston, C. C., Bonnell, J. W., Clausen, L., & Angelopoulos, V. 2012, J. Geophys. Res.: Space Phys., 117 [Google Scholar]
  18. Chaston, C. C., Bonnell, J. W., Wygant, J. R., et al. 2014, Geophys. Res. Lett., 41, 209 [NASA ADS] [CrossRef] [Google Scholar]
  19. Chaston, C. C., Bonnell, J. W., Wygant, J. R., et al. 2015, Geophys. Res. Lett., 42, 531 [NASA ADS] [Google Scholar]
  20. Chen, C. H., & Boldyrev, S. 2017, ApJ, 842, 122 [NASA ADS] [CrossRef] [Google Scholar]
  21. Choi, C. R., Woo, M.-H., Ryu, K., Lee, D.-Y., & Yoon, P. H. 2023, Phys. Plasmas, 30, 092901 [CrossRef] [Google Scholar]
  22. Damiano, P. A., Delamere, P. A., Kim, E., Johnson, J. R., & Ng, C. S. 2023, Geophys. Res. Lett., 50 [CrossRef] [Google Scholar]
  23. Gary, S. P. 1986, J. Plasma Phys., 35, 431 [NASA ADS] [CrossRef] [Google Scholar]
  24. Gary, S. P. 1992, Eos, Transactions American Geophysical Union, 73, 529 [NASA ADS] [CrossRef] [Google Scholar]
  25. Gershman, D. J., Viñas, A. F., Dorelli, J. C., et al. 2017, Nat. Commun., 8, 7813 [NASA ADS] [CrossRef] [Google Scholar]
  26. Gershman, D. J., Connerney, J. E., Kotsiaros, S., et al. 2019, Geophys. Res. Lett., 46, 7157 [Google Scholar]
  27. Goertz, C. K., & Boswell, R. W. 1979, J. Geophys. Res., 84, 7239 [NASA ADS] [CrossRef] [Google Scholar]
  28. Grigorenko, E. E., Kronberg, E. A., Daly, P. W., et al. 2016, J. Geophys. Res.: Space Phys., 121, 9985 [NASA ADS] [CrossRef] [Google Scholar]
  29. Hasegawa, A. 1977, Indian Acad. Sci. Proc. Sect., 86A, 151 [NASA ADS] [CrossRef] [Google Scholar]
  30. He, J., Tu, C., Marsch, E., & Yao, S. 2011, ApJ, 745, 85 [NASA ADS] [CrossRef] [Google Scholar]
  31. He, J., Wang, L., Tu, C., Marsch, E., & Zong, Q. 2015, ApJ, 800, L31 [Google Scholar]
  32. Hollweg, J. V. 1999, J. Geophys. Res.: Space Phys., 104, 14811P [NASA ADS] [CrossRef] [Google Scholar]
  33. Howes, G. G. 2009, Nonlin. Proc. Geophys., 16, 219 [CrossRef] [Google Scholar]
  34. Huang, S. Y., Zhang, J., Sahraoui, F., et al. 2020, ApJ, 897, L3 [NASA ADS] [CrossRef] [Google Scholar]
  35. Hunana, P., Goldstein, M. L., Passot, T., et al. 2013, ApJ, 766, 93 [NASA ADS] [CrossRef] [Google Scholar]
  36. Isenberg, P. A. 1984, J. Geophys. Res., 89, 2133 [NASA ADS] [CrossRef] [Google Scholar]
  37. Jana, S., Ghosh, S., & Chakrabarti, N. 2017, Phys. Plasmas, 24, 102307P [NASA ADS] [CrossRef] [Google Scholar]
  38. Kato, T. N. 2007, ApJ, 668, 974 [Google Scholar]
  39. Krauss-Varban, D., Omidi, N., & Quest, K. B. 1994, J. Geophys. Res.: Space Phys., 99, 5987 [NASA ADS] [CrossRef] [Google Scholar]
  40. Lakhina, G. S. 1990, Astrophys. Space Sci., 165, 153 [CrossRef] [Google Scholar]
  41. Lakhina, G. 2008, AdSpR, 41, 1688 [NASA ADS] [Google Scholar]
  42. Landau, L. D. 1965, Collected Papers of L.D. Landau, 445 [Google Scholar]
  43. Landau, L. D., Lifshitz, E. M., & Pitaevskij, L. P. 1981, Course of Theoretical Physics. vol. 10: Physical Kinetics (Oxford) [Google Scholar]
  44. Livadiotis, G. 2017, Kappa Distributions: Theory and Applications in Plasmas (Elsevier) [Google Scholar]
  45. López, R. A. 2023, DIS-K: Dispersion Solver for Kappa Plasmas [Google Scholar]
  46. López, R. A., Shaaban, S. M., & Lazar, M. 2021, J. Plasma Phys., 87, 905870310 [CrossRef] [Google Scholar]
  47. López, R. A., Micera, A., Lazar, M., et al. 2022, ApJ, 930, 158 [CrossRef] [Google Scholar]
  48. Lysak, R. L., & Lotko, W. 1996, J. Geophys. Res.: Space Phys., 101, 5085 [NASA ADS] [CrossRef] [Google Scholar]
  49. Malaspina, D. M., Claudepierre, S. G., Takahashi, K., et al. 2015, Geophys. Res. Lett., 42, 9203 [NASA ADS] [CrossRef] [Google Scholar]
  50. Maneva, Y., Lazar, M., Viñas, A., & Poedts, S. 2016, ApJ, 832, 64 [Google Scholar]
  51. Matthaeus, W. H., Yang, Y., Wan, M., et al. 2020, ApJ, 891, 101 [NASA ADS] [CrossRef] [Google Scholar]
  52. Mizuno, Y., Fromm, C. M., Younsi, Z., et al. 2021, MNRAS, 506, 741 [NASA ADS] [CrossRef] [Google Scholar]
  53. Moya, P. S., Pinto, V. A., Viñas, A. F., et al. 2015, J. Geophys. Res.: Space Phys., 120, 5504 [NASA ADS] [CrossRef] [Google Scholar]
  54. Moya, P. S., Gallo-Méndez, I., & Zenteno-Quinteros, B. 2021, J. Atmosph. Solar-Terrest. Phys., 219, 105630 [Google Scholar]
  55. Moya, P. S., Zenteno-Quinteros, B., Gallo-Méndez, I., & Pinto, V. A. 2022, ApJ, 933, 32 [NASA ADS] [CrossRef] [Google Scholar]
  56. Nandal, P., Yadav, N., Sharma, R., & Goldstein, M. 2016, Astrophys. Space Sci., 361, 239 [Google Scholar]
  57. Perschke, C., Narita, Y., Gary, S., Motschmann, U., & Glassmeier, K. 2013, Ann. Geophys., 31, 1949 [NASA ADS] [CrossRef] [Google Scholar]
  58. Podesta, J. J. 2012, J. Geophys. Res.: Space Phys., 117 [Google Scholar]
  59. Quataert, E. 1998, ApJ, 500, 978 [NASA ADS] [CrossRef] [Google Scholar]
  60. Quataert, E., & Narayan, R. 1999, ApJ, 516, 399 [NASA ADS] [CrossRef] [Google Scholar]
  61. Raymond, J. C., Ghavamian, P., Bohdan, A., et al. 2023, ApJ, 949, 50 [NASA ADS] [CrossRef] [Google Scholar]
  62. Roberts, O. W., Narita, Y., Nakamura, R., Vörös, Z., & Verscharen, D. 2022, Phys. Plasmas, 29, 012308 [NASA ADS] [CrossRef] [Google Scholar]
  63. Sahraoui, F., Belmont, G., & Goldstein, M. L. 2012, ApJ, 748, 100 [NASA ADS] [CrossRef] [Google Scholar]
  64. Saikin, A. A., Zhang, J., Allen, R. C., et al. 2015, J. Geophys. Res.: Space Phys., 120, 7477 [NASA ADS] [CrossRef] [Google Scholar]
  65. Salem, C. S., Howes, G. G., Sundkvist, D., et al. 2012, ApJ, 745, L9 [NASA ADS] [CrossRef] [Google Scholar]
  66. Shapiro, S. L., Lightman, A. P., & Eardley, D. M. 1976, ApJ, 204, 187 [NASA ADS] [CrossRef] [Google Scholar]
  67. Stawarz, J. E., Eastwood, J. P., Varsani, A., et al. 2017, Geophys. Res. Lett., 44, 7106 [NASA ADS] [CrossRef] [Google Scholar]
  68. Stix, T. 1992, Waves in Plasmas (American Inst. of Physics) [Google Scholar]
  69. Sulaiman, A. H., Hospodarsky, G. B., Elliott, S. S., et al. 2020, Geophys. Res. Lett., 47, e2020GL089732 [CrossRef] [Google Scholar]
  70. Tian, S., Lyons, L. R., Nishimura, Y., et al. 2022, Geophys. Res. Lett., 49, e2022GL098457 [Google Scholar]
  71. Tong, Y., Bale, S. D., Chen, C. H., Salem, C. S., & Verscharen, D. 2015, ApJ, 804, L36 [NASA ADS] [CrossRef] [Google Scholar]
  72. Trávníček, P. M., & Chaston, C. C. 2022, ApJ, 935, 106 [CrossRef] [Google Scholar]
  73. Usanova, M. E. 2021, Front. Astron. Space Sci., 8, 204 [NASA ADS] [CrossRef] [Google Scholar]
  74. Usanova, M. E., & Mann, I. R. 2016, Waves, Particles, and Storms in Geospace, 244 [CrossRef] [Google Scholar]
  75. van Adelsberg, M., Heng, K., McCray, R., & Raymond, J. C. 2008, ApJ, 689, 1089 [CrossRef] [Google Scholar]
  76. Verscharen, D., & Chandran, B. D. G. 2018, Res. Notes AAS, 2, 13 [CrossRef] [Google Scholar]
  77. Verscharen, D., Klein, K. G., & Maruca, B. A. 2019, Liv. Rev. Sol. Phys., 16, 5 [Google Scholar]
  78. Villarroel-Sepúlveda, N., López, R. A., & Moya, P. 2023, A&A, 675, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Wang, C.-P., Gkioulidou, M., Lyons, L. R., & Angelopoulos, V. 2012, J. Geophys. Res.: Space Phys., 117, 132 [Google Scholar]
  80. Wilson, L. B., III, Stevens, M. L., Kasper, J. C., et al. 2018, ApJS, 236, 41 [NASA ADS] [CrossRef] [Google Scholar]
  81. Wu, D. J., & Yang, L. 2006, A&A, 452, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  82. Wygant, J. R., Keiling, A., Cattell, C. A., et al. 2002, J. Geophys. Res.: Space Phys., 107, 24 [Google Scholar]
  83. Yang, L., Wu, D. J., Wang, S. J., & Lee, L. C. 2014, ApJ, 792, 36 [Google Scholar]
  84. Yao, Y., Chaston, C. C., Glassmeier, K.-H., & Angelopoulos, V. 2011, Geophys. Res. Lett., 38 [Google Scholar]
  85. Zhang, Z., Yuan, Z., Huang, S., et al. 2022, Earth Planet. Phys., 6, 465 [Google Scholar]
  86. Zhao, J. 2015, Phys. Plasmas, 22, 032505 [NASA ADS] [CrossRef] [Google Scholar]
  87. Zhao, J., Lee, L., Xie, H., et al. 2022, ApJ, 930, 95 [Google Scholar]
  88. Zhou, M., Liu, Z., & Loureiro, N. F. 2023, Proc. Natl. Acad. Sci., 120 [Google Scholar]

All Figures

thumbnail Fig. 1.

Real (ω) and imaginary (γ) frequency of the Alfvén wave and its transverse polarisation for different electron-to-proton temperature ratios, with βp = 0.1 (top) and βp = 1.0 (bottom). The dispersion relation is plotted with continuous lines for |γ|< |ω| and in dotted lines for |γ|> |ω|, indicating that the mode is strongly damped. Dash-dotted lines indicate k⊥ρ = 1 for the different configurations, and the segmented line in the real frequency panels corresponds to the MHD dispersion relation of the Alfvén wave.
In the text
thumbnail Fig. 2.

Magnitude of the real part of the magnetic ratio iBz/By for different values of Te/Tp. Continuous lines are the results obtained from kinetic theory and indicate the rough predictions from the two-fluid theory given in Eq. (13a).
In the text
thumbnail Fig. 3.

Real and imaginary frequency, transverse electrical polarisation, and magnetic polarisation of the Alfvén wave. The summed β of the plasma, β = βe + βp, was fixed at 0.12, 0.60, 1.20, and for each value of β different electron-to-proton temperature ratios were considered. Dash-dotted lines indicate k⊥ρL = 1 for the different values of βe + βp. The segmented line in the real frequency panels corresponds to the MHD dispersion relation of the Alfvén wave. In the two middle panels it indicates the line corresponding to zero, and in the bottom panel it represents the improved two-fluid approximation of this quantity given in Eq. (13b).
In the text
thumbnail Fig. 4.

Amplitude of the perturbed electric field ratios for different values of Te/Tp and different propagation angles. Results are displayed for βp = 0.1 and βp = 1.0. Vertical dashed lines correspond to k⊥ρL = 1.0 for the corresponding electron-to-proton temperature ratio indicated by the color code.
In the text
thumbnail Fig. 5.

Amplitude of the squared parallel electric field ratio, Ez/|E|, real part of the transverse electric polarisation, iEx/Ey, and magnitude of the real part of the magnetic polarisation, iBz/By, for different values of βp and propagation angles. The results are displayed as functions of the electron-to-proton temperature ratio contained in βe/βp for kρp = 0.5 and kρp = 1.0.
In the text
thumbnail Fig. 6.

Heat maps displaying the transverse electric polarisation for a wide range of propagation angles and different combinations of βp and βe/βp as a function of the wavenumber in units of ρ L − 1 $ \rho_{\mathrm{L}}^{-1} $ and for different combinations of βp and kρp as functions of βe/βp. The white lines indicate the contour of Re[iEx/Ey] = 0 and black lines represent contours of characteristic values of −γ/Ωp, where γ is the imaginary part of the wave frequency.
In the text
thumbnail Fig. 7.

Contours of Re[iEx/Ey] = 0 for different electron-to-proton temperature ratios and βp as functions of the propagation angle and kρL in the top two panels, and for different combinations of the βp and kρp as functions of the propagation angle and the ratio βe/βp in the bottom two panels.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.