| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A8 | |
| Number of page(s) | 15 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201423518 | |
| Published online | 22 May 2015 | |
Measuring star formation with resolved observations: the test case of M 33⋆
1 Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
e-mail: mboquien@ast.cam.ac.uk
2 Aix-Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique de Marseille) UMR 7326, 13388 Marseille, France
3 Department of Astronomy, University of Massachusetts, Amherst, MA 01003, USA
4 Department of Earth and Space Sciences, Chalmers University of Technology, Onsala Observatory, 43994 Onsala, Sweden
5 Laboratoire d’Astrophysique de Bordeaux, Université de Bordeaux, CNRS UMR 5804, 33271 Floirac, France
6 Observatoire de Paris, LERMA, CNRS, 61 Av. de l’Observatoire, 75014 Paris, France
7 Sterrewacht Leiden, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
8 Instituto Radioastronomia Milimetrica, 18012 Granada, Spain
9 Infrared Processing and Analysis Center, California Institute of Technology, MS 100–22, Pasadena, CA 91125, USA
10 Department Física Teórica y del Cosmos, Universidad de Granada 18071, Granada, Spain
11 Department of Physics, University of Alberta, 2–115 Centennial Centre for Interdisciplinary Science, Edmonton T6G2E1, Canada
12 Department of Astronomy, Cornell University, Ithaca, NY 14853, USA
13 Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
14 SRON Netherlands Institute for Space Research, Landleven 12, 9747 AD Groningen, The Netherlands
15 Kapteyn Astronomical Institute, University of Groningen, 9712 Groningen, The Netherlands
16 Institute for Astronomy, Astrophysics, Space Applications and Remote Sensing, National Observatory of Athens, 15236 Athens, Greece
Received: 28 January 2014
Accepted: 4 February 2015
Context. Measuring star formation on a local scale is important to constrain star formation laws. It is not clear yet, however, whether and how the measure of star formation is affected by the spatial scale at which a galaxy is observed.
Aims. We wish to understand the impact of the resolution on the determination of the spatially resolved star formation rate (SFR) and other directly associated physical parameters such as the attenuation.
Methods. We carried out a multi-scale, pixel-by-pixel study of the nearby galaxy M 33. Assembling FUV, Hα, 8 μm, 24 μm, 70 μm, and 100 μm maps, we have systematically compared the emission in individual bands with various SFR estimators from a resolution of 33 pc to 2084 pc.
Results. There are strong, scale-dependent, discrepancies of up to a factor 3 between monochromatic SFR estimators and Hα+24 μm. The scaling factors between individual IR bands and the SFR show a strong dependence on the spatial scale and on the intensity of star formation. Finally, strong variations of the differential reddening between the nebular emission and the stellar continuum are seen, depending on the specific SFR (sSFR) and on the resolution. At the finest spatial scales, there is little differential reddening at high sSFR. The differential reddening increases with decreasing sSFR. At the coarsest spatial scales the differential reddening is compatible with the canonical value found for starburst galaxies.
Conclusions. Our results confirm that monochromatic estimators of the SFR are unreliable at scales smaller than 1 kpc. Furthermore, the extension of local calibrations to high-redshift galaxies presents non-trivial challenges because the properties of these systems may be poorly known.
Key words: galaxies: individual: M 33 / galaxies: ISM / galaxies: star formation
The maps (FITS files) and the data cube used in this article are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/578/A8
© ESO, 2015
1. Introduction
As we observe galaxies across the Universe, their evolution from highly disturbed proto-galaxies at high redshift to the highly organised systems common in the zoo of objects we see in the nearby Universe is striking. One of the most important processes that drives this evolution is the transformation of the primordial gas reservoir into stars, which form heavy elements that are ejected into the intergalactic medium during intense episodes of feedback. In other words, if we wish to understand galaxy formation and evolution across cosmic times, we need to understand the process of star formation in galaxies. To do so, it is paramount to be able to measure star formation as accurately as possible.
The most direct way to trace star formation is through the photospheric emission of massive stars with lifetimes of up to ~100 Myr, which dominate the ultraviolet (UV) energy budget of star-forming galaxies. An indirect star formation tracer is the Hα recombination line (or any other hydrogen recombination line) from gas ionised by the most massive stars that are around for up to ~10 Myr. However, both the UV emission and the Hα line are severely affected by the presence of dust, which absorbs energetic photons and reemits their energy at longer wavelengths. From the inception of the far-infrared era with the launch of the Infrared Astronomical Satellite (IRAS, Neugebauer et al. 1984), the emission of the dust has been used as a powerful tracer of star formation from local galaxies up to high-redshift objects, resulting in a tremendous progress of our understanding of galaxy evolution in general and of the physical processes of star formation in particular.
The launch of the Herschel Space Observatory (Pilbratt et al. 2010) has opened new avenues for the investigation of star formation in the far-infrared not only in entire galaxies, but also within nearby galaxies at scales where physical processes such as heating and cooling are localised. Herschel matches the angular resolution of 5−6′′ of Spitzer in the mid-infrared (Fazio et al. 2004; Rieke et al. 2004), and of GALEX in the UV (Galaxy Evolution Explorer, Martin et al. 2005).
Measuring local star formation in galaxies still remains an important challenge. For instance, Kennicutt et al. (2007); Bigiel et al. (2008) found seemingly incompatible star formation laws with the same dataset. Such a difference could be due to the distinct ways star formation is measured in galaxies (Liu et al. 2011); different star formation rate (SFR) estimates lead to variations of 10−50% of the molecular gas depletion timescale (Leroy et al. 2012, 2013).
The measurement of star formation relies upon three main assumptions.
-
First of all, a well-defined and fully sampled initial mass function(IMF) is assumed. This is necessary to relate the measured poweroutput from massive, short-lived stars to the total mass of thestellar population of the same age. Massive stars only account for aminor fraction of the total mass of stellar populations, even in theyoungest star-forming regions, which contain the highestproportion of such stars.
-
Star-formation-tracing bands need to be sensitive mainly to the most recent episode of star formation. Contamination from emission unrelated to recent star formation, such as active nuclei and older stellar populations, needs to be negligible.
-
A well-defined star formation history is assumed. Too few star-forming regions would induce rapid variations of the SFR with time.
These assumptions, which are not exhaustive, may already be problematic for some entire galaxies (Boselli et al. 2009). At small scales, they are unlikely to hold true across an entire spiral disk.
If we wish to understand star formation laws in the era of resolved observations, it is therefore crucial to understand when, how, and from which spatial scale we can measure star formation reliably. In particular, we need to understand how star formation tracers relate to each other in galaxies from the finest spatial scale, at which H ii regions are resolved, to large portions of a spiral disk. Recent results show a systematic variation of star formation tracers with spatial scale, which could be due to the presence of diffuse emission unrelated to recent star formation (Li et al. 2013): ~20−30% of the far-UV (FUV) luminosity from a galaxy is due to stars older than 100 Myr (Johnson et al. 2013; Boquien et al. 2014) and 30% to 50% of Hα is diffuse (Thilker et al. 2005; Crocker et al. 2013). Measuring local star formation is made even more difficult by the fact that indirect tracers of star formation (the ionised gas and dust emission) may not be spatially coincident with the direct tracer of star formation, the UV emission (Calzetti et al. 2005; Relaño & Kennicutt 2009; Verley et al. 2010; Louie et al. 2013; Relaño et al. 2013). Such offsets can also be seen in the Milky Way in NGC 3603, Carina, or the OB associations in Orion for instance. This challenges the real meaning of SFR measurements on local scales.
These offsets along with other processes such as stochastic sampling of the IMF or the insufficient number of star-forming regions and/or molecular clouds in a given region could be one of several reasons for the observational breakdown of the Schmidt-Kennicutt law on scales of the order of ~100−300 pc (Calzetti et al. 2012), which has been found in M 33 by Onodera et al. (2010) and Schruba et al. (2010). The complex interplay between various processes at the origin of the breakdown of the Schmidt-Kennicutt law on small spatial scales has recently been analysed by Kruijssen & Longmore (2014).
With the availability of resolved observations of high-redshift objects with ALMA and the JWST by the end of the decade, understanding whether and how we can measure star formation on local scales is also of increasing importance. We address this question through a detailed study of star formation tracers on all scales in the nearby late-type galaxy M 33. Thanks to its proximity (840 kpc, corresponding to 4.07 pc/′′, Freedman et al. 1991), relatively low inclination (56°, Regan & Vogel 1994), and large angular size (over 1° across), M 33 is an outstanding galaxy for such a study. It has been a popular target for a large number of multi-wavelength observations and surveys in star-formation-tracing bands from the FUV with the GALEX Nearby Galaxies Survey (NGS, Gil de Paz et al. 2007), to the FIR with Herschel in the context of the HerM33es survey (Kramer et al. 2010), including Spitzer mid-infrared data (Verley et al. 2007) as well as Hα narrow-band imaging (Hoopes & Walterbos 2000).
In Sect. 2 we present the data, including new observations recently obtained by our team, and how data processing was carried out. We compare various SFR estimators at different scales in Sect. 3. We examine in detail the properties of dust emission with scale to measure the SFR from monochromatic infrared bands in Sect. 4. We investigate the relative fraction of attenuated and unattenuated star formation with scale in Sect. 5. Finally, we discuss our results in Sect. 6 and conclude in Sect. 7.
2. Observations and data processing
2.1. Observations
To carry out this study, we considered the main star formation tracers used in the literature: the emission from young, massive stars in the FUV, the ionised gas recombination line Hα, and the emission of the dust at 8 μm, 24 μm, 70 μm, and 100 μm. We did not explore dust emission beyond 100 μm because previous work has shown that longer wavelengths are poor tracers of star formation (Bendo et al. 2010, 2012; Boquien et al. 2011) and the scale sampled with Herschel becomes coarser. Neither did we investigate radio tracers, because they are not as widely used.
The FUV GALEX data from NGS were obtained directly from the GALEX website through galexview1. The observation was carried out on 25 November 2003 for a total exposure time of 3334 s.
Hα+[Nii] observations were carried out in November 1995 on the Burrel Schmidt telescope at Kitt Peak National Observatory. They consisted of 20 exposures of 900 s, each covering a final area of 1.75 × 1.75 deg2. This map has been continuum-subtracted by scaling an off-band image using foreground stars. The observations and the data processing are analysed in detail in Hoopes & Walterbos (2000).
The Spitzer/IRAC 8 μm image, which is sensitive to the emission of polycyclic aromatic hydrocarbons (PAH), and the MIPS 24 μm image, which is sensitive to the emission of very small grains (VSG), were obtained from the NASA Extragalactic Database and have been analysed by Hinz et al. (2004) and Verley et al. (2007).
The PACS data at 70 μm and 100 μm, which are sensitive to the warm dust heated by massive stars, come from two different programmes. The 100 μm image was obtained in the context of the Herschel HerM33es open time key project (Kramer et al. 2010, observation ID 1342189079 and 1342189080). The observation was carried out in parallel mode on 7 January 2010 for a duration of 6.3 h. It consisted of two orthogonal scans at a speed of 20′′/s, with a leg length of 70′. The 70 μm image was obtained as a follow-up open time cycle 2 programme (OT2_mboquien_4, observation ID 1342247408 and 1342247409). M 33 was scanned on 25 June 2012 at a speed of 20′′/s in two orthogonal directions over 50′ with five repetitions of this scheme so as to match the depth of the 100 μm image. The total duration of the observation was 9.9 h. Reduced maps are available on the Herschel user-provided data product website2.
2.2. Additional data processing
The GALEX data we obtained from galexview were already fully processed and calibrated, we therefore did not carry out any additional processing.
We corrected the continuum-subtracted Hα map for [N ii] contamination, which according to Hoopes & Walterbos (2000) accounts for 5% of the Hα flux in the narrow-band filter. We have also removed subtraction artefacts caused by bright foreground stars. To do so, we used iraf’s imedit procedure, replacing these artefacts with data similar to that of the neighbouring background.
The Spitzer/IRAC and MIPS data we used were processed in the context of the Local Volume Legacy survey (LVL, Dale et al. 2009). No further processing was performed.
Even though in the context of the HerM33es project we already reduced and published 100 μm data (Boquien et al. 2010b, 2011), these observations were processed with older versions of the data reduction pipeline. To work on a fully consistent set of Herschel PACS data and to take advantage of the recent improvements of the pipeline, we reprocessed the 100 μm from the HerM33es survey along with the new 70 μm data. To do so, we took the raw data to level 1 with HIPE version 9 (Ott 2010), flagging bad pixels, masking saturated pixels, adding pointing information, and calibrating each frame. In a second step, to remove the intrinsic 1 /f noise of the bolometers and make the maps, we used the Scanamorphos software (Roussel 2013), version 19. We present the new 70 μm map obtained for this project in Fig. 1.
 |
Fig. 1 Map of M 33 at 70 μm obtained with the Herschel PACS instrument in the context of a cycle 2 programme (OT2_mboquien_4, observation ID 1342247408 and 1342247409; the original map is available from the link given in footnote 2). The image is in Jy/arcsec2, and the colours follow an arcsinh scale indicated by the bar on the right side of the figure. The physical scale is indicated by the white line in the bottom right corner of the figure, representing 1 kpc. Each pixel has a size of 1.4′′. |
2.3. Correction for the Galactic foreground extinction
To correct the FUV and Hα fluxes for the Galactic foreground extinction, we used the extinction curve reported by Cardelli et al. (1989), including the update of O’Donnell (1994). We assumed E(B−V) = 0.0413, as indicated by NASA/IPAC Infrared Science Archive’s dust extinction tool from the extinction maps of Schlegel et al. (1998). This yields a correction of 0.34 mag in FUV and 0.11 mag in Hα.
2.4. Astrometry
To carry out a pixel-by-pixel analysis, it is important that the relative astrometric accuracy of all the bands is significantly better than the pixel size. A first visual inspection reveals a clear offset between the new 70 μm data we present in this paper and the 100 μm data presented in Boquien et al. (2010b, 2011). When comparing the 70 μm and 100 μm images with the Hα image of Hoopes & Walterbos (2000), we found that the 70 μm map corresponded more closely to the Hα emission across the galaxy and was consistent with data at other wavelengths. We therefore decided to shift the 100 μm image to match the 70 μm map astrometry. To determine the offset, we compared the relative astrometry of the 160 μm images obtained in the context of HerM33es and the OT2_mboquien_4 programme. As the 160 μm is observed in parallel with the 70 μm or the 100 μm, they have the same astrometry. The offset between the 160 μm maps between these two programmes is therefore the same as the offset between the 70 μm and the 100 μm maps. We determined an offset of ~5″ (4.83′′ towards the east and 1.25′′ towards the north) and applied this to the 100 μm image. When comparing the corrected 100 μm band with the 8 μm and 24 μm images, we can see small region-dependent offsets of the order of 1−2′′. The variation of this offset from one region to another leads us to think that at least part of it reflects physical variations in the emission of the various dust components in M 33. In addition, as we describe below, we carried out this study at a minimum pixel size of 8′′, much larger than any possible systematic offset. We conclude that the relative astrometry of our images is sufficient to reach our goals.
2.5. Pixel-by-pixel matching
Because pixel-by-pixel analysis is central for this study, it is crucial to match all the images to a common reference frame. To do so, it is important that all bands share a common point spread function (PSF). To ensure this, in a first step we convolved all the images to the PACS 100 μm PSF using the dedicated kernels provided by Aniano et al. (2011). We then registered these images to a common reference frame with a pixel size ranging from 8′′, slightly larger than the PACS 100 μm PSF, to 512′′, by increments of 1′′ in terms of pixel size, using iraf’s wregister procedure with the drizzle interpolant. This allowed us to sample all scales from fractions of H ii regions at 33 pc (8′′) to large portions of the disk at 2084 pc (512′′). The upper bound is limited by the size of the galaxy. Increasing to larger physical scales would leave us with too few pixels in M 33. We present some of the final, convolved, registered, and background-subtracted maps used in this study for a broad range of pixel sizes in Fig. 2.
 |
Fig. 2 Convolved images registered to a common reference frame at 33 pc (8′′/pixel, left), 260 pc (64′′/pixel, centre), and 2084 pc (512′′/pixel, right). Each row represents a different star-formation-tracing band, from top to bottom: GALEX FUV, Hα, IRAC 8 μm, MIPS 24 μm, PACS 70 μm, and PACS 100 μm. Blue pixels have a low flux density, whereas red pixels have a high flux density, following an arcsinh scale. The colours used are simply chosen to best represent the wide dynamical range of intensities across all bands and all pixel sizes and should be used in a qualitative sense only. |
To compute flux uncertainties, we relied on the 33 pc scale maps. We took into account the uncertainty on the background determination, which is due to large-scale variations, and the pixel-to-pixel noise. The former was measured as the standard deviation of the background level measured within 10 × 10 pixel square apertures around the galaxy using iraf’s imexamine procedure. The latter was measured as the mean of the standard deviation of pixel fluxes in these apertures around the galaxy. We then summed these uncertainties in quadrature. For maps at lower resolution, we simply scaled the uncertainties on the background with the square of the pixel size, and the pixel-to-pixel uncertainties with the pixel size. Direct measurements on lower resolution maps yielded uncertainties consistent with the scaled ones.
2.6. Removal of the stellar pollution in infrared bands
In a final data processing step, we removed the stellar contamination in the 8 μm and 24 μm bands. To do so, we assumed that the Spitzer/IRAC 3.6 μm image is dominated by stellar emission, following the analysis of Meidt et al. (2012). We then scaled this image to predict the stellar emission at 8 μm and 24 μm and subtracted it from these images. We assumed a scaling factor of 0.232 at 8 μm and 0.032 at 24 μm, following Helou et al. (2004). We note that this scaling factor can change quite significantly with the star formation history (e.g. Calapa et al. 2014; Ciesla et al. 2014).
3. Comparison of SFR estimators at different scales
3.1. Presentation of monochromatic and composite SFR estimators
Ideally, a good SFR estimator has a solid physical basis and is devoid of biases. Thus, because they directly or indirectly trace the emission from young, massive stars, the attenuation3-corrected FUV or Hα should in principle be ideal estimators. In practice, however, the presence of biases is a real problem since it shows that other factors unrelated to recent star formation can contribute to the emission in star-formation-tracing bands. For instance, for monochromatic IR tracers, such factors are the contribution from old stars, changes in the opacity of the ISM (interstellar medium), or in the IR SED (spectral energy distribution).
When no attenuation measurement is available, a popular method developed over the past few years has been to combine attenuated and attenuation-free tracers (Calzetti et al. 2007; Kennicutt et al. 2007, 2009; Leroy et al. 2008; Hao et al. 2011). Unfortunately, how to combine such tracers remains uncertain. Calzetti et al. (2007) and Kennicutt et al. (2009) found different scaling factors when combining dust emission at 24 μm with Hα, probably because of different scales probed: 500 pc for the former and entire galaxies for the latter, and therefore different timescales (Calzetti 2013). According to Leroy et al. (2012), the universality of composite estimators remains in doubt. One of the main problems comes from the diffuse emission and whether it is linked to recent star formation or not. In M 33, the fraction of diffuse emission is high: 65% in FUV, and from 60% to 80% in the 8 μm and 24 μm bands, with clear variations across the disk for the latter two (Verley et al. 2009). While some methods have been suggested to remove the diffuse emission linked to old stars (Leroy et al. 2012), they rely on uncertain assumptions. We therefore cannot rely a priori on such tracers as an absolute reference. But how monochromatic and hybrid SFR estimators compare may still yield useful information on star formation in M 33. We consider the restricted set of monochromatic and hybrid SFR estimators presented in Table 1.
SFR estimators.
Before comparing these SFR estimators, we add a word of caution. In some cases, especially at the smallest spatial scales, the concept of an SFR in itself may not be valid (for a description of the reasons see Sect. 3.9 of Kennicutt & Evans 2012, in particular: IMF sampling, age effects, and the spatial extension of the emission in star-formation-tracing bands in comparison to the resolution). In the context of this study, IMF sampling is probably no particular problem. A scale of 33 pc corresponds to the Strömgren radius of a 3000−5000 M⊙, 4−5 Myr old stellar cluster. Such a cluster would already be massive enough not to be too affected by stochastic sampling (Fouesneau et al. 2012). However, we cannot necessarily assume that other assumptions are fulfilled: age effects may be strong and star-forming regions may be individually resolved (Kennicutt & Evans 2012; Kruijssen & Longmore 2014). This means that care must be taken when interpreting the SFR. In this case, it may be preferable to interpret the SFR as a proxy for the local radiation field intensity. The dust emission may come from heating by local old stellar populations or because of heating by energic photons emitted by stars in neighbouring pixels rather than being driven by local massive stars.
 |
Fig. 3 Comparison of monochromatic SFR estimators with the reference SFR(Hα+24 μm) estimator versus the spatial scale. The colour indicates the monochromatic band: FUV (blue), Hα (cyan), 24 μm (green), 70 μm (magenta), and 100 μm (red). Left panel: correlation coefficient between the monochromatic and reference estimators. Right panel: mean offset (solid line) and the standard deviation (shaded area) of the difference between the estimators. |
3.2. Comparison between monochromatic and hybrid SFR estimators
We now compare popular monochromatic SFR estimators in the FUV, Hα (both uncorrected for the attenuation), 24 μm, 70 μm, and 100 μm bands with SFR(Hα+24 μm), which we take as the refererence, to understand how their relation changes with the scale considered. We selected SFR(Hα+24 μm) over SFR(FUV+24 μm) because as we show in Sect. 6, at local scales the 24 μm and the Hα are more closely related. We note that we are here not so much interested in the absolute SFR, which we cannot compute reliably at all scales, as in the consistency of SFR estimators with one another and their relative variations with spatial scale. These relative variations bring us important information on star formation in M 33. In addition, if different estimators give systematically different results, this shows that they cannot all be simultaneously reliable. The relations between the various aforementioned SFR estimators are shown in Fig. 3.
We first observe that monochromatic SFR estimates are well correlated with the reference estimates (0.67 ≤ ρ ≤ 1.00, with ρ the Spearman correlation coefficient). There is a rapid increase of the correlation coefficient up to a scale of 150−200 pc for all estimators but Hα. Beyond 200 pc, IR estimators show a regular increase. The FUV correlation coefficient remains relatively stable until a scale of 1700 pc and then rapidly increases. The Hα estimator globally shows little variation with scale. At scales beyond 2 kpc, all estimators are strongly correlated with the reference one.
However, if they are all well correlated, this does not necessarily mean that they provide consistent results. In the right panel of Fig. 3, we show the mean offset and the dispersion between monochromatic SFR estimators and the reference one. The FUV, Hα, and 24 μm estimates are lower than the reference one. This is naturally expected for Hα because it is part of the reference SFR estimator. The FUV being subject to the attenuation will also naturally yield lower estimates. The amplitude of the offset at 24 μm (0.14 dex at 33 pc to 0.10 dex at 2084 pc) can be more surprising as the 24 μm estimator used here is non-linear to take into account that only a fraction of photons are attenuated by dust. This is probably due to a metallicity effect. Magrini et al. (2009) measured the metallicity of M 33 H ii regions at 12 + log O / H = 8.3, placing it near the limit between the high (12 + log O / H > 8.35) and intermediate (8.00 < 12 + log O / H ≤ 8.35) metallicity samples of Calzetti et al. (2007). In turn, intermediate metallicity galaxies show some deficiency in their 24 μm emission relative to higher metallicity galaxies. This is due to reduced dust content of the ISM, which increases its transparency (Calzetti et al. 2007).
If we compare the SFR at 24 μm and 70 μm, the relative offset ranges from 0.57 dex at 33 pc to 0.53 dex at 2084 pc. This discrepancy has several possible origins. First, these infrared estimators have been determined only for a limited range in terms of ΣSFR. Li et al. (2013) computed their estimators for −1.5 ≤ log ΣSFR ≤ 0.5 M⊙ yr-1 kpc-2. The 24 μm estimator of Calzetti et al. (2007) benefited from a much broader range: −3.0 ≤ log ΣSFR ≤ 1.0 M⊙ yr-1 kpc-2. If we consider only the definition range of SFR(70 μm), at the finest pixel size, the disagreement between SFR(70 μm) and SFR(Hα+24 μm) is not as strong. Another possible source of disagreement lies in the scale on which estimators have been derived. Indeed, increasing the pixel sizes means averaging over larger regions and including a larger fraction of diffuse emission. Li et al. (2013) determined their estimators on two galaxies on a scale of about 200 pc. They estimated that 50% of the emission at this scale comes from dust heated by stellar populations unrelated to the latest episode of star formation. But even if this diffuse emission were exclusive to the 70 μm band, this would not be sufficient to explain the full extent of the offset. Calzetti et al. (2007) combined data of a much more diverse sample of galaxies on a physical scale ranging from 30 pc to 1.26 kpc, averaging out specificities of individual galaxies. To gain further insight on these differences, we examine in detail the origin of dust emission on different scales in Sect. 4.
 |
Fig. 4 Relations at 33 pc (left), 260 pc (centre), and 2084 pc (right) of Lν(70 μm) versus Lν(24 μm) (top), and Lν(100 μm) versus Lν(70 μm) (bottom). All luminosities have been multiplied by a constant factor corresponding to a linear SFR estimator (a24 = 2.04 × 10-36M⊙ yr-1 W-1, a70 = 5.89 × 10-37M⊙ yr-1 W-1, and a100 = 5.17 × 10-37M⊙ yr-1 W-1) to place them on a similar scale. The colour of each point indicates ΣSFR following the colour bar at the right of each row. The red line indicates a one-to-one relation. We see the non-linear relations between the luminosities in different bands. These non-linearities are particularly apparent on the finest pixel scales. On coarser scales, the relations appear more linear, which is probably due to a mixing between diffuse and star-forming regions. |
As a concluding remark, these discrepancies must serve as a warning when using SFR estimators. Applying them beyond their validity range in terms of surface brightness, physical scale, and metallicity may yield important biases. This is especially important when applying SFR estimators on higher redshift galaxies because their physical properties may be more poorly known.
4. Understanding dust emission to measure the SFR on different scales
4.1. What the infrared emission traces from 24 μm to 100 μm
To understand what the emission of the dust traces on which scale and under which conditions, we examine the change in the relative emission at 24 μm, 70 μm, and 100 μm. To facilitate the comparison, we first convert the luminosity surface densities into SFR using the linear estimators of Rieke et al. (2009) at 24 μm and Li et al. (2013) at 70 μm and 100 μm. We stress that we are not interested here in the absolute values of SFR, only in their relative variations. These linear estimators only serve to place the luminosities on a comparable scale.
In Fig. 4 we compare the dust emission at 24 μm, 70 μm, and 100 μm from 33 pc to 2084 pc. In general, the emission in these three bands correlates excellently well (0.90 ≤ ρ ≤ 0.98) across all scales. Unsurprisingly, the luminosity of individual regions in all bands also varies with ΣSFR. When examining relations on a scale of 33 pc, we find that there is a systematic sub-linear trend between shorter and longer wavelength bands. For higher luminosity surface densities, Lν(24 μm) is stronger relatively to Lν(70 μm) than what can be seen at lower Lν(24 μm) or Lν(70 μm). The same behaviour is clearly observed when comparing Lν(70 μm) with Lν(100 μm). Interestingly, towards coarser resolutions this trend progressively disappears, and at 2084 pc the relations between the various bands appear more linear. The important aspect to note is not so much that the dispersion diminishes with coarser spatial scales, but that there is a progressive transition from a non-linear relation to a linear relation. This phenomenon could be due to the progressive mixing of diffuse and star-forming regions.
To understand how the relative infrared emission varies with the spatial scale, we compare the observed dust at 24 μm, 70 μm, and 100 μm with the model of Draine & Li (2007). We refer to Rosolowsky et al. (in prep.) for a full description of the dust SED modelling of M 33 with the models of Draine & Li (2007). In a nutshell, the emission of the dust is modelled by combining two components. The first component is illuminated by a starlight intensity Umin, corresponding to the diffuse emission. The other component corresponds to dust in star-forming regions, illuminated with a starlight intensity ranging from Umin to Umax following a power law. We considered all available values for Umin, from 0.10 to 25. Following Draine et al. (2007), we adopted a fixed Umax = 106. The fraction of the dust mass linked to star-forming regions is γ, and as a consequence, 1−γ is the mass fraction of the diffuse component. We considered γ ranging from 0.00 to 0.20 by steps of 0.01. Because M 33 has a sub-solar metallicity, we adopted the so-called MW3.1_30 dust composition, which corresponds to a Milky Way dust mix with a PAH mass fraction relative to the total dust mass of 2.50%, lower than the Milky Way mass fraction of 4.58%. We compare this grid of physical models to the observations in Fig. 5 for a resolution of 33 pc, and at a resolution of 260 pc.
 |
Fig. 5 70-to-100 versus 24-to-70 flux density ratios for each pixel at a resolution of 33 pc (left) and 260 pc (right). The colour of each symbol corresponds to ΣSFR, according to the colour bar on the right. The grid represents the models of Draine & Li (2007), with the MW3.1_30 dust composition, 0.10 ≤ Umin ≤ 25, and 0.00 ≤ γ ≤ 0.20. The red dashed lines indicate the locus corresponding to the one-to-one relations shown in Fig. 4. The 3σ uncertainties are shown in the bottom right corner. The 24-to-70 ratio is well correlated with γ and ΣSFR, especially at 33 pc. At 260 pc, due to mixing between diffuse and star-forming regions, excursions in γ are strongly reduced. Note that when considering the galaxy as a whole, a large part of the emission is due to the handful of luminous regions and not to the larger number of faint regions. |
The parameter space spanned by the grid of models reproduces the observations very well except for a fraction of points at low 24-to-70 and 70-to-100 ratios, for which even models with γ = 0 fail. Most points are concentrated in regions with simultaneously low values for γ and Umin, which also correspond to low SFR estimates. Regions at higher SFR seem to have a higher value for Umin, and there is a clear trend with γ, strongly star-forming regions having a larger γ. In other words, this means that the relative increase of the 24 μm emission compared to the 70 μm one that we saw in Fig. 4 is probably due to the transition between a regime entirely driven by the diffuse emission and a nearly complete lack of dust heated in star-forming regions (0.00 ≤ γ ≤ 0.01), to a regime with a strong contribution from dust heated in star-forming regions. When the resolution is coarser, the emission from star-forming regions is increasingly mixed with the emission from dust illuminated by the diffuse radiation field, reducing the excursions to high values of γ required to have a strong emission at 24 μm compared to the emission at 70 μm. If we assume that on average in star-forming galaxies γ = 1−2% (e.g. Draine et al. 2007), a significant fraction of the luminosity at 70 μm comes from star-forming regions. Considering a resolution of 33 pc, these values of γ typically correspond to regions with log ΣSFR ≥ −2 to −1.5 M⊙ yr-1 kpc-2. The 70 μm luminosity contributed by regions brighter than log ΣSFR = −2 and −1.5 is 58% and 27%, respectively. This is consistent with what we would expect from Fig. 5 as a small fraction of pixels with a high ΣSFR contributes a large part to the total luminosity compared to the more numerous but much fainter pixels.
We can also understand the observed trends by examining the physical origin of dust emission in relation to the SFR. At high SFR, the emission at 24 μm and 70 μm is caused by dust at the equilibrium and by a stochastically heated component. In low SFR regions only the stochastically heated component remains at 24 μm, contrary to what occurs at 70 μm (see in particular Fig. 15 in Draine & Li 2007). This means that the 24 μm emission should drop more quickly than the 70 μm emission with decreasing SFR. This accounts for the difference in behaviour seen in Fig. 5. The preceding explanation for M 33 seems consistent with the findings of Calzetti et al. (2007, 2010), who have studied this problem in great detail. Combining several samples totalling almost 200 star-forming galaxies, Calzetti et al. (2010) also found a clear positive correlation between the measured SFR and the 24-to-70 ratio.
 |
Fig. 6 Scaling coefficients from the luminosity in infrared bands to ΣSFR versus the pixel size, at 8 μm, 24 μm, 70 μm, and 100 μm, from the top left corner to the bottom right corner. The blue line indicates the value of the scaling factor when taking into account all pixels detected at a 3σ level in all six bands. The red (green) line indicates the scaling factor when considering only pixels with a ΣSFR higher (lower) than the median ΣSFR at a given resolution. The cyan and magenta lines represent regions in the top and bottom 15% in terms of ΣSFR. The shaded areas of the corresponding colours indicate the 1σ uncertainties. The horizontal dashed line at 24 μm (resp. 70 μm) indicates the scaling factor determined by Rieke et al. (2009), Calzetti et al. (2010) for entire galaxies. The crosses for the 70 μm and 100 μm bands indicate the scaling factor determined for individual galaxies on a scale of 200 pc (Li et al. 2013) and 700 pc (Li et al. 2010). The squares indicate mean values over several galaxies. The empty squares denote that no background subtraction was performed. |
4.2. Effect of the scale on the SFR measure from monochromatic infrared bands
4.2.1. Computation of SFR scaling relations
The determination of the SFR is paramount to understanding galaxy formation and evolution. Initially, such estimates in the mid- and far-infrared were limited to entire galaxies because of the coarse resolution of the first generations of space-based IR instruments. Spitzer has enabled computing dust emission in galaxies on a local scale in nearby galaxies (e.g., Boquien et al. 2010a). Thanks to its outstanding resolution, Herschel has enabled such studies at the peak of the emission of the dust on ever smaller spatial scales (Boquien et al. 2010b, 2011; Galametz et al. 2013). But such a broad and homogeneous spectral sampling represents an ideal case. More commonly, just one or a handful of infrared bands are available at sufficient spatial resolution. It is therefore important not only to be able to estimate the SFR from just one or a few IR bands, but also to understand how this is dependent on the spatial scale.
To do so, we simply determined at each resolution the scaling factor Cband between the luminosity in a given band and ΣSFR from the combination of Hα and 24 μm. This is done by carrying out an orthogonal distance regression using the odr module from the scipy python library on the following relation: 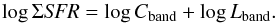 (1)To examine the difference between intense and quiescent regions, at each resolution we also separated the regions into four bins in addition to fitting the complete sample: top and bottom 50%, and top and bottom 15%, in terms of ΣSFR from the combination of Hα and 24 μm. The most extreme bins ensure that we only selected the most star-forming (top) or the most diffuse (bottom) regions in the galaxy.
(1)To examine the difference between intense and quiescent regions, at each resolution we also separated the regions into four bins in addition to fitting the complete sample: top and bottom 50%, and top and bottom 15%, in terms of ΣSFR from the combination of Hα and 24 μm. The most extreme bins ensure that we only selected the most star-forming (top) or the most diffuse (bottom) regions in the galaxy.
4.2.2. Dependence of SFR scaling relations on the pixel size
The dependence of the scaling factors on resolution at 8 μm, 24 μm, 70 μm, and 100 μm is presented in Fig. 6.
Description of the scaling relations.
It clearly appears that regions with strong and weak ΣSFR have markedly different scaling factors and a different evolution with pixel size. Compared to the entire sample, at 33 pc the scaling factor for the 50% (15%) brightest pixels is higher by a factor 1.06 to 1.16 (1.12 to 1.55). Conversely, the scaling factor for the 50% (15%) faintest pixels is lower by a factor 0.71 to 0.84 (0.56 to 0.74). When increasing the pixel size from 33 pc to 2084 pc, the scaling factor for pixels with a weak ΣSFR strongly increases. On the other hand, the scaling factor for pixels with a strong ΣSFR generally shows a slightly decreasing trend. From a typical scale of 400 pc to 1200 pc, depending on the infrared band, there is no significant difference in the scaling factors between pixels with weak and strong ΣSFR.
Impact of the relative fraction of diffuse emission.
As we have already explained, our reference SFR estimator combining Hα and 24 μm is unfortunately not perfect because it is also sensitive to diffuse emission that may or may not actually be related to star formation. We now consider only the 15% brightest pixels at 33 pc. They most likely correspond to pure star-forming regions with little or no diffuse emission. Conversely, the 15% faintest pixels will be almost exclusively made of diffuse emission with little or no local star formation. That way the scaling factor will be higher for the former compared to the latter. If we move to coarser resolutions, individual pixels will increasingly be made of a mix of star-forming and diffuse regions such that the brightest and faintest regions will be less different at 2084 pc than they are at 33 pc. This naturally yields increasingly similar scaling factors that progressively lose their dependence on the intensity of star formation. In other words, this means that on a scale larger than roughly 1 kpc, monochromatic IR bands from 8 μm to 100 μm may be as reliable for estimating the SFR as the combination of Hα and 24 μm. This scale is probably indicative of the typical scale from which there is always a similar fraction of diffuse and star-forming regions in each pixel, bright or faint. This scale is likely to vary depending on intensity of star formation in a given galaxy and on its physical propeties. This aspect should be explored in a broader sample of spiral galaxies. Moreover, this result is also affected by the transparency of the ISM as we show below, or by non-linearities that are not accounted for here. For instance, in intense star-forming regions the 8 μm emission may become depressed because of the PAH destruction by the strong radiation field (Boselli et al. 2004; Helou et al. 2004; Bendo et al. 2006), or because the 8 μm has a strong stochastic component that is proportionally more important than at 24 μm. These processes can induce a non-proportionality between the 8 μm emission and the SFR. Finally, we note that the difference in the scaling factor between the faintest and the brightest bins is minimal at 24 μm. This is most likely because the 24 μm emission affects both sides of Eq. (1).
Comparison with the literature.
When comparing the scaling factors determined in M 33 with those determined in the literature from both individual star-forming regions in galaxies and entire galaxies, we find instructive discrepancies. On a scale of 200 pc, the scaling factors at 70 μm determined by Li et al. (2013) for NGC 5055 and NGC 6946 are systematically higher. As discussed in this article, this may be due to background subtraction. Indeed, their study is based on the selection of individual H ii regions, allowing for the subtraction of the local background, which is not easily achieved with accuracy when carrying out a systematic pixel-by-pixel analysis we perform in this article. Without background subtraction, they obtained a scaling factor that is very similar to the factor we find when selecting pixels with a strong SFR. A similar study carried out on a scale of 700 pc by Li et al. (2010) led to a similar result.
When we compare our scaling factors to the factors obtained on entire galaxies at 24 μm by Rieke et al. (2009) and at 70 μm by Calzetti et al. (2010), there is a clear discrepancy: their scaling factors are lower. Because we see little trend with pixel size on larger scales, it appears unlikely that the scaling factor will diminish strongly at scales larger than 2084 pc. A possible explanation is that this could be due to the increased ISM transparency in M 33. In other words, this could be because a smaller fraction of the energetic radiation emitted by young stars is reprocessed by dust into the infrared. In the case of M 33, about 75% of star formation is seen in Hα and only 25% in the infrared. Indeed, Li et al. (2010) found a trend of the scaling factor with the oxygen abundance, with more metal-poor galaxies having a higher coefficient. If we consider the relation Li et al. (2010) found between the oxygen abundance and the scaling factor, the change in the coefficient from 12 + log O / H ≃ 8.3 (for M 33) to 12 + log O / H ≃ 8.7 (for the sample of Calzetti et al. 2010), would explain the observed discrepancy. At the same time, we note that the discrepancy with Rieke et al. (2009) at 24 μm is stronger than with Calzetti et al. (2010) at 70 μm. This is expected because the former sample consists of the most deeply dust-embedded galaxies ([ultra] luminous infrared galaxies), in contrast to the latter one, which is made of galaxies that are more transparent at short wavelength. We note, however, that at a given metallicity, Li et al. (2010) found a strong dispersion. This is exemplified by the case of NGC 5055 and NGC 6946, which despite having very similar metallicities yield very different scaling factors. In addition, a galaxy like the Large Magellanic Cloud, which has a metallicity similar to that of M 33, has a scaling factor similar to that of galaxies with 12 + log O / H ≃ 8.7, perhaps because it has been calibrated with HII regions, with diffuse emission having been subtracted, but accounting only for the obscured part of star formation (Lawton et al. 2010; Li et al. 2010). A dedicated study to distinguish the respective effects of the metallicity and the diffuse emission on the scaling factors at various scales would be required to fully understand this point.
5. Obscured versus unobscured star formation
5.1. FUV and Hα attenuation in M 33
Because of the dust, we only see a fraction of star formation in the UV or Hα. Following Kennicutt et al. (2009), hybrid SFR estimators allow us to easily compute a proxy (noted 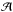 ) for the attenuation (noted A) of the UV and Hα fluxes.
) for the attenuation (noted A) of the UV and Hα fluxes.
![\begin{eqnarray} && \mathcal{A}\mathrm{_{FUV}} = \mathrm{2.5\log\left[{\it SFR}(FUV+24~\mu m)/{\it SFR}(FUV)\right]},\\ && \mathcal{A}\mathrm{_{H\alpha}} = \mathrm{2.5\log\left[{\it SFR}(H\alpha+24~\mu m)/{\it SFR}(H\alpha)\right]}.\label{eqn:AHalpha} \end{eqnarray}](/articles/aa/full_html/2015/06/aa23518-14/aa23518-14-eq74.png) We can also write this more directly in terms of luminosities:
We can also write this more directly in terms of luminosities:
![\begin{eqnarray} &&\mathcal{A}\mathrm{_{FUV}} = \mathrm{2.5\log\left[1+{\it k}_{FUV-24}\times {\it L}(24~\mu m)/{\it L}(FUV)\right]},\\ &&\mathcal{A}\mathrm{_{H\alpha}} = \mathrm{2.5\log\left[1+{\it k}_{H\alpha-24}\times{\it L}(24~\mu m)/{\it L}(H\alpha)\right]}, \end{eqnarray}](/articles/aa/full_html/2015/06/aa23518-14/aa23518-14-eq75.png) with kband1 - band2 defined as in Sect. 3.1 and Table 1. These expressions can also be written equivalently in terms of surface brightnesses. Before proceeding, we recall that these estimators have been defined for star-forming regions and may not provide accurate estimates outside of their definition range.
with kband1 - band2 defined as in Sect. 3.1 and Table 1. These expressions can also be written equivalently in terms of surface brightnesses. Before proceeding, we recall that these estimators have been defined for star-forming regions and may not provide accurate estimates outside of their definition range.
Because the attenuation increases with decreasing wavelength, the attenuation in the FUV is higher than in the optical. For instance, if we consider the Milky Way extinction curve of Cardelli et al. (1989) with the update of O’Donnell (1994), for AV = 1, AHα ≃ 0.8 and AFUV ≃ 2.6. However, nebular emission is more closely linked to the most recent star formation episode, and therefore to dust, than the underlying stellar continuum. As a consequence, the Hα line is actually more attenuated than the stellar continuum at the same wavelength than what we could expect from the extinction by a simple dust screen affecting both components the same way (Calzetti et al. 1994, 2000; Charlot & Fall 2000). In reality, this differential attenuation strongly depends on the geometry between the dust and the stars as well as on the star formation history. Given the broad range of physical conditions and scales in M 33, we can expect the attenuation law between Hα and the FUV band to vary strongly across the galaxy and across scales. Such variations would provide useful information on the effective attenuation curve between these two popular star formation tracers. The relations between Hα and FUV attenuations as a function of ΣSFR and the specific SFR (sSFR, the SFR per unit stellar mass) are shown in Fig. 7.
 |
Fig. 7 Attenuation in the FUV band versus the attenuation in Hα. The colour of each point indicates ΣSFR (upper row) or the sSFR (lower row), following the bar to the right. In the bottom row, the number of regions N and the Spearman correlation coefficient ρ are indicated. To compute the sSFR, the stellar mass in each region was computed from the 3.6 μm emission using the linear conversion factor of Zhu et al. (2010). The red line shows the one-to-one relation. The black, magenta, and cyan lines represent the attenuation for a starburst, a Milky Way, and an LMC average curve with differential reddening (f ≡ E(B−V)continuum/E(B−V)gas = 0.44, solid, with E(B−V)continuum being the reddening between the V and B bands of the stellar continuum and E(B−V)gas being that of the ionised gas) and without (f = 1, dashed). For the starburst relation, we assumed that even though the stellar continuum follows the starburst curve, the gas still follows a Milky Way curve. Note that the black and cyan solid lines are nearly overlap. At the finest resolution, there is a broad range in terms of differential reddening. Intense star-forming regions have little differential reddening, whereas diffuse regions present a strong differential reddening. On coarser scales, the averaging between diffuse and star-forming regions yields a differential reddening that is similar to that of starburst galaxies. The overall shape of the attenuation law is only weakly constrained, however, and may vary across the galaxy. |
On average, the attenuation in M 33 is relatively low for a spiral galaxy. There are peaks of attenuation reaching 2.5 mag in the FUV band at a resolution of 33 pc, but when we consider large sections of the galaxy on 2 kpc scales, the typical attenuation is around 0.6 mag in the FUV band and 0.4 mag in Hα, making M 33 mostly transparent in star-formation-tracing bands on large scales. While this is lower than the typical FUV attenuation in nearby spiral galaxies (Boquien et al. 2012, 2013), it is consistent with previous findings in M 33 (Tabatabaei et al. 2007; Verley et al. 2009). This difference compared to local spirals is probably due to the more metal-poor nature of M 33.
Overall, we find that at the finest resolution, regions in M 33 span a broad range in terms of absolute and relative attenuations in FUV and Hα. This does not appear to be due to random noise, however, because the locus of the regions is structured according the the intensity of star formation. Regions with intense star formation as traced by the combination of Hα with 24 μm tend to have a higher  than
than  . This is especially visible at the finest spatial resolution. Intensely star-forming regions such as NGC 604 show a peak in
. This is especially visible at the finest spatial resolution. Intensely star-forming regions such as NGC 604 show a peak in 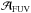 , whereas no particular increase is seen in
, whereas no particular increase is seen in 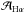 . If we select all pixels with ΣSFR(Hα + 24 μm) ≥ 0.1 M⊙ yr-1 kpc-2 at 33 pc, we find
. If we select all pixels with ΣSFR(Hα + 24 μm) ≥ 0.1 M⊙ yr-1 kpc-2 at 33 pc, we find 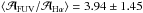 , versus
, versus 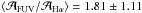 for less active regions. As the resolution becomes coarser, excursions in attenuation become more moderate and the range covered in terms of FUV and Hα attenuations becomes much smaller. At the coarsest resolution,
for less active regions. As the resolution becomes coarser, excursions in attenuation become more moderate and the range covered in terms of FUV and Hα attenuations becomes much smaller. At the coarsest resolution, 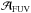 and
and 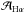 show little scatter, and they are consistent with a starburst or a Milky Way law with a differential reddening (see Sect. 5.2) between the stellar continuum and the gas. What probably happens is that at coarser resolutions, intensely star-forming regions and quiescent regions merge, which decreases the dynamic range in terms of attenuation properties. At the coarsest resolution, all regions have broadly similar properties, which is why they all have similar attenuation laws. We detail this aspect in Sect. 5.2.
show little scatter, and they are consistent with a starburst or a Milky Way law with a differential reddening (see Sect. 5.2) between the stellar continuum and the gas. What probably happens is that at coarser resolutions, intensely star-forming regions and quiescent regions merge, which decreases the dynamic range in terms of attenuation properties. At the coarsest resolution, all regions have broadly similar properties, which is why they all have similar attenuation laws. We detail this aspect in Sect. 5.2.
Finally, we also mention the possibility that there is a change in the intrinsic extinction laws because of changes in the dust composition. Regions at low ΣSFR are located in the outskirts of the galaxy. However, this is probably a minor effect. M 33 has a very modest metallicity gradient of −0.027 ± 0.012 dex/kpc (Rosolowsky & Simon 2008). As we can see in Fig. 7, a variation of the differential reddening has a much stronger effect than a change in the intrinsic extinction curve from the Milky Way to the LMC average.
5.2. Variations of attenuation laws with scale
At first sight, these variations may seem at odds with the now well-established picture of differential attenuation between the gas and the stars in galaxies (Calzetti et al. 1994, 2000; Charlot & Fall 2000). However, this description was conceived in the particular context of starburst galaxies and may not apply directly to resolved and more quiescent galaxies. We first consider M 33 at a resolution of 33 pc. As mentioned earlier, a low value for ΣSFR corresponds to diffuse emission with at most very little local star formation. Because gas is intimately linked with dust, the Hα radiation in this environment always undergoes some attenuation. The stellar emission may be relatively attenuation-free, however, as it is not particularly linked to dust, depending on the actual geometry. This would explain the relatively shallow effective FUV-Hα attenuation curve that is normally seen in starburst galaxies. Now, if we consider star-forming regions, the FUV-emitting stars will on average be younger and still closely linked to their birth cloud, hence undergoing a much higher attenuation than in diffuse regions. Because Hα is always linked to dust, the increase of the attenuation is not as strong. If we now consider coarser resolutions, we increasingly mix diffuse and star-forming regions. On a local scale, 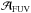 is on average much larger than
is on average much larger than 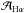 in star-forming regions but more similar in diffuse regions, as we have seen above. This means that on a global scale, the effective Hα-UV attenuation curve should be shallower than intrinsic extinction curves. This agrees with what we see on a scale of 2 kpc,
in star-forming regions but more similar in diffuse regions, as we have seen above. This means that on a global scale, the effective Hα-UV attenuation curve should be shallower than intrinsic extinction curves. This agrees with what we see on a scale of 2 kpc, 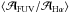 = 1.46 ± 0.24.
= 1.46 ± 0.24.
Using FUV to FIR broadband data on a sample of nearby, resolved galaxies on a typical scale of 1 kpc, Boquien et al. (2012) found hints of an evolution of the attenuation curve of the stellar continuum, with the age of star-forming regions, from a starburst-like curve in young regions to LMC-like curves in older regions. A consistent result was found on the scale of entire galaxies by Kriek & Conroy (2013). They showed that 0.5 <z< 2.0 galaxies with a high sSFR have a shallower attenuation curve. If we assume that a high ΣSFR is an indication of a young age, this would appear to be opposite of the trend we see in M 33. However, a direct comparison is not straightforward because here we are comparing the nebular attenuation to the stellar continuum attenuation, and with measurements at only two wavelengths. In other words, we consider the difference between the gas and the stellar attenuation curves, measuring each at only a single wavelength.
A major and poorly constrained factor that is important for this comparison is the differential reddening we mentioned earlier, which we can write as f = E(B−V)continuum/E(B−V)gas. This can also be expressed in terms of attenuations. Considering that E(B−V) = AV/RV, f = AV,continuum/AV,gas × RV,gas/RV,continuum. As we have stated earlier, in diffuse regions FUV-emitting stars are probably more weakly linked to the dust than the ionised gas. As such, in diffuse regions f may be much smaller than it is in pure star-forming regions where it should be closer to f = 1. This means that in diffuse regions the attenuation of the stellar continuum would be much smaller than the attenuation of the nebular emission at a given wavelength. Based on a sample of galaxies observed by the SDSS, Wild et al. (2011) found that the optical depth of nebular emission compared to that of the continuum is significantly higher for galaxies at low sSFR. They attributed this to a variation of the relative weight of diffuse and star-forming regions. This means that f is smaller in these more quiescent galaxies. Similar results have been obtained by Price et al. (2014) based on the 3D-HST survey and by Kashino et al. (2013) using ground-based spectra of galaxies at z = 1.6. To verify these results in M 33, in Fig. 7 we have also colour-coded the relation between 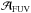 and
and 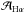 as a function of the sSFR. We find a result consistent with that of the aforementioned works. Regions with a high sSFR have a high value of f, whereas regions with a low sSFR have a low value of f. This way, considering a variation of f, it is possible that the effective FUV-Hα attenuation curve would show an evolution different from the attenuation curve of the stellar continuum emission. Our results suggest both a variation of f across the galaxy on a given scale from diffuse regions to star-forming regions, and a variation depending on the scale due to averaging of star-forming and diffuse regions that have different values of f. At the finest resolution, a range of f is required to explain the observations across the galaxy. Towards coarser resolutions, however, the observations can be explained with f = 0.44.
as a function of the sSFR. We find a result consistent with that of the aforementioned works. Regions with a high sSFR have a high value of f, whereas regions with a low sSFR have a low value of f. This way, considering a variation of f, it is possible that the effective FUV-Hα attenuation curve would show an evolution different from the attenuation curve of the stellar continuum emission. Our results suggest both a variation of f across the galaxy on a given scale from diffuse regions to star-forming regions, and a variation depending on the scale due to averaging of star-forming and diffuse regions that have different values of f. At the finest resolution, a range of f is required to explain the observations across the galaxy. Towards coarser resolutions, however, the observations can be explained with f = 0.44.
5.3. Limits on determining the attenuation
This discussion relies on the assumption that no systematic bias is introduced by the way we compute the attenuation and ΣSFR. If we consider ΣSFR from FUV and 24 μm rather than from Hα and 24 μm, the trends are not as clear. There is a fraction of pixels at 33 pc with very low FUV attenuation (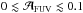 ) and moderately high ΣSFR. This probably corresponds to regions with a low level of 24 μm and Hα emission but with strong FUV. That could be the case for instance in a region where recently formed clusters have blown away much of the dust and the gas of their parent clouds. Such regions were found by Relaño et al. (2013), especially in the outskirts of M 33.
) and moderately high ΣSFR. This probably corresponds to regions with a low level of 24 μm and Hα emission but with strong FUV. That could be the case for instance in a region where recently formed clusters have blown away much of the dust and the gas of their parent clouds. Such regions were found by Relaño et al. (2013), especially in the outskirts of M 33.
A specific bias may affect some diffuse regions. The most extreme have 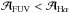 , which would require a particularly strong differential attenuation. A close inspection reveals that these regions are also somewhat fainter in Hα. The relatively higher uncertainties would then propagate into the attenuation estimates, yielding spuriously low
, which would require a particularly strong differential attenuation. A close inspection reveals that these regions are also somewhat fainter in Hα. The relatively higher uncertainties would then propagate into the attenuation estimates, yielding spuriously low 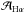 . In practice, they could also be affected by very strong age and radiation transfer effects such as the escape of ionising photons, which would reduce the local Hα luminosity, independent of the actual attenuation underwent by Hα photons. In that case, with a lower Hα and for the same amount of 24 μm, the selected estimators will then naturally overestimate AHα. These regions would in reality not present a differential attenuation as extreme as could be inferred from our estimates. To ensure that these uncertainties on diffuse regions do not affect our results, we have selected only regions with ΣSFR(Hα + 24 μm) > 10-2M⊙ yr-1 kpc-2, which means that we removed purely diffuse regions. We still see the clear gradients described in Fig. 7. This means that if in the most extreme regions, the differential attenuation is likely to be overestimated, there is still a clear variation of the differential attenuation depending on the sSFR.
. In practice, they could also be affected by very strong age and radiation transfer effects such as the escape of ionising photons, which would reduce the local Hα luminosity, independent of the actual attenuation underwent by Hα photons. In that case, with a lower Hα and for the same amount of 24 μm, the selected estimators will then naturally overestimate AHα. These regions would in reality not present a differential attenuation as extreme as could be inferred from our estimates. To ensure that these uncertainties on diffuse regions do not affect our results, we have selected only regions with ΣSFR(Hα + 24 μm) > 10-2M⊙ yr-1 kpc-2, which means that we removed purely diffuse regions. We still see the clear gradients described in Fig. 7. This means that if in the most extreme regions, the differential attenuation is likely to be overestimated, there is still a clear variation of the differential attenuation depending on the sSFR.
The issues we have presented show the sensitivity of such an analysis on the selected SFR estimators and the great caution that must be used when interpreting such results. A promising way to reduce such potential problems would be to compute the attenuation with a full SED modelling for the stellar continuum and from the Balmer decrement for the nebular emission. The increasing availability of spectral maps using integral field spectrographs (IFS), and large multi-wavelength surveys now makes this possible for nearby galaxies (e.g., Sánchez et al. 2012; Blanc et al. 2013). Recently, Kreckel et al. (2013) have used such IFS data on a sample of eight nearby galaxies, deriving the nebular attenuation from the Balmer decrement and the stellar attenuation from the shape of the continuum between 500 nm and 700 nm. Interestingly, in contrast to our results and that of Wild et al. (2011), they found that in diffuse regions the attenuation of the stars increases compared to that of the gas. In the most extreme cases, in the V band the stellar attenuation is ten times higher than that of the gas. Conversely, for regions with ΣSFR> 10-1M⊙ yr-1 kpc-2, they converge on f = 0.47, close to what we find at the coarsest resolution. The discrepancy at low ΣSFR may be due to systematics in the way the attenuation is computed for the diffuse medium, both for the stars and the gas. For similar-sized regions at high ΣSFR, the discrepancy is probably due to the fact we measure the continuum attenuation in the FUV, whereas Kreckel et al. (2013) measured it in the optical. In their case, even in star-forming regions the continuum emission is generally dominated by older stellar populations, which is not necessarily the case in the FUV, inducing a different f. This effect is probably prevalent mainly on the smallest scales.
To summarise, great care must be used when correcting star-formation-tracing bands for the attenuation. We have shown that there are clear variations of the effective FUV-Hα attenuation curves that depend on the sSFR and ΣSFR, with regions at higher SFR having steeper attenuation curves. This is due to a strong variation of the differential reddening between the stars and the gas. Intense star-forming regions have little differential reddening (f ≃ 1), in contrast to more quiescent regions. Finally, there is also a strong variation with the resolution, which is due to averaging regions with different physical properties. At the coarsest resolution, the effective attenuation curve is compatible a differential reddening of f = 0.44, which is the value for the starburst curve, for instance. It is not possible to distinguish between different laws at fixed differential reddening, however.
6. Discussion
We have found that the differential attenuation in M 33 varies strongly on both the spatial scale and the sSFR. At the same time, it appears that resolution effects become weak beyond a scale of 1 kpc. In light of these results, we now have a better insight into the relation between UV-emitting stars and dust in galaxies (Sect. 6.1). They also allow us to understand how the measure of the SFR will be affected by high-resolution observations with upcoming instruments (Sect. 6.2).
6.1. Constraints on the relative geometry of stars and dust in star-forming galaxies
The actual geometry between the stars and the dust in galaxies is undoubtedly complex, but a simple generalised model has emerged for starburst and more quiescent star-forming galaxies (Calzetti et al. 1994; Wild et al. 2011; Price et al. 2014). These descriptions generally rely on a two-component model framework (e.g., Charlot & Fall 2000): dense star-forming regions and a diffuse medium with a lower density. We do not revisit the general descriptions of galaxies that have been discussed in detail in the literature (e.g., Wild et al. 2011). Our multi-scale analysis sheds light on the distribution between FUV-emitting stars and the dust on a local scale, however.
We have found that the differential reddening in diffuse regions is high. This shows that the FUV-emitting stars are relatively unassociated with dust. This requires these stars to have escaped their birth cocoon or stellar feedback to have induced a physical displacement between the young stars on one hand and the gas and dust on the other hand. Conversely, the nebular emission is more strongly attenuated. This means that the ionised gas is more associated with dust than the stars. Several mechanisms can be invoked. First, this emission may originate from gas ionised by nearby massive stars or created by ionising radiation that has escaped from more distant star-forming regions. Hoopes & Walterbos (2000) found that massive stars in the field can account for 40% of the ionisation of the diffuse ionised gas in M 33. An alternative is that it comes from Hα photons that have travelled a long distance in the plane of the disk before being scattered in the direction of the line of sight. The latter possibility is less likely because it would locally boost the Hα luminosity relative to the 24 μm one, thereby reducing the attenuation inferred from Eq. (3).
Conversely, in star-forming regions there is very little differential reddening. This suggests that the UV-emitting stars, the dust, and the gas are well mixed and follow similar distributions. The actual geometry drives the transformation of the extinction curve, which describes the case when there is a simple dust screen in front of the sources, into an attenuation curve. Constraining the geometry would require additional data to attempt to break the various degeneracies affecting the determination of the attenuation curve. This is a notoriously difficult task, especially since the structure of the ISM is much more complex than the simple assumptions that are usually made.
The progressive convergence towards the canonical differential reddening of f = 0.44 at larger scales shows the effect of the distribution of gas and stars on local scales on the galaxy seen at coarser scales. But this also shows the danger of assuming similar geometries and attenuation curves across all scales and all regions in resolved galaxies. Assuming a differential reddening different from what it is in reality can lead to errors of a factor of several on the determination of the attenuation, and therefore on the determination of the SFR. In other words: there is no unique attenuation law that is valid under all circumstances. However, considering regions of at least 1 kpc across strongly limits resolution effects to compute the SFR. This is probably due to the broad mixing between star-forming and diffuse regions. We explore in the next section for which conditions this scale dependence is most likely to have an effect in the era of high-resolution observations.
We present a simplified graphical description of the relative geometry of stars, gas, and dust in diffuse and in star-forming regions in Fig. 8. It is conceptually similar to Fig. 8 in Calzetti (2001), but at the same time, it shows the fundamental difference between normal star-forming galaxies and starburst galaxies.
 |
Fig. 8 Simplified description of the relative distribution of stars, gas, and dust on a local scale in diffuse regions (top) and in star-forming regions (bottom). The FUV emitting stars are shown in blue, whereas older stellar populations are plotted in yellow or orange. The clouds of gas and dust are symbolised with grey patches. |
6.2. Measuring high-redshift star formation in the era of high-resolution ALMA and the JWST observations
As we have shown in this article, the determination of the SFR or the attenuation does not only depend on luminosity, but also on scale. With the recent commissioning of ALMA and the launch of the JWST by the end of the decade, it will finally be possible to carry out highly resolved observations of star formation not only in the nearby Universe, but also well beyond. With such opportunities also come the complexities inherent to high-resolution studies. To examine in which cases the interpretation of the observations may be affected by the resolution, we have plotted in Fig. 9 the physical scale that can be reached in the UV and in the IR with the JWST and ALMA.
It is expected that the highest resolution will be achieved in the rest-frame 200 nm, which will allow us to distinguish 500 pc details all the way to z = 10. Unless degraded to lower resolution, these images may prove problematic to derive reliably the local physical parameters. Conversely, the resolution of rest-frame 8 μm rapidly degrades with increasing redshift, reaching 9 kpc at the maximum redshift of z = 2.5. It would still be considerably useful to carry out resolved studies of low-redshift galaxies; a resolution of 1 kpc is already achieved at z = 0.15.
To probe the peak of dust emission at 100 μm with ALMA, a baseline of 1 km appears nearly perfect, with the resolution only slightly varying around 1 kpc from z = 3.2 to z = 9.9. A baseline of only 150 m would only provide us with a much coarser resolution of 4 to 5 kpc. An additional complexity not taken into account here would be the loss of uv coverage from the lack of short baselines, which would be especially problematic at low redshift. This would require complementary observations with the Atacama Compact Array. The addition in the future of bands 10 and perhaps 11 will allow the use of shorter baselines while extending the window to lower redshift galaxies. Band 11 would be able to detect 100 μm emission down to z = 1.
Overall, the synergy between ALMA and the JWST is excellent for probing star formation on a well-resolved scale while also gaining valuable insight into triggering or feedback. The combination of these instruments will extend the spatially resolved multi-wavelength studies to much higher redshifts, which currently can only be done for nearby galaxies.
 |
Fig. 9 Spatial resolution versus z for a rest frame wavelength of 200 nm (yellow) and 8 μm (red) with the JWST, and at 100 μm with ALMA for baselines of 150 m (blue) and 1 km (green). We adopted the cosmological parameters of Planck Collaboration XVI et al. (2014). The solid lines show at which redshifts the observations can be carried out. With the JWST, observations below 200 nm are not possible below z = 2, while observations beyond z = 2.5 are not possible at 8 μm. Conversely, the rest frame emission at 100 μm cannot be observed with ALMA below z = 3.2. There are several gaps at longer wavelengths corresponding to the gaps between different ALMA bands. These bands correspond to those available for cycle 2. Band 10 will strongly improve the capabilities of ALMA to map the main infrared star formation bands at moderate redshifts, while band 11 will allow us to probe the peak of dust emission down to z = 1. Finally, the hatched area corresponds to a resolution lower than 1 kpc, where there may be a strong effect on the measure of star formation. |
7. Conclusion
To understand how SFR measurements of galaxies depend on the physical scale, we have carried out an analysis of the emission of the local group galaxy M 33 from 33 pc to 2084 pc. We have found the following results:
-
1.
Monochromatic SFR estimators can be strongly discrepantcompared to a reference Hα+24 μm estimator. Thesediscrepancies depend on the scale of the study and on ΣSFR. Theymay be due to be combined effects of the age, the geometry, thetransparency of the ISM, and the importance of diffuse emission.
-
2.
The scaling factors from individual infrared bands to ΣSFR show a vigorous evolution with physical size, up to a factor 2. Star-forming and diffuse regions show a different evolution with the spatial scale. The scaling factors converge at large scales, however.
-
3.
More generally, such variations with the physical scale and the discrepancies of the scaling relations compared to those obtained from different samples show that it is especially dangerous to apply SFR estimators beyond their validity range in terms of surface brightness, physical scale, and metallicity. This problem is especially important when applying SFR estimators on higher redshift galaxies because their physical properties may be more poorly known. This is why we made no attempt to derive a multi-scale SFR estimator, because it would be strongly tied with M 33. That being said, carrying out studies at a scale coarser than 1 kpc strongly limits resolution effects. Such resolutions will be routinely achieved at high redshift with ALMA and the JWST.
-
4.
Finally, there is a clear change in the differential reddening between the nebular emission and the stellar continuum depending on both the physical scale and on the ΣSFR or the sSFR. Star-forming regions have nearly no differential reddening, whereas diffuse regions have a strong differential reddening. This change in the reddening is especially visible at the finest spatial resolution. At coarser resolutions, the differential reddening converges to values compatible with the canonical 0.44 value derived for starburst galaxies by Calzetti et al. (2000). These results allow us to obtain new insights into the relative geometry between the stars and the dust on a local scale in galaxies, from diffuse regions to star-forming regions.
We distinguish between the extinction, which includes the absorption and the scattering out of the line of sight, and the attenuation, which also includes the scattering into the line of sight. In practice, we here only have access to the attenuation and not to the extinction. See for instance Sect. 1.4.1 of Calzetti (2013).
Acknowledgments
M.B. thanks Robert Kennicutt, Kathryn Kreckel, Yiming Li, and Vivienne Wild for useful discussions that have helped improve the paper. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. This research has made use of the NASA/IPAC Infrared Science Archive, which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. This research made use of Astropy, a community-developed core Python package for Astronomy (Astropy Collaboration et al. 2013). This research made use of APLpy, an open-source plotting package for Python hosted at http://aplpy.github.com.
References
- Aniano, G., Draine, B. T., Gordon, K. D., & Sandstrom, K. 2011, PASP, 123, 1218 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration, Robitaille, T. P., Tollerud, E. J., et al. 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bendo, G. J., Dale, D. A., Draine, B. T., et al. 2006, ApJ, 652, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Bendo, G. J., Wilson, C. D., Pohlen, M., et al. 2010, A&A, 518, L65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bendo, G. J., Boselli, A., Dariush, A., et al. 2012, MNRAS, 419, 1833 [NASA ADS] [CrossRef] [Google Scholar]
- Bigiel, F., Leroy, A., Walter, F., et al. 2008, AJ, 136, 2846 [NASA ADS] [CrossRef] [Google Scholar]
- Blanc, G. A., Weinzirl, T., Song, M., et al. 2013, AJ, 145, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Boquien, M., Bendo, G., Calzetti, D., et al. 2010a, ApJ, 713, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Boquien, M., Calzetti, D., Kramer, C., et al. 2010b, A&A, 518, L70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boquien, M., Calzetti, D., Combes, F., et al. 2011, AJ, 142, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Boquien, M., Buat, V., Boselli, A., et al. 2012, A&A, 539, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boquien, M., Boselli, A., Buat, V., et al. 2013, A&A, 554, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boquien, M., Buat, V., & Perret, V. 2014, A&A, 571, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Lequeux, J., & Gavazzi, G. 2004, A&A, 428, 409 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Boissier, S., Cortese, L., et al. 2009, ApJ, 706, 1527 [NASA ADS] [CrossRef] [Google Scholar]
- Calapa, M. D., Calzetti, D., Draine, B. T., et al. 2014, ApJ, 784, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D. 2001, PASP, 113, 1449 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D. 2013, in Secular Evolution of galaxies, eds. J. Falcón-Barroso, & J. H. Knapen (Cambridge University Press), 419 [Google Scholar]
- Calzetti, D., Kinney, A. L., & Storchi-Bergmann, T. 1994, ApJ, 429, 582 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Kennicutt, R. C., Bianchi, L., et al. 2005, ApJ, 633, 871 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Kennicutt, R. C., Engelbracht, C. W., et al. 2007, ApJ, 666, 870 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Wu, S., Hong, S., et al. 2010, ApJ, 714, 1256 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Liu, G., & Koda, J. 2012, ApJ, 752, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Charlot, S., & Fall, S. M. 2000, ApJ, 539, 718 [NASA ADS] [CrossRef] [Google Scholar]
- Ciesla, L., Boquien, M., Boselli, A., et al. 2014, A&A, 565, A128 [Google Scholar]
- Crocker, A. F., Calzetti, D., Thilker, D. A., et al. 2013, ApJ, 762, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, D. A., Cohen, S. A., Johnson, L. C., et al. 2009, ApJ, 703, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., Dale, D. A., Bendo, G., et al. 2007, ApJ, 663, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Fazio, G. G., Hora, J. L., Allen, L. E., et al. 2004, ApJS, 154, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Fouesneau, M., Lançon, A., Chandar, R., & Whitmore, B. C. 2012, ApJ, 750, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Freedman, W. L., Wilson, C. D., & Madore, B. F. 1991, ApJ, 372, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Galametz, M., Kennicutt, R. C., Calzetti, D., et al. 2013, MNRAS, 431, 1956 [NASA ADS] [CrossRef] [Google Scholar]
- Gil de Paz, A., Boissier, S., Madore, B. F., et al. 2007, ApJS, 173, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Hao, C.-N., Kennicutt, R. C., Johnson, B. D., et al. 2011, ApJ, 741, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Helou, G., Roussel, H., Appleton, P., et al. 2004, ApJS, 154, 253 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hinz, J. L., Rieke, G. H., Gordon, K. D., et al. 2004, ApJS, 154, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Hoopes, C. G., & Walterbos, R. A. M. 2000, ApJ, 541, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, B. D., Weisz, D. R., Dalcanton, J. J., et al. 2013, ApJ, 772, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Kashino, D., Silverman, J. D., Rodighiero, G., et al. 2013, ApJ, 777, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C., Calzetti, D., Walter, F., et al. 2007, ApJ, 671, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Hao, C., Calzetti, D., et al. 2009, ApJ, 703, 1672 [NASA ADS] [CrossRef] [Google Scholar]
- Kramer, C., Buchbender, C., Xilouris, E. M., et al. 2010, A&A, 518, L67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kreckel, K., Groves, B., Schinnerer, E., et al. 2013, ApJ, 771, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Kriek, M., & Conroy, C. 2013, ApJ, 775, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Kruijssen, J. M. D., & Longmore, S. N. 2014, MNRAS, 439, 3239 [NASA ADS] [CrossRef] [Google Scholar]
- Lawton, B., Gordon, K. D., Babler, B., et al. 2010, ApJ, 716, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2782 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Bigiel, F., de Blok, W. J. G., et al. 2012, AJ, 144, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Sandstrom, K., et al. 2013, AJ, 146, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Y., Calzetti, D., Kennicutt, R. C., et al. 2010, ApJ, 725, 677 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Y., Crocker, A. F., Calzetti, D., et al. 2013, ApJ, 768, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, G., Koda, J., Calzetti, D., Fukuhara, M., & Momose, R. 2011, ApJ, 735, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Louie, M., Koda, J., & Egusa, F. 2013, ApJ, 763, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Magrini, L., Stanghellini, L., & Villaver, E. 2009, ApJ, 696, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, D. C., Fanson, J., Schiminovich, D., et al. 2005, ApJ, 619, L1 [Google Scholar]
- Meidt, S. E., Schinnerer, E., Knapen, J. H., et al. 2012, ApJ, 744, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, E. J., Condon, J. J., Schinnerer, E., et al. 2011, ApJ, 737, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Neugebauer, G., Habing, H. J., van Duinen, R., et al. 1984, ApJ, 278, L1 [Google Scholar]
- O’Donnell, J. E. 1994, ApJ, 422, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Onodera, S., Kuno, N., Tosaki, T., et al. 2010, ApJ, 722, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Ott, S. 2010, Astronomical Data Analysis Software and Systems XIX, eds. Y. Mizumoto, K.-I. Morita, & M. Ohishi, ASP Conf. Ser. [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XVI. 2014, A&A, 571, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Price, S. H., Kriek, M., Brammer, G. B., et al. 2014, ApJ, 788, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Regan, M. W., & Vogel, S. N. 1994, ApJ, 434, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Relaño, M., & Kennicutt, Jr., R. C. 2009, ApJ, 699, 1125 [NASA ADS] [CrossRef] [Google Scholar]
- Relaño, M., Verley, S., Pérez, I., et al. 2013, A&A, 552, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieke, G. H., Young, E. T., Engelbracht, C. W., et al. 2004, ApJS, 154, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Rieke, G. H., Alonso-Herrero, A., Weiner, B. J., et al. 2009, ApJ, 692, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Rosolowsky, E., & Simon, J. D. 2008, ApJ, 675, 1213 [NASA ADS] [CrossRef] [Google Scholar]
- Roussel, H. 2013, PASP, 125, 1126 [Google Scholar]
- Sánchez, S. F., Kennicutt, R. C., Gil de Paz, A., et al. 2012, A&A, 538, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schruba, A., Leroy, A. K., Walter, F., Sandstrom, K., & Rosolowsky, E. 2010, ApJ, 722, 1699 [NASA ADS] [CrossRef] [Google Scholar]
- Tabatabaei, F. S., Beck, R., Krügel, E., et al. 2007, A&A, 475, 133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thilker, D. A., Hoopes, C. G., Bianchi, L., et al. 2005, ApJ, 619, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Verley, S., Hunt, L. K., Corbelli, E., & Giovanardi, C. 2007, A&A, 476, 1161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verley, S., Corbelli, E., Giovanardi, C., & Hunt, L. K. 2009, A&A, 493, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verley, S., Relaño, M., Kramer, C., et al. 2010, A&A, 518, L68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wild, V., Charlot, S., Brinchmann, J., et al. 2011, MNRAS, 417, 1760 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, Y.-N., Wu, H., Li, H.-N., & Cao, C. 2010, Res. Astron. Astrophys., 10, 329 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Map of M 33 at 70 μm obtained with the Herschel PACS instrument in the context of a cycle 2 programme (OT2_mboquien_4, observation ID 1342247408 and 1342247409; the original map is available from the link given in footnote 2). The image is in Jy/arcsec2, and the colours follow an arcsinh scale indicated by the bar on the right side of the figure. The physical scale is indicated by the white line in the bottom right corner of the figure, representing 1 kpc. Each pixel has a size of 1.4′′. |
| In the text | |
 |
Fig. 2 Convolved images registered to a common reference frame at 33 pc (8′′/pixel, left), 260 pc (64′′/pixel, centre), and 2084 pc (512′′/pixel, right). Each row represents a different star-formation-tracing band, from top to bottom: GALEX FUV, Hα, IRAC 8 μm, MIPS 24 μm, PACS 70 μm, and PACS 100 μm. Blue pixels have a low flux density, whereas red pixels have a high flux density, following an arcsinh scale. The colours used are simply chosen to best represent the wide dynamical range of intensities across all bands and all pixel sizes and should be used in a qualitative sense only. |
| In the text | |
 |
Fig. 3 Comparison of monochromatic SFR estimators with the reference SFR(Hα+24 μm) estimator versus the spatial scale. The colour indicates the monochromatic band: FUV (blue), Hα (cyan), 24 μm (green), 70 μm (magenta), and 100 μm (red). Left panel: correlation coefficient between the monochromatic and reference estimators. Right panel: mean offset (solid line) and the standard deviation (shaded area) of the difference between the estimators. |
| In the text | |
 |
Fig. 4 Relations at 33 pc (left), 260 pc (centre), and 2084 pc (right) of Lν(70 μm) versus Lν(24 μm) (top), and Lν(100 μm) versus Lν(70 μm) (bottom). All luminosities have been multiplied by a constant factor corresponding to a linear SFR estimator (a24 = 2.04 × 10-36M⊙ yr-1 W-1, a70 = 5.89 × 10-37M⊙ yr-1 W-1, and a100 = 5.17 × 10-37M⊙ yr-1 W-1) to place them on a similar scale. The colour of each point indicates ΣSFR following the colour bar at the right of each row. The red line indicates a one-to-one relation. We see the non-linear relations between the luminosities in different bands. These non-linearities are particularly apparent on the finest pixel scales. On coarser scales, the relations appear more linear, which is probably due to a mixing between diffuse and star-forming regions. |
| In the text | |
 |
Fig. 5 70-to-100 versus 24-to-70 flux density ratios for each pixel at a resolution of 33 pc (left) and 260 pc (right). The colour of each symbol corresponds to ΣSFR, according to the colour bar on the right. The grid represents the models of Draine & Li (2007), with the MW3.1_30 dust composition, 0.10 ≤ Umin ≤ 25, and 0.00 ≤ γ ≤ 0.20. The red dashed lines indicate the locus corresponding to the one-to-one relations shown in Fig. 4. The 3σ uncertainties are shown in the bottom right corner. The 24-to-70 ratio is well correlated with γ and ΣSFR, especially at 33 pc. At 260 pc, due to mixing between diffuse and star-forming regions, excursions in γ are strongly reduced. Note that when considering the galaxy as a whole, a large part of the emission is due to the handful of luminous regions and not to the larger number of faint regions. |
| In the text | |
 |
Fig. 6 Scaling coefficients from the luminosity in infrared bands to ΣSFR versus the pixel size, at 8 μm, 24 μm, 70 μm, and 100 μm, from the top left corner to the bottom right corner. The blue line indicates the value of the scaling factor when taking into account all pixels detected at a 3σ level in all six bands. The red (green) line indicates the scaling factor when considering only pixels with a ΣSFR higher (lower) than the median ΣSFR at a given resolution. The cyan and magenta lines represent regions in the top and bottom 15% in terms of ΣSFR. The shaded areas of the corresponding colours indicate the 1σ uncertainties. The horizontal dashed line at 24 μm (resp. 70 μm) indicates the scaling factor determined by Rieke et al. (2009), Calzetti et al. (2010) for entire galaxies. The crosses for the 70 μm and 100 μm bands indicate the scaling factor determined for individual galaxies on a scale of 200 pc (Li et al. 2013) and 700 pc (Li et al. 2010). The squares indicate mean values over several galaxies. The empty squares denote that no background subtraction was performed. |
| In the text | |
 |
Fig. 7 Attenuation in the FUV band versus the attenuation in Hα. The colour of each point indicates ΣSFR (upper row) or the sSFR (lower row), following the bar to the right. In the bottom row, the number of regions N and the Spearman correlation coefficient ρ are indicated. To compute the sSFR, the stellar mass in each region was computed from the 3.6 μm emission using the linear conversion factor of Zhu et al. (2010). The red line shows the one-to-one relation. The black, magenta, and cyan lines represent the attenuation for a starburst, a Milky Way, and an LMC average curve with differential reddening (f ≡ E(B−V)continuum/E(B−V)gas = 0.44, solid, with E(B−V)continuum being the reddening between the V and B bands of the stellar continuum and E(B−V)gas being that of the ionised gas) and without (f = 1, dashed). For the starburst relation, we assumed that even though the stellar continuum follows the starburst curve, the gas still follows a Milky Way curve. Note that the black and cyan solid lines are nearly overlap. At the finest resolution, there is a broad range in terms of differential reddening. Intense star-forming regions have little differential reddening, whereas diffuse regions present a strong differential reddening. On coarser scales, the averaging between diffuse and star-forming regions yields a differential reddening that is similar to that of starburst galaxies. The overall shape of the attenuation law is only weakly constrained, however, and may vary across the galaxy. |
| In the text | |
 |
Fig. 8 Simplified description of the relative distribution of stars, gas, and dust on a local scale in diffuse regions (top) and in star-forming regions (bottom). The FUV emitting stars are shown in blue, whereas older stellar populations are plotted in yellow or orange. The clouds of gas and dust are symbolised with grey patches. |
| In the text | |
 |
Fig. 9 Spatial resolution versus z for a rest frame wavelength of 200 nm (yellow) and 8 μm (red) with the JWST, and at 100 μm with ALMA for baselines of 150 m (blue) and 1 km (green). We adopted the cosmological parameters of Planck Collaboration XVI et al. (2014). The solid lines show at which redshifts the observations can be carried out. With the JWST, observations below 200 nm are not possible below z = 2, while observations beyond z = 2.5 are not possible at 8 μm. Conversely, the rest frame emission at 100 μm cannot be observed with ALMA below z = 3.2. There are several gaps at longer wavelengths corresponding to the gaps between different ALMA bands. These bands correspond to those available for cycle 2. Band 10 will strongly improve the capabilities of ALMA to map the main infrared star formation bands at moderate redshifts, while band 11 will allow us to probe the peak of dust emission down to z = 1. Finally, the hatched area corresponds to a resolution lower than 1 kpc, where there may be a strong effect on the measure of star formation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


