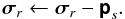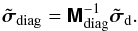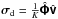| Issue |
A&A
Volume 577, May 2015
|
|
|---|---|---|
| Article Number | A56 | |
| Number of page(s) | 11 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201425492 | |
| Published online | 01 May 2015 | |
Efficient correction for both direction-dependent and baseline-dependent effects in interferometric imaging: An A-stacking framework
1
Department of Electrical and Electronic EngineeringStellenbosch
University,
7599
Stellenbosch,
South Africa
e-mail:
ayoung.at.sun@gmail.com
2
Netherlands Institute for Radio Astronomy (ASTRON),
7990AA
Dwingeloo, The
Netherlands
3
Department of Earth and Space Sciences, Chalmers University of
Technology, 412
58
Gothenburg,
Sweden
4
Department of Signals and Systems, Chalmers University of
Technology, 412
58
Gothenburg,
Sweden
Received: 10 December 2014
Accepted: 23 February 2015
A general framework is presented for modeling direction-dependent effects that are also baseline-dependent, as part of the calibration and imaging process. Within this framework such effects are represented as a parametric linear model in which basis functions account for direction dependence, whereas expansion coefficients account for the baseline dependence. This separation enables the use of a multiple fast Fourier transform-based implementation of the forward calculation (sky to visibility) in a manner similar to the W-stacking solution for non-coplanar baselines, and offers a potential improvement in computational efficiency in scenarios where the gridding operation in a convolution-based approach to direction-dependent effects may be too costly. Two novel imaging approaches that are possible within this framework are also presented.
Key words: methods: analytical / methods: numerical / techniques: image processing
© ESO, 2015
1. Introduction
Without properly correcting for various direction-dependent (DD) effects, such as the antenna radiation patterns, ionospheric phase delay, and non-coplanar baselines, the imaging performance of existing and future interferometer arrays may be limited (Smirnov 2011). One aspect of this problem concerns the determination of the various DD effects at the time of an observation, and in this context the characteristic basis function pattern (CBFP) method has been developed to provide an efficient parametrized model (i.e. high accuracy for very few parameters) with which unknown antenna radiation patterns may be solved (Maaskant et al. 2012). However, even when DD effects are known exactly, accurately correcting for them in a computationally efficient manner during the imaging process is difficult since these effects often vary over time as well as among the antenna elements in the array. The latter variation results in such effects also being baseline-dependent (BD), and in turn causes a breakdown of the Fourier transform relationship between the visibility data measured by an interferometer array and the sky brightness distribution (Offringa et al. 2014). This has a significant impact on the computational cost of estimating the sky (imaging), which is often performed iteratively (Bhatnagar et al. 2008; Tasse et al. 2013), and relies on the efficiency of the fast Fourier transform (FFT) to transform between the image and visibility planes.
One class of solutions to this problem accounts for DD effects, which enter as multiplicative distortions to the intensity distribution on the sky, in the visibility domain through utilization of the convolution theorem. Since the visibility sampling provided by a typical array is not regularly spaced on a rectangular grid, as is required by the use of the FFT, additional gridding and degridding steps in the form of a convolution are usually employed to relate visibilities on the FFT grid to those at the array sampling positions (Briggs et al. 1999). Exploiting this already-required convolution step to include DD effects is at the heart of these solutions, which include the W-projection (Cornwell et al. 2008) algorithm, which corrects for the non-coplanar baselines effect, and the A-projection (Bhatnagar et al. 2008) algorithm which corrects for more general DD effects.
Accurate implementation of these approaches, however, requires a visibility domain convolution kernel of which the support is dependent on the spatial frequency content of the DD effect accounted for, and may result in the computational cost of convolution significantly overshadowing that of the FFT. For non-coplanar baselines an alternative method, called W-stacking (Humphreys & Cornwell 2011; Offringa et al. 2014) has been developed to exploit the relatively cheap cost of the FFT by trading a slow convolution operation followed by a single FFT for a faster convolution and repeated FFTs. This method is based on grouping visibilities having similar w-terms together and then performing separate FFTs for each of these visibility groups.
In this paper a novel framework is presented that allows a similar approach to account for more general BD-DD effects. Owing to the similarity to W-stacking, and the extension from non-coplanar baselines to more general DD effects, our approach is called A-stacking. Within this framework the prevailing BD-DD effects are represented as a linear model in which the basis functions are DD but baseline-independent, while the expansion coefficients are BD but direction-independent. Mathematically this separation of direction-dependence and baseline-dependence is convenient, as it results in the forward calculation (sky to visibility) assuming the form of a combination of separate Fourier transforms, and thus allows fast computation via repeated FFTs. Furthermore, the accuracy of the calculation is determined by the number of terms in the model, thus allowing a simple trade-off between computational cost and accuracy. In the next section the response of an interferometer array is reviewed, followed by Sect. 3 where the A-stacking formulation is presented. In Sect. 4 two alternative imaging approaches that are possible within this framework are developed, and Sect. 5 describes a procedure by which an appropriate linear model may be derived for prior characterized BD-DD effects via the singular value decomposition (SVD). Finally, in Sect. 6 some simulation results are presented to assess the performance of A-stacking based BD-DD models.
Although the framework presented here is generally applicable to any BD-DD effects, results will show that the method is most efficient when these effects are accurately described by low-order (relatively few terms) models. This typically applies to the BD-DD gain associated with the primary beams in an array comprising similar antennas, and the scope of this paper is limited to this particular effect. Furthermore, it is assumed throughout that the BD-DD antenna gains are known a priori; modeling and solving for unknown gains is the subject of ongoing work and will not be discussed herein.
2. Interferometer array response
The full-polarization response on one baseline of a narrow-band phase-tracking interferometer array is given by (see Hamaker et al. 1996; Thompson et al. 2004; Tasse et al. 2013) 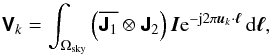 (1)where 1 and 2 denote the antennas that comprise the interferometer formed on the kth baseline, ⊗ is the Kronecker product, and
(1)where 1 and 2 denote the antennas that comprise the interferometer formed on the kth baseline, ⊗ is the Kronecker product, and 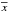 indicates the complex conjugate of x. J1 is the 2 × 2 Jones-matrix which represents all instrumental effects introduced in the received signal1 along channel 1. For a non-isotropic antenna the Jones-matrix term is DD and evaluating the Kronecker product in (1)yields a 4 × 4 direction-dependent matrix Ak. The 4 × 1 vector I represents the sky coherency in the polarization coordinates of the antennas.
indicates the complex conjugate of x. J1 is the 2 × 2 Jones-matrix which represents all instrumental effects introduced in the received signal1 along channel 1. For a non-isotropic antenna the Jones-matrix term is DD and evaluating the Kronecker product in (1)yields a 4 × 4 direction-dependent matrix Ak. The 4 × 1 vector I represents the sky coherency in the polarization coordinates of the antennas.
The vector uk is the baseline between the antenna pair (1,2) expressed in the wavelength normalized Cartesian coordinates (u,v,w) with w pointing towards the center of the field of view (FoV) being tracked, and ℓ is a vector representing a direction on the sky relative to the FoV center. Using direction cosines l and m relative to u and v, respectively, to express the direction on the sky yields 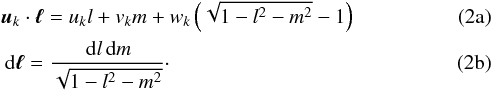 For the sake of simplifying notation, the denominator in (2b)is subsumed into the sky coherency. Furthermore, the w-term may be subsumed into the BD-DD gain Ak as a scalar factor and is omitted in the following. We consider for now only a single cross-correlation product, and assume the antennas have zero cross-polarization2. The measurement in (1)can be seen as sampling at the point (uk,vk) the visibility function
For the sake of simplifying notation, the denominator in (2b)is subsumed into the sky coherency. Furthermore, the w-term may be subsumed into the BD-DD gain Ak as a scalar factor and is omitted in the following. We consider for now only a single cross-correlation product, and assume the antennas have zero cross-polarization2. The measurement in (1)can be seen as sampling at the point (uk,vk) the visibility function 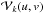 which is related to an apparent sky
which is related to an apparent sky 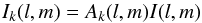 (3)through
(3)through 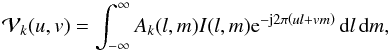 (4)where the support of Ik spans only the visible region of the sky Ωsky. Here the term Ak(l,m) is used to indicate the entry in the first row and first column in Ak and its direction-dependence is explicitly stated. The subscript k in
(4)where the support of Ik spans only the visible region of the sky Ωsky. Here the term Ak(l,m) is used to indicate the entry in the first row and first column in Ak and its direction-dependence is explicitly stated. The subscript k in 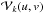 indicates the baseline-dependence of the sampled visibility function: for a fixed point in the uv-plane,
indicates the baseline-dependence of the sampled visibility function: for a fixed point in the uv-plane, 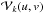 may vary depending on which antenna pair is used to sample the visibility at that point.
may vary depending on which antenna pair is used to sample the visibility at that point.
Equation (4)forms the basis of synthesis imaging: by measuring visibilities on a large number of unique baselines, the inversion of this relationship becomes more tractable. To this end, we consider the discrete form of (4). We let an Np × Np pixel image of the sky be represented by the 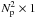 vector σ. Then the visibility measured on the kth baseline may be written as
vector σ. Then the visibility measured on the kth baseline may be written as 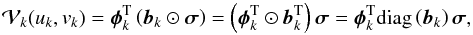 (5)where ⊙ is the Hadamard or element-wise product, diag(x) forms a diagonal matrix by placing the elements in the vector x on the diagonal, bk is the
(5)where ⊙ is the Hadamard or element-wise product, diag(x) forms a diagonal matrix by placing the elements in the vector x on the diagonal, bk is the 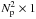 vector discretization of Ak(l,m) over the image plane, and φk is the
vector discretization of Ak(l,m) over the image plane, and φk is the 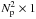 vector in which the element associated with the nth image pixel is
vector in which the element associated with the nth image pixel is 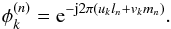 (6)Grouping all visibilities measured on K unique baselines into a single K × 1 vector yields
(6)Grouping all visibilities measured on K unique baselines into a single K × 1 vector yields 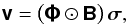 (7)where
(7)where 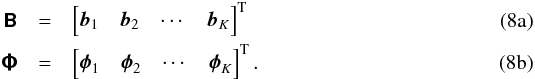 Even though the relation between the measured visibilities and the discretized sky in (7)is relatively simple, for long observations with large arrays the scale of this linear system precludes its direct inversion, and even its direct evaluation as part of an iterative solution may prove too costly (Tasse et al. 2013). An approach that is typically employed to circumvent this problem makes use of the Fourier transform relationship in (4)to enable more efficient calculations via the FFT (Briggs et al. 1999; Jackson et al. 1991). In order to illustrate this approach, we consider the visibility function
Even though the relation between the measured visibilities and the discretized sky in (7)is relatively simple, for long observations with large arrays the scale of this linear system precludes its direct inversion, and even its direct evaluation as part of an iterative solution may prove too costly (Tasse et al. 2013). An approach that is typically employed to circumvent this problem makes use of the Fourier transform relationship in (4)to enable more efficient calculations via the FFT (Briggs et al. 1999; Jackson et al. 1991). In order to illustrate this approach, we consider the visibility function 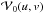 that would be measured by a hypothetical interferometer array for which Ak(l,m) = 1,
that would be measured by a hypothetical interferometer array for which Ak(l,m) = 1, 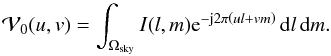 (9)Since all baselines measure the same visibility function, the true sky I(l,m) may be computed simply using the inverse Fourier transform. Furthermore, if the hypothetical array samples
(9)Since all baselines measure the same visibility function, the true sky I(l,m) may be computed simply using the inverse Fourier transform. Furthermore, if the hypothetical array samples 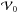 on an Np × Np rectangular grid
on an Np × Np rectangular grid 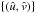 which satisfies the following spacing requirements
which satisfies the following spacing requirements 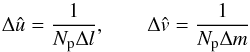 (10)over the uv-plane, where Δl and Δm are the spacing between pixels in the image, then arranging the corresponding visibility samples in the
(10)over the uv-plane, where Δl and Δm are the spacing between pixels in the image, then arranging the corresponding visibility samples in the 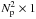 vector
vector 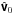 yields
yields 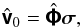 (11a)where
(11a)where 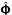 is a discrete Fourier transform (DFT) matrix. Using the unitary property of
is a discrete Fourier transform (DFT) matrix. Using the unitary property of 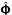 the inverse transform is easily computed as
the inverse transform is easily computed as 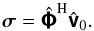 (11b)Moreover, owing to the structure of
(11b)Moreover, owing to the structure of 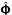 the transforms in (11)may be computed efficiently using the FFT. This approach is depicted in Fig. 1a.
the transforms in (11)may be computed efficiently using the FFT. This approach is depicted in Fig. 1a.
 |
Fig. 1 Transformations between image and visibility domains a) for FFT compatible visibility plane sampling, and b) for irregular visibility plane sampling which requires an additional (de)gridding operation in order to utilize the FFT. |
There are two caveats associated with the above outlined procedure. Firstly, the uv-sampling provided by any practical interferometer typically does not fall on a rectangular grid, and as such does not satisfy the requirements in (10). This means that, in order to utilize the efficiency of the FFT, it is necessary to relate the visibility samples on the rectangular grid 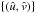 , or gridded visibilities, to the irregularly sampled visibilities on {(uk,vk)}. That is, the following operators are required, for gridding
, or gridded visibilities, to the irregularly sampled visibilities on {(uk,vk)}. That is, the following operators are required, for gridding 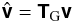 (12a)and for degridding
(12a)and for degridding  (12b)This workaround is illustrated in Fig. 1b.
(12b)This workaround is illustrated in Fig. 1b.
Secondly, the use of the FFT is based on the assumption that the same visibility function, which may be related to the same apparent sky, is sampled on all baselines. However, it is well known that under certain conditions this assumption breaks down (Smirnov 2011), e.g. for non-coplanar baselines or non-identical primary beams. This problem is indicated by the dependence on k of both the left hand side of (4), as well as the integrand on its right hand side, as opposed to the form in (9)which is identical for all k. In such a case it is desirable to find some corrective transformation which can relate the baseline-dependent apparent skies (visibility functions) to a single apparent sky (visibility function) common to all baselines.
The A/W-projection algorithms present such a solution and are based on the observation that the image plane multiplicative distortions introduced by the BD-DD term Ak in (4)enter as convolutions in the visibility domain (Cornwell et al. 2008; Bhatnagar et al. 2008). This, combined with the fact that convolution is generally used to approximate the required gridding operations (Briggs et al. 1999; Jackson et al. 1991), means that BD-DD effects may be accounted for through a proper choice of gridding convolution kernel. For instance, given the visibility function 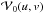 uncorrupted by the effects of Ak, the irregularly sampled visibilities may be computed by evaluating
uncorrupted by the effects of Ak, the irregularly sampled visibilities may be computed by evaluating 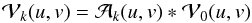 (13)at each point (uk,vk), and where
(13)at each point (uk,vk), and where 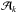 is the Fourier transform of Ak. Practical implementation of this approach requires the support of
is the Fourier transform of Ak. Practical implementation of this approach requires the support of 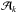 to be limited to some finite region, which depends on the image plane spatial frequency content of Ak and the required accuracy of the calculation in (13). Consequently the cost of gridding may increase substantially in certain instances by correcting for BD-DD effects in this way.
to be limited to some finite region, which depends on the image plane spatial frequency content of Ak and the required accuracy of the calculation in (13). Consequently the cost of gridding may increase substantially in certain instances by correcting for BD-DD effects in this way.
Alternatively, provided that the computational bottleneck in the transformation between the image and visibility planes is not the FFT itself but the gridding step, a grouping together of baselines for which the direction-dependent effects are sufficiently similar and performing separate Fourier transforms for each group may provide a more efficient solution if it allows the computational cost of gridding to be reduced. This is the approach used in W-stacking to account for non-coplanar baselines (Humphreys & Cornwell 2011; Offringa et al. 2014). In the following it will be shown how the use of a linear model to represent a general BD-DD effect Ak(l,m) results in a similar solution.
3. A-Stacking formulation: forward calculation
Suppose the factor Ak(l,m) in (3)can be written in an exact form as the weighted combination of NB basis functions3, 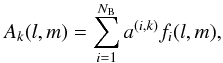 (14)where each of the coefficients a(i,k) pertains to the specific baseline k, and the DD expansion functions fi(l,m) are common to all baselines. Using fi to denote the
(14)where each of the coefficients a(i,k) pertains to the specific baseline k, and the DD expansion functions fi(l,m) are common to all baselines. Using fi to denote the 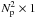 vector discretization of fi on the image plane, the discrete form of (14)becomes
vector discretization of fi on the image plane, the discrete form of (14)becomes 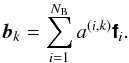 (15)Substituting this expression into (5)gives
(15)Substituting this expression into (5)gives ![\begin{eqnarray} \mathcal{V}_k(u_k,v_k) & =& \Transpose{\Matrix{\phi}}_k \left[ \left(\sum_{i=1}^{N_{\rm B}} a^{(i,k)} \Matrix{f}_i\right) \Hadamard \Matrix{\sigma} \right] = \sum_{i=1}^{N_{\rm B}} a^{(i,k)} \Transpose{\Matrix{\phi}}_k\left( \Matrix{f}_i \Hadamard \Matrix{\sigma} \right)\nonumber\\ & =& \sum_{i=1}^{N_{\rm B}} a^{(i,k)} \Transpose{\Matrix{\phi}}_k \text{diag}\left(\Matrix{f}_i\right) \Matrix{\sigma}. \end{eqnarray}](/articles/aa/full_html/2015/05/aa25492-14/aa25492-14-eq78.png) (16)Using
(16)Using 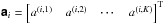 the result for all baselines can be written as
the result for all baselines can be written as ![\begin{equation} \label{eq:efficientexact} \Matrix{v} = \sum_{i=1}^{N_{\rm B}} \Matrix{a}_i \Hadamard \left[\Matrix{\Phi} \left( \Matrix{f}_i \Hadamard \Matrix{\sigma} \right)\right] = \sum_{i=1}^{N_{\rm B}} \text{diag}\left(\Matrix{a}_i\right)\Matrix{\Phi}\text{diag}\left(\Matrix{f}_i\right)\Matrix{\sigma}, \end{equation}](/articles/aa/full_html/2015/05/aa25492-14/aa25492-14-eq80.png) (17)which is the desired form relating the visibilities to the discretized sky.
(17)which is the desired form relating the visibilities to the discretized sky.
Equation (17)states that the visibilities pertaining to a model sky may be calculated as follows, while fully accounting for the BD-DD effects contained in Ak:
-
1.
Apply a per basis function image domain cor-rection in the form of an element-wise multipli-cation to calculate a corresponding apparent sky,
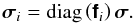 (18a)
(18a) -
2.
Fourier transform each apparent sky using the FFT, followed by a degridding step, to compute per basis function sets of visibilities,

-
3.
Apply a visibility domain correction in the form of an element-wise multiplication to each visibility set, and sum the resulting visibility sets,
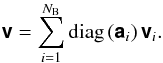 (18d)
(18d)
3.1. Computational complexity
In order to identify conditions under which A-stacking may present an efficient alternative to a convolution based approach for the forward calculation, the computational complexity of the algorithm is compared here to that of A-projection. The algorithms are illustrated in Fig. 2.
 |
Fig. 2 a) Forward calculation in the A-stacking framework, subdivided into the algorithmic steps described by (18). b) Forward calculation using A-projection. The A-projection convolution kernel size is NgA × NgA, as determined by the spatial frequency content of the direction-dependent effects on the sky, and can result in a relatively expensive gridding cost. A-stacking aims to reduce this cost by decreasing the size of the gridding convolution kernel to Ng × Ng, as determined by the required image dynamic range; the penalty is that multiple FFTs and gridding operations are required. |
Assuming a gridding convolution kernel of size Ng × Ng is required to meet dynamic range requirements (Duijndam & Schonewille 1999), the overall cost incurred by (18)can be shown to scale as 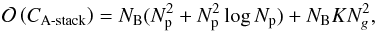 (19)where the first term on the right-hand side accounts for the per basis function image plane correction and FFT, and second term accounts for the gridding and visibility plane correction. In comparison the overall cost of an A-projection implementation, assuming a convolution kernel of size NgA × NgA is required to accurately account for the associated DD effects, scales as (Jongerius et al. 2014; Offringa et al. 2014)
(19)where the first term on the right-hand side accounts for the per basis function image plane correction and FFT, and second term accounts for the gridding and visibility plane correction. In comparison the overall cost of an A-projection implementation, assuming a convolution kernel of size NgA × NgA is required to accurately account for the associated DD effects, scales as (Jongerius et al. 2014; Offringa et al. 2014) 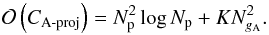 (20)If the overall cost in both cases is dominated by the gridding step, that is
(20)If the overall cost in both cases is dominated by the gridding step, that is 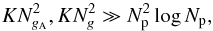 (21)then A-stacking presents a more efficient alternative to A-projection on condition that
(21)then A-stacking presents a more efficient alternative to A-projection on condition that 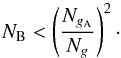 (22)The total storage required to perform the A-stacking forward calculation in Fig. 2a completely in memory scales as
(22)The total storage required to perform the A-stacking forward calculation in Fig. 2a completely in memory scales as 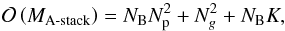 (23)where the first term accounts for the per basis function image domain correction, the second accounts for the storage of the single gridding convolution kernel, and the last term accounts for the per basis function visibility domain corrections. In comparison, the total storage required to perform the A-projection forward calculation in Fig. 2b completely in memory scales as
(23)where the first term accounts for the per basis function image domain correction, the second accounts for the storage of the single gridding convolution kernel, and the last term accounts for the per basis function visibility domain corrections. In comparison, the total storage required to perform the A-projection forward calculation in Fig. 2b completely in memory scales as 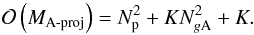 (24)Here storage of only a single image and visibility map are required, however a (potentially) different convolution kernel needs to be stored per baseline. The storage required or A-stacking is less than that for A-projection if
(24)Here storage of only a single image and visibility map are required, however a (potentially) different convolution kernel needs to be stored per baseline. The storage required or A-stacking is less than that for A-projection if 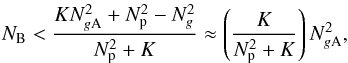 (25)where the approximation assumes that gridding dominates the computational cost as in (21)(which implies that
(25)where the approximation assumes that gridding dominates the computational cost as in (21)(which implies that 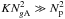 ), and that
), and that 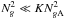 .
.
Since NgA depends on the spatial frequency content of the primary beam patterns on the sky, and NB depends on the inter-element variation among the primary beams, a clear distinction between cases where one algorithm should outperform the other (in the asymptotic limit) in terms of computing time and memory requirements is possible in principle. We also note that the cost of a convolution-based approach scales quadratically with an increase in NgA, whereas that of the stacking approach in (18)scales linearly with an increase in NB. This means that even with a moderately sized NgA a relatively large number of basis functions NB may still render the proposed method more efficient.
Finally, since the efficiency of A-stacking depends on reducing the required size of the visibility plane convolution kernel, it may be necessary to avoid a convolution based approach to correct for non-coplanar baselines. As stated earlier, the w-term is easily included in the BD-DD modeling approach presented here, however, this may increase the number NB of terms in (14)required to yield an accurate model. Alternatively, A-stacking may be combined with W-stacking (Offringa et al. 2014), which does not affect the cost of gridding, but does result in the number of image plane corrections and FFTs increasing by a factor Nw (number of w-layers). This means that the cost of repeated FFTs may become more expensive than gridding for fewer Nw than when combing W-stacking with A-projection in the so-called hybrid w-stacking (see Tasse et al. 2013).
4. Imaging with A-stacking: backward calculation
Imaging is concerned with the inversion of (7). As was already stated, the scale of this system of equations precludes the use of a direct method, so that a different approach to imaging is required. In this section two approaches possible within the A-stacking framework are derived.
4.1. Adaptation to the CLEAN algorithm
In theory, the Fourier relationship in (4)allows the apparent sky Ik to be determined from the visibility function 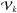 via the inverse Fourier transform. Given the discretization inherent to the limited sampling provided by any practical interferometer array and the image representation of the sky, the result of the practical equivalent of this is
via the inverse Fourier transform. Given the discretization inherent to the limited sampling provided by any practical interferometer array and the image representation of the sky, the result of the practical equivalent of this is 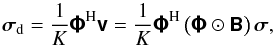 (26)which is the so-called dirty image4. Apart from the effects associated with B, the limited sampling of the array also adds a distortion in the form of a convolution with the Fourier transform of the visibility plane sampling function, or point spread function (PSF) (Jackson et al. 1991). Not only does this limit the resolution of the obtained image to the scale of the PSF main lobe, but sidelobes in the PSF can also produce artifacts that may produce false sources, hide existing ones, or distort other sources in the image. Removing this corruption requires some deconvolution procedure. However, owing to the imperfect sampling of the array in general the solution is not unique, so that a non-linear deconvolution procedure is usually required (Cornwell et al. 1999). The algorithm perhaps most widely used for this purpose is CLEAN and its derivatives (Högbom 1974; Clark 1980; Schwab 1984). In general this algorithm is based on identifying a peak in the dirty image as the location of a point-like source, and then removing the effect of that source by subtracting an appropriately scaled and shifted PSF.
(26)which is the so-called dirty image4. Apart from the effects associated with B, the limited sampling of the array also adds a distortion in the form of a convolution with the Fourier transform of the visibility plane sampling function, or point spread function (PSF) (Jackson et al. 1991). Not only does this limit the resolution of the obtained image to the scale of the PSF main lobe, but sidelobes in the PSF can also produce artifacts that may produce false sources, hide existing ones, or distort other sources in the image. Removing this corruption requires some deconvolution procedure. However, owing to the imperfect sampling of the array in general the solution is not unique, so that a non-linear deconvolution procedure is usually required (Cornwell et al. 1999). The algorithm perhaps most widely used for this purpose is CLEAN and its derivatives (Högbom 1974; Clark 1980; Schwab 1984). In general this algorithm is based on identifying a peak in the dirty image as the location of a point-like source, and then removing the effect of that source by subtracting an appropriately scaled and shifted PSF.
In order to demonstrate how this algorithm may be adapted within the A-stacking framework, we consider the dirty image produced by applying ΦH to the visibilities in (17)![\begin{eqnarray} \Matrix{\sigma}_{\rm d} & = &\frac{1}{K}\Hermitian{\Matrix{\Phi}}\Matrix{v} = \frac{1}{K}\Hermitian{\Matrix{\Phi}} \sum_{i=1}^{N_{\rm B}} \text{diag}\left(\Matrix{a}_i\right)\Matrix{\Phi}\text{diag}\left(\Matrix{f}_i\right)\Matrix{\sigma}\nonumber\\[3mm] \label{eq:dirtyimage} & = &\frac{1}{K}\sum_{i=1}^{N_{\rm B}} \Hermitian{\Matrix{\Phi}} \text{diag}\left(\Matrix{a}_i\right)\Matrix{\Phi}\text{diag}\left(\Matrix{f}_i\right)\Matrix{\sigma}. \end{eqnarray}](/articles/aa/full_html/2015/05/aa25492-14/aa25492-14-eq102.png) (27)Replacing the true sky image vector σ with an image es corresponding to a single point source of unit intensity at the location (ls,ms) and an otherwise empty sky, yields the PSF
(27)Replacing the true sky image vector σ with an image es corresponding to a single point source of unit intensity at the location (ls,ms) and an otherwise empty sky, yields the PSF ![\begin{eqnarray} \Matrix{p}_{s} & =& \sum_{i=1}^{N_{\rm B}} f_i(l_s,m_s) \left[ \frac{1}{K} \Hermitian{\Matrix{\Phi}} \text{diag}\left(\Matrix{a}_i\right)\Matrix{\Phi}\Matrix{e}_{s} \right]\nonumber\\[3mm] \label{eq:bcleanpsf} &=& \sum_{i=1}^{N_{\rm B}} f_i(l_s,m_s) \Matrix{q}_i(s). \end{eqnarray}](/articles/aa/full_html/2015/05/aa25492-14/aa25492-14-eq105.png) (28)Herein qi(s) is the PSF, centered at (ls,ms), and associated with applying the weights ai to the visibilities. Although each qi represents a shift-invariant PSF, that represented by ps is not shift-invariant, because of the direction-dependent weighting fi(ls,ms) applied to each qi. Assuming a sky composed of a number Ns of point sources allows the following representation
(28)Herein qi(s) is the PSF, centered at (ls,ms), and associated with applying the weights ai to the visibilities. Although each qi represents a shift-invariant PSF, that represented by ps is not shift-invariant, because of the direction-dependent weighting fi(ls,ms) applied to each qi. Assuming a sky composed of a number Ns of point sources allows the following representation 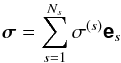 (29)which, when substituted into (27)and using (28)gives the desired result,
(29)which, when substituted into (27)and using (28)gives the desired result, 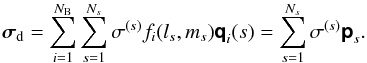 (30)This expression presents an interesting decomposition of the dirty image: it is the superposition of a number of sub-images, each of which is a different apparent sky σi convolved with an associated PSF qi. More importantly, this interpretation can be used to adapt the PSF subtraction in the CLEAN algorithm to account more accurately for the BD-DD effects.
(30)This expression presents an interesting decomposition of the dirty image: it is the superposition of a number of sub-images, each of which is a different apparent sky σi convolved with an associated PSF qi. More importantly, this interpretation can be used to adapt the PSF subtraction in the CLEAN algorithm to account more accurately for the BD-DD effects.
We let the NB different PSFs 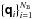 be pre-computed as part of initializing the CLEAN algorithm, and we let σr be the residual dirty image at the start of a PSF subtraction iteration. With a point source identified at location s in σr the PSF subtraction now proceeds as follows:
be pre-computed as part of initializing the CLEAN algorithm, and we let σr be the residual dirty image at the start of a PSF subtraction iteration. With a point source identified at location s in σr the PSF subtraction now proceeds as follows:
-
1.
Weigh each PSF qi(s) by the value of its corresponding DD basis function towards the direction of the source fi(ls,ms), and accumulate the result for all NB basis functions to yield the total PSF ps as in (28).
-
2.
Scale ps according to the intensity of the identified source and the loop gain parameter γ,
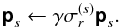 (31a)
(31a) - 3.
4.2. Diagonal correction
Using the BD-DD effect model in (14)also produces a useful imaging approach for the case where deconvolution is not necessary, either because the image dynamic range is not high enough or because the spatial selectivity is very good, so that artifacts produced by the PSF sidelobe structure do not have a dominant effect on the image quality.
Suppose an overdetermined system in (7), that is, 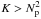 . The well-known linear least squares (LLS) solution to such a system is
. The well-known linear least squares (LLS) solution to such a system is ![\begin{equation} \tilde{\Matrix{\sigma}} = \MoorePenrose{\left(\Matrix{\Phi}\Hadamard\Matrix{B}\right)}\Matrix{v} = \Inverse{\left[\Hermitian{\left(\Matrix{\Phi}\Hadamard\Matrix{B}\right)}\left(\Matrix{\Phi}\Hadamard\Matrix{B}\right)\right]} \Hermitian{\left(\Matrix{\Phi}\Hadamard\Matrix{B}\right)}\Matrix{v}, \end{equation}](/articles/aa/full_html/2015/05/aa25492-14/aa25492-14-eq122.png) (32)where † denotes the Moore-Penrose pseudoinverse. Using the model in (15)and the result in (17), the LSS solution becomes
(32)where † denotes the Moore-Penrose pseudoinverse. Using the model in (15)and the result in (17), the LSS solution becomes  (33)where the deconvolution matrix M-1 and the dirty image vector5
(33)where the deconvolution matrix M-1 and the dirty image vector5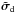 have been introduced,
have been introduced, 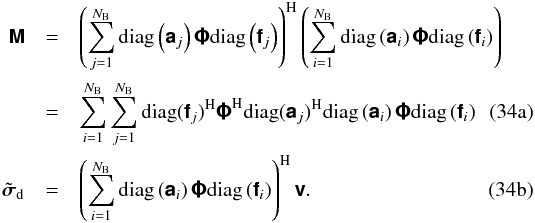 Because of the computational costs involved for typically encountered image sizes, direct evaluation of (33)may not be practicable. However, given the condition that deconvolution is unnecessary, the inversion of M becomes tractable in that it may be approximated as being diagonal6. This results from the fact that the off-diagonal entries in this matrix represent the flux leakage between different pixels in the image, the very effect deconvolution aims to correct.
Because of the computational costs involved for typically encountered image sizes, direct evaluation of (33)may not be practicable. However, given the condition that deconvolution is unnecessary, the inversion of M becomes tractable in that it may be approximated as being diagonal6. This results from the fact that the off-diagonal entries in this matrix represent the flux leakage between different pixels in the image, the very effect deconvolution aims to correct.
We let Mdiag be the matrix formed by setting all off-diagonal entries in M equal to zero. In order to determine the structure of this matrix, we consider the qth diagonal element in ![\begin{eqnarray} \left[ \Hermitian{\Matrix{\Phi}} \Hermitian{\text{diag}(\Matrix{a}_j)} \text{diag}\left(\Matrix{a}_i\right) \Matrix{\Phi}\right]^{(q,q)} & =& \sum_{k=1}^{K} \Conjugate{\Phi^{(k,q)}} \Conjugate{a^{(j,k)}} a^{(i,k)} \Phi^{(k,q)}\nonumber\\ & = &\Hermitian{\Matrix{a}_j}\Matrix{a}_i, \end{eqnarray}](/articles/aa/full_html/2015/05/aa25492-14/aa25492-14-eq131.png) (35)where the relation
(35)where the relation 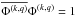 has been used. Since the result is independent of q, we can write
has been used. Since the result is independent of q, we can write ![\begin{eqnarray} \label{eq:diagM} \Matrix{M}_{\text{diag}} & = & \sum_{i=1}^{N_{\rm B}}\sum_{j=1}^{N_{\rm B}} \Hermitian{\text{diag}(\Matrix{f}_j)} \left[\Hermitian{\Matrix{a}_j}\Matrix{a}_i \vec{I}\right] \text{diag}\left(\Matrix{f}_i\right)\nonumber\\ & = & \sum_{i=1}^{N_{\rm B}}\sum_{j=1}^{N_{\rm B}} \Hermitian{\Matrix{a}_j}\Matrix{a}_i \text{diag}\left(\Conjugate{\Matrix{f}_j} \Hadamard \Matrix{f}_i\right), \end{eqnarray}](/articles/aa/full_html/2015/05/aa25492-14/aa25492-14-eq133.png) (36)since
(36)since 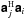 is scalar, and where I is an appropriately sized identity matrix.
is scalar, and where I is an appropriately sized identity matrix.
This naturally leads to the following imaging procedure:
-
1.
Compute the dirty image
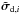 for each basis function by applying the weights
for each basis function by applying the weights
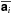 to the visibilities, Fourier transforming to the image plane (via gridding and using
the FFT), and then weighting the image values by
to the visibilities, Fourier transforming to the image plane (via gridding and using
the FFT), and then weighting the image values by
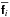 ,
,
![% subequation 2148 0 \begin{equation} \tilde{\Matrix{\sigma}}_{{\rm d},i} = \Hermitian{\text{diag}(\Matrix{f}_i)}\left[\Hermitian{\Grid{\Matrix{\Phi}}} \Matrix{T}_{\rm G}\left(\Hermitian{\text{diag}(\Matrix{a}_i)}\Matrix{v}\right)\right]. \end{equation}](/articles/aa/full_html/2015/05/aa25492-14/aa25492-14-eq138.png) (37a)This is simply a
practical implementation of each term in (34b).
(37a)This is simply a
practical implementation of each term in (34b). -
2.
Accumulate the result for the NB basis functions to yield the dirty image,
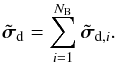 (37b)
(37b) -
3.
Compute the diagonal version of the deconvolution matrix Mdiag using (36).
- 4.
5. Basis function construction
Although the above results are generally applicable for any exact expansion of Ak which has the form of (14), it is obviously desirable to obtain such an expansion which requires the least number of terms, since the cost of the above derived algorithms generally scale with NB. In this section an approach aimed at producing such a model from a prior characterized Ak is presented.
For imaging purposes it is sufficient to obtain a model for the discretization of Ak on the image grid, that is bk as in (15). From (8a)it is clear that finding a set of expansion functions 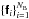 with which each bk may be expressed as in (15)is equivalent to finding a basis for the row space of B. One such basis may be obtained by computing the truncated Singular Value Decomposition (SVD),
with which each bk may be expressed as in (15)is equivalent to finding a basis for the row space of B. One such basis may be obtained by computing the truncated Singular Value Decomposition (SVD),  (38)Selecting the columns in the
(38)Selecting the columns in the 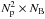 matrix U (left-singular vectors) as the basis functions {fi} in (15), it can be shown that each expansion coefficient a(i,k) is the entry on the ith row and kth column in the matrix7
matrix U (left-singular vectors) as the basis functions {fi} in (15), it can be shown that each expansion coefficient a(i,k) is the entry on the ith row and kth column in the matrix7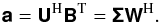 (39)This produces an exact expansion with
(39)This produces an exact expansion with 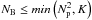 number of terms, where the inequality may result from a linear dependence among the DD gains associated with each of the baselines8.
number of terms, where the inequality may result from a linear dependence among the DD gains associated with each of the baselines8.
Since the computational burden resulting from the use of the linear model in (15)scales linearly with the number of basis functions, it may be desirable to rather use nB<NB number of terms, thus trading computational cost for accuracy. Furthermore, since the accuracy of transformations between the image and visibility planes is also affected by other factors (e.g. noise, gridding/degridding), the required accuracy may need to be only such that it does not limit the overall accuracy. With these considerations in mind, the aim is to produce a model which yields the highest precision for a given number of terms. For this reason, the model provided through the use of the SVD is especially useful in the case where nB<NB. Specifically, the sum of the squared distances between each of the rows in B and the vector space spanned by nB left-singular vectors is minimized by choosing those left-singular vectors corresponding to the nB largest singular values on the diagonal of Σ (Jolliffe 1986).
It should be noted that the computational cost incurred by evaluating (38)and (39)does not need to enter into the overall cost of the algorithms presented in the previous sections, since the result need only be determined once and can be stored for repeated use over the course of one or more observations9. Nevertheless, one way to alleviate the cost of constructing the BD-DD model is to sample Ak over a sparser grid prior to computing the basis functions. The motivation for this approach is that the resolution obtainable with the entire array may be much higher than that required to accurately represent the radiation pattern of a single antenna element in such an array. We let 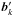 be such a discretization of Ak over an Nq × Nq grid { (l′,m′) } in the image plane, where Np = αNq with α> 1, and
be such a discretization of Ak over an Nq × Nq grid { (l′,m′) } in the image plane, where Np = αNq with α> 1, and  (40)Using this discretization of the BD-DD effects the matrix B′ is constructed, and the SVD is computed to yield
(40)Using this discretization of the BD-DD effects the matrix B′ is constructed, and the SVD is computed to yield 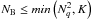 left-singular vectors
left-singular vectors 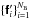 . The model basis functions are now obtained by first interpolating each singular vector to extend its support onto the Np × Np grid,
. The model basis functions are now obtained by first interpolating each singular vector to extend its support onto the Np × Np grid, 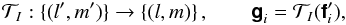 (41)and then orthonormalizing the resulting set of vectors to yield
(41)and then orthonormalizing the resulting set of vectors to yield 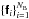 . Each model coefficient a(i,k) is then computed by projecting the ith basis function onto the kth column of BT.
. Each model coefficient a(i,k) is then computed by projecting the ith basis function onto the kth column of BT.
6. Results
In this section simulation results are presented in order to assess the performance of the A-stacking approach. First the impact of various factors on the accuracy of the forward calculation is considered, followed by a demonstration of the performance of the CLEAN algorithm when combined with the A-stacking approach.
Simulations pertain to a snapshot observation in a narrow frequency band around 50 MHz, using one polarization of the LOFAR Low Band Antenna (LBA) station at Onsala, Sweden as an interferometer array. A full-wave numerical model was analyzed in FEKO10 to determine the radiation patterns of all the elements in the array (Young et al. 2014); see Fig. 3. Because of the effects of mutual coupling, which was fully accounted for in the numerical model, the primary beams exhibited a variation over the elements in the array so that a single primary beam approximation would not suffice. The phase reference for each pattern was located at the corresponding antenna position in the array, as used to determine the baseline uv-coordinates. Sky models were generated by randomly placing ten point sources of varying intensity on an image grid, so that the source statistics were in agreement with that reported in Bregman (2012) for frequencies below 1.4 GHz. The sky models were then used as input to various observation simulations. For each simulation the reference (exact) visibilities vexact were calculated via direct evaluation of (7), which were then used as input for further analysis.
 |
Fig. 3 a) The LOFAR LBA station at Onsala Space Observatory, Sweden. Photograph courtesy of Leif Helldner. b) FEKO model of the 96 element LBA station showing the radiation patterns (magnitude) of each antenna in the array. The array comprises dual-polarized inverted-V antennas above a ground plane (not shown in model). Generally a larger degree of inter-element variability is observed among the patterns of the antennas that are closely spaced than in the patterns of those that are more isolated. |
6.1. Accuracy of the forward calculation
Model visibilities were calculated from the input sky using various approaches, and then compared to the exact visibilities. The sky model extended over the region | l | , | m | ≤ 0.5 and was discretized with Np = 64 pixels along each dimension (i.e. 64 × 64 pixel image). The following model visibilities were computed:
-
1.
vavg – Visibilities are calculated using (7), but the DD gain on all baselines is assumed identical and equal to b0, for which the average power pattern over all antennas in the array is used.
-
2.
vavg - fft – Again an identical b0 is used for all baselines, but the visibilities are calculated via the FFT, followed by a degridding step which is implemented as cubic interpolation.
-
3.
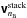 – Visibilities are calculated using (17), but truncating the summation over i after nB<NB terms and using basis functions computed via the SVD in (38).
– Visibilities are calculated using (17), but truncating the summation over i after nB<NB terms and using basis functions computed via the SVD in (38). -
4.
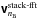 – Using again only nB model terms, visibilities are calculated via the procedure outlined in (18), that is, using the FFT and degridding.
– Using again only nB model terms, visibilities are calculated via the procedure outlined in (18), that is, using the FFT and degridding. -
5.
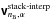 – Here
– Here 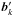 was calculated on an Nq × Nq grid with Np = αNq in the lm-plane prior to computing the SVD in (38). Cubic interpolation was used to extend the support of the basis functions onto the image grid, and the Gram-Schmidt method was then used to orthonormalize the basis functions. Finally, visibilities were computed using (17)and truncating the summation over i after nB<NB terms.
was calculated on an Nq × Nq grid with Np = αNq in the lm-plane prior to computing the SVD in (38). Cubic interpolation was used to extend the support of the basis functions onto the image grid, and the Gram-Schmidt method was then used to orthonormalize the basis functions. Finally, visibilities were computed using (17)and truncating the summation over i after nB<NB terms.
In all cases the error between a reference visibility vector and model visibility vector was computed as 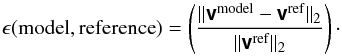 (42)Figure 4 shows the accuracy of the forward calculation obtained with various truncated A-stacking based BD-DD gain models. The result shown is the average of ϵ(model,exact) over 1000 different generated sky models. As can be expected, in all cases the accuracy improves with an increase in the number nB of model terms. The highest accuracy is achieved by using the direct Fourier transform in (17), combined with basis functions derived directly from a discretization of Ak on the full image grid (stack model). Since the visibilities computed in this manner converge to the exact visibilities for nB = NB this result can be used to estimate the highest accuracy that may be obtained with a model of a given number of terms. The error decays rapidly as nB is increased for the first few terms (nB ≲ 10), and thereafter at a somewhat slower rate, until nB ≈ 192 where a sharp drop in the error occurs. This sudden decrease in error is related to a similar sudden decrease in the Singular Value (SV) spectrum of BT at twice the number of antennas in the array, 2 × 96 = 192. Using a sparser discretization of Ak to expedite the construction of the basis functions via the SVD (stack-interp models) is seen to introduce an error between about 10-2.6 and 10-2.9, depending on the sparsity of the grid, and only represents a significant loss in accuracy for a model with more than about nB = 60 terms. Similarly, utilizing the FFT-based calculation (stack-fft model), an error of around 10-2.3 and associated with the degridding operation is introduced which only has a significant impact on the accuracy for a model with more than roughly nB = 40 terms.
(42)Figure 4 shows the accuracy of the forward calculation obtained with various truncated A-stacking based BD-DD gain models. The result shown is the average of ϵ(model,exact) over 1000 different generated sky models. As can be expected, in all cases the accuracy improves with an increase in the number nB of model terms. The highest accuracy is achieved by using the direct Fourier transform in (17), combined with basis functions derived directly from a discretization of Ak on the full image grid (stack model). Since the visibilities computed in this manner converge to the exact visibilities for nB = NB this result can be used to estimate the highest accuracy that may be obtained with a model of a given number of terms. The error decays rapidly as nB is increased for the first few terms (nB ≲ 10), and thereafter at a somewhat slower rate, until nB ≈ 192 where a sharp drop in the error occurs. This sudden decrease in error is related to a similar sudden decrease in the Singular Value (SV) spectrum of BT at twice the number of antennas in the array, 2 × 96 = 192. Using a sparser discretization of Ak to expedite the construction of the basis functions via the SVD (stack-interp models) is seen to introduce an error between about 10-2.6 and 10-2.9, depending on the sparsity of the grid, and only represents a significant loss in accuracy for a model with more than about nB = 60 terms. Similarly, utilizing the FFT-based calculation (stack-fft model), an error of around 10-2.3 and associated with the degridding operation is introduced which only has a significant impact on the accuracy for a model with more than roughly nB = 40 terms.
 |
Fig. 4 Error in model visibilities as a function of number of BD-DD gain model terms. The error was computed using the exact visibilities as reference. |
In order to put the results in Fig. 4 in perspective, we consider the accuracy for various models reported in Table 1. The error incurred by using a baseline-independent DD gain to compute the visibilities is around −1.404. Using nB = 10 terms of the A-stacking model and computing visibilities via the FFT already reduces the error by more than 50%, and using nB = 40 the error is reduced by more than 75%. (With nB = 40 and using the direct Fourier transform reduces the error slightly more, by about 80%.) This indicates that a large improvement over using a baseline-independent DD gain model is possible with just the first few terms of the BD-DD model, even when the calculation is performed using the FFT followed by a degridding step. Finally, the error in the avg-fft model when using avg model as the reference confirms the error introduced by the degridding operation to be around the 10-2.3 level.
Memory usage statistics for the A-stacking forward calculations based on (23)are listed in Table 2. Results show how the memory requirement increases with the number of terms nB in the BD-DD model for the Np = 64 images used here, and also for Np = 1024 to indicate the requirements for larger images. Since the overall cost scales linearly with the number of terms in the model a simple trade-off between computational cost and calculation accuracy is available. For comparison, the memory requirements for A-stacking are also shown for different convolution kernel sizes. We note that number of baselines relative to the image sizes considered means that the memory requirements for A-projection is almost independent of image size.
6.2. CLEAN performance
In order to demonstrate how A-stacking may impact on the imaging performance, two simple CLEAN algorithms were implemented to use BD-DD gain models of various levels of accuracy. Here the direct transforms in (17)and (27)were used for the forward and backward calculations, respectively, so that the impact of the accuracy of the BD-DD model on the result could be isolated. The sky models used here extended over the same region as before, but used a coarser grid with Np = 16 pixels along each dimension (i.e. 16 × 16 pixel image).
 |
Fig. 5 Convergence of VDSS-CLEAN implementation for DD gain models of various levels of accuracy. Figure shows how the residual image norm is reduced over iterations of source subtraction in the visibility plane. |
Visibility domain source subtraction: VDSS-CLEAN algorithm
The first CLEAN algorithm is based on using the accurate A-stacking forward calculation, and proceeds as follows:
-
1.
Initialize the model sky σm and residual image σr as
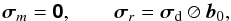 (43)where ⊘ indicates element-wise division, 0 is the zero vector, b0 is the average power pattern over all antennas in the array, and σd is obtained by computing (27)from the visibilities vexact.
(43)where ⊘ indicates element-wise division, 0 is the zero vector, b0 is the average power pattern over all antennas in the array, and σd is obtained by computing (27)from the visibilities vexact. -
2.
The residual norm is calculated as r = log 10( ∥ σr ∥ 2).
-
3.
The peak in σr is identified, and its location (ls,ms) and intensity
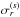 used to update the model sky
used to update the model sky 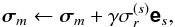 (44)where γ is the loop gain.
(44)where γ is the loop gain. -
4.
Model visibilities vmodel are calculated using the model sky σm in either (5)with the baseline-independent gain b0, or in (17)with the A-stacking model and truncating the summation over i after nB ≤ NB basis functions. This is used to compute residual visibilities,
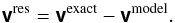 (45)
(45) -
5.
The residual image is updated by substituting vres for the visibilities in (27), and applying a DD correction in the form of element-wise division by b0 to the result.
-
6.
Steps 2 through 5 are repeated for a fixed number of iterations.
Figure 5 shows how the residual norm is reduced over the number of iterations of the VDSS-CLEAN algorithm, and the result displayed is the mean of r over 1000 different generated input skies. Assuming that at each iteration a source is correctly identified, and its intensity underestimated, the energy in the residual image should ideally decrease monotonically with each subtraction. A comparison is shown between DD models of various levels of accuracy, ranging from the same average antenna power pattern over all baselines (avg) to the exact A-stacking model (stack, nB = NB = 256). The intermediate models correspond to keeping only those terms corresponding to Singular Values (SVs) in (38)that are above 1.0% (nB = 3) and 0.1% (nB = 61) relative to the maximum; nB = 96 uses as many terms in the model as antennas in the array, and nB = 192 uses twice as many terms. The latter model is of interest since the SV spectrum exhibits a sharp drop after the 192th SV. In general the algorithm is seen to converge at ever lower values of the residual norm as the model accuracy is increased. The results for each model after the final iteration are summarized in Table 3. Compared to the result for using the average DD gain, using A-stacking with just 3 terms the residual is reduced by about 29%, and with 61 terms by 89%.
Mean residual norms (log-scale) after 300 iterations of each CLEAN algorithm for various BD-DD models.
Image dynamic range after 300 iterations of each CLEAN algorithm for various BD-DD models.
The distributions of residual norms after 300 iterations and for all 1000 simulations are shown in Fig. 7 for four different DD models. In 95% of the simulations the average beam model yielded r < 0.55, and the A-stack model with nB = 3 and nB = 61 yielded r < 0.45, and r < −0.35, respectively. Using the exact model resulted in r < −5.65 for the same percentage of simulations. For a small fraction of the simulations the algorithm converged to a relatively large residual irrespective of the DD gain model used.
Image domain source subtraction: IDSS-CLEAN algorithm
The second CLEAN implementation is based on the procedure outlined in (31)from Sect. 4.1. Using the measured visibilities vexact the dirty image is computed using (27), and the residual image σr is initialized to this dirty image without any DD correction as was done for the VDSS-CLEAN algorithm. The algorithm then proceeds by repeatedly performing PSF subtraction via (31)to update σr for a fixed number of iterations, and computing the residual norm r = log 10( ∥ σr ∥) at each iteration.
Figure 6 shows how the residual norm is reduced over the number of iterations for the IDSS-CLEAN algorithm. The result shown is the mean of r over 1000 different generated sky models and a comparison is shown for various DD gain models. Initially the residual decreases at a steady rate for all DD gain models; beyond a certain number of iterations this decrease slows down significantly, and the residual level at which this occurs depends once again on the accuracy of the DD gain model. For comparison, the results after 300 iterations of IDSS-CLEAN for the different gain models are also shown in Table 3. Apart from somewhat higher residuals after the same number of iterations as compared to that in VDSS-CLEAN, the decrease in the residual with the increase in the number of terms in the gain model is similar for both algorithms. To help put these results into perspective, the dynamic range of the images obtained after 300 iterations of either CLEAN algorithm was calculated and listed in Table 4.
 |
Fig. 6 Convergence of IDSS-CLEAN implementation for DD gain models of various levels of accuracy. Figure shows how the residual image norm is reduced over iterations of source subtraction in the image plane. |
 |
Fig. 7 Distribution of the residual norms after 300 VDSS-CLEAN iterations for 1000 different generated skies. Results are shown for different DD models. We note that the upper limit of the vertical axis has been reduced to improve the clarity of results at lower densities. |
Assuming that a distinct source (in a distinct location) is identified in each iteration of the IDSS-CLEAN algorithm, a differently weighted combination of the PSFs associated with each of the DD basis functions may be required at each iteration. This combination step requires up to 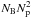 complex multiplications and is the computational bottleneck for this image domain deconvolution approach. As can be expected the cost of a single iteration of this algorithm is much cheaper than that for the VDSS-CLEAN algorithm, which includes an image domain correction that also scales as
complex multiplications and is the computational bottleneck for this image domain deconvolution approach. As can be expected the cost of a single iteration of this algorithm is much cheaper than that for the VDSS-CLEAN algorithm, which includes an image domain correction that also scales as 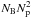 , as well as the costs associated with transforming between the image and visibility planes. This holds even when utilizing the efficiency of an FFT-based implementation, see (19).
, as well as the costs associated with transforming between the image and visibility planes. This holds even when utilizing the efficiency of an FFT-based implementation, see (19).
7. Conclusion
A novel framework for modeling baseline-dependent direction-dependent effects was presented. The approach is based on the expansion of BD-DD effects in the form of a weighted sum of basis functions, where the basis functions are direction-dependent, and the coefficients account for the baseline-dependence. Related to the W-stacking method which accounts for non-coplanar baselines, the present approach, called A-stacking, offers an alternative method to the convolution based algorithm A-projection. As such it offers a potential improvement in computational efficiency in scenarios where A-projection results in a significant increase in the gridding cost.
Using the proposed modeling technique the calculation from sky to visibilities is achieved by combining the result from a number of separate Fourier transforms, which may be implemented to utilize the efficiency of the FFT. The accuracy of this calculation is directly controlled by the number of terms retained in the model, and yields a simple trade-off between accuracy and computational cost. Furthermore, results have shown that good performance may be achieved with relatively few terms, given that an appropriate basis is chosen for the linear model. A method to obtain such a basis for a prior characterized BD-DD effect was presented, and is based on the use of the SVD.
Within this framework, two different imaging strategies were also derived. One strategy takes the form of an adaptation of the PSF subtraction cycle in a typical CLEAN deconvolution process, while the other presents an imaging approach where deconvolution is deemed unnecessary. The use of A-stacking model in two different CLEAN algorithms was also used to demonstrate how this modeling approach may affect image quality. In either case the image residual after a fixed number of iterations was seen to decrease steadily as the model accuracy was improved.
Since the model relies on an accurate characterization of the BD-DD effects, further work focuses on the development of a solvable BD-DD model which is compatible with the A-stacking approach.
The scalar formulation is presented without loss of generality, and the impact of the full-polarization form of (1)is considered subsequently.
This is not the same dirty image as in (26).
In fact, the diagonal approximation may also be used to speed up deconvolution via an
optimization procedure such as the Levenberg-Marquardt algorithm (Marquardt 1963). Such an approximation reduces the Jacobian (and hence
the approximate Hessian) of the deconvolution problem
 to a diagonal matrix,
which reduces the order of complexity of the algorithm from
to a diagonal matrix,
which reduces the order of complexity of the algorithm from
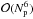 to
to
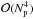 .
.
The rows in a
are mutually orthogonal owing to the unitary property of W, so that
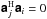 for
i ≠
j. This result may be used to reduce the complexity of
evaluating (36)from
for
i ≠
j. This result may be used to reduce the complexity of
evaluating (36)from
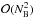 to
to
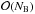 .
.
For instance, this may apply to earth rotation synthesis where multiple visibility measurements are obtained between the same antenna pair, resulting in identical rows in B. Even when the primary beams are varying in time, e.g. rotating primary beams on the sky for alt-az mount reflector antennas, a linear dependence will still be present if such variation is negligible over time scales much larger than the integration time.
Acknowledgments
This work is supported by SKA South Africa, the South African Research Chairs Initiative of the Department of Science and Technology, the National Research Foundation, and the Swedish Vinnova and VR grants. This publication is supported by Samenwerkingsverband Noord Nederland (SNN), SKA-TSM project, and the European Community FP7 program, MIDPREP, Grant Agreement PIRSES-GA-2013-612599.
References
- Bhatnagar, S., Cornwell, T. J., Golap, K., & Uson, J. M. 2008, A&A, 487, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bregman, J. D. 2012, Ph.D. Thesis, University of Groningen [Google Scholar]
- Briggs, D. S., Schwab, F. R., & Sramek, R. A. 1999, in Synthesis Imaging in Radio Astronomy II, ASP Conf. Ser., 180, 127 [NASA ADS] [Google Scholar]
- Clark, B. G. 1980, A&A, 89, 377 [NASA ADS] [Google Scholar]
- Cornwell, T., Braun, R., & Briggs, D. S. 1999, in Synthesis Imaging in Radio Astronomy II, ASP Conf. Ser., 180, 151 [Google Scholar]
- Cornwell, T. J., Golap, K., & Bhatnagar, S. 2008, IEEE J. Select. Topics Signal Process., 2, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Duijndam, A. J. W., & Schonewille, M. A. 1999, Geophysics, 64, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Hamaker, J. P., Bregman, J. D., & Sault, R. J. 1996, A&AS, 117, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Högbom, J. A. 1974, A&AS, 15, 417 [NASA ADS] [Google Scholar]
- Humphreys, B., & Cornwell, T. J. 2011, Analysis of convolutional resampling algorithm performance, Tech. Rep. 132, SKA Memo [Google Scholar]
- Jackson, J. I., Meyer, C. H., Nishimura, D. G., & Macovski, A. 1991, IEEE Trans. Medical Imaging, 10, 473 [Google Scholar]
- Jolliffe, I. 1986, Principal Component Analysis (Springer) [Google Scholar]
- Jongerius, R., Wijnholds, S., Nijboer, R., & Corporaal, H. 2014, Computer, 47, 48 [CrossRef] [Google Scholar]
- Maaskant, R., Ivashina, M. V., Wijnholds, S. J., & Warnick, K. F. 2012, IEEE Trans. Antennas Propag., 60, 3614 [NASA ADS] [CrossRef] [Google Scholar]
- Marquardt, D. W. 1963, J. Soc. Industr. Appl. Math., 11, 431 [Google Scholar]
- Offringa, A. R., McKinley, B., Hurley-Walker, N., et al. 2014, MNRAS, 444, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Schwab, F. R. 1984, AJ, 89, 1076 [NASA ADS] [CrossRef] [Google Scholar]
- Smirnov, O. M. 2011, A&A, 527, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tasse, C., van der Tol, S., van Zwieten, J., van Diepen, G., & Bhatnagar, S. 2013, A&A, 553, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thompson, A. R., Moran, J. M., & Swenson, G. 2004, Interferometry and Synthesis in Radio Astronomy, 2nd edn. (Wiley) [Google Scholar]
- Young, A., Carozzi, T., Maaskant, R., Ivashina, M. V., & Davidson, D. B. 2014, in Int. Conf. Electromagnetics in Advanced Applications (ICEAA), 462 [Google Scholar]
All Tables
Mean residual norms (log-scale) after 300 iterations of each CLEAN algorithm for various BD-DD models.
Image dynamic range after 300 iterations of each CLEAN algorithm for various BD-DD models.
All Figures
 |
Fig. 1 Transformations between image and visibility domains a) for FFT compatible visibility plane sampling, and b) for irregular visibility plane sampling which requires an additional (de)gridding operation in order to utilize the FFT. |
| In the text | |
 |
Fig. 2 a) Forward calculation in the A-stacking framework, subdivided into the algorithmic steps described by (18). b) Forward calculation using A-projection. The A-projection convolution kernel size is NgA × NgA, as determined by the spatial frequency content of the direction-dependent effects on the sky, and can result in a relatively expensive gridding cost. A-stacking aims to reduce this cost by decreasing the size of the gridding convolution kernel to Ng × Ng, as determined by the required image dynamic range; the penalty is that multiple FFTs and gridding operations are required. |
| In the text | |
 |
Fig. 3 a) The LOFAR LBA station at Onsala Space Observatory, Sweden. Photograph courtesy of Leif Helldner. b) FEKO model of the 96 element LBA station showing the radiation patterns (magnitude) of each antenna in the array. The array comprises dual-polarized inverted-V antennas above a ground plane (not shown in model). Generally a larger degree of inter-element variability is observed among the patterns of the antennas that are closely spaced than in the patterns of those that are more isolated. |
| In the text | |
 |
Fig. 4 Error in model visibilities as a function of number of BD-DD gain model terms. The error was computed using the exact visibilities as reference. |
| In the text | |
 |
Fig. 5 Convergence of VDSS-CLEAN implementation for DD gain models of various levels of accuracy. Figure shows how the residual image norm is reduced over iterations of source subtraction in the visibility plane. |
| In the text | |
 |
Fig. 6 Convergence of IDSS-CLEAN implementation for DD gain models of various levels of accuracy. Figure shows how the residual image norm is reduced over iterations of source subtraction in the image plane. |
| In the text | |
 |
Fig. 7 Distribution of the residual norms after 300 VDSS-CLEAN iterations for 1000 different generated skies. Results are shown for different DD models. We note that the upper limit of the vertical axis has been reduced to improve the clarity of results at lower densities. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.