| Issue |
A&A
Volume 577, May 2015
|
|
|---|---|---|
| Article Number | A4 | |
| Number of page(s) | 12 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201424960 | |
| Published online | 22 April 2015 | |
Excitation of kink oscillations of coronal loops: statistical study ⋆
1 Centre for Fusion, Space and Astrophysics, Department of
Physics, University of Warwick, CV4 7AL, UK
e-mail:
V.Nakariakov@warwick.ac.uk
2
Space Research Institute (IKI), Russian Academy of
Sciences, Profsoyuznaya St.
84/32, 117997
Moscow,
Russia
e-mail:
ivanzim@iki.rssi.ru
3
Astronomical Observatory at Pulkovo, Russian Academy of
Sciences, 196140
St. Petersburg,
Russia
4 School of Space Research, Kyung Hee University, 446-701
Yongin, Gyeonggi, Korea
Received: 11 September 2014
Accepted: 17 December 2014
Context. Solar flares are often accompanied by kink (transverse) oscillations of coronal loops. Despite intensive study of these oscillations in recent years, the mechanisms that excite them are still not known.
Aims. We aim to clarify the excitation mechanisms for these kink oscillations of coronal loops.
Methods. We analysed 58 kink-oscillation events observed by the Atmospheric Imaging Assembly (AIA) onboard the Solar Dynamics Observatory (SDO) during its first four years (2010–2014) with the use of the JHelioviewer. Association of these oscillation events with flares, lower coronal (r ≲ 1.4 R⊙) eruptions and plasma ejections, coronal mass ejections (CMEs), and coronal Type-II radio bursts is studied.
Results. We find that 44 of these 58 oscillation events (76%) were associated with CMEs observed in the white light emission. Moreover, 57 events (98%) were accompanied by lower coronal eruptions/ejections (LCEs) observed in the extreme-ultraviolet band in the parental active regions. In the remaining event an LCE was not clearly seen, but it was definitely associated with a CME too. The main observational finding is that the kink oscillations were excited by the deviation of loops from their equilibria by a nearby LCE in 55 events (95%). In three remaining events, it was difficult to reliably determine the cause of the oscillations because of limitations in the observational data. We also found that 53 events (91%) were associated with flares. In five remaining events, the parental active regions were behind the limb and we could not directly see flare sites. It indicates that there is a close relationship between these two kinds of solar activity. However, the estimated speeds of a hypothetical driver of kink oscillations by flares were found to be lower than 500 km s-1 in 80% of the cases. Such low speeds do not favour the association of the oscillation excitation with a shock wave, as usually assumed. That only 23 (40%) of the oscillation events were found to be associated with coronal Type-II radio bursts also goes against the shock wave mechanism for the excitation of kink oscillations.
Conclusions. The statistical analysis shows that the most probable mechanism for exciting the kink oscillations of coronal loops is the deviation of loops from their equilibrium by nearby eruptions or plasma ejections rather than a blast shock wave ignited by a flare.
Key words: Sun: magnetic fields / Sun: oscillations / Sun: flares / Sun: coronal mass ejections (CMEs) / shock waves
Table 1 is available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Kink oscillations of coronal loops are one of the most debated physical phenomena in solar physics. The oscillations are usually seen as periodic harmonic displacements of the axes of loops seen in 171 Å and 195 Å bandpasses of coronal extreme ultraviolet (EUV) imagers (Aschwanden et al. 1999; Nakariakov et al. 1999). Evidence of kink oscillations of coronal loops has recently been found with the use of the radio observations (e.g. Inglis & Nakariakov 2009; Khodachenko et al. 2011; Mossessian & Fleishman 2012; Kupriyanova et al. 2013; Zaqarashvili et al. 2013). The typical periods of these oscillations are several minutes, and the displacement amplitude is typically several Mm (see De Moortel & Nakariakov 2012; Liu & Ofman 2014, for recent comprehensive reviews).
Kink oscillations of neighbouring loops usually have different periods, amplitudes, and phases. In the majority of cases, only the fundamental spatial harmonics is observed, with the maximum of the transverse displacement near the loop top and the node of the oscillations at the footpoints. However, in several cases the second harmonics was detected, too. In the vast majority of observed cases, the oscillations are seen to have horizontal polarisation. Kink oscillations are detected in two regimes, the high-amplitude rapidly decaying oscillations (Nakariakov et al. 1999) and the recently discovered low-amplitude decayless oscillations (Nisticò et al. 2013). In the following, we concentrate on the high-amplitude, rapidly decaying oscillations.
The interest in the kink oscillation is connected with its intensive use for the remote diagnostics of active region plasmas (e.g. Stepanov et al. 2012). Comparison of the observed properties of kink oscillations with theoretical modelling allows estimating the absolute value of the magnetic field in the oscillating loop (e.g. Nakariakov & Ofman 2001), the density scale height (e.g. Andries et al. 2005), and the height variation of the loop minor radius (e.g. Verth & Erdélyi 2008). Also, understanding basic physical mechanisms operating in kink oscillations is important for revealing the enigmatic problem of solar and stellar coronal heating (e.g. Goossens et al. 2013).
It is commonly accepted that kink oscillations are a manifestation of the kink (m = 1) magnetohydrodynamic (MHD) standing mode of a plasma cylinder (e.g. Zaitsev & Stepanov 1982; Edwin & Roberts 1983). But, there is no agreement on the physical mechanisms for their excitation. The observed timing of the appearance of kink oscillations soon after solar flares suggests that the oscillations were excited by a blast wave generated by a flare (e.g. Aschwanden et al. 1999; Nakariakov et al. 1999; Schrijver et al. 2002; Hudson & Warmuth 2004; Tothova et al. 2011). However, numerical simulations of this process have shown that it is difficult to excite perturbations of the observed displacement amplitude of several minor radii of the loop (e.g. McLaughlin & Ofman 2008; Ofman 2009) in a loop with a low ratio of the internal to external mass densities.
There have been several alternative mechanisms proposed. The apparent proximity of some oscillating loops to topologically unstable magnetic regions, such as near the magnetic separatrix, have led to the idea that the oscillations highlight rocking motions at the photospheric level. In this case, a small displacement of the loop footpoint is magnified by the “sensitivity” of the equilibrium magnetic topology to a small perturbation (Schrijver & Brown 2000; Schrijver et al. 2002; White et al. 2013). The apparent association of kink oscillation events with the phenomenon of coronal EUV dimming led to the development of a mechanism based on the resonant excitation of the oscillations by the aerodynamic drag force caused by periodic shedding of Alfvénic vortices (Nakariakov et al. 2009; Gruszecki et al. 2010). Another mechanism based upon the presence of field-aligned electric currents in loops, causing their inductive interaction, was developed in Khodachenko et al. (2009). Uralov (2003) propose that the oscillatory pattern is not an oscillation of the individual loop but a tracer of an oscillatory wake behind a flare-generated MHD disturbance propagating across the field. Distinguishing between these mechanisms requires detailed information about the relationship between the kink oscillation events and their potential drivers, such as flares, plasma ejections, and eruptions.
The aim of this work is to perform a detailed study of the statistical association between events of kink oscillations and dynamical processes in the corona, that could potentially excite them. The study is based upon using high time and spatial resolution observational data and online catalogues. The paper is organised as follows. In Sect. 2 we describe the data used, Sect. 3 contains the results obtained, and Sect. 4 presents our conclusions.
2. Observations
2.1. Kink oscillations of coronal loops
The main object of the study is high-amplitude, rapidly decaying kink oscillations of coronal loops observed in the EUV band with the Atmospheric Imaging Assembly (AIA, Lemen et al. 2012) onboard the Solar Dynamics Observatory (SDO). The term “high-amplitude” means that the amplitude of the oscillations is at least a few minor radii of the loop, which is about the linear size of the AIA pixel, or about 0.6″ or 435 km at the Sun. The period of the studied oscillations is longer than a few time steps between two successive AIA images in the EUV channels, which is 12 s. Thus, our study is restricted to analysing loop oscillations that are well resolved with AIA and that can be seen with the naked eye in a sequence of AIA images without using any special detection techniques, such as the time-distant mapping or periodmapping.
Our search for kink oscillation events is restricted by the first four years of the AIA observations, the time period from 20 May 2010 to 20 May 2014. The search for kink oscillations was performed with the Heliophysics Events Knowledgebase (HEK1). We found 96 events marked as “Oscillation” in the HEK within this time interval, but not all of them were found to satisfy the purpose of our study. First of all, we excluded from further consideration all (15) events (reported in the HEK) associated with oscillations of cold and dense filaments/prominences. This left 81 events in the preliminary list for the further analysis.
It was very time consuming to analyse rough AIA data for all 81 events, each lasting several tens of minutes or longer. But, this task was efficiently done with JHelioviewer, which is a visualisation tool for solar images based on the JPEG2000 compression standard (Mueller et al. 20092). Its capacity is sufficient for our purposes. It allows for visualising time series of AIA images with the average cadence of 24 s. An important advantage of the JHelioviewer is the possibility to determine the solar coordinates (x,y) of each image pixel, allowing for finding the coordinates of the studied objects at the Sun at any given time.
With the JHelioviewer we found that kink oscillations of coronal loops were not obvious in 37 out of 81 events in the preliminary list. These 37 events were indeed accompanied by some oscillatory-like processes in the corona. However, available observational datasets did not allow us to assert with confidence that these processes were really kink oscillations of coronal loops and not some other processes, such as turbulent eddies, longitudinal oscillations, complex motions of multi-loop multi-temperature structures, or something else. For this reason, we excluded these events from further analysis. We also found that the AIA data were not available in the JHelioviewer for three other events from the preliminary list. Thus, only 41 out of 81 events were left in the list.
It should be noted that some of these 41 oscillatory events lasted for several hours according to the HEK. Careful consideration of such events with the JHelioviewer showed that they consisted of several separate events, although occurring sequentially in the same active regions. The term “separate” here means that excitation of the decaying kink oscillations in these events happened several times. Each of these sub-events we classified as a separate event. Thus, our list extended from 41 to 51 events.
Finally, we added seven other events to the list, which were not reported in the HEK. Three of them were found by the authors of this paper (20 October 2012, 17 February 2013, 19 November 2013) and four others were reported in the literature: 2 August 2010 (White & Verwichte 2012), 6 September 2011 (Verwichte et al. 2013), 8 May 2012 (White et al. 2013), and 30 May 2012 (Nisticò et al. 2013). It should be noted that White & Verwichte (2012) have also analysed an oscillatory event of 13 June 2010, which was not reported in the HEK. But the AIA data for this event was not available within the JHelioviewer, so we did not include it in our final list.
Thus, our final list (catalogue) contains 58 events that were the clear examples of high-amplitude, decaying kink oscillations of coronal loops. These events are summarised in Table 1. We should note that we did not thoroughly check all the literature on the kink oscillations detected by AIA. Therefore, it is possible that some kink oscillation events observed by AIA during the time interval of 20 May 2010–20 May 2014 were missing in our list. Nevertheless, we assume that the sample of 58 events is large enough to draw statistically robust conclusions about the excitation mechanisms of the kink oscillations of EUV coronal loops.
Columns 1 and 2 of Table 1 contain the index number and date of each event. Column 3 contains the start times of oscillations (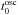 ). Since oscillations were detected by naked eye, the accuracy of the determination of their start times is not high. Since in some events there were almost simultaneous oscillations of several spatially separated loops, Col. 3 may contain several different start times. Only start times of the most obvious (high-amplitude) loop oscillations are given. From the total set of 58 events we identified 169 different oscillating loops. Solar coordinates (xosc,yosc) of these oscillating loops are shown in Col. 4. These coordinates correspond to the part of a loop that had the highest visible oscillation amplitude for the given loop. In most cases this corresponded to the top of the loop, indicating that, most probably, the fundamental harmonics of the kink oscillations were detected.
). Since oscillations were detected by naked eye, the accuracy of the determination of their start times is not high. Since in some events there were almost simultaneous oscillations of several spatially separated loops, Col. 3 may contain several different start times. Only start times of the most obvious (high-amplitude) loop oscillations are given. From the total set of 58 events we identified 169 different oscillating loops. Solar coordinates (xosc,yosc) of these oscillating loops are shown in Col. 4. These coordinates correspond to the part of a loop that had the highest visible oscillation amplitude for the given loop. In most cases this corresponded to the top of the loop, indicating that, most probably, the fundamental harmonics of the kink oscillations were detected.
2.2. Flares
To check the possible solar flare activity associated with the selected loop oscillation events we used the soft X-ray reports provided by the National Oceanic and Atmospheric Administration (NOAA). These reports are provided by the National Geophysical Data Center (NGDC3). Columns 5 and 6 of Table 1 contain the start (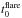 ) and peak (
) and peak (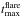 ) times of the associated flare X-ray emission detected in the 1–8 Å wavelength band, determined with the X-Ray Sensor (XRS) onboard the Geostationary Operational Environmental Satellites (GOES) in the studied events. Column 8 shows the X-ray class of each associated flare.
) times of the associated flare X-ray emission detected in the 1–8 Å wavelength band, determined with the X-Ray Sensor (XRS) onboard the Geostationary Operational Environmental Satellites (GOES) in the studied events. Column 8 shows the X-ray class of each associated flare.
Flares were not reported by the NGDC for all studied events. For those events without reported flares we checked the original three-second GOES data using the “GOES”package in the Solar SoftWare (SSW). In the cases where we found an increase in the solar soft X-ray flux with respect to the background level for several consecutive data points in a half-hour vicinity of the corresponding oscillation event, we added the start and peak times, as well as the X-ray class of this flare event to our catalogue. Such flares (8 cases) are marked by “(ZN)” label in Col. 5.
It can be seen in Table 1 that 53 out of the total 58 oscillation events were definitely accompanied by flares, although in the majority of them these flares were quite weak: 10 out of 53 flares (19%) were of the B class, 25 (47%) of the C class, 14 (26%) of the M class, and only 4 (8%) of the X class. In the remaining five events, there were no obvious increases in the solar soft X-ray flux (in the GOES data) above the background level. In those events the parental active regions (and probably flares) were behind the solar limb. A look at the data obtained with the EUVI/SECCHI (Howard et al. 2008) onboard the STEREO-A and STEREO-B spacecraft revealed that all five events were accompanied by some increases in the EUV brightness, localised in time and space in the corresponding active regions. This indicates that all 58 studied oscillation events were accompanied by some flaring activities related to localised releases of energy.
Column 7 of Table 1 contains solar coordinates 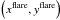 of each detected flare. These are coordinates of the brightest pixels of the flaring site close to its geometrical centre observed in the AIA “hottest” (131 Å) channel in the vicinity of the flare X-ray peak time. These coordinates were identified using the JHelioviewer. When the flare site (at the photosphere) was obviously behind the east or west limb of the Sun, we added “(BEL)” or “(BWL)” marks respectively to Col. 7.
of each detected flare. These are coordinates of the brightest pixels of the flaring site close to its geometrical centre observed in the AIA “hottest” (131 Å) channel in the vicinity of the flare X-ray peak time. These coordinates were identified using the JHelioviewer. When the flare site (at the photosphere) was obviously behind the east or west limb of the Sun, we added “(BEL)” or “(BWL)” marks respectively to Col. 7.
The time difference 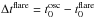 is shown in Col. 9 of Table 1. It can be seen that the flares started earlier than the loop oscillations in all events except only two: N 13 and 36. This may indicate that the loop oscillations are a consequence of the flares. We estimated the speeds of a possible (hypothetical) flare driver of the oscillations in each event as a ratio of the distance between the oscillating loop and the flare site, and Δtflare, i.e.
is shown in Col. 9 of Table 1. It can be seen that the flares started earlier than the loop oscillations in all events except only two: N 13 and 36. This may indicate that the loop oscillations are a consequence of the flares. We estimated the speeds of a possible (hypothetical) flare driver of the oscillations in each event as a ratio of the distance between the oscillating loop and the flare site, and Δtflare, i.e. 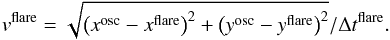 (1)The speeds are shown in Col. 10. Figure 1 gives the histogram of vflare values. It is seen that in the majority of cases (in 102 out of 132 cases, where it was possible to calculate vflare, i.e. in 77%) vflare< 500 km s-1. We restricted the horizontal axis of the histogram in Fig. 1 by the value of vflare = 2000 km s-1 for clarity. Anomalously high values of vflare, greater than 2000 km s-1 for events N 13, 18, 48, and 52, were not included in the statistics. These values are not likely to be physically meaningful. They indicate that in this event the loop oscillations were excited by a different agent (see Sect. 2.3) rather than by a hypothetical wave driven by a flare.
(1)The speeds are shown in Col. 10. Figure 1 gives the histogram of vflare values. It is seen that in the majority of cases (in 102 out of 132 cases, where it was possible to calculate vflare, i.e. in 77%) vflare< 500 km s-1. We restricted the horizontal axis of the histogram in Fig. 1 by the value of vflare = 2000 km s-1 for clarity. Anomalously high values of vflare, greater than 2000 km s-1 for events N 13, 18, 48, and 52, were not included in the statistics. These values are not likely to be physically meaningful. They indicate that in this event the loop oscillations were excited by a different agent (see Sect. 2.3) rather than by a hypothetical wave driven by a flare.
 |
Fig. 1 Distributions of the speeds required for hypothetical agents exciting kink oscillations of coronal loops to reach the oscillation sites from the starting point of the lower coronal eruptions/ejections (vLCE, solid line) and the location of the flares (vflare, dotted lines). |
2.3. Eruptions and plasma ejections in the lower corona
Owing to continuous observations of the Sun’s hemisphere that is visible from the Earth with the SDO/AIA simultaneously in different channels covering a broad range of plasma temperatures, we have a good opportunity to carefully examine the presence or absence of eruptions and/or plasma ejections in the lower corona (r ≲ 1.4 R⊙) co-existing with the studied loop oscillation events. This information may help us to identify a relationship between eruptions (ejections) and excitation of kink oscillations. By the eruption we mean a sudden destabilisation and ejection of some plasma configuration in the active region of interest. It can be a cold and dense filament, a flux rope, a system of magnetic loops (a loop arcade or a more complex structure), or something else. By the plasma ejection we mean an ejection of plasmoids or jets from the flaring site along magnetic flux tubes (closed or open) of the active region.
Using the JHelioviewer we found that 57 out of the total 58 studied kink oscillation events (except event N 55), i.e. 98% of cases, were accompanied by evident lower coronal eruptions/ejections (LCEs) from the parental active regions. The start times (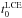 ) of each detected LCE and solar coordinates of its initial appearance (xLCE,yLCE) are given respectively in Cols. 11 and 12 of Table 1. We should note here that event N 55 was behind the solar limb and was not accompanied by an obvious increase in the soft X-ray flux, i.e. by a flare visible from the Earth’s orbit with GOES/XRS. Nevertheless, it was accompanied by a coronal mass ejection (CME, see Sect. 2.4). Consequently, this event should also be taken as being accompanied by an eruption/ejection in the lower corona, but it was not obviously seen with the AIA/SDO by some reason. One of the possibilities is that it was a faint eruption. Analysis of the white-light CME observations with the LASCO/SOHO (Brueckner et al. 1995) in this event confirms this simple interpretation. Thus, it can be concluded that all studied kink oscillation events were accompanied by LCEs in the corresponding parental active regions. This fact is crucial for understanding the excitation mechanisms of coronal loop oscillations (see the discussion below).
) of each detected LCE and solar coordinates of its initial appearance (xLCE,yLCE) are given respectively in Cols. 11 and 12 of Table 1. We should note here that event N 55 was behind the solar limb and was not accompanied by an obvious increase in the soft X-ray flux, i.e. by a flare visible from the Earth’s orbit with GOES/XRS. Nevertheless, it was accompanied by a coronal mass ejection (CME, see Sect. 2.4). Consequently, this event should also be taken as being accompanied by an eruption/ejection in the lower corona, but it was not obviously seen with the AIA/SDO by some reason. One of the possibilities is that it was a faint eruption. Analysis of the white-light CME observations with the LASCO/SOHO (Brueckner et al. 1995) in this event confirms this simple interpretation. Thus, it can be concluded that all studied kink oscillation events were accompanied by LCEs in the corresponding parental active regions. This fact is crucial for understanding the excitation mechanisms of coronal loop oscillations (see the discussion below).
All the observed LCEs started several tens or hundreds of seconds before the loop oscillations. The time differences between the start times of the oscillations and LCEs, 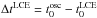 , is given in Col. 13 of Table 1. As in the case of the flares, the positive values of ΔtLCE illustrate that excitation of the loop oscillations can be related to the LCEs. The time lag between the LCEs’ starting times
, is given in Col. 13 of Table 1. As in the case of the flares, the positive values of ΔtLCE illustrate that excitation of the loop oscillations can be related to the LCEs. The time lag between the LCEs’ starting times 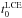 and the onset of the oscillation corresponds to the LCE development time from its initial location
and the onset of the oscillation corresponds to the LCE development time from its initial location 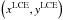 up to its contact with the loops.
up to its contact with the loops.
Thanks to the high time cadence, sensitivity, and multi-wavelength (thus, multi-temperature) character of the SDO/AIA observations, it was possible to observe the impact (influence) of the LCEs to the nearby plasma structures in detail, in particular, to coronal loops in each event (except event N 55 mentioned above and event N 2, see below). Careful analysis of the sequences of the AIA images (movies) in different channels within the JHelioviewer showed that in almost all events the excitation of kink oscillations was caused by the displacement of the loops from their equilibrium state, made by a nearby LCE, and subsequent oscillatory relaxation of the loops to the pre-eruption equilibrium or to a new equilibrium state. This is the main result of the entire work.
 |
Fig. 2 Schematic illustration of the mechanism for the excitation of kink oscillations of coronal loops, observed in the majority of the studied events. a) Pre-eruption state of the active region. b) Displacement of a coronal loop (solid black curve) from its equilibrium state (dashed black line) by an erupting and expanding plasma structure, e.g. a flux rope (grey loop-shaped structure). c) Oscillatory relaxation of the loop to its equilibrium state after the eruption. |
Schematic illustration of the most common situation observed is sketched in Fig. 2. We marked this situation as Type 1 in Col. 18 of Table 1. It was observed in 50 out of 58 events (86% of cases). For these cases it was found that coronal loops of the active region were in their equilibrium state before the flare and/or eruption (Fig. 2a). During the eruption an erupting plasma structure, i.e. a magnetic flux rope or a subsystem of unstable loops, interacts with some (but not necessarily all) coronal loops of the active region by ram and/or magnetic pressure, causing the loops to deviate from their equilibrium state (Fig. 2b). In other words, the loops are mechanically pushed away from the equilibrium by the moving plasma structure. After the erupting object has left the interaction region and reached greater heights in the corona, the disturbed loops relax to the pre-eruption or a new state of equilibrium (Fig. 2c). Because of the inertia, the loops overshoot the equilibrium and the kink oscillation occurs. The efficiency of this effect probably depends on how rapidly the displacing forces cease, in comparison with the period of the kink oscillation. Obviously, the proposed illustration is very schematic and should only be considered as a cartoon. The studied active regions had a broader variety of plasma configurations. In a more thorough study, the specific details of the active region and LCE geometries should be taken into account. In particular, the LCE can interact simultaneously with several loops situated at different angles with respect to the LCE axes of symmetry.
As an example of this mechanism, we show a sequence of images taken with AIA at 171 Å during event N 44. Figure 3a shows the pre-event state of the active region, which is situated close to the west limb. The active region consisted of a set of several loops of different sizes and inclined at different angles to the vertical. Figure 3b shows the active region at the moment when a flux-rope-like LCE was clearly visible. This LCE propagated upwards in the region between the loops and pushed them away from their equilibria in the transverse direction. The flare position and the LCE starting point close to the solar surface, found with the JHelioviewer (see Table 1), are indicated in the figure. Figure 3c shows the instant of time when the LCE was already at some distance from the loops. The lower row of images (Fig. 3d–h) represents the dynamics of the top of one particular loop bundle shown in the upper rows of images by the white square box. The oscillatory dynamics of the loop-top is clearly seen. Only two periods of oscillations are shown for clarity.
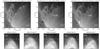 |
Fig. 3 Sequence of AIA 171 Å images taken during event N 44. Crosses indicate the positions of the oscillating loops found with JHelioviewer and shown in Col. 4 of Table 1. The black asterisk and triangle indicate positions of the flare and the starting point of the LCE, given in Cols. 7 and 12 of Table 1, respectively. The white square boxes in the upper images show the region that is zoomed in the lower row of panels. The solar limb is shown by the thin white curve. Solar coordinates of the black cross in all images are the same. The dashed horizontal line is an arbitrary reference level to highlight the oscillatory behaviour of the loops. |
We also found that in six events kink oscillations of loops were excited in a somewhat different way. We marked these events as Type 2 in Col. 18 of Table 1. In these events the LCEs are also clearly seen, but it is not clear how exactly the loops become displaced. The mechanism for the excitation of kink oscillations in those cases requires a detailed dedicated study, but it is definitely connected with an LCE. It should be noted here that White et al. (2013) proposed another excitation mechanism for the kink oscillations observed in event N 29. We mentioned this possibility by adding the “type 3” mark into Col. 18 of Table 1. This event occurred far from the limb, and the projection effect should be taken into account. Also the AIA images of this event were saturated by high fluxes of the EUV emission from the flare kernel. These factors strongly complicated revealing the processes operating in this active region. Both interpretations should not be excluded for this event.
In event N 2 the observations do not allow us to state unambiguously whether the mechanism for the excitation of the oscillation was connected with the interaction of loops with an LCE. Even though this event was undoubtedly accompanied by an LCE, as well as by a CME (see Sect. 2.4), direct interaction of loops with this LCE was not evident from the AIA images. This could be due to the projection effect or because of the low brightness of the LCE. However, the loop oscillations in this event were apparently excited by the interaction of the loops with the flanks of an expanding LCE (close to its bases), the apex of which was already at a high altitude (thus, not well seen by the AIA) during the interaction. See also the paper by Aschwanden & Schrijver (2011) where this event was studied in detail and some other possible mechanisms for the excitation of the loop oscillations were discussed.
Since we found that the main physical agent (driver) that excited oscillations of coronal loops was an LCE we can roughly estimate its speed for each event as 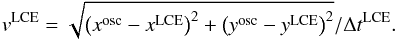 (2)The values of vLCE are given in Col. 15 of Table 1. Figure 1 gives the histogram of the vLCE values. It can be seen that, in general, values of vLCE are comparable to the values of vflare and are lower than 500 km s-1 in 91 out of 165 cases, i.e. for 55% of the oscillating loops. However, the high-speed tail in the histograms is more pronounced for vLCE than for vflare. Furthermore we compare the distributions of vLCE values for events with and without CMEs and for events with and without Type II radio bursts.
(2)The values of vLCE are given in Col. 15 of Table 1. Figure 1 gives the histogram of the vLCE values. It can be seen that, in general, values of vLCE are comparable to the values of vflare and are lower than 500 km s-1 in 91 out of 165 cases, i.e. for 55% of the oscillating loops. However, the high-speed tail in the histograms is more pronounced for vLCE than for vflare. Furthermore we compare the distributions of vLCE values for events with and without CMEs and for events with and without Type II radio bursts.
2.4. Coronal mass ejections
We used two sources of information to check whether the studied oscillation events were accompanied by CMEs or not. The first one is the SOHO/LASCO CME catalogue (Gopalswamy et al. 20094). The second one is the CACTus CME list (Robbrecht & Berghmans 2004; Robbrecht et al. 20095). The main difference between these two sources is that the SOHO/LASCO CME catalogue contains the CMEs manually defined from the SOHO/LASCO (Brueckner et al. 1995) data, while the CACTus CME list contains the CMEs detected with a special automatic technique from both the SOHO/LASCO and STEREO/SECCHI/COR2 (Howard et al. 2008) data. The simultaneous use of these two catalogues allows for the more reliable identification of the presence or absence of CMEs in the studied events.
We consider a loop oscillation event to be accompanied by a CME if: 1) a CME was observed within a one and a half hour interval after the start time of the first loop oscillation; and 2) the central position angle of the oscillating loops (measured counterclockwise from the north pole of the Sun) was in the range ![\hbox{$\left[ {\rm PA}^\mathrm{CME} - \alpha/2, {\rm PA}^\mathrm{CME} + \alpha/2 \right]$}](/articles/aa/full_html/2015/05/aa24960-14/aa24960-14-eq26.png) , where PACME is the central position angle of the CME and α is its angular width measured with the SOHO/LASCO observations. The second criterion was omitted when we considered the STEREO/COR1 observations. As the first step, we checked reports in the SOHO/LASCO CME catalogue. If a CME satisfying the two criteria mentioned above was in this catalogue, we marked the time of its first appearance, (
, where PACME is the central position angle of the CME and α is its angular width measured with the SOHO/LASCO observations. The second criterion was omitted when we considered the STEREO/COR1 observations. As the first step, we checked reports in the SOHO/LASCO CME catalogue. If a CME satisfying the two criteria mentioned above was in this catalogue, we marked the time of its first appearance, (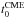 , measured with an accuracy of one minute) in Col. 15 of Table 1. If there was no report in the SOHO/LASCO CME catalogue, we checked in the CACTus list of the CMEs detected with the SOHO/LASCO observations. If we found an appropriate CME there, we added its
, measured with an accuracy of one minute) in Col. 15 of Table 1. If there was no report in the SOHO/LASCO CME catalogue, we checked in the CACTus list of the CMEs detected with the SOHO/LASCO observations. If we found an appropriate CME there, we added its 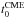 to Col. 15, labelling it with the “(C/L)” mark. If we did not find an appropriate report, we checked further for the CACTus list of the CMEs detected with the STEREO/COR2 data. In the positive identification case, we added the appropriate
to Col. 15, labelling it with the “(C/L)” mark. If we did not find an appropriate report, we checked further for the CACTus list of the CMEs detected with the STEREO/COR2 data. In the positive identification case, we added the appropriate 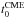 to Col. 15, labelling it with the “(C/SA)” or “(C/SB)” marks, depending on which spacecraft – respectively the STEREO-A or STEREO-B – detected the CME.
to Col. 15, labelling it with the “(C/SA)” or “(C/SB)” marks, depending on which spacecraft – respectively the STEREO-A or STEREO-B – detected the CME.
 |
Fig. 4 Distributions of the speeds required for the excitation of kink oscillations by lower coronal eruptions/ejections, vLCE, in the events: a) with (solid line) and without (dotted line) CMEs; b) with (solid line) and without (dotted line) coronal Type-II radio bursts. |
We found that 44 out of total 58 loop oscillation events (76%) were accompanied by a CME. This means that the statistical association of loop oscillation events with the CMEs is slightly worse than with the LCEs. This is not surprising, since some of the LCEs were confined (failed) CMEs; i.e. they did not reach the heights in the corona (r ≈ 2 R⊙) where they could be identified as a CME in the white light emission with the coronagraphic observations. We checked whether there was some difference between the speeds (vLCE) estimated for the LCE-induced agents possibly exciting the oscillations in the events with and without CMEs. Distributions of vLCE for both these types of events are shown in Fig. 4a.
One can see that there is no obvious difference between the distributions of vLCE in these two types of events, except that the statistics of the events without CMEs is three times poorer than for the events with CMEs. This indicates that the ability of an LCE to become a CME does not depend strongly on its average speed. Indeed, there are multiple proofs that the major factor determining whether an LCE will be confined (failed) or full (will become a CME) is the character of an overlying magnetic field decrease with height (e.g. Török & Kliem 2005, 2007; Liu 2008; Guo et al. 2010). Another possibility is that the estimated values of vLCE do not accurately represent of the real speeds of the studied LCEs. This could be because our estimates do not consider possible acceleration or deceleration of the LCEs during the studied time intervals. The lack of the significant difference between the vLCE-distributions in the events with and without coronal Type-II radio bursts (Fig. 4b and Sect. 2.5) confirms that our estimations of vLCE are not very precise.
2.5. Coronal Type-II radio bursts
To find out whether the studied loop oscillation events were associated with large-scale shock waves in the corona, we checked the presence of coronal (decimetric, metric, decametric) Type-II radio bursts in each case. For the first look, for each oscillation event in Table 1, we used the daily reports of the solar and geophysical activity produced by the Space Weather Prediction Center (SWPC) of the NOAA6 and also the monthly reports of the solar radio events detected with the Culgoora and Learmonth Radiospectrographs7. After this first step we checked the original radio spectrograms obtained with radio telescopes from around the globe, which performed observations of the Sun in a one-hour vicinity of each oscillation event. Radio spectrograms from the Radio Solar Telescope Network8 and the e-Callisto International Network of Solar Radio Spectrometers9 were mainly used.
 |
Fig. 5 Distributions of the speeds, vflare, required for the excitation of kink oscillations by a flare, in the events with (solid line) and without (dotted line) coronal type II radio bursts. |
The start times (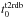 ) of the found Type-II radio bursts and their starting frequencies (
) of the found Type-II radio bursts and their starting frequencies (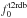 ) are shown in Cols. 16 and 17 of Table 1 with an accuracy of 1 min and 10 MHz, respectively. The symbol “∗” before the starting frequencies of some Type-II bursts means that the starting frequencies of these bursts were most probably higher than the given values, but radio spectrograms for the higher frequency range were not available for these events. We found that only 23 out of the total 58 loop oscillation events (40%) were associated with coronal Type-II bursts. This ratio is similar to the 43% found by Hudson & Warmuth (2004). Moreover, 16 out of these 23 Type-II bursts (70%) were found to start more than one minute later than the beginning of the loop oscillations. This indicates that the shock waves are not the exciting agent of the loop oscillations. The shock waves highlighted by the Type-II radio bursts are rather only a secondary phenomenon accompanying a fraction of the observed LCEs and CMEs. Indeed, all 23 Type-II bursts (100%) were associated with the LCEs, and 22 Type-II bursts (96%) were associated with the CMEs. The lack of differences between the vflare-distributions (see Sect. 2.2) in the events with and without coronal Type-II bursts (Fig. 5) further confirms that the Type-II bursts in the studied events (hence the shock waves) were not the result of the flares, but the phenomenon accompanying the LCEs and CMEs (see also Gopalswamy 2006, for a comprehensive review of this issue).
) are shown in Cols. 16 and 17 of Table 1 with an accuracy of 1 min and 10 MHz, respectively. The symbol “∗” before the starting frequencies of some Type-II bursts means that the starting frequencies of these bursts were most probably higher than the given values, but radio spectrograms for the higher frequency range were not available for these events. We found that only 23 out of the total 58 loop oscillation events (40%) were associated with coronal Type-II bursts. This ratio is similar to the 43% found by Hudson & Warmuth (2004). Moreover, 16 out of these 23 Type-II bursts (70%) were found to start more than one minute later than the beginning of the loop oscillations. This indicates that the shock waves are not the exciting agent of the loop oscillations. The shock waves highlighted by the Type-II radio bursts are rather only a secondary phenomenon accompanying a fraction of the observed LCEs and CMEs. Indeed, all 23 Type-II bursts (100%) were associated with the LCEs, and 22 Type-II bursts (96%) were associated with the CMEs. The lack of differences between the vflare-distributions (see Sect. 2.2) in the events with and without coronal Type-II bursts (Fig. 5) further confirms that the Type-II bursts in the studied events (hence the shock waves) were not the result of the flares, but the phenomenon accompanying the LCEs and CMEs (see also Gopalswamy 2006, for a comprehensive review of this issue).
It should also be noted here that in the considered cases we found that almost every event with a flare was accompanied by an LCE. However, it was not possible to establish whether the flares were triggered by LCEs or if it was the other way around. Figure 6 shows the histogram of the time differences between the beginning times of the studied LCEs and flares, and the distribution is almost symmetric with respect to zero.
 |
Fig. 6 Distributions of the differences between the beginning times of LCEs and flares. The time is measured in minutes. The bin size is one minute. |
3. Results
We briefly summarise the results of this work. We selected 58 events of kink oscillation of EUV coronal loops, observed well by the AIA onboard the SDO during its first four years (May of 2010 to May of 2014). One hundred sixty-nine individual loops performing well-pronounced kink oscillations were selected in these events for the analysis (see Table 1). The actual number of oscillating loops in these 58 events may have even been larger than 169, since we restricted our analysis to consideration of the most prominent oscillating loops.
We found that 53 out of the total 58 oscillation events (i.e. 91%) were associated with flares, and in five remaining events the flare sites were obviously behind the solar limb for an observer near Earth. This may indicate a close relationship between flares and oscillations of coronal loops. Assuming this, we estimated the speeds of a hypothetical driver of loop oscillations caused by a nearby flare. The speed was calculated as the ratio of (i) the distance between the flare site and (ii) the location of the highest amplitude of the oscillation and the time between the flare onset and the beginning of the oscillation. This hypothetical driver is usually assumed to be a fast magnetoacoustic blast wave (e.g. Aschwanden et al. 1999, Nakariakov et al. 1999, Schrijver et al. 2002, Hudson & Warmuth 2004). These speeds were found to be lower than 500 km s-1 in 80% of the cases. Such low speeds do not favour the blast wave mechanism, since the Alfvén speed in oscillating loops is usually higher than about 800–1000 km s-1 (e.g. Nakariakov & Ofman 2001, De Moortel & Nakariakov 2012, Stepanov et al. 2012). The Alfvén speed outside the oscillating loops – in the medium where the hypothetical driver propagates – should not be less than these values since the magnetic field outside the loops is slightly higher than inside them, while the plasma concentration inside the loop is slightly higher than outside it (e.g. Edwin & Roberts 1983). Thus, to be a shock wave, the hypothetical driver of loop oscillations should propagate from the flare site to the oscillating loop at a speed higher than at least 800 km s-1, which was not found in the majority of the cases analysed in this study. Moreover, we found that only 23 (i.e. 40%) of the loop oscillation events were associated with coronal Type-II radio bursts, which are associated with coronal blast waves. Our finding is in good agreement with the result of Hudson & Warmuth (2004). In our opinion, as opposed to the conclusion of Hudson & Warmuth (2004), the 40% association is too low to favour the blast wave mechanism for the excitation of kink oscillations.
On the other hand, we found that 44 out of the 58 analysed oscillation events (76%) were associated with CMEs observed in the white-light emission. Even more informative is that 57 out of the 58 loop oscillation events (i.e. 98%) were accompanied by lower coronal eruptions or plasma ejections (LCEs) observed in the EUV band with the SDO/AIA in the parental active regions, and the remaining one was a faint event associated with a CME. Careful consideration of each loop oscillation event with the JHelioviewer revealed that in 55 events (95%), kink oscillations were definitely excited by the deviation of the loops from their pre-event equilibrium state by a nearby LCEs. This is the main result of this statistical study. Recent observational results (e.g. Harra et al. 2014, for an individual event) are consistent with this conclusion.
Two main scenarios of the excitation of kink oscillations by LCEs were thus identified as follows. The Type-1 excitation was seen in 50 out of total 58 events. In the scenario of this type, kink oscillations were excited by the displacement of the loops from their equilibria by a moving (e.g. erupting and/or expanding) plasma structure, such as an unstable flux rope or a system of magnetic loops. In five other events the excitation of kink oscillations is seen to be associated with LCEs too, while there is no clear evidence of the Type-1 mechanism. In three remaining events it was difficult to unambiguously find out the driver of kink oscillations owing to observational limitations. We would like to point out that there are other well-known examples of kink oscillations that are not excited by the proposed mechanisms, e.g. the “harmonica event”studied by Verwichte et al. (2004).
As a byproduct of our analysis it was found that almost all the studied kink oscillation events were associated with both flares and LCEs, which occurred in the same parental active regions. This shows a close link between these two kinds of the solar activity. However, our analysis does not allow us to unambiguously conclude whether the flares drive LCEs, LCEs drive the flares, or both these phenomena are caused by a common reason. This conclusion is based on the finding that in about one half of the studied events, the flares began prior to LCEs, and in the other half of the events the LCEs started before the flares (see Fig. 6). This problem has a long history (e.g. Sheeley et al. 1983; Dryer 1996; Jing et al. 2004; Schrijver 2009), and requires a dedicated investigation. Also, our study gives a useful catalogue (Table 1) of the kink oscillation events that can be used for follow-up studies of this interesting phenomenon.
4. Conclusions
Our statistical analysis shows that the most probable mechanism for exciting the kink oscillations of coronal loops is the initial displacement of the loops from their equilibria by an eruption of some unstable plasma configuration, such as a flux rope or a system (arcade) of magnetic loops, or by a plasma ejection from a nearby flare site, rather than a blast shock wave excited by a flare. The ascending motion of the plasma structures, or their temporary expansion, displaces coronal loops situated around them in the horizontal direction. After the passage of an ascending structure, the loops return to the previous or gain new equilibrium, then overshoot it, and oscillate with the period prescribed by their length and the kink speed (Type-1 mechanism). This mechanism is consistent with the observed domination of the horizontally polarisation of kink oscillations.
In conclusion, we would like to emphasise that we performed a very basic and preliminary analysis of the 169 kink oscillation loops in the 58 events summarised in Table 1. A more detailed study of this catalogue can reveal new, statistically significant properties of the oscillations.
Online material
List of the coronal loop kink oscillation events detected with the AIA/SDO and their association with other phenomena in the solar atmosphere.
Acknowledgments
The data used are courtesy of the SDO/AIA, STEREO/SECCHI, and GOES consortia. The SOHO LASCO CME catalogue is generated and maintained at the CDAW Data Center by NASA and The Catholic University of America in cooperation with the Naval Research Laboratory. SOHO is a project of international cooperation between ESA and NASA. The work was supported by the Marie Curie PIRSES GA-2011-295272 RadioSun Project, by the grants MK-3931.2013.2 and NSh-248.2014.2 of the President of the Russian Federation for the State Support of Young Russian PhDs and Leading Scientific Schools of the Russian Federation, by the Russian Foundation for Basic Research (project No 13-02-91165-GFEN_A) (IVZ); STFC consolidated grant ST/L000733/1, the European Research Council under the SeismoSun Research Project No. 321141 and the BK21 plus program through the National Research Foundation funded by the Ministry of Education of Korea (VMN).
References
- Andries, J., Arregui, I., & Goossens, M. 2005, ApJ, 624, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., & Schrijver, C. J. 2011, ApJ, 736, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Fletcher, L., Schrijver, C. J., & Alexander, D. 1999, ApJ, 520, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Brueckner, G. E., Howard, R. A., Koomen, M. J., et al. 1995, Sol. Phys., 162, 357 [NASA ADS] [CrossRef] [Google Scholar]
- De Moortel, I., & Nakariakov, V. M. 2012, Roy. Soc. London Philos. Trans. Ser. A, 370, 3193 [Google Scholar]
- Dryer, M. 1996, Sol. Phys., 169, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Edwin, P. M., & Roberts, B. 1983, Sol. Phys., 88, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Goossens, M., Van Doorsselaere, T., Soler, R., & Verth, G. 2013, ApJ, 768, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Gopalswamy, N. 2006, Geophysical Monograph Series, 165, 207 [Google Scholar]
- Gopalswamy, N., Yashiro, S., Michalek, G., et al. 2009, Earth Moon Planets, 104, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Gruszecki, M., Nakariakov, V. M., van Doorsselaere, T., & Arber, T. D. 2010, Phys. Rev. Lett., 105, 055004 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Guo, Y., Ding, M. D., Schmieder, B., et al. 2010, ApJ, 725, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Harra, L. K., Matthews, S. A., Long, D. M., Doschek, G. A., & De Pontieu, B. 2014, ApJ, 792, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, R. A., Moses, J. D., Vourlidas, A., et al. 2008, Space Sci. Rev., 136, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Hudson, H. S., & Warmuth, A. 2004, ApJ, 614, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Inglis, A. R., & Nakariakov, V. M. 2009, A&A, 493, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jing, J., Yurchyshyn, V. B., Yang, G., Xu, Y., & Wang, H. 2004, ApJ, 614, 1054 [NASA ADS] [CrossRef] [Google Scholar]
- Khodachenko, M. L., Zaitsev, V. V., Kislyakov, A. G., & Stepanov, A. V. 2009, Space Sci. Rev., 149, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Khodachenko, M. L., Kislyakova, K. G., Zaqarashvili, T. V., et al. 2011, A&A, 525, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kupriyanova, E. G., Melnikov, V. F., & Shibasaki, K. 2013, Sol. Phys., 284, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Y. 2008, ApJ, 679, L151 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W., & Ofman, L. 2014, Sol. Phys., 289, 3233 [NASA ADS] [CrossRef] [Google Scholar]
- McLaughlin, J. A., & Ofman, L. 2008, ApJ, 682, 1338 [NASA ADS] [CrossRef] [Google Scholar]
- Mossessian, G., & Fleishman, G. D. 2012, ApJ, 748, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Mueller, D., Dimitoglou, G., Caplins, B., et al. 2009 [arXiv:0906.1582] [Google Scholar]
- Nakariakov, V. M., & Ofman, L. 2001, A&A, 372, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakariakov, V. M., Ofman, L., Deluca, E. E., Roberts, B., & Davila, J. M. 1999, Science, 285, 862 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Nakariakov, V. M., Aschwanden, M. J., & van Doorsselaere, T. 2009, A&A, 502, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nisticò, G., Nakariakov, V. M., & Verwichte, E. 2013, A&A, 552, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ofman, L. 2009, Space Sci. Rev., 149, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Robbrecht, E., & Berghmans, D. 2004, A&A, 425, 1097 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robbrecht, E., Berghmans, D., & Van der Linden, R. A. M. 2009, ApJ, 691, 1222 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J. 2009, Adv. Space Res., 43, 739 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., & Brown, D. S. 2000, ApJ, 537, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., Aschwanden, M. J., & Title, A. M. 2002, Sol. Phys., 206, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Sheeley, Jr., N. R., Howard, R. A., Koomen, M. J., & Michels, D. J. 1983, ApJ, 272, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Stepanov, A. V., Zaitsev, V. V., & Nakariakov, V. M. 2012, Physics Uspekhi, 55, A4 [Google Scholar]
- Török, T., & Kliem, B. 2005, ApJ, 630, L97 [Google Scholar]
- Török, T., & Kliem, B. 2007, Astron. Nachr., 328, 743 [NASA ADS] [CrossRef] [Google Scholar]
- Tothova, D., Innes, D. E., & Stenborg, G. 2011, A&A, 528, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Uralov, A. M. 2003, Astron. Lett., 29, 486 [NASA ADS] [CrossRef] [Google Scholar]
- Verth, G., & Erdélyi, R. 2008, A&A, 486, 1015 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verwichte, E., Nakariakov, V. M., Ofman, L., & Deluca, E. E. 2004, Sol. Phys., 223, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Verwichte, E., Van Doorsselaere, T., Foullon, C., & White, R. S. 2013, ApJ, 767, 16 [NASA ADS] [CrossRef] [Google Scholar]
- White, R. S., & Verwichte, E. 2012, A&A, 537, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- White, R. S., Verwichte, E., & Foullon, C. 2013, ApJ, 774, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Zaitsev, V. V., & Stepanov, A. V. 1982, AZh, 59, 563 [NASA ADS] [Google Scholar]
- Zaqarashvili, T. V., Melnik, V. N., Brazhenko, A. I., et al. 2013, A&A, 555, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
List of the coronal loop kink oscillation events detected with the AIA/SDO and their association with other phenomena in the solar atmosphere.
All Figures
 |
Fig. 1 Distributions of the speeds required for hypothetical agents exciting kink oscillations of coronal loops to reach the oscillation sites from the starting point of the lower coronal eruptions/ejections (vLCE, solid line) and the location of the flares (vflare, dotted lines). |
| In the text | |
 |
Fig. 2 Schematic illustration of the mechanism for the excitation of kink oscillations of coronal loops, observed in the majority of the studied events. a) Pre-eruption state of the active region. b) Displacement of a coronal loop (solid black curve) from its equilibrium state (dashed black line) by an erupting and expanding plasma structure, e.g. a flux rope (grey loop-shaped structure). c) Oscillatory relaxation of the loop to its equilibrium state after the eruption. |
| In the text | |
 |
Fig. 3 Sequence of AIA 171 Å images taken during event N 44. Crosses indicate the positions of the oscillating loops found with JHelioviewer and shown in Col. 4 of Table 1. The black asterisk and triangle indicate positions of the flare and the starting point of the LCE, given in Cols. 7 and 12 of Table 1, respectively. The white square boxes in the upper images show the region that is zoomed in the lower row of panels. The solar limb is shown by the thin white curve. Solar coordinates of the black cross in all images are the same. The dashed horizontal line is an arbitrary reference level to highlight the oscillatory behaviour of the loops. |
| In the text | |
 |
Fig. 4 Distributions of the speeds required for the excitation of kink oscillations by lower coronal eruptions/ejections, vLCE, in the events: a) with (solid line) and without (dotted line) CMEs; b) with (solid line) and without (dotted line) coronal Type-II radio bursts. |
| In the text | |
 |
Fig. 5 Distributions of the speeds, vflare, required for the excitation of kink oscillations by a flare, in the events with (solid line) and without (dotted line) coronal type II radio bursts. |
| In the text | |
 |
Fig. 6 Distributions of the differences between the beginning times of LCEs and flares. The time is measured in minutes. The bin size is one minute. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


