| Issue |
A&A
Volume 577, May 2015
|
|
|---|---|---|
| Article Number | A87 | |
| Number of page(s) | 5 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201424889 | |
| Published online | 08 May 2015 | |
Gravity-darkening exponents for neutron and non-relativistic stars
Instituto de Astrofísica de AndalucíaCSIC, Apartado 3004 18080 Granada Spain
e-mail:
claret@iaa.es
Received: 31 August 2014
Accepted: 2 April 2015
Context. Rotation affects various aspects of the stellar structure and evolution. For example, it distorts the star and causes the energy flow to be dependent on the local gravity (von Zeipel effect). Recent advances in the semi-empirical derivation of the gravity-darkening exponents in eclipsing binaries and very fast rotators require new theoretical calculations so that the results can be compared with these observations.
Aims. Using an analytical alternative method, we studied how the temperature is distributed over distorted neutron star (NS) surfaces through the gravity-darkening exponent (GDE). We also extended these investigations to non-relativistic stars.
Methods. The envelopes of NS, whose properties are necessary to derive the GDE, were computed using routines of the code mesa. The non-relativistic stellar models were computed following the code granada.
Results. We use a perturbation theory to derive an equation for the GDE for neutron and non-relativistic stars as a function of the rotation law, of the colatitude, and of the logarithmic derivatives of the opacity. Significant deviations from the von Zeipel’s theorem were found for differentially rotating NS as well as for non-relativistic stars. This equation is also capable of predicting the transition zone in the GDE around log Teff = 3.9 for non-relativistic stars, in good agreement with observational data. We use this equation to explore the effects of differential rotation to explain the anomalous values of semi-empirical GDE found in some early-type eclipsing binaries. We also analysed the role of convection and of the change of the main thermonuclear energy source in the GDE calculations for late-type stars.
Key words: stars: interiors / binaries: eclipsing / stars: neutron / stars: rotation / stars: evolution / stars: fundamental parameters
© ESO, 2015
1. Introduction
According to von Zeipel (1924), the flux is not constant on the surface of a distorted star, that is, 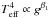 , where g is the local gravity, Teff is the effective temperature, and β1 is the gravity-darkening exponent (GDE). If the configuration is in radiative equilibrium, β1 = 1.0. This relationship is only valid for pseudo-barotropes. In 1967, the GDEs of convective stars were investigated by Lucy. The method used by Lucy (1967) is based on numerical calculations of the adiabatic constant for a series of stellar envelopes. He found
, where g is the local gravity, Teff is the effective temperature, and β1 is the gravity-darkening exponent (GDE). If the configuration is in radiative equilibrium, β1 = 1.0. This relationship is only valid for pseudo-barotropes. In 1967, the GDEs of convective stars were investigated by Lucy. The method used by Lucy (1967) is based on numerical calculations of the adiabatic constant for a series of stellar envelopes. He found 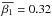 , which is significantly lower than von Zeipel’s value. Webbink (1976), using a simple opacity law, found that if the entropy is constant in an envelope, the values of β1 are consistent with the values reported by Lucy. Still concerning convective envelopes, Anderson & Shu (1977) argued that there is no relation between the effective temperature and effective gravity, that is, β1 = 0.0. However, some years later, Sarna (1989) confirmed the results obtained by Lucy, although a slight variation with mass was also detected. Claret (1998) introduced a numerical method for deriving the GDE based on the triangle strategy. This method embraced both convective and radiative envelopes. In addition to computing GDE for radiative and convective envelopes, such a method has the following advantages: a) one can go as deep as necessary into the interior of the model to impose the boundary conditions; b) the GDEs are computed as a function of the mass, effective temperature, radius, chemical composition, and time; c) the changes in the chemical profile of the envelopes are taken into account; and d) more realistic atmosphere models can be introduced as external boundary conditions, as was done for brown- dwarfs stars. Using this method, Claret (1998) also found that β1 is lower than 1.0 for late-type stars, which again confirmed Lucy’s calculations. Very simple arguments can be used to support these results. We summarize them here for completeness. In the classical HR diagram log g × log Teff, we plot two stellar evolutionary tracks for which the radiative and convective transport mechanisms are predominant in their envelopes, for example, 10 and 1 M⊙, respectively. Both tracks can be roughly approximated to straight lines (see Fig. 3 in Claret 1998), whose slopes are 0.25 and 0.06. By making an analogy between these slopes and the respective GDEs we have β1(radiative) ≈ 1.0 and β1(convective) ≈ 0.24. In the first case, we recover the von Zeipel theorem, and in the second case we obtain a GDE lower than 1.0 for late-type stars, which is consistent with the results reported by Lucy (1967), Sarna (1989), and Claret (1998). We note that the properties of the equation of transport are implicit in the calculations of the two stellar models used in this simple argument.
, which is significantly lower than von Zeipel’s value. Webbink (1976), using a simple opacity law, found that if the entropy is constant in an envelope, the values of β1 are consistent with the values reported by Lucy. Still concerning convective envelopes, Anderson & Shu (1977) argued that there is no relation between the effective temperature and effective gravity, that is, β1 = 0.0. However, some years later, Sarna (1989) confirmed the results obtained by Lucy, although a slight variation with mass was also detected. Claret (1998) introduced a numerical method for deriving the GDE based on the triangle strategy. This method embraced both convective and radiative envelopes. In addition to computing GDE for radiative and convective envelopes, such a method has the following advantages: a) one can go as deep as necessary into the interior of the model to impose the boundary conditions; b) the GDEs are computed as a function of the mass, effective temperature, radius, chemical composition, and time; c) the changes in the chemical profile of the envelopes are taken into account; and d) more realistic atmosphere models can be introduced as external boundary conditions, as was done for brown- dwarfs stars. Using this method, Claret (1998) also found that β1 is lower than 1.0 for late-type stars, which again confirmed Lucy’s calculations. Very simple arguments can be used to support these results. We summarize them here for completeness. In the classical HR diagram log g × log Teff, we plot two stellar evolutionary tracks for which the radiative and convective transport mechanisms are predominant in their envelopes, for example, 10 and 1 M⊙, respectively. Both tracks can be roughly approximated to straight lines (see Fig. 3 in Claret 1998), whose slopes are 0.25 and 0.06. By making an analogy between these slopes and the respective GDEs we have β1(radiative) ≈ 1.0 and β1(convective) ≈ 0.24. In the first case, we recover the von Zeipel theorem, and in the second case we obtain a GDE lower than 1.0 for late-type stars, which is consistent with the results reported by Lucy (1967), Sarna (1989), and Claret (1998). We note that the properties of the equation of transport are implicit in the calculations of the two stellar models used in this simple argument.
The GDE has also been the object of recent theoretical investigations that adopted different approaches (Claret 1998, 2000, 2012; Espinosa Lara & Rieutord 2011, 2012; McGill et al. 2013). Since the pioneering work by Rafert & Twigg (1980), some important systematic studies have been conducted on observational data that used eclipsing binaries (Kitamura & Nakamura 1987; Pantazis & Niarchos 1998; Niarchos 2000; Djurasevic et al. 2003, 2006). A considerable effort was also made by several authors who derived the GDE for very rapid isolated rotating stars, for example, van Belle et al. (2001, 2006), Domiciano de Souza et al. (2003, 2012), Aufdenberg et al. (2006), Peterson et al. (2006), Monnier et al. (2007), Zhao et al. (2009), and Che et al. (2011).
In our previous investigations, we have introduced a numerical method for deriving the GDE that is based on the triangle strategy, as commented above. In the present paper we introduce a new insight into the GDE problem using a perturbation theory to derive an analytical expression for the GDE for rotating neutron stars (NS) that is extensible to non-relativistic stars. The GDE are presented as a function of the rotation law, colatitude, and opacity derivatives that are to be compared with the corresponding observational data. We adopted this equation to explore the effects of differential rotation to explain the anomalous values of semi-empirical GDE found in some early-type eclipsing binaries.
2. Gravity-darkening exponent for neutron stars
The observations of NS show that they are rotating with frequencies between 0.1 mHz up to around of 1 kHz. Because of their high rotational rates, it is expected that they are flattened at the poles. Belvedere et al. (2014) computed rotating models of NS and show in their Fig. 16 that the eccentricity of a rotating NS can reach 0.7, where e = [ 1 − (Rp/Re)2 ] 1/2, Rp and Re being the polar and equatorial radius. In these typical conditions, the gravity-darkening may play an important role in the interpretation of observations of NS.
To calculate the GDE (β1) for an NS, we adopted a modified version of the formalism by Claret (2012), which is based on the work of Kippenhahn (1977). We focus our attention on the envelope (r ≈ R) where we can neglect the pressure contribution to the source function, and the enclosed mass in the differential equations can be substituted by M (the total mass). More details on the NS envelope structure can be found in Appendix A. First, we used the Roche model to calculate the polar and the equatorial gravities. Next, we used the equation of radiative transport to derive the respective fluxes at the pole and at the equator. When these quantities are calculated, we are able to derive the gravity-darkening exponents β1.
By adopting the aforementioned approximations, we can write following Gudmunsson et al. (1983) 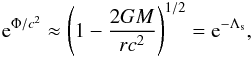 (1)where Φ is the gravitational potential, G is the constant of gravitation, M is the NS mass, r the radial coordinate, c is the speed of light, and the subscript s refers to the surface value. The total potential, including rotation, can be approximated by
(1)where Φ is the gravitational potential, G is the constant of gravitation, M is the NS mass, r the radial coordinate, c is the speed of light, and the subscript s refers to the surface value. The total potential, including rotation, can be approximated by 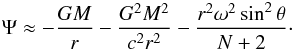 (2)In this equation we adopt a rotation law of the form ω2 = h(r)sinNθ, where θ is the colatitude, ω is the angular velocity, N indicates the degree of asymmetry of the angular velocity, and h(r) a generic function. If the effects of the centrifugal force on the NS structure are weak, the integrating factor for the potential equation is given by
(2)In this equation we adopt a rotation law of the form ω2 = h(r)sinNθ, where θ is the colatitude, ω is the angular velocity, N indicates the degree of asymmetry of the angular velocity, and h(r) a generic function. If the effects of the centrifugal force on the NS structure are weak, the integrating factor for the potential equation is given by 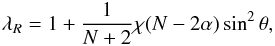 (3)where α = ∂lnω/∂lnr and χ = r3ω2/(GM). The radius of a given equipotential is
(3)where α = ∂lnω/∂lnr and χ = r3ω2/(GM). The radius of a given equipotential is 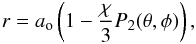 (4)ao being the mean radius of the level surface, and P2(θ,φ) is the second surface harmonic. We note that in our approximation the term G2M2/(c2r2) in the gravitational potential is small and therefore Eq. (4) is still an acceptable approximation for the radius of an equipotential. The local gravity can be computed by using
(4)ao being the mean radius of the level surface, and P2(θ,φ) is the second surface harmonic. We note that in our approximation the term G2M2/(c2r2) in the gravitational potential is small and therefore Eq. (4) is still an acceptable approximation for the radius of an equipotential. The local gravity can be computed by using ![\begin{eqnarray} {g} = {\partial\Psi\over{\partial n}} = \left[ \left({\partial\Psi\over{\partial r}}\right)^2 + \left({1\over r}{\partial\Psi\over{\partial \theta}}\right)^2 \right]^{1/2}\cdot \end{eqnarray}](/articles/aa/full_html/2015/05/aa24889-14/aa24889-14-eq37.png) (5)The values of g at the pole and at the equator are related by
(5)The values of g at the pole and at the equator are related by ![\begin{eqnarray} \lefteqn{{{g_{\rm e}-g_{\rm p}}\over{g_{\rm p}}} \approx} \nonumber \\ && {\chi}{{\left[ a_{\rm o} c^2 G M (2- 3 N) + 10 G^2 M^2 (2 + N) -2 a_{\rm o}^2 c^4(4 + N)\right]} \over{2(a_{\rm o}^2 c^4 - 4 G^2 M^2) (2 + N)}}\cdot \end{eqnarray}](/articles/aa/full_html/2015/05/aa24889-14/aa24889-14-eq38.png) (6)On the other hand, the energy transport equation for the envelope can be written as (see for example, Gudmunsson et al. 1983; and Thorne 1966)
(6)On the other hand, the energy transport equation for the envelope can be written as (see for example, Gudmunsson et al. 1983; and Thorne 1966) 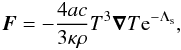 (7)where T is the temperature, a is the radiation pressure constant, ρ is the density, and κ is the total opacity, that is, the radiative and the conductive contributions are considered. We assume that the density and temperature are functions of the total potential, that is, ρ = d(Ψ)λR and T = t(Ψ) /λR. Therefore
(7)where T is the temperature, a is the radiation pressure constant, ρ is the density, and κ is the total opacity, that is, the radiative and the conductive contributions are considered. We assume that the density and temperature are functions of the total potential, that is, ρ = d(Ψ)λR and T = t(Ψ) /λR. Therefore 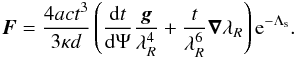 (8)By introducing the appropriate values in Eq. (8) for the pole and for the equator, we obtain the quantity (Fe − Fp) /Fp, which will be approximated as a logarithmic derivative necessary to calculate β1. Finally, we have
(8)By introducing the appropriate values in Eq. (8) for the pole and for the equator, we obtain the quantity (Fe − Fp) /Fp, which will be approximated as a logarithmic derivative necessary to calculate β1. Finally, we have ![\begin{eqnarray} {\beta_1}&\approx& {{{F_{\rm e}-F_{\rm p}}\over{F_{\rm p}}}\over{{{g_{\rm e}-g_{\rm p}}\over{g_{\rm p}}}}} \nonumber \\ &\approx& {1} + {\left[(4+\kappa_{\rho}- \kappa_T)(N-2\alpha)\over{4 + N}\right]} \nonumber \\ &&+\,{ G M\over{2 a_{\rm o} c^2 (4 +N)^2}}\left [-8 + 2(1+ \kappa_{\rho}- \kappa_T)N \right. \nonumber \\ && \left. + \,(-13 - 3\kappa_{\rho} + 3\kappa_T)N^2 + 2\alpha (4+\kappa_{\rho}- \kappa_T) (3N - 2)\right] \nonumber \\ && +\, G_{\rm rot}\left(a_{\rm o}, M, N,t, {{\rm d}t\over{{\rm d}\Psi}}, {\partial\! \ln\alpha\over{\partial r}}, {\partial\! \ln\chi\over{\partial r}}\right), \end{eqnarray}](/articles/aa/full_html/2015/05/aa24889-14/aa24889-14-eq48.png) (9)where κρ ≡ (∂lnκ/∂lnρ)T and κT ≡ (∂lnκ/∂lnT)ρ. The function Grot is proportional to ∂lnχ/∂r and ∂lnα/∂r. As explained in Kippenhahn (1977) and Claret (2012), these derivatives are very small and therefore we can neglect this function in the calculation of β1. For N = 2α and/or (4 + κρ − κT) = 0 and for non-relativistic stars we recover the classical von Zeipel result, β1 = 1. The simplest solution for the first condition implies solid body rotation, α = 0. To analyse the second case, we consider that the opacity has the form κ ≈ κoρnT− s. Therefore, the second condition can be written as 4 + n + s = 0. This is a known relationship often found in the analysis of stability of the radiative gradient in stellar envelopes (for a more detailed and interesting discussion on this subject, see Cox & Giuli 1968).
(9)where κρ ≡ (∂lnκ/∂lnρ)T and κT ≡ (∂lnκ/∂lnT)ρ. The function Grot is proportional to ∂lnχ/∂r and ∂lnα/∂r. As explained in Kippenhahn (1977) and Claret (2012), these derivatives are very small and therefore we can neglect this function in the calculation of β1. For N = 2α and/or (4 + κρ − κT) = 0 and for non-relativistic stars we recover the classical von Zeipel result, β1 = 1. The simplest solution for the first condition implies solid body rotation, α = 0. To analyse the second case, we consider that the opacity has the form κ ≈ κoρnT− s. Therefore, the second condition can be written as 4 + n + s = 0. This is a known relationship often found in the analysis of stability of the radiative gradient in stellar envelopes (for a more detailed and interesting discussion on this subject, see Cox & Giuli 1968).
 |
Fig. 1 Gravity-darkening exponent for neutron stars. The continuous line indicates β1 for the case α = −0.1, the dashed line denotes α = −0.2, and the dashed-dotted line represents the case α = 0.1. Envelope model for an NS with 1.4 M⊙. |
We focus on the spherical symmetric case, N = 0. To evaluate the GDE of an NS we need, in addition to assuming a rotation law, the surface values of κρ and κT in the NS envelopes. To derive these quantities, we have computed NS envelopes with the code mesa (Paxton et al. 2011). These routines produce an envelope of an NS with MNS = 1.4 M⊙ and RNS = 106 cm, accreting 12C at a rate of 1.7 × 10-9M⊙/yr. This envelope consists of 56Fe (log P> 20.0) and 4He. The logarithmic derivatives were numerically evaluated at the surface and are κρ = −0.33 and κT = −0.94. The GDE expressed by Eq. (9) depends primarily upon the degree of the differential rotation and upon the properties of the opacity. For example, for moderate differential rotation (α = −0.1) we obtain β1 = 1.2, while for α = −0.2 we correspondingly obtain β1 = 1.5. These values are practically constant over the envelope, as can be seen by inspecting Fig. 1. There are strong variations in β1 around log T = 7.8, but they are not fully shown in the figure for the sake of clarity. These variations are due to the chemical composition discontinuity (4He → 56Fe). The resulting GDE are very interesting since they indicate that the von Zeipel theorem is no longer valid for NS rotating differentially. To check this point, we computed several NS envelopes with slightly different radii to simulate configurations distorted by rotation and/or tides. This method is based on the triangles strategy commonly used in stellar evolution calculations we mentioned in the introduction; for more details see Claret (2000). The value of β1 resulting from these envelopes is on average equal to 1.4, thus confirming the deviation of the von Zeipel theorem for rotating NS.
A hypothetical but interesting possibility is α> 0 (Fig. 1). This could be the case of a star with an accretion disk whose forming belt rotates faster than the stellar surface. For a moderately rotating belt, for example α = 0.1, we have β1 = 0.7, which also contradicts the classical von Zeipel theorem.
 |
Fig. 2 Theoretical gravity-darkening exponents and observed values for TT Aur (open square) and V Pup (open triangle). The semi-empirical values of β1 reported by Rafert & Twigg (1980) and Djurasevic et al. (2003, 2006) are represented by asterisks and full squares, respectively. The continuous line indicates the theoretical β1 (Eq. (9)) for the case α = −0.1, the dashed line denotes α = −0.3, and the dotted line indicates the case α = −0.2 for the Kramer law. The dashed-dotted line represents the calculations adopting the triangle strategy method (Claret 2000). |
3. Gravity-darkening exponent for non-relativistic stars: an approach
Equation (9) can be also used to predict the GDE for non-relativistic stars neglecting the term dependent on GM/(2aoc2). Some time ago it was a difficult task to compare the theoretical β1 with the observational counterparts obtained from eclipsing binary data because the reliable semi-empirical data were very hard to obtain and there were only two theoretical GDE values to be compared: stars with radiative envelopes (β1 = 1.0, von Zeipel 1924) and β1 = 0.32 for convective envelopes (Lucy 1967). Fortunately, some decades ago, Rafert & Twigg (1980) inferred the GDE from a systematic light curve analysis covering a wide range of effective temperatures. A preliminary comparison of the theoretical GDE with this observational sample showed a scattering around the von Zeipel value for higher effective temperatures. In this comparison the numerical method described in Claret (1998, 2000) was adopted. However, the predicted theoretical drop-off in β1 agreed well with the semi-empirical values (Claret 1998, Fig. 7). More recently, Djurasevic et al. (2003, 2006) estimated the GDE for several semi-detached systems. Of particular interest for us are the early-type systems TT Aur and V Pup, which present notorious deviations from the von Zeipel value and whose observational GDE are controversial. Both systems were previously analysed by Kitamura & Nakamura (1987), who found β1 = 4.14 and 5.44, respectively. Applying a different method but using the same observational material, Djurasevic et al. (2003) found 1.48 and 1.53. These high discrepancies between the semi-empirical β1 for the two systems are an example of the difficulties of inferring the GDE from observations, even when the same set of observational data is adopted.
These data now serve as a preliminary test for Eq. (9). To compare the theoretical GDE with the semi-empirical ones, we computed stellar models that cover the range of the observed effective temperatures of the observational sample: ZAMS (zero-age main-sequence) configurations with masses ranging from 1.7 up to 125 M⊙ with X = 0.70,Z = 0.02, a mixing-length parameter αMLT = 1.68, and a core-overshooting parameter αov = 0.2 using the code granada, described in Claret (2004). We used the properties of the uppermost layers of these models to evaluate the contribution of κρ and κT in calculating the theoretical GDE. The comparison is shown in Fig. 2, where the asterisks represent the observational data used by Rafert & Twigg (1980) and the full squares denote the data reported by Djurasevic et al. (2003, 2006). The anomalous values of β1 for the two systems can be satisfactorily explained if we assume moderate differential rotation rates (α = −0.1 and − 0.3). The semi-empirical β1 lower than 1.0 for early-type stars might also be explained by Eq. (9) assuming α ≈ 0.1 (see last paragraph of the previous subsection). It would be of interest if observers of eclipsing binaries or even of isolated fast rotators were to search for some evidence of such a disk. We note that the comparison shown in Fig. 2 is only preliminary since the evolutionary effects were not taken into account in the theoretical GDE calculations.
The drop-off in the theoretical GDE for log Teff ≈ 3.9 predicted by Eq. (9) is very interesting. This can be explained, at least partially, by the behaviour of the opacity in the upper layers of solar-type stars. In these stars the dominant opacity source in their atmospheres is due to the negative hydrogen ion. This opacity can be expressed by κH− ≈ κoZ1/2ρ1/2T7.7, which gives κρ = 0.5 and κT = 7.7. Thus, the resulting β1 assuming for example α = −0.2, is equal to 0.68, which is significantly lower than the von Zeipel standard value and could explain in part the theoretical drop-off/transition zone for the GDE around log Teff ≈ 3.9.
This transition zone approximately coincides with the onset of convection. The radiative and convective transport mechanisms can be acting simultaneously in this region of the HR diagram. To evaluate the impact of convection on the GDE of late-type stars, we start with defining the mean convective flux (Cox & Giuli 1968) 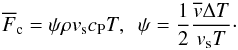 (10)In these equations, vs is the local velocity of sound,
(10)In these equations, vs is the local velocity of sound, 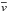 the mean convective velocity, ΔT is the excess of temperature of a convective cell with respect to its neighbouring cell, and cP is the specific heat at constant pressure. It can be shown that the convective efficiency is proportional to
the mean convective velocity, ΔT is the excess of temperature of a convective cell with respect to its neighbouring cell, and cP is the specific heat at constant pressure. It can be shown that the convective efficiency is proportional to 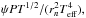 where rn is the stellar radius (in normalized units). Finally, for a constant convective efficiency, we derive Teff ∝ g1/17, that is, β1 ≈ 0.24. This low value of β1 for convective envelopes confirms the tendency we found by applying the opacity derivatives of the negative hydrogen ion to Eq. (9). This tendency is also confirmed by the radiation hydrodynamics simulations, as shown in Fig. 8 by Claret (2000). However, to take the structure of the envelopes of late-type stars fully into account, one must use the physical properties of the upper layers of evolutionary stellar models and consider the effects of convection in Eq. (9). In fact, the position and shape of the transition zone depends on the structure of these envelopes: the stellar mass, the evolutionary status, the chemical composition (including dredge-up), the adopted convection theory, etc.
where rn is the stellar radius (in normalized units). Finally, for a constant convective efficiency, we derive Teff ∝ g1/17, that is, β1 ≈ 0.24. This low value of β1 for convective envelopes confirms the tendency we found by applying the opacity derivatives of the negative hydrogen ion to Eq. (9). This tendency is also confirmed by the radiation hydrodynamics simulations, as shown in Fig. 8 by Claret (2000). However, to take the structure of the envelopes of late-type stars fully into account, one must use the physical properties of the upper layers of evolutionary stellar models and consider the effects of convection in Eq. (9). In fact, the position and shape of the transition zone depends on the structure of these envelopes: the stellar mass, the evolutionary status, the chemical composition (including dredge-up), the adopted convection theory, etc.
Another phenomenon that takes place in the neighbouring of the transition zone is the change of the predominant source of thermonuclear energy from CNO cycle to proton-proton chain. This change is accompanied by a readjustment of the density profile and has clear repercussions on how a star would react to rotational distortions. Indeed, the quantity (ge − gp) /gp, which is primordial to compute β1, can be written as a function of k2, the apsidal-motion constant that gives a measure of the mass concentration. Equation (9) embraces both phenomena, the change of the main thermonuclear energy source and the onset of convection, through (ge − gp) /gp, κρ, and κT. Moreover, the drop-off/transition zone predicted by this equation is observationally supported by the data reported by Rafert & Twigg (1980) and Djurasevic et al. (2003, 2006).
At this point, it is interesting to compare the theoretical predictions of Eq. (9) with previous works, for example that by Espinosa Lara & Rieutord (2011). In this paper the authors assumed that the energy flux is a divergence-free vector antiparallel to the effective gravity and that the star can be represented by the Roche model. As a result, they obtained that the latitudinal variations of Teff only depend on the ratio of the equatorial to the Keplerian velocity. They also compared their β1, as a function of the rotational distortions, with interferometric observations of fast rotators (their Fig. 4). According to these authors, the agreement is good for Altair and α Leo, but only fair for α Cep. However, for the fourth system, β Cas, the authors found a discrepancy with their theoretical prediction and explained it to be due to the small inclination angle of this system. More recent comparisons with observations can be found in Domiciano et al. (2014), where six fast rotators were compared with the mentioned theoretical predictions. The authors concluded (their Fig. 13) that there are two systems – α Cep and β Cas – that are not satisfactorily matched by the theoretical predictions by Espinosa Lara & Rieutord (2011).
On the other hand, Eq. (9) was derived under the assumption of small distortions, and its theoretical predictions are not directly comparable to the results by Espinosa Lara & Rieutord (2011). Despite this difference in the interval of validity of both theories, some comparisons can be made. For example, their Fig. 4 predicts a systematic decrease of β1 with the stellar distortions and that the original von Zeipel value is only recovered for small rotational distortions. As we have seen before, this is just the prediction of our Eq. (9) when N = 2α and/or (4 + κρ − κT) = 0. However, using typical values extracted from evolutionary stellar models, Eq. (9) predicts a family of curves of β1 that depend on the nature of the rotational law, on the colatitude, and on the physical conditions of the stellar envelopes (Fig. 2). We relate the decreasing of β1 around log Teff ≈ 3.9 to the onset of convection and with the change of the main source of thermonuclear energy, as explained previously. This may be the cases of the fast rotators β Cassiopeiae, Altair, and α Cep, whose mean effective temperatures are within the drop-off region predicted by Eq. (9) (see also Fig. 9 by Che et al. 2011).
The low values of β1 for the systems on the right side of Fig. 2 can be explained by the role of convection in the envelopes of late-type stars as well as by the changes in internal structure of these stars, which tend to decrease the GDE values (see a more detailed discussion of this topic in Claret 2000, Fig. 1). In addition, the theoretical drop-off is confirmed by observations of binary stars (Rafert & Twigg 1980; Djurasevic et al. 2003, 2006), as commented above. The cases of the fast rotators α Lyr, α Leo (preliminarily analysed by Claret 2012), α Cep, α Eri, α Aql, and β Cas will be investigated in more detail using a variant of the method presented here and those previously introduced by us (Claret, in prep.).
The observational data for the hotter systems shown in Fig. 2 can also be used to compare the theoretical predictions of Eq. (9) and those by Espinosa Lara & Rieutord (2011). There are some systems that cannot be satisfactorily explained on the basis of their Fig. 4, or their Table 1 (Espinosa Lara & Rieutord 2012), in particular, the binaries TT Aur and V Pup, whose revised observational values of β1 are 1.48 and 1.53, respectively. By using Eq. (9) and adopting moderate differential rotation – which is a reasonable assumption – a good agreement with observations is achieved. On the other hand, there are some detached binaries with low effective temperatures with an average GDE of 0.3−0.4 that cannot be explained by the calculations of Espinosa Lara & Rieutord (2012 because these systems are only slightly distorted, and following these authors, β1 would be ≈1.0.
Equation (9) is only valid for slow rotation. Although we consider this equation as an exploratory tool, its sensitivity to the stellar structural changes and the observational support gives us confidence to further investigate its applicability to the surface temperature distribution of rotating stars.
Acknowledgments
I would like to thank B. Rufino and the anonymous referee for their comments. The Spanish MEC (AYA2012-39727-C03-01) is gratefully acknowledged for its support during the development of this work. This research has made use of the SIMBAD database, operated at the CDS, Strasbourg, France, and of NASA’s Astrophysics Data System Abstract Service.
References
- Anderson, L., & Shu, F. H. 1977, ApJ, 214, 798 [NASA ADS] [CrossRef] [Google Scholar]
- Aufdenberg, J. P., Mérand, A., Coudé du Foresto, V., et al. 2006, ApJ, 645, 664 [NASA ADS] [CrossRef] [Google Scholar]
- Belvedere, R., Boshkayev, K., Rueda, J. A., & Ruffini, R. 2014, Nucl. Phy. A, 921, 33 [Google Scholar]
- Che, X., Monnier, J. D., Zhao, M., et al. 2011, ApJ, 732, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A. 1998, A&AS, 131, 123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A. 2000, A&A, 359, 289 [NASA ADS] [Google Scholar]
- Claret, A. 2004, A&A, 424, 919 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A. 2012, A&A, 538, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cox, J. P., & Giuli, R. T. 1968, Principles of Stellar Structure, Vol. 1 (New York: Gordon & Breach) [Google Scholar]
- Djurasevic, G., Rovithis-Livaniou, H., Rovithis, P., et al. 2003, A&A, 402, 667 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Djurasevic, G., Rovithis-Livaniou, H., Rovithis, P., et al. 2006, A&A, 445, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Domiciano de Souza, A., Kervella, P., Jankov, S., et al. 2003, A&A, 407, L47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Domiciano de Souza, A., Hadjara, M., Vakili, F., et al. 2012, A&A, 545, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Domiciano de Souza, A., Kervella, P., MoserFaes, D., et al. 2014, A&A, 569, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Espinosa Lara, F., & Rieutord, M. 2011, A&A, 533, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Espinosa Lara, F., & Rieutord, M. 2012, A&A, 547, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gudmunsson, E. H., Pethick, C. J., & Epstein, R. I. 1983, ApJ, 272, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R. 1977, A&A, 58, 267 [NASA ADS] [Google Scholar]
- Kitamura, M., & Nakamura, Y. 1987, Ann. Tokyo Astron. Obs., 2nd Ser, 21, 387 [Google Scholar]
- Lucy, L. B. 1967, Z. Astrophys., 65, 89 [Google Scholar]
- McGill, M. A., Sigut, T. A. A., & Jones, C. E. 2013, ApJS, 204, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Monnier, J. D., Zhao, M., Pedretti, E., et al. 2007, Science, 317, 342 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Niarchos, P. G. 2000, in Variable Stars as Essential Astrophysical Tools, ed. C. Ibanoglu, 631 [Google Scholar]
- Pantazis, G., & Niarchos, P. G. 1998, A&A, 335, 199 [NASA ADS] [Google Scholar]
- Paxton, B., & Bildsten, L., & Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Peterson, D. M., Hummel, C. A., Pauls, T. A., et al. 2006, Nature, 440, 896 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Rafert, J. B., & Twigg, L. W. 1980, MNRAS, 193, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Sarna, M. J. 1989, A&A, 224, 98 [NASA ADS] [Google Scholar]
- Thorne, K. S. 1966, Proc. International School of Physics Enrico Fermi, ed. L. Gratton (New York: Academic Press), 166 [Google Scholar]
- van Belle, G. T., Ciardi, D. R., tenBrummelaar, T., et al. 2006, ApJ, 637, 494 [NASA ADS] [CrossRef] [Google Scholar]
- von Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Webbink, R. F. 1976, ApJ, 209, 829 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, M., Monnier, J. D., Pedretti, E., et al. 2009, ApJ, 701, 209 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Some notes on the structure of a neutron star envelope
The structure of a spherically symmetrical and non-magnetic NS is determined by solving six ordinary differential equations: a) the Tolman-Oppenheimer-Volkoff (TOV) equation of hydrostatic equilibrium; b) the heat transport equation; c) the potential source equation; d) the neutrino luminosity equation; e) the equation of energy conservation, and finally; f) the continuity equation that determines the enclosed gravitational mass (see for example Eqs. (4)−(9) by Gudmunsson et al. 1983). These equations reduce to the usual differential equations of the stellar structure and evolution in the non-relativistic case. The boundary conditions are the same as those required by the traditional stellar structure, that is, m(0) = 0,L(0) = 0 and Lν(0) = 0, where m is the enclosed gravitational mass, L is the net luminosity, and Lν is the neutrino luminosity. Note that L = Lcr + Lν, where Lcr is the luminosity due to the radiation and thermal conduction.
If we only focus on the envelope, some simplifications can be introduced. For example, we
can approximate m(r) ≈ M
(M is the
total gravitational mass). In these conditions, the redshift factor is given by Eq. (1).
It can also be shown that the Λ is practically invariant over the whole envelope. In addition, by
neglecting the pressure, the simplified TOV equation can be expressed
by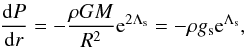 (A.1)where
gs is the surface gravity of a neutron
star. The transfer equation is given by
(A.1)where
gs is the surface gravity of a neutron
star. The transfer equation is given by
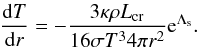 (A.2)\newpage\noindentFrom
(A.1) and (A.2), we have
(A.2)\newpage\noindentFrom
(A.1) and (A.2), we have 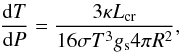 (A.3)which
is the differential equation that determines the thermal structure of the envelope. These
equations must be integrated by means of numerical methods. This was done in this paper
using some subroutines of the code mesa.
(A.3)which
is the differential equation that determines the thermal structure of the envelope. These
equations must be integrated by means of numerical methods. This was done in this paper
using some subroutines of the code mesa.
All Figures
 |
Fig. 1 Gravity-darkening exponent for neutron stars. The continuous line indicates β1 for the case α = −0.1, the dashed line denotes α = −0.2, and the dashed-dotted line represents the case α = 0.1. Envelope model for an NS with 1.4 M⊙. |
| In the text | |
 |
Fig. 2 Theoretical gravity-darkening exponents and observed values for TT Aur (open square) and V Pup (open triangle). The semi-empirical values of β1 reported by Rafert & Twigg (1980) and Djurasevic et al. (2003, 2006) are represented by asterisks and full squares, respectively. The continuous line indicates the theoretical β1 (Eq. (9)) for the case α = −0.1, the dashed line denotes α = −0.3, and the dotted line indicates the case α = −0.2 for the Kramer law. The dashed-dotted line represents the calculations adopting the triangle strategy method (Claret 2000). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


