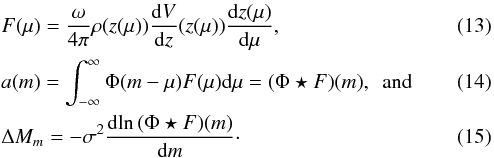| Issue |
A&A
Volume 576, April 2015
|
|
|---|---|---|
| Article Number | A75 | |
| Number of page(s) | 5 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201425489 | |
| Published online | 01 April 2015 | |
Eddington-Malmquist bias in a cosmological context
Tuorla ObservatoryDepartment of Physics and Astronomy, University of
Turku,
21500
Piikkiö,
Finland
e-mail:
pekkatee@utu.fi
Received: 9 December 2014
Accepted: 27 February 2015
Aims. In 1914, Eddington derived a formula for the difference between the mean absolute magnitudes of stars “in space” or gathered “from the sky”. In 1920, Malmquist derived a general relation for this difference in Euclidean space. Here we study this statistical bias in cosmology, clarifying and expanding previous work.
Methods. We derived the Malmquist relation within a general cosmological framework, including Friedmann’s model, analogously to the way Malmquist showed in 1936 that his formula is also valid in the presence of extinction in Euclidean space. We also discuss some conceptual aspects that explain the wide scope of the bias relation.
Results. The Malmquist formula for the intrinsic difference ⟨ M ⟩ m − M0 = −σM2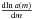 is also valid for observations made in an expanding Friedmann universe. This holds true for bolometric and finite-band magnitudes when a(m) refers to the distribution of observed (uncorrected for K-effect or z-dependent extinction) apparent magnitudes.
is also valid for observations made in an expanding Friedmann universe. This holds true for bolometric and finite-band magnitudes when a(m) refers to the distribution of observed (uncorrected for K-effect or z-dependent extinction) apparent magnitudes.
Key words: methods: statistical / galaxies: distances and redshifts / distance scale
© ESO, 2015
1. Introduction
Although not an astronomer, but a philosophical and cosmological thinker, Giordano Bruno already understood that our fixed position in the Universe leads to problems for the observer. When he discussed his vision of the cosmos filled with stars and planetary systems, he pointed out some reasons why we cannot see all those planets: 1) they may be too faint; 2) they may be too far away; and 3) they may reflect the light of their central star only poorly (in the third dialog of his book “Of the infinite universe and worlds”, 1584).
Thus Bruno was faintly aware of some selection effects that make the life (or at least the task) of an astronomer difficult. Before the telescopic era, Bruno had in mind visual observations, but similar problems affect observations made with instruments. The fact that celestial bodies have a range of luminosities and are scattered in space leads to interesting effects that the observer should take into account.
1.1. Eddington’s contribution
In his book “Stellar movements and the structure of the universe”, Eddington (1914) discusses in the chapter “Phenomena associated with spectral type” among other topics the distribution of stars in the Hertzsprung-Russel (HR) diagram (absolute magnitude vs. spectral type) that had recently been introduced by Hertzsprung and Russell. They had proposed the existence of “giant” and “dwarf” stars. Eddington begins by considering what happens when one chooses Type A and Type M stars “at random out of the stars in space”, and then he says:
We say intentionally “out of the stars in space”, because, for example, the stars visible to the naked eye are a very special selection by no means representative of the true distribution of the stars.
When discussing the reality of the dwarfs and giants division, Eddington then ponders the possibility of a selection effect. As the stars for which the parallaxes had been derived had been chosen either for brightness or for nearness (large proper motion), he asks if the two groups might result “from the double mode of selection, without implying any real division in the intrinsic luminosities”.
Then he shows in a few strokes that for a normal distribution of absolute magnitudes M with the mean M0 and the dispersion 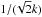 (his notation), the frequency of M among stars in a magnitude-limited sample is a normal distribution with the same dispersion, but a brighter mean value M0 − 0.69 /k2. With this formula at hand, Eddington shows that to explain in this way the wide gap of 11 mag between giants and dwarfs for the M spectral type would require a dispersion of almost 3 mag, while Russell had derived a mean value of 1.14 mag for all spectral types. Thus he concludes that the selection effect, which he had just discovered, cannot explain dwarfs and giants.
(his notation), the frequency of M among stars in a magnitude-limited sample is a normal distribution with the same dispersion, but a brighter mean value M0 − 0.69 /k2. With this formula at hand, Eddington shows that to explain in this way the wide gap of 11 mag between giants and dwarfs for the M spectral type would require a dispersion of almost 3 mag, while Russell had derived a mean value of 1.14 mag for all spectral types. Thus he concludes that the selection effect, which he had just discovered, cannot explain dwarfs and giants.
In the current notation Eddington’s formula is written 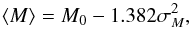 (1)where ⟨ M ⟩ is the mean absolute magnitude when a stellar class with a Gaussian luminosity function (LF; M0 = the mean absolute magnitude, σM = the dispersion) is sampled from the sky as a magnitude-limited sample. Such a class may be called a Gaussian standard candle.
(1)where ⟨ M ⟩ is the mean absolute magnitude when a stellar class with a Gaussian luminosity function (LF; M0 = the mean absolute magnitude, σM = the dispersion) is sampled from the sky as a magnitude-limited sample. Such a class may be called a Gaussian standard candle.
1.2. General Malmquist formula
Equation (1) is valid for a homogeneous spatial distribution. It is a special case of the more general formula derived by Malmquist (1920, 1922). He investigated how the LF of A-type stars may be derived from their distances (in fact, proper motions), provided that it is Gaussian and one knows the distribution a(m) of apparent magnitudes up to a limiting magnitude. One result was the Malmquist formula for the mean value of M of a sample gathered through the apparent magnitude “window” 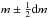 :
: 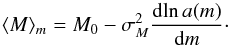 (2)The a(m) term in Eq. (2) depends on the spatial distribution of stars. It has a simple constant form, when the number density reads r− α, where r is the distance:
(2)The a(m) term in Eq. (2) depends on the spatial distribution of stars. It has a simple constant form, when the number density reads r− α, where r is the distance: 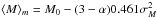 . With α = 0, the Eddington Eq. (1) is obtained. A strongly thinning density with α = 3 is required for no bias, ⟨ M ⟩ m = M0. Then the large volume at large distances, which contributes high-luminosity stars to the sample, is fully compensated for by the lower number density of stars.
. With α = 0, the Eddington Eq. (1) is obtained. A strongly thinning density with α = 3 is required for no bias, ⟨ M ⟩ m = M0. Then the large volume at large distances, which contributes high-luminosity stars to the sample, is fully compensated for by the lower number density of stars.
1.3. About terminology
The Eddington-Malmquist (or Malmquist) bias refers to the major difference in sampling luminous objects “from space” versus “from sky”. The Malmquist relation is the general Eq. (2), while the Eddington formula is the special case, Eq. (1).
Butkevich et al. (2005) termed the bias in Eq. (2) differential, while integral bias was used to denote Malmquist’s other formula, 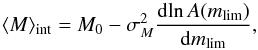 (3)where ⟨ M ⟩ int is the mean for the whole magnitude-limited sample and A(m) is the cumulative distribution up to the magnitude limit mlim.
(3)where ⟨ M ⟩ int is the mean for the whole magnitude-limited sample and A(m) is the cumulative distribution up to the magnitude limit mlim.
When standard candle data are inspected as ⟨ M ⟩ vs. m or ⟨ M ⟩ vs. r (r = distance), respective biases of Type 1 and Type 2 appear (as reviewed by Teerikorpi 1997, especially Table 1 therein), which were also called classical and distance-dependent by Sandage (1994).
Type 1 relates to the bias treated here, that is, how ⟨ M ⟩ m differs from M0. Type 2 refers to the magnitude cut-off effect when for instance a Hubble diagram is inspected as m versus log z. Often the Type 2 aspect is also called, a little misleadingly, the Malmquist bias.
Another parameter is the Eddington bias, which denotes the influence of random measurement errors on derived distribution functions (Eddington 1913, 1940). The Eddington bias was discussed by Teerikorpi (2004), who also considered how it works in concert with the Malmquist bias, Eq. (2).
We derive in Sect. 2 the Malmquist relation in a general cosmological context, first using the bolometric magnitude and then for a finite-band magnitude. In Sect. 3, the result is illustrated and compared with our earlier studies. Section 4 contains concluding remarks.
2. Malmquist equation in a cosmological context
We have previously discussed cosmological Malmquist bias in the Hubble diagram at high redshifts (Teerikorpi 1998, 2003; or T98, T03). This was made by calculating the behaviour of the average ⟨ log z ⟩ m for a Gaussian standard candle, taking into account the different foreground and background volumes as given by Friedmann models. The Malmquist formula was not directly considered.
An early work on the Malmquist bias in cosmology was made by Bigot & Triay (1990), kindly communicated by them to us after the paper T98 was published. The present discussion should facilitate access to their technical treatment, where one result is the Malmquist integral relation, Eq. (3), and where they conclude that the constant correction (Eq. (1)) is no longer valid for distant objects.
Here we derive the general formula using the cosmological route, but analogously to the way Malmquist (1936) remarkably showed that Eq. (2) is valid not only in transparent Euclidean space, but also in the presence of interstellar extinction. We first assume fully transparent space and start with the differential bias (Eq. (2)), whose derivation illustrates well the classical and cosmological aspects of the bias and from which it is easy to derive the integral bias.
2.1. Bolometric magnitude
We begin with the necessary formulae using the bolometric magnitude. Instead of the classical distance, we use the redshift z as the parameter indicating the distance. Then the observed apparent (bolometric) magnitude m is related to the absolute (bolometric) magnitude M as M = m − μ(z), where μ(z) is the Friedmann model-dependent distance modulus of an object at redshift z1.
We consider a class of objects with a Gaussian LF Φ(M) for the bolometric magnitudes. Then the number of objects in the sky observed with the apparent magnitude 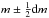 (differential counts) may be obtained using the analogue of the equation of von Seeliger (1898), now summing over the redshift:
(differential counts) may be obtained using the analogue of the equation of von Seeliger (1898), now summing over the redshift: 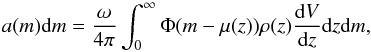 (4)where ρ(z) gives the co-moving spatial number density of objects, possibly varying as a function of redshift, V(z) is the co-moving volume up to redshift z, and ω is the solid angle covered by the region under survey (
(4)where ρ(z) gives the co-moving spatial number density of objects, possibly varying as a function of redshift, V(z) is the co-moving volume up to redshift z, and ω is the solid angle covered by the region under survey (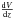 is the co-moving volume derivative).
is the co-moving volume derivative).
By derivation, one obtains another needed expression 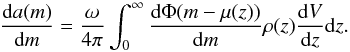 (5)Using Eq. (4), the average value of the absolute magnitude of the objects observed at
(5)Using Eq. (4), the average value of the absolute magnitude of the objects observed at 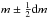 reads
reads 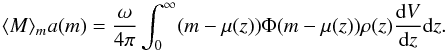 (6)Inserting the Gaussian LF, Eq. (5) becomes
(6)Inserting the Gaussian LF, Eq. (5) becomes 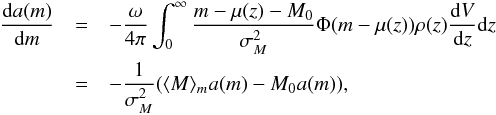 (7)from which one finally obtains
(7)from which one finally obtains 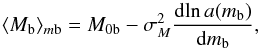 (8)where b means that the magnitudes are bolometric. Equation (8) is the same as the classical Malmquist formula. Below we discuss some further aspects of the result.
(8)where b means that the magnitudes are bolometric. Equation (8) is the same as the classical Malmquist formula. Below we discuss some further aspects of the result.
2.2. K-correction K(z) and extinction E(z)
The above derivation, with the bolometric magnitude in cosmology, corresponds to the case of transparent Euclidean space in Malmquist’s original study, where the apparent magnitude could be bolometric or finite-band (no redshift).
In practice, a finite-band magnitude mi is measured that gives rise to a redshift-dependent K-effect Ki(z). In that case, one replaces M = m − μ(z) by Mi,c = mi − Ki(z) − μ(z), and the end result is similar to Eq. (8), now for the K-corrected Mi-magnitude Mi,c and the observed mi magnitude: 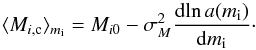 (9)We emphasize a subtlety in the magnitudes in Eq. (9). The difference ⟨ Mi,c ⟩ mi − Mi0 indicates how much the mean value of the intrinsic (K-corrected) absolute magnitude of the objects at the observed apperent magnitude mi differs from the actual mean Mi0 of the Gaussian LF. In the right-side expression, the distribution a(mi) is that of the observed (uncorrected) apparent magnitude.
(9)We emphasize a subtlety in the magnitudes in Eq. (9). The difference ⟨ Mi,c ⟩ mi − Mi0 indicates how much the mean value of the intrinsic (K-corrected) absolute magnitude of the objects at the observed apperent magnitude mi differs from the actual mean Mi0 of the Gaussian LF. In the right-side expression, the distribution a(mi) is that of the observed (uncorrected) apparent magnitude.
Adding a z-dependent extinction E(z) to the model (Mi,c = mi − Ki(z) − E(z) − μ(z)) leads to the same result.
The symbol m may designate either a bolometric or (as in practice) a finite-band magnitude in the remaining text.
2.3. Integral relation
In the integral bias the relevant variable is the limiting magnitude mlim up to which the sample is complete in the inspected region of the sky (in the derivation of the differential bias it is not required that the sample is complete in this sense). Then up to mlim, the number of objects is 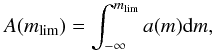 (10)and the mean absolute magnitude for the whole sample is
(10)and the mean absolute magnitude for the whole sample is 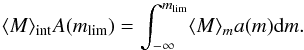 (11)From what was discussed above, we know what ⟨ M ⟩ m is (i.e., Eq. (9)) both classically and cosmologically for a Gaussian LF, and inserting this into Eq. (11) results in
(11)From what was discussed above, we know what ⟨ M ⟩ m is (i.e., Eq. (9)) both classically and cosmologically for a Gaussian LF, and inserting this into Eq. (11) results in 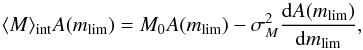 (12)from which follows Eq. (3).
(12)from which follows Eq. (3).
It is interesting to note that the Malmquist differential and integral relations also apply to the extreme spatial distribution z = constant. This is considered in Appendix A.
 |
Fig. 1 log a(m) vs. bolometric magnitude m (Eq.(4)) for a standard candle with M0 = −23.0 and σM = 0.4 mag (the E-deS model, see text). The upper figures above the curve are the mean values ⟨ M ⟩ m calculated from Eq. (6) for m = 8, 16 and 22 mag, respectively. The lower figures (Δ) are the Malmquist bias values as calculated from the slopes shown below the curve. |
2.4. Malmquist relation via convolution
The Malmquist relation can also be considered via convolution. Namely, the distribution a(m) results from a convolution of a Gaussian function Φ and a function F when (e.g., in the cosmological context) one considers the distance modulus μ as a variable instead of z. Then
Here we have the essential mathematical reason for the wide scope of the Malmquist relation because it is based on the simple Gaussian convolution of the function F, which carries all cosmological factors (geometry, luminosity distance, possible number density evolution), and the distance modulus μ may be viewed as a dummy integration variable. With the K-effect (Sect. 2.2), the new variable is constructed from μ(z) + K(z), which is normally a monotonically increasing function2.
3. Discussion
To illustrate the result in a concrete way, it is instructive to make numerical calculations of the left and right sides of the Malmquist equation in Friedmann space.
3.1. Illustrations of the result
For example, consider a class of Gaussian standard candles with M0 = −23 mag and σM = 0.4 mag. Bolometric magnitudes are first assumed and the Einstein-de Sitter model with H0 = 50 km s-1 Mpc-1 is used (the exact value of H0 is not relevant). Then the distance modulus is μ = 5log (1 + z − (1 + z)1/2) + 45.4 and the co-moving volume derivative is 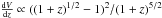 .
.
Using these relations in Eqs. (4) and (6), with ρ(z) = constant (no number evolution), we calculate the logarithmic distribution of apparent magnitudes a(m) as shown in Fig. 1 (an arbitrary zero-point) and the average M at different observed m, or ⟨ M ⟩ m. The slope of log a(m) is indicated for a few apparent magnitudes. Note the expected classical slope 0.6 at bright magnitudes (low redshifts).
Calculation shows that the expression 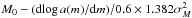 indeed reproduces the numerically calculated ⟨ M ⟩ m (see the upper part of Fig. 1).
indeed reproduces the numerically calculated ⟨ M ⟩ m (see the upper part of Fig. 1).
Of course, this agreement is just as expected from the derived Malmquist relation. However, in presenting Fig. 1, we wish to underline several aspects. In the distribution a(m), m is the observed, uncorrected apparent magnitude. The difference ⟨ M ⟩ m − M0 for intrinsic absolute magnitudes can be derived without detailed information on the Friedmann model in question. This is also true for some number evolution (ρ(z)). As the slope of log a(m) decreases starting from 0.6, the Malmquist bias decreases for this model as well.
Figure 2 presents similar calculations, but now assuming finite-band apparent magnitudes subject to a K-effect. For simple illustration, the K-correction is taken to be K(z) = 2.5z mag, roughly like for elliptical galaxies in optical wavebands (Coleman et al. 1980), making them apparently fainter than would be the bolometric expectation at increasing redshifts. Again, here a(m) is the raw distribution of observed magnitudes, without the K-correction.
 |
Fig. 2 log a(m) vs. finite-band apparent magnitude m for a Gaussian standard candle. Here the K-effect needed in the calculations of a(m) and the average absolute magnitude ⟨ M ⟩ m corresponds to the correction K(z) = 2.5z. Other parameters have the same values as in Fig. 1. This and Fig. 1 also show roughly where the redshift distribution peaks around m = 22 mag. |
3.2. Comparison with the bias analysis in T98
We have explained what happens to the Malmquist bias in cosmology in terms of the luminosity distance and the corresponding comoving volume (T98). As the cosmological distances and volumes are related in a way different from the classical distances, the bias is generally not constant in Friedmann models, but depends on apparent magnitude.
In the cited analysis, instead of ⟨ M ⟩ m, we calculated the quantity ⟨ log z ⟩ m, which is directly suitable to analyse the Hubble log z vs. m diagram. A uniform spatial distribution was assumed with no comoving number evolution.
We conclude that the curves of Mattig (1958) for Friedmann models need to be corrected for a non-constant Malmquist bias in the log z vs. m Hubble diagram (T98; also Bigot & Triay 1990).
It was found that at bright m (low z) the Malmquist shift is close to classical, as expected. Then it generally decreases (in absolute value) towards fainter magnitudes. The same can now be seen from the Malmquist relation.
When changing the model for example by adding the cosmological constant Λ, one simply asks how the slope of the counts a(m) changes. While the comoving volume derivative V′(z) becomes steeper with increasing z when a positive Λ is added, (tending to increase the slope), the luminosity distance also increases (diminishing the slope).
The rapidly increasing volume is more important; it results in steeper a(m), which means a larger Malmquist bias, that is, closer to the classical one. For example, referring to Fig. 1, at m = 22 mag the pure flat Λ model, ΩΛ = 1, would lead to the bias −0.15 instead of −0.08 for the E-deS flat model. Thus the Λ-model leads to a weaker m-dependence of the bias, as also derived in T98 and T03.
For the K-effect, it was pointed out in T98 that if K(z) increases with z so that the objects become fainter quicker than when they are only due to the bolometric factor, then the backside volume effectively decreases and the trend in the Malmquist bias away from the classical case increases, as also seen here in Figs. 1 and 2. The K-effect can be important and increase the deviation of the bias from the classical constant value.
3.3. Practical note
That we can derive the difference of the intrinsic magnitudes ⟨ M ⟩ m and M0 in principle from minimal information (σM) and raw data (a(m)) does not mean that we may generally forget factors such as the K-correction when applying this result.
For example, we consider a Gaussian standard candle in a test of the Friedmann model, assuming that we have been able to determine a(m) and know σM.
At the observed m the average ⟨ M ⟩ m is predicted to be 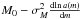 . This value is compared with the average ⟨ M ⟩ m,data derived from the K-corrected apparent magnitudes of the objects at the observed (uncorrected) magnitude m. Each object has a known redshift, so one may calculate for each its K-corrected absolute magnitude for a given Friedmann model. Therefore the test requires knowing K(z) and the expression for the luminosity distance.
. This value is compared with the average ⟨ M ⟩ m,data derived from the K-corrected apparent magnitudes of the objects at the observed (uncorrected) magnitude m. Each object has a known redshift, so one may calculate for each its K-corrected absolute magnitude for a given Friedmann model. Therefore the test requires knowing K(z) and the expression for the luminosity distance.
Referring to Fig. 2, one might have derived the slope 0.46 at m = 16 and hence the bias −0.17 mag. Then the Friedmann model is correct, which gives ⟨ M ⟩ 16,data = −23.17 mag, as derived from the K-corrected apparent magnitudes of the objects at the uncorrected m = 16 mag.
With all the data, one requires that the difference 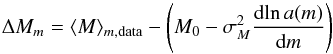 (16)does not depend on m. In addition, ⟨ ΔMm ⟩ ≈ 0 for the correct Hubble constant and M03.
(16)does not depend on m. In addition, ⟨ ΔMm ⟩ ≈ 0 for the correct Hubble constant and M03.
4. Concluding remarks
Malmquist (1936) reported that his relation is also valid when light extinction is added to the static Euclidean space he considered. His study inspired the present work, which shows the scope of the Malmquist relation from classical situations to Friedmann cosmological models.
The cosmological factors (luminosity distance, comoving volume derivative, and number evolution) are all reflected in the slope of the (log) counts vs. observed apparent magnitude. The K-effect for finite-band magnitude and also possible z-dependent extinction are automatically included in the right side of the Malmquist relation.
We emphasized conceptual aspects of the Malmquist relation in view of its important role in stellar statistics. However, prospects for its practical use for high-luminosity objects in extragalactic astronomy are not so immediate.
First, a constant Gaussian LF is rare or absent for objects found at low and high redshifts. Second, it requires many data to determine 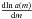 with good accuracy. In addition, the Type 1 Malmquist analysis is too simplistic if the objects are not detected on the basis of non-variable brightness, but there is a chain of measurement and luminosity inference as for Ia supernovae.
with good accuracy. In addition, the Type 1 Malmquist analysis is too simplistic if the objects are not detected on the basis of non-variable brightness, but there is a chain of measurement and luminosity inference as for Ia supernovae.
The Type 2 approach is often applied in luminosity-bias analysis in extragalactic astronomy, where the redshift offers a good relative distance indicator. This concerns the classical determination of the Hubble constant as well as the detection of universal acceleration from the Hubble diagram of Ia SNe (e.g., Perrett et al. 2010). Bayesian approaches are also currently used when considering general LFs and inferring cosmological model parameters (e.g., March et al. 2011).
The Malmquist correction may be viewed as a Bayesian approach to the problem of deriving ⟨ M ⟩ m (and perhaps using it in distance estimation) when the standard candle has a known Gaussian LF as prior, while the Type 2 approach corresponds to the frequentist view of probability (Hendry & Simmons 1994). In the Gaussian case, the mean value of the posterior distribution P(M | m) in the Bayesian formula 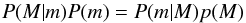 (17)can be solved directly, essentially following Sect. 2.
(17)can be solved directly, essentially following Sect. 2.
One may write μ(z) = 5log rlum(z)/10 pc. The luminosity distance rlum(z) is obtained using the well-known Mattig equation and its generalizations (e.g., Baryshev & Teerikorpi 2012), once the values of the Friedmann model parameters are fixed.
The same is valid in stellar statistics if the Malmquist relation is to be used to derive the mean absolute magnitude of a stellar class. ⟨ M ⟩ data − M0 is derived from the histogram of the apparent magnitudes. Then to infer M0, ⟨ M ⟩ data must be computed, which requires distances and extinctions for each sample star.
Acknowledgments
I thank Alexei Butkevich for help in providing me with the relevant chapter in Eddington’s rare 1914 book and for discussions on different aspects of the Malmquist bias. Good remarks by the referee are also acknowledged.
References
- Baryshev, Yu., & Teerikorpi, P. 2012, Fundamental Questions of Practical Cosmology (Berlin: Springer) [Google Scholar]
- Bigot, G., & Triay, R. 1990, Phys. Lett. A, 150, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Butkevich, A., Berdyugin, A., & Teerikorpi, P. 2005, MNRAS, 362, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Coleman, G. D., Wu, C.-C., & Weedman, D. W. 1980, ApJSS, 43, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Eddington, A. S. 1913, MNRAS, 73, 359 [Google Scholar]
- Eddington, A. S. 1914, Stellar Movements and the Structure of the Universe (London: Macmillan) [Google Scholar]
- Eddington, A. S. 1940, MNRAS, 100, 35 [Google Scholar]
- Hendry, M. A., & Simmons, J. F. L. 1994, ApJ, 435, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Kapteyn, J. C. 1914, ApJ, 40, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Malmquist, K. G. 1920, Lund Medd. Ser. II, 22 [Google Scholar]
- Malmquist, K. G. 1922, Lund Medd. Ser. I, No.100, Arkiv Mat. Astr. Fys., 16, 23 [Google Scholar]
- Malmquist, K. G. 1936, Arkiv Mat. Astr. Fys. A., 25, 14 [Google Scholar]
- March, M. C., Trotta, R., Berkes, P., Starkman, G. D., & Vaudrevange, P. M. 2011, MNRAS, 418, 2308 [NASA ADS] [CrossRef] [Google Scholar]
- Mattig, W. 1958, Astron. Nachr., 284, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Perrett, K., Balam, D., Sullivan, M., et al. 2010, AJ, 140, 518 [NASA ADS] [CrossRef] [Google Scholar]
- Sandage, A. 1994, ApJ, 430, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Teerikorpi, P. 1997, ARA&A, 35, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Teerikorpi, P. 1998, A&A, 339, 647 (T98) [NASA ADS] [Google Scholar]
- Teerikorpi, P. 2003, A&A, 399, 829 (T03) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Teerikorpi, P. 2004, A&A, 424, 73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Seeliger, H. 1898, Abh. K. Bayer Akad Wiss. Ser II KI, 19, 564 [Google Scholar]
Appendix A: Case of a cluster (z = const.)
In the integrations of Sect. 2 (e.g., in Eq. (4)) integration can be restricted to a finite z range (where the objects in question exist). The density law ρ(z) takes care of this.
Equation (9) also applies for a δ-function-like ρ(z), for instance, for a cluster at z = z0. Then a(m) is proportional to a Gaussian function with the mean m0 = M0 + μ(z0) and is observed up to the sample limit mlim. The second term in the right side of Eq. (9) for any m<mlim becomes after derivation m − M0 − μ(z0) = Mm − M0. This is equal to ⟨ M ⟩ m − M0 in this case and gives the difference between m and the magnitude m0 corresponding to the maximum of the LF at M0 even if this is not reached by the sample.
 |
Fig. A.1 Differential Malmquist relation as applied to the case of a cluster at distance modulus μ = 10. The LF is Gaussian with M0 = −5 and σ = 1 mag. The slope of the lna(m) curve at any m, multiplied by σ2, gives the difference m0 − m. |
The slope of the lna(m) distribution at any m gives, via the Malmquist Eq. (9), the absolute magnitude Mm corresponding to the observed m and hence the distance modulus (see Fig. A.1 for a graphic representation). For a good Gaussian LF the same result is obtained for any other m in the complete part of the sample.
It is interesting to note that in the same year as Eddington published his Eq. (1), Kapteyn (1914) discussed the derivation of the distance of a star cluster with a Gaussian LF. He considered the observational cut-off effect and derived an integral equation
that took into account the magnitude limit mlim and contained the distance modulus as unknown. Essentially, in that method the cluster is moved along the line of sight up to the distance modulus μ where the observed average apparent magnitude is equal to the value predicted from μ, mlim, and the known Gaussian LF. Of course, the end result will be the same as in the approach where the slope of lna(m) is used.
In fact, the formula (69) in the study by Kapteyn is a special case of the Malmquist integral bias relation, Eq. (3). Therefore both the differential and integral bias relations by Malmquist are formally applicable to the extreme spatial distribution represented by z = constant.
All Figures
 |
Fig. 1 log a(m) vs. bolometric magnitude m (Eq.(4)) for a standard candle with M0 = −23.0 and σM = 0.4 mag (the E-deS model, see text). The upper figures above the curve are the mean values ⟨ M ⟩ m calculated from Eq. (6) for m = 8, 16 and 22 mag, respectively. The lower figures (Δ) are the Malmquist bias values as calculated from the slopes shown below the curve. |
| In the text | |
 |
Fig. 2 log a(m) vs. finite-band apparent magnitude m for a Gaussian standard candle. Here the K-effect needed in the calculations of a(m) and the average absolute magnitude ⟨ M ⟩ m corresponds to the correction K(z) = 2.5z. Other parameters have the same values as in Fig. 1. This and Fig. 1 also show roughly where the redshift distribution peaks around m = 22 mag. |
| In the text | |
 |
Fig. A.1 Differential Malmquist relation as applied to the case of a cluster at distance modulus μ = 10. The LF is Gaussian with M0 = −5 and σ = 1 mag. The slope of the lna(m) curve at any m, multiplied by σ2, gives the difference m0 − m. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.