EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 576 (April 2015) A&A, 576 (2015) A133 Full HTML
Issue
A&A
Volume 576, April 2015
Article Number A133
Number of page(s) 10
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/201425185
Published online 20 April 2015

© ESO, 2015

1. Introduction

Detecting exoplanets and characterizing their atmospheres and system architectures using direct imaging is one of the most difficult challenges in modern astronomy. Optimized observing strategy and data analysis are required to overcome the high contrasts (≳104) and the small separations (a few tenths of an arcsecond) between a star and a planet. The development of adaptive optics systems, coronagraphic devices, and differential imaging techniques in the past fifteen years allowed detection of planetary-mass objects in favorable situations: young and nearby host star, large orbital separation, and/or low star/planet mass ratio (e.g., Chauvin et al. 2005; Marois et al. 2008, 2010b; Lagrange et al. 2010; Lafrenière et al. 2010; Kuzuhara et al. 2013; Rameau et al. 2013; Bailey et al. 2014). A new generation of instruments dedicated to the search and characterization of young exoplanets down to the Jupiter mass has started operations (Tamura & SEEDS Team 2010; Hinkley et al. 2011; Close et al. 2013; Skemer et al. 2014a; Macintosh et al. 2014; Beuzit et al. 2012).

One main topic in the study of exoplanetary systems using direct imaging is their architecture. This can be investigated using indirect or direct observational evidence of the presence of planets. The modeling of the dust spatial distribution in resolved circumstellar debris disks can provide predictions of the orbital parameters and the mass of one or more putative planets which gravitationnally perturb the disk (e.g., Mouillet et al. 1997; Wyatt et al. 1999; Ozernoy et al. 2000; Augereau et al. 2001; Kalas et al. 2005). These predictions may be followed by direct detection of a planet (Lagrange et al. 2009, 2010) or a substellar-mass object (Kalas et al. 2008; Currie et al. 2012; Galicher et al. 2013; Kalas et al. 2013). When an object is detected, accurate astrometric follow-up is needed to determine its orbital elements (Chauvin et al. 2012; Kalas et al. 2013). Since most of the directly-imaged exoplanets have long orbital periods (>20 AU), this analysis is challenging when based on data acquired on timescales of a few years and usually with different instruments. For multiple-planet systems, the study of the dynamical stability allows putting constraints on the planet masses (Fabrycky & Murray-Clay 2010; Goździewski & Migaszewski 2009, 2014; Reidemeister et al. 2009; Moro-Martín et al. 2010; Marois et al. 2010b; Currie et al. 2011; Sudol & Haghighipour 2012; Esposito et al. 2013). These estimates do not depend on evolutionary models of giant planets (e.g., Burrows et al. 1997; Chabrier et al. 2000; Baraffe et al. 2003; Marley et al. 2007), which rely on unknown initial conditions (Marley et al. 2007; Spiegel & Burrows 2012; Marleau & Cumming 2014), and on poorly constrained stellar ages. Thus, the derivation of the dynamical mass of young low-mass companions may help to calibrate the evolutionary models (e.g., Close et al. 2005; Boden et al. 2005; Crepp et al. 2012; Bonnefoy et al. 2014b).

Table 1

Log of the observations.

The LBT Exozodi Exoplanet Common Hunt (LEECH, Skemer et al. 2014a) survey to search for and characterize young and adolescent exoplanets in L′ band (3.8 ¯m) started at the Large Binocular Telescope in February 2013. This ~130-night survey exploits the adaptive optics system FLAO (Esposito et al. 2010), which combines Strehl ratio performance superior to 80% in H band and to 95% in L′ band with low thermal emissivity, the LBT Interferometer (LBTI, Hinz et al. 2008), and the L/M-band InfraRed Camera (LMIRCam, Skrutskie et al. 2010; Leisenring et al. 2012). The selection of the L′ band is strategic, because AO systems provide better Strehl ratios, and the star/planet brightness ratios are reduced for this spectral band with respect to shorter wavelengths. LEECH complements the other current or future large imaging surveys for young (≲200 Myr) giant exoplanets by covering longer wavelengths and probing northern, nearby (≲30–55 pc), and older (≲1 Gyr) stars. The first data obtained with LBTI/LMIRCam prior to the LEECH survey allowed the multiwavelength photometric analysis in the L band (3–4 ¯m) of the four planets of HR 8799 (Skemer et al. 2012, 2014b), and the M-band detection and photometric characterization of κ And b (Bonnefoy et al. 2014a).

One important aspect of a high-contrast imaging survey is accurate determination of the astrometry of the detected exoplanet candidates. To date, only one astrometric analysis based on LBTI/LMIRCam data and not related to the LEECH primary goals has been performed for the white dwarf companion to HD 114174 (Matthews et al. 2014b), using observations of an astrometric binary, but without correcting for the distortion effects of the camera.

We present in this paper the first reliable LEECH astrometry of an exoplanetary system, HR 8799. The host star is a young (30 Myr, Marois et al. 2010b; Baines et al. 2012) and nearby (d = 39.4 ± 1.0 pc, van Leeuwen 2007) late-A or early-F star (Gray & Kaye 1999; Gray & Corbally 2014). It is orbited by at least four giant planets at projected separations of 15, 24, 38, and 68 AU (Marois et al. 2008, 2010b). The system is also composed of a complex debris disk (Su et al. 2009) seen with an inclination of 26° (Matthews et al. 2014a), with a warm (T ~ 150 K) and unresolved inner dust component between about 6 and 15 AU, a cold (T ~ 35 K) planetesimal belt extending from ~100 to 310 AU, and a cold halo of dust grains that extends from 310 to ~2000 AU. We also describe the astrometric calibration and characterization of the LMIRCam distortion, which are of general interest for users of the instrument (now offered to the LBT community). We also present new orbital fitting of all four planets and further constraints on the properties of a putative fifth planet inside these planets. We describe the observations and the data reduction in Sect. 2 and Appendix A. We present the astrometric analysis in Sect. 3. We report the planet photometry and the detection limits in Sects. 4 and 5. We perform new orbital fitting of the astrometric measurements in Sect. 6. We discuss our results and assumptions in Sect. 7.

2. Observations and data reduction

The observations of HR 8799 and the Θ1 Ori C field were carried out during the same observing run in October 2013 (Table 1). The LBTI is located at a bent Gregorian focus with no field rotator, so all observations are performed in pupil-stabilized mode. This mode allows the use of angular differential imaging (Marois et al. 2006a) to subtract the point-spread function (PSF) for high-contrast imaging. The LMIRCam camera is designed to be Nyquist-sampled for the full 22.8-m aperture of the LBT when used in interferometric mode. When LMIRCam is used with one of the two apertures of 8.4 m, the images are oversampled. For the high-contrast imaging observations (HR 8799 in this paper), we bin the pixels two by two.

The Θ1 Ori C field was observed on October 24 UT with the right side (also known as the “DX” side) of the LBT at twelve different dither patterns, with each dither position consisting of ten frames. Each group of ten frames was corrected for the distortion effects of the camera (Appendix A) and the bad pixels, then sky-subtracted and averaged. The mean measured PSF full-width at half maximum is about ten pixels estimated, by several methods (Gaussian fitting, radial profile).

HR 8799 (L′ = 5.220 ± 0.018, Hinz et al. 2010) was observed on October 21 UT with the “DX” side of the telescope at two different nods simultaneously. We selected the individual exposure time so that the readout noise is kept below the sky background. The star is thus saturated on the detector. After applying frame selection, distortion correction, cosmetic removal, sky subtraction, 2 × 2 binning, and frame registration (using cross-correlation), the data were processed using our implementation of the principal component analysis approach (PCA, Soummer et al. 2012; Amara & Quanz 2012). Figure 1 shows the resulting image. HR 8799 bcde are detected with signal-to-noise ratio 81, 154, 62, and 32 (see below for the method used for the noise estimation). Immediately after observing HR 8799, we observed another star, HIP 18859, in the same mode as HR 8799 but with a calibrated 1% neutral density filter.

When observing a bright star in the L′ band, the LMIRCam PSF is very stable, so this photometric standard is more than adequate for approximating the relatively low signal-to-noise core of an exoplanet. Since the point-source self-subtraction of angular differential imaging biases the astrometric and photometric measurements, we calibrated these effects using injection of synthetic point sources (based on the measured PSF) with different brightness and insertion positions into the preprocessed data (Skemer et al. 2012). More precisely, we inserted negative artificial planets (Marois et al. 2010a; Bonnefoy et al. 2011) at the positions of the real planets in the preprocessed data before performing the differential imaging part of the data analysis. This is repeated as part of a Levenberg-Marquardt fit (Markwardt 2009)1 until the flux at the positions of the true planets is minimized. The procedure minimizes the planet flux over an annulus centered on the star with a radius equal to the planet separation and a width of 0.3′′. Using an annulus for the minimization zone instead of an aperture around the planet PSF has negligible effects on the results of the minimization process because a planet signal spans a small region of the annulus. The Levenberg-Marquardt code outputs error bars, based on the cross-correlation matrix and the number of free parameters (i.e., the number of resolution elements) in the annulus.

thumbnail Fig. 1

LMIRCam image in L′ band of the HR 8799 multiple-planet system. The field of view is ~4′′. The point-spread function is subtracted using our PCA pipeline (see text). The image is binned (2 × 2 binning). The intensity scale is linear.

We constructed a contrast curve (discussed in Sect. 5) using the preprocessed frames with HR 8799 bcde artificially removed. At every radius, we inserted a fake planet in these data and performed a complete re-reduction, iterating until we reached a 5σ detection2 (our nominal contrast benchmark). For each separation to the star, the noise level was estimated using the standard deviation of the intensity of the pixels at this separation. For deriving the signal-to-noise of the planets, the noise level was scaled to the same aperture size (1 λ/D) as used to estimate the flux of the fake planets assuming white noise. We repeated this analysis at eight position angles for every radius, and averaged the results to suppress random speckle error.

3. Astrometric analysis

3.1. The Θ1 Ori C field

The stellar positions in the images are derived using the centroid IDL routine cntrd3 adapted from the DAOphot software (Stetson 1987). For the catalog positions, we use the astrometry published in Close et al. (2012), based on LBT/PISCES observations acquired on October 16, 2011, which is referenced to the HST/ACS observations of Ricci et al. (2008). In each of the dithered frames of the observing sequence (Sect. 2), we typically select three to four stars with signal-to-noise ratios greater than 10 for the calibration. We use all the available stellar pairs for the analysis.

Table 2

Astrometric measurements of the HR 8799 planets with respect to the star at epoch 2013.81.

Combining the results obtained for the whole dataset, we derive forty individual measurements for the platescale and the true north orientation with respect to the detector y-axis (counted positively in the counterclockwise direction). The mean value and the corresponding error are

  • Platescale: 10.707 ± 0.012 mas/pix;

  • True north: −0.430 ± 0.076°.

The errors on the platescale and true north orientation translate into astrometric accuracies at a separation of 1′′ of 1.1 mas and 1.3 mas, respectively.

We do not correct the catalog positions for the differential stellar proper motions. The absolute motions are expected to be ~1.5 mas/yr (Close et al. 2012). The error on the platescale produced by the differential stellar proper motions is negligible for the separations of the stellar pairs considered in this work (mean value 5′′) with respect to the errors induced by the platescale estimation (relative error 0.1%, Table 3) and the detector distortion (relative error ~0.1% after correction, see Appendix A).

Table 3

1σ astrometric error budget (in mas) for the HR 8799 planets for both observations (see text).

3.2. The HR 8799 planetary system

HR 8799 was observed once during the night of October 21 2013 simultaneously at two different nods. We combined the individual measurements of these two datasets for each of the four planets and derived the astrometric measurements in Table 2. We give the error budget for both datasets in Table 3. We note a bias of ~0.015′′ between the two sets of measurements for the relative vertical position. This may be due to a less accurate centering of the frames (Sect. 2). We account for this bias in the derivation of the error on the relative vertical position given in Table 2. The star center and the fitting error are the dominant error sources. For planets b and d, both sources have similar contributions. For planet c, the star center is the main error source. For planet e, the fitting error is the largest error. The accuracies on our measurements are similar to those measured by Currie et al. (2014) in Keck L′ data for the three outer planets. For the innermost planet, the accuracy is worse with respect to the work of Currie et al. (2014) because of the large fitting error, but similar to the values measured in Keck L′ data in the discovery paper (Marois et al. 2010b).

Table 4

LBTI/LMIRCam relative and absolute photometry of the HR 8799 planets in L′ band.

4. Photometry

thumbnail Fig. 2

5σ detection limits in L′ band for the LMIRCam data of HR 8799 expressed in contrast (left) and in planet mass (right), with the four planets shown (filled circles in the left panel and gray areas in the right panel). The positions of a putative fifth planet in resonance 3:1 and 2:1 with planet e according to the models of Goździewski & Migaszewski (2014) are also indicated (assuming a face-on and circular orbit). For the right plot, the detection limits are derived for an age of 30 Myr from the “hot-start” COND model (Baraffe et al. 2003) coupled to the atmosphere model BT-Settl (Allard et al. 2012) and the “warm-start” evolutionary+atmosphere model of Spiegel & Burrows (2012) for an initial entropy of 9 kB/baryon (see text). The range of masses for HR 8799 bcde is delimited by the predictions of the two evolutionary models assumed for deriving the detection limits (lower limit: BT-Settl+COND; upper limit: SB12 with initial entropy of 9 kB/baryon). The range of physical separations for the planets is computed using the errors on the planet separation and the star distance.

We did not acquire any unsaturated images of HR 8799 during the observations, so we derived the relative photometry of planets b, d, and e with respect to planet c and used the absolute photometry of HR 8799 c reported in Marois et al. (2008) and its uncertainty (0.09 mag) to determine the absolute photometry and the associated error bars. We combined two sets of photometric measurements and derived the values reported in Table 4. The statistical error on the individual measurements includes the fitting error and the stellar flux variations during the observation. We estimated the latter errors to be 1.1% using the photometric variations of an unsaturated optical ghost in the frames. Given the error bars, our values agree with the values in the literature and achieve similar accuracies (Marois et al. 2008, 2010b; Currie et al. 2014). For these reasons, we did not attempt to carry out atmospheric modeling (Skemer et al. 2012, 2014b) using these new photometric data.

5. Constraints on the properties of a fifth planet

We now discuss the constraints on the separation and mass of a putative fifth planet closer in, “HR 8799 f”, based on the data presented in this paper and the theoretical predictions in Goździewski & Migaszewski (2014). We show both the 5σ detection contrast curve measured in the reduced image (after removing the signals of the four planets) and corrected for the self-subtraction of off-axis point sources (Skemer et al. 2012, and Sect. 2) in the lefthand panel of Fig. 2, and the location of the four known planets. The locations of the resonances 3:1 and 2:1 with planet e according to the models of Goździewski & Migaszewski (2014) are also indicated, assuming for simplicity a face-on and circular orbit for planet “f”. For resonance 3e:1f, Goździewski & Migaszewski (2014) predict a separation and a mass range for “HR 8799 f” of ~7.4 AU and about two to eight Jupiter masses (MJ), while for resonance 2e:1f, they derive values of ~9.7 AU and ~1.5–5 MJ. Given the contrast curve in the lefthand panel of Fig. 2, we are able to exclude a fifth planet slightly brighter or more massive than planet b at the location of 2e:1f resonance and a fifth planet about twice as bright as planets c–e at the location of 3e:1f resonance.

In the righthand panel of Fig. 2, we show the detection limits in planet mass. We assume an age for HR 8799 of 30 Myr (Marois et al. 2010b; Baines et al. 2012). The planet masses and the detection limits are derived from two models: the “hot-start” model COND (Baraffe et al. 2003) coupled with the atmosphere model BT-Settl (Allard et al. 2012) and the “warm-start” evolutionary and atmosphere model of Spiegel & Burrows (2012) corresponding to an initial entropy of 9 kB/baryon and a cloudy atmosphere of one solar metallicity4. The value for the initial entropy is selected based on the work of Marleau & Cumming (2014), assuming an upper limit for the planet masses of 12 MJ according to the dynamical analysis of Goździewski & Migaszewski (2014)5. The selected value for the initial entropy is thus the approximate minimum value allowed for the formation of the planets independently from the details of the formation scenario. We cannot reject a “warm-start” model for the formation and evolution of the HR 8799 planets given the dynamical mass constraints.

The constraints on a planet mass for a given initial entropy still depend on the assumption on the star age. Thus, the detection limits in the righthand panel of Fig. 2 define the range of possible values, assuming HR 8799 is a 30-Myr star. The range will be shifted towards higher masses when assuming older ages. However, constraints from the stellar properties (Marois et al. 2008; Baines et al. 2012), the mass of the disk (Su et al. 2009), and models of dynamical stability of the four planets (Esposito et al. 2013; Goździewski & Migaszewski 2014) suggest that the system is young. Other hints for small radii or low masses of the planets come from the fitting of their spectral energy distribution (e.g., Marois et al. 2008; Bowler et al. 2010; Currie et al. 2011; Barman et al. 2011; Madhusudhan et al. 2011; Galicher et al. 2011; Ingraham et al. 2014), although there are uncertainties on the atmospheric composition and the physical processes governing their atmospheres assumed for the models (e.g., solar/non-solar metallicity, physics of the clouds, non-equilibrium chemistry).

Directly south of the star at ~0.2′′, we find an excess at the ~3–4σ level (see Fig. 1), which is below our planet detection threshold. The excess is detected at a higher signal-to-noise ratio for one sequence recorded at one nod. Thus, it could be a speckle correlated between the nods. The excess is not seen in other LBTI datasets from the same run, although these datasets were taken in worse conditions. As noted by Mawet et al. (2014), high standard deviation residuals become increasingly common at small separations, so we note the excess, but categorize it as most likely a PSF residual. We do not detect any excess at the location of the residual reported in Currie et al. (2014).

thumbnail Fig. 3

Relative astrometry of the HR 8799 planets for all the measurements available in the literature (small filled circles) and the measurements derived in this work (purple filled squares). The solid blue lines represent the orbital solution labeled “A” in Table 5. Red lines connect the predicted and observed positions for all the data points. The dotted line in the panel for HR 8799 e indicates the orbital solution labeled “B” in Table 5. The orange circles indicate the ephemeris predicted in Goździewski & Migaszewski (2014).

6. Orbital architecture

It has been proposed that mean motion resonances maintain the dynamical stability of the compact four-giant planet system of HR 8799 on timescales of at least the stellar lifetime (>30 Myr, Marois et al. 2010b). The architecture of the system is still not completely understood, and two families of orbital solutions have been investigated in the literature: non-circular and coplanar orbits (Goździewski & Migaszewski 2009, 2014; Fabrycky & Murray-Clay 2010; Soummer et al. 2011) and circular and non-coplanar orbits (Esposito et al. 2013). Recently, Goździewski & Migaszewski (2014) have built a long-term stable model of the system, with all planets on quasi-circular coplanar orbits and likely involved in 8b:4c:2d:1e mean motion resonance. We first tested the predictions of Goździewski & Migaszewski (2014) with respect to the astrometric measurements presented in this paper. We gathered all the relative astrometric measurements available in the literature (Marois et al. 2008, 2010b; Lafrenière et al. 2009; Fukagawa et al. 2009; Metchev et al. 2009; Hinz et al. 2010; Currie et al. 2011, 2012, 2014; Bergfors et al. 2011; Galicher et al. 2011; Soummer et al. 2011; Esposito et al. 2013; Pueyo et al. 2015) and included the LEECH measurements (Table 2) to represent Fig. 3. We also indicate in Fig. 3 the ephemeris predicted by Goździewski & Migaszewski (2014) for a four-planet system (see their Appendix B.1) at the epoch of the observations presented in this paper. The presence of a putative fifth planet inside the known planets does not affect the ephemeris of the known planets significantly. Given the error bars, our measurements agree within 3σ with the ephemeris.

To complement the analysis of Goździewski & Migaszewski (2014), based on astrometric data obtained before 2012, we performed new orbital fitting of the planets assuming circular and non-coplanar orbits using the more extended baseline offered by the measurements of Currie et al. (2014), Pueyo et al. (2015), and the data reported in this work. We used the orbital fitting procedure described in Esposito et al. (2013), i.e., a best-fit, least-squares orbital fitting of the four planets simultaneously, based on the Levenberg-Marquardt algorithm (see note 1). We did not intend to perform an in-depth orbital analysis like the study presented in Pueyo et al. (2015), because such a study would soon be altered with the availability of more recent astrometric data.

Table 5

Orbital elements fitted on the astrometric data in Fig. 3.

In Fig. 3, we show the orbital fits (Table 5) assuming two orbital solutions proposed by Esposito et al. (2013): A. circular and non-coplanar orbits, with all planets involved in 8b:4c:2d:1e mean motion resonance; and B. circular and non-coplanar orbits, assuming 4b:2c:1d and 5d:2e mean motion resonances. Esposito et al. (2013) are not able to distinguish them with the available data, but predict that the orbits would diverge significantly within two to three years. We assumed the same ranges of allowed values for the orbital elements as found by Esposito et al. (2013) using Monte Carlo simulations (see their Fig. 8). The semi-major axes were derived by assuming a mass for the host star of 1.51 M⊙, following the work of Baines et al. (2012). We estimated the error bars on the orbital parameters in Table 5 based on the sensitivity of the orbital fits with the errors on the astrometric data (Fig. 3). We generated 1000 random sets of astrometric measurements for each planet assuming Gaussian distributions around the nominal astrometric measurements. We then performed the fitting of these measurements assuming the properties of each orbital solution. Except for a few solutions, all the fitted solutions produce a square root of the reduced χ2 below two for each planet. There are no clear minima in the distribution of the orbital parameters. The error bar on each orbital parameter is the standard deviation of the fitted values. The astrometric measurements obtained in 2012 by Pueyo et al. (2015) and Currie et al. (2014) and in 2013 by us allow a modest increase in the time baselines for the three outer planets but a significant improvement for planet e. In particular, our measurement for planet e favors the orbital solution “A” (Table 5), i.e., an orbital architecture based on the mean motion resonance 8:4:2:1. Nevertheless, the LEECH measurement lies out of solution “B” by only ~2σ, so this solution is not firmly excluded from a statistical point of view. We note that Goździewski & Migaszewski (2014) find that the most likely mean motion resonance for the planets is 8:4:2:1 under the assumption of quasi-circular and coplanar orbits.

7. Discussion

We discuss in this section the assumptions and the results for the planet architecture described in Sect. 6 in light of the recent analysis of Pueyo et al. (2015). These authors performed a Bayesian analysis based on Markov Chain Monte Carlo techniques of the astrometric measurements of all the four planets compiled in Esposito et al. (2013) and P1640 measurements obtained in June 2012. The main motivation of their work is to complement the previous analyses, which are based on least-squares orbital fitting and/or dynamical studies and consider strong assumptions for the orbits (coplanarity, circularity, and/or mean motion resonances). These assumptions are used because of the degeneracies inherent to the determination of the six Keplerian elements of an orbit based on data covering only a small portion of the latter. However, as outlined by Pueyo et al. (2015), Markov Chain Monte Carlo techniques are sensitive to underestimated biases that are not accounted for in the error bars6. Such biases can come from measurements obtained with different instruments and/or data analyses.

Our work belongs to the category of orbital fitting studies and is based on the assumption of circular and non-coplanar orbits and the use of Monte Carlo simulations for estimating broad ranges for the orbital parameters. Monte Carlo methods are sensitive to the same kind of biases as Markov Chain Monte Carlo methods, so we cannot exclude biases in our results, in particular the mean motion resonances between the planets.

We first focus on the relative inclinations of the planets. We consider non-coplanar orbits in this paper. Our estimates in Table 5 do not allow concluding that the orbit of one planet is outside the plane of the orbits of the other planets. Pueyo et al. (2015) find that planets b, c, and e would have similar inclinations, but that planet d would have a more inclined orbit (~15–20°). Looking at Fig. 3, we note the discrepancy of the P1640 data for planet d (ΔRA = −0.323 ± 0.006′′, ΔDec = −0.529 ± 0.006′′) with respect to the October 2012 data reported in Currie et al. (2014) (ΔRA = −0.343 ± 0.006′′, ΔDec = −0.555 ± 0.006′′) and our 2013 October measurement. The P1640 measurement is likely the cause for the orbital solutions found for this planet by Pueyo et al. (2015). Our motivation for exploring non-coplanar orbits for the planets in Esposito et al. (2013) and this work is to complement the available studies, which assume coplanarity. It is also suggested by asteroseismology studies that indicate that the star has a more edge-on inclination (≥40°, Wright et al. 2011) with respect to the planes of the planet orbits and of the disk (Su et al. 2009). A recent analysis of the MOST photometric data of the star (Sódor et al. 2014) does not give clear evidence of rotational splitting of the modes, which would imply a stellar inclination similar to those of the planes of the planet orbits and of the disk. Thus, we cannot draw sound conclusions for either a misalignment or alignment of the star equator with respect to the plane of the planet orbits. Nevertheless, we note that under the extreme assumption of circular orbits, we find that HR 8799 bc would have orbits that are roughly coplanar with the disk of the host star (i = 26 ± 3° and Ω = 62 ± 3°, Matthews et al. 2014a). HR 8799 d might have a slightly inclined (~8–11°) orbit with respect to the disk plane, although our study does not allow any conclusion on this point. According to the orbital solution favored in our analysis (solution “A”, Table 5), HR 8799 e might have an orbit that is significantly misaligned with respect to the position angle of the disk (the difference between the longitudes of ascending node is ~75–78°).

We now test the hypothesis of circular orbits for all planets that we made in our analysis (Sect. 6). Previous analyses indicate that planets b and c have roughly circular orbits, while planet d would have a moderately eccentric orbit (≲0.15, Fabrycky & Murray-Clay 2010; Bergfors et al. 2011; Soummer et al. 2011; Goździewski & Migaszewski 2014). For planet e, studies suggest an eccentric orbit (≲0.15, Sudol & Haghighipour 2012; Goździewski & Migaszewski 2014). Pueyo et al. (2015) find roughly circular orbits for planets b and c, but a very eccentric (≤0.3 at 1σ) orbit for planet d. As mentioned above, the P1640 data for planet d appears discrepant to the 2012 measurement by Currie et al. (2014), which probably biases their results for this planet. We performed several orbital fitting tests assuming non-circular and coplanar orbits for all planets, using the values of inclination (i ~ 26°) and longitude of ascending node (Ω ~ 62°) derived in Matthews et al. (2014a), and found moderate eccentricities for planet d (≲0.15), in agreement with the previous analyses mentioned above. For planet e, the time baseline used by Pueyo et al. (2015) is limited, preventing them from placing strong constraints. Our tests suggest an eccentricity similar to that of planet d or higher (up to ~0.25), depending on the assumed mean motion resonance between planets d and e.

We finally discuss the mean motion resonances. Given the broad ranges of orbital parameters indicated by the Monte Carlo simulations performed in Esposito et al. (2013) assuming circular orbits (see their Fig. 8), we find that the hypothesis of 4:2:1 mean motion resonance for the three outer planets produces the best-fitting solution to the data. This result agrees with previous analyses (Fabrycky & Murray-Clay 2010; Goździewski & Migaszewski 2009, 2014; Reidemeister et al. 2009; Soummer et al. 2011). For planets d and e, our analysis favors a period ratio of 2:1 over 5:2. The analysis described in Pueyo et al. (2015) rules out a 2:1 mean motion resonance for the two outermost planets and favors a period ratio between 3:1 and 5:2. They find that a 2:1 period ratio for planets c and d is still favored. Finally, Pueyo et al. (2015) suggest that the most likely period ratio for planets d and e would be 3:2, but cannot rule out a value of 2:1. We tested the hypothesis of 3:2 period ratio for planets d and e assuming circular and non-coplanar orbits and found that it cannot be excluded given our dataset, although it would induce an orbit for planet e that is strongly misaligned (i ~ 45° and Ω ~ 149°) with respect to the orbit of planet d (i ~ 37° and Ω ~ + 58°, Table 5). The inclinations of planets d and e and the longitude of ascending node of planet e might be diminished toward values closer to those of planets b and c when relaxing the constraint of circular orbits.

8. Conclusions

In this paper, we presented the first reliable astrometric analysis of an exoplanetary system which was observed in the context of LEECH, the high-contrast imaging survey to search for and characterize young and adolescent exoplanets in L′ band using LBTI/LMIRCam. To achieve this, we first performed the astrometric calibration of the LMIRCam camera using the Θ1 Ori C field. We characterized the distortion of this new instrument and refined the estimates of platescale and true north with respect to previous works, which did not account for the distortion effects. Applying the results of this analysis to HR 8799 data obtained in October 2013, we were able to further constrain the orbit of HR 8799 e, based on the previous analysis described in Esposito et al. (2013), who used data covering only a 2.3-yr baseline between mid 2009 and late 2011. In particular, the new measurements favor an orbital model with all planets in multiple double Laplace resonance, assuming circular and non-coplanar orbits. Our results agree with the recent models of Goździewski & Migaszewski (2014), who assume quasi-coplanar and eccentric orbits. Astrometric monitoring in the coming years with the current and new-generation high-contrast imaging instruments will improve the time baseline even more and maybe confirm these conclusions.

We also presented deep constraints on a putative fifth planet inside the known planets. We were able to rule out a planet slightly brighter or more massive than HR 8799 b at the location of the 2:1 mean motion resonance with HR 8799 e and a planet twice as bright as HR 8799 cde at the location of the 3:1 mean motion resonance with HR 8799 e. However, Goździewski & Migaszewski (2014) predict that this fifth planet is less massive or luminous than planet b in the first case and has a mass inferior to 8 MJ in the second case. The corresponding physical separations (~7–9 AU) translate into angular separations of ~0.20–0.25′′. Detecting a faint planet at these very short separations could be challenging in the coming years, even with the new generation of high-contrast imaging instruments on 8–10-m telescopes (SPHERE, GPI, SCExAO+CHARIS).

One of the most significant errors in current astrometric measurements from high-contrast imaging is the estimation of the star center in saturated or coronagraphic images. This is also the case for our LBTI/LMIRCam measurements, because of the saturation of the star. This error could be reduced using the adaptive secondary mirror to create several faint replica of the star at a given separation in the field of view in order to accurately derive the star center (Marois et al. 2006b; Sivaramakrishnan & Oppenheimer 2006). The use of star replica for estimating the center of coronagraphic or saturated images is employed in the new high-contrast imaging instruments SPHERE (Beuzit et al. 2012; Zurlo et al. 2014; Mesa et al. 2015) and GPI (Macintosh et al. 2014). On-sky tests are foreseen in the coming months to implement this technique for the LEECH observations.

Finally, for astrometric analyses based on data with high signal-to-noise ratios, we outlined that if the error budget related to the instrument (uncertainties on platescale, true north, and distortion) and to the estimation of the star center are reduced to levels of about 1–2 mas, the errors on the stellar positions in standard astrometric fields are no longer negligible. The main source of the latter errors are the differential proper motions of the stars between the epoch of the reference data (typically Hubble Space Telescope data) and the epoch of the science observations to be calibrated. It would be very useful to define a common set of reliable astrometric calibrators to be used for the ongoing or upcoming high-contrast imaging surveys (P1640, LMIRCam, GPI, SPHERE, MagAO), to improve the accuracy of analyses based on combinations of datasets. We note that the Gaia all-sky survey will contribute significantly to providing good astrometric calibrators in the coming years.

2

As recently discussed in Mawet et al. (2014), the confidence level associated to a given σ threshold decreases when the separation decreases owing to the small sample statistics of the noise realizations. For the separation range considered in this work (≳2 λ/D), it is superior to the confidence level corresponding to a 3σ Gaussian threshold.

4

We note that the atmospheric properties (presence/absence of clouds, metallicity) also affect an object’s luminosity, but the effect is less significant with respect to the choice of initial conditions (initial entropy).

5

The entropy value of 9 kB/baryon refers to the predictions of Spiegel & Burrows (2012). To obtain this value, we decreased the value predicted by Marleau & Cumming (2014) by an offset of 0.45 kB/baryon. This offset stems from different assumptions for the equation of state between the predictions of Spiegel & Burrows (2012) and Marleau & Cumming (2014, see for details).

6

Nevertheless, as noted by Pueyo et al. (2015), these biases could be included in the Markov Chain Monte Carlo state vectors.

Acknowledgments

We thank the referee for a detailed and constructive report that helped to improve the manuscript. We thank Thayne Currie and Gabriel-Dominique Marleau for useful comments. A.-L.M. thanks Arthur Vigan for helping on distortion correction and Dimitri Mawet for discussions on contrast estimation at small separations. A.-L.M., S.D., R.G., R.U.C., and D.M. acknowledge support from the “Progetti Premiali” funding scheme of the Italian Ministry of Education, University, and Research. Support for A.J.S. provided by the National Aeronautics and Space Administration through Hubble Fellowship grant HST-HF2-51349 awarded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., for NASA, under contract NAS 5-26555. E.B. was supported by the Swiss National Science Foundation (SNSF). The research of J.E.S. was supported in part by an appointment to the NASA Postdoctoral Program at NASA Ames Research Center, administered by Oak Ridge Associated Universities through a contract with NASA. LEECH is funded by the NASA Origins of Solar Systems Program, grant NNX13AJ17G. The Large Binocular Telescope Interferometer is funded by NASA as part of its Exoplanet Exploration program. LMIRCam is funded by the National Science Foundation through grant NSF AST-0705296.

References

  1. Allard, F., Homeier, D., Freytag, B., & Sharp, C. M. 2012, in EAS Pub. Ser. 57, eds. C. Reylé, C. Charbonnel, & M. Schultheis, 3 [Google Scholar]
  2. Amara, A., & Quanz, S. P. 2012, MNRAS, 427, 948 [NASA ADS] [CrossRef] [Google Scholar]
  3. Augereau, J.-C., Nelson, R. P., Lagrange, A.-M., Papaloizou, J. C. B., & Mouillet, D. 2001, A&A, 370, 447 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Bailey, V., Meshkat, T., Reiter, M., et al. 2014, ApJ, 780, L4 [Google Scholar]
  5. Baines, E. K., White, R. J., Huber, D., et al. 2012, ApJ, 761, 57 [NASA ADS] [CrossRef] [Google Scholar]
  6. Baraffe, I., Chabrier, G., Barman, T. S., Allard, F., & Hauschildt, P. H. 2003, A&A, 402, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Barman, T. S., Macintosh, B., Konopacky, Q. M., & Marois, C. 2011, ApJ, 733, 65 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bergfors, C., Brandner, W., Janson, M., Köhler, R., & Henning, T. 2011, A&A, 528, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Beuzit, J.-L., Feldt, M., Mouillet, D., et al. 2012, in SPIE Conf. Ser. 8446, eds. I. S. McLean, S. K. Ramsay, & H. Takami [Google Scholar]
  10. Boden, A. F., Sargent, A. I., Akeson, R. L., et al. 2005, ApJ, 635, 442 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bonnefoy, M., Lagrange, A.-M., Boccaletti, A., et al. 2011, A&A, 528, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Bonnefoy, M., Currie, T., Marleau, G.-D., et al. 2014a, A&A, 562, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Bonnefoy, M., Marleau, G.-D., Galicher, R., et al. 2014b, A&A, 567, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Bowler, B. P., Liu, M. C., Dupuy, T. J., & Cushing, M. C. 2010, ApJ, 723, 850 [NASA ADS] [CrossRef] [Google Scholar]
  15. Burrows, A., Marley, M., Hubbard, W. B., et al. 1997, ApJ, 491, 856 [NASA ADS] [CrossRef] [Google Scholar]
  16. Chabrier, G., Baraffe, I., Allard, F., & Hauschildt, P. 2000, ApJ, 542, 464 [NASA ADS] [CrossRef] [Google Scholar]
  17. Chauvin, G., Lagrange, A.-M., Dumas, C., et al. 2005, A&A, 438, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Chauvin, G., Lagrange, A.-M., Beust, H., et al. 2012, A&A, 542, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Close, L. M., Lenzen, R., Guirado, J. C., et al. 2005, Nature, 433, 286 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  20. Close, L. M., Puglisi, A., Males, J. R., et al. 2012, ApJ, 749, 180 [NASA ADS] [CrossRef] [Google Scholar]
  21. Close, L., Males, J., Morzinski, K., et al. 2013, in Proc. Third AO4ELT Conf., eds. S. Esposito, & L. Fini, 91 [Google Scholar]
  22. Crepp, J. R., Johnson, J. A., Fischer, D. A., et al. 2012, ApJ, 751, 97 [NASA ADS] [CrossRef] [Google Scholar]
  23. Currie, T., Burrows, A., Itoh, Y., et al. 2011, ApJ, 729, 128 [NASA ADS] [CrossRef] [Google Scholar]
  24. Currie, T., Fukagawa, M., Thalmann, C., Matsumura, S., & Plavchan, P. 2012, ApJ, 755, L34 [NASA ADS] [CrossRef] [Google Scholar]
  25. Currie, T., Burrows, A., Girard, J. H., et al. 2014, ApJ, 795, 133 [NASA ADS] [CrossRef] [Google Scholar]
  26. Esposito, S., Riccardi, A., Fini, L., et al. 2010, in SPIE Conf. Ser., 7736, 09 [Google Scholar]
  27. Esposito, S., Mesa, D., Skemer, A., et al. 2013, A&A, 549, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Fabrycky, D. C., & Murray-Clay, R. A. 2010, ApJ, 710, 1408 [NASA ADS] [CrossRef] [Google Scholar]
  29. Fukagawa, M., Itoh, Y., Tamura, M., et al. 2009, ApJ, 696, L1 [Google Scholar]
  30. Galicher, R., Marois, C., Macintosh, B., Barman, T., & Konopacky, Q. 2011, ApJ, 739, L41 [Google Scholar]
  31. Galicher, R., Marois, C., Zuckerman, B., & Macintosh, B. 2013, ApJ, 769, 42 [Google Scholar]
  32. Goździewski, K., & Migaszewski, C. 2009, MNRAS, 397, L16 [NASA ADS] [CrossRef] [Google Scholar]
  33. Goździewski, K., & Migaszewski, C. 2014, MNRAS, 440, 3140 [NASA ADS] [CrossRef] [Google Scholar]
  34. Gray, R. O., & Corbally, C. J. 2014, AJ, 147, 80 [NASA ADS] [CrossRef] [Google Scholar]
  35. Gray, R. O., & Kaye, A. B. 1999, AJ, 118, 2993 [NASA ADS] [CrossRef] [Google Scholar]
  36. Hinkley, S., Oppenheimer, B. R., Zimmerman, N., et al. 2011, PASP, 123, 74 [NASA ADS] [CrossRef] [Google Scholar]
  37. Hinz, P. M., Bippert-Plymate, T., Breuninger, A., et al. 2008, in SPIE Conf. Ser., 7013 [Google Scholar]
  38. Hinz, P. M., Rodigas, T. J., Kenworthy, M. A., et al. 2010, ApJ, 716, 417 [NASA ADS] [CrossRef] [Google Scholar]
  39. Ingraham, P., Marley, M. S., Saumon, D., et al. 2014, ApJ, 794, L15 [NASA ADS] [CrossRef] [Google Scholar]
  40. Kalas, P., Graham, J. R., & Clampin, M. 2005, Nature, 435, 1067 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  41. Kalas, P., Graham, J. R., Chiang, E., et al. 2008, Science, 322, 1345 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  42. Kalas, P., Graham, J. R., Fitzgerald, M. P., & Clampin, M. 2013, ApJ, 775, 56 [NASA ADS] [CrossRef] [Google Scholar]
  43. Kuzuhara, M., Tamura, M., Kudo, T., et al. 2013, ApJ, 774, 11 [NASA ADS] [CrossRef] [Google Scholar]
  44. Lafrenière, D., Marois, C., Doyon, R., & Barman, T. 2009, ApJ, 694, L148 [NASA ADS] [CrossRef] [Google Scholar]
  45. Lafrenière, D., Jayawardhana, R., & van Kerkwijk, M. H. 2010, ApJ, 719, 497 [NASA ADS] [CrossRef] [Google Scholar]
  46. Lagrange, A.-M., Gratadour, D., Chauvin, G., et al. 2009, A&A, 493, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Lagrange, A.-M., Bonnefoy, M., Chauvin, G., et al. 2010, Science, 329, 57 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  48. Leisenring, J. M., Skrutskie, M. F., Hinz, P. M., et al. 2012, in SPIE Conf. Ser., 8446 [Google Scholar]
  49. Macintosh, B., Graham, J. R., Ingraham, P., et al. 2014, Proc. Nat. Acad. Sci., 111, 12661 [Google Scholar]
  50. Madhusudhan, N., Burrows, A., & Currie, T. 2011, ApJ, 737, 34 [Google Scholar]
  51. Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [Google Scholar]
  52. Marleau, G.-D., & Cumming, A. 2014, MNRAS, 437, 1378 [NASA ADS] [CrossRef] [Google Scholar]
  53. Marley, M. S., Fortney, J. J., Hubickyj, O., Bodenheimer, P., & Lissauer, J. 2007, ApJ, 655, 541 [NASA ADS] [CrossRef] [Google Scholar]
  54. Marois, C., Lafrenière, D., Doyon, R., Macintosh, B., & Nadeau, D. 2006a, ApJ, 641, 556 [Google Scholar]
  55. Marois, C., Lafrenière, D., Macintosh, B., & Doyon, R. 2006b, ApJ, 647, 612 [NASA ADS] [CrossRef] [Google Scholar]
  56. Marois, C., Macintosh, B., Barman, T., et al. 2008, Science, 322, 1348 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  57. Marois, C., Macintosh, B., & Véran, J.-P. 2010a, in SPIE Conf. Ser. 7736, eds. B. L. Ellerbroek, M. Hart, N. Hubin, & P. L. Wizinowich [Google Scholar]
  58. Marois, C., Zuckerman, B., Konopacky, Q., Macintosh, B., & Barman, T. 2010b, Nature, 468, 1080 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  59. Matthews, B. C., Kennedy, G., Sibthorpe, B., et al. 2014a, ApJ, 780, 97 [NASA ADS] [CrossRef] [Google Scholar]
  60. Matthews, C. T., Crepp, J. R., Skemer, A., et al. 2014b, ApJ, 783, L25 [NASA ADS] [CrossRef] [Google Scholar]
  61. Mawet, D., Milli, J., Wahhaj, Z., et al. 2014, ApJ, 792, 97 [NASA ADS] [CrossRef] [Google Scholar]
  62. Mesa, D., Gratton, R., Zurol, A. et al. 2015, A&A, in press, DOI: 10.1051/0004-6361/201423910 [Google Scholar]
  63. Metchev, S., Marois, C., & Zuckerman, B. 2009, ApJ, 705, L204 [NASA ADS] [CrossRef] [Google Scholar]
  64. Moro-Martín, A., Rieke, G. H., & Su, K. Y. L. 2010, ApJ, 721, L199 [NASA ADS] [CrossRef] [Google Scholar]
  65. Mouillet, D., Larwood, J. D., Papaloizou, J. C. B., & Lagrange, A.-M. 1997, MNRAS, 292, 896 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  66. Ozernoy, L. M., Gorkavyi, N. N., Mather, J. C., & Taidakova, T. A. 2000, ApJ, 537, L147 [NASA ADS] [CrossRef] [Google Scholar]
  67. Pueyo, L., Soummer, R., Hoffmann, J., et al. 2015, ApJ, 803, 31 [NASA ADS] [CrossRef] [Google Scholar]
  68. Rameau, J., Chauvin, G., Lagrange, A.-M., et al. 2013, ApJ, 772, L15 [NASA ADS] [CrossRef] [Google Scholar]
  69. Reidemeister, M., Krivov, A. V., Schmidt, T. O. B., et al. 2009, A&A, 503, 247 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Ricci, L., Robberto, M., & Soderblom, D. R. 2008, AJ, 136, 2136 [NASA ADS] [CrossRef] [Google Scholar]
  71. Sivaramakrishnan, A., & Oppenheimer, B. R. 2006, ApJ, 647, 620 [NASA ADS] [CrossRef] [Google Scholar]
  72. Skemer, A. J., Hinz, P. M., Esposito, S., et al. 2012, ApJ, 753, 14 [NASA ADS] [CrossRef] [Google Scholar]
  73. Skemer, A. J., Hinz, P., Esposito, S., et al. 2014a, in SPIE Conf. Ser., 9148 [Google Scholar]
  74. Skemer, A. J., Marley, M. S., Hinz, P. M., et al. 2014b, ApJ, 792, 17 [NASA ADS] [CrossRef] [Google Scholar]
  75. Skrutskie, M. F., Jones, T., Hinz, P., et al. 2010, in SPIE Conf. Ser., 7735 [Google Scholar]
  76. Sódor, Á., Chené, A.-N., De Cat, P., et al. 2014, A&A, 568, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Soummer, R., Brendan Hagan, J., Pueyo, L., et al. 2011, ApJ, 741, 55 [NASA ADS] [CrossRef] [Google Scholar]
  78. Soummer, R., Pueyo, L., & Larkin, J. 2012, ApJ, 755, L28 [NASA ADS] [CrossRef] [Google Scholar]
  79. Spiegel, D. S., & Burrows, A. 2012, ApJ, 745, 174 [NASA ADS] [CrossRef] [Google Scholar]
  80. Stetson, P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef] [Google Scholar]
  81. Su, K. Y. L., Rieke, G. H., Stapelfeldt, K. R., et al. 2009, ApJ, 705, 314 [NASA ADS] [CrossRef] [Google Scholar]
  82. Sudol, J. J., & Haghighipour, N. 2012, ApJ, 755, 38 [NASA ADS] [CrossRef] [Google Scholar]
  83. Tamura, M., & SEEDS Team 2010, in Proc. Conf. In the Spirit of Lyot 2010 [Google Scholar]
  84. van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  85. Wright, D. J., Chené, A.-N., De Cat, P., et al. 2011, ApJ, 728, L20 [NASA ADS] [CrossRef] [Google Scholar]
  86. Wyatt, M. C., Dermott, S. F., Telesco, C. M., et al. 1999, ApJ, 527, 918 [NASA ADS] [CrossRef] [Google Scholar]
  87. Zurlo, A., Vigan, A., Mesa, D., et al. 2014, A&A, 572, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

Appendix A: Distortion correction

A new distortion grid was installed in LMIRCam in late July 2014. The purpose of this grid is to measure the distortion effects of the camera, which are expected to be much more significant than the distortion induced by the telescope and the light combiner. The grid is formed of holes of diameter 381 ¯m regularly spaced by 838 ¯m (<6% accuracy) following a square pattern. The sampling of the grid spots in the images is ~48 pixels. In Table A.1, we give the coefficients of the polynomial laws used to correct for the measured distortion effects. The solution is accurate to ~0.1% on the separation at 1σ. We expect the distortion to be roughly constant with time, depending on the optical properties, so we use this distortion calibration for the HR 8799 data taken in October 2013. In the future, the distortion calibration will be regularly performed to monitor passive temporal variations due to, e.g., temperature variations. Assuming the position of the image center is (x0, y0), the distortion-corrected coordinates (x, y) are related to the raw coordinates (x′, y′) by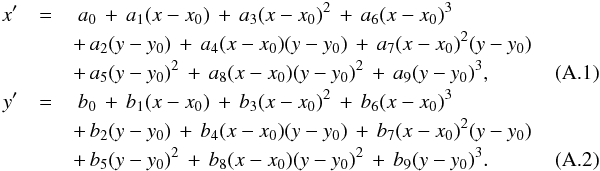

Table A.1

Coefficients of the distortion solution for the LMIRCam camera.

All Tables

Table 1

Log of the observations.

In the text
Table 2

Astrometric measurements of the HR 8799 planets with respect to the star at epoch 2013.81.

In the text
Table 3

1σ astrometric error budget (in mas) for the HR 8799 planets for both observations (see text).

In the text
Table 4

LBTI/LMIRCam relative and absolute photometry of the HR 8799 planets in L′ band.

In the text
Table 5

Orbital elements fitted on the astrometric data in Fig. 3.

In the text
Table A.1

Coefficients of the distortion solution for the LMIRCam camera.

In the text

All Figures

thumbnail Fig. 1

LMIRCam image in L′ band of the HR 8799 multiple-planet system. The field of view is ~4′′. The point-spread function is subtracted using our PCA pipeline (see text). The image is binned (2 × 2 binning). The intensity scale is linear.
In the text
thumbnail Fig. 2

5σ detection limits in L′ band for the LMIRCam data of HR 8799 expressed in contrast (left) and in planet mass (right), with the four planets shown (filled circles in the left panel and gray areas in the right panel). The positions of a putative fifth planet in resonance 3:1 and 2:1 with planet e according to the models of Goździewski & Migaszewski (2014) are also indicated (assuming a face-on and circular orbit). For the right plot, the detection limits are derived for an age of 30 Myr from the “hot-start” COND model (Baraffe et al. 2003) coupled to the atmosphere model BT-Settl (Allard et al. 2012) and the “warm-start” evolutionary+atmosphere model of Spiegel & Burrows (2012) for an initial entropy of 9 kB/baryon (see text). The range of masses for HR 8799 bcde is delimited by the predictions of the two evolutionary models assumed for deriving the detection limits (lower limit: BT-Settl+COND; upper limit: SB12 with initial entropy of 9 kB/baryon). The range of physical separations for the planets is computed using the errors on the planet separation and the star distance.
In the text
thumbnail Fig. 3

Relative astrometry of the HR 8799 planets for all the measurements available in the literature (small filled circles) and the measurements derived in this work (purple filled squares). The solid blue lines represent the orbital solution labeled “A” in Table 5. Red lines connect the predicted and observed positions for all the data points. The dotted line in the panel for HR 8799 e indicates the orbital solution labeled “B” in Table 5. The orange circles indicate the ephemeris predicted in Goździewski & Migaszewski (2014).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.