| Issue |
A&A
Volume 576, April 2015
|
|
|---|---|---|
| Article Number | A61 | |
| Number of page(s) | 12 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201425124 | |
| Published online | 27 March 2015 | |
XMMFITCAT: The XMM-Newton spectral-fit database⋆
1
IAASARS, National Observatory of Athens, 15236
Penteli, Greece
e-mail: acorral@noa.gr
2
Department of Physics & Astronomy, University of
Leicester, Leicester,
LE1 7RH,
UK
3
Institut de Recherche en Astrophysique et Planétologie
(IRAP), 9 Avenue du Colonel
Roche, 31028
Toulouse Cedex 4,
France
Received: 8 October 2014
Accepted: 2 December 2014
The XMM-Newton spectral-fit database (XMMFITCAT) is a catalogue of spectral fitting results for the source detections within the XMM-Newton serendipitous source catalogue with more than 50 net (background-subtracted) counts per detector in the 0.5–10 keV energy band. Its most recent version, constructed from the latest version of the XMM-Newton catalogue, the 3XMM Data Release 4 (3XMM-DR4), contains spectral-fitting results for ≳114 000 detections, corresponding to ≃78 000 unique sources. Three energy bands are defined and used in the construction of XMMFITCAT: Soft (0.5–2 keV), Hard (2–10 keV), and Full (0.5–10 keV) bands. Six spectral models, three simple and three more complex models, were implemented and applied to the spectral data. Simple models are applied to all sources, whereas complex models are applied to observations with more than 500 counts (30%). XMMFITCAT includes best-fit parameters and errors, fluxes, and goodness of fit estimates for all fitted models. XMMFITCAT has been conceived to provide the astronomical community with a tool to construct large and representative samples of X-ray sources by allowing source selection according to spectral properties, as well as characterise the X-ray properties of samples selected in different wavelengths. We present in this paper the main details of the construction of this database, and summarise its main characteristics.
Key words: X-rays: general / catalogs / surveys
© ESO, 2015
1. Introduction
X-rays observations have expanded our knowledge of the most energetic phenomena in the Universe, and the astronomical sources in which they take place, such as stars, galaxies, clusters, and active galactic nuclei (AGN). Besides, and thanks to their penetrating ability, X-ray observations detect sources hidden behind large amount of gas, and up to high distances. Serendipitous X-ray surveys conducted by the XMM-Newton1 and Chandra2 observatories, have almost completely resolved the X-ray cosmic background (CXB) below 10 keV, showing that the X-ray sky is dominated by AGN emission (Gilli et al. 2007; Treister et al. 2009).
Thanks to its large collecting area and its large field of view, XMM-Newton has proven to be an extraordinary instrument to perform X-ray surveys. The European Photon Imaging Camera (EPIC3) on-board XMM-Newton works in a photon-counting mode. This characteristic, along with its large effective area, allows us, from a single observation, to extract images, light curves, and spectral data not only for the proposed target, but also for many of the detected sources within the field of view. Data from this camera have been used to construct the largest catalogue of X-ray sources ever built, the XMM-Newton serendipitous source catalogue. The latest version of the XMM-Newton catalogue, 3XMM Data Release 4 (3XMM-DR44), contains high-quality photometric information for more than 500 000 source detections, and light curves and spectral data for more than 120 000 of them.
The XMM-Newton spectral-fit database is an ESA funded project aimed to provide the astronomical community with a tool to construct large and representative samples of X-ray sources according to their spectral properties. To this end, the database is built from the spectral data within the XMM-Newton catalogue, which are then used to produce a new catalogue composed of X-ray spectral fitting results.
2. The XMM-Newton serendipitous source catalogue
The 3XMM-DR4 source catalogue is the largest catalogue of X-ray sources compiled to date (see Rosen et al., in prep., and Watson et al. 2009). It derives from 7427 pointed X-ray observations, covering ~2% of the sky, taken with the EPIC camera pn and MOS instruments on board the XMM-Newton satellite. The 3XMM-DR4 catalogue, which contains more than 500 000 detections from ~372 000 unique X-ray sources, was produced by the XMM-Newton Survey Science Centre (SSC5) (Watson et al. 2001) on behalf of ESA.
2.1. Catalogue production
Only data from the three EPIC (pn, MOS-1 and MOS-2) instruments are used in the 3XMM-DR4 catalogue. These instruments operate in photon-counting mode such that, from a single observation, spectra and time series can be extracted from every source detected in the observed field of view. During routine pipeline processing of the XMM-Newton EPIC data, photometric measurements are obtained for every detected source in a number of distinct energy bands over the 0.2–12 keV range (see Watson et al. 2009). In parallel, for brighter sources (>100 counts, summed over all 3 instruments), spectra and time series are extracted.
The 3XMM-DR4 catalogue reflects both an increased number of detections, due to the increased (3.2 yr) observation baseline since its predecessor, 2XMMi-DR3, and improvements to the processing system and calibration information. The number of public observations contained in 3XMM-DR4 increased by ~50% relative to 2XMMi-DR3. At the same time, the science data processing has taken advantage of significant improvements within the XMM-Newton Science Analysis Software (SAS) and calibration data. The key science-driven gains include:
-
improved source characterisation and reduced spurious source detections;
-
improved astrometric precision of sources;
-
greater net sensitivity for source detection;
-
extraction of spectra and time series for fainter sources, with improved signal-to-noise ratio (SNR).
The resulting catalogue contains spectra for more than 120 000 detections corresponding to ~80 000 unique sources.
2.2. Spectral extraction
The pipeline processing automatically extracts spectra and time series (source-specific products, SSPs), from suitable exposures, for detections that meet certain brightness criteria.
In previous versions of the processing pipeline, extractions were attempted for any source which had at least 500 EPIC counts. In such cases, source data were extracted from a circular aperture of fixed radius (28 arcsec), centred on the detection position, while background data were accumulated from a co-centred annular region with inner and outer radii of 60 and 180 arcsec, respectively. Other sources that lay within or overlapped the background region were masked during the processing. In most cases this process worked well. However, in some cases, especially when extracting SSPs from sources within the small central window of MOS Small-Window mode observations, the background region could comprise very little usable background, with the bulk of the region lying in the gap between the central CCD and the peripheral ones. This resulted in very small (or even zero) areas for background rate scaling during background subtraction, often leading to incorrect background subtraction during the analysis of spectra in Xspec6, the standard package for X-ray spectral analysis.
For the bulk reprocessing leading to 3XMM-DR4, two new approaches have been adopted and implemented in the pipeline.
-
1.
The extraction of data for the source takes place from an aperture whose radius is chosen to maximise the signal-to-noise (SNR) of the source data. This is achieved by a curve-of-growth analysis, performed by the SAS task, eregionanalyse. This is especially useful for fainter sources where the relative background level is high.
-
2.
To address the problem of locating an adequately filled background region for each source, the centre of a circular background aperture of radius, rb = 168 arcsec (comparable area to the previously used annulus) is stepped around the source along a circle centred on the source position. Up to 40 uniformly spaced azimuthal trials are tested along each circle. A suitable background region is found if, after masking out other contaminating sources and allowing for empty regions, a filling factor of at least 70% usable area remains. If no background trial along a given circle yields sufficient residual background area, the aperture is moved out to a circle of larger radius and the azimuthal trials are repeated. The smallest trial circle has a radius of rc = rb + 60 arcsec so that the inner edge of the background region is at least 60 arcsec from the source centre – for the case of MOS Small-Window mode, the smallest test circle for a source in the central CCD is set to a radius that already lies on the peripheral CCDs. Other than for the MOS Small-Window cases, a further constraint is that, ideally, the background region should lie on the same instrument CCD as the source.
If no solution is found with at least a 70% filling factor, the background trial with the largest filling factor is adopted.
For the vast majority of detections where SSP extraction is attempted, this process obtains a solution in the first radial step, and a strong bias to early azimuthal steps, i.e. in most cases an acceptable solution is found very rapidly. For detections in the MOS instruments, about 1.7% lie in the central window in Small-Window mode and have a background region located on the peripheral CCDs. Importantly, in contrast to earlier pipelines, this process always yields a usable background spectrum for objects in the central window of MOS Small-Window mode observations.
In addition, the current pipeline permits extraction of SSPs for fainter sources. Extraction is considered for any detection with at least 100 EPIC source counts in the full catalogue band (0.2–12 keV), instead of the 500 EPIC counts limit used in the previous pipeline. Where this condition is met, spectra and time series are extracted. For a more detailed description of the 3XMM-DR4 catalogue production consult the catalogue’s user guide7. Catalogue spectra and time series can be retrieved from the XMM-Newton Science Archive (XSA8), as well as from the web services listed at the end of Sect. 4.
3. The XMM-Newton spectral-fit database
The XMM-Newton spectral-fit database is a project aimed to take advantage of the great wealth of data and information contained within the XMM-Newton serendipitous source catalogue to construct a database composed of spectral-fitting results. The possible applications of this database include: the construction of large and representative samples of X-ray sources according to spectral properties; the possibility of pinpoint sources with interesting spectral properties; and the cross-correlation with samples selected in other wavelengths so as to obtain a first-order description of the sources X-ray spectral-properties.
3.1. Automated spectral fitting
The XMM-Newton spectral-fit database (XMMFITCAT) is constructed by using automated spectral fits applied to the pipeline extracted spectra within the 3XMM-DR4 catalogue. The software used to perform the spectral fits was Xspec v12.7 (Arnaud 1996). In the case of multiple observations available for the same source, each observation is fitted separately. The fitting scripts were designed to jointly fit all the available spectra for the same source detection. As a result, the database contains spectral-fitting results for each source observation, not for each observed source.
The data used in the construction of the database are spectral data (source and background spectra), as well as ancillary matrices, retrieved from the 3XMM-DR4 catalogue products. Redistribution matrices are the canned matrices provided by the XMM-Newton SOC (Science Operations Centre).
The spectral-fitting pipeline is composed of tcl (Tool Command Language), and Perl scripts. The default fitting algorithm that Xspec uses to find the best-fit values for each model parameter is a modified Levenberg-Marquardt algorithm. This default algorithm is the one used in the construction of the database so as to optimise the fitting speed. However, this algorithm is local rather than global, so it is possible for the fitting process not to find the global best-fit, but a local minimum. To prevent this, the scripts include an optimisation algorithm that tries to avoid the fit to fall into a local minimum by computing the errors on all variable parameters at the 95% confidence level. If a better fit is found, the optimisation algorithm starts again. In the case non-monotonicity is detected during the error computation, the confidence level in the error computation is increased until a better minimum is found. Once the best-fit is found, errors are computed and reported within the database at the 90% confidence level.
Energy bands.
The energy bands used in the automated fits are listed in Table 1. As a comparison, the energy bands used in the construction of the 3XMM-DR4 catalogue are also listed in the same table.
3.2. Spectral data selection
Cash statistics, implemented as C-stat in Xspec, are used to fit the data. This statistic was selected, instead of the more commonly used χ2 statistic, to optimise the spectral fitting in the case of low count spectra. The 3XMM-DR4 spectra are unbinned and then binned to 1 count/bin. The combined use of spectra binned to 1 count/bin plus C-stat fitting has been proven to work very well when fitting spectral data down to 40 counts (Krumpe et al. 2008).
During the spectral fits, all variable parameters for different instruments and exposures are tied together except for a relative normalisation, which accounts for the differences between different flux calibrations. Given that each additional instrument spectrum adds a new parameter to the fit, and to ensure a minimum quality on the spectral fits, a lower limit on the number of counts in each individual spectrum is imposed: only spectra corresponding to a single EPIC instrument, with more than 50 source counts in the Full band are included in the spectral fits. Note that this implies that not all available spectra within 3XMM-DR4 for a given observation are used in some cases. A table listing the spectra used for each source observation is also publicly available, along with the one containing the spectral fitting results, at the database’s webpage (see Sect. 4).
3.3. Spectral models
 |
Fig. 1 Examples of spectral-fitting results for the models (from top to bottom and left to right): absorbed power-law model; absorbed thermal model; absorbed black-body model; thermal plus power-law model; double power-law model; and black-body plus power-law model. |
Three simple, and three more complex models have been implemented. All these models are applied to the spectral data if the following conditions are fulfilled:
-
simple models: total number of counts (all instruments added together) larger than 50 counts in the energy band under consideration;
-
complex models: total number of counts larger than 500 counts in the Full band.
The models are selected to represent the most commonly observed spectral shapes in astronomical sources in a phenomenological way. The preferred model (among the implemented ones) for each observation is selected according to the goodness of each fit (see Sect. 3.5), but spectral-fitting results for all the models applied are included in the database. It is important to note that the automated procedure is only intended to obtain a good representation of the spectral shape so, given the limited number of spectral models applied, the preferred model should not be interpreted as a “best-fit model” in the way it is when carrying out manual fits.
The simple models (models 1 to 3), and the more complex models (models 4 to 6) are:
-
1.
Absorbed power-law model ( wabs*pow in Xspec notation): a power-law model modified by photoelectric absorption.
-
2.
Absorbed thermal model (wabs*mekal): a thermal model modified by photoelectric absorption.
-
3.
Absorbed black-body model (wabs*bb): a photoelectrically absorbed black-body model.
-
4.
Absorbed power-law model plus thermal model (wabs(mekal+wabs*pow)): a thermal plus a power-law model in which both components are modified by absorption, and the power-law is additionally absorbed.
-
5.
Double power-law model (wabs*(pow+wabs*pow)): a double power-law model, with different photon indices, modify by photoelectric absorption, and additional absorption only affecting one of the power-law components.
-
6.
Black-body plus power-law model (wabs*(bb+pow)): a black-body plus a power-law component modified by photoelectric absorption.
A component is considered not-significant in a complex-model fit if its corresponding normalisation is consistent with zero at the 90% confidence level. In those cases, spectral-fitting results for that model are not included in the database. Plots corresponding to each of the implemented models are shown in Fig. 1. Each model and its corresponding spectral-fitting process are described in Sects. 3.3.1 to 3.3.6. Parameters and allowed ranges for them that are not described in these sections are set to their Xspec default values. The initial value and allowed range of values for the column density for all absorption components (wabs) is the same for all simple models: initial value NH = 1021 cm-2; allowed range: 1020 to 1024 cm-2.
As part of the spectral fits, errors are computed at the 90% confidence level for every variable parameter. If Xspec cannot constrain the value of a certain parameter, i.e. the error computation pegs at the lower and upper limits of the allowed range, the parameter is fixed. Fixed values are not the same for all observations, but they are computed during each spectral fit (see below), and they depend on the spectral model, energy band, and data quality.
3.3.1. Absorbed power-law model
A power-law component is the most common spectral shape displayed by X-ray sources, including active galactic nuclei (AGN, the most abundant X-ray sources), and X-ray binaries. This model is applied in the Full, Soft, and Hard bands to get a first-order characterisation of the full spectral shape. Besides, a simple absorbed power-law model is found to be a good representation of most low to medium quality AGN spectra. The variable parameters of the model are the column density of the absorption component, and the photon index (initial value Γ = 2; range: 0–4), and normalisation of the power-law component.
The first step of the spectral fit for this model in the Full band is to compute the photon index in the Hard band without including absorption. The resulting value is the one used to fix the photon index of the model if it cannot be constrained. Sometimes the number of counts above 2 keV is <20 counts, and this value cannot be computed. In those cases, the fixed value is the initial value, Γ = 2. If the parameter that cannot be constrained is the column density, its fixed value is the one obtained by carrying out the spectral fit in the Soft band with Γ fixed to the value obtained in the Hard band. If the number of counts below 2 keV is <20 counts, the fixed value is NH = 1022 cm-2. This is a reasonable approximation since spectra with >50 counts in the Full band but <20 counts below 2 keV are most likely absorbed by column densities above that value.
The fixed values for the photon index and the column density when fitting in the Soft and Hard bands are Γ = 2 and NH = 1022 cm-2, respectively. We adopted these values because it is very difficult to constrain both the photon index and the column density in the Soft band in the case of low-count spectra, and the spectral fit is insensitive to column densities below that value in the Hard band. The spectral-fitting results of this model applied in these narrow bands are used as initial parameters and fixed values in the complex models.
3.3.2. Absorbed thermal model
The absorbed thermal model is applied in the Full and Soft bands. It is intended to model emission from stars, galaxies, and galaxy clusters. The Xspec mekal model is used, instead of the more up to date apec model, to maximise the fitting speed. The only variable parameters are the column density of the wabs component, the plasma temperature of the mekal component (initial value kT = 0.5 keV; range: 0.08–20 keV), and its normalisation. As a consequence, this model is not always an acceptable fit for these kind of sources, but it is better, in terms of goodness (see Sect. 3.5), than a power-law model in most cases.
Similarly to the absorbed power-law model fit, the plasma temperature is computed by removing the absorption component and fitting this simple thermal model in the Soft band. The resulting temperature is the one used to fix this parameter in the case it cannot be constrained. In the case the number of counts in the Soft band is <20 counts, a value of kT = 1 keV is used instead. The fixed value used in case the column density cannot be constrained is NH = 1020 cm-2 in all cases.
The spectral-fitting results of this model applied in the Soft band are the ones used in the complex model: mekal plus power-law model.
3.3.3. Absorbed black-body model
This model is only applied in the Soft band to model, for example, soft emission in AGN, X-ray binaries, and supersoft novae. The variable parameters are the column density of the wabs component, and the black-body temperature (initial value kT: 0.5 keV; range: 0.01–10 keV), and its normalisation.
The spectral fitting of this model is carried out in the same way as the absorbed thermal model. The only difference in this case is that the fixed value of the temperature in the case of low number of counts is kT = 0.1 keV.
The spectral-fitting results of this model are used as input parameters and fixed values in the black-body plus power-law model fit.
3.3.4. Absorbed thermal plus power-law model
This model includes two absorption components: one affecting both the thermal, and power-law components; and a second one only affecting the power law component. In the case of AGN for example, this model could represent the host-galaxy soft emission (thermal component), and the more absorbed intrinsic AGN emission (power-law component), although it could also model appropriately emission from X-ray binaries.
The initial parameters are extracted from the absorbed thermal model fitting in the Soft band, and the absorbed power-law model fitting in the Hard band. If the number of counts in either of those bands is lower than 50 counts and thus, either of these models has not been fitted, this complex model is not fitted either. Taking into account the limit of 500 counts to apply complex modes, it is reasonable to assume that spectra that lack enough counts in the Hard/Soft band do not need an additional power-law/thermal component to model the spectral shape.
3.3.5. Double power-law model
As the previous model, this model also includes two absorption components. The photon indices of the two power-law components are not fixed together so this model could represent several physical scenarios: an absorbed power-law plus a scattered component; a partial covering absorber affecting intrinsic power-law emission; and even a hard power-law plus a soft thermal component if the data at low energies are of low quality. In this case, the initial values and fixed parameters are extracted from the absorbed power-law model fittings in the Soft, and Hard bands. As for the previous model, if either of these fits has not been performed, this complex model fit is not carried out.
3.3.6. Absorbed black-body plus power-law model
In this case there is only one absorption component covering both the black-body and the power-law components. The black-body component is often used to phenomenologically represent soft emission in AGN, but it can also account for disk emission in X-ray binaries. The initial and fixed values for the parameters are extracted from the absorbed black-body model fit, and the absorbed power-law model fit in the Hard band.
3.4. Fluxes
For each model applied, the observed flux and its errors (at the 90% confidence level) are computed in the band used in the spectral fit. In the case of multiple instrument spectra being jointly fitted, the flux included in the database corresponds to the average of all available instruments and exposures for that observation. Fluxes and errors are reported in erg cm-2 s-1. In a small number of cases (<1%), Xspec fails to compute the errors on the fluxes. In those cases, only fluxes values are reported in the database.
A direct comparison between fluxes reported in this database and within the 3XMM-DR4 catalogue is not possible for all energy bands (see Table 1), but only in the database Soft band. The observed fluxes in the Soft band obtained from the automated fits are plotted against the one reported in 3XMM-DR4 in Fig. 2. Values in both catalogues agree in 70% of cases. Significant differences between both values correspond to one of the following preferred models: black-body or thermal model; and power-law models with steep photon indices. The larger number of consistent fluxes below the on-to-one line is due to larger errors in the XMMFITCAT fluxes computed in the Soft band, sometimes consistent with zero at the 90% confidence level.
 |
Fig. 2 Observed fluxes in the Soft band (in erg cm-2 s-1) from the automated fits against the ones reported in the 3XMM-DR4 catalogue. Filled circles correspond to consistent fluxes between both catalogues, whereas small points correspond to non-consistent ones. Square points with error bars represent average error sizes at each flux interval. |
3.5. Goodness of fit
C-stat does not provide goodness of fit. As an estimate, the Xspec command goodness is used. This command performs a number of simulations, 1000 simulations in the case of this database, and returns the percentage of simulations that gives a lower value of the statistic. For large return values of this command, the model can be rejected at the goodness value confidence level.
As another proxy of the goodness of fit, the reduced χ2 value, after C-stat fitting, is also computed and included in the database. There is not direct correspondence between goodness and reduced χ2 values computed this way, although low goodness values (<50%) correspond to low reduced χ2 values (<1.5) in 97% of cases. As it is implemented in Xspec, C-stat/d.o.f values tend to reduced χ2 values for large number of counts. However, most observations (80%) within the 3XMM-DR4 catalogue have <1000 counts. A conservative approach is adopted in the database to decide if a spectral-fit is an acceptable fit or not. Instead of using the χ2 values from the C-stat fits, we used only the value of goodness. We consider a fit as an acceptable fit if the return value of goodness is lower than 50%. Although both estimates behave in a similar way, i.e. they are similarly “good” in separating acceptable from unacceptable fits, by using goodness a smaller number of unacceptable fits are included within our acceptable criteria (see Sect. A.1).
As a guide to the user, the simplest model applied in the Full band with the lowest value of goodness is considered as the preferred model for that observation. However, since both goodness and reduced χ2 values are provided within the database, the user could decide between both estimates to select the best-fit model.
4. Database overview
The final XMM-Newton spectral-fit database contains spectral-fitting
results for 114 166 observations, corresponding to 77 954 unique sources. Acceptable fits
are found for 90% of the observations with less than 500 counts (70% of all the
observations), whereas they are found for 80% of the observations with more than 500 counts.
This is a remarkable result given the limited number of spectral models used, and the
difficulty often found to obtain acceptable fits in the case of high number of counts even
in manual fits. The distribution of counts in the XMMFITCAT is shown in Fig. 3. The vertical line correspond to the limit of 500 counts
above which complex models are applied. The distribution of photon indices (excluding
detections for which it had to be fixed) for the sources best-fitted by an absorbed
power-law model is plotted in Fig. 4. As expected,
since most X-ray sources are likely AGN, the distribution is very similar to the one usually
obtained from X-ray analyses of AGN. We separated observations with fewer than 500, and more
than 500 counts and found and average 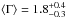 and a standard deviation of 0.64, and
and a standard deviation of 0.64, and
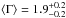 and a standard deviation of 0.54,
respectively. Both distributions are very similar, the lower value for the average
Γ for detections with
<500 counts likely due to
the higher tail towards lower photon index values.
and a standard deviation of 0.54,
respectively. Both distributions are very similar, the lower value for the average
Γ for detections with
<500 counts likely due to
the higher tail towards lower photon index values.
 |
Fig. 3 Distribution of net source counts per detection in XMMFITCAT. |
 |
Fig. 4 Photon index distribution for the XMMFITCAT detections for which an absorbed power-law model is the preferred model. Empty histogram corresponds to detections with <500 counts, and line-shaded histogram to detections with >500 counts. |
 |
Fig. 5 Hardness ratios from 3XMM-DR4 against best-fit parameters (photon index and column density) from XMMFITCAT. Left panel: high Galactic latitude sample (|b| > 20). Right panel: low Galactic latitude sample (|b| < 20). |
Hardness ratios (or X-colors) are used as a proxy of the spectral shape, and to estimate
the column density. Following the band numbering in Table 1, hardness ratios are defined within 3XMM-DR4 as:
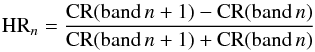 (1)where CR(band n) is the count rate in the
band number n. Therefore, a correlation is expected between hardness ratio values and
spectral parameters. To check the consistency between the results in 3XMM-DR4 and XMMFITCAT,
we compared the HR2+HR3 values from 3XMM-DR4, against the best-fit parameters from the
absorbed power-law fit in XMMFITCAT (see Fig. 5). As it
can be seen in Fig. 5, we find a very good agreement
between both catalogues.
(1)where CR(band n) is the count rate in the
band number n. Therefore, a correlation is expected between hardness ratio values and
spectral parameters. To check the consistency between the results in 3XMM-DR4 and XMMFITCAT,
we compared the HR2+HR3 values from 3XMM-DR4, against the best-fit parameters from the
absorbed power-law fit in XMMFITCAT (see Fig. 5). As it
can be seen in Fig. 5, we find a very good agreement
between both catalogues.
Less than 1% of the observations in XMMFITCAT are affected by Xspec errors. This means that these observations lack spectral fitting results for one or more, but not all, of the spectral models that were applied according to their spectral counts. These errors occur when the model is a very bad representation of the spectral shape and/or the allowed ranges for the parameters did not encompass the best-fit values. As a consequence, Xspec fails in finding a minimum and/or falls into an infinite loop.
More than 18% of the sources within XMMFITCAT have multiple observations with spectra available. This represents an incredible source of information for spectral variability studies, that are usually observationally expensive.
This database has been already been successfully used to devise a selection technique for highly absorbed AGN (Corral et al. 2014). That work was envisioned as a test of the capabilities of XMMFITCAT in constructing representative samples of different X-ray sources. We used the automated spectral-fitting results as a starting point from which to pinpoint candidate sources, and then confirmed their obscured nature by using manual fits. We derived an efficiency of our automated method of ~80% in selecting highly absorbed AGN.
The database, and the list of spectra used in the spectral fits, can be retrieved in FITS format from the database project webpage9. The spectral-fitting results can be also be queried by accessing the LEDAS10 (LEicester Database and Archive Service), and the XCAT-DB11, that also includes a data visualisation tool.
The verification tests carried out, as well as a description of the database columns can be found in the Appendix.
Acknowledgments
We thank the anonymous referee for providing us with constructive comments and suggestions. A. Corral acknowledges financial support by the European Space Agency (ESA) under the PRODEX program.
References
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
- Corral, A., Della Ceca, R., Caccianiga, A., et al. 2011, A&A, 530, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Corral, A., Georgantopoulos, I., Watson, M. G., et al. 2014, A&A, 569, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Della Ceca, R., Maccacaro, T., Caccianiga, A., et al. 2004, A&A, 428, 383 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilli, R., Comastri, A., & Hasinger, G. 2007, A&A, 463, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krumpe, M., Lamer, G., Corral, A., et al. 2008, A&A, 483, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, Q. Z., van Paradijs, J., & van den Heuvel, E. P. J. 2006, A&A, 455, 1165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, Q. Z., van Paradijs, J., & van den Heuvel, E. P. J. 2007, A&A, 469, 807 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pye, J., Fyfe, D., Rosen, S., & Schröder, A. 2008, in The X-ray Universe 2008, Symp. held in Granada, Spain, 21 [Google Scholar]
- Treister, E., Urry, C. M., & Virani, S. 2009, ApJ, 696, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, M. G., Auguères, J.-L., Ballet, J., et al. 2001, A&A, 365, L51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Watson, M. G., Schröder, A. C., Fyfe, D., et al. 2009, A&A, 493, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Verification procedures
In the following sections of the appendix we describe some of the quality verification tests that have been carried out during the construction of the database.
 |
Fig. A.1 Goodness values versus reduced χ2 values for the same spectral fits. Circles and crosses correspond to acceptable and unacceptable fits, respectively, according to χ2 fitting. |
Appendix A.1: Goodness of fit: C-stat versus χ2 fitting
χ2 fitting has the advantage of providing goodness of fit, reduced values (χ2/d.o.f.) ~1 indicating that the model is a good representation of the data. However, a relatively high number of counts is needed in order to use this statistic. C-stat fitting works very well down to 40 spectral counts, but it does not provide goodness of fit. Two possible solutions to this problem are: to use the command goodness in Xspec; and to use C-stat as fitting statistic but χ2 as the test statistic (see Sect. 3.5).
 |
Fig. A.2 Photon index distribution for XBS AGN obtained from the automated spectral fit (line-shaded histogram) and from the manual fit in Corral et al. (2011) (empty histogram). |
To compare both goodness estimates to define acceptable fits in the database, a random
sample (~2000
detections with more than 200 net counts) was selected from the 3XMM-DR4 catalogue. The
automated fitting procedure was applied both using C-stat fitting to spectra binned to 1
count/bin, and χ2 fitting to spectra binned to 20
count/bin. In the second case, χ2 values are true representations of
the goodness of fit. In Fig. A.1, the values of
goodness are plotted against derived χ2 values from C-stat fitting
(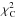 ). Different symbols represent acceptable
(filled circles), and unacceptable (crosses) fits from the χ2 fitting of
the same observations. We define as an acceptable fit a χ2 fit with a
reduced χ2 value <1.5. The arrows on the plot indicate
that 50% of the unacceptable fits according to χ2 fitting lie
above
). Different symbols represent acceptable
(filled circles), and unacceptable (crosses) fits from the χ2 fitting of
the same observations. We define as an acceptable fit a χ2 fit with a
reduced χ2 value <1.5. The arrows on the plot indicate
that 50% of the unacceptable fits according to χ2 fitting lie
above 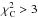 and goodness > 80. We find that there
are no limits for goodness or
and goodness > 80. We find that there
are no limits for goodness or 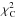 that allow us to distinguish
unambiguously between acceptable and unacceptable fits by using these estimates. The
compromise adopted in the database is to define an acceptable fit as a fit with a
goodness value <50%, that
roughly corresponds to reduced
that allow us to distinguish
unambiguously between acceptable and unacceptable fits by using these estimates. The
compromise adopted in the database is to define an acceptable fit as a fit with a
goodness value <50%, that
roughly corresponds to reduced 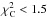 , but classify less probably-bad fits as
acceptable fits.
, but classify less probably-bad fits as
acceptable fits.
It is important to note that both estimates, goodness <50% and
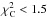 , distinguish between acceptable and
unacceptable fits (as defined by χ2< 1.5, or >1.5, respectively),
similarly well. We find that both criteria classify correctly 90% of the spectral fits.
The disadvantage of each criterion is to include more bad fits within the acceptable
fits in the case of
, distinguish between acceptable and
unacceptable fits (as defined by χ2< 1.5, or >1.5, respectively),
similarly well. We find that both criteria classify correctly 90% of the spectral fits.
The disadvantage of each criterion is to include more bad fits within the acceptable
fits in the case of 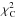 , and classifying more good fits as
unacceptable, in the case of goodness.
, and classifying more good fits as
unacceptable, in the case of goodness.
For lower number of counts, the comparison is more difficult since χ2 fitting is
less reliable. To compare the reliability of both estimates we made use of simulations.
We simulated ~4000
observations with fewer than 200 counts, using an absorbed power-law and an absorbed
thermal model, and considering a wide range of values for the photon index, the thermal
component temperature, and the column density. Assuming that power-law simulated models
should be well-fitted by a power-law, we find again that using goodness we miss a larger
number of good fits than using 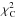 (17% fits are considered unacceptable
according to goodness values, whereas only 2% are according to
(17% fits are considered unacceptable
according to goodness values, whereas only 2% are according to
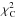 values). However, simulated thermal
models are classified as acceptable fitted by a power-law model according to
values). However, simulated thermal
models are classified as acceptable fitted by a power-law model according to
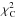 in 70% of the cases, whereas they are
only classified as acceptable according to goodness in 50% of them. Both criteria seem
to classify correctly the same fraction of spectral fits (~80%, lower than the 90% for more
than 200 counts), but again using goodness we miss more good fits, and using
in 70% of the cases, whereas they are
only classified as acceptable according to goodness in 50% of them. Both criteria seem
to classify correctly the same fraction of spectral fits (~80%, lower than the 90% for more
than 200 counts), but again using goodness we miss more good fits, and using
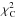 we miss-classify more bad fits as good
fits.
we miss-classify more bad fits as good
fits.
 |
Fig. A.3 Column density distribution for XBS AGN obtained from the automated spectral fit (line-shaded histogram) and from the manual fit in Corral et al. (2011) (empty histogram). |
Although it is not the purpose of this database to decide between models but to provide
as much information as possible about the spectral shape, the goodness values are used,
as a guide to the user, to both distinguish between acceptable and unacceptable fits,
and to select the best-fit model within the database. However, goodness and
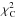 values are both included in the database
so the users may consider either or both values to define their own
acceptable/unacceptable classification or to select the best-fit model.
values are both included in the database
so the users may consider either or both values to define their own
acceptable/unacceptable classification or to select the best-fit model.
Appendix A.2: Dependence on source type
To study if the automated preferred models and best-fit parameters are in agreement with what is often found from manual spectral analyses, we constructed a sample of ~500 sources including stars (2XMM/Tycho sample, Pye et al. 2008), Low Mass X-ray binaries, (LMXB, from the catalogue in Liu et al. 2007), High Mass X-ray Binaries (HMXB, from the catalogue in Liu et al. 2006), normal galaxies, and Active Galactic Nuclei (AGN from the XMM-Newton Bright Sample, XBS, Della Ceca et al. 2004). These kinds of sources are representative of the most common types expected to be found within the XMM-Newton catalogue. This test sample also includes a great variety in spectral quality, including bright targeted sources as well as serendipitous much more fainter sources.
 |
Fig. A.4 Best-fit parameters (left: photon index, right: absorbing column density) from the manual fits compared to the ones obtained from the automated fits. Empty symbols and arrows on the right panel correspond to upper limits. Square points with errors represent average error sizes. |
We then applied the automated spectral-fitting process to the 500 sources. In 6% of cases an acceptable fit was not found (goodness of fit larger than 50% for all models). All these cases correspond to X-ray binaries and stars with large numbers of net counts (>15 000), and a very complex spectral shape, and for which a much more detailed spectral analysis has already been published in the literature. Most sources with less than 1000 counts are well-fitted by using simple models. But it is also important to note that a good fit is also found for 20% of the sources with more than 15 000 counts.
The large majority of AGN (95%) are well-fitted by using a simple absorbed power-law model. The photon index distribution is in good agreement with published results from manual spectral analyses of X-ray selected AGN. A manual spectral fitting analysis of the same sample of AGN was presented in Corral et al. (2011), which has been used to compare our results. The individual values for the photon index from the automated fits are systematically lower than the ones presented in Corral et al. (2011) (see Fig. A.2), but consistent within errors in most cases. The same applies for the column density values (see Fig. A.3), the values in Corral et al. (2011) being higher likely because of the also higher values of the photon indices and the effect of redshift, but consistent with the automated ones within errors. These small differences are likely caused by one or more of the following intrinsic differences between both analysis:
-
Different energy channels taken into account: the fitting statistics used in Corral et al. (2011) was χ2 instead of C-stat. One of the main differences between the two statistics is that spectral channels were added together to contain at least a minimum number of counts in Corral et al. (2011). This can lead to the removal of high energy spectral channels (usually less populated) and as a consequence, the lost of counts at high energies, whereas using C-stat almost all detected photons in the energy range in use are taken into account. These high energy channels usually contain only a small number of counts, so they are often removed if only added channels with a minimum number of counts are considered, which can result in a softer spectrum used during the spectral fit, and a resulting higher value for the photon index.
-
Different fitting statistics: the systematic differences can be produced by the use of C-stat instead of χ2 too, and it could be simply due to the fact that C-stat fitting is better in the low-count mode. In fact, the higher the number of counts, the closer the parameter values become between C-stat and χ2 fitting.
-
Different spectral-fitting methods: it is also important to note that, unlike previously reported manual analysis of these samples, the automated fits do not make use of any assumptions regarding the type of source under consideration, nor do they include information about the source redshifts. Besides, very hard photon indices (<1.4) were not allowed in Corral et al. (2011). If a very hard photon index was found, either it was fixed to 1.9, or additional spectral components were added to the fit.
The results for the rest of source types are also in agreement with published results. Most stars, normal galaxies, and LMXBs are better-fitted by using soft models, i.e. by power law models with a steep (most of them >2) photon index, or by thermal models. HMXBs are better-fitted by hard models, i.e. by models including a power-law component with a flat photon index (most of them <2).
Appendix A.2.1: Manual testing
We constructed another randomly selected sample of 500 sources, extracted from 3XMM-DR4, in order to manually check the spectral results. The strategy was to apply the automated spectral fitting procedure to these sources and then, to fit them also manually by using the same set of models and compare the results. The selected sample spans a wide range in spectral quality very similar to the one spanned by the full XMMFITCAT.
As a first step, we compared the values of the resulting spectral parameters, such as the power-law photon index, the temperature of the thermal component, or the inferred flux. We find an excellent agreement between these values in almost all cases. Significant deviations between values derived from different methods only occur if the model is not an acceptable fit. The values obtained from the automated fits against the ones obtained manually, for the photon index and the absorbing column density, are plotted in Fig. A.4. Note that the most significant differences, although consistent within errors, for the column density values occur only for low values of this parameter, i.e., when the absorption component does not affect significantly the spectral shape.
We also checked if the model considered as our best-fit model was the same for the manual and automated fits. For the one-component models, the model selected as our best-fit model by the automated process was the same as for the manual process in 95% of the cases. In the case of two-components models, it is extremely difficult to decide between two acceptable models even if we could take into consideration the source type. Nevertheless, the manually derived spectral parameters are in agreement with the ones obtained from the automated fits in almost all cases (see, for example, the computed fluxes plotted in Fig. A.5).
 |
Fig. A.5 Fluxes (in erg cm-2 s-1) computed by using manual fits versus the ones obtained by the automated fits. Square points with errors correspond to the average error at each flux. |
 |
Fig. A.6 Simulated photon indices versus the ones obtained from the automated spectral fits. Square point with error bar represents the average error size. |
Appendix A.2.2: Simulated data
Finally, we tested the ability of the automated procedure to distinguish between spectral models, and its accuracy at retrieving the intrinsic shape. To this end, we selected yet another random sample from 3XMM-DR4 of 1000 detections with the same count distribution as the full XMMFITCAT. Then, we used the preferred model and parameters to simulate 10 times each source and background spectra, and applied the automated procedure to the simulated data.
We find that the simulated model and the preferred model after the automated fits agree in ~87% of the cases. Nevertheless, the preferred model is given as a guide to the user, and it is not the aim of this database to distinguish between models, but to provide a good representation of the spectral shape. We find that the vast majority of the best-fit parameters from the automated fits are consistent within errors with the input parameters of the simulations. Therefore, the automated procedure is very successful in recovering the simulated spectral shape. As an example, the simulated photon indices are plotted against the ones obtained after the automated fits in Fig. A.6.
Appendix B: Database columns
The catalogue contains 214 columns. A description of each column is given in the following sections. The name is given in capital letters, the FITS data format in brackets, and the unit in square brackets. For easier reference the columns are grouped into five sections. Non-available data are represented by a –99 value within the FITS table.
Appendix B.1: Identification of the detection
The first eight columns of the database are also contained within the 3XMM-DR4 catalogue, and their purpose is to identify each source detection and spectral products, and to this end, they share the same column name, format, and values as in 3XMM-DR4. IAUNAME (21A): the IAU name assigned to the unique SRCID. DETID (J): a consecutive number which identifies each entry (detection) in the catalogue. The DETID numbering assignments in 3XMM-DR4 bear no relation to those in 2XMMi-DR3 but the DETID of the nearest matching detection from the 2XMMi-DR3 catalogue to the 3XMM-DR4 detection is provided via the DR3DETID column (not included in the XMMFITCAT table) within 3XMM-DR4. SRCID (J): a unique number assigned to a group of catalogue entries which are assumed to be the same source. The process of grouping detections in to unique sources has changed since the 2XMM catalogue series. The SRCID assignments in 3XMM-DR4 bear no relation to those in 2XMMi-DR3 but the nearest unique sources from the 2XMMi-DR3 catalogue to the 3XMM-DR4 unique source is provided via the DR3SRCID column (not included in XMMFITCAT). OBS_ID (10A): the XMM-Newton observation identification. SRC_NUM (J): the (decimal) source number in the individual source list for this observation as determined during the source fitting stage; in the hexadecimal system it identifies the source-specific product files belonging to this detection. SRC_HEX (4A): source number expressed in the hexadecimal system to identify the source-specific product files belonging to this detection. SC_RA (D) [deg]: the mean Right Ascension in degrees (J2000) of all the detections of the source SRCID weighted by the positional errors. SC_DEC (D) [deg]: the mean Declination in degrees (J2000) of all the detections of the source SRCID weighted by the positional errors.
Appendix B.2: Spectral source counts
Given the restriction imposed on the number of counts per individual instrument spectra, all available spectra for each observation are not always used in the spectral analysis. The number of counts reported in the table correspond to the number of counts used during the spectral fit. This number is computed by adding the number of source (background subtracted) counts for all instruments and exposures used in the spectral analysis. T_COUNTS (D) [count]: spectral background subtracted counts in the Full band (0.5–10 keV) computed by adding all instruments and exposures for the corresponding observation. A number of counts equal to –99 means that the number of counts is <50 counts and the spectral fit in this band is not performed. H_COUNTS (D) [count]: spectral background subtracted counts in the Hard band (2–10 keV) computed by adding all instruments and exposures for the corresponding observation. A number of counts equal to –99 means that the number of counts is <50 counts and the spectral fit in this band is not performed. S_COUNTS (D) [count]: spectral background subtracted counts in the Soft band (0.5–2 keV) computed by adding all instruments and exposures for the corresponding observation. A number of counts equal to –99 means that the number of counts is <50 counts and the spectral fit in this band is not performed.
Appendix B.2.1: Galactic column density
GNH (D) [1022cm-2]: galactic column density in the direction of the source from the Leiden/Argentine/Bonn (LAB) Survey of Galactic HI (Kalberla et al. 2005).
Appendix B.3: Spectral model names
Model related columns start with the model name. Model names are as follows:
-
WAPO: absorbed power-law model applied in the Full band.
-
WAPOS: absorbed power-law model applied in the Soft band.
-
WAPOH: absorbed power-law model applied in the Hard band.
-
WAMEKAL: absorbed thermal model applied in the Full band.
-
WAMEKALS: absorbed thermal model applied in the Soft band.
-
WABBS: absorbed black-body model applied in the Soft band.
-
WAMEKALPO: absorbed thermal plus power-law model applied in the Full band.
-
WAPOPO: absorbed double power-law model applied in the Full band.
-
WABBPO: absorbed black-body plus power-law model applied in the Full band.
Appendix B.4: Spectral-fit summary columns
A_FIT (L): the value is set to True, if an acceptable fit, i.e. goodness value <50%, has been found for the models applied in the Full band, and to False otherwise.
P_MODEL (J): the data preferred model, i.e., the simplest spectral model with the lowest goodness value among the models applied in the Full band. Each model is assigned a number as follows:
-
0.
WAPO;
-
1.
WAMEKAL;
-
2.
WABBPO;
-
3.
WAMEKALPO;
-
4.
WAPOPO.
Appendix B.5: Columns containing spectral fitting results
The remaining columns refer to the spectral-fitting results for the different models applied. Columns for a single model start with the model name as listed in Sect. B.3.
Appendix B.5.1: Spectral-fit summary for a specific model
MODEL_FIT (J): spectral-fit summary for the model MODEL. The possible values for this column correspond to the different situations that may occur during the spectral fits, and they are described as follows:
-
0.
The spectral fit was performed, and the model is considered an acceptable fit, i.e, the value returned by the command goodness is lower than 50%.
-
1.
The spectral fit was performed, but the value returned by the command goodness is greater than 50%.
-
2.
The spectral fit was not performed because the number of counts in the Soft band is lower than 50 counts.
-
3.
The spectral fit was not performed because the number of counts in the Hard band is lower than 50 counts.
-
4.
Complex-model (WAMEKALPO, WABBPO, or WAPOPO) spectral fit was not performed because the number of counts in the full band is lower than 500 counts.
-
5.
Complex-model (WAMEKALPO, WABBPO, or WAPOPO) fit results not reported because soft model component (thermal or black-body) is not significant, i.e., its normalisation is consistent with 0 at the 90% confidence level.
-
6.
Complex-model (WAMEKALPO, WABBPO, or WAPOPO) fit results not reported because hard model component (power-law) is not significant, i.e., its normalisation is consistent with 0 at the 90% confidence level.
-
7.
No best-fit parameters found. This may occur if the allowed ranges for the parameters to vary and/or the spectral model are not a good representation of the data, and Xspec falls into an infinite loop or fails to find a minimum.
Appendix B.5.2: Parameters and errors
In the case of absorption components, the column density and errors reported are in units of 1022 cm-2. In the case of thermal and black-body components, the temperatures reported are in keV. Power-law component normalisation and errors are in photons keV-1 cm-2 s-1.
MODEL_PARAMETER (D): parameter value.
MODEL_PARAMETER_HI (D): upper error (at the 90% confidence level). In the case of fixed parameters, the error values are equal to –99.
MODEL_PARAMETER_LO (D): upper error (at the 90% confidence level). In the case of fixed parameters, the error values are equal to –99.
MODEL_PARAMETER_ERR (J): Flag on the parameter error calculation. The different flags are:
-
0.
no errors occurred during the parameter error computation.
-
1.
parameter error computation hit hard lower/upper limit.
-
2.
parameter fixed to the value computed in the Soft band by using a simple model.
-
3.
parameter fixed to the value computed in the Hard band by using a simple model.
-
4.
parameter fixed to its initial value.
Appendix B.5.3: Fluxes
Reported fluxes are computed in the band used in the spectral fit.
MODEL_FLUX (D) (erg cm-2 s-1): the mean observed flux of all instruments and exposures for the corresponding observation, in the energy band used in the spectral fit.
MODEL_FLUX_HI (D) (erg cm-2 s-1): flux upper error at the 90% confidence level. If Xspec failed to compute the errors, a –99 value is listed.
MODEL_FLUX_LO (D) (erg cm-2 s-1): flux lower error at the 90% confidence level. If Xspec failed to compute the errors, a –99 value is listed.
Appendix B.5.4: Fitting statistics
MODEL_CSTAT (D): C-stat value.
MODEL_DOF (I): degrees of freedom.
MODEL_REDCHI (D): reduced χ2 from the C-stat fitting.
MODEL_GOODNESS (D): return value of the command goodness in Xspec.
All Tables
All Figures
 |
Fig. 1 Examples of spectral-fitting results for the models (from top to bottom and left to right): absorbed power-law model; absorbed thermal model; absorbed black-body model; thermal plus power-law model; double power-law model; and black-body plus power-law model. |
| In the text | |
 |
Fig. 2 Observed fluxes in the Soft band (in erg cm-2 s-1) from the automated fits against the ones reported in the 3XMM-DR4 catalogue. Filled circles correspond to consistent fluxes between both catalogues, whereas small points correspond to non-consistent ones. Square points with error bars represent average error sizes at each flux interval. |
| In the text | |
 |
Fig. 3 Distribution of net source counts per detection in XMMFITCAT. |
| In the text | |
 |
Fig. 4 Photon index distribution for the XMMFITCAT detections for which an absorbed power-law model is the preferred model. Empty histogram corresponds to detections with <500 counts, and line-shaded histogram to detections with >500 counts. |
| In the text | |
 |
Fig. 5 Hardness ratios from 3XMM-DR4 against best-fit parameters (photon index and column density) from XMMFITCAT. Left panel: high Galactic latitude sample (|b| > 20). Right panel: low Galactic latitude sample (|b| < 20). |
| In the text | |
 |
Fig. A.1 Goodness values versus reduced χ2 values for the same spectral fits. Circles and crosses correspond to acceptable and unacceptable fits, respectively, according to χ2 fitting. |
| In the text | |
 |
Fig. A.2 Photon index distribution for XBS AGN obtained from the automated spectral fit (line-shaded histogram) and from the manual fit in Corral et al. (2011) (empty histogram). |
| In the text | |
 |
Fig. A.3 Column density distribution for XBS AGN obtained from the automated spectral fit (line-shaded histogram) and from the manual fit in Corral et al. (2011) (empty histogram). |
| In the text | |
 |
Fig. A.4 Best-fit parameters (left: photon index, right: absorbing column density) from the manual fits compared to the ones obtained from the automated fits. Empty symbols and arrows on the right panel correspond to upper limits. Square points with errors represent average error sizes. |
| In the text | |
 |
Fig. A.5 Fluxes (in erg cm-2 s-1) computed by using manual fits versus the ones obtained by the automated fits. Square points with errors correspond to the average error at each flux. |
| In the text | |
 |
Fig. A.6 Simulated photon indices versus the ones obtained from the automated spectral fits. Square point with error bar represents the average error size. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


