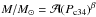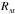| Issue |
A&A
Volume 576, April 2015
|
|
|---|---|---|
| Article Number | A68 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201424800 | |
| Published online | 01 April 2015 | |
Neutron stars with hyperon cores: stellar radii and equation of state near nuclear density
N. Copernicus Astronomical Center, Polish Academy of Sciences, Bartycka 18, 00-716 Warszawa, Poland
e-mail: fortin@camk.edu.pl; jlz@camk.edu.pl; haensel@camk.edu.pl; bejger@camk.edu.pl
Received: 13 August 2014
Accepted: 23 January 2015
Context. The existence of 2 M⊙ pulsars puts very strong constraints on the equation of state (EOS) of neutron stars (NSs) with hyperon cores, which can be satisfied only by special models of hadronic matter. The radius-mass relation for these models is sufficiently specific that it could be subjected to an observational test with future X-ray observatories.
Aims. We want to study the impact of the presence of hyperon cores on the radius-mass relation for NS. We aim to find out how, and for which particular stellar mass range, a specific relation R(M), where M is the gravitational mass, and R is the circumferential radius, is associated with the presence of a hyperon core.
Methods. We consider a set of 14 theoretical EOS of dense matter, based on the relativistic mean-field approximation, allowing for the presence of hyperons in NSs. We also discuss a recent EOS based on non-relativistic G-matrix theory yielding NSs with hyperonic cores and M> 2M⊙. We seek correlations between R(M) and the stiffness of the EOS below the hyperon threshold needed to pass the 2 M⊙ test.
Results. For NS masses 1.0 <M/M⊙< 1.6, we get R> 13 km, because of a very stiff pre-hyperon segment of the EOS. At nuclear density (n0 = 0.16 fm-3), the pressure is significantly higher than a robust upper bound obtained recently using chiral effective field theory.
Conclusions. If massive NSs do have a sizable hyperon core, then according to current models the radii for M = 1.0 − 1.6 M⊙ are necessarily >13 km. If, on the contrary, a NS with a radius R(obs)< 12 km is observed in this mass domain, then sizable hyperon cores in NSs, as we model them now, are ruled out. Future X-ray missions with <5% precision for a simultaneous M and R measurement will have the potential to solve the problem with observations of NSs. Irrespective of this observational test, present EOS allowing for hyperons that fulfill condition Mmax> 2 M⊙ yield a pressure at nuclear density that is too high relative to up-to-date microscopic calculations of this quantity.
Key words: dense matter / equation of state / stars: neutron
© ESO, 2015
1. Introduction
Hyperons, which are baryons containing at least one strange quark, were discovered more than 50 years ago. They are frequently studied in terrestrial laboratories. Although unstable on Earth, it is expected however that they are stably present in the dense interiors of neutrons stars (NSs). Recent measurements of 2M⊙ pulsars (Demorest et al. 2010; Antoniadis et al. 2013) represent a challenge for equations of state (EOS) of NSs with hyperon cores. The difficulty of reaching a high mass is related to a significant softening of the EOS associated with the hyperonization of the matter. With one exception, only EOS based on the relativistic mean-field (RMF) models, after tuning of their Lagrangians, turned out to be able to produce NS with maximum allowable mass Mmax> 2M⊙ and sizable hyperon cores (see Colucci & Sedrakian 2013 and references therein). A very recent paper of Yamamoto et al. (2014) is based on the non-relativistic G-matrix theory of dense baryon matter. Their MPa model yields Mmax> 2M⊙ for NSs with hyperon cores. As we will see, however, the properties of NS models for MPa EOS are consistent with those obtained by our set of RMF EOS.
These successful models with hyperonization of NS matter (one of them being hereafter referred to as EOS.H) merit a careful inspection. We will focus here on two specific features of these models: NS radii and EOS at pre-hyperon density; as we will show, both features are interrelated.
The EOS below nuclear density ρ0 = 2.7 × 1014g cm-3 (corresponding to the baryon number density n0 = 0.16 fm-3) is commonly believed to be rather well known (see Hebeler et al. 2013). However, to construct a complete family of NS models, up to the maximum allowable mass Mmax, one needs the EOS for up to ~8ρ0. Nuclear densities 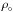 and
and 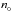 are suitable units for the mass-energy density ρ and the baryon number density nb in the NS core. In what follows we will use dimensionless (reduced) densities
are suitable units for the mass-energy density ρ and the baryon number density nb in the NS core. In what follows we will use dimensionless (reduced) densities 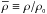 and
and 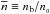 . Because of uncertainties in the theory of dense matter, the only chance to unveil the actual EOS of degenerate matter at supra-nuclear density relies on the observations of NSs.
. Because of uncertainties in the theory of dense matter, the only chance to unveil the actual EOS of degenerate matter at supra-nuclear density relies on the observations of NSs.
Mathematically, both Mmax and the radius of NS of (gravitational) mass M, RM ≡ R(M), are functionals of the EOS. We expect that NS matter at 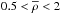 (the so-called outer core) is composed mostly of neutrons, with a few percent admixture of protons, electrons, and muons. At higher densities, hyperons or even quark gluon plasma might appear, forming a strangeness carrying NS core. In the present paper, we restrict ourselves to the NSs cores where quarks are confined into baryons: nucleons and hyperons. The EOS fulfilling Mmax> 2M⊙ and allowing for the presence of hyperons in NSs cores form the set EOS.H.
(the so-called outer core) is composed mostly of neutrons, with a few percent admixture of protons, electrons, and muons. At higher densities, hyperons or even quark gluon plasma might appear, forming a strangeness carrying NS core. In the present paper, we restrict ourselves to the NSs cores where quarks are confined into baryons: nucleons and hyperons. The EOS fulfilling Mmax> 2M⊙ and allowing for the presence of hyperons in NSs cores form the set EOS.H.
Independent of the uncertainties related to the structure of the cores of NSs, any theoretical EOS.H has to be consistent with the semi-empirical parameters of nuclear matter at 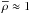 . Moreover, the hyperon component should be consistent with semi-empirical estimates (potential wells, ΛΛ-interaction) coming from hypernuclear physics (Schaffner-Bielich 2008). Basic features of EOS.H resulting from various theoretical models and puzzles, which are as yet not resolved, are briefly summarized in Sect.2. Another constraint, related to the value of the pressure P at nuclear (saturation) density, is discussed in Sect.3.
. Moreover, the hyperon component should be consistent with semi-empirical estimates (potential wells, ΛΛ-interaction) coming from hypernuclear physics (Schaffner-Bielich 2008). Basic features of EOS.H resulting from various theoretical models and puzzles, which are as yet not resolved, are briefly summarized in Sect.2. Another constraint, related to the value of the pressure P at nuclear (saturation) density, is discussed in Sect.3.
The impact of the uncertainty in the EOS on the mass vs. central density dependence for NS is described in Sect.4. We prefer to use 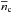 instead of
instead of 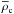 because the former characterizes the degree of packing of baryons at the NS centre. Different segments (domains) of the EOS
because the former characterizes the degree of packing of baryons at the NS centre. Different segments (domains) of the EOS 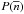 determine measurable global stellar parameters in different NS mass domains. The radius of a 1.4M⊙ NS, R1.4, is mostly determined by EOS
determine measurable global stellar parameters in different NS mass domains. The radius of a 1.4M⊙ NS, R1.4, is mostly determined by EOS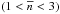 , while the value of Mmax is to a large extent determined by EOS
, while the value of Mmax is to a large extent determined by EOS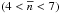 .
.
As we show in Sect.5, the NS radius for 1.0M⊙<M< 1.6M⊙ for EOS.H is larger than 13 km. This seems to be an unavoidable consequence of Mmax> 2.0M⊙ condition, which implies a very high stiffness of the pre-hyperon (i.e., purely nucleon) segment  of EOS.H.
of EOS.H.
Section6 explores the difference in the values of NS masses at a given central pressure and connects it with the difference in pressure distribution within NS models. In Sect.7 the causal-limit EOS is used to provide a bound on the NS radius, R(M). Section8 is devoted to the effects of NS rotation.
In Sect.9 we discuss a possible meaning of large radii of NSs with hyperon cores in the context of recent measurements of radii of NSs. Our conclusions are formulated in Sect.10.
Equations of state. For EOS.Nref (upper part) we selected three widely used EOS, which produce standard values of NS parameters.
2. Equation of state of neutron-star matter
Except for a very outer layer, whose contribution to NS mass and radius can be neglected, the matter in NS interior is strongly degenerate, and can be approximated by that calculated at T = 0, assuming the ground state composition (cold catalyzed matter, see e.g. Haensel et al. 2007). For these EOS, pressure depends on the density only.
In general theory of relativity (GTR) the matter density is defined as ρ = ℰ /c2, where ℰ is the total energy density (including rest energy of particles). Baryon density nb is defined as the baryon number (baryon charge) in a unit volume. Using elementary thermodynamics one obtains the relation between P and ρ from the calculated function ℰ(nb), 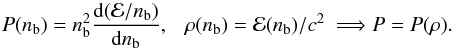 (1)
(1)
2.1. EOS satisfying the semi-empirical nuclear-hypernuclear constraints and Mmax> 2.0 M⊙
The models of the EOS.H set reproduce (within some tolerance) four semi-empirical values of parameters of nuclear matter at saturation: saturation density ns, energy per nucleon Es, symmetry energy Ss and incompressibility Ks. The semi-empirical value of a fifth parameter, the density slope of symmetry energy Ls, is relatively poorly known (Hebeler et al. 2013) and hence it is not imposed as a constraint. Together with Mmax> 2M⊙, this amounts to five constraints imposed on an EOS belonging to EOS.H.
Apart from the five constraints described above, a given EOS.H has to reproduce additional semi-empirical values of three potential wells of (zero momentum) hyperons in nuclear matter at ns: these include the sixth, seventh, and eighth constraints on EOS.H. Moreover, for most of the EOS.H models, a ninth condition, fitting a semi-empirical estimate of the depth of potential well of Λ in Λ-matter, is also imposed. In summary, there are eight or nine constraints to be satisfied by an EOS.H. Constructing an EOS of the EOS.H set is therefore associated with a strong tuning of the dense matter models. With the exception of a very recent EOS.H of Yamamoto et al. (2014), only the EOS based on the non-linear RMF theories can satisfy these conditions.
Selecting a very specific type of approximation, the RMF, is a first tuning of the dense matter model. Moreover, to satisfy Mmax> 2M⊙, baryon fields are not only coupled to (standard) σ, ω, and ρ meson fields. Namely, the hyperon fields are additionally coupled to the vector φ meson field. The addition of φ (and possibly also of a σ⋆ meson field, which provides a scalar coupling between hyperons only) is a second tuning. All EOS from EOS.H are able to satisfy Mmax> 2.0M⊙ due to repulsion produced by the φ-meson coupled only to hyperons. Moreover, in some cases, an amplification of the hyperon repulsion due to SU(6)-symmetry breaking in the vector-meson coupling to hyperons is introduced, which is a third tuning. Finally, some models have density-dependent coupling constants of baryons to meson fields. This allows for a fourth tuning. The models included in EOS.H set are listed in Table 1 together with brief characteristics and references.
Among the eight models consistent with a 2M⊙ NS in Sulaksono & Agrawal (2012), we selected four of them, three with SU(6) symmetry, the stiffest, the softest and an intermediate one, and one with SU(6) symmetry broken. Lopes & Menezes (2014) obtain similar results to Weissenborn et al. (2012) and their EOS are not included in Table 1. We also restrict ourselves to EOS calculated for a zero temperature. The EOS at finite temperature, such that they are suitable for supernova and proto-neutron star modelling and including a transition to hyperonic matter, have also been developed. In particular Banik et al. (2014) using a RMF model obtain a maximum mass for cold NS of Mmax = 2.1M⊙. Gulminelli et al. (2013), extending the EOS by Lattimer & Swesty (1991) to include hyperons with the model by Balberg & Gal (1997), reach Mmax = 2.04M⊙; however, they include only the Λ hyperon.
In order to have a reference set of models of widely used purely nucleon EOS, denoted as EOS.Nref, we selected three models listed in the upper part of Table 1. These EOS produce “standard NS”, are consistent with all semi-empirical constraints and yield Mmax> 2.0M⊙. We note that not only is Ls for EOS.H widely scattered (62−118 MeV) but it is also typically much higher than for EOS.Nref (37−59 MeV).
The EOS of the core is supplemented with an EOS of NS crust. We assume that the crust is composed of cold catalyzed matter. For the very outer layer with ρ< 108 g cm-3 we use classical BPS EOS (Baym et al. 1971). The outer crust with ρ> 108 g cm-3 is described by the EOS of Haensel & Pichon (1994), while for the inner crust we apply the SLy EOS of Douchin & Haensel (2001). A smooth matching with an interpolation between the crust and core EOS is applied to get a complete EOS of NS interior1.
3. Overpressure of EOS.H at nuclear density
We start our comparative study of EOS.H and EOS.Nref by calculating the pressure at nuclear density, P(N)(n0) and P(H)(n0), respectively. Results are collected in the Appendix Table A.1. In the following P33 refers to the pressure P in the units of 1033 dyn cm-2. We notice a striking difference between EOS.H and EOS.Nref. The values of 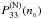 are concentrated within 3.3 ± 0.3, while the values of
are concentrated within 3.3 ± 0.3, while the values of 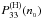 are significantly higher, within 8 ± 2.5.
are significantly higher, within 8 ± 2.5.
Hebeler et al. (2013) argue that the EOS of pure neutron matter at nb ≤ n0 can be reliably calculated using the up-to-date many-body theory of nuclear matter. Their results are in remarkable agreement with those by Gandolfi et al. (2012) using an approach completely different from that adopted by Hebeler et al. (2013). At this density, NS matter in beta equilibrium is expected to be somewhat softer than the pure neutron matter. Hebeler et al. (2013) calculate the effect of the presence of an admixture of protons and electrons in beta equilibrium on the EOS, combining the EOS of neutron matter and available semi-empirical information about nuclear symmetry energy and its density dependence (slope parameter Ls). Interpolating between the values in their Table 5, we conclude that Hebeler et al. (2013) provide the following constraint on the pressure of NS matter at 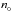 :
: 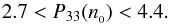 (2)This constraint is satisfied by EOS.Nref. On the contrary, it is badly violated by EOS from EOS.H, which give P33(n0) significantly higher than the upper bound in Eq.(2). Before considering consequences of the “overpressure” of the nucleon (pre-hyperon) segment of EOS.H for NS radii, we discuss two different parametrizations of NS models.
(2)This constraint is satisfied by EOS.Nref. On the contrary, it is badly violated by EOS from EOS.H, which give P33(n0) significantly higher than the upper bound in Eq.(2). Before considering consequences of the “overpressure” of the nucleon (pre-hyperon) segment of EOS.H for NS radii, we discuss two different parametrizations of NS models.
 |
Fig. 1 Mass density ρ = ℰ /c2 vs. baryon density nb for NS matter for the set of EOS presented in Figs. 2−4. Dotted segments correspond to the central densities of NS models, which are unstable with respect to radial oscillations. Relation ρ = ρ(nb) deviates from linearity for nb> 0.3fm-3. Non-linearity grows with increasing nb and is EOS-dependent. For nb ≲ 0.2fm-3, the linear approximation ρ ≈ nbmn (where mn is neutron mass) is valid. (Colour online.) |
4. Two densities and two parametrizations of neutron star models
When investigating the EOS of NS matter, we have to consider two distinct densities, ρ = ℰ /c2 and nb (Sect.2). While ρ is the relevant quantity for GTR calculations of the NS structure, it is nb that is associated with an average distance between baryons (treated as point-like objects),  . Therefore, knowing nb, we can compare an actual rb with the average distance between nucleons in nuclear matter at normal nuclear density,
. Therefore, knowing nb, we can compare an actual rb with the average distance between nucleons in nuclear matter at normal nuclear density, 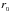 ,
, 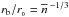 . At subnuclear densities, ρ of NS matter can be very well approximated by nbmn, where mn is neutron rest mass. However, at supranuclear densities ρ grows non-linearly with nb. This non-linear dependence is model dependent, see Fig. 1, and actually determines the EOS, see Eq. (1).
. At subnuclear densities, ρ of NS matter can be very well approximated by nbmn, where mn is neutron rest mass. However, at supranuclear densities ρ grows non-linearly with nb. This non-linear dependence is model dependent, see Fig. 1, and actually determines the EOS, see Eq. (1).
 |
Fig. 2 Gravitational mass M vs. central baryon density nc for non-rotating NS models based on the sets EOS.H (blue lines – H) and EOS.Nref (black lines – Nref). In Nref: A is APR, B is BSk20, C is DH; in H: a is SA.BSR2, b indicates BM165, c indicates GM1Z0, d is UU1, e is G.TM1C. EOS labels from Table 1. Solid lines: stable NS configurations. Dotted lines: configurations unstable with respect to small radial perturbations. Vertical lines crossing the M(nc) curves indicate configurations with nc/n0 = 2,3,.... Hatched strip correspond to M = 1.4 ± 0.05M⊙, and the observational constraints for J1614-2230 and J0348+0432 are marked in blue and magenta, respectively (1-σ errors). (Colour online.) |
In Fig.2 we plot the relations between M and the central baryon density nc for non-rotating NS models. Several conclusions result from this figure. First, the central density in a 2M⊙ NS is typically  , so that at the star’s centre rb/r0 ≈ 0.6. Second, the N segment of EOS.H, corresponding to
, so that at the star’s centre rb/r0 ≈ 0.6. Second, the N segment of EOS.H, corresponding to 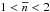 , is so much stiffer than a similar segment of the EOS.Nref, that
, is so much stiffer than a similar segment of the EOS.Nref, that 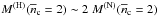 . In other words, to yield Mmax> 2.0 M⊙ despite the hyperon softening, the pre-hyperon (nucleon) segment
. In other words, to yield Mmax> 2.0 M⊙ despite the hyperon softening, the pre-hyperon (nucleon) segment 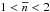 of EOS.H has to be very stiff.
of EOS.H has to be very stiff.
Figure 3 shows the 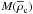 curves. The
curves. The 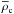 in 2M⊙ stars can be as high as 6−7, significantly larger than the corresponding values of
in 2M⊙ stars can be as high as 6−7, significantly larger than the corresponding values of 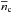 . For the Mmax configurations, the difference is even larger. However, it is nc and not ρc that determines the mean inter-baryon distance at the centre of the star.
. For the Mmax configurations, the difference is even larger. However, it is nc and not ρc that determines the mean inter-baryon distance at the centre of the star.
The value of 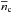 for 2M⊙ stars can be used to evaluate the importance of relativistic effects in the relevant many-body problem. The number density ni of baryon species i = n,p,Λ,... with a mass mi can be related to their mean velocity ⟨ vi ⟩. In the free Fermi gas approximation,
for 2M⊙ stars can be used to evaluate the importance of relativistic effects in the relevant many-body problem. The number density ni of baryon species i = n,p,Λ,... with a mass mi can be related to their mean velocity ⟨ vi ⟩. In the free Fermi gas approximation, 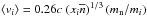 , where xi = ni/nb and mn is the neutron mass. At the centre of a 2M⊙ star we expect
, where xi = ni/nb and mn is the neutron mass. At the centre of a 2M⊙ star we expect 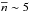 so that
so that  . The multi-component character of dense baryon matter implies lower ⟨ vi ⟩ as compared to a pure neutron matter case and, consequently, smaller relativistic effects in the many-body system, as stressed in the classical paper of Bethe & Johnson (1974) to justify the use of a non-relativistic many-body theory of dense matter. Therefore, we might expect that not only RMF but also some non-relativistic models, consistent with semi-empirical nuclear and hypernuclear matter constraints, could yield 2M⊙ stars with hyperonic cores. However, as far as we know, there is only one such a non-relativistic dense matter model satisfying these conditions (Yamamoto et al. 2014).
. The multi-component character of dense baryon matter implies lower ⟨ vi ⟩ as compared to a pure neutron matter case and, consequently, smaller relativistic effects in the many-body system, as stressed in the classical paper of Bethe & Johnson (1974) to justify the use of a non-relativistic many-body theory of dense matter. Therefore, we might expect that not only RMF but also some non-relativistic models, consistent with semi-empirical nuclear and hypernuclear matter constraints, could yield 2M⊙ stars with hyperonic cores. However, as far as we know, there is only one such a non-relativistic dense matter model satisfying these conditions (Yamamoto et al. 2014).
A very recent calculation of Katayama & Saito (2014) is performed using a relativistic formulation of G-matrix theory (Dirac-Brueckner-Hartree-Fock approximation). Some models from this work give Mmax> 2M⊙, but they do not satisfactorily reproduce the semi-empirical parameters of nuclear matter (see Table 1 of Katayama & Saito 2014).
 |
Fig. 4 Gravitational mass M vs. circumferential radius R for non-rotating NS models. For the labels, see details in the caption of Fig. 2. (Colour online.) |
5. Radii of neutron stars with hyperon cores
The radius R is a measurable NS parameter and therefore large radii of NS with hyperon cores could be subject to an observational test. The M(R) lines for selected EOS from EOS.H are plotted in Fig.4. By construction, selected EOS.H include those producing an envelope of a complete H-bundle of M(R) curves.
 |
Fig. 5 Pressure at nuclear density vs. NS radius for 1.4M⊙ for EOS.H and EOS.Nref (see Table 1 for the labels). Grey horizontal strip – range of P(n0) determined by Hebeler et al. (2013). Circles correspond to EOS with the TM1, squares with NL3, pentagons with GM1 model for the nucleon sector, respectively. Triangles indicate EOS built with RMF models with density-dependent couplings. (Colour online.) |
In the mass range 1 <M/M⊙< 1.6, the H-bundle is centred around ~14.2 km. There is a wide >1 km gap between the H and Nref bundles in this mass range. More specifically, we find a lower bound R(H)> 13 km in the considered mass range. In Fig. 5 we plot the points calculated for EOS.H in the P33(n0) − R1.4 plane, where R1.4 ≡ R(1.4M⊙). Large values of 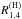 are correlated2 with a high P(n0) violating the upper bound of Hebeler et al. (2013).
are correlated2 with a high P(n0) violating the upper bound of Hebeler et al. (2013).
 |
Fig. 6 NS radius for 2.0M⊙ vs. radius at maximum allowable mass. EOS labels from Table 1. (Colour online.) |
Consider the largest, up-to-date, measured pulsar mass, 2.0M⊙, and EOS-dependent (theoretical) maximum allowable mass Mmax. The EOS-dependent radius of 2.0M⊙ star and the radius at Mmax are denoted by R2.0 and RMmax, respectively. Calculated points in the RMmax-R2.0 plane are shown in Fig.6. Those for EOS.Nref are tightly grouped (within less than 1 km) around R2.0 = 11 km. The points calculated for EOS.H are loosely distributed along the diagonal of the bounding box, with 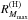 ranging within 10.5−12.5 km, and
ranging within 10.5−12.5 km, and 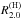 within 11.5−14 km.
within 11.5−14 km.
 |
Fig. 7 Dependence of M on the central pressure, for non-rotating NS models, for M< 1.6M⊙. Dashed and dashed-dotted lines describe the |
6. Mass vs. central pressure for neutron stars with hyperon cores
The difference between M − R relations for EOS.Nref and EOS.H and in particular an R-gap for 1.0 <M/M⊙< 1.6 reflects a difference in the pressure distributions within NS models of a given M. This is visualized in Fig.7 where we show M(Pc) plots for EOS.Nref and EOS.H families. For M ≲ 1.6M⊙ we find that M = M(Pc) is well approximated by  (3)where P34 = P/ 1034erg cm-3 and βH ≈ βN = 0.52, while prefactor
(3)where P34 = P/ 1034erg cm-3 and βH ≈ βN = 0.52, while prefactor 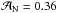 for the Nref-bundle is significantly smaller than
for the Nref-bundle is significantly smaller than 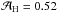 for the H-bundle.
for the H-bundle.
There is a sizable gap between M(N)(Pc) and M(H)(Pc) bundles. The M-gap ranges from ~0.2M⊙ at Pc,34 = 3 to ~0.7M⊙ at Pc,34 = 8. The fit 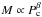 with β = const. breaks down for the H-family for M> 1.6M⊙ because of the hyperon softening of the EOS. For M ~ 2M⊙ (not shown in Fig.7), the gap between the Nref and H bundles disappears.
with β = const. breaks down for the H-family for M> 1.6M⊙ because of the hyperon softening of the EOS. For M ~ 2M⊙ (not shown in Fig.7), the gap between the Nref and H bundles disappears.
7. On the causal bounds on R(M)
The radius of a neutron star of given mass M, based on a causal EOS, cannot exceed a limit that is calculated by replacing this EOS above some “fiducial density” n⋆ by the causal-limit (speed of sound = c) continuation. The causal-limit (CL) segment of the EOS.CL is: 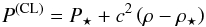 (4)for nb ≥ n⋆, whereas P⋆ and ρ⋆ are calculated from the original EOS, P⋆ = P(n⋆), ρ⋆ = ρ(n⋆).
(4)for nb ≥ n⋆, whereas P⋆ and ρ⋆ are calculated from the original EOS, P⋆ = P(n⋆), ρ⋆ = ρ(n⋆).
 |
Fig. 8 Solid lines: mass-radius relations for an EOS.N(DH) and an EOS.H (DS08), respectively. Long-dash line: causal-limit upper bound on RM for these EOS, assuming n⋆ = n0. Dotted line: similar upper bound on |
We choose n⋆ = n0. Our choice is more conservative, for the reasons explained later in this section, than 1.8n0 used by Hebeler et al. (2013). We fix the model for the crust segment of all EOS, i.e. for nb< 0.5n0, we use the EOS described in the final fragment of Sect. 2.1.
In Fig.8 we show M(R) curves for selected models from EOS.Nref and EOS.H (DH and DS08 EOS, respectively), together with their causal-limit (CL) bounds. The CL curves bifurcate from the actual M(R) curves at nc = n⋆, corresponding to M = M⋆. For a given M>M⋆, the CL-bound is denoted by Rmax(M).
Consider first 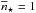 . We get
. We get 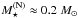 and
and  . As
. As 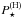 is significantly higher than
is significantly higher than 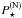 ,
, 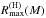 is larger than
is larger than 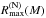 , e.g. by about 1 km at 1.4M⊙. The difference decreases to 0.5 km at 2M⊙.
, e.g. by about 1 km at 1.4M⊙. The difference decreases to 0.5 km at 2M⊙.
Consider now 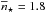 chosen by Hebeler et al. (2013). We then get
chosen by Hebeler et al. (2013). We then get 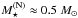 and
and 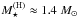 . At 1.4M⊙ the actual R(H)(M) is larger than
. At 1.4M⊙ the actual R(H)(M) is larger than 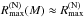 by about 1.4 km. The H configuration there violates the condition Pc ≫ P(H) needed for a weak dependence of Rmax(M) on the EOS below n⋆. Therefore, a CL-bound derived for EOS.Nref should not be applied to EOS.H stars. Even at 2M⊙ the CL-bound for H is larger by 1 km than the N-bound. We conclude that
by about 1.4 km. The H configuration there violates the condition Pc ≫ P(H) needed for a weak dependence of Rmax(M) on the EOS below n⋆. Therefore, a CL-bound derived for EOS.Nref should not be applied to EOS.H stars. Even at 2M⊙ the CL-bound for H is larger by 1 km than the N-bound. We conclude that 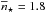 chosen by Hebeler et al. (2013) is too large to yield a unique CL-bound for radii of the Nref and H families simultaneously.
chosen by Hebeler et al. (2013) is too large to yield a unique CL-bound for radii of the Nref and H families simultaneously.
 |
Fig. 9 M(Req) for two selected EOS: N (DH) and H (DS08). The Req is defined in the text. Solid curves: non-rotating configurations. Dashed lines: configurations rotating uniformly at f = 300 and 600 Hz. (Colour online.) |
8. Effect of neutron star rotation
The fact that NSs rotate should be taken into account when comparing their radii; the values will differ from a non-rotating solution because of the effect of the centrifugal force. Mature NSs, and especially extremely stably spinning millisecond pulsars (spin frequencies larger than 100 Hz) may be, to an excellent approximation, described using the assumption of uniform rotation3. Non-axial deformations supported by the elastic strain accumulated in the crust, as well as non-axiality generated by the internal magnetic field, are small for the rotating NSs that we are modelling. Therefore, in what follows we will assume that the configurations are stationary and axisymmetric, and we will define the circumferential equatorial radius Req as the proper length of the equator divided by 2π. For a given mass M, the value 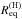 for EOS.H-based NS increases with rotation rate more rapidly than for EOS.Nref. This is a direct consequence of larger radii of hyperonic NSs. In Newtonian terms, for fixed mass M and spin frequency f, the gravitational pull at the equator is weaker, while the centrifugal force is stronger in the case of EOS.H stars: both effects increase the value of Req. Figure 9 compares M(Req) curves calculated for f = 300Hz and f = 600Hz with the non-rotating (f = 0) case. Frequencies ~300 Hz are measured for many radio and X-ray millisecond pulsars, while f ~ 600 Hz is characteristic of a group of the fastest (Lorimer 2008; Patruno & Watts 2012).
for EOS.H-based NS increases with rotation rate more rapidly than for EOS.Nref. This is a direct consequence of larger radii of hyperonic NSs. In Newtonian terms, for fixed mass M and spin frequency f, the gravitational pull at the equator is weaker, while the centrifugal force is stronger in the case of EOS.H stars: both effects increase the value of Req. Figure 9 compares M(Req) curves calculated for f = 300Hz and f = 600Hz with the non-rotating (f = 0) case. Frequencies ~300 Hz are measured for many radio and X-ray millisecond pulsars, while f ~ 600 Hz is characteristic of a group of the fastest (Lorimer 2008; Patruno & Watts 2012).
For the EOS in Fig.9, the rotational increase of ΔReq is roughly twice as large for EOS.H compared with EOS.N. It can be well approximated, for a fixed EOS and mass M, as a quadratic function in f: 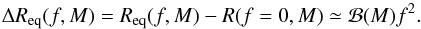 (5)For M = 1.4M⊙, one has ℬH = 3.1km / kHz2 and ℬN = 1.6km / kHz2. At a given f, ΔReq decreases with increasing M. For an astrophysically motivated range of masses between 1.2M⊙ and 1.8M⊙, the decrease of ΔReq with an increasing mass is approximately linear: ℬ(M) changes from 2.0km / kHz2 to 1.2km / kHz2 for EOS.N, and from 3.8km / kHz2 to 2.2km / kHz2 for EOS.H. These linear approximations for ℬ and relation (5) may be used to estimate the increase of Req for rotating nucleonic and hyperonic NSs.
(5)For M = 1.4M⊙, one has ℬH = 3.1km / kHz2 and ℬN = 1.6km / kHz2. At a given f, ΔReq decreases with increasing M. For an astrophysically motivated range of masses between 1.2M⊙ and 1.8M⊙, the decrease of ΔReq with an increasing mass is approximately linear: ℬ(M) changes from 2.0km / kHz2 to 1.2km / kHz2 for EOS.N, and from 3.8km / kHz2 to 2.2km / kHz2 for EOS.H. These linear approximations for ℬ and relation (5) may be used to estimate the increase of Req for rotating nucleonic and hyperonic NSs.
Radius determination: most recent publications.
9. Observational determination of radii of neutron stars
The radius R can be extracted from the analysis of X-ray spectra emitted by the NS atmosphere. Recent attempts are based on the modelling of X-ray emission from four different types of objects (see Potekhin 2014, for a review):
-
isolated NSs (INSs);
quiescent X-ray transients (QXTs) in low-mass X-ray binaries (LMXBs), i.e. NSs in a binary system observed when the accretion of matter from their binary companion has stopped or is strongly reduced;
bursting NSs (BNSs) i.e. NSs from which recurring and very powerful bursts, so-called photospheric radius expansion (PRE) bursts, are observed;
rotation-powered radio millisecond pulsars (RP-MSPs).
 .
.
While the magnetic field and the chemical composition of the atmosphere of INSs are unknown and difficult to determine, QXTs have a low magnetic field, as a result of its decay due to the accretion of matter, and an atmosphere likely to be composed of light elements (H, possibly He; see Catuneanu et al. 2013; Heinke et al. 2014). In addition, QXTs in globular clusters are promising sources for the mass-radius determination since their distances are well known. BNSs that also have low magnetic fields and a light-element atmosphere are interesting sources, all the more if the distance to them is known. However the modelling of the PRE bursts is still subject to uncertainties and debates (see Poutanen et al. 2014; Steiner et al. 2013; Güver & Özel 2013). Finally, constraints can be derived from the modelling of the shape of the X-ray pulses observed from RP-MSPs, in particular, if the mass is known from radio observations (Bogdanov 2013).
Conflicting constraints on the radius from the X-ray emission of QXTs, BNSs, and RP-MSPs have been obtained by different groups. In what follows, we restrict ourselves to the most recent publications, indicated in Table 2. Figure 10 shows the constraints with 2-σ error bars derived in these papers for the radius R1.4 of a NS with a mass of 1.4 M⊙.
Performing a simultaneous spectral analysis of six QXTs assuming unmagnetized hydrogen atmosphere, Guillot & Rutledge (2014) derive a constraint suggesting a small radius: R = 9.4 ± 1.2 km (90% confidence level) consistent with their previous results (Guillot et al. 2013). Heinke et al. (2014), using new and archival X-ray data, re-performed an analysis of the spectrum of the one of these QXTs, NGC 6397 and argue that a helium atmosphere is favoured over a hydrogen atmosphere such as the one used in Guillot et al. (2013), which favours a larger radius.
For all papers in Table 2, if not available, constraints on R1.4 with a 2-σ error bars were derived assuming a Gaussian distribution for the radius, which makes the comparison between the results easier. The constraint from Güver & Özel (2013) is extracted from their Fig. 3.
 |
Fig. 10 Observational constraints on the radius R1.4 of a 1.4 M⊙ NS from the most recent publications. See Table 2 for the labels and text for details. The 2-σ error-bars are plotted. |
Formally, at 2-σ level, all constraints on R1.4 but those by Poutanen et al. (2014) and Guillot & Rutledge (2014) are consistent with one another and give the radius of ~12.8km for M = 1.4M⊙. All present EOS.H have a substantially larger radius R1.4 ≥ 13.51 km as indicated in Table A.1 and Fig. 5 and thus violate this upper bound. They are consequently consistent only with the lower bounds on R1.4 obtained by Poutanen & Suleimanov (2013) and Bogdanov (2013).
However, the determination of the radius of NSs is subject to many assumptions, uncertainties, and systematic effects, (see e.g. Table 1 in Potekhin 2014). In addition, the inclusion of rotation strongly complicates the analysis of the collected X-ray spectra from both QXTs and BNSs, which are likely to rotate at a frequency of few hundreds of Hz. Rotation is expected to affect the radius determination by ~10% according to Poutanen et al. (2014) and Baubock et al. (2015).
10. Summary, discussion, and conclusions
The observational constraint that Mmax> 2.0M⊙ for NS with hyperon cores imposes a fine tuning of the dense matter model, which has to be simultaneously consistent with semi-empirical nuclear and hyper-nuclear parameters. With one very recent exception (Yamamoto et al. 2014), which will be discussed separately, only specific types of non-linear RMF models are able to satisfy this constraint. The EOS of NS matter for these models, forming the set EOS.H, have the features that are described below.
Overpressure at 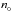 . Pressures P(H)(n0) are significantly higher than the robust upper bound obtained by Hebeler et al. (2013). Introducing a density-dependence for the coupling constants in the RMF Lagrangian does not help in this respect.
. Pressures P(H)(n0) are significantly higher than the robust upper bound obtained by Hebeler et al. (2013). Introducing a density-dependence for the coupling constants in the RMF Lagrangian does not help in this respect.
Large radii. For 1.0 <M/M⊙< 1.6, one obtains 13 <R(H)/ km < 15. These radii are consistent at 2-σ confidence level only with two lower bounds out of the five most recent constraints, derived by analyzing and modelling the X-ray emission from NSs in quiescent LMXBs, from those exhibiting photospheric expansion bursts, and from radio millisecond pulsars. Future simultaneous determinations of M and R through analysis of the X-ray spectra with a ~5% precision, thanks to the forthcoming NICER (Gendreau et al. 2012), Athena+ (Motch et al. 2013) and possibly LOFT (Feroci et al. 2012) missions, could either rule out hyperon cores in NS or leave open the possibility of sizable hyperon cores.
Overpressure at 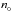 and large radii are likely to be interrelated. To get Mmax> 2M⊙, an EOS.H should necessarily have unusually stiff pre-hyperon segment, and this results in large radii for M ≲ 1.6M⊙. However, in our opinion the upper bound on P(n0) by Hebeler et al. (2013) is sufficiently robust to be respected. Therefore, we propose including this constraint in the procedure of determination of the RMF Lagrangian coupling constants, in addition to the standard fitting four parameters Es,ns,Esym,Ks. In the weakest form, this constraint would read
and large radii are likely to be interrelated. To get Mmax> 2M⊙, an EOS.H should necessarily have unusually stiff pre-hyperon segment, and this results in large radii for M ≲ 1.6M⊙. However, in our opinion the upper bound on P(n0) by Hebeler et al. (2013) is sufficiently robust to be respected. Therefore, we propose including this constraint in the procedure of determination of the RMF Lagrangian coupling constants, in addition to the standard fitting four parameters Es,ns,Esym,Ks. In the weakest form, this constraint would read 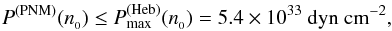 (6)where P(PNM) is the pressure of pure neutron matter (PNM) calculated for a given RMF model, and
(6)where P(PNM) is the pressure of pure neutron matter (PNM) calculated for a given RMF model, and  is the upper bound to this pressure obtained by Hebeler et al. (2013). We prefer to use constraint (6) instead of fitting the very uncertain Ls, referring to weakly asymmetric nuclear matter. We are now studying the possibility of imposing both the PNM constraint (6) and getting Mmax> 2M⊙ to narrow the EOS.H family of RMF models.
is the upper bound to this pressure obtained by Hebeler et al. (2013). We prefer to use constraint (6) instead of fitting the very uncertain Ls, referring to weakly asymmetric nuclear matter. We are now studying the possibility of imposing both the PNM constraint (6) and getting Mmax> 2M⊙ to narrow the EOS.H family of RMF models.
A very recent model of EOS.H fulfilling Mmax> 2M⊙ (Yamamoto et al. 2014) deserves a separate discussion. This model does not rely on the RMF approximation, rather it is calculated using the G-matrix theory. A crucial new element is a strong three- and four-baryon repulsion resulting from the multi-pomeron exchanges between baryons. The many-body theory is applied to a number of terrestrial nuclear and hyper-nuclear data, which are sufficient to fit three sets of parameters of the models. The set MPa yields the stiffest hyperon NS-cores and is the only set satisfying Mmax> 2M⊙. The MPa curves in Figs. 8, 9 and 11 of Yamamoto et al. (2014) indicate that the MPa EOS has similar basic features as those characteristic of the RMF models of our EOS.H set. Namely, R(MPa) ≳ 13.5 km for 1.2 <M/M⊙< 1.6 and 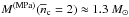 , which is twice the value characteristic of our EOS.Nref set. This indicates that the pre-hyperon segment of the MPa EOS is very stiff, in particular, with a large overpressure at
, which is twice the value characteristic of our EOS.Nref set. This indicates that the pre-hyperon segment of the MPa EOS is very stiff, in particular, with a large overpressure at  . In conclusion, these features of the MPa EOS coincide with those of our RMF-EOS.H set, and should be subject to the same tests.
. In conclusion, these features of the MPa EOS coincide with those of our RMF-EOS.H set, and should be subject to the same tests.
As far as observations are concerned, owing to the current large uncertainties on the radius determination that exist because of assumptions in the models and systematic effects, no stringent conclusion on the radius of a 1.4M⊙ NS can be derived.
In our opinion, a robust observational upper bound on R will become available only with advent of high-precision X-ray astronomy, like that promised by the NICER, Athena+, and LOFT projects. A simultaneous measurement of M and R within a few percent error is expected to be achieved, and then used in combination with a maximum measured pulsar mass (at present 2.01 ± 0.04M⊙) as a robust criterion in our quest to unveil the structure of neutron star cores.
The non-uniqueness of the crust-core matching in the EOS introduces some indeterminacy, which only disappears for unified EOS where the crust and core EOS are based on the same nuclear many-body model, starting from the same nucleon interaction (see e.g. Douchin & Haensel 2001; Grill et al. 2014).
To a good approximation  , consistently with Lattimer & Prakash (2001) (Blaschke, priv. comm.).
, consistently with Lattimer & Prakash (2001) (Blaschke, priv. comm.).
At the NS birth, the temperature is high enough to allow for differential rotation, but as soon as the star cools, physical processes such as convection, turbulent motions, and shear viscosity promptly enforce uniform rotation. At sufficiently low temperatures, the NS interior becomes superfluid. Total stellar angular momentum is then represented by a sum of quantized vortices, but on scales much larger than the vortex separation (which is typically much smaller than 1 cm for known pulsars’ rotation rates) fluid motion averages out and may be considered uniform (see e.g. Sonin 1987).
Acknowledgments
We thank V. Dexheimer, M. Oertel, A. Sulaksono, H. Uechi, and Y. Yamamoto for providing us with the EOS tables. We are grateful to H. Uechi and Y. Yamamoto for helpful comments concerning their EOS. Correspondence with N. Chamel and A. Fantina about the BSk EOS was very helpful. We are grateful to J.M. Lattimer for his comments after a talk by one of the authors (PH) during the EMMI meeting a FIAS (Frankfurt, Germany, November 2013). We thank M. Oertel and M. Hempel for useful discussions. We are also grateful to D. Blaschke for his helpful remarks on the meaning of Fig. 5. One of the authors (MF) was supported by the French-Polish LIA HECOLS and by the Polish NCN HARMONIA grant DEC-2013/08/M/ST9/00664. This work was partially supported by the Polish NCN grant No. 2011/01/B/ST9/04838.
References
- Akmal, A., Pandharipande, V. R., & Ravenhall, D. G. 1998, Phys. Rev. C, 58, 1804 [NASA ADS] [CrossRef] [Google Scholar]
- Antoniadis, J., Freire, P. C. C., Wex, N., et al. 2013, Science, 340, 6131 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Balberg, S., & Gal, A. 1997, Nucl. Phys. A, 625, 435 [Google Scholar]
- Banik, S., Hempel, M., & Bandyopadhyay, D. 2014, ApJS, 214, 22 [Google Scholar]
- Baubock, M., Ozel, F., Psaltis, D., & Morsink, S. M. 2015, ApJ, 799, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Baym, G., Pethick, C. J., & Sutherland, P. 1971, ApJ, 170, 299 [Google Scholar]
- Bednarek, I., Haensel, P., Zdunik, J. L., Bejger, M., & Mańka, R. 2012, A&A, 543, A157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bethe, H. A., & Johnson, M. B. 1974, Nucl. Phys. A, 230, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bogdanov, S. 2013, ApJ, 762, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Catuneanu, A., Heinke, C. O., Sivakoff, G. R., Ho, W. C. G., & Servillat, M. 2013, ApJ, 764, 145 [Google Scholar]
- Colucci, G., & Sedrakian, A. 2013, Phys. Rev. C, 87, 055807 [Google Scholar]
- Demorest, P. B., Pennucci, T., Ransom, S. M., Roberts, M. S. E., & Hessels, J. W. T. 2010, Nature, 467, 1081 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dexheimer, V., & Schramm, S. 2008, ApJ, 683, 943 [Google Scholar]
- Douchin, F., & Haensel, P. 2001, A&A, 380, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fantina, A. F., Chamel, N., Pearson, J. M., & Goriely, S. 2013, A&A, 559, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feroci, M., den Herder, J. W., Bozzo, E., et al. 2012, Proc. SPIE, 8443 [Google Scholar]
- Gandolfi, S., Carlson, J., & Reddy, S. 2012, Phys. Rev. C, 85, 032801 [NASA ADS] [CrossRef] [Google Scholar]
- Gendreau, K. C., Arzoumanian, Z., & Okajima, T. 2012, Proc. SPIE, 8443 [Google Scholar]
- Grill, F., Pais, H., Providência, C., Vidaña, I., & Avancini, S. S. 2014, Phys. Rev. C, 90, 045803 [NASA ADS] [CrossRef] [Google Scholar]
- Guillot, S., & Rutledge, R. E. 2014, ApJ, 796, L3 [Google Scholar]
- Guillot, S., Servillat, M., Webb, N. A., Rutledge, R. E. 2013, ApJ, 772, 7 [Google Scholar]
- Gulminelli, F., Raduta, A. R., Oertel, M., & Margueron, J. 2013, Phys. Rev. C, 87, 055809 [NASA ADS] [CrossRef] [Google Scholar]
- Gusakov, M. E., Haensel, P., & Kantor, E. M. 2014, MNRAS, 439, 318 [Google Scholar]
- Güver, T., & Özel, F. 2013, ApJ, 765, L1 [Google Scholar]
- Haensel, P., & Pichon, B. 1994, A&A, 283, 313 [NASA ADS] [Google Scholar]
- Haensel, P., Potekhin, A. Y., & Yakovlev, D. G. 2007, Neutron Stars 1, Equation of State and Structure (New York: Springer) [Google Scholar]
- Hebeler, K., Lattimer, J. M., Pethick, C. J., & Schwenk, A. 2013, ApJ, 773, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Heinke, C. O., Cohn, H. N., Lugger, P. M., et al. 2014, MNRAS, 444, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Katayama, T., & Saito, K. 2014 [arXiv:1410.7166] [Google Scholar]
- Lattimer, J. M., & Douglas Swesty, F. 1991, Nucl. Phys. A, 535, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Lattimer, J. M., & Prakash, M. 2001, ApJ, 550, 426 [Google Scholar]
- Lopes, L. L., & Menezes, D. P. 2014, Phys. Rev. C, 89, 025805 [NASA ADS] [CrossRef] [Google Scholar]
- Lorimer, D. R. 2008, Liv. Rev. Rel., 11, 8 [Google Scholar]
- Miyatsu, T., Cheoun, M.-K., & Saito, K. 2013, Phys. Rev. C, 88, 015802 [NASA ADS] [CrossRef] [Google Scholar]
- Motch, C., Wilms, J., Barret, D., et al. 2013 [arXiv:1306.2334] [Google Scholar]
- Patruno, A., & Watts, A. L. 2012 [arXiv:1206.2727] [Google Scholar]
- Potekhin, A. Y. 2014, Phys. Uspekhi, 57, 735 [NASA ADS] [CrossRef] [Google Scholar]
- Poutanen, J., & Suleimanov, V. 2013, Proc. IAU Symp. 291, ed. J. van Leeuven (Cambridge, UK: Cambridge University Press), 145 [Google Scholar]
- Poutanen, J., Nättilä, J., Kajava, J. J. E., et al. 2014, MNRAS, 442, 3777 [NASA ADS] [CrossRef] [Google Scholar]
- Schaffner-Bielich, J. 2008, Nucl. Phys. A, 804, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Sonin, E. B. 1987, Rev. Mod. Phys., 59, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, A. W., Lattimer, J. M., & Brown, E. F. 2013, ApJ, 765, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Sulaksono, A., & Agrawal, B. K. 2012, Nucl. Phys. A, 895, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Uechi, S. T., & Uechi, H. 2009, Adv. High Energy Phys., 2009, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Verbiest, J. P. W., Bailes, M., van Straten, W., et al. 2008, ApJ, 679, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Weissenborn, S., Chatterjee, D., & Schaeffner-Bielich, J. 2012, Phys. Rev. C, 85, 065802 [NASA ADS] [CrossRef] [Google Scholar]
- Yamamoto, Y., Furumoto, T., Yasutake, N., & Rijken, T. A. 2014, Phys. Rev. C, 90, 045805 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Collected numerical results for EOS.N and EOS.H
Parameters of the EOS and of NS models based on them.
All Tables
Equations of state. For EOS.Nref (upper part) we selected three widely used EOS, which produce standard values of NS parameters.
All Figures
 |
Fig. 1 Mass density ρ = ℰ /c2 vs. baryon density nb for NS matter for the set of EOS presented in Figs. 2−4. Dotted segments correspond to the central densities of NS models, which are unstable with respect to radial oscillations. Relation ρ = ρ(nb) deviates from linearity for nb> 0.3fm-3. Non-linearity grows with increasing nb and is EOS-dependent. For nb ≲ 0.2fm-3, the linear approximation ρ ≈ nbmn (where mn is neutron mass) is valid. (Colour online.) |
| In the text | |
 |
Fig. 2 Gravitational mass M vs. central baryon density nc for non-rotating NS models based on the sets EOS.H (blue lines – H) and EOS.Nref (black lines – Nref). In Nref: A is APR, B is BSk20, C is DH; in H: a is SA.BSR2, b indicates BM165, c indicates GM1Z0, d is UU1, e is G.TM1C. EOS labels from Table 1. Solid lines: stable NS configurations. Dotted lines: configurations unstable with respect to small radial perturbations. Vertical lines crossing the M(nc) curves indicate configurations with nc/n0 = 2,3,.... Hatched strip correspond to M = 1.4 ± 0.05M⊙, and the observational constraints for J1614-2230 and J0348+0432 are marked in blue and magenta, respectively (1-σ errors). (Colour online.) |
| In the text | |
 |
Fig. 3 Same as in Fig.2, except with nc replaced by ρc. (Colour online.) |
| In the text | |
 |
Fig. 4 Gravitational mass M vs. circumferential radius R for non-rotating NS models. For the labels, see details in the caption of Fig. 2. (Colour online.) |
| In the text | |
 |
Fig. 5 Pressure at nuclear density vs. NS radius for 1.4M⊙ for EOS.H and EOS.Nref (see Table 1 for the labels). Grey horizontal strip – range of P(n0) determined by Hebeler et al. (2013). Circles correspond to EOS with the TM1, squares with NL3, pentagons with GM1 model for the nucleon sector, respectively. Triangles indicate EOS built with RMF models with density-dependent couplings. (Colour online.) |
| In the text | |
 |
Fig. 6 NS radius for 2.0M⊙ vs. radius at maximum allowable mass. EOS labels from Table 1. (Colour online.) |
| In the text | |
 |
Fig. 7 Dependence of M on the central pressure, for non-rotating NS models, for M< 1.6M⊙. Dashed and dashed-dotted lines describe the |
| In the text | |
 |
Fig. 8 Solid lines: mass-radius relations for an EOS.N(DH) and an EOS.H (DS08), respectively. Long-dash line: causal-limit upper bound on RM for these EOS, assuming n⋆ = n0. Dotted line: similar upper bound on |
| In the text | |
 |
Fig. 9 M(Req) for two selected EOS: N (DH) and H (DS08). The Req is defined in the text. Solid curves: non-rotating configurations. Dashed lines: configurations rotating uniformly at f = 300 and 600 Hz. (Colour online.) |
| In the text | |
 |
Fig. 10 Observational constraints on the radius R1.4 of a 1.4 M⊙ NS from the most recent publications. See Table 2 for the labels and text for details. The 2-σ error-bars are plotted. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.