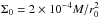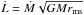| Issue |
A&A
Volume 576, April 2015
|
|
|---|---|---|
| Article Number | A29 | |
| Number of page(s) | 23 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201424359 | |
| Published online | 18 March 2015 | |
The evolution of a binary in a retrograde circular orbit embedded in an accretion disk⋆
1 DAMTP, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
e-mail: pbi20@cam.ac.uk
2 Astro Space Centre, P. N. Lebedev Physical Institute, 84/32 Profsoyuznaya st., 117997 Moscow, Russia
3 Astronomy Unit, Queen Mary University of London, Mile end Road, London, E1 4NS, UK
Received: 9 June 2014
Accepted: 8 October 2014
Aims. Supermassive black hole binaries may form as a consequence of galaxy mergers. Both prograde and retrograde orbits have been proposed. We study a binary with a small mass ratio, q, in a retrograde orbit immersed in and interacting with a gaseous accretion disk in order to estimate the time scales for inward migration that leads to coalescence and the accretion rate to the secondary component.
Methods. We employed both semi-analytic methods and two-dimensional numerical simulations, focusing on the case where the binary mass ratio is small but large enough to significantly perturb the disk.
Results. We develop the theory of type I migration in this case and go on to determine the conditions for gap formation. We find that when this happens inward migration occurs on a time scale equal to the time required for one half of the secondary mass to be accreted through the unperturbed accretion disk. The accretion rate onto the secondary itself is found to only play a minor role in the orbital evolution as it is of the order of q1/3 of that to the primary. We obtain good general agreement between the semi-analytic and fully numerical approaches and note that the former can be applied to disks with a wide dynamic range on long time scales.
Conclusions. We conclude that inward migration induced by interaction with the disk can enable the binary to migrate inwards, alleviating the so-called final parsec problem. When q is sufficiently small, there is no well-pronounced cavity inside the binary orbit, unlike the prograde case. The accretion rate to the secondary does not influence the binary orbital evolution much, but can lead to some interesting observational consequences, provided the accretion efficiency is sufficiently large. In this case the binary may be detected as, for example, two sources of radiation rotating around each other. However, the study should be extended to consider orbits with significant eccentricity and the effects of gravitational radiation at small length scales. Also, torques acting between a circumbinary accretion disk, which has a non-zero inclination with respect to a retrograde binary orbit at large distances, may cause the inclination to increase on a time scale that can be similar to, or smaller than, the time scale of orbital evolution, depending on the disk parameters and binary mass ratio. This is also an aspect for future study.
Key words: accretion, accretion disks / black hole physics / hydrodynamics / planet-disk interactions / binaries: general / quasars: supermassive black holes
The movies are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
The merger of two galaxies could lead to formation of a supermassive binary black hole (SBBH) in the centre of the newly formed more massive galaxy as a result of dynamical friction, (see e.g. Komberg 1968; Begelman et al. 1980). The coalescence of supermassive black holes results in a burst of gravitational radiation, which can in principle be detected by planned space-based gravitational antennae, when originating at cosmological distances, (see e.g. Grishchuk et al. 2001; Amaro-Seoane et al. 2013).
The orbit of a SBBH shrinks towards coalescence as a result of the operation of a number of mechanisms. These include frictional interaction with a gaseous component that may reside in the form of an accretion disk, gravitational interaction with the stars of a central star cluster, and the emission of gravitational waves. It was noted by Begelman et al. (1980) that orbital evolution of the SBBH induced by gravitational radiation and gravitational interaction with a star cluster may not be efficient at intermediate scales in the range of 0.01–1 pc so that it may stall when its semi-major axis reaches these scales. This has been called the final parsec problem.
This problem may be alleviated by taking the interaction with a gaseous component of the system into account, which is assumed to be in the form of a circumbinary accretion disk; see for example Ivanov et al. (1999, hereafter IPP), Gould & Rix (2000), and more recently, Cuadra et al. (2009), Haiman et al. (2009), Lodato et al. (2009), Rossi et al. (2010), Farris et al. (2011), Roedig et al. (2012), Kocsis et al. (2012), Tanaka et al. (2012), Hayasaki et al. (2013), Rafikov (2013), and Gold et al. (2014), and references therein. Apart from providing a possible solution to the final parsec problem, the time variability of the accretion rate supplied by an accretion disk around a SBBH, peculiarities in emission spectra, etc., may serve to indicate its presence (Rieger & Mannheim 2000; Yu & Lu 2001; Armitage & Natarajan 2002; Liu 2004; Lobanov & Roland 2005; Komossa 2006; MacFadyen & Milosavljevic 2008; Bogdanovic et al. 2008, 2009; Montuori et al. 2011, 2012; Sesana et al. 2012; Valtonen et al. 2012; Burke-Spolaor 2013; Ju et al. 2013; Farris et al. 2014; McKernan et al. 2014; Roedig et al. 2014, and references therein). In addition, filling the central regions of the accretion disk after SBBH coalescence under various circumstances may also provide indirect observational evidence that the event of SBBH coalescence actually is taking place (see e.g. Loeb 2007; Shapiro 2010).
It has been commonly assumed that the direction of motion of the disk gas and the orbital motion of the SBBH coincide. However, as noted by Nixon et al. (2011a,b), this may not always be the case, since the direction of the binary orbital motion may not be correlated with the initial direction of the gas motion within the disk. For example, the system considered may correspond to the inner regions of a disk galaxy, which on large scales consists of counter-rotating gas and stars (see e.g. Corsini 2014, for a review), with the gas containing a relatively small part of the total angular momentum content. In that case gas starting with extreme orbital inclination relative to the stellar component is naturally expected to settle into a counter rotating state (e.g. Thakar & Ryden 1998).
Thus the SBBH may be aligned with orbital motion being either prograde or retrograde with respect to the direction of orbital motion of the disk gas. This can be understood as follows. We consider a SBBH consisting of a primary with mass M and a secondary with mass Mp, and assume for simplicity that the mass ratio q is small, q ≪ 1. We assume that there is an inclined thin circumbinary accretion disk with a typical mass, Md, within the scale of the SBBH semi-major axis, a, which is much smaller than Mp. At distances much larger than a the gravitational field of the SBBH may be approximated by its time average form, namely the gravitational field due to a ring of mass Mp and radius a. It was shown by IPP that the disk must align into the binary plane on a scale larger than a. Clearly, when the mass of the secondary greatly exceeds the disk mass on this alignment scale, and as here only the time averaged potential of the binary matters, the direction of alignment will not depend on the direction of SBBH orbital rotation, and the disk may align with either prograde or retrograde orbital motion, depending on which of these requires the inclination change of least magnitude (see King et al. 2005)1.
In this paper we assume that the configuration of the system and source of disk gas enables retrograde binary orbital motion with respect to the disk to be set up; however, after the initial alignment process, gravitational torques exerted between a twisted circumbinary disk and a slightly misaligned binary orbit, through which there is an accretion flow, may tend to overturn the orbital plane of the binary on a long time scale when there is counterrotation (see e.g. Scheuer & Feiler 1996; IPP; King et al. 2005; Nixon et al. 2011). The time scale associated with this process is determined by the magnitude of the gravitational torque exerted by the twisted accretion disk on the binary. In the linear regime of small mutual inclinations, this torque can be quite large when the effective Shakura-Sunyaev α parameter (Shakura & Sunyaev 1973) governing the evolution of the twisted disk is small. However, once the inclination of the disk with respect to the orbital plane at large distances is significant, non-linear effects come into play and are expected to reduce the value of the torque (see e.g. Ogilvie 1999). In this situation we estimate the time scale of the evolution of binary orbital plane assuming that the effective α ~ 1 as was done in IPP (see their Eq. (23)). We discuss this estimate further in Sect. 12.3, showing that the time scale is expected to be comparable to or even slightly smaller than the time scale of evolution of the binary semi-major axis, depending on the disk parameters and binary mass ratio. Also depending on them, the binary may thus be expected to evolve in the state of retrograde rotation long enough to undergo significant changes to its orbit, and in some cases the effect of secular changes of its orientation may become important. However, for simplicity, we neglect this possibility in what follows, assuming that the planes of the binary and the disk are aligned.
The evolution of a SBBH immersed in the accretion disk and rotating in the retrograde sense has recently been explored numerically using the SPH method for a relatively large mass ratio q ≥ 0.1 (see e.g. Roedig & Sesana 2014). In addition McKernan et al. (2014) have recently considered the opposite limit of an extremely small mass ratio q = 10-4 using the grid-based PENCIL CODE.
This paper presents a simple semi-analytic theory of a retrograde binary immersed in and interacting with a thin accretion disk. This theory is presented together with the results of two-dimensional numerical hydrodynamical simulations of representative systems. Unlike the works mentioned above, we consider the case where the mass ratio q ≤ 2 × 10-2 is small but still large enough to significantly affect the evolution of the disk surface density. We consider both disks of formally infinite extent and disks with a finite outer boundary and with various prescriptions for the effective viscosity. Because two-dimensional numerical simulations become problematic for disks with a wide dynamic range likely to be relevant for SBBH, we develop a simpler applicable one-dimensional approach that is validated by making comparisons with the two-dimensional simulations. For this first treatment we focus on the simplest case of a binary with a circular orbit interacting only with the disk, while briefly discussing features that should be tackled in future work, such as orbital eccentricity and orbital evolution induced by gravitational radiation.
The plan of this paper is as follows. We give the basic definitions and set-up in Sect. 2 and go on to describe a framework for a one-dimensional model for calculating the evolution of the disk and binary orbit in Sect. 3. In this model, the evolution of the disk surface density is governed by a diffusion equation that incorporates a simple model of the angular momentum exchange between the perturber and disk through gravitational scattering. For small mass ratios, the perturber remains embedded in the disk, producing a linear response that induces type I migration. The theory of this is presented in Sect. 4 and expressions for the migration rate given. A comparison with migration rates obtained from two-dimensional numerical simulations is then undertaken in Sect. 5. The two approaches are found to be in good agreement. Angular momentum exchange with the disk is expected to result in gap formation for sufficiently massive perturbers. This process is studied in Sect. 6 using the one-dimensional model set up in Sect. 3. Gap formation was determined to occur for perturber mass ratios exceeding an estimated value ~1.57δ2, with δ being the disk aspect ratio. Simple 1D modelling of the gap surface density profile for the case of relatively large mass ratio is described in Sect. 7.
Since two-dimensional simulations are time consuming and impractical for disks with a very wide dynamic range, we go on to develop the more applicable simple one-dimensional model in Sect. 8. This is later validated by making additional detailed comparisons between the two approaches. In the one-dimensional model, one can calculate the evolution of the disk surface density in the first instance by assuming the radius of the assumed circular orbit is a fixed parameter. One can then use this solution to determine how the orbit evolves. It turns out that when a deep gap is formed, only the disk outside the perturber has to be considered as explained in Sect. 8.1. A relevant similarity solution for an accretion disk of infinite extent is given in 8.2 and the time scale for orbital evolution induced through the action of disk torques discussed in Sect. 9. In addition, the accretion rate onto the perturber is estimated in Sect. 10.
We compare the results of the one-dimensional model regarding gap formation and migration for larger mass perturbers, with two-dimensional numerical simulations in Sect. 11. The two approaches are again found to be in good agreement.
We go on to briefly discuss additional features that should be considered in future work, such as the possible effects of (i) a moderate-to-large, imposed orbital eccentricity; (ii) orbital evolution driven by the emission of gravitational waves, a process that may dominate when the perturber reaches the inner regions of the disk; and (iii) the secular evolution of the direction of binary’s angular momentum due to interaction with a twisted accretion disk, in Sect. 12. Finally we summarise our results and conclusions in Sect. 13.
2. Basic definitions and set-up
We consider a binary consisting of a primary of mass M and a secondary of mass Mp that is embedded in an accretion disk. The binary orbit is taken to be coplanar with the disk mid-plane and is approximately circular with a sense of rotation that is opposite to that of the disk gas. We suppose that the primary is much more massive than the secondary such that the mass ratio q = Mp/M ≪ 1. Thus disk material inside the orbit of the secondary revolves approximately in circles centred on the primary.
We determine the modification of the disk structure due to the presence of the binary and the evolution of the binary separation distance, rp, induced by torques exerted by the disk material. To do this we employ a simple numerical approach based on an azimuthally averaged, hence simplified, one-dimensional description of the accretion disk, as well as an additional simplified analytic treatment of the problem. We go on to relate these to two-dimensional numerical simulations of the disk’s interaction with the binary. In the work presented below, we adopt a cylindrical coordinate system (r,φ,z) with its origin at the primary and with the z axis directed perpendicular to the orbital plane. We assume that the disk material and the binary orbit with increasing and decreasing azimuthal angle, thus in a prograde and retrograde sense, respectively.
3. A one-dimensional model for the evolution of the disk and binary orbit
We have developed a simplified one-dimensional model for the evolution of the binary orbit taking the gravitational interaction with the disk into account (e.g. Lin & Papaloizou 1986), which itself undergoes viscous evolution due to angular momentum transport (e.g. Lynden-Bell & Pringle 1974).
3.1. The evolution of the accretion disk and its interaction with the binary orbit
To find the torque T due to the disk acting on the binary, it is necessary to determine how the presence of the perturbing body affects the structure of the disk. Following the discussion of Lin & Papaloizou (1986), which is applicable to the case where the binary and disk rotate in the same direction, we assume that the gravitational interaction results in locally induced angular momentum transport to the disk. This in turn determines the evolution of the disk surface density Σ, together with internal angular momentum transport induced by the action of an effective turbulent viscosity.
The evolution of Σ can be obtained from considering the conservation of mass and angular momentum. The former is expressed by the continuity equation, which can be written as 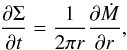 (1)where the mass flux through radius r is given by
(1)where the mass flux through radius r is given by 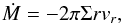 (2)with vr being the radial velocity of the disk material.
(2)with vr being the radial velocity of the disk material.
The conservation of the z-component of angular momentum is expressed by the equation 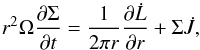 (3)where the inwardly directed angular momentum flux through radius r is given by
(3)where the inwardly directed angular momentum flux through radius r is given by 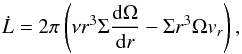 (4)with ν being the kinematic viscosity of the disk material,
(4)with ν being the kinematic viscosity of the disk material, 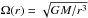 is its angular velocity which is assumed to be Keplerian, and G is the gravitational constant. The torque exerted per unit mass by the perturber on the disk is
is its angular velocity which is assumed to be Keplerian, and G is the gravitational constant. The torque exerted per unit mass by the perturber on the disk is 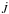 . Thus the total torque exerted on the disk by the perturber is given by
. Thus the total torque exerted on the disk by the perturber is given by 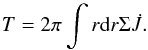 (5)Unlike the prograde case there are no Lindblad resonances in the retrograde circular case, and, accordingly, their contribution is not included in (5). However, they can operate when a retrograde binary has some eccentricity. This effect is briefly discussed in Sect. 12.1 below.
(5)Unlike the prograde case there are no Lindblad resonances in the retrograde circular case, and, accordingly, their contribution is not included in (5). However, they can operate when a retrograde binary has some eccentricity. This effect is briefly discussed in Sect. 12.1 below.
3.2. The evolution of the binary orbit
By Newton’s third law, the total torque exerted on the binary will be −T. Provided that it remains approximately circular, angular momentum conservation for the orbit determines the evolution of rp through 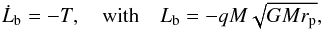 (6)being the orbital angular momentum, which has a negative sign on account of the orbit being retrograde. From Eq. (6) we find
(6)being the orbital angular momentum, which has a negative sign on account of the orbit being retrograde. From Eq. (6) we find 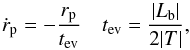 (7)which defines a characteristic time scale, tev, for the orbital evolution.
(7)which defines a characteristic time scale, tev, for the orbital evolution.
For the configuration considered here, the binary is expected to transfer retrograde angular momentum to the disk, causing it to slowly spiral inwards. Thus we expect 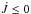 and T ≤ 0. As a consequence the disk will gain retrograde or, equivalently, lose prograde, angular momentum. We expect
and T ≤ 0. As a consequence the disk will gain retrograde or, equivalently, lose prograde, angular momentum. We expect 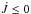 everywhere. Thus unlike the case for which the binary is prograde,
everywhere. Thus unlike the case for which the binary is prograde, 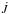 does not change sign on crossing the orbit.
does not change sign on crossing the orbit.
We now consider two regimes of perturber disk interaction. The first, appropriate for small mass ratios, is when the disk surface density is only slightly modified such that the interaction can be regarded as linear. It corresponds to the type I migration regime. The second, appropriate for large enough mass ratios, is when the interaction is non-linear such that a gap is formed in the disk. In this case, corresponding to type II migration, migration rates become significantly reduced relative to the type I regime.
4. Small mass ratios and type I migration
In this case we assume that the perturber has a small enough mass such that the disk surface density remains unchanged by the embedded perturber, at least on long enough time scales for significant migration to occur. In this regime, the torque exerted on the perturber through interaction with the disk occurs through the excitation, transport and dissipation of density waves. To find the resulting torque, Twave, exerted on the binary, we perform a linear calculation of the disk response. This approach is standard when considering the type I migration regime in the prograde case (see e.g. Baruteau et al. 2014).
We begin by performing a Fourier expansion of the gravitational potential of the perturber, ψp, in the form ![\begin{eqnarray} \psi_{\rm p}\,\,& =& {\cal{R}}e\sum_{m=0}^{\infty} W_m\exp[{\rm i}m(\varphi +\omega t)]\quad {\rm with} \nonumber \\ W_m &= &-\frac{GM_{\rm p}}{\pi}\int_{0}^{2\pi}\frac{\cos m\varphi {\rm d}\varphi}{\sqrt{r_{\rm p}^2+r^2+\Delta_{\rm s}^2 -2rr_{\rm p}\cos\varphi}}\nonumber \\ &&\sim -\frac{2GM_{\rm p}}{\pi r_{\rm p}}K_0\left( \frac{m\sqrt{\Delta^2+\Delta_{\rm s}^2}}{r_{\rm p}} \right) \hspace{2mm} {\rm for}\hspace{2mm} m > 0. \label{potexp} \end{eqnarray}](/articles/aa/full_html/2015/04/aa24359-14/aa24359-14-eq42.png) (8)Here m is the azimuthal mode number, and we recall that Δ = |r − rp |,
(8)Here m is the azimuthal mode number, and we recall that Δ = |r − rp |, 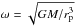 is the binary orbital frequency and that K0 denotes the modified Bessel function of the second kind. A gravitational softening length, Δs, is included. This is regularly used to approximately account for 3D effects (e.g. Baruteau et al. 2014). The representation of the Fourier coefficient through a Bessel function, as well as the neglect of the indirect term in the perturbing potential, should be accurate either for small
is the binary orbital frequency and that K0 denotes the modified Bessel function of the second kind. A gravitational softening length, Δs, is included. This is regularly used to approximately account for 3D effects (e.g. Baruteau et al. 2014). The representation of the Fourier coefficient through a Bessel function, as well as the neglect of the indirect term in the perturbing potential, should be accurate either for small 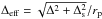 or for mΔeff up to of order unity in the limit of large m. We assume that one of these conditions is appropriate from now on.
or for mΔeff up to of order unity in the limit of large m. We assume that one of these conditions is appropriate from now on.
For a barotropic equation of state, the disk response to the action of the perturbing potential (8) can be obtained from Eqs. (45) and (46) of Lin & Papaloizou (1993) with a forcing frequency applicable to a secondary in a retrograde circular orbit. These take the form 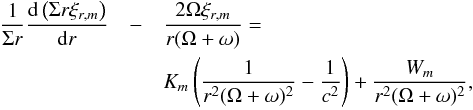 (9)and
(9)and ![\begin{eqnarray} \frac{{\rm d} K_m }{{\rm d}r}&+ & \frac{2\Omega K_m }{r(\Omega+\omega)} = \nonumber\\ & &\left[m^2(\Omega+\omega)^2 - \Omega^2\right]\xi_{r,m} - \frac{{\rm d} W_m }{{\rm d}r} - \frac{2\Omega W_m}{r(\Omega+\omega)}\cdot \label{cr2} \end{eqnarray}](/articles/aa/full_html/2015/04/aa24359-14/aa24359-14-eq51.png) (10)Here ξr,m and Km are the Fourier coefficients in the expansions analogous to (8) for the radial component of the Lagrangian displacement and W = Σ′c2/ Σ, respectively, with Σ′ being the induced surface density perturbation. The local sound speed is c.
(10)Here ξr,m and Km are the Fourier coefficients in the expansions analogous to (8) for the radial component of the Lagrangian displacement and W = Σ′c2/ Σ, respectively, with Σ′ being the induced surface density perturbation. The local sound speed is c.
Local approximation
Because the typical wavelength of the density wave response is ~c/ (mω) ≪ r even for m = 1, we expect that they attain the form of outgoing waves for | r − rp| /rp ≪ 1. Thus it is appropriate to look for local solutions for which outgoing wave boundary conditions are applied at radii close to the orbital radius of the perturber.
We thus assume Σ and c2 are constant and replace r and Ω where they appear explicitly by rp and ω, respectively. As c2 ≪ r2ω2, the second term on the LHS and first term on the RHS of Eq. (9) are neglected. This then becomes 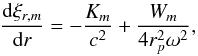 (11)and using the same approximation scheme (10) becomes
(11)and using the same approximation scheme (10) becomes 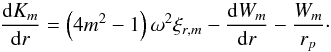 (12)We now use (11) to eliminate Km in (12), noting that it turns out that the second term on the RHS of (11) may be neglected in our approximation scheme. We thus obtain a governing equation for ξr,m of the form
(12)We now use (11) to eliminate Km in (12), noting that it turns out that the second term on the RHS of (11) may be neglected in our approximation scheme. We thus obtain a governing equation for ξr,m of the form 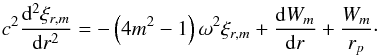 (13)This is seen to be an equation for a forced simple harmonic oscillator. However, it is important to note that, through its dependence on the gravitational potential of the perturber, the effective forcing term involving W varies rapidly in its vicinity and cannot be assumed to be constant. It is convenient to write the governing equation in the compact form
(13)This is seen to be an equation for a forced simple harmonic oscillator. However, it is important to note that, through its dependence on the gravitational potential of the perturber, the effective forcing term involving W varies rapidly in its vicinity and cannot be assumed to be constant. It is convenient to write the governing equation in the compact form 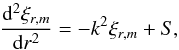 (14)where k2 = (4m2 − 1)ω2/c2 and
(14)where k2 = (4m2 − 1)ω2/c2 and 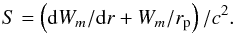
Solution of the governing equation for the linear response
Equation (14) is solved subject to radiation boundary conditions. For convenience we adopt the convention that ω and k are positive. The free solutions of (14) corresponding to inward and outward propagating density waves are then ![\begin{eqnarray} \xi_{r,m}& =& C_1 \exp({\rm i}kx)\quad {\rm and}\nonumber \\[2mm] \xi_{r,m} &= &C_2 \exp(-{\rm i}kx), \end{eqnarray}](/articles/aa/full_html/2015/04/aa24359-14/aa24359-14-eq72.png) (15)where x = r − rp and C1 and C2 are arbitrary constant amplitude factors, respectively, and real parts are taken to obtain physical solutions here and below when needed. The solution to the forced problem is determined such that it takes a multiple of the above forms at large distances (measured in terms of wavelengths) inside and outside the source, respectively.
(15)where x = r − rp and C1 and C2 are arbitrary constant amplitude factors, respectively, and real parts are taken to obtain physical solutions here and below when needed. The solution to the forced problem is determined such that it takes a multiple of the above forms at large distances (measured in terms of wavelengths) inside and outside the source, respectively.
The required solution is found by standard methods to be given by 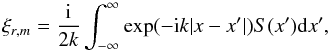 (16)with the constants C1 and C2, which specify the amplitude of the inwardly and outwardly propagating waves at large distances, readily seen as given by
(16)with the constants C1 and C2, which specify the amplitude of the inwardly and outwardly propagating waves at large distances, readily seen as given by 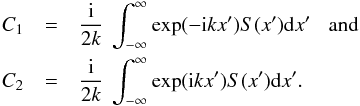 (17)
(17)
Rate of angular momentum transport
Each of the waves described above transfers angular momentum from the orbit to the disk at the locations where they eventually dissipate. In a low viscosity disk, dissipation occurs as a result of non-linear steepening and shock formation. Depending on their amplitudes, this may be some distance away from the location of the orbit. Because the orbit is retrograde with respect to the disk, the transfer removes positive angular momentum from the disk, potentially causing it to accrete onto the central object. The rate of flow of angular momentum through a circle of radius, r, associated with either of the waves is 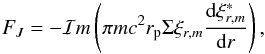 (18)where ℐm denotes that the imaginary part is to be taken.
(18)where ℐm denotes that the imaginary part is to be taken.
We evaluate this expression for ingoing and outgoing waves with a particular value of m. They both remove negative angular momentum from the binary orbit and ultimately transfer it to the disk, accordingly giving additive contributions to the torque acting on the disk, which we write as −Twave. The corresponding torque acting on the perturber will then be Twave, which is positive. On account of it being retrograde, this acts so as to make the perturber spiral inwards. For a particular value of m, we thus obtain 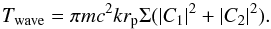 (19)This quantity is directly related to the Fourier transform of the source, S(x), through Eq. (17). A useful result that enables its evaluation is provided by the standard integral
(19)This quantity is directly related to the Fourier transform of the source, S(x), through Eq. (17). A useful result that enables its evaluation is provided by the standard integral 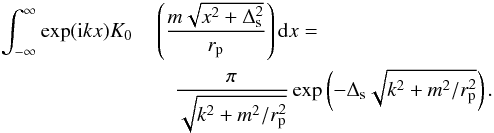 (20)Making use of (17) and (20), from Eq. (19) we find that
(20)Making use of (17) and (20), from Eq. (19) we find that 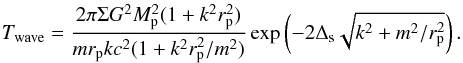 (21)As k ≫ m/rp for all m ≥ 1, we simplify (21) to read
(21)As k ≫ m/rp for all m ≥ 1, we simplify (21) to read 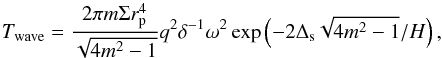 (22)and we recall that q = Mp/M and δ = H/r. This shows that when Δs ~ H, as is expected to be appropriate for approximately accounting for the finite disk thickness and as adopted in many of our numerical simulations, the dominant contributions come from the smallest m. This is unlike the prograde case for which the dominant contributions come from m ~ rp/H. Taking only m = 1 into account, we calculate a migration time for the perturber using (7) with | T| = |Twave |, thus obtaining
(22)and we recall that q = Mp/M and δ = H/r. This shows that when Δs ~ H, as is expected to be appropriate for approximately accounting for the finite disk thickness and as adopted in many of our numerical simulations, the dominant contributions come from the smallest m. This is unlike the prograde case for which the dominant contributions come from m ~ rp/H. Taking only m = 1 into account, we calculate a migration time for the perturber using (7) with | T| = |Twave |, thus obtaining 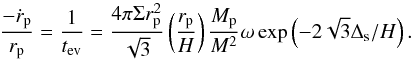 (23)Comparing this expression with the corresponding one given by Tanaka et al. (2002) for the prograde case and a uniform surface density, we find that tmig is slower by a factor
(23)Comparing this expression with the corresponding one given by Tanaka et al. (2002) for the prograde case and a uniform surface density, we find that tmig is slower by a factor 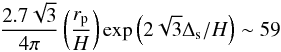 for the parameters of the two-dimensional simulations we performed to test (23).
for the parameters of the two-dimensional simulations we performed to test (23).
4.1. Total torques obtained by summing over m
When a sum of the contributions from all values of m is performed, the analytic theory indicates that the total torque should be ∝ as the softening length tends to zero. However, our derivation of the expression (22) relies on the assumption that the linear theory is valid. Clearly, this falls when a typical inverse wave number associated with the disk response, k-1 ~ δrp/ (2m), becomes comparable to or less than the accretion radius ra ~ qrp/ 2. (This defines the impact parameter for significant scattering if the response is purely ballistic.) Using the equality ra = k-1 to define a maximal cutoff value of m, mmax, we obtain mmax ~ δ/q. Summing contributions from different values of m given by (22) up to this cut off, we obtain an estimate of the total torque corresponding to the small mass retrograde case for zero softening as
as the softening length tends to zero. However, our derivation of the expression (22) relies on the assumption that the linear theory is valid. Clearly, this falls when a typical inverse wave number associated with the disk response, k-1 ~ δrp/ (2m), becomes comparable to or less than the accretion radius ra ~ qrp/ 2. (This defines the impact parameter for significant scattering if the response is purely ballistic.) Using the equality ra = k-1 to define a maximal cutoff value of m, mmax, we obtain mmax ~ δ/q. Summing contributions from different values of m given by (22) up to this cut off, we obtain an estimate of the total torque corresponding to the small mass retrograde case for zero softening as 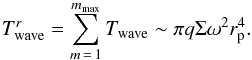 (24)
(24)
4.2. Type I migration rates
We notice that (24) gives the migration torque with the cut off scale assumed to be governed by the accretion radius. However, if the accretion radius is less than the scale height, the cut off is more likely to be determined by the latter. To deal with that case we replace ra by 0.3πH in the above determination of mmax. To take both possibilities into account, we multiply the torque given by (24) by a factor f, where f = min(1,5q/ (3πδ)). Thus 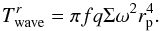 (25)It is instructive to compare (25) with the corresponding expression for the prograde case,
(25)It is instructive to compare (25) with the corresponding expression for the prograde case, 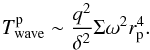 (26)From (25) we see that the ratio
(26)From (25) we see that the ratio 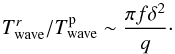 (27)Thus, small mass objects immersed in the disk and rotating in different directions could drift with different radial velocities determined by the disk half-thickness and their mass ratios. In principal, this could lead to some interesting consequences, such as a possibility of collision between the objects since, in this situation, for comparable mass ratios, the radial separation between them will in general decrease relatively rapidly with time.
(27)Thus, small mass objects immersed in the disk and rotating in different directions could drift with different radial velocities determined by the disk half-thickness and their mass ratios. In principal, this could lead to some interesting consequences, such as a possibility of collision between the objects since, in this situation, for comparable mass ratios, the radial separation between them will in general decrease relatively rapidly with time.
5. Numerical simulations of embedded perturbers
We have performed numerical simulations using the two-dimensional code NIRVANA (see e.g. Podlewska-Gaca et al. 2012, and references therein) and also the ROe solver for Disk Embedded Objects (RODEO) method (see e.g. Paardekooper & Papaloizou 2009). In the context of the results presented here, these independent methods were found to give almost identical results.
In this section we consider numerical simulations for which the perturber remained embedded without forming a significant gap. The initial surface density was specified to be ∝r− 1/2 and scaled so that the total mass interior to the initial orbital radius of the perturber was 10-3 in units of the dominant central mass. The perturber was initiated on a retrograde circular orbit of radius r0 that is taken to be the simulation unit of length. For simulation unit of time, we take the orbital period of a circular orbit with this radius. We adopted H/r = 0.05, and the kinematic viscosity was taken to be 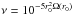 . The computational domain was taken to be (0.2r0,5r0). The outer radial boundary was considered to be rigid and the inner radial boundary open. Gravitational softening lengths were considered ranging from Δs = 0.6H, denoted as standard softening, to Δs = 0.1H, denoted as small softening. Grid resolutions with NR = 350 and Nφ = 400 equally spaced grid points in the radial and azimuthal directions, respectively, were typically adopted for cases with standard softening. For smaller softening lengths, the resolution was increased to NR = 700 and Nφ = 1200. For simulations presented in this section, there was no accretion onto the perturber.
. The computational domain was taken to be (0.2r0,5r0). The outer radial boundary was considered to be rigid and the inner radial boundary open. Gravitational softening lengths were considered ranging from Δs = 0.6H, denoted as standard softening, to Δs = 0.1H, denoted as small softening. Grid resolutions with NR = 350 and Nφ = 400 equally spaced grid points in the radial and azimuthal directions, respectively, were typically adopted for cases with standard softening. For smaller softening lengths, the resolution was increased to NR = 700 and Nφ = 1200. For simulations presented in this section, there was no accretion onto the perturber.
The results of a numerical simulation that was performed for q = 0.001 for standard softening and with no accretion onto the perturber are illustrated in Fig. 1. The semi-major axis is plotted as a function of time in units of the initial orbital radius. In addition, the evolution expected from the analytic theory, obtained from Eq. (7) with | T | evaluated by summing the values of Twave calculated using (22) for m ≤ 100.
 |
Fig. 1 Semi-major axis, in units of the initial orbital radius as a function of time in orbits for q = 0.001. The solid curve give the results from numerical simulation, and the curve with imposed crosses is obtained using Eq. (7) with contributions to the total torque for m ≤ 100 obtained from Eq. (22). However, the main contribution comes from m = 1 in this case (see Sect. 5.1 below). The numerical simulation was performed with no accretion onto the companion. |
 |
Fig. 2 log Σ contours for q = 0.001 with softening length 0.6H after 100 orbits (left panel) and after 840 orbits (right panel). In these simulations, the companion was not allowed to accrete: its position in each case is at the centre of the small superposed red circle, located on the line at an angle of ~315° to the x axis (left panel) and at an angle of ~45° to the x axis (right panel). Short wavelength density waves are visible on both sides of the quasi-circular orbit. The relative density changes are similar in both these plots. However, the density in the interior regions of the disk decreases at later times on account of accretion through the inner boundary as is manifest in both panels. |
There is seen to be very good agreement between the two with the total amount of radial migration differing by less than 10% over 900 orbits. The form of the surface density after 100 and 840 orbits is illustrated in Fig. 2. Apart from the central regions where the surface density becomes small on account of the outflow boundary condition, the surface density remains relatively unperturbed with small amplitude density waves apparent in the vicinity of the orbit.
5.1. The dependence on the mass ratio and softening length
A comparison of orbital evolution rates calculated analytically as indicated above with those obtained from our numerical simulations for different mass ratios with standard softening and no accretion are presented in Table 1. In addition, Fig. 3 indicates the contributions from m = 1 and all m< 100 to the analytic evolution rates. There is good agreement between the numerical and analytic results given in Table 1, which differ by no more than 25%, with the maximum deviation occurring for the smallest mass ratio case.
Evolution rates calculated numerically, (drp/ dt)n, and analytically as indicated above, (drp/ dt)a, for different values of the mass ratio q.
The dependence on the softening length was also investigated for the case with q = 0.005, and the results of a comparison between numerical and analytic migration rates are shown in Fig. 3. One can see that in this case there is very good agreement between the analytical and numerical results down to softening lengths ~0.1 H.
 |
Fig. 3 Inverse of the evolution time scale defined according to Eq. (23), as a function of the dimensionless softening length Δs/H. It is expressed in units of |
6. Gap formation and migration for larger mass perturbers
We now consider perturbers massive enough to make the interaction between the disk and perturber non-linear. We first consider simplified semi-analytic models for calculating gap profiles and migration rates, subsequently comparing results with direct numerical simulations.
6.1. A simplified description of the interaction between the perturber and disk
In general 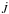 can be determined by considering the disk’s response to the perturber as disk gas streams by. When dissipation is efficient enough to prevent angular momentum being carried away by waves, the process can be modelled as a direct transfer of angular momentum to the gas particles when they are scattered by the perturber while undergoing a close approach to it (see Lin & Papaloizou 1979a,b). When dissipation is ineffective, the transferred angular momentum is carried away by waves that may dissipate in some other location, making the process non local (see e.g. Papaloizou & Lin 1984). When the disk viscosity is small, waves are expected to be excited when the perturbation is linear. On the other hand, when the perturbation is non-linear, shocks are likely to occur, resulting in the local transfer of angular momentum.
can be determined by considering the disk’s response to the perturber as disk gas streams by. When dissipation is efficient enough to prevent angular momentum being carried away by waves, the process can be modelled as a direct transfer of angular momentum to the gas particles when they are scattered by the perturber while undergoing a close approach to it (see Lin & Papaloizou 1979a,b). When dissipation is ineffective, the transferred angular momentum is carried away by waves that may dissipate in some other location, making the process non local (see e.g. Papaloizou & Lin 1984). When the disk viscosity is small, waves are expected to be excited when the perturbation is linear. On the other hand, when the perturbation is non-linear, shocks are likely to occur, resulting in the local transfer of angular momentum.
For the regions of the disk where dissipation is effective locally, we adopt the impulse approximation employed by Lin & Papaloizou (1979a,b; see also Papaloizou & Terquem 2006) in the prograde case. However, here we modify the analysis to allow for the perturber moving in the direction opposite to that of the gas. Then we find that approximately ![\begin{eqnarray} \dot J& = & -{1\over 4\pi}q^{2} (\Omega r)^{2}{r^{2}\over \Delta^2 +\Delta_{\rm s}^2} \quad {\rm when} \quad |\Delta|< r_{\rm c} \quad {\rm and} \nonumber \\[2mm] \dot J &= & 0 \quad {\rm when } \quad |\Delta|> r_{\rm c}. \label{e3} \end{eqnarray}](/articles/aa/full_html/2015/04/aa24359-14/aa24359-14-eq144.png) (28)Here Δ = r − rp, and we have introduced a gravitational softening length, Δs, which prevents a divergence when Δ → 0.
(28)Here Δ = r − rp, and we have introduced a gravitational softening length, Δs, which prevents a divergence when Δ → 0.
The cut-off radius rc gives the distance inside which the perturbation is non-linear and the impulse approximation can be employed. At greater distances we assume that the angular momentum transferred is carried away by waves, so does not affect the disk locally. We estimate that rc = min(rh,rs), where rh ≈ (q/ 3)1/3rp is the Hill radius. The “sound” radius, rs, is defined through rs = (q/δ)rp, where δ = H/r and H is the disk semi-thickness. This radius is defined as the impact parameter such that the radial velocity component of a gas particle induced by the scattering event is equal to the sound speed. When the sound radius exceeds the Hill radius, the latter is taken to be the cut-off distance.
The angular momentum carried away by waves does not affect the disk locally but should be taken into account when considering the evolution of the orbit. However, this is only a weak effect once the interaction becomes significantly non-linear since linearity then only applies at large scattering impact parameters for which the interaction is weak. Thus in that regime it may be neglected.
We here note that the linear estimate (24) can be obtained from the above arguments based on treating the disk response to the perturber using the impulse approximation. To obtain it, Eqs. (5) and (28) are used under the assumption that the latter is approximately valid even when Δ ~ ra. Approximating (5), taking the disk on both sides of the perturber into account, as 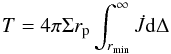 (29)and making use of (28) with Δs = 0, we recover the expression (24) when the inner cut off radius, rmin ≪ rc is set equal to 2ra/π.
(29)and making use of (28) with Δs = 0, we recover the expression (24) when the inner cut off radius, rmin ≪ rc is set equal to 2ra/π.
6.2. Evolution of the disk surface density
Multiplying Eq. (1) by r2Ω and subtracting the result from (3) we obtain an expression for vr in the form 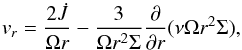 (30)and, accordingly,
(30)and, accordingly,
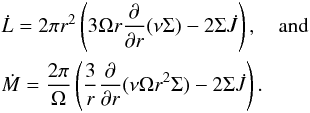 (31)Substituting Eq. (30) into Eq. (1) and making use of (28), we obtain a single equation for the evolution of the surface density in the form
(31)Substituting Eq. (30) into Eq. (1) and making use of (28), we obtain a single equation for the evolution of the surface density in the form 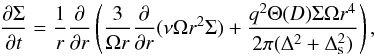 (32)where Θ(D) is the step function and D = rc − |Δ |.
(32)where Θ(D) is the step function and D = rc − |Δ |.
It is convenient to introduce dimensionless variables  and
and 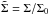 , where r0 and Σ0 are the initial orbital radius of the perturber and surface density at its initial location, respectively. In addition, we use
, where r0 and Σ0 are the initial orbital radius of the perturber and surface density at its initial location, respectively. In addition, we use 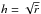 as spatial coordinate. We also assume power law dependences of ν on r and Σ through the relation
as spatial coordinate. We also assume power law dependences of ν on r and Σ through the relation 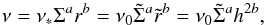 (33)where ν∗, ν0, a, and b are constants. Then Eq. (32) takes the form
(33)where ν∗, ν0, a, and b are constants. Then Eq. (32) takes the form
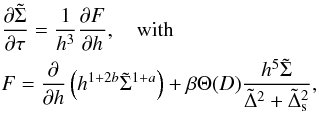 (34)and
(34)and 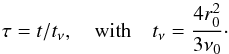 (35)Here tν is a characteristic time scale of viscous evolution of the disk at r ~ r0,
(35)Here tν is a characteristic time scale of viscous evolution of the disk at r ~ r0, 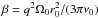 , Ω0 = Ω(r0),
, Ω0 = Ω(r0), 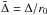 and
and 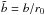 .
.
From Eqs. (31) and (34) it then follows that the mass and angular momentum fluxes can be expressed in the form 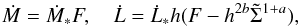 (36)where Ṁ∗ = 3πΣ0ν0 and
(36)where Ṁ∗ = 3πΣ0ν0 and 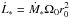 .
.
For our estimates below we use the standard representation of ν0 through the Shakura-Sunyaev parameter α (Shakura 1973; Shakura & Sunyaev 1973) as 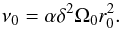 (37)The coefficient ν∗ defined through (33) can then be expressed in terms of quantities characterising opacity law in the disk and α; for an explicit expression, see Lyubarskiy & Shakura (1987) and IPP. From Eq. (37) we obtain
(37)The coefficient ν∗ defined through (33) can then be expressed in terms of quantities characterising opacity law in the disk and α; for an explicit expression, see Lyubarskiy & Shakura (1987) and IPP. From Eq. (37) we obtain 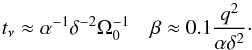 (38)
(38)
6.3. Initial and boundary conditions for a disk structured by a perturber
We assume that the disk is in a steady state at time t = 0 when the binary is introduced. In the steady state the dependence of 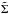 on h follows from Eqs. (34) with time derivatives and q set to zero. Thus dF/dh = 0, and therefore
on h follows from Eqs. (34) with time derivatives and q set to zero. Thus dF/dh = 0, and therefore 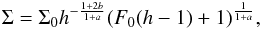 (39)and
(39)and 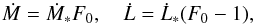 (40)where F0 is a constant of integration, and we have ensured that Σ(h = 1) = Σ0 as required by definition. Of special interest are the cases with F0 = 1 and F0 = 0. These correspond to cases with zero angular momentum flux and zero mass flux through the disk, respectively. The former case corresponds to a disk of formally infinite extent with constant mass flux equal to Ṁ∗. Recalling that the angular momentum flux in a stationary disk is determined by an inner boundary condition and is typically small, we can consider the case F0 = 1 as appropriate for astrophysical systems of interest such as a disk interacting with a binary black hole, since we expect the secondary to be immersed in the disk at radii that are much larger than its inner boundary radius2.
(40)where F0 is a constant of integration, and we have ensured that Σ(h = 1) = Σ0 as required by definition. Of special interest are the cases with F0 = 1 and F0 = 0. These correspond to cases with zero angular momentum flux and zero mass flux through the disk, respectively. The former case corresponds to a disk of formally infinite extent with constant mass flux equal to Ṁ∗. Recalling that the angular momentum flux in a stationary disk is determined by an inner boundary condition and is typically small, we can consider the case F0 = 1 as appropriate for astrophysical systems of interest such as a disk interacting with a binary black hole, since we expect the secondary to be immersed in the disk at radii that are much larger than its inner boundary radius2.
The case with F0 = 0 can approximately describe a circumbinary disk around a massive binary rotating in the same direction as the disk gas (e.g. Ivanov et al. 1999). Although there is no direct relation to situations considered in this paper, we use 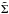 distributions for such models in several numerical runs to test different initial conditions.
distributions for such models in several numerical runs to test different initial conditions.
It is instructive to express the steady state surface density and the angular momentum flux in terms of the mass flux, the quantity h∗ = (F0 − 1) /F0, and the viscosity coefficient ν∗ defined through (33). We obtain ![\begin{eqnarray} \Sigma &=& \left({\dot M\over 3\pi \nu_*r_0^b}\right)^{1/( 1+a)} h^{-(1+2b)/( 1+a)}(h-h_*)^{1/( 1+a)} \hspace{2mm} {\rm with }\nonumber \\[2mm] \dot L&=&\dot M \Omega_0r_0^2 h_*. \label{en10a} \end{eqnarray}](/articles/aa/full_html/2015/04/aa24359-14/aa24359-14-eq204.png) (41)From (41) it is clear that h = h∗ corresponds to the inner edge of the disk, where the surface density drops to zero.
(41)From (41) it is clear that h = h∗ corresponds to the inner edge of the disk, where the surface density drops to zero.
Because we cannot perform two-dimensional numerical simulations of accretion disks of an arbitrary radial extent, we developed an approximate theory of the evolution of the disk and orbit that is valid both for disks of finite and infinite extent. This is tested against numerical simulations for the case of disks of finite extent.
6.4. Conditions for gap formation
The action of the impulsive torque per unit of mass exerted on the disk by the perturber given by (28) is to cause gas elements to lose angular momentum as they encounter and are scattered by the perturber. This causes them to move to smaller radii, enhancing any inward drift resulting from viscous evolution. Since the disk gas in the vicinity of the orbit is supplied from the outer regions of the disk at a rate determined by viscous evolution and the presence of the perturber increases the magnitude of the radial velocity, vr, that is directed inwards, a surface density depression must form close to the perturber orbit so that the continuity equation is satisfied. We hereafter describe this depression as “a gap” but emphasise that the way the gap is formed differs from what is applicable to the well known case where the perturber is in a prograde orbit (see e.g. Papaloizou & Terquem 2006).
As indicated above, the impulsive torque is efficient only when the distance from the perturber, Δ is smaller than both the Hill radius rh ≈ (q/ 3)1/3rp and “the sound radius”, rs ~ (q/δ)rp. When the mass ratio is very small and, accordingly, impulsive interactions are not effective, the angular momentum transferred between the perturber and the disk is transported away by waves, and a pronounced gap in the disk is not produced.
We make a simple estimate for when this should occur by requiring that rs be smaller than πδrp/ 2, which is half the longest wavelength associated with density waves launched by the perturber that occurs for m = 1 (see above). This gives rs<πδrp/ 2, from which we obtain 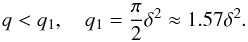 (42)We emphasise that on account of it being obtained from simple estimates, this criterion is uncertain to within a numerical factor of order unity. Nonetheless, we find that our numerical results agree with it. We adopt δ = 0.05 in our numerical calculations. Then we obtained q1 ≈ 5 × 10-3. We observed gap formation in the case of the somewhat larger q = 0.01 and did not observe it for q = 0.001.
(42)We emphasise that on account of it being obtained from simple estimates, this criterion is uncertain to within a numerical factor of order unity. Nonetheless, we find that our numerical results agree with it. We adopt δ = 0.05 in our numerical calculations. Then we obtained q1 ≈ 5 × 10-3. We observed gap formation in the case of the somewhat larger q = 0.01 and did not observe it for q = 0.001.
6.4.1. Secondary mass larger than the local disk mass
In the opposite limiting case of a large mass ratio such that the secondary mass Mp is much larger than a characteristic disk mass within its orbital radius 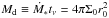 , the local viscous evolution time scale of the disk is expected to be much smaller than the evolution time scale of the binary orbit. In this case one can find the time scale for evolution of the orbit in two steps. At first, one can determine the modification of the disk structure induced by the binary assuming that its separation distance rp is fixed and then calculate the interaction torque T. One can use this in Eq. (7) to find the evolution time scale. From the condition Mp>Md we obtain
, the local viscous evolution time scale of the disk is expected to be much smaller than the evolution time scale of the binary orbit. In this case one can find the time scale for evolution of the orbit in two steps. At first, one can determine the modification of the disk structure induced by the binary assuming that its separation distance rp is fixed and then calculate the interaction torque T. One can use this in Eq. (7) to find the evolution time scale. From the condition Mp>Md we obtain 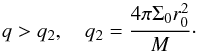 (43)
(43)
6.4.2. Issue of gravitational stability
The ratio of the local disk mass, Md, to the mass of the primary should be of the order of or smaller than δ for the disk to be gravitationally stable according to the Toomre stability criterion. It is, therefore, sufficient to have 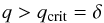 (44)for q to be larger than both q1 and q2. This case is analogous to what is considered in Ivanov et al. (1999) for systems with prograde rotation. Inequality (44) typically holds for supermassive black hole masses appropriate to galactic centres.
(44)for q to be larger than both q1 and q2. This case is analogous to what is considered in Ivanov et al. (1999) for systems with prograde rotation. Inequality (44) typically holds for supermassive black hole masses appropriate to galactic centres.
7. Simple 1D modelling of the surface density profile for the case of a relatively large mass ratio
In this section we assume that although the mass ratio q ≪ 1, the conditions q>q1 and (43) are both fulfilled and, accordingly, the ratio of the perturber mass to a characteristic mass of the disk is large. As we discussed above, in this situation the characteristic time for evolution of the perturber’s orbit is much longer than that of the disk, so that in order to model the evolution in a simple way, we can calculate quantities characterising the evolution of the system iteratively, assuming at first that the perturber’s orbital distance is fixed, analysing properties of the disk, and then calculating the evolution rate of the binary.
7.1. Structure of the gap around perturber’s orbit obtained by solving the diffusion equation and incorporating the effect of torques due to the perturber
As seen, a depression in the profile of the surface density called a gap is formed in the neighbourhood of the perturber’s orbit. Gravitational interaction with the perturber removes angular momentum from disk gas elements as they stream past it, thus increasing their radial drift velocity in the vicinity of the orbit. The formation of the gap can be described by Eq. (34), which incorporates the effects of viscosity and torques due to the perturber. It may be shown that after some relatively short period of time, the solution to (34) in the neighbourhood of r ~ rp becomes quasi-stationary. This implies that in order to find the form of 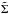 , we can assume that the dimensionless mass flux, F, defined there, does not depend on the radial coordinate h, and, accordingly, obtain an equation for
, we can assume that the dimensionless mass flux, F, defined there, does not depend on the radial coordinate h, and, accordingly, obtain an equation for 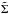 of the form
of the form 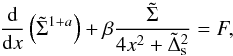 (45)where x = h − 1, the ratio rc/r0 is assumed to be small, and we also consider the region, where
(45)where x = h − 1, the ratio rc/r0 is assumed to be small, and we also consider the region, where 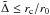 , and, accordingly, the coordinate x should be such that x− ≤ x ≤ x+, where x± = ± rc/ (2r0).
, and, accordingly, the coordinate x should be such that x− ≤ x ≤ x+, where x± = ± rc/ (2r0).
The condition (44), together with Eq. (38), imply that for α< 0.1, β should be of the order of or larger than unity, and in the limit that q ≫ qcrit we accordingly have β ≫ 1.
Since the detailed shape of 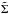 close to the orbit does not influence our results, we only consider, for simplicity, the linear case a = 0, for which the general solution to (45) can be written down in the form
close to the orbit does not influence our results, we only consider, for simplicity, the linear case a = 0, for which the general solution to (45) can be written down in the form 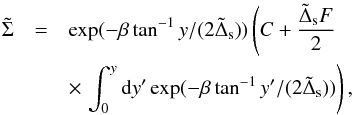 (46)where
(46)where 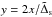 and C is an integration constant.
and C is an integration constant.
In general the integral in (46) can be expressed in terms of hypergeometric functions, but the resulting expression is cumbersome and difficult to use. The expression simplifies, however, when 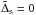 . In this case we have
. In this case we have ![\begin{eqnarray} \hspace{-4mm}\tilde \Sigma &=& {\beta F\over 4}\left({1\over z}-{\rm e}^z{\rm E}_1(z)\right ) + C_{+}{\rm e}^{z} \quad {\rm for} \quad x > 0, \nonumber \\[2mm] \hspace{-4mm} \quad \tilde \Sigma &=& {\beta F\over 4}\left ({\rm e}^{-z}{\rm Ei}(z)-{1\over z}\right ) + C_{-} {\rm e}^{-z}\quad {\rm for} \quad x < 0, \label{e10} \end{eqnarray}](/articles/aa/full_html/2015/04/aa24359-14/aa24359-14-eq241.png) (47)where z = β/ (4|x|),
(47)where z = β/ (4|x|),![\begin{eqnarray} {\rm E} _1(z)&=&\int^{\infty}_z {{\rm e}^{-t}\over t} {\rm d}t \quad {\rm and}\nonumber\\[2mm] {\rm Ei} (z)&=&\dashint^z_{-\infty} {{\rm e}^{t}\over t} {\rm d}t . \end{eqnarray}](/articles/aa/full_html/2015/04/aa24359-14/aa24359-14-eq243.png) (48)When x → 0, z → ∞ the term proportional to C+ diverges exponentially. That means that we have to set C+ = 0. In this case we have
(48)When x → 0, z → ∞ the term proportional to C+ diverges exponentially. That means that we have to set C+ = 0. In this case we have 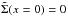 .
.
When 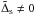 , the expression for
, the expression for 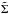 is different from (47) with the most important qualitative difference due to the fact that in this case the value of the surface density at its minimum is non-zero. Assuming that the position of the minimum,
is different from (47) with the most important qualitative difference due to the fact that in this case the value of the surface density at its minimum is non-zero. Assuming that the position of the minimum, 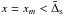 , from Eq. (45) it follows that
, from Eq. (45) it follows that 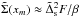 . On the other hand,
. On the other hand, 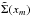 is much smaller than other terms in the expression (47) when
is much smaller than other terms in the expression (47) when 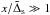 , and therefore, to account approximately for a non-zero value of the minimum, we simply add
, and therefore, to account approximately for a non-zero value of the minimum, we simply add 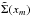 to the expression given by (47). In this way we finally obtain
to the expression given by (47). In this way we finally obtain ![\begin{eqnarray} \tilde \Sigma &\approx& {\beta F\over 4}\left({1\over z}-{\rm e}^z{\rm E}_1(z)+ 4{{\tilde \Delta_{\rm s}}^2\over \beta^2}\right ) \quad {\rm for } \quad x > 0, \quad \nonumber \\[2mm] \tilde \Sigma &=& {\beta F\over 4}\left ({\rm e}^{-z}{\rm Ei}(z)-{1\over z} + 4{{\tilde \Delta_{\rm s}}^2\over \beta^2}\right)+C_{-}{\rm e}^{-z} \hspace{2mm} {\rm for} \hspace{1mm} x < 0. \label{e10aa} \end{eqnarray}](/articles/aa/full_html/2015/04/aa24359-14/aa24359-14-eq254.png) (49)The value of the variable z, corresponding to the boundary values of x of the zone where the impulsive interactions operate, x± = ± rc/ (2r0), namely zb = βr0/ (2rc), is expected to be large. Since z ≥ zb throughout the region x− ≤ x ≤ x+ when zb ≫ 1, we can simplify the expression (49) using the corresponding asymptotic expressions of the functions E1(z) and Ei(z) for large z. In this way we get
(49)The value of the variable z, corresponding to the boundary values of x of the zone where the impulsive interactions operate, x± = ± rc/ (2r0), namely zb = βr0/ (2rc), is expected to be large. Since z ≥ zb throughout the region x− ≤ x ≤ x+ when zb ≫ 1, we can simplify the expression (49) using the corresponding asymptotic expressions of the functions E1(z) and Ei(z) for large z. In this way we get ![\begin{eqnarray} \tilde \Sigma &\approx & {F\over \beta}(4x^2 + {\tilde \Delta_{\rm s}}^2) \quad {\rm for} \quad x > 0, \quad\nonumber\\[2mm] \tilde \Sigma &= & {F\over \beta}(4x^2 + {\tilde \Delta_{\rm s}}^2)+C_{-}{\rm e}^{-z} \quad {\rm for} \quad x < 0, \label{e12} \end{eqnarray}](/articles/aa/full_html/2015/04/aa24359-14/aa24359-14-eq262.png) (50)and we recall that
(50)and we recall that 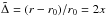 .
.
From (50) it follows that when F is fixed, β → ∞, and Δs → 0, all terms in (50) tend to zero apart from the term, proportional to the constant C−, which can be made arbitrarily large. This means that when q is large, we expect the surface density at the outer edge of the gap to be smaller than the surface density at the inner edge where there is a jump in 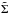 of magnitude C−.
of magnitude C−.
However, as we see below, the above analysis predicts a minimum surface density in the gap that is too small. We investigate the possibility that this is because the scattering process is not entirely localised at one radial location as has been assumed. This effect is expected to have greater significance close to the perturber.
7.1.1. Modification of the gap profile close to the perturber
When the dimensionless distance from the perturber, 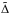 , is sufficiently small, Eq. (34) may not be adequate for describing the surface density distribution. We note that from Eq. (28) it follows that during one orbital period, the quantity,
, is sufficiently small, Eq. (34) may not be adequate for describing the surface density distribution. We note that from Eq. (28) it follows that during one orbital period, the quantity,  , for a particular gas element, changes according to
, for a particular gas element, changes according to 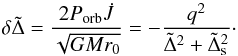 (51)When
(51)When  is sufficiently small, the magnitude of
is sufficiently small, the magnitude of  can be of the order of the magnitude of
can be of the order of the magnitude of 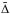 itself. In this situation, a particular gas element crosses the perturber position such that
itself. In this situation, a particular gas element crosses the perturber position such that 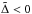 . Subsequently after each close encounter with the perturber the surface density associated with this element changes by order of itself until
. Subsequently after each close encounter with the perturber the surface density associated with this element changes by order of itself until 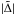 becomes large enough so that
becomes large enough so that 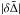 becomes smaller than
becomes smaller than 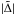 .
.
Clearly, we expect a non-zero value of the surface density even when 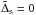 , and Eq. (50) predicts that
, and Eq. (50) predicts that 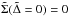 . From the condition
. From the condition 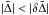 , we have
, we have 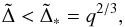 (52)and the value of the surface density at
(52)and the value of the surface density at 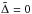 may be simply estimated with the help of Eq. (50) as
may be simply estimated with the help of Eq. (50) as 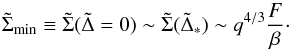 (53)We note that we have simply assumed here that the azimuthally averaged Σ does not decrease below the value at
(53)We note that we have simply assumed here that the azimuthally averaged Σ does not decrease below the value at 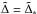 . This ignores azimuthally localised phenomena such as accretion onto the perturber, but this is not found to affect the azimuthally averaged profile much in two-dimensional simulations.
. This ignores azimuthally localised phenomena such as accretion onto the perturber, but this is not found to affect the azimuthally averaged profile much in two-dimensional simulations.
Let us consider this effect in more detail. We first introduce a new variable 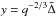 and consider a map defined by
and consider a map defined by 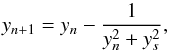 (54)where
(54)where 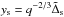 . Here yn denotes the value of y obtained after n iterations, the starting value being y0. This map describes successive changes to y for a gas element occurring as a result of scattering, obtained by application of (51). The corresponding values of the surface density
. Here yn denotes the value of y obtained after n iterations, the starting value being y0. This map describes successive changes to y for a gas element occurring as a result of scattering, obtained by application of (51). The corresponding values of the surface density 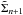 and
and 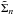 are related through conservation of mass such that
are related through conservation of mass such that 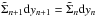 :
: 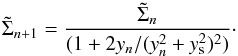 (55)The map given by (54) together with (55) can be iterated from some initial y0 ≫ 1, where the distribution (50) is valid, and we have, accordingly,
(55)The map given by (54) together with (55) can be iterated from some initial y0 ≫ 1, where the distribution (50) is valid, and we have, accordingly, 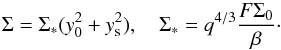 (56)We iterate the map numerically starting from several initial values of y0 to take a dependence of this procedure on initial conditions into account. They are chosen according to the rule y0 = 20 + dy(i − 1), dy = 0.01528π, and i = 1,2,3...N. An iteration proceeds until yn< 0. Then, we define a minimum surface density corresponding to a particular y0 as
(56)We iterate the map numerically starting from several initial values of y0 to take a dependence of this procedure on initial conditions into account. They are chosen according to the rule y0 = 20 + dy(i − 1), dy = 0.01528π, and i = 1,2,3...N. An iteration proceeds until yn< 0. Then, we define a minimum surface density corresponding to a particular y0 as 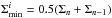 . We then average over the results obtained for different y0. The result of this calculation is shown in Fig. 4, where we plot the quantity
. We then average over the results obtained for different y0. The result of this calculation is shown in Fig. 4, where we plot the quantity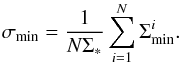 (57)for N = 1000. As seen from Fig. 4, we can approximate the dependence of σmin on ys as3
(57)for N = 1000. As seen from Fig. 4, we can approximate the dependence of σmin on ys as3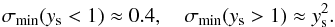 (58)From Eqs. (56) and (58), together with the definition of the parameter β, we can obtain an estimate of the minimum surface density in the gap as
(58)From Eqs. (56) and (58), together with the definition of the parameter β, we can obtain an estimate of the minimum surface density in the gap as ![\begin{eqnarray} \Sigma_{\min}\left(y_{\rm s} < 1\right)&\approx& \frac {1.2\pi q^{-2/3}F\nu_0\Sigma_0}{ \Omega_0 r_0^2}, \quad\nonumber \\[3mm] \Sigma_{\min}\left(y_{\rm s} > 1\right)&\approx& \frac{3\pi F\nu_0\Sigma_0}{\Omega_0 r_0^2} \left({{\tilde \Delta_{\rm s}}\over q}\right)^2 \cdot \label{g9} \end{eqnarray}](/articles/aa/full_html/2015/04/aa24359-14/aa24359-14-eq306.png) (59)We emphasise the approximate nature of these estimates, which are found to generally be too small by a factor of a few (see below). This is probably on account of the neglect of smoothing the profile due to the action of pressure. Finally we would like to stress that although we effectively assumed above that the orbital radius of perturber rp is close to its initial value r0, the analytic expressions are valid for any rp, by simply replacing r0 by rp in them.
(59)We emphasise the approximate nature of these estimates, which are found to generally be too small by a factor of a few (see below). This is probably on account of the neglect of smoothing the profile due to the action of pressure. Finally we would like to stress that although we effectively assumed above that the orbital radius of perturber rp is close to its initial value r0, the analytic expressions are valid for any rp, by simply replacing r0 by rp in them.
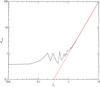 |
Fig. 4 Dependence of the mean ratio of the minimum surface density in the gap on the characteristic disk surface density Σ∗, σmin, as a function of the parameter ys. The solid curve represents the result obtained from the numerical iterations of the map based on the solution of Eqs. (54) and (55), while the dashed curve shows the analytic expression |
8. A simple procedure for calculating the accretion disk evolution together with the orbital evolution of the perturber occurring through torques exerted by the disk
As discussed above, after the perturber has been present in the disk for a time that is longer than its characteristic evolution time scale, but less than the characteristic time scale for orbital evolution, the disk structure at radii, r ~ rp, should be close to a quasi-stationary one. In this situation, the mass flux Ṁ and the dimensionless value of the specific angular momentum at the inner disk that appears in Eq. (41) may be assumed to be functions of time only with a characteristic time scale for change being much larger than required for local disk evolution.
On the other hand, in the limit q ≪ 1, the region in the vicinity of the perturber, where impulsive interaction operates, is very small, with a typical dimension ≪rp. Therefore, in the simplest treatment of the problem, we describe the influence of the perturber on the disk as providing a jump condition on the surface density, to be applied at the perturber’s orbital location in a disk otherwise evolving only under the influence of internal viscosity.
As indicated above, the mass flux through the gap is approximately constant in this limit. In addition, from the steady state solution given by Eq. (41), it can be seen that when the mass flux is fixed, stationary solutions depend only on one constant, h∗, which is proportional to the flux of angular momentum through the disk 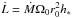 .
.
In Sect. 7 we showed that the outer disk for which r>rp should attain Σ(rp +) ~ 0 (see discussion in the penultimate paragraph of Sect. 7.1). This means that the flux of angular momentum through the disk at radii r>rp and r ~ rp, 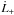 should be ~
should be ~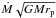 , and we must set
, and we must set 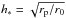 in Eq. (41) for this to be applicable to the outer disk.
in Eq. (41) for this to be applicable to the outer disk.
On the other hand, the flux of angular momentum through the inner disk, at radii <rp, 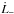 , should be equal to the angular momentum accreted per unit time by the component with the dominant mass, M. Assuming that rp is much larger than the size of the last stable orbit of that component, we can set
, should be equal to the angular momentum accreted per unit time by the component with the dominant mass, M. Assuming that rp is much larger than the size of the last stable orbit of that component, we can set 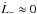 . Therefore, we set h∗ = 0 in Eq. (41) in order to apply that to the inner disk located at radii r<rp. We accordingly obtain
. Therefore, we set h∗ = 0 in Eq. (41) in order to apply that to the inner disk located at radii r<rp. We accordingly obtain
![\begin{eqnarray} && \Sigma(r)= \left({\dot M(t)\over 3\pi \nu_*r_0^b}\right)^{1/( 1+a)} \hspace{-3mm}h^{-2b/( 1+a)}, \quad {\rm for}\quad r < r_{\rm p} \quad {\rm and}\nonumber \\[2mm] && \Sigma (r)={\left({\dot M(t)\over 3\pi \nu_*r_0^b}\right)}^{1/( 1+a)}\hspace{-3mm} h^{-(1+2b)/( 1+a)}\left(h-\sqrt{r_{\rm p}/r_0}\right)^{1/( 1+a)}\nonumber \\[2mm] && {\rm for}\quad r > r_{\rm p}. \label{e13} \end{eqnarray}](/articles/aa/full_html/2015/04/aa24359-14/aa24359-14-eq325.png) (60)We notice that the first of the solutions that are appropriate to the outer disk corresponds to a steady state disk with zero couple at r = rp +, while the second solution appropriate to the inner disk corresponds to a steady state disk with zero couple at a very small inner-boundary radius.
(60)We notice that the first of the solutions that are appropriate to the outer disk corresponds to a steady state disk with zero couple at r = rp +, while the second solution appropriate to the inner disk corresponds to a steady state disk with zero couple at a very small inner-boundary radius.
For r<rp, Eq. (60) gives the value of the surface density at the inner edge of the gap for the linear case with a = b = 0 as 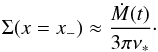 (61)This can be used to estimate the constant C− entering (47). In particular, in the limit β → ∞, for finite F, C− becomes equal to Σ(x = x−).
(61)This can be used to estimate the constant C− entering (47). In particular, in the limit β → ∞, for finite F, C− becomes equal to Σ(x = x−).
We stress again that the solution (60) is approximately valid only on scales where r is of order rp. It clearly becomes invalid on a length scale that is large enough that the characteristic time scale for evolution of the disk tdiff becomes equal to or larger than the time t, after which either the perturber is embedded in the disk or it changes its orbital radius by an amount comparable to rp. To calculate the disk evolution at large radii, it is necessary to use Eq. (34) with the time dependence retained.
Since the total angular momentum of the system is conserved and there is no angular momentum flux through the inner disk, the outward angular momentum flux through the outer disk, T, must be equal and opposite to the torque acting on the perturber due to the disk, the latter thus being −T. We have, therefore,  (62)and we recall that as Ṁ(t) > 0, T< 0 (see Sect. 3.2).
(62)and we recall that as Ṁ(t) > 0, T< 0 (see Sect. 3.2).
8.1. Evolution of the surface density in the outer disk
To model the evolution of the disk surface density along with the orbital evolution of the binary, we implemented a procedure that updates the disk surface density using Eq. (34) with the torque terms corresponding to interaction with the disk set to zero.
In our analytical work we have so far assumed, for simplicity, that the binary semi-major axis, rp, is close to its initial position, r0. However, many expressions, such as the distribution of the surface density in the gap, remain approximately valid even when rp is noticeably smaller than r0, provided that we substitute rp for r0. This can be understood as follows.
When the perturber is sufficiently heavy, the discussion in the previous section shows that the solution close to its orbit is quasi-stationary and largely unaffected by a changing rp. In this situation, it is convenient to change the unit of length in (34) from r0 to rp neglecting ṙp when carrying out this transformation. Accordingly, from now on we switch the unit of length from r0 to rp in the definition of the variable h in (34) so that 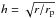 . This coincides with the previous definition
. This coincides with the previous definition 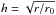 only when t = 0. Other quantities are appropriately rescaled apart from those involving Σ0, which as before denotes the initial surface density at r = r0. Then we can continue to use the kinematic viscosity prescription defined through (33). We further notice that when these changes are made, the second term in brackets in the second expression in (60) is equal to unity.
only when t = 0. Other quantities are appropriately rescaled apart from those involving Σ0, which as before denotes the initial surface density at r = r0. Then we can continue to use the kinematic viscosity prescription defined through (33). We further notice that when these changes are made, the second term in brackets in the second expression in (60) is equal to unity.
Under the above conditions, Eq. (34) gives the equation for the evolution of the surface density as 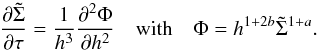 (63)in the region h> 1 with the initial conditions defined by Eq. (39) with F0 = 1 and the inner boundary condition
(63)in the region h> 1 with the initial conditions defined by Eq. (39) with F0 = 1 and the inner boundary condition 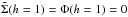 4. We adopt an outer boundary condition that either corresponds to a disk of formally infinite extent or corresponds to a finite boundary at an outer radial distance, taken to be
4. We adopt an outer boundary condition that either corresponds to a disk of formally infinite extent or corresponds to a finite boundary at an outer radial distance, taken to be  . In the former case we assume that asymptotically, when h → ∞, the angular momentum flux tends to zero; i.e., the disk approaches solution (39) with F0 = 1. Then, we find the mass flux using equation (36) with F = ∂Φ /∂h. In the latter case we assume that there is no mass flux through the outer boundary at
. In the former case we assume that asymptotically, when h → ∞, the angular momentum flux tends to zero; i.e., the disk approaches solution (39) with F0 = 1. Then, we find the mass flux using equation (36) with F = ∂Φ /∂h. In the latter case we assume that there is no mass flux through the outer boundary at 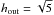 . The results obtained with this boundary condition can be directly compared with numerical simulations, most of which have adopted this boundary condition.
. The results obtained with this boundary condition can be directly compared with numerical simulations, most of which have adopted this boundary condition.
While the surface density is being updated using the above procedure, we use Eqs. (6), (7), and (62) to simultaneously find the orbital evolution of the perturber. However, after the unit of length has been changed from r0 to rp, the value of hout corresponding to a fixed pre-scaled radius grows with time. The effect of this can be taken into account within the framework of our approximation scheme by using a grid of solutions to (63) corresponding to different hout. The situation can be further simplified for the case of a constant kinematic viscosity when Eq. (63) becomes linear. In this case, its late time solution is mainly determined by the smallest eigenvalue of the linear eigenvalue problem determining the associated normal modes. The dependence of this on hout is discussed in the Appendix where it is illustrated in Fig. A.1. In our numerical work we have only considered modest changes in rp for which this effect turns out to be unimportant. It is not, accordingly, considered in the rest of the paper.
8.2. A similarity solution for an accretion disk of infinite extent
For arbitrary a and b, Eq. (63) must in general be solved numerically. However, simple arguments allow us to show that when τ ≫ 1, the accretion rate close to the perturber is approximately equal to the rate at infinity. To find the corresponding approximate non-stationary solution to (63), we note that it must have the property that ![\begin{eqnarray} \Phi(r)& \sim & h-1, \quad {\rm for} \hspace{2mm} r < r_{\rm diff}(\tau) \quad {\rm and}\nonumber\\[2mm] \Phi (r) & \rightarrow h& \quad {\rm for} \quad r \rightarrow \infty \label{e16} \end{eqnarray}](/articles/aa/full_html/2015/04/aa24359-14/aa24359-14-eq349.png) (64)to satisfy the inner boundary condition and the requirement that the disk tends asymptotically to the stationary solution with zero angular momentum flux. We recall that rdiff(τ) is the radius at which the local viscous diffusion time is equal to the current time τ in dimensionless form. Assuming that rdiff ≫ rp, the difference φ = Φ − h should be small at r>rdiff, and we can treat it as a perturbation. In this case we can obtain a linear equation for φ by linearizing (63). This takes the form
(64)to satisfy the inner boundary condition and the requirement that the disk tends asymptotically to the stationary solution with zero angular momentum flux. We recall that rdiff(τ) is the radius at which the local viscous diffusion time is equal to the current time τ in dimensionless form. Assuming that rdiff ≫ rp, the difference φ = Φ − h should be small at r>rdiff, and we can treat it as a perturbation. In this case we can obtain a linear equation for φ by linearizing (63). This takes the form 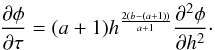 (65)We look for a self-similar solution to (65) of the form φ = φ(ξ), where the similarity variable ξ = hτ− γ and γ = (a + 1)/2c, with c = 2(a + 1) − b. The function φ then satisfies the ordinary differential equation
(65)We look for a self-similar solution to (65) of the form φ = φ(ξ), where the similarity variable ξ = hτ− γ and γ = (a + 1)/2c, with c = 2(a + 1) − b. The function φ then satisfies the ordinary differential equation 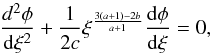 (66)and we assume from now on that c> 0. We note that rdiff(τ) can be found from the requirement ξ(rdiff,τ) = 1 and we, accordingly, have rdiff = rpτ2γ. The general solution to (66) is
(66)and we assume from now on that c> 0. We note that rdiff(τ) can be found from the requirement ξ(rdiff,τ) = 1 and we, accordingly, have rdiff = rpτ2γ. The general solution to (66) is 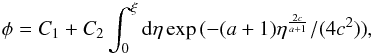 (67)where C1 and C2 are constants of integration. These are determined by the requirement that the solution should satisfy the conditions that φ → − 1 for ξ → 0 and φ → 0 for ξ → ∞5. These ensure that the surface density profile matches the required forms for h = 1 as τ → ∞, and h → ∞ for all τ. We therefore find
(67)where C1 and C2 are constants of integration. These are determined by the requirement that the solution should satisfy the conditions that φ → − 1 for ξ → 0 and φ → 0 for ξ → ∞5. These ensure that the surface density profile matches the required forms for h = 1 as τ → ∞, and h → ∞ for all τ. We therefore find 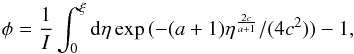 (68)where
(68)where ![\begin{eqnarray} I&=&\int_{0}^{\infty}{\rm d}\eta \exp{(-(a+1)\eta^{{2c\over a+1}}/(4c^2))}\nonumber \\[2mm] &=&{(a+1)\over 2c}\left({a+1\over 4c^2}\right )^{-{(a+1)\over2 c}} \Gamma ({(a+1)/2 c}) \end{eqnarray}](/articles/aa/full_html/2015/04/aa24359-14/aa24359-14-eq374.png) (69)with Γ denoting the gamma function.
(69)with Γ denoting the gamma function.
 |
Fig. 5 Difference φ = Φ − h is shown as a function of the radial coordinate h, at τ = 5, 20, and 100, see the text for details. |
To demonstrate the applicability of the similarity solution described above, we illustrate a numerical solution of Eq. (63) in Figs. 5 and 6. In Fig. 5 the quantity φ = Φ − h is shown at times τ = 5, 20, 100 with curves passing through larger values at the same h corresponding to later times. The solid curves are obtained by numerical solution of Eq. (63), while the dashed curves represent the analytical expression (68). For the solution shown, a = 2/3 and b = 1 (solid curve), which are the values expected for a disk with Thompson opacity being dominant. For initial condition we took Φ = h, with the adjustment as described in Sect. 8.1 , which corresponds to the distribution given by (39) with F0 = 1.
One can see that the quantity φ does have the form predicted by the expression (68). It tends to −1 at small values of h and to zero at large values of h with intermediate values being gradually shifted towards larger h with time. In Fig. 6 the dimensionless mass flux Ṁ/Ṁ∗, where Ṁ∗ = 3πΣ0ν0, is shown as a function of time for the case a = 2/3, b = 1, and the case of a = 3/7 and b = 15/14, the last corresponding to a disk opacity dominated by free-free transitions. It is clear that the mass flux tends asymptotically to its unperturbed value when τ → ∞. It can also be seen that the ratio Ṁ/Ṁ∗ never exceeds ~1.6 for all times.
 |
Fig. 6 Dimensionless mass flux Ṁ/Ṁ∗ shown as a function of time τ. The solid and dashed curves correspond to a = 2/3, b = 1 and a = 3/7, b = 15/14, respectively. |
9. Orbital evolution time scale
Since the time-dependent mass flux never significantly exceeds its unperturbed value, and tends asymptotically to this value, we estimate the mass flux in (62) as Ṁ(t) ≈ Ṁ, where Ṁ is the unperturbed mass flux, i.e. the one that existed in the disk before the secondary had been embedded. Substituting the result for T in Eqs. (6) and (7), we get 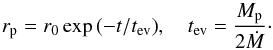 (70)In this case the orbital evolution time scale is therefore equal to the time that would be required for the steady state accretion flow through the unperturbed disk to amount to half of the perturber mass, Mp/ 2. We note that this evolution time scale was given by Nixon et al. (2011) and Roedig et al. (2014; see Eq. (9) in the latter paper in the limit of small mass ratio and small eccentricity with no accretion onto the perturber). This was obtained by simply assuming that mass flowing through the orbit transfers all its angular momentum to the companion. Here we have considered the process of gap formation, which is necessary for this time scale to be valid, as well as demonstrated compatibility with the evolution of the accretion disk that supplies the mass flow via material on approximately circular orbits.
(70)In this case the orbital evolution time scale is therefore equal to the time that would be required for the steady state accretion flow through the unperturbed disk to amount to half of the perturber mass, Mp/ 2. We note that this evolution time scale was given by Nixon et al. (2011) and Roedig et al. (2014; see Eq. (9) in the latter paper in the limit of small mass ratio and small eccentricity with no accretion onto the perturber). This was obtained by simply assuming that mass flowing through the orbit transfers all its angular momentum to the companion. Here we have considered the process of gap formation, which is necessary for this time scale to be valid, as well as demonstrated compatibility with the evolution of the accretion disk that supplies the mass flow via material on approximately circular orbits.
10. Estimating the accretion rate onto the secondary
We now give simple estimates for the possible accretion rate onto the perturber in the spirit of our simplified 1D modelling approach and conclude that this is not expected to have significant effects on orbital evolution. However, it can lead to non-trivial activity and be relevant to studies aimed at investigating the means of detecting SBBH and other similar systems.
To estimate the accretion rate, ṁ, to the secondary, we assume that all gas elements, which approach the secondary within an accretion radius, ra, are accreted to the secondary. The value of ra is estimated as in standard Bondi-Hoyle accretion (Bondi & Hoyle 1944) noting that a typical relative velocity of a gas element with respect to the secondary, vrel, is twice the Keplerian value. Accordingly, we obtain ra = qrp/ 2. By adopting these assumptions, the accretion rate to the secondary, ṁ, can be easily estimated in two limiting cases ra ≫ H and ra ≪ H6 as 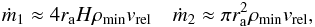 (71)where indices 1 and 2 correspond to the former and latter cases, respectively, ρmin ≈ Σmin/ (2H), and we use the first expression in (59) to estimate Σmin, making the assumption that the softening length is sufficiently small. Using the explicit expressions of all quantities entering (71), we obtain
(71)where indices 1 and 2 correspond to the former and latter cases, respectively, ρmin ≈ Σmin/ (2H), and we use the first expression in (59) to estimate Σmin, making the assumption that the softening length is sufficiently small. Using the explicit expressions of all quantities entering (71), we obtain 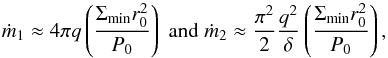 (72)where we have assumed for simplicity that rp ~ r0.
(72)where we have assumed for simplicity that rp ~ r0.
We now use the estimate of the minimum surface density given by (59) in (72) thus obtaining 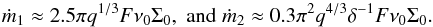 (73)The expressions (73) can be further simplified for a disk of infinite extent. From the discussion in Sect. 8.2, it follows that in this case F ~ 1 and, accordingly, the accretion rate through the disk Ṁ ~ Ṁ∗ = 3πΣ0ν0. Therefore, from the first expression in (73) we expect that
(73)The expressions (73) can be further simplified for a disk of infinite extent. From the discussion in Sect. 8.2, it follows that in this case F ~ 1 and, accordingly, the accretion rate through the disk Ṁ ~ Ṁ∗ = 3πΣ0ν0. Therefore, from the first expression in (73) we expect that 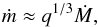 (74)where we have neglected a numerical factor order of unity. It then follows from the expression (70) for the orbital evolution time that the mass of the secondary can only increase by a fraction q1/3/ 2 during significant orbital evolution, even when the disk is very thin. This fraction will be smaller for a thick disk. We note that, in addition, the disk could be thickened locally as a result of radiative processes, producing a back reaction on the accretion flow. Thus accretion is not expected to affect the orbital evolution significantly. It is important to stress that although we have assumed that rp ~ r0 when deriving (74), this expression is, in fact, valid for any rp.
(74)where we have neglected a numerical factor order of unity. It then follows from the expression (70) for the orbital evolution time that the mass of the secondary can only increase by a fraction q1/3/ 2 during significant orbital evolution, even when the disk is very thin. This fraction will be smaller for a thick disk. We note that, in addition, the disk could be thickened locally as a result of radiative processes, producing a back reaction on the accretion flow. Thus accretion is not expected to affect the orbital evolution significantly. It is important to stress that although we have assumed that rp ~ r0 when deriving (74), this expression is, in fact, valid for any rp.
11. Numerical simulations of gap formation, migration, and accretion onto the perturber
In this section we consider numerical simulations that resulted in gap formation. They were performed for q = 0.01 with standard softening and for q = 0.02 and q = 0.01 with small softening (see Sect. 5). For cases with standard softening, the computational domain was taken to be (0.2r0,5r0). For the other cases, it was (0.4r0,4r0). Other features of the simulations were as described in Sect. 5.
11.1. Accretion and migration
Some simulations were performed with the perturber allowed to accrete mass from the disk. Following the approach of Bondi & Hoyle (1944), the accretion rate is then taken to be 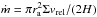 (see Eq. (71)). In implementing this we removed mass uniformly from the grid cell containing the perturber and its eight nearest neighbours. In this context we notice that in the small softening cases, the grid size is approximately equal to, or somewhat less than, both the softening length and the accretion radius. Furthermore, tests showed that results, in particular for the total amount of mass accreted over long periods of time, were not sensitive to the detailed implementation, since they were not significantly changed even when the mass was only removed from the grid cell that contained the perturber.
(see Eq. (71)). In implementing this we removed mass uniformly from the grid cell containing the perturber and its eight nearest neighbours. In this context we notice that in the small softening cases, the grid size is approximately equal to, or somewhat less than, both the softening length and the accretion radius. Furthermore, tests showed that results, in particular for the total amount of mass accreted over long periods of time, were not sensitive to the detailed implementation, since they were not significantly changed even when the mass was only removed from the grid cell that contained the perturber.
To calculate the torque acting on the perturber, contributions arising from gravitational torques from the disk, as well as the mass and momentum accreted by the perturber, were taken into account. The latter effects were found to only play a minor role for the simulations reported here. As indicated above, simulations with q < ~ 0.003 did not readily exhibit gap formation, with the perturber remaining in a type-I migration regime, at least on time scales of a few hundred orbits, although this picture could potentially be modified on very long time scales through the cumulative dissipation of weak shock waves.
 |
Fig. 7 Log Σ contours for q = 0.02 with softening length 0.1H after 50 orbits (left panel) and after 100 orbits (right panel). In these simulations the companion, its position in each case being at the centre of the small red circle located within the gap region, was allowed to accrete. The widths of the gaps slowly increase, while the accretion rates, on average, decrease slowly with time. Short wavelength density waves in the outer disks are just visible. Values of log Σ below the minimum indicated on the colour bar are plotted as that minimum value. |
 |
Fig. 8 As in Fig. 7 but for q = 0.01 with softening length 0.6H after 100 orbits (left panel) and 800 orbits (right panel). As the mass ratio is smaller in this case than for Fig. 7, the gap in the disk is narrower. The companion, indicated by a small red circle, is found in general to orbit closer to the inner disk edge at earlier times. In the left-hand panel, the companion grazes the inner edge slightly above the x axis for x< 0. This enhances the accretion rate at that stage. |
The structure of the disk gaps for q = 0.02 and q = 0.01 is illustrated in the surface density contour plots presented in Figs. 7 and 8 at various times. The runs illustrated respectively correspond to the strongest and weakest gap-forming cases considered in this section. The gap is indeed significantly wider and deeper for q = 0.02, as expected, and in addition the gap edges define significantly non-circular boundaries as mentioned above. Material crossing the gap in the form of streamers is also present7.
The semi-major axis is shown as a function of time for q = 0.02 and q = 0.01 for small softening and for q = 0.01 with standard softening in Fig. 9. The behaviour depends only very weakly on whether the perturber is allowed to accrete from the disk or not. At early times the cases with q = 0.01 have the migration rates expected in the type I regime (see Fig. 9), which is approximately ∝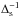 in agreement with the discussion in Sect. 5.1 above. However, after a few orbits, the effects of gap formation become noticeable, and the migration starts to slow down. For the case with q = 0.02, the initial migration rate is a factor of two less than the expected type I migration rate with the effects of gap formation being noticeable immediately. At longer times the migration rates for q = 0.01 with different softening lengths slow to become approximately equal, as would be expected if the migration was governed by the viscous evolution of the disk. There was a deeper and wider gap in the small softening case, the ultimate migration being somewhat slower. This might be expected on account of the wave excitation and associated angular momentum removal, which was apparently more effective in the case with standard softening.
in agreement with the discussion in Sect. 5.1 above. However, after a few orbits, the effects of gap formation become noticeable, and the migration starts to slow down. For the case with q = 0.02, the initial migration rate is a factor of two less than the expected type I migration rate with the effects of gap formation being noticeable immediately. At longer times the migration rates for q = 0.01 with different softening lengths slow to become approximately equal, as would be expected if the migration was governed by the viscous evolution of the disk. There was a deeper and wider gap in the small softening case, the ultimate migration being somewhat slower. This might be expected on account of the wave excitation and associated angular momentum removal, which was apparently more effective in the case with standard softening.
 |
Fig. 9 Semi-major axis, in units of the initial orbital radius, as a function of time for q = 0.02 and q = 0.01 for small softening and for q = 0.01 with standard softening. Two curves without imposed crosses, which are very close together, are shown for each of these three cases. The uppermost pair of curves corresponds to q = 0.01 with standard softening and the lowermost pair for q = 0.01 with small softening. The central pair corresponds to q = 0.02 with small softening. The lower of the pair of curves for the cases with small softening corresponds to runs with accretion from the disk included (see text). For the case with standard softening, this situation is reversed. The straight lines with superimposed crosses are obtained by adopting the initial type I migration rate with contributions from all m ≤ 100 included. The line with the more widely separated crosses corresponds to q = 0.01 with small softening, while the other line corresponds to q = 0.01 with standard softening. |
 |
Fig. 10 Mass accreted, in units of M, as a function of time for runs with accretion illustrated in Fig. 9. The uppermost curve corresponds to q = 0.01 with standard softening, the central curve to q = 0.01 with small softening, and the lowermost curve to q = 0.02 with small softening. Although the accretion rate shows large variations, these curves do not because they time average this quantity effectively. |
On the other hand, the larger open inner boundary radius adopted for the simulations with smaller softening, on account of necessary numerical convenience, results in a relatively larger angular momentum loss as material passes through it.
This angular momentum is not available to be transferred to the secondary mass resulting in an expected slowing of the inward migration rate as compared to simulations with a smaller inner boundary radius (see discussion in Sect. 8 below). The case with q = 0.02 ends with the slowest migration rate as expected. In all cases the characteristic time scale becomes comparable to or greater than that for the viscous evolution of the disk. To consider this issue more precisely, a comparison between the orbital evolution obtained from some of these simulations and the semi-analytic model for which the orbital evolution is driven by the viscous evolution of the disk is given in Sect. 9.
Accretion onto the secondary from the disk plays only a minor role in these simulations as illustrated in Fig. 10. We note that the accretion rate can show large variations on an orbital time scale. These are due to the disk edges not being circular, enabling the secondary to approach, in particular the inner disk edge, where the accretion rate naturally increases, quasi-periodically on an orbital time scale. In spite of this, it is found that the time-averaged accretion rate is well behaved and significantly slower for cases with wider and deeper gaps as expected. This is discussed further in Sect. 11.3 below. For the simulations presented here, the accretion rate is never large enough to double the perturber’s mass on its migration time scale.
11.2. Comparison of analytical and numerical results on the gap profile
 |
Fig. 11 Surface density Σ in units |
We compare results of a numerical simulation of the type described in Sect. 11 with results obtained from the numerical solution of Eq. (34) within the framework of the simplified one-dimensional model and also with an analytic surface density profile obtained (49) in Fig. 11. The adopted simulation corresponds to the case with mass ratio q = 10-2 and standard softening described in Sect. 11. The initial surface density profile was taken to be Σ = Σ0(r/r0)− 1/2, which corresponds to F0 = 0 in Eqs. (39) and (40). The value 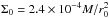 was adopted to correspond to the numerical simulation.
was adopted to correspond to the numerical simulation.
In Fig. 11 the surface density Σ is shown as a function of r/r0 for t = 1500P0. We recall that 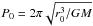 and point out that we determine the constants F and C− in (49) using the solution obtained with the help of our one-dimensional numerical approach, by matching the values of mass flux through the gap and a value of the surface density at the inner edge of the gap. We see from Fig. 11 that the profiles of Σ given by the analytical expression (49) and the numerical solution of Eq. (34) almost coincide. There is also a good agreement between the surface density profiles obtained from these approaches and those obtained from two-dimensional numerical simulations apart from the region very close to the surface density minimum.
and point out that we determine the constants F and C− in (49) using the solution obtained with the help of our one-dimensional numerical approach, by matching the values of mass flux through the gap and a value of the surface density at the inner edge of the gap. We see from Fig. 11 that the profiles of Σ given by the analytical expression (49) and the numerical solution of Eq. (34) almost coincide. There is also a good agreement between the surface density profiles obtained from these approaches and those obtained from two-dimensional numerical simulations apart from the region very close to the surface density minimum.
In this region the two-dimensional simulations give values of Σ that are roughly five times larger than the other approaches. This can be explained by having adopted an over-simplified treatment of the angular momentum exchange within the framework of the impulsive approximation. Also we note that the estimate of the minimum surface density based on Eq. (59) gives practically the same values as obtained from (49), so it is not shown. In that context we compare numerical simulation results for the minimum surface density in the gap with expression (59) in Fig. 12. The parameters of the numerical simulation we consider are the same as described above except that the mass ratio is q = 2 × 10-2 and 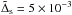 . The value of the dimensionless flux F entering (59) is calculated as outlined in Appendix A. As seen from Fig. 12, apart from the times t = 10P0 and t = 70P0, where the analytical results give a much smaller value of Σmin, the analytical and numerical results are in reasonable agreement with the numerical results giving two to three times larger values of Σmin as indicated in Sect. 7.1.1.
. The value of the dimensionless flux F entering (59) is calculated as outlined in Appendix A. As seen from Fig. 12, apart from the times t = 10P0 and t = 70P0, where the analytical results give a much smaller value of Σmin, the analytical and numerical results are in reasonable agreement with the numerical results giving two to three times larger values of Σmin as indicated in Sect. 7.1.1.
 |
Fig. 12 Minimum value of surface density Σmin in the gap in units of initial surface density |
11.3. Comparison of the analytic estimate of the accretion rate with the results of a simulation
 |
Fig. 13 Accretion rate onto the secondary in units M/P0 as a function of time. The dotted curve, showing large variations, is obtained numerically, the solid curve represents the numerical results time averaged over 7.5 periods, while the dashed curve represents ṁ2 as specified through one of the Eqs. (73). |
We consider the run with q = 2 × 10-2 and δ = 0.05 described in Sect. 11. A comparison of the accretion rate measured in the numerical simulation with our analytical estimate is shown in Fig. 13. Since in this case ra<h, we use the second expression in (73) to make the comparison. The numerical data show sharp variations in the accretion rate. These variations are due to the secondary approaching the inner disk edge where the surface density is larger. Such approaches can occur because the inner disk edge is not circular, and they repeat approximately periodically on the orbital time scale. This effect may have important observational consequences since it may lead to variation in the secondary luminosity.
When the numerical data is averaged over time intervals of 7.5 orbital periods, there is good agreement between both approaches with the analytical curve giving somewhat smaller values of ṁ. This may be because our analytical expression for Σmin underestimates the minimum values of the azimuthally averaged surface density in the gap that is found in simulations. But the accretion rate can reach values that are an order of magnitude larger than the locally averaged value.
11.4. A comparison of semi-analytic models and numerical simulations of migration in an accretion disk of finite extent in which a gap forms
Here we compare orbital migration determined using Eqs. (6), (7), and (62), together with (63) (see Sect. 9) with results of numerical simulations. We performed several two-dimensional numerical simulations of accretion disks of finite radial extent, 0.25 ≤ r/r0 ≤ 5. We notice that for these disks the dependence of Ṁ on t differs from what is appropriate to the case of a disk of formally infinite extent. In this case, a slightly different calculation of the dependence of Ṁ(t) needs to be undertaken to compare with the orbital evolution obtained from simulations.
Here we make a comparison for a sufficiently large mass ratio, q = 10-2, and two disk models. Model 1 employed the non-linear viscosity law with a = 2/3, b = 1, and the initial surface density profile corresponding to zero angular momentum flux through the disk, i.e. given by Eq. (39) with F0 = 1. Model 2 adopted a constant viscosity for which a = b = 0 and the initial surface density profile as for Model 1. In both cases the dimensionless viscosity coefficient ν0 = 10-5, δ = 0.05, we adopted standard softening and the initial disk mass, Md = 3 × 10-3M.
For Model 1 we solve Eq. (63) numerically, and use Eqs. (6), (7), (62), and the definition of Ṁ∗ to find the dependence of rp on time. The dimensionless mass flux for this model is shown in Fig. 14 as a function of time τ, and the binary separation distance as a function of t/P0 is shown in Fig. 15 together with the results obtained from the two-dimensional numerical simulation. One can see that both approaches give excellent agreement. The result based on the solution of (63) also predicts that the evolution stalls eventually, since on account of its being finite, all the disk mass is eventually accreted by the primary in this model.
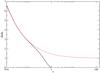 |
Fig. 14 Dimensionless mass flux Ṁ/Ṁ∗ as a function of time τ for the case a = 2/3, b = 1 (model 1). The solid curve corresponds to our model of the disk of finite size. The dashed curve shows, for comparison, the same dependence for the disk of formally infinite extent. |
 |
Fig. 15 Dependence of the binary separation distance, rp/r0, as a function of t/P0 for Model 2. We recall that r0 and P0 are the binary separation distance and orbital period at the initial time t = 0. The solid curve is obtained from the solution of Eq. (63), while the dashed curve represents the results of a two-dimensional numerical simulation. |
For Model 2 we develop an analytic approach to calculating the evolution of rp in Appendix A. The result is given by Eq. (A.13) and is compared with a two-dimensional simulation in Fig. 16. As for the non-linear case, we again have very good agreement between the numerical and analytical approaches.
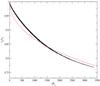 |
Fig. 16 Dependence of the binary separation distance on time. The solid curve shows the result of numerical simulation with the mass ratio q = 10-2 and other parameters described in the text. The dashed curve is calculated from Eq. (A.13). |
12. Discussion
This paper has studied the evolution of a secondary mass embedded in an accretion disk in a quasi-circular retrograde orbit. Before summarising our conclusions, we briefly discuss some additional phenomena and processes that may be important under some circumstances. We consider both the effects that could occur if the binary orbit possessed a moderate-to-large eccentricity and the importance of orbital evolution arising from the radiation of gravitational waves for perturbers orbiting close to the central mass.
Additional phenomena and processes
12.1. A binary with large orbital eccentricity
A binary black hole may have large eccentricity at the stage where interaction with the disk becomes important (see e.g. Polnarev & Rees 1994). In other potential astrophysical applications of the scenario considered in this paper, such as to exoplanetary systems, the orbital motion of a massive planet can, in principle, be oppositely directed to that of the protoplanetary disk, only as a result of its gravitation interaction with other objects. In this case, large eccentricities would also be expected. Perhaps, the most important qualitative difference between the case of an eccentric binary and the case of circular binary considered in this paper is that in the former case, outer Lindblad resonances are still possible, though with amplitudes significantly reduced in comparison to the prograde case. Unlike the impulsive and non-resonant torques considered in this paper, the Lindblad torques are necessarily positive with respect to the direction of gas motion, see for instance Goldreich & Tremaine (1979). Thus, if a disk is sufficiently thin, there is a possibility of gap formation in the “standard sense” with the disk gas being repelled from the binary orbit radii as the result of an outward flux of positive angular momentum supplied by waves launched at the resonances. We briefly consider this possibility and estimate typical disk parameters for which a gap could be opened, assuming that the binary has an eccentricity e ~ 1.
We use the standard expressions for the resonant torques, Tml, associated with perturbations with a particular azimuthal mode number, m, and a particular time harmonic number l using expressions from Artymowicz & Lubow (1994, hereafter AL) for the corresponding component of the gravitational potential due to the perturber assuming that the binary mean motion, or orbital angular velocity, ω, entering these expressions is negative. Then, terms with negative values of l correspond to waves propagating in the direction of the disk’s rotation. It is readily found (see e.g. AL) that the torques Tml scale approximately as e2|m − l | in the limit of small eccentricities. Therefore, we parametrise them through the expression 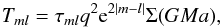 (75)where a is the semi-major axis that is such that a = rp when e = 0.
(75)where a is the semi-major axis that is such that a = rp when e = 0.
The most important torques Tml are those corresponding to the smallest difference | m − l | with l< 0, i.e. terms with m = 1 and l = −1, m = 2 and l = −1 and so on. Assuming that e is small, one can use expressions in AL to obtain  (76)and the corresponding resonances reside at radii
(76)and the corresponding resonances reside at radii  (77)A general dependence of these quantities on e can be obtained numerically. This is shown in Fig. 17 together with a corresponding calculation with m = 2,l = 1 evaluated for a prograde orbit, which is shown for comparison.
(77)A general dependence of these quantities on e can be obtained numerically. This is shown in Fig. 17 together with a corresponding calculation with m = 2,l = 1 evaluated for a prograde orbit, which is shown for comparison.
 |
Fig. 17 Dimensionless torques τml for the cases m = 1,l = −1 (solid curve), m = 2,l = −1 (dashed curve), and m = 2,l = 1 (dotted curve) as functions of eccentricity e. The solid curve ends at e = 0.58. At this value of eccentricity, the apocentre distance rp = a(1 + e) is equal to r(1, − 1) given by Eq. (77). At larger values of e, the corresponding resonance lies within the binary orbit. Also, the case m = 2,l = 1 shown for illustration corresponds to prograde orbital motion of the binary. |
As indicated by Fig. 17, the asymptotic expressions (76) are approximately valid even in case of rather large eccentricities. In particular, the numerical factor in the (1, − 1) term changes from 0.69 to 0.76 when e grows from zero to its maximal value ≈0.58 corresponding to the position of the resonance situated at the apocentre distance. Analogously, the numerical factor of the (2, − 1) term is smaller than unity for eccentricities smaller than 0.72. Thus, the expressions (76) can be used for estimates of the corresponding torques at moderate values of eccentricity. Accordingly, we use expressions for our estimates of conditions for gap formation below.
To proceed we use the criterion proposed in Lin & Papaloizou (1979b), see also AL. Namely, we assume that a gap can be opened provided the angular momentum flux due to viscous forces, 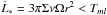 . We note that
. We note that 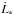 is evaluated at r = r(m,l). Using this condition, Eqs. (37), (75), and assuming that α and δ are small, we obtain a condition for gap formation in the form
is evaluated at r = r(m,l). Using this condition, Eqs. (37), (75), and assuming that α and δ are small, we obtain a condition for gap formation in the form 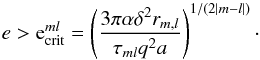 (78)Now we use (76) and (77) to obtain
(78)Now we use (76) and (77) to obtain 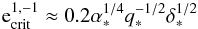 (79)and
(79)and 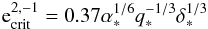 (80)for m = 1, l = −1, and m = 2, l = −1, respectively, where α∗ = α/ 10-2, q∗ = q/ 10-2, and δ∗ = δ/ 10-3.
(80)for m = 1, l = −1, and m = 2, l = −1, respectively, where α∗ = α/ 10-2, q∗ = q/ 10-2, and δ∗ = δ/ 10-3.
Since the critical eccentricities are in the range of 0.2 − 0.4 for very thin accretion disks, which may be present in galactic nuclei, this effect may operate there. The situation is less favourable for protoplanetary disks, where we typically have δ ~ 0.05, and, accordingly, δ∗ ~ 50. In this case we have the critical eccentricities formally exceeding unity for α∗ = 1, and this effect is, therefore, unlikely to operate unless α is very small.
We comment that the gap opening process considered here differs from the one considered in previous sections for near circular orbits for which the disk edges are relatively close to the perturber. For the case of a perturber in an eccentric orbit considered here, the gap is maintained by interactions at Lindblad resonances such that the outer disk edge may be a distance of order a even from apocentre. Angular momentum transfer to the perturber from material streaming through the cavity due to viscous evolution of the disk may occur and also contribute to maintaining the gap. However, on account of a gap being produced through their action, Lindblad torques are at least comparable to viscous torques. Accordingly angular momentum exchange with the perturber due to Lindblad torques and streaming material are potentially comparable.
If the gap opening by Lindblad resonances can indeed be realised and these are important for the angular momentum exchange, the binary evolution would be quite different from what is described in this paper. It may be closer to the regime discussed by IPP. Non-resonant effects may, however, interfere with gap formation owing to resonances when the apocentre approaches the radius of a resonance.
Also, when resonances give the main contribution in the energy and angular momentum exchange between the binary and the disk, the binary eccentricity decreases with time, and, therefore, the gap can be eventually overrun by the disk gas, after which, the evolution will proceed in a manner similar to the one discussed in this paper8. The effects discussed above are in need of further investigation.
In this context we notice that the evolution of massive binary immersed in a circumbinary disk is also potentially interesting in the context of disk-planet interactions (see e.g. Papaloizou et al. 2007, for a review). Although it is generally accepted that the planets are formed in the protoplanetary disk rotating in the prograde sense, a gravitational interaction between a group of planets (see e.g. Rasio & Ford 1996; Papaloizou & Terquem 2001) may, in principle, lead to the formation of a planetary orbit of large eccentricity with the direction of orbital rotation opposite to that of a disk of finite extent in which it is partially embedded. Physically, this may be achieved by different generalisations of the well-known Lidov-Kozai effect, such as in Ziglin (1975), Farago & Laskar (2010), Katz et al. (2011), and Li et al. (2013).
12.2. The influence of the emission of gravitational waves on the orbital evolution and accretion rate for SBBH
In the case of SBBH there is an additional important mechanism for driving orbital evolution through emission of gravitational waves. For a circular orbit and q ≪ 1, the corresponding time scale can be easily obtained from expressions given by Landau & Lifshitz (1975), among others, as 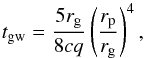 (81)where rq = 2GM/c2 ≈ 3 × 1013M8 cm, with M8 = M/ 108M⊙, and c denoting the speed of light from now on.
(81)where rq = 2GM/c2 ≈ 3 × 1013M8 cm, with M8 = M/ 108M⊙, and c denoting the speed of light from now on.
From Eq. (70) it follows that the time scale for orbital evolution due to interaction with the disk can be written in the form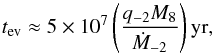 (82)where q-2 = q/ 10-2 and Ṁ-2 = Ṁ/ (10-2M⊙ yr-1). From the condition tgw<tev we conclude that gravitational waves will determine the orbital evolution when
(82)where q-2 = q/ 10-2 and Ṁ-2 = Ṁ/ (10-2M⊙ yr-1). From the condition tgw<tev we conclude that gravitational waves will determine the orbital evolution when 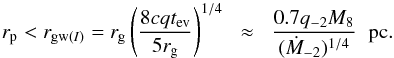 (83)The orbital period at rp ~ rgw(I) being given by
(83)The orbital period at rp ~ rgw(I) being given by 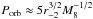 yr, where r-2 = rp/ (10-2 pc) is expected to be a few years. From the definition of rgw(I), and (81) it also follows that
yr, where r-2 = rp/ (10-2 pc) is expected to be a few years. From the definition of rgw(I), and (81) it also follows that 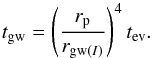 (84)Another important scale, rgw(ν), is determined by the condition that the time scale for orbital evolution due to gravitational radiation be less than the time scale for viscous evolution of the disk, or tgw(rp<rgw(ν)) <tν. Making use of (37) we obtain
(84)Another important scale, rgw(ν), is determined by the condition that the time scale for orbital evolution due to gravitational radiation be less than the time scale for viscous evolution of the disk, or tgw(rp<rgw(ν)) <tν. Making use of (37) we obtain ![\begin{equation} r_{{\rm gw}(\nu)}=r_{\rm g} \left[\frac{32\sqrt{2}q}{15\alpha\delta^2 }\right]^{2/5} \approx 5\times 10^{-3}M_{8}\,(q_{-2})^{2/5}\alpha_{*}^{-2/5} \delta_{*}^{-4/5}~{\rm pc}. \label{w5} \end{equation}](/articles/aa/full_html/2015/04/aa24359-14/aa24359-14-eq504.png) (85)When r<rgw(ν), the absolute value of the radial velocity of the perturber exceeds that of the disk gas. In this regime the disk gas is transferred from the inner part of the disk to the outer part opposite to the regime considered above. However, arguments leading to expression (74) remain essentially the same if instead of the accretion rate through the disk, Ṁ, the rate of transfer of the disk gas through perturber’s orbit, Ṁtr, is used. Here, Ṁtr is defined in the frame, where the perturber is at rest. We can estimate it as Ṁtr ~ Md(r<rp) /tgw, where the disk mass inside the perturber’s orbit can be found from the first expression of (60). On the other hand, as discussed above, the disk inside the perturber’s orbit may be approximated as a stationary disk characterised by the accretion rate Ṁ, and, therefore, its mass can be estimated as Md(r<rp) ~ Ṁtν. Taking these considerations into account, we obtain
(85)When r<rgw(ν), the absolute value of the radial velocity of the perturber exceeds that of the disk gas. In this regime the disk gas is transferred from the inner part of the disk to the outer part opposite to the regime considered above. However, arguments leading to expression (74) remain essentially the same if instead of the accretion rate through the disk, Ṁ, the rate of transfer of the disk gas through perturber’s orbit, Ṁtr, is used. Here, Ṁtr is defined in the frame, where the perturber is at rest. We can estimate it as Ṁtr ~ Md(r<rp) /tgw, where the disk mass inside the perturber’s orbit can be found from the first expression of (60). On the other hand, as discussed above, the disk inside the perturber’s orbit may be approximated as a stationary disk characterised by the accretion rate Ṁ, and, therefore, its mass can be estimated as Md(r<rp) ~ Ṁtν. Taking these considerations into account, we obtain 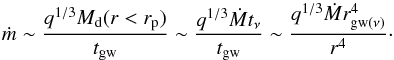 (86)This indicates that the accretion rate onto the secondary can exceed the rate onto the primary, ~Ṁ, provided that
(86)This indicates that the accretion rate onto the secondary can exceed the rate onto the primary, ~Ṁ, provided that 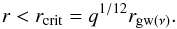 (87)Since the power of q in (87) is small, we find that typically rcrit ~ rgw(ν); however, even when r<rcrit, the luminosity of the secondary does not necessarily exceed that of the primary. This is also determined whether the mode of accretion onto the secondary is disk-like or more approximately spherical. This issue is one for future investigation.
(87)Since the power of q in (87) is small, we find that typically rcrit ~ rgw(ν); however, even when r<rcrit, the luminosity of the secondary does not necessarily exceed that of the primary. This is also determined whether the mode of accretion onto the secondary is disk-like or more approximately spherical. This issue is one for future investigation.
12.3. Secular evolution of directions of angular momenta of the binary and the disk
As mentioned in the Introduction, the gravitational torque exerted by a stationary twisted circumbinary disk on the binary orbit changes its orientation on a long time scale tor. It is assumed that the disk is aligned with the binary orbital plane on smaller scales than the alignement radius ral, but misaligned on scales ral with some inclination angle, which may be initially small but subsequently may become large enough for non-linear effects to become important. The action of the disk torque tends to overturn the binary orbit when it is retrograde (see e.g. IPP).
When the inclination angle is large enough, non-linear effects are important, and for an estimate of the time tor, we formally assume that the effective α for the twisted disk ~1; see, for example, Ogilvie (1999) for a theoretical justification and also Lodato & Price (2010) for numerical SPH simulations of the evolution of twisted disks in the regime of large gradients of the disk’s tilt9. We then use the simple estimate of tor given in IPP as 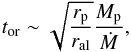 (88)where the alignement radius
(88)where the alignement radius 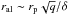 (see Eq. (23) of IPP). Recalling that the orbital evolution time scale tev = Mp/ (2Ṁ), we get
(see Eq. (23) of IPP). Recalling that the orbital evolution time scale tev = Mp/ (2Ṁ), we get 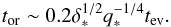 (89)Although the numerical factor in (89) is clearly approximate, it would increase if a smaller effective value of α had been used as long as it exceeded δ. One sees that as long as ral ~ rp, as is the case for the gap-forming simulations discussed in Sect. 11, tor ~ tev, which occurs because the process inducing inclination changes works at the same rate as the one producing changes to the semi-major axis. In that case changes in the orientation of the orbit may not be significant. On the other hand, for some values of q and δ, ral could exceed rp enough that the time scale for the orientation evolution could be somewhat smaller than the orbital evolution time scale leading to significant changes in inclination. This is an aspect to consider in future study.
(89)Although the numerical factor in (89) is clearly approximate, it would increase if a smaller effective value of α had been used as long as it exceeded δ. One sees that as long as ral ~ rp, as is the case for the gap-forming simulations discussed in Sect. 11, tor ~ tev, which occurs because the process inducing inclination changes works at the same rate as the one producing changes to the semi-major axis. In that case changes in the orientation of the orbit may not be significant. On the other hand, for some values of q and δ, ral could exceed rp enough that the time scale for the orientation evolution could be somewhat smaller than the orbital evolution time scale leading to significant changes in inclination. This is an aspect to consider in future study.
13. Summary of results and conclusions
This paper has considered a binary with a small mass ratio q ≪ 1 embedded in an accretion disk with the direction of orbital motion being retrograde with respect to the rotation of the disk. We studied the evolution of the semi-major axis and the mass accretion rate onto the secondary component, focusing on the case of a quasi-circular orbit.
We employed several approaches to the problem. A simple semi-analytic approach based on solving a one-dimensional diffusion equation for the disk surface density that incorporated a local scattering model for estimating the rate of angular momentum exchange between the orbit and disk, which resulted in the orbit evolving. In addition to this, we presented a simplified, purely analytic calculation of the surface density profile in the vicinity of the perturber and the construction of a similarity solution for the outer disk that was applicable when the latter had an infinite extent. Under the assumption of slow orbit evolution, which is valid when the secondary mass is much larger than the local disk mass, the rate of orbital evolution in the form of an inward migration could be readily calculated. In addition to these approaches, we performed two-dimensional numerical hydrodynamical simulations. All methods were found to be in qualitative, and often in quantitative agreement, as in the context of orbital semi-major axis evolution.
We found that for binaries with very small mass ratios, the secondary component migrated through the disk, leaving the surface density virtually unchanged. This corresponds to the usual type I migration regime for prograde orbits. The orbital evolution is due to the launching of tightly wound density waves that propagate away from the orbit (see Sect. 4). We calculate the evolution rate, which is much less than in the prograde case.
When the mass ratio is large enough, q > ~ 1.57δ2, ~10-3−10-2, for the typical parameters being considered, a gap in the disk opens in the vicinity of the perturber’s orbit (see Sects. 6.4 and 11). However, the form of the gap and the way it opens are not the same as in the prograde case. In the retrograde case, gap opening is produced by efficient removal of angular momentum in the vicinity of the orbit as the disk material passes through it. This leads to a depression of the surface density profile near the orbit that we are able to match quite well using simplified analytic modelling.
Provided that the secondary mass is significantly larger than the typical disk mass in the vicinity of its orbit, the disk outside the gap over a length scale of order rp relaxes to a quasi-stationary state characterised by the rate of mass flow through the disk, Ṁ, on a time scale that is characteristic of the local viscous time scale, but significantly shorter than the characteristic time scale of orbital evolution, tev. For a disk of large radial extent Ṁ is comparable to the accretion rate at large distances. The orbital evolution time scale, tev, was found to be Mp/ (2Ṁ), where Mp is the secondary mass (see Sect. 9).
When the orbital evolution is solely determined by interaction with the disk, the time-averaged accretion rate onto the secondary, ṁ, is estimated to be at most ṁ ~ q1/3Ṁ, which is significantly smaller than the accretion rate onto the primary ~Ṁ (see Sect. 10). This behaviour is different from what is seen in the prograde case, where the accretion rates can be reduced due to the presence of a deep cavity in the disk on scales ~rp. Our numerical results also show large variations of the accretion rate on the orbital time scale. If the radiative efficiency of the accretion onto the secondary is large enough, the binary may manifest itself as a non-stationary source of radiation with a typical time scale for variability close to the orbital period. It may also be observed as two nearby sources of radiation being blue-shifted and red-shifted with respect to each other.
In the case of a supermassive binary black hole, the orbital evolution is also influenced significantly by the emission of gravitational waves. This effect becomes more important than the interaction with the disk when rp< 10-2 pc, for typical parameters of the problem. When the evolution is governed by gravitational wave emission such that its inward radial drift speed exceeds the gas radial velocity induced by disk viscosity, it is expected that the accretion rate onto the perturber would increase, possibly becoming greater than Ṁ for a brief period of time (see Sect. 12.2). Another open issue for future study is the behaviour of the system when the orbit has an appreciable eccentricity. We indicated in Sect. 12.1 that when the binary is very eccentric and the disk is very thin, a conventional gap may be opened because of the effect Lindblad resonances, which are present in this case even for binaries with retrograde orbital motion relative to the disk. In addition to a systematic detailed study of effects arising from orbital eccentricity, another issue for future consideration is the influence of the mutual inclination of the binary orbital plane with respect to the disk mid-plane and the effect of secular evolution of the binary inclination with respect to the disk plane at large distances.
Online material
Movie 1 Access here
Movie 2 Access here
Hydrodynamic interaction of the secondary with the accretion disk during the alignment process is discussed in e.g. Ivanov et al. (1998).
In fact the initial distribution (39) is not compatible with the inner boundary condition; accordingly, in practice, when solving (63) numerically we modify the stationary solution (39) by adjusting the surface density profile within a small transitional region 1 ≤ h ≤ 1 + Δh, Δh< 1, in order that 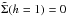 . An exact form of the surface density profile in the transitional region is not important for the solution at large time τ> 1.
. An exact form of the surface density profile in the transitional region is not important for the solution at large time τ> 1.
The latter case formally violates the sufficient condition for a “sufficiently massive” binary (44). Nonetheless we consider it to compare our analytical estimates with the results of numerical simulations, for which the disk is relatively thick and which marginally corresponds to this case even though q exceeds both q1 and q2 so that the binary is in fact “sufficiently massive”.
Animations of the process of gap formation can be found online or at http://astro.qmul.ac.uk/people/sijme-jan-paardekooper/publications
We also point out that SPH simulations with a large mass ratio, q = 1, indicate that when the eccentricity is sufficiently large, the inclination angle between the binary and the disk may grow with time (see Roedig & Sesana 2014).
There are non-linear effects operating in twisted disks with finite inclination angles, which are not considered in Ogilvie (1999), such as a possibility of standing shocks; see e.g. Fragile & Blaes (2008). These effects could lead to additional damping of non-stationary twisted disturbances once the inclination to the binary orbit exceeds ~ δ; see e.g. Sorathia et al. (2013), and may act so as to produce an increase in the effective α. Also, the presence of shocks may increase the disk thickness since they provide an additional source of energy dissipation.
Acknowledgments
We are grateful to R. R. Rafikov, V. V. Sidorenko, and the referee for useful comments. P.B.I. was supported in part by RFBR grant 15-02-08476-a and programmes 9 and 22 of the Russian Academy of Sciences and in part by the Grant of the President of the Russian Federation for Support of Leading Scientific Schools of the Russian Federation NSh-4235.2014.2.
References
- Amaro-Seoane, P., Aoudia, S., Babak, S., et al. 2013,GWN, 6, 4 [Google Scholar]
- Armitage, P. J., & Natarajan, P. 2002, ApJ, 567, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Artymowicz, P., & Lubow, S. H. 1994, ApJ, 421, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Begelman, M. C., Blandford, R. D., & Rees, M. J. 1980, Nature, 287, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Bogdanovic, T., Smith, B. D., Sigurdsson, S., & Eracleous, M. 2008, ApJS, 174, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Bogdanovic, T., Eracleous, M., & Sigurdsson, S. 2009, New Astron., 53, 113 [CrossRef] [Google Scholar]
- Bondi, H., & Hoyle, F. 1944, MNRAS, 104, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Burke-Spolaor, S. 2013, CQGRA, 30, 4013 [CrossRef] [Google Scholar]
- Corsini, E. M. 2014, in Counter-Rotation in Disk Galaxies, eds. E. Iodice, & E. M. Corsini (San Francisco: ASP), ASP Conf. Ser., 486, 51 [Google Scholar]
- Cuadra, J., Armitage, P. J., Alexander, R. D., & Begelman, M. C. 2009, MNRAS, 393, 1423 [NASA ADS] [CrossRef] [Google Scholar]
- Farago, F., & Laskar, J. 2010, MNRAS, 401, 1189 [NASA ADS] [CrossRef] [Google Scholar]
- Farris, B. D., Liu, Y. T., & Shapiro, S. L. 2011, Phys. Rev. D, 84, 4024 [Google Scholar]
- Farris, B. D., Duffell, P., MacFadyen, A. I., & Haiman, Z. 2014, ApJ, 783, 73 [Google Scholar]
- Fragile, P. C., & Blaes, O. M. 2008, ApJ, 687, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Grishchuk, L. P., Lipunov, V. M., Postnov, K. A., Prokhorov, M. E., & Sathyaprakash, B. S. 2001, Physics Uspekhi, 44, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Gold, R., Paschalidis, V., Etienne, Z. B., Shapiro, S. L., & Pfeiffer, H. P. 2014, Phys. Rev. D, 89, 4060 [Google Scholar]
- Goldreich, P., & Tremaine, S. 1979, ApJ, 233, 857 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Gould, A., & Rix, H.-W. 2000, ApJ, 532, L29 [Google Scholar]
- Haiman, Z., Kocsis, B., & Menou, K. 2009, ApJ, 700, 1952 [NASA ADS] [CrossRef] [Google Scholar]
- Hayasaki, K., Saito, H., & Mineshige, S. 2013, PASJ, 65, 86 [NASA ADS] [Google Scholar]
- Ivanov, P. B., Igumenshchev, I. V., & Novikov, I. D. 1998, ApJ, 507, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanov, P. B., Papaloizou, J. C. B., & Polnarev, A. G. 1999, MNRAS, 307, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Ju, W., Greene, J. E., Rafikov, R. R., Bickerton, S. J., & Badenes, C. 2013, ApJ, 777, 44 [Google Scholar]
- Katz, B., Dong, S., & Malhotra, R. 2011, Phys. Rev. Lett., 107, 1101 [Google Scholar]
- King, A. R., Lubow, S. H., Ogilvie, G. I., & Pringle, J. E. 2005, MNRAS, 363, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Kocsis, B., Haiman, Z., & Loeb, A. 2012, MNRAS, 427, 2680 [NASA ADS] [CrossRef] [Google Scholar]
- Komberg, B. V. 1968, Sov. Astron., 11, 727 [NASA ADS] [Google Scholar]
- Komossa, S. 2006, Mem. Soc. Astron. It., 77, 733 [Google Scholar]
- Landau, L. D., & Lifshitz, E. M. 1975, The Classical Theory of Fields, Vol. 2, 4th edn. (Butterworth-Heinemann) [Google Scholar]
- Li, G., Naoz, S., Kocsis, B., & Loeb, A. 2013, ApJ, 785, 116 [Google Scholar]
- Lin, D. N. C., & Papaloizou, J. 1979a, MNRAS, 186, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, D. N. C., & Papaloizou, J. 1979b, MNRAS, 188, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, D. N. C., & Papaloizou, J. 1986, ApJ, 309, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, D. N. C., & Papaloizou, J. C. B. 1993, in Protostars and planets III (A93-42937 17-90), 749 [Google Scholar]
- Liu, F. K. 2004, MNRAS, 347, 1357 [NASA ADS] [CrossRef] [Google Scholar]
- Lobanov, A. P., & Roland, J. 2005, A&A, 431, 831 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lodato, G., & Price, D. J. 2010, MNRAS, 405, 1212 [NASA ADS] [Google Scholar]
- Lodato, G., Nayakshin, S., King, A. R., & Pringle, J. E. 2009, MNRAS, 398, 1392 [NASA ADS] [CrossRef] [Google Scholar]
- Loeb, A. 2007, Phys. Rev. Lett., 99, 1103 [Google Scholar]
- Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Lyubarskiy, Y. E., & Shakura, N. I. 1987, Sov. Astron. Lett., 13, 386 [NASA ADS] [Google Scholar]
- MacFadyen, A. L., & Milosavljevic, M. 2008, ApJ, 672, 83 [Google Scholar]
- McKernan, B., Ford, K. E. S., Kocsis, B., Lyra, W., & Winter, L. M. 2014, MNRAS, 441, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Montuori, C., Dotti, M., Colpi, P., Decarli, R., & Haart, F. 2011, MNRAS, 412, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Montuori, C., Dotti, M., Haardt, F., Colpi, M., & Decarli, R. 2012, MNRAS, 425, 1633 [NASA ADS] [CrossRef] [Google Scholar]
- Nixon, C. J., King, A. R., & Pringle, J. E. 2011a, MNRAS, 417, L66 [NASA ADS] [CrossRef] [Google Scholar]
- Nixon, C. J., Cossins, P. J., King, A. R., & Pringle, J. E. 2011b, MNRAS, 412, 1591 [NASA ADS] [CrossRef] [Google Scholar]
- Ogilvie, G. I. 1999, MNRAS, 304, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Paardekooper, S.-J., & Papaloizou, J. C. B. 2009, MNRAS, 394, 2297 [NASA ADS] [CrossRef] [Google Scholar]
- Papaloizou, J., & Lin, D. N. C. 1984, ApJ, 285, 818 [NASA ADS] [CrossRef] [Google Scholar]
- Papaloizou, J. C. B., & Terquem, C. 2001, MNRAS, 325, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Papaloizou, J. C. B., & Terquem, C. 2006, Rep. Prog. Phys., 69, 119 [Google Scholar]
- Podlewska-Gaca, E., Papaloizou, J. C. B., & Szuszkiewicz, E. 2012, MNRAS, 421, 1736 [NASA ADS] [CrossRef] [Google Scholar]
- Polnarev, A. G., & Rees, M. J. 1994, A&A, 283, 301 [NASA ADS] [Google Scholar]
- Rafikov, R. 2013, ApJ, 774, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Rasio, F. A., & Ford, E. R. 1996, Science, 274, 954 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Rieger, F. M., & Mannheim, K. 2000, A&A, 359, 948 [NASA ADS] [Google Scholar]
- Roedig, C., & Sesana, A. 2014, MNRAS, 439, 3476 [NASA ADS] [CrossRef] [Google Scholar]
- Roedig, C., Sesana, A., Dotti, M., et al. 2012, A&A, 545, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roedig, C., Krolik, J., & Miller, M. 2014, ApJ, 785, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Rossi, E. M., Lodato, G., Armitage, P. J., Pringle, J. E., & King, A. R. 2010, MNRAS, 401, 2021 [NASA ADS] [CrossRef] [Google Scholar]
- Scheuer, P. A. G., & Feiler, R. 1996, MNRAS, 282, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Sesana, A., Roedig, C., Reynolds, M., & Dotti, M. 2012, MNRAS, 420, 860 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I. 1973, SvA, 16, 756 [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shapiro, S. L. 2010, Phys. Rev. D, 81, 4019 [NASA ADS] [CrossRef] [Google Scholar]
- Sorathia, K. A., Krolik, J. H., & Hawley, J. F. 2013, ApJ, 768, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, H., Takeuchi, T., & Ward, W. R. 2002, ApJ, 565, 1257 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, T., Menou, K., & Haiman, Z. 2012, MNRAS, 420, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Thakar, A. R., & Ryden, B. S. 1998, ApJ, 506, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Valtonen, M. J., Ciprini, S., & Lehto, H. J. 2012, MNRAS, 427, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, Q., & Lu, Y. 2001, A&A, 377, 17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ziglin, S. L. 1975, Sov. Astron. Lett., 1, 194 [NASA ADS] [Google Scholar]
Appendix A: The evolution of a finite disk with a = b = 0
When a = b = 0, Eq. (63) becomes a linear equation taking on the simple form 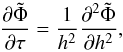 (A.1)where
(A.1)where 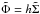 . We express the solution of (A.1) for h ∈ (1,hout) as a linear combination of normal modes in the form
. We express the solution of (A.1) for h ∈ (1,hout) as a linear combination of normal modes in the form 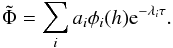 (A.2)The boundary conditions satisfied by Φ(h,τ) (and also φi(h), i = 1,2...) are
(A.2)The boundary conditions satisfied by Φ(h,τ) (and also φi(h), i = 1,2...) are 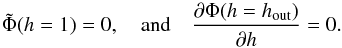 (A.3)The required solution to (A.2) should also satisfy the initial condition Φ(τ = 0) = 1.
(A.3)The required solution to (A.2) should also satisfy the initial condition Φ(τ = 0) = 1.
We recall that in order to express the surface density in physical units, we must multiply 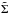 by the product of a numerical factor and
by the product of a numerical factor and 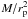 , where the numerical factor is determined by the specification of the ratio of the disk mass to the mass of the central body within the computational domain. For the particular numerical simulations discussed in this paper, the numerical factor relating the quantity
, where the numerical factor is determined by the specification of the ratio of the disk mass to the mass of the central body within the computational domain. For the particular numerical simulations discussed in this paper, the numerical factor relating the quantity 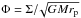 to
to 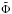 , Φ0, is approximately equal to 2.4 × 10-4. However, the initial condition is incompatible with the inner boundary condition (A.3), because our boundary conditions are strictly valid only after some period of time has elapsed. Nonetheless, the choice of the functions φi(h) enables the initial condition to be satisfied everywhere apart from at h = 1, see below. After substitution of (A.2) to (A.1), we get
, Φ0, is approximately equal to 2.4 × 10-4. However, the initial condition is incompatible with the inner boundary condition (A.3), because our boundary conditions are strictly valid only after some period of time has elapsed. Nonetheless, the choice of the functions φi(h) enables the initial condition to be satisfied everywhere apart from at h = 1, see below. After substitution of (A.2) to (A.1), we get 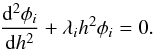 (A.4)The solutions to (A.4) are orthogonal with respect to the scalar product
(A.4)The solutions to (A.4) are orthogonal with respect to the scalar product 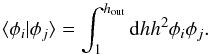 (A.5)They can be expressed in terms of Bessel functions as
(A.5)They can be expressed in terms of Bessel functions as  (A.6)where z = λih2/ 2. The boundary conditions (A.3) then define an eigenvalue problem leading to a discrete set of positive λi bounded from below. We arrange the eigenvalues in such a way that larger eigenvalues correspond to larger values of i, and calculate them numerically for i = 0,1,...13, with i = 0 corresponding to the mode with the smallest value of λ for a given hout. The dependence λ0 on hout is shown in Fig. A.1.
(A.6)where z = λih2/ 2. The boundary conditions (A.3) then define an eigenvalue problem leading to a discrete set of positive λi bounded from below. We arrange the eigenvalues in such a way that larger eigenvalues correspond to larger values of i, and calculate them numerically for i = 0,1,...13, with i = 0 corresponding to the mode with the smallest value of λ for a given hout. The dependence λ0 on hout is shown in Fig. A.1.
 |
Fig. A.1 Minimum eigenvalue λ0 as a function of the outer boundary location of the computational domain. |
When λi ≫ 1, we can use the asymptotic representation of the Bessel functions corresponding to large values of their arguments. In this case it is easy to show that λi approximately satisfy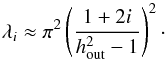 (A.7)We have checked that the approximate values (A.7) are close to the ones obtained numerically even for i = 1.
(A.7)We have checked that the approximate values (A.7) are close to the ones obtained numerically even for i = 1.
To find the coefficients ai in (A.2), we use the formal identity 1 = ∑ iaiφi(h) and the orthogonality condition (A.5) to get 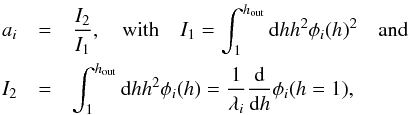 (A.8)where we have used Eq. (A.4) to obtain the last equality. For our purposes we need to know the value of the quantity
(A.8)where we have used Eq. (A.4) to obtain the last equality. For our purposes we need to know the value of the quantity 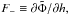 evaluated at h = 1. It is easy to see that this can be represented in the form
evaluated at h = 1. It is easy to see that this can be represented in the form 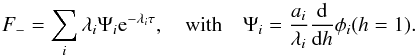 (A.9)In general the coefficients Ψi have to be be calculated numerically. Thus we obtain Ψ0 = 3.1. For large values of i the asymptotic representation of the Bessel functions may be used, as for eigenvalue determination, with the result
(A.9)In general the coefficients Ψi have to be be calculated numerically. Thus we obtain Ψ0 = 3.1. For large values of i the asymptotic representation of the Bessel functions may be used, as for eigenvalue determination, with the result 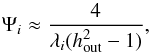 (A.10)where we can use Eq. (A.7) to specify λi. Equation (A.10) is found to give reasonable values for Ψi even when i is small. Thus for i = 1, the numerical value of Ψ1 ≈ 0.2, whereas Eq. (A.10) gives Ψ1 ≈ 0.18.
(A.10)where we can use Eq. (A.7) to specify λi. Equation (A.10) is found to give reasonable values for Ψi even when i is small. Thus for i = 1, the numerical value of Ψ1 ≈ 0.2, whereas Eq. (A.10) gives Ψ1 ≈ 0.18.
Appendix A.1: Orbital evolution
Now let us consider the orbital evolution. To find the dependence of rp on time, we again use Eqs. (6), (7), and (62), recalling the relationship between the mass flux Ṁ and the quantity F− as given by 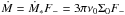 (see Eq. (36) and preceding discussion). We account for the effect of the evolution of perturber’s orbital distance rp with time on the surface density profile, in the simplest possible manner, by utilising an appropriate scaling of quantities of interest with the ratio rp/r0 as in the main text. We recall that since the inner boundary condition in (A.3) assumes that the variable h is always equal to unity at the perturber’s position, it is convenient to redefine this quantity according to
(see Eq. (36) and preceding discussion). We account for the effect of the evolution of perturber’s orbital distance rp with time on the surface density profile, in the simplest possible manner, by utilising an appropriate scaling of quantities of interest with the ratio rp/r0 as in the main text. We recall that since the inner boundary condition in (A.3) assumes that the variable h is always equal to unity at the perturber’s position, it is convenient to redefine this quantity according to 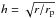 , which strictly coincides with the older definition only when t = 0. Furthermore, we redefine the dimensionless time τ assuming that in Eq. (35) rp replaces r0. Thus we have
, which strictly coincides with the older definition only when t = 0. Furthermore, we redefine the dimensionless time τ assuming that in Eq. (35) rp replaces r0. Thus we have 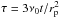 . However, the definition of the dimensionless surface density
. However, the definition of the dimensionless surface density 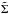 and the relation between ν and Σ given by Eq. (33) remains unchanged.
and the relation between ν and Σ given by Eq. (33) remains unchanged.
We proceed by introducing the dimensionless time variable 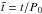 , where
, where 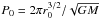 and the dimensionless orbital distance
and the dimensionless orbital distance 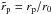 . Utilising Eqs. (6), (7) and (62), it is straightforward to obtain an equation governing the orbital evolution in terms of these quantities. This takes the form
. Utilising Eqs. (6), (7) and (62), it is straightforward to obtain an equation governing the orbital evolution in terms of these quantities. This takes the form 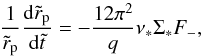 (A.11)where
(A.11)where 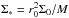 and
and 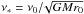 . For the simulation discussed above, Σ∗ ≈ 2.4 × 10-4 and ν∗ = 10-5.
. For the simulation discussed above, Σ∗ ≈ 2.4 × 10-4 and ν∗ = 10-5.
From Eq. (A.9) it follows that F− can be written in the form 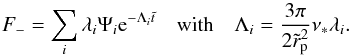 (A.12)We integrate (A.12) formally assuming that rp does not depend on time on the right-hand side to obtain
(A.12)We integrate (A.12) formally assuming that rp does not depend on time on the right-hand side to obtain 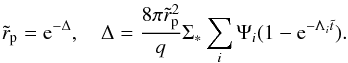 (A.13)Equation (A.13) provides an implicit dependence of
(A.13)Equation (A.13) provides an implicit dependence of  on time since
on time since 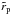 enters both sides of the equation. Its numerical solution by a standard iterative procedure is shown in Fig. 16.
enters both sides of the equation. Its numerical solution by a standard iterative procedure is shown in Fig. 16.
All Tables
Evolution rates calculated numerically, (drp/ dt)n, and analytically as indicated above, (drp/ dt)a, for different values of the mass ratio q.
All Figures
 |
Fig. 1 Semi-major axis, in units of the initial orbital radius as a function of time in orbits for q = 0.001. The solid curve give the results from numerical simulation, and the curve with imposed crosses is obtained using Eq. (7) with contributions to the total torque for m ≤ 100 obtained from Eq. (22). However, the main contribution comes from m = 1 in this case (see Sect. 5.1 below). The numerical simulation was performed with no accretion onto the companion. |
| In the text | |
 |
Fig. 2 log Σ contours for q = 0.001 with softening length 0.6H after 100 orbits (left panel) and after 840 orbits (right panel). In these simulations, the companion was not allowed to accrete: its position in each case is at the centre of the small superposed red circle, located on the line at an angle of ~315° to the x axis (left panel) and at an angle of ~45° to the x axis (right panel). Short wavelength density waves are visible on both sides of the quasi-circular orbit. The relative density changes are similar in both these plots. However, the density in the interior regions of the disk decreases at later times on account of accretion through the inner boundary as is manifest in both panels. |
| In the text | |
 |
Fig. 3 Inverse of the evolution time scale defined according to Eq. (23), as a function of the dimensionless softening length Δs/H. It is expressed in units of |
| In the text | |
 |
Fig. 4 Dependence of the mean ratio of the minimum surface density in the gap on the characteristic disk surface density Σ∗, σmin, as a function of the parameter ys. The solid curve represents the result obtained from the numerical iterations of the map based on the solution of Eqs. (54) and (55), while the dashed curve shows the analytic expression |
| In the text | |
 |
Fig. 5 Difference φ = Φ − h is shown as a function of the radial coordinate h, at τ = 5, 20, and 100, see the text for details. |
| In the text | |
 |
Fig. 6 Dimensionless mass flux Ṁ/Ṁ∗ shown as a function of time τ. The solid and dashed curves correspond to a = 2/3, b = 1 and a = 3/7, b = 15/14, respectively. |
| In the text | |
 |
Fig. 7 Log Σ contours for q = 0.02 with softening length 0.1H after 50 orbits (left panel) and after 100 orbits (right panel). In these simulations the companion, its position in each case being at the centre of the small red circle located within the gap region, was allowed to accrete. The widths of the gaps slowly increase, while the accretion rates, on average, decrease slowly with time. Short wavelength density waves in the outer disks are just visible. Values of log Σ below the minimum indicated on the colour bar are plotted as that minimum value. |
| In the text | |
 |
Fig. 8 As in Fig. 7 but for q = 0.01 with softening length 0.6H after 100 orbits (left panel) and 800 orbits (right panel). As the mass ratio is smaller in this case than for Fig. 7, the gap in the disk is narrower. The companion, indicated by a small red circle, is found in general to orbit closer to the inner disk edge at earlier times. In the left-hand panel, the companion grazes the inner edge slightly above the x axis for x< 0. This enhances the accretion rate at that stage. |
| In the text | |
 |
Fig. 9 Semi-major axis, in units of the initial orbital radius, as a function of time for q = 0.02 and q = 0.01 for small softening and for q = 0.01 with standard softening. Two curves without imposed crosses, which are very close together, are shown for each of these three cases. The uppermost pair of curves corresponds to q = 0.01 with standard softening and the lowermost pair for q = 0.01 with small softening. The central pair corresponds to q = 0.02 with small softening. The lower of the pair of curves for the cases with small softening corresponds to runs with accretion from the disk included (see text). For the case with standard softening, this situation is reversed. The straight lines with superimposed crosses are obtained by adopting the initial type I migration rate with contributions from all m ≤ 100 included. The line with the more widely separated crosses corresponds to q = 0.01 with small softening, while the other line corresponds to q = 0.01 with standard softening. |
| In the text | |
 |
Fig. 10 Mass accreted, in units of M, as a function of time for runs with accretion illustrated in Fig. 9. The uppermost curve corresponds to q = 0.01 with standard softening, the central curve to q = 0.01 with small softening, and the lowermost curve to q = 0.02 with small softening. Although the accretion rate shows large variations, these curves do not because they time average this quantity effectively. |
| In the text | |
 |
Fig. 11 Surface density Σ in units |
| In the text | |
 |
Fig. 12 Minimum value of surface density Σmin in the gap in units of initial surface density |
| In the text | |
 |
Fig. 13 Accretion rate onto the secondary in units M/P0 as a function of time. The dotted curve, showing large variations, is obtained numerically, the solid curve represents the numerical results time averaged over 7.5 periods, while the dashed curve represents ṁ2 as specified through one of the Eqs. (73). |
| In the text | |
 |
Fig. 14 Dimensionless mass flux Ṁ/Ṁ∗ as a function of time τ for the case a = 2/3, b = 1 (model 1). The solid curve corresponds to our model of the disk of finite size. The dashed curve shows, for comparison, the same dependence for the disk of formally infinite extent. |
| In the text | |
 |
Fig. 15 Dependence of the binary separation distance, rp/r0, as a function of t/P0 for Model 2. We recall that r0 and P0 are the binary separation distance and orbital period at the initial time t = 0. The solid curve is obtained from the solution of Eq. (63), while the dashed curve represents the results of a two-dimensional numerical simulation. |
| In the text | |
 |
Fig. 16 Dependence of the binary separation distance on time. The solid curve shows the result of numerical simulation with the mass ratio q = 10-2 and other parameters described in the text. The dashed curve is calculated from Eq. (A.13). |
| In the text | |
 |
Fig. 17 Dimensionless torques τml for the cases m = 1,l = −1 (solid curve), m = 2,l = −1 (dashed curve), and m = 2,l = 1 (dotted curve) as functions of eccentricity e. The solid curve ends at e = 0.58. At this value of eccentricity, the apocentre distance rp = a(1 + e) is equal to r(1, − 1) given by Eq. (77). At larger values of e, the corresponding resonance lies within the binary orbit. Also, the case m = 2,l = 1 shown for illustration corresponds to prograde orbital motion of the binary. |
| In the text | |
 |
Fig. A.1 Minimum eigenvalue λ0 as a function of the outer boundary location of the computational domain. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.