| Issue |
A&A
Volume 575, March 2015
|
|
|---|---|---|
| Article Number | L9 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201525643 | |
| Published online | 27 February 2015 | |
Long-term OVRO monitoring of LS I +61°303: confirmation of the two close periodicities
1
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69, 53121
Bonn,
Germany
e-mail: mmassi@mpifr-bonn.mpg.de; fjaron@mpifr-bonn.mpg.de
2
Aalto University Metsähovi Radio Observatory,
Metsähovintie 114, 02540
Kylmälä,
Finland
e-mail:
talvikki.hovatta@aalto.fi
3
Cahill Center for Astronomy and Astrophysics, California Institute
of Technology, Pasadena
CA, 91125, USA
Received: 12 January 2015
Accepted: 26 January 2015
Context. The gamma-ray binary LS I +61°303 shows multiple periodicities. The timing analysis of 6.7 yr of GBI radio data and of 6 yr of Fermi-LAT GeV gamma-ray data both have found two close periodicities P1,GBI = 26.49 ± 0.07 d, P2,GBI = 26.92 ± 0.07 d and P1,γ = 26.48 ± 0.08 d, P2,γ = 26.99 ± 0.08 d.
Aims. The system LS I +61°303 is the object of several continuous monitoring programs at low and high energies. The frequency difference between ν1 and ν2 of only 0.0006 d-1 requires long-term monitoring because the frequency resolution in timing analysis is related to the inverse of the overall time interval. The Owens Valley Radio Observatory (OVRO) 40 m telescope has been monitoring the source at 15 GHz for five years and overlaps with Fermi-LAT monitoring. The aim of this work is to establish whether the two frequencies are also resolved in the OVRO monitoring.
Methods. We analysed OVRO data with the Lomb-Scargle method. We also updated the timing analysis of Fermi-LAT observations.
Results. The periodograms of OVRO data confirm the two periodicities and .
Conclusions. The three independent measurements of P1 and P2 with GBI, OVRO, and Fermi-LAT observations confirm that the periodicities are permanent features of the system LS I +61°303. The similar behaviours of the emission at high (GeV) and low (radio) energy when the compact object in LS I +61°303 is toward apastron suggest that the emission is caused by the same periodically (P1) ejected population of electrons in a precessing (P2) jet.
Key words: radio continuum: stars / X-rays: binaries / X-rays: individuals: LSI +61°303 / gamma rays: stars
© ESO, 2015
1. Introduction
The stellar system LS I +61°303 is formed by a compact object and a Be star in an eccentric orbit (e = 0.72 ± 0.15, Casares et al., 2005). Fermi-LAT observations (Abdo et al., 2009) reveal a large outburst toward periastron (Φperiastron = 0.23 ± 0.02, Casares et al., 2005) along with a smaller outburst toward apastron (Jaron & Massi, 2014). Radio observations of the system show a large radio outburst toward apastron exhibiting a modulation of ~ 1667 days (Paredes et al., 1990; Gregory, 2002; Massi & Kaufman Bernadó, 2009, and here Fig. 1).
 |
Fig. 1 Left: OVRO data vs. MJD. Centre: OVRO (filled squares, black) data and GBI 8 GHz data (empty squares, red) vs. Θ; Θ is the fractional part of (t − t0) / 1667 with t0 = JD 2 443 366.775 (Gregory, 2002). Right: OVRO (black) data and GBI 8 GHz data (red) vs. Φ, where Φ is the orbital phase, i.e., the fractional part of (t − t0) /P1, with P1 = 26.496 days (Gregory, 2002). The largest radio outbursts occur around Φ = 0.6. At Φ = 0.23, i.e., at periastron, only a low level of emission is present. |
 |
Fig. 2 Lomb-Scargle periodograms of three independent long-term monitorings of LS I +61°303. Top: OVRO at 15 GHz. Centre: Fermi-LAT in the energy range 100 MeV to 300 GeV using only data from the orbital phase interval Φ = 0.5−1.0 (see Jaron & Massi, 2014). Bottom: GBI at 2 GHz (empty circles) and 8 GHz (filled squares) (see Massi & Jaron, 2013). In all periodograms there are two periodicities with a false-alarm probability of between 0.00 and 0.01 (see Sect. 2). The ratio (R) between the intensity of the two spetral features at P1 and P2 is different in the different periodograms and is R = 1.9 at 2 GHz and R = 1.5 at 8 GHz for GBI data, R = 1.4 at 15 GHz and R = 1.3 for GeV data. |
Two distinct outbursts along the orbit are well understood in the context of accretion along an eccentric orbit (Bondi & Hoyle, 1944). The expression of the accretion rate is 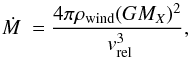 (1)where ρwind is the density, and vrel is the relative velocity between the compact object and the Be equatorial wind. As shown by several authors for the eccentric orbit of LS I +61303, two peaks result: one peak corresponds to the periastron passage because of the highest density; the second peak occurs in the phase interval (toward apastron) where the reduced velocity of the compact object compensates for the decrease in density (Taylor et al., 1992; Marti & Paredes, 1995; Bosch-Ramon et al., 2006; Romero et al., 2007). At each accretion peak, matter is assumed to be ejected outward in two jets perpendicular to the accretion disk plane as for microquasars, but for the two ejections different energetic losses for the particles occur. Ejected relativistic electrons around periastron suffer severe inverse Compton losses because of the proximity to the Be star (Bosch-Ramon et al., 2006): the electrons upscatter stellar photons to higher energies, and by doing so, they loose their energy and become unable to generate synchrotron emission in the radio band. The consequence is that around periastron a high-energy outburst caused by inverse Compton process results, but no or negligible radio emission (Bosch-Ramon et al., 2006). This first predicted gamma-ray outburst has been confirmed by Fermi-LAT observations (Abdo et al., 2009; Hadasch et al., 2012; Ackermann et al., 2013; Jaron & Massi, 2014). During the second accretion peak, the compact object is much farther away from the Be star, and inverse Compton losses are lower: the electrons can propagate out of the orbital plane and generate synchrotron emission in the radio band and a minor gamma-ray outburst (see the predicted outbursts in Fig. 2 of Bosch-Ramon et al., 2006). Indeed, as quoted above, radio and gamma-ray observations confirm the predicted radio and minor gamma-ray outburst toward apastron. The spectrum of the radio outburst has been reported to be flat from 1.5 to 22 GHz by Gregory et al. (1979), and recently, Zimmermann (2013) observed a flat spectrum up to 33 GHz. These radio observations corroborate the microquasar hypothesis for LS I +61°303 because a flat radio spectrum is indeed associated with the conical radio jet of microquasars (Fender et al., 2000; Fender, 2001; Kaiser, 2006).
(1)where ρwind is the density, and vrel is the relative velocity between the compact object and the Be equatorial wind. As shown by several authors for the eccentric orbit of LS I +61303, two peaks result: one peak corresponds to the periastron passage because of the highest density; the second peak occurs in the phase interval (toward apastron) where the reduced velocity of the compact object compensates for the decrease in density (Taylor et al., 1992; Marti & Paredes, 1995; Bosch-Ramon et al., 2006; Romero et al., 2007). At each accretion peak, matter is assumed to be ejected outward in two jets perpendicular to the accretion disk plane as for microquasars, but for the two ejections different energetic losses for the particles occur. Ejected relativistic electrons around periastron suffer severe inverse Compton losses because of the proximity to the Be star (Bosch-Ramon et al., 2006): the electrons upscatter stellar photons to higher energies, and by doing so, they loose their energy and become unable to generate synchrotron emission in the radio band. The consequence is that around periastron a high-energy outburst caused by inverse Compton process results, but no or negligible radio emission (Bosch-Ramon et al., 2006). This first predicted gamma-ray outburst has been confirmed by Fermi-LAT observations (Abdo et al., 2009; Hadasch et al., 2012; Ackermann et al., 2013; Jaron & Massi, 2014). During the second accretion peak, the compact object is much farther away from the Be star, and inverse Compton losses are lower: the electrons can propagate out of the orbital plane and generate synchrotron emission in the radio band and a minor gamma-ray outburst (see the predicted outbursts in Fig. 2 of Bosch-Ramon et al., 2006). Indeed, as quoted above, radio and gamma-ray observations confirm the predicted radio and minor gamma-ray outburst toward apastron. The spectrum of the radio outburst has been reported to be flat from 1.5 to 22 GHz by Gregory et al. (1979), and recently, Zimmermann (2013) observed a flat spectrum up to 33 GHz. These radio observations corroborate the microquasar hypothesis for LS I +61°303 because a flat radio spectrum is indeed associated with the conical radio jet of microquasars (Fender et al., 2000; Fender, 2001; Kaiser, 2006).
In 1993, the radio-emitting source was resolved with high-resolution radio observations showing a structure of milliarcsecond (mas) size corresponding to a few AU at the distance of 2.0 kpc (Massi et al., 1993). Successive observations revealed that the radio morphology not only changes position angle, but it is even sometimes one-sided and at other times two-sided (Peracaula et al., 1998; Paredes et al., 1998; Taylor et al., 2000; Massi et al., 2001, 2004). This suggested that LS I +61°303 might be a precessing microquasar (Kaufman Bernadó et al., 2002; Massi et al., 2004). A precession of the jet leads to a variation in the angle between the jet and the line of sight and therefore to variable Doppler boosting. The result is a continuous variation in both the position angle of the radio-emitting structure and its flux density (Massi, 2007). Concerning the precession time-scale, rather fast position angle variations of almost 60°/day measured by MERLIN observations (Massi et al., 2004) were confirmed by VLBA observations (Dhawan et al., 2006), which measured a rotation of roughly 5°−7° in 2.5 h (i.e., ~ 60°/day). Radio astrometry resulted in a precessing period of 27–28 days (Massi et al., 2012).
A timing analysis of the GBI radio data of LS I +61°303 has revealed two rather close frequencies: and (Massi & Jaron, 2013). The period P1 agrees with the value of (Gregory, 2002) associated with the orbital period of the binary system and with the predicted periodical accretion peak. Period P2 agrees well with the estimate by radio astrometry of 27–28 days for the precession period.
Recently, a Lomb-Scargle analysis of Fermi-LAT data around apastron revealed the same periodicities and (Jaron & Massi, 2014). The similar behaviours of the emission at high (GeV) and low (radio) energy would imply that the emission is caused by the same population of electrons in a precessing jet. This important result must be confirmed by simultaneous observations. GBI observations were made from January 1994 until October 2000. Fermi-LAT has observed since August 2008. The fact that the two archives do not even overlap shows the persistence of ν1 and ν2 and characterizes them as permanent features of the system LS I +61°303. However, to investigate the electron population, one needs simultaneous monitorings. Fortunately, a new radio long-term monitoring is available. The Owens Valley Radio Observatory (OVRO) 40 m telescope monitoring at 15 GHz began in March 2009. In this Letter we present a timing analysis of these data. Section 2 describes the data reduction and the results. Section 3 presents our conclusions.
2. Data analysis and results
2.1. OVRO observations
Regular 15 GHz observations of LS I +61°303 from 54 908.8 MJD (March 2009) to 56 795.0 MJD (May 2014) were carried out approximately twice per week using the OVRO telescope (Richards et al., 2011). The OVRO 40 m uses off-axis dual-beam optics and a cryogenic high electron mobility transistor (HEMT) low-noise amplifier with a 15.0 GHz centre frequency and 3 GHz bandwidth. The two sky beams are Dicke-switched using the off-source beam as a reference, and the source is alternated between the two beams in an ON-ON fashion to remove atmospheric and ground contamination. Calibration is achieved using a temperature-stable diode noise source to remove receiver gain drifts, and the flux density scale is derived from observations of 3C 286 assuming the Baars et al. (1977) value of 3.44 Jy at 15.0 GHz. The systematic uncertainty of about 5% in the flux density scale is not included in the error bars. Complete details of the reduction and calibration procedure are found in Richards et al. (2011). OVRO data vs. time, long-term, and orbital phase are shown in Fig. 1
2.2. Timing analysis
To search for possible periodicities, we used the Lomb-Scargle method, which is very efficient for irregularly sampled data (Lomb, 1976; Scargle, 1982). We used the algorithms of the UK Starlink software package, PERIOD1. The statistical significance of a period is calculated in PERIOD following the method of Fisher randomization as outlined in Linnel Nemec & Nemec (1985). The advantage of using a Monte Carlo- or randomization test is that it is distribution-free and is not constrained by any specific noise models (Poisson, Gaussian, etc.). The fundamental assumption is that if there is no periodic signal in the time series data, then the measured values are independent of their observation times and could have occurred in any other order. One thousand randomized time series are formed, and the periodograms are calculated. The proportion of permutations that give a peak power higher than that of the original time series would then provide an estimate of p, the probability that for a given frequency window there is no periodic component present in the data with this period. A derived period is defined as significant for p< 1%, and a marginally significant one for 1% <p< 10% (Linnel Nemec & Nemec, 1985). Figure 2 shows the result for OVRO data. There are two periodicities and . The periods are both significant: they result in the randomization test with a false-alarm probability of p< 1%.
2.3. Fermi-LAT
The timing analysis in Jaron & Massi (2014) for the whole data set gave P2 as significant (p< 1%) in the randomization tests even if it is a rather weak feature in the periodograms of their Fig. 3a–c. In other words, the timing analysis performed on the whole Fermi data set yields that P2 is significant even if the spectral feature is much lower than that at P1. When the timing analysis is performed for emission in the orbital phase Φ = 0.5–1.0, as described in Jaron & Massi (2014), the spectral feature at P2 is comparable with that at P1, but the randomization tests find a probability of false detection of p = 4%. The γ-ray data used in that analysis did span the time period MJD 54 683 (August 05, 2008) to MJD 56 838 (June 30, 2014). Now we have five more months of Fermi-LAT observations. The data reduction was performed as reported in Jaron & Massi (2014). The periodogram for data in the orbital phase Φ = 0.5–1.0 shown in Fig. 2 has the same periodicities as in Jaron & Massi (2014), but with the important difference that now the randomization test gives both frequencies as significant, with a false-alarm probability of p< 1%.
 |
Fig. 3 Lomb-Scargle periodograms of 385 days of GBI radio data at 2 GHz to be compared with the periodogram in Trushkin et al. (2014) also of 385 days. The spectral resolution of only 0.00065 d-1 cannot resolve the separation of 0.0006 d-1 between and determined by Massi & Jaron (2013) with 6.7 yr of GBI data. |
2.4. 385 days of GBI data vs. RATAN results
The frequency resolution in a periodogram is related to the inverse of the overall time interval of observations. The resolution for GBI of covers six times the difference in frequency between and determined by Massi & Jaron (2013). Indeed, the two spectral features are evident in the GBI periodogram shown here in Fig. 2. Very recently, Trushkin et al. (2014) reported that the timing analysis of RATAN-600 radio telescope data did not find the two frequencies. The reported daily monitoring with the RATAN-600 radio telescope includes the time from 16 November 2013 (MJD 56 612) to 6 December 2014 (MJD 56 997), that is, 385 days. This corresponds to a frequency resolution of 0.00065 d-1 that is even higher than the difference in frequency between ν1 and ν2 of 0.00060 d-1. We tested the insufficient frequency resolution by performing the timing analysis on 385 days of GBI data. The resulting periodogram, shown in Fig. 3, is well comparable with that of Trushkin et al. (2014). The two frequencies ν1 and ν2 are plotted in Fig. 3 by arrows. The low spectral resolution is still unable to resolve the frequency separation.
Timing analysis results.
3. Conclusions and discussion
The spectral resolution in the timing analysis of OVRO data is able to distinguish the two spectral features found in GBI and Fermi-LAT data (Table 1).
These two periodicities are physically related to the periodical ejection (P1) of electrons in a particular orbital phase toward apastron and to the precession (P2) of the jet. The beating of these two periodicities probably causes the so-called long-term modulation. The peak flux density of the periodical radio outburst exhibits in fact a modulation of 1667 ± 8 d (Gregory, 2002). Massi & Jaron (2013) have shown the consistency between the long-term modulation and the beating of the two frequencies determined in the GBI timing analysis, that is, 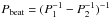 (Table 1). Moreover, Massi & Torricelli-Ciamponi (2014) have shown that a physical model for LS I +61°303 of synchrotron emission from a precessing (P2) jet, periodically (P1) refilled with relativistic particles, produces a maximum when the jet electron density is at its maximum and the approaching jet forms the smallest possible angle with the line of sight. This coincidence of the highest number of emitting particles and the strongest Doppler boosting of their emission occurs with a period of
(Table 1). Moreover, Massi & Torricelli-Ciamponi (2014) have shown that a physical model for LS I +61°303 of synchrotron emission from a precessing (P2) jet, periodically (P1) refilled with relativistic particles, produces a maximum when the jet electron density is at its maximum and the approaching jet forms the smallest possible angle with the line of sight. This coincidence of the highest number of emitting particles and the strongest Doppler boosting of their emission occurs with a period of 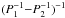 , that is, Pbeat , or the long-term periodicity.
, that is, Pbeat , or the long-term periodicity.
The open question now is: why is the precession so close to the orbital period? While the microquasar SS433 and several known precessing X-ray binaries (Larwood, 1998) have a precession period longer by an order of magnitude than the orbital period (as predicted for a tidally forced precession by the companion star), the different case of the microquasar GRO J1655−40 was discovered in 1995 (Hjellming & Rupen, 1995). This system has an orbital period of 2.601 ± 0.027 days (Bailyn et al., 1995). Hjellming & Rupen (1995) discovered a radio jet in this object with a precessional period of 3.0 ± 0.2 days (Hjellming & Rupen, 1995). LS I +61°303 seems to be the second case of this new class of objects with orbital and precession periods that are rather close to each other.
Acknowledgments
The OVRO 40 M Telescope Monitoring Program is supported by NASA under awards NNX08AW31G and NNX11A043G, and by the NSF under awards AST-0808050 and AST-1109911. We would like to thank Jürgen Neidhöfer, Giammarco Quaglia, and Eduardo Ros for helpful comments. This work has made use of public Fermi data obtained from the High Energy Astrophysics Science Archive Research Center (HEASARC), provided by NASA Goddard Space Flight Center. The Green Bank Interferometer is a facility of the National Science Foundation operated by the NRAO in support of NASA High Energy Astrophysics programs.
References
- Abdo, A. A, Ackermann, M., Ajello, M., et al. 2009, ApJ, 701, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Ballet, J., et al. 2013, ApJ, 773, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Baars, J. W. M., Genzel, R., Paulini-Toth, I. I. K., & Witzel, A. 1977, A&A, 61, 91 [Google Scholar]
- Bailyn, C. D., Orosz, J. A., McClintock, J. E., & Remillard, R. A. 1995, Nature, 378, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Bondi, H., & Hoyle, F. 1944, MNRAS, 104, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Bosch-Ramon, V., Paredes, J. M., Romero, G. E., & Ribó, M. 2006, A&A, 459, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casares, J., Ribas, I., Paredes, J. M., Martí, J., & Allen de Prieto, C. 2005, MNRAS, 360, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Dhawan, V., Mioduszewski, A., & Rupen, M. 2006, Proc. of the VI Microquasar Workshop, 52.1 [Google Scholar]
- Fender, R. P. 2001, MNRAS, 322, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Fender, R. P., Pooley, G. G., Durouchoux, P., Tilanus, R. P. J., & Brocksopp, C. 2000, MNRAS, 312, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Gregory, P. C. 2002, ApJ, 575, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Gregory, P. C., Taylor, A. R., Crampton, D., et al. 1979, AJ, 84, 1030 [NASA ADS] [CrossRef] [Google Scholar]
- Hadasch, D., Torres, D. F., Tanaka, T., et al. 2012, ApJ, 749, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Hjellming, R. M., & Rupen, M. P. 1995, Nature, 375, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Jaron, F., & Massi, M. 2014, A&A, 572, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnston, S., Manchester, R. N., & McConnell, D. 2002, MNRAS, 336, 1201 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, C. R. 2006, MNRAS, 367, 1083 [NASA ADS] [CrossRef] [Google Scholar]
- Kaufman Bernadó, M. M., Romero, G. E., & Mirabel, I. F. 2002, A&A, 385, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larwood, J. 1998, MNRAS, 299, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Linnell Nemec, A. F., & Nemec, J. M. 1985, AJ, 90, 2317 [NASA ADS] [CrossRef] [Google Scholar]
- Lomb, N. R. 1976, Ap&SS, 39, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Marti, J., & Paredes, J. M. 1995, A&A, 298, 151 [NASA ADS] [Google Scholar]
- Massi, M. 2007, The Multicolored Landscape of Compact Objects and Their Explosive Origins, 924, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Massi, M., & Jaron, F. 2013, A&A, 554, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massi, M., & Kaufman Bernadó, M. 2009, ApJ, 702, 1179 [NASA ADS] [CrossRef] [Google Scholar]
- Massi, M., & Torricelli-Ciamponi, G. 2014, A&A, 564, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massi, M., & Zimmermann, L. 2010, A&A, 515, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massi, M., Paredes, J. M., Estalella, R., & Felli, M. 1993, A&A, 269, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Massi, M., Ribó, M., Paredes, J. M., Peracaula, M., & Estalella, R. 2001, A&A, 376, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massi, M., Ribó, M, Paredes, J. M., et al. 2004, A&A, 414, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massi, M., Ros, E., & Zimmermann, L. 2012, A&A, 540, A14 [Google Scholar]
- Paredes, J. M., Estalella, R., & Rius, A. 1990, A&A, 232, 377 [NASA ADS] [Google Scholar]
- Paredes, J. M., Massi, M., Estalella, R., & Peracaula, M. 1998, A&A, 335, 539 [NASA ADS] [Google Scholar]
- Peracaula, M., Gabuzda, D. C., & Taylor, A. R. 1998, A&A, 330, 612 [NASA ADS] [Google Scholar]
- Ray, P. S., Foster, R. S., Waltman, E. B., Tavani, M., & Ghigo, F. D. 1997, ApJ, 491, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Reig, P. 2011, Ap&SS, 332, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, J. L. et al. 2011, ApJS, 194, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Romero, G. E., Okazaki, A. T., Orellana, M., & Owocki, S. P. 2007, A&A, 474, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, A. R., Kenny, H. T., Spencer, R. E., & Tzioumis, A. 1992, ApJ, 395, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, A. R., Dougherty, S. M., Scott, W. K., Peracaula, M., & Paredes, J. M. 2000, in Astrophysical Phenomena Revealed by Space VLBI (Institute of Space and Astronautical Science), 223 [Google Scholar]
- Trushkin, S. A., Nizhelskij N. A., & Tsybulev P. G. 2014, ATel, 6786 [Google Scholar]
- Zimmermann L. 2013, Variability of radio and TeV emitting X-ray binary systems The case of LS I +61°303. Univ. Bonn, Diss., URN:urn:nbn:de:hbz:5n-33175 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Left: OVRO data vs. MJD. Centre: OVRO (filled squares, black) data and GBI 8 GHz data (empty squares, red) vs. Θ; Θ is the fractional part of (t − t0) / 1667 with t0 = JD 2 443 366.775 (Gregory, 2002). Right: OVRO (black) data and GBI 8 GHz data (red) vs. Φ, where Φ is the orbital phase, i.e., the fractional part of (t − t0) /P1, with P1 = 26.496 days (Gregory, 2002). The largest radio outbursts occur around Φ = 0.6. At Φ = 0.23, i.e., at periastron, only a low level of emission is present. |
| In the text | |
 |
Fig. 2 Lomb-Scargle periodograms of three independent long-term monitorings of LS I +61°303. Top: OVRO at 15 GHz. Centre: Fermi-LAT in the energy range 100 MeV to 300 GeV using only data from the orbital phase interval Φ = 0.5−1.0 (see Jaron & Massi, 2014). Bottom: GBI at 2 GHz (empty circles) and 8 GHz (filled squares) (see Massi & Jaron, 2013). In all periodograms there are two periodicities with a false-alarm probability of between 0.00 and 0.01 (see Sect. 2). The ratio (R) between the intensity of the two spetral features at P1 and P2 is different in the different periodograms and is R = 1.9 at 2 GHz and R = 1.5 at 8 GHz for GBI data, R = 1.4 at 15 GHz and R = 1.3 for GeV data. |
| In the text | |
 |
Fig. 3 Lomb-Scargle periodograms of 385 days of GBI radio data at 2 GHz to be compared with the periodogram in Trushkin et al. (2014) also of 385 days. The spectral resolution of only 0.00065 d-1 cannot resolve the separation of 0.0006 d-1 between and determined by Massi & Jaron (2013) with 6.7 yr of GBI data. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


