| Issue |
A&A
Volume 575, March 2015
|
|
|---|---|---|
| Article Number | A107 | |
| Number of page(s) | 7 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201425400 | |
| Published online | 04 March 2015 | |
A new look at microlensing limits on dark matter in the Galactic halo
Institute for Astronomy (IfA), University of Edinburgh, Royal Observatory, Blackford Hill Edinburgh EH9 3HJ UK
e-mail:
mrsh@roe.ac.uk
Received: 25 November 2014
Accepted: 28 January 2015
Context. The motivation for this paper is to review the limits set on the MACHO content of the Galactic halo by microlensing experiments in the direction of the Large Magellanic Cloud. This has been prompted by recent measurements of the Galactic rotation curve, which suggest that the limits have been biassed by the assumption of an over-massive halo.
Aims. The paper first discusses the security of the detection efficiency calculations which are central to deriving the MACHO content of the Galactic halo. It then sets out to compare the rotation curves from various halo models with recent observations, with a view to establishing what limits can be put on an all-MACHO halo.
Methods. The main thrust of the paper is to investigate whether lighter halo models which are consistent with microlensing by an all-MACHO halo are also consistent with recent measures of the Galactic rotation curve. In this case the population of bodies discovered by the MACHO collaboration would make up the entire dark matter content of the Galactic halo.
Results. The main result of this paper is that it is easy to find low mass halo models consistent with the observed Galactic rotation curve, which also imply an optical depth to microlensing similar to that found by the MACHO collaboration. This means that all-MACHO halos cannot be ruled out on the basis of their observations.
Conclusions. Limits placed on the MACHO content of the Galactic halo from microlensing surveys in the Magellanic Clouds are inconsistent and model dependent, and do not provide a secure basis for rejecting an all-MACHO halo.
Key words: dark matter / gravitational lensing: micro / Galaxy: halo
© ESO, 2015
1. Introduction
Over the last three decades it has generally been accepted that studies of galactic dynamics and the velocity dispersion of galaxy clusters imply a large component of dark matter which cannot be accounted for by observable stellar populations, gas and other baryonic material (Trimble, 1987). This finding is supported by results from cosmic microwave background (CMB) experiments where dark matter is found to make up some 83% of the mass density of the Universe (Dunkley et al., 2009). When Virginia Trimble wrote her review in 1987 it was already clear that dark matter must be in a non-baryonic form, and compact bodies were seen as plausible candidates alongside various supersymmetric particles. At that time there was no reason to favour elementary particles over compact bodies, as little if any direct evidence had emerged to support the existence of either category of dark matter.
The situation changed dramatically during the 1990s with the first results from the MACHO collaboration (Alcock et al., 1996). This well known experiment was designed to detect the microlensing of stars in the Magellanic Clouds by compact bodies in the Galactic halo. The project was a success, and after 5.7 years of observation some 15 microlensing events were observed (Alcock et al., 2000). This was far more than expected for microlensing by the stellar content of the halo and disc, but the MACHO collaboration concluded that the resulting optical depth to microlensing τ corresponded to a contribution to the Galactic dark matter halo from compact bodies of only ~20%. Other groups, notably the EROS and OGLE collaborations, undertook similar surveys which appeared to put the limit even lower. Taken together, these results were widely seen as ruling out any significant component of dark matter in the form of compact bodies of around a solar mass, and had a major impact on cosmology.
The limitation on the halo fraction in compact bodies derived from the microlensing of the Magellanic Cloud stars is based on three distinct components. Firstly, the events must be detected by searching through the millions of light curves for the characteristic variation due to microlensing. Secondly, the efficiency of the detection procedure must be estimated to allow a measure of the true optical depth to microlensing in the Galactic halo. Thirdly, the Galactic halo must be modelled so that the optical depth to microlensing can be calculated on the basis that the dark matter component is composed entirely of compact bodies. This can then be compared with the observed optical depth.
The idea behind this paper is to re-examine the limits on compact bodies in the Galactic halo set by the MACHO collaboration and other groups in the light of recent improvements in the measurement of the dynamical and structural parameters of the Galaxy. Modern observations imply a falling Galactic rotation curve and a relatively light halo. This has major consequences for the expected number of microlensing events, which is reduced to as little as 25% of the previously accepted value. The main conclusion from this is that even though there is still room for discussion on the predicted value for τ, an all-MACHO halo can no longer be ruled out with any confidence. Given the importance of identifying the nature of dark matter, and the current lack of success in detecting a convincing elementary particle candidate, it is surely time to look again at the possibility that dark matter is in the form of compact bodies.
2. Microlensing limits from the MACHO project
The idea of detecting dark halo objects by looking for the microlensing of Magellanic Cloud stars was first suggested by Paczyński (1986). Paczyński proposed monitoring a few million stars to search for the characteristic light curve of a microlensing event which would indicate the presence of a dark halo object. The proposal was taken up by the MACHO collaboration which set up a nightly CCD monitoring programme of the Magellanic Clouds to measure the light curves of around 12 million stars (Griest, 1991). Given the crowded nature of the star fields, the implementation of a satisfactory automated data reduction pipeline was in itself a major challenge. Nonetheless, the first light curve fitting their criteria for a microlensing event was soon detected (Alcock et al., 1993), and the project was shown to be observationally feasible. The monitoring programme was completed in 1999 by which time between 13 and 17 events had been detected, depending on the exact nature of the selection criteria.
2.1. Detection efficiency
Galactic models for LMC microlensing.
Although the detection of a sample of candidate microlensing events formed the bulk of the enormous effort put into the MACHO project, the next step of determining the detection efficiency is arguably more critical to the reliability of the final result. In an ideal situation the source stars would be well separated from each other with standard point spread functions, and the light curves would be adequately sampled with evenly spaced observations. The expectation would be that every microlensing event with given parameters of duration and amplitude would be detected. In such a case, from a knowledge of the total number of sources being monitored the frequency of detection of microlensing events is a direct measure of the optical depth to microlensing, or equivalently the surface density, of compact bodies in a given mass range in the Galactic halo.
In fact, the data obtained from the microlensing survey in the Magellanic Clouds were very far from this ideal. Perhaps the most straightforward problem was the variable sampling of the light curves due to unfavourable weather, mechanical failure and other interruptions to the observing programme. Gaps in the light curves will result in events being missed which would otherwise be detected in adequately sampled data. The MACHO collaboration’s solution to this was to use a Monte Carlo technique to model the actual epochs of observation and estimate the probability of missing detections (Alcock et al., 2001a). In these simulations they made the assumption that each light curve was from a single resolved star.
More serious problems arose from the overlapping of images in the dense star fields of the Magellanic Clouds. For example, any star-like image may actually consist of two or more stars, leading to an underestimation of the probability of microlensing. On the other hand, any microlensing amplification will be reduced as a result of dilution by light from the other images, and may well result in a colour change if the contaminating stars are of different spectral types. This problem is well illustrated by Alcock et al. (2001b) where they show a Hubble Space Telescope image of one of their microlensing candidates which splits the original single CCD source into four separate stars. The MACHO team came to the conclusion that to attempt to incorporate these effects into more complex Monte Carlo simulations would not be feasible, and addressed the problem of changes in photometry from overlapping images in the dense star fields of the Magellanic by injecting synthetic microlensing events into a sample of observed light curves (Alcock et al., 2001a). This is a complex process in which the stellar population must be modelled accurately as a function of position in the Magellanic Cloud galaxies to allow for changes in the point spread function from frame to frame, resulting in star images being resolved in some frames and not in others. Not only will this reduce the chances of a microlensing event being detected due to spurious variation, but it will also produce apparent changes in colour.
There are a number of other effects which must be allowed for in estimating detection efficiency. Some of these are listed in Table 4 of Alcock et al. (2001a) and include hard to estimate or unknown parameters. Particularly problematic is how to allow for the accidental inclusion of unforeseen types of variable stars such as “bumpers”, and the exclusion of real halo microlensing effects for spurious reasons such as the distortion of the light curve by the presence of a planetary or binary companion. This point has been made by Calchi Novati & Mancini (2011) in discussing the OGLE results when they “stress the potential difficulty within the evaluation of the detection efficiency to correctly take into account the risk of excluding bona fide microlensing candidates”. The question of whether the detected events really are microlensing events by compact halo objects has been the subject of extensive debate (Bennett et al., 2005; Griest & Thomas, 2005; Bennett, 2005; Evans & Belokurov, 2007), although the outcome of this exchange seems to support, with minor modifications, the original claims of Alcock et al. (2000). Rather than simply removing suspect microlensing candidates, Bennett (2005) employs a likelihood anaysis to assign microlensing probabilities to the candidates. This a posteriori procedure will in general have the effect of reducing the observed optical depth to microlensing, and raises the question of a possible bias as real microlensing events which were inadvertently missed will not be recovered by subsequent analysis. As Bennett (2005) points out, this should be allowed for in the selection criteria, but it is clearly problematic to anticipate every situation in which a microlensing profile can be masked. To illustrate the problem of deciding how to deal with microlensing events which are discovered after the definition of the survey sample, and which plausibly might have been contained in it, we can consider the events detected by one of the MACHO, OGLE or EROS projects, which although also observed by one of the other two, were not identified as microlensing events. Although a posteriori reasons were usually found to explain this, these events were never included in other samples because they were assumed to be taken into account in the detection efficiency calculation.
The possibility that candidate microlensing events might be attributed to “self-lensing” by lenses in the Magellanic Clouds rather than the Galactic halo was first suggested by Sahu (1994), and has received much attention. This is essentially a part of the calculation of detection efficiency, and has been addressed in some detail by several groups (Alcock et al., 2000; Gyuk et al., 2000; Mancini et al., 2004). Their conclusion was that self-lensing in the LMC would have only a small effect on the observed optical depth to microlensing, and certainly could not account for the observed signal. An interesting paper by Evans & Kerins (2000) proposes that the LMC is surrounded by a large microlensing cloud sufficient to reproduce the observed microlensing signal by lensing background source stars. The main problem with this idea is that all known stellar populations in the LMC have too small a velocity dispersion for such a cloud. The situation in the SMC is more complicated as we appear to be observing the galaxy end on, resulting in a much higher optical depth to self-lensing. For this reason, most of the discussion in this paper will be focussed on the LMC, which in any case dominates in any microlensing statistics.
The MACHO collaboration faced a formidable challenge in confronting the issues raised above, and tackled it with remarkable thoroughness. However, given the importance of their result in ruling out compact bodies as dark matter candidates, the uncertainties in their procedure cannot be ignored. Given the lack of knowledge of the underlying starfield, the population of variable stars and the frequency and effect of binary and planetary systems it is difficult to see how any firm estimate of the detection efficiency can be made, let alone a hard lower limit. It only needs to drop from around 30% to 15% for their favoured halo model to be consistent with the observed optical depth to microlensing.
2.2. Halo models
To determine the fraction of the Galactic halo made up of compact bodies, the sample of microlensing events must be combined with the detection efficiency to give the observed optical depth to microlensing τ. This can then be compared with the predicted value of τ for a chosen Galactic halo model composed entirely of MACHOs. It is this choice of halo model which provides the greatest uncertainty in the limit on dark matter in the form of compact bodies. The difficulty which confronted the MACHO collaboration was that at that time little was known about the rotation curve, and hence the mass profile, of the Galaxy. The solution that they adopted was to define eight model halos incorporating a wide range of galaxy parameters. They then calculated the optical depth to microlensing τ for each halo on the assumption that it was composed entirely of compact bodies. By comparing these computed values for τ with their observed value they could then determine which, if any, halo models for the Galaxy could be made up of MACHOs. The model which they describe (Alcock et al., 1996) as a “standard” halo with a core radius and flat rotation curve, has a density profile of the form: 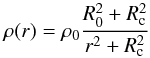 (1)where r and R0 are the Galactocentric radius and Galactocentric distance of the sun respectively, and Rc is the halo core radius. They also include a set of power law models (Evans, 1994), covering a wide range of halo parameters, including small and maximal discs. The calculated values of τ for their models are shown in Table 2 of Alcock et al. (1996), and it will be seen that all but two have predicted values for τ which are inconsistent with their measured value. In fact the authors consider these two Models E and F too extreme to be taken seriously, although their low optical depths to microlensing are actually consistent with an all-MACHO halo. To quote from Alcock et al. (1996) referring to their model E, “almost no useful limits f< 1 can be placed for any MACHO mass”, and indeed model E implies a lower value of τ than that observed by the MACHO collaboration (Alcock et al., 1996, 2000). The reason the MACHO collaboration rejected Model E was that it “has an asymptotic rotation speed of only 83 km s-1 and is probably inconsistent with other estimates of the mass of the Milky Way halo”. Actually, this figure for the asymptotic rotation speed is close to recently measured values (Sofue, 2013; Bhattacharjee et al., 2014). With regard to their Model F, Alcock et al. (2000) state that it has “an extremely low mass halo, somewhat inconsistent with the known Galactic rotation curve”. It is possible that at the time of writing this seemed to be the case, but the latest measurements of stellar velocity dispersion in the outer part of the Galaxy no longer support this. Figure 1 shows recent measurements of stellar velocity dispersion (Battaglia et al., 2005; Deason et al., 2012b) which imply a falling rotation curve and a relatively low mass halo. The actual values of the rotation speeds are still somewhat uncertain, depending on the values of the Galactic constants and the velocity anisotropy of the tracer orbits (Bhattacharjee et al., 2014), but the declining trend seems clear. Observations appear to indicate a radially biassed velocity anisotropy (Deason et al., 2012a; Rashkov et al., 2013) which would favour a lower halo mass. In fact high values for the Milky Way halo mass all come from the analyses of the kinematics of the satellite galaxies including the anomalous object Leo I (Boylan-Kolchin et al., 2013). If Leo I is taken out of the sample on the grounds that it may not be gravitationally bound to the Milky Way, or the entire local group is modelled (Peñarrubia et al., 2014), then the kinematics are also consistent with a low mass halo. Further support for a low mass halo comes from the analysis of the Sagittarius stream (Gibbons et al., 2014), which gives a result free from many of the assumptions inherent in other approaches.
(1)where r and R0 are the Galactocentric radius and Galactocentric distance of the sun respectively, and Rc is the halo core radius. They also include a set of power law models (Evans, 1994), covering a wide range of halo parameters, including small and maximal discs. The calculated values of τ for their models are shown in Table 2 of Alcock et al. (1996), and it will be seen that all but two have predicted values for τ which are inconsistent with their measured value. In fact the authors consider these two Models E and F too extreme to be taken seriously, although their low optical depths to microlensing are actually consistent with an all-MACHO halo. To quote from Alcock et al. (1996) referring to their model E, “almost no useful limits f< 1 can be placed for any MACHO mass”, and indeed model E implies a lower value of τ than that observed by the MACHO collaboration (Alcock et al., 1996, 2000). The reason the MACHO collaboration rejected Model E was that it “has an asymptotic rotation speed of only 83 km s-1 and is probably inconsistent with other estimates of the mass of the Milky Way halo”. Actually, this figure for the asymptotic rotation speed is close to recently measured values (Sofue, 2013; Bhattacharjee et al., 2014). With regard to their Model F, Alcock et al. (2000) state that it has “an extremely low mass halo, somewhat inconsistent with the known Galactic rotation curve”. It is possible that at the time of writing this seemed to be the case, but the latest measurements of stellar velocity dispersion in the outer part of the Galaxy no longer support this. Figure 1 shows recent measurements of stellar velocity dispersion (Battaglia et al., 2005; Deason et al., 2012b) which imply a falling rotation curve and a relatively low mass halo. The actual values of the rotation speeds are still somewhat uncertain, depending on the values of the Galactic constants and the velocity anisotropy of the tracer orbits (Bhattacharjee et al., 2014), but the declining trend seems clear. Observations appear to indicate a radially biassed velocity anisotropy (Deason et al., 2012a; Rashkov et al., 2013) which would favour a lower halo mass. In fact high values for the Milky Way halo mass all come from the analyses of the kinematics of the satellite galaxies including the anomalous object Leo I (Boylan-Kolchin et al., 2013). If Leo I is taken out of the sample on the grounds that it may not be gravitationally bound to the Milky Way, or the entire local group is modelled (Peñarrubia et al., 2014), then the kinematics are also consistent with a low mass halo. Further support for a low mass halo comes from the analysis of the Sagittarius stream (Gibbons et al., 2014), which gives a result free from many of the assumptions inherent in other approaches.
 |
Fig. 1 Stellar velocity dispersion as a function of Galactocentric distance. Filled circles are from Battaglia et al. (2005) and open circles from Deason et al. (2012b). |
 |
Fig. 2 Rotation curves for models for the outer part of the Galaxy. The observed rotation curves are shown as filled circles (Sofue, 2013) and open circles (Bhattacharjee et al., 2014). The red (dashed), green (dot-dash), blue (dotted) and purple (dash-dot-dot-dot) curves are for Models B, S, F and E respectively from Alcock et al. (1996). |
For the final analysis of the MACHO microlensing data (Alcock et al., 2000) just three halo models were considered, namely S, B and F from Table 2 of Alcock et al. (1996). Model E was not included because, as mentioned above, it was considered incompatible with observations of the Galactic rotation curve. Parameters for these models are given in Table 1, including model E, together with the optical depth to microlensing resulting from an all-MACHO halo. Figure 2 shows the rotation curves of these models, and measurements of the circular velocity from Sofue (2013) and Bhattacharjee et al. (2014) in the outer part of the Galactic halo. Goodness-of-fit of each model to the data can be assessed from the values of χ2 given in Table 1, with 8 degrees of freedom. It will be seen that Models B and S are inconsistent with the data at very high confidence levels, Model E is marginally rejected, while Model F provides an adequate fit. In fact, as quoted above, Model F was rejected by the MACHO collaboration for being inconsistent with the Galactic rotation curve as it was known at that time. The fact that their preferred Model S appears to be incompatible with recent observations is undoubtedly a matter for debate, as the calculation of rotation speed is somewhat model dependent. However, whether or not Model S should be seen as a valid model for the Galactic halo, the point to be emphasised is that all-MACHO Galaxy halos were rejected for reasons which are no longer valid.
2.3. Comparison with other surveys
The importance of establishing whether a population of compact bodies could account for the dark matter in the Galaxy halo prompted other groups to embark on microlensing surveys in the Magellanic Clouds. The EROS collaboration undertook a series of monitoring programmes, the first of which was based on Schmidt telescope photographic plates. During the three seasons of this programme only one ultimately acceptable microlensing event was detected from the 4 million stars being monitored. This initial programme was supplemented by a CCD based survey which monitored four times as many stars in the LMC and resulted in the detection of a further two microlensing events. The combined EROS programme was then analysed by Lasserre et al. (2000) to put constraints on the MACHO content of the Galactic halo. They found that for their “standard” halo model, a solar mass MACHO component can make up no more than 40%, at the 95% confidence limit. This may be compared with the equivalent figure of 50% for the MACHO project (Alcock et al., 2000). The EROS monitoring programme was subsequently extended in scope as EROS2 and re-analysed by Tisserand et al. (2007) who restricted the sample to bright stars with R< 19.7, reducing the parent sample of stars to around 6 million, in the process eliminating all three previously discovered microlensing events on the basis that they were observed to brighten again. Their subsequent analysis failed to identify any new events, and on this basis they claimed an upper limit of 12% for the MACHO content of the Model S halo.
The statistical incompatibility of the MACHO and EROS results has been the subject of extensive discussion (Tisserand et al., 2007; Moniez, 2010). One of the most obvious differences between the MACHO and EROS experiments is the respective use of faint and bright star samples. Only 2 of the 17 MACHO microlensing candidates were bright enough to be included in the EROS Bright-Stars sample (Tisserand et al., 2007), which is consistent with the low detection rate for bright microlensing events in the EROS survey. Although there are clearly advantages in the restriction of the EROS analysis to relatively bright stars, it may have resulted in a problem associated with the resolution of the stellar discs. A sample of luminous LMC source stars will contain a high proportion of giants, with diameters of the order of the Einstein radii of substellar mass lenses. This can limit the observed microlensing amplitude to as little as a factor of two (Schneider et al., 1992), making the events less likely to be detected than those associated with smaller, less luminous sources.
As well as including fainter stars in their sample, the MACHO collaboration also tended to cover more crowded fields in their survey. This has raised the possibility that their microlensing detections are more likely to be caused by self-lensing than in the sparser fields of the EROS survey. However, this would contradict results from models of the LMC which imply that any self-lensing will be small (Gyuk et al., 2000; Mancini et al., 2004). Another potential problem arising from the use of crowded fields is that poor photometry resulting from blending will result in spurious microlensing events being selected. In fact, most of the MACHO microlensing candidates have withstood subsequent scrutiny and are still accepted as microlensing events (Bennett, 2005). It is more of an open question as to how many events have been missed, and whether they have been correctly allowed for in the detection efficiency calculation.
In reviewing the discrepancy between the MACHO and EROS results, Moniez (2010) concludes that the best way to reconcile them is to drop the assumption of a homogeneous distribution of microlenses tracing out a smooth dark matter halo, and to postulate a clumpy halo which the two surveys sample differently. This idea has been examined in some detail by Holopainen et al. (2006) using N-body simulations of dark matter halos. They found that triaxiality and substructure can have major effects on the observed optical depth to microlensing and event rate. However, as Moniez (2010) points out, convincing proof of the existence of such structures is still to be provided.
We have already discussed the difficulties of calculating the detection efficiency in Sect. 2.1, and this does provide another possible explanation for at least part of the difference between the MACHO and EROS detection rates. A useful way of comparing detection efficiencies is to look at the statistics of events detected by one group but not by the other. There was in fact a considerable overlap between the MACHO and EROS2 surveys, both in time and fields monitored. Two of the MACHO events which fell in this overlap region (MACHO-LMC-18 and 25) were bright enough to be included in the EROS2 Bright-Stars sample (Tisserand et al., 2007), although neither of them was accepted as a microlensing candidate by the EROS software. In the case of MACHO-LMC-18 this was because it was merged with a nearby star (Tisserand et al., 2007). These non-detections will of course have been allowed for in the detection efficiency calculation, but they also allow a simple Bayesian estimate of that detection efficiency. Given that no common detections were made, no finite figure can be put on this, but it clearly implies a very low detection efficiency for the EROS2 Bright-Stars sample. This seems to be at odds with their published detection efficiencies which are similar to those of the MACHO collaboration. If the EROS2 collaboration have used detection efficiencies which are too large, it would go a long way to explaining the discrepancies between the two groups.
A third group to investigate the MACHO content of the Galactic halo, the OGLE collaboration, commenced observations in 1996 using broadly the same techniques as the MACHO and EROS experiments. The OGLE project went through a number of phases, the results of which were summarised by Wyrzykowski et al. (2011b). The survey was divided into “Bright” and “All Stars” samples to facilitate comparison with the MACHO and EROS results, and their automated search procedure detected two microlensing candidates (Wyrzykowski et al., 2011a), both from the Bright Star sample. This is broadly in line with the MACHO collaboration’s bright star detections, but the lack of faint star microlensing candidates is not consistent with the MACHO result, and hard to explain. Given that the OGLE All Stars sample contains some three times as many stars as the Bright sample (Wyrzykowski et al., 2011a), there should be three times as many microlensing candidates, unless the fainter events are harder to detect. This of course is probably the case due to blending and other magnitude dependent effects, but should be allowed for in the dection efficiency calculation. In fact, the detection efficiencies for the All Stars and Bright samples used for the analysis were around 15% and 20% respectively (Wyrzykowski et al., 2011a), implying that magnitude dependent effects were not very important. This raises the possibility that the difference in the detection rate between the MACHO and OGLE programmes could be due to over-estimation of the detection efficiency for faint stars in the OGLE analysis.
3. New microlensing limits for the Galactic halo
 |
Fig. 3 Rotation curves for models of the Galaxy out to 60 kpc. The observed rotation curves are shown as filled circles (Xue et al., 2008), open circles (Sofue, 2013) and filled triangles (Bhattacharjee et al., 2014). The red (dashed), green (dot-dash), blue (dotted) and purple (dash-dot-dot-dot) curves are for Models B, S, F and E respectively from Alcock et al. (1996). |
In Sect. 2.2 it has been argued that in the light of recent observations of the asymptotic rotation speed of the Galaxy, the idea of an all-MACHO Galactic halo was rejected prematurely. In this section we address the question of whether one can find model all-MACHO halos consistent with current observational constraints. For this purpose, attention needs to be focussed on Galactic structure out to the distance of the LMC. Figure 3 shows recent measurements of the Galactic rotation curve out to 60 kpc together with rotation curves for Models S, B, F and E from Alcock et al. (2000). Goodness-of-fit may be assessed from the χ2 values given in the bottom line of Table 1, with 37 degrees of freedom. It will be seen that Models B, S and E are inconsistent with the observations at very high significance levels. Model F provides an adequate fit to the data, with an associated optical depth to microlensing marginally consistent with an all-MACHO halo. However, the Galactic parameters for Model F do not agree well with recent measurements. It is nonetheless quite easy to find halo models with acceptable Galactic parameters that provide a good fit to the data in Fig. 3, as well as predicting an optical depth to microlensing consistent with the MACHO observations and hence an all-MACHO halo. Examples of 8 such models are illustrated in Fig. 4 as coloured lines, with halo parameters given in Table 1. The values of these parameters are within the range used by Alcock et al. (1996), and supported by more recent measurements such as Ojiha (2001) and Siebert et al. (2003). As may be seen from Table 1, the values of τ for these halos are consistent with microlensing by a 100% MACHO halo. Two of the halos (H4 and H5) are not consistent with measures of the outer rotation curve, but the remainder provide a good fit at all Galactocentric distances. This implies that not only are all-MACHO halos not ruled out, but that they can actually provide a better fit to the data than the preferred models of the MACHO collaboration.
 |
Fig. 4 Rotation curves for models of the Galaxy out to 60 kpc. The observed rotation curves are shown as filled circles (Xue et al., 2008), open circles (Sofue, 2013) and filled triangles (Bhattacharjee et al., 2014). The coloured curves are for Models H1 to H8 from Table 1. |
It is important to emphasise that the purpose of this analysis is not to demonstrate that Model S is inconsistent with the data, but that other models which imply a low optical depth to microlensing provide as good a fit. The question that we address here is whether there is a sound basis for ruling out an all-MACHO halo from the microlensing observations of the MACHO collaboration.
4. Discussion
The dark matter problem is widely considered to be one of the most important in physics, and the search for a dark matter particle absorbs huge resources. The assumption that dark matter is a particle is rarely questioned these days, and rests largely on the seminal work of the MACHO collaboration, and later microlensing surveys in the Magellanic Clouds. The most remarkable thing about the results of the MACHO project is that it discovered a population of compact bodies which still have no plausible identity. Whatever the explanation for the failure of the EROS and OGLE experiments to detect a similar sample of microlensing events, the MACHO result has withstood scrutiny and needs explanation. Additional support for their conclusions comes from the preliminary results of the SuperMACHO project (Rest et al., 2005) which in 2003 alone reported the detection of 10 high quality microlensing events (Becker et al., 2005). Although the full analysis of the SuperMACHO results is yet to be published, the detection rate of microlensing events appears to favour that found by the MACHO collaboration rather than the very few events detected by the EROS and OGLE projects.
More supporting evidence for the MACHO result comes from observations of pixel lensing in M31. Some 30 candidate microlensing events have now been reported towards M31 (Calchi Novati, 2010), but the question of how many of these are self-lensing events is still a matter of discussion. The POINT-AGAPE collaboration conclude that at least 20% of the halo mass in the direction of M31 must be in the form of MACHOs (Calchi Novati et al., 2005), whereas the MEGA collaboration (de Jong et al., 2006) claim an upper limit for a MACHO halo fraction of 30%. They did however concede that their result was model dependent, and some of the events where hard to explain as self-lensing due to their position relative to the centre of M31.
The distribution of microlensing candidates across the disc of M31 is an important way of determining whether the events can be attributed to self-lensing. There should be more events from sources in M31 which are furthest from us, as they would be seen through a greater optical depth of compact bodies in the M31 halo. This asymmetry is indeed seen, but the situation is confused by results that show a similar asymmetry for variable stars (An et al., 2004), which in this case is due to differential extinction across the disc of M31. This coincidence has the effect of blurring the difference between microlensing events and variable stars which in the absence of extinction would be distinguishable by their different distributions. In fact many of the problems associated with microlensing surveys in the Magellanic Clouds are exacerbated in pixel lensing projects. In particular, the detection efficiency calculation is made much more difficult by the large number of sources in each pixel.
The usefulness of a common halo model to convert optical depth τ to MACHO halo fraction has resulted in the widespread adoption of the MACHO collaboration Model S as a standard for comparison. In summarising the OGLE LMC results Wyrzykowski et al. (2011a) use Model S to calculate the halo mass fraction, and it is also used by Ansari et al. (1996) together with related models in the analysis of the EROS results. In reviewing the results from the first 20 years of microlensing studies Moniez (2010) concludes that a substantial contribution of compact objects to a standard halo is now excluded. However, the ‘standard’ halo to which he explicitly refers is the MACHO collaboration’s Model S. Although a common standard is clearly useful, it has perhaps obscured the fact that any conclusions rely on Model S being an accurate description of the Galactic halo. In fact, as may be seen Fig. 2 and illustrated in Table 1, the asymptotic rotation speed for Model S is not consistent with the observed rotation curve. More importantly, in the region out to the distance of the Magellanic Clouds where any microlensing from bodies in the Galactic halo will take place Table 1 and Fig. 3 show that Model S is rejected at high significance level as a fit to the rotation curve measurements. By contrast, MACHO Model F is consistent with measurements of the Galactic rotation curve at all distances, although its associated predicted microlensing rate for an all-MACHO halo is 1.8σ greater than that found by Alcock et al. (2000).
In addition to the halos from Alcock et al. (1996), Table 1 also shows data for 8 halos with parameters in line with recent observations. All these halos have associated optical depths to microlensing within around 1σ of the value observed by Alcock et al. (2000). The halos were selected to be consistent with the recent measurements of the Galactic rotation curve out to the distance of the LMC, and most of them also have the low asymptotic rotation speed which is a feature of current observations. The values of τ for all these model halos imply that they would not be excluded by the results of Alcock et al. (2000) as models for the Galactic halo, and thus that a 100% MACHO halo cannot be ruled out for the Galaxy. The issue here is not how well Model S fits the data, but whether there are viable halo models which are consistent with a Galactic halo made up of compact bodies. Given the importance of this question, it seems premature to abandon this route to the identification of dark matter, especially in light of the current lack of progress in detecting a dark matter particle.
There is still much to be understood about the MACHO content of the Galactic halo, and in particular the apparent discrepancy between the results from different groups. However, the claim that stellar mass compact bodies have been ruled out as dark matter candidates on the basis of the Magellanic Cloud microlensing experiments does not seem to be supportable any more. A result which has such important consequences needs to be secure at a high confidence level, and free from inconsistencies and unquantifiable systematic errors. The reliability of the event detection efficiency is fundamental to the confidence that can be placed on limits to the MACHO content of the Galactic halo. So far, no objective way has been found for checking the accuracy of the Monte Carlo process on which it is largely based. Moreover, the apparent inconsistencies between groups in the detection efficiencies for bright and faint sources that were discussed in Sect. 2.3 need to be clarified. More important however is the choice of a realistic halo model that is consistent with observations of the structure and dynamics of the Galaxy. We have shown here that models which have been used to rule out a significant population of compact bodies in the Galactic halo are not consistent with recent measurements of the Galactic rotation curve. On the other hand, halo models that do provide an adequate fit to the data would, if made up of solar mass compact bodies, produce a microlensing signal similar to that observed by the MACHO project.
5. Conclusions
In this paper we re-examine the claim that the Magellanic Cloud microlensing results of the MACHO collaboration rule out a Galactic halo composed predominantly of compact bodies. The MACHO collaboration’s measurement of the optical depth to microlensing, combined with their preferred Galactic halo model, implies a MACHO fraction of around 20%. This result has withstood extensive scrutiny, and the population of compact objects which it revealed has yet to be satisfactorily identified.
Recent measurements of the Galactic rotation curve and other structural and dynamical parameters imply a falling rotation curve and a relatively light Galactic halo. We show here that the standard halo model used by the MACHO collaboration and other microlensing groups is not consistent with these observations, and consequently cannot be used to put reliable limits on the MACHO content of the halo. We then show that it is easy to find more realistic halo models compatible with the measurements of Galactic rotation, which if made up of compact bodies would imply an optical depth to microlensing similar to that found by the MACHO collaboration. On this basis we suggest that it is premature to rule out a Galactic halo composed entirely of compact bodies. This result could help to throw light on the current difficulties in detecting a dark matter particle.
Acknowledgments
I would like to thank the anonymous referee for some very helpful suggestions.
References
- Alcock, C., Akerlof, C. W., Allsman, R. A., et al. 1993, Nature, 365, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Alcock, C., Allsman, R. A., Axelrod, T. S., et al. 1996, ApJ, 461, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Alcock, C., Allsman, R. A., Alves, D. R., et al. 2000, ApJ, 542, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Alcock, C., Allsman, R. A., Alves, D. R., et al. 2001a, ApJS, 136, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Alcock, C., Allsman, R. A., Alves, D. R., et al. 2001b, ApJ, 552, 582 [NASA ADS] [CrossRef] [Google Scholar]
- An, J. H., Evans, N. W., Hewett, P., et al. 2004, MNRAS, 351, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Ansari, R., Cavalier, F., Moniez, M., et al. 1996, A&A, 314, 94 [NASA ADS] [Google Scholar]
- Battaglia, G., Helmi, A., Morrison, H., et al. 2005, MNRAS, 364, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, A. C., Rest, A., Stubbs, C., et al. 2005, in Impact of Gravitational Lensing on Cosmology, eds. Y. Mellier, & G. Meylan (Cambridge: Cambridge Univ. Press), IAU Symp., 225, 357 [Google Scholar]
- Bennett, D. P. 2005, ApJ, 633, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, D. P., Becker, A. C., & Tomaney, A. 2005, ApJ, 631, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Bhattacharjee, P., Chaudhury, S., & Kundu, S. 2014, ApJ, 785, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Boylan-Kolchin, M., Bullock, J. S., Sohn, S. T., Besla, G., & van der Marel, R. P. 2013, ApJ, 768, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Calchi Novati, S. 2010, Gen. Rel. Grav., 42, 2101 [NASA ADS] [CrossRef] [Google Scholar]
- Calchi Novati, S., & Mancini, L. 2011, MNRAS, 416, 1292 [NASA ADS] [CrossRef] [Google Scholar]
- Calchi Novati, S., Paulin-Henriksson, S., An, J., et al. 2005, A&A, 443, 911 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Jong, J. T. A., Widrow, L. M., Cseresnjes, P., et al. 2006, A&A, 446, 855 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deason, A. J., Belokurov, V., Evans, N. W., & An, J. 2012a, MNRAS, 424, L44 [NASA ADS] [CrossRef] [Google Scholar]
- Deason, A. J., Belokurov, V., Evans, N. W., et al. 2012b, MNRAS, 425, 2840 [NASA ADS] [CrossRef] [Google Scholar]
- Dunkley, J., Komatsu, E., Nolta, M. R., et al. 2009, ApJS, 180, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, N. W. 1994, MNRAS, 267, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, N. W., & Belokurov, V. 2007, MNRAS, 374, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, N. W., & Kerins, E. 2000, ApJ, 529, 917 [NASA ADS] [CrossRef] [Google Scholar]
- Gibbons, S. L. J., Belokurov, V., & Evans, N. W. 2014, MNRAS, 445, 3788 [NASA ADS] [CrossRef] [Google Scholar]
- Griest, K. 1991, ApJ, 366, 412 [NASA ADS] [CrossRef] [Google Scholar]
- Griest, K., & Thomas, C. L. 2005, MNRAS, 359, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Gyuk, G., Dalal, N., & Griest, K. 2000, ApJ, 535, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Holopainen, J., Flynn, C., Knebe, A., Gill, S. P., & Gibson, B. K. 2006, MNRAS, 368, 1209 [NASA ADS] [CrossRef] [Google Scholar]
- Lasserre, T., Afonso, C., Albert, J. N., et al. 2000, A&A, 355, L39 [NASA ADS] [Google Scholar]
- Mancini, L., Calchi Novati, S., Jetzer, P., & Scarpetta, G. 2004, A&A, 427, 61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moniez, M. 2010, Gen. Rel. Grav., 42, 2047 [NASA ADS] [CrossRef] [Google Scholar]
- Ojiha, D. K. 2001, MNRAS, 322, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Paczyński, B. 1986, ApJ, 304, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Peñarrubia, J. 2014, MNRAS, 443, 2204 [NASA ADS] [CrossRef] [Google Scholar]
- Rashkov, V., Pillepich, A., Deasan, A. J., et al. 2013, ApJ, 773, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Rest, A., Stubbs, C., Becker, A. C., et al. 2005, ApJ, 634, 1103 [NASA ADS] [CrossRef] [Google Scholar]
- Sahu, K. C. 1994, Nature, 370, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, P., Ehlers, J., Falco, E. E. 1992, Gravitational Lenses (New York: Springer) [Google Scholar]
- Siebert, A., Bienyame, O., Soubiran, C. 2003, A&A, 399, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sofue, Y. 2013, PASJ, 65, 118 [NASA ADS] [Google Scholar]
- Tisserand, P., Le Guillou, L., Afonso, C., et al. 2007, A&A, 469, 387 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trimble, V. 1987, ARA&A, 25, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Wyrzykowski, Ł., Kozłowski, S., Skowrom, J., et al. 2011a, MNRAS, 413, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Wyrzykowski, Ł., Skowrom, J., Kozłowski, S., et al. 2011b, MNRAS, 416, 2949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xue, X. X., Rix, H. W., Zhao, G., et al. 2008, ApJ, 684, 1143 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Stellar velocity dispersion as a function of Galactocentric distance. Filled circles are from Battaglia et al. (2005) and open circles from Deason et al. (2012b). |
| In the text | |
 |
Fig. 2 Rotation curves for models for the outer part of the Galaxy. The observed rotation curves are shown as filled circles (Sofue, 2013) and open circles (Bhattacharjee et al., 2014). The red (dashed), green (dot-dash), blue (dotted) and purple (dash-dot-dot-dot) curves are for Models B, S, F and E respectively from Alcock et al. (1996). |
| In the text | |
 |
Fig. 3 Rotation curves for models of the Galaxy out to 60 kpc. The observed rotation curves are shown as filled circles (Xue et al., 2008), open circles (Sofue, 2013) and filled triangles (Bhattacharjee et al., 2014). The red (dashed), green (dot-dash), blue (dotted) and purple (dash-dot-dot-dot) curves are for Models B, S, F and E respectively from Alcock et al. (1996). |
| In the text | |
 |
Fig. 4 Rotation curves for models of the Galaxy out to 60 kpc. The observed rotation curves are shown as filled circles (Xue et al., 2008), open circles (Sofue, 2013) and filled triangles (Bhattacharjee et al., 2014). The coloured curves are for Models H1 to H8 from Table 1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


