| Issue |
A&A
Volume 575, March 2015
|
|
|---|---|---|
| Article Number | A97 | |
| Number of page(s) | 13 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201425271 | |
| Published online | 03 March 2015 | |
2D He+ pickup ion velocity distribution functions: STEREO PLASTIC observations
Institut für Experimentelle und Angewandte Physik (IEAP), Christian
Albrechts-Universität zu Kiel,
Leibnizstrasse 11,
24118
Kiel,
Germany
e-mail:
drews@physik.uni-kiel.de
Received: 4 November 2014
Accepted: 21 January 2015
Context. He+ pickup ions are either born from the ionization of interstellar neutral helium inside our heliosphere, the so-called interstellar pickup ions, or through the interaction of solar wind ions with small dust particles, the so-called inner source of pickup ions. Until now, most observations of pickup ions were limited to reduced 1D velocity spectra, which are insufficient to study certain characteristics of the He+ velocity distribution function (VDF).
Aims. It is generally assumed that rapid pitch-angle scattering of freshly created pickup ions quickly leads to a fully isotropic He+ VDF. In light of recent observations, this assumption has found to be oversimplified and needs to be reinvestigated.
Methods. Using He+ pickup ion data from the PLASTIC instrument on board the STEREO A spacecraft, we reconstruct a reduced form of the He+ VDF in two dimensions. This allows us to study relative changes of the 2D He+ VDF as a function of the configuration of the heliospheric magnetic field.
Results. Our observations show that the He+ VDF is highly anisotropic and even indicates that, at least for certain configurations of B, it is not fully gyrotropic. Our results further suggest, that the observed velocity and pitch angle of He+ depends strongly on the local solar magnetic field vector, B, the ecliptic longitude, λ, the solar wind speed, vsw, and the global distribution of B.
Conclusions. We found two distinct signatures that systematically change as a function of the alignment of B: (1) a ring beam distribution that is most pronounced at wsw> 0.5 and likely attributed to interstellar He+; (2) a beam signature aligned parallel to B that is most pronounced at wsw < 0.5 and attributed to inner-source He+. The strong anisotropy and the aforementioned dependencies of the He+ VDF also imply that observations of 1D velocity spectra of He+ pickup ions are potentially deceiving.
Key words: Sun: heliosphere / solar wind / plasmas / magnetic fields / scattering
© ESO, 2015
1. Introduction
Pickup ions are created when neutral particles inside the heliosphere are ionised by either solar UV ionization, charge exchange with solar wind H+ or electron impact ionization. The neutral seed population for the creation of these ions can either be of interstellar origin, which was first predicted by Semar (1970); Fahr (1971) and subsequently confirmed with the AMPTE spacecraft near Earth (Moebius et al. 1985), or of lunar-, cometary- or inner-source origin as reported in Wenzel et al. (1986); Hilchenbach et al. (1992); Geiss et al. (1995) respectively. Despite their diverse potential origins pickup ions share certain kinetic characteristics, i.e. they show highly non-thermal velocity distributions and their maximum velocity typically exceeds the bulk speed of the solar wind by a factor between ~ 1 to ~ 2.
The initial pickup ion velocity distribution function (VDF) directly after the pickup process is generally assumed to resemble the form of a torus, which is shown in the upper left panel of Fig. 1. In a solar wind frame of reference, interstellar atoms, which make up the bulk of the seed population for pickup ions, have relative speeds of ~ vsw with respect to the solar wind. After the ionization the interaction with the solar magnetic field forces the pickup ions on gyro orbits perpendicular to the local magnetic field vector, B, with an orbital velocity that is given by the relative velocity between the former interstellar neutral and the solar wind bulk velocity. The inclination of the resulting toroidal ring distribution is therefore determined by the local magnetic field vector, which in a solar wind frame of reference is necessarily perpendicular to the velocity vector of the freshly injected pickup ion (see Fig. 1).
For a few years after the original prediction of the existence of pickup ions, it remained relatively unclear how the toroidal ring distribution of pickup ions would develop once convected outwards with the solar wind (Chalov & Fahr 1998). A study by Vasyliunas & Siscoe (1976) proposed that the pickup ion ring distribution is transformed into an isotropic shell distribution because of the influence of resonant wave-particle interactions and further altered by an adiabatic cooling effect due to the expansion of the pickup ion distribution inside the expanding solar wind. Since then, the process of rapid pitch-angle scattering and subsequent alteration of the pickup ion VDF by e.g. adiabatic cooling has been generally accepted to be one of the main drivers for the evolution of pickup ion VDFs (see top right and bottom left panel of Fig. 1). However, observations made by the AMPTE spacecraft of interstellar He+ (Möbius et al. 1998) and by the Ulysses spacecraft of interstellar H+ (Gloeckler et al. 1995) revealed that the pickup ion VDF can exhibit strong anisotropic features. Subsequent studies argued that these anisotropic features could either be because of the predominant injection of interstellar pickup ions into the sunward hemisphere of velocity space, which then escape detection (Isenberg 1997), and/or because of ineffective pitch-angle scattering under certain conditions (Fisk et al. 1997).
Numerical studies on the behaviour of interstellar pickup ions by Chalov & Fahr (1998), which include processes of diffusion, adiabatic cooling, pitch-angle scattering, drifts and energy diffusion, further introduced an important concept for the evolution of pickup ions inside the heliosphere. Pickup ions spatially diffuse, which means that a pickup ion injected inside a certain solar wind plasma parcel will systematically move away from that parcel during its evolution. The spatial diffusion of pickup ions has a severe influence not only on the in-situ pickup ion VDF, but also on the spatial distribution of these ions inside the heliosphere. A subsequent study by Chalov & Fahr (1999) has shown that the derivation of interstellar helium parameters from He+ observations (summarised in Möbius et al. 2004) is therefore very much impeded as pickup ions systematically lose/change the characteristic imprint of their spatial injection pattern.
Until 2002 almost all observations of pickup ion VDFs were limited to observations of reduced 1D velocity spectra. This means that certain characteristics of pickup ions that were already predicted in theory, such as pitch-angle scattering, spatial diffusion, or adiabatic cooling, were – and still are – very difficult to quantify. This is mainly because a 1D representation of the pickup ion VDF does not allow for a study of the relevant processes for the evolution of pickup ion VDFs individually. Instead, studying a particular process for the evolution of pickup ions is much impeded as the 1D velocity spectrum is strongly influenced and shaped by other processes as well. It is therefore highly beneficial to transit from a purely 1D observation to at least 2D or 3D observations, which facilitate the interpretation of the pickup ion VDF and the comparison between the theoretical model and observations.
The first 2D observation of an interstellar pickup ion VDF was performed with the GEOTAIL satellite near Earth’s orbit over the course of six years (Oka et al. 2002). They found that the observation probability of a He+ torus distribution is nearly 20% and that the distribution strongly depends on turbulence levels and the local magnetic field. However, the angular resolution in velocity space, i.e. the angle between the radial and tangential velocity component of He+, was limited to ~ 20°, and their study could only be used to show the existence of a torus distribution and not to present the detailed structure of the pickup ion VDF. A subsequent study by Drews et al. (2013) used the STEREO Ahead spacecraft to investigate the interstellar He+ VDF. The Plasma and Suprathermal Ion Composition instrument used for this investigation, provided a higher angular resolution in velocity space of ~ 2°, and the authors were able to show that the inclination of the He+ torus systematically changes with the inclination of the local solar magnetic field. It was therefore argued that past observations by Möbius et al. (1998) of a significant flux decrease of interstellar He+ from quasi-perpendicular to quasi-parallel configurations of the interplanetary magnetic field (IMF) should not be solely attributed to the predominant sunward injection and inefficient pitch-angle scattering across 90° (Isenberg 1997; Fisk et al. 1997) of He+ but should also be attributed to the systematic variation of the inclination of the He+ torus distribution. During quasi-radial magnetic field orientations the torus or ring beam distribution of He+ escapes detection because of the limited and sunward pointing field of view of mass and time-of-flight spectrometers such as SWICS, PLASTIC, or SULEICA. For orientations of the local magnetic field in which the ring beam lies inside the instrument’s aperture, the inclination of the torus strongly influences the observed 1D pickup ion VDF (Drews et al. 2013). As a consequence, understanding the formation and evolution of pickup ion ring-beam distributions is of fundamental importance for the interpretation of 1D observations of pickup ion velocity spectra.
 |
Fig. 1 Velocity space diagrams of a He+ ring beam signature (top left) under the influence of pitch angle scattering (top right), adiabatic cooling (bottom left), and a rapid change of the solar magnetic field vector, B, (bottom right) are shown. To illustrate the torus character of the distribution the (vx, vy)-plane is slightly tilted in this diagram. |
In general, the formation and evolution of pickup ion VDFs is very complex and depends on a wide range of heliospheric conditions. A detailed summary of observations and theoretical work of the He+ VDF made over the last three decades would certainly be beyond the scope of this work. However, we will provide a short and incomplete list of important parameters and processes that have undoubtedly influenced the observation of the 2D He+ VDF presented in this work.
-
Resonant wave-particle interactions: resonant interactions of pickup ions and Alfvén waves embedded inside the solar magnetic field change the pitch-angle of interstellar He+ and therefore determines the degree of anisotropy of the He+ VDF. A detailed description of this interaction and its dependency on magnetic turbulence levels is summarised in Vasyliunas & Siscoe (1976); Fisk et al. (1997); Saul et al. (2007) and sketched in the upper right panel of Fig. 1.
-
Deceleration and acceleration processes: the radial expansion of the solar wind, which carries the solar magnetic field, forces pickup ions to expand as well. The pickup ion VDF therefore suffers from adiabatic cooling (Vasyliunas & Siscoe 1976; Moebius et al. 1988; Chen et al. 2013), which gradually decreases the pickup ion velocity over time (see lower left panel of Fig. 1). In addition, pickup ions can experience strong acceleration during their evolution through the heliosphere, which results in the formation of suprathermal tails that exceed the typical velocity of interstellar pickup ions, v> 2·vsw (e.g. Isenberg 1987; Chalov & Fahr 1996; Fahr & Fichtner 2011; Fisk & Gloeckler 2012).
-
The Local and Global Solar Magnetic Field Orientation: the local solar magnetic field determines the inclination of the He+ torus distribution directly after the injection process. The global field on the other hand influences the evolution of the pickup ion VDF (compare bottom right panel of Fig. 1) and is tightly related to the spatial diffusion and transport of pickup ions (e.g. Chalov & Fahr 1998; Oka et al. 2002; Drews et al. 2013; Chalov 2014).
-
Ionization rates: the interplay between ionization of neutral atoms by either charge exchange, UV- or electron-impact, and its resulting imprint on the pickup ion VDF is discussed in e.g. Rucinski & Fahr (1989); Cummings et al. (2002).
-
The neutral seed population: the velocity, temperature, and spatial distribution of the neutral seed population strongly influences the initial form of the pickup ion VDF. We will mainly focus on the interstellar and inner-source constituents of the seed population, which are described in Kallenbach et al. (2000); Drews et al. (2012) and Geiss et al. (1995); Allegrini et al. (2005), respectively.
The numerical description for the formation and evolution of the He+ VDF has made substantial progress over the last three decades. In fact, theoretical predictions for the He+ VDF often precede the actual observations of corresponding signatures by several years. In comparison, the quality of observations of the He+ VDF is almost stagnating, which is mainly due to the time consuming, costly, and difficult task to deploy new instruments into space. Most observations are therefore still limited to 1D representations of the VDF that are, on the one hand, potentially deceiving when dealing with 2D signatures like the toroidal ring distribution of He+, and on the other hand, limiting for the interpretation of the complex processes associated with the formation and evolution of the He+ VDF. In this study we plan to utilise the unique capabilities of the PLASTIC instrument on board the STEREO Ahead mission to infer a 2D representation of the He+ VDF and close the aforementioned gap between observations and predictions made by theoretical considerations. However, the novelty of this observation and long history of theoretical prediction for the He+ VDF, makes it difficult to properly address all relevant concepts associated with the phase space transport of He+ from a (2D) observational point of view. Furthermore, the observation of the initial torus distribution of interstellar He+ at 1 AU, presented in Oka et al. (2002); Drews et al. (2013) and this work, has not yet been addressed in theoretical studies. The aim of this study is therefore first and foremost to describe and present the 2D observations of the He+ VDF, while the interpretation and context with respect to theory is given only for a few selected topics.
2. Observations and analysis technique
The observations of the 2D He+ VDF that we present here are based on measurements of He+ pickup ions with the PLAsma and SupraThermal Ion Composition (PLASTIC) instrument (Galvin et al. 2008) and the in-situ solar magnetic field vector B with the magnetometers of the In situ Measurements of PArticles and Coronal mass ejection Transients (IMPACT) instrument suite (Acuña et al. 2008). Both instruments are mounted on board the Solar Terrestrial RElations Observatory Ahead (STEREO A) spacecraft, which launched in October, 2006. PLASTIC is a time-of-flight mass spectrometer that is used to infer the composition, flux, and velocity of solar wind as well as suprathermal ions, such as pickup ions. This is achieved by the combined measurements of a particle’s energy, E, time-of-flight, τ, and energy-per-charge, E/q, which allows us to determine an ion’s mass, m, mass-per-charge, m/q, and velocity, vion. The PLASTIC instrument encompasses three different apertures that accept particles from varying directions and speeds. The He+ analysis presented here is performed with the Solar Wind Section (SWS) of PLASTIC, which is centred along the line connecting the Sun and the spacecraft and provides a limited field of view of ± 22.5° in- and ± 20.0° out of the ecliptic plane. One of the unique capabilities of the PLASTIC instrument is that it also measures the incident angle of ions in azimuth, α, and polar direction, θ, by utilizing a resistive anode and electrostatic deflection system, respectively. Thus, PLASTIC is capable of distinguishing between 32 different angles of incidence of incoming ions that are linear spaced between [αacc = ± 22.5°,Δα = 1.4°] in azimuth and [θacc = ± 20.0°,Δα = 1.3°] in polar direction. For this study we use the pulse height analysis data of PLASTIC, which have already been described in Drews et al. (2010, 2012, 2013) to determine the He+ VDF in the (vx,vy) plane of velocity space.
The aim of this analysis is to study changes of the He+ VDF as a function of the alignment of the solar magnetic field vector B. The provided pulse height analysis data by PLASTIC, which includes information about the total velocity and angle of incidence, α, of He+ pickup ions, are sufficient to determine the vx- and vy-component of the He+ velocity vector, vHe. The instrumental response of PLASTIC I(E/q,α), which describes the efficiency of detecting ions of a given energy-per-charge E/q and incident angle α, is unfortunately not well characterised. This means that we are not able to convert He+ count rates into absolute fluxes and consequently cannot study absolute changes of the He+ VDF as a function of B. However, we can resolve relative changes of the VDF for each angle of incidence α as a function of B, which then allows us to circumvent the unknown instrumental response I(E/q,α) as it does not depend on the alignment of the solar magnetic field vector, B. The relative change of the He+ VDF as a function of the alignment of B (reduced form of the He+ VDF – RVDF) preserves the angular information of all features of the He+ VDF that show a systematic variation with B.
 |
Fig. 2 Top left: phase space diagram in a spacecraft frame of reference. The white shaded area is the instrumental coverage of PLASTIC in phase space. The angle α denotes the azimuthal angle of an ion’s velocity vector in a resting frame of reference. Within the highlighted phase space volumes in red, yellow, and blue, only He+ particles with velocities of 1.9 <w < 2.0 and angles of α = (−15°,0°,15°) are measured. Top right: mean count rates of He+, CHe+ detected in the three different phase space volumes (in corresponding colours) as a function of φB. Bottom: probability density η(φB) (see Eq. (2)) plotted for the range −180°<φB < 180°. The vertical lines denote the expected magnetic field configurations in which the He+ ring beam distribution lies within the respective phase space volumes. |
Figure 2 shows a step-by-step illustration of the analysis method to determine the RVDF for three different phase space volumes. We restrict our analysis to the (vx,vy)-plane and periods in which B lies inside the ecliptic plane, i.e. θB = 90° ± 10°. Thus the orientation of the solar magnetic field vector can be expressed with a single parameter, φB, i.e. the azimuthal angle between B and the line connecting the Sun and the spacecraft. The top left panel of Fig. 2 shows a sketch of the phase space diagram in spacecraft coordinates. Velocities are expressed in terms of 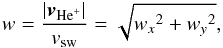 (1)i.e. w is the speed of He+, | vHe+ |, with respect to vsw (green dot). The white shaded area denotes the He+ coverage of the PLASTIC instrument in phase space, which is mainly determined by the instrumental E/q range and resolution, and the instrumental angular coverage. The angle α describes the azimuthal angle of incidence of He+ ions entering the instrument in a spacecraft frame of reference. He+ pickup ions with velocities of 1.9 <w < 2.0 and incident angles α of −15°,0°, and 15° lie inside the phase space volumes highlighted in red, yellow, and blue, respectively. The expected position of a He+ ring beam distribution for φB = 75° projected onto the (wx,wy)-plane is shown as a red dashed line. In the top right panel of Fig. 2, we provide the mean count rates with respect to φB, CHe+(φB) for the highlighted phase space volumes. The observation period started in March 2007 and ended in July 2013 and is based on 5-min resolution data of both the magnetic field and He+ pickup ions. For each phase space volume, clear structures can be seen, but all three distributions clearly differ in intensity. As stated before, the instrumental efficiency is not well defined and we cannot determine whether relative intensity differences are due to the instrumental response or not. However, the instrumental efficiency does certainly not depend on the alignment of the solar magnetic field, φB. Thus, we can derive the probability density, η(φB), for each phase space volume (α,w) with
(1)i.e. w is the speed of He+, | vHe+ |, with respect to vsw (green dot). The white shaded area denotes the He+ coverage of the PLASTIC instrument in phase space, which is mainly determined by the instrumental E/q range and resolution, and the instrumental angular coverage. The angle α describes the azimuthal angle of incidence of He+ ions entering the instrument in a spacecraft frame of reference. He+ pickup ions with velocities of 1.9 <w < 2.0 and incident angles α of −15°,0°, and 15° lie inside the phase space volumes highlighted in red, yellow, and blue, respectively. The expected position of a He+ ring beam distribution for φB = 75° projected onto the (wx,wy)-plane is shown as a red dashed line. In the top right panel of Fig. 2, we provide the mean count rates with respect to φB, CHe+(φB) for the highlighted phase space volumes. The observation period started in March 2007 and ended in July 2013 and is based on 5-min resolution data of both the magnetic field and He+ pickup ions. For each phase space volume, clear structures can be seen, but all three distributions clearly differ in intensity. As stated before, the instrumental efficiency is not well defined and we cannot determine whether relative intensity differences are due to the instrumental response or not. However, the instrumental efficiency does certainly not depend on the alignment of the solar magnetic field, φB. Thus, we can derive the probability density, η(φB), for each phase space volume (α,w) with 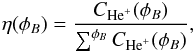 (2)where CHe+ are the observed count rates in the given phase space volume. The probability density η(φB) is shown in the bottom panel of Fig. 2 and denotes the change of the total He+ pickup ion flux in the given phase space volumes relative to φB. The distributions η(φB) are, in particular, no longer influenced by the α-dependence of the instrumental efficiency. As a consequence, we can use η(φB) to study signatures of the RVDF that change with the solar magnetic field configuration, φB. The most prominent features of η(φB) at velocities of 1.9 <w < 2.0 and α = (−15°,0°,15°) are two intensity peaks separated by ΔΦB = 180°, which match the expected magnetic field configurations of the He+ ring beam indicated by the red, yellow, and blue vertical lines at φB = (−105°,−90°,−75°) and φB = (75°,90°,115°), respectively.
(2)where CHe+ are the observed count rates in the given phase space volume. The probability density η(φB) is shown in the bottom panel of Fig. 2 and denotes the change of the total He+ pickup ion flux in the given phase space volumes relative to φB. The distributions η(φB) are, in particular, no longer influenced by the α-dependence of the instrumental efficiency. As a consequence, we can use η(φB) to study signatures of the RVDF that change with the solar magnetic field configuration, φB. The most prominent features of η(φB) at velocities of 1.9 <w < 2.0 and α = (−15°,0°,15°) are two intensity peaks separated by ΔΦB = 180°, which match the expected magnetic field configurations of the He+ ring beam indicated by the red, yellow, and blue vertical lines at φB = (−105°,−90°,−75°) and φB = (75°,90°,115°), respectively.
 |
Fig. 3 Top: average He+ counts observed per φ bin, α bin, and 5 min in a velocity range of 1.8 <w < 2.2 plotted as a function of φB (x-axis) and α (y-axis). Centre: probability density η(φB) plotted as a function of α and φB in a spacecraft frame of reference. Bottom: same as centre panel, except for He+ pickup ions with velocities of 0.8 <wsw < 1.2 coming from certain direction β in a solar wind frame of reference. The solid black lines denote the expected positions of the He+ ring beam distributions. |
In order to derive the RVDF in a velocity window of 1.8 <w < 2.2, i.e. velocities in which the He+ ring beam signature is the most prominent feature (Drews et al. 2013), we compute η(φB) for each instrumental angle of incidence, α, in the range −22.5°<α < 22.5°. The results are shown in Fig. 3. The top panel shows He+ count rates, CHe+, for each α (y-axis) as a function of φB (x-axis). Signatures of the He+ ring beam are visible (solid black lines) but disturbed by the α-dependence of the instrumental response. As discussed before, we can eliminate the influence of α on the detection efficiency by computing the probability density, η(φB), which is shown in the centre panel. The two-peak structure of η(φB) shown in Fig. 2 is visible for all α values and occurs at the expected ring beam configuration of φB.
 |
Fig. 4 Illustration of the two coordinate systems used throughout the analysis. Construction of the angle β and wsw of the solar wind frame of reference from the instrumental incident angles α and relative velocities w of the spacecraft frame of reference. A grid of the respective coordinate system is shown in both the solar wind (top) and spacecraft (bottom) frame of reference in grey. |
The injection of interstellar pickup ions and the initial He+ ring beam signature is well described in the frame of the former interstellar neutral atoms, i.e. in a spacecraft frame of reference (Figs. 2 and 4). However, their evolution is best described in a solar wind frame of reference as e.g. wave-particle interactions also occur in the frame of the solar wind (Saul et al. 2007). The angle β and wsw in a frame of reference of the solar wind are illustrated in Fig. 4 and defined as ![\begin{eqnarray} \label{eqw} &&\beta = \arctan{\left(\frac{\sin{(\alpha)\sin{(\theta)}} \cdot v_{\rm{He}^+}}{\cos{(\alpha)\sin{(\theta)}} \cdot v_{\rm{He}^+} - v_{\rm sw}}\right)} \\ &&w_{\rm sw}=\sqrt{\frac{\left[\sin{(\alpha)}\sin{(\theta)} \cdot v_{\rm{He}^+}\right]^2 + \left[\cos{(\alpha)}\sin{(\theta)} \cdot v_{\rm{He}^+}\right]^2}{v_{\rm sw}^2}}\cdot\quad\quad\quad \end{eqnarray}](/articles/aa/full_html/2015/03/aa25271-14/aa25271-14-eq60.png) Note that the polar angle, θ, of the He+ velocity vector, although required for a transition to the solar-wind frame of reference, is not shown in Fig. 4.
Note that the polar angle, θ, of the He+ velocity vector, although required for a transition to the solar-wind frame of reference, is not shown in Fig. 4.
The bottom panel of Fig. 3 shows η(φB) as a function of β for 0.8 <wsw < 1.2. Both β and wsw were corrected for the eigen-velocity of the STEREO spacecraft of ~ 35 km s-1. It is worth noting that the observed signatures in both frames of reference (centre and bottom panel) look very similar because β ≃ 2α for wsw ≃ 1.0. If the He+ VDF were fully isotropic, as was proposed in Vasyliunas & Siscoe (1976), He+ pickup ions of constant relative velocity wsw would show a uniform distribution in β (note that this is not equivalent to a uniform distribution in α). In our analysis method, pickup ions coming from a constant direction, β, with a constant velocity, wsw, would show a uniform distribution of the solar magnetic field angle, φB, if the He+ VDF is fully isotropic, i.e. the bottom panel of Fig. 3 would show no structure.
 |
Fig. 5 Probability density η(φB) for He+ pickup ions of varying velocities (different panels) coming from varying directions β (y-axis) plotted as a function of φB (x-axis). The expected positions of the He+ ring beam distributions are plotted as black lines. Positions in which the pitch angle of He+ is 0° are marked with red dashed lines. |
 |
Fig. 6 The He+ RVDF (see text for details) for different configurations of the in-ecliptic solar magnetic field angle φB. The top six panels show a configuration in which B is almost perpendicular with respect to vsw, i.e. a configuration in which the ring beam distribution lies within the aperture of the PLASTIC instrument. The bottom three panels show almost radial configurations of B for which no ring beam distribution is expected to be observed within the instruments aperture. |
By applying the approach previously described for different velocity windows, we finally obtain the RVDF within the limits of PLASTIC’s phase space coverage. Figure 5 shows the results of the analysis in the same manner as that shown in Fig. 3 (bottom panel) except for nine different velocity windows within 0.3 <wsw < 1.2 and Δw = 0.1. In each panel, the probability density η(φB) is colour coded as a function of φB (ΔφB = 3°) for each incident angle β (Δβ = 3°). The observation period started in March 2007 and ended in July 2013 and was limited to periods in which 80°<θB < 100°, wHe+> 1.3, and 200 km s-1<vsw < 500 km s-1. To guide the eye, the expected signature of the He+ ring beam is plotted as a black line in each panel for both magnetic polarities. Regions in which the velocity vector of He+ and the solar magnetic field vector, B, are parallel, i.e. the pitch angle is μ = 0° or cos(μ) = 1, are indicated by the red dashed lines. In each panel, slices parallel to the φB-axes denote the probability density, η(φB), for a constant incident angle β and relative velocity wsw similar to that shown in Fig. 2. More importantly, slices parallel to the β-axes in each panel can now be used to reconstruct the RVDF of He+.
For every magnetic field configuration φB, we use the slices parallel to the y-axes of Fig. 5 for all analysed wsw to reconstruct the reduced form of the velocity distribution function of He+. The resulting RVDF is shown in Fig. 6 for nine configurations of φB. The expected position of the He+ ring beam projected into 2D phase space is shown with red dashed lines. The red dots denote the intersection of the ring beam with the (wx, wy)-plane. Note, that the intersection of an undisturbed ring beam always lies at wsw ~ 1.0. As previously mentioned, the RVDF preserves the angular information of features of the He+ VDF. This means that the RVDF representation of the VDF allows us to study systematic variations of the ring beam orientation with varying inclinations of B, the angular distribution of the ring beam, i.e. the shape of the ring beam at a constant velocity wsw, and the relative intensity of the ring beam compared to structures that do not systematically change with the orientation of B. Of course, the RVDF representation is not limited to the ring beam distribution, but applies to all structures of the He+ VDF that systematically change with the orientation of B. On the other hand, the RVDF cannot preserve information of the absolute intensity of the VDF, i.e. the intensity of the RVDF is a measure for relative intensity changes of the VDF as a function of the local magnetic field orientation. The RVDF is also not applicable to study the shape of He+ velocity spectra considering that only a fraction of the He+ systematically changes with the orientation of B.
To show how the RVDF representation compares to the He+ VDF, we constructed the RVDF from an artificial He+ VDF. The top three panels of Fig. 7 show this artificial VDF for three alignments of B, i.e. φB = −90°,0°,90° from left to right. The artificial VDF is composed of three components: (1) a background distribution that is constant with respect to β, φB, and wsw; (2) a Gaussian feature of a constant intensity that does not change with B, and is similar to particles that are always streaming along a certain direction β, in this case along β = 40°; (3) a Gaussian feature of a constant intensity that does change with B, and is a general representation for the ring beam. This VDF is by no means a realistic representation of a He+ VDF, rather it is used to validate our analysis method. The centre three panels show the artificial He+ VDF convoluted with an arbitrary angular response function, i.e. each β-slice is multiplied by a random number between zero and one that simulates the unknown efficiency for the detection of He+ ion coming from different directions β. If the instrumental response were well known, the VDF in the upper three panels could be reconstructed from the observation shown in the centre three panels. In particular, angular features as well as absolute intensities could be resolved. As previously mentioned, the angular response is not known with sufficient accuracy and the VDF cannot be reconstructed from the three centre panels directly. Instead we can derive the RVDF as discussed above. The RVDF is basically a difference spectrum of the VDF with respect to φB and shown in the bottom three panels of Fig. 7. Angular information of features of the original VDF that show a systematic variation with φB are clearly resolved. However, the absolute intensity of these features is influenced by the underlying background of the original VDF, i.e. if the background is high the intensity of features that systematically change with the orientation of B decreases. Furthermore, features of the VDF that show no variation with the orientation of B, cannot be resolved with the RVDF, which is especially clear if one compares the Gaussian feature at β = 40° of the original VDF (top three panels in Fig. 7) to the RVDF shown in the bottom three panels of Fig. 7.
In conclusion, our analysis technique is clearly capable to resolve features of the He+ VDF that systematically change with a varying orientation of B. In particular, the anisotropic ring beam feature of the He+ VDF, which was originally observed in Oka et al. (2002) and Drews et al. (2013), is visible and together with Fig. 7 a good indicator for the validity of our analysis method. Furthermore, the analysis does not require any assumptions for the He+ VDF. With the observation shown in Figs. 5 and 6, we now summarise and describe the two most prominent features of the He+ RVDF:
-
(1) Interstellar He+ ring beam.
-
(2) Inner-source He+ feature.
2.1. Interstellar He+ ring beam signature
As previously mentioned, the ring beam of He+ is simply a result of the gyro motion of freshly ionised He+ pickup ions perpendicular to the local solar magnetic field B. The geometry of this set-up predicts that the incident angle of He+ pickup ions from the ring beam in a resting frame of reference is given by αHe,RB = φB−90°. The expected signature of the He+ ring beam in a frame of reference of the solar wind is indicated with black solid lines in Fig. 5 for both magnetic polarities. For He+ pickup ions that have been produced close to the spacecraft, i.e. wsw> 0.9 (bottom three panels of Fig. 5), the He+ ring beam signature is the most prominent feature of the RVDF. The ring beam is observed at its expected position, i.e. αHe,RB = φB−90°, which can be seen in the centre three panels of Fig. 6. As previously described, the strong contrast of the ring beam feature in the RVDF is an indicator that it is also the most dominant feature of the He+ VDF at wsw> 0.9. Between 0.6 <wsw < 0.9 the ring beam intensity seemingly decreases with an increasing asymmetry with respect to β. By asymmetry we explicitly mean that the ring beam feature is only visible for a confined range of incident angles β that seem to decrease with decreasing relative velocities wsw. The ring beam remains barely visible especially at wsw < 0.6 . As already described, at high relative velocities wsw> 0.9 the expected ring beam position is given by αHe,RB = φB−90°, which translates into βHe,RB with Eq. (3). The top three panels of Fig. 6 show a clear asymmetry of the ring beam with respect to its expected position, βHe,RB, i.e. the intensity of the RVDF is increased for β>βHe,RB.
2.2. Inner-source He+ feature
Another population of He+ pickup ions seems to systematically stream along B, i.e. vHe ∥ B, as evidenced by an increase of η(φB) around cos(μ) = 1 for each velocity in Fig. 5 (red dashed line). In contrast to the ring beam, it seems that this feature is most pronounced at small relative velocities of wsw < 0.8. Based on the RVDF shown in the bottom three panels of Fig. 6, it is also clear that the feature is centred around B with a distinct asymmetry towards β<φB opposed to the ring beam. Although the intensity of this feature is less pronounced compared to the He+ ring beam, the RVDF intensity significantly increases by almost a factor 2 with respect to the background due to this feature.
 |
Fig. 7 Top three panels: an artificial He+ VDF as a function of the He+ angle of incidence β and relative velocity wsw. Centre three panels: the same distribution convolved with a complex angular response function. Bottom three panels: reconstruction of the reduced He+ VDF (RVDF) with the proposed analysis technique based on data from the centre three panels. The RVDF representation of the VDF is only able to reconstruct structures that systematically change with the orientation of B (Gaussian feature at wsw = 1.1). Structures that stay constant over different orientations of B (Gaussian feature at wsw = 0.6) are not resolved. |
 |
Fig. 8 Reduced 1D He+ count rate spectra as a function of w − 1 (blue) and wsw (red) for periods in which 95°<φB < 105°. |
3. Discussion
Before we start to discuss the two previously mentioned He+ populations in detail, we emphasise the key difference of the He+ observation presented in this work compared to He+ observation made by other instruments, e.g. the Solar Wind Ion Composition Spectrometer (SWICS) on the Advanced Composition Explorer (ACE) and the Ulysses missions. First of all, PLASTIC’s angular resolution in azimuth, α, and polar angle, θ, allows us to determine the three components of the velocity vector vHe. With vHe we can determine a reduced form of the 2D He+ VDF, and make the correct transition from a spacecraft to a solar-wind frame of reference, i.e. we are able to derive wsw from the combination of w, α, and θ (see Fig. 4). Figure 8 shows a comparison between 1D He+ spectra in the two frames of reference for an observation period in which 95°<φB < 105°. While the assumption of a fully isotropic He+ VDF would allow for the transition from the spacecraft to a solar-wind frame of reference even without knowing the three components of the He+ velocity vector, vHe, a non-isotropic He+ VDF, as evidenced by the ring beam observation shown in Fig. 6, will result in a significant difference in shape and intensity of the observed He+ spectra between the two frames of reference (see Fig. 8). Because most instruments, in particular SWICS, are limited to 1D velocity spectra in a spacecraft frame of reference, deduced quantities from the observed w-spectra, like an adiabatic cooling index γ (e.g. Chen et al. 2013) or a pitch-angle scattering rate τ (e.g. Saul et al. 2007), are systematically altered by the anisotropic nature of the He+ VDF and therefore questionable.
Furthermore, several additional consideration have to be made if one tries to derive physical quantities from the observations of 1D spectra of He+. First of all, and contrary to the often applied simplification, He+ pickup ions do not have an initial velocity of wsw = 1 directly after their ionization. The relative velocity, wsw, is influenced by the velocity of the former neutral helium atom vN at 1 AU, the solar wind speed vsw, and therefore the ecliptic longitude, λ, in which the measurement is performed (e.g. Moebius et al. 1995). The initial speed of He+ is determined by the relative speed of the former neutral particle with respect to the solar wind, i.e. 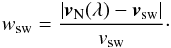 (5)In the upwind direction (λ ≈ 258°) interstellar neutrals will move anti-parallel to the solar wind while on the downwind side of the Sun (λ ≈ 78°) they move parallel to the solar wind. Assuming that | vN | = 45 km s-1, the initial velocity of interstellar He+ pickup ions can therefore vary between 0.85 <wsw < 1.15 for vsw = 300 km s-1 and 0.93 <wsw < 1.08 for vsw = 600 km s-1 purely due to a change of ecliptic longitude.
(5)In the upwind direction (λ ≈ 258°) interstellar neutrals will move anti-parallel to the solar wind while on the downwind side of the Sun (λ ≈ 78°) they move parallel to the solar wind. Assuming that | vN | = 45 km s-1, the initial velocity of interstellar He+ pickup ions can therefore vary between 0.85 <wsw < 1.15 for vsw = 300 km s-1 and 0.93 <wsw < 1.08 for vsw = 600 km s-1 purely due to a change of ecliptic longitude.
In addition, observations of He+ velocity spectra made by SWICS are limited to the quantity w = | vHe | /vsw, i.e. the velocity of He+ relative to the solar wind speed in a resting frame of reference. As was shown in Drews et al. (2013) and discussed in our introduction, the observed relative velocity of He+ pickup ions of the initial ring beam is determined by the magnetic configuration, i.e. 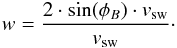 (6)This means that even during quasi-perpendicular configurations of B, 70°<φB < 110° and θB = 90°, and a constant solar wind velocity and ecliptic longitude, a relative velocity of wsw = 1 results in a w range of 1.88 <w < 2.0. The PLASTIC instrument, which although it is capable of transforming from w to the correct frame of reference wsw, is, on the other hand, heavily biased by the insufficiently characterised instrumental efficiency. This renders 1D observations with PLASTIC, as shown in Fig. , unsuited to obtain meaningful quantities for γ or τ as well. As discussed before, 1D observations of He+ spectra in general seem to be a poor indicator for the phase space transport of pickup ions. However, the transition from 1D to 2D observations and the approach to study relative differences of the He+ VDF with respect to φB enables us to circumvent the poorly characterised instrumental response of PLASTIC and to investigate several new and unexpected characteristics of the He+ VDF.
(6)This means that even during quasi-perpendicular configurations of B, 70°<φB < 110° and θB = 90°, and a constant solar wind velocity and ecliptic longitude, a relative velocity of wsw = 1 results in a w range of 1.88 <w < 2.0. The PLASTIC instrument, which although it is capable of transforming from w to the correct frame of reference wsw, is, on the other hand, heavily biased by the insufficiently characterised instrumental efficiency. This renders 1D observations with PLASTIC, as shown in Fig. , unsuited to obtain meaningful quantities for γ or τ as well. As discussed before, 1D observations of He+ spectra in general seem to be a poor indicator for the phase space transport of pickup ions. However, the transition from 1D to 2D observations and the approach to study relative differences of the He+ VDF with respect to φB enables us to circumvent the poorly characterised instrumental response of PLASTIC and to investigate several new and unexpected characteristics of the He+ VDF.
3.1. The He+ ring beam signature
The initial phase space distribution of He+ pickup ions resembles the form of a torus. A sketch of this, so-called, ring beam distribution is shown in Figs. 1 and 4. The observation of a He+ ring beam feature was already presented in Oka et al. (2002) and Drews et al. (2013), although these observations were limited by an insufficient phase space resolution and a rather indirect method to visualise the ring beam feature. Because the ring beam distribution is expected to show systematic changes with the configuration of the solar magnetic field, the He+ RVDF we developed is ideal for studying the characteristic of the He+ ring beam.
The geometry of the ring beam (see Figs. 1 and 4) predicts (1) that the plane of the ring beam is perpendicular to B; (2) that the two intersections of the torus distribution with the vz = 0 plane lie at | wsw | = 1 and requires that the He+ distribution has not been severely disturbed by wave-particle interactions or other disturbances. Characteristic (1) can be verified with our observation in Fig. 5, which shows a good alignment of the observed ring beam signature compared to its expected position (black lines). The RVDF representation of the ring beam (Fig. 6) shows that the plane orientation of the torus distribution changes linearly with B, which in terms of a difference image results in a ring beam distribution that co-rotates with B through the instrument’s aperture. Furthermore, a distinct intensity asymmetry between different magnetic configurations is evident, i.e. the RVDF intensity of the ring beam increases with increasing βHe,RB. However, this special characteristic is unlikely to be a direct result of the initial ring beam distribution and will be further discussed in the next chapter. Characteristic (2), i.e. that the initial ring beam is most pronounced at | wsw | = 1, is also fulfilled within the limits of the previously discussed uncertainty of the initial relative speed, wsw, of He+ pickup ions. Considering that our measurement of the RVDF is based on an observation period of almost five years and consists of a relatively uniform mixture of ecliptic longitudes and concurrent solar wind velocities, the initial velocity of He+ directly after the ionization is expected to lie in the range of 0.85 ≲ wsw ≲ 1.15 (see Eq. (5)) and therefore in agreement with our observations (Fig. 5). Nonetheless, signatures of the He+ ring beam remain visible down to wsw> 0.4. This could either indicate that the initial ring beam distribution can persist for a prolonged period, i.e. adiabatic cooling happens on much faster timescales than pitch-angle scattering, or that the range of the initial velocity of He+ is much broader than predicted by Eq. (5) due to, for example, the thermal velocity of the former interstellar neutrals.
Our RVDF representation of the He+ VDF would allow us to determine estimates for both the angular width of the ring beam signature as well as its significance compared to the isotropic background. These two estimates are obtained under the assumption of a constant interstellar neutral helium velocity, vN, a constant solar wind velocity, vsw, and a simple heliospheric magnetic field, e.g. a Parker field configuration. With this configuration these two estimates itself are a direct measure of the amount of disturbances, e.g. wave-particle interactions, that the interstellar He+ pickup ion population has undergone. However, as indicated by the observed RVDF in Fig. 6, the He+ VDF is much more complex in nature than generally assumed. The VDF is especially not isotropic, partially not gyrotropic (discussed in the next section), and significantly different for varying velocities wsw. This is partially because the velocity of the neutral seed population and the solar wind is not constant but highly variable in time and space. Especially the heliospheric magnetic field is not an ideal Parker field and is disturbed both on local and global scales within the heliosphere. To our knowledge, existing models for the He+ VDF (e.g. Isenberg 1997; Chalov & Fahr 1998; Chalov 2014) currently rely on the aforementioned simplification to solve the transport equation of pickup ions and are therefore inapplicable for a comparison to the observations presented in this work, which of course have been made under realistic conditions. We also point out that signatures of the initial He+ torus distribution at 1 AU as observed in this work have neither been predicted nor sufficiently discussed in the existing theory. Because of the strong discrepancy between observations and predictions and the aforementioned simplification made in theoretical studies, we deliberately refrain from a quantitative parameter study or comparison of the He+ ring beam RVDF observation to pre-existing theoretical studies.
 |
Fig. 9 Left: phase space diagram of the injection of He+ pickup ions for the most likely configuration of the solar magnetic field vector, i.e. φB = 45° ± 15°. For this configuration, most He+ ions are injected in the sunward hemisphere of phase space (w < 1.0) and will not be detected by an instrument like SWICS, CTOF, or PLASTIC. Right: during almost perpendicular configurations of B, the He+ ring beam (red line) lies within the instrument aperture at an angle of incidence of ~ 0°. However, He+ ions that have been ionised prior to the perpendicular configuration of B, i.e. the phase space density shown in the left panel, are now also scattered into the anti-sunward hemisphere of phase space. This scenario causes a distinct one-sided asymmetry of the observed He+ ring beam distributions during perpendicular configurations of B. |
3.2. The asymmetry of the He+ ring beam
As described in the previous chapter, the He+ ring beam signature seems to be asymmetrically distributed around the expected incident angle of βHe,RB (Fig. 6, top six panels). More specifically, the likelihood of observing He+ pickup ions is significantly increased for He+ pickup ions that are measured with incident angles of β>βHe,RB. Neither influences of the temperature of the neutral helium atoms nor the fluctuations of the solar magnetic field are expected to cause an asymmetric distribution of β around the expected incident angle of He+ ring beam particles. However, until now we have neglected the influence of the spatial diffusion of pickup ions for the discussion of the He+ VDF (Chalov & Fahr 1998). As already discussed, pickup ions only co-move with the solar wind if they are injected at magnetic field configurations that are perfectly perpendicular to the solar wind velocity vector, i.e. B ⊥ vsw. For any given configuration of B with θB = 90°, the guiding centre velocity of the pickup ion is given by 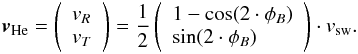 (7)The parameter vHe describes the velocity vector of the pickup ion relative to the solar wind velocity vector vsw in which it was born. For the sake of simplicity, we will assume in the following discussion that the influence of resonant wave-particle interactions is negligible and that the solar magnetic field angle, φB, is constant.
(7)The parameter vHe describes the velocity vector of the pickup ion relative to the solar wind velocity vector vsw in which it was born. For the sake of simplicity, we will assume in the following discussion that the influence of resonant wave-particle interactions is negligible and that the solar magnetic field angle, φB, is constant.
A He+ pickup ion that is injected into the heliosphere at a distance from the Sun of R = 0.6 AU and a solar magnetic field angle of φB = 45° will have a relative speed compared to the solar wind of vHe = (0.5·vsw,0.5·vsw). The solar wind will take ~ 2 days to travel the distance from 0.6 AU to 1 AU for a solar wind speed of vsw = 400 km s-1. During that time, the pickup ion will move with a total velocity of ~ 280 km s-1 relative to the solar wind. As a result, once the solar wind has travelled from 0.6 AU to 1 AU, the pickup ion will be located in a distance of ~ 0.3 AU away from the solar wind parcel in which it was originally born. The pickup ion will also take ~ 1 day longer to reach 1 AU compared to the solar wind. Although this is an over-simplified picture of the transport of pickup ions, it introduces a very important concept for the investigation of the He+ VDF. Influences of these so-called transport effects on the heliospheric distribution and 1D velocity spectra of He+ pickup ions have already been investigated in e.g. Chalov & Fahr (1998); Chalov (2014) for a simplified set of heliospheric conditions, e.g. a constant solar wind speed and an ideal heliospheric magnetic Parker field. However, a more realistic, e.g. fluctuating, magnetic field combined with varying solar wind speeds and strong spatial diffusion would allow pickup ions to change from one solar wind or, rather, magnetic field regime into another. This also introduces a process that may change the shape of the He+ VDF without the influence of resonant wave-particle interaction. Consequently, numerical pickup ion models that assume a constant solar wind speed and a simple solar magnetic Parker field are likely insufficient to make quantitative predictions for the He+ VDF at 1 AU.
Figure 9 shows an example of how the spatial diffusion of pickup ions can influence the observed He+ VDF. The left panel shows a phase space diagram of the VDF for the most likely magnetic field configuration at ~1 AU, i.e. the Parker configuration in which φB = (−45°,135°). Here, almost all pickup ions are injected inside the sunward hemisphere of phase space (red shaded area) with a guiding centre velocity that is significantly different compared to the solar wind. As discussed earlier, this pickup ion population can change from one solar wind regime into another in which, for example, the solar magnetic field vector is more perpendicular (right panel of Fig. 9). The distribution shown in the left panel of Fig. 9 is then scattered (or mirrored) into the anti-sunward hemisphere of phase space if the change of B happens rapidly, i.e. B changes on timescales τS smaller then the gyration period of the pickup ions, τG. For τS ≫ τG, the distribution shown on the left will slowly rotate into the instrument aperture instead. Thus, during a perpendicular configuration of B we will likely see a mixture of the pickup ion ring beam feature and a pickup ion population that has been injected during completely different magnetic field configurations. This will also produce a significant asymmetry of the observed pitch-angle distribution of these pickup ions (sketched in the right panel of Fig. 9), as was observed for the He+ ring beam feature shown in Fig. 6. This asymmetry also results in the intensity asymmetry of the ring beam for different magnetic configurations. Because the RVDF shown in Fig. 6 is only a representation of relative changes of the VDF with respect to φB, a He+ population that is scattered (or mirrored) into the instrument’s aperture can produce different amounts of background depending on the orientation of B. Although both processes previously discussed seem to have a measurable impact on the observed pitch-angle distribution of pickup ions, they are obviously very difficult to quantify as they depend on the global distribution of the solar magnetic field, which is not observed and therefore unknown. Nonetheless, the implication is that the spatial diffusion of pickup ions can easily change the observed pitch-angle distribution without the influence of resonant wave-particle interactions.
We also point out that the spatial diffusion and its influence on the 1D spatial, pitch-angle, and velocity profile of interstellar pickup ions has already been addressed in Chalov & Fahr (1998) and subsequent studies. In their studies, the authors have shown that the diffusion in combination with a highly anisotropic VDF of interstellar pickup ions has a significant impact on the spatial and spectral pattern of interstellar pickup ions. Their study is, however, not readily applicable to our observations because of two simplifications made in their numerical approach. They assumed that the solar wind is constant everywhere in the heliosphere and that the global solar magnetic field is well described by an undisturbed Parker field. We argue, on the other hand, that the asymmetry of the ring beam is due to a predominantly injection of interstellar He+ during the Parker configuration. Due only to the spatial diffusion of He+ and consequent change of the global solar magnetic field properties for these ions, He+ ions that were originally injected at e.g. Bφ = 45° can be scattered into the anti-sunward hemisphere of velocity space during local magnetic field configurations in which Bφ = 90°. The resulting He+ VDF then shows the superposition of He+ ions that were just injected at Bφ = 90°, i.e. an undisturbed torus distribution, and He+ ions that were mirrored/scattered into the anti-sunward hemisphere of velocity space because of a change of the solar magnetic field properties (see Fig. 9). Changes of the global solar magnetic field properties as seen by pickup ions, e.g. a disturbance of the global field or change of the inclination of B due to the diffusion of pickup ions from a low- to high-speed solar wind stream, are not properly considered in Chalov & Fahr (1998). Theses changes are, however, undoubtedly significant for the He+ VDF, as evidenced by our observation of a distinct asymmetry of the ring beam distribution of He+ pickup ions.
3.3. Inner-source feature of the He+ VDF
At small velocities, in particular, wsw < 0.8, the He+ VDF shows a significant anisotropic feature that seems to follow the solar magnetic field vector; i.e. He+ pickup ions are streaming along the local magnetic field. This feature can be seen in the top six panels of Fig. 5 as a broad diagonal structure distributed around the cos(μ) = 1 line. Furthermore, the bottom three panels of Fig. 6 show that the most likely incident angle for particles of this population is not symmetrically distributed around B. This behaviour somewhat contradicts the expectation of a charged particle inside an external magnetic field, which, at least, should show gyrotropy around B. Of course, one can only assume a gryotropic distribution if the measurement is averaged over time periods that are larger than the gyro period of the particle, which for the example given in Fig. 6 is obviously fulfilled.
In contrast to the ring beam observation at high relative velocities wsw> 0.8, we have to make sure that the observation of this feature at lower relative velocities, wsw < 0.8, is not systematically biased by solar wind background. At He+ velocities close to the solar wind velocity, it is very difficult to distinguish He+ pickup ions from solar wind Si7+, Fe13+, and Fe14+ ions due to their similar mass-per-charge ratio compared to He+. Because we identify the He+ pickup ion data from the PLASTIC instrument by means of an ion’s mass-per-charge (or rather the combination of an ion’s energy-per-charge and time-of-flight), we might be affected by instrumental background from the aforementioned solar wind ions. In order to check whether this is true, we investigated the time-of-flight distribution of He+ as a function of wsw and β. For this purpose, we defined a He+ time-of-flight signal, CS, as τS = τHe ± 5, where τHe denotes the most probable time-of-flight position of He+, and a solar wind background signal, CB, as τHe + 10 <τB<τHe + 30. In fact, both of the ranges defined for CS and CB lie inside the range of the expected He+ time-of-flight distribution. However, CS covers the core of the He+ time-of-flight distribution and therefore provides a significantly better He+ to solar-wind background ratio compared to CB. The signal CB on the other hand covers the right flank of the He+ time-of-flight distribution in which solar wind background, e.g. Si7+ and Fe13+,14+, can contribute significantly to the observed count rate. The ratio CB/CS is therefore an indicator of the degree of contamination of the He+ signal by solar wind ions, i.e. higher values denote higher contamination, but not an absolute measure for the ratio of He+ ions to solar wind background.
 |
Fig. 10 Ratio of the instrumental time-of-flight background (τHe + 10 <τB<τHe + 30) and the He+ time-of-flight signal (τS ≈ τHe ± 5) plotted as a function of wsw and β, whereas τHe denotes the expected time-of-flight position of He+ in instrumental channel numbers. |
Figure 10 shows the count ratio of CB/CS as a function of the incident angle β and He+ velocity wsw. Based on the observations of Fig. 10, it is clear that our analysis of the He+ RVDF might be systematically biased by solar wind background, i.e. especially at low wsw and β < 0°, the He+ RVDF is more contaminated by solar wind background compared to high wsw and β> 0°. Consequently, we need to test whether structures of the He+ RVDF occurring at small relative speeds and β < 0° are related to the higher contamination of solar wind ions. In order to see whether the discussed anisotropy during radial configurations of B is in fact caused by the solar wind contamination shown in Fig. 10, we repeated our analysis shown in Fig. 5 for solar wind Fe11+ and O6+. Both O6+ and Fe11+ show the same anisotropic signature around the solar magnetic field vector B, indicating that this feature is a characteristic of heavy solar wind ions and likely related to heavy ion-proton differential streaming, which is known to be aligned with B (Berger et al. 2011).
In a next step we compared the RVDF of the He+ signal CS (τS = τHe ± 5) and the background signal CB (τHe + 10 <τB<τHe + 30). Considering that CB is much more contaminated by solar wind background than CS, CB should show a significantly stronger signature of heavy ion-proton streaming compared to CS if the feature is really related to solar wind contamination. However, we found that CB and CS show the same feature aligned with B without significant intensity differences (see bottom three panels of Fig. 6). The fact that heavy solar wind ions show this feature and the mixture of heavy solar wind and He+ ions is different in CB and CS, therefore indicates that He+ pickup ions in fact share characteristics of heavy solar wind ions at low relative velocities wsw. The anisotropic features of O6+, Fe11+, and He+ are most prominent at small relative velocities wsw < 0.5, i.e. the feature is ordered by the solar wind velocity vsw, and therefore unlikely to be related to instrumental biases.
We further point out that He+ not only originates from interstellar neutral helium atoms but also from the so-called inner source. This inner source was first reported in Geiss et al. (1995) in an observation of C+ pickup ions with the SWICS instrument on board Ulysses. Interstellar He+ is expected to be much more abundant than inner-source He+. Consequently, contributions of inner-source He+ pickup ions are very difficult to resolve in 1D velocity spectra of He+. However, we know from observations of inner-source pickup ions heavier than helium that the inner source of pickup ions is dominant at relative velocities wsw < 0.5 (Berger et al. 2013). Because the composition of the inner source resembles the composition of the solar wind (Allegrini et al. 2005; Gloeckler et al. 2000; Taut et al. 2015) and the inner-source pickup ion flux is correlated to the flux of the corresponding element in the solar wind (Berger et al. 2015), the seed population of inner-source pickup ions is likely the solar wind.
Of all proposed scenarios for the production of inner-source pickup ions (Allegrini et al. 2005), the scenario proposed by Wimmer-Schweingruber & Bochsler (2003) has turned out to be the most likely candidate. In this scenario, solar wind ions penetrate thin (nm-sized) dust grains and leave them as neutral or low-charged particles. If the interaction is weak, i.e. there is no significant energy loss or scattering of the solar wind ion during grain passage, the particles would leave the grain with a small wsw, and the shape of the original solar wind VDF would be partially preserved in the resulting inner-source population.
The aforementioned streaming signature parallel to B is visible for heavy solar wind ions as well as He+ and the signature is most dominant at wsw < 0.5, i.e. the expected range for inner-source pickup ions due to their predominant injection close to the Sun and consequent adiabatic deceleration. In particular, these two observational constraints are in agreement with the production scenario for the inner source proposed by Wimmer-Schweingruber & Bochsler (2003). Thus we argue that the beam distribution of He+ is related to inner-source He+ pickup ions. Therefore, our 2D observation of the He+ RVDF can provide a way to identify inner-source He+ despite the predominant contribution of interstellar helium. However, the non-gyrotropic feature of the He+ beam and the fact that the beam is located at significantly higher velocities compared to the expected velocity of a solar wind He2+ beam at vB = vsw + vA, with vA being the Alfvén speed, is not yet fully understood and requires further investigation.
4. Conclusions and outlook
In summary, our observations have shown that the He+ VDF is not isotropic. The observations in Figs. 5 and 6 unambiguously show that, during all magnetic field configurations of B and all relative velocities of He+, wsw, the observed VDF is neither uniform nor symmetrically distributed around B. At velocities close to the injection velocity of He+, 0.8 <wsw < 1.2, the ring beam signature seems to be the most prominent feature of the He+ VDF (see Fig. 5). Thus the state of the He+ VDF strongly depends on the local solar magnetic field vector B, the relative speed of the former neutral helium with respect to the solar wind, which in turn is a function of the ecliptic longitude, λ, and the solar wind speed, vsw. For that reason, we argue that the relative velocity of He+ measured in a spacecraft frame of reference, w, is a very poor indicator to obtain values for either the pitch-angle scattering rate or adiabatic cooling index of He+ pickup ions, because of the dependence of w on the aforementioned quantities vsw, B, and λ.
A close investigation of the He+ ring beam signature also revealed an asymmetric distribution of the He+ ring beam around its expected position. We propose that this asymmetry is caused by spatial diffusion of pickup ions (see Fig. 9), which only co-move with the solar wind when B ⊥ vsw (Chalov & Fahr 1998). The relative velocity of He+ with respect to the solar wind, therefore, allows He+ to change from one solar magnetic field regime into another, i.e. from the most likely Parker field configuration, φB = 45°, to a configuration in which B ⊥ vsw. Following the scenario illustrated in Fig. 9, the ring beam distribution is therefore expected to show a distinct asymmetry around its expected position. This indicates that rapid changes of the IMF, e.g. a spatial distortion of the IMF due to magnetic flux tubes, have a significant influence on the evolution of the He+ VDF.
At relative velocities outside the typical interstellar pickup ion range, wsw < 0.5, the ring beam is far less pronounced. Instead, the RVDF is dominated by a beam of He+ ions aligned along B (see bottom three panels of Fig. 6). The He+ beam is also not strictly symmetrically distributed around B, indicating that the He+ VDF is unlikely to be fully gyrotropic. Investigation of the RVDF for solar wind O6+ and Fe11+ revealed that solar wind ions show the same beam signature at wsw < 0.3, which is likely related to a ion-proton differential streaming signature. Considering the inner-source production scenario proposed by Wimmer-Schweingruber & Bochsler (2003), we argue that the observation of a beam-like He+ signature at low wsw parallel to B can be attributed to the inner source. In this scenario, signatures of the solar wind, i.e. the seed population of the inner source, are passed on to the corresponding inner-source population. However, the non-gyrotropic feature of the He+ beam and the extension of the beam towards higher wsw is not yet fully understood and requires further investigations.
In general, our study of relative changes of the 2D He+ VDF with varying configurations of the IMF revealed several new characteristics of interstellar and inner-source He+ pickup ions. In particular, the formation of a beam signature of He+ aligned along B and the observed asymmetry of the ring beam implies that the He+ VDF is more complex than originally thought. To some degree, our analysis might also be applicable for other pickup ions as well, especially a comparison between He+ and C+, which is solely attributed to the inner source (Geiss et al. 1995), might clarify whether the He+ beam at wsw < 0.5 is indeed caused by an inner-source He+ population. Furthermore, a systematic investigations of the ring beam of interstellar He+ and O+ in different regimes of solar- or magnetic activity would help to study the stability of the ring beam during varying conditions of the solar wind and by that address the importance of resonant wave-particle interaction on the initial ring beam distribution of interstellar pickup ions.
As already mentioned, the phase space transport of pickup ions is highly complex and connected to, e.g., adiabatic deceleration, resonant wave-particle interactions, the spatial and spectral distribution of the neutral seed population, and the local and global solar magnetic field. While most of these topics can be addressed individually by numerical studies, observations of the He+ VDF necessarily include the combined interactions of the aforementioned aspects of the phase space transport of He+. This especially complicates the investigations of individual signatures of the VDF that might have been predicted in the past by theoretical studies, such as an imprint of the spatial and spectral injection pattern due to electron impact ionization close to the Sun (Rucinski & Fahr 1989) or spatial diffusion (Chalov & Fahr 1998). However, observations at 1 AU of a He+ torus or ring beam distribution presented in Oka et al. (2002); Drews et al. (2013) and this work have, to our knowledge, not been predicted by past theoretical studies of the VDF of pickup ions. This demonstrates the necessity to improve on the existing numerical description for the formation and evolution of the pickup ion VDF, and that a 1D examination of either the spatial, velocity and pitch-angle distributions in both theoretical and observational studies are too limiting to make meaningful predictions for the pickup ion phase space transport. We emphasise that a detailed discussion of the pickup ion phase space transport can not rely on an individual 2D observations of the He+ VDF, but requires complementary support by theoretical studies to deconvolve the complex interplay of processes relevant for the formation and evolution of the He+ VDF.
Acknowledgments
We like to thank the PLASTIC and IMPACT teams for providing the necessary data for this work (Galvin et al. 2008; Acuña et al. 2008). Part of this work was supported by the German Deutsche Forschungsgemeinschaft, DFG (project number: Wi2139/7-1).
References
- Acuña, M. H., Curtis, D., Scheifele, J. L., et al. 2008, Space Sci. Rev., 136, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Allegrini, F., Schwadron, N. A., McComas, D. J., Gloeckler, G., & Geiss, J. 2005, J. Geophys. Res. (Space Phys.), 110, 5105 [Google Scholar]
- Berger, L., Wimmer-Schweingruber, R. F., & Gloeckler, G. 2011, Phys. Rev. Lett., 106, 151103 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, L., Drews, C., Taut, A., & Wimmer-Schweingruber, R. F. 2013, AIP Conf. Ser., 1539, 386 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, L., Drews, C., Taut, A., Wimmer-Schweingruber, R. F. 2015, A&A, in press, DOI: 10.1051/0004-6361/201425116 [Google Scholar]
- Chalov, S. V. 2014, MNRAS, 443, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Chalov, S. V., & Fahr, H. J. 1996, Sol. Phys., 168, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Chalov, S. V., & Fahr, H. J. 1998, A&A, 335, 746 [NASA ADS] [Google Scholar]
- Chalov, S. V., & Fahr, H. J. 1999, Sol. Phys., 187, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, J. H., Möbius, E., Gloeckler, G., et al. 2013, J. Geophys. Res. (Space Phys.), 118, 3946 [NASA ADS] [CrossRef] [Google Scholar]
- Cummings, A. C., Stone, E. C., & Steenberg, C. D. 2002, ApJ, 578, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Drews, C., Berger, L., Wimmer-Schweingruber, R. F., et al. 2010, J. Geophys. Res., 115, 10108 [Google Scholar]
- Drews, C., Berger, L., Wimmer-Schweingruber, R. F., et al. 2012, J. Geophys. Res., 117, 9106 [Google Scholar]
- Drews, C., Berger, L., Wimmer-Schweingruber, R. F., & Galvin, A. B. 2013, Geophys. Res. Lett., 40, 1468 [NASA ADS] [CrossRef] [Google Scholar]
- Fahr, H. J. 1971, Planet. Space Sci., 19, 1121 [NASA ADS] [CrossRef] [Google Scholar]
- Fahr, H. J., & Fichtner, H. 2011, A&A, 533, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fisk, L. A., & Gloeckler, G. 2012, Space Sci. Rev., 173, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Fisk, L. A., Schwadron, N. A., & Gloeckler, G. 1997, Geophys. Res. Lett., 24, 93 [Google Scholar]
- Galvin, A. B., Kistler, L. M., Popecki, M. A., et al. 2008, Space Sci. Rev., 136, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Gloeckler, G., Schwadron, N. A., Fisk, L. A., & Geiss, J. 1995, Geophys. Res. Lett., 22, 2665 [NASA ADS] [CrossRef] [Google Scholar]
- Gloeckler, G., Fisk, L. A., Geiss, J., Schwadron, N. A., & Zurbuchen, T. H. 2000, J. Geophys. Res., 105, 7459 [NASA ADS] [CrossRef] [Google Scholar]
- Geiss, J., Gloeckler, G., Fisk, L. A., & von Steiger, R. 1995, J. Geophys. Res., 100, 23373 [NASA ADS] [CrossRef] [Google Scholar]
- Hilchenbach, M., Hovestadt, D., Klecker, B., & Moebius, E. 1992, in Solar Wind Seven, Proc. of the 3rd COSPAR Colloquium, 349 [Google Scholar]
- Isenberg, P. A. 1987, J. Geophys. Res., 92, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Isenberg, P. A. 1997, J. Geophys. Res., 102, 4719 [NASA ADS] [CrossRef] [Google Scholar]
- Kallenbach, R., Geiss, J., Gloeckler, G., & von Steiger, R. 2000, Ap&SS, 274, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Marsch, E., Rosenbauer, H., Schwenn, R., Muehlhaeuser, K.-H., & Denskat, K. U. 1981, J. Geophys. Res., 86, 9199 [NASA ADS] [CrossRef] [Google Scholar]
- Moebius, E., Hovestadt, D., Klecker, B., Scholer, M., & Gloeckler, G. 1985, Nature, 318, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Moebius, E., Klecker, B., Hovestadt, D., & Scholer, M. 1988, Ap&SS, 144, 487 [NASA ADS] [Google Scholar]
- Moebius, E., Rucinski, D., Hovestadt, D., & Klecker, B. 1995, A&A, 304, 505 [NASA ADS] [Google Scholar]
- Möbius, E., Rucinski, D., Lee, M. A., & Isenberg, P. A. 1998, J. Geophys. Res., 103, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Möbius, E., Bzowski, M., Chalov, S., et al. 2004, A&A, 426, 897 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oka, M., Terasawa, T., Noda, H., Saito, Y., & Mukai, T. 2002, Geophys. Res. Lett., 29, 1612 [NASA ADS] [CrossRef] [Google Scholar]
- Rucinski, D., & Fahr, H. J. 1989, A&A, 224, 290 [NASA ADS] [Google Scholar]
- Saul, L., Möbius, E., Isenberg, P., & Bochsler, P. 2007, ApJ, 655, 672 [NASA ADS] [CrossRef] [Google Scholar]
- Saul, L., Wurz, P., & Kallenbach, R. 2009, ApJ, 703, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Semar, C. L. 1970, J. Geophys. Res., 75, 6892 [NASA ADS] [CrossRef] [Google Scholar]
- Schwadron, N. A. 1998, J. Geophys. Res., 103, 20643 [NASA ADS] [CrossRef] [Google Scholar]
- Taut, A., Berger, L., Drews, C. Wimmer-Schweingruber, R. F., & Galvin, A. B. 2015, A&A, in press, DOI: 10.1051/0004-6361/201425139 [Google Scholar]
- Vasyliunas, V. M., & Siscoe, G. L. 1976, J. Geophys. Res., 81, 1247 [NASA ADS] [CrossRef] [Google Scholar]
- Wenzel, K.-P., Sanderson, T. R., Richardson, I. G., et al. 1986, Geophys. Res. Lett., 13, 861 [NASA ADS] [CrossRef] [Google Scholar]
- Wimmer-Schweingruber, R. F., & Bochsler, P. 2003, Geophys. Res. Lett., 30, 1077 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Velocity space diagrams of a He+ ring beam signature (top left) under the influence of pitch angle scattering (top right), adiabatic cooling (bottom left), and a rapid change of the solar magnetic field vector, B, (bottom right) are shown. To illustrate the torus character of the distribution the (vx, vy)-plane is slightly tilted in this diagram. |
| In the text | |
 |
Fig. 2 Top left: phase space diagram in a spacecraft frame of reference. The white shaded area is the instrumental coverage of PLASTIC in phase space. The angle α denotes the azimuthal angle of an ion’s velocity vector in a resting frame of reference. Within the highlighted phase space volumes in red, yellow, and blue, only He+ particles with velocities of 1.9 <w < 2.0 and angles of α = (−15°,0°,15°) are measured. Top right: mean count rates of He+, CHe+ detected in the three different phase space volumes (in corresponding colours) as a function of φB. Bottom: probability density η(φB) (see Eq. (2)) plotted for the range −180°<φB < 180°. The vertical lines denote the expected magnetic field configurations in which the He+ ring beam distribution lies within the respective phase space volumes. |
| In the text | |
 |
Fig. 3 Top: average He+ counts observed per φ bin, α bin, and 5 min in a velocity range of 1.8 <w < 2.2 plotted as a function of φB (x-axis) and α (y-axis). Centre: probability density η(φB) plotted as a function of α and φB in a spacecraft frame of reference. Bottom: same as centre panel, except for He+ pickup ions with velocities of 0.8 <wsw < 1.2 coming from certain direction β in a solar wind frame of reference. The solid black lines denote the expected positions of the He+ ring beam distributions. |
| In the text | |
 |
Fig. 4 Illustration of the two coordinate systems used throughout the analysis. Construction of the angle β and wsw of the solar wind frame of reference from the instrumental incident angles α and relative velocities w of the spacecraft frame of reference. A grid of the respective coordinate system is shown in both the solar wind (top) and spacecraft (bottom) frame of reference in grey. |
| In the text | |
 |
Fig. 5 Probability density η(φB) for He+ pickup ions of varying velocities (different panels) coming from varying directions β (y-axis) plotted as a function of φB (x-axis). The expected positions of the He+ ring beam distributions are plotted as black lines. Positions in which the pitch angle of He+ is 0° are marked with red dashed lines. |
| In the text | |
 |
Fig. 6 The He+ RVDF (see text for details) for different configurations of the in-ecliptic solar magnetic field angle φB. The top six panels show a configuration in which B is almost perpendicular with respect to vsw, i.e. a configuration in which the ring beam distribution lies within the aperture of the PLASTIC instrument. The bottom three panels show almost radial configurations of B for which no ring beam distribution is expected to be observed within the instruments aperture. |
| In the text | |
 |
Fig. 7 Top three panels: an artificial He+ VDF as a function of the He+ angle of incidence β and relative velocity wsw. Centre three panels: the same distribution convolved with a complex angular response function. Bottom three panels: reconstruction of the reduced He+ VDF (RVDF) with the proposed analysis technique based on data from the centre three panels. The RVDF representation of the VDF is only able to reconstruct structures that systematically change with the orientation of B (Gaussian feature at wsw = 1.1). Structures that stay constant over different orientations of B (Gaussian feature at wsw = 0.6) are not resolved. |
| In the text | |
 |
Fig. 8 Reduced 1D He+ count rate spectra as a function of w − 1 (blue) and wsw (red) for periods in which 95°<φB < 105°. |
| In the text | |
 |
Fig. 9 Left: phase space diagram of the injection of He+ pickup ions for the most likely configuration of the solar magnetic field vector, i.e. φB = 45° ± 15°. For this configuration, most He+ ions are injected in the sunward hemisphere of phase space (w < 1.0) and will not be detected by an instrument like SWICS, CTOF, or PLASTIC. Right: during almost perpendicular configurations of B, the He+ ring beam (red line) lies within the instrument aperture at an angle of incidence of ~ 0°. However, He+ ions that have been ionised prior to the perpendicular configuration of B, i.e. the phase space density shown in the left panel, are now also scattered into the anti-sunward hemisphere of phase space. This scenario causes a distinct one-sided asymmetry of the observed He+ ring beam distributions during perpendicular configurations of B. |
| In the text | |
 |
Fig. 10 Ratio of the instrumental time-of-flight background (τHe + 10 <τB<τHe + 30) and the He+ time-of-flight signal (τS ≈ τHe ± 5) plotted as a function of wsw and β, whereas τHe denotes the expected time-of-flight position of He+ in instrumental channel numbers. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


