EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 575 (March 2015) A&A, 575 (2015) A66 Full HTML
Free Access
Issue
A&A
Volume 575, March 2015
Article Number A66
Number of page(s) 7
Section Stellar atmospheres
DOI https://doi.org/10.1051/0004-6361/201425193
Published online 24 February 2015

© ESO, 2015

1. Introduction

Colliding-wind massive binaries (CWB) are binary systems composed of two stars of O, early-B, or WR type. Their main feature is a wind-wind interaction region where the shocked gas is very hot (107 K). This wind interaction region is likely to contribute to the thermal radio emission, together with the free-free radiation due to thermal electrons in single-star winds (Dougherty et al. 2003).

In addition to this thermal emission, non-thermal radio emission was discovered in some systems. It is related to the synchrotron radiation caused by relativistic electrons (Pittard et al. 2006). These synchrotron emitters are called particle-accelerating colliding-wind binaries (PACWB). As well as by the synchrotron emission, these systems can be revealed by exceptionally large radio fluxes, a spectral index significantly lower than the thermal value, and an orbital modulation of the radio flux. De Becker & Raucq (2013) recently provided the latest catalogue of such systems.

High angular resolution observations of some PACWB have allowed to distinguish the thermal from the non-thermal emissions (e.g. OB2 #5, Dzib et al. 2013) and showed that the synchrotron emission is associated with the wind-wind interaction region. This region is a source of thermal X-rays, in addition to the intrinsic X-ray emission produced in the stellar winds of the individual components. The X-ray spectrum produced in the wind interaction region is generally significantly harder than that of massive single stars, and the X-ray emission is variable with the orbital phase (e.g. De Becker et al. 2011; Cazorla et al. 2014).

Finally, it was discovered more recently that PACWB may also emit γ rays through inverse Compton scattering by the relativistic electrons and neutral pion decay. However, only one such example is currently known (η Car, Farnier et al. 2011).

These many characteristics make PACWB very interesting objects in which to study extreme physical processes. However, it has become increasingly clear over the past few years that PACWB cover a very wide range of parameters (mass loss, wind velocity, orbital period, etc.), and the fundamental difference between the PACWB and “normal” CWB is unknown (De Becker & Raucq 2013).

The synchrotron emission in PACWB immediately points towards a magnetic field. Indeed, synchrotron emission results from the modified movement of relativistic electrons in a magnetic field. Moreover, the acceleration of particles in PACWB can be explained either by strong shocks in the colliding winds (e.g. Pittard et al. 2006) or by magnetic reconnection or annihilation (e.g. Jardine et al. 1996). It has thus been speculated that the fundamental difference between CWB and PACWB is the presence of a magnetic field.

Over the past two decades, magnetic fields have been detected in ~7% of single massive stars (Wade et al. 2014b). While the fraction of PACWB among CWB is not known and the catalogue by De Becker & Raucq (2013) certainly underestimates the number of PACWB, ~7% might be a plausible proportion considering that only 43 possible PACWB have been identified as of today (De Becker & Raucq 2013), while most massive stars are probably binaries (Sana et al. 2012, 2014). Therefore, the presence of a magnetic field might indeed be the difference between PACWB and normal CWB.

The magnetic field in PACWB might be of stellar origin, but it might also possibly be generated in the colliding winds themselves. From synchrotron observations, one can estimate the magnetic field strength in the wind-wind interaction region to be of the order of a few mG (see e.g. Dougherty et al. 2003). Extrapolating this to the surface of the stars with typical distances between the stagnation point and the photosphere, we obtain values of the stellar magnetic field strength between one G and a few thousand G, depending on the system and on the assumptions (e.g. Parkin et al. 2014). Magnetic fields detected in single massive stars have a polar field strength between one hundred and several thousand G (see e.g. Petit et al. 2013), which are compatible with the fields speculated to exist in PACWB models.

Therefore, measuring magnetic fields in PACWB is an ideal way to test these assumptions, constrain models of colliding winds, and understand the difference between PACWB and normal CWB.

2. Archival spectropolarimetric observations

An updated census of 43 PACWB has been published recently (De Becker & Raucq 2013). It includes clear PACWB detected through their synchrotron emission as well as candidates from indirect indicators (e.g. radio flux).

We have gathered all high-resolution spectropolarimetric data of these PACWB available in archives, that is, those observed with Narval at the Télescope Bernard Lyot (TBL) in France, ESPaDOnS at the Canada-France-Hawaii telescope (CFHT) in Hawaii, or HarpsPol at ESO in Chile. Circular polarisation data are available for 9 of the 43 known PACWB. When several consecutive spectra were available for the same night, we averaged them. The 9 stars and 21 (average) observations are listed in Table 1.

Table 1

21 archival spectropolarimetric observations of 9 PACWB.

For each star, we normalised the data to the intensity continuum level and extracted Stokes V and null (N) polarisation spectra. N spectra allow us to check that the magnetic measurements (in the Stokes V spectra) have not been polluted by spurious signal, for example by instrumental polarisation.

We then proceeded to use the least squares deconvolution (LSD) technique (Donati et al. 1997) to search for weak Zeeman signatures in the mean Stokes V profile. The input LSD masks for each star were extracted from line lists provided by VALD (Piskunov et al. 1995; Kupka et al. 1999) according to the spectral type of each target. These line lists orginally contain all lines with predicted line depths greater than 1%, assuming solar abundances. We proceeded to remove all hydrogen lines, lines that were blended with H lines, and lines that are strongly contaminated by telluric regions. We then automatically adjusted the line depths of each remaining line to provide the best fit to the observed Stokes I spectra.

Using these final line masks, a mean wavelength of 5000 Å and a mean Landé factor of 1.2, we extracted LSD Stokes I and V profiles for each spectropolarimetric measurements. We also extracted LSD N polarisation profiles to check for spurious signatures. All LSD N profiles are flat, showing that the LSD V measurements do reflect the stellar magnetic field. The LSD I and Stokes V profiles of the nine stars are shown in Fig. 1. LSD V profiles are also flat, showing no sign of a magnetic signature in any of the nine PACWB.

3. LSD I profile fitting

To proceed and evaluate the magnetic field in the studied PACWB, we first needed to separate the individual spectra of each component in the LSD I profiles, because PACWB are binary stars.

For each spectrum we fitted the mean LSD Stokes I profile to determine the radial velocity Vrad, the projected rotational broadening (vsini), and any contribution from non-rotational broadening that we considered to be macroturbulent broadening (Vmac).

thumbnail Fig. 1

LSD I (bottom panels) and Stokes V (top panels, y-axis multiplied by 10 000) profiles of the nine PACWB available in spectropolarimetric archives. When only one spectrum is available (left panels), observations are indicated in black and the fit in red. If there are several components, the fit of the primary/secondary/tertiary component is shown in blue/green/pink, while the combined fit is shown in red. When several spectra are available for one star (middle and right panels), observations are indicated with various colours, and the fits are indicated in black with primary and secondary component fits indicated in green and blue. In these cases, profiles are artificially shifted upwards for clarity.

Table 2

Parameters derived from the fit of LSD I profiles of each star.

Ideally, fits to the observed profiles should be computed with Fourier techniques (e.g. Gray 2005; Simón-Díaz & Herrero 2014) directly on the intensity profiles (rather than the LSD profiles). However, this is very time consuming and not necessary here since the exact value of the parameters are not important for our purpose. We only need a good fit to the LSD profiles. Therefore, the profiles were computed as the convolution of a rotationally broadened profile and a radial-tangential broadened profile following the parametrisation of Gray (2005), assuming equal contributions from the radial and tangential (RT) component. While this form of macroturbulence is not commonly used in the study of early-type stars (typically a Gaussian profile is used to characterise Vmac), Simón-Díaz & Herrero (2014) showed that it provides a good agreement with the Fourier techniques.

The code uses the mpfit library (Moré 1978; Markwardt 2009) to find the best-fit solution. Using a radial-tangential profile for Vmac tends to maximise vsini. Therefore, the values we obtain for vsini can be considered as upper limits.

For profiles that show obvious signs of spectroscopic companions (HD 37468, HD 47839 and HD 167971), we simultaneously fitted multiple profiles, one for each component, to determine the overall best solution for the given SB2 (or SB3) profile. For HD 47839 the average profile was fitted because the various spectra show no significant variations. The simultaneous fitting of multiple profiles for one spectrum is a difficult task and the solution is often degenerate. We therefore attempted to constrain each fit based on previous studies published in the literature whenever possible. Only one component was fitted for the other stars (SB1).

Table 3

Measured longitudinal field Bl and null polarization Nl, with their error bars σ.

The various components and the resulting parameters are listed in Table 2. These parameters are only calculated to derive upper limits on the magnetic field strength. They should be used with care for other studies, because they do not necessarily have a physical meaning. From running the fits several times with different initial guess values, and by visually comparing the quality of the fit when changing the parameters, we estimate that the uncertainty on vsini and Vmac is of the order of 10 km s-1. The uncertainty on Vrad is of the order of a few km s-1. The fits of each individual component, as well as the combined fit of all components, are shown in Fig. 1.

thumbnail Fig. 2

Detection probability for each spectrum of each star as a function of the magnetic polar field strength. The horizontal dashed line indicates the 90% detection probability.

4. Magnetic field measurements

4.1. Longitudinal field measurements

From the LSD profiles we computed the longitudinal magnetic field (Bl) value, the corresponding null measurement Nl and their error bars σ using the first-order moment method of Rees & Semel (1979) in the form given in Wade et al. (2000). We applied this measurement to the individual components of each stars, when visible.

The results are reported in Table 3. We find that the Bl and Nl values are all compatible with 0 within 3σ. This confirms that no field is detected in any of the nine PACWB.

The magnetic field of one of our targets, HD 93250, has already been analysed with low-resolution FORS data by Nazé et al. (2012). They did not detect a magnetic field in this star either, obtaining an even more stringent error bar of σ ~ 80 G.

4.2. Upper limit on undetected fields

Since we did not detect a magnetic field signature in the nine PACWB we studied, we proceeded to determine the upper limit of the strength of a magnetic field that could have remained hidden in the spectral noise.

For this aim, we calculated 1000 oblique dipole models for various values of the polar magnetic field Bpol of each of the LSD Stokes V profiles with random inclination angle i and obliquity angle β, random rotational phase, and a white Gaussian noise with a null average and a variance corresponding to the S/N of each observed profile. Using the fitted LSD I profiles, we calculated local Stokes V profiles assuming the weak-field case and integrated over the visible hemisphere of the star. We obtained synthetic Stokes V profiles, which we normalised to the intensity continuum. We used the same mean Landé factor (1.2) and wavelength (5000 Å) as in the observations.

We then computed the probability of detection of a field in this set of models by applying the Neyman-Pearson likelihood ratio test (see e.g. Helstrom 1995; Kay 1998; Levy 2008) to decide between two hypotheses, H0 and H1, where H0 corresponds to noise alone and H1 to a noisy simulated Stokes V signal. This rule selects the hypothesis that maximises the detection probability while ensuring that the false-alarm probability PFA is not higher than a prescribed value considered acceptable. Following values commonly assumed in the literature for magnetic field detections (e.g. Donati et al. 1997), we used PFA = 10-3 for a marginal magnetic detection. We then calculated the rate of detections among the 1000 models for each of the profiles of the primary and secondary stars depending on the field strength (see Fig. 2).

We required a 90% detection rate to consider that the field would statistically be detected. This translates into an upper limit for the possible undetected dipolar field strength for each star and spectrum. These upper limits are listed in Table 2. Since the computation of the upper limits rely on fitted I profiles, the uncertainty in the fits may introduce an error in the field strength we derive. Comparing limits derived from various fits of the same profile, we estimated that the error on the upper limits might be up to ~20%.

For the three PACWB for which each binary component was fitted (HD 37468, HD 47839, and HD 167971), we provide an upper limit for each star. For the other six PACWB, however, the result is contaminated by the undetected companion. For two of these PACWB, either the companion has never been detected (HD 151804) or it is known to be a faint cool star (HD 152804, see Mason et al. 1998), and therefore the contamination can be neglected. In the case of HD 190918, the companion is a Wolf-Rayet star that contributes to the spectrum with emission lines and continuum flux. Since the extracted LSD profile is normalised to the total continuum flux, it can be treated as a single star.

For HD 36486, HD 93250, and HD 164794, however, the contribution from the companion to the spectrum cannot be neglected. For HD 36486 and HD 93250, each component contributes with about 50% of the flux and the vsini values of the primary and secondary are similar (see Harvin et al. 2002 for HD 36486, and Sana et al. 2011 for HD 93250). For these two stars, the upper limit values should thus be considered with care and are probably underestimated by a factor of ~2. For HD 164794, the vsini values of the two components are not very different either (87 and 57 km s-1 according to Rauw et al. 2012), but the secondary has deeper lines than the primary. For this star, the upper limit value should therefore likewise be considered with care and might be significantly underestimated.

In addition, for stars with several available observations, statistics can be combined to extract a stricter upper limit taking into account that the field has not been detected in any of the observations, using the following equation: Pcomb=100[1−􏽙i=1n(100−Pi)100],\begin{eqnarray*} P_{\rm comb} = 100 \left[ 1 - \prod_{i=1}^n \frac{\left(100-P_i\right)}{100} \right], \end{eqnarray*}where Pi is the detection probability for the ith observation, and Pcomb is the detection probability for n observations combined. All probabilities are expressed in percent.

As an example, if two observations of one star were obtained with a detection probability of 80% and 90% that no field stronger than 1000 G was detected, then the combined probability that such a 1000 G field was detected in none of the two observations would be 98%.

The final upper limit derived from this combined probability for each star for a 90% detection probability is listed in Table 4.

Table 4

Upper dipolar field strength limit in G, combining all available data for each detected component of each star.

Finally, for one of our targets, HD 190918, de la Chevrotière et al. (2014) searched for a magnetic field in the stellar wind from its emission lines in the same ESPaDOnS spectrum as we used. They detected no field and determined an upper limit on the wind magnetic field of 329 G for a 95.4% credible region using a Bayesian analysis. Their method assumes prior knowledge on the properties of the star, in particular a pole-on orientation for the magnetic geometry, and therefore leads to much more optimistic upper limits than the method presented here. The upper limit on the wind magnetic field they obtained can therefore not be directly compared with the upper limit on the stellar magnetic field we obtained here.

5. Discussion and conclusions

Parkin et al. (2014) showed that the surface magnetic field of the PACWB Cyg OB #9 would be between 0.3 and 52 G if one assumed a simple magnetic field radial dependence, no or slow rotation, and a ratio of the energy density in the magnetic field to the local thermal energy density (ζB) of 5 × 10-5, or between 30 and 5200 G if that ratio is assumed to be 0.5. In their work, the magnetic field strength scales with 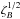ζB1/2\hbox{$\zeta_B^{1/2}$} and Vrot.

The assumptions on the field configuration and slow rotation used by Parkin et al. (2014) are probably generally not adapted to PACWB. In particular, if the field is strong, the impact of the magnetic field on the wind, for example, magnetic wind confinement, should be taken into account (ud-Doula & Owocki 2002; ud-Doula et al. 2008), and massive stars are often rapid rotators (e.g. Grunhut et al. 2013). Nevertheless, their work provides an idea of the typical field strengths that one might expect in PACWB.

Our analysis of archival spectropolarimetric data shows no magnetic detection in any of the nine PACWB for which data are available. However, the precision reached by these archival observations is between 7 and 211 G for the measured longitudinal field. These values are typical of the precision reached for the measurements of fields in massive stars by the MiMeS collaboration (Grunhut et al., in prep.). Assuming an oblique dipole field, as observed in the vast majority of single massive stars, this leads to an upper limit of the undetected magnetic field at 3σ and a 90% detection probability between 178 and 4367 G at the stellar pole, depending on the star.

While for some stars these archival observations are not really constraining (e.g. HD 93250), for several cases we can clearly exclude fields above 1000 G, and thus high ζB values are certainly rare in PACWB. The results obtained for HD 36486, HD 37468, and HD 47839 show that even dipolar fields above a few hundreds G, that is, more moderate ζB, do not seem common in PACWB, while this corresponds to the typical field strength observed in magnetic massive stars (Petit et al. 2013). While the proportion of magnetic stars among OB stars (~7%) could fit with the proportion of PACWB among massive binary stars, our results clearly show that PACWB are not particularly magnetic compared to other massive stars. Therefore, no link can be established between a magnetic field typical of a magnetic massive star and synchrotron emission.

These archival data cannot exclude fields of a few tens of G or lower, however. Field values like this would point towards low ζB values and would be sufficient to produce synchrotron emission. However, studies of magnetism in OB stars show that magnetic fields detected in these stars are always relatively strong (with Bl> 100 G). Weak magnetic fields are generally not found in massive stars, even when low detection thresholds are used. This is known as the magnetic dichotomy in massive stars (Aurière et al. 2007; Lignières et al. 2014).

However, ultra-weak magnetic fields have recently been detected in some A stars (Lignières et al. 2009; Petit et al. 2011; Blazère et al. 2014). These fields might possibly also exist in higher mass stars, although attempts to detect them in B stars have been unsuccessful so far (Neiner et al. 2014; Wade et al. 2014a). Magnetic field amplification might exist in PACWB (Lucek & Bell 2000; Bell & Lucek 2001; Falceta-Gonçalves & Abraham 2012), and an ultra-weak stellar surface magnetic field could then be sufficient to produce synchrotron emission.

As a consequence, while this work represents the first effort to detect magnetic field signatures in PACWB, provide quantitative estimates of its possible value and constraints for models, and clearly excludes the presence of magnetic fields typical of massive stars as the origin of synchrotron emission in PACWB, more precise spectropolarimetric measurements of magnetic fields in PACWB are necessary before one can exclude very weak magnetic fields at the surface of PACWB stars. We plan to acquire such precise observations for very bright PACWB in the near future.

Nevertheless, even if the ultra-weak magnetic fields were present at the surface of PACWB and magnetic field amplification was at work, the question remains: if PACWB are not different from typical massive stars as far as their magnetic field is concerned, why are they particle accelerators? A possible scenario would be the production of a magnetic field at the location of the wind shock itself.

Acknowledgments

This research has made use of the SIMBAD database operated at CDS, Strasbourg (France), and of NASA’s Astrophysics Data System (ADS). We thank the referee, M. Leutenegger, for his constructive feedback.

References

  1. Aurière, M., Wade, G. A., Silvester, J., et al. 2007, A&A, 475, 1053 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Bell, A. R., & Lucek, S. G. 2001, MNRAS, 321, 433 [NASA ADS] [CrossRef] [Google Scholar]
  3. Blazère, A., Petit, P., Lignières, F., et al. 2014, in SP2A-2014: Proc. of the Annual meeting of the French Society of Astronomy and Astrophysics, eds. J. Ballet, F. Martins, F. Bournaud, R. Monier, & C. Reylé, 463 [Google Scholar]
  4. Cazorla, C., Nazé, Y., & Rauw, G. 2014, A&A, 561, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. De Becker, M., & Raucq, F. 2013, A&A, 558, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. De Becker, M., Pittard, J. M., Williams, P., & WR140 Consortium 2011, Bull. Soc. Roy. Sci. Liège, 80, 653 [NASA ADS] [Google Scholar]
  7. de la Chevrotière, A., St-Louis, N., Moffat, A. F. J., & MiMeS Collaboration 2014, ApJ, 781, 73 [NASA ADS] [CrossRef] [Google Scholar]
  8. Donati, J.-F., Semel, M., Carter, B. D., Rees, D. E., & Collier Cameron, A. 1997, MNRAS, 291, 658 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  9. Dougherty, S. M., Pittard, J. M., Kasian, L., et al. 2003, A&A, 409, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Dzib, S. A., Rodríguez, L. F., Loinard, L., et al. 2013, ApJ, 763, 139 [NASA ADS] [CrossRef] [Google Scholar]
  11. Falceta-Gonçalves, D., & Abraham, Z. 2012, MNRAS, 423, 1562 [NASA ADS] [CrossRef] [Google Scholar]
  12. Farnier, C., Walter, R., & Leyder, J.-C. 2011, A&A, 526, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Gray, D. F. 2005, The Observation and Analysis of Stellar Photospheres (Cambridge University Press) [Google Scholar]
  14. Grunhut, J. H., Wade, G. A., Leutenegger, M., et al. 2013, MNRAS, 428, 1686 [NASA ADS] [CrossRef] [Google Scholar]
  15. Harvin, J. A., Gies, D. R., Bagnuolo, Jr., W. G., Penny, L. R., & Thaller, M. L. 2002, ApJ, 565, 1216 [NASA ADS] [CrossRef] [Google Scholar]
  16. Helstrom, C. W. 1995, Elements of Signal Detection and Estimation (Prentice Hall) [Google Scholar]
  17. Jardine, M., Allen, H. R., & Pollock, A. M. T. 1996, A&A, 314, 594 [NASA ADS] [Google Scholar]
  18. Kay, S. M. 1998, in Fundamentals of Statistical Signal Processing, Detection Theory (Prentice Hall), 2 [Google Scholar]
  19. Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
  20. Levy, B. C. 2008, Principles of Signal Detection and Parameter Estimation (Springer) [Google Scholar]
  21. Lignières, F., Petit, P., Böhm, T., & Aurière, M. 2009, A&A, 500, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Lignières, F., Petit, P., Aurière, M., Wade, G. A., & Böhm, T. 2014, IAU Symp., 302, 338 [NASA ADS] [Google Scholar]
  23. Lucek, S. G., & Bell, A. R. 2000, MNRAS, 314, 65 [NASA ADS] [CrossRef] [Google Scholar]
  24. Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [Google Scholar]
  25. Mason, B. D., Gies, D. R., Hartkopf, W. I., et al. 1998, AJ, 115, 821 [NASA ADS] [CrossRef] [Google Scholar]
  26. Moré, J. 1978, in Numerical Analysis, ed. G. Watson (Berlin, Heidelberg: Springer), Lecture Notes in Mathematics, 630, 105 [Google Scholar]
  27. Nazé, Y., Bagnulo, S., Petit, V., et al. 2012, MNRAS, 423, 3413 [NASA ADS] [CrossRef] [Google Scholar]
  28. Neiner, C., Monin, D., Leroy, B., Mathis, S., & Bohlender, D. 2014, A&A, 562, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Parkin, E. R., Pittard, J. M., Nazé, Y., & Blomme, R. 2014, A&A, 570, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Petit, P., Lignières, F., Aurière, M., et al. 2011, A&A, 532, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Petit, V., Owocki, S. P., Wade, G. A., et al. 2013, MNRAS, 429, 398 [NASA ADS] [CrossRef] [Google Scholar]
  32. Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [NASA ADS] [Google Scholar]
  33. Pittard, J. M., Dougherty, S. M., Coker, R. F., O’Connor, E., & Bolingbroke, N. J. 2006, A&A, 446, 1001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Rauw, G., Sana, H., Spano, M., et al. 2012, A&A, 542, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Rees, D. E., & Semel, M. D. 1979, A&A, 74, 1 [NASA ADS] [Google Scholar]
  36. Sana, H., Le Bouquin, J.-B., De Becker, M., et al. 2011, ApJS, 740, L43 [Google Scholar]
  37. Sana, H., de Mink, S. E., de Koter, A., et al. 2012, Science, 337, 444 [Google Scholar]
  38. Sana, H., Le Bouquin, J.-B., Lacour, S., et al. 2014, ApJS, 215, 15 [NASA ADS] [CrossRef] [Google Scholar]
  39. Simón-Díaz, S., & Herrero, A. 2014, A&A, 562, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. ud-Doula, A., & Owocki, S. P. 2002, ApJ, 576, 413 [NASA ADS] [CrossRef] [Google Scholar]
  41. ud-Doula, A., Owocki, S. P., & Townsend, R. H. D. 2008, MNRAS, 385, 97 [NASA ADS] [CrossRef] [Google Scholar]
  42. Wade, G. A., Donati, J.-F., Landstreet, J. D., & Shorlin, S. L. S. 2000, MNRAS, 313, 851 [NASA ADS] [CrossRef] [Google Scholar]
  43. Wade, G. A., Folsom, C. P., Petit, P., et al. 2014a, MNRAS, 444, 1993 [NASA ADS] [CrossRef] [Google Scholar]
  44. Wade, G. A., Grunhut, J., Alecian, E., et al. 2014b, IAU Symp., 302, 265 [Google Scholar]

All Tables

Table 1

21 archival spectropolarimetric observations of 9 PACWB.

In the text
Table 2

Parameters derived from the fit of LSD I profiles of each star.

In the text
Table 3

Measured longitudinal field Bl and null polarization Nl, with their error bars σ.

In the text
Table 4

Upper dipolar field strength limit in G, combining all available data for each detected component of each star.

In the text

All Figures

thumbnail Fig. 1

LSD I (bottom panels) and Stokes V (top panels, y-axis multiplied by 10 000) profiles of the nine PACWB available in spectropolarimetric archives. When only one spectrum is available (left panels), observations are indicated in black and the fit in red. If there are several components, the fit of the primary/secondary/tertiary component is shown in blue/green/pink, while the combined fit is shown in red. When several spectra are available for one star (middle and right panels), observations are indicated with various colours, and the fits are indicated in black with primary and secondary component fits indicated in green and blue. In these cases, profiles are artificially shifted upwards for clarity.
In the text
thumbnail Fig. 2

Detection probability for each spectrum of each star as a function of the magnetic polar field strength. The horizontal dashed line indicates the 90% detection probability.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.