| Issue |
A&A
Volume 575, March 2015
|
|
|---|---|---|
| Article Number | A81 | |
| Number of page(s) | 6 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201424805 | |
| Published online | 27 February 2015 | |
Research Note
H.E.S.S. reveals a lack of TeV emission from the supernova remnant Puppis A
1
Universität Hamburg, Institut für Experimentalphysik,
Luruper Chaussee 149,
22761
Hamburg,
Germany
2
Max-Planck-Institut für Kernphysik, PO Box 103980, 69031
Heidelberg,
Germany
3
Dublin Institute for Advanced Studies, 31 Fitzwilliam Place, Dublin 2,
Ireland
4
National Academy of Sciences of the Republic of Armenia, Marshall Baghramian
Avenue, 24, 0019 Yerevan, Republic of Armenia
5
Yerevan Physics Institute, 2 Alikhanian Brothers St., 375036
Yerevan,
Armenia
6
Institut für Physik, Humboldt-Universität zu Berlin,
Newtonstr. 15, 12489
Berlin,
Germany
7
University of Namibia, Department of Physics, Private Bag 13301, Windhoek,
Namibia
8
University of Durham, Department of Physics,
South Road, Durham
DH1 3LE,
UK
9
GRAPPA, Anton Pannekoek Institute for Astronomy, University of
Amsterdam, Science Park
904, 1098 XH
Amsterdam, The
Netherlands
10
Obserwatorium Astronomiczne, Uniwersytet Jagielloński, ul. Orla
171, 30-244
Kraków,
Poland
11
now at Harvard-Smithsonian Center for Astrophysics, 60 Garden St,
MS-20, Cambridge,
MA
02138,
USA
12
Department of Physics and Electrical Engineering, Linnaeus
University, 351
95
Växjö,
Sweden
13
Institut für Theoretische Physik, Lehrstuhl IV: Weltraum und
Astrophysik, Ruhr-Universität Bochum, 44780
Bochum,
Germany
14
GRAPPA, Anton Pannekoek Institute for Astronomy and Institute of
High-Energy Physics, University of Amsterdam, Science Park 904, 1098 XH
Amsterdam, The
Netherlands
15
Institut für Astro- und Teilchenphysik,
Leopold-Franzens-Universität Innsbruck, 6020
Innsbruck,
Austria
16
Laboratoire Leprince-Ringuet, École Polytechnique,
CNRS/IN2P3, 91128
Palaiseau,
France
17
now at Santa Cruz Institute for Particle Physics, Department of
Physics, University of California at Santa Cruz, Santa Cruz, CA
95064,
USA
18
Centre for Space Research, North-West University,
2520
Potchefstroom, South
Africa
19
LUTH, Observatoire de Paris, CNRS, Université Paris
Diderot, 5 Place Jules
Janssen, 92190
Meudon,
France
20
LPNHE, Université Pierre et Marie Curie Paris 6, Université Denis
Diderot Paris 7, CNRS/IN2P3, 4
PlaceJussieu, 75252
Paris Cedex 5,
France
21
Institut für Astronomie und Astrophysik, Universität
Tübingen, Sand 1,
72076
Tübingen,
Germany
22
Laboratoire Univers et Particules de Montpellier, Université
Montpellier 2, CNRS/IN2P3, CC 72,
Place Eugène Bataillon, 34095
Montpellier Cedex 5,
France
23
DSM/Irfu, CEA Saclay, 91191
Gif-Sur-Yvette Cedex,
France
24
Astronomical Observatory, The University of Warsaw,
Al. Ujazdowskie 4, 00-478
Warsaw,
Poland
25
Instytut Fizyki Ja¸drowej PAN, ul. Radzikowskiego
152, 31-342
Kraków,
Poland
26
School of Physics, University of the Witwatersrand,
1 Jan Smuts Avenue, Braamfontein,
2050
Johannesburg, South
Africa
27
Landessternwarte, Universität Heidelberg,
Königstuhl, 69117
Heidelberg,
Germany
28
Oskar Klein Centre, Department of Physics, Stockholm University,
Albanova University Center, 10691
Stockholm,
Sweden
29
School of Chemistry & Physics, University of
Adelaide, 5005
Adelaide,
Australia
30
APC, AstroParticule et Cosmologie, Université Paris Diderot,
CNRS/IN2P3, CEA/Irfu, Observatoire de Paris, Sorbonne Paris Cité, 10 rue Alice Domon et Léonie
Duquet, 75205
Paris Cedex 13,
France
31
Univ. Grenoble Alpes, IPAG, 38000
Grenoble,
France
32
CNRS, IPAG, 38000
Grenoble,
France
33
Department of Physics and Astronomy, The University of Leicester,
University Road, Leicester, LE1
7RH, UK
34
Nicolaus Copernicus Astronomical Center, ul. Bartycka
18, 00-716
Warsaw,
Poland
35
Institut für Physik und Astronomie, Universität
Potsdam, Karl-Liebknecht-Strasse
24/25, 14476
Potsdam,
Germany
36
Laboratoire d’Annecy-le-Vieux de Physique des Particules,
Université de Savoie, CNRS/IN2P3, 74941
Annecy-le-Vieux,
France
37
DESY, 15738
Zeuthen,
Germany
38
Université Bordeaux 1, CNRS/IN2P3, Centre d’Études Nucléaires de Bordeaux
Gradignan, 33175
Gradignan,
France
39
Universität Erlangen-Nürnberg, Physikalisches
Institut, Erwin-Rommel-Str.
1, 91058
Erlangen,
Germany
40
Centre for Astronomy, Faculty of Physics, Astronomy and
Informatics, Nicolaus Copernicus University, Grudziadzka 5, 87-100
Torun,
Poland
41
Department of Physics, University of the Free State,
PO Box 339, 9300
Bloemfontein, South
Africa
42
GRAPPA, Institute of High-Energy Physics, University of
Amsterdam, Science Park
904, 1098 XH
Amsterdam, The
Netherlands
Received: 14 August 2014
Accepted: 20 December 2014
Context. Puppis A is an interesting ~4 kyr-old supernova remnant (SNR) that shows strong evidence of interaction between the forward shock and a molecular cloud. It has been studied in detail from radio frequencies to high-energy (HE, 0.1−100 GeV) γ-rays. An analysis of the Fermi-LAT data has shown extended HE γ-ray emission with a 0.2−100 GeV spectrum exhibiting no significant deviation from a power law, unlike most of the GeV-emitting SNRs known to be interacting with molecular clouds. This makes it a promising target for imaging atmospheric Cherenkov telescopes (IACTs) to probe the γ-ray emission above 100 GeV.
Aims. Very-high-energy (VHE, E ≥ 0.1 TeV) γ-ray emission from Puppis A has been, for the first time, searched for with the High Energy Stereoscopic System (H.E.S.S.).
Methods. Stereoscopic imaging of Cherenkov radiation from extensive air showers is used to reconstruct the direction and energy of the incident γ-rays in order to produce sky images and source spectra. The profile likelihood method is applied to find constraints on the existence of a potential break or cutoff in the photon spectrum.
Results. The analysis of the H.E.S.S. data does not reveal any significant emission towards Puppis A. The derived upper limits on the differential photon flux imply that its broadband γ-ray spectrum must exhibit a spectral break or cutoff. By combining Fermi-LAT and H.E.S.S. measurements, the 99% confidence-level upper limits on such a cutoff are found to be 450 and 280 GeV, assuming a power law with a simple exponential and a sub-exponential cutoff, respectively. It is concluded that none of the standard limitations (age, size, radiative losses) on the particle acceleration mechanism, assumed to be continuing at present, can explain the lack of VHE signal. The scenario in which particle acceleration has ceased some time ago is considered as an alternative explanation. The HE/VHE spectrum of Puppis A could then exhibit a break of non-radiative origin (as observed in several other interacting SNRs, albeit at somewhat higher energies), owing to the interaction with dense and neutral material, in particular towards the NE region.
Key words: gamma rays: ISM / ISM: individual objects: Puppis A / radiation mechanisms: non-thermal / cosmic rays / acceleration of particles
© ESO, 2015
1. Introduction
Supernova remnants (SNRs) have long been considered as the main sources of Galactic cosmic rays (CRs, Ginzburg & Syrovatskii 1964). Direct measurements of CRs from SNRs are impossible because of Galactic magnetic fields, but γ-rays can provide an indirect signature of their presence (see e.g. Reynolds 2008, for a review). On one hand, several middle-aged SNRs interacting with molecular clouds (MCs) have been observed with the Fermi Large Area Telescope (Fermi-LAT) and Astro-Rivelatore Gamma a Immagini Leggero (AGILE) telescope as luminous high-energy (HE, 0.1−100 GeV) γ-ray sources. The strong HE γ-ray emission from these sources is thought to arise from neutral pion decay subsequent to the interactions between accelerated CR particles and the dense gas, and whose unique spectral feature, referred to as the pion bump at ~200 MeV, was recently revealed in two such SNRs with Fermi-LAT (Ackermann et al. 2013). Some examples are W28 (Abdo et al. 2010a), W51C (Abdo et al. 2009), W44 (Abdo et al. 2010b), and IC 443 (Abdo et al. 2010c), which furthermore all exhibit power-law spectral breaks in the 1−20 GeV range. As a consequence of these breaks, the associated very-high-energy (VHE, E ≥ 0.1 TeV) emission is usually soft and faint (e.g. Albert et al. 2007; Aharonian et al. 2008). On the other hand, young, shell-type SNRs, with bright and hard spectra in the VHE domain (such as RX J1713.7−3946, Aharonian et al. 2007) and without clear evidence for cloud interaction, exhibit hard and relatively faint spectra in the HE domain (Abdo et al. 2011). In these cases, inverse Compton (IC) emission from accelerated electrons naturally explains the observed γ-ray emission (e.g. Lee et al. 2012).
Puppis A (G260.4−3.4) represents an interesting case in between these two SNR categories. At a distance of 2.2 ± 0.3 kpc1 (Reynoso et al. 2003), it is a well-studied Galactic SNR in most energy bands from radio to HE γ-rays. It is one of the three oxygen-rich SNRs (Winkler & Kirshner 1985) known today in the Galaxy. This, together with the presence of a central compact object (CCO; Becker et al. 2012, and references therein), strongly supports the idea that Puppis A originates in a core-collapse SN explosion. Based on the motions of both optical filaments and CCO, its age is estimated to be (4450± 750) yr (Becker et al. 2012), implying that the SNR is currently in the Sedov-Taylor evolutionary phase (see e.g. Chevalier 1977). The strong X-ray emission from Puppis A is mostly dominated by the shock-heated interstellar medium (ISM, e.g. Hwang et al. 2005), except for some isolated O-Ne-Mg-rich features associated with the SN ejecta (Hwang et al. 2008; Katsuda et al. 2008, 2010), the kinematics of which have been fully measured (Katsuda et al. 2013, and references therein). The SNR also has another interesting characteristic: together with W49B (Abdo et al. 2010d) and G349.7+0.2 (Lazendic et al. 2010), it is amongst the youngest Galactic SNRs known to be interacting at several locations throughout the shell with dense gas seen as a complex of H i and CO clouds surrounding most of the SNR (Dubner & Arnal 1988; Reynoso et al. 1995; Dubner et al. 2013). In particular, spectro-imaging X-ray studies towards the so-called bright eastern knot (BEK) have presented evidence for a shock-cloud interaction (Hwang et al. 2005). Recent high-resolution X-ray observations of the whole SNR (Dubner et al. 2013) have confirmed the presence of a decreasing gradient in the emission from NE to SW and also revealed a highly structured and filamentary morphology with unprecedented detail, indicating that Puppis A is evolving in an inhomogeneous, knotty ISM. Observations with Spitzer have shown a clear correlation between infrared (IR) and X-rays at all spatial scales, demonstrating that the thermal IR emission arises from dust collisionally heated by the hot, shocked plasma (Arendt et al. 2010).
Hewitt et al. (2012) have reported the detection of Puppis A in the HE γ-ray domain with the Fermi-LAT. Its luminosity of 2.7 × 1034(d/2.2 kpc)2 erg s-1 in the 1−100 GeV band is slightly higher than those of the low-luminosity, HE-emitting SNRs such as Cygnus Loop, S147 and HB21 (Reichardt et al. 2012 and references therein), and about a factor ten lower than those measured from the archetypal SNRs known to be interacting with MCs (Abdo et al. 2009, 2010c,d). The morphology of the HE γ-ray emission is described well by a uniform disc of radius 0.38° ± 0.04° and compatible with the radio and X-ray morphologies. The HE γ-ray spectrum is described well by a power law (PL) with no indication of a break or cutoff, and a spectral variation at the ~2σ level between the E and the W hemispheres was found. Such a PL HE spectrum, together with a hint of a radio break at ~40 GHz in the WMAP data (Hewitt et al. 2012), makes Puppis A quite peculiar with respect to most of the HE-emitting SNRs. Puppis A can be considered as an intermediate case between the young, isolated, and bright VHE γ-ray emitting SNRs and the middle-aged, bright HE γ-ray emitting ones interacting with MCs. To probe its emission in the VHE domain, observations towards Puppis A obtained with the High Energy Stereoscopic System (H.E.S.S.) are reported in this article.
2. Observations and analysis
2.1. H.E.S.S. observations and analysis results
H.E.S.S. is an array of five imaging atmospheric Cherenkov telescopes (IACTs) located in Namibia and designed to detect VHE γ-rays (Bernlöhr et al. 2003). The fifth telescope (28-m diameter) has been operating since September 2012, but the data exploited here were taken from 2005 to 2013 with the four-telescope array alone. In this configuration, the instrument covers a field of view of 5°. The primary particle direction and energy are reconstructed above a threshold of ~100 GeV with an angular resolution of ~0.1° and energy resolution of ~15%, (e.g. Aharonian et al. 2006a). The whole dataset on Puppis A amounts to 24 h including 17 h of dedicated observations taken using the wobble mode and 7 h of runs towards nearby sources in the Vela region (in particular, Vela X, Aharonian et al. 2006b; Abramowski et al. 2012). These observations were performed at zenith angles between 18° and 45° with a median value of 22°, and a median offset from the source of 1.0°.
Data were analysed with the model analysis described in de Naurois & Rolland (2009) and using Standard cuts2. The main analysis results were confirmed with an independent data calibration chain and a multivariate analysis method (Ohm et al. 2009). The resulting energy threshold of the main analysis, which is conservatively defined as the energy above which the acceptance is larger than 15% of its maximum value, is Eth = 0.26 TeV. The analysis ON-region (i.e. signal integration region) was defined as a circular region of radius 0.38°, centred on 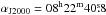 ,
, 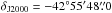 , to match the best-fit values of the HE γ-ray emission extent and position measured with the Fermi-LAT3. The statistical significance of a potential VHE γ-ray emission from Puppis A was determined by using Eq. (17) in Li & Ma (1983) after background subtraction with the reflected background method (Berge et al. 2007). No significant signal was found within the ON-region. In total, eight excess counts were measured, corresponding to a significance of 0.1σ. Similar analyses have been performed for two half-disc regions corresponding to the E and W hemispheres as defined in Hewitt et al. (2012). Figure 1 shows an image of the γ-ray excess counts, where the background level is estimated following the template background method and cross-checked with the ring background method (Berge et al. 2007), together with the ON-region and contours of the radio continuum emission at 1.4 GHz (Castelletti et al. 2006).
, to match the best-fit values of the HE γ-ray emission extent and position measured with the Fermi-LAT3. The statistical significance of a potential VHE γ-ray emission from Puppis A was determined by using Eq. (17) in Li & Ma (1983) after background subtraction with the reflected background method (Berge et al. 2007). No significant signal was found within the ON-region. In total, eight excess counts were measured, corresponding to a significance of 0.1σ. Similar analyses have been performed for two half-disc regions corresponding to the E and W hemispheres as defined in Hewitt et al. (2012). Figure 1 shows an image of the γ-ray excess counts, where the background level is estimated following the template background method and cross-checked with the ring background method (Berge et al. 2007), together with the ON-region and contours of the radio continuum emission at 1.4 GHz (Castelletti et al. 2006).
 |
Fig. 1 Image of the H.E.S.S. γ-ray excess centred on the Puppis A SNR. The excess was smoothed with a Gaussian kernel of width 0.06° corresponding to the H.E.S.S. angular resolution (68% containment radius) for this analysis (shown in the bottom left inset). The colour scale represents the excess counts per surface area of π(0.06°)2. The circular analysis region of radius 0.38°, matching the Fermi-LAT best-fit morphological model, is shown as a dashed circle. The two hemispheres are separated by a dashed line along the north/south axis in celestial coordinates. The black contours represent the 1.4 GHz continuum emission (Castelletti et al. 2006) at the 5, 10, 20 and 50 mJy/beam levels. The yellow cross indicates the position of the BEK (Hwang et al. 2005). |
Following the method of Feldman & Cousins (1998), differential flux upper limits (ULs) at the 99% confidence level (CL) and for a spectral index Γ = 2.1 (as measured with Fermi-LAT, Hewitt et al. 2012) were extracted in the 0.26−10 TeV energy range within the circular and the two half-disc ON-regions. These ULs are not very sensitive to the choice of the photon index; assuming Γ = 3 instead changes the values by less than 5%. To ensure that these ULs account for the full source emission, they have been corrected for the underestimation caused by events reconstructed outside the analysis regions due to the H.E.S.S. point spread function (PSF). By convolving a disc of 0.38° radius with the H.E.S.S. PSF, the flux outside of the ON-region was estimated to be 10% of the total flux. The H.E.S.S. ULs do not vary by more than 10% by changing the integration radius between 0.35° and 0.48°. The resulting H.E.S.S. ULs are shown in Fig. 2 together with the Fermi-LAT spectra.
 |
Fig. 2 H.E.S.S. 99% CL upper limits on the differential flux (arrows), together with the Fermi-LAT spectra from Puppis A, as reported in Hewitt et al. (2012). Red, blue and green symbols correspond to Fermi-LAT and H.E.S.S. measurements for the whole SNR, the E and W hemisphere, respectively. The data points show the LAT fluxes and 1σ statistical and systematic errors, whilst the bow-tie areas define the 68% CL bands. The solid and dashed lines indicate the preferred γ-ray spectra for the exponential and sub-exponential cutoff models, respectively. |
While the H.E.S.S. ULs derived from the W hemisphere are not constraining, owing to a steeper HE spectrum, those from the E hemisphere and from the whole SNR exclude the possibility that their respective PL spectra extend up to the VHE domain at more than the 99% CL. This indicates the existence of a spectral feature (break or cutoff) at intermediate energies, i.e. between the HE and VHE domains.
2.2. Constraints on the CR particle spectrum
Presuming that the accelerated particle spectra are PLs with exponential cutoffs as predicted by the diffusive shock acceleration (DSA) mechanism (e.g. Krymskii 1977; Blandford & Ostriker 1978; Bell 1978a,b), the γ-ray spectrum resulting from the different emission processes should also follow a PL with exponential cutoff: dN/ dE = N0E− Γe− (E/Ecut)β, where Ecut is the cutoff energy and β defines the spectral shape in the cutoff region. To evaluate the existence of such a cutoff energy in the spectrum of the whole SNR4, a likelihood estimator ℒ was defined as the combination of the likelihoods from the Fermi-LAT data points and H.E.S.S. measurements. The Fermi-LAT likelihood value was estimated by computing χ2 from the available data points and 1σ errors. The H.E.S.S. likelihood is calculated by comparing the number of detected excess events (following Poisson statistics) with the expected number in each reconstructed energy bin. To cover a wide range of physically possible scenarios, two values for the β parameter were chosen: β = 1 (defining the exponential cutoff model hereafter) corresponds to the most commonly used case and β = 0.5 (defining the sub-exponential cutoff model hereafter) is more physically motivated in both leptonic (under the assumption that electrons suffer from SC losses and that diffusion proceeds in Bohm regime, Zirakashvili & Aharonian 2007) and hadronic (for a proton spectrum exhibiting a simple exponential cutoff, Kelner et al. 2006) scenarios. The method used to derive the exclusion domain of Ecut is based on a likelihood ratio test statistic (Rolke et al. 2005): 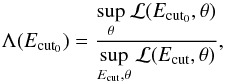 (1)where Ecut0 is the tested hypothesis and Ecut all the allowed values. The unknown spectral index Γ and normalisation N0 are considered as nuisance parameters under the θ variable. The profile of the log-likelihood ratio test statistic −2 ln Λ has an approximate χ2 distribution with one degree of freedom (Rolke et al. 2005). The minimum is reached at around ~55 GeV and 150 GeV for β = 0.5 and 1, respectively. Below these energies, −2 ln Λ increases rapidly because of the constraints imposed by the Fermi-LAT detection. Above that, the H.E.S.S. data become more constraining and lead to an increase in the −2 ln Λ value. The 99% CL ULs on the cutoff energy correspond to 280 and 450 GeV for β = 0.5 and 1, respectively5.
(1)where Ecut0 is the tested hypothesis and Ecut all the allowed values. The unknown spectral index Γ and normalisation N0 are considered as nuisance parameters under the θ variable. The profile of the log-likelihood ratio test statistic −2 ln Λ has an approximate χ2 distribution with one degree of freedom (Rolke et al. 2005). The minimum is reached at around ~55 GeV and 150 GeV for β = 0.5 and 1, respectively. Below these energies, −2 ln Λ increases rapidly because of the constraints imposed by the Fermi-LAT detection. Above that, the H.E.S.S. data become more constraining and lead to an increase in the −2 ln Λ value. The 99% CL ULs on the cutoff energy correspond to 280 and 450 GeV for β = 0.5 and 1, respectively5.
Broken PL spectra have been observed in several SNRs interacting with MCs (e.g. Abdo et al. 2010a,b), and this could also be the case for Puppis A. A spectral index variation ΔΓ ~ 1 can be explained by radiative cooling of electrons or escape of protons in the case of a SNR encountering a dense and neutral medium (Malkov et al. 2012). The derived UL on the sub-exponential cutoff energy (280 GeV) can be used as a conservative UL on the energy of any spectral break as long as ΔΓ ≲ 1.
3. Discussion
Throughout the SNR evolution, particles are accelerated at the forward shock up to a maximum energy Emax, typically determined by the SNR’s finite age, finite size, or radiative losses. These effects become relevant when the characteristic timescales are close to the acceleration timescale, leading to cutoffs in the spectra of accelerated particles residing in the SNR. Additionally, a radiative spectral break can be present at the particle energy Ebreak for which the radiative loss timescales equal the SNR age. The conservative ULs on the cutoff energy in the γ-ray spectrum derived from the Fermi-LAT and H.E.S.S. measurements translate into ULs on Emax of ~2 TeV, ~3 TeV, or ~5 TeV depending on whether the γ-ray emission results from Bremsstrahlung (Br), IC or proton-nucleus interactions (e.g. p-p) radiation mechanisms. These limits can in turn be compared with the expectations from DSA theory taken in its simplest form and applied to the case of Puppis A whose main parameters are an age of ~4500 yr (Becker et al. 2012), a shock radius Rsh = 15 pc (for Rsh = 24′ at 2.2 kpc), and a shock velocity vsh ranging from 700 to 2500 km s-1. The last velocity value was estimated by Katsuda et al. (2013) based on the electron temperatures and ionisation timescales in the ejecta knots, whilst the former was derived from the shock temperature of ~0.7 keV (Hwang et al. 2008) by assuming full equipartition of the shock energy between ions and electrons. These shock-velocity estimates concern the NE region of the SNR, which is also the region coincident with the bulk of GeV emission. Based on these SNR parameters, constraints on the magnetic field and ISM density can be derived and compared to independent estimates (Hewitt et al. 2012; Dubner et al. 2013). In these calculations, the acceleration is assumed to proceed in a steady-state manner from the SN until now, and the derived contraints are implicitely considered as having been constant. Assuming Bohm diffusion, the acceleration timescale6 and the diffusion coefficient are 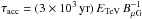
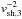 and
and 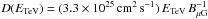 (Parizot et al. 2006), where BμG is the downstream magnetic field in units of μG, ETeV the particle energy in units of TeV, and vsh,3 the shock velocity in units of 103 km s-1. Synchrotron (syn), p-p, and Br radiative loss timescales are
(Parizot et al. 2006), where BμG is the downstream magnetic field in units of μG, ETeV the particle energy in units of TeV, and vsh,3 the shock velocity in units of 103 km s-1. Synchrotron (syn), p-p, and Br radiative loss timescales are 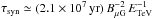 (Parizot et al. 2006),
(Parizot et al. 2006), 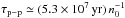 , and
, and 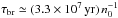 (Gabici et al. 2009), with n0 the ISM density in units of cm-3, and BμG is the downstream magnetic field in units of μG. The derived constraints are shown in Table 1.
(Gabici et al. 2009), with n0 the ISM density in units of cm-3, and BμG is the downstream magnetic field in units of μG. The derived constraints are shown in Table 1.
Constraints on BμG and n0 based on standard DSA predictions (assuming Bohm diffusion) and the ULs on the maximum particle energy derived from the Fermi-LAT and H.E.S.S. measurements.
In the age- and size-limited scenarios, the derived ULs on the magnetic field are lower than both the estimates of Hewitt et al. (2012), based on a simple one-zone modelling of Puppis A broadband emission (between 8 and 35 μG), and those of Dubner et al. (2013) and Arbutina et al. (2012), based on equipartition arguments (~26–100 μG). In other words, higher magnetic field values would have led to higher Emax and hence to VHE γ-ray emission from Puppis A detectable with the H.E.S.S. array. The ULs in Table 1 depend on the diffusion coefficient, which could depart from the traditional Bohm assumption (see e.g. Parizot et al. 2006). However, strong deviations from the Bohm regime would be required to make the non-detection with H.E.S.S. compatible with the Fermi-LAT detection. In particular, for the hadronic scenario in the size-limited case, diffusion about two orders of magnitude slower than the Bohm one would be needed. In the loss-limited cases due to p-p and Br interactions, lower limits on the density are much higher than estimated from IR observations towards the NE rim (~4 cm-3, Arendt et al. 2010), for any acceptable value of the magnetic field. Nonetheless, this density estimate, together with a realistic amount of energy in accelerated particles of ~ (1−4) × 1049 erg, can account for the GeV emission (Hewitt et al. 2012). The synchrotron limited case leads to a lower limit on the magnetic field that is far too high for a SNR of age ~4500 yr. Hewitt et al. (2012) have treated Emax as a free parameter in their broadband modelling, fixing it to 0.5 (resp. 0.8) TeV in their leptonic (resp. hadronic) modelling in order not to violate the Fermi-LAT measurements, but without imposing any physical constraint. By applying the same reasoning as above with only these Fermi-LAT lower limits on Emax, non-constraining limits on BμG and n0 are obtained.
The hypothesis of a break in the particle spectrum of Puppis A owing to synchrotron losses results in a realistic lower limit on the magnetic field (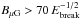 , Ebreak in TeV). However, leptonic-dominated scenarios would require an unusually high electron-to-proton ratio (greater than 0.1), in excess of the observed CR abundances (Hewitt et al. 2012). Radiative breaks due to p-p and Br mechanisms imply a constraint on n0 ≳ 104 cm-3 that is much stronger than the density estimates reported in Puppis A. Therefore, it turns out that none of the known limitations in the simple context of a single population of particles continuously accelerated at the SNR shock can explain the lack of VHE emission from the Puppis A SNR, except if the diffusion has been proceeding far from the Bohm limit.
, Ebreak in TeV). However, leptonic-dominated scenarios would require an unusually high electron-to-proton ratio (greater than 0.1), in excess of the observed CR abundances (Hewitt et al. 2012). Radiative breaks due to p-p and Br mechanisms imply a constraint on n0 ≳ 104 cm-3 that is much stronger than the density estimates reported in Puppis A. Therefore, it turns out that none of the known limitations in the simple context of a single population of particles continuously accelerated at the SNR shock can explain the lack of VHE emission from the Puppis A SNR, except if the diffusion has been proceeding far from the Bohm limit.
However, if the SNR shock has encountered a MC some time ago, the acceleration of particles could have ceased because of ion-neutral damping. In such a case, a radiative cutoff would appear at an energy for which τrad = Δt, with Δt the time elapsed since the beginning of the interaction. This would imply n0 ≳ 103 cm-3 and B ≳ 50 μG for the Br/p-p and syn radiative losses, respectively. These values seem to be very reasonable for a MC (Crutcher 1999).
Alternatively, other scenarios that could explain a break in the HE regime deal with particle escape and diffusion in SNRs (e.g. Ohira et al. 2010; Malkov et al. 2012). Although these spectral breaks are generally observed at energies of ~1−20 GeV (Abdo et al. 2009, 2010a,b,c,d), so lower than the constraints presented here, it is not clear whether the detection of such breaks in this energy range is entirely due to a Fermi-LAT statistical selection effect or not. Some localised regions along the Puppis A outer rim are known to have interacted with dense surrounding material (such as the BEK, Hwang et al. 2005), but due to their very small sizes and positions along the SNR rim they may not be representative of the bulk of the GeV emission observed with Fermi-LAT. The GeV emission is more compatible with the (hard) X-ray morphology shown in Dubner et al. (2013) pointing towards the NE region adjacent to a cloud traced in the far-IR domain that either still needs to be hit or that has already being shocked by the Puppis A SNR. Such a cloud interaction could be responsible for a break in the HE/VHE γ-ray spectrum through the above-mentioned mechanisms, but at somewhat higher energies than observed in the more evolved interacting SNRs.
4. Conclusion
The H.E.S.S. observations of Puppis A in the VHE domain reveal an unexpected lack of emission from the SNR. The extrapolation from the Fermi-LAT HE power-law spectrum to the VHE domain contrasts with the absence of VHE emission. The comparison of these two measurements indicates that a spectral feature (a break or a cutoff) must exist at energies around a few hundred GeV. By assuming a PL with an exponential (resp. sub-exponential) cutoff, such a feature should occur below 450 GeV (resp. 280 GeV) at the 99% CL. The latter value provides a conservative UL on any break energy as long as ΔΓ ≲ 1. In the context of a single population of particles continuously accelerated at the SNR forward shock through an on-going DSA process, and under the assumption of Bohm diffusion, it is difficult to reconcile the constraints on the magnetic field and ISM density derived from the broadband emission modelling (Hewitt et al. 2012) with those obtained here based on the predicted maximum/break particle energies. However, multi-wavelength data suggest that Puppis A has already interacted with MCs in some localised regions along the shell and that the NE region coincident with the bulk of GeV emission is possibly interacting with a far-IR MC (Dubner et al. 2013). If this is true, the acceleration of particles could have ceased some time ago, and either a radiative cutoff or a break of a non-radiative origin could be expected. In the latter case, the break is expected at somewhat higher energies than those measured in several SNRs known to be interacting with MCs, which lie in the 1−20 GeV energy range (Abdo et al. 2009, 2010d,a; Ackermann et al. 2013). Upcoming observations with the five-telescope H.E.S.S. II will allow the unexplored ~100−300 GeV domain, where this spectral feature is predicted to exist, to be probed for the first time.
Although a smaller distance of 1.3 kpc, with large uncertainties of +0.6/–0.8 kpc, has been previously determined by Woermann et al. (2000) based on OH line observations, a distance of 2.2 kpc is assumed throughout this paper.
The HE spectral parameters were obtained with the ROSAT X-ray template. However, as shown in Table 3 of Hewitt et al. (2012), those derived under the assumption of a uniform disc are fully compatible.
By setting the coefficient k0 from Eq. (14) of Parizot et al. (2006) equal to unity.
Acknowledgments
The support of the Namibian authorities and of the University of Namibia in facilitating the construction and operation of H.E.S.S. is gratefully acknowledged, as is the support by the German Ministry for Education and Research (BMBF), the Max Planck Society, the German Research Foundation (DFG), the French Ministry for Research, the CNRS-IN2P3, and the Astroparticle Interdisciplinary Programme of the CNRS, the UK Science and Technology Facilities Council (STFC), the IPNP of the Charles University, the Czech Science Foundation, the Polish Ministry of Science and Higher Education, the South African Department of Science and Technology and National Research Foundation, and by the University of Namibia. We appreciate the excellent work of the technical support staff in Berlin, Durham, Hamburg, Heidelberg, Palaiseau, Paris, Saclay, and in Namibia in the construction and operation of the equipment. We thank Gloria Dubner for providing the 1.4 GHz radio image of Puppis A.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, ApJ, 706, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010a, ApJ, 718, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010b, Science, 327, 1103 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010c, ApJ, 712, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010d, ApJ, 722, 1303 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2011, ApJ, 734, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Abramowski, A., Acero, F., Aharonian, F., et al. 2012, A&A, 548, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ackermann, M., Ajello, M., Allafort, A., et al. 2013, Science, 339, 807 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006a, A&A, 457, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006b, A&A, 448, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2007, A&A, 464, 235 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2008, A&A, 481, 401 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2007, ApJ, 664, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Arbutina, B., Urošević, D., Andjelić, M. M., Pavlović, M. Z., & Vukotić, B. 2012, ApJ, 746, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Arendt, R. G., Dwek, E., Blair, W. P., et al. 2010, ApJ, 725, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, W., Prinz, T., Winkler, P. F., & Petre, R. 2012, ApJ, 755, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, A. R. 1978a, MNRAS, 182, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, A. R. 1978b, MNRAS, 182, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Berge, D., Funk, S., & Hinton, J. 2007, A&A, 466, 1219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bernlöhr, K., Carrol, O., Cornils, R., et al. 2003, Astropart. Phys., 20, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Ostriker, J. P. 1978, ApJ, 221, L29 [Google Scholar]
- Castelletti, G., Dubner, G., Golap, K., & Goss, W. M. 2006, A&A, 459, 535 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chevalier, R. A. 1977, ARA&A, 15, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Crutcher, R. M. 1999, ApJ, 520, 706 [NASA ADS] [CrossRef] [Google Scholar]
- de Naurois, M., & Rolland, L. 2009, Astropart. Phys., 32, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Dubner, G., Loiseau, N., Rodríguez-Pascual, P., et al. 2013, A&A, 555, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dubner, G. M., & Arnal, E. M. 1988, A&AS, 75, 363 [NASA ADS] [Google Scholar]
- Feldman, G. J., & Cousins, R. D. 1998, Phys. Rev. D, 57, 3873 [Google Scholar]
- Gabici, S., Aharonian, F. A., & Casanova, S. 2009, MNRAS, 396, 1629 [NASA ADS] [CrossRef] [Google Scholar]
- Ginzburg, V. L., & Syrovatskii, S. I. 1964, Sov. Astron., 8, 342 [NASA ADS] [Google Scholar]
- Hewitt, J. W., Grondin, M.-H., Lemoine-Goumard, M., et al. 2012, ApJ, 759, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Hwang, U., Flanagan, K. A., & Petre, R. 2005, ApJ, 635, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Hwang, U., Petre, R., & Flanagan, K. A. 2008, ApJ, 676, 378 [NASA ADS] [CrossRef] [Google Scholar]
- Katsuda, S., Mori, K., Tsunemi, H., et al. 2008, ApJ, 678, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Katsuda, S., Hwang, U., Petre, R., et al. 2010, ApJ, 714, 1725 [NASA ADS] [CrossRef] [Google Scholar]
- Katsuda, S., Ohira, Y., Mori, K., et al. 2013, ApJ, 768, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Kelner, S. R., Aharonian, F. A., & Bugayov, V. V. 2006, Phys. Rev. D, 74, 034018 [NASA ADS] [CrossRef] [Google Scholar]
- Krymskii, G. F. 1977, Sov. Phys. Doklady, 22, 327 [Google Scholar]
- Lazendic, J. S., Wardle, M., Whiteoak, J. B., Burton, M. G., & Green, A. J. 2010, MNRAS, 409, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, S.-H., Ellison, D. C., & Nagataki, S. 2012, ApJ, 750, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Li, T.-P., & Ma, Y.-Q. 1983, ApJ, 272, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Malkov, M. A., Diamond, P. H., & Sagdeev, R. Z. 2012, Phys. Plasmas, 19, 082901 [NASA ADS] [CrossRef] [Google Scholar]
- Ohira, Y., Murase, K., & Yamazaki, R. 2010, A&A, 513, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ohm, S., van Eldik, C., & Egberts, K. 2009, Astropart. Phys., 31, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Parizot, E., Marcowith, A., Ballet, J., & Gallant, Y. A. 2006, A&A, 453, 387 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reichardt, I., de Oña-Wilhelmi, E., Rico, J., & Yang, R. 2012, A&A, 546, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reynolds, S. P. 2008, ARA&A, 46, 89 [Google Scholar]
- Reynoso, E. M., Dubner, G. M., Goss, W. M., & Arnal, E. M. 1995, AJ, 110, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Reynoso, E. M., Green, A. J., Johnston, S., et al. 2003, MNRAS, 345, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Rolke, W. A., López, A. M., & Conrad, J. 2005, Nucl. Instr. Meth. Phys. Res. A, 551, 493 [CrossRef] [Google Scholar]
- Winkler, P. F., & Kirshner, R. P. 1985, ApJ, 299, 981 [NASA ADS] [CrossRef] [Google Scholar]
- Woermann, B., Gaylard, M. J., & Otrupcek, R. 2000, MNRAS, 317, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Zirakashvili, V. N., & Aharonian, F. 2007, A&A, 465, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zirakashvili, V. N., & Ptuskin, V. S. 2008, ApJ, 678, 939 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Constraints on BμG and n0 based on standard DSA predictions (assuming Bohm diffusion) and the ULs on the maximum particle energy derived from the Fermi-LAT and H.E.S.S. measurements.
All Figures
 |
Fig. 1 Image of the H.E.S.S. γ-ray excess centred on the Puppis A SNR. The excess was smoothed with a Gaussian kernel of width 0.06° corresponding to the H.E.S.S. angular resolution (68% containment radius) for this analysis (shown in the bottom left inset). The colour scale represents the excess counts per surface area of π(0.06°)2. The circular analysis region of radius 0.38°, matching the Fermi-LAT best-fit morphological model, is shown as a dashed circle. The two hemispheres are separated by a dashed line along the north/south axis in celestial coordinates. The black contours represent the 1.4 GHz continuum emission (Castelletti et al. 2006) at the 5, 10, 20 and 50 mJy/beam levels. The yellow cross indicates the position of the BEK (Hwang et al. 2005). |
| In the text | |
 |
Fig. 2 H.E.S.S. 99% CL upper limits on the differential flux (arrows), together with the Fermi-LAT spectra from Puppis A, as reported in Hewitt et al. (2012). Red, blue and green symbols correspond to Fermi-LAT and H.E.S.S. measurements for the whole SNR, the E and W hemisphere, respectively. The data points show the LAT fluxes and 1σ statistical and systematic errors, whilst the bow-tie areas define the 68% CL bands. The solid and dashed lines indicate the preferred γ-ray spectra for the exponential and sub-exponential cutoff models, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


