| Issue |
A&A
Volume 574, February 2015
|
|
|---|---|---|
| Article Number | L6 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201425234 | |
| Published online | 22 January 2015 | |
Formation of dense structures induced by filament collisions
Correlation of density, kinematics, and magnetic field in the Pipe nebula⋆
1 Instituto de Ciencia de Materiales de
Madrid (CSIC), Sor Juana Inés de la
Cruz 3, 28049 Madrid, Spain
e-mail: pfrau@icmm.csic.es
2 Observatorio Astronómico Nacional, Alfonso XII 3,
28014
Madrid,
Spain
3 Institut de Ciències de l’Espai
(CSIC–IEEC), Campus UAB, Facultat de Ciències, C5p 2, 08193 Bellaterra, Catalonia,
Spain
4 Max-Planck-Institut für
extraterrestrische Physik, Giessenbachstr. 1, 85748
Garching,
Germany
5 Departamento de Física–ICEx–UFMG, Caixa Postal 702,
30.123-970
Belo Horizonte,
Brazil
6 Department of Physical Science, Osaka
Prefecture University, Gakuen 1–1,
Sakai, 599-8531
Osaka,
Japan
7 Instituto de Astronomía – UNAM, Unidad Académica en Ensenada,
Ensenada BC 22860, México, Mexico
Received:
28
October
2014
Accepted:
10
December
2014
Context. The Pipe nebula is a molecular cloud that lacks star formation feedback and has a relatively simple morphology and velocity structure. This makes it an ideal target for testing cloud evolution through collisions.
Aims. We aim at drawing a comprehensive picture of this relatively simple cloud to better understand the formation and evolution of molecular clouds on large scales.
Methods. We use archival data to compare the optical polarization properties, the visual extinction, and the 13CO velocities and linewidths of the entire cloud in order to identify trends among the observables.
Results. The Pipe nebula can be roughly divided into two filaments with different orientations and gas velocity ranges: E–W at 2−4 km s-1 and N–S at 6–7 km s-1. The two filaments overlap at the bowl, where the gas shows a velocity gradient spanning from 2 to 7 km s-1. Compared to the rest of the Pipe nebula, the bowl gas appears to be denser and exhibits larger linewidths. In addition, the polarization data at the bowl shows lower angular dispersion and higher polarization degree. Cores in the bowl tend to cluster in space and to follow the 13CO velocity gradient. In the stem, cores tend to cluster in regions with properties similar to those of the bowl.
Conclusions. The velocity pattern points to a collision between the filaments in the bowl region. The magnetic field seems to be compressed and strengthened in the shocked region. The proportional increase in density and magnetic field strength by a factor similar to the Alfvénic Mach number suggests a continuous shock at low Alfvénic Mach number under the flux-freezing condition. Shocked regions seem to enhance the formation and clustering of dense cores.
Key words: ISM: clouds / ISM: magnetic fields / ISM: individual objects: Pipe nebula / dust, extinction / evolution / ISM: kinematics and dynamics
A movie associated to Fig. 2 is available at http://www.aanda.org
© ESO, 2015
1. Introduction
The Pipe nebula is an ideal test site for studying early cloud formation. From this massive, nearby, elongated cloud (104M⊙; 145 pc away; 18 pc × 3 pc in size) 12CO 1–0 emission arises that shows two filamentary structures: one elongated along the N–S direction at a vLSR range of 6−7 km s-1, and the other one along the E–W direction at 2−4 km s-1 (Onishi et al. 1999). The magnetic field is strikingly uniform along the N–S direction with optical polarization degrees up to an outstanding 15% value (Alves et al. 2008, hereafter AFG08; Alves et al. 2014). Overall, the cloud seems to be magnetically dominated and turbulence seems to be sub-Alfvénic (Franco et al. 2010). Besides the simple structure, the cloud is at a very early stage of evolution with little to no star-formation feedback. Only 14 young stars have been detected, mostly in the B59 region at the west end, delivering a very low ~0.06% star formation efficiency (Forbrich et al. 2009). In addition, the cloud harbors more than 150 starless cores with very early chemistry that seem to be gravitationally unbound and pressure confined (Lada et al. 2008; Rathborne et al. 2008; Román-Zúñiga et al. 2009, 2010; Frau et al. 2010, 2012a).
2. Datasets and data process
The three datasets used in this work have been published in different articles. We limit ourselves to providing the basic information, and we refer the reader to the original publications. The dust extinction maps were derived by Román-Zúñiga et al. (2009, 2010) through the NICER infrared color excess technique (Lombardi & Alves 2001). The angular resolution is 20′′ and the typical rms is <1 mag. The 13CO 1–0 map was presented by Onishi et al. (1999) and has spectral and angular resolution of ~0.1 km s-1 and 4′, respectively. The 13CO emission is enclosed in the 5 mag contour of the Av map (Fig. 1). As a result, 13CO is a good tracer of the gas kinematics (Sect. 4.1). The optical linear polarization data were published by AFG08 and Franco et al. (2010). They observed 46 fields of 12′ × 12′ in the R band, covering most of the Pipe nebula. We used the ~6600 stars detected with P/σP ≥ 10.
Our data-processing followed two steps. First, the 13CO datacube was converted to spectra on a pixel-by-pixel basis. A semi-automatic algorithm detected the number of peaks in each spectrum and carried out a Gaussian fit to derive the peak velocity, vi, and the linewidth, FWHMi, of the different components. For each pixel, we also derived the first-order moment of the 13CO emission (vm1). Second, we paired the position of each R-band star to its pixel in the Av and 13CO map. After a positional match, we composed a set of properties for each pixel: Av, vm1, vi, FWHMi, polarization angle (Pang), and degree (Pdeg). The effects of the different angular resolutions are discussed in Sect. 4.1.
 |
Fig. 1 Velocity and polarization distribution of the Pipe nebula. Color code: blue and red for field groups NS and S, respectively. Central maps: Grayscale maps: top and bottom panels show the regions with 13CO vm1 in the >4 km s-1 and <4 km s-1, respectively (fitted to the map by Onishi et al. 1999). The N–S filament is evident in 12CO emission (Onishi et al. 1999). Contours: visual extinction map (Lombardi et al. 2006). Levels are 5.5 and 20 mag. Segments: average polarization segment on each observed field (AFG08; Franco et al. 2010). Length is proportional to ⟨ Pdeg ⟩. Circles: positions of the embedded dense cores with extinction peaks > 10 mag (Román-Zúñiga et al. 2009, 2010). Lefthand side panels: data averaged over the fields observed by AFG08. Top panel: ⟨ ΔPang ⟩ versus ⟨ Pdeg ⟩ as in AFG08. Central panels: ⟨ ΔPang ⟩ and ⟨ Pdeg ⟩ versus ⟨ vm1 ⟩, where m1 stands for the first-order moment of the 13CO emission. Bottom panel: average linewidth of the 13CO velocity components as a function of vi for the different cloud regions. vi is sampled in 0.25 km s-1–wide bins. Error bars indicate 1σ dispersion. Righthand side panels: data for every pixel separated by groups. Top panel: Pang versus Pdeg. Bottom panels: Pang and Pdeg versus vm1. |
3. Results and analysis
3.1. Dual large-scale velocity structure
Figure 1 outlines the main velocity structures of the Pipe nebula derived from the 13CO spectra. The cloud can be separated into two different filaments with narrow velocity ranges: one oriented E−W at <4 km s-1 and another one oriented N–S at >4 km s-1. (This filament is better seen in the 12CO map: see Onishi et al. 1999.) The spectra from the E−W filament typically have one velocity component, or two in some cases. Instead, the spectra from the N–S filament show a richer velocity structure with up to four components. Both structures overlap along the line of sight (LOS) at the bowl (Fig. 1). The velocities in the overlapping region cover the entire range between those of the two filaments. This transition is illustrated in Fig. 2 through two orthogonal projections of the position-position-velocity cube (see Hacar et al. 2013) that show distinct patterns (Sect. 4.2).
We define two regions: the non-shocked gas – group NS – that roughly includes B59 and the stem (⟨ Pdeg ⟩≲ 5%) and the shocked gas – group S – that roughly coincides with the bowl (⟨ Pdeg ⟩≳ 5%). These groups appear color-coded in Fig. 1 and also have distinct properties in polarimetry, density, and turbulence (Sect. 3.2).
3.2. Bimodal trends in velocity, polarization, and linewidth
The top lefthand panel in Fig. 1 replicates Fig. 2 by Alves et al. (2008). They report a systematic anti–correlation between ⟨ ΔPang ⟩ and ⟨ Pdeg ⟩. The color-coded NS and S groups appear clearly differentiated: S fields have high ⟨ Pdeg ⟩ and low ⟨ ΔPang ⟩, oppositely to NS fields. This differentiation goes beyond field averages and holds at a single pixel level (top right panels).
The central lefthand panels in Fig. 1 show the distinct distribution of ⟨ ΔPang ⟩ and ⟨ Pdeg ⟩ as a function of ⟨ vm1 ⟩. The bottom righthand panels of Fig. 1 show similar plots but for all the pixels. These panels show that the clear polarization differences between groups S and NS are mostly independent of the velocity of the gas, thus suggesting different scenarios for the two regions. Group S gas at 4–5 km s-1 shows the highest polarization degree.
The bottom lefthand panel of Fig. 1 and top panel of Fig. 2 show that the gas in the bowl has a larger linewidth than in B59 and the stem. Strikingly, the star-forming B59 complex has a smaller linewidth than group S. This suggests that the Bowl gas is more disturbed than that of B59.
4. Discussion
4.1. Data suitability and spatial resolution
The polarization data trace material with Av ≲ 15 mag that includes 99.1% of the Av map pixels, and Franco et al. (2010) show that Pdeg and Av grow roughly proportionally. As a result, optical data are good tracers of the magnetic field of the cloud. The NICER Av maps are very accurate: a comparison to 1.2 mm emission maps of dense cores shows a perfect within-the-errors agreement for up to 45 mag (Frau 2012b). The spatial resolution of the Av map is ~0.015 pc. This is significantly lower than the typical 0.1 pc diameter of dense cores, and the map resolution is thus more than enough for the large scales. 13CO is a good tracer of the dense gas (Fig. 1). The 13CO pixel size is ~0.17 pc, comparable to a dense core. With a mean 13CO linewidth of 0.6 ± 0.3 km s-1, the pixel crossing time is ~0.28 Myr. The dense core formation timescale is 0.5−1 Myr (Bergin & Tafalla 2007), and thus, it seems unlikely that any velocity substructure would form. Therefore, the 13CO map should suffice to reflect all significant variations in the gas velocity.
 |
Fig. 2 Top panels: projections of the position-position-velocity cube in two perpendicular position-velocity planes. The orientation of the projection planes is indicated as blue lines in the Av map subpanels. Bottom panel: velocity as a function of position. The projection plane is at an angle of 124° (shock direction: projection on the plane of the sky of the velocity difference of the filaments). Top panels: vi and FWHMi as a function of position. The projection plane is at an angle of 34° (perpendicular to the shock direction). Circles: dense cores as in Fig. 1. Cartoon: proposed scenario. The antenna represents the observer. Blue and red cylinders represent the E–W and N–S filaments, respectively. The LOS velocities of the filaments are shown as arrows, and the stem and bowl regions are labeled. The translucent plane shows the shock direction on the plane of the sky extended along the line-of-sight direction (blue line in bottom panel above). The velocities of the filaments along the shock are shown as arrows. Green arrows represent the tentative direction of the magnetic field (Sect. 4.3). An associated movie is available online. |
4.2. Interaction of gas filaments and core formation
The two filaments overlap at the bowl, and the gas velocities cover the entire range between the original velocities (Fig. 2). This fact points to an interaction, possibly a collision, as reported toward denser and more massive IRDCs (Duarte-Cabral et al. 2011; Henshaw et al. 2013; Nakamura et al. 2014). The sound speed at 12 K is cs = 0.27 km s-1 and the pre-shock Alfvén speed1 is vA = 0.78 km s-1. The magnetosonic speed 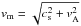 is 0.83 km s-1, less than the velocity separation of the filaments. Therefore, an MHD wave is slower than the velocity difference between the filaments, and a shock would indeed form. In the Pipe nebula it is therefore possible to compare the evolution from non-shocked (stem) to shocked (bowl) gas.
is 0.83 km s-1, less than the velocity separation of the filaments. Therefore, an MHD wave is slower than the velocity difference between the filaments, and a shock would indeed form. In the Pipe nebula it is therefore possible to compare the evolution from non-shocked (stem) to shocked (bowl) gas.
The two orthogonal projections of the position-position-velocity cube show that LOS velocities are anisotropic (Fig. 2). On the one hand, the bottom panel shows highly ordered velocities likely to be the velocity gradient generated along the direction of the collision. On the other hand, the middle panel shows a large velocity dispersion likely to be the projection across the shock. This identified direction for the plausible shock is the projection on the plane of the sky of the velocity difference between the filaments. In addition, for the collision to happen, the N–S filament must be closer to us because it is going away faster than the E–W filament. The total shock velocity would be a combination of two components: (a) the line-of-sight velocity and (b) the plane-of-the-sky velocity whose direction is deduced from the projections of the position-position-velocity cube. Figure 2 shows a cartoon of the proposed scenario.
Figure 1 shows that linewidths increase only at the bowl and for the velocities between the two filaments (roughly 4 to 6 km s-1). This points to a more turbulent region where the interaction takes place. The interaction would settle the gas at the observed intermediate velocities and result in sub- and trans-Alfvénic gas motions (Franco et al. 2010). The accumulation of material would cause the increase in density and would lead to the formation of the bowl. In fact, the average column density of 6.0 ± 1.8 mag at the bowl is twice as high as the average 3.0 ± 1.3 mag at the stem. This increase reflects an increase in volume density owing to the plausible filament collision.
The bowl is the region with the highest column density and the most fertile one in number of dense cores (Fig. 1). B59, the other region rich in dense cores, is also proposed as being formed through an external shock that triggered star formation (Peretto et al. 2012). Cores have velocities in good agreement with gas velocities. At the bowl, cores cover the entire velocity range between the filaments, follow the velocity gradient along the shock, and tend to cluster at the higher velocities (bottom panel in Fig. 2). This combined structure of cores and gas is the “molecular ring” reported by Muench et al. (2007). There are other clusters of cores, one in B59 and two in the stem (middle panel in Fig. 2). The gas surrounding these clusters shows similar properties: a larger dispersion of velocities and increases in linewidth, 13CO brightness, and column density. These properties resemble those of the shocked bowl but with lower values and on a smaller spatial scale. In general, it seems that in the slowed, shocked gas, the higher density and sub-Alfvénic motions enhance the creation of cores.
4.3. Magnetic field compression and polarization increase
The high Pdeg values – close to the theoretical maximum (Whittet 2003) – suggest that the magnetic field direction is close to the plane of the sky AFG08. The higher Pdeg values are detected toward the bowl, where the two filaments interact. The shock can have reoriented the magnetic field, placing it closer to the plane of the sky (Fig. 2). This scenario could explain the variation in Pdeg. Moreover, the peak of Pdeg is at a velocity of ~4.5 km s-1, the intermediate velocity between the filaments where the shock would have the strongest effects.
The material traced by the optical polarization is dominated by magnetic field over gravity and turbulence (Franco et al. 2010). This low-density gas is in flux-freezing conditions, this is, matter and magnetic field are tied. As expected in this regime, the large-scale gas compression that causes the column density to double also doubles the magnetic field strength: from 30 μG at the stem to 65 μG at the bowl (AFG08). This implies that the magnetic energy density is four times higher in the bowl than in the stem (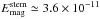 erg cm-3 and
erg cm-3 and 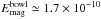 erg cm-3). Similarly, the larger line widths in the bowl than in the stem (0.6 ± 0.3 and 0.48 ± 0.19 km s-1, respectively) give a turbulent kinetic energy density about 40% higher in the bowl (
erg cm-3). Similarly, the larger line widths in the bowl than in the stem (0.6 ± 0.3 and 0.48 ± 0.19 km s-1, respectively) give a turbulent kinetic energy density about 40% higher in the bowl (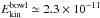 erg cm-3). This generates an increase in the surface pressure on dense cores, reported to be ~60% higher in the bowl with respect to the stem (Lada et al. 2008). The energy increase can be explained by the plausible shock scenario: assuming an average volume density of 3 × 103 cm-3 (AFG08) and assuming that the shock velocity is the velocity difference between the two filaments, 2.5 km s-1, then the shock energy density is Eshock ≃ 3.7 × 10-10 erg cm-3, which is twice the energy increase from the stem to the bowl. Consequently, the kinetic energy of the collision could increase the measured turbulence levels, and then drag and compress the magnetic field, thereby transferring and storing some of the kinetic energy into magnetic field energy.
erg cm-3). This generates an increase in the surface pressure on dense cores, reported to be ~60% higher in the bowl with respect to the stem (Lada et al. 2008). The energy increase can be explained by the plausible shock scenario: assuming an average volume density of 3 × 103 cm-3 (AFG08) and assuming that the shock velocity is the velocity difference between the two filaments, 2.5 km s-1, then the shock energy density is Eshock ≃ 3.7 × 10-10 erg cm-3, which is twice the energy increase from the stem to the bowl. Consequently, the kinetic energy of the collision could increase the measured turbulence levels, and then drag and compress the magnetic field, thereby transferring and storing some of the kinetic energy into magnetic field energy.
The Alfvénic Mach number MA = vshock/vA of the plausible shock is ~3.0. Simulations of low MA (highly magnetized) collisions predict the formation of shocks (Lesaffre et al. 2013). Indeed, models with low Alfvénic Mach numbers (MA ~ 4−5) drive more energy into compressing the magnetic field (Pon et al. 2012). In particular, for clouds of similar temperature and density to the Pipe nebula colliding at 2−3 km s-1, the density and magnetic field strength increase by a factor similar to MA. Moreover, 20% to 50% of the shock energy is stored in the magnetic field. These predictions match our results at the Pipe nebula, also if taking the factor of 2 error in the measured quantities into account. This provides a plausible theoretical framework
that reproduces our observations. The majority of the remaining energy is expected to be radiated away through mid-J CO lines that can be used to test this scenario further.
5. Conclusions
We combined visual extinction, optical polarimetry, and 13CO data of the Pipe nebula. Here, we summarize the conclusions.
-
1.
The velocity patterns of the gas suggest that the N−S and E−W filaments are colliding along the NW-SE direction at the bowl, where turbulence increases.
-
2.
There is a good correlation between polarization properties and velocity of the gas, suggesting that magnetization increases at the interaction site. The column density and magnetic field strength double with respect to the non-shocked gas, pointing to a highly magnetized, continuous collision under flux-freezing.
-
3.
Cores in the bowl tend to cluster in space and tend to follow the 13CO velocity gradient. Dense cores tend to form in regions similar to the bowl where the cloud gas has large velocity dispersion, linewidths, column density, and 13CO emission. It seems that in the slowed, shocked gas, the higher density and sub-Alfvénic motions enhance the creation of cores.
Online material
Movie of Fig. 2 Access here
Acknowledgments
We thank Daniele Galli and Andy Pon for useful comments and suggestions that are greatly appreciated. P.F. is supported by the CONSOLIDER project CSD2009-00038, Spain. P.F. and J.M.G. are supported by the MINECO project AYA2011-30228-C03-02, Spain. G.A.P.F. is supported by the CNPq agency, Brazil. CRZ is supported by program CONACYT CB-2010 152160, México.
References
- Alves, F. O., Franco, G. A. P., & Girart, J. M. 2008, A&A, 486, L13 (AFG08) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alves, F. O., Frau, P., Girart, J. M., et al. 2014, A&A, 569, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergin, E. A., & Tafalla, M. 2007, ARA&A, 45, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Duarte-Cabral, A., Dobbs, C. L., Peretto, N., & Fuller, G. A. 2011, A&A, 528, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Forbrich, J., Lada, C. J., Muench, A. A., Alves, J., & Lombardi, M. 2009, ApJ, 704, 292 [NASA ADS] [CrossRef] [Google Scholar]
- Franco, G. A. P., Alves, F. O., & Girart, J. M. 2010, ApJ, 723, 146 [Google Scholar]
- Frau, P. 2012, Ph.D. thesis [Google Scholar]
- Frau, P., Girart, J. M., Beltrán, M. T., et al. 2010, ApJ, 723, 1665 [NASA ADS] [CrossRef] [Google Scholar]
- Frau, P., Girart, J. M., Beltrán, M. T., et al. 2012, ApJ, 759, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Hacar, A., Tafalla, M., Kauffmann, J., & Kovács, A. 2013, A&A, 554, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henshaw, J. D., Caselli, P., Fontani, F., et al. 2013, MNRAS, 428, 3425 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Muench, A. A., Rathborne, J. M., Alves, J. F., & Lombardi, M. 2008, ApJ, 672, 410 [NASA ADS] [CrossRef] [Google Scholar]
- Lesaffre, P., Pineau des Forêts, G., Godard, B., et al. 2013, A&A, 550, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lombardi, M., & Alves, J. 2001, A&A, 377, 1023 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lombardi, M., Alves, J., & Lada, C. J. 2006, A&A, 454, 781 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muench, A. A., Lada, C. J., Rathborne, J. M., Alves, J. F., & Lombardi, M. 2007, ApJ, 671, 1820 [NASA ADS] [CrossRef] [Google Scholar]
- Nakamura, F., Sugitani, K., Tanaka, T., et al. 2014, ApJ, 791, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Onishi, T., Kawamura, A., Abe, R., et al. 1999, PASJ, 51, 871 [Google Scholar]
- Peretto, N., André, P., Könyves, V., et al. 2012, A&A, 541, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pon, A., Johnstone, D., & Kaufman, M. J. 2012, ApJ, 748, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Rathborne, J. M., Lada, C. J., Muench, A. A., Alves, J. F., & Lombardi, M. 2008, ApJS, 174, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Román-Zúñiga, C., Lada, C. J., & Alves, J. F. 2009, ApJ, 704, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Román-Zúñiga, C., Alves, J. F., Lada, C. J., & Lombardi, M. 2010, ApJ, 725, 2232 [NASA ADS] [CrossRef] [Google Scholar]
- Whittet, D. C. B. 2003, Dust in the Galactic Environment, 2nd edn. (Bristol: Institute of Physics Publishing) [Google Scholar]
All Figures
 |
Fig. 1 Velocity and polarization distribution of the Pipe nebula. Color code: blue and red for field groups NS and S, respectively. Central maps: Grayscale maps: top and bottom panels show the regions with 13CO vm1 in the >4 km s-1 and <4 km s-1, respectively (fitted to the map by Onishi et al. 1999). The N–S filament is evident in 12CO emission (Onishi et al. 1999). Contours: visual extinction map (Lombardi et al. 2006). Levels are 5.5 and 20 mag. Segments: average polarization segment on each observed field (AFG08; Franco et al. 2010). Length is proportional to ⟨ Pdeg ⟩. Circles: positions of the embedded dense cores with extinction peaks > 10 mag (Román-Zúñiga et al. 2009, 2010). Lefthand side panels: data averaged over the fields observed by AFG08. Top panel: ⟨ ΔPang ⟩ versus ⟨ Pdeg ⟩ as in AFG08. Central panels: ⟨ ΔPang ⟩ and ⟨ Pdeg ⟩ versus ⟨ vm1 ⟩, where m1 stands for the first-order moment of the 13CO emission. Bottom panel: average linewidth of the 13CO velocity components as a function of vi for the different cloud regions. vi is sampled in 0.25 km s-1–wide bins. Error bars indicate 1σ dispersion. Righthand side panels: data for every pixel separated by groups. Top panel: Pang versus Pdeg. Bottom panels: Pang and Pdeg versus vm1. |
| In the text | |
 |
Fig. 2 Top panels: projections of the position-position-velocity cube in two perpendicular position-velocity planes. The orientation of the projection planes is indicated as blue lines in the Av map subpanels. Bottom panel: velocity as a function of position. The projection plane is at an angle of 124° (shock direction: projection on the plane of the sky of the velocity difference of the filaments). Top panels: vi and FWHMi as a function of position. The projection plane is at an angle of 34° (perpendicular to the shock direction). Circles: dense cores as in Fig. 1. Cartoon: proposed scenario. The antenna represents the observer. Blue and red cylinders represent the E–W and N–S filaments, respectively. The LOS velocities of the filaments are shown as arrows, and the stem and bowl regions are labeled. The translucent plane shows the shock direction on the plane of the sky extended along the line-of-sight direction (blue line in bottom panel above). The velocities of the filaments along the shock are shown as arrows. Green arrows represent the tentative direction of the magnetic field (Sect. 4.3). An associated movie is available online. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


