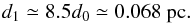| Issue |
A&A
Volume 574, February 2015
|
|
|---|---|---|
| Article Number | A143 | |
| Number of page(s) | 7 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201425015 | |
| Published online | 10 February 2015 | |
The SS433 jet from subparsec to parsec scales
1
Centre for mathematical Plasma Astrophysics, Department of
Mathematics,
KU Leuven, Celestijnenlaan 200B,
3001
Leuven,
Belgium
e-mail: Remi.MonceauBaroux@wis.kuleuven.be
2
Department of Applied Mathematics, The University of
Leeds, Leeds,
LS2 9JT,
UK
3
LUTh, Observatoire de Paris, France
Received:
17
September
2014
Accepted:
8
November
2014
Context. Relativistic jets associated with compact objects, as in the X-ray binary SS433, are known to be multiscale because they spawn over many orders of magnitude in distance. Here we model the precessing SS433 jet and study its dynamics from 𝒪 (0.01) to 𝒪(1) parsec scales.
Aims. We aim to solve the discrepancy between the observations on a 0.1 pc scale of SS433, where the jet is clearly precessing with an angle of 20°, and the larger scale observations where the jet of SS433 interacts with the associated supernova remnant W50, requiring a precessing angle of 10°.
Methods. We use 3D special relativistic hydrodynamical simulations on a domain of a scale of 1 pc. We use the finite volume code MPI-AMRVAC, solving the relativistic variant of the Euler equations. To cover lengthscale variations from 𝒪(0.001) pc as the jet beam width up to the domain size, we take full advantage of code parallelization and its adaptive mesh refinement scheme.
Results. We found that by means of a simple hydrodynamical process, the jet of SS433 can transit from a precessing jet with an angle of 20°, to a continuous hollow non-precessing jet with a smaller opening angle of about 10°. Successive windings of the precessing jet helix undergo gradual deceleration by ISM interaction, to ultimately merge in a hollow straight jet at distances where the ram pressure of individual jet elements match the ISM pressure at about 0.068 pc from the source.
Conclusions. We solve the discrepancy with an elegant and simple model that does not require the jet of SS433 to undergo any temporal changes in jet injection dynamics, but does so as a consequence of a hydrodynamically enforced spatial recollimation. Our simulation thus serves to validate simpler model prescriptions for SS433 on large scales, where a continuous jet profile suffices.
Key words: hydrodynamics / relativistic processes / ISM: jets and outflows / X-rays: binaries
© ESO, 2015
1. Introduction
Relativistic jets are associated with many astrophysical objects from high energy jets associated with active galactic nuclei (AGN) to mildly relativistic jets associated with X-ray binaries (XRB). One thing all relativistic jets have in common is their multiscale nature. This was perfectly illustrated by Harris et al. (2005), where in a review of observations of 3C 120, this AGN jet was essentially traced for distances from 5 pc up to 150 kpc.
Here, we are interested in the mildly relativistic jet associated with SS433, an XRB system discovered in 1977 (Stephenson & Sanduleak 1977). This jet has also been observed well on many different scales. In 1998, this jet was observed through its interaction with the supernova remnant W50 (Dubner et al. 1998) with the VLA ground base array on a scale of 50 pc. Roberts et al. (2008) and Bell et al. (2011) observed SS433 on a scale of about 0.1 pc again with the VLA instrument. Going to smaller scales yet (down to order 10-4 pc), there are VLBA observations (Mioduszewski et al. 2004), and an online version exists of the resulting VLBA radio map movie, covering about 40 days of observations that shows dynamics and the jet precession close to its launch area. Finally, Roberts et al. (2014) have recently started analyzing Jansky VLA observations on the scale of the source system, which is about 10-6 pc.
SS433 is an XRB system from which the accretion disk and the associated jet are precessing. Many publications, starting from 1979, studied this system and constructed a model known today as the canonical kinematic model (Fabian & Rees 1979; Milgrom 1979b,a; Margon et al. 1979). This model describes the jet from SS433 as a precessing jet with a beam of opening angle 1.5°, inclined with an angle of 20° to the precession axis. The jet material has a Lorentz factor of 1.036 (or a velocity of 0.26c) and a beam luminosity of 1039 erg s-1 (Brinkmann et al. 2005). We validated this model by means of 3D special relativistic hydrodynamical simulations in Monceau-Baroux et al. (2014, hereafter, M14). We pointed out that this model has to be corrected for the interaction with the medium and the linked deceleration. These M14 simulations were targeted to the region of scale 0.1 pc. In Zavala et al. (2008) and Goodall et al. (2011), the authors reproduced the observations for the scales where the jet interacts with the supernova remnant W50 at about 50 pc from the source. The main finding of their simulations was that they could only reproduce the observation for a precessing angle of about 10°. Zavala et al. (2008) also use a hollow conical jet instead of a precessing jet with the argument that they cannot resolve the timescale needed to see the successive windings.
Therefore, we end up with a discrepancy between the larger scales of the jet of SS433 and its inner region. No observations give insight into the dynamics of the SS433 jet in this transition region because the jet itself becomes too faint for the sensitivity of the VLA instrument. On larger scales, the jet is visible indirectly through its deformation of W50. Numerical modeling is therefore needed to understand how the precessing jet of SS433 can evolve in this transition region. This is the problem we address in this article. One can easily imagine two scenarios for resolving the discrepancy: a temporal evolution of the precessing motion. This scenario invokes a change in the source of the jet itself. The second scenario is a spatial evolution of the precessing jet, meaning where some degree of reconfinement in its propagation is at work. This scenario invokes interactions with the medium. We show how we found the second scenario to be more likely by following the jet progression on a large domain.
General parameters for the 3D simulation studying the spatial evolution of SS433.
2. Simulation setup
The setting for the simulation is similar to case A in M14. We used 3D cartesian geometry. The difference resides in the size of the domain that is increased tenfold in each dimension. The number of cells in each direction of the simulation is increased by a factor 8 by allowing the simulation to use three extra levels of mesh refinement for a total of seven adaptive mesh refinement (AMR) levels. This results in a physical resolution that is somewhat less but close to the smaller simulations in M14. The initial conditions of the simulation can be found in Table 1, where we introduce and adopt the same notation as in M14. We recall that its case A was found to give the best correspondence with VLA radiomaps, when compared to simulations where the same kinetic flux Lkin was realized at a slightly different beam Lorentz factor γb or density contrast between jet beam and interstellar medium (ISM). The normalization to convert code units to their physical counterpart is as follows: speeds are normalize to the speed of light, the distance to the parsec, the time to 1.027 × 108 s (≃ 3.3 years) and the density to 1.66 × 10-24 g cm-3. As in our previous work on SS433, during simulation time, we follow the evolution of an electron population defined by its density and power-law energy spectrum that will allow us to produce a synthetic radio map of the simulation.
The AMR scheme (in a block-octree fashion) is manually enforced to its maximum resolution near the injection of the jet, which again uses a sphere of radius 0.008 pc to inject a precessing jet of finite opening angle and SS433 parameter settings into the domain. For the rest of the domain, the AMR is automatically triggered by following the spatial variation of the density, Lorentz factor, and pressure. To keep the size of the data and the simulation time manageable, the domain resolution is not allowed to go farther than the fifth level of mesh refinement beyond a sphere with radius equal to three radii of injection of the jet (i.e., r> 0.024 pc).
By using the same data analysis tools as developed in M14, we can always distinguish physically distinct regions in our domain. A tracer follows the presence of material coming from the jet. Together with the relativistic beam velocity, this allows us to locate the ‘active beam’ where the material is not yet fully decelerated. Using instantaneous quantities like the vorticity of the velocity field and the energy content, we can also locate the cocoon and the shocked interstellar medium (SISM) regions precisely, as detailed in M14. We then, for exemple calculate the radial velocity profile vb(r) (Fig. 5), which quantifies the maximal velocity found on a sphere of increasing radius r to the central source. We also calculate the width of the various domain regions (Fig. 3) along with their excess energy content (Fig. 2), to collect quantitative information on jet-affected ISM volumes and the energy redistribution.
3. Early spatial evolution and long-term energy balance
 |
Fig. 1 Overall view of the large simulation of SS433 zoomed to the scale reached at t = 2 (6.5 years), i.e. |
 |
Fig. 2 Energy transfer from jet to cocoon and SISM regions as a function of time (in years). |
Up to time t = 2 of the simulation (6.5 years), the precessing jet keeps the helical pattern that we know from our previous studies for the same parameter values (case A of M14). At this point the jet has propagated for a distance of 0.1 pc. A visual comparison between case A (see Fig. 3, left panel in M14) and the present Fig. 1 shows matching results. Both snapshots are taken at the same physical time (t = 6.5 years), so they are at the same stage of their precessing jet evolution. We can see the same helical pattern, with three stable windings for each jet, plus a fourth highly decelerated and unstable winding. The only difference up to this point is that our domain is larger and that the local resolution on injection is close, but slightly smaller than for the smaller domain.
The larger domain size now allows us to analyze energy redistribution of the jet without suffering from losses through the domain walls. Previously, this hampered our analysis of energy deposition and transfer. The same quantification, but now for the entire duration of up to 30 years of our large scale run is plotted in Fig. 2, showing energy fractions in jet, cocoon and SISM regions as a function of time. Unlike to M14 (their Fig. 5), we do not see any significant decrease in the energy fraction present in the SISM region up to time t = 6.5 years (which was previously due to energy leaving through the boundaries of our domain). This study of the energy content redistribution for the precessing SS433 jet shown in Fig. 2 extends our study from case A in M14. The transition from the initial conditions to the steady injection causes the abrupt changeover within the first (few) years, but the percentages are accurate for the subsequent decades of evolution, since all dynamics stay well within the boundaries of our domain. We see that the fraction of energy present in the jet decreases steadily as it gets transferred to cocoon and SISM regions, while there is a slight bump at time t ≈ 13 years, which coincides with the formation of a more hollow, steady jet farther down the jet path (see Sect. 4). The establishment of a self-collimated jet beyond 0.068 parsec is thus seen to influence overall energy redistribution fractions.
 |
Fig. 3 Farthest radial reach of SISM, cocoon, and jet regions over time, extending the analysis of M14 (their Fig. 4) to cover larger scales. |
4. Morphological changeover at later times
 |
Fig. 4 Horizontal cuts along the (x,z) plane (precession axis along the here horizontal z-axis) of the SS433 jet simulation at times (from left to right): t = 6.5 year, t = 10.5 years, t = 15.5 years, and t = 29.25 years. The plot shows the Lorentz factor with the color scale as indicated and shared for all panels. |
As already pointed out in M14, the morphology of the precessing jet has a direct impact on the deceleration of the jet head. In contrast to a static case, an element of the jet interacts not only with the surrounding medium when it reaches the jet head, but also all along its path. As a result, the farther away from the source an element of the jet is, the more decelerated it is. We have already discussed in M14 that even though the jet as a whole precesses, individual fluid elements largely follow a radial (bullet-like) propagation. We then consider two different fluid elements of the jet corresponding to the same phase in a precession cycle (later on referred to as “pulses” on the 2D cuts), for two consecutive cycles of the continuous regim. We label A as the element in front, and B the one behind it. As they propagate into the medium, A gets more decelerated than B, because it is farther away and has spent more time interacting with the medium. As a result the radial distance between them reduces, and at some point they start interacting as B catches up with the tail of A. Such a case can be seen clearly in Fig. 4 where we show horizontal cuts through the precession axis, quantifying the Lorentz factor at selected times. At a certain distance from the source, it is not possible anymore to distinguish the different precession cycles. This is a spatial evolution and not a temporal evolution: at all times the region of the jet close to the source stays helical. This spatial evolution of the jet generally leads to a stationary state. Figure 5 shows that as the jet head progresses, it dynamically establishes a steady velocity profile vb(r), which then remains constant in time in the beam: up to 0.08,0.13,0.17, and 0.21 pc for time t = 10.5 years, t = 15.5 years, and t = 29.25 years, respectively. Beyond the point where the overall jet progression has established a stationary pattern, the material from the jet reaches the jet head where it is quickly decelerated. The velocity profile evolution reveals another feature: for the first part of its propagation, the jet beam is decelerated in a similar fashion as discussed in M14. But upon reaching the transition to a continuous jet (as shown below happening at about 0.068 parsec), this deceleration becomes more gradual before reaching the end of the jet where it is quickly fully decelerated. From an injection velocity of 0.26c, the jet beam slows down to 0.2c, at which point it slowly decreases to velocities of 0.12c (and lower ahead).
Looking back at Fig. 3, where we used the instantaneous masks to distinguish the different regions and quantify their width as a function of time, we can again see this pattern as the jet, cocoon, and SISM all propagate quickly up to time t = 2.5 years, after which time the jet pushes all other regions steadily outward. After this point, the overreaching bow shocks propagate freely in the SISM with a constant supersonic speed of 0.05c. The expansions of jet and cocoon remain similar, decreasing slowly to an asymptotic propagation that we fit with a velocity of 0.02c.
5. Synthetic views and recollimation analysis
 |
Fig. 5 Radial speed profiles vb(r) at several times. |
As shown clearly in the horizontal cuts with Lorentz factor from Fig. 4, there is a clear spatial transition as judged from the jet morphology, realized at about t ≃ 10 years. We now wish to generate more observationally relevant maps on this spatial evolution, which we do using two means for generating synthetic radio views. The first method is already described in detail in Porth et al. (2014a) and used in M14, and uses post treatment on saved data files, where a python script generates a line-of-sight-aligned new ray grids, and subsequently interpolates this data to then integrate to a 2D intensity map. In doing so, effects of projection in any direction, as well as Doppler boosting effects, are fully incorporated. Here we also employ a simplified method that yields mock images during the runtime of the simulation. During the simulation, we quantify a mock-up local instantaneous synchrotron emission of the matter in the jet je(x,y,z,t). je(x,y,z,t) express in the observer frame as 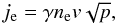 (1)where γ is the local Lorentz factor, ne the electron density, p the local instantaneous pressure acting as a proxy for the strength of the magnetic field, and v the local velocity. We point out that the emission is isotropic since we do not take the relativistic beaming into account. The electron density ne is taken in both emission mapping as the density of the electron population that evolves during simulation time. This evolution only takes into account adiabatic expansion and compression of the density and energy of the electrons. It does not account for the emission losses and possible reacceleration at shocks. By collapsing the octree AMR structure along one coordinate direction using the collapse option as described in Porth et al. (2014b), we obtain a mock line-of-sight integration of this emission, along rays aligned with the x, y, or z coordinates. Those mock intensity maps are shown in Fig. 6 for four selected time frames (like those from Fig. 4), where we show views that collapse information along the y axis. The main downsides of this simplified method are that it uses the electron density but not the information on their power spectrums, and that the integration has to be done along one of the axies of the simulation, corresponding here to a line of sight of 90°. In reality, SS433 is seen with a line of sight of 80°. Its main advantage, on the other hand, is its operation during simulation time and the short time needed to be executed, since no interpolations are required.
(1)where γ is the local Lorentz factor, ne the electron density, p the local instantaneous pressure acting as a proxy for the strength of the magnetic field, and v the local velocity. We point out that the emission is isotropic since we do not take the relativistic beaming into account. The electron density ne is taken in both emission mapping as the density of the electron population that evolves during simulation time. This evolution only takes into account adiabatic expansion and compression of the density and energy of the electrons. It does not account for the emission losses and possible reacceleration at shocks. By collapsing the octree AMR structure along one coordinate direction using the collapse option as described in Porth et al. (2014b), we obtain a mock line-of-sight integration of this emission, along rays aligned with the x, y, or z coordinates. Those mock intensity maps are shown in Fig. 6 for four selected time frames (like those from Fig. 4), where we show views that collapse information along the y axis. The main downsides of this simplified method are that it uses the electron density but not the information on their power spectrums, and that the integration has to be done along one of the axies of the simulation, corresponding here to a line of sight of 90°. In reality, SS433 is seen with a line of sight of 80°. Its main advantage, on the other hand, is its operation during simulation time and the short time needed to be executed, since no interpolations are required.
 |
Fig. 6 Collapsed emission images of SS433 at times (from left to right): t = 6.5 years, t = 10.5 years, t = 15.5 years, and t = 29.25 years. Logarithm of the intensity from Eq. (1). Scale is indicated and is the same for all panels. |
The obtained mock-up synchrotron views using Eq. (1) allow drawing the following conclusions. Looking at the first panel, we can see the helical shape we already know. Taken at the same time intervals, the horizontal cuts through the jet in the (x,z) plane (Fig. 4) show the pulsing nature of the jet along any line on the precessing cone. This gives this helical path which is, also frequently approximated with the canonical kinematic model. This section of the domain will keep the same geometry in all subsequent panels of Fig. 6, with a constant precessing angle. Starting in the second panel, the jet adopts a continuous conical geometry at a certain distance from the source. We note a core region of the beam, where we identify successive precession pulses as mentioned before, with a high Lorentz factor. It is surrounded by a continuous region with lower Lorentz factor. This is mostly material from the medium accelerated by the jet.
 |
Fig. 7 Cuts along the (x,y) plane (precession axis along the z axis) of our SS433 jet simulation at (negative) distances z = −0.15 pc, z = −0.07 pc, and z = −0.02 pc at time t = 29.25 years. Top: Lorentz factor. Bottom: material coming from the jet as located with the weighted tracer. Scale is indicated and shared for all panels. |
Additional 2D cuts in Fig. 7 further reveal this jet to be hollow. The cuts perpendicular to the precession axis also reveal extra features: at first we can clearly see the helix of SS433 which propagates unperturbed even if subject to deceleration and adiabatic expansion. We also note that around the jet the medium is accelerated as the successive windings go through it. As the jet moves through the transition region at z ≃ 0.068 pc, we can see that the new element of the helix catches up with the tail of the previous winding. This is particularly clear in the plot of the material coming from the jet (bottom panels of Fig. 7). Later we can see that the jet becomes a continuous jet. The density tracer of the material originating in the jet reveals an annulus shape. It also starts being subject to hydrodynamical turbulence triggered by fluid instabilities in the shear flow between jet and ambient medium, as can be seen in the left hand panels of Fig. 7. We note that there is no rotation of the jet in the plane perpendicular to the precession axis. In the bottom left hand panel of Fig. 7 we also observe cocoon material with very low Lorentz factor surrounding the jet annulus.
We now quantify this transitional behavior by collecting profiles as a function of distance z from the central region, where we at every z-value quantify the maximum jet reach Rmax(z) and the jet axis Rj(z) location as measured in cylindrical distance R from the precession axis. Here, Rmax(z) is using the cocoon filter described in M14. Rj(z) is calculated by locating the element with maximum velocity in the plane of coordinate z and included in the filter for the jet as described in M14. This is done in Fig. 8, where we see the maximum distance from the precession axis reached by the jet material Rmax(z) evolving over time and showing a clear recollimation beyond a critical | z |-value. The same is seen when quantifying the position of the beam axis from the precession axis Rj(z). It is important to note that we consider a profile here that in essence integrates around the axis of precession by quantifying distances to this axis and that in that manner we do not consider the jet as a helix, but as a cone.
By fitting the slope of this expansion with distance from the source we can find the maximal opening angle of the jet. The first thing we notice is an asymmetry between the two oppositely directed jets. At some point during the transition phase, the two counter propagating jets evolve differently. For the jet at negative z values up to 0.08 pc, the jet material is confined in an angle of 36°, while its beam axis follows a precession axis of 20° as expected. As the jet is over dense, we can postulate that the larger extension of the jet material results from cocoon dynamics that manifest a “bursting” scenario added to the adopted 5° jet opening angle due to the jet being overdense.
Between 0.08 pc and 0.14 pc this (left) jet material undergoes a first recollimation down to 19°. After 0.14 pc the jet material almost becomes fully recollimated. For the jet at positive z-values, the first recollimation happens almost at the same distance of 0.09 pc and only to an angle of 25° for the jet material. But quickly after that at 0.11 pc, it reaches a geometry taht is similar to its left counterpart. Looking at the fit of the jet axis between the transition region (z = 0.07 pc) and the position where the jet gets deflected (z = 0.17 pc), the curve for t = 29.25 years is fit for the negative z with 9.8° and the positive z with 11.6° angles. Although the opposing jet asymmetry is likely to be influenced by numerical effects, the observed recollimation beyond 0.07−0.08 pc is a robust result as happens in both jet parts.
 |
Fig. 8 Top: maximum distance Rmax(z) from the precession axis reached by the jet material, at various times. Middle: distance Rj(z) from the precession axis of the jet beam axis, at the same times. Bottom: fit of Rj(z) for t = 29.25 years. The dashed line represents a precessing angle of 20°. The two continuous lines fits a ax+b function between the transition region (z = 0.07 pc) and the position where the jet gets deflected (z = 0.17 pc). The curve is fit for the negative z with 9.8° and the positive z with 11.6° precessing angles. |
This result can be understood by making the assumption that this transition will happen where the ram pressure of the jet elements is matched by the pressure that this element will encounter from the medium. We can express this dynamical equilibrium by 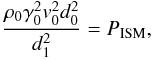 (2)where ρ0, γ0, and v0 are respectively the density, Lorentz factor, and velocity at the distance from the source d0 where the jet is injected in the numerical domain, d1 the distance of the transition region, or distance of dynamical equilibrium, and PISM taken as the medium pressure. In our case this reduces to
(2)where ρ0, γ0, and v0 are respectively the density, Lorentz factor, and velocity at the distance from the source d0 where the jet is injected in the numerical domain, d1 the distance of the transition region, or distance of dynamical equilibrium, and PISM taken as the medium pressure. In our case this reduces to 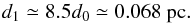 (3)If we compare this estimated distance to where the transition starts, it is consistent with the distances obtained. At about 0.068 pc from the SS433 source, we now find that the jet beam realizes approximate dynamical equilibrium with the surroundings and that this distance also locates where successive windings catch up with each other. In all, this acts as a dynamical reconfinement scenario, where radio images show a clear morphological changeover.
(3)If we compare this estimated distance to where the transition starts, it is consistent with the distances obtained. At about 0.068 pc from the SS433 source, we now find that the jet beam realizes approximate dynamical equilibrium with the surroundings and that this distance also locates where successive windings catch up with each other. In all, this acts as a dynamical reconfinement scenario, where radio images show a clear morphological changeover.
6. Synthetic radio map views and conclusions
 |
Fig. 9 Radio map of the spatial evolution of SS433 in VLA conditions. The reconstruction beam is equivalent to 0.005 pc. We show a dynamical range of 40 contours with incremental levels of |
We finally use the ray tracing script described in Porth et al. (2014a) and M14, which accounts for the evolution of a passive electron distribution was it is subjected to adiabatic compressions and expansions, to see what the VLA instrument could see of this spatial evolution of the jet. We recall that the line of sight for SS433 is 80°. The result in this setting can be seen in Fig. 9. The center of the image up to 0.05 pc is similar, with a different scaling, to the canonical case shown in M14, which gave the best correspondence with actual observations from Roberts et al. (2008). In this section of the jet, which is located before the transition, the helical pattern is clearly marked. The radio map gives us a clear transition of the jet around 0.068 pc. Here the jet is no longer seen as a helix but as two nearly parallel intensity lines. The asymmetry between the approaching and receding jets mentioned previously does not strongly influence the radio maps because both jets seem similar.
Despite the inclination of the line of sight, we observe no visible effect of Doppler boosting on the intensity contrast between the paired jets. This is easily explained by the clear deceleration of the jet, compared to its higher velocity in its helical section. The more striking feature is that the continuous part is relatively faint compare to the central helical part as seen in Fig. 9. Looking at the observational views shown in Roberts et al. (2008), the radio elements farther away from the source seem to fade under the observational sensitivity. For this reason, the predicted appearance as a double-line pattern farther along in the continuous section of SS433 may well be below the sensitivity of VLA. We point out that we find a inertia ratio of about 28.6 between the jet and its medium (see Table 1). In their observations, Bell et al. (2011) give an inertia ratio of around 300. The main difference is that we take the density value for the medium typical for the ISM where the jet of SS433 is propagating in a supernovae remnant (SNR). This would locate the position of the transition region even farther away from the source. Investigation of more realistic SNR atmosphere are planned for future work.
In conclusion, the precessing jet of SS433 evolves spatially, by means of its gradual deceleration along its helical path and the unavoidable dynamical interaction that results. We find a clear transition at finite radial distances, estimated to be at about 0.068 pc from pressure-matching arguments, to a new continuous jet that has characteristics of its own. Its beam velocity is 0.12c and head velocity is 0.02c. But the more notable feature is that this new jet is recollimated dynamically to an opening angle equal or inferior to 10°. This solves the discrepancy between the smaller scale 20° opening angle of the SS433 VLA observations (see Roberts et al. 2008 and M14) and the 10° opening angle deduced from the observations of its interaction with W50 (see Dubner et al. 1998; Zavala et al. 2008, and Goodall et al. 2011).
Acknowledgments
For part of the simulations, we used the infrastructure of the VSC-Flemish Supercomputer Center, funded by the Hercules Foundation and the Flemish Government, department EWI. We acknowledge financial support from FWO-Vlaanderen, grant G.0238.12 and from project GOA/2015-014 (KU Leuven). OP is supported by STFC under grant ST/I001816/1.
References
- Bell, M. R., Roberts, D. H., & Wardle, J. F. C. 2011, ApJ, 736, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Brinkmann, W., Kotani, T., & Kawai, N. 2005, A&A, 431, 575 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dubner, G. M., Holdaway, M., Goss, W. M., & Mirabel, I. F. 1998, AJ, 116, 1842 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., & Rees, M. J. 1979, MNRAS, 187, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Goodall, P. T., Alouani-Bibi, F., & Blundell, K. M. 2011, MNRAS, 414, 2838 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, D. E., Mossman, A. E., & Walker, R. C. 2005, in X-Ray and Radio Connections, eds. L. O. Sjouwerman, & K. K. Dyer [Google Scholar]
- Margon, B., Grandi, S. A., Stone, R. P. S., & Ford, H. C. 1979, ApJ, 233, 63 [Google Scholar]
- Milgrom, M. 1979a, A&A, 76, 3 [Google Scholar]
- Milgrom, M. 1979b, A&A, 78, 17 [NASA ADS] [Google Scholar]
- Mioduszewski, A. J., Rupen, M. P., Walker, R. C., Schillemat, K. M., & Taylor, G. B. 2004, in AAS High Energy Astrophysics Division #8, BAAS, 36, 967 [Google Scholar]
- Monceau-Baroux, R., Porth, O., Meliani, Z., & Keppens, R. 2014, A&A, 561, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Porth, O., Komissarov, S. S., & Keppens, R. 2014a, MNRAS, 438, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Porth, O., Xia, C., Hendrix, T., Moschou, S. P., & Keppens, R. 2014b [arXiv:1407.2052] [Google Scholar]
- Roberts, D. H., Wardle, J. F. C., Lipnick, S. L., Selesnick, P. L., & Slutsky, S. 2008, ApJ, 676, 584 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, D. H., Kosowsky, M., & Wardle, J. F. C. 2014, in AAS Meet. Abstr., 224, 219.24 [Google Scholar]
- Stephenson, C. B., & Sanduleak, N. 1977, BAAS, 33, 459 [Google Scholar]
- Zavala, J., Velázquez, P. F., Cerqueira, A. H., & Dubner, G. M. 2008, MNRAS, 387, 839 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
General parameters for the 3D simulation studying the spatial evolution of SS433.
All Figures
 |
Fig. 1 Overall view of the large simulation of SS433 zoomed to the scale reached at t = 2 (6.5 years), i.e. |
| In the text | |
 |
Fig. 2 Energy transfer from jet to cocoon and SISM regions as a function of time (in years). |
| In the text | |
 |
Fig. 3 Farthest radial reach of SISM, cocoon, and jet regions over time, extending the analysis of M14 (their Fig. 4) to cover larger scales. |
| In the text | |
 |
Fig. 4 Horizontal cuts along the (x,z) plane (precession axis along the here horizontal z-axis) of the SS433 jet simulation at times (from left to right): t = 6.5 year, t = 10.5 years, t = 15.5 years, and t = 29.25 years. The plot shows the Lorentz factor with the color scale as indicated and shared for all panels. |
| In the text | |
 |
Fig. 5 Radial speed profiles vb(r) at several times. |
| In the text | |
 |
Fig. 6 Collapsed emission images of SS433 at times (from left to right): t = 6.5 years, t = 10.5 years, t = 15.5 years, and t = 29.25 years. Logarithm of the intensity from Eq. (1). Scale is indicated and is the same for all panels. |
| In the text | |
 |
Fig. 7 Cuts along the (x,y) plane (precession axis along the z axis) of our SS433 jet simulation at (negative) distances z = −0.15 pc, z = −0.07 pc, and z = −0.02 pc at time t = 29.25 years. Top: Lorentz factor. Bottom: material coming from the jet as located with the weighted tracer. Scale is indicated and shared for all panels. |
| In the text | |
 |
Fig. 8 Top: maximum distance Rmax(z) from the precession axis reached by the jet material, at various times. Middle: distance Rj(z) from the precession axis of the jet beam axis, at the same times. Bottom: fit of Rj(z) for t = 29.25 years. The dashed line represents a precessing angle of 20°. The two continuous lines fits a ax+b function between the transition region (z = 0.07 pc) and the position where the jet gets deflected (z = 0.17 pc). The curve is fit for the negative z with 9.8° and the positive z with 11.6° precessing angles. |
| In the text | |
 |
Fig. 9 Radio map of the spatial evolution of SS433 in VLA conditions. The reconstruction beam is equivalent to 0.005 pc. We show a dynamical range of 40 contours with incremental levels of |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.