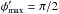| Issue |
A&A
Volume 573, January 2015
|
|
|---|---|---|
| Article Number | A8 | |
| Number of page(s) | 5 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201424779 | |
| Published online | 09 December 2014 | |
Wind mass transfer in S-type symbiotic binaries
I. Focusing by the wind compression model
Astronomical Institute, Slovak Academy of Sciences,
059 60
Tatranská Lomnica,
Slovakia
e-mail:
skopal@astro.sk
Received: 8 August 2014
Accepted: 12 October 2014
Context. Luminosities of hot components in symbiotic binaries require accretion rates that are higher than those that can be achieved via a standard Bondi-Hoyle accretion. This implies that the wind mass transfer in symbiotic binaries has to be more efficient.
Aims. We suggest that the accretion rate onto the white dwarfs (WDs) in S-type symbiotic binaries can be enhanced sufficiently by focusing the wind from their slowly rotating normal giants towards the binary orbital plane.
Methods. We applied the wind compression model to the stellar wind of slowly rotating red giants in S-type symbiotic binaries.
Results. Our analysis reveals that for typical terminal velocities of the giant wind, 20 to 50 km s-1, and measured rotational velocities between 6 and 10 km s-1, the densities of the compressed wind at a typical distance of the accretor from its donor correspond to the mass-loss rate, which can be a factor of ~10 higher than for the spherically symmetric wind. This allows the WD to accrete at rates of 10-8−10-7 M⊙ yr-1, and thus to power its luminosity.
Conclusions. We show that the high wind-mass-transfer efficiency in S-type symbiotic stars can be caused by compression of the wind from their slowly rotating normal giants, whereas in D-type symbiotic stars, the high mass transfer ratio can be achieved via the gravitational focusing, which has recently been suggested for very slow winds in Mira-type binaries.
Key words: stars: activity / binaries: symbiotic / stars: winds, outflows
© ESO, 2014
1. Introduction
Symbiotic stars are long-period interacting binary systems that include a cool giant as the donor star and a compact star, in most cases a white dwarf (WD), as the accretor. On the basis of their infrared properties, we distinguish between S-type (stellar) and D-type (dusty) symbiotic stars (Webster & Allen 1975). The former is represented by a stellar type of the IR continuum from a normal giant, whereas the latter contains additional strong emission from the dust produced by a Mira-type variable. For D-type systems, the orbital periods are, in general, unknown, but considered to be in the range of a few times 10 to 100 years. The cases of V1016 Cyg (Porb ~ 15 years, Parimucha et al. 2002) and Mira AB with the projected separation of components of ~65 AU (Matthews & Karovska 2006) represent the well-measured examples. Most of S-type systems has orbital periods between 200 and 1000 days (e.g. Belczynski et al. 2000), which correspond to the binary extension of a few AU for their typical total mass of ≈2 M⊙ (e.g. Schild et al. 1996). Based on a strong correlation between the spectral type of the cool giant and the orbital period, Mürset & Schmid (1999) suggested that symbiotic stars are well detached binary systems. Thus the symbiotic activity on the WD companion is triggered by the wind mass transfer.
The WD therefore accretes a fraction of the giant wind, which leads to its heating up to ≳105 K and increasing its luminosity to ~102−104 L⊙. This hot WD then ionizes a portion of the wind from the giant giving rise to the nebular radiation (e.g. Seaquist et al. 1984). Without any sudden optical brightenings, this configuration is called the quiescent phase of a symbiotic star. In most cases, the observed large energy output is believed to be caused by stable nuclear hydrogen burning on the WD surface (e.g. Tutukov & Yungelson 1976), which requires accretion onto a low mass WD at rates of 10-8−10-7 M⊙ yr-1 (see Fig. 2 of Shen & Bildsten 2007). However, such high accretion rates cannot be achieved by a standard Bondi-Hoyle wind accretion, because of its low efficiency (=the mass transfer ratio) of a few percent (Bondi & Hoyle 1944; Livio & Warner 1984) and the mass-loss rates from red giants (RGs) in S-type systems of ≈10-7 M⊙ yr-1 (e.g. Mürset et al. 1991; Mikołajewska et al. 2002; Skopal 2005; Walder et al. 2008). Similar results were obtained by even more sophisticated three-dimensional simulations of wind accretion in well separated binaries. Depending on the binary configuration, the mass transfer ratio (=mass accretion rate/mass loss rate) was found to be in the range of 0.6–10% (e.g. Theuns et al. 1996; Walder 1997; Dumm et al. 2000; Nagae et al. 2004; Walder et al. 2008).
The long-standing problem of the large energetic output from hot components in symbiotic binaries and its deficient fuelling by the giant in the canonical Bondi-Hoyle picture was first pointed out by Kenyon & Gallagher (1983). A promising solution of the problem has recently been suggested for Mira-type interacting binaries, whose slow and dense winds from evolved AGB giants can be gravitationally focused on the binary orbital plane (Mohamed & Podsiadlowski 2007, 2012; de Val-Borro et al. 2009). This mass transfer mode, where the wind is filling the Roche lobe instead of the star itself, is called wind Roche-lobe overflow (WRLOF, Mohamed & Podsiadlowski 2007). In the model, material is gravitationally confined to the Roche lobe and falls into the potential of the companion through the L1 point, similarly to standard RLOF. In general, WRLOF can occur in systems where the wind acceleration zone lies close to, or is a significant fraction of, the Roche lobe radius. Corresponding mass transfer efficiencies are at least an order of magnitude more than the analogous Bondi-Hoyle values (Mohamed & Podsiadlowski 2012).
In this contribution we suggest that the wind from normal giants in S-type symbiotic stars can be focused by their rotation according to the wind compression disk (WCD) model elaborated by Bjorkman & Cassinelli (1993). This possibility insists on the fact that normal giants in these systems rotate slowly, with the equatorial velocity around of 8 km s-1 (e.g. Zamanov et al. 2007). In addition, a wind-focusing effect was also proven observationally (Blind et al. 2011; Boffin et al. 2014a,b). Accordingly, Sect. 2 outlines the WCD model, and Sect. 3 presents results of its application. Their discussion and conclusion are found in Sects. 4 and 5, respectively.
2. The method
2.1. Wind compression model
Rotation of a star with radiation-driven wind leads to its compression towards the equatorial regions, where it can create a disk-like formation (Bjorkman & Cassinelli 1993). There are two main simplifications in the model: (i) the model neglects the gas pressure gradients at and beyond the sonic point; and (ii) it assumes the spherical stars with only the radial acting of gravity and radiation forces on wind elements, which then move as independent particles ejected with a non-radial initial velocity. Furthermore, in a star-centred spherical coordinate system (r,θ,φ) with the spin axis θ = 0, the WCD model assumes an azimuthal symmetry of the wind density. Therefore, it is a function of the radial distance r from the star’s centre and the polar angle θ. According to the mass continuity equation, the mass density distribution in the WCD model, ρc(r,θ), is expressed as 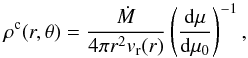 (1)where Ṁ is the mass-loss rate from the star, vr(r) is the radial component of the wind velocity and the geometrical factor dμ/dμ0 describes the compression of the wind due to rotation of the star (see below).
(1)where Ṁ is the mass-loss rate from the star, vr(r) is the radial component of the wind velocity and the geometrical factor dμ/dμ0 describes the compression of the wind due to rotation of the star (see below).
For the wind velocity profile, we used the β-law as introduced by Lamers & Cassinelli (1999), 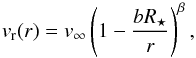 (2)where R⋆ is the radius of the star, β characterizes acceleration of its wind, and the parameter b is given by
(2)where R⋆ is the radius of the star, β characterizes acceleration of its wind, and the parameter b is given by 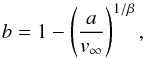 (3)where a is the initial velocity of the wind at its origin R⋆, and v∞ its terminal velocity. In comparison with Bjorkman & Cassinelli (1993), we assume that v∞ does not depend on the polar angle θ.
(3)where a is the initial velocity of the wind at its origin R⋆, and v∞ its terminal velocity. In comparison with Bjorkman & Cassinelli (1993), we assume that v∞ does not depend on the polar angle θ.
The geometrical factor in Eq. (1) is expressed as 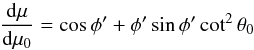 (4)(Bjorkman & Cassinelli 1993), where μ = cosθ, μ0 = cosθ0, and the relation between the initial polar angle θ0 of the parcel of gas in the streamline (i.e. the polar angle at the radius of the star R⋆) and the actual θ (see Fig. 2 therein) is given by
(4)(Bjorkman & Cassinelli 1993), where μ = cosθ, μ0 = cosθ0, and the relation between the initial polar angle θ0 of the parcel of gas in the streamline (i.e. the polar angle at the radius of the star R⋆) and the actual θ (see Fig. 2 therein) is given by 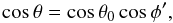 (5)where the angle
(5)where the angle ![\begin{equation} \phi'(r) = \frac{v_{\rm rot} \sin \theta_{0}}{v_{\infty}} \frac{1}{b(1-\beta)} \left[\left(1-\frac{bR_{\star}}{r} \right)^{1-\beta}-(1-b)^{1-\beta}\right] . \label{eqn:fi} \end{equation}](/articles/aa/full_html/2015/01/aa24779-14/aa24779-14-eq41.png) (6)The angle φ′ is called the “displacement angle”, which determines deflection of a streamline from the radial direction. It describes the trajectory of the mass launched from the star’s surface at θ0 in its own orbital plane. The larger the angle φ′, the closer the material gets to the equatorial plane of the star. For r → ∞, φ′(r) has an asymptotic value
(6)The angle φ′ is called the “displacement angle”, which determines deflection of a streamline from the radial direction. It describes the trajectory of the mass launched from the star’s surface at θ0 in its own orbital plane. The larger the angle φ′, the closer the material gets to the equatorial plane of the star. For r → ∞, φ′(r) has an asymptotic value 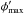 , which means that the trajectory becomes radial at this direction owing to the dominance of the radiation forces. Using the β-law wind as above, the asymptotic deflection of the rotating wind particles is given by (see Lamers & Cassinelli 1999)
, which means that the trajectory becomes radial at this direction owing to the dominance of the radiation forces. Using the β-law wind as above, the asymptotic deflection of the rotating wind particles is given by (see Lamers & Cassinelli 1999) ![\begin{equation} \phi'_{\rm max} = \frac{v_{\rm rot}\sin \theta_{0}}{v_{\infty}} \frac{1}{b(1-\beta)}\left[1-(1-b)^{1-\beta}\right], \label{eqn:max} \end{equation}](/articles/aa/full_html/2015/01/aa24779-14/aa24779-14-eq46.png) (7)where vrot is the equatorial rotation velocity of the star. In our application we consider only models with trajectories that do not cross the star’s equator (the so-called wind compression zone (WCZ) model, see Ignace et al. 1996), which means that
(7)where vrot is the equatorial rotation velocity of the star. In our application we consider only models with trajectories that do not cross the star’s equator (the so-called wind compression zone (WCZ) model, see Ignace et al. 1996), which means that 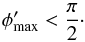 (8)This condition constrains a maximum of vrot for given parameters of the stellar wind to form a WCZ. Table 1 gives some examples of its value for the wind parameters in Sect. 2.3.
(8)This condition constrains a maximum of vrot for given parameters of the stellar wind to form a WCZ. Table 1 gives some examples of its value for the wind parameters in Sect. 2.3.
In our application the rotating star in the model is considered to be the RG in S-type symbiotic binaries. Assuming that the wind from the giant is isothermal at the same temperature as the stellar photosphere (≈3000 K), the speed of sound is a few times km s-1. Then, according to Bjorkman & Cassinelli (1993), the gas pressure gradient force will be negligible, because the terminal velocity of the wind and the stellar rotation are greater than the isothermal speed of sound (parameters in Sects. 2.3 and 2.4). A negligible oblateness of the slowly rotating RG (see Cariková & Skopal 2014) and dropping pressure gradient force result in the purely radial radiative drag on wind particles. These properties satisfy main simplifications of the WCD model (see above), and thus justify its applicability to normal giants in S-type symbiotic stars.
2.2. Mass-loss ratio
To compare densities of the compressed and spherically symmetric wind, we determine mass-loss ratio f, which we define as the ratio of the mass-loss rate Ṁc(r,θ), given by the local density ρc(r,θ), to the mass-loss rate from the star Ṁ, that is, 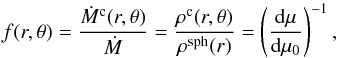 (9)where ρsph(r) is the mass density distribution of spherically symmetric wind. Owing to the compression of the wind towards the equatorial plane and a constant value of Ṁ, the mass-loss ratio f(r,θ) > 1 near the equatorial plane, but <1 in directions around the pole. Figure 1 shows two examples of f(r,θ) for r< 6 R⋆ and all θ.
(9)where ρsph(r) is the mass density distribution of spherically symmetric wind. Owing to the compression of the wind towards the equatorial plane and a constant value of Ṁ, the mass-loss ratio f(r,θ) > 1 near the equatorial plane, but <1 in directions around the pole. Figure 1 shows two examples of f(r,θ) for r< 6 R⋆ and all θ.
To estimate the accretion from the compressed wind onto the WD, we need to determine the mass-loss ratio around the orbital plane, which is assumed to coincide with the equatorial plane of the rotating star. According to Eq. (9) it is given by the reciprocal value of the geometrical factor (4), which depends on the parameters of the wind and the rotational velocity of the star.
 |
Fig. 1 Mass-loss ratio, f(r,θ) = Ṁc(r,θ) /Ṁ, calculated for parameters of the model A (left) and H (right) in Table 2, depicted in the plane perpendicular to the equatorial plane containing the giant at (0, 0). This demonstrates compression of the wind to the equatorial plane with a factor of > 5−9 at r = 5−6 R⋆ relative to the spherically symmetric density distribution. |
2.3. Parameters of the RG wind
We assume that the parameters of the wind from the giant are characterized by the initial velocity a =1 km s-1, terminal velocities v∞ = 20−50 km s-1, and the acceleration parameter β = 2.5 (Schröder 1985).
2.4. Rotational velocities of RGs
Soker (2002) has predicted theoretically that the cool components in symbiotic systems are likely to rotate much faster than isolated cool giants or those in wide binary systems. Zamanov et al. (2008) support this suggestion by measuring projected rotational velocities, vrotsin(i), in a number of symbiotic stars and isolated giants. They find that in S-type symbiotics the K giants rotate two to four times faster than the field K giants, and M giants rotate on average 1.5 times faster than the field M giants. Using high-resolution spectroscopic observations and the cross-correlation function method, Zamanov et al. (2007) find a typical rotational velocity of the K and M giants in S-type symbiotic stars to be 4.5 <vrotsin(i) < 11.7 km s-1. These results were confirmed by Zamanov & Stoyanov (2012). Using new data for 55 field M0 III – M6 III giants, they indicated a mean vrotsin(i) = 5.0 km s-1 and median vrotsin(i) = 4.3 km s-1. For 33 M0 III – M6 III giants in symbiotic systems, they have confirmed a mean vrotsin(i) = 7.8 km s-1 and median vrotsin(i) = 8 km s-1. As a result of these studies, we assumed the rotational velocities of the cool giants to be in the range of 6–9.5 km s-1.
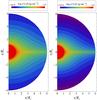 |
Fig. 2 Density distribution in the compressed wind calculated according to Eq. (1) for Ṁ = 10-7 M⊙ yr-1 and R⋆ = 100 R⊙. The step of isodensities is 0.17. Selection of models and the plane of depiction are as in Fig. 1. |
 |
Fig. 3 Left and middle panels: mass-loss ratio f(r,π/ 2) at the equatorial plane as a function of the radial distance. Parameters of the models are in Table 2. The right panel demonstrates an increase of f(6R⋆,π/ 2) for vrot/vrot,max → 1 and different v∞ (labelled on the right side). |
Mass-loss ratio f at r = 6 R⋆ and θ = π/ 2 calculated for selected values of v∞ and vrot (in km s-1).
3. Results
To demonstrate focusing of the giant’s wind towards the equatorial plane (assumed to be coincident with the orbital plane) due to its rotation, we calculated the mass-loss ratio f(r,θ) (Eq. (9)) for parameters of the wind v∞ = 20−50 km s-1, a = 1 km s-1, and β = 2.5 (Sect. 2.3), and the equatorial rotation velocity of the giant vrot = 6−9.5 km s-1 (Sect. 2.4). Selected models are summarized in Table 2. Models A–D correspond to vrot ~ 0.9 × vrot,max, while models E–H have vrot ≳ 0.95 × vrot,max.
Figure 1 shows f, for r< 6 R⋆, all θ and parameters of models A and H in Table 2. Compression to the equatorial plane is fairly significant: f> 1 for θ ≳ 75° and f ~ 5−10 for θ = 90° at r = 5−6 R⋆. This means that the wind from slowly rotating giants is compressed to its equatorial plane with the factor f ~ 5−10 with respect to the density distribution of the spherically symmetric wind that has the same overall Ṁ.
Figure 2 shows examples of the mass density distribution in the compressed wind calculated according to Eq. (1) for typical quantities of RGs in S-type symbiotic stars, Ṁ = 10-7 M⊙ yr-1, R⋆ = 100 R⊙, and parameters of models A and H as in Fig. 1. A compression of the wind is clearly seen.
Figure 3 shows the dependence of f on the radial distance at the equatorial plane (left and middle panels) and on the rotation rate vrot/vrot,max (right panel). For the fixed v∞ the density gradient in the direction perpendicular to the equatorial plane is larger for higher vrot. This implies an increase of f when vrot approaches its threshold value vrot,max for forming a WCZ, and thus a more efficient wind mass transfer (the right panel of the figure).
Our results suggest that for a typical separation between the binary components of 5–6 R⋆ (2–3 AU), the wind compression can increase the local mass-loss rate around the orbital plane, and thus also the accretion rate onto the WD, by a factor of ~5–10 with respect to the spherically symmetric wind.
4. Discussion
Because of the low mass transfer ratio in the wind accreting binaries (see Sect. 1), the only way to get the required high accretion rate, which maintains the high luminosity of WDs in symbiotic systems, is to focus the giant wind in the direction of their compact companions. Our findings that the rotating giant can compress its wind around the WD by a factor of f ~ 5−10 (Figs. 1 and 3) suggests a relevant increase in the accretion rate, Ṁacc, onto the WD. It can be formally expressed as 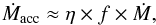 (10)where η is the mass transfer ratio (a few times 0.01 as summarized in Sect. 1), f is the mass-loss ratio (Eq. (9), Fig. 3) and Ṁ is the mass-loss rate from giants in S-type symbiotic stars. Thus, Ṁ = a few × 10-7 M⊙ yr-1 yields Ṁacc ~ 10-8−10-7 M⊙ yr-1, which is sufficient to power the WD luminosity by a stable hydrogen-burning regime for the WD mass <1 M⊙.
(10)where η is the mass transfer ratio (a few times 0.01 as summarized in Sect. 1), f is the mass-loss ratio (Eq. (9), Fig. 3) and Ṁ is the mass-loss rate from giants in S-type symbiotic stars. Thus, Ṁ = a few × 10-7 M⊙ yr-1 yields Ṁacc ~ 10-8−10-7 M⊙ yr-1, which is sufficient to power the WD luminosity by a stable hydrogen-burning regime for the WD mass <1 M⊙.
The WRLOF represents a different type of the wind focusing (Sect. 1), which has recently been applied to the nearest D-type symbiotic binary, Mira AB (o Ceti), to explain its unusual activity (Mohamed & Podsiadlowski 2012). It was shown that the WRLOF mode is applicable for slow dense winds from evolved AGB objects with the acceleration zone extending to their Roche lobes (see Fig. 1 of Abate et al. 2013). Measuring and modelling the circumstellar envelope around o Ceti, the prototype of Mira variables, showed that the terminal expansion velocity of its wind is only 4.6–2.5 km s-1 (Bowers & Knapp 1988; Ryde & Schöier 2001). This suggests that the gravitational focusing by the WRLOF mode may also be in the effect in other D-type symbiotic stars, because they comprise a Mira-type variable as the cool component.
On the other hand, the winds from normal giants in S-type symbiotic stars are typically one order of magnitude faster than those produced by Mira variables. Therefore, focusing of the wind in S-type symbiotic stars by the rotation of their normal giants probably represents a more suitable alternative to the WRLOF. However, this idea should be tested further by applying the WRLOF mode also to faster winds to better understand which type of the mass transfer mode is dominant in different wide-interacting binaries.
5. Conclusion
We tested a possibility of the wind focusing towards the orbital plane of S-type symbiotic binaries by rotation of their RGs. In this way we attempted to explain a high wind mass transfer efficiency required to power the observed luminosity of their WD accretors.
For the measured rotational velocities of the giant, 6–10 km s-1, and terminal velocities of its wind, 20–50 km s-1, the densities of the compressed wind around the WD, hence the accretion rate, can be a factor of ~10 higher than in the case of spherically symmetric wind (Figs. 1 and 3, Eq. (10)). As a result, the WD can accrete at rates of 10-8−10-7 M⊙ yr-1 (Sect. 4), which is sufficient to power its luminosity of a few times 1000 L⊙ measured during quiescent phases of symbiotic stars (Sect. 1).
Being aware of the simplicity of the WCD model for the purpose of our application, more sophisticated calculations should be done to prove (or disprove) our result. Using the WCD model we can suggest only the way to get enough wind from the RG to the vicinity of the WD in S-type symbiotic binaries. However, to find out the structure of the wind from the rotating giant in these systems and to understand the process of its accretion, 3D hydrodynamic models (e.g., as cited in Sect. 1 and/or that was recently presented by Hadrava & Čechura 2012), including the idea of the WCD model, should gone into in more detail. From this point of view, our approach to solving the problem of a high wind mass transfer efficiency in S-type symbiotic binaries represents a direction for future theoretical modelling.
Acknowledgments
The authors would like to thank the anonymous referee for useful comments that helped to improve the clarity of this paper. This research made use of NASA’s Astrophysics Data System Service. This project was supported by the Slovak Academy of Sciences under grant VEGA No. 2/0002/13.
References
- Abate, C., Pols, O. R., Izzard, R. G., Mohamed, S. S., & de Mink, S. E. 2013, A&A, 552, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belczynski, K., Mikolajewska, J., Munari, U., Ivison, R. J., & Friedjung, M. 2000, A&AS, 146, 407 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bjorkman, J. E., & Cassinelli, J. P. 1993, ApJ, 409, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Blind, N., Boffin, H. M. J., Berger, J.-P., et al. 2011, A&A, 536, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boffin, H. M. J., Blind, N., Hillen, M., et al. 2014a, Messenger, 156 [Google Scholar]
- Boffin, H. M. J., Hillen, M., Berger, J. P., et al. 2014b, A&A, 564, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bondi, H., & Hoyle, F. 1944, MNRAS, 114, 195 [Google Scholar]
- Bowers, P. F., & Knapp, G. R. 1988, ApJ, 332, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Cariková, Z., & Skopal, A. 2014, A&A, 570, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Val-Borro, M., Karovska, M., & Sasselov, D. 2009, ApJ, 700, 1148 [NASA ADS] [CrossRef] [Google Scholar]
- Dumm, T., Folini, D., Nussbaumer, H., et al. 2000, A&A, 354, 1014 [NASA ADS] [Google Scholar]
- Hadrava, P., & Čechura, J. 2012, A&A, 542, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ignace, R., Cassinelli, J. P., & Bjorkman, J. E. 1996, ApJ, 459, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Kenyon, S. J., & Gallagher, J. S. 1983, AJ, 88, 666 [NASA ADS] [CrossRef] [Google Scholar]
- Lamers, H. J. G. L. M., & Cassinelli, J. P. 1999, Introduction to stellar winds (Cambridge University Press) [Google Scholar]
- Livio, M., & Warner, B. 1984, The Observatory, 104, 152 [NASA ADS] [Google Scholar]
- Matthews, L. D., & Karovska, M. 2006, ApJ, 637, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Mikołajewska, J., Ivison, R. J., & Omont, A. 2002, Adv. Space Res., 30, 2045 [NASA ADS] [CrossRef] [Google Scholar]
- Mohamed, S., & Podsiadlowski, Ph. 2007, in 15th European Workshop on White Dwarfs, eds. R. Napiwotzki, & M. R. Burleigh, ASP Conf. Ser., 372, 397 [Google Scholar]
- Mohamed, S., & Podsiadlowski, Ph. 2012, Balt. Astron., 21, 88 [Google Scholar]
- Mürset, U., & Schmid, H. M. 1999, A&AS, 137, 473 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mürset, U., Nussbaumer, H., Schmid, H. M., & Vogel, M. 1991, A&A, 248, 458 [NASA ADS] [Google Scholar]
- Nagae, T., Oka, K., Matsuda, T., et al. 2004, A&A, 419, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parimucha, Š., Chochol, D., Pribulla, T., Buson, L. M., & Vittone, A. A. 2002, A&A, 391, 999 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ryde, N., & Schöier, F. L. 2001, ApJ, 547, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Schild, H., Mürset, U., & Schmutz, W. 1996, A&A, 306, 477 [NASA ADS] [Google Scholar]
- Schröder, K.-P. 1985, A&A, 147, 103 [NASA ADS] [Google Scholar]
- Seaquist, E. R., Taylor, A. R., & Button, S. 1984, ApJ, 284, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, K. J., & Bildsten, L. 2007, ApJ, 660, 1444 [NASA ADS] [CrossRef] [Google Scholar]
- Skopal, A. 2005, A&A, 440, 995 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soker, N. 2002, MNRAS, 337, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Theuns, T., Boffin, H. M. J., & Jorissen, A. 1996, MNRAS, 280, 1264 [NASA ADS] [CrossRef] [Google Scholar]
- Tutukov, A. V., & Yungelson, L. R. 1976, Astrophys., 12, 342 [Google Scholar]
- Walder, R. 1997, in Accretion phenomena and related outflows, eds. D. T. Wichramasinghe, L. Ferrario, & G. V. Bicknell, IAU Coll. 163 (San Francisco: ASP), ASP Conf. Ser., 121, 822 [Google Scholar]
- Walder, R., Folini, D., & Shore, S. N. 2008, A&A, 484, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Webster, B. L., & Allen, D. A. 1975, MNRAS, 171, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Zamanov, R. K., & Stoyanov, K. A. 2012, Bulgarian Astron. J., 18, 41 [Google Scholar]
- Zamanov, R. K., Bode, M. F., Melo, C. H. F., et al. 2007, MNRAS, 380, 1053 [NASA ADS] [CrossRef] [Google Scholar]
- Zamanov, R. K., Bode, M. F., Melo, C. H. F., et al. 2008, MNRAS, 390, 377 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Mass-loss ratio f at r = 6 R⋆ and θ = π/ 2 calculated for selected values of v∞ and vrot (in km s-1).
All Figures
 |
Fig. 1 Mass-loss ratio, f(r,θ) = Ṁc(r,θ) /Ṁ, calculated for parameters of the model A (left) and H (right) in Table 2, depicted in the plane perpendicular to the equatorial plane containing the giant at (0, 0). This demonstrates compression of the wind to the equatorial plane with a factor of > 5−9 at r = 5−6 R⋆ relative to the spherically symmetric density distribution. |
| In the text | |
 |
Fig. 2 Density distribution in the compressed wind calculated according to Eq. (1) for Ṁ = 10-7 M⊙ yr-1 and R⋆ = 100 R⊙. The step of isodensities is 0.17. Selection of models and the plane of depiction are as in Fig. 1. |
| In the text | |
 |
Fig. 3 Left and middle panels: mass-loss ratio f(r,π/ 2) at the equatorial plane as a function of the radial distance. Parameters of the models are in Table 2. The right panel demonstrates an increase of f(6R⋆,π/ 2) for vrot/vrot,max → 1 and different v∞ (labelled on the right side). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.