| Issue |
A&A
Volume 573, January 2015
|
|
|---|---|---|
| Article Number | A62 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201424735 | |
| Published online | 18 December 2014 | |
67P/Churyumov-Gerasimenko: Activity between March and June 2014 as observed from Rosetta/OSIRIS
1
Max-Planck-Institut für Sonnensystemforschung,
Justus-von-Liebig-Weg 3,
37077
Göttingen,
Germany
e-mail:
tubiana@mps.mpg.de
2
Planetary and Space Sciences, Department of Physical Sciences, The
Open University, Walton
Hall, Milton
Keynes, MK7 6AA,
UK
3
Center of Studies and Activities for Space (CISAS) “G. Colombo”,
University of Padova, via Venezia
15, 35131
Padova,
Italy
4
Institute of Planetary Research, DLR, Rutherfordstrasse 2, 12489
Berlin,
Germany
5
Instituto de Astrofísica de Andalucía – CSIC,
18080
Granada,
Spain
6
LESIA, Obs. de Paris, CNRS, Univ Paris 06, Univ. Paris-Diderot, 5 Place J.
Janssen, 92195
Meudon,
France
7
Physikalisches Institut, Sidlerstrasse 5, University of
Bern, 3012
Bern,
Switzerland
8
INAF – Osservatorio Astronomico di Trieste, via Tiepolo
11, 34143
Trieste,
Italy
9
Department for Astronomy, University of Maryland,
College Park, MD
20742-2421,
USA
10
Department of Physics and Astronomy “G. Galilei”, University of
Padova, Vic. Osservatorio
3, 35122
Padova,
Italy
11
Centre for Astrophysics and Planetary Science, School of Physical
Sciences, The University of Kent, Canterbury, CT2
7NH, UK
12
Centro de Astrobiología, CSIC-INTA, 28850 Torrejón de
Ardoz, Madrid,
Spain
13
International Space Science Institute,
Hallerstrasse 6, 3012
Bern,
Switzerland
14
University of Padova, Department of Physics and
Astronomy, vicolo dell’Osservatorio
3, 35122
Padova,
Italy
15
LATMOS, CNRS/UVSQ/IPSL, 11 Boulevard d’Alembert, 78280
Guyancourt,
France
16
INAF–Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio
5, 35122
Padova,
Italy
17
CNR–IFN UOS Padova LUXOR, via Trasea 7,
35131
Padova,
Italy
18
Department of Physics and Astronomy, Uppsala
University, 75120
Uppsala,
Sweden
19
UNITN, Universitá di Trento, via Mesiano 77, 38100
Trento,
Italy
20
Department of Mechanical Engineering – University of
Padova, via Venezia
1, 35131
Padova,
Italy
21
Aix Marseille Université, CNRS, LAM (Laboratoire d’Astro-physique
de Marseille) UMR 7326, 13388
Marseille,
France
22
Institute for Space Science, National Central
University, 32054
Chung-Li,
Taiwan
23
Institute for Geophysics and Extraterrestrial
Physics, TU
Braunschweig, 38106
Braunschweig,
Germany
24
Research and Scientific Support Department,
European Space Agency, 2201
Noordwijk, The
Netherlands
25
ESA/ESAC, PO Box 78, 28691
Villanueva de la Cañada,
Spain
26
Dept. Physics, University of Padova, 35122
Padova,
Italy
27
Institut für Datentechnik und Kommunikationsnetze,
38106
Braunschweig,
Germany
28
Department of Information Engineering – University of
Padova, via Gradenigo
6, 35131
Padova,
Italy
29
PAS Space Reserch Center, Bartycka 18A,
00716
Warszawa,
Poland
30
Instituto Nacional de Técnica Aeroespacial,
28850
Torrejon de Ardoz,
Spain
Received: 1 August 2014
Accepted: 27 October 2014
Aims. 67P/Churyumov-Gerasimenko is the target comet of the ESA’s Rosetta mission. After commissioning at the end of March 2014, the Optical, Spectroscopic, and Infrared Remote Imaging System (OSIRIS) onboard Rosetta, started imaging the comet and its dust environment to investigate how they change and evolve while approaching the Sun.
Methods. We focused our work on Narrow Angle Camera (NAC) orange images and Wide Angle Camera (WAC) red and visible-610 images acquired between 2014 March 23 and June 24 when the nucleus of 67P was unresolved and moving from approximately 4.3 AU to 3.8 AU inbound. During this period the 67P – Rosetta distance decreased from 5 million to 120 thousand km.
Results. Through aperture photometry, we investigated how the comet brightness varies with heliocentric distance. 67P was likely already weakly active at the end of March 2014, with excess flux above that expected for the nucleus. The comet’s brightness was mostly constant during the three months of approach observations, apart from one outburst that occurred around April 30 and a second increase in flux after June 20. Coma was resolved in the profiles from mid-April. Analysis of the coma morphology suggests that most of the activity comes from a source towards the celestial north pole of the comet, but the outburst that occurred on April 30 released material in a different direction.
Key words: comets: general / comets: individual: 67P/Churyumov-Gerasimenko
© ESO, 2014
Observational circumstances.
1. Introduction
67P/Churyumov-Gerasimenko (67P) is the target comet of the ESA’s Rosetta mission. Launched in 2004, the Rosetta spacecraft woke up on 2014 January 20 after 30 months of deep space hibernation, and will follow 67P along its orbit, investigating how the comet changes and evolves while approaching the Sun.
The Optical, Spectroscopic, and Infrared Remote Imaging System (OSIRIS, Keller et al. 2007), is the scientific camera system onboard Rosetta. It comprises a Narrow Angle Camera (NAC) with a wavelength range 250−1000 nm and a Wide Angle Camera (WAC) with wavelength range 240−720 nm. The field of view (FOV) of NAC and WAC is 2.20°× 2.22° and 11.35°× 12.11°, respectively. Both camera use a 2048 × 2048 pixel CCD. After commissioning at the end of March 2014, OSIRIS began imaging 67P and its dust and gas environment. Ground-based observations performed in 2007/08 when the comet was in the same orbital arc as it was in March−April 2014, show that 67P was already active at 4.3 AU inbound and that its behaviour was repetitive during the last three apparitions (Snodgrass et al. 2013).
The aim of this work is to study the comet’s dust environment and its evolution with time, from the unique viewpoint of the approaching spacecraft: close enough to obtain regular high signal-to-noise images, but still at large enough distance to see the whole coma. We focused on the images of 67P acquired by OSIRIS between March and June 2014 when the comet nucleus was unresolved at heliocentric distances of approximately 4.3 AU to 3.8 AU inbound, and the comet–spacecraft distance decreased from 5 × 106 km to 120 × 103 km.
Images of 67P were acquired with the OSIRIS camera between 2014 March 23 and June 24 with the NAC orange (λc = 649.2 nm, FWHM = 84.5 nm), WAC red (λc = 629.8 nm, FWHM = 156.8 nm), and WAC visible-610 (λc = 612.6 nm, FWHM = 9.8 nm) filters.
The exposure times varied between 10 s and 12 min, decreasing as the distance to the comet narrowed. The acquisition sequences interleaved short, full-frame time series acquired for the purpose of optical navigation, with long series (lasting typically 13 h) of windowed images, exposed for the purpose of light curve studies. The dataset comprises a total of 282 images. The raw frames were pre-processed with the standard OSIRIS calibration pipeline: the images were bias subtracted, flat-fielded, normalised to 1 s exposure, radiometrically calibrated – using standard stars (16Cyg and Vega) acquired during calibration campaigns – and distortion corrected.
The data set is the first ever detailed view of the dust environment of a Jupiter family comet as it becomes active at large heliocentric distance, with regular sampling and resolution to see small coma that is invisible from Earth. We describe how the coma brightness varies (Sect. 2), and discuss some preliminary conclusions on the properties of the dust in the coma (Sects. 3 and 4), including analysis of the morphology of the coma once it was resolved (Sect. 5).
2. Surface brightness
To investigate how the comet’s brightness varies with heliocentric distance, we used images acquired with NAC orange filter from March 23 to June 20 and WAC red filter from June 20 to June 24. The photometric reduction was performed with AstPhot, a synthetic aperture photometry tool (Mottola et al. 1995).
The observational details are summarised in Table 1.
We measured the brightness of the comet in each frame using aperture photometry. The size of the photometric aperture was varied as a function of the target distance, thereby achieving a constant projected circle at the comet with the radius of 270 km. This aperture size was chosen in order to integrate at least 99.5% of the point spread function when the object was at its largest range. Consequently, the radius of the integration aperture changed between 4 to 97 pixels for the NAC images and between 19 to 24 pixels for the WAC frames. Faint field stars present in the integration aperture were removed by a procedure in which the stars were manually identified, and the corresponding pixels were substituted with the median value of the surrounding region. No attempt was made to remove stars in the immediate vicinity of the nucleus, or with brightness comparable to that of the comet or higher, as the added photon noise and the removal artefacts would have unnecessarily degraded the photometric accuracy. Given the wealth of excellent data returned by OSIRIS, such frames were simply discarded. The typical signal-to-noise ratio (S/N) for the integrated photometry of 67P ranged between 100 and 400 in each frame.
Standard stars acquired during calibration campaigns were used to transform the instrumental magnitudes into the Kron-Cousins R band. The typical photometric uncertainty of the measurements is 0.01 mag, while the systematic uncertainty of the absolute calibration is estimated to be of the order of 0.03 mag (1σ). In order to compare the brightness of observations obtained at different heliocentric and topocentric distances, we further reduced the observed magnitudes to the standard geometry of 1 AU from the Sun and from the observer. We did not apply a phase function correction as the phase angle remains approximately constant at 32°–35° throughout the approach phase.
Mottola et al. (2014) performed a full analysis of the rotational state of 67P between March and June 2014, using the same data that we used for our study. Since the observing geometry varied very little during the three months of observations covered in this study, both the synodic period of the light curve and its amplitude stayed constant (Mottola et al. 2014). Therefore we could combine all photometric series into a single composite light curve by using the Fourier fitting technique described by Harris et al. (1989). The resulting zeroth order Fourier coefficient for each individual data set represents its average magnitude. Figure 1 displays the mid- light curve magnitude as function of time, which therefore shows the evolution of the brightness of the comet without the modulation due to rotation. Unfortunately, the last three data points in the plot (marked as asterisks) have a saturated central pixel and therefore they represent a lower bound to the flux. The typical RMS error of these data points is in the range of a few millimag. The total error budget is therefore dominated by the absolute calibration error, which is reported in the graph as error bar.
Figure 1 clearly shows an outburst occurring between April 27 and April 30. The increase of intensity occurring after June 20 can be either a second less intense outburst (with an uncertain amplitude due to saturation) or the start of more continuing activity. We estimated the dust production rate during the outburst by considering that the observation of April 30 shows an increase of 65% in the observed flux, with respect to the pre-outburst observations. Given that the exact time of the onset of the activity was probably not observed, this increase represents a lower bound. By assuming that the dust has similar optical properties to the comet nucleus in terms of albedo and phase function and that the coma contribution was negligible in the pre-outburst observations, we can estimate the dust optical cross section within the 270 km aperture. Adopting a nucleus effective radius of 2.04 km (Kelley et al. 2009), that gives a nucleus average cross section of 13.1 km2, we determine a dust optical cross section of 8.5 km2 and a corresponding filling factor of 2.95 × 10-5 which, assuming an albedo of 0.054 (Kelley et al. 2009) results in Afρ = 43 cm. Care should be taken in comparing this value to other Afρ measurements, as the assumption of similar optical properties between the dust and nucleus is likely to be incorrect at these large phase angles, and of course Afρ is derived for a steady state coma, which was clearly not the case in these observations.
 |
Fig. 1 Magnitude versus time and heliocentric distance, measured in an aperture of 270 km at the comet. T0 = 56 739.0 MJD = 2014 March 23.0. |
To investigate whether 67P was already active or not when OSIRIS started observing it, we compared the surface brightness profile of 67P with the one of a background star, following the method described in Tubiana et al. (2008).
 |
Fig. 2 Surface brightness profiles of 67P for March 23 and April 14. The brightness corresponds to the measured brightness, no correction for heliocentric and Rosetta-comet distance is applied. The open circles are the comet profile and the solid line is the star profile. The increase of brightness at ρ > 40′′ in the March 23 profile and at ρ > 50′′ in the April 14 profile is caused by background stars. The error bars associated to each datapoint are smaller than the symbol used, thus they are not visible in the plot. |
Figure 2 shows the radial profiles of 67P for March 23 and April 14. In March, the comet’s profile looks star-like, suggesting that no detectable activity is present around the nucleus. From April 14 on, the 67P’s profile broadens indicating that a coma has developed. However, the aperture photometry (see Fig. 1) shows that the magnitude of the comet is constant between March and April 2014 and again after the outburst, when clear activity was visible in the images of the comet. This suggests that 67P was already active on March 23, when the first images from OSIRIS were acquired and that the comet’s profile looks stellar because, due to the comet-Rosetta distance, the coma was unresolved and did not appear in the radial profile. To investigate this further, using an albedo A = 0.054 ± 0.006, effective radius for the nucleus of 67P Reff = 2.04 ± 0.11 km (Kelley et al. 2009) and a linear phase function coefficient β = 0.059 ± 0.006 mag/° (Lowry et al. 2012), we calculated that the expected brightness for the bare nucleus on March 23 is R(1,1,α) = 17.28 ± 0.03 mag. This value is significantly larger (i.e. the nucleus is fainter) than the magnitude measured in the OSIRIS images in the same date and we conclude that the difference is to be attributed to unresolved coma in the OSIRIS images.
In conclusion, our analysis suggests that 67P was already active on March 23 at 4.3 AU, as expected based on ground based observations of the comet, as Snodgrass et al. (2013) showed was true at this heliocentric distance at previous apparitions.
3. Dust environment
We analysed the overall dust coma behaviour through the azimuthally averaged profiles of the continuum intensity around the comet’s optocenter in NAC orange and WAC visible-610 (only for June 14 and June 24) images. Examples of the profiles sampling the time interval spanned by our observations are plotted in Fig. 3. All profiles have been measured up to 100 pix from the optocenter, that corresponds to a different projected distance ρ in each profile since the Rosetta-67P distance changed during the observations. An uncertainty of 3% in flux for each measurement has been used. The corresponding error bar is not appreciable in the plot due to the logarithmic scale used.
 |
Fig. 3 Coma brightness B(ρ) vs. ρ in log-log scale for March 23, April 17, April 24, April 30, May 7, May 18, June 14, and June 24. The 3% uncertainty in flux associated with each single measurement is not appreciable in the plot due to the logarithmic scale used. |
The measure of the coma brightness, B(ρ), plotted against ρ in a log-log representation can be described by a straight line with slope m = −1 in case of an idealised steady-state coma (Eddington 1910; Wallace et al. 1958). Steeper profiles up to m = −1.5 are still indicating a steady-state in case of a coma profile distorted by solar radiation pressure if measured at distances larger than the extent of the coma in the Sun direction (Jewitt & Meech 1987).
We discarded the first pixel around the optocenter to remove from the analysis the artificial flattening of the profiles caused by the nucleus point spread function (PSF) close to the nucleus itself. We found that 67P has a stellar profile, characterised by a steep profile (with m ~ −5), from the first data in March until mid-April. Although this usually indicates that no coma is present around the nucleus, we believe that the appearance is due to unresolved coma that did not show up in the profile, as discussed in Sect. 2.
Starting from mid April, a small coma is visible, although often contaminated by the intense stellar background, and the overall profiles get shallower when measured within the first ~300 km from the nucleus position. On April 30 the spatial profile is even shallower (m ~ −2), as a clear consequence of the outburst. In May the spatial profiles assume a bimodal trend, with a steep stellar-like profiles up to ~100 km from the nucleus and a shallower profiles with m ~ −1 for larger nucleocentric distances up to ~400 km. One possible interpretation is that the comet’s coma is in a stationary state from 100 km to 400 km from the nucleus. However, what we observe could as well be the outburst expanding cloud, with decreasing surface brightness because it is expanding, plus some activity (weaker than the outburst) occurring afterwards. The bimodal distribution is still present in the profiles measured in June. For distances larger than 60−100 km from the nucleus (depending on the date), the profiles are characterised by m close to − 2, thus steeper than the ones in May.
Morphology in the coma can also introduce slope differences. Activity from rotating jets, even if the jets are unresolved, can produce unusual and changing slopes in the coma. This could be a possible explanation for the different slope measured in the June profile.
We estimated that the root mean-square error on the slope measurements to be on average <7%. These uncertainties, larger than the usual 1% associated to this kind of measurements in other comets (Lara et al. 2006; Bertini et al. 2009, 2012) are essentially due to the small size of the comet projected on the sky plane and the consequent rather small number of pixels involved in our measurements.
4. Outburst
We used NAC orange images acquired on April 24, April 27, April 30, May 5, May 7, and May 11 to study the comet outburst that occurred on April 30. Background stars close to the comet were removed by interpolation from the surrounding area. The projected distance (R) from the center of brightness was computed; multiplying the image brightness by R, we obtained a distance corrected intensity map (Fig. 4).
 |
Fig. 4 Intensity maps for April 24 a); April 27 b); April 30 c); May 5 d); May 7 e); and May 11 f). Each image corresponds to an area of 1600 × 1600 km and the comet is place in the centre. The orientation of the images is shown in the first panel. |
The outburst appears as a broad (in angular extension) intensity maximum on April 30 (Fig. 4c). Close to the nucleus the direction of the maximum intensity is 338° (measured counterclockwise from north over east), while at larger distance it becomes 15°, as it can be seen from the azimuthal average shown in Fig. 5. In the following days the feature gets weaker in intensity and also narrower in angular extent (FWHM ~ 60−70°). The maximum intensity direction is 338°.
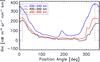 |
Fig. 5 Azimuthal average for R = 200−240 km (blue line), R = 400−500 km (red line), and R = 200−600 km (black line), obtained for April 30. |
The change in direction of maximum intensity on April 30 could be explained in two ways:
-
1.
The nucleus has one active region that is the main source ofactivity; the outburst produces a burst of particles from a secondactive region that gives rise to the emission maximum at15°.
-
2.
Only one active region is present on the nucleus; the outburst produces a time limited emission of particles in a direction different from the one of the main activity. This produces the observed change in the position angle of maximum intensity.
The data do not allow us to identify where the outburst come from, thus the aforementioned explanations are equally probable.
To quantify the dust activity between April 20 to May 18 we measured ΣAf as a function of the cometocentric distance ρ. ΣAf (Tozzi & Licandro 2002) is defined as the total Af measured in an area enclosed by two concentric circles of radius ρ and ρ + dρ: 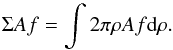 (1)For a comet with a production of dust described by a simple radial outflow model (i.e., a comet with constant dust production rate, without destruction, fragmentation, or acceleration of dust grains) ΣAf is constant since the Af profile is proportional to ρ-1. The profiles are affected in the inner coma by the PSF, which makes the quantities approach zero close to the photometric nucleus, and in the outer coma by an incorrect background subtraction that can make the two functions linearly dependent on ρ. We measured ΣAf vs. ρ profiles in NAC orange images acquired on April 20, April 24, April 27, April 30, May 4, May, May 11 and May 18. The profiles are displayed in Fig. 6.
(1)For a comet with a production of dust described by a simple radial outflow model (i.e., a comet with constant dust production rate, without destruction, fragmentation, or acceleration of dust grains) ΣAf is constant since the Af profile is proportional to ρ-1. The profiles are affected in the inner coma by the PSF, which makes the quantities approach zero close to the photometric nucleus, and in the outer coma by an incorrect background subtraction that can make the two functions linearly dependent on ρ. We measured ΣAf vs. ρ profiles in NAC orange images acquired on April 20, April 24, April 27, April 30, May 4, May, May 11 and May 18. The profiles are displayed in Fig. 6.
 |
Fig. 6 ΣAf vs. ρ for NAC orange images of 67P/Churyumov-Gerasimenko obtained on April 20: black line (55 km/pix), April 24: red line (51.2 km/pix), April 27: green line (47.2 km/pix), April 30: blue line (43.8 km/pix), May 4: yellow line (38.9 km/pix), May 11: magenta line (30 km/pix), and May 18: cyan line (21.7 km/pix). For each observation, the pixel scale (in km per pixel at the comet distance) is indicated. The x-axis is in km and for each date, the spacecraft-comet distance is taken into account to convert pixel to km, whereas the y-axis is in arbitrary units. |
ΣAf shows a steady coma from April 20 to 27. The size of the coma is 3 times the NAC pixel value, thus a contamination by the nucleus PSF to the coma is probable. In the case of a steady coma, its size depends on the size distribution of the ice/dust grains and on their ejection velocity. Since the effects of solar radiation pressure on the length scale of NAC images is negligible, it is impossible to fix both the distribution and the velocity.
On April 30, 67P underwent a clear outburst, with the coma brightness increasing at all nucleus distances. The following days, the coma showed a constant decay, first in the central part and later in the outer one, as it is expected in case of the expansion of a ice/dust shell ejected in a single burst occurred between April 27 and 30. This provides an upper limit of the shell age at the first observation on April 30 of 3 days. On April 30, the observed size of the shell reaches at most 800 km, a value given by the image noise level, where the coma signal becomes flat due to dominant image noise. The outburst can have occurred any time, with uniform probability, during the time interval Δt between the outburst observation time T and the previous observation. If the outburst occurred at T − Δt, the dust speed would be V< 800 km/3 days = 3 m/s; if it occurred at T − 0.1 × Δt, the speed would be V< 30 m/s; if it occurred at T − 0.01 × Δt, the speed would be V< 300 m/s. Only very small (μm sized) and slow moving (just above the nucleus escape velocity, of order 1 m/s) dust will see the effects of radiation pressure within the OSIRIS field of view. Although the dust speeds and size distribution are not known, calculations based on the expected gas flux at 4.1 AU indicate that μm sized grains are likely to be accelerated to considerably higher speeds (at least 10 s of m/s), so it is probable that we do not see the effects of radiation pressure within the OSIRIS images.
We can also estimate the total ejected dust mass during the outburst by analysing the intensity of scattered light in the coma some time after the outburst has stopped. In Fig. 7, an image of the coma on May 14 at 12:37:41 in NAC orange is shown. A background star image acquired some days earlier has been subtracted. The area of the image used for the calculation is shown by the white line. The faint coma outside the displayed region has been ignored. The region around the nucleus and strong stellar residuals were eliminated for the integration. Hence we are obtaining a lower limit to the integrated radiance. In combination with errors expected from the absolute calibration, we estimate the total error made in the computation of the integrated radiance to be around 25%.
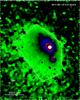 |
Fig. 7 Comet 67P/Churyumov-Gerasimenko observed with the OSIRIS NAC orange on May 14 at 12:37:41. A background star image has been subtracted. The directions to the Sun and celestial north are marked. The white polygon indicates the image area used to compute the total mass lost. |
Under the assumption of zero optical depth, the observed radiance can be summed and compared to the expected radiance of a column of dust with a specified size distribution and of unit mass. We adopt the differential size distribution: 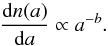 (2)The scattering has been calculated using Mie theory (e.g. Bohren & Huffman 1983) for different values of b, at the wavelength of OSIRIS NAC orange filter, and at a scattering angle of 145°. The resulting diagram (Fig. 8) shows the total mass required to produce the observed integrated radiance. Particles of size, a, in the range 1 nm to 1 mm have been considered. If larger particles were to be included in the calculation, the roll-over seen at low values of b would not occur. There is a minimum mass at around b = 4. As b decreases, the mass is increasingly in the larger particles with smaller cross-sectional areas per unit mass and hence the mass required to produce the observed radiance rises. On the other hand, as shown mostly recently by Fink & Rubin (2012), particles with a< 0.1μm are extremely inefficient scatters. Hence, as b increases the mass concentrates more in the highly inefficient scatters so that again more mass is required to produce the observed radiance. The consequence of these competing processes is the clear minimum mass seen in Fig. 8.
(2)The scattering has been calculated using Mie theory (e.g. Bohren & Huffman 1983) for different values of b, at the wavelength of OSIRIS NAC orange filter, and at a scattering angle of 145°. The resulting diagram (Fig. 8) shows the total mass required to produce the observed integrated radiance. Particles of size, a, in the range 1 nm to 1 mm have been considered. If larger particles were to be included in the calculation, the roll-over seen at low values of b would not occur. There is a minimum mass at around b = 4. As b decreases, the mass is increasingly in the larger particles with smaller cross-sectional areas per unit mass and hence the mass required to produce the observed radiance rises. On the other hand, as shown mostly recently by Fink & Rubin (2012), particles with a< 0.1μm are extremely inefficient scatters. Hence, as b increases the mass concentrates more in the highly inefficient scatters so that again more mass is required to produce the observed radiance. The consequence of these competing processes is the clear minimum mass seen in Fig. 8.
A similar calculation was done for data from May 5. In this dataset 67P already shows a significant coma. To determine the total columnar mass, we used an image acquired on April 27 to determine the nucleus contribution to the image. A subtraction of the nucleus brightness was performed taking into account the changes in heliocentric distance, comet – Rosetta distance, and the rotational phase (which necessitated a 15% reduction in the flux from the nucleus for the May 5 observation Mottola et al. 2014) between the two images. Once the integrated brightness was computed, the total columnar mass was computed in an identical manner to that for the May 14 data set and the result for one beta value has been plotted on Fig. 8. The total columnar mass on May 14 is lower than that computed for May 5, indicating that the total mass of the dust coma decreased between May 5 and May 14 although it should be noted that the error on the May 14 calculation is such that the results for the two dates should be considered as similar within error.
Although the errors in the integrated radiance and the lack of knowledge of the refractive index of the particles (especially the complex part) contribute to the uncertainty, the largest uncertainty in the ejected mass determination comes from the unknown particle size distribution. Figure 8 show that particle mass in the coma barely changed over a period of 9 days indicating that slow-moving large particles dominated the mass loss. This is consistent with the model by Fulle et al. (2010) according to which before perihelion the dominant optical scattering is coming from large grains, of a typical mass of 1 mg (thus mm – cm size particles), i.e. the typical components of cometary trails.
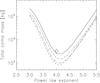 |
Fig. 8 Mie calculations of the mass required to produce the observed radiance in the data from May 14. The lines correspond to different refractive indices for the dust particles. Solid line: n = 1.55 + 0.1i, dashed: n = 1.8 + 0.01i, dot-dash: n = 1.8 + 0.4i, dot-dot-dash: n = 2.0 + 0.1i. The size distribution cut-offs at 1 mm. If larger particles were to be included in the calculation, the roll-over seen at low values of b would not occur. The diamond indicates a similar calculation for data from May 5. Here, the radiance from the nucleus (obtained prior to the outburst) was subtracted from the data to leave the residual from the outburst itself. The radiance was converted to a mass at b = 4. If the calculation were extended over all size distributions, the curve shape would be identical to those shown. |
5. Coma structures
NAC orange images acquired between March 23 and June 4 and WAC visible-610 images acquired between May 25 and June 24 were analysed with image enhancing techniques to reveal possible anisotropic structures around the comet’s optocenter. We used the rotational gradient Larson-Sekanina (Larson & Sekanina 1984) and derivative adaptive Laplace (Boehnhardt & Birkle 1994, and references therein) filtering. After extensive tests in order to obtain the best enhancement of the structures, we chose a Laplace filter width of 15 pix. The best enhancement parameter for the Larson-Sekanina was found to be a rotation of 40° around the optocenter. We also checked for isophote anisotropies in order to have an independent verification of the real existence of the features.
Geometry of coma structures found with Larson-Sekanina image-enhancing technique.
Image enhancement revealed the presence of one structure close to the celestial north direction. Images of the enhanced structure in various dates are shown in Fig. 9.
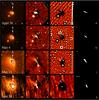 |
Fig. 9 Coma structures found in NAC orange (April 30, May 4, and May 14) and WAC visible-610 (June 24) data with image-enhancing techniques. First, second, and third column shows an isophotal representation of the corresponding original image, Larson-Sekanina, and adaptive Laplace filtering results, respectively. The last column shows dynamical simulations of the coma structures for the same observing dates. Each white pixel indicates the presence of dust particles, without photometric information. Arrows pointing S give the direction of the Sun in the frames. The north-east orientation is given in images in the second column. The horizontal bar in the upper left corners corresponds to a scale length of 400 km for NAC images and 150 km for WAC images. The size of each image is 180 × 180 pix for NAC and 80 × 80 pix for WAC. |
The structure (marked with A in Fig. 9) is clearly visible in NAC orange images between April 14 and May 18. In the images acquired before mid-April the coma is still unresolved and after mid-May structures are not detected anymore because of the low exposure time used that affects significantly their S/N. The structure is not detected in WAC visible-610 images acquired between May 25 and June 9 and it is extremely faint in the ones acquired on June 13 and June 14 because of a combination of two factors: first, due to the large Rosetta-comet distance the coma was not well resolved and second, the S/N of the structure was reduced due to the short exposure times used. WAC visible-610 images acquired on June 24 clearly show the structure.
We measured the position angle and the width of the structure in the sky plane at the nucloecentric distance of 400 km in NAC orange images and of 150 km (where we could still obtain a good S/N of the structure) in WAC visible-610 images. The position angle is determined as the center position of the Gaussian fit to the structure azimuth profile and the width corresponds to Full Width at Half Maximum of the fit itself. The measured values are summarised in Table 2. If we compare the position angle and the FWHM of the structure for April 30 as measured in Figs. 4 and 9 and reported in Fig. 5 and Table 2, respectively, we noticed that they are slightly different. This is because the two images have been treated with two difference image enhancing techniques (distance corrected intensity map vs. Larson-Sekanina filtering) and the method used to measure the position angle is also different: the PA in Fig. 5 is obtained as the maximum of intensity, while the PA in Table 2 is obtained as the center of the gaussian profile fitting the observed profile (that not always coincides with the intensity maximum). In addition, it should be noticed that for the determination of the direction of maximum intensity, it matters at what distance exactly one considers the azimuthal profile because of the change in coma shape due to the outburst.
The Larson-Sekanina filtering effectively enhanced the structure in all images acquired between April 14 and May 18, while the adaptive Laplace filtering reveals the structure only in a few days. We therefore decided to measure the structure position using only Larson-Sekanina enhanced images. The structure has an almost constant position angle in the sky-plane during April (Fig. 9a–c). After the outburst, that took place on April 30, the structure changed its position in the sky-plane of about 20° (Fig. 9e–g). After the first week of May, the position angle of the structure starts increasing, reaching in mid-May values close to the April ones (Fig. 9i–k).
A likely interpretation of these measurements points towards an active zone on the nucleus which produces the observed structure, which appears to be the brightness feature in the coma, probably indicating the main coma source. During the outburst that occurred at the end of April another source region of the nucleus may have been activated and the envelope of the dust produced by the two sources resulted in a net change of the structure position angle as seen from the spacecraft. Then the source connected with the outburst got exhausted and the activity was produced again mainly by the April source, leading the structure back to its pre-outburst position. Another possibility is that the outburst triggered a time-limited emission of dust particles from the main active area but in a different direction. Also in this case, the envelope of dust emitted in the different directions resulted in a net change of the position angle of the structure as seen by Rosetta.
 |
Fig. 10 Position in Equatorial J2000 coordinates of the unit vectors centred in the comet’s center of mass which projection in the image plane is within half degree from the measured structure direction. Filled circles represent the possible coordinates of the fan, while open circles refers to the anti-fan position. Previous determinations of the comet rotational axis are shown for comparison. |
5.1. 67P’s pole measure
The structure is projected towards the Sun direction on the sky plane throughout all our observations. Its position angle is measured to be almost constant from April to May, except for a 20° deviation after the end of April outburst. In that phase of the mission the viewing geometry from Rosetta is not changing as we approach the comet. Therefore, any variation in the orientation of coma structures is only related to physical processes on the nucleus, for instance a change of spatial distribution of the activity, or a change in the direction of emission as the nucleus rotates. Features with constant orientation are typically explained by being created by sources close to the rotation pole, sweeping the edges of a cone with the daily spinning of the nucleus. By tracking the shape of this cone in several images one can derive the orientation of the pole (Sekanina 1987); this approach has been successfully applied to several comets (i.e. 9P/Tempel 1 by Vincent et al. 2010 or 67P/C-G by Vincent et al. 2013).
In the current case, the analysis is complicated by the fact that the dust grains involved are possibly emitted with very low relative velocity, compared to the typical 10 s of m/s we observe close to perihelion. This makes the grains trajectory far from the nucleus more sensitive to the radiation pressure. With a phase angle of only ~30°, it effectively pushes the fan away from the observer. It is therefore difficult to conclude unambiguously whether the opening angle of the fan is an intrinsic property of the source, or an effect of the rotation. However, as discussed in Sect. 4, only very small and slow moving grains see radiation pressure effects within the near-nucleus region imaged by OSIRIS, so we assume that radiation pressure is negligible in this analysis.
We used a Monte Carlo code to determine the orientation of the structure axis in a comet centred reference frame starting from its observed projection in the sky-plane. Modelling done by Sekanina (1987) indicates that a long-lasting fixed projected position of a coma jet over a large period of time could be the axis of such a jet close to the rotation axis of the comet. We de-projected the position angle of the structure measured in the sky-plane to Equatorial J2000 in the comet’s body reference frame using appropriate spice kernels. We used 10 000 unit vectors having origin in the assumed center of mass of the comet and randomly oriented in the 3D space, and selected the ones that, projected in the image plane, stay within half degree from the measured direction of the structure. The (α, δ) position in the sky of the selected vectors, giving the possible direction of the structure axis, is shown in Fig. 10 for all observing dates (coloured circles). For comparison, we overplot the newly determined position of the structure axis to previous determinations of the comet rotational axis: areas where the the structure axis position overplap the rotational axis determinations exist (Fig. 10). This confirms the possibility that the structure axis is the tracer of the comet rotational axis.
We also used simulations performed with the COSSIM code (Vincent et al. 2010) to constrain better the activity (see Fig. 9). We found that the observed structure can be reproduced with the current spin solution (Lamy et al. 2007), and a source location within 30° of latitude away from the pole. This is compatible with previous determinations of active sources from ground based observations (source “C” in Vincent et al. 2013), and the spin analysis detailed above.
We also underline that some of the structure position solutions are in agreement, considering the possible distance from the rotational pole derived with COSSIM, with the pole solution clusters measured in Mottola et al. (2014) using OSIRIS light-curve data acquired between 2014 March and June.
6. Summary and conclusions
We presented photometry and images of the early activity of 67P, taken at large heliocentric distance but at close range, using the OSIRIS images taken while Rosetta approached the comet. We find that:
-
1.
The comet was likely already weakly active when Rosetta’sinstruments were recommissioned, with excess flux above thatexpected from the nucleus, in line with predictions fromground-based observations in the previous orbit (Snodgrasset al. 2013).
-
2.
This activity was mostly constant (in terms of brightness), but did not produce a resolvable coma in profiles until mid April.
-
3.
One outburst occurred during the 3 months of approach observations, increasing the flux by at least 65% for a short period.
-
4.
Morphological analysis suggests that most of the activity seems come from source towards the (celestial) north pole of the comet, although the large outburst released material in a different direction.
-
5.
No motion of the released dust due to radiation pressure is detectable on the small scale of the OSIRIS imaging, preventing the use of modelling dust motions to constrain grain sizes.
Acknowledgments
OSIRIS was built by a consortium led by the Max-Planck-Institut für Sonnensystemforschung, Katlenburg-Lindau, Germany, in collaboration with CISAS, University of Padova, Italy, the Laboratoire d’Astrophysique de Marseille, France, the Instituto de Astrofísica de Andalucia, CSIC, Granada, Spain, the Scientific Support Office of the European Space Agency, Noordwijk, The Netherlands, the Instituto Nacional de Técnica Aeroespacial, Madrid, Spain, the Universidad Politéchnica de Madrid, Spain, the Department of Physics and Astronomy of Uppsala University, Sweden, and the Institut für Datentechnik und Kommunikationsnetze der Technischen Universität Braunschweig, Germany. The support of the national funding agencies of Germany (DLR), France (CNES), Italy (ASI), Spain (MEC), Sweden (SNSB), and the ESA Technical Directorate is gratefully acknowledged. We thank the Rosetta Science Ground Segment at ESAC, the Rosetta Mission Operations Centre at ESOC and the Rosetta Project at ESTEC for their outstanding work enabling the science return of the Rosetta Mission.
References
- Bertini, I., Lara, L. M., Vincent, J.-B., et al. 2009, A&A, 496, 235 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertini, I., Barbieri, C., Ho, T.-M., et al. 2012, A&A, 541, A159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boehnhardt, H., & Birkle, K. 1994, A&AS, 107, 101 [NASA ADS] [Google Scholar]
- Bohren, C. F., & Huffman, D. R. 1983, Absorption and scattering of light by small particles (New York: John Wiley & Sons) [Google Scholar]
- Eddington, A. S. 1910, MNRAS, 70, 442 [NASA ADS] [Google Scholar]
- Fink, U., & Rubin, M. 2012, Icarus, 221, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Fulle, M., Colangeli, L., Agarwal, J., et al. 2010, A&A, 522, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, A. W., Young, J. W., Bowell, E., et al. 1989, Icarus, 77, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Jewitt, D. C., & Meech, K. J. 1987, ApJ, 317, 992 [NASA ADS] [CrossRef] [Google Scholar]
- Keller, H. U., Barbieri, C., Lamy, P., et al. 2007, Space Sci. Rev., 128, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Kelley, M. S., Wooden, D. H., Tubiana, C., et al. 2009, AJ, 137, 4633 [NASA ADS] [CrossRef] [Google Scholar]
- Lamy, P. L., Toth, I., Davidsson, B. J. R., et al. 2007, Space Sci. Rev., 128, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Lara, L. M., Boehnhardt, H., Gredel, R., et al. 2006, A&A, 445, 1151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larson, S. M., & Sekanina, Z. 1984, AJ, 89, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Lowry, S., Duddy, S. R., Rozitis, B., et al. 2012, A&A, 548, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mottola, S., De Angelis, G., Di Martino, M., et al. 1995, Icarus, 117, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Mottola, S., Lowry, S., Snodgrass, C., et al. 2014, A&A, 569, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sekanina, Z. 1987, in Diversity and Similarity of Comets, eds. E. J. Rolfe, & B. Battrick, ESA SP, 278, 315 [Google Scholar]
- Snodgrass, C., Tubiana, C., Bramich, D. M., et al. 2013, A&A, 557, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tozzi, G. P., & Licandro, J. 2002, Icarus, 157, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Tubiana, C., Barrera, L., Drahus, M., & Böhnhardt, H. 2008, A&A, 490, 377 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vincent, J.-B., Böhnhardt, H., & Lara, L. M. 2010, A&A, 512, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vincent, J.-B., Lara, L. M., Tozzi, G. P., Lin, Z.-Y., & Sierks, H. 2013, A&A, 549, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wallace, L. V., Miller, I., & Freeman, D. 1958, AJ, 63, 213 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Geometry of coma structures found with Larson-Sekanina image-enhancing technique.
All Figures
 |
Fig. 1 Magnitude versus time and heliocentric distance, measured in an aperture of 270 km at the comet. T0 = 56 739.0 MJD = 2014 March 23.0. |
| In the text | |
 |
Fig. 2 Surface brightness profiles of 67P for March 23 and April 14. The brightness corresponds to the measured brightness, no correction for heliocentric and Rosetta-comet distance is applied. The open circles are the comet profile and the solid line is the star profile. The increase of brightness at ρ > 40′′ in the March 23 profile and at ρ > 50′′ in the April 14 profile is caused by background stars. The error bars associated to each datapoint are smaller than the symbol used, thus they are not visible in the plot. |
| In the text | |
 |
Fig. 3 Coma brightness B(ρ) vs. ρ in log-log scale for March 23, April 17, April 24, April 30, May 7, May 18, June 14, and June 24. The 3% uncertainty in flux associated with each single measurement is not appreciable in the plot due to the logarithmic scale used. |
| In the text | |
 |
Fig. 4 Intensity maps for April 24 a); April 27 b); April 30 c); May 5 d); May 7 e); and May 11 f). Each image corresponds to an area of 1600 × 1600 km and the comet is place in the centre. The orientation of the images is shown in the first panel. |
| In the text | |
 |
Fig. 5 Azimuthal average for R = 200−240 km (blue line), R = 400−500 km (red line), and R = 200−600 km (black line), obtained for April 30. |
| In the text | |
 |
Fig. 6 ΣAf vs. ρ for NAC orange images of 67P/Churyumov-Gerasimenko obtained on April 20: black line (55 km/pix), April 24: red line (51.2 km/pix), April 27: green line (47.2 km/pix), April 30: blue line (43.8 km/pix), May 4: yellow line (38.9 km/pix), May 11: magenta line (30 km/pix), and May 18: cyan line (21.7 km/pix). For each observation, the pixel scale (in km per pixel at the comet distance) is indicated. The x-axis is in km and for each date, the spacecraft-comet distance is taken into account to convert pixel to km, whereas the y-axis is in arbitrary units. |
| In the text | |
 |
Fig. 7 Comet 67P/Churyumov-Gerasimenko observed with the OSIRIS NAC orange on May 14 at 12:37:41. A background star image has been subtracted. The directions to the Sun and celestial north are marked. The white polygon indicates the image area used to compute the total mass lost. |
| In the text | |
 |
Fig. 8 Mie calculations of the mass required to produce the observed radiance in the data from May 14. The lines correspond to different refractive indices for the dust particles. Solid line: n = 1.55 + 0.1i, dashed: n = 1.8 + 0.01i, dot-dash: n = 1.8 + 0.4i, dot-dot-dash: n = 2.0 + 0.1i. The size distribution cut-offs at 1 mm. If larger particles were to be included in the calculation, the roll-over seen at low values of b would not occur. The diamond indicates a similar calculation for data from May 5. Here, the radiance from the nucleus (obtained prior to the outburst) was subtracted from the data to leave the residual from the outburst itself. The radiance was converted to a mass at b = 4. If the calculation were extended over all size distributions, the curve shape would be identical to those shown. |
| In the text | |
 |
Fig. 9 Coma structures found in NAC orange (April 30, May 4, and May 14) and WAC visible-610 (June 24) data with image-enhancing techniques. First, second, and third column shows an isophotal representation of the corresponding original image, Larson-Sekanina, and adaptive Laplace filtering results, respectively. The last column shows dynamical simulations of the coma structures for the same observing dates. Each white pixel indicates the presence of dust particles, without photometric information. Arrows pointing S give the direction of the Sun in the frames. The north-east orientation is given in images in the second column. The horizontal bar in the upper left corners corresponds to a scale length of 400 km for NAC images and 150 km for WAC images. The size of each image is 180 × 180 pix for NAC and 80 × 80 pix for WAC. |
| In the text | |
 |
Fig. 10 Position in Equatorial J2000 coordinates of the unit vectors centred in the comet’s center of mass which projection in the image plane is within half degree from the measured structure direction. Filled circles represent the possible coordinates of the fan, while open circles refers to the anti-fan position. Previous determinations of the comet rotational axis are shown for comparison. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


