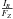| Issue |
A&A
Volume 573, January 2015
|
|
|---|---|---|
| Article Number | A91 | |
| Number of page(s) | 8 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201424675 | |
| Published online | 23 December 2014 | |
On the local dark matter density
1 Instituto de Astronomía, Universidad Católica del NorteAv. Angamos 0610 Antofagasta Chile
e-mail:
cmoni@ucn.cl
2 Departamento de Astronomía, Universidad de Concepción, Casilla 160- C Concepción, Chile
3 European Southern Observatory, 3107 Alonso de Cordova, Vitacura, Santiago, Chile
4 Dipartimento di Fisica e Astronomia, Universitá di Padova, Vicolo Osservatorio 3, 35122 Padova, Italy
5 Universidad de Chile, Departamento de Astronomía, Casilla 36- D Santiago, Chile
Received: 24 July 2014
Accepted: 17 September 2014
Context. In 2012, we applied a three-dimensional formulation to kinematic measurements of the Galactic thick disk and derived a surprisingly low dark matter density at the solar position. This result was challenged by Bovy & Tremaine (2012, ApJ, 756, 89), who claimed that the observational data are consistent with the expected local dark matter density if a one-dimensional approach is adopted.
Aims. We aim at clarifying whether their work definitively explains our result by analyzing the assumption at the base of their formulation and their claim that this returns a lower limit for the local dark matter density, which is accurate within 20%.
Methods. We find that the validity of their formulation depends on the underlying mass distribution. We therefore analyze the predictions that their hypothesis casts on the radial gradient of the azimuthal velocity ∂Rv̅ and compare it with observational data as a testbed for the validity of their formulation.
Results. We find that their hypothesis requires too steep a profile of ∂Rv̅(Z), which is inconsistent with the observational data both in the Milky Way and in external galaxies. As a consequence, their results are biased and largely overestimate the mass density. Dynamical simulations also show that, contrary to their claims, low values of ∂Rv̅ are compatible with a Milky Way-like potential with radially constant circular velocity. We nevertheless confirm that, according to their criticism, our assumption ∂Rv̅ = 0 is only an approximation. If this hypothesis is released, and the available information about ∂Rv̅ in the thick disk is used, the resulting local dark matter density increases by a tiny amount, from 0 ± 1 to 2 ± 3 mM⊙ pc-3, with an upper limit of ~3.5 mM⊙ pc-3. Hence, this approximation has negligible influence on our results.
Conclusions. Our analysis shows that their criticism is not a viable explanation for the inferred lack of dark matter at the solar position detected by us. More studies are required to understand these unexpected results.
Key words: Galaxy: kinematics and dynamics / Galaxy: structure / dark matter
© ESO, 2014
1. Introduction
Dark matter (DM) plays a key role in many fields of modern astrophysics, and it is recognized as a fundamental component of the Universe. Despite this general agreement, its density at the solar position (ρ⊙ ,DM) is still poorly constrained. Even recent measurements are compatible within 1σ with both a null local density (e.g., Creze et al. 1998; Holmberg & Flynn 2000) and with a value as high1 as 37 mM⊙ pc-3 (Garbari et al. 2012). The predictions of current models of spherical Galactic DM halo span the range ρ⊙ ,DM = 5–13 mM⊙ pc-3 (e.g., Olling & Merrifield 2001; Weber & de Boer 2010), but the density could be much lower in the case of a non-spherical or a more centrally concentrated distribution (Olling 1995; Einasto 1965, 1968), or higher by up to a factor of two in the presence of dark substructures, such as a dark matter disk or ring (Kalberla 2003; Read et al. 2008; Purcell et al. 2009).
Recently, Moni Bidin et al. (2012b, hereafter M12b) have proposed a new formulation to measure the dynamical mass of the Galactic disk up to large heights from the plane, by using the full three-dimensional kinematics and spatial distribution of a test stellar population. The hypotheses at the basis of their calculations are not innovative, and they were (often implicitly) assumed in most of the previous estimates. Applying this formulation to the kinematical measurements of Moni Bidin et al. (2012a, herafter M12a), Moni Bidin et al. (2010, 2012b) found a surprising lack of DM at the solar position (ρ⊙ ,DM = 0 ± 1 mM⊙ pc-3), at variance with most of the one-dimensional estimates even recently proposed (e.g., Zhang et al. 2013). A strong effort followed their work to understand the reliability of these unexpected results.
Sanders (2012) argues, by means of numerical simulations, that M12a underestimated the gradients of the velocity dispersions with Galactic height by up to a factor of three. His work impels further investigation to derive more reliable kinematical data, but it has negligible effects on the results of M12b. In fact, they obtained identical results by adopting alternative data sets, where the kinematical quantities were measured with different methods. Moreover, the mass derived with their three-dimensional formulation is largely insensitive to an isotropic change in the dispersions, because a steeper gradient of the vertical component (σW) induces an increase in the inferred mass that is compensated by the larger negative contribution of the radial and azimuthal ones (σU and σV, respectively).
If the vertical trend of σW is expressed by a linear relation 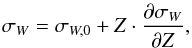 (1)and we isolate the terms containing
(1)and we isolate the terms containing 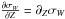 in Eq. (14) of M12b, their contribution to the surface density is
in Eq. (14) of M12b, their contribution to the surface density is 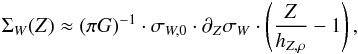 (2)where we neglected quadratic terms in ∂ZσW, whose contribution is smaller by one order of magnitude. With the parameter definition of M12b and the kinematical values of M12a, we obtain ΣW(4 kpc) ≈ 20 M⊙ pc-2. Thus, enhancing ∂ZσW by a factor of three, the DM density increases by
(2)where we neglected quadratic terms in ∂ZσW, whose contribution is smaller by one order of magnitude. With the parameter definition of M12b and the kinematical values of M12a, we obtain ΣW(4 kpc) ≈ 20 M⊙ pc-2. Thus, enhancing ∂ZσW by a factor of three, the DM density increases by 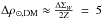 mM⊙ pc-2. However, repeating the same exercise for the other two components, we find (ΣU + ΣV) ≈ (−10−4) M⊙ pc-2 ≈ −0.7·ΣW. As a consequence, the increase of ρ⊙ ,DM in response to an isotropic increase in the dispersion gradients is damped by 70%, when σU and σV are taken into account. Even enhancing the vertical gradients by a factor of three, the derived local mass density increases by only 1.5 mM⊙ pc-3. A gradient of σW steeper than that of the other components is required to obtain a significantly higher DM density. Figure 6 of Sanders (2012) also shows that the large underestimate claimed by the author is introduced by the offset measurements at Z ≤ 2.5 kpc, while in the range Z = 2.5–4 kpc, the M12a method underestimates the dispersions by only ~5%, and their gradient by ~15%, both compatible with their quoted errors. This discontinuity at Z = 2.5 kpc is not observed in the real data of M12a (see their Fig. 6), where the gradients change by less than 0.5σ if the points at Z ≤ 2.5 kpc are excluded. This suggests that Sanders’ simulations did not reproduce the measurements at lower heights well and that they introduced a systematic offset not present in the measurements of M12a, whose gradient estimates should be accurate within 15%.
mM⊙ pc-2. However, repeating the same exercise for the other two components, we find (ΣU + ΣV) ≈ (−10−4) M⊙ pc-2 ≈ −0.7·ΣW. As a consequence, the increase of ρ⊙ ,DM in response to an isotropic increase in the dispersion gradients is damped by 70%, when σU and σV are taken into account. Even enhancing the vertical gradients by a factor of three, the derived local mass density increases by only 1.5 mM⊙ pc-3. A gradient of σW steeper than that of the other components is required to obtain a significantly higher DM density. Figure 6 of Sanders (2012) also shows that the large underestimate claimed by the author is introduced by the offset measurements at Z ≤ 2.5 kpc, while in the range Z = 2.5–4 kpc, the M12a method underestimates the dispersions by only ~5%, and their gradient by ~15%, both compatible with their quoted errors. This discontinuity at Z = 2.5 kpc is not observed in the real data of M12a (see their Fig. 6), where the gradients change by less than 0.5σ if the points at Z ≤ 2.5 kpc are excluded. This suggests that Sanders’ simulations did not reproduce the measurements at lower heights well and that they introduced a systematic offset not present in the measurements of M12a, whose gradient estimates should be accurate within 15%.
Bovy & Tremaine (2012, hereafter BT12) also argue that M12b results are flawed. They claimed that the same data of M12a are fully consistent with the standard value ρ⊙ ,DM = 10 mM⊙ pc-3, with a lower limit of ρ⊙ ,DM ≥ 5 mM⊙ pc-3, if a more classical one-dimensional approach is adopted. In this paper, we analyze the hypotheses underlying their formulation in more detail, to verify that their criticism explains the results of M12b and that this is the correct solution to the puzzle. Following M12b and BT12, we use the cylindrical Galactic coordinates (R,θ,Z), where R is the Galactocentric distance, θ is directed in the direction of Galactic rotation, and Z is positive toward the north Galactic pole. The respective velocity components are 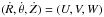 .
.
2. Bovy & Tremaine’s assumptions
Both M12b and BT12 estimate the mass surface density Σ(Z) within ±Z kpc of the Galactic plane by means of the integrated Poisson equation in cylindrical coordinates: 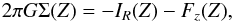 (3)with
(3)with 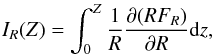 (4)where G is the gravitational constant, and FR and FZ are the radial and vertical components of the force per unit mass, respectively. If FR in Eq. (4) is expressed by means of the radial Jeans equation for a population in steady state,
(4)where G is the gravitational constant, and FR and FZ are the radial and vertical components of the force per unit mass, respectively. If FR in Eq. (4) is expressed by means of the radial Jeans equation for a population in steady state, 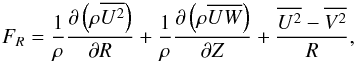 (5)the radial gradient of the mean azimuthal velocity
(5)the radial gradient of the mean azimuthal velocity 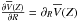 is introduced in the formulation, because
is introduced in the formulation, because ![\begin{eqnarray} \frac{\partial (R F_{R})}{\partial R}=\frac{\partial}{\partial R}\left[ \frac{R}{\rho}\frac{\partial \left(\rho\overline{U^2}\right)}{\partial R}+\frac{R}{\rho}\frac{\partial \left(\rho\overline{UW}\right)}{\partial Z}+ \overline{U^2}\right]-\frac{\partial \overline{V^2}}{\partial R}, \label{e_dRFR} \end{eqnarray}](/articles/aa/full_html/2015/01/aa24675-14/aa24675-14-eq44.png) (6)and
(6)and 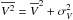 . This quantity is poorly known observationally, and M12b assumed
. This quantity is poorly known observationally, and M12b assumed 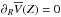 at any Z. They referred to
at any Z. They referred to 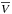 as the “rotational” velocity and to
as the “rotational” velocity and to 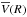 as the “rotation curve” henceforth. This terminology is not new in the literature (e.g., Yoachim & Dalcanton 2005), but very unfortunate, because the same terms are used more often for the circular velocity Vc. Nevertheless, their Eq. (11) unambiguously stated their hypothesis. BT12 exposed this source of confusion, and arguing against the M12b assumption, they removed the source of the problematic term, setting IR(Z) = 0 at any Z. This reduced the three-dimensional formulation of M12b to a one-dimensional approach, similar to the previous works (e.g., Kuijken & Gilmore 1989; Holmberg & Flynn 2000), but for the first time extended beyond 1.1 kpc from the Galactic plane. They also claim that IR(Z) < 0 and
as the “rotation curve” henceforth. This terminology is not new in the literature (e.g., Yoachim & Dalcanton 2005), but very unfortunate, because the same terms are used more often for the circular velocity Vc. Nevertheless, their Eq. (11) unambiguously stated their hypothesis. BT12 exposed this source of confusion, and arguing against the M12b assumption, they removed the source of the problematic term, setting IR(Z) = 0 at any Z. This reduced the three-dimensional formulation of M12b to a one-dimensional approach, similar to the previous works (e.g., Kuijken & Gilmore 1989; Holmberg & Flynn 2000), but for the first time extended beyond 1.1 kpc from the Galactic plane. They also claim that IR(Z) < 0 and 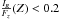 . The first inequality implies that their assumption IR(Z) = 0 returns a lower limit of ρ⊙ ,DM, because IR enters with negative sign in the calculation of the surface mass density. In addition, if
. The first inequality implies that their assumption IR(Z) = 0 returns a lower limit of ρ⊙ ,DM, because IR enters with negative sign in the calculation of the surface mass density. In addition, if 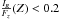 , the resulting estimate of Σ(Z) is accurate within 20% (see Eq. (3)). They claim that they only substitute the M12b assumption with the observationally-proven fact
, the resulting estimate of Σ(Z) is accurate within 20% (see Eq. (3)). They claim that they only substitute the M12b assumption with the observationally-proven fact 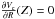 (e.g., Sofue et al. 2009), but all their calculations were actually based on the implicit assumption that
(e.g., Sofue et al. 2009), but all their calculations were actually based on the implicit assumption that 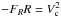 up to Z = 4 kpc. However, this equation is strictly valid only on the plane. Assuming hR = 3.8 kpc and hσ = 3.5 kpc for the radial scale length of the thick disk mass density and velocity dispersions, respectively, they derived ρ⊙ ,DM = 5.5 mM⊙ pc-3, with a slope of Σ(Z) compatible with ρ⊙ ,DM = 7 mM⊙ pc-3. They also argue that hR = 2 kpc should be preferred, and they obtained ρ⊙ ,DM = 8.5 ± 1.5 mM⊙ pc-3 in this case. In this section, we analyze in more detail the BT12 assumption IR(Z) = 0 that leads to these results.
up to Z = 4 kpc. However, this equation is strictly valid only on the plane. Assuming hR = 3.8 kpc and hσ = 3.5 kpc for the radial scale length of the thick disk mass density and velocity dispersions, respectively, they derived ρ⊙ ,DM = 5.5 mM⊙ pc-3, with a slope of Σ(Z) compatible with ρ⊙ ,DM = 7 mM⊙ pc-3. They also argue that hR = 2 kpc should be preferred, and they obtained ρ⊙ ,DM = 8.5 ± 1.5 mM⊙ pc-3 in this case. In this section, we analyze in more detail the BT12 assumption IR(Z) = 0 that leads to these results.
 |
Fig. 1 Trend of IR (solid line) and |
 |
Fig. 2 Trend of IR(Z) with Z at R = 8 kpc, for a Miyamoto-Nagai disk (gray curves) with b = 0.3 kpc and a = 2.5, 3.5, 4.5 kpc, and a NFW halo model with ρ⊙ ,DM = 8 mM⊙ pc-3 (black curve). |
2.1. The universality of the IR(Z) = 0 assumption
We first analyze the BT12 claim that IR(Z) < 0 and 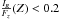 . The sign of IR(Z) and its weight in the calculation of Σ(Z) depend critically on the mass density distribution. BT12 prove the validity of their claims at R = 8 kpc for an exponential disk model with scale length hR = 3.4 kpc and for a spherical NFW (Navarro et al. 1997) dark halo. However, alternative mass distributions lead to completely different conclusions. For example, as shown in Fig. 1, IR(Z) is positive up to Z = 4 kpc for the Galactic disk model of Flynn et al. (1996) at R/hD> 2.4, where hD is the radial scale length of the disk mass density. This condition is most likely verified at the solar position, where R ≈ 8–8.5 kpc and hD = 2–3 kpc (Jurić et al. 2008; Bovy et al. 2012b). Figure 1 also shows the trend of
. The sign of IR(Z) and its weight in the calculation of Σ(Z) depend critically on the mass density distribution. BT12 prove the validity of their claims at R = 8 kpc for an exponential disk model with scale length hR = 3.4 kpc and for a spherical NFW (Navarro et al. 1997) dark halo. However, alternative mass distributions lead to completely different conclusions. For example, as shown in Fig. 1, IR(Z) is positive up to Z = 4 kpc for the Galactic disk model of Flynn et al. (1996) at R/hD> 2.4, where hD is the radial scale length of the disk mass density. This condition is most likely verified at the solar position, where R ≈ 8–8.5 kpc and hD = 2–3 kpc (Jurić et al. 2008; Bovy et al. 2012b). Figure 1 also shows the trend of 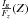 , which exceeds 0.2 if R/hD> 3, i.e. if hD ≲ 2.7 kpc.
, which exceeds 0.2 if R/hD> 3, i.e. if hD ≲ 2.7 kpc.
In Fig. 2 we show the trend of IR(Z) at R = 8 kpc for a family of Miyamoto-Nagai (MN) disk models 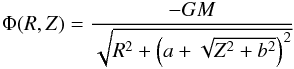 (7)(Miyamoto & Nagai 1975) with b = 0.3 kpc and total mass M = 6 × 1011M⊙. The figure shows that IR(Z) is positive up to Z = 3.5 kpc for the MN disk with a = 4 kpc used by Qu et al. (2011) and Bovy et al. (2012b) to model the Galactic disk. More in general, IR(Z) > 0 up to Z = 4 kpc for a MN disk with a< 4 kpc. The parameter a must be increased to a/R0> 0.63 if we want IR(Z) < 0 at R = R0 in the whole range Z = 0–4 kpc.
(7)(Miyamoto & Nagai 1975) with b = 0.3 kpc and total mass M = 6 × 1011M⊙. The figure shows that IR(Z) is positive up to Z = 3.5 kpc for the MN disk with a = 4 kpc used by Qu et al. (2011) and Bovy et al. (2012b) to model the Galactic disk. More in general, IR(Z) > 0 up to Z = 4 kpc for a MN disk with a< 4 kpc. The parameter a must be increased to a/R0> 0.63 if we want IR(Z) < 0 at R = R0 in the whole range Z = 0–4 kpc.
The sign of IR(Z) and its incidence in Eq. (3) depend on the relative weight of the individual mass components, due to the additive property of the potential. A spherical extended feature such as a DM halo gives a negative contribution, as shown for example in Fig. 2 for a NFW dark halo with ρ⊙ ,DM = 8 mM⊙ pc-3. If the Galactic disk is approximated by the aforementioned MN model with a = 4, the presence of such a dark halo is required to have IR(Z) < 0 up to Z = 4 kpc.
It must be considered that, when IR(Z) is positive and neglected, the total mass is overestimated, leading to a larger overestimate of ρ⊙ ,DM, because the spurious excess of visible mass is ascribed to a higher DM density. For example, if ρ⊙ ,DM = 5 mM⊙ pc-3, a mass overestimate of 20% at Z = 2.5 kpc would increase the derived ρ⊙ ,DM to 8.5 mM⊙ pc-3, thus overestimating the DM density by ~70%.
In conclusion, our counterexamples show that IR(Z) is not negative and negligible for any Galactic mass model. As a consequence, the BT12 formulation is not generally valid. It is a good approximation if the underlying mass distribution is close to the Galactic models implicitly assumed, but if it differs, the resulting estimate is not necessarily a lower limit to ρ⊙ ,DM, nor is it accurate within 20%. Such implicit assumptions should obviously be avoided in a formulation aimed at measuring the local mass density itself.
2.2. Tests of the validity of the IR(Z) = 0 assumption
Given the results of the previous section, we test the BT12 assumption here, to verify that their formulation is coincidentally reliable in the specific case under study. The hypothesis IR(Z) = 0 requires 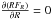 at any Z. When FR is expressed by means of Eq. (5), this translates to:
at any Z. When FR is expressed by means of Eq. (5), this translates to: 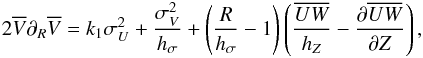 (8)with
(8)with 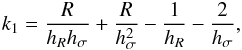 (9)where we assumed a mass density distribution described by a double exponential law (ρ ∝ exp(−R/hR− | Z | /hZ)) and an exponential radial decay of the velocity dispersions with scale length hσ. Both these assumptions were discussed, justified, and adopted by BT12 and M12b.
(9)where we assumed a mass density distribution described by a double exponential law (ρ ∝ exp(−R/hR− | Z | /hZ)) and an exponential radial decay of the velocity dispersions with scale length hσ. Both these assumptions were discussed, justified, and adopted by BT12 and M12b.
Equation (8) must be satisfied if the BT12 hypothesis is correct. BT12 claim a good match between the predictions on 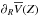 obtained from this equation and the observational results of Casetti-Dinescu et al. (2011, hereafter CD11). Here we study those predictions in more detail, re-analyze this comparison, and extend it to additional data sets. We assume hσ = 3.8 kpc (M12b; BT12) and a circular velocity at the solar position Vc = 215 ± 30 km s-1 (Salucci et al. 2010), which is indistinguishable from 220 km s-1 of BT12 for our purposes, but more compatible with the assumed solar Galactocentric distance R⊙ = 8 kpc (Kerr & Lynden-Bell 1986; Reid et al. 1999). Following the results of Sanders (2012) discussed in Sect. 1, we increase the velocity dispersions of M12a by 5%, and their vertical gradient by 15%, although this correction has negligible effects on the results.
obtained from this equation and the observational results of Casetti-Dinescu et al. (2011, hereafter CD11). Here we study those predictions in more detail, re-analyze this comparison, and extend it to additional data sets. We assume hσ = 3.8 kpc (M12b; BT12) and a circular velocity at the solar position Vc = 215 ± 30 km s-1 (Salucci et al. 2010), which is indistinguishable from 220 km s-1 of BT12 for our purposes, but more compatible with the assumed solar Galactocentric distance R⊙ = 8 kpc (Kerr & Lynden-Bell 1986; Reid et al. 1999). Following the results of Sanders (2012) discussed in Sect. 1, we increase the velocity dispersions of M12a by 5%, and their vertical gradient by 15%, although this correction has negligible effects on the results.
 |
Fig. 3 Vertical trend of |
In Fig. 3, we show the expectations for 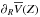 obtained by inserting in Eq. (8) the kinematical results of M12a (their Eqs. (3) to (5), with
obtained by inserting in Eq. (8) the kinematical results of M12a (their Eqs. (3) to (5), with 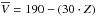 km s-1) and CD11 (their Table 1, with
km s-1) and CD11 (their Table 1, with 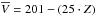 km s-1), with
km s-1), with 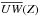 from M12b (compatible with both data sets, see M12b). The hypothesis IR(Z) = 0 requires high values of
from M12b (compatible with both data sets, see M12b). The hypothesis IR(Z) = 0 requires high values of 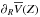 , and its steep increase with Z. Assuming hR = 3.8 kpc and hZ = 0.9 kpc, it grows from ≈10 km s-1 kpc-1 at Z = 1 kpc to ≈45 km s-1 kpc-1 at Z = 4 kpc. Assuming hR = 2 kpc, hσ = 3.5 kpc, and hZ = 0.7 kpc, as preferred by BT12,
, and its steep increase with Z. Assuming hR = 3.8 kpc and hZ = 0.9 kpc, it grows from ≈10 km s-1 kpc-1 at Z = 1 kpc to ≈45 km s-1 kpc-1 at Z = 4 kpc. Assuming hR = 2 kpc, hσ = 3.5 kpc, and hZ = 0.7 kpc, as preferred by BT12, 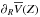 increases even more, up to ≈80 km s-1 kpc-1 at Z = 4 kpc. In other words, the BT12 assumption requires that the thick disk rotation increases rapidly with distance from the Galactic center and much more rapidly at larger Galactic heights. For any parameter set, the radial gradient of
increases even more, up to ≈80 km s-1 kpc-1 at Z = 4 kpc. In other words, the BT12 assumption requires that the thick disk rotation increases rapidly with distance from the Galactic center and much more rapidly at larger Galactic heights. For any parameter set, the radial gradient of 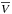 is six to eight times higher at Z = 4 kpc than on the Galactic plane. Thus, while the thick disk rotation decreases with distance from the plane by
is six to eight times higher at Z = 4 kpc than on the Galactic plane. Thus, while the thick disk rotation decreases with distance from the plane by 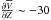 km s-1 kpc-1 at the solar position (e.g., Majewski 1992; Chiba & Beers 2000; Girard et al. 2006), this vertical shear would disappear within 3 kpc of the Sun (R< 11 kpc), where the stars at Z = 4 kpc would be corotating with those on the plane. This shear would be inverted farther out, with stars outside the plane rotating faster. This peculiar thick disk kinematics have never been observed in edge-on external galaxies, where
km s-1 kpc-1 at the solar position (e.g., Majewski 1992; Chiba & Beers 2000; Girard et al. 2006), this vertical shear would disappear within 3 kpc of the Sun (R< 11 kpc), where the stars at Z = 4 kpc would be corotating with those on the plane. This shear would be inverted farther out, with stars outside the plane rotating faster. This peculiar thick disk kinematics have never been observed in edge-on external galaxies, where 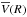 is rather flat outside the central regions at any height (Kregel et al. 2004), and the off-plane thick disk rotation is always slower than on the plane with no appreciable change in the radial gradient (Yoachim & Dalcanton 2005, 2008).
is rather flat outside the central regions at any height (Kregel et al. 2004), and the off-plane thick disk rotation is always slower than on the plane with no appreciable change in the radial gradient (Yoachim & Dalcanton 2005, 2008).
2.2.1. Comparison with Casetti-Dinescu et al. (2011)
The measurements of CD11 for the Galactic thick disk are shown in Fig. 3. They confirm that the assumption 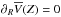 is only a rough approximation, because
is only a rough approximation, because 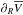 is in general not zero. However, the solution predicted by the hypothesis IR(Z) = 0, coupled with the BT12 preferred parameters, is clearly ruled out by the observations. Even when assuming the parameter set criticized by BT12, the inferred
is in general not zero. However, the solution predicted by the hypothesis IR(Z) = 0, coupled with the BT12 preferred parameters, is clearly ruled out by the observations. Even when assuming the parameter set criticized by BT12, the inferred 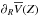 is systematically higher than all the measurements, barely matching the two larger error bars. Moreover, the measurements of CD11 are most likely only upper limits of
is systematically higher than all the measurements, barely matching the two larger error bars. Moreover, the measurements of CD11 are most likely only upper limits of 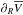 . In fact, the radial profile of
. In fact, the radial profile of 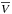 , similar to Vc, is steeper in the inner Galaxy and flattens at larger R (see, e.g., the theoretical radial profiles of Jałocha et al. 2010, or our Fig. 6), and a linear fit in the range R = 6–9 kpc can easily overestimate
, similar to Vc, is steeper in the inner Galaxy and flattens at larger R (see, e.g., the theoretical radial profiles of Jałocha et al. 2010, or our Fig. 6), and a linear fit in the range R = 6–9 kpc can easily overestimate 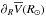 . More reliable estimates can be derived by considering only the stars within 1 kpc from the Sun (R = 7–9 kpc). We thus obtain
. More reliable estimates can be derived by considering only the stars within 1 kpc from the Sun (R = 7–9 kpc). We thus obtain 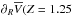 kpc)= 4.9 ± 1.4 km s-1 kpc-1 and
kpc)= 4.9 ± 1.4 km s-1 kpc-1 and 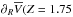 kpc)= 7 ± 4 km s-1 kpc-1, while the new fit at Z = 2.25 kpc is affected by uncertainties that are too large (close to 100%) for a reliable re-estimate. As shown in Fig. 3, the expectations of the BT12 hypothesis are even more discrepant when compared to these revised values. The comparison with the black curves is particularly relevant, because both the empirical points and the expectations are obtained from the same data set.
kpc)= 7 ± 4 km s-1 kpc-1, while the new fit at Z = 2.25 kpc is affected by uncertainties that are too large (close to 100%) for a reliable re-estimate. As shown in Fig. 3, the expectations of the BT12 hypothesis are even more discrepant when compared to these revised values. The comparison with the black curves is particularly relevant, because both the empirical points and the expectations are obtained from the same data set.
BT12 performed a similar comparison with CD11 data and claimed to prove the validity of their formulation. However, their adopted input quantities differ from the results of CD11 in many cases. For example, they assumed σU = 60 km s-1 in the nearest bin, but Table 1 of CD11 quotes 70.4 km s-1 (see also their Fig. 12). Similar problems can be found for σV and 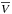 in the same bin, all in the direction of decreasing the expected
in the same bin, all in the direction of decreasing the expected 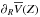 . Moreover, they fix Z at the lower end of the CD11 bins, thus decreasing the expectations further by 2–3 km s-1 kpc-1 in all the bins. They also never test their preferred set of parameters, which hugely offsets the expected
. Moreover, they fix Z at the lower end of the CD11 bins, thus decreasing the expectations further by 2–3 km s-1 kpc-1 in all the bins. They also never test their preferred set of parameters, which hugely offsets the expected 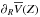 to higher values (Fig. 3).
to higher values (Fig. 3).
2.2.2. Comparison with SDSS data
 |
Fig. 4 Vertical trend of azimuthal velocity for our SDSS sample of thick disk stars. The linear fit to the data is indicated by the solid line. |
We collected from the Sloan Digital Sky Survey (SDSS, York et al. 2000) DR7 database2 the photometric and spectroscopic data of stars with r0< 20.2, 0.48 < (g−r)0< 0.55, S/N> 15, log g> 4.2, 0.25 ≤ [α/Fe] ≤ 0.3, −0.9 ≤ [Fe/H] ≤ −0.5, and error on metallicity and α-elements abundance lower than 0.25 dex. These criteria were adopted to select old, intermediate-metallicity G-type dwarf stars, as discussed in Carrell et al. (2012) and Bovy et al. (2012b). Their distance was estimated photometrically as in Ivezić et al. (2008). The Galactic coordinates, radial velocity, proper motion, and distance of each star were then transformed into (R,θ,Z) cylindrical coordinates and the respective (U,V,W) spatial velocities, and the errors on the former quantities were propagated to derive the final uncertainties. Only the 1096 stars with R = 7–9 kpc were considered in the analysis.
The azimuthal velocity of the resulting sample decreases with Z by −30 ± 2 km s-1 kpc-1, as shown in Fig. 4. This vertical shear is identical to what is found by M12a (see M12a for a comparison with previous studies). The rotational properties of the two samples are therefore very similar, indicating that they probe the same Galactic stellar population. The SDSS sample can therefore be used to study 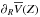 for the test population studied by M12b and BT12.
for the test population studied by M12b and BT12.
We fitted a linear relation to 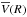 in Z bins of width 0.5 kpc in steps of ΔZ = 0.1 kpc. A 2σ clipping algorithm was adopted to remove outliers, which are mainly residual halo contaminators and bad measurements. The mean azimuthal velocity of these stars is constant with R in both cases. As a consequence,
in Z bins of width 0.5 kpc in steps of ΔZ = 0.1 kpc. A 2σ clipping algorithm was adopted to remove outliers, which are mainly residual halo contaminators and bad measurements. The mean azimuthal velocity of these stars is constant with R in both cases. As a consequence, 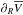 decreased at all heights if this clipping was not applied, while the results were stable if the cut was stronger. The results are plotted in Fig. 5, where they are compared to the expectations of the BT12 assumption. The quantity
decreased at all heights if this clipping was not applied, while the results were stable if the cut was stronger. The results are plotted in Fig. 5, where they are compared to the expectations of the BT12 assumption. The quantity 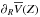 increases slowly from ~5 km s-1 kpc-1 at Z = 1 kpc to ~13 km s-1 kpc-1 at Z = 2.5–3 kpc. This trend matches the results of CD11 extremely well. The SDSS data thus confirm all the conclusions drawn in Sect. 2.2.1 and, in particular, confirm that the BT12 hypothesis largely overestimates
increases slowly from ~5 km s-1 kpc-1 at Z = 1 kpc to ~13 km s-1 kpc-1 at Z = 2.5–3 kpc. This trend matches the results of CD11 extremely well. The SDSS data thus confirm all the conclusions drawn in Sect. 2.2.1 and, in particular, confirm that the BT12 hypothesis largely overestimates 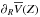 at any heights.
at any heights.
2.2.3. Comparison with simulations
BT12 claim that the M12b hypothesis 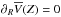 is inconsistent with a flat radial profile of Vc, while the steep increase in
is inconsistent with a flat radial profile of Vc, while the steep increase in 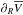 with Z discussed in Sect. 2.2 is its natural consequence. We tested this claim by means of orbit integration of a synthetic sample of stars. We adopted the Galactic potential model of Flynn et al. (1996), where the disk is represented by the sum of three MN disks and the dark halo by a spherical logarithmic potential. The contribution of the Galactic bulge and stellar halo are also included. The radial profile of Vc in this model Galaxy is flat outside the solar circle. The test particles were spatially distributed as a double exponential disk with hZ = 0.9 kpc and hR = 3.5 kpc. Their initial kinematics was fixed to match the trends of σU(Z), σV(Z), σW(Z), and
with Z discussed in Sect. 2.2 is its natural consequence. We tested this claim by means of orbit integration of a synthetic sample of stars. We adopted the Galactic potential model of Flynn et al. (1996), where the disk is represented by the sum of three MN disks and the dark halo by a spherical logarithmic potential. The contribution of the Galactic bulge and stellar halo are also included. The radial profile of Vc in this model Galaxy is flat outside the solar circle. The test particles were spatially distributed as a double exponential disk with hZ = 0.9 kpc and hR = 3.5 kpc. Their initial kinematics was fixed to match the trends of σU(Z), σV(Z), σW(Z), and 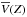 observed by M12a with the condition
observed by M12a with the condition 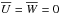 and an exponential radial decay of the dispersions with scale length hσ = 3.5 kpc. The system was then left to relax in the potential, and it rapidly achieved its steady state within the first Gyr of integration, although the experiment was stopped only after 5 Gyr. We then divided the sample in non-overlapping bins of 1000 stars with increasing Z, and we measured
and an exponential radial decay of the dispersions with scale length hσ = 3.5 kpc. The system was then left to relax in the potential, and it rapidly achieved its steady state within the first Gyr of integration, although the experiment was stopped only after 5 Gyr. We then divided the sample in non-overlapping bins of 1000 stars with increasing Z, and we measured 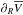 in each bin fitting the function
in each bin fitting the function ![\begin{eqnarray} V(R)=A\cdot\left[ 1-\exp{\left( -\frac{R}{B}\right) }\right]+C\cdot R, \label{eq_Vsym} \end{eqnarray}](/articles/aa/full_html/2015/01/aa24675-14/aa24675-14-eq142.png) (10)where A, B, and C are the fit parameters. This functional form of the radial profile was chosen to account for the deviations from linearity at lower R, as discussed in Sect. 2.2.1. An example of these fits is shown in Fig. 6 for the 1000 stars with Z = 2.0–2.1 kpc.
(10)where A, B, and C are the fit parameters. This functional form of the radial profile was chosen to account for the deviations from linearity at lower R, as discussed in Sect. 2.2.1. An example of these fits is shown in Fig. 6 for the 1000 stars with Z = 2.0–2.1 kpc.
 |
Fig. 6 Azimuthal velocity V as a function of distance from the center, for the stars of our simulated sample in the bin Z = 1.0–1.09 kpc. The solid line indicates the linear fit in the range R = 6–10 kpc. |
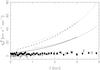 |
Fig. 7 Same as Fig. 3, but the expectations of BT12 are compared with the results of our symulations. The full dots indicate the results when |
The results of our experiment are shown in Fig. 7. We first imposed 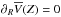 at any Z as the initial condition, and
at any Z as the initial condition, and 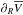 slightly increased during the integration. The system relaxed to tiny non-zero values with
slightly increased during the integration. The system relaxed to tiny non-zero values with 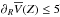 km s-1 kpc-1 up to Z = 4 kpc. This result indicates that the M12b hypothesis is wrong in this specific Galactic model, because a flat radial gradient of
km s-1 kpc-1 up to Z = 4 kpc. This result indicates that the M12b hypothesis is wrong in this specific Galactic model, because a flat radial gradient of 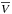 is not an equilibrium solution. In the second run, we imposed as initial condition the lowest BT12 expectation, obtained from Eq. (8) assuming the M12b parameters and the kinematical data of CD11 (Figs. 3, 5, and 7). Very surprisingly, the system relaxed to a
is not an equilibrium solution. In the second run, we imposed as initial condition the lowest BT12 expectation, obtained from Eq. (8) assuming the M12b parameters and the kinematical data of CD11 (Figs. 3, 5, and 7). Very surprisingly, the system relaxed to a 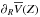 profile identical to the first run, indicating that this is the real equilibrium configuration regardless of the initial conditions. This solution is much lower than the curves expected by the IR(Z) = 0 hypothesis, whose steep profile is therefore unstable in this Galactic potential model. This test demonstrates that low values of
profile identical to the first run, indicating that this is the real equilibrium configuration regardless of the initial conditions. This solution is much lower than the curves expected by the IR(Z) = 0 hypothesis, whose steep profile is therefore unstable in this Galactic potential model. This test demonstrates that low values of 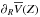 are consistent with a Milky Way-like galaxy, where
are consistent with a Milky Way-like galaxy, where 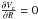 at the solar position, and a thick disk-like kinematics. The steep profile implied by the BT12 formulation is therefore not a natural consequence of a radially constant circular velocity. It must be noted, however, that this counterexample alone does not prove that
at the solar position, and a thick disk-like kinematics. The steep profile implied by the BT12 formulation is therefore not a natural consequence of a radially constant circular velocity. It must be noted, however, that this counterexample alone does not prove that 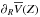 must be small for any Galactic potential model and initial conditions.
must be small for any Galactic potential model and initial conditions.
2.2.4. The validity of the IR(Z) = 0 assumption
We have shown that the observations, both in the Milky Way and in external galaxies, rule out the very peculiar thick disk kinematics required by the hypothesis IR(Z) = 0, which is at the basis of the BT12 formulation. Experiments of orbit integrations indicate that it is not a requirement of a flat radial profile of Vc, and it is even an unstable configuration in the Milky Way-like potential adopted in the simulations.
The failure of the underlying assumption necessarily flaws the results of BT12. It also invalidates the claim that their estimate is a lower limit to ρ⊙ ,DM accurate within 20%. All evidence points to IR(Z) > 0, because 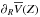 is much lower than the values required to have IR(Z) = 0. BT12 thus overestimate the mass density, because they neglect a negative contribution in Eq. (3) or, equivalently, because they implicitly assume values of
is much lower than the values required to have IR(Z) = 0. BT12 thus overestimate the mass density, because they neglect a negative contribution in Eq. (3) or, equivalently, because they implicitly assume values of 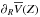 that are too high (see Figs. 3, 5, and 7), whose integral gives a positive contribution to Σ(Z) (see Eq. (11)). This bias is severe for their preferred solution (Figs. 3, 5, and 7), which yields ρ⊙ ,DM = 8.5 mM⊙ pc-3. However, this overestimate is present even when assuming hZ = 0.9 kpc and hR = 3.8 kpc, and the corresponding BT12 solution for Σ> 1.5kpc(Z) (compatible with ρ⊙ ,DM ≈ 7 mM⊙ pc-3) must also be biased.
that are too high (see Figs. 3, 5, and 7), whose integral gives a positive contribution to Σ(Z) (see Eq. (11)). This bias is severe for their preferred solution (Figs. 3, 5, and 7), which yields ρ⊙ ,DM = 8.5 mM⊙ pc-3. However, this overestimate is present even when assuming hZ = 0.9 kpc and hR = 3.8 kpc, and the corresponding BT12 solution for Σ> 1.5kpc(Z) (compatible with ρ⊙ ,DM ≈ 7 mM⊙ pc-3) must also be biased.
3. Moni Bidin et al. (2012) revisited
The results presented in Sect. 2.2 evidence that the M12b hypothesis 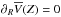 is only a rough approximation, and a more precise estimate of the mass density can be derived if it is dropped. In this case, the M12b expression becomes
is only a rough approximation, and a more precise estimate of the mass density can be derived if it is dropped. In this case, the M12b expression becomes 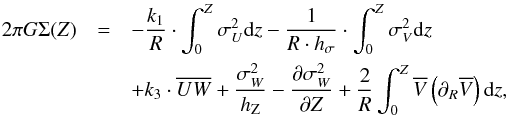 (11)where
(11)where 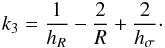 (12)The quantity
(12)The quantity 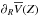 cannot be estimated from M12a data, but the CD11 results can be used. In fact, the two data sets probe the same stellar population (the intermediate-metallicity thick disk), as demonstrated by the fact that their kinematical results are fully compatible. A small mismatch in the mean metallicity would only have tiny effects on the kinematics (Bovy et al. 2012a). In any case, our aim here is not a complete revision of the M12b results, but to check to what extent these are biased by the assumption
cannot be estimated from M12a data, but the CD11 results can be used. In fact, the two data sets probe the same stellar population (the intermediate-metallicity thick disk), as demonstrated by the fact that their kinematical results are fully compatible. A small mismatch in the mean metallicity would only have tiny effects on the kinematics (Bovy et al. 2012a). In any case, our aim here is not a complete revision of the M12b results, but to check to what extent these are biased by the assumption 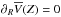 .
.
The studies of the Galactic disk measure the kinematical quantities only beyond a minimum Galactic height Z0, because many observational limitations prevent us from tracking their trend down to the Galactic plane. The estimate of Σ(Z) thus requires the extrapolation of the kinematics for Z<Z0. Calculating the surface density of the mass enclosed between Z0 and Z, 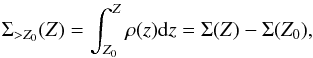 (13)is more appropriate in this case. M12b argue that their estimate of Σ(Z) is not biased by the extension of the integration to lower Z, and they obtained identical results analyzing both Σ(Z) and Σ> 1.5 kpc(Z). Nevertheless, the general reliability of this extrapolation is not proven, and it is even less safe for Eq. (11), which includes the previously neglected quantity
(13)is more appropriate in this case. M12b argue that their estimate of Σ(Z) is not biased by the extension of the integration to lower Z, and they obtained identical results analyzing both Σ(Z) and Σ> 1.5 kpc(Z). Nevertheless, the general reliability of this extrapolation is not proven, and it is even less safe for Eq. (11), which includes the previously neglected quantity 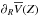 . We therefore do not extend the calculation beyond the interval where we have information about it, and we study Σ> 1 kpc(Z) up to Z = 2.5 kpc. BT12 also gave more importance to the increment of Σ(Z) above Z0 than to its absolute value. Subtracting the expected visible mass from the result, as defined by M12b, we derive the mean DM density in the range Z = 1–2.5 kpc,
. We therefore do not extend the calculation beyond the interval where we have information about it, and we study Σ> 1 kpc(Z) up to Z = 2.5 kpc. BT12 also gave more importance to the increment of Σ(Z) above Z0 than to its absolute value. Subtracting the expected visible mass from the result, as defined by M12b, we derive the mean DM density in the range Z = 1–2.5 kpc, 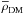 (1–2.5 kpc). It must be noted that the DM density derived from Σ>Z0(Z) is nearly insensitive to the assumed visible mass model when Z0 ≥ 1 kpc, because most of it lies below the volume under analysis. In fact, had different estimates from the literature been assumed (e.g., Holmberg & Flynn 2000; Garbari et al. 2011), the
(1–2.5 kpc). It must be noted that the DM density derived from Σ>Z0(Z) is nearly insensitive to the assumed visible mass model when Z0 ≥ 1 kpc, because most of it lies below the volume under analysis. In fact, had different estimates from the literature been assumed (e.g., Holmberg & Flynn 2000; Garbari et al. 2011), the 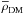 (1–2.5 kpc) would vary by less than 0.2 mM⊙ pc-3.
(1–2.5 kpc) would vary by less than 0.2 mM⊙ pc-3.
 |
Fig. 8 Surface density of the mass at Z> 1 kpc, calculated by inserting the kinematical results of M12a, with the thick disk parameters of Jurić et al. (2008, , and BT12 (lower panel), in Eq. (11). The dashed lines with arrows indicate the upper limit derived from the estimates of CD11 for |
Our results are shown in Fig. 8, overplotted to a set of curves of constant DM density. We first estimated 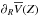 by fitting the three measurements of CD11 shown in Fig. 3. By inserting the result in Eq. (11) along with the other kinematical quantities from M12a and the thick disk parameters preferred by BT12 (hR = 2.0 kpc, hσ = 3.5 kpc, and hZ = 0.7 kpc), the curve of Σ> 1kpc(Z) returns
by fitting the three measurements of CD11 shown in Fig. 3. By inserting the result in Eq. (11) along with the other kinematical quantities from M12a and the thick disk parameters preferred by BT12 (hR = 2.0 kpc, hσ = 3.5 kpc, and hZ = 0.7 kpc), the curve of Σ> 1kpc(Z) returns 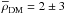 mM⊙ pc-3. A higher DM density (3.6 ± 3.0 mM⊙ pc-3) can be recovered assuming the geometrical parameters hR = 3.6 kpc and hZ = 0.9 kpc from the extensive survey of Jurić et al. (2008). Nevertheless, these results are only upper limits because, as discussed in Sect. 2.2.1, CD11 probably overestimate
mM⊙ pc-3. A higher DM density (3.6 ± 3.0 mM⊙ pc-3) can be recovered assuming the geometrical parameters hR = 3.6 kpc and hZ = 0.9 kpc from the extensive survey of Jurić et al. (2008). Nevertheless, these results are only upper limits because, as discussed in Sect. 2.2.1, CD11 probably overestimate 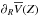 . If the expression for
. If the expression for 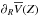 is derived from the revised values of
is derived from the revised values of 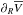 presented in Sect. 2.2.1 (Fig. 3), we obtain
presented in Sect. 2.2.1 (Fig. 3), we obtain 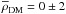 mM⊙ pc-3 when using the BT12 geometrical parameters, and
mM⊙ pc-3 when using the BT12 geometrical parameters, and 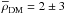 mM⊙ pc-3 when adopting the values from Jurić et al. (2008).
mM⊙ pc-3 when adopting the values from Jurić et al. (2008).
Similar results are found when σU(Z),σV(Z), and σW(Z) are taken from CD11, and we obtain 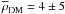 mM⊙ pc-3, with an upper limit of
mM⊙ pc-3, with an upper limit of 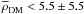 mM⊙ pc-3. These estimates are consistent with those obtained above, but they are poorly informative because of the large errors.
mM⊙ pc-3. These estimates are consistent with those obtained above, but they are poorly informative because of the large errors.
4. Discussion and conclusions
We have shown that the validity of the BT12 hypothesis IR(Z) = 0 depends on the underlying mass distribution. This means that they implicitly constrain the mass distribution to measure the mass density in a given volume. Even the validity of their claim that their estimate is a lower limit to ρ⊙ ,DM accurate within 20% depends on these constraints.
The assumption IR(Z) = 0 predicts a very peculiar behavior for the Galactic thick disk rotation, ruled out by the observations of both the Milky Way and external galaxies. The results of BT12 are flawed by this hypothesis. More specifically, they overestimate the mass density, because their formulation implicitly assumes values of 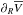 that are too large (see Eq. (11)). The observations also indicate that the M12b assumption
that are too large (see Eq. (11)). The observations also indicate that the M12b assumption 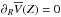 is only a rough approximation, but we find that it does not bias the results noticeably. In fact, when this assumption is dropped and
is only a rough approximation, but we find that it does not bias the results noticeably. In fact, when this assumption is dropped and 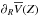 is taken from literature measurements, the resulting mean DM density at the solar position between Z = 1 and 2.5 kpc is
is taken from literature measurements, the resulting mean DM density at the solar position between Z = 1 and 2.5 kpc is 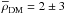 mM⊙ pc-3, with an upper limit of
mM⊙ pc-3, with an upper limit of 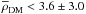 mM⊙ pc-3. The thick disk parameters preferred by BT12 return much lower values. These results agree well with those of M12b, demonstrating that the incidence of
mM⊙ pc-3. The thick disk parameters preferred by BT12 return much lower values. These results agree well with those of M12b, demonstrating that the incidence of 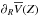 on the calculation is small. The resulting lack of DM is therefore not a systematic effect introduced by the aforementioned assumption. More investigation is needed to understand the peculiar results found by M12b.
on the calculation is small. The resulting lack of DM is therefore not a systematic effect introduced by the aforementioned assumption. More investigation is needed to understand the peculiar results found by M12b.
The uncertainties quoted here and in M12b result from rigorous propagation of errors on the input quantities, and they represent the statistical uncertainties well. Possible systematic errors are not considered in the error budget, but M12b analyzed most of their hypotheses and found no relevant bias. Their uncertainties are small when compared to the literature, but it must be considered that their calculation is extended in a volume that is four times larger than before. In fact, the extrapolation of the expected small DM contribution in the first kpc from the Galactic plane (25% of the total mass) is necessarily more uncertain than its estimate in a volume where it exceeds the quantity of visible mass. For example, a 10% uncertainty on the total mass and on the visible component propagates to a ≈40% error on ρ⊙ ,DM at Z< 1 kpc, but this reduces to 20% and 10% at Z< 4 kpc, respectively. The volume analyzed here is smaller than M12b, and the resulting errors are larger by a factor of three. Our uncertainties are also partially enhanced by 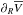 , an additional source of error not constrained very well by the data. As a result, our final errors are 30% larger than those quoted by Zhang et al. (2013), although our volume is comparable to theirs.
, an additional source of error not constrained very well by the data. As a result, our final errors are 30% larger than those quoted by Zhang et al. (2013), although our volume is comparable to theirs.
The results presented here are at variance with the expectations of a classical spherical DM halo with ρ⊙ ,DM> 5 mM⊙ pc-3, whose density decreases by only ~5% between Z = 0 and 2 kpc. A deeper comprehension of the power and limitations of the M12b three-dimensional approach is required to fully understand this discrepancy. We nevertheless note that, while a low density on the plane is compatible only with a highly prolate halo (see M12b), a low mean density in the range Z = 1–2.5 kpc is compatible even with a very flat (oblate) distribution, if the bulk of the dark mass is found at Z< 1 kpc. It is also important to point out that the results obtained here are not directly comparable to previous estimates, because all similar measurements in the literature are limited to Z< 1.2 kpc.
All the literature measurements of the mass density at the solar position have adopted a one-dimensional approach, where the Galactic potential was modeled to match the observational data (but see Korchagin et al. 2003, for an exception). Both BT12 and M12b make use of a direct equation, which relates the mass density to the kinematical quantities. BT12 used the same kinematical data as M12b, and share most of the assumptions with them but, after reducing the three-dimensional formulation of M12b to a one-dimensional approximation, found results in agreement with both classical works (e.g. Kuijken & Gilmore 1989; Holmberg & Flynn 2000) and more recent studies (e.g. Siebert et al. 2003; Zhang et al. 2013). Thus, they eventually prove that the discrepancy between the M12b results and the literature is most likely due neither to their use of a direct equation nor to a bias in the kinematical measurements. Their unexpected results most likely stem from their innovative three-dimensional approach, and more investigation is needed to understand them.
Acknowledgments
R.A.M. acknowledges support from the Chilean Centro de Excelencia en Astrofísica y Tecnologías Afines (CATA) BASAL PFB/06, and by Project IC120009 “Millennium Institute of Astrophysics (MAS)” of the Iniciativa Científica Milenio del Ministerio de Economía, Fomento y Turismo de Chile. R.S. was financed by FONDECYT grant 3120135. Funding for SDSS-III has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, and the US Department of Energy Office of Science. R.A.M. acknowledges ESO/Chile for hosting him during his sabbatical leave.
References
- Bovy, J., & Tremaine, S. 2012, ApJ, 756, 89 [Google Scholar]
- Bovy, J., Rix, H.-W., Hogg, D. W., et al. 2012a, ApJ, 755, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Bovy, J., Rix, H.-W., Liu, C., et al. 2012b, ApJ, 753, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Carrell, K., Chen, Y., & Zhao, G. 2012, AJ, 144, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Casetti-Dinescu, D. I., Girard, T. M., Korchagin, V. I., & van Altena, W. F. 2011, ApJ, 728, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Chiba, M., & Beers, T. C. 2000, AJ, 119, 2843 [NASA ADS] [CrossRef] [Google Scholar]
- Creze, M., Chereul, E., Bienayme, O., & Pichon, C. 1998, A&A, 329, 920 [NASA ADS] [Google Scholar]
- Einasto, J. 1965, Trudy Astrofizicheskogo Instituta Alma-Ata, 5, 87 [NASA ADS] [Google Scholar]
- Einasto, J. 1968, Publications of the Tartu Astrofizica Observatory, 36, 414 [Google Scholar]
- Flynn, C., Sommer-Larsen, J., & Christensen, P. R. 1996, MNRAS, 281, 1027 [NASA ADS] [CrossRef] [Google Scholar]
- Garbari, S., Read, J. I., & Lake, G. 2011, MNRAS, 416, 2318 [NASA ADS] [CrossRef] [Google Scholar]
- Garbari, S., Liu, C., Read, J. I., & Lake, G. 2012, MNRAS, 425, 1445 [NASA ADS] [CrossRef] [Google Scholar]
- Girard, T. M., Korchagin, V. I., Casetti-Dinescu, D. I., et al. 2006, AJ, 132, 1768 [NASA ADS] [CrossRef] [Google Scholar]
- Holmberg, J., & Flynn, C. 2000, MNRAS, 313, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezić, Ž., Sesar, B., Jurić, M., et al. 2008, ApJ, 684, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Jałocha, J., Bratek, Ł., Kutschera, M., & Skindzier, P. 2010, MNRAS, 407, 1689 [NASA ADS] [CrossRef] [Google Scholar]
- Jurić, M., Ivezić, Ž., Brooks, A., et al. 2008, ApJ, 673, 864 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kalberla, P. M. W. 2003, ApJ, 588, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Kerr, F. J., & Lynden-Bell, D. 1986, MNRAS, 221, 1023 [NASA ADS] [CrossRef] [Google Scholar]
- Korchagin, V. I., Girard, T. M., Borkova, T. V., Dinescu, D. I., & van Altena, W. F. 2003, AJ, 126, 2896 [NASA ADS] [CrossRef] [Google Scholar]
- Kregel, M., van der Kruit, P. C., & Freeman, K. C. 2004, MNRAS, 351, 1247 [NASA ADS] [CrossRef] [Google Scholar]
- Kuijken, K., & Gilmore, G. 1989, MNRAS, 239, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Majewski, S. R. 1992, ApJS, 78, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Miyamoto, M., & Nagai, R. 1975, PASJ, 27, 533 [NASA ADS] [Google Scholar]
- Moni Bidin, C., Carraro, G., Méndez, R. A., & van Altena, W. F. 2010, ApJ, 724, L122 [NASA ADS] [CrossRef] [Google Scholar]
- Moni Bidin, C., Carraro, G., & Méndez, R. A. 2012a, ApJ, 747, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Moni Bidin, C., Carraro, G., Méndez, R. A., & Smith, R. 2012b, ApJ, 751, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Olling, R. P. 1995, AJ, 110, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Olling, R. P., & Merrifield, M. R. 2001, MNRAS, 326, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Purcell, C. W., Bullock, J. S., & Kaplinghat, M. 2009, ApJ, 703, 2275 [NASA ADS] [CrossRef] [Google Scholar]
- Qu, Y., Di Matteo, P., Lehnert, M. D., & van Driel, W. 2011, A&A, 530, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Read, J. I., Lake, G., Agertz, O., & Debattista, V. P. 2008, MNRAS, 389, 1041 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, M. J., Readhead, A. C. S., Vermeulen, R. C., & Treuhaft, R. N. 1999, ApJ, 524, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Salucci, P., Nesti, F., Gentile, G., & Frigerio Martins, C. 2010, A&A, 523, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanders, J. 2012, MNRAS, 425, 2228 [NASA ADS] [CrossRef] [Google Scholar]
- Siebert, A., Bienaymé, O., & Soubiran, C. 2003, A&A, 399, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sofue, Y., Honma, M., & Omodaka, T. 2009, PASJ, 61, 227 [NASA ADS] [Google Scholar]
- Weber, M., & de Boer, W. 2010, A&A, 509, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoachim, P., & Dalcanton, J. J. 2005, ApJ, 624, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Yoachim, P., & Dalcanton, J. J. 2008, ApJ, 682, 1004 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, Jr., J. E., et al. 2000, AJ, 120, 1579 [Google Scholar]
- Zhang, L., Rix, H.-W., van de Ven, G., et al. 2013, ApJ, 772, 108 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Trend of IR (solid line) and |
| In the text | |
 |
Fig. 2 Trend of IR(Z) with Z at R = 8 kpc, for a Miyamoto-Nagai disk (gray curves) with b = 0.3 kpc and a = 2.5, 3.5, 4.5 kpc, and a NFW halo model with ρ⊙ ,DM = 8 mM⊙ pc-3 (black curve). |
| In the text | |
 |
Fig. 3 Vertical trend of |
| In the text | |
 |
Fig. 4 Vertical trend of azimuthal velocity for our SDSS sample of thick disk stars. The linear fit to the data is indicated by the solid line. |
| In the text | |
 |
Fig. 5 Comparison of BT12 expectations for |
| In the text | |
 |
Fig. 6 Azimuthal velocity V as a function of distance from the center, for the stars of our simulated sample in the bin Z = 1.0–1.09 kpc. The solid line indicates the linear fit in the range R = 6–10 kpc. |
| In the text | |
 |
Fig. 7 Same as Fig. 3, but the expectations of BT12 are compared with the results of our symulations. The full dots indicate the results when |
| In the text | |
 |
Fig. 8 Surface density of the mass at Z> 1 kpc, calculated by inserting the kinematical results of M12a, with the thick disk parameters of Jurić et al. (2008, , and BT12 (lower panel), in Eq. (11). The dashed lines with arrows indicate the upper limit derived from the estimates of CD11 for |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.