| Issue |
A&A
Volume 572, December 2014
|
|
|---|---|---|
| Article Number | A120 | |
| Number of page(s) | 9 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201423854 | |
| Published online | 09 December 2014 | |
The PHEMU09 catalogue and astrometric results of the observations of the mutual occultations and eclipses of the Galilean satellites of Jupiter made in 2009
1 Institut de mécanique céleste et de calcul des éphémérides-Observatoire de Paris, UMR 8028 CNRS, UPMC, USTL, 77 avenue Denfert-Rochereau, 75014 Paris, France
e-mail: Jean-Eudes.Arlot@imcce.fr
2 Sternberg Astronomical Institute, Lomonosov Moscow State University, 119991 Moscow, Russia
3 Association Jonckheere-Les Amis de l’Observatoire de Lille, 1 Impasse de l’Observatoire, 59000 Lille, France
4 Gruppo Astrofili Catanesi, 95128 Catania, Italy
5 Associazione Astrofili Bolognesi, 95128 Bologna, Italy
6 viale L.Pirandello, 26, 21052 Busto Arsizio (VA), Italy
7 Im Erlenhof 2a, 51429 Bergisch Gladbach, Germany
8 Agrupació Astronómica de Sabadell, Carrer Prat de la Riba, s/n, 08206 Sabadell, Catalonia, Spain
9 Armagh Observatory, College Hill, Armagh BT61 9DG, UK
10 CALA, Place de la nation, 69120 Vaulx-en-Velin, France
11 Observatorul Astronomic Amiral Vasile Urseanu, no.21, Lascar Catargiu Boulevard, 71111 Bucharest, Romania
12 Nonndorf 12, 3830, Austria
13 2112 Maple Leaf Trail, Columbia, TN, 38401, USA
14 2 rue de l’Ardèche, 31170 Tournefeuille, France
15 Univ. Bordeaux, LAB, UMR 5804, 33270 Floirac, France
16 Astronomical Union of Sparta, 23100 Sparta, Greece
17 Plantation, FL, USA
18 1155 Hartford St Elgin, Oregon 97827, USA
19 22 Booker Road, Hawkesbury Heights NSW 2777, Australia
20 136 Rio Senda, Umatilla, Oregon 97882, USA
21 Bartlesville, Oklahoma, USA
22 Shandong University at Weihai, 264209 Weihai, PR China
23 1-4-17, Okino, Higashi-Ohmi, 527-0034 Shiga, Japan
24 Central Astronomical Observatory of the Russian Academy of Sciences, St. Petersburg, Pulkovo, Russia
25 Astronomical observatory of Odessa University, Marazlievskaya st. 1-B, Odessa, Ukraine
26 Department of Astrophysics, Astronomy and Mechanics, University of Athens, 15784 Zografos, Athens, Greece
27 Shanghai Astronomical Observatory, Chinese Academy of Sciences, 200030 Shanghai, PR China
28 14 Craigieburn Street, 7510 Darfield, New Zealand
29 Istituto Spezzino Ricerche Astronomiche, 19125 La Spezia, Italy
30 Astronomical Observatory University of Siena, 53100 Siena, Italy
31 Astrocampania, 80063 Piano di Sorrento, Italy
32 4368-1, Akashina-Nanaki, Azumino, 399-7104 Nagano, Japan
33 University of Namur, NAmur Center for CompleX SYStems (naXys), Rempart de la Vierge 8, 5000 Namur, Belgium
34 Koninklijke Sterrenwacht van België, Ringlaan 3, 1180 Brussels, Belgium
35 45/192 Vimiera Rd, Marsfield, NSW 2122, Australia
36 Department of computer Science, Jinan University, 510632 Guangzhou, PR China
37 Institut de Ciéncies de l’Espai (IEEC-CSIC), Campus UAB, Facultat de Ciéncies, Torre C5 parell 2n pis, 08193 Bellaterra, Catalonia, Spain
38 Observatory and Planetarium Praha, Kralovska obora 233 170 21 Praha 7, Czech Republic
39 26 impasse des Forsythias, 06560 Valbonne, France
40 Observatório do Valongo/UFRJ, Ladeira Pedro Antonio 43, RJ 23. 070-200 Rio de Janeiro, Brazil
41 Organizzazione Ricerche e Studi di Astronomia, Palermo, Italy
42 Kourovskaya observatory of the Ural Federal University, Prospect Lenina 51, 620000 Ecaterinbourg, Russia
43 Gruppo Astrofili di Piacenza, Italy
44 Scaggsville, Maryland, USA
45 Fessenkov Astrophysical Institute, Alma-Ata, Kazakhstan
46 RASNZ Occultation Section, 3 Hughes Street, Waikanae Beach, New Zealand
47 Newark, New York, USA
48 Associazione Iblea Divulgazione Astronomica, 497100 Ragusa, Italy
49 9 Payling Lane, 8052 Christchurch, Christchurch, New Zealand
50 PO Box 117, Chester, GA 31012, USA
51 8 rue des Ormes, 67450 Mundolsheim, France
52 281, Kasadashinden, Inabe, Mie, 511-0205, Japan
53 Virtual Telescope Project, Via Madonna de Loco 47, 03023 Ceccano (FR), Italy
54 Observatorio Nacional/MCTI, R. General Jose Cristino 77, RJ 20. 921-400 Rio de Janeiro, Brazil
55 Centro Universitário Estadual da Zona Oeste, Av. Manuel Caldeira de Alvarenga 1203, RJ 23. 070-200 Rio de Janeiro, Brazil
56 3 Lupin Pl, Murrumbateman, NSW 2582, Australia
57 CNRS, LAB, UMR 5804, 33270 Floirac, France
Received: 20 March 2014
Accepted: 15 May 2014
Context. In 2009, the Sun and the Earth passed through the equatorial plane of Jupiter and therefore the orbital planes of its main satellites. It was the equinox on Jupiter. This occurrence made mutual occultations and eclipses between the satellites possible. Experience has shown that the observations of such events provide accurate astrometric data able to bring new information on the dynamics of the Galilean satellites. Observations are made under the form of photometric measurements, but need to be made through the organization of a worldwide observation campaign maximizing the number and the quality of the data obtained.
Aims. This work focuses on processing the complete database of photometric observations of the mutual occultations and eclipses of the Galilean satellites of Jupiter made during the international campaign in 2009. The final goal is to derive new accurate astrometric data.
Methods. We used an accurate photometric model of mutual events adequate with the accuracy of the observation. Our original method was applied to derive astrometric data from photometric observations of mutual occultations and eclipses of the Galilean satellites of Jupiter.
Results. We processed the 457 lightcurves obtained during the international campaign of photometric observations of the Galilean satellites of Jupiter in 2009. Compared with the theory, for successful observations, the r.m.s. of O–C residuals are equal to 45.8 mas and 81.1 mas in right ascension and declination, respectively; the mean O–C residuals are equal to –2 mas and –9 mas in right ascension and declination, respectively, for mutual occultations; and –6 mas and +1 mas in right ascension and declination, respectively, for mutual eclipses.
Key words: astronomical databases: miscellaneous / planets and satellites: general / occultations / eclipses / ephemerides
© ESO, 2014
1. Introduction
Photometric observations of mutual occultations and eclipses of natural satellites of planets offer an efficient source of new astrometric data. We took the opportunity of the 2009 occurrence to organize a worldwide observational campaign that allowed us to gather very accurate astrometric observations. We report in this paper the results of the campaign under the form of photometric and astrometric data.
2. The mutual events
The Earth and the Sun cross the equatorial plane of Jupiter every six years at the time of the Jovian equinox. The Jovian declinations of the Earth and the Sun then become zero and, since the orbital plane of the Galilean satellites is close to the equatorial plane of Jupiter, the satellites occult and eclipse each other.
The 2009 period was favorable because the equatorial plane crossing occurred near the opposition of Jupiter and the Sun making the observations easier.
Arlot (2008) compiled predictions of all 2009 events using the G5 ephemerides based on Lieske’s theory (Lieske 1977) and the newer L1 ephemerides from Lainey et al. (2004a,b) for the motion of the Galilean satellites; 370 observable mutual events were computed. Before 2009, several observational campaigns were completed during previous occurrences (Arlot 1992, 1997, 2006, 2009). Table 1 presents the results derived for each campaign up to the present campaign. Our goal was to observe as many events as possible. At least two observations of each event were desirable to eliminate any biases in the present observations.
Since no thick atmosphere surrounds any of the Galilean satellites, the photometric observations of these phenomena are extremely accurate for astrometric purposes. The results previously obtained after similar observations of the Galilean satellites demonstrated that high astrometric accuracy could be achieved; an accuracy higher than 30 mas was expected (Lainey et al. 2004b).
This accuracy allowed us to provide the data necessary to improve the theoretical models of the orbital motions and to determine the tidal effects in the dynamics of the Galilean satellites through the measurement of a shift in longitude of the satellites, signature of an acceleration in their motions.
Results of the past observation campaigns.
3. The PHEMU09 campaign
We coordinated an international PHEMU09 campaign to acquire a significant number of events. These events occurred in a short period of time, so numerous observers located in several sites were necessary to help avoiding meteorological problems and to observe different events from different longitudes. This is why observers previously involved in PHEMU observational campaigns of mutual events of the Galilean satellites were invited to join the new campaign.
The observational data of the international campaign PHEMU09 were provided from different sources and were processed in three different ways.
Source R: the photometric observations of mutual occultations and eclipses of the Galilean satellites of Jupiter in 2009 were made in five observatories in Russia. The 89 lightcurves were processed with the procedure explained in the present paper. A description of this series of observations and obtained astrometric results was published in Emelyanov et al. (2011).
Source B: a series of observations was made in the observatory of Itajuba, Brazil. The 30 lightcurves were provided to the Institut de Mécanique Céleste et de Calcul des Éphémérides (IMCCE). We processed these photometric results with the procedure described here and present the obtained photometric and astrometric data. We note that 25 out of 30 of these lightcurves were processed by an original method and published by Dias-Oliveira et al. (2013). The astrometric results are slightly different from ours.
Source A: other numerous observations were made in several sites around the world. The results were provided to IMCCE. This series of data includes 384 lightcurves. From 338 of them astrometric results were successfully obtained; 46 other lightcurves yielded no astrometric results for the reasons listed below.
For this campaign, 370 events were observable, 172 different events were successfully observed. In total 457 lightcurves were successfully obtained and reduced.
3.1. Detectors
When observing mutual events, only relative photometry can generally be completed. Since the elevation of Jupiter above the horizon may be small, the air mass is often too high and absolute photometry is then impossible. Telescopes were equipped with the detectors listed in the tables. Two kinds of detectors were used, the video cameras (Table 2) providing movies and the two-dimensional CCD detectors (Table 3) providing series of images. Visual observations and observations using single channel photoelectric photometers are no longer performed. The codes for the detectors used are given in Tables 4 for each site of observation.
Video detectors used for the observations.
3.2. Observation sites
Coordinated by the Institut de Mécanique Céleste et de Calcul des Éphémérides (IMCCE), this campaign included 74 observation sites (81 different telescopes). The different locations are given in Tables 4. These tables give the codes, locations, and telescopes used (T means reflector, L refractor, SCT Schmidt-Cassegrain-telescope, MCT Maksutov-Cassegrain telescope) followed by the aperture in cm, and longitudes, latitudes, and altitudes of the observational sites. The observation codes (Obs. codes) are also given in Tables 5 and 6 which provide the data for each observation. The column labelled O gives the number of observations received from the observers, R the number of observations from which the astrometric results were obtained, N the number of observations where the light curves show no events, L the number of observations with incorrect data or missing metadata.
4. Lightcurve reduction procedure
Lightcurves are the results of a series of successive images. Such a series may have different forms: a simple analogic or numeric video movie or a set of images of successive fits files. In both cases, each image is dated in Universal Time or in a time scale linked to Universal Time with an accuracy better than 0.1 s.
The photometry of each image had to be made with care even if we were doing relative photometry not absolute. In order to perform relative photometry, each recording of an event must have either two objects on each image (the occulted or eclipsed satellite with another reference satellite) or a reference taken before and after the event if only the satellites involved in the event are present on each image. The reference is necessary and its flux should be constant during the event. If not, it is due to the passage of light clouds. Then, the reference will be used to rebuild the fluxes by dividing event flux/reference flux. At any time this ratio is dependent on any variation of the global received light flux. In addition, the background light had to be removed especially for observations made during twilight when it varies rapidly.
Then, the light reflected by the satellites has to be measured on each image. It is necessary to tell if the measured light corresponds to one or two satellites (and sometimes three if the satellites are too close together) and a file is built providing for each image a series of data as follows: the dates in UTC and the light fluxes of the satellites involved in the event followed when possible by the light from a reference object and the light from the background. These files are provided by the observers but it is not these files which are provided in our database rather the files described in Sect. 6.11.
Figures 1 to 5 show examples of lightcurves. We note that the determination of the light flux on each image may be made either through a Gaussian fit of the object or an aperture photometry integrating all the light in a specific area with the careful elimination of the light from the sky background.
CCD detectors used for the observations.
5. Extracting astrometric data from the photometry of satellites during the mutual occultations and eclipses
We use our original method to derive positional and astrometric data from the measurements of satellite fluxes during their mutual occultations and eclipses (see Emelyanov 2000; Emel’yanov 2003; Emelyanov & Gilbert 2006), for a description of the method, also used in Emelyanov (2009) and Emelyanov & Vashkovyak (2009).
We adopt Hapke’s light scattering law in our solution (Hapke 1981, 1984). His scattering function depends on five parameters, which are constant for a given satellite and spectral band. McEwen et al. (1988) give the Hapke parameters for the rough surface of the Io satellite, whereas Domingue & Verbiscer (1997) refined the Hapke function for rough surfaces and, in particular, for the other three Galilean satellites. Given that most of the observations of the Galilean satellites were made with the V filter, or with no filter at all, we adopt the set of parameters from Domingue & Verbiscer (1997) for the 0.55 μm spectral band. During the event, almost half of the leading and half of the trailing hemisphere of each satellite were viewed from the Earth, and we therefore use the mean values for the corresponding parameters. We allow for solar limb darkening as described by Emel’yanov (2003) and Emelyanov & Gilbert (2006), and use tables from Makarova et al. (1998) to this end. In our solution, we use the dependence of the magnitudes of the Galilean satellites on the angle of rotation based on the ground-based photometry by Morrison & Morrison (1977). Some revision of this dependence was adopted for Ganymede and Callisto using observations made by Prokof’eva-Mikhailovskaya et al. (2010).
The main idea of our method consists in modelling the deviation of the observed relative satellite motion from the theoretical motion provided by the relevant ephemeris, rather than analysing the apparent relative motion of one satellite with respect to the other.
The measured flux E(t) during an event at time t can be expressed by 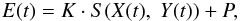 (1)where X(t) and Y(t) are the projections of the differences of planetocentric Cartesian coordinates of the two satellites onto the tangent plane of the event. In the case of mutual occultations, this plane coincides with the plane passing through the occulted satellite perpendicular to the line of sight of the observer. In the case of a mutual eclipse, the plane of the event passes through the eclipsed satellite perpendicular to the line connecting the satellite with the center of the Sun. The coordinate origin is placed at the center of the passive (occulted or eclipsed) satellite. The occulting or eclipsing satellite is referred to as the active satellite.
(1)where X(t) and Y(t) are the projections of the differences of planetocentric Cartesian coordinates of the two satellites onto the tangent plane of the event. In the case of mutual occultations, this plane coincides with the plane passing through the occulted satellite perpendicular to the line of sight of the observer. In the case of a mutual eclipse, the plane of the event passes through the eclipsed satellite perpendicular to the line connecting the satellite with the center of the Sun. The coordinate origin is placed at the center of the passive (occulted or eclipsed) satellite. The occulting or eclipsing satellite is referred to as the active satellite.
The function S(X(t),Y(t)) describes the model of the phenomenon. In a general case we have
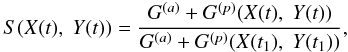 where G(a) is the light flux from the occulting or eclipsing satellite and G(p)(X(t),Y(t)) is the light flux from the occulted or eclipsed one. Here t is an instant in time during the event and t1 denotes the instant immediately before the start of the event. In the case of mutual eclipse when the light flux from eclipsed satellite only is measured G(a) = 0. In our calculations we partition the surface of the eclipsed or occulted satellite into finite elements. For each element the flux received is calculated separately according to the assumed photometric model. We compute the total luminous flux from the surface of the satellite as the sum of the fluxes from all partition elements. It is evident that S(X(t),Y(t)) = 1 off event. The parameter K is a scale factor for the flux drop during the event and it is equal to the total flux measured outside the event. We refer to the part of the photometric count that is not due to the satellite flux as the background and denote it as P.
where G(a) is the light flux from the occulting or eclipsing satellite and G(p)(X(t),Y(t)) is the light flux from the occulted or eclipsed one. Here t is an instant in time during the event and t1 denotes the instant immediately before the start of the event. In the case of mutual eclipse when the light flux from eclipsed satellite only is measured G(a) = 0. In our calculations we partition the surface of the eclipsed or occulted satellite into finite elements. For each element the flux received is calculated separately according to the assumed photometric model. We compute the total luminous flux from the surface of the satellite as the sum of the fluxes from all partition elements. It is evident that S(X(t),Y(t)) = 1 off event. The parameter K is a scale factor for the flux drop during the event and it is equal to the total flux measured outside the event. We refer to the part of the photometric count that is not due to the satellite flux as the background and denote it as P.
Theories of the motion of planets and satellites can be used to compute the theoretical values of functions X(t),Y(t), i.e., Xth(ti), Yth(ti) at times ti(i = 1,2,...,m) for each photometric measurement. Here m is the number of photometric counts during a single event. The actual values of X(ti), Y(ti) differ from Xth(ti), Yth(ti) by the corrections Dx,Dy.
Our method consists in solving conditional equations 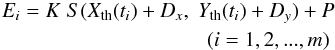 (2)for constants Dx,Dy,K, and P. Here Ei is the photometric count made at time ti. We linearize conditional equations with respect to the parameters Dx,Dy and then solve them using the least-squares method.
(2)for constants Dx,Dy,K, and P. Here Ei is the photometric count made at time ti. We linearize conditional equations with respect to the parameters Dx,Dy and then solve them using the least-squares method.
In our final solution we use the theory of the motion of the Galilean satellites developed by Lainey et al. (2009) to compute the theoretical values Xth(ti), Yth(ti) and then the corrections Dx, Dy.
Astrometric results of the observations may have the form of any corrected relative position of satellites X(t∗) = Xth(t∗) + Dx,Y(t∗) = Yth(t∗) + Dy together with the associated time instant t∗ inside the time interval of the event. Although this is not mandatory, we assume that t∗ is the time instant when 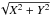 takes its minimum value, t∗ is the time of the closest apparent approach of the satellites.
takes its minimum value, t∗ is the time of the closest apparent approach of the satellites.
Modern data fitting procedures can use the X,Y coordinates directly. Given that in published results of observations there are differences of the topocentric angular coordinates X′′,Y′′, we prefer to present our final results in these coordinates as well. We note that in the cases of mutual eclipses angular coordinates are heliocentric.
Observation sites for the PHEMU09 campaign.
Given the topocentric or heliocentric distance R of the passive satellite one can compute X′′,Y′′ from X,Y using precise equations. In the cases of ground-based observations of the mutual events of natural satellites approximate relations
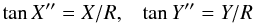 can be used, which are accurate for these observations to 0.00001 arcsec. In a similar way we designate by
can be used, which are accurate for these observations to 0.00001 arcsec. In a similar way we designate by 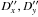 the angular values corresponding to the corrections Dx,Dy. In the case where the same event was observed at two observatories the time instants t∗ may differ because of observational errors and hence the differences between the coordinates X(t∗),Y(t∗) obtained at two observatories cannot be viewed as bias indicators. The quantities
the angular values corresponding to the corrections Dx,Dy. In the case where the same event was observed at two observatories the time instants t∗ may differ because of observational errors and hence the differences between the coordinates X(t∗),Y(t∗) obtained at two observatories cannot be viewed as bias indicators. The quantities 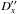 ,
, 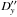 characterize the agreement between theory and observations. These quantities can be used to compare the results of observations made at different observatories. The errors σx and σy of the derived parameters X′′(t∗), Y′′(t∗) characterize the internal accuracy of photometry estimated via the least-squares method.
characterize the agreement between theory and observations. These quantities can be used to compare the results of observations made at different observatories. The errors σx and σy of the derived parameters X′′(t∗), Y′′(t∗) characterize the internal accuracy of photometry estimated via the least-squares method.
After computing the Dx,Dy values we determine the minimum value Smin of the normalized flux S(Xth(t) + Dx,Yth(t) + Dy) based on observations. The maximum flux drop during the event is then equal to 1 − Smin. In certain cases, where the corrections Dx, Dy could not be reliably determined, we converted the coordinates X,Y into the coordinates connected with the apparent trajectory of the relative satellite motion. Once determined in this coordinate system, the corrections were converted into the Dx, Dy values.
The occulting satellite may pass above or below the occulted satellite at the same distance from the latter producing the same dips in the total flux. Thus, any observed lightcurve of the satellites has two solutions for the corresponding coordinate differences of apparent coordinates of satellites. For each observation the minimum values of Dx, Dy was a factor taken into account when choosing between the two solutions. Most of our astrometric results come from processing the mutual event observations where both corrections Dx, Dy could be obtained.
In the case where the apparent disc of one of the satellites overlaps fully with that of the other satellite, the solution becomes uncertain in one of the relative coordinates. Similar effects also occur in the case of mutual eclipses of satellites. In such cases observations yield only the correction to the position of the satellite along the trajectory of its relative motion. As a result, only position angle A defined with the equation
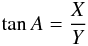 can be determined for a certain time instant (t∗) near the time of minimum apparent distance between the satellites. The data obtained in such cases form a separate section of our astrometric results.
can be determined for a certain time instant (t∗) near the time of minimum apparent distance between the satellites. The data obtained in such cases form a separate section of our astrometric results.
In our final solution for astrometric coordinates we assume that the effect of the background on the result of photometric measurements is already eliminated by the observers and therefore we set P = 0.
6. The catalogue
6.1. The data
The catalogue of the data gathered after the observation campaign of the mutual events of the Galilean satellites is provided under the form of 457 files (one for each observation) containing a series of photometric measurements: the lightcurve obtained from the photometry of the mutual event calibrated using the flux scale coefficient K obtained after the fit of the parameters on the observations, so that the measured flux must be equal to 1 when no event occurs and to 0 if no light is received from the observed objects (if only the flux from the eclipsed satellite is measured and if this satellite has disappeared). The calibrated value of the measured flux is supplied with the theoretical value of the flux obtained after the fit of the parameters to the observation. On each line of the file, we provide three numbers as follows: first the time in minutes counted from 0 h (UTC) of the day of the event; second, the calibrated value of the observed measured flux (the value Ei/K, see the Eq. (2)), and third, the light flux modelled after the fit of the parameters on the observation as explained above (the value S(Xth(ti) + Dx,Yth(ti) + Dy) in Eq. (2)).
Fragment of the first section of astrometric results.
Fragment of the second section of astrometric results.
The catalogue also contains a file of relative astrometric positions of the two satellites involved in each mutual event (one line per event) as described in the Sect. 6.2 and in Tables 5 and 6.
Figures 1 to 5 show examples of observed lightcurves: the dots are the observations and the line is the model as explained in Sects. 4 and 5.
The lightcurves and the astrometric results are available for anyone interested from the electronic database of the Natural Satellite Data Center (NSDC) server2.
6.2. Astrometric results
We subdivide our final astrometric results into two sections. The first section includes the results obtained from the observations where two coordinates X′′(t∗), Y′′(t∗) could be successfully determined. The second section contains the results obtained in the cases where only the position angle could be determined.
 |
Fig. 1 J2 occults J3 on May 23, 2009: this observation shows a grazing event with a small magnitude drop. The signal is noisy. The noise could be reduced with a longer integrating time for each point. |
In the first section each final result of the observation of a single mutual phenomenon at a given observatory is presented by the following fields: the date, the type of the phenomenon (eclipse or occultation) including the satellite numbers, the observatory code, the time instant t∗ in the UTC scale, X′′(t∗), Y′′(t∗), σx, σy, 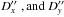 . The type of phenomenon is coded as naonp or naenp for a mutual occultation or eclipse, respectively. Here na is the number of the occulting or eclipsing satellite and np is the number of the occulted or eclipsed satellite. We give the results in the form of the angular separation s (in arcseconds) and position angle A (in degrees) corresponding to X′′(t∗), Y′′(t∗). The angular separation s is determined by the equation
. The type of phenomenon is coded as naonp or naenp for a mutual occultation or eclipse, respectively. Here na is the number of the occulting or eclipsing satellite and np is the number of the occulted or eclipsed satellite. We give the results in the form of the angular separation s (in arcseconds) and position angle A (in degrees) corresponding to X′′(t∗), Y′′(t∗). The angular separation s is determined by the equation
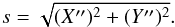 We also give the minimum level Smin of normalized flux. We assign flag Q to each observation in order to indicate the quality and the reliability of the result. Flag Q may have acquired one of the following four values: 0 for normally determined coordinates, 1 for the cases doubtful photometric data, 2 for results following from low-quality photometry, and 3 for results very different from those from other observatories. Right ascensions and declinations are measured in the international celestial reference frame (ICRF). All angular quantities are in arcseconds. In the case of a mutual occultation, t∗ is the time of topocentric observation of satellites. In the case of mutual eclipse, t∗ is the time of topocentric observation of the eclipsed satellite.
We also give the minimum level Smin of normalized flux. We assign flag Q to each observation in order to indicate the quality and the reliability of the result. Flag Q may have acquired one of the following four values: 0 for normally determined coordinates, 1 for the cases doubtful photometric data, 2 for results following from low-quality photometry, and 3 for results very different from those from other observatories. Right ascensions and declinations are measured in the international celestial reference frame (ICRF). All angular quantities are in arcseconds. In the case of a mutual occultation, t∗ is the time of topocentric observation of satellites. In the case of mutual eclipse, t∗ is the time of topocentric observation of the eclipsed satellite.
 |
Fig. 2 J3 eclipses J2 on August 12, 2009: the flat bottom of the lightcurve for the model and for the observation. |
 |
Fig. 3 J3 eclipses J2 on July 28, 2009: the observation started a little late. The minimum of the lightcurve is clearly visible allowing the reduction. |
 |
Fig. 4 J4 eclipses J1 on May 16, 2009: the lightcurve is perfectly modelled and the observation is not noisy. |
 |
Fig. 5 J1 occults J3 on May 8, 2009: the observation is noisy, but the lightcurve is perfectly modelled. As in Fig. 1, a longer integrating time for each point could decrease the noise. |
The quantities σx and σy can be interpreted as internal errors of Δαcosδp and Δδ, respectively, and 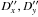 are the residuals with respect to the theory of Lainey et al. (2009).
are the residuals with respect to the theory of Lainey et al. (2009).
Table 5 gives a fragment of the first section of astrometric results.
The data in the second section are given by the following set of fields: the date, the type of the phenomenon (eclipse or occultation) including the satellite numbers, the observatory code, the time instant t∗ in the UTC scale, the position angle A, the precision σalong of the apparent position along the apparent relative trajectory of the satellite as obtained with the least-squares method. Differences in the apparent relative position of the satellites along the apparent relative trajectory obtained from observation and determined from the theory of Lainey et al. (2009) are given in the column (O–C)along. In addition, a sign R is assigned showing the reason why only one coordinate was determined: 0 for a total mutual eclipse or occultation observed, 1 for the results following from low-quality photometry. In these cases the apparent relative position of the satellite measured across the apparent trajectory cannot be determined accurately enough and therefore position angles can be determined only up to ±180° (A ± 180°).
Table 6 gives a fragment of the second section of the astrometric results.
Tables 5 and 6 are available in electronic form from the Natural Satellites Data Center service3.
7. Estimation of the accuracy of the derived astrometric results
The following estimates of the accuracy of the derived astrometric results were made. The least-squares method yields standard errors σx, σy for the parameters 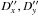 derived from the observed lightcurves. These errors are due to random errors of photometry and characterize the internal accuracy of astrometric results. We have calculated the r.m.s. values of these estimates for the 365 best astrometric results taken from Table 5 with Q = 0 (some 15 observations with Q> 0 were also excluded). These estimates are listed in Table 7 as total random errors.
derived from the observed lightcurves. These errors are due to random errors of photometry and characterize the internal accuracy of astrometric results. We have calculated the r.m.s. values of these estimates for the 365 best astrometric results taken from Table 5 with Q = 0 (some 15 observations with Q> 0 were also excluded). These estimates are listed in Table 7 as total random errors.
The values 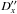 and
and 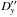 show an agreement of the theory by Lainey et al. (2009) with the obtained astrometric results. The values
show an agreement of the theory by Lainey et al. (2009) with the obtained astrometric results. The values 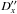 are residuals in right ascension and
are residuals in right ascension and 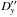 in declination. Therefore we have also calculated the total r.m.s. of all
in declination. Therefore we have also calculated the total r.m.s. of all 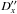 and
and 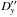 computed over the 365 best observations mentioned above. These estimates are given in Table 7 as r.m.s. of O–C.
computed over the 365 best observations mentioned above. These estimates are given in Table 7 as r.m.s. of O–C.
Estimates of the accuracy of the results of astrometric reduction performed to determine two relative coordinates of satellites X′′(t∗), Y′′(t∗).
8. Conclusions
We reduced the entire database of photometric observations of the mutual occultations and eclipses of the Galilean satellites of Jupiter made during the international campaign in 2009 to determine the topocentric or heliocentric angular differences for satellite pairs at 457 time instants on the time interval from April 17, 2009 to December 24, 2009.
The standard errors of the relative satellite coordinates due to the random errors of the photometry are equal to 18.4 mas and 15.6 mas in right ascension and declination, respectively. For successful observations, the r.m.s. of O–C residuals with respect to the theory by Lainey et al. (2009) are equal to 45.8 mas and 81.1 mas in right ascension and declination, respectively, and the mean O–C residuals are equal to –2 mas and –9 mas in right ascension and declination, respectively, for mutual occultations and –6 mas and +1 mas in right ascension and declination, respectively, for mutual eclipses. For 23 observations only the position angle was derived.
We now look forward to observing the next mutual events: the occurrence will take place from September 2014 to July 2015. The occurrence will be very favorable since the maximum of events will occur at the opposition of Jupiter with the Sun. Contrary to the 2009 occurrence that was more favorable for the southern hemisphere (Jupiter had a delination equal to –10 degrees), the 2014–15 occurrence will be more favorable for the northern hemisphere (Jupiter will have a declination equal to +20 degrees). The site of the campaign is available at the address: http://www.imcce.fr/phemu/.
Ephemerides of the mutual eclipses and occultations of the Galilean satellites of Jupiter in 2014–2015 with local observational conditions is available at the address: http://www.imcce.fr/hosted_sites/saimirror /nsszph515he.htm.
http://www.imcce.fr/ nsdc or on the ftp server at ftp://ftp.imcce.fr/ pub/NSDC/ jupiter/raw_data/ phenomena/ mutual/2009/ and at http://www.sai.msu.ru/neb/nss/index.htm
Acknowledgments
This work was supported by the Russian Foundation for Basic Research (project no. 12-02-00294), by The European contract ESPaCE (FP7-grant agreement 263466), by the Scientific Council of Paris Observatory, by the CNRS PICS 3840 France-Russia, by the Programme National de Planétologie (CNES and CNRS) and by the National Science Foundation of China (Grant No 11273014) and the Fundamental Research Funds for the Central Universities.
References
- Arlot, J. E. 2008, A&A, 478, 285 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arlot, J. E., Thuillot, W., Barroso, J., et al. 1992, A&AS, 92, 151 [NASA ADS] [Google Scholar]
- Arlot, J. E., Ruatti, C., Thuillot, W., et al. 1997, A&AS, 125, 399 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arlot, J.-E., Thuillot, W., Ruatti, C., et al. 2006, A&A, 451, 733 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arlot, J. E., Thuillot, W., Ruatti, C., et al. 2009, A&A, 493, 1171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dias-Oliveira, A., Vieira-Martins, R., Assafin, M., et al. 2013, MNRAS, 432, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Domingue, D., & Verbiscer, A. 1997, Icarus, 128, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Emel’yanov, N. V. 2000, Sol. Syst. Res., 34, 226 [Google Scholar]
- Emel’yanov, N. V. 2003, Sol. Syst. Res., 37, 314 [Google Scholar]
- Emelyanov, N. V. 2009, MNRAS, 394, 1037 [NASA ADS] [CrossRef] [Google Scholar]
- Emelyanov, N. V., & Gilbert, R. 2006, A&A, 453, 1141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Emelyanov, N. V., & Vashkov’yak, S. N. 2009, Sol. Syst. Res., 43, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Emelyanov, N. V., Andreev, M. V., Berezhnoi, A. A., et al. 2011, Sol. Syst. Res., 45, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Hapke, B. 1981, J. Geophys. Res., 86, 3039 [Google Scholar]
- Hapke, B. 1984, Icarus, 59, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Lainey, V., Duriez, J. E., & Vienne, A. 2004a, A&A, 420, 1171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lainey, V., Arlot, J. E., & Vienne, A. 2004b, A&A, 427, 371 [Google Scholar]
- Lainey, V., Arlot, J. E., Karatekin, O., & van Hoolst, T. 2009, Nature, 459, 957 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lieske, J. H., 1977, A&A, 56, 333 [NASA ADS] [Google Scholar]
- Makarova, E. A., Kharitonov, A. V., Kaznachevskaja, T. V., et al. 1998, Balt. Astron., 7, 467 [Google Scholar]
- McEwen, A. S., Johnson, T. V., & Matson, D. L. 1988, Icarus, 75, 450 [NASA ADS] [CrossRef] [Google Scholar]
- Morrison, D., & Morrison, N. D. 1977, in Planetary satellites (Tucson: University of Arizona Press), 363 [Google Scholar]
- Prokof’eva-Mikhailovskaya, V. V., Abramenko, A. N., Baida, G. V., et al. 2010, Bull. Crimean Astrophys. Obs., 106, 68 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Estimates of the accuracy of the results of astrometric reduction performed to determine two relative coordinates of satellites X′′(t∗), Y′′(t∗).
All Figures
 |
Fig. 1 J2 occults J3 on May 23, 2009: this observation shows a grazing event with a small magnitude drop. The signal is noisy. The noise could be reduced with a longer integrating time for each point. |
| In the text | |
 |
Fig. 2 J3 eclipses J2 on August 12, 2009: the flat bottom of the lightcurve for the model and for the observation. |
| In the text | |
 |
Fig. 3 J3 eclipses J2 on July 28, 2009: the observation started a little late. The minimum of the lightcurve is clearly visible allowing the reduction. |
| In the text | |
 |
Fig. 4 J4 eclipses J1 on May 16, 2009: the lightcurve is perfectly modelled and the observation is not noisy. |
| In the text | |
 |
Fig. 5 J1 occults J3 on May 8, 2009: the observation is noisy, but the lightcurve is perfectly modelled. As in Fig. 1, a longer integrating time for each point could decrease the noise. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


