| Issue |
A&A
Volume 572, December 2014
|
|
|---|---|---|
| Article Number | A6 | |
| Number of page(s) | 13 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201323139 | |
| Published online | 18 November 2014 | |
HST observations of the limb polarization of Titan
1 ETH Zurich, Institute of Astronomy, Wolfgang-Pauli-Str. 27, 8093 Zurich, Switzerland
e-mail: bazzon@astro.phys.ethz.ch
2 Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
Received: 27 November 2013
Accepted: 5 September 2014
Context. Titan is an excellent test case for detailed studies of the scattering polarization from thick hazy atmospheres. Accurate scattering and polarization parameters have been provided by the in situ measurements of the Cassini-Huygens landing probe. For Earth-bound observations Titan can only be observed at a backscattering situation, where the disk-integrated polarization is close to zero. However, with resolved imaging polarimetry a second order polarization signal along the entire limb of Titan can be measured.
Aims. We present the first limb polarization measurements of Titan, which are compared as a test to our limb polarization models.
Methods. Previously unpublished imaging polarimetry from the HST archive is presented, which resolves the disk of Titan. We determine flux-weighted averages of the limb polarization and radial limb polarization profiles, and investigate the degradation and cancelation effects in the polarization signal due to the limited spatial resolution of our observations. Taking this into account we derive corrected values for the limb polarization in Titan. The results are compared with limb polarization models, using atmosphere and haze scattering parameters from the literature.
Results. In the wavelength bands between 250 nm and 2 μm a strong limb polarization of about 2 − 7% is detected with a position angle perpendicular to the limb. The fractional polarization is highest around 1 μm. As a first approximation, the polarization seems to be equally strong along the entire limb. The comparison of our data with model calculations and the literature shows that the detected polarization is compatible with expectations from previous polarimetric observations taken with Voyager 2, Pioneer 11, and the Huygens probe.
Conclusions. Our results indicate that ground-based monitoring measurements of the limb-polarization of Titan could be useful for investigating local haze properties and the impact of short-term and seasonal variations of the hazy atmosphere of Titan. Planets with hazy atmospheres similar to Titan are particularly good candidates for detection with the polarimetric mode of the upcoming planet finder instrument at the VLT. Therefore, a good knowledge of the polarization properties of Titan is also important for the search and investigation of extra-solar planets.
Key words: polarization / planets and satellites: atmospheres / scattering / radiative transfer / instrumentation: polarimeters
© ESO, 2014
1. Introduction
Solar light reflected from planets, moons, and smaller objects is polarized. This basic property of light reflection provides a powerful diagnostic tool for the remote investigation of the scattering particles in atmospheres and the reflecting surfaces of solar system bodies.
Polarization studies of Titan are particularly well suited to studying the scattering polarization from a hazy atmosphere. The hazy atmosphere of Titan produces a very strong polarization signal over a wide wavelength range. At quadrature phase α ≈ 90°, the fractional polarization of Titan from the UV to the R band is p ≈ 50%, as measured by the Pioneer 11 (Tomasko & Smith 1982) and Voyager 2 (West et al. 1983) spacecrafts. Furthermore, thanks to the joint NASA-ESA Cassini-Huygens satellite mission, Titan’s surface and atmospheric structure are known in great detail. In particular, the measurements made inside Titan’s atmosphere, made available by the Huygens landing probe, have provided accurate scattering and polarization parameters for the haze particles (e.g., Brown et al. 2010; Tomasko et al. 2008).
For Earth-bound instruments the atmosphere of Titan can only be observed at very limited phase angles α ≲ 5°, where the disk-integrated polarization is close to zero, and the polarimetric properties can only be investigated if disk-resolved imaging polarimetry is available. In this work we present previously unpublished imaging polarimetry from the HST archive which resolves the disk of Titan and clearly shows a strong limb polarization effect. Together with literature values for the albedo Ag and the quadrature polarization p(90°) of Titan, our limb polarization measurements can now be used to test polarization models for a haze scattering atmosphere, and we can make predictions for the detection and characterization of reflected light of extra-solar planets.
The limb polarization is a well-known second order scattering effect of reflecting atmospheres with predominantly Rayleigh-type scattering processes (e.g., van de Hulst 1980). In general, single backscattering with scattering angles ~180° would produce a very small polarization signal or no signal at all. Thus, the polarization measured at the limb arises from second order and also higher order scatterings by light that is scattered sideways, i.e., more or less parallel to the limb, and then scattered back to the observer. The polarization angle induced by Rayleigh scattering, i.e. single dipole-type scattering, is perpendicular to the propagation direction of the incoming photon. Hence, the position angle of polarization is perpendicular to the limb everywhere.
Over the last 20 years, Titan’s thick and hazy atmosphere has been monitored and intensively studied by spectral HST observations, revealing strong local albedo variations mainly caused by seasonal migration of haze from one hemisphere to another (Lorenz et al. 2004, and references therein). The most prominent features are a varying north-south asymmetry, a dark polar hood that is most prominent in the UV, and a detached haze layer lying only ~200 km above the optical limb of Titan (e.g., Lorenz et al. 2004, 2006). Observations of Titan from the ground, e.g., using the upcoming SPHERE instrument at the VLT (Beuzit et al. 2008), consisting of state-of-the-art imagers and polarimeters, will have the advantage of a much higher spatial resolution and a broader wavelength coverage. Therefore, a consistent monitoring program of Titan’s atmosphere from the ground could potentially be useful for investigating the temporal changes in the polarization structure along the limb, and for constraining local haze properties of Titan.
After the description of the observational data and the basic data reduction in Sects. 2 and 3 respectively, we discuss the intensity images in Sect. 4 and compare them with the literature. In Sect. 5 we derive the Stokes images for all our wavelength bands, which are then converted into radial limb polarization images in Sect. 6. There, we discuss the radial polarization profiles and the advantage of disk-integrated radial polarization measurements, and we explain how we correct our images for the polarization degradation caused by a PSF smearing effect. In Sect. 7 we describe our radiative transfer model for Titan, and we compare the model with our limb polarization results and literature values for the geometric albedo Ag and the quadrature polarization p(90°) of Titan. The last section gives a summary and discusses the prospects for a polarimetric monitoring program of Titan and for the detection and investigation of extra-solar haze planets.
2. Observations
We reduced and analyzed imaging polarimetry of Titan from the HST archive1 for which only the intensity images have been published (Lorenz et al. 2006) but not the polarization data. The data were recorded with the ACS HRC and the NICMOS instruments in seven filters covering wavelengths 0.25 μm−2 μm. Polarimetry is achieved with three subsequent measurements, using three polarizers with different orientations. Titan was observed in 2002 during two visits on November 27 and December 2, i.e., shortly after southern summer solstice that occurred in late October 2002, and with the north pole of Titan on the hidden hemisphere. Table 1 gives an overview of the observational parameters, the used instruments and corresponding filters, the total exposure times, and the plate scales.
For broad-band observations the nominal filter wavelength may differ significantly from the average wavelength of the photons registered in the polarization map. Similarly the evaluation of the reflected-flux weighted albedo Ag,eff for a given filter considers a weighting with the effective spectral distribution of the registered photons, taking into account the wavelength dependence of the instrument, the solar photon spectrum, and the albedo of Titan.
 |
Fig. 1 Upper panel: geometric albedo of Titan (full line) and effective albedos Ag,eff and wavelengths λeff for the HST filter polarimetry (crosses). The dashed line illustrates the solar spectrum. Lower panel: normalized filter efficiency curves and the normalized wavelength distribution of the registered photons. |
Figure 1 illustrates the spectral dependence of the full disk albedo of Titan from the mid-UV to the near-IR (McGrath et al. 1998 for the UV, Karkoschka 1998 for the visual, Negrão et al. 2006 for the near-IR) assuming Titan’s optical radius varying with λ according to the Toon et al. (1992) radius RT. The solar irradiance photon spectrum derived from Thuillier et al. (2004) is given by the dashed line. The normalized instrument efficiencies in the different HST filters and the calculated spectral distribution of the registered photons are also indicated. We use the median wavelengths of the individual photon distributions as effective filter wavelengths λeff, and the reflected-flux weighted values for the effective albedos Ag,eff for each filter. The corresponding values are indicated in Fig. 1 and Table 3 lists the derived values and RT(λeff).
We note that when looking specifically at the limb the methane bands are weaker and center-to-limb differences in the albedo spectrum are present (e.g., Smith et al. 1996; Lorenz et al. 2004, 2006). However, we mainly focus on the derivation of disk-integrated albedo and limb polarization values (Sect. 6.3).
The effective filter wavelengths λeff are shifted to longer wavelength for the UV/blue filters because of the steep photon spectrum. The effective albedos Ag,eff are relevant for the filters covering spectral regions with strong CH4 absorption bands. They are about 20% higher for the NIC1 and 40% higher for the NIC2 passbands than the simple mean. For the F250W and the F330W filters the difference is < 5%, and for the other filters the difference is ~10% or less (steep flux gradient combined with systematic albedo gradient).
Observational parameters and summary of the HST polarimetry used in this work.
3. Basic data reduction
The data provided by the HST data reduction pipeline are already corrected for bias, dark, flatfield, and image distortion. However, in the case of the ACS data the pipeline drizzled, combined images showed a strange stripe pattern which was caused by incorrectly set bits in the data quality mask that are used for identifying pixels flagged as cosmic rays by MultiDrizzle2. Using the instructions provided by the stsdas3 helpdesk we reset the dq_bits and re-run multidrizzle using the standard settings.
Both the ACS and the NICMOS instrument contain sets of three linear polarizer filters with their relative polarization directions oriented according to 0°, 60°, 120° and 0°, 120°, 240° respectively. In the first data reduction step the basic pipeline processed images were cut out and aligned to subpixel accuracy of ± 0.1 pixel. Then the images corresponding to the Stokes parameters I, Q, and U were calculated and corrected for instrumental polarization.
3.1. Calculation of Stokes parameters for ACS
In case of ACS the Stokes parameters are calculated according to: ![\begin{eqnarray*} I &=& \left(\frac{2}{3}\right)\left[i_0 \cdot c_{0}(\lambda) + i_{60} \cdot c_{60}(\lambda) + i_{120} \cdot c_{120}(\lambda)\right], \\ Q& =& \left(\frac{2}{3}\right)\left[2 i_0 \cdot c_{0}(\lambda) - i_{60} \cdot c_{60}(\lambda) - i_{120} \cdot c_{120}(\lambda)\right] \left( \frac{T_{\parallel} + T_{\perp} }{T_{\parallel} - T_{\perp}} \right) , \\ U &= &\left(\frac{2}{\sqrt{3}}\right)\left[i_{60} \cdot c_{60}(\lambda) - i_{120} \cdot c_{120}(\lambda)\right] \left( \frac{T_{\parallel} + T_{\perp} }{T_{\parallel} - T_{\perp}} \right), \end{eqnarray*}](/articles/aa/full_html/2014/12/aa23139-13/aa23139-13-eq42.png) whereas i∗ indicate the intensity images corresponding to the three polarizer orientations, c∗ are corresponding correction factors calibrating the polarization zero-point, and the T∗ parameters correct for polarization cross-talks caused by leakages of the polarizing filters. The calibration parameters are given in the HST calibration handbook (Fig. 5.3, Table 6.3) which we summarize in Table 2. According to the handbook for the ACS camera the residual instrumental polarization uncertainty should be at the one-part-in-ten level for highly polarized sources and at the 1% level for weakly polarized targets.
whereas i∗ indicate the intensity images corresponding to the three polarizer orientations, c∗ are corresponding correction factors calibrating the polarization zero-point, and the T∗ parameters correct for polarization cross-talks caused by leakages of the polarizing filters. The calibration parameters are given in the HST calibration handbook (Fig. 5.3, Table 6.3) which we summarize in Table 2. According to the handbook for the ACS camera the residual instrumental polarization uncertainty should be at the one-part-in-ten level for highly polarized sources and at the 1% level for weakly polarized targets.
For the F250W filter no calibration parameters are provided by the HST handbook. However, because of symmetry reasons one can assume that to first order the fractional polarization at the center of the apparent disk of Titan should be zero: 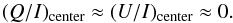 Therefore, by using extrapolated values for c∗ as starting points, and by minimizing the fractional polarization around the center of Titan, we determined estimates for the F250W calibration parameters indicated in Table 2. Especially for the integrated radial polarization described in Sect. 6 these calibration parameters produce very reasonable results which are consistent with the other wavelengths.
Therefore, by using extrapolated values for c∗ as starting points, and by minimizing the fractional polarization around the center of Titan, we determined estimates for the F250W calibration parameters indicated in Table 2. Especially for the integrated radial polarization described in Sect. 6 these calibration parameters produce very reasonable results which are consistent with the other wavelengths.
Calibration parameters for ACS polarimetry.
3.2. Calculation of Stokes parameters for NICMOS
In case of NICMOS the HST handbook provides the user with two coefficient matrices M1;2 to calculate the Stokes parameters of NIC1 and NIC2 respectively: 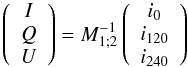 with the matrices
with the matrices 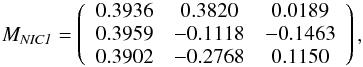
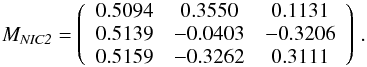 For NIC1 the coefficient matrix calibration is not perfect and a residual instrumental polarization at a level of pinst. ≈ 1.2 − 1.5% was reported (see Batcheldor et al. 2009). Furthermore, for bright targets ghost images are present in two NIC1 polarization filters (i0°,i240°). In case of NIC2 the instrumental effects are very well calibrated, and uncertainties as low as pinst. ≈ 0.2% should be achievable with bright objects. Both for NIC1 and NIC2, this is in good agreement with our findings for the Titan polarization in the disk center in Sect. 5.
For NIC1 the coefficient matrix calibration is not perfect and a residual instrumental polarization at a level of pinst. ≈ 1.2 − 1.5% was reported (see Batcheldor et al. 2009). Furthermore, for bright targets ghost images are present in two NIC1 polarization filters (i0°,i240°). In case of NIC2 the instrumental effects are very well calibrated, and uncertainties as low as pinst. ≈ 0.2% should be achievable with bright objects. Both for NIC1 and NIC2, this is in good agreement with our findings for the Titan polarization in the disk center in Sect. 5.
4. Intensity images
The used HST-dataset was mainly taken to study seasonal effects of the stratospheric haze on Titan, and an analysis of the spectro-photometric data is given by Lorenz et al. (2004, 2006). In particular, they describe and explain in detail the varying dark polar hood and the north-south asymmetry measured in different narrow-band filters.
The dark polar hood was first seen in 1980 by Voyager 1 around the north, and disappeared from the south pole in 2002−2003 (Lorenz et al. 2006). Most probably, the polar hood is associated to a downwelling during the long polar night, redistributing haze from the summer hemisphere towards the winter pole (Rannou et al. 2002; Lorenz et al. 2006). This process then also creates the detached haze layer as the haze is horizontally drawn from beneath the formation zone.
Lorenz et al. (2004) find that in the narrow-band filters the north-south asymmetry is reversed between the blue (439 nm) and the red (889 nm), and almost absent at 619 nm. In the blue Titan is brighter in the south than in the north and vice versa in the red methane bands. In the near-IR, the variation of the asymmetry with wavelength is dramatic, and different narrow-band filters may see different reversions of the north-south asymmetry as they are probing different altitude regions.
 |
Fig. 2 Intensity cuts/profiles through the disk center for the F250W band (bottom), the F435W band (middle), and the NIC1 band (top). The solid line indicates the north-south profile through the planetary poles, and the dashed line is the east-west profile perpendicular to the polar axis respectively. |
The north-south asymmetry is also visible in our broad-band images ranging from 0.3−2 μm of the same HST visit as the narrow-band data of Lorenz et al. (2004), and it is in qualitative agreement with the spectro-photometric analysis by Lorenz et al. (2004, 2006). Figure 2 shows N-S and E-W profiles of Titan for the F330W band, the F435W band, and the NIC1 band. Intensity images for the bands F330W, F435W, F625W, NIC1, and NIC2 are given in the left panel of Fig. 5. The nominal optical radius of Titan, the south pole, and the equator are also indicated. The images are normalized such that 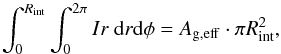 (1)where Ag,eff indicates the effective albedo given in Table 3 and Fig. 1, and Rint = 0.75″ is the integration radius, which is greater than the nominal radius of Titan RTitan = 0.44″.
(1)where Ag,eff indicates the effective albedo given in Table 3 and Fig. 1, and Rint = 0.75″ is the integration radius, which is greater than the nominal radius of Titan RTitan = 0.44″.
5. Stokes Q and U images for Titan
In Fig. 3 Stokes Q and U images in the F775W band are shown. The same highly symmetric quadrant pattern is present in all of our data. This butterfly pattern is real and it is practically impossible to artificially create such a pattern by misalignments of the three polarization images i∗ or other spurious effects. The gray scale is normalized to the central intensity Icenter of the planetary disk and goes from −0.02 Icenter (black) to + 0.02 Icenter (white). At the center Q and U are essentially zero (Q/I,U/I ≲ ± 0.2%).
The butterfly polarization pattern is typical for a centro-symmetric scattering geometry. For example, the Rayleigh-scattering atmospheres of Uranus and Neptune show this pattern of radial limb polarization (Schmid et al. 2006b). For all our data the pattern is highly symmetric, indicating that the limb polarization has similar strength along the entire limb of Titan. The strength of the limb polarization increases with wavelength until it peaks in the 1 μm band measurement after which it decreases again.
 |
Fig. 3 Stokes Q (left) and U (right) images in the F775W band. The south pole and the equator are indicated. The gray scale is normalized to the central intensity of Stokes I by ± 0.02 Icenter. |
Polarization results for Titan.
We do not see a significant imprint of the north-south asymmetry of Titan (Sect. 4) in the polarization images. To study the polarization along the north-south (and east-west) direction the polarization pattern was aligned with respect to the polar axis of Titan by 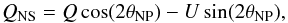 where θNP is the angle between the polarizer reference axis and the polar axis of Titan.
where θNP is the angle between the polarizer reference axis and the polar axis of Titan.
For all filters we calculate disk-integrated Stokes fluxes ΣI, ΣQ, and ΣU by summing up all counts within the integration radius Rint = 0.75″ from the apparent disk center of the I, Q, and U images respectively. Rint includes the halo of the planet which is greater than the nominal limb at RTitan = 0.44″. We then calculate disk-integrated fractional polarization parameters for Stokes Q (and similarly U): 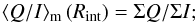 (2)⟨ Q/I ⟩ m and ⟨ U/I ⟩ m are equivalent to a measurement with aperture polarimetry, where the aperture is larger than the planet. The results for all filters are given in Table 3. The disk-integrated polarization of Titan is essentially zero (p< 0.2%) for all filters in agreement with Veverka (1973) and Zellner (1973), except for F330W and for NIC1; these results are not real and can be explained by instrumental effects.
(2)⟨ Q/I ⟩ m and ⟨ U/I ⟩ m are equivalent to a measurement with aperture polarimetry, where the aperture is larger than the planet. The results for all filters are given in Table 3. The disk-integrated polarization of Titan is essentially zero (p< 0.2%) for all filters in agreement with Veverka (1973) and Zellner (1973), except for F330W and for NIC1; these results are not real and can be explained by instrumental effects.
As explained in Sect. 3.2NIC1 is not well calibrated for instrumental polarization and between pinst. ≈ 1.2% − 1.5% residual polarization is expected. We are measuring ⟨ Q/I ⟩ m = 1.5% despite the expectation that Titan has zero net polarization. The same instrument offset is also seen at the center of the disk which should be zero because of symmetry reasons. Similarly for the F330W measurement the center of the Stokes Q and U images is not zero indicating residual instrumental polarization at the level of pinst. ≈ 0.8% in Q and pinst. ≈ 0.2% in U respectively.
The absence of a net polarization in the disk averages indicates that the limb polarization has a similar strength along the entire limb for all observed bands. We note that the disk-integrated parameters ⟨ Q/I ⟩ m and ⟨ U/I ⟩ m can hardly be affected by inaccuracies in the image centering procedure or other spurious effects due to the data reduction. The statistical 1σ measuring error is Δp< 0.1% as estimated for the measuring error of the integrated radial polarization ⟨ Ur/I ⟩ m in Sect. 6 which is independent of any residual instrumental offset.
6. The radial polarization
The polarization flux of an object is given by 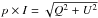 . However, because of the squares in this formula, large systematic bias errors are introduced if the absolute value of one or both measured signals | Q | and | U | is not significantly higher than the measuring noise ΔQ and ΔU. In our Titan data there is ΔQ ≈ | Q | and ΔU ≈ | U | in the middle of the planetary disk, and between positive and negative quadrants in the butterfly pattern. Therefore one should not use the polarized flux p × I or the normalized polarization p as measuring parameter. We adopt radial Stokes parameters, which are particularly well-suited for characterizing centro-symmetric polarization patterns of planets (e.g., Schmid et al. 2006b).
. However, because of the squares in this formula, large systematic bias errors are introduced if the absolute value of one or both measured signals | Q | and | U | is not significantly higher than the measuring noise ΔQ and ΔU. In our Titan data there is ΔQ ≈ | Q | and ΔU ≈ | U | in the middle of the planetary disk, and between positive and negative quadrants in the butterfly pattern. Therefore one should not use the polarized flux p × I or the normalized polarization p as measuring parameter. We adopt radial Stokes parameters, which are particularly well-suited for characterizing centro-symmetric polarization patterns of planets (e.g., Schmid et al. 2006b).
The radial Stokes parameters Qr and Ur describe the polarization in radial and tangential direction on the disk of Titan. They are given by 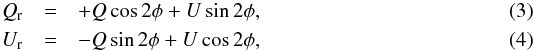 where φ is the polar angle of a given position (x,y) on the apparent planetary disk (disk center (x0,y0)) with respect to the polarizer reference direction:
where φ is the polar angle of a given position (x,y) on the apparent planetary disk (disk center (x0,y0)) with respect to the polarizer reference direction: 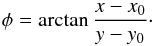 Qr> 0 is equivalent to a radial polarization or a polarization perpendicular to the limb, while Qr< 0 indicates a tangential polarization component. Ur describes the polarization in the directions ± 45° with respect to the radial direction.
Qr> 0 is equivalent to a radial polarization or a polarization perpendicular to the limb, while Qr< 0 indicates a tangential polarization component. Ur describes the polarization in the directions ± 45° with respect to the radial direction.
6.1. Radial stokes Qr and Ur images for Titan
For all observed bands we calculated radial polarization images Qr and Ur. In case of the F330W and NIC1 observations the Stokes Q and U images were first corrected for residual instrumental polarization (see Sect. 5), derived from the disk center which is expected to be unpolarized. Figure 4 shows Qr and Ur for Titan in the F775W filter. In all of our data the limb polarization is clearly visible as a bright ring with positive Qr polarization and essentially zero Ur polarization. Except for the F250W filter, the level of the Ur polarization is typically about 10 times lower than the positive Qr signal along the limb. For the F250W filter the Ur polarization is about 3 times lower than Qr. Thus Qr dominates in all filters. In Fig. 5 we show images of Qr as well as corresponding Stokes I for the rest of our data. The gray scale of the radial polarization images in Figs. 4 and 5 is scaled to the central intensity Icenter by ± 0.02·Icenter, and the intensity images are normalized to the effective albedo Ag,eff according to Eq. (1).
 |
Fig. 4 Radial Stokes Qr (left) and Ur (right) images in the F775W band. The south pole and the equator are indicated. The gray scale is normalized to the central intensity of Stokes I by ± 0.02 Icenter. |
6.2. Polarization as function of radius
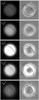 |
Fig. 5 Intensity (left) and radial polarization images Qr (right) in the F330W, F435W, F625W, NIC1, and NIC2 band (top to bottom). The intensity images are normalized to |
 |
Fig. 6 Titan radial profiles for intensity I (upper panel, thick lines) and radial polarization Qr (upper panel, thin lines) in the F435W (dash-dot), F775W (dash) and NIC1 (solid) filters. Both I and Qr are normalized to the peak flux at r = 0. The lower panel shows the corresponding normalized radial polarization Qr/I. |
The observed polarization of Titan is essentially centro-symmetric, and contrary to the strong north-south albedo asymmetry, the corresponding imprint in the radial polarization flux is either absent or much weaker. In the fractional radial polarization images Qr/I we see marginal north-south differences with higher polarization in the north for the bands shorter than 1 μm, the opposite effect in the NIC1 band, and about equal polarization for the NIC2 band. However, these results are not significant and on the order of our systematic uncertainties Δp/p ≈ 0.05 − 0.1.
In the infrared there is a similar weak indication for an east-west asymmetry of Qr/I, whereas for the NIC1 band the polarization seems to be higher in the east, which is inverted for the NIC2 band. It also seems that for wavelengths shorter than 1 μm the maximum polarization is higher at the eastern and western limbs than in the north and south, whereas for the NIC1 band the polarization in east-west and north-south is of about equal strength, and for NIC2 the polarization is higher at the poles. However, the quality of our data is not good enough to draw firm conclusions, and at least part of the polarization differences mentioned above could be due to systematics in the data reduction, e.g., slight misalignments of corresponding polarization images coupled with strong intensity gradients at the limb.
The detection of structure in the limb polarization would be very interesting for investigating local haze properties, e.g., such as particle size differences of the photochemical haze between the morning and the evening limb of Titan. Observations with higher polarimetric sensitivity and higher spatial resolution are required for such studies.
For the moment, assuming a rotational symmetry for the polarization structure seems to be a reasonable first approximation, and we construct rotationally averaged, radial profiles for the polarization, the normalized polarization, and the intensity. The results for the F435W, F775W, and NIC2 filters are shown in Fig. 6.
In all filters the radial profiles look very similar. The polarization Qr in the disk center at R = 0 is essentially zero. The normalized radial polarization Qr/I increases steadily with radius until it peaks at around RTitan = 0.44″ after which it decreases again until the photon noise starts dominating the measurements. Similarly, the radial polarization flux Qr also increases with radius but only up to a radius slightly smaller than RTitan, and then it decreases farther out to zero in step with the intensity profile.
Both Qr/I and Qr increase with wavelength until they peak in the NIC1 band at 1 μm. Then, in the NIC2 band at 2 μm the polarization has again significantly dropped. Using tentative fits for the radial profiles, we measure maximum fractional radial polarization values Qr/I of 1.8% for the F250W band, up to 6.9% for the NIC1 band, and 3.4% for the NIC2 band. The values for all filters are given in Table 3. However we note that these values are not yet corrected for the PSF smearing effect described in Sect. 6.4.
6.3. Disk-integrated radial polarization
Similar to the calculation of disk-integrated Stokes parameters in Sect. 5 disk-integrated radial Stokes parameters ⟨ Qr/I ⟩ m and ⟨ Ur/I ⟩ m are calculated for all filters. Because of the intrinsic rotational symmetry of Eqs. (2)−(4), ⟨ Qr/I ⟩ m and ⟨ Ur/I ⟩ m have the additional advantage that any instrumental polarization offset or gradient cancels out. Therefore, we do not need to correct the instrumental offset described in Sect. 5 for the F330W and NIC1 filter to calculate corresponding disk-integrated radial polarization values. This was also verified by calculating ⟨ Qr/I ⟩ m and ⟨ Ur/I ⟩ m for the NIC1 data, both with and without correction of the instrumental offset, which showed that the difference is less than Δp = 0.01%.
A strong positive signal is obtained for the disk-integrated radial polarization ⟨ Qr/I ⟩ m, while ⟨ Ur/I ⟩ m is essentially zero (Table 3). The 1σ measuring error is Δp< 0.1% as estimated from the assumption ⟨ U/I ⟩ m = 0. Both ⟨ Qr/I ⟩ m and ⟨ Ur/I ⟩ m are only very weakly affected by small asymmetries caused by inaccuracies in the image centering procedure or other spurious effects due to the data reduction. However, strong asymmetric perturbations such as strong ghosts could probably bias the result. Anyway, except for NIC1 we do not see any ghosts in our Qr and Ur images (Sect. 6.1). In case for NIC1 it is known that weak ghosting is present for bright sources but we estimate that the impact on the integrated radial polarization is less than Δp/p = 0.01 (see also Sect. 7.3).
The integrated radial polarization ⟨ Qr/I ⟩ is a good parameter for characterizing the overall limb polarization of a planet. Since Qr is either positive or close to zero everywhere on the disk no polarization compensation effect is present. Furthermore, there is ⟨ Qr/I ⟩ ≫ ⟨ Ur/I ⟩ ≈ 0, so that we can approximate 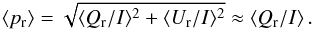
6.4. Correction for the PSF smearing effect
The point spread functions (PSFs) of HST ACS and NICMOS have a finite width given by the telescope diffraction ~λ/D, and they are affected by optical aberrations, geometric distortions, and in case of ACS a long-wavelength halo produced by the detector itself. This leads to extended PSF wings which limit the resolution of the HST observations. Therefore, the measured integrated limb polarizations ⟨ Qr/I ⟩ m and ⟨ Ur/I ⟩ m need to be corrected by the inverse of a degradation factor CPSF, accounting for a polarization cancelation due to PSF smearing.
We produced simulated ACS and NICMOS PSFs for all wavelengths, using the Tiny Tim4 PSF simulation software package for the HST (see Krist et al. 2011). Figure 7 compares the encircled energy of these PSFs to the encircled energy of Gaussian PSFs with FWHM = λ/D. One can see that for the Gaussian PSFs essentially all the energy is contained within half the radius of Titan. However, in the NIC2 band up to 45% of the energy is smeared over an area larger than half of the radius of Titan. For the ACS filters and NIC1 the fraction originating from R> 0.5 RTitan is considerably smaller but still about 15% and 20% respectively.
 |
Fig. 7 Encircled energies for HST PSFs (thick lines) and Gaussian PSFs (thin lines): ACS F625W (solid), NIC1 POL0S (dashed), and NIC2 POL0L (dash-dot). |
Because of these extended PSF wings, the opposite polarization components + Q and −Q overlap and cause a reduction in the resulting net polarization. In the most extreme case of an unresolved centro-symmetric planetary disk, the polarization cancelation would be perfect and only a zero net polarization level could be measured. The compensation effect is stronger for longer wavelengths, where the diffraction limited spatial resolution of HST is not as good, and at the same time the PSF wings are stronger.
For an estimate of the polarization cancelation, we adopted our haze scattering model for the expected polarization pattern (see Sect. 7.2). From the model we constructed two-dimensional intensity images for i0, i90, i45, and i135, from which the corresponding Stokes Q and U images can be calculated by Q = i0 − i90 and U = i45 − i135. Similarly, we constructed smeared Stokes images Qs and Us by folding the i∗ images with the simulated HST PSFs. Figure 8 illustrates the cancelation effect in the Stokes Q image due to the HST PSF of ACS at F625W, NIC1 at 1 μm, and NIC2 at 2 μm.
 |
Fig. 8 Modeling of the degradation of the Titan polarization Q due to the cancelation of opposite polarization components + Q and −Q caused by the limited resolution; a) unlimited resolution; b) HST PSF at 630 nm (F625W); c) HST PSF at 1 μm (NIC1); and d) HST PSF at 2 μm (NIC2). The gray scale spans for all panels the range from −2% (black) to + 2% (white) of the peak intensity of the initial perfect intensity image. |
The Q and U images can then be converted into radial polarization images Qr and Ur, as for the observations. From Qr the integrated radial polarizations ⟨ Qr/I ⟩ and ⟨ Qr/I ⟩ s are calculated for the different filters in the same way as for the observations. The ratio between the clean and the smeared polarization then yields the factor for the expected degradation of the disk-integrated radial polarization 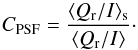 (5)The corresponding values of CPSF and the corrected limb polarization ⟨ Qr/I ⟩ for all filters are given in Table 3. Especially for NIC2 the degradation factor CPSF = 0.58 is low, while for the ACS bands and for NIC1 the degradation factor is about CPSF = 0.85 and CPSF = 0.74 respectively. The statistical 1σ error of the degradation factor is estimated to be about ΔCPSF = ± 0.01.
(5)The corresponding values of CPSF and the corrected limb polarization ⟨ Qr/I ⟩ for all filters are given in Table 3. Especially for NIC2 the degradation factor CPSF = 0.58 is low, while for the ACS bands and for NIC1 the degradation factor is about CPSF = 0.85 and CPSF = 0.74 respectively. The statistical 1σ error of the degradation factor is estimated to be about ΔCPSF = ± 0.01.
The polarization cancelation depends not on the strength, but on the geometric structure of the polarization pattern. Rayleigh scattering models indicate that the polarization pattern is very similar for the different model parameters (see Schmid et al. 2006b). Thus the degradation depends not significantly on the exact haze scattering parameters of the planet. A sanity check by recalculating CPSF using a Rayleigh scattering model indeed shows that within our 1σ error bars the results for CPSF were identical.
7. Comparison with limb polarization models
Titan is an excellent test case for detailed studies of the scattering polarization from a hazy atmosphere, and accurate scattering and polarization parameters are available from the in situ measurements of the Huygens landing probe (e.g., Brown et al. 2010; Tomasko et al. 2008). In the next section we describe the basic atmospheric structure that we used for our radiative transfer model, which is described in Sect. 7.2, and in Sect. 7.3 we compare the model with our limb polarization measurements and literature values for the geometric albedo Ag and the quadrature polarization p(90°) of Titan.
7.1. Atmospheric parameters
For our model we assume an atmosphere ranging from 0−1300 km. This includes Titan’s troposphere with its well defined tropopause at ~44 km (112 mbar), the stratosphere with the stratopause located at ~260−310 km (0.22−0.08 mbar; Fulchignoni et al. 2005; Vinatier et al. 2007), the mesosphere with the mesopause at ~494 km (0.002 mbar; Fulchignoni et al. 2005), and the thermosphere ranging up to ~1300 km (1.4 × 10-8 mbar).
The atmospheric composition is predominantly N2, with CH4 and H2 the second and third most abundant molecules respectively. Near the surface CH4 has an abundance of ~5%, falling to ~1.4% in the stratosphere (Brown et al. 2010). Because of its long chemical lifetime H2 is essentially uniformly mixed throughout the atmosphere with a mixing ratio ~0.1% (Courtin et al. 2008). A thick haze layer is located in the stratosphere, and a second detached haze layer lies just above the mesopause at around 500 km altitude (Porco et al. 2005). Above 700−800 km most of the methane is destroyed by photolysis.
 |
Fig. 9 Vertical optical depth τ for λ = 445 nm (dash-dot), λ = 775 nm (dash), λ = 940 nm (dot), λ = 1000 nm (methane absorption band, solid), and for λ = 1580 nm. |
For simplification, we assume the atmospheric composition to be solely made out of methane and nitrogen. The methane mole fraction fCH4(h) between h = 0 − 144 km altitude was taken from Brown et al. (2010), whereas above 140 km fCH4(h) was assumed to linearly drop to zero at an altitude of 600 km. We use the temperature T(h) and density ρ(h) profiles provided by the Huygens Atmospheric Structure Instrument (HASI)5, and the total molecular number densities and the Rayleigh scattering optical depth τRay(h,λ) are then calculated from the ideal gas law and the gas column density (see Appendix).
For the methane absorption coefficients κ(T,λ) we use the formula given by Karkoschka & Tomasko (2010). We note that below λ = 1 μm these coefficients are generally close to those by Karkoschka (1998).
A detailed model of the aerosol properties of Titan is given by Tomasko et al. (2008), based on measurements of the DISR instrument on the Huygens landing probe (Tomasko et al. 2002). The haze optical depth per unit path length τhaze(h,λ) is derived for three altitude regions, i.e., above 80 km, between 30−80 km, and below 30 km. On the one hand, Tomasko et al. (2008) describe the wavelength dependence by three different power laws, corresponding to the three altitude regions. Then on the other hand, the cumulative optical depth increases with decreasing altitude. Between 0−30 km and 30−80 km the increase is linear but with two different slopes, and above 80 km the increase is exponential with a scale height of 65 km.
The vertical optical depth is shown in Fig. 9 for five different wavelengths between λ = 445 nm and λ = 1580 nm, including the methane absorption band at λ = 1 μm. For wavelengths λ< 1 μm most of the light is scattered in the stratosphere between ~100−300 km altitude where τ ≈ 1, whereas for λ = 1.6 μm the light penetrates down to about 30 km altitude. The impact of the methane absorption is particularly strong in the troposphere but has almost no effect for higher altitudes.
Similar to τ, the single scattering albedo ωhaze(h,λ) can be split into wavelength and altitude dependent parts, whereas typically ωhaze(h,λ) ≈ 0.8 − 1. We adopt the altitude model of Tomasko et al. (2008). Between 0−30 km, 30−80 km, and above 144 km respectively, we assume ωhaze(h,λ) to be constant with altitude, using the values given in Table 2 of Tomasko et al. (2008), whereas between 80−144 km we linearly interpolate between the adjacent regions. For the region between 80 km to 144 km Tomasko et al. (2008) suggest that new material is incorporated in the aerosols as they fall, and that the aerosols grow in size. In the few kilometers above the surface they also see some weak evidence of a decrease of ωhaze(h,λ), i.e., reversing the general trend with altitude. The wavelength dependence of ωhaze for the region above 144 km and 30−80 km is given in Fig. 48 of Tomasko et al. (2008), and the same dependence is assumed for the region 80−144 km. For the region below 30 km we adopt a three-dimensional polynomial fit to the values given in Table 2 of Tomasko et al. (2008).
For the surface we assume a diffusely scattering surface with constant albedo As = 0.2 for all wavelengths. This is a strong simplification and according to the literature the surface albedo of Titan varies between As = 0.1 − 0.3, depending on wavelength and also the season of Titan (e.g., McKay et al. 1989; Tomasko et al. 1997, 2008). Anyway, we tested different models using a range of As = 0.1 − 0.3, and the variation from p(0°) | As = 0.2 is less than Δp(0°) /p(0°) ≈ 0.1.
The wavelength range of our model is restricted by the Tomasko et al. (2008) values for τhaze(h,λ) and ωhaze(h,λ), which are only given for a wavelength range of 400−1600 nm. On the one hand, we extended this range towards the UV by extrapolating the parameters down to 200 nm. To first order this is valid because between 200−400 nm we do not expect strong spectral or altitudinal features in τhaze(h,λ) and ωhaze(h,λ). On the other hand, we did not extrapolate the parameter range towards the red end because above λ ≈ 1 μm the spectral variation in ωhaze is more complex, and because the extrapolation interval to include the NIC2 band at 2.2 μm was too large. Therefore, the final spectral range of the model covers 200−1600 nm, which includes all our polarization data except the NIC2 polarimetry.
7.2. Radiative transfer code
We use an extended version of the Monte Carlo scattering code described by Buenzli & Schmid (2009). Basically, the code calculates random walk histories of many photons entering the atmosphere, and follows their direction and polarization change until they are absorbed or they escape. The intensity and polarization spectra of the planet can then be established for different lines of sight, and in the case for backscattering (α = 0°) as a function of radial distance from the disk center. For the calculation, the spherical model atmosphere is assumed to be rotationally homogeneous, consisting of multiple locally plane parallel layers. The incident radiation is a parallel beam of unpolarized photons, whereas despite multiple scattering, the photons emerge at the same point where they entered into the atmosphere.
The scattering processes are described by probability density functions, derived from the appropriate phase matrices of the scattering particles (see also Schmid 1992). For scattering on haze particles, the code allows for scattering matrices of the form 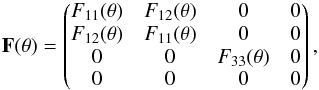 (6)where θ is the scattering angle. The code does not consider circular polarization because these effects are expected to be very small and negligible for a simple scattering model.
(6)where θ is the scattering angle. The code does not consider circular polarization because these effects are expected to be very small and negligible for a simple scattering model.
 |
Fig. 10 Wavelength dependence of the single scattering polarization parameter pm defined by Eq. (7). The fit values to the Tomasko et al. (2008) curves for the blue and the red channel are also indicated. |
We used the aerosol scattering phase functions F11(θ) given in tabulated form by Tomasko et al. (2008) for two altitude regions, above 80 km and below 80 km, and for different wavelengths ranging between 355 nm to 5166 nm. Typically a phase function is given about every 100 nm for λ< 1μm and about every 200 nm for 1 μm <λ< 1.5 μm, and for our model calculations we linearly interpolate between these values. Anyway, it turned out that for the polarization results the dependence on λ is very weak. This was tested by running different model implementations using only the tabulated phase functions with the closest match to λ, and within our observational error bars the calculated limb polarization was the same.
Tomasko et al. (2008) also derive a single scattering polarization fraction (−F12/F11) for the blue (470 − 530 nm) and the red (880 − 970 nm). To first order, we find a very tight fit to their model using a scaled Rayleigh-like single scattering polarization dependence according to 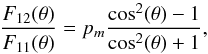 (7)with pm = 0.920 for the blue channel and pm = 0.975 for the red channel. For our model we use pm(λ) with a linear slope, going through the values of the red and blue channel, and pm(λ) = 1 above λ ≈ 1 μm as shown in Fig. 10.
(7)with pm = 0.920 for the blue channel and pm = 0.975 for the red channel. For our model we use pm(λ) with a linear slope, going through the values of the red and blue channel, and pm(λ) = 1 above λ ≈ 1 μm as shown in Fig. 10.
For F33(θ) we use the same dependence as for Rayleigh scattering according to 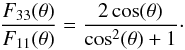 (8)The atmospheric parameters used for our model are described in the previous section. Our calculations include Rayleigh scattering, aerosol scattering, and methane absorption but we neglect Raman scattering, which has only a very small effect on the reflectivity and polarization (e.g., Sromovsky 2005). The model atmosphere consists of 47 different layers above a diffusely scattering surface, and the models are run with 109 − 1010 photons depending on wavelength, such that the statistical error of the fractional polarization is Δp ≤ ± 0.1%.
(8)The atmospheric parameters used for our model are described in the previous section. Our calculations include Rayleigh scattering, aerosol scattering, and methane absorption but we neglect Raman scattering, which has only a very small effect on the reflectivity and polarization (e.g., Sromovsky 2005). The model atmosphere consists of 47 different layers above a diffusely scattering surface, and the models are run with 109 − 1010 photons depending on wavelength, such that the statistical error of the fractional polarization is Δp ≤ ± 0.1%.
7.3. Results
Our model calculates the geometric albedo Ag, the quadrature polarization p(90°) = ⟨ Q/I ⟩ (90°), and the limb polarization p(0°) = ⟨ Qr/I ⟩. Figure 11 compares in the top panel the calculated geometric albedo with observational data (see Sect. 2). We find a good qualitative agreement for the complete wavelength range. Above 500 nm the agreement outside strong absorption bands is better than ΔAg/Ag = 0.2, whereas for the strong absorption around 1.15 μm and 1.45 μm the agreement is ΔAg/Ag ≈ 0.3. Below 500 nm the agreement gets worse with decreasing wavelength. At 400 nm it is ΔAg/Ag ≈ 0.4 and at 300 nm it is only ΔAg/Ag ≈ 0.75. We note that the disagreement below 400 nm is not alarming because there the albedo is very low. Furthermore, it could also origin from our questionable extrapolation of the Tomasko et al. (2008) haze parameters from 400 nm to 200 nm.
 |
Fig. 11 Comparison of our model results for the limb polarization with literature values. Top panel: geometric albedo Ag from the literature (dashed, see also Fig. 1) and from our model (solid). Bottom panel: integrated limb polarization p(0°) of our model for the complete wavelength range (solid), and the HST filter pass bands (+), as well as our HST polarimetry observations (×) given in Table 3. |
 |
Fig. 12 Comparison of our model results at quadrature phase α = 90° with literature values. Top panel: reflectivity f(90°). Middle panel: integrated quadrature polarization p(90°) of our model for the complete wavelength range (solid), and the results from the Pioneer 11 (⋄) and Voyager 2 (□) spacecrafts. The model results in the Pioneer 11 pass bands are also indicated (+). Bottom panel: integrated polarization flux p × f (90°). |
The limb polarization results for the model and our measurements are shown in the bottom panel of Fig. 11. Between 400 − 900 nm the agreement is good with Δp/p ≈ 0.1 for the F625W pass band, and Δp/p ≤ 0.05 for the F435W and F775 pass bands. Below 400 nm the model seems to systematically overestimate the polarization, yielding a discrepancy of Δp/p ≈ 0.3. Qualitatively this UV-offset agrees with our result for the geometric albedo Ag, which also seems to be systematically too high in the UV. Above 900 nm our NIC1 polarization is much higher than the model result and Δp/p ≈ 0.25. We could not conclusively determine whether this discrepancy is caused by an issue of the measurement, the modeling, or both.
It is known that the polarimetric calibration of NIC1 has some deficiencies such as residual instrumental polarization of pinst. ~ 1.5% and weak ghosting (see Sect. 3.2). However, because of the intrinsic symmetry of the radial Stokes parameters Qr and Ur the residual instrument polarization has no effect on ⟨ Qr/I ⟩ (see Sect. 6.3). The ghosting on the other hand is asymmetric and thus could have an impact on ⟨ Qr/I ⟩. However, in our data we only see very weak ghosts which we do not believe to have an effect at the percent level. Finally, it could also be that the real PSF is different from the adopted PSF used for the efficiency correction CPSF (Sect. 6.4). An overcompensation of the PSF smearing could explain a Δp/p of a few percent but certainly not the full discrepancy between model and data.
Concerning the model parameters for the NIC1 wavelength range and their impact on ⟨ Qr/I ⟩, we tested the effect of the surface albedo As, the single scattering polarization parameter pm, and the methane fraction as functions of altitude. Using a range of As = 0.1 − 0.3 showed that the impact of As is less than Δp/p ≈ 0.1. Similarly, setting pm = 1 everywhere cannot explain the discrepancy and the effect is less than Δp/p ≈ 0.05. Finally, we set the methane mole fraction fCH4 = 0 for h> 80 km to check the impact of the methane absorption in the stratosphere and mesosphere. This basically gets rid of the absorption dips in ⟨ Qr/I ⟩ but only has a minor impact outside the absorption bands. Since ⟨ Qr/I ⟩ is flux weighted, we conclude that the overall impact of the methane absorption on the limb polarization is much less than Δp/p ≈ 0.1. Therefore, the cause of the disagreement between the model and the NIC1 measurement remains uncertain.
Titan full disk phase curves for intensity and polarization have been obtained by the Pioneer 11 (Tomasko & Smith 1982) and the Voyager 2 (West et al. 1983) spacecrafts. The Pioneer 11 data were obtained in the B and R bands, covering phase angles between α = 28° − 96°, whereas the Voyager 2 data were taken in the near UV at 264 nm and the near IR at 750 nm, covering phase angles α = 2.7° − 154°. The second panel of Fig. 12 compares our model with the quadrature polarization at α = 90° measured by Pioneer 11 and Voyager 2. For three bands we find a good agreement better than Δp/p ≈ 0.1, whereas for the Pioneer 11 R band the agreement is not as tight but still at the level Δp/p ≈ 0.25.
We note that the quadrature polarization p(90°) is generally higher in the absorption bands because multiple scattering is strongly reduced, and the reflection is dominated by strongly polarized single scattering at ~90°. For the limb polarization p(0°) this Ag − p correlation is reversed. Multiple scattering and a low single scattering albedo ω are required for producing a strong polarization signal since the total polarization is mainly produced by second order but also higher order scatterings.
8. Discussion and conclusions
We present disk resolved imaging polarimetry of Titan, measured with the HST for the UV to the near-IR spectral region. From these observations, we derive the disk-integrated radial limb polarization ⟨ Qr/I ⟩ (Table 3) for various filter pass bands, and we compare our results with the polarization of a model atmosphere. For the model we use a radiative transfer code presented in Buenzli & Schmid (2009), adopting Titan atmosphere parameters from the literature, which were mainly derived from the Huygens landing probe (e.g., Tomasko et al. 2008).
The geometric albedo Ag and the quadrature polarization p(90°) are important reference quantities for characterizing the scattering properties of a reflecting atmosphere. Therefore, we derive the reflected-flux weighted geometric albedo Ag,eff for the used filter pass bands (Table 3), using the spectrophotometry of McGrath et al. (1998), Karkoschka (1998), and Negrão et al. (2006); and we compare our model results for p(90°) with measurements obtained by the Pioneer 11 (Tomasko & Smith 1982) and the Voyager 2 (West et al. 1983) spacecrafts.
A comparison between the model and our observations for ⟨ Qr/I ⟩ (λ), as well as a comparison between our model and literature values for the geometric albedo Ag(λ) and the quadrature polarization p(90°,λ) are given in Figs. 11 and 12.
8.1. Detection of the limb polarization.
For all observed filter bands, our data show a strong limb polarization of several percent, as expected from previous polarization measurements of Titan taken at larger phase angles. To our knowledge, this is the first time that the limb polarization of Titan has been measured, and we did not find any previous earth-bound imaging polarimetry which resolved Titan.
Within the resolution limits of the observations, the measured limb polarization for Titan is centro-symmetric. This is similar to observations of Uranus and Neptune (Schmid et al. 2006b) but for Titan the polarization is much stronger. On the other hand, similar polarization strength can be found in observations of Jupiter but there the limb polarization is essentially only present at the poles (e.g., Schmid et al. 2011), indicating thick polar haze layers and non-polarizing reflection from the clouds along the equator.
The polarimetric sensitivity and the resolution of our data are not sufficient to detect variations of the polarization signal along the limb of Titan, as it is seen in albedo observations. In Sect. 6.2 we pointed to some tentative limb polarization structure, which could be present in our data. Additional observations of Titan with increased polarimetric sensitivity and resolution are required to progress in this direction.
Assuming rotational symmetry, we derive center-to-limb profiles for the radial Stokes parameter Qr(r) /I(r). Because of the scattering symmetry, Qr(r) /I(r) is essentially zero in the disk center, whereas the polarization increases for larger radii, reaching a maximum in the seeing halo at Rmax>RTitan. Depending on wavelength, we measured maximum fractional polarization values in the range of ~2−7% with the highest value obtained in the NIC1 band at 1 μm.
The observed maximum limb polarization is averaged down by the limited resolution and the PSF structure of HST. This has been taken into account in our analysis of the measured disk-integrated radial polarization ⟨ Qr/I ⟩ m. Using synthetic PSF profiles for HST we have modeled the resolution effect on the polarization, and we derive corrected values for the intrinsic ⟨ Qr/I ⟩ of Titan (Table 3). We find ⟨ Qr/I ⟩ ≈ 1.2% in the UV, increasing to about 5.5% at 1 μm, and then decreasing again to about 3.4% at 2 μm. For comparison, a semi-infinite, conservative (ω = 1) Rayleigh-scattering atmosphere produces a disk-integrated limb polarization ⟨ Qr/I ⟩ ≈ 2.75 % (Buenzli & Schmid 2009).
Using our radiative transfer model for Titan we predict the maximum limb polarization without PSF smearing, e.g., for observations with larger earth-bound telescopes or from spacecrafts close to Titan. We find (Qr/I)max ≈ 4.2% for the F250W band, up to (Qr/I)max ≈ 8.7% for the F775W and (Qr/I)max ≈ 10.5% for the NIC1 band, which is even larger than ≈ 8% for a semi-infinite conservative Rayleigh-scattering atmosphere (Buenzli & Schmid 2009). The modeled (Qr/I)max for all filters are also given in Table 3, and Fig. 13 compares the measured F775W radial polarization profile with the model result. In the figure one can see both the polarization dilution, as well as the decreased resolution provided by the HST.
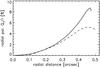 |
Fig. 13 Measured radial polarization profile for Titan in the F775W band (dashed) versus the modeled profile without PSF smearing (solid). |
8.2. Comparison with model calculations
Our model calculates the intensity and the polarization spectra of the planet at different phase angles α = 0° − 180°, and in case of backscattering (α = 0°), the limb polarization as a function of the radial distance from the disk center.
Overall, we find a good agreement at the level of (ΔAg) /Ag ≈ 0.1 − 0.2 or (Δp) /p ≈ 0.1 respectively between model, literature values, and our observations. In one filter (NIC1 at 1 μm) we find a discrepancy of Δp/p = 0.25 between the measured limb polarization ⟨ Qr/I ⟩ and our model, for which the cause is still uncertain. Despite this outlier, our analysis shows that limb-polarization measurements potentially offer an additional diagnostic tool for investigating the properties of scattering particles in Titan with earth-bound observations. Since our model assumes a rotationally homogeneous atmosphere, our results further show that the locally derived haze and atmosphere parameters from the Huygens probe are indeed representative for Titan.
Additional observations of Titan with increased resolution and a high polarimetric sensitivity better than 0.1%, e.g., using the upcoming SPHERE instrument at the VLT (Beuzit et al. 2008), might reveal structure along the limb and temporal changes in the polarization. Such limb polarization measurements could be useful for investigating local haze properties of Titan, and the impact of short-term and seasonal variations. In particular, the limb polarization is very sensitive to the maximum haze single scattering polarization pm, which is strongly depending on the monomer size of the small haze aggregates (e.g., Tomasko et al. 2008). Changing pm in the F775W band from, e.g., pm = 0.96 to pm = 0.94, i.e., corresponding to an increase of the monomer radius of about 15% (rough estimate based on Fig. 18 by Tomasko et al. 2008), reduces the limb polarization by Δp/p ≈ 0.1, while the albedo remains essentially unchanged.
For other atmospheric parameters like τhaze, ωhaze, or the CH4 fraction the geometric albedo Ag and the limb polarization Qr/I will change together (ωhaze) or in opposite direction (τhaze). Thus no structure in the limb polarization is expected if there is no strong albedo feature, like a north-south asymmetry.
8.3. Prospects for extra-solar planets
Differential polarimetric imaging is a particularly promising technique for the detection and characterization of extra-solar planets. With sensitive polarimetry the measurable contrast between star and planet can be enhanced by searching for the polarized signal of the scattered light from the planet within the halo of the unpolarized light from the star (e.g., Schmid et al. 2006b). The upcoming planet finder instruments SPHERE (Beuzit et al. 2008) and GPI (Macintosh et al. 2012) will both provide improved performance for substantial progress in this direction.
The measurable polarization contrast can be described by 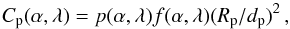 (9)where α is the phase angle, Rp the radius of the planet, dp its separation to the star, f(α,λ) is the phase-dependent reflectivity, and p(α,λ) is the integrated fractional polarization. Therefore, the investigation of p(α,λ) and the polarization flux p(α,λ) × f(α,λ) of Titan is important for planning future observing projects on extrasolar planetary systems and interpreting observational data.
(9)where α is the phase angle, Rp the radius of the planet, dp its separation to the star, f(α,λ) is the phase-dependent reflectivity, and p(α,λ) is the integrated fractional polarization. Therefore, the investigation of p(α,λ) and the polarization flux p(α,λ) × f(α,λ) of Titan is important for planning future observing projects on extrasolar planetary systems and interpreting observational data.
On the one hand, Titan shows that atmospheres with thick layers of small aggregate haze particles produce a very strong polarization signal of p(α ≈ 90°) ≈ 50% over a wide wavelength range from the UV at 300 nm to the near-IR at 2 μm. The bottom panel of Fig. 12 gives the expected polarized flux p × f of Titan if we would observe the object at quadrature phase α = 90°. In the optical p × f (90°) is increasing with wavelength with p × f (90°) ≈ 0.02 at λ = 450 nm, up to p × f (90°) ≳ 0.03 at λ = 850 nm. Above 850 nm the polarized flux is strongly decreased in the methane absorption bands. Therefore, planets with hazy atmospheres and aerosol properties similar to Titan could be particularly good candidates for detection with ZIMPOL/SPHERE (Beuzit et al. 2008; Schmid et al. 2006a) because of their large polarization over the entire wavelength range of the instrument (520−900 nm).
On the other hand, the polarization signal could be strongly reduced for a planet with a Titan-like atmosphere but consisting of larger aggregates. If the monomers were about a factor of two larger then the single scattering polarization in the F775W band is reduced by about Δpm/pm ≈ 0.2 (rough estimate based on Tomasko et al. 2008), and the quadrature polarization will be reduced by Δp/p ≈ 0.4 to about p(90°) ≈ 25%. The polarization signal of a pure Rayleigh scattering atmosphere would also be different with a high signal in shorter wavelength bands between 550-700 nm, and a significantly lower signal for the longer filter bands between 700−800 nm (Buenzli & Schmid 2009). Therefore, a good knowledge of the polarization properties of the hazy atmosphere of Titan is useful for the search and investigation of the polarimetric signal of extra-solar planets.
Acknowledgments
We thank the referee for very thoughtful comments and suggestions which lead to a much improved revised version of the paper. Part of this work was supported by the FINES research fund by a grant through the Swiss National Science Foundation (SNF).
References
- Batcheldor, D., Schneider, G., Hines, D. C., et al. 2009, PASP, 121, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Beuzit, J.-L., Feldt, M., Dohlen, K., et al. 2008, in SPIE Conf. Ser., 7014, 18 [Google Scholar]
- Brown, R. H., Lebreton, J.-P., & Waite, J. H. 2010, Titan from Cassini-Huygens (Springer Science) [Google Scholar]
- Buenzli, E., & Schmid, H. M. 2009, A&A, 504, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Courtin, R. D., Sim, C., Kim, S., Gautier, D., & Jennings, D. E. 2008, BAAS, 40, 446 [NASA ADS] [Google Scholar]
- Fulchignoni, M., Ferri, F., Angrilli, F., et al. 2005, Nature, 438, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Karkoschka, E. 1998, Icarus, 133, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Karkoschka, E., & Tomasko, M. G. 2010, Icarus, 205, 674 [NASA ADS] [CrossRef] [Google Scholar]
- Krist, J. E., Hook, R. N., & Stoehr, F. 2011, in SPIE Conf. Ser., 8127 [Google Scholar]
- Lorenz, R. D., Smith, P. H., & Lemmon, M. T. 2004, Geophys. Res. Lett., 31, 10702 [NASA ADS] [CrossRef] [Google Scholar]
- Lorenz, R. D., Lemmon, M. T., & Smith, P. H. 2006, MNRAS, 369, 1683 [NASA ADS] [CrossRef] [Google Scholar]
- Macintosh, B. A., Anthony, A., Atwood, J., et al. 2012, in SPIE Conf. Ser., 8446 [Google Scholar]
- McGrath, M. A., Courtin, R., Smith, T. E., Feldman, P. D., & Strobel, D. F. 1998, Icarus, 131, 382 [NASA ADS] [CrossRef] [Google Scholar]
- McKay, C. P., Pollack, J. B., & Courtin, R. 1989, Icarus, 80, 23 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Negrão, A., Coustenis, A., Lellouch, E., et al. 2006, Planet. Space Sci., 54, 1225 [NASA ADS] [CrossRef] [Google Scholar]
- Porco, C. C., Baker, E., Barbara, J., et al. 2005, Nature, 434, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Rannou, P., Hourdin, F., & McKay, C. P. 2002, Nature, 418, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Schmid, H. M. 1992, A&A, 254, 224 [Google Scholar]
- Schmid, H. M., Beuzit, J.-L., Feldt, M., et al. 2006a, in Direct Imaging of Exoplanets: Science & Techniques, eds. C. Aime, & F. Vakili, IAU Colloq. 200, 165 [Google Scholar]
- Schmid, H. M., Joos, F., & Tschan, D. 2006b, A&A, 452, 657 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmid, H. M., Joos, F., Buenzli, E., & Gisler, D. 2011, Icarus, 212, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, P. H., Lemmon, M. T., Lorenz, R. D., et al. 1996, Icarus, 119, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Sromovsky, L. A. 2005, Icarus, 173, 254 [NASA ADS] [CrossRef] [Google Scholar]
- Thuillier, G., Floyd, L., Woods, T. N., et al. 2004, Adv. Space Res., 34, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Tomasko, M. G., & Smith, P. H. 1982, Icarus, 51, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Tomasko, M. G., Lemmon, M., Doose, L. R., et al. 1997, in Huygens: Science, Payload and Mission, ed. A. Wilson, ESA SP, 1177, 345 [Google Scholar]
- Tomasko, M. G., Buchhauser, D., Bushroe, M., et al. 2002, Space Sci. Rev., 104, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Tomasko, M. G., Doose, L., Engel, S., et al. 2008, Planet. Space Sci., 56, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Toon, O. B., McKay, C. P., Griffith, C. A., & Turco, R. P. 1992, Icarus, 95, 24 [NASA ADS] [CrossRef] [Google Scholar]
- US Naval Observatory & Royal Greenwich Observatory 2000, The Astronomical Almanac for the year 2002 (Washington, USA, London, UK: US Government Printing Office (USGPO) and The Stationary Office) [Google Scholar]
- van de Hulst, H. C. 1980, Multiple light scattering, 2 (New York, NY: Academic Press) [Google Scholar]
- Veverka, J. 1973, Icarus, 18, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Vinatier, S., Bézard, B., Fouchet, T., et al. 2007, Icarus, 188, 120 [NASA ADS] [CrossRef] [Google Scholar]
- West, R. A., Hart, H., Simmons, K. E., et al. 1983, J. Geophys. Res., 88, 8699 [NASA ADS] [CrossRef] [Google Scholar]
- Zellner, B. 1973, Icarus, 18, 661 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Titan scattering model parameters
Appendix A.1: Number densities and column density
For the calculation of the methane number density nCH4 and the scale height ZCH4 the following formulas are used: ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{eq: number density CH4} n_{\rm CH_4} &=& \frac{\rho~[{\rm g/cm}^3] \times 6.02 \times 10^{23}}{28/f_{\rm CH_4} - 12} \\\label{eq: number density N2} n_{\rm N_2} &=& n_{\rm CH_4} \cdot \frac{f_{\rm N_2}}{f_{\rm CH_4}} = n_{\rm CH_4} \cdot \frac{1- f_{\rm CH_4}}{f_{\rm CH_4}}\cdot \end{eqnarray}](/articles/aa/full_html/2014/12/aa23139-13/aa23139-13-eq295.png) Derivation:
Derivation:
-
![\hbox{$n_{\rm tot} = \frac{\rho\,[{\rm g/cm}^3] \cdot \rm N_{\rm A}}{\mu} = n_{\rm CH_4} + n_{\rm N_2}$}](/articles/aa/full_html/2014/12/aa23139-13/aa23139-13-eq296.png)
-
μ = 28·(1 − fCH4) + 16·fCH4
-
![\hbox{$n_{\rm CH_4} = f_{\rm CH_4} n_{\rm tot} = \frac{f_{\rm CH_4}\, \rho\,\left[{\rm g/cm}^3\right] \cdot \rm N_{\rm A}}{28\left(1-f_{\rm CH_4}\right) + 16 f_{\rm CH_4}}\cdot$}](/articles/aa/full_html/2014/12/aa23139-13/aa23139-13-eq298.png)
Column density in km-am6: ![\appendix \setcounter{section}{1} \begin{equation} Z ~[1/\rm{km^2}] = 10^{15} \int n~[1/\rm{cm^3}]\,\rm d h = 2.687 \times 10^{34} \times Z ~[\textnormal{km-am}]. \end{equation}](/articles/aa/full_html/2014/12/aa23139-13/aa23139-13-eq299.png) (A.3)
(A.3)
Appendix A.2: Rayleigh scattering optical depth
This is from PDS7: 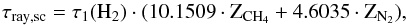 (A.4)with Zi [km - am] and the optical depth per km-am of hydrogen given as (λ [Å]):
(A.4)with Zi [km - am] and the optical depth per km-am of hydrogen given as (λ [Å]): 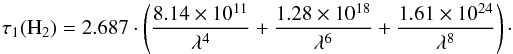 (A.5)
(A.5)
Appendix A.3: Methane absorption
Methane absorption from Karkoschka & Tomasko (2010). Below 1 μm these methane absorption coefficients are generally close to those by Karkoschka (1998), 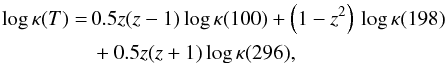 (A.6)with z = (T − 198)/98; and κ(100), κ(198), and κ(296) are given in Table 4 of the supplementary material of Karkoschka & Tomasko (2010). Therefore, we get
(A.6)with z = (T − 198)/98; and κ(100), κ(198), and κ(296) are given in Table 4 of the supplementary material of Karkoschka & Tomasko (2010). Therefore, we get 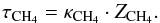 (A.7)
(A.7)
Appendix A.4: Haze optical depth and single scattering albedo
The haze optical depth τh and single scattering albedo ωhaze are taken from Tomasko et al. (2008). τh is given for three altitude regions, above 80 km, 30−80 km, and below 30 km (see Figs. 47, 50). Above 80 km, the cumulative optical depth increases with decreasing altitude with a scale height of 65 km. Between 80 and 30 km, and below 30 km the variation is linear with two different slopes. The wavelength dependence for the three regions is taken from Fig. 47 of Tomasko et al. (2008): ![\appendix \setcounter{section}{1} \begin{eqnarray} &&\tau_{80} (\lambda) = 1.012 \times 10^7 \times \lambda^{-2.339} \\[1mm] &&\tau_{30} (\lambda) = 2.029 \times 10^4 \times \lambda^{-1.409} \\[1mm] &&\tau_{0} (\lambda) = 6.270 \times 10^2 \times \lambda^{-0.9706} \\[1mm] &&\tau_{>80} (h, \lambda) = \tau_{80}(\lambda) \cdot e^{-\frac{h-80 \, {\rm km}}{65 \, {\rm km}}} \\[1mm] &&\tau_{30-80}(h, \lambda) = \tau_{80}(\lambda) + \tau_{30} (\lambda)\left(1-\frac{h-30\,{\rm km}}{50\,{\rm km}}\right) \\[1mm] &&\tau_{<30}(h, \lambda) = \tau_{80}(\lambda) + \tau_{30}(\lambda) + \tau_{0}(\lambda)\left(1-\frac{h}{30\,{\rm km}}\right) \cdot \end{eqnarray}](/articles/aa/full_html/2014/12/aa23139-13/aa23139-13-eq311.png) The single scattering albedo ωhaze is given in Tomasko et al. (2008) for three altitude regions (Fig. 48, Table 2), above 144 km, 30−80 km, and below 30 km. The wavelength dependence of ωhaze for the region above 144 km and 30−80 km is given in Fig. 48 of Tomasko et al. (2008) whereas for the region below 30 km we adopt a three-dimensional polynomial fit to the values given in Table 2 of Tomasko et al. (2008). For the regions below 30 km, 30−80 km, and above 144 km, we assume ωhaze to be constant with altitude, whereas for the region 80−144 km we linearly interpolate between the values at 80 km and 144 km:
The single scattering albedo ωhaze is given in Tomasko et al. (2008) for three altitude regions (Fig. 48, Table 2), above 144 km, 30−80 km, and below 30 km. The wavelength dependence of ωhaze for the region above 144 km and 30−80 km is given in Fig. 48 of Tomasko et al. (2008) whereas for the region below 30 km we adopt a three-dimensional polynomial fit to the values given in Table 2 of Tomasko et al. (2008). For the regions below 30 km, 30−80 km, and above 144 km, we assume ωhaze to be constant with altitude, whereas for the region 80−144 km we linearly interpolate between the values at 80 km and 144 km: ![\appendix \setcounter{section}{1} \begin{eqnarray} &&\omega_{\rm haze, >144} (h, \lambda) = \omega_{\rm haze, 144} (\lambda) \\[1mm] &&\omega_{\rm haze, 80-144} (h, \lambda) = \omega_{\rm haze, 30-80} (\lambda) \notag \\[1mm] &&\hspace*{2.5cm}+ \frac{\omega_{\rm haze, 144} - \omega_{\rm haze, 30-80}}{64\,{\rm km}} \cdot (h-80\,{\rm km}) \\[1mm] &&\omega_{\rm haze, 30-80} (h, \lambda) = \omega_{\rm haze, 30-80} (\lambda) \\[1mm] &&\omega_{\rm haze, <30} (h, \lambda) = \omega_{\rm haze, <30} (\lambda) . \end{eqnarray}](/articles/aa/full_html/2014/12/aa23139-13/aa23139-13-eq312.png)
Appendix A.5: Effective single scattering albedo
All Tables
All Figures
 |
Fig. 1 Upper panel: geometric albedo of Titan (full line) and effective albedos Ag,eff and wavelengths λeff for the HST filter polarimetry (crosses). The dashed line illustrates the solar spectrum. Lower panel: normalized filter efficiency curves and the normalized wavelength distribution of the registered photons. |
| In the text | |
 |
Fig. 2 Intensity cuts/profiles through the disk center for the F250W band (bottom), the F435W band (middle), and the NIC1 band (top). The solid line indicates the north-south profile through the planetary poles, and the dashed line is the east-west profile perpendicular to the polar axis respectively. |
| In the text | |
 |
Fig. 3 Stokes Q (left) and U (right) images in the F775W band. The south pole and the equator are indicated. The gray scale is normalized to the central intensity of Stokes I by ± 0.02 Icenter. |
| In the text | |
 |
Fig. 4 Radial Stokes Qr (left) and Ur (right) images in the F775W band. The south pole and the equator are indicated. The gray scale is normalized to the central intensity of Stokes I by ± 0.02 Icenter. |
| In the text | |
 |
Fig. 5 Intensity (left) and radial polarization images Qr (right) in the F330W, F435W, F625W, NIC1, and NIC2 band (top to bottom). The intensity images are normalized to |
| In the text | |
 |
Fig. 6 Titan radial profiles for intensity I (upper panel, thick lines) and radial polarization Qr (upper panel, thin lines) in the F435W (dash-dot), F775W (dash) and NIC1 (solid) filters. Both I and Qr are normalized to the peak flux at r = 0. The lower panel shows the corresponding normalized radial polarization Qr/I. |
| In the text | |
 |
Fig. 7 Encircled energies for HST PSFs (thick lines) and Gaussian PSFs (thin lines): ACS F625W (solid), NIC1 POL0S (dashed), and NIC2 POL0L (dash-dot). |
| In the text | |
 |
Fig. 8 Modeling of the degradation of the Titan polarization Q due to the cancelation of opposite polarization components + Q and −Q caused by the limited resolution; a) unlimited resolution; b) HST PSF at 630 nm (F625W); c) HST PSF at 1 μm (NIC1); and d) HST PSF at 2 μm (NIC2). The gray scale spans for all panels the range from −2% (black) to + 2% (white) of the peak intensity of the initial perfect intensity image. |
| In the text | |
 |
Fig. 9 Vertical optical depth τ for λ = 445 nm (dash-dot), λ = 775 nm (dash), λ = 940 nm (dot), λ = 1000 nm (methane absorption band, solid), and for λ = 1580 nm. |
| In the text | |
 |
Fig. 10 Wavelength dependence of the single scattering polarization parameter pm defined by Eq. (7). The fit values to the Tomasko et al. (2008) curves for the blue and the red channel are also indicated. |
| In the text | |
 |
Fig. 11 Comparison of our model results for the limb polarization with literature values. Top panel: geometric albedo Ag from the literature (dashed, see also Fig. 1) and from our model (solid). Bottom panel: integrated limb polarization p(0°) of our model for the complete wavelength range (solid), and the HST filter pass bands (+), as well as our HST polarimetry observations (×) given in Table 3. |
| In the text | |
 |
Fig. 12 Comparison of our model results at quadrature phase α = 90° with literature values. Top panel: reflectivity f(90°). Middle panel: integrated quadrature polarization p(90°) of our model for the complete wavelength range (solid), and the results from the Pioneer 11 (⋄) and Voyager 2 (□) spacecrafts. The model results in the Pioneer 11 pass bands are also indicated (+). Bottom panel: integrated polarization flux p × f (90°). |
| In the text | |
 |
Fig. 13 Measured radial polarization profile for Titan in the F775W band (dashed) versus the modeled profile without PSF smearing (solid). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.