| Issue |
A&A
Volume 571, November 2014
|
|
|---|---|---|
| Article Number | A82 | |
| Number of page(s) | 8 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201424990 | |
| Published online | 14 November 2014 | |
Bulge formation in disk galaxies with MOND
Observatoire de Paris, LERMA (CNRS: UMR 8112), 61 Av. de l’Observatoire, 75014 Paris, France
e-mail: francoise.combes@obspm.fr
Received: 15 September 2014
Accepted: 24 September 2014
The formation of galaxies and their various components can be stringent tests of dark matter models and of gravity theories. In the standard cold dark matter (CDM) model, spheroids are formed through mergers in a strongly hierarchical scenario and also in the early universe through dynamical friction in clumpy galaxies. More secularly, pseudo-bulges are formed by the inner vertical resonance with bars. The high efficiency of bulge formation is in tension with observations in the local universe of a large amount of bulgeless spiral galaxies. In the present work, the formation of bulges in very gas-rich galaxies, such as those in the early universe, is studied in Milgrom’s MOdified Newtonian Dynamics (MOND) through multigrid simulations of the nonlinear gravity, including gas dissipation, star formation, and feedback. Clumpy disks are rapidly formed, as in the equivalent Newtonian systems. However, the dynamical friction is not as efficient in the absence of dark matter halos, and the clumps have no time to coalesce into the center to form bulges before they are eroded by stellar feedback and shear forces. Previous work has established that mergers are less frequent in MOND, and classical bulges are expected less massive. We now show that gas-rich clumpy galaxies in the early universe do not form bulges. Disks with a low bulge fraction, which is compatible with the observations, are therefore a natural result in MOND. Since pseudo-bulges are formed by bars with a similar rate to those in the Newtonian equivalent systems, it can be expected that the contribution of pseudo-bulges is significantly higher in MOND.
Key words: galaxies: bulges / galaxies: evolution / galaxies: formation / galaxies: halos / galaxies: kinematics and dynamics
© ESO, 2014
1. Introduction
Many problems in cosmology that are related either to the missing mass in galaxies and clusters or to the formation of large-scale structures and galaxies are solved by the existence of a dark sector, dark matter, and dark energy, dominating the content of the universe (e.g., Blumenthal et al. 1984; Peebles & Ratra 2003). The standard hypothesis for dark matter is the cold and massive elementary particle (CDM) coming from supersymmetry (Bertone et al. 2005), although there is also a recent revival of warm dark matter models that are able to reproduce the power spectrum of structures better at galactic scales and below (Bode et al. 2001). All dark matter models, however, encounter persistent problems at galactic scales, such as the predicted cusps and abundance of dark matter in galaxies that is too high (e.g., Wang & White 2009; Kennedy et al. 2014; Boylan-Kolchin et al. 2011, 2012).
An alternative to dark matter models that work in Einstein gravity is to assume that a modification of the gravity could account for the apparent dark sector and, in particular, the MOdified Newtonian Dynamics (MOND) proposed by Milgrom (1983), which accounts for the missing mass on galaxy scales very well (see the review by Sanders & McGaugh 2002 and Famaey & McGaugh 2012). The fundamental idea is based on the observation that mass discrepancies mainly occur when the acceleration falls below the critical value of a0 ~ 2 × 10-10 m/s2. At low acceleration, the gravitational force varies as 1/r instead of 1/r2. The outer parts of giant galaxies and dwarf galaxies should fall entirely into this regime.
In standard dark matter models, bulges in galaxies are thought to be formed mainly through major or minor mergers (e.g., Toomre 1977; Barnes & Hernquist 1991; Naab & Burkert 2003; Bournaud et al. 2005, 2007a). The time scale of a merger is short, on the order of 10% of Hubble time or less, because of the existence of extended and massive dark halos, which take the orbital angular momentum of baryons away (Barnes 1988). In modified gravity models and in the absence of halos, the spiral-in of companion galaxies occur on a much larger time scale, and the frequency of mergers is low (Tiret & Combes 2008b). The prediction of the number and mass of bulges in spiral galaxies could then be a discriminant between models. Another way to form bulges occurs in the early universe, when gas-rich disks are unstable to collapsing into massive clumps, which spiral in and form a bulge and thick disk (e.g., Noguchi 1999; Bournaud et al. 2007b). Dynamical friction is thought to bring the clumps inward, faster than their destruction through star formation feedback, and this could also constrain dark matter models.
There is a third main dynamical process able to form bulges in spiral galaxies, the vertical resonance with a stellar bar (Combes et al. 1990; Kormendy & Kennicutt 2004). These are called pseudo-bulges, since they show more rotation, more flattening, and a radial distribution closer to an exponential than do “classical” bulges. Bars form at comparable frequency in MOND and Newtonian models with dark matter (Tiret & Combes 2007, 2008a), and pseudo-bulges are expected to form as frequently in the two models.
The goal of the present article is to compare the formation of bulges in clumpy disks in the frame of dark matter and MOND models, to probe early bulge formation. The methods for the simulations are described in Sect. 2, and the galaxy models used in Sect. 3. The results are first presented for dynamical friction in dissipationless models (Sect. 4.1), and then all the phenomena of gas-rich disks forming clumpy galaxies with star formation and feedback are included in Sect. 4.2, and discussed in Sect. 5. The conclusions of bulge formation in the different models are then summarized in Sect. 6.
2. Simulation methods
Since the MOND equations are nonlinear, it is not possible to use normal Poisson solvers, such as the Tree code, but instead the full differential equations should be solved on a grid. This is very efficiently done with the multigrid algorithm (cf. Press et al. 1992; Brada & Milgrom 1999; Tiret & Combes 2007, hereafer TC07). Both the MOND simulations and the Newtonian gravity comparison runs were carried out with the same multigrid method. For the modified gravity runs, the self-consistent Lagrangian theory AQUAL, developed by Bekenstein & Milgrom (1984) was used, where the Poisson equation is written as ![\begin{equation} \label{eq:mondaqual} \nabla [\mu(|\nabla\Phi|/a_0) \nabla\Phi] = 4 \pi G \rho, \end{equation}](/articles/aa/full_html/2014/11/aa24990-14/aa24990-14-eq3.png) (1)where μ(x) is the interpolation function that is equal to unity at large x (Newtonian regime), and it tends to x when x ≪ 1 in the MOND regime. Various functions have been used in the literature, and for fitting rotation curves of spiral galaxies, the best one appears to be the standard function μ(x) = x/ (1 + x2)1/2 (Sanders & McGaugh 2002), while for the Milky Way, the best fit is obtained with the so-called “simple” function μ(x) = x/ (1 + x) (Famaey & Binney 2005). The values of a0 range between 1 and 2 × 10-10 m/s2, according to the μ function used: with the simple function, the MOND regime is reached with an acceleration about one order of magnitude greater than with the standard function (e.g., Tiret & Combes 2008a). There are other uncertain parameters that could influence the choice of the coupled parameters (μ, a0), such as the unknown fraction of dark baryons in galaxy disks (Tiret & Combes 2009) or the impact of the external field effect (Zhao & Famaey 2006).
(1)where μ(x) is the interpolation function that is equal to unity at large x (Newtonian regime), and it tends to x when x ≪ 1 in the MOND regime. Various functions have been used in the literature, and for fitting rotation curves of spiral galaxies, the best one appears to be the standard function μ(x) = x/ (1 + x2)1/2 (Sanders & McGaugh 2002), while for the Milky Way, the best fit is obtained with the so-called “simple” function μ(x) = x/ (1 + x) (Famaey & Binney 2005). The values of a0 range between 1 and 2 × 10-10 m/s2, according to the μ function used: with the simple function, the MOND regime is reached with an acceleration about one order of magnitude greater than with the standard function (e.g., Tiret & Combes 2008a). There are other uncertain parameters that could influence the choice of the coupled parameters (μ, a0), such as the unknown fraction of dark baryons in galaxy disks (Tiret & Combes 2009) or the impact of the external field effect (Zhao & Famaey 2006).
The multigrid method developed in the present work has been described at length and tested in TC07, in particular the problem of boundary conditions. Equation (1) has been discretized similarly, and the Gauss-Seidel relaxation with red and black ordering was followed. If the convergence is very quick with the linear Newtonian Poisson equation, the analogous MOND equations take a much longer CPU time. Then to be able to run many more simulations in a given time, I used the quasi linear formulation of MOND, call QUMOND developed by Milgrom (2010).
This formulation has the advantage of being much easier to solve, since the interpolation function of a/a0 has been transferred to its inverse equivalent as a function of aN/a0, with aN the Newtonian acceleration. It is a non-relativistic complete theory, derivable from an action, but the nonlinearity can be reduced to solve the linear Poisson equation several times. Indeed, the equation to solve is the following: ![\begin{equation} \label{eq:qumond} \nabla^2 \Phi = \nabla [\nu(|\nabla\Phi_N|/a_0) \nabla\Phi_N] \end{equation}](/articles/aa/full_html/2014/11/aa24990-14/aa24990-14-eq15.png) (2)where Φ is the Milgromian potential and ΦN the Newtonian one. Since the normal Poisson equation links ΦN and the density ρ by the relation ∇2ΦN = 4πGρ, Eq. (2) can be written as the function of two densities:
(2)where Φ is the Milgromian potential and ΦN the Newtonian one. Since the normal Poisson equation links ΦN and the density ρ by the relation ∇2ΦN = 4πGρ, Eq. (2) can be written as the function of two densities: 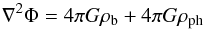 where ρb is the baryonic density, and ρph the so-called phantom density, which is the equivalent of the missing mass within the Newtonian gravity. Examples of the phantom density distribution are given by Lüghausen et al. (2013), it can sometimes (rarely) be negative. The phantom density can be computed by
where ρb is the baryonic density, and ρph the so-called phantom density, which is the equivalent of the missing mass within the Newtonian gravity. Examples of the phantom density distribution are given by Lüghausen et al. (2013), it can sometimes (rarely) be negative. The phantom density can be computed by ![\begin{equation} \label{eq:phantom} \rho_{\rm ph}= \frac{1}{ 4 \pi G} \nabla [(\nu -1) \nabla\Phi_N]. \end{equation}](/articles/aa/full_html/2014/11/aa24990-14/aa24990-14-eq23.png) (3)The computation of the Milgromian potential therefore can be carried out in two linear steps. First, the Newtonian potential ΦN is computed on the grid from the baryonic density ρb, and the phantom density ρph is derived on the same grid, through discretization of Eq. (3) (see, e.g., Famaey & McGaugh 2012), in a similar manner to Eq. (1). Then the linear Newtonian Poisson solver is used again, this time with ρb + ρph. The interpolation function ν(aN/a0) corresponding to the standard μ function can easily be computed as
(3)The computation of the Milgromian potential therefore can be carried out in two linear steps. First, the Newtonian potential ΦN is computed on the grid from the baryonic density ρb, and the phantom density ρph is derived on the same grid, through discretization of Eq. (3) (see, e.g., Famaey & McGaugh 2012), in a similar manner to Eq. (1). Then the linear Newtonian Poisson solver is used again, this time with ρb + ρph. The interpolation function ν(aN/a0) corresponding to the standard μ function can easily be computed as 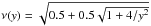 . The two MOND formulations AQUAL and QUMOND are not completely equivalent, since their forces differ by a curl field (Zhao & Famaey 2010). The two are very close in symmetric systems, however, and in what follows, the results from the two formulations were checked for similarity.
. The two MOND formulations AQUAL and QUMOND are not completely equivalent, since their forces differ by a curl field (Zhao & Famaey 2010). The two are very close in symmetric systems, however, and in what follows, the results from the two formulations were checked for similarity.
Simulation models.
The grid used in the present work is 2573 in size. The simulation box covers a 60 kpc cube, and the spatial resolution is about 230 pc. The rest of the simulation code works like a particle-mesh (PM) code. Up to 0.75 million particles are initially distributed on the grid. The density is computed on the grid by a cloud-in-cell (CIC) algorithm, and once the potential is computed, particles are advanced using a leap-frog method. For the purpose of distinguishing the various physical mechanisms, simulations with only stars (and dark matter in the Newtonian equivalent systems) were run, followed by simulations that included gas, star formation, and feedback. The gas dissipation was taken into account with a sticky-particle code, as described in Tiret & Combes (2008a). The rebound parameters were varied from 0.4 to 1, which essentially affected the amount of dissipation and the time scales of clump formation. The runs presented in the following are all with βr = βt = 0.5. The variety of results obtained with a changing gas dissipation does not fundamentally change the conclusions.
Star formation follows a Schmidt law; i.e., the star formation rate (SFR) is proportional to a power n of the local volumic density with a density threshold. The exponent n has been taken equal to 1.4 (Kennicutt 1998). This nonlinear relation means that gas clumps will primarily be the site of star formation. The proportionality factor is selected to give a depletion time scale for a homogeneous gas disk of 5 Gyr in its initial state. When clumps form, the consumption time scale is considerably reduced owing to the higher star formation efficiency in dense clumps. A continuous mass loss from stars into the gas is taken into account as in Jungwiert et al. (2001). The mass loss by stars is distributed through the gas on neighboring particles, with a velocity dispersion to schematize the feedback energy.
 |
Fig. 1 Left: circular and rotational velocities, together with the velocity dispersions for the stellar component in the Newtonian+DM (top) and MOND (bottom) initial galaxy models with stars and gas. Right: same for the giant galaxy model. |
3. The model galaxies
The goal of the present work is to study the formation of bulges in the early universe, therefore the initial conditions are gas-rich galaxies with a gas fraction of 50% of the baryonic mass and no bulge to start with.
The stellar disk follows a Miyamoto-Nagai density profile: ![\begin{eqnarray} \label{stdisk} \rho_{*}(R,Z)&=&\left(\frac{{z_{*}}^2 M_{*}}{4 \pi}\right)\nonumber\\ &&\times~\frac{r_{*} R^2+(r_{*}+3\sqrt{Z^2+{z_{*}}^2})\left(r_{*}+\sqrt{Z^2+{z_{*}}^2}\right)^2} {\left[R^2+\left(r_{*}+\sqrt{Z^2+{z_{*}}^2}\right)^2\right]^{5/2}\left(Z^2+{z_*}^2\right)^{3/2}} \end{eqnarray}](/articles/aa/full_html/2014/11/aa24990-14/aa24990-14-eq50.png) (4)with mass M∗ and radial and vertical scale lengths r∗ and z∗, respectively. The gas disk follows the same distribution with characteristic parameters Mg, rg, and zg, respectively. All values of parameters are displayed in Table 1. The simulation resolution (230 pc) is barely enough to study the vertical structure of the gas disk (500 pc). All components are truncated at three times the value of their characteristic scale, therefore the extent of the disk is initially 15 kpc in radius.
(4)with mass M∗ and radial and vertical scale lengths r∗ and z∗, respectively. The gas disk follows the same distribution with characteristic parameters Mg, rg, and zg, respectively. All values of parameters are displayed in Table 1. The simulation resolution (230 pc) is barely enough to study the vertical structure of the gas disk (500 pc). All components are truncated at three times the value of their characteristic scale, therefore the extent of the disk is initially 15 kpc in radius.
In the equivalent Newtonian galaxies, the dark halo is modeled as a Plummer sphere with characteristic mass MH and characteristic radius RH. Its density is given by the following analytical formula: 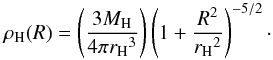 (5)The values of these parameters MH and rH are selected so that the Newtonian equivalent model has the same rotation curve as the disk in the modified dynamics. The dark matter halo is truncated at 21 kpc, and the halo masses indicated in Table 1 are relevant to this radius.
(5)The values of these parameters MH and rH are selected so that the Newtonian equivalent model has the same rotation curve as the disk in the modified dynamics. The dark matter halo is truncated at 21 kpc, and the halo masses indicated in Table 1 are relevant to this radius.
The stability of these galaxy models is controlled initially through a Toomre parameter for the stellar disk of Qstar = 1.5 and for the gas component, Qgas = 1.1. The initial rotation curves of the model galaxies are shown in Fig. 1. To avoid artificial initial relaxation of the disks, particles are advanced during a typical rotation period in the frozen initial potential, computed with the multigrid potential solver. No gas dissipation or star formation are included in this relaxation phase.
4. Results
To isolate the main physical parameters, purely stellar models are run first, although they do not correspond to the reality of galaxies in the early universe. They are compared to analogous simulations, where half of the baryonic mass is gas, which emphasizes the role of dissipation, star formation, and feedback.
Estimate of decay time scales for Newton+dark matter models.
4.1. Dissipationless models
Two extreme mass models, dwarf and giant galaxies, were run with the same characteristic scales, but with masses that are different by an order of magnitude (see Table 1). To quantify the effects of dynamical friction, initial clumps were simulated by massive particles, in two options: either five clumps in all containing 25% of the disk mass or three clumps containing 30% of the disk mass were distributed randomly with the same initial velocity distribution as the rest of particles.
In total, eight types of runs were carried out with two mass models, with two types of clumps, and for the two gravity models. For each type of run, ten different random realizations of the initial conditions were used, to average out the results. The decay of the clumps through dynamical friction is illustrated in some of these runs in Fig. 2. An estimate of the decay time scale (time for the clumps to fall from their initial radius to the central region at 1–2 kpc where their orbit reaches a stationary state) is obtained through averaging of these clump orbits, and is gathered in Table 2 for the Newton+DM runs. All realizations of a given run type are averaged out, with all orbits that are selected randomly. This procedure looks more realistic than launching a given clump alone at an external radius, since the dynamical effects of all the clumps interfere in the deformations they impact on the dark halo and other particles in the disk. This interference of several clumps can reduce and sometimes increase the dynamical friction effect (Weinberg 1989). Also the decay time scales depend on the launching radius, and in the same run, the clumps starting at smaller radii have a shorter decay time scale.
 |
Fig. 2 Left: decay of the 5 clumps containing globally 25% of the baryonic disk as a function of time, in the Newtonian +DM (top) and MOND (bottom), for the purely stellar galaxy models. Right: same for the giant galaxy model. |
Although these final averaged values have relative error bars of 10% to 20%, they are compatible in their mass and density dependency with the Chandrasekhar formula for dynamical friction (Chandrasekhar 1943). The decay time is predicted to be inversely proportional to the clump mass, for a given background distribution, and with the present assumptions on radii and mass ratios between clumps and disk, roughly inversely proportional to the square root of the total host mass. It is only an approximation of course, since many other parameters enter into account, such as the initial velocity of the clump and the dark and baryonic radial mass distributions. It was not possible to measure the corresponding values in the MOND models, because of weak dynamical friction.
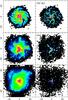 |
Fig. 3 All baryons (left) and gas (right) surface densities of the dwarf clumpy galaxy, simulated with MOND gravity, at epochs 0.5, 1, and 2 Gyr. Each panel is 60 kpc in size. The color scale is logarithmic and is the same for all plots. |
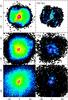 |
Fig. 4 All baryons (left) and gas (right) surface densities of the giant clumpy galaxy, simulated with MOND gravity, at epochs 0.5, 1, and 2 Gyr. Each panel is 60 kpc in size. The color scale is logarithmic and is the same for all plots. |
 |
Fig. 5 Evolution of the star formation rate (black line, left scale) and the remaining amount of gas (red lines and middle scale) in the giant galaxy, with MOND (left), and Newtonian dynamics (right). |
4.2. Models with gas, star formation, and feedback
Figures 3, 4, and 6 show the evolution of the gas and total baryonic component of some models with gas. The disks are highly unstable to clump formation owing to the high gas fraction of 50% and the absence of a bulge. Control runs with only stars were relatively stable, but they formed a strong bar, after 500 Myr for the MOND disks and more than 2 Gyr for the Newtonian ones. The mass in clumps increases at the beginning with the gravitational instability due to the gas dissipation and large gas fraction. But these overdense regions are very efficient at forming stars, and the gas fraction in clumps decreases, as does the global gas fraction. Figure 5 shows the evolution of the SFR with time and the corresponding consumption of the gas. Since the SFR law adopted is nonlinear, the formation of dense clumps leads to intense starbursts with an episodic character, which consume the gas much more quickly than the analogous quiescent, almost homogeneous disk galaxy, which was used to calibrate depletion time.
In the absence of external gas accretion and replenishment of the gas content, the disk becomes more stable. Through both the star formation feedback and the gravitational shear on the stellar clumps, the mass fraction in clumps slowly decreases. The dynamical friction due to the dark halo on the clumps is, however, fast enough to bring the clumps towards the center and build a bulge in the Newtonian runs. In the MOND models, the stellar fragments are maintained in the disk, because of the weaker dynamical friction from the disk.
The evolution of the stellar surface density Σ as a function of time is shown in Fig. 7 for the giant galaxy in the Newtonian model and in Fig. 7 in the MOND gravity. Initially, there is an exponential distribution in the disk, while a second component is progressively accumulated toward the center in the clumpy galaxy with dark matter. An edge-on view reveals that there is indeed a small spheroid in the center, along with a thick disk (Fig. 9). This initial bulge formation due to massive clumps has been discussed widely in the literature (Noguchi 1999; Immeli et al. 2004; Bournaud et al. 2007b; Elmegreen et al. 2008), along with the formation of a thick disk from star formation in a turbulent gas disk (Bournaud et al. 2009). We show that this rapid and early bulge formation does not occur in the MOND gravity model. The disk remains clumpy until 2 Gyr, as revealed by Fig. 7. This is the natural consequence of a much longer dynamical friction time scale.
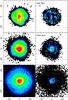 |
Fig. 6 All baryons (left) and gas (right) surface densities of the giant clumpy galaxy, simulated with Newtonian+DM gravity, at epochs 0.5, 1, and 2 Gyr. Each panel is 60 kpc in size. The color scale is logarithmic and the same for all plots. |
The mass fraction in clumps was monitored as a function of time, in the same manner as described by Bournaud et al. (2007b). The surface density of the baryonic component was computed at each snapshot. It was first smoothed at a resolution of 700 pc to reduce noise, and the azimutal average surface density Σ(r) computed at each radius. When the local surface density was higher than three times Σ(r), it was considered to belong to a clump. When plotted together, these regions do correspond to the main clumps seen in the maps. There is no ambiguity with spiral arms, since the clumps are dominating the global spiral structure (see Fig. 3). The number of clumps found by this method is typically 10 to 20. The fraction of the disk mass in clumps can reach at the maximum of the starburst of the order of 30%. Figure 10 displays the clump mass fraction evolution for the giant model galaxy. It is remarkable that in the MOND regime, the disk galaxy remains highly clumpy, while in the Newtonian gravity with a massive dark matter halo, the clumps are driven toward the center, and the disk becomes more homogeneous after some last starbursts have consumed the remaining gas.
 |
Fig. 7 Stellar profile of the giant galaxy in the Newtonian dynamics, at various epochs (0, 0.5, 1, and 2 Gyr). A bulge is building alongside the exponential disk. |
 |
Fig. 9 Evolution of the edge-on morphology of the giant galaxy, in the Newtonian gravity model with gas and star formation. |
 |
Fig. 10 Evolution of the clump mass fraction (see text for the definition) for the giant galaxy, in the MOND gravity (left) and in the Newtonian gravity (right). |
4.3. Dynamical friction
The different dynamical friction efficiency in the two gravity models is the key to understanding the morphology of clumpy galaxies in the early universe and the bulge formation. The main phenomenon at the origin of the drag on the clumps is the deformation or wake that a massive body imprints on the background distribution of particles. When the bodies have low mass with respect to the total system, their wake is a small perturbation, and the process can be handled analytically. However, with massive bodies, it is not an intuitive process to derive the actual effect of the friction, especially when the massive bodies are numerous, and their wakes interfere. They can perturb the system significantly, so that it cannot be considered as an infinite reservoir of energy and angular momentum.
Results that may look controversial at first glance have been claimed in the literature. A perturbation study by Ciotti & Binney (2004) concludes that dynamical friction is stronger in MOND. They consider only very low-mass bodies, like star clusters, with a negligible effect on the full stellar background, and adopt an impulse approximation for deflection or orbits and linear summation of effects. For the Newtonian model with dark matter, they consider the dark matter halo as a rigid background that does not participate in the dynamical friction. They find that the two-body relaxation time is shorter for disks in the MOND regime and extrapolate these results to the dynamical friction time, obtained for test particles in the local formula of Chandrasekhar (1943). The consequences would be that globular clusters should spiral inwards to the center in dwarf galaxies on a few dynamical time scales, as well as galaxies in groups and in clusters. Simulations by Nipoti et al. (2008) confirm these findings in the context of tiny perturbations: the massive bodies subject to the friction, either globular clusters or a rigid bar, have to contain less than 5% of the baryonic mass, so that particles in the stellar background absorbing the energy and angular momentum are not significantly perturbed. In realistic systems though, Nipoti et al. (2007) find that the merging time scales for spherical systems are significantly longer in MOND than in Newtonian gravity with dark matter, and Tiret & Combes (2007) found that bars keep their pattern speed constant in MOND, while they are strongly slowed down in the Newtonian equivalent system with a dark matter halo.
The main conclusion of these apparently different claims is that the dynamical friction time scale is greater in MOND for satellite galaxy interactions and for stellar bars, since galaxies are not embedded in extended and massive spheroids of dark matter particles, which are able to accept the orbital angular momentum. Although the impact of very small fluctuations could be greater in MOND than in Newtonian dynamics, the effect saturates quickly when the perturbation is no longer infinitesimal. In contrast, the equivalent Newtonian system with dark matter has shorter dynamical time scales, and common satellites and bars are slowed down in a few rotation times. The present results extend these conclusions for clumpy galaxies, which are typical of high-redshift systems, where the total clump mass fraction can reach 30% of the disk mass, with individual clumps of 108–109 M⊙. The typical time scale for the clumps to be driven to the center and form the bulge in the Newtonian model with dark matter is about 1 Gyr for the giant galaxy and 3 Gyr for the dwarf. For the MOND model, the dynamical friction is not efficient enough to form a bulge before the clumps are destroyed or reduced by the star formation feedback and the tidal and shear forces.
5. Discussion
The present simulations are based on the simple model of sticky particles for the gas physics and dissipative character. Previous works have used different methods, either sticky particles (Noguchi 1999; Immeli et al. 2004; Bournaud et al. 2007a; Elmegreen et al. 2008), AMR hydro-code (Dekel et al. 2009; Ceverino et al. 2010; Behrendt et al. 2014), or Tree-SPH code (Hopkins et al. 2012). The results are very similar, as far as the instability of the early galaxies is concerned. Massive clumps are formed, reproducing clumpy galaxies at high redshift. The importance of the bulge formation is variable according to the stellar feedback adopted. Clumps are driven to the center through dynamical friction in less than 1 Gyr for massive galaxies of ~7 × 1010 M⊙ in baryons, but extreme supernovae feedback could significantly reduce the mass of clumps ending in the bulge (Hopkins et al. 2012). The bulge in all cases has a stabilizing influence on the disk, and after the clumpy phase, the disk remains quite homogeneous, even in the case of abundant external gas accretion (Ceverino et al. 2010). We have tried several degrees of dissipation, and the variation of the collisional parameters β between 0.3 and 0.7 did not have a strong influence on the results, confirming the conclusions of Bournaud et al. (2007a). The essential point is to have sufficient dissipation in the gas to allow its collapse into dense clumps and to enhance the SFR through a nonlinear Schmidt law.
It is also necessary to check that the spatial resolution of the simulations is not perturbing the main conclusions. The 2573 grid means a resolution of 230 pc for the potential solver, it is always lower than the Jeans scales. From initial conditions, it is possible to predict the range in sizes and masses of clumps in the unstable disks (but see Behrendt et al. 2014). The Jeans length in an axisymmetric disk is 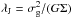 , where σg is the gas velocity dispersion, and Σ the disk’s surface density. These range from 0.5 to 1 kpc in the dwarf galaxy model and from 1.4 to 2 kpc for the giant. The corresponding ranges in mass of the clumps are
, where σg is the gas velocity dispersion, and Σ the disk’s surface density. These range from 0.5 to 1 kpc in the dwarf galaxy model and from 1.4 to 2 kpc for the giant. The corresponding ranges in mass of the clumps are 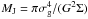 , between 106–108 M⊙ for the dwarf galaxy, and 108–109 M⊙ for the giant model. A higher resolution simulation with 5133 grid has been run for the dwarf galaxy model, increasing the number of particles to six million. The clump mass fraction is plotted in Fig. 11. In general, the evolution is similar, with the clump fraction determined with the smoothing length adapted to a factor-2 higher spatial resolution.
, between 106–108 M⊙ for the dwarf galaxy, and 108–109 M⊙ for the giant model. A higher resolution simulation with 5133 grid has been run for the dwarf galaxy model, increasing the number of particles to six million. The clump mass fraction is plotted in Fig. 11. In general, the evolution is similar, with the clump fraction determined with the smoothing length adapted to a factor-2 higher spatial resolution.
 |
Fig. 11 Evolution of the clump mass fraction for the dwarf galaxy in the MOND gravity (left) and in the Newtonian gravity (right). The high-resolution run with a 5133 grid and 8 times the number of particles is plotted in red. |
Another interesting issue is the stability of the considered disks to large-scale waves, although small-scale fragmentation is dominant. The critical wavelength λcrit above which disks should be stabilized by differential rotation, even without pressure (dispersion) terms, indicating that the self-gravity scale is λcrit = 4π2GΣ /κ, where κ is the epicyclic frequency. It ranges from 1–3 kpc in the dwarf galaxy and from 2–6 kpc for the giant. The role of the dark matter halo is proportionally much higher in the dwarf. The X-Toomre parameter, X = λ/λcrit, where λ ~ 2πr controls the self-gravitating response of the disk through the swing amplifier; waves develop more efficiently when X ~ 2 (Toomre 1981). In the present galaxy models, a central region always exists where X ~ 1–2.
6. Summary
Simulations have been carried out of the dynamical processes occurring early in the Universe, in galaxies that are very rich in gas, and corresponding to the clumpy galaxies observed at high redshift (e.g., Elmegreen & Elmegreen 2005; Elmegreen 2007). Previous works have established that bulge formation is rapid in those galaxies through dynamical friction driving the clumps to coalesce in the galaxy centers (Noguchi 1999; Bournaud et al. 2007b; Elmegreen et al. 2008). The present work explores the analogous phenomena in modified gravity (MOND, Milgrom 1983). A multigrid code is used to solve the nonlinear equations, both from the original AQUAL Lagrangian (Bekenstein & Milgrom 1984) and the QUMOND solution, recently developed by Milgrom (2010). Both appear to give similar results, and most runs were performed in the faster method of QUMOND. For each galaxy model, the corresponding rotation curve is first computed in MOND, and then an equivalent Newtonian system is built with a dark matter halo added, in order to get exactly the same rotation curve as in Tiret & Combes (2007, 2008a). The efficiency of dynamical friction was first compared between the two gravity models, with academic purely stellar runs, where an ensemble of clumps were randomly distributed initially with 20–30% of the baryonic mass. A series of such simulations show that clumps should spiral inwards to the center in the Newtonian galaxies in about 1 Gyr or less, while the clumps remain orbiting in the disk for more than 2–3 Gyr in the MOND regime.
The most realistic simulations include gas dissipation, star formation, and feedback. Disks are initially composed of 50% stars and 50% gas. Rapid fragmentation occurs in these unstable disks, and clumpy galaxies that are similar to what is observed at high redshift are formed in both gravity models. This clumpy morphology lasts less than 1 Gyr in the giant galaxy model of baryonic mass 5.7 × 1010 M⊙ and 3 Gyr in the dwarf galaxy, with ten times less mass. Clumps are driven inwards by dynamical friction, and form a spheroidal bulge. This is very compatible with previous works. However, in the MOND gravity model, the clumps remain in the disk for a much longer time, are eventually destroyed or reduced by stellar feedback and shear, and have no time to fall in the center to form a bulge. The lower bulge formation efficiency in MOND is more in line with the large number of observed bulgeless galaxies today (Kormendy et al. 2010).
Fisher & Drory (2011) also find that the galaxies that contain either a pseudo-bulge or no bulge represent more than 80% of galaxies above a stellar mass of 109 M⊙ in the local volume of 11 Mpc radius. This is difficult to explain in the standard Newton plus dark matter models. Weinzirl et al. (2009) compare the observations of the bulge mass and frequency in present-day galaxies with the predictions of the CDM model. Massive galaxies can have less than 20% of their baryonic mass in a bulge if they experience mergers only before z = 4. But galaxies having later mergers and larger fractions of their mass in a bulge are about 30 times more abundant in CDM simulations than observed. Zavala et al. (2012) and Avila-Reese et al. (2014) revisit the CDM predictions, with semi-enpirical recipes and an analytical treatment to follow the transfer of stellar masses to bulges after a merger. They assign the stars coming from merging satellites to the classical bulges and stars coming from the primary during the merger to pseudo-bulges. But they do not consider the pseudo-bulges formed by secular evolution of bars. They then claim to form less classical bulges, since there is now only one path to form them. Also the result depends on the adopted evolution of the stellar-to-halo mass relation, the mass assembly in their models resembling more a monolithic scenario than a hierarchical one. In any case, there are still problems explaining the large fraction of bulgeless galaxies observed locally.
In the framework of MOND, classical bulges are hardly formed in early times in the clumpy phase of galaxy formation, when gas is dominating the surface density of galaxy disks. They can form later through hierarchical merging with a frequency that is smaller than what occurs in the analogous Newtonian systems with dark matter. Pseudo-bulges, however, form with equivalent frequency through secular evolution by vertical resonances with bars. It is therefore expected that the relative frequency of pseudo-bulges is higher in MOND. More quantitative statements will require many more simulations with a cosmological context.
Acknowledgments
I warmly thank the referee, Stacy McGaugh, for constructive comments and suggestions. The idea of this work came when Eija Laurikainen asked me to write a review article on bulge formation with MOND. The European Research Council for the Advanced Grant Program Number 267399-Momentum is acknowledged. Most simulations have been run on the cluster provided by this ERC grant.
References
- Avila-Reese, V., Zavala, J., & Lacerna, I. 2014, MNRAS, 441, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J. E. 1988, ApJ, 331, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J. E., & Hernquist, L. E. 1991, ApJ, 370, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Behrendt, M., Burkert, A., & Schartmann, M. 2014, MNRAS, submitted [arXiv:1408.5902] [Google Scholar]
- Bekenstein, J., & Milgrom, M. 1984, ApJ, 286, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Bertone, G., Hooper, D., & Silk, J. 2005, Phys. Rep., 405, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Blumenthal, G. R., Faber, S. M., Primack, J. R., & Rees, M. J. 1984, Nature, 311, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Bode, P., Ostriker, J. P., & Turok, N. 2001, ApJ, 556, 93 [Google Scholar]
- Bournaud, F., Jog, C. J., & Combes, F. 2005, A&A, 437, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bournaud, F., Jog, C. J., & Combes, F. 2007a, A&A, 476, 1179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bournaud, F., Elmegreen, B. G., & Elmegreen, D. M. 2007b, ApJ, 670, 237 [Google Scholar]
- Bournaud, F., Elmegreen, B. G., & Martig, M. 2009, ApJ, 707, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Boylan-Kolchin, M., Bullock, J. S., & Kaplinghat, M. 2011, MNRAS, 415, L40 [CrossRef] [Google Scholar]
- Boylan-Kolchin, M., Bullock, J. S., & Kaplinghat, M. 2012, MNRAS, 422, 1203 [NASA ADS] [CrossRef] [Google Scholar]
- Brada, R., & Milgrom, M. 1999, ApJ, 519, 590 [NASA ADS] [CrossRef] [Google Scholar]
- Ceverino, D., Dekel, A., & Bournaud, F. 2010, MNRAS, 404, 2151 [NASA ADS] [Google Scholar]
- Chandrasekhar, S. 1943, ApJ, 97, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Ciotti, L., & Binney, J. 2004, MNRAS, 351, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Combes, F., Debbasch, F., Friedli, D., & Pfenniger, D. 1990, A&A, 233, 82 [NASA ADS] [Google Scholar]
- Dekel, A., Sari, R., & Ceverino, D. 2009, ApJ, 703, 785 [Google Scholar]
- Elmegreen, D. M. 2007, in IAU Symp. 235, eds. F. Combes, & J. Palous (Cambridge University Press), 376 [Google Scholar]
- Elmegreen, B. G., & Elmegreen, D. M. 2005, ApJ, 627, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., Bournaud, F., & Elmegreen, D. M. 2008, ApJ, 688, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Famaey, B., & Binney, J. 2005, MNRAS, 363, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Famaey, B., & McGaugh, S. S. 2012, Liv. Rev. Rel., 15, 10 [Google Scholar]
- Fisher, D. B., & Drory, N. 2011, ApJ, 733, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Keres, D., Murray, N., et al. 2012, MNRAS, 427, 968 [NASA ADS] [CrossRef] [Google Scholar]
- Immeli, A., Samland, M., Gerhard, O., & Westera, P. 2004, A&A, 413, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jungwiert, B., Combes, F., & Palous, J. 2001, A&A, 376, 85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kennedy, R., Frenk, C., Cole, S., & Benson, A. 2014, MNRAS, 442, 2487 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Kennicutt, R. C. 2004, ARA&A, 42, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., Drory, N., Bender, R., & Cornell, M. E., 2010, ApJ, 723, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Lüghausen, F., Famaey, B., Kroupa, P., et al. 2013, MNRAS, 432, 2846 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 1983, ApJ, 270, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 2010, MNRAS, 403, 886 [NASA ADS] [CrossRef] [Google Scholar]
- Naab, T., & Burkert, A. 2003, ApJ, 597, 893 [NASA ADS] [CrossRef] [Google Scholar]
- Nipoti, C., Londrillo, P., & Ciotti, L. 2007, MNRAS, 381, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Nipoti, C., Ciotti, L., Binney, J., & Londrillo, P. 2008, MNRAS, 386, 2194 [NASA ADS] [CrossRef] [Google Scholar]
- Noguchi, M. 1999, ApJ, 514, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E., & Ratra, B. 2003, Rev. Mod. Phys., 75, 559 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in Fortran 77, 2nd edn. (Cambridge University Press) [Google Scholar]
- Sanders, R. H., & McGaugh, S. 2002, ARA&A, 40, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Tiret, O., & Combes, F. 2007, A&A, 464, 517 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tiret, O., & Combes, F. 2008a, A&A, 483, 719 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tiret, O., & Combes, F. 2008b, ASP Conf. Ser., 396, 259 [Google Scholar]
- Tiret, O., & Combes, F. 2009, A&A, 496, 659 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Toomre, A. 1977, in Evolution of Galaxies and Stellar Populations, Proc. of a Conference at Yale University, 401 [Google Scholar]
- Toomre, A. 1981, Proc. of the Advanced Study Institute, Cambridge, England (Cambridge, New York: Cambridge University Press), 111 [Google Scholar]
- Wang, J., & White, S. D. M. 2009, MNRAS, 396, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Weinberg, M. D. 1989, MNRAS, 239, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Weinzirl, T., Jogee, S., Khochfar, S., et al. 2009, ApJ, 696, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Zavala, J., Avila-Reese, V., Firmani, C., & Boylan-Kolchin, M. 2012, MNRAS, 427, 1503 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, H. S., & Famaey, B. 2006, ApJ, 638, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, H. S., & Famaey, B. 2010, Phys. Rev. D, 81, 7304 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Left: circular and rotational velocities, together with the velocity dispersions for the stellar component in the Newtonian+DM (top) and MOND (bottom) initial galaxy models with stars and gas. Right: same for the giant galaxy model. |
| In the text | |
 |
Fig. 2 Left: decay of the 5 clumps containing globally 25% of the baryonic disk as a function of time, in the Newtonian +DM (top) and MOND (bottom), for the purely stellar galaxy models. Right: same for the giant galaxy model. |
| In the text | |
 |
Fig. 3 All baryons (left) and gas (right) surface densities of the dwarf clumpy galaxy, simulated with MOND gravity, at epochs 0.5, 1, and 2 Gyr. Each panel is 60 kpc in size. The color scale is logarithmic and is the same for all plots. |
| In the text | |
 |
Fig. 4 All baryons (left) and gas (right) surface densities of the giant clumpy galaxy, simulated with MOND gravity, at epochs 0.5, 1, and 2 Gyr. Each panel is 60 kpc in size. The color scale is logarithmic and is the same for all plots. |
| In the text | |
 |
Fig. 5 Evolution of the star formation rate (black line, left scale) and the remaining amount of gas (red lines and middle scale) in the giant galaxy, with MOND (left), and Newtonian dynamics (right). |
| In the text | |
 |
Fig. 6 All baryons (left) and gas (right) surface densities of the giant clumpy galaxy, simulated with Newtonian+DM gravity, at epochs 0.5, 1, and 2 Gyr. Each panel is 60 kpc in size. The color scale is logarithmic and the same for all plots. |
| In the text | |
 |
Fig. 7 Stellar profile of the giant galaxy in the Newtonian dynamics, at various epochs (0, 0.5, 1, and 2 Gyr). A bulge is building alongside the exponential disk. |
| In the text | |
 |
Fig. 8 Same as Fig. 7 for the MOND model. |
| In the text | |
 |
Fig. 9 Evolution of the edge-on morphology of the giant galaxy, in the Newtonian gravity model with gas and star formation. |
| In the text | |
 |
Fig. 10 Evolution of the clump mass fraction (see text for the definition) for the giant galaxy, in the MOND gravity (left) and in the Newtonian gravity (right). |
| In the text | |
 |
Fig. 11 Evolution of the clump mass fraction for the dwarf galaxy in the MOND gravity (left) and in the Newtonian gravity (right). The high-resolution run with a 5133 grid and 8 times the number of particles is plotted in red. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


