| Issue |
A&A
Volume 571, November 2014
|
|
|---|---|---|
| Article Number | L1 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201424420 | |
| Published online | 04 November 2014 | |
PRISM: Recovery of the primordial spectrum from Planck data
1
Laboratoire AIM, UMR CEA-CNRS-Paris 7, Irfu, SAp, CEA Saclay,
91191
Gif-sur-Yvette Cedex,
France
e-mail: francois.lanusse@cea.fr; paniez.paykari@cea.fr
2
Laboratoire d’Astrophysique, École Polytechnique Fédérale de
Lausanne (EPFL), Observatoire de Sauverny, 1290, Versoix, Switzerland
Received: 17 June 2014
Accepted: 9 October 2014
Aims. The primordial power spectrum describes the initial perturbations that seeded the large-scale structure we observe today. It provides an indirect probe of inflation or other structure-formation mechanisms. In this Letter, we recover the primordial power spectrum from the Planck PR1 dataset, using our recently published algorithm PRISM.
Methods. PRISM is a sparsity-based inversion method that aims at recovering features in the primordial power spectrum from the empirical power spectrum of the cosmic microwave background (CMB). This ill-posed inverse problem is regularised using a sparsity prior on features in the primordial power spectrum in a wavelet dictionary. Although this non-parametric method does not assume a strong prior on the shape of the primordial power spectrum, it is able to recover both its general shape and localised features. As a results, this approach presents a reliable way of detecting deviations from the currently favoured scale-invariant spectrum.
Results. We applied PRISM to 100 simulated Planck data to investigate its performance on Planck-like data. We then applied PRISM to the Planck PR1 power spectrum to recover the primordial power spectrum. We also tested the algorithm’s ability to recover a small localised feature at k ~ 0.125 Mpc-1, which caused a large dip at ℓ ~ 1800 in the angular power spectrum.
Conclusions. We find no significant departures from the fiducial Planck PR1 near scale-invariant primordial power spectrum with As = 2.215 × 10-9 and ns = 0.9624.
Key words: cosmic background radiation / methods: data analysis / methods: statistical
© ESO, 2014
1. Introduction
The primordial power spectrum describes the initial curvature perturbations that over time evolved to form the large-scale structure we observe today. Because the physics of the early Universe are encoded in the primordial power spectrum, it represents an invaluable probe of primordial cosmology, and measuring it is a crucial research area in modern cosmology. The currently favoured model describing the physics of the early Universe, inflation (Guth 1981; Linde 1982), produces initial perturbations from quantum fluctuations during an epoch of accelerated exponential expansion. This inflation process produces a power spectrum of specific shape and can leave characteristic features. For the simplest inflation models, the power spectrum, generated by almost purely adiabatic perturbations, which is predicted to be nearly scale invariant. Hence, it is often expressed in terms of an amplitude As and a spectral index ns with an optional “running” αs, 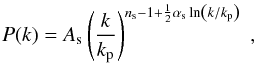 (1)where kp is a pivot scale. We consider here only the first-order expansion of the spectral index, although higher orders can be considered (e.g., Debono et al. 2010). Exact scale invariance, known as the Harrison-Zeldovich (HZ) model, which sets ns = 1 (and αs = 0) (Harrison 1970; Zeldovich 1972), has been ruled out by different datasets. Instead, the near scale-invariant spectrum with ns< 1 fits the current observations very well (e.g., Planck Collaboration XVI 2014). There exist more complex models that generate deviations from scale invariance. For a short review of inflation we refer to Planck Collaboration XXII (2014).
(1)where kp is a pivot scale. We consider here only the first-order expansion of the spectral index, although higher orders can be considered (e.g., Debono et al. 2010). Exact scale invariance, known as the Harrison-Zeldovich (HZ) model, which sets ns = 1 (and αs = 0) (Harrison 1970; Zeldovich 1972), has been ruled out by different datasets. Instead, the near scale-invariant spectrum with ns< 1 fits the current observations very well (e.g., Planck Collaboration XVI 2014). There exist more complex models that generate deviations from scale invariance. For a short review of inflation we refer to Planck Collaboration XXII (2014).
The recent Planck mission cosmic microwave background (CMB) temperature anisotropy data, combined with the WMAP large-scale polarisation, constrain the spectral index to ns = 0.9603 ± 0.0073 (Planck Collaboration XVI 2014), ruling out exact scale invariance at over 5σ. Planck also failed to find a statistically significant running of the scalar spectral index, obtaining αs = −0.0134 ± 0.0090. On the other hand, high-resolution CMB experiments, such as the South Pole Telescope (SPT)1, report a small running of the spectral index; −0.046 <αs< −0.003 at 95% confidence (Hou et al. 2014). However, in general, any such detections have been weak and were consistent with zero.
Planck Collaboration XVI (2014) extensively investigated features in the primordial power spectrum. A penalised likelihood approach indicated that there might be a feature near the highest wavenumbers probed by Planck at an estimated significance of ~3σ. This nominally statistically significant feature is detected around k ~ 0.13Mpc-1. It has been confirmed that the large dip at ℓ ~ 1800 in the CMB power spectrum, which is associated with residual electromagnetic interference generated by the drive electronics of the 4 K cooler, is in fact responsible for the features detected at these high wavenumbers.
With the recent release of BICEP2 B-mode polarisation data there has been a variety of studies investigating the shape of both the scalar and the tensor primordial power spectrum in light of these new data. Hazra et al. (2014) have combined Planck CMB temperature and BICEP2 B-mode polarisation data (BICEP2 Collaboration et al. 2014; Ade et al. 2014) to show that, assuming inflationary consistency relation, the power-law form of the scalar primordial spectrum is ruled out at more than 3σ confidence level. In fact, a break or step at large scales in the primordial scalar perturbation spectrum is more favourable.
Determining the shape of the primordial spectrum generally consists of two approaches, one by parametrisation, the second by reconstruction. Non-parametric methods suffer from the non-invertibility of the transfer function that describes the transfer from P(k) to the CMB power spectrum. The dependence on the transfer function has the form 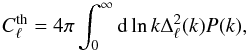 (2)where ℓ is the angular wavenumber that corresponds to an angular scale via ℓ ~ 180°/θ and Δℓ(k) is the radiation transfer function holding the cosmological parameters responsible for the evolution of the Universe. Because of the singularity of the transfer function and the limitations on the data from effects such as projection, cosmic variance, instrumental noise, and point sources, a robust algorithm is necessary to an accurately reconstruct the primordial power spectrum from CMB data.
(2)where ℓ is the angular wavenumber that corresponds to an angular scale via ℓ ~ 180°/θ and Δℓ(k) is the radiation transfer function holding the cosmological parameters responsible for the evolution of the Universe. Because of the singularity of the transfer function and the limitations on the data from effects such as projection, cosmic variance, instrumental noise, and point sources, a robust algorithm is necessary to an accurately reconstruct the primordial power spectrum from CMB data.
In this Letter, we use our recently published algorithm PRISM (Paykari et al. 2014) to reconstruct this spectrum from the LGMCA Planck PR1 data (Bobin et al. 2014).
2. PRISM
A CMB experiment, such as Planck, measures the anisotropies in the CMB temperature Θ(p) in direction p, which is described as T(p) = TCMB [ 1 + Θ(p) ]. This anisotropy field can be expanded in terms of spherical harmonic functions Yℓm as Θ(p) = ∑ ℓ ∑ maℓmYℓm(p), where aℓm are the spherical harmonic coefficients that have a Gaussian distribution with zero mean, ⟨ aℓm ⟩ = 0, and variance 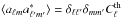 .
.
In practice, we only observe a realisation of this underlying power spectrum on our sky, meaning we are restricted by cosmic variance, especially on large scales. In addition, data are contaminated with additive instrumental noise on small scales and, because of different Galactic foregrounds, some areas of the observed CMB map need to be masked, which induces correlations between modes. Taking these effects into account and following the MASTER method from Hivon et al. (2002), the pseudo power spectrum 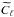 and the empirical power spectrum
and the empirical power spectrum 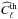 , which is defined as
, which is defined as 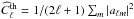 , can be related through their ensemble averages
, can be related through their ensemble averages 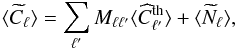 (3)where Mℓℓ′ describes the mode-mode coupling between modes ℓ and ℓ′ resulting from computing the transform on the masked sky. We note that in this expression
(3)where Mℓℓ′ describes the mode-mode coupling between modes ℓ and ℓ′ resulting from computing the transform on the masked sky. We note that in this expression 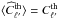 , and we set
, and we set 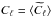 and
and 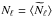 , where Cℓ and Nℓ refer to the CMB and the noise power spectra of the masked maps, respectively. We have assumed that the pseudo power spectrum
, where Cℓ and Nℓ refer to the CMB and the noise power spectra of the masked maps, respectively. We have assumed that the pseudo power spectrum 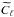 follows a χ2 distribution with 2ℓ + 1 degrees of freedom and hence can be modelled as
follows a χ2 distribution with 2ℓ + 1 degrees of freedom and hence can be modelled as 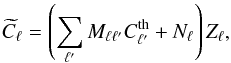 (4)where Zℓ is a random variable distributed according to (2ℓ + 1)
(4)where Zℓ is a random variable distributed according to (2ℓ + 1)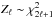 .
.
2.1. Formulation of the inverse problem
The relation between the discretised primordial power spectrum Pk and the measured pseudo power spectrum 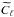 , computed on a masked noisy map of the sky, can be condensed into the following form:
, computed on a masked noisy map of the sky, can be condensed into the following form: 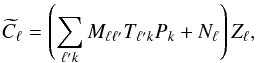 (5)with matrix elements
(5)with matrix elements 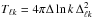 , where Δlnk is the logarithmic k interval for the discrete sampling chosen in the integration of the system of equations. Because of the non-invertibility of the T operator, recovering the primordial power spectrum Pk from the true CMB power spectrum
, where Δlnk is the logarithmic k interval for the discrete sampling chosen in the integration of the system of equations. Because of the non-invertibility of the T operator, recovering the primordial power spectrum Pk from the true CMB power spectrum 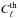 already constitutes an ill-posed inverse problem, made even more difficult by the mask and cosmic variance affecting the observed
already constitutes an ill-posed inverse problem, made even more difficult by the mask and cosmic variance affecting the observed 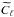 . In PRISM, we address both the inversion problem and the control of the noise on the CMB spectrum due to sample variance in the framework of sparse recovery. The inversion problem in Eq. (5) can be regularised in a robust way by using the sparse nature of the reconstructed signal as a prior.
. In PRISM, we address both the inversion problem and the control of the noise on the CMB spectrum due to sample variance in the framework of sparse recovery. The inversion problem in Eq. (5) can be regularised in a robust way by using the sparse nature of the reconstructed signal as a prior.
2.2. Pk sparse recovery formulation
If the signal to recover, Pk in our case, can be sparsely represented in an adapted dictionary Φ, then this problem, known as the basis pursuit denoising BPDN, can be recast as an optimisation problem. In our case, the optimisation problem can be formulated as 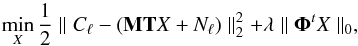 (6)where X is the reconstructed estimate for the primordial power spectrum Pk. The first term in Eq. (6) imposes an ℓ2 fidelity constraint to the data, while the second term promotes the sparsity of the solution in dictionary Φ. The parameter λ tunes the sparsity constraint.
(6)where X is the reconstructed estimate for the primordial power spectrum Pk. The first term in Eq. (6) imposes an ℓ2 fidelity constraint to the data, while the second term promotes the sparsity of the solution in dictionary Φ. The parameter λ tunes the sparsity constraint.
Although the ℓ0 optimisation problem stated in Eq. (6)cannot be solved directly, its solution can be estimated by solving a sequence of weighted ℓ1 minimisation problems (Candes et al. 2008) of the form ![\begin{equation} \min\limits_X \frac{1}{2} \parallel \frac{1}{\sigma_\ell}\overline{R}_\ell(X) \parallel_2^2 + K \sum_i \lambda_i | [ \mathbf{W} \mathbf{\Phi}^t X ]_i |, \label{eq:reweighted-bp-lagragian} \end{equation}](/articles/aa/full_html/2014/11/aa24420-14/aa24420-14-eq70.png) (7)where W is a diagonal matrix applying a different weight for each wavelet coefficient,
(7)where W is a diagonal matrix applying a different weight for each wavelet coefficient, 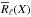 is an estimate of the residual Cℓ − (MTX + Nℓ), and σℓ is its standard deviation. The parameters λi are set with respect to the expected standard variation σ(wi) of each wavelet coefficient such that λi = Kσ(wi), where K is a global regularisation parameter (usually set to K = 3 or K = 4), which translates into a significance level threshold for the detection of features. The weighted ℓ1 problem (7)is solved several times using the popular iterative soft-thresholding algorithm (ISTA) and updating each time the weights W based on the solution of the previous iteration. This procedure is fully described in Paykari et al. (2014).
is an estimate of the residual Cℓ − (MTX + Nℓ), and σℓ is its standard deviation. The parameters λi are set with respect to the expected standard variation σ(wi) of each wavelet coefficient such that λi = Kσ(wi), where K is a global regularisation parameter (usually set to K = 3 or K = 4), which translates into a significance level threshold for the detection of features. The weighted ℓ1 problem (7)is solved several times using the popular iterative soft-thresholding algorithm (ISTA) and updating each time the weights W based on the solution of the previous iteration. This procedure is fully described in Paykari et al. (2014).
3. Results
Before applying the PRISM algorithm to the Planck data processed with the LGMCA2 pipeline, we investigate the performance of the algorithm on a set of simulations. The Planck team provides 100 of their 1000 CMB and instrumental noise simulated maps3. The cosmology used to set up these CMB simulations is different from the PR1 best-fit cosmology. Because we wish to have the exact same pipeline applied to both the data and the simulations (hence the same radiation transfer function), we created our own 100 CMB simulations based on PR1 fiducial cosmology. However, we used the simulated noise maps provided by the Planck team. To enable a thorough comparison between the simulations and the Planck PR1 data, we ran the simulations through the same pipeline as the Planck data, that is, through the LGMCA pipeline. For each simulation, we processed the nine frequency channels through LGMCA, with the precomputed set of parameters (Bobin et al. 2014). Full-sky noisy maps with a 5 arcmin resolution were obtained, which were then masked using a Galactic and point sources mask with fsky = 0.76. The pseudo power spectra were obtained by applying the empirical power spectrum estimator to the masked maps. We also built an estimate of the instrumental noise power spectrum Nℓ by processing the noise maps through the same pipeline in LGMCA, masking the resulting noise maps and applying the pseudo spectrum estimator to these masked maps. We set our estimate of Nℓ to the average of the 100 noise pseudo spectra.
To apply PRISM to the simulated data, we built a transfer function T′ adapted to the simulations, so that it includes the effects of the beam bℓ and the HEALPix window hℓ represented by the two diagonal matrices 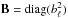 and
and 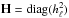 ; T′ = HBT. The radiation transfer function T was computed for the PR1 fiducial cosmology using CAMB4. The lensing contribution to the CMB temperature power spectrum, also computed with CAMB for the PR1 fiducial cosmology, is taken into account as an additional contribution to Nℓ.
; T′ = HBT. The radiation transfer function T was computed for the PR1 fiducial cosmology using CAMB4. The lensing contribution to the CMB temperature power spectrum, also computed with CAMB for the PR1 fiducial cosmology, is taken into account as an additional contribution to Nℓ.
In contrast to Paykari et al. (2014), where the algorithm was initialised to a scale-invariant power spectrum, in this work we initialised the algorithm to the best-fit Planck PR1 primordial power spectrum because we search for small deviations from the best-fit power law that already fits the data. With this choice of initialisation, the reconstruction will not depart from the best-fit power law in the absence of evidence from the data. To reconstruct the simulations and the Planck data, we fixed the regularisation parameter K to K = 4 which robustly removes the noise due to sampling variance, and we used bi-orthogonal Battle-Lemarié wavelets of order 1 with nine dyadic scales. This choice of wavelet dictionary is generic and not specifically tuned to recover physically motivated features, but these wavelets exhibit limited oscillations and have two vanishing moments, which makes them well suited to recover a near scale-invariant power spectrum in logarithmic scale.
We note that reconstructing the primordial power spectrum is limited by different effects on different scales. On very large scales, the recovery is limited by cosmic variance and geometrical projection of the modes, and on small scales we are limited by effects such as instrumental noise and point sources. These limitations leave us a window through which the primordial power spectrum can be constrained with good accuracy and through which features can be detected. For the Planck data, we expect this window to be in the range k ~ 0.005−0.20Mpc-1.
 |
Fig. 1 Reconstructions for the primordial power spectra from 100 simulations and Planck PR1 data. The 1σ and 2σ dispersion of the reconstructed spectra from the simulations are shown as blue bands around the mean of the reconstructions (blue line). We note that these bands do not include the errors due to point sources and beam uncertainties. The Planck fiducial power spectrum used for the simulations, with As = 2.215 × 10-9 and ns = 0.9626, is shown as a yellow dashed line. The inset shows a close-up of the main figure. |
In Fig. 1 we show the reconstructed spectra from the simulations and the data. The mean reconstructed power spectrum perfectly fits the input PR1 best-fit power law in the entire reconstructed range. Of course this does not mean that the algorithm is able to perfectly reconstruct an unknown power spectrum over this entire range, but that with the regularisation level used for these reconstructions, no significant departures from the best-fit power law have been detected. The reconstructed spectrum from the LGMCA PR1 power spectrum remains within the 1σ bar of the reconstructed spectra from the PR1 best-fit power law. Thus, we find no significant departure from the PR1 best-fit near scale-invariant spectrum.
As a complementary test of PRISM on Planck-like data we assessed the algorithm’s ability to recover a small local departure from the best-fit PR1 power law. We created a set of CMB simulations from a fiducial primordial power spectrum with a small localised test feature causing a dip in the angular power spectrum around ℓ ~ 1800. The aim of this set of simulations was to mimic the feature that Planck Collaboration XVI (2014) proposed to be accountable for the large dip in the angular power spectrum, which was later confirmed as being caused by residual electromagnetic interferences. Our test primordial power spectrum was built from the best-fit PR1 power law with an added feature around k = 0.125 which causes a dip in the angular power spectrum around ℓ ~ 1800. This feature and the residuals ΔCℓ between the fiducial angular power spectrum and the PR1 best fit Cℓ are shown in Fig. 2.
From this test primordial power spectrum, we generated a set of 100 CMB simulations using the exact same procedure as previously mentioned, and we applied PRISM to the measured angular pseudo-power spectra with the exact same parameters. As can be seen in Fig. 2, the feature is successfully detected, and the reconstruction shows little bias in position and amplitude. Using the primordial power spectrum reconstructed with PRISM enables a much better fit to the data than a power law, and the reconstructed angular power spectra fall inside the 1σ region due to cosmic variance. If such a feature existed in the LGMCA processed Planck PR1 data, PRISM would therefore have been able to detect it.
 |
Fig. 2 Top panel: fiducial primordial power spectrum with a feature around k = 0.125 Mpc-1 in red and in green contours the 1σ and 2σ dispersion of 100 reconstructions from simulated CMB spectra. The mean of reconstructions is shown in yellow. Bottom panel: residuals ΔCℓ between the Cℓ for the fiducial primordial power spectrum with a feature and the Cℓ for the best-fit Planck power law in red and for the mean reconstructed primordial power spectrum in yellow. The green bands indicate the 1σ and 2σ bands for the ΔCℓ from the simulations, the dashed blue lines show the 1σ region due to cosmic variance. |
4. Conclusions
The simplest inflation models are currently favoured the most by the data and predict a near scale-invariant power spectrum with a possible small running. The CMB spectrum provides a possibility to measure the primordial spectrum. However, the singular nature of the radiation transfer function, the joint estimation of the cosmological parameters and the primordial power
spectrum, along with the different sources of noise, impede the full recovery of the primordial spectrum. Therefore, devising a robust technique able to detect deviations from scale invariance is important.
We have applied our recently published algorithm PRISM (Paykari et al. 2014) to the Planck PR1 data to recover the primordial power spectrum. PRISM is a sparse recovery method, that uses the sparsity of the primordial power spectrum as well as an adapted modelling for the noise of the CMB power spectrum. This algorithm assumes no prior shape for the primordial spectrum and does not require a coarse binning of the power spectrum, making it sensitive to both general smooth features (e.g. running of the spectral index) and local sharp features (e.g. a bump or an oscillatory feature). We reconstructed the primordial power spectrum from the LGMCA PR1 Planck dataset in the range k ~ 0.005−0.20Mpc-1. We did not detect any significant deviations from the best-fit Planck near scale-invariant power spectrum with As = 2.215 × 10-9 and ns = 0.9624. However, we tested that PRISM would have been able to recover a small localised feature around k ~ 0.125, similar to the feature that was proposed in Planck Collaboration XVI (2014) to be accountable for a dip in the angular power spectrum at around ℓ ~ 1800, if it were present on the LGMCA Planck PR1 data.
LGMCA codes and Planck PR1 data are available at http://www.cosmostat.org/planck_pr1.html
Acknowledgments
This work is supported by the European Research Council grant SparseAstro (ERC-228261).
References
- Ade, P. A. R., Aikin, R. W., Barkats, D., et al. 2014, Phys. Rev. Lett., 112, 241101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- BICEP2 Collaboration, Ade, P. A. R., Aikin, R. W., et al. 2014, ApJ, 792, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Bobin, J., Sureau, F., Starck, J.-L., Rassat, A., & Paykari, P. 2014, A&A, 563, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Candes, E. J., Wakin, M. B., & Boyd, S. P. 2008, J. Fourier Anal. Appl., 14, 877 [Google Scholar]
- Debono, I., Rassat, A., Réfrégier, A., Amara, A., & Kitching, T. D. 2010, MNRAS, 404, 110 [NASA ADS] [Google Scholar]
- Guth, A. H. 1981, Phys. Rev. D, 23, 347 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Harrison, E. R. 1970, Phys. Rev. D, 1, 2726 [NASA ADS] [CrossRef] [Google Scholar]
- Hazra, D. K., Shafieloo, A., Smoot, G. F., & Starobinsky, A. A. 2014, J. Cosmology Astropart. Phys., 6, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Hivon, E., Górski, K. M., Netterfield, C. B., et al. 2002, ApJ, 567, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Hou, Z., Reichardt, C. L., Story, K. T., et al. 2014, ApJ, 782, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Linde, A. D. 1982, Phys. Lett. B, 108, 389 [Google Scholar]
- Paykari, P., Lanusse, F., Starck, J.-L., Sureau, F., & Bobin, J. 2014, A&A, 566, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XVI. 2014, A&A, 571, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXII. 2014, A&A, 571, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zeldovich, Y. B. 1972, MNRAS, 160, 1 [Google Scholar]
All Figures
 |
Fig. 1 Reconstructions for the primordial power spectra from 100 simulations and Planck PR1 data. The 1σ and 2σ dispersion of the reconstructed spectra from the simulations are shown as blue bands around the mean of the reconstructions (blue line). We note that these bands do not include the errors due to point sources and beam uncertainties. The Planck fiducial power spectrum used for the simulations, with As = 2.215 × 10-9 and ns = 0.9626, is shown as a yellow dashed line. The inset shows a close-up of the main figure. |
| In the text | |
 |
Fig. 2 Top panel: fiducial primordial power spectrum with a feature around k = 0.125 Mpc-1 in red and in green contours the 1σ and 2σ dispersion of 100 reconstructions from simulated CMB spectra. The mean of reconstructions is shown in yellow. Bottom panel: residuals ΔCℓ between the Cℓ for the fiducial primordial power spectrum with a feature and the Cℓ for the best-fit Planck power law in red and for the mean reconstructed primordial power spectrum in yellow. The green bands indicate the 1σ and 2σ bands for the ΔCℓ from the simulations, the dashed blue lines show the 1σ region due to cosmic variance. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


